摘要: 很多关于等离子体鞘层的研究工作都是基于电子满足经典的麦克斯韦速度分布函数, 而等离子体中的粒子具有长程电磁相互作用, 使用Tsallis提出的非广延分布来描述电子更为恰当. 本文建立一个具有非广延分布电子的碰撞等离子体磁鞘模型, 理论推导出受非广延参数
q 影响的玻姆判据, 离子马赫数的下限数值会随着参数
q 的增大而减小. 经过数值模拟, 发现与具有麦克斯韦分布(
q = 1)电子的碰撞等离子体磁鞘对比, 具有超广延分布(
q < 1)和亚广延分布(
q > 1)电子的碰撞等离子体磁鞘的结构各有不同, 包括空间电势分布、离子电子密度分布、空间电荷密度分布. 模拟结果显示非广延分布的参数
q 对碰撞等离子体磁鞘的结构具有不可忽略的影响. 希望这些结论对相关的天体物理、等离子体边界问题的研究有参考价值.
关键词: 非广延分布 /
等离子体 /
鞘层 English Abstract Structure of collisional magnetized plasma sheath with non-extensive distribution of electrons Zou Xiu Liu Hui-Ping Zhang Xiao-Nan Qiu Ming-Hui School of Science, Dalian Jiaotong University, Dalian 116028, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 10605008) and the Scientific Research Foundation of the Education Department of Liaoning Province, China (Grant Nos. L2011069, JDL2017012)Received Date: 26 May 2020Accepted Date: 15 July 2020Available Online: 14 December 2020Published Online: 05 January 2021Abstract: Many previous researches on the plasma sheath were based on the fact that the electrons satisfy the classical Maxwell velocity distribution function, while the particles in the plasma have long-range electromagnetic interactions. It is more appropriate to use the non-extensive distribution proposed by Tsallis to describe the electrons. In this paper, a collisional magnetized plasma sheath model with non-extensive distribution of electrons is established. Bohm criterion is derived theoretically. With the ion drift motion in the plasma pre-sheath region taken into consideration, the ion Mach number is only related to the angle of the magnetic field, the collision parameters, the electric field at the sheath edge, and non-extensive parameter $ q $ . The influence of parameter $ q $ on the criterion is discussed in this paper. The lower limit of the ion Mach number changes with the value of parameter $ q $ . The lower limit of the ion Mach number increases for $ q < 1 $ . And the lower limit of the ion Mach number decreases for $ q>1 $ . With the increase of $ q $ , the number of electrons with lower speed increases, ions need less kinetic energy to enter into the sheath and thus enter into the sheath more easily. Through numerical simulation, it is found that compared with the structure of the plasma magnetized sheath with Maxwell distribution ($ q=1 $ ), the structure of the plasma magnetized sheath with super-extensive distribution ($ q < 1 $ ) and that with sub-extensive ($ q>1 $ ) are different, including the distribution of the space potential, the ion density, the electron density, and the space charge density. When $ q < 1 $ , the space potential, the electron density and the ion density fall more slowly, and the peak of the space charge density curve is closer to the wall. When $ q>1 $ , the space potential and the ion electron density fall faster, especially the electron density drops to zero faster, and the peak of the space charge density curve is far away from the wall. The simulation results show that the non-extensive parameter $ q $ has a significant influence on the structure of collisional plasma magnetized sheath. The influence of the collision on the magnetized plasma sheath with non-extensive distribution is similar to that with the Maxwell distribution. These conclusions may be useful in solving the problems of plasma boundary.Keywords: non-extensive distribution /plasma /sheath 全文HTML --> --> --> 1.引 言 实验室里, 在等离子体与其周围器壁、电极或是工件之间会形成一个很窄的正空间电荷层, 厚度相当于几个电子德拜长度, 称为等离子体鞘层. 研究等离子体鞘层的结构对等离子体刻蚀、材料表面改性等很多工艺具有极其重要的作用, 所以相关的理论和实验的研究工作也从未间断[1 -30 ] . 这些工作研究了很多具有不同物理条件的等离子体鞘层, 例如: 离子与中性粒子的碰撞, 离子温度和外加磁场等. 然而, 很多情况下, 对等离子体鞘层的研究工作是基于电子满足经典的麦克斯韦速度分布函数[1 -13 ] . 等离子体中的粒子具有长程电磁相互作用, 分布会偏离麦克斯韦分布. 为了描述这种系统, 1988年Tsallis[31 ] 提出非广延熵的概念, 表达为${S}_{q}=k\dfrac{1-\sum {P}_{i}^{q}}{q-1}$ , 其中: $ k $ 为玻尔兹曼常数, $ {P}_{i} $ 是第$ i $ 个微观态出现的概率, $ q $ 是无量纲化的描述系统非广延性质的参量. Tsallis以非广延熵为基础建立了非广延统计力学, 已经为长程相互作用系统找到了很好的描述框架. 当参数$ q=1 $ 时, 粒子分布又回到了广延的$ \mathrm{e} $ 指数情形, 所有的结果可以回到粒子满足经典的麦克斯韦分布时的结论. $ q < 1 $ 和 $ q>1 $ 分别对应超广延分布和亚广延分布情况. 非广延统计是一种新的统计力学, 近年来得到了广泛的应用, 尤其是成功地应用于解决各种天体物理以及等离子体物理问题, 包括等离子体不稳定性、等离子体鞘层和非线性波等. 研究具有非广延分布的等离子体已成为国际上一个新的研究热点[14 -26 ] .[14 ,15 ] 在2015年研究了无碰撞和有碰撞的两种鞘层模型, 修正了鞘层判据. 研究结果表明: 鞘层边缘离子的速度与非广延参数$ q $ 的数值成反比. 之后, Hatami等[16 ] 又在磁鞘模型中对德拜长度进行了修正. Borgohain等[17 ] 与Borgohain和Saharia[18 ] 分别研究了包含两种温度的非广延分布电子和热离子的系统和考虑了正离子中性碰撞的电负性等离子体鞘, 数值研究了鞘层中的粒子数密度、电位、净空间电荷密度. 结果是$ q $ 值的增加会导致鞘层厚度降低. 2019年, 赵晓云等[19 ] 研究了电子的非广延分布对等离子体鞘层中的二次电子发射的影响, 结果显示: 随着非广延参量的增大, 鞘层厚度减小、鞘层中二次电子数密度增加. 此外, 还有Liu等[20 ,21 ] 在含有非广延分布电子的尘埃等离子体鞘层模型基础上研究了德拜长度和玻姆判据. Tantawy等[22 ] 研究了存在非广延分布的电子和正电子的等离子体系统的非线性结构. Emamuddin等[23 ] 和Safa等[24 ] 分别研究了含有非广延分布电子的尘埃等离子体鞘层. Mehdipoor和Mohsenpour[25 ] 研究了具有非广延分布的电负性等离子体磁鞘的双层结构.[12 ] 与非广延分布两种碰撞磁鞘的玻姆判据, 以及由参数$ q $ 引起的电子离子密度、电势和空间电荷密度等物理量分布的变化. 研究所得到的结果对相关的天体物理、等离子体边界等问题的研究具有参考价值.2.基本物理模型 根据研究的需要, 并且考虑鞘层的厚度远远小于器壁尺度的条件, 我们建立一个一维坐标空间, 三维速度空间的碰撞等离子体磁鞘模型(图1 ). 外加的磁场在$ (x, z) $ 平面内, 磁场与$ x $ 轴的夹角为$ \theta $ . 在等离子体鞘层和等离子体的分界处, 即坐标$ x=0 $ 处, 空间静电势为$ \varphi =0 $ .图 1 等离子体磁鞘模型示意图Figure1. Schematic diagram of plasma magnetic sheath model.${C_q} \!=\! \left\{ \begin{aligned}& {{n_{{\rm{e}}0}}\dfrac{{{\Gamma }\Big( {\dfrac{1}{{1 \!-\! q}}} \Big)}}{{{\Gamma }\Big( {\dfrac{1}{{1 \!-\! q}} - \dfrac{1}{2}} \Big)}}{{\left[ {\dfrac{{{m_{\rm{e}}}\left( {1 \!-\! q} \right)}}{{2\pi k{T_{\rm{e}}}}}} \right]}^{\tfrac{1}{2}}},~ -\! 1 \! < \! q \! < \! 1}\\& {{n_{{\rm{e}}0}}\dfrac{{q + 1}}{2}\dfrac{{{\Gamma }\Big( {\dfrac{1}{{1 \!-\! q}} \!+\! \dfrac{1}{2}} \Big)}}{{{\Gamma }\Big( {\dfrac{1}{{1 \!-\! q}}} \Big)}}{{\left[ {\dfrac{{{m_{\rm{e}}}\left( {q \!-\! 1} \right)}}{{2\pi k{T_{\rm{e}}}}}} \right]}^{\tfrac{1}{2}}},~ q \! > \! 1}\end{aligned}\right.$ ${m}_{\mathrm{e}}, {v}_{\mathrm{e}}{\text{和}}{T}_{\rm e}$ 分别是电子的质量、速度和温度; ${n}_{\mathrm{e}0} $ 是电子在鞘边的数密度; $ \Gamma $ 是标准伽马函数. 对速率分布函数求导可得最概然速率, ${v}_{\mathrm{m}\mathrm{a}\mathrm{x}}=\dfrac{\mathrm{d}{f}_{\mathrm{e}}\left(v\right)}{\mathrm{d}v}=\sqrt{\dfrac{2 k{T}_{\mathrm{e}}}{{m}_{\mathrm{e}}(q-1)}-\dfrac{2 e\varphi }{{m}_{\mathrm{e}}}}$ [18 ] . 对速率分布函数积分, 可得电子的密度为[14 ,15 ,18 ,19 ] $ {n}_{\mathrm{e}} $ 是电子的数密度.[8 ,10 ,12 ] :$ {n}_{\mathrm{i}} $ , $ {{v}}_{\mathrm{i}} $ 和$ {m}_{\mathrm{i}} $ 分别是正离子的数密度、速度以及质量; $ {n}_{\mathrm{n}} $ 是中性气体的数密度; $ \mu ={\mu }_{\mathrm{s}}({v}_{\mathrm{i}}/{c}_{\mathrm{i}\mathrm{s}}{)}^{\beta } $ 是离子与中性粒子间碰撞时动量传递的截面, $ {\mu }_{\mathrm{s}} $ 是正离子声速的测量截面, $ {c}_{\mathrm{i}\mathrm{s}}=(k{T}_{\mathrm{e}}/{m}_{\mathrm{i}}{)}^{1/2} $ 是离子声速, $ \beta $ 是无量纲化参数, 取值范围为$ -1—0 $ . 这个取值范围包含了两种特殊情况: $ \beta =0 $ 对应恒定的离子平均自由程; $ \beta =-1 $ 对应恒定的离子碰撞频率.$ {\varphi }_{\mathrm{w}} $ , 离子和电子的电流守恒, $ {j}_{\mathrm{i}}={j}_{\mathrm{e}} $ , $ j $ 是电流密度.$ \varPhi =e\varphi /{kT}_{\mathrm{e}} $ , $ \xi =x/{\lambda }_{\mathrm{D}} $ , $ {{u}}_{\mathrm{i}}={{v}}_{\mathrm{i}}/{c}_{\mathrm{i}\mathrm{s}} $ , $ {N}_{\mathrm{e}}={n}_{\mathrm{e}}/{n}_{\mathrm{e}0} $ , $ {N}_{\mathrm{i}}={n}_{\mathrm{i}}/{n}_{\mathrm{i}0} $ , $ \nu ={\lambda }_{\mathrm{D}}{n}_{\mathrm{n}}{\mu }_{\mathrm{s}} $ . 这里$ {\lambda }_{\mathrm{D}}=({{\epsilon }_{0}kT}_{\mathrm{e}}/{n}_{\mathrm{e}0}{e}^{2}{)}^{1/2} $ 是电子德拜长度, $ {\omega }_{\mathrm{i}\mathrm{c}}=eB/{m}_{\mathrm{i}} $ 是离子回旋频率. $ {\omega }_{\mathrm{i}\mathrm{c}} $ 和$ {\lambda }_{\mathrm{D}} $ 分别是离子回旋频率和电子德拜长度. 令${B}_{0}=\mathrm{c}\mathrm{o}\mathrm{s}\theta {{i}}+ \mathrm{s}\mathrm{i}\mathrm{n}\theta {{k}}$ , 如果取物理量只有$ x $ 方向的空间变化, 即$\nabla \to \partial /\partial x\hat{i}$ , 则由(2 )式—(7 )/式, 可以得到9 )式中$ {Ma}_{\mathrm{i}}={v}_{\mathrm{i}x0}/{c}_{\mathrm{i}\mathrm{s}} $ 为离子马赫数. (10 )式中$ {\gamma }_{\mathrm{i}}={\omega }_{\mathrm{i}\mathrm{c}}/{\omega }_{\mathrm{p}\mathrm{i}} $ 为离子回旋频率$ {\omega }_{\mathrm{i}\mathrm{c}} $ 与离子等离子体频率$ {\omega }_{\mathrm{p}\mathrm{i}} $ 之比, $ {\omega }_{\mathrm{p}\mathrm{i}}=({n}_{\mathrm{i}0}{e}^{2}/{{\epsilon }_{0}m}_{\mathrm{i}}{)}^{1/2} $ , (14 )式中$\mu = ({m}_{\mathrm{e}}/{m}_{\mathrm{i}}{)}^{1/2}$ , $ {A}_{q}={C}_{q}(k{T}_{\mathrm{e}}/{m}_{\mathrm{e}}{)}^{1/2}/{n}_{\mathrm{e}0} $ .8 )式, (9 )式和(13 )式可得赛格捷夫势:$ V\left(\varPhi =0\right)=0 $ , ${\left.\dfrac{\partial V(\varPhi)}{\partial \varPhi }\right|}_{\varPhi =0}=0$ , 和${\left.\dfrac{{\partial }^{2}V(\varPhi)}{\partial {\varPhi }^{2}}\right|}_{\Phi =0}\leqslant 0$ .8 )式可得9 )式和(10 )式, 再考虑鞘层的边界条件: $ x=0 $ , $ \varPhi \to 0 $ , $ {N}_{i}\to 1 $ , $ \partial \varPhi /\partial \xi ={-E}_{0}\ne 0 $ , 可得$ {{E}}\times {{B} }$ 漂移运动[13 ,27 -30 ] , 离子进入鞘层初始速度的$ y $ 轴和$ z $ 轴分量分别为$ {u}_{\mathrm{i}y0}=-{E}_{0}\mathrm{s}\mathrm{i}\mathrm{n}\theta /{\gamma }_{\mathrm{i}} $ 和 $ {u}_{\mathrm{i}z0}={Ma}_{\mathrm{i}}\mathrm{t}\mathrm{a}\mathrm{n}\theta $ , 则:16 )和(17 )式, 可得$ \beta =0 $ 时, ${Ma}_{\mathrm{i}}\geqslant \dfrac{\mathrm{cos}\theta }{\Big({\dfrac{\nu }{{E}_{0}}+\dfrac{q+1}{2}\Big)}^{1/2}}$ ;$\beta \!=\!-\!1$ 时, ${Ma}_{\mathrm{i}}\!\geqslant\! \dfrac{\Big[\!{{\Big(\!\dfrac{\nu }{{E}_{0}}\!\Big)}^{2}\!+\!2\left(q\!+\!1\right){\mathrm{c}\mathrm{o}\mathrm{s}\theta }^{2}\!\Big]}^{1/2}\!-\!\dfrac{\nu }{{E}_{0}}}{q+1}$ .$ q=1 $ 时, (18 )式与电子满足麦克斯韦分布时的等离子体磁鞘的下限条件[12 ] 一致. 由Tsallis的非广延分布理论, 当$ q=1 $ 时, 所有的结果可以回到经典的麦克斯韦分布对应的结论. 由(18 )式代入条件参数($q=1, \theta =0, \nu =0$ )可得到${Ma}^{2}\geqslant 1,$ 这是我们非常熟悉的无外加磁场且不考虑碰撞效应的电子离子鞘层的玻姆判据. 当不考虑碰撞效应时, 离子马赫数与鞘边电场没有关系. 从(18 )式可以得到${Ma}_{\mathrm{i}}^{2}\geqslant \dfrac{{\mathrm{c}\mathrm{o}\mathrm{s}\theta }^{2}}{(q \!+\! 1)/2}$ , 当电子采用麦克斯韦分布来描述时($ q=1 $ ), 就可以得到Chodura[1 ] 研究工作的结果${Ma}_{\mathrm{i}}\geqslant\mathrm{c}\mathrm{o}\mathrm{s}\theta$ . 很多研究鞘层判据的工作[13 ,27 -30 ] 在考虑离子的$ {{E}}\times {{B} }$ 漂移运动之后都得到了类似的结果: 磁场的角度对离子马赫数是有影响. 等离子体预鞘区存在一个微弱的电场加速离子, 在考虑碰撞的情况下, 鞘边电场对离子马赫数是有影响的, 有限边界电场是克服碰撞摩擦的必要条件. 没有碰撞和电离时, 边界电场可以设置为无穷小, 采用无碰撞情况下的鞘判据, 可以利用$ {j}_{\mathrm{i}}={j}_{\mathrm{e}} $ 的条件来确定鞘层电势, 而鞘边电场也不是一个独立的变量. 本文研究的是碰撞磁鞘, 对离子进入鞘层的判据进行了修正, 在数值模拟中鞘边电场需要给出一个初始值.15 )式, $V(\varPhi)\leqslant 0$ 可得离子马赫数应当满足的上限条件:$ q $ 有关.3.数值结果与讨论 在图2 —图7 的数值模拟中, 采用氩等离子体实验中常用的数据, 例如: 碰撞参数$ \nu =0.134 $ , 相应的气体压强为$ 13\;\mathrm{P}\mathrm{a} $ , 温度为 $ 290\;\mathrm{K} $ . 取等离子体密度为$ 5\times {10}^{14}/{\mathrm{m}}^{3} $ , 电子温度为$ 3.48\times {10}^{4}\;\mathrm{K} $ .图 2 离子马赫数的下限随参数$ q $ 的变化 ($B=0.3~\mathrm{T}$ , $ {E}_{0}=0.1 $ )Figure2. Ion Mach number versus non-extensive parameter $ q $ ($B=0.3~\mathrm{T}$ , $ {E}_{0}=0.1 $ ).图2 显示了$ \beta =0 $ 和$ \beta =-1 $ 时离子马赫数下限的数值随$ q $ 值的变化关系, 并且对比了磁场角度对离子马赫数的影响. 如图2 所示, 外加磁场角度增大会使离子马赫数下限的数值减小. 因为在磁场强度不变的前提下, 磁场角度增大也就是磁场$ z $ 轴分量增强, 这个方向的磁场分量对离子的洛伦兹力会明显影响离子$ x $ 轴的速度分量, 从而影响离子的密度分布, 关于磁场角度对鞘层结构($ q=1 $ )的影响, 可以参考文献[10 ]的相关结论. 无论磁场角度取何值, 离子马赫数的下限的数值都会随着非广延分布参数$ q $ 值增大而减小, 相比$ \beta =-1 $ 情形, $ \beta =0 $ 时这个减小的趋势更加明显, 这个结论与Hatami[14 ] 的研究结果相似. 当非广延分布参数$ q < 1 $ 时离子马赫数的下限值会增大; 而当$ q>1 $ 时, 离子马赫数的下限值会减小. 随着$ q $ 值增加, 离子马赫数下限会降低, 意味着当低速运动的电子数目增多时, 离子进入鞘层需要具有较少的动能, 更容易进入鞘层.图3 —图5 显示了非广延分布对碰撞磁鞘的影响. 图3 显示了非广延分布参数$ q $ 值对碰撞磁鞘电势的影响. 与麦克斯韦分布的磁鞘($ q=1 $ )相比, 当$ q < 1 $ 时, 非广延分布磁鞘的空间电势下降得慢些, 而当$ q>1 $ 时, 对应的电势下降得更快些. 与麦克斯韦分布相比, 超广延分布($ q < 1 $ )的电子平均速度相对较快, 高速运动的电子数量增加; 亚广延分布($ q>1 $ )的电子平均速度相对较慢, 低速运动的电子数量增加. 电子的速度影响空间电势分布, 也影响到达器壁的电子数量. 器壁悬浮电势与参数$ q $ 的关系与文献[19 ]类似, 这里不做赘述.图 3 具有不同参数$ q $ 值的鞘层空间电势($B=0.3~\mathrm{T}$ , $ \theta =15° $ , $ {E}_{0}=0.1 $ , $ \beta =0 $ )Figure3. Sheath potential for different values of non-extensive parameter$ q $ ($B=0.3~\mathrm{T}$ , $ \theta =15° $ , $ {E}_{0}=0.1 $ , $ \beta =0 $ ).图 5 具有不同参数$ q $ 值的鞘层空间电荷密度分布 ($B= 0.3~\mathrm{T}$ , $ \theta =15° $ , $ {E}_{0}=0.1 $ , $ \beta =0 $ )Figure5. Normalized space charge density for different values of non-extensive parameter $ q $ ($B=0.3~\mathrm{T}$ , $ \theta =15° $ , ${E}_{0}= 0.1$ , $ \beta =0 $ ).图4 显示了非广延分布的碰撞等离子体磁鞘的电子离子密度分布跟麦克斯韦分布碰撞磁鞘的对比. 由图4(a) 可知, 当$ q < 1 $ 时, 电子数密度降落得也相对较慢, 而且$ q $ 值越小, 高速运动的电子数量越多, 密度分布曲线下降得越慢. 由图4(b) 可知, 当$ q>1 $ 时, 随着$ q $ 值的增大, 高速运动的电子数量越少, 电子数密度更快地降为零, 离子的密度分布也下降得更快.图 4 具有不同参数$ q $ 值的离子电子密度分布($B=0.3~\mathrm{T}$ , $ \theta =15° $ , $ {E}_{0}=0.1 $ , $ \beta =0 $ ) (a)$ q < 1 $ ; (b$ )q>1 $ Figure4. Normalized density of ions and electrons for different values of non-extensive parameter $ q $ ($B=0.3~\mathrm{T}$ , $ \theta =15° $ , $ {E}_{0}=0.1 $ , $ \beta =0 $ ): (a)$ q < 1 $ ; (b)$ q>1 $ 图5 显示了$ q $ 取不同值时非广延分布的碰撞等离子体磁鞘的空间电荷密度分布. 与麦克斯韦分布($ q=1 $ )的碰撞磁鞘的对比, 当$ q < 1 $ 时, 由于电子的密度分布降落得较慢, 所以空间电荷曲线的峰值更小而且更加靠近器壁或是工件. 也就是在这种情况下, 更多更高能量的电子进入鞘层区域, 结果净空间电荷密度降低. 当$ q>1 $ 时, 对应的电子数密度下降得较快, 这也导致空间净电荷曲线的峰值较大, 而且远离器壁或是工件.图6 和图7 显示了碰撞对非广延分布等离子体磁鞘的影响, 取参数$ q=0.9 $ . 本文讨论的碰撞是发生在离子与中性粒子间的碰撞. 由于碰撞, 离子损失了动能. 与无碰撞时相比较, 离子向极板运动的速度会降低, 相应的密度分布的降落会减缓, 如图6 所示. 离子密度分布的变化会影响鞘层的电势分布和电子密度分布, 也会影响鞘层空间电荷密度分布(如图7 所示). 由于离子的密度分布降落得较慢, 所以空间电荷曲线的峰值更高. 通过以上结果可见碰撞对非广延分布磁鞘的影响同在麦克斯韦分布磁鞘得到结论[11 ] 类似.图 6 具有不同碰撞参数$ \nu $ 值的离子电子密度分布($B= 0.3~\mathrm{T}$ , $ \theta =15° $ , $ {E}_{0}=0.5 $ , $ \beta =0 $ , $ q=0.9 $ )Figure6. Normalized density of ions and electrons for different values of collision parameter $ \nu $ ($B=0.3~\mathrm{T}$ , $ \theta =15° $ , $ {E}_{0}=0.5, \beta =0 $ , $ q=0.9 $ ).图 7 具有不同碰撞参数$ \nu $ 值的鞘层空间电荷密度分布 ($B= 0.3~\mathrm{T}$ , $ \theta =15° $ , $ {E}_{0}=0.5 $ , $ \beta =0 $ , $ q=0.9 $ )Figure7. Normalized space charge density for different values of collision parameter $ \nu $ ($B=0.3~\mathrm{T}$ , $ \theta =15° $ , $ {E}_{0}=0.5 $ , $ \beta =0 $ , $ q=0.9 $ )4.结 论 本文建立一个具有非广延分布电子的碰撞等离子体磁鞘模型, 理论推导出与非广延参数$ q $ 有关的玻姆判据, 离子马赫数下限的数值随参数$ q $ 的增大而减小. 与具有麦克斯韦分布($ q=1) $ 电子的碰撞等离子体磁鞘对比, 当$ q < 1 $ 时, 离子马赫数的下限的数值会增加; 当$ q>1 $ 时, 离子马赫数的下限的数值会降低. 经过数值模拟, 得出结论: 与具有麦克斯韦分布($ q=1) $ 的碰撞等离子体磁鞘对比, 当$ q < 1 $ 时, 非广延分布的碰撞等离子体磁鞘的空间电势降落得更慢, 离子电子密度降落得更慢, 空间电荷密度曲线的峰值更加靠近器壁; 当$ q>1 $ 时, 非广延分布的等离子体磁鞘的空间电势降落得更快, 离子电子密度降落得更快, 尤其是电子密度更快地降为零, 空间电荷密度曲线的峰值远离器壁. 以上模拟结果显示出非广延分布的参数$ q $ 对等离子体磁鞘的结构具有不可忽略的影响, 而碰撞对非广延分布磁鞘的影响同在麦克斯韦分布磁鞘得到的结论类似, 这些结论对相关的等离子体边界问题或者等离子体工艺的研究具有参考价值. 


















 图 1 等离子体磁鞘模型示意图
图 1 等离子体磁鞘模型示意图













































































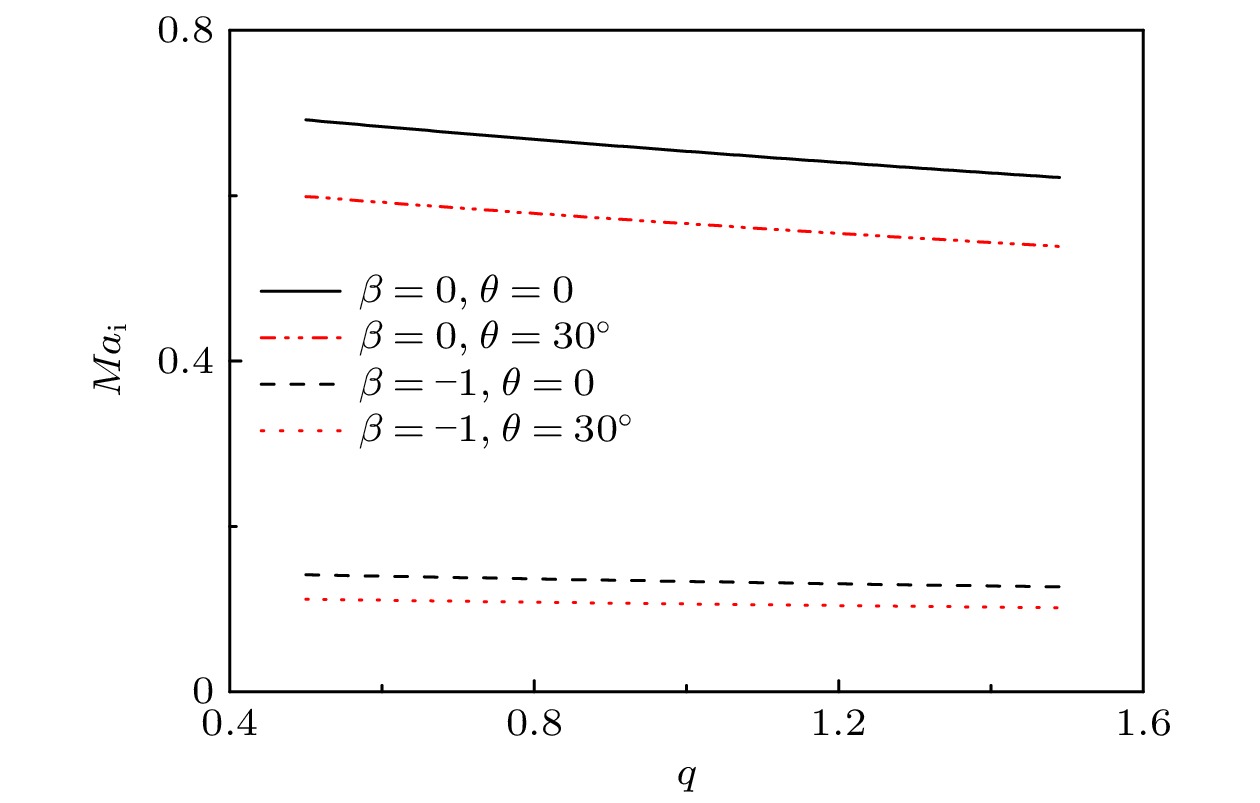 图 2 离子马赫数的下限随参数
图 2 离子马赫数的下限随参数








































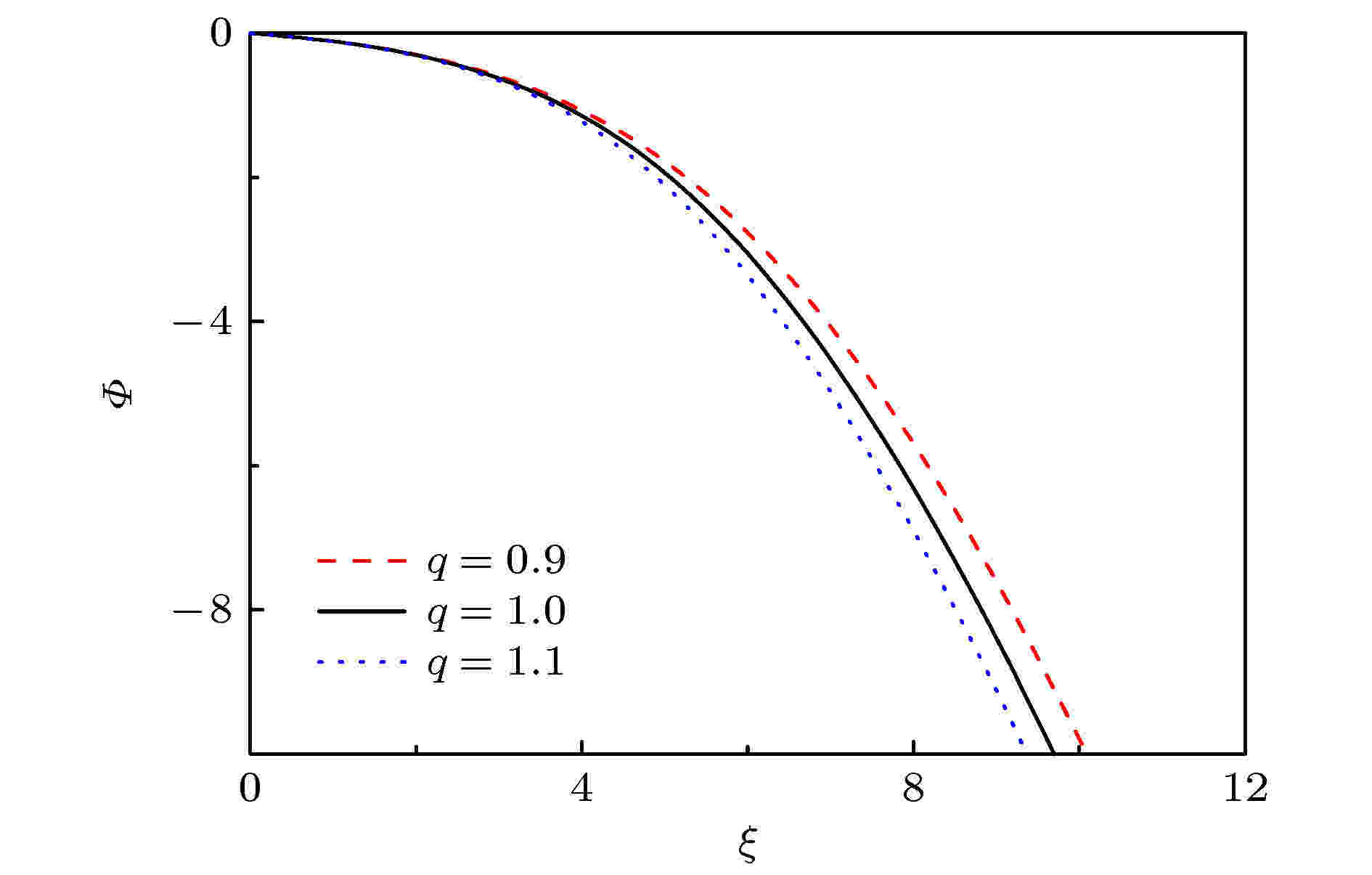 图 3 具有不同参数
图 3 具有不同参数









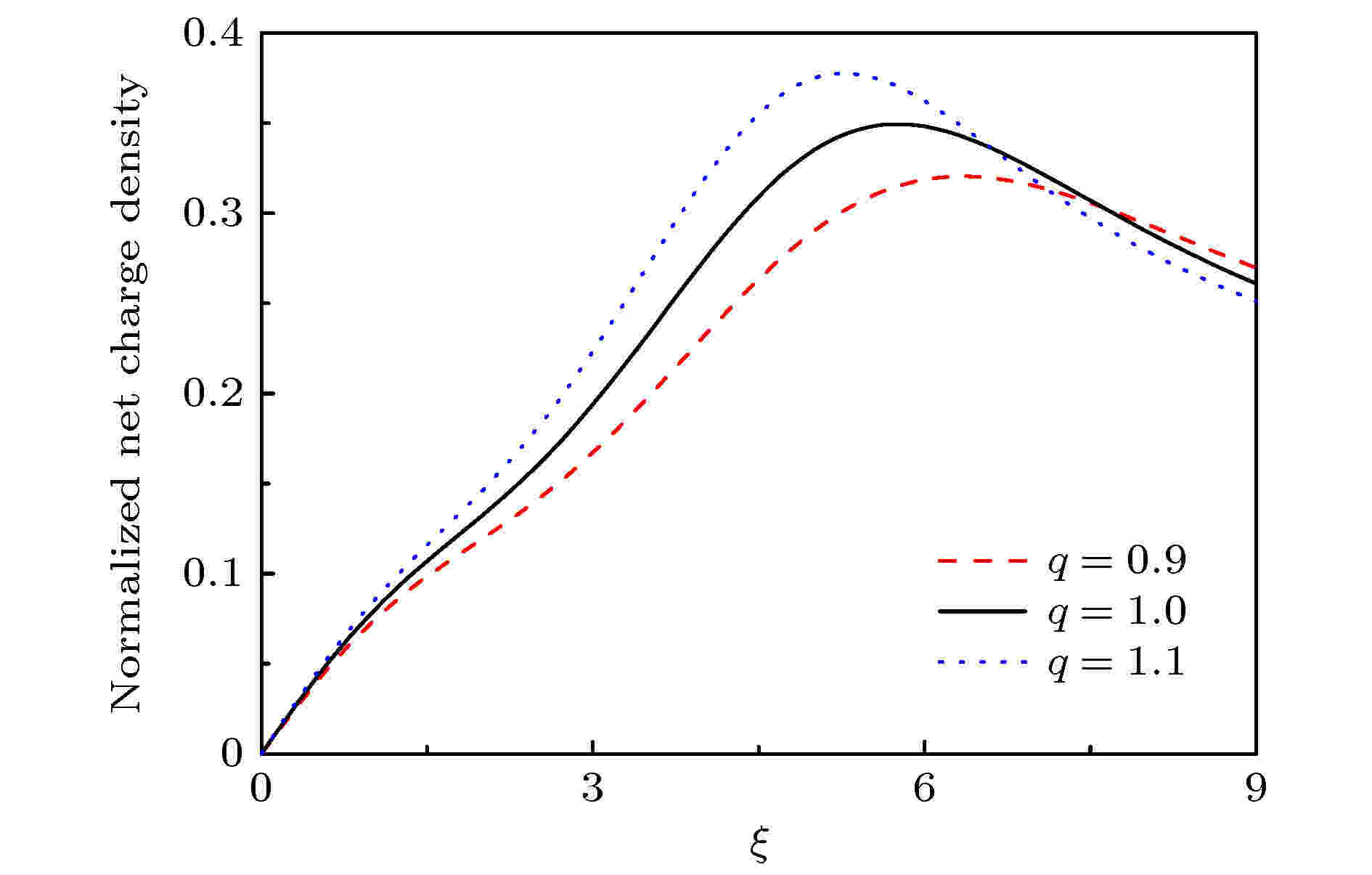 图 5 具有不同参数
图 5 具有不同参数















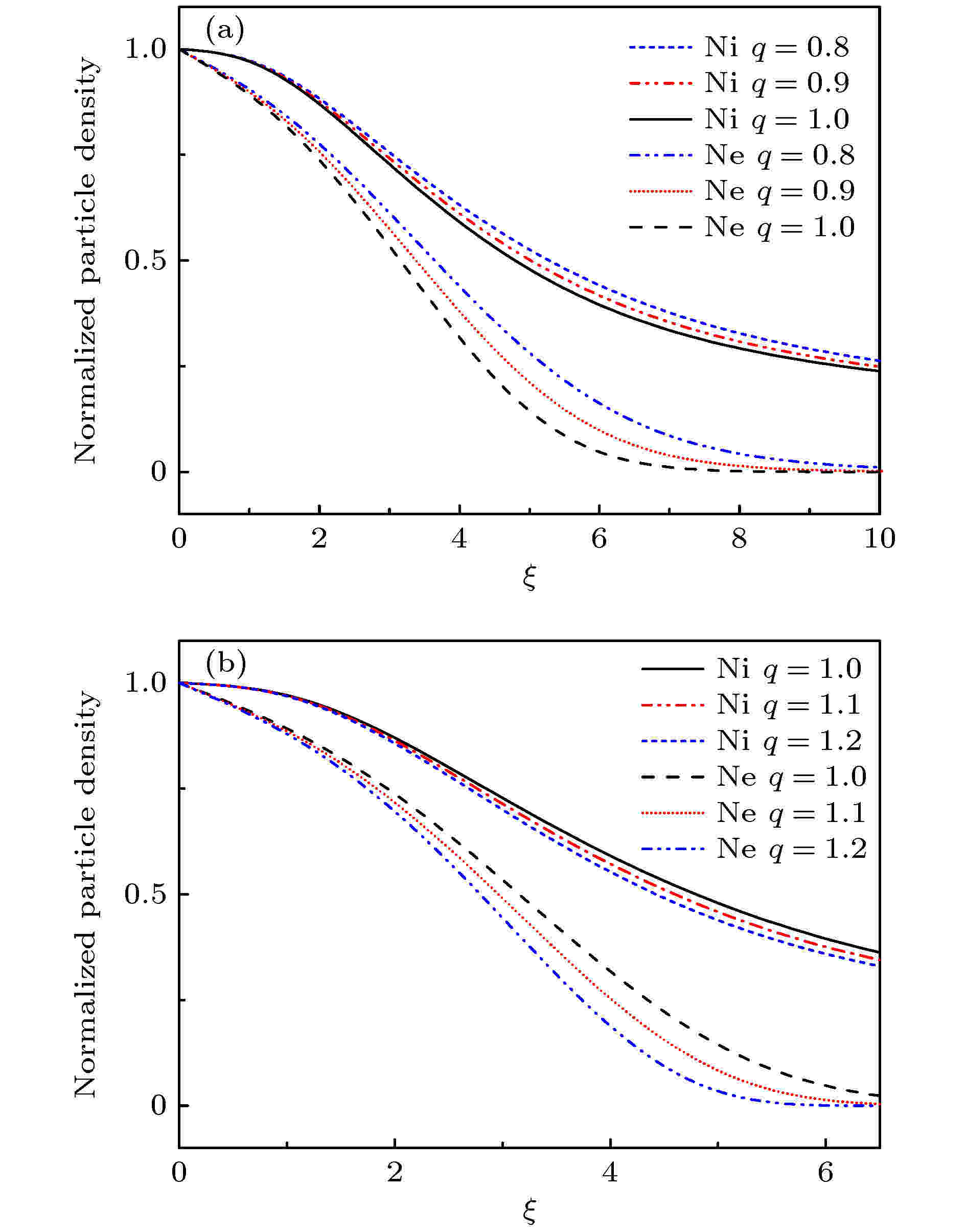 图 4 具有不同参数
图 4 具有不同参数


















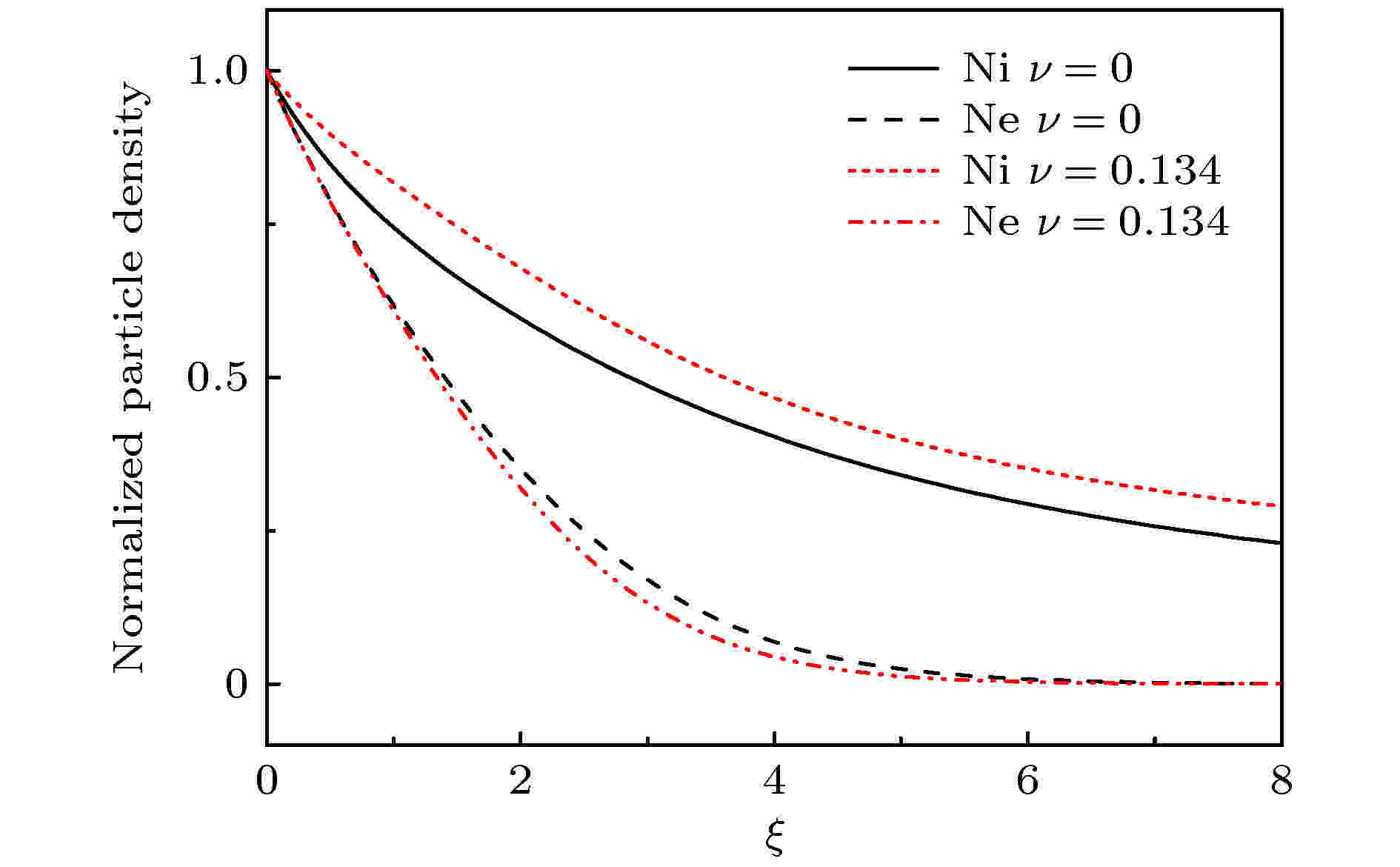 图 6 具有不同碰撞参数
图 6 具有不同碰撞参数










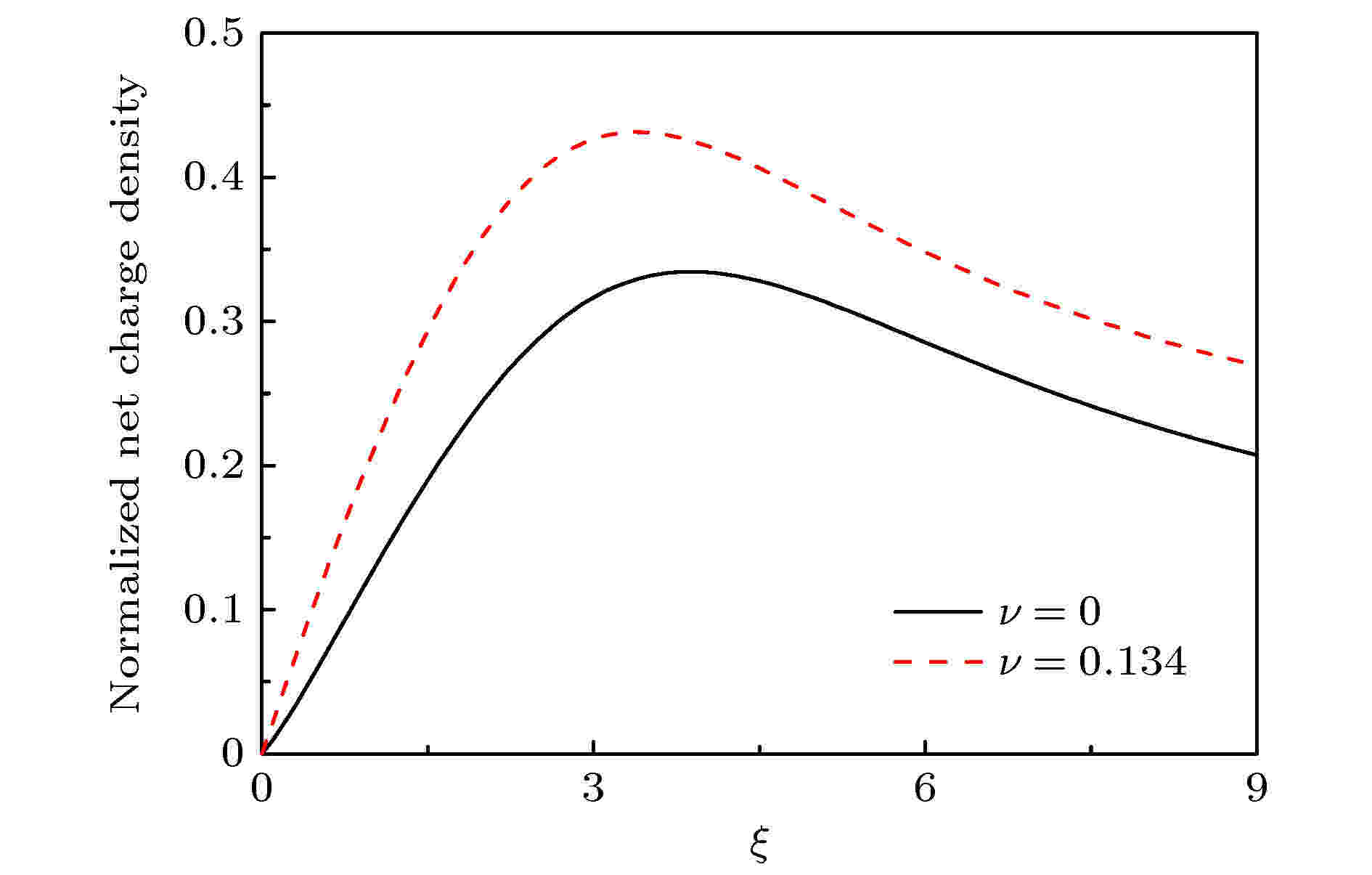 图 7 具有不同碰撞参数
图 7 具有不同碰撞参数




































