摘要:多功能器件的设计是推动新一代电磁系统发展的重要力量, 而超构表面因其对电磁波的幅度、相位和极化等特性的灵活调控在多功能器件领域备受关注. 传统的多功能超构表面是利用各向异性单元对相互正交的线极化波具有不同响应的特性, 从而设计出适用于线极化的多功能器件. 本文提出了一种缝隙加载的环I形复合超构表面单元, 通过单元臂长和旋转角度的调整实现了对圆极化电磁波传输和几何相位的独立控制. 利用上述两种相位的共同作用, 打破了左旋和右旋圆极化电磁波操控中存在的固有关系, 为圆极化双功能器件的设计提供了新的思路. 在此基础上, 利用复合超构表面分别设计了异面偏折器和定向/涡旋光束产生器, 实验结果表明, 本文设计的两种反射型圆极化双功能器件在9—13 GHz的宽频带范围内均能良好工作.
关键词: 复合超构表面/
多功能/
圆极化/
传输相位/
几何相位

English Abstract

全文HTML

--> --> -->

电磁波包括光的调控是一项古老而又与时俱进的话题, 主要是依照一定的规律去改变电磁波的相位、幅度以及极化状态等特性, 从而达到调控电磁波传播方向、形成特定的电磁波前或者赋予电磁波一些能够用于探测、成像和通信的特殊信息的目标. 近年来, 超构表面通过在二维平面上引入不连续的参数变化, 打破体材料对传输长度的依赖, 在电磁波波前调制领域受到****们的广泛关注^[1]. 它主要是通过在介质表面上合理地布局一些亚波长结构的周期或者准周期单元来实现对电磁波相位、幅度以及极化状态的灵活调控. 目前, 超构表面的研究理论逐渐完善, 其在奇异偏折^[2-5]、波束聚焦^[6-8]、表面波耦合^[9,10]、雷达散射截面减缩^[11-13]、极化变换^[14]、特殊波形产生器^[15-18]和多功能器件设计^[19-26]等领域应用广泛.
随着电子设备的快速发展, 为满足各种设备间日益增长的通信需求, 电子通信系统必须包含各种不同功能的电磁器件, 导致通信设备的体积增大同时兼容性变差. 如何将不同的功能集成到同一个器件中, 从而设计出多功能电磁器件, 成为了现代通信设备尤其是移动设备小型化设计的重要手段. 近年来, 超构表面因其灵活的电磁特性在多功能器件领域受到****的密切关注. Cai等^[19]设计了双极化双功能超构表面, 同时实现了汇聚水平极化波的功能以及将垂直极化波耦合成表面波的两种功能. Guo等^[20]利用超薄的单层超构表面实现了贴片天线增益的提高并且将圆极化入射波分离成为两束线极化波. Qi等^[21]设计出了不同极化的电磁波携带不同模式的双涡旋光束. Arbabi等^[22]则设计出双频双焦点的介质透镜. Ling等^[23]则同时实现了表面等离子激元(surface plasmon polaritons, SPP)耦合和聚焦两种功能. 上述工作主要是利用各向异性超构表面对不同线极化波的响应不同, 从而设计出线极化多功能器件. 近年来, 关于圆极化的多功能器件也逐渐被报道, Zentgraf等^[24]设计出不同旋向圆极化激励产生不同全息图案的多功能全息表面; Tian等^[25]在THz频段实现了不同旋向圆极化入射波波在超构表面前向和后向的奇异偏折效应; Chen等^[26]设计出正常反射左旋圆极化波而全吸收右旋圆极化波的多功能器件. 本文结合传输相位和几何相位, 通过优化成功解锁了左旋和右旋电磁波调制过程中的固定相位关系, 提供了实现圆极化任意双功能器件设计的一种新方法, 并设计了两款反射型宽带圆极化双功能器件, 验证了方法的有效性.

2

-->

2.1.圆极化电磁波相位的复合调制方法

在微波频段, 无源超构表面对电磁波相位的控制方法主要分为两种: 一种是改变单元结构关于对称轴的旋转角度; 另一种是改变单元结构的物理尺寸. 其中, 改变旋转角度的方法主要依据Pancharatnam-Berry (PB)原理, 仅对圆极化(circular polarization, CP)电磁波起到调制作用, 通常将旋转角度决定的相位称作几何相位(geometric phase, GP). 而且超构表面单元是半波片时, 能够实现最佳的调控效率.
为了便于描述单元的电磁特性, 利用如下式表述单元在线极化入射波下的反射系数${{{R}}_{{l}}}$:

${{{R}}_{ {l}}} = \left( {\begin{array}{*{20}{c}} {{r_{xx}}}&{{r_{yx}}} \\ {{r_{xy}}}&{{r_{yy}}} \end{array}} \right),$

其中${r_{xx}}$和${r_{yy}}$表示主极化的反射系数, ${r_{yx}}$和${r_{xy}}$表示交叉极化的反射系数. 其中, 下标的前一个字母表示出射波的极化而后一个字母代表入射波的极化. 如图1(a)所示, 假设电磁波沿z轴负方向入射到超构表面单元上(沿x和y方向均设置为周期边界), 左旋和右旋入射波在线极化基${{l}} = {\left( {x, y} \right)^{\rm{T}}}$下的系数$A_{_ - }^{\rm{i}}$和$A_{_ + }^{\rm{i}}$由下式表示, 初始相位为0:
图 1 反射型PB单元示意图　(a) 自由视图; (b) 原始单元俯视图; (c)旋转单元俯视图
Figure1. Schematic diagram of reflected PB unit cell: (a) Free view of the unit cell; (b) top view of the original unit cell; (c) top view of the rotated unit cell.

$\left\{ \begin{aligned} &{A_{_ - }^{\rm{i}} = \left( {1, - {\rm{j}}} \right){{\rm{e}}^{{\rm{j}}kz}}{{,}}} \\ &{A_{_ + }^{\rm{i}} = \left( {1,{\rm{j}}} \right){{\rm{e}}^{{\rm{j}}kz}}{{,}}} \end{aligned} \right.$

其中k表示自由空间波数; 上标符号i表示入射波; 下标符号$ -{\text{和}}+$分别代表左旋圆极化和右旋圆极化电磁波. 在线极化激励下, 当单元主极化反射系数(反射波和入射波极化相同)幅度相等且为1, 相位相差 ± 180°, 交叉极化(反射波与入射波极化正交)分量为0, 表明单元满足半波片条件. 依据PB原理, 图1(b)和图1(c)所示单元反射电磁波在线极化基l下的系数可以分别用下面公式表示:

$\left\{ \begin{aligned} &{A_{_{{ - }}}^{\rm{o}} = \left( {1,{\rm{j}}} \right){{\rm{e}}^{ - {\rm{j}}kz}}{{,}}} \\ &{A_{{ + }}^{\rm{o}} = \left( {1, - {\rm{j}}} \right){{\rm{e}}^{ - {\rm{j}}kz}}{{,}}} \end{aligned}\right.$

$ \left\{ \begin{aligned} &{C}_{{-}}^{\rm{o}}=\left(1,{\rm{j}}\right){\rm{e}}^{-{\rm{j}}kz}{\rm{e}}^{-{\rm{j}}2\beta } , \\ &{C}_{{+}}^{\rm{o}}=\left(1,-{\rm{j}}\right){\rm{e}}^{-{\rm{j}}kz}{\rm{e}}^{{\rm{j}}2\beta } , \end{aligned} \right.$

其中$A_{_ - }^{\rm{o}}$和$A_ + ^{\rm{o}}$表示原始单元的左旋和右旋出射波在l下的系数, $C_{{ - }}^{\rm{o}}$和$C_{{ + }}^{\rm{o}}$表示旋转$\beta $角单元的左旋和右旋出射波在l下的系数. (3)式和(4)式表明, 当入射波为左旋圆极化时, 反射波表现为左旋圆极化, 且旋转后和旋转前的反射波表达式相差${{\rm{e}}^{ - {\rm{j}}2\beta }}$算符; 当入射波为右旋圆极化时, 反射波则表现为右旋圆极化, 此时旋转后和旋转前的透射波表达式相差${{\rm{e}}^{{\rm{j}}2\beta }}$算符. 除了改变单元的旋转角度以外, 改变物理尺寸同样是调控相位的常用手段. 尺寸的改变会带来谐振频率的变化, 并且这种变化对左旋和右旋圆极化(circular polarization, CP)电磁波具有相同的效果, 通常将由物理尺寸决定的相位称为传输相位(propagating phase, PP).
综上所述, 单独旋转角度或变化尺寸时, 左旋和右旋圆极化波的相位变化存在相反和相同的变化关系. 因此, 仅仅旋转角度或者仅仅改变物理尺寸均不能实现对左旋和右旋圆极化电磁波相位的独立控制. 为了打破左旋和右旋圆极化电磁波在传统调制方法中的固定关系, 需要同时旋转单元角度和改变单元物理尺寸. 为了获得最佳的操控效率, 单元物理尺寸的改变不能破坏半波片条件. 对于反射PB单元, 在上述复合相位调制的方法下, 反射电磁波在线极化基${{l}} = {\left( {x, y} \right)^{\rm{T}}}$下的表达式为:

$ \left\{ \begin{aligned} &{C}_{-}^{\rm{o}}=\left(1,{\rm{j}}\right){\rm{e}}^{-{\rm{j}}kz}{\rm{e}}^{{\rm{j}}(\varphi -2\beta )} , \\ &{C}_{+}^{\rm{o}}=\left(1,-{\rm{j}}\right){\rm{e}}^{-{\rm{j}}kz}{\rm{e}}^{{\rm{j}}(\varphi +2\beta )} {.}\end{aligned} \right.$

为了更直观地表示圆极化间的相互转换关系, 利用下面公式中所示的${{{R}}_{\rm{c}}}$表示超构单元的圆极化透射系数, 其中, ${r_{ - - }}$和${r_{ + + }}$表示主极化的反射系数, ${r_{ + - }}$和${r_{ - + }}$表示交叉极化的反射系数, 下标的前一个字符表示出射波的极化而后一个字符代表入射波的极化.

${{{R}}_{\rm{c}}} = \left( {\begin{array}{*{20}{c}} {{r_{ - - }}}&{{r_{ + - }}} \\ {{r_{ - + }}}&{{r_{ + + }}} \end{array}} \right).$

当单元旋转β角的同时变化一定的尺寸, 根据(5)式, 可得到其反射系数满足下面公式, 从如下式可以看出右旋和左旋圆极化反射波具有不同的相位:

$\left\{ \begin{aligned} &{{r_{ + - }} = {r_{ - + }} = 0{{ ,}}}\\ &{\left| {{r_{ - - }}} \right| = \left| {{r_{ + + }}} \right| = 1{{ }},}\\ &{\varphi \left( {{r_{ - - }}} \right) = \varphi - 2\beta {{ }},}\\ &{\varphi \left( {{r_{ + + }}} \right) = \varphi + 2\beta {{ }}{{.}}} \end{aligned} \right.$

设定反射右旋圆极化电磁波的相位为$\varphi \left( + \right)$而左旋圆极化电磁波为$\varphi \left( - \right)$, 此时根据(7)式可以计算出几何相位算符和传输相位算符满足下面的公式:

$ \left\{ \begin{aligned} &\varphi =\frac{\varphi (+)+\varphi (-)}{2} , \\ &\beta =\frac{\varphi (+)-\varphi (-)}{4} {.}\end{aligned} \right.$

不同的$\varphi \left( + \right)$和$\varphi \left( - \right)$分布将对应不同的β和φ的分布, 进而得到不同的尺寸和旋转角度分布, 依此构建的复合超构表面将实现对左旋和右旋圆极化电磁波的独立控制, 从而设计出任意的圆极化双功能器件.
2 -->

2.2.宽带反射型复合超构表面单元设计

如图2(a)所示, 单元整体采用金属-介质-金属的结构, 其中底层为全金属结构, 中间介质层采用厚度为3 mm的聚四氟乙烯玻璃布板(F4B, ε_r = 2.65, tanδ = 0.003), 外层金属结构由传统的I形单元演化而来, 单元的两臂呈环状且加载有缝隙结构, 本节将这种新型单元称作缝隙加载的环I形单元. 单元具体结构参数如下, 内侧圆环半径r = 1.5 mm, 金属条宽度w = 0.6 mm, 环形缝隙宽度s = 0.5 mm, 介质板厚度d = 3 mm, 单元周期p = 7 mm, 金属臂对应的角度α和旋转角度β分别用来控制反射波的传输相位和几何相位. 为了便于描述单元的电磁特性, 选取了三种典型的单元C1, C2和C3, 首先分析它们的电磁特性. 单元的旋转角β均为0°, C1, C2和C3金属臂长对应的角度α分别为87°, 61°和15°.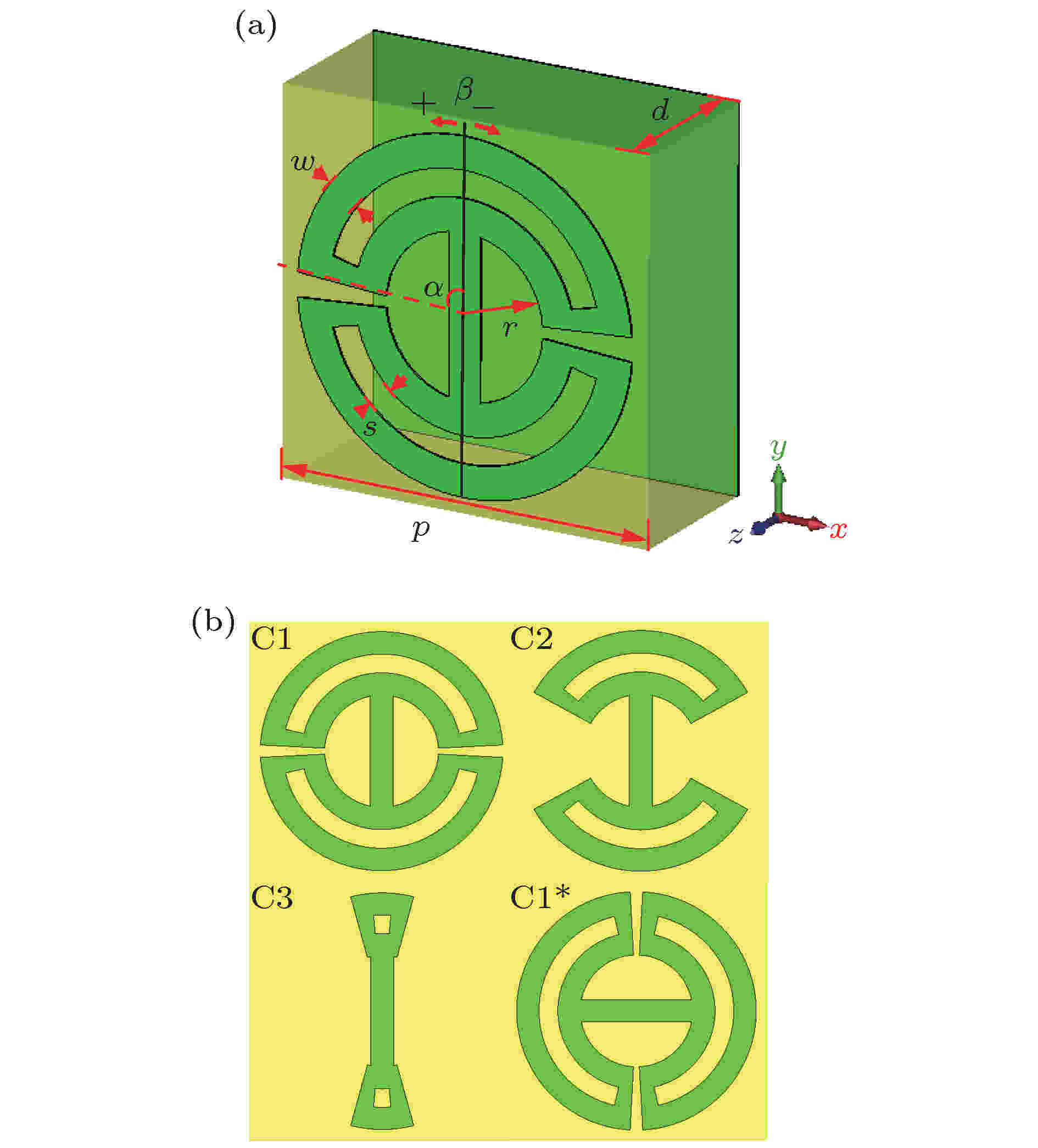
图 2 复合超构表面单元结构参数　(a) 单元模型及相关参数; (b) 典型单元俯视图
Figure2. Structural parameters of the composite metasurface: (a) Model and parameters of the unit cell; (b) top view of the typical unit cell.

选取C1单元作为参考单元, 图3(a)给出了C1的线极化反射系数, 从图中可以看出入射波分别为x和y极化时, 单元的主极化反射系数的相位在10 GHz周围满足180°的相位差, 同时反射系数幅度几乎相等且接近1, 满足半波片的条件. 此时, 改用圆极化的入射波, 依据PB原理, 反射电磁波的主极化与入射相同, 相比于金属板而言实现了与入射波旋向相同的圆极化辐射. 如图3(b)所示, 单元C1在很宽的频带内保持了较高的主极化反射率, 尤其在8—12 GHz范围内, 主极化反射系数幅度超过了0.95. 同时, 图3(b)还给出了半波片C2和C3的主极化反射系数. 从图中可以看出, 单元C2和C3在宽带范围内实现了高效的圆极化反射, 同时, 它们的传输相位分别与单元C1相差90°和180°.
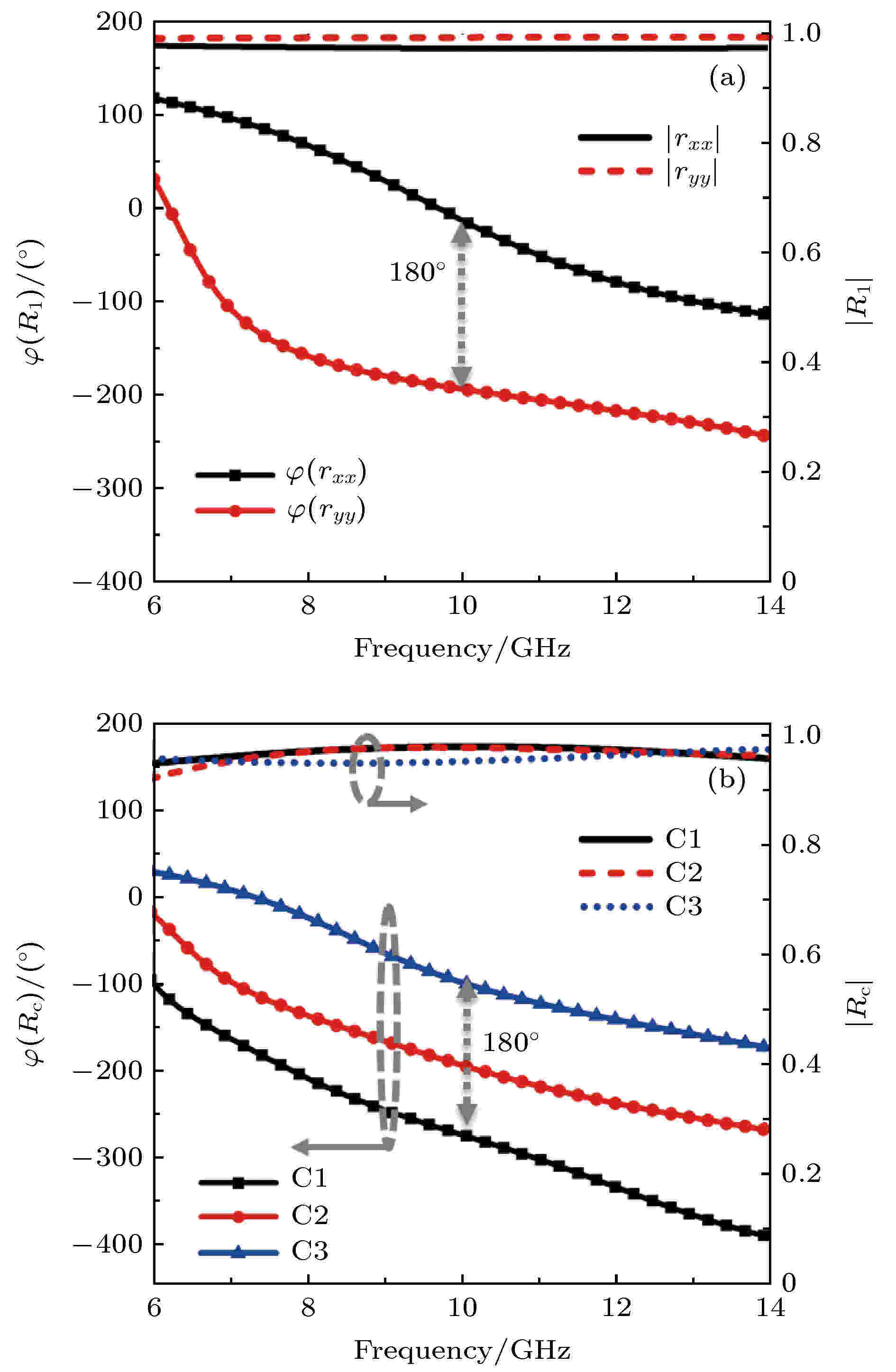图 3 复合超构表面单元反射系数随频率变化曲线 　(a) C1单元线极化反射系数; (b) C1, C2和C3单元的圆极化反射系数
Figure3. The curves of reflection coefficient versus frequency for the unit cells: (a) Linear polarization reflection coefficient of C1; (b) circular polarization reflection coefficients of C1, C2 and C3.

接下来, 需要进一步验证旋转时单元的相位变化. 如图4(a)所示, 当β从0°变化到180°时, 三种单元右旋和左旋反射系数的相位变化分别满足2β和–2β的变化, 幅度的变化相同且始终高于0.9. 为了实现对物理相位的连续控制, 对α进行参数扫描, 扫描范围从15°到87°, 间隔为1°, 扫描结果如图4(b)所示. 从图4(b)中可以看出, 随着α的变化, 单元传输相位平缓变化, 且在幅度高于0.9的前提下, 实现了传输相位的180°连续可调, 而另外180°的传输相位调制可以通过单元旋转90°来实现. 如图2(b)所示, 单元C1*由C1旋转90°得来. 根据PB原理, 与C1相比, C1*的右旋反射波相位为180°, 而左旋反射波的相位为–180°. 由于相位变化的周期为360°, 此时可以认为右旋和左旋反射波的相位变化均为180°, 这同时也符合传输相位变化的特点, 所以单元旋转90°可以作为一种特殊的尺寸变化. 在这种变化下, 左旋和右旋反射波的几何相位差值不发生改变, 绝对相位却存在180°的跃变. 在超构表面设计中, 确定α和β的具体方法如下:
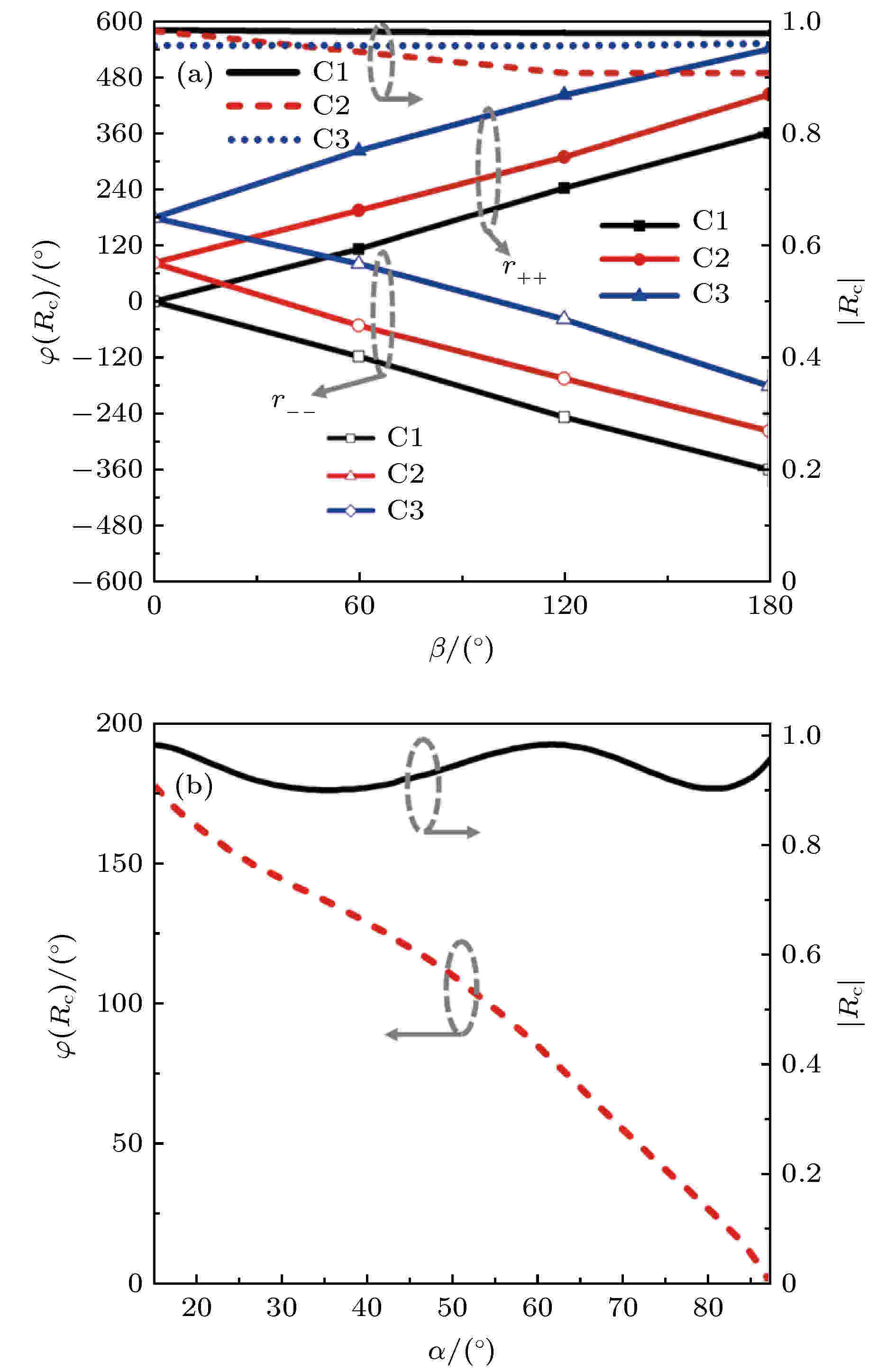图 4 复合超构表面单元反射系数随参数的变化曲线 (a) 10 GHz处, C1, C2和C3单元随旋转角β变化的幅度和相位曲线; (b) 10 GHz处, β = 0°时, 单元传输相位随α变化的幅度和相位曲线
Figure4. The curves of the reflection coefficient versus structural parameters for unit cells: (a) The curves of the amplitude and phase versus β for C1, C2, and C3 at 10 GHz; (b) the curves of the propagating phase and amplitude versus α at 10 GHz and β = 0°.

1) 依据左旋和右旋的目标相位计算得到传输相位(P)和几何相位(G)分布;
2) 利用相位周期(360°)且参考C1单元, 将传输相位划归到0°—360°区间;
3) 当0° ≤ P ≤ 180°时, α根据图4(b)所示的P与α关系直接确定, β则等于G/2;
4) 当180° ≤ P ≤ 360°时, 则令P = P –180°, 此时α依然根据图4(b)所示的P与α关系直接确定, β则等于G/2 – 90°.
2 -->

2.3.奇异偏折线性阵列仿真

单元设计完成后, 通过仿真奇异偏折线性阵列验证复合超构表面单元对左旋和右旋反射电磁波的独立控制.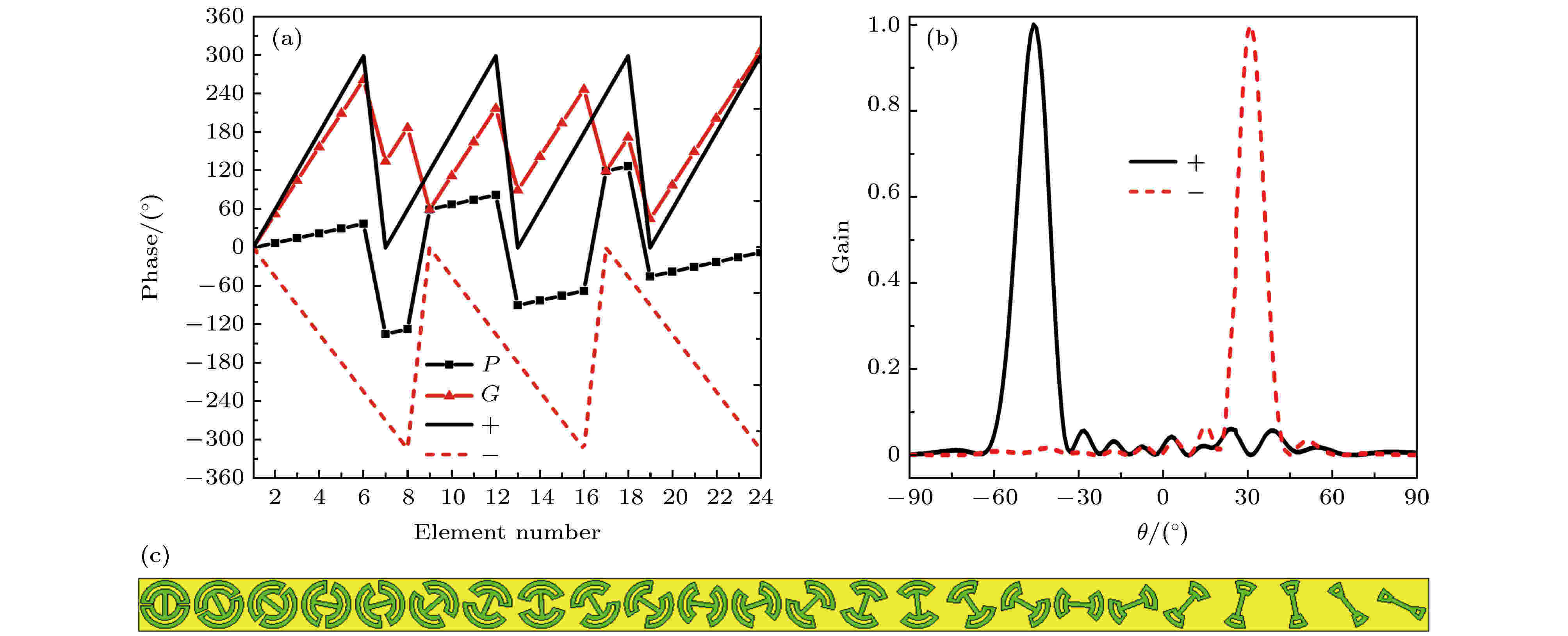

$ \left\{ \begin{aligned} & \Delta \varphi (+) = \varphi (+) - P({\rm{C1}}) = 60(n - 1), \\ & \Delta \varphi (-) \!=\! \varphi(-) \!-\! P({\rm{C1}}) = - 45(n - 1)\;{{,}} \\ & n \!=\! 1,2 \cdots, N. \end{aligned} \right. $

$\left\{\begin{aligned} & \Delta P = P - P({\rm{C1}}) \!=\! \frac{\Delta \varphi (+) + \Delta \varphi (-)}{2} \\ & \;\;\quad = 7.5(n - 1) ,\\ &{G = \frac{{\Delta \varphi \left( + \right) - \Delta \varphi \left( - \right)}}{2} = 52.5(n - 1){{ }}{{.}}} \end{aligned} \right.$

线性阵列的相位分布满足(9)式, 其中, n表示单元的序号, 右旋和左旋的相位梯度分别为60°和–45°, 依据公式可以计算出阵列的传输和几何相位分布, 如图5(a)所示. 然后依据2.2节中的参数确定方法得到24个单元的α和β取值, 进而建立如图5(c)所示的线性阵列. 为了观察线性阵列的偏折效果, 图5(b)给出了xoz面内的二维远场方向图. 从图5(b)中可以看出, 右旋和左旋反射波的偏折角度分别为–46°和32°, 这与广义反射定率的理论计算值(–45.6°和32.4°)吻合很好. 由此, 验证了本节设计的缝隙加载的环I形单元能够有效实现反射传输和几何相位的完全调制.
图 5 线性阵列的相位分布、仿真结果及模型　(a) 左旋、右旋、传输和几何相位的线性分布; (b)左旋和右旋反射波的归一化远场方向图; (c)阵列模型
Figure5. The phase distribution, simulated results and model of the linear array: (a) Linear distribution of left-handed, right-handed, propagating and geometric phase; (b) normalized far-field patterns of left-hand and right-hand reflected waves; (c) model of the linear array.

2

-->

3.1.异面偏折器设计

利用上述单元, 首先设计一款圆极化异面偏折器, 其中, 右旋反射波在xoz面内发生偏折, 左旋透射波在yoz面内发生偏折. 馈源天线采用Vivaldi天线, 馈源天线结构及驻波比(voltage standing wave ratio, VSWR, 电压最大和最小值的比)图6(a)所示. 其结构图和驻波比如图6(a)所示, 结构参数如下w₁ = 14 mm, w₂ = 1 mm, w₃ = 0.95 mm, l₁ = 41.2 mm, l₂ = 50 mm, g₁ = 0.5 mm, g₂ = 1.0 mm, r = 1.9 mm. Vivaldi天线介质板为厚度为0.73 mm的F4B, 采用微带扇形枝节耦合槽线的馈电方式. 从图6(a)中可以看出, Vivaldi天线在8—18 GHz频段范围内驻波比均小于2, 其在10 GHz处相位中心距离天线末端23 mm.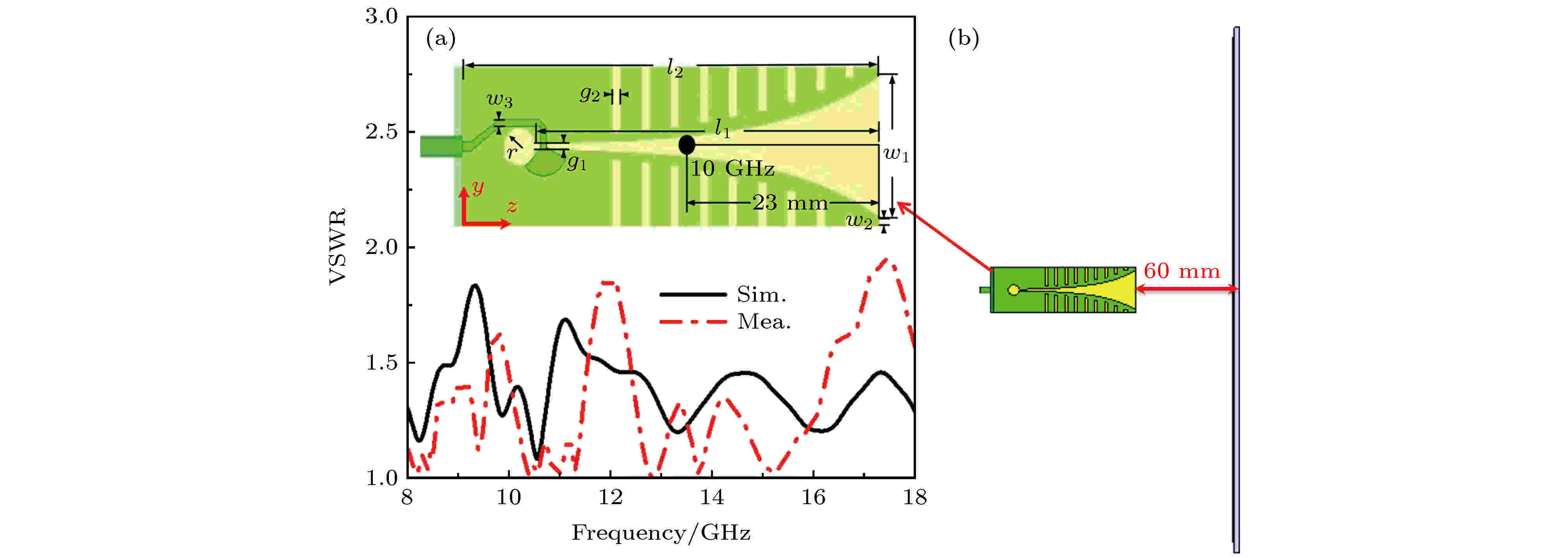
图 6 Vivaldi天线及其与超构表面之间的位置关系　(a) Vivaldi天线结构图和VSWR; (b) Vivaldi天线与超构表面位置关系
Figure6. Structure and location of the Vivaldi antenna: (a) Structure and VSWR of the Vivaldi antenna; (b) location of the Vivaldi antenna.

为了实现点源发出的球面波到一定角度偏折的平面波, 超构表面需要满足聚焦相位叠加线性偏折相位的条件. 考虑到右旋和左旋电磁波分别在不同的平面发生偏折, 它们的相位分别满足下面的公式:

$\begin{split} &\varDelta {\varPhi _ + }(m,n) = {\varPhi _ + }(m,n) - P({\rm{C1}}) \\ &= \frac{{2\pi }}{{{\lambda _0}}}\left(\sqrt {{{(mp)}^2} + {{(np)}^2} + {L^2}} - L\right) + \delta mp,\end{split}$

$\begin{split} &\varDelta {\varPhi _ - }(m,n) = {\varPhi _ - }(m,n) - P({\rm{C1}}) \\ &= \frac{{2\pi }}{{{\lambda _0}}}\left(\sqrt {{{(mp)}^2} + {{(np)}^2} + {L^2}} - L\right) - \delta np,\end{split}$

其中m和n分别为沿x和y轴的单元序号; p为单元周期; ${\varPhi _ + }(m, n)$和${\varPhi _ - }(m, n)$表示$(m, n)$处单元的右旋和左旋圆极化相位; $\varDelta {\varPhi _ + }(m, n)$和$\varDelta {\varPhi _ - }(m, n)$则表示它们相对于参考单元C1的相位; ${\lambda _0}$为设计频率对应的自由空间波长; L为聚焦相位分布的焦距. 由于左旋和右旋透射波的偏折角度均为30°, 依据广义反射定律计算得到相位梯度δ为42°. 中心频率为10 GHz, 焦距为L = 83 mm, 此时天线末端距离表面60 mm, 如图6(b)所示.
超构表面整体尺寸为133 mm × 133 mm, 单元个数19 × 19, 依据(11)式和(12)式计算得到右旋和左旋的目标相位分布如图7(a)和图7(b)所示, 并进一步得到如图7(c)和图7(d)所示的传输和几何相位分布. 依据参数确定方法, 得到超构表面每个单元的臂长和旋转角度, 进而建立如图8(a)所示的模型.
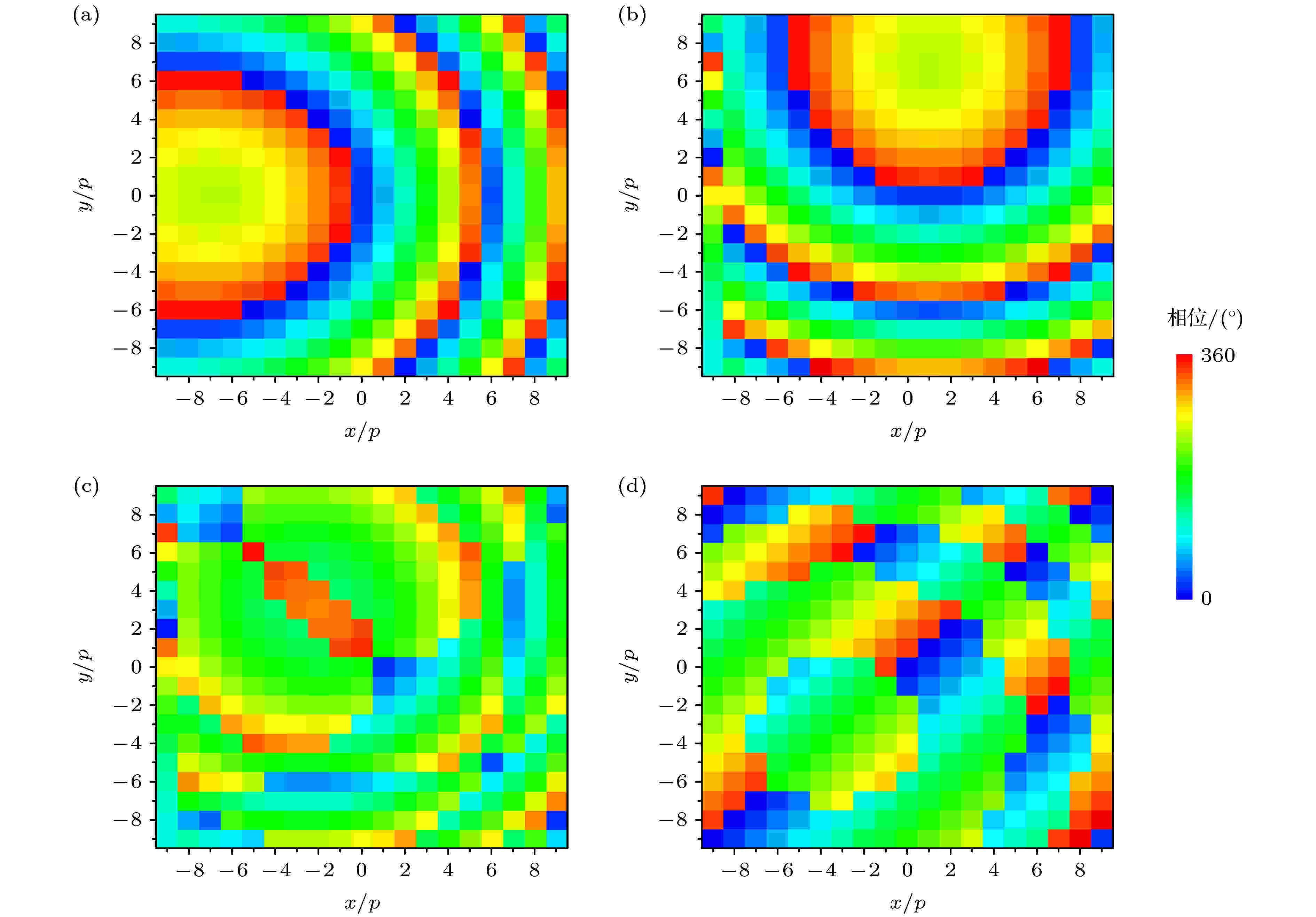图 7 圆极化异面偏折器的相位分布　(a)右旋相位分布; (b)左旋相位分布; (c)传输相位分布; (d)几何相位分布;
Figure7. Phase distributions of circularly polarized deflector with reflections in different planes: (a) Right-handed circular polarization; (b) left-handed circular polarization; (c) propagating phase; (d) geometric phase.

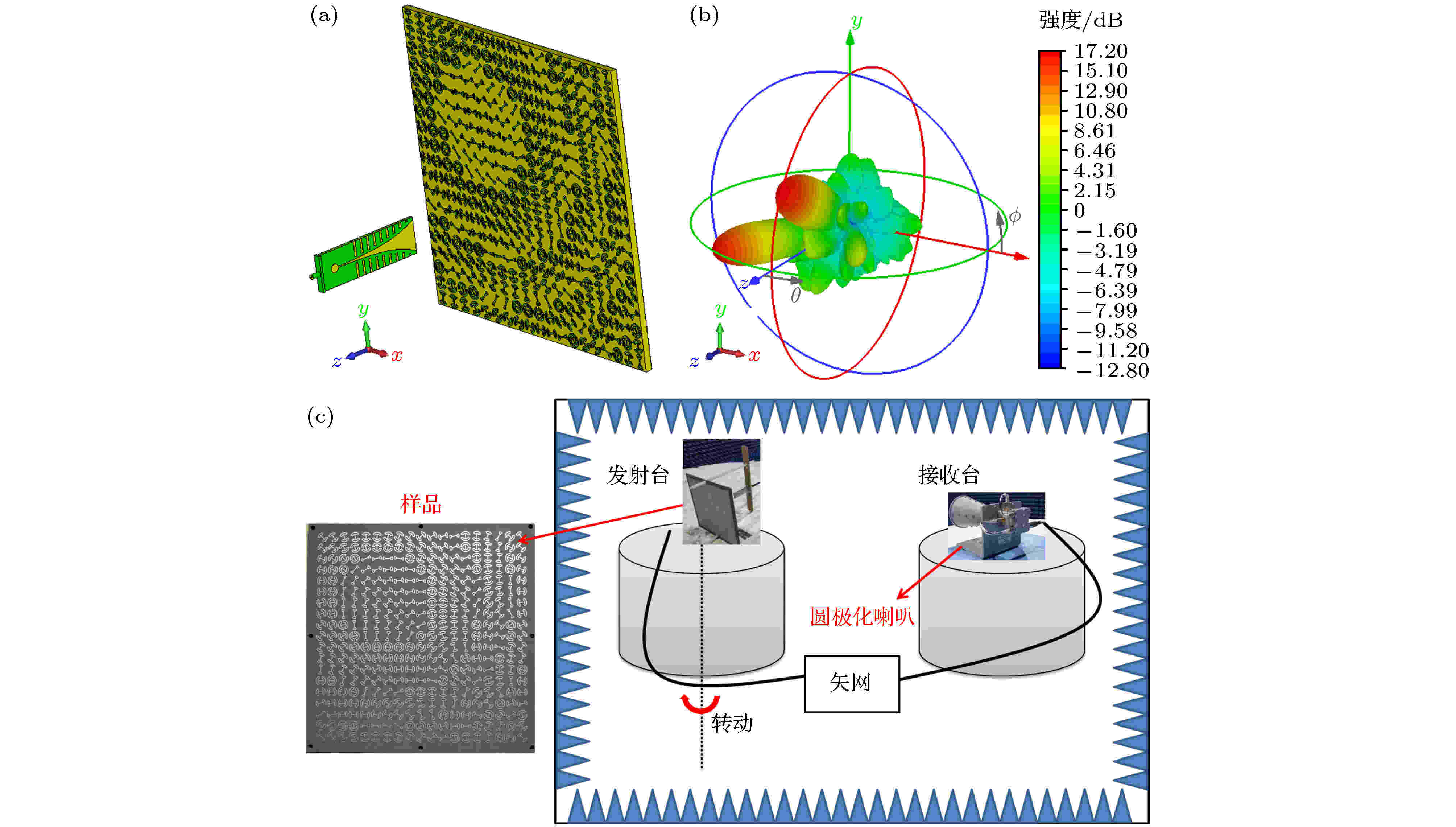图 8 圆极化异面偏折器仿真及测试　(a) 仿真模型; (b) 总能量在10 GHz处的三维仿真远场方向图; (c) 暗室测试示意图
Figure8. Model and total power farfield radiation pattern of the circularly polarized deflector with reflections in different planes: (a) Simulated model; (b) three-dimensional farfield radiation pattern of total power at 10 GHz.; (c) schematic of the measurement in the anechoic chamber.

为了观察超构表面反射波的异面偏折效果, 图8(b)给出了10 GHz处偏折器的总能量仿真方向图, 从图8(b)中可以明显的观察到两支分别在xoz面和yoz面发生偏折的主波束. 样品加工完成后, 利用介质柱和木板将Vivaldi天线固定在需要的位置处, 如图8(c)所示. 样品在微波暗室中完成测试, 测试中超构表面和馈源被置于发射转台上, 转台旋转360o, 围绕转台一周的远场电平就被另一平台上的圆极化喇叭天线接收并传递给矢量网络分析仪记录下来. 其中, 测试用的喇叭为双圆极化, 接入不同的接口可以实现左旋和右旋圆极化的切换, 从而便于在测试中区分反射波的旋向. 进一步, 在CST中增加左旋和右旋分量的远场监视器, 图9给出了左旋和右旋分量的三维远场方向图, 从图中可以看出, 右旋反射波偏向x轴负方向而左旋反射波偏向y轴正方向, 仿真的增益分别达到了17 dB和17.2 dB, 与理论预测一致.
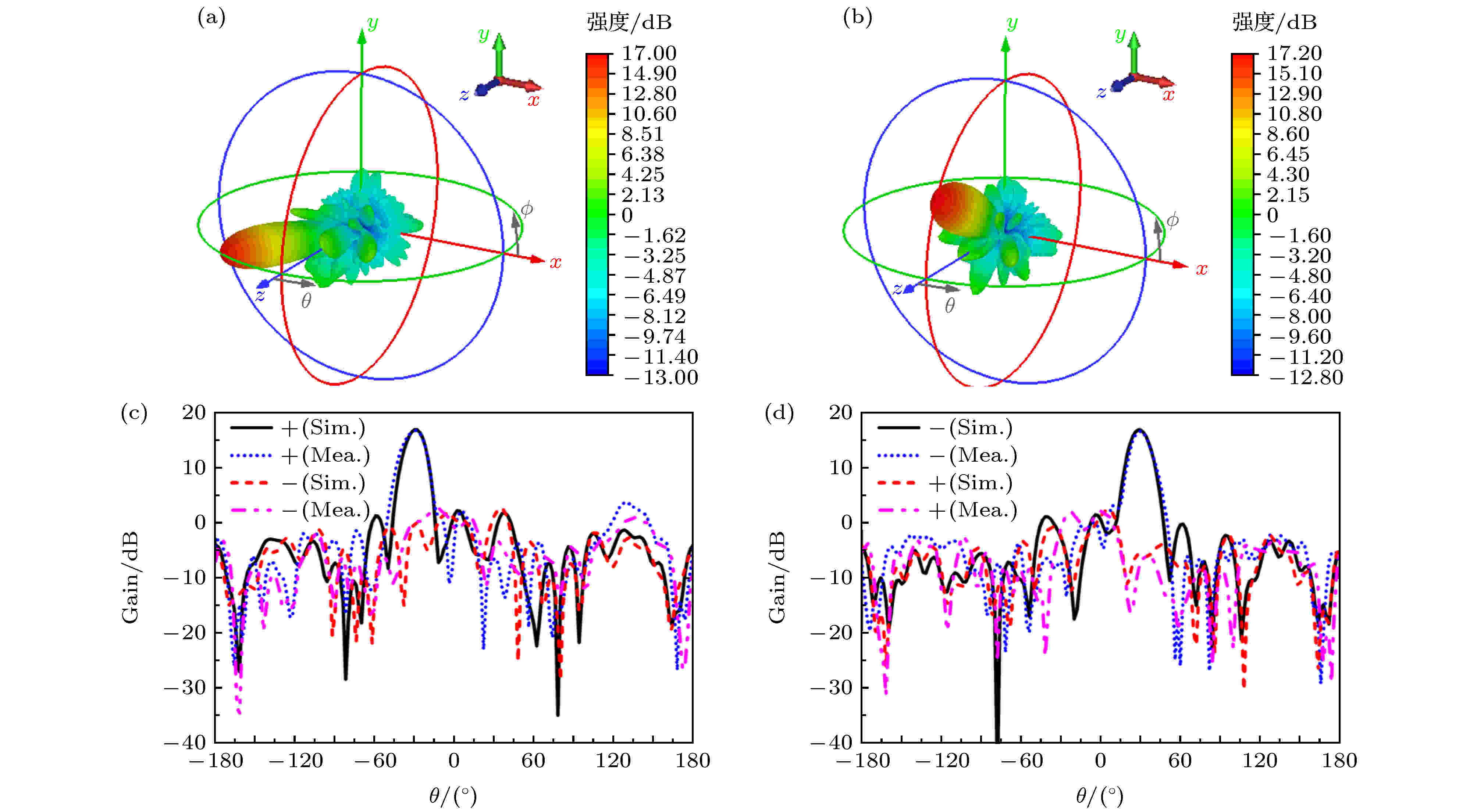图 9 异面偏折器右旋和左旋分量的远场方向图. 仿真三维方向图　(a) 右旋; (b) 左旋. 仿真和测试二维方向图 (c) xoz面; (d) yoz面
Figure9. Farfield radiation patterns of right-handed and left-handed components. Simulated three-dimensional patterns of (a) right-handed component and (b) left-handed component. Simulated and measured two-dimensional patterns on (c) xoz and (d) yoz plane.

为了明确左旋和右旋波束的具体偏折角度, 图9(c)和图9(d)分别给出了xoz面和yoz面内的仿真和测试的二维远场方向图. 从图9(c)和图9(d)中可以看出, 波束偏转角在xoz面和yoz面内分别为–30°和30°, 与理论计算保持一致. 另外, 仿真和测试结果的主波束吻合很好, 在10 GHz处, 二者的副瓣和交叉极化电平值均低于–15 dB. 进一步观察异面偏折器的工作带宽, 图10给出了8—14 GHz范围内其他整数频点处的三维远场方向图. 从图10中可以看出, 偏折器在9, 11, 12和13 GHz均呈现出很好的异面偏折效果, 8 GHz处略有恶化, 14 GHz处已经出现较大的旁瓣. 此外, 图11给出了仿真和测试的二维方向图随频率变化谱图, 从图11中可以看出偏折角度与广义反射定律的理论计算值吻合较好, 且谱图在整个9—13 GHz范围内比较纯净, 波束分离效果比较好.
图 10 异面偏折器在其他频点处的三维总能量仿真远场方向图　(a) 8 GHz; (b) 9 GHz; (c) 11 GHz; (d) 12 GHz; (e) 13 GHz; (f) 14 GHz
Figure10. Simulated three-dimensional farfield radiation patterns at other frequencies for the circularly polarized deflector with reflections in different planes: (a) 8 GHz; (b) 9 GHz; (c) 11 GHz; (d) 12 GHz; (e) 13 GHz; (f) 14 GHz.

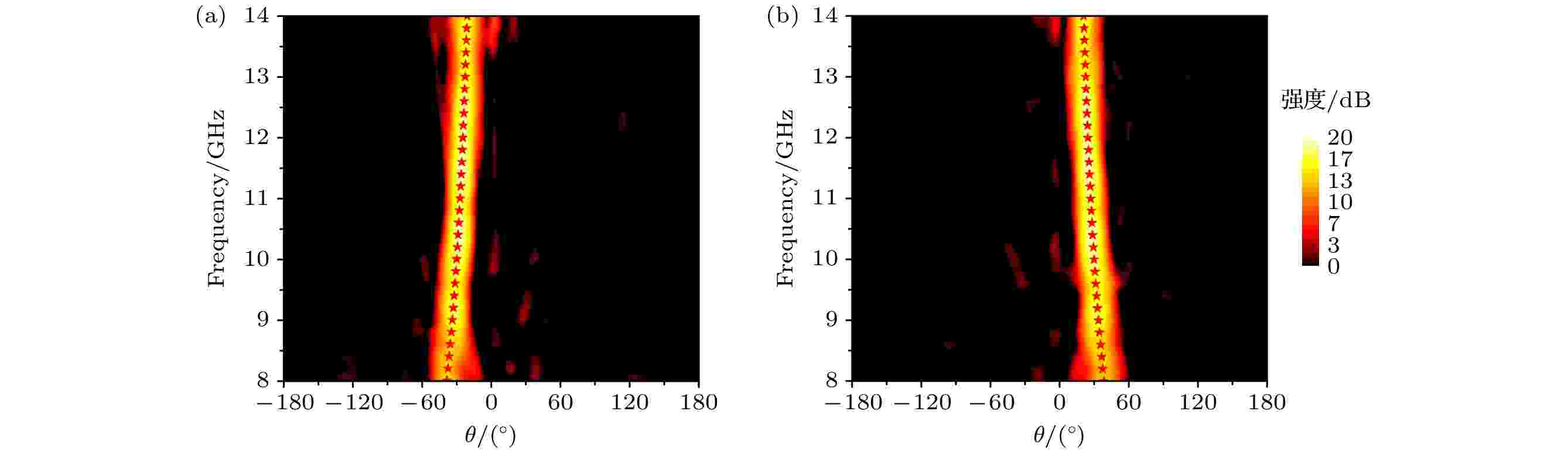图 11 异面偏折器的二维方向图随频率变化谱图(红色★为理论计算值)　(a) xoz面; (b) yoz面
Figure11. Maps of the two-dimensional far-field pattern versus frequency on different planes for the circularly polarized deflector with reflections on different planes: (a) xoz plane; (b) yoz plane (The symbols marked by red ★ are the theoretical values).

2 -->

3.2.定向和涡旋光束产生器设计

3.1节设计了反射型的异面偏折器, 本节将设计一款反射型的定向和涡旋波束产生器. 右旋定向波束设定为指向x轴–30°的定向波束, 此时右旋电磁波相位分布满足(13)式, 其中δ = 42°. 而左旋设定为1阶的涡旋波束. 相位分布满足(14)式(且拓扑荷数l为1. 由此计算出如图12(a)和图12(b)所示的目标相位分布.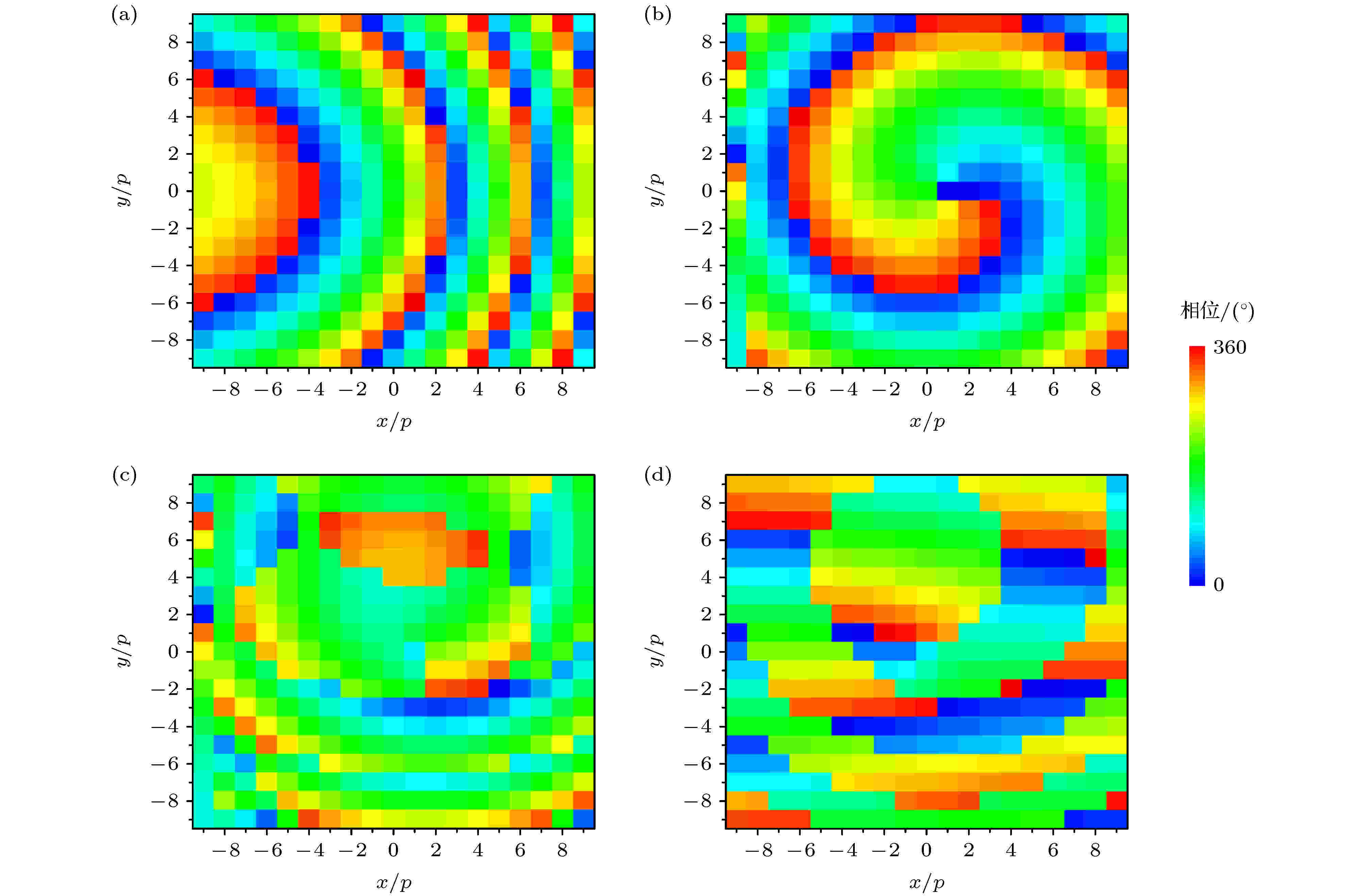
图 12 定向和涡旋光束产生器的相位分布　(a) 右旋相位分布; (b) 左旋相位分布; (c) 传输相位分布; (d) 几何相位分布
Figure12. Phase distributions of the circularly polarized generator with directional and vortex-shape beams: (a) Right-handed circular polarization; (b) left-handed circular polarization; (c) propagating phase; (d) geometric phase.

$\begin{split} &{{\Delta }}{\varPhi _ + }(m,n) = {\varPhi _ + }(m,n) - P({\rm{C1}}) \\ &= \frac{{2\pi }}{{{\lambda _0}}}\left(\sqrt {{{(mp)}^2} + {{(np)}^2} + {L^2}} - L\right) + \delta mp,\end{split}$

${{\Delta }}{\varPhi _ - }(m,n) = \left\{ \begin{aligned} & \frac{{2{\rm{\pi }}}}{{{\lambda _0}}}\left(\sqrt {{{(mp)}^2} + {{(np)}^2} + {L^2}} - L\right) \\ &+ l{{\tan }^{ - 1}}\left( {\frac{n}{m}} \right) + 2\pi,\;\;\;m \geqslant 0{{,}} \\ & \frac{{2\pi }}{{{\lambda _0}}}\left(\sqrt {{{(mp)}^2} + {{(np)}^2} + {L^2}} - L\right) \\ &+ l{{\tan }^{ - 1}}\left( {\frac{n}{m}} \right) + \pi,\;\;\;m < 0\;{{.}} \end{aligned} \right.$

根据上述目标相位分布, 计算得到如图12(c)和图12(d)所示的传输和几何相位分布, 然后依据参数确立原则得到超构表面上每个单元α和β的取值, 从而建立如图13(a)所示的仿真模型. 为了观察波束产生器的性能, 图13(b)首先给出了10 GHz处总能量的三维远场方向图. 从图13(b)中可以看出, 方向图两个主波束分别为指向–30°(x轴)的笔形波束和处于法向的中空状锥形波束. 其中第一种波束为右旋反射波形成的定向光束而第二种为左旋反射波形成的涡旋光束, 如图13(c)和图13(d)所示, 定向和涡旋光束的仿真增益分别达到了16.9 dB和13.7 dB. 此时, 左旋和右旋能量分散到不同的方向, 可以单独观察左旋反射波的线极化分量验证涡旋光束的模式. 在超构表面上方90 mm处设置监视器平面, 平面上x极化电场分量的近场分布如图14(a)所示. 从图14(a)中可以观察到一对比较明显的涡旋臂, 与模式数l = 1相对应. 进一步考察波束产生器的带宽特性, 图14(b)给出了部分典型频点处总能量的三维方向图, 图中显示超构表面在9—13 GHz范围内能够同时产生较好的定向波束和涡旋波束. 最后, 图14(c)和图14(d)给出了波束产生器在10 GHz处的仿真和测试二维方向图, 从图中可以看出, 右旋反射波在xoz面内发生–30°的偏折, 左旋反射波在xoz和yoz面内的两支波束分别出现在–10°和10°, 与理论预测相符. 同时, 仿真和测试的主波束以及峰值增益均吻合较好, 其测试方法与异面偏折器相同.
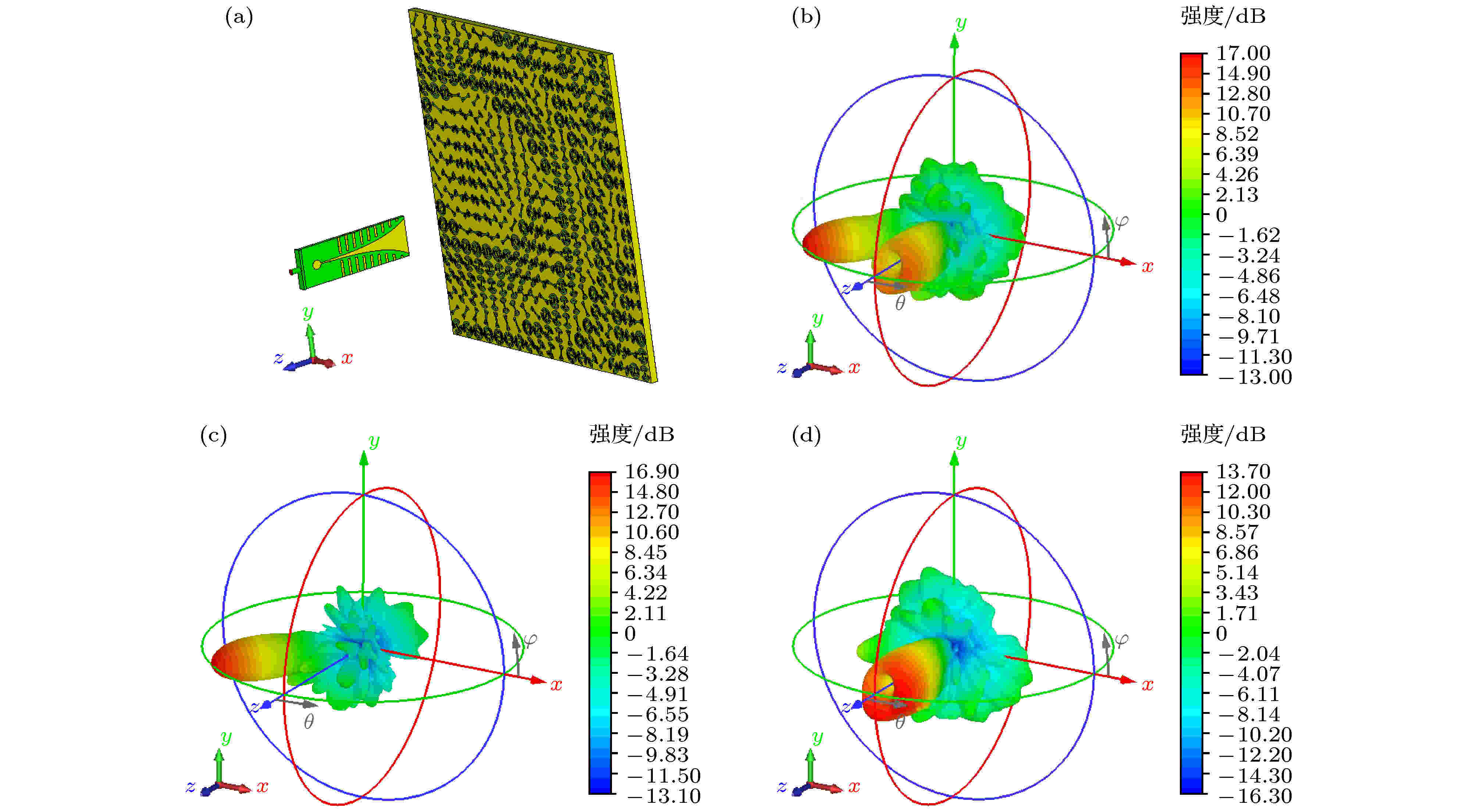图 13 定向和涡旋光束产生器的模型和三维仿真方向图　(a) 模型; 10 GHz处的总能量(b), 右旋分量(c); 左旋分量(d)的三维远场方向图
Figure13. Model and radiation patterns of the circularly polarized generator with directional and vortex-shape beams: (a) Simulation model; three-dimensional patterns of the total power (b), right-handed component (c), and (d) left-handed component at 10 GHz.

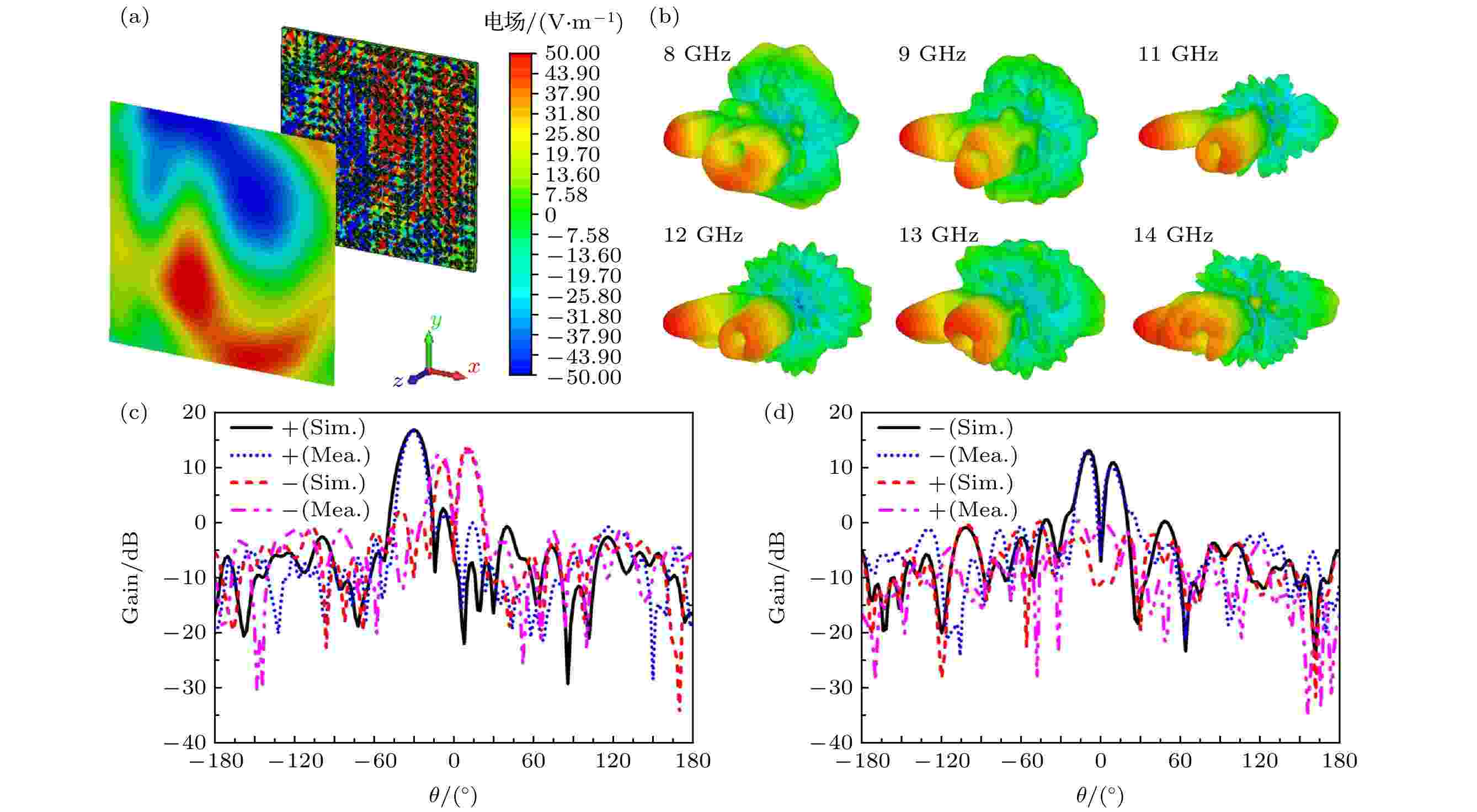图 14 (a) x极化电场分量在10 GHz处的涡旋近场分布; (b) 其他频点处的三维总能量仿真远场方向图; (c) xoz面和(d) yoz面的仿真和测试二维远场方向图
Figure14. (a) The x-component electric field distribution at 10 GHz; (b) three-dimensional farfield radiation patterns at other frequencies. Simulated and measured two-dimensional radiation patterns on xoz-plane (c) and yoz-plane (d) at 10 GHz.

尺寸渐变超构表面对左旋和右旋圆极化电磁波具有相同的调制作用, 而几何相位超构表面对左旋和右旋圆极化电磁波具有相反的调制作用. 利用传输和几何相位复合的超构表面可以完全解锁不同旋向圆极化波的相位关系, 进而实现任意双功能的圆极化器件. 本文提出了一种新型缝隙加载的环I形单元, 可以通过调整单一参数完成传输相位的高效调制, 进而在较宽的频带范围内实现反射传输相位和几何相位的高效操控, 最终设计出异面偏折器以及定向和涡旋波束产生器两种宽带的圆极化双功能器件.