摘要:锆合金(如: 锆铌(Zr-Nb)合金)的辐照损伤问题是裂变堆结构材料和燃料棒包壳材料设计的关键, 而深入理解辐照损伤的物理机制, 往往需借助于原子尺度的计算模拟, 如: 分子动力学和第一性原理等. 针对随机置换固溶体合金的模拟, 首先需构建能反映合金元素随机分布特征的大尺寸超胞, 然而第一性原理计算量大, 不宜使用过大(如 ≥ 200原子)超胞. 通常第一性原理计算使用的是特殊准随机(SQS)超胞, SQS超胞可部分反映合金元素的随机分布特性, 但对于特定组分只对应一种构型, 这种模型是否能反映真实随机置换固溶体中多种局域构型的统计平均还有待进一步研究验证. 分子动力学可在更大的尺度上进行计算模拟, 能够通过随机取代(RSS)模型研究更多的合金构型, 因此, 本文基于RSS超胞模型及SQS扩展超胞模型, 运用分子动力学方法对Zr-Nb合金进行了研究. 首先通过构型误差分析确定了能真实反映固溶体合金性能统计性的RSS超胞的临界尺寸; 然后计算比较了Zr-Nb合金SQS扩展超胞和一系列RSS超胞的晶格常数、形成能和能量-体积关系. 研究表明, 利用SQS超胞模拟得到的固溶体的晶格常数、形成能和能量体积曲线与一系列RSS超胞的对应统计值接近, 因而SQS超胞可用于研究随机置换固溶体合金.
关键词: 锆铌合金/
分子动力学/
SQS模型/
临界超胞

English Abstract

全文HTML

--> --> -->

锆(Zr)合金因其热中子吸收截面低, 较好的力学性能、加工性能和抗腐蚀性能, 常被用作核反应堆的结构材料和燃料包壳材料^[1]. 在常温常压下, Zr的稳定结构是密排六方(hcp)结构(α-Zr); 温度升到1135 K, α-Zr转变为β-Zr (体心立方, bcc); β-Zr熔点为2128 K^[2]. 当在Zr中加入少量合金元素Nb时, 能够显著提高合金材料的耐腐蚀性能, 同时减弱Zr的氢化作用^[3], 因而一系列含Nb元素的Zr合金被开发出来, 如: 用于压水堆燃料包壳的M5 (Zr-1%Nb-O)合金^[4]和ZIRLO (Zr-1%Nb-1%Sn-0.1%Fe)合金^[5], 用于水冷堆VVER和RMBK核心的E110 (Zr-1%Nb)合金和E635 (Zr-1.3%Sn-1%Nb-0.4%Fe)合金^[6]. 为了获得Zr-Nb合金的基本性质, 可以利用分子模拟技术中的第一性原理(first principles, FP)^[7]和分子动力学(molecular dynamics, MD)^[8]对其展开研究. FP基于密度泛函理论, 可获得材料的热力学参数及动力学过程的能垒等信息; 而MD相对于FP来说计算量要小得多, 因而能够采用更大的计算体系, 模拟材料内部微观结构的产生和演化过程.
实际合金中合金元素浓度在局部区域存在起伏从而引起合金局部性质的涨落, 然而对于合金块体, 由于存在大量的随机局域构型, 因而从整体上来看, 合金的物理性能是大量局域构型物理性能的统计平均. 因此针对随机置换固溶体合金的计算模拟思路可包括, 研究大量的随机构型的小尺寸超胞, 然后进行统计平均, 或者构建尺寸较大的超胞进行研究. 分子动力学模拟用超胞中原子数目可以达到上百万个, 因而可以通过用溶质原子随机取代溶剂原子的方式来模拟真实随机置换固溶体中的原子分布, 按这种方式得到的结构叫做随机取代结构(random substitution structure, RSS); 而FP计算量大, 使用的体系大小有限, 因此Wei等^[9]提出了SQS (special quasirandom structure)模型. 在SQS模型中, 通过调整一定成分的小超胞中各原子的排列方式, 以使得一定距离范围内(比如前四近邻)的对关联函数与实际晶体尽可能接近, 从而实现小超胞模拟随机固溶体合金体系. 前期FP计算^[10,11]表明小尺寸SQS超胞能够获得部分与实验结果接近的物理性能, 因此Hu等^[12]将SQS模型用于高熵合金的研究. 但含有特定成分的SQS超胞往往仅对应一种构型, 其模拟结果与分子动力学通过随机取代结构模型得到的多构型统计平均值的相似性还有待进一步深入研究. 因此, 本文针对Zr-Nb合金, 运用分子动力学方法对小尺寸SQS超胞模拟随机置换固溶体合金的可行性进行了研究. 首先, 确定了能真实反映固溶体合金物理性能统计性的RSS模型超胞的临界尺寸; 然后比较了两种模型获得的Zr-Nb合金的晶格常数、形成能和能量-体积关系. 研究表明, 利用SQS超胞得到的合金的物理性能与利用一系列RSS超胞得到的对应统计值接近, 因而SQS超胞可用于研究随机置换固溶体合金.
本文的第2部分给出了分子动力学模拟所使用的势函数和具体的模拟细节. 第3部分是结果与讨论, 包括RSS模型超胞临界尺寸的确定、Zr-Nb合金晶格常数、形成能和能量-体积关系的研究, 以及SQS模型与RSS模型结果差异的分析讨论. 最后是全文的结论.

2

-->

2.1.Zr-Nb势函数

势函数是MD计算的关键. 金属中常用嵌入原子法(EAM)^[13]来描述原子间的相互作用. 在EAM势函数中, N个原子构成的系统总能量(E_total)可以表示为

$ {E}_{\rm{total}}=\sum \limits_{i}^{N}F\left({\rho }_{i}\right)+\sum \limits_{i=1}^{N-1}\sum \limits_{j=i+1}^{N}V\left({r}_{ij}\right), $

$ {\rho }_{i}=\sum \limits_{j\ne i}\varphi \left({r}_{ij}\right),$

其中r_ij是原子i和原子j的距离, $ {\rho }_{i} $是体系中原子i以外的原子在原子i处产生的电子密度, $ F\left({\rho }_{i}\right) $是原子i的嵌入能, $ \varphi \left({r}_{ij}\right) $是原子i的电子密度; V(r_ij)原子i和原子j的对势.
针对Zr-Zr和Nb-Nb的势函数, 采用Wadley的EAM势^[14,15], 对势V(r_ij)和电子密度$ \varphi \left({r}_{ij}\right) $为

$ \begin{split} V\left({r}_{ij}\right)=\;&\frac{A{\rm{exp}}\left[-\alpha \left(\dfrac{{r}_{ij}}{{r}_{\rm{e}}}-1\right)\right]}{1+{\left(\dfrac{{r}_{ij}}{{r}_{\rm{e}}}-\kappa \right)}^{m}}\\ &-\frac{B{\rm{exp}}\left[-\beta \left(\dfrac{{r}_{ij}}{{r}_{\rm{e}}}-1\right)\right]}{1+{\left(\dfrac{{r}_{ij}}{{r}_{\rm{e}}}-\lambda \right)}^{n}}, \end{split}$

$\varphi \left({r}_{ij}\right)=\frac{{E}_{{\rm{c}}\exp}\left[-\beta \left(\dfrac{{r}_{ij}}{{r}_{\rm{e}}}-1\right)\right]}{{V}^{1/3}\left[1+{\left(\dfrac{{r}_{ij}}{{r}_{\rm{e}}}-\lambda \right)}^{n}\right]},$

其中A, B, $ \alpha , \;\beta $, m, n, $ \kappa , \;\lambda $, r_e是势参数; E_c是结合能; V是原子体积.
嵌入能为

$F\left(\rho \right)=\left\{\begin{aligned}&\sum \limits_{i=0}^{3}\begin{array}{l}{{F}_{{n}_{i}}\left(\dfrac{\rho }{{\rho }_{\rm{n}}}-1\right)}^{i},\;\;\;\;\;\;\;\;\;\;\;\rho <{\rho }_{\rm{n}}=0.85{\rho }_{\rm{e}}, \;\;\;\;\;\;\;\;\; \qquad\qquad \qquad (5)\\ \end{array}\\ &\sum\limits _{i=0}^{3}\begin{array}{c}{{F}_{i}\left(\dfrac{\rho }{{\rho }_{\rm{e}}}-1\right)}^{i},\;\;\;\;\;\;\;\;\;\;{\rho }_{\rm{n}}\leqslant \rho <{\rho }_{0}=1.15{\rho }_{\rm{e}}, \;\;\;\;\qquad \qquad \qquad \left(6\right)\\ \end{array}\\ &{F}_{\rm{e}}\left[1-{{\rm{ln}}\left(\frac{\rho }{{\rho }_{\rm{e}}}\right)}^{\eta }\right]{\left(\frac{\rho }{{\rho }_{\rm{e}}}\right)}^{\eta },\;\;\;\;\;\;\;\;\rho \geqslant {\rho }_{0},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\qquad \qquad\qquad \left(7\right)\end{aligned}\right.$

其中$ {\rho }_{\rm{e}} $是平衡电子密度; $ {F}_{{n}_{i}} $, F_i, F_e和$ \eta $是嵌入函数的参数.
关于Zr-Nb对势$ {V}_{\rm{ZrNb}} $, Johnson^[16]提出了一种根据各元素的EAM势构建合金中异种原子相互作用势的方法, 我们采用该方法构造了Zr-Nb对势, 但在模拟时发现超胞中出现了空洞等非物理现象, 这表明Johnson的方法不适用于Zr-Nb合金. 因此, 本文采用文献[17]给出的Zr-Nb势函数. 该势函数采用三次多项式的形式, 并利用第一性原理计算获得的Zr-Nb固溶体的基本性质来拟合得到势参数, 其具体表达式如下:

${V}_{\rm{ZrNb}}\left(r\right)=\sum\limits _{k=1}^{10}{{A}_{k}({x}_{k}-r)}^{3}H({x}_{k}-r), $

其中H(x)是Heaviside阶跃函数; A_k和x_k是势参数. 以上各公式的势参数采用文献[17]的拟合结果.
2 -->

2.2.模拟细节

本文分别针对hcp结构超胞和bcc结构超胞进行了模拟. bcc结构超胞的x, y和z轴分别为[100], [010]和[001]晶向; hcp结构超胞的x, y和z轴分别为$[ {\bar 1} 2 {\bar 1} 0]$, $ [10{\bar 1} 0]$和[0001]; 晶胞参数c/a取Zr的实验值1.5929^[18]. 超胞3个轴均采用周期性边界条件. 采用的软件为GPU并行加速分子动力学程序包(MDPSCU)^[19]. 势函数截断距离取2.2a, 时间步长选用0.5 fs, 模拟过程为, 在初始2.5 ps内将超胞热化到400 K, 热化时采用不同的随机数依据Maxwell分布随机抽样获得各原子速度, 然后采用最陡下降法淬火到0 K.
以bcc结构为例说明确定RSS超胞临界尺寸的方法: 首先构建了6 × 6 × 6, 8 × 8 × 8, 10 × 10 × 10和20 × 20 × 20四种尺寸的超胞, 分别含有432, 1024, 2000和16000个原子; 为了研究的系统性, 对每一种尺寸下的每一种浓度(10%—90%, 以10%为间隔, 共9种浓度), 分别构造50组不同的RSS超胞进行模拟, 不同浓度合金的初始晶格常数通过Vegard定律估算获得. 该定律指出, 当组成相的键合性质相似时, 连续置换固溶体的晶体学参数在恒温条件下随浓度线性变化^[20].
对于hcp结构超胞的临界尺寸研究, 除了所用的超胞尺寸(分别为5 × 5 × 5, 10 × 5 × 5, 10 × 10 × 10和20 × 20 × 20)与bcc结构略有不同外, 其构型误差的研究过程与bcc结构相同, 此处不再赘述.
本文所用的SQS超胞是将初始SQS超胞沿3个晶格矢量方向扩展后得到的. SQS超胞中原子的排列方式受到晶体结构、合金元素成分以及超胞尺寸的影响. 对于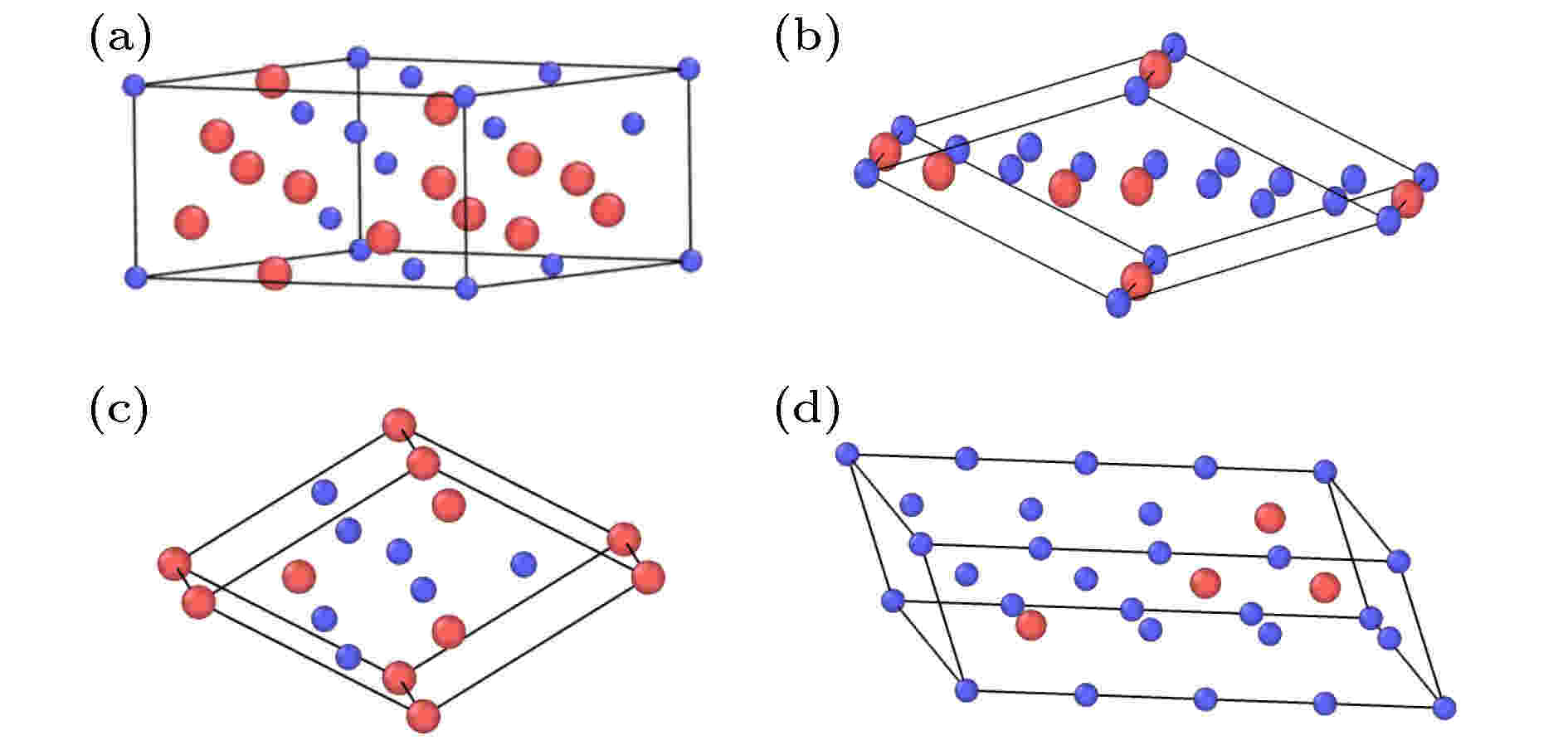$ {A}_{x}{B}_{1-x} $型随机置换固溶体的初始SQS超胞, bcc结构超胞采用Jiang等^[10]开发的SQS-16模型, hcp结构超胞采用Shin等^[11]的SQS-16模型(x = 0.25或0.75)和SQS-8模型(x = 0.5), 四种超胞结构如图1所示, 原子显示使用了OVITO软件^[21].
图 1 $ {A}_{x}{B}_{1-x} $随机置换固溶体SQS模型超胞　(a) x = 0.5, SQS-16, bcc晶格; (b) x = 0.25或x = 0.75, SQS-16, bcc晶格; (c) x = 0.5, SQS-8, hcp晶格; (d) x = 0.25或x = 0.75, SQS-16, hcp晶格
Figure1. Supercells of the $ {A}_{x}{B}_{1-x} $ random solid solution: (a) x = 0.5, SQS-16, bcc lattice; (b) x = 0.25 or x = 0.75, SQS-16, bcc lattice; (c) x = 0.5, SQS-8, hcp lattice; (d) x = 0.25 or x = 0.75, SQS-16, hcp lattice.

2

-->

3.1.RSS超胞临界尺寸

如前文所述, 在随机置换固溶体合金中, 每一个原子附近其他原子的排布方式(配位情况)是随机的, 真实合金中包含有大量的这种排布方式, 因而固溶体合金性质是大量的这种微观排布的统计平均. 如果要反映固溶体物理性能的这种统计性, 模拟用的超胞就需要足够大的尺寸, 但为了保证计算的效率与速度, 又不宜采用太大的超胞. 因此, 必须确定能兼顾这两个因素的RSS超胞的临界尺寸.
在确定RSS超胞临界尺寸时, 本文的判断依据是不同构型合金形成能相对误差, 即构型误差. 模拟时出现构型误差是因为RSS模型在随机取代溶剂原子时, 会得到不同的原子构型(原子的不同配位和这些局域构型不同排列方式), 在小尺寸超胞模拟中, 固溶体性质可能存在较大的涨落. 本文中构型误差定义如下:

$\eta =\frac{{\Delta E}^{{A}_{x}{B}_{1-x}}}{{H}_{\rm{f}}\left({A}_{x}{B}_{1-x}\right)}\times 100\%,$

式中, $ {\Delta E}^{{A}_{x}{B}_{1-x}}$表示由构型引起的随机固溶体的能量标准差; $ {H}_{\rm{f}}\left({A}_{x}{B}_{1-x}\right) $为平均合金形成能, 其计算公式为

${H}_{\rm{f}}\left({A}_{x}{B}_{1-x}\right)={E}_{0}^{{A}_{x}{B}_{1-x}}-x{E}_{0}^{A}-\left(1-x\right){E}_{0}^{B},$

其中$ {E}_{0}^{A} $, $ {E}_{0}^{B} $, $ {E}_{0}^{{A}_{x}{B}_{1-x}} $ 分别为纯元素A, B和它们按特定组分形成的固溶体 $ {A}_{x}{B}_{1-x} $的基态能量. 计算形成能时, 以Vegard定律预测的晶格常数值作为输入参数, 得到固溶体基态能量.
不同尺寸超胞中的形成能误差如图2所示, 这里应该指出的是, 图中的构型误差是9种浓度下分别计算的构型误差的算术平均值($ {\bar \eta } $). 从图2可以看出, 当bcc超胞内包含432个原子时, 随机取代原子的位置不同, 对形成能有很大影响, 误差在8%左右; 当原子个数增加到2000个和16000个时, 构型误差分别约为0.8%和0.3%, 均在1%以下, 表明当原子个数超过2000时, bcc超胞中RSS模型可以很好地体现置换固溶体物理性能的统计性. 对于hcp超胞, 将尺寸从500个原子增大到32000个原子后, 构型误差也从2.4%降到了0.4%. 因此, 在后文MD模拟中, 对于SQS超胞和RSS超胞, bcc晶格的原子数设置为16000, hcp晶格的原子数设置为32000.
图 2 不同超胞尺寸的bcc和hcp结构Zr-Nb合金的构型误差(形成能的相对误差)
Figure2. Configuration Errors of Zr-Nb alloy with bcc and hcp structure in different supercell sizes (relative errors of formation energy).

2 -->

3.2.SQS超胞的分子动力学模拟

类似于RSS模型的超胞, 我们将SQS模型小尺寸超胞扩展成大于临界尺寸的超胞, 然后对这些超胞进行了分子动力学模拟, 得到了固溶体合金的晶格常数、形成能以及能量-体积曲线, 并与50种不同构型的RSS超胞的统计平均值进行比较分析.
3 -->

3.2.1.晶格常数

晶格常数是晶体物质的基本结构参数, 晶格常数的变化通常反映了晶体内部的成分、受力状态等的变化. 平衡晶格常数对应于体系能量最小时的晶格常数, 本节通过调整晶格常数找到合金的最低能量, 从而确定对应浓度合金的平衡晶格常数. bcc结构的Zr-60%Nb合金的体系能量与晶格常数变化如图3所示, 可以看到晶格产生在3.41 ?时, 能量最低, 因而确定该合金的晶格常数为3.41 ?. 采用该方法确定了SQS超胞和RSS超胞在各个浓度下的平衡晶格常数, 结果如图4所示, 图中还比较了Smirnova和Starikov^[2]采用ADP (angular-dependent potential)势计算得到的合金晶格常数.
图 3 bcc结构Zr-60%Nb合金能量与晶格常数的关系
Figure3. Relationship between solid solution energy and lattice constant of Zr-60%Nb alloy in bcc lattice.

图 4 由SQS和RSS模型得到的合金晶格常数与Nb浓度的关系　(a) bcc晶格; (b) hcp晶格; (a)中实验值取自文献[22, 23], ADP势函数计算的晶格常数取自Smirnova和Starikov^[2]
Figure4. Relationships between the alloy lattice constant and Nb concentration obtained from SQS and RSS models: (a) The bcc lattice; (b) the hcp lattice. In Fig. 4(a), the experimental values were obtained from literatures^[22,23], and the lattice constant calculated from the ADP potential function was taken from Smirnova and Starikov^[2].

图4(a)展示的是bcc结构Zr-Nb合金的晶格常数, 可以看到, SQS超胞和RSS超胞得到的平衡晶格常数接近, 差异较小; 而且从图4(a)还可以看到, 随着Nb原子浓度的增加, 合金平衡晶格常数线性减小, 与实验值^[22,23]和Vegard定律预测值接近, 但Smirnova和Starikov^[2]拟合的ADP势函数计算获得的晶格常数偏大. 图4(b)展示的是hcp结构Zr-Nb合金的晶格常数, 同样可以看到, SQS超胞和RSS超胞得到的平衡晶格常数接近, 但相对于bcc结构, hcp结构中两种模型的差异偏大. 应该指出的是, 在计算过程发现当Nb原子浓度超过40%时, 合金能量与晶格常数不是单调递增或递减关系, 而是出现了能量起伏, 因而不能使用上述方法来确定平衡晶胞参数. 另外, 由于核材料领域中hcp晶格Zr-Nb合金的Nb原子比例通常都低于10%^[22,24], 因而图4(b)仅展示了Nb原子比例0—50%的结果.
3 -->

3.2.2.随机固溶体形成能

形成能是表征合金原子合金化($ {H}_{\rm{f}} < 0$)或偏析($ {H}_{\rm{f}} > 0$)的重要参数. 图5(a)和图5(b)分别给出了0 K时bcc晶格和hcp晶格随机置换固溶体的总形成能. 此处总形成能的计算公式与方程(10)类似, 方程右边纯A和纯B的能量取最稳定结构的能量^[25].
图 5 SQS模型与RSS模型计算的Zr-Nb合金的总形成能　(a) bcc晶格; (b) hcp晶格
Figure5. Total formation energies of Zr-Nb alloy calculated from the RSS and SQS structures: (a) The bcc lattice; (b) the hcp lattice.

从图5(a)可以看到bcc结构的Zr-Nb随机置换固溶体的形成能都是正值, 表明易产生偏析现象, 这与Zr-Nb相图^[26]中在10%—90%Nb原子浓度范围内, 温度低于400 ℃时, 合金均为α-Zr与β-Nb两相共存的现象相一致. 我们还发现, 随着Nb原子浓度的增加, 固溶体形成能先增大后减小, 说明在富Zr和富Nb的固溶体中, 合金偏析能力有所下降. 另外可以看到SQS模型与RSS模型的总形成能在25%, 50%, 75% 三个浓度处接近, 且两者样条插值曲线也基本重合, 表明两者对bcc晶格Zr-Nb固溶体的形成能描述是基本一致的. 但是两个模型给出的形成能仍存在细微差异, 比如在25%和75%浓度处, SQS超胞和RSS超胞的形成能差值在0.3 kJ/mol左右, 大于RSS模型的统计误差(图5(a)中已标出了RSS模型的误差棒, ～10^–2 kJ/mol).
与晶格常数部分类似, 图5(b)仅显示了Nb原子浓度在0—50%范围内hcp结构Zr-Nb合金的总形成能, 可以看到SQS模型与RSS模型的总形成能基本接近, 随着Nb浓度的升高, 形成能也随之增大, 且均为正值, 这与bcc晶格趋势类似. 同样两种模型仍存在差异, 对于25%Nb, 形成能差异约为1 kJ/mol (大于RSS模型统计误差 ～0.01 kJ/mol); 对于50%Nb, 形成能差异约为2 kJ/mol (大于RSS超胞误差0.3 kJ/mol). 对比图5(a)可知, hcp结构的两种模型的形成能差异要大于bcc晶格的形成能差异, 其原因可能是, 本文使用的hcp晶格SQS超胞, 构造时仅拟合前四($ x=0.5 $)和前三(x = 0.25或0.75)近邻的原子对关联函数, 而bcc晶格SQS超胞在构造时, 拟合了前四(x = 0.25或0.75)和前五(x = 0.5)近邻的原子对关联函数.
3 -->

3.2.3.能量-体积曲线

晶格常数和总形成能是固溶体合金的平衡态性质, 而能量-体积(E-V )关系可以给出体系在远离平衡态(如: 压缩或膨胀)时的性质. E-V关系可用Rose等^[27]提出的状态方程(EOS)来描述:

$E\left(V\right)=-{E}_{{\rm{c}}}\left(1+{a}^{*}+0.05{a}^{*3}\right){e}^{-{a}^{*}},$

${a}^{*}=\sqrt{\frac{9{B}_{0}{V}_{0}}{{E}_{{\rm{c}}}}}\Big[{\Big(\frac{V}{{V}_{0}}\Big)}^{\frac{1}{3}}-1\Big], $

其中V是原子体积; E是单个原子总能量; E_c, B₀和V₀分别是平衡状态下结合能、体积弹性模量和原子体积.
通过分子动力学模拟得到的SQS模型和RSS模型的E-V关系曲线如图6(bcc晶格)和图7(hcp晶格)所示. 从图6和图7可以看到, EOS方程能较好地描述Zr-Nb随机置换固溶体的E-V关系. SQS模型和RSS模型的E-V关系曲线几乎完全重合, 固溶体能量随着Nb浓度的增大而降低. 由于势函数的不同, Smirnova和Starikov^[2]的E-V曲线与相应随机置换固溶体合金的E-V关系明显偏离. 需要指出的是, 图中Smirnova和Starikov的E-V曲线(由ADP势函数计算获得)对应的是金属化合物L1₂和B2, 而非随机置换固溶体.
图 6 bcc晶格RSS超胞和SQS超胞的E-V曲线, 以及ADP势的计算结果, 其中, 多边形和圆形图标为对应的SQS和RSS模型的能量计算值, 对应的曲线是用EOS方程^[27]拟合得到的E-V曲线; 单点划线、双点划线和短划线是Smirnova和Starikov^[2]得到的ADP势模拟结果
Figure6. Energy-volume curves of RSS and SQS supercells in bcc lattice, and the calculation results of ADP potential. The polygon and circular icons are the energy calculation values of the corresponding SQS and RSS structure, and the corresponding curves are the E-V curves obtained by fitting EOS equation^[27]. Single dotted line, double dotted line and short dotted line are the calculated results of ADP potential obtained by Smirnova and Starikov^[2].

图 7 hcp晶格SQS超胞和RSS超胞的Zr-25%Nb合金E-V曲线, 以及ADP势的计算结果^[2]
Figure7. E-V curves of Zr-25%Nb alloy obtained by SQS supercells and RSS supercells in hcp lattice, and the calculation results of ADP potential^[2].

通过拟合Rose状态方程, 可获得材料的平衡性质, 包括晶胞参数、结合能和体弹性模量, 拟合结果如表1所列. 另外表1中还列出文献[17]中拟合数据. 可以看到, SQS超胞和RSS超胞得到的结合能差异均小于0.01 eV (远小于不同势函数之间的能量差), 体弹模量的差异也都在4 GPa以下, 证明两种超胞的模拟结果是十分一致的. 因此可以认为, 两种模型对固溶体非平衡态E-V关系的模拟是一致的.

Alloy	a/?	c/?	Ec/(eV·atom–1)	B0/GPa
Zr0.75Nb0.25(bcc)	3.527		6.450	96
	3.531		6.447	100
Zr0.75Nb0.25(hcp)	3.200	5.097	6.468	144
	3.202	5.100	6.477	142
*L12-Zr3Nb	4.49		6.45	107
Zr0.5Nb0.5(bcc)	3.442		6.745	118
	3.441		6.744	117
*B2-ZrNb	3.48		6.69	116
Zr0.25Nb0.75(bcc)	3.366		7.127	153
	3.367		7.124	156
*L12-ZrNb3	4.34		6.96	100

表1由EOS方程拟合得到的Zr-Nb合金性质(带“*”的为文献[17]的拟合结果; 第一行对应RSS超胞, 第二行对应SQS超胞)
Table1.Properties of Zr-Nb alloy obtained by fitting EOS equation, and the “ * ” is the fitting result of literature^[17]. The first line corresponds RSS structure, and the second line corresponds SQS structure.

为了验证SQS模型在物理性能上的广延性, 本文利用SQS模型对Zr-Nb随机置换固溶体进行了分子动力学模拟, 并将SQS模拟结果与一系列RSS超胞的统计平均值进行比较.
为了使RSS模型既能准确体现固溶体物理性质统计性的同时又能保证计算速度, 首先确定了RSS超胞的临界尺寸, 然后分别将SQS模型超胞和RSS模型超胞用于分子动力学模拟, 并给出了两种模型在不同Nb原子浓度下的晶格常数、合金形成能以及能量-体积曲线. 模拟结果表明, 无论是平衡态的晶格常数、形成能, 还是非平衡态的能量-体积曲线, SQS模型的模拟结果与RSS模型的统计平均值相比, 虽然有细微的差别, 但在数值上都十分接近, 表明利用小尺寸SQS超胞模拟随机置换固溶体的方法是可靠的. 因此, 对于二元随机置换固溶体的模拟, 在分子动力学势函数开发难度很大的情况下, 可以利用SQS模型进行第一性原理计算, 并为MD势函数开发提供重要的物理性质.