摘要:人为操控电子的内禀自由度是现代电子器件的核心和关键. 如今电子的电荷和自旋自由度已经被广泛地应用于逻辑计算与信息存储. 以二维过渡金属硫属化合物为代表的二维原子层材料由于其具有独特的谷自由度和优异的物理性质, 成为了新型谷电子学器件研究的优选材料体系. 本文介绍了能谷的基本概念、谷材料的基本物理性质、谷效应的调控和谷电子学器件的研究进展, 并对谷电子学材料和器件的研究进行了总结与展望.
关键词: 二维过渡金属硫属化合物/
谷电子学

English Abstract

全文HTML

--> --> -->

1965年英特尔创始人之一戈登·摩尔提出了著名的摩尔定律: 集成电路上可容纳的元器件数目, 每隔18个月便会增加1倍. 现今十分成熟的硅基光刻工艺保证了芯片元件特征尺寸可以做到几个纳米的量级. 但当芯片尺寸继续降低, 由于能耗和量子效应的影响, 电路集成度、器件运行速度接近理论极限. 在此背景下, 寻找新型电子自由度、发展新型电子器件成为重要的研究方向之一.
近年来, 电子的一种新型内禀自由度“能谷”被发现并被用来研究和发展新型电子学器件. 能谷是晶体布洛赫电子能带的极值点, 其形似“山谷”而得名. 类似于电子自旋自由度, 能谷自由度也被称作赝自旋. 能谷器件相比传统器件有着运算速度快、集成度高、信息不易失真、能耗低等优点, 因此“谷电子学”近年来成为凝聚态方向研究的热点^[1-5].
谷电子学的发展与二维原子层材料的研究密不可分. 早期石墨烯被证实通过人为手段打破空间反演对称性可以出现依赖于能谷的光学、电学性质^[6,7]. 与石墨烯不同, 单层过渡金属硫属化合物(transition metal dichalcogenides, TMDCs)晶体结构不具有空间反演对称性, 贝里曲率非零, 另外能谷与自旋之间存在强耦合^[8], 通过光^[9]或电磁注入自旋^[10]的方法可以实现特定能谷的极化. 单层与多层TMDCs材料之间对称性的不同也提供了人为调控能谷性质的途径. 因此TMDCs材料成为了研究能谷效应、构建能谷器件的重要研究平台.
本文将从以下几个方面介绍原子层材料的能谷性质与器件: 首先简要介绍能谷的物理概念及能谷效应; 在第3节介绍TMDCs材料能带性质; 第4节介绍多层TMDCs材料的能谷效应; 第5节介绍能谷极化的实现手段; 最后简要介绍能谷器件的研究进展.

能谷, 指的是晶体中电子能量在动量空间中的极值. 在一些半导体材料能带中, 会出现几个能量简并但不等价的能谷. 谷电子学就是在合适的能谷材料基础上, 对不同能谷态进行调控和信息处理^[11,12].
能谷的研究最早可以追溯到20世纪70年代^[13,14]. 21世纪初开始, 一些传统材料, 例如AlAs异质结构^[15,16], 硅^[17,18], 金刚石^[19], 铋^[20]的能谷性质逐步被研究, 但这些材料能谷极化与调控难以实现. 随着石墨烯、二维TMDCs等材料的出现, 具有六角晶格结构的二维原子层材料在谷电子学研究材料体系中脱颖而出. 以石墨烯为例, 其晶格由两套布拉伐格子子晶格嵌套而成, 在倒空间形成一组由时间反演对称性联系的两重简并能谷, 记为K, K'. K能谷与K' 能谷在宏观上的性质主要取决于能谷中的贝里曲率^[6,7,21]. 贝里曲率是贝里相位的拓展, 是描述电子布洛赫态的函数, 代表了晶体自身结构的性质. 贝里相位是系统哈密顿量依赖的参数在参数空间中缓慢变换一个回路时系统波函数改变的相位. 在晶体中, 系统哈密顿量与晶体倒空间波矢有关, 由此当波矢在倒空间布里渊区进行一个回路的演化时, 晶体系统布洛赫波函数会演变出贝里相位, 如下公式计算^[21]:

${\gamma _n} \!=\! \oint\nolimits_C {\left\langle {{\mu _{n,{{k}}}}} \right| {\rm i} {\nabla _k}\left| {{\mu _{n,{{k}}}}} \right\rangle \cdot {\rm{d}}{{k}}} \!=\! \oint\nolimits_C {{{{A}}_n}({{k}}) \cdot {\rm{d}}{{k}}} ,$

其中, ${\mu _{n, {{k}}}}$是第n个晶体能带在倒空间动量坐标k处的布洛赫波周期函数部分, C为闭合回路, ${{{A}}_n}({{k}})$被称为贝里联络(Berry Connection). 通过(1)式可发现相位不依赖于时间并且形式与电动力学中的磁通量$\phi = \displaystyle\oint\nolimits_C {{A}} \cdot {\rm{d}}{{r}} = \iint\nolimits_S {(\nabla \times {{A}})} \cdot {\rm{d}}{{S}}$类似. 贝里相位中的被积函数${{{A}}_n}({{k}})$的环路积分可以化为函数旋度在环路所包围的面上积分, 此时$\nabla \times {{{A}}_n}({{k}})$为规范不变量, 被称为贝里曲率, 可以证明得到^[21]:

${{{\varOmega }}_n}({{k}}) = {\nabla _k} \times \left\langle {{\mu _{n,{{k}}}}} \right|{\rm i} {\nabla _k}\left| {{\mu _{n,{{k}}}}} \right\rangle ,$

根据贝里曲率的表达式可以发现${{{\varOmega }}_n}({{k}})$由系统的对称性决定. 当系统仅具有空间反演对称性时, 贝里曲率满足${{{\varOmega }}_n}({{k}}) = {{{\varOmega }}_n}( - {{k}})$; 当体系仅具有时间反演对称性时, 贝里曲率满足${{{\varOmega }}_n}({{k}}) = - {{{\varOmega }}_n}( - {{k}})$. 因而当空间反演对称与时间反演对称同时被保护时, 贝里曲率为零, 能谷效应消失. 理论研究曾提出石墨烯材料的能谷性质需要利用外界手段打破空间反演对称^[6,7], 空间反演破缺的能隙石墨烯的哈密顿量为: $H{{ = }}at({\tau _z}{k_x}{ \sigma _x} + {k_y}{ \sigma _y}) + \dfrac{{{\varDelta }}}{2}{ \sigma _z}$^[6], 其中, a是晶格常数, t是最近邻碳原子之间的跃迁概率, ${\tau _z}{{ = }} \pm 1$为能谷序数, ${\varDelta }$是能隙大小. 在此哈密顿量下, 导带能谷电子的贝里曲率为: $\varOmega (k) = {\tau _z}\dfrac{{3{a^2}{{\varDelta }}{t^2}}}{{2{{({{{\varDelta }}^2} + 3{k^2}{a^2}{t^2})}^{\tfrac{3}{2}}}}}$^[6], 方向垂直于样品面, 显然从理论结果中也可以看出当石墨烯能隙为零时, 贝里曲率也为零.
伴随能谷电子布洛赫态非零贝里曲率出现的是能谷的轨道磁矩^[6,7,21], 代表着布洛赫电子波包围绕其中心的转动. 在两带模型近似下, 能谷的轨道磁矩与贝里曲率之间有简单的关系: $m(k) = \dfrac{e}{\hbar }\varepsilon (k)\varOmega (k)$. 由于时间反演对称性, K谷与K' 谷的贝里曲率满足关系${{{\varOmega }}_n}({{k}}) = - {{{\varOmega }}_n}( - {{k}})$, 因此两个能谷有着大小相同方向相反的轨道磁矩. 类比于自由电子上自旋和下自旋, 不同能谷可以由轨道磁矩区分, 与之相关的贝里曲率则可以被描述为参数空间的有效磁场. 在空间反演对称性破缺石墨烯体系中, 导带轨道磁矩在倒空间的分布如图1所示^[6], 贝里曲率有着与其类似的分布.
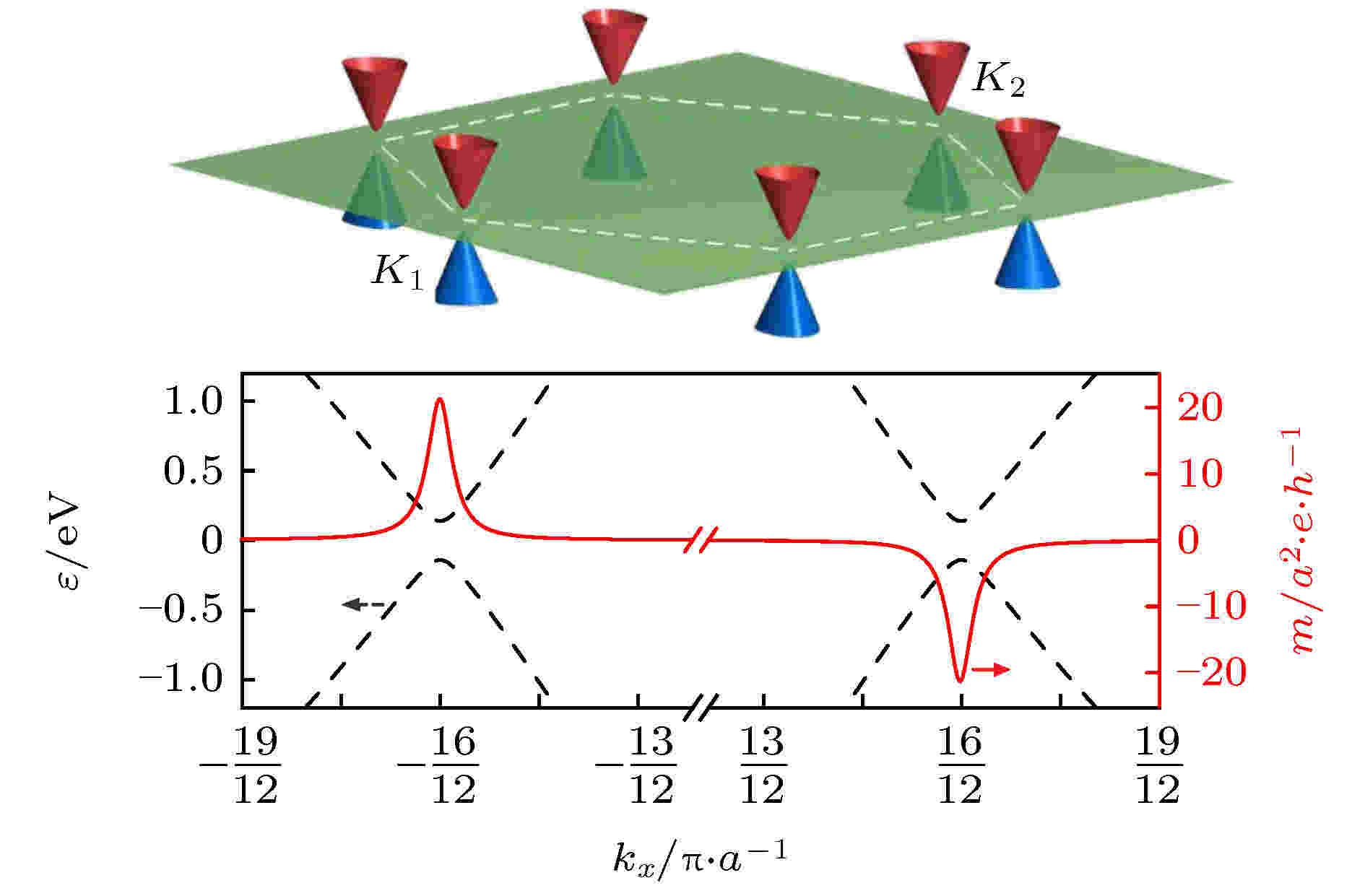图 1 空间反演对称性破缺的石墨烯的能带(上半部分)和导带轨道磁矩(下半部分). 贝里曲率分布和轨道磁矩类似^[6]
Figure1. Energy bands (top panel) and orbital magnetic moment of the conduction bands (bottom panel) of a graphene sheet with broken inversion symmetry. The Berry curvature Ω(k) has a distribution similar to that of m(k)^[6].

如上所述, 贝里联络和贝里曲率分别等效于波矢空间中的磁矢势和磁场. 与存在磁场时电子会发生霍尔效应的情况类似, 当系统存在非零贝里曲率时, 载流子运动同样会受其影响产生谷霍尔效应. 在外磁场为零时, 晶体中电子的运动方程需要在经典表达式中加入与贝里曲率有关的反常速度项, 即^[21]

${{v}}({{k}}) = \frac{1}{\hbar }{\nabla _k}\varepsilon ({{k}}) - \frac{e}{\hbar }{{E}} \times {{\varOmega }}({{k}}),$

其中$\varepsilon ({{k}})$是电子能量. 在经典体系中载流子速度与外加电场方向一致; 而当系统存在非零贝里曲率时, (3)式中的反常速度项会引起电子垂直于电场方向的横向运动. 由(3)式可见, 反常速度与贝里曲率的大小方向有着重要的联系. 对于空间对称性破缺的石墨烯, 其本征谷霍尔电导率为${\sigma _{\rm H}}({\tau _z}) = {\tau _z}\dfrac{{{e^2}}}{h}\left[ {1 - \dfrac{\varDelta }{{2\mu }} - \dfrac{{3\varDelta {t^2}k_{\rm F}^2{a^2}}}{{8{\mu ^3}}}} \right]$, 其中化学势$\mu $与费米波矢${k_{\rm F}}$的关系为$\mu = \sqrt {{{{\varDelta }}^2} + 3 k_{\rm F}^2{a^2}{t^2}}\big/2$^[6].
不同于石墨烯, 以单层MoS₂为代表的单层TMDCs材料本身具有时间反演对称性而缺乏空间反演对称性, 贝里曲率满足${{{\varOmega }}_n}({{k}}) = - {{{\varOmega }}_n} ( - {{k}}) \ne 0$, 因而早期能谷研究利用TMDCs材料围绕发现、验证能谷自由度展开了大量的工作. 单层TMDCs材料中K谷和K' 谷中的贝里曲率大小相等方向相反, 在外加电场的作用下, 根据(3)式, K谷和K' 谷中的载流子在垂直于电场方向具有不同方向的反常速度, 导致K谷与K' 谷的载流子分别向沟道两侧进行偏转, 实现谷霍尔效应^[8]. 值得注意的是, 在贝里曲率的影响下, 谷霍尔效应和自旋霍尔效应会在沟道两侧积累不同能谷和自旋序数的电子与空穴, 因而复合过程要通过谷间散射来辅助完成^[8].
TMDCs材料的谷霍尔效应最早在单层MoS₂中被实验观测到^[22]. 由于谷霍尔效应在能谷简并的材料中产生的能谷流并不能直接在沟道两侧形成电势差, 因此需要外加圆偏振光辅助. 这是由于TMDCs材料具有圆偏振光选择性, 特定手性的圆偏振光会产生K和K'谷的极化. 实验结果如图2所示, 单层MoS₂在左旋或右旋圆偏光的作用下, 沟道两侧均能观测到和源漏电压成正比的霍尔电压; 双层MoS₂由于空间反演对称性的保护不能测到霍尔电压.
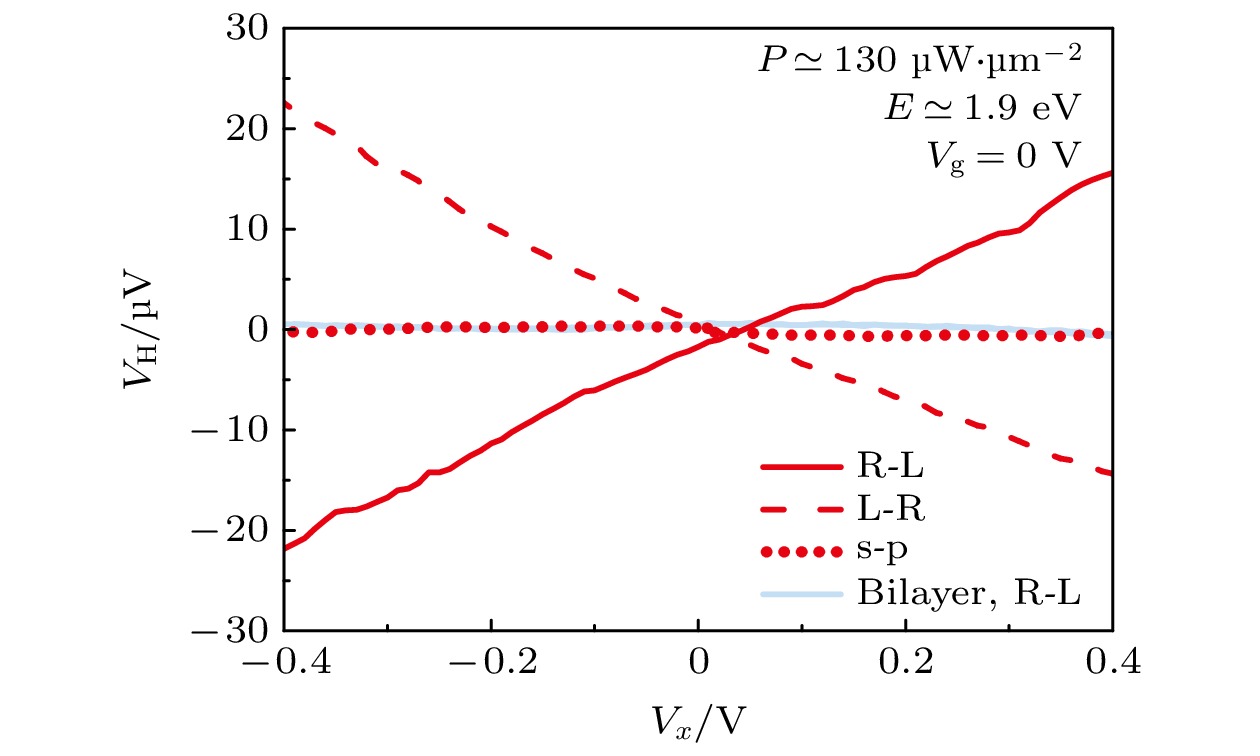图 2 单层器件和双层器件霍尔电压随着源漏偏压的变化关系^[22]
Figure2. The source-drain bias dependence of the Hall voltage for the monolayer device and bilayer device^[22].

在之后几年, TMDCs材料的谷霍尔效应研究受到了广泛的关注. 2016年宾夕法尼亚大学研究团队在双层MoS₂体系中通过栅电场打破材料空间反演对称性, 成功诱导出谷霍尔效应^[23], 此实验说明了能谷效应可以在过原子层面通过人为调控来实现. 2017年, 单层TMDCs材料圆偏振光激发诱导的谷霍尔效应被证实来源于激子和带电激子的贡献^[24]; 2019年, n型和p型的单层WSe₂晶体管通过低温克尔(Kerr)光谱观测到了谷霍尔效应^[25]. 同年, 单层MoS₂的霍尔结构器件在输运实验中被测量到了非局域霍尔电压, 成功在TMDCs体系中实现了纯电学的谷霍尔效应观测^[26,27], 实验示意图如图3所示^[26].
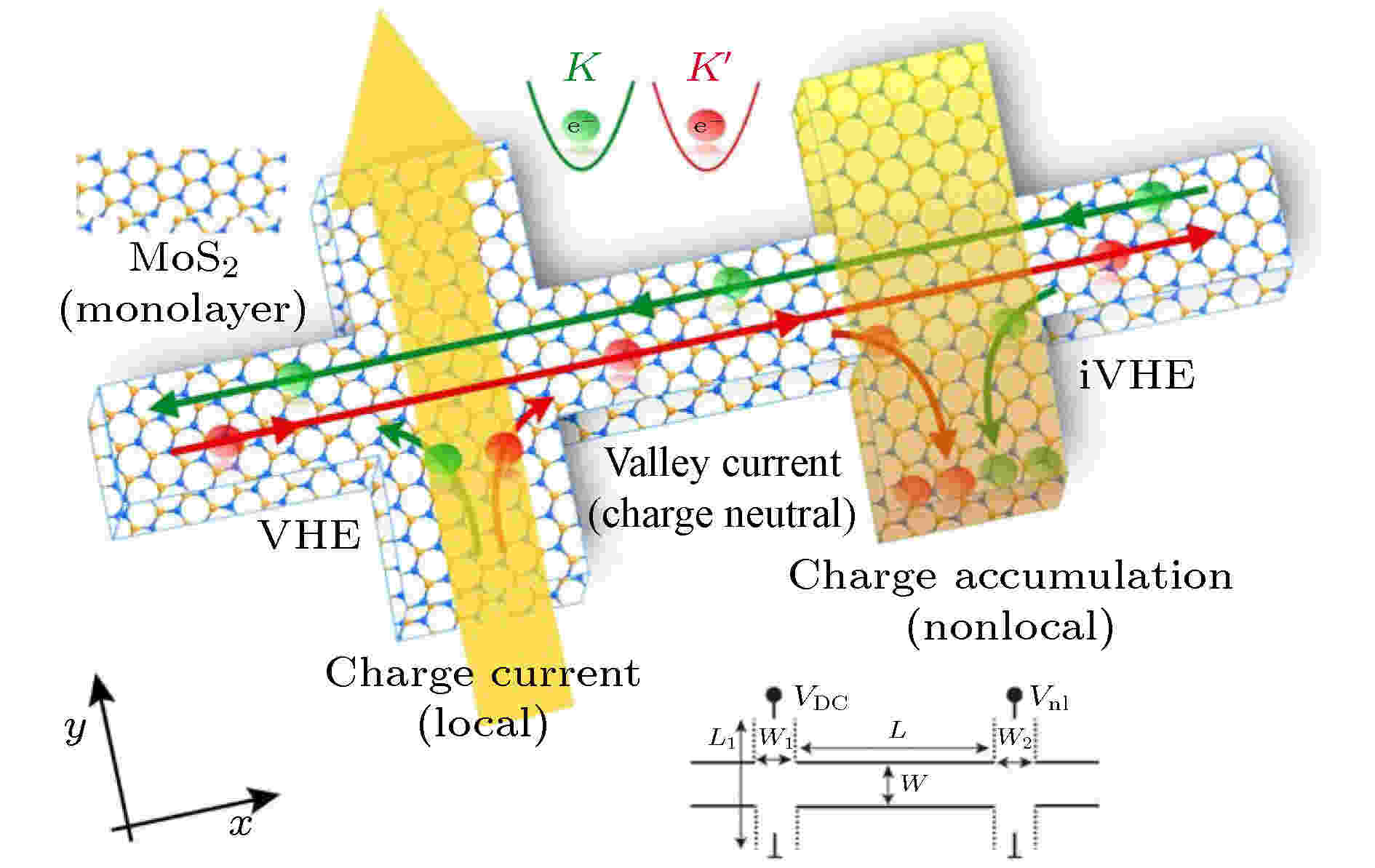图 3 单层MoS₂中谷霍尔效应与逆谷霍尔效应导致的能谷流示意图^[26]
Figure3. Schematic of valley-coupled topological current due to VHE and inverse VHE (iVHE) in monolayer MoS₂^[26].

上述研究中提到了二维原子层材料能谷的另一个重要性质—圆偏振光选择定则. 众所周知, 半导体光学跃迁需要满足能量守恒、动量守恒及角动量守恒. 角动量守恒要求在跃迁前后磁量子数保持守恒, 而这一守恒条件直接导致了材料对左右旋光选择性的吸收. 二维原子层材料能谷圆偏振选择定则的理论研究早期在石墨烯体系中完成^[7]. 研究人员计算得到在空间反演对称性打破的石墨烯材料中, 圆偏振光跃迁极化度与能谷的轨道磁矩及体系贝里曲率有着如下关系. 圆偏振光极化定义为

$\eta (k) = \dfrac{{{{\left| {{P_ + }(k)} \right|}^2} - {{\left| {{P_ - }(k)} \right|}^2}}}{{{{\left| {{P_ + }(k)} \right|}^2} + {{\left| {{P_ - }(k)} \right|}^2}}},$

其中${P_ \pm }(k) = \langle c| {p_x} \pm {\rm{i}}{p_y} |v \rangle$是带间跃迁矩阵, 表示k点的电子在旋光激发下从价带到导带的跃迁. 在两带模型近似下, 圆偏振光极化度^[7]可表示为

$\eta (k) \!=\!-\dfrac{m(k) \cdot \hat{z}}{{\mu }_{\rm B}^{{*}}(k)} \!=\! -\dfrac{\varOmega (k) \cdot \hat{z}}{{\mu }_{\rm B}^{{*}}(k)}[{\varepsilon }_{c}(k)-{\varepsilon }_{v}(k)]\dfrac{e}{2\hslash }.$

在能谷的极值点, $\eta (k) = - {\tau _z}$, 即K谷的跃迁只与左旋光耦合, K' 谷的跃迁只与右旋光耦合. 这一性质使得光学激发、调控、探测能谷极化成为可能.
单层和多层的石墨烯在不同外界手段打破对称性的条件下, 被理论计算验证了圆偏振选择定则^[7]. 但由于石墨烯本身缺乏带隙, 能谷圆偏振光选择定则很难通过实验验证, 因而单层TMDCs材料成为实验验证能谷光学响应的理想材料^[28-30]. 单层MoS₂中的圆偏振光选择定则在2012年基于科恩-沈吕九(Kohn-Sham)波函数密度泛函微扰理论计算结合圆偏振荧光(photoluminescence, PL)谱实验成功验证^[28]. 实验中利用了633 nm光激发的圆偏振PL谱对能谷进行表征, 结果如图4所示^[28].
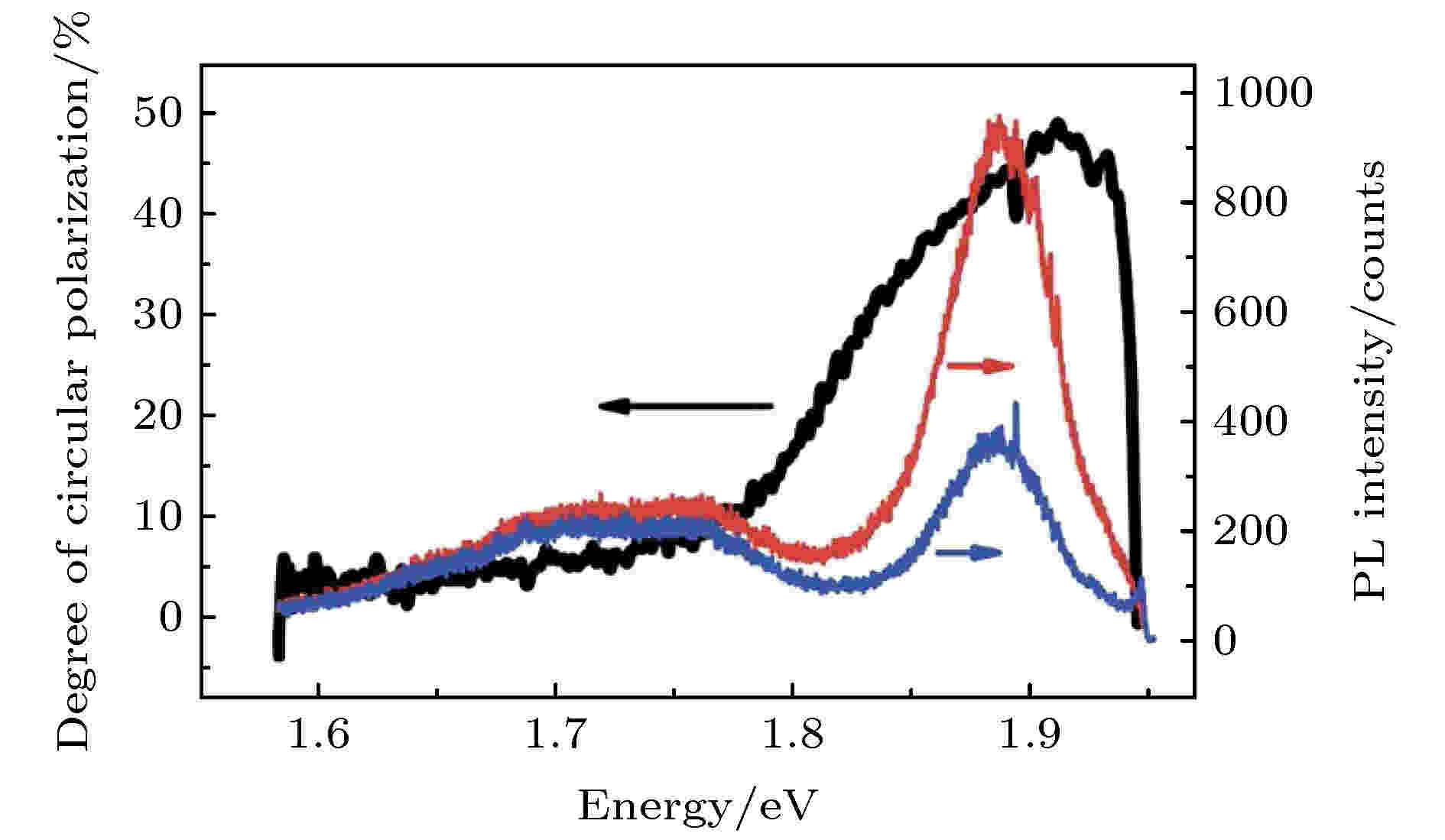图 4 单层MoS₂在83 K下的圆偏振极化PL谱和PL谱的圆偏振极化程度. 红色和蓝色曲线分别对应于发光光谱中${\sigma ^ + }$和${\sigma ^ - }$极化强度, 黑色曲线是净极化的大小^[28]
Figure4. Circularly polarized micro-PL of monolayer MoS₂ at 83 K, along with the degree of circular polarization of the PL spectra. The red and blue curves correspond to the intensities of ${\sigma ^ + }$ and ${\sigma ^ - }$ polarizations, respectively, in the luminescence spectrum. The black curve is the net degree of polarization^[28].

可以发现在左旋${\sigma ^ + }$的激发下, ${\sigma ^ + }$的荧光强度要显著大于${\sigma ^ - }$的荧光强度. 荧光的偏振度即表征着K与K' 谷的谷极化度, 可以由下式计算:

$p = \frac{{I({\sigma ^ + }) - I({\sigma ^ - })}}{{I({\sigma ^ + }) + I({\sigma ^ - })}},$

其中, $I({\sigma ^ + })$和$I({\sigma ^ - })$分别代表${\sigma ^ + }$和${\sigma ^ - }$的荧光强度. 实验测得了50%的谷极化度, 谷极化度无法达到理论中的100%的原因是光子复合跃迁会伴随着声子参与的K和K' 谷间散射. 实验在激发K(K')谷的同时在K'(K)谷中也会产生复合发光的过程. 同年, 另外两个研究组在实验上也验证了单层MoS₂材料中的圆偏光选择定则^[29,30], 并讨论了谷间弛豫及温度对圆偏光极化率的影响. 在低温区域, 能谷间散射主要由缺陷、杂质和边界引起; 而当温度大于90 K时, 荧光谱的极化率随着温度的升高快速下降, 表明较高温度下谷间散射由声子辅助占主导^[30]. 为了能在室温下应用能谷效应, 研究人员曾利用调制样品质量的手段在室温下测量到了能谷的圆二向色性^[31,32], 而在2018年通过将MoS₂生长在(0001)方向的纤锌矿GaN衬底, 能谷的圆偏振荧光极化度在室温下达到了33%^[33]. 对于能谷圆二向色性的实验研究也不仅局限于PL谱的测量, 2015年单层WSe₂材料体系通过测量左旋和右旋抽运光产生的Kerr旋转信号探测到能谷圆偏振光选择性吸收的现象^[34]. 而以能谷圆二向色性为基础的时间分辨Kerr实验又成功探测了电子^[35]、空穴^[36]及受栅压调控的单层WSe₂载流子能谷寿命^[37].
如上所述, 大量实验结果验证了二维TMDCs材料体系中能谷圆偏振选择定则与谷霍尔效应, 这两种能谷效应也成为了研究和利用能谷自由度的重要手段.

随着晶体生长和原子层尺度加工技术的提升, MoS₂为代表的二维TMDCs材料在电子器件、光电器件、传感器、析氢反应催化剂等领域开始显现重要的应用前景^[38]. 在谷电子学方面, 其单层材料天然具有反演破缺的性质, 具有谷电子学性质^[8,22-30]. 为了更深入理解TMDCs材料能谷性质, 我们将以MoS₂为例介绍单层、多层TMDCs材料的能带结构.
TMDCs材料的化学分子式为MX₂, M为过渡金属元素, X为硫属元素. 单层TMDCs材料结构类似于“三明治”, 中间的Mo原子被两层外侧的S原子以共价键相结合; 体材料由单层通过范德瓦耳斯相互作用结合形成, 层间距约为6.5 ?^[39]. 层与层之间堆垛方式的不同可以将TMDCs体材料分为2H, 3R, 以及1T相3类^[40], 一般情况下体材料多以2H与1T形式存在, 其中2H是半导体性质, 1T是金属态.
谷电子学材料的性质取决于能带结构. 在TMDCs材料中, 能带结构会随着原子层数的变化产生奇特的转变. 随着层数的减少, TMDCs材料会由间接带隙半导体转变为直接带隙半导体^[41,42], 这是源于单层材料量子限制所导致的Mo原子的d轨道与S原子的p_z轨道杂化形式变化^[42]. 第一性原理计算得到的不同层数MoS₂能带结构如图5所示^[42].
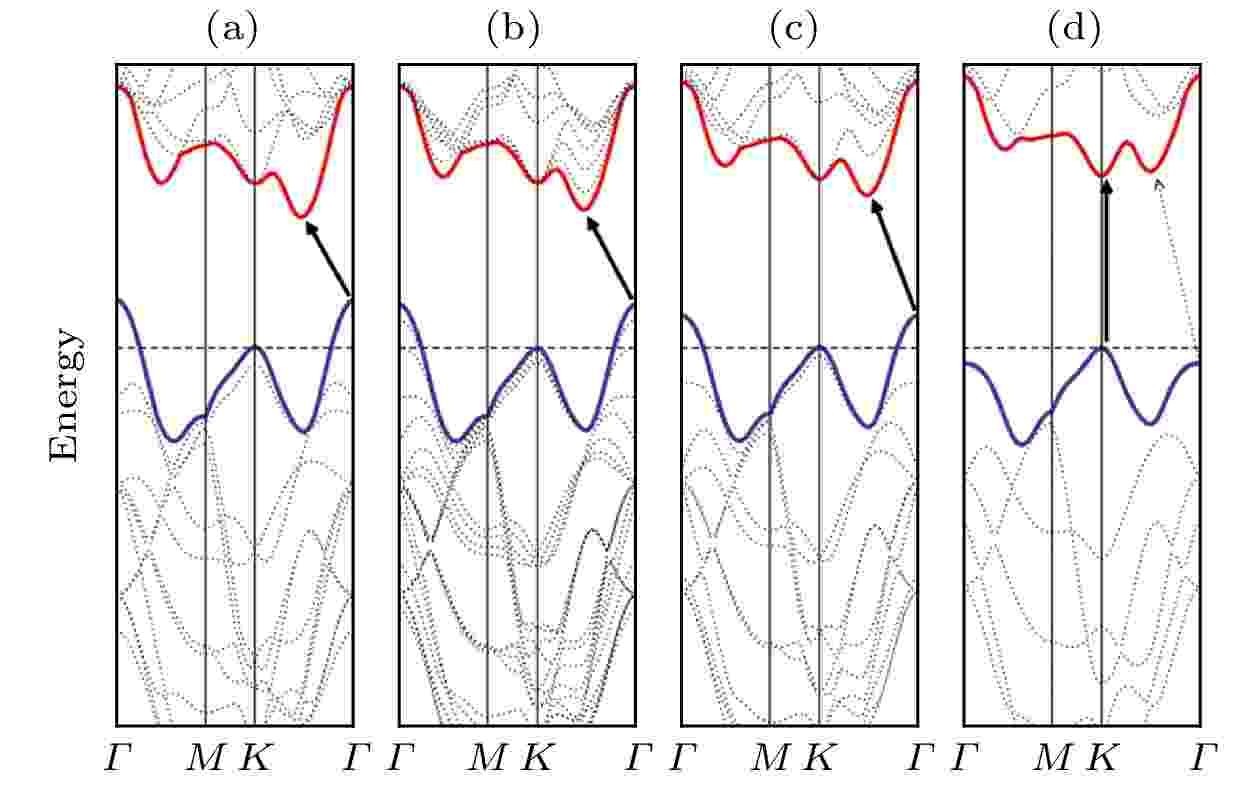图 5 (a)体MoS₂, (b)四层MoS₂, (c)双层MoS₂和(d)单层MoS₂的能带结构. 实心箭头表示最低能量跃迁. 体和多层MoS₂具有间接带隙特性. 对于单层MoS₂, 它变为直接带隙半导体^[42]
Figure5. Calculated band structures of (a) bulk MoS₂, (b) quadrilayer MoS₂, (c) bilayer MoS₂, and (d) monolayer MoS₂. The solid arrows indicate the lowest energy transitions. Bulk MoS₂ is characterized by an indirect bandgap. For monolayer MoS₂, it becomes a direct bandgap semiconductor^[42].

单层MoS₂直接带隙位于K点. 随着层数的增加, 层间耦合作用增强, 导带底移至Λ点, 价带顶移至${{\varGamma }}$点. 此时带间的光学跃迁需要声子的协助才能实现, 因此其PL谱不同于单层^[41], 如图6所示.
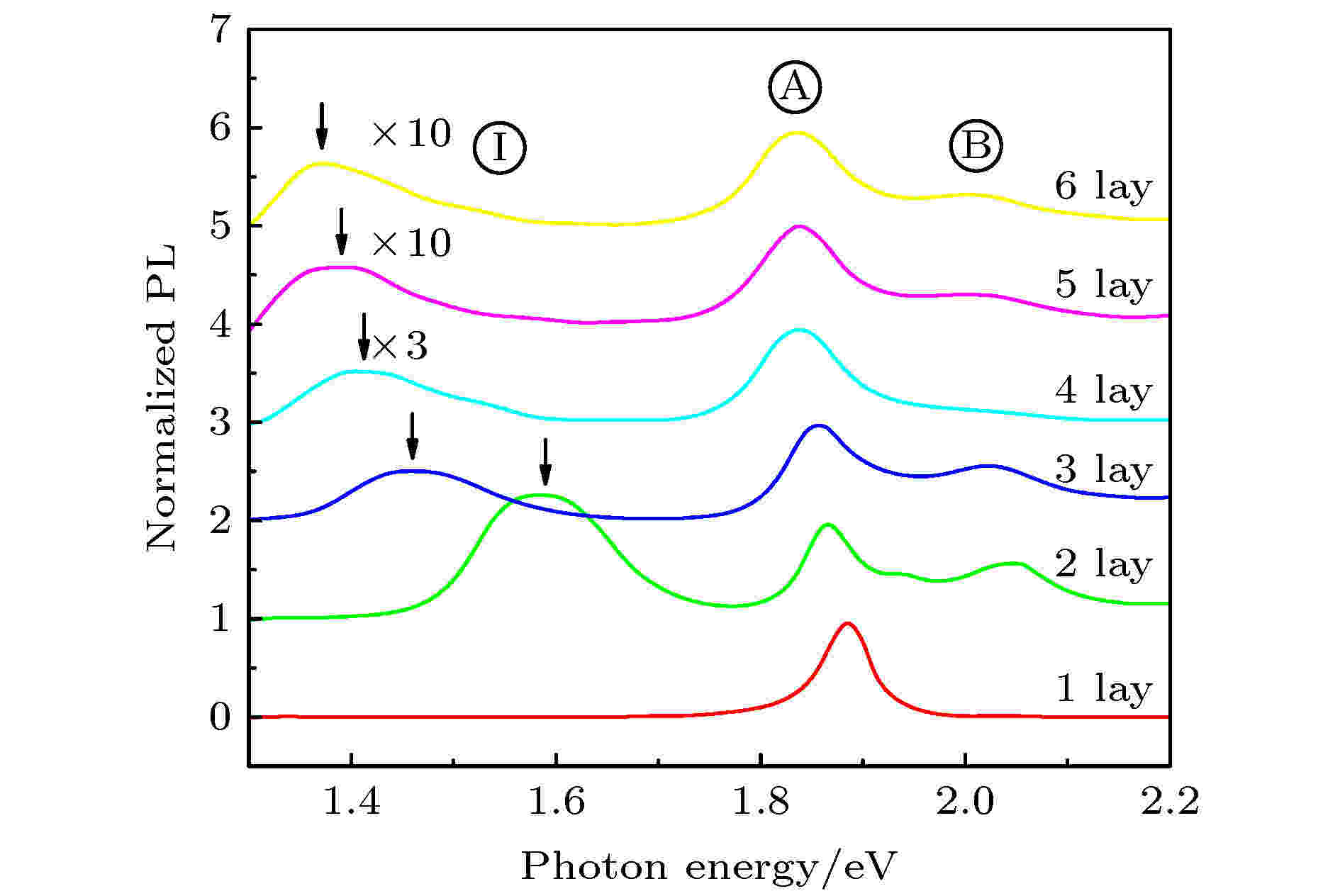图 6 单层到6层MoS₂样品A激子峰强度的归一化PL光谱^[41]
Figure6. Normalized PL spectra by the intensity of peak A of thin layers of MoS₂ for number of layers = 1–6^[41].

从PL谱中可以明显看到多层材料在1.4—1.6 eV范围内出现较宽的发光峰, 此峰来源于带间的间接跃迁. 而在1.90 eV和2.05 eV处出现两个发光峰, 其代表着K-K跃迁的两种激子态, 即A激子与B激子. 二者150 meV的能量差主要来源于价带自旋轨道耦合作用导致的能量分裂^[41]. 由于金属原子d 轨道的性质, 二维 TMDCs 中带边的电子和空穴存在强烈的自旋轨道耦合. 在单层材料中空间反演对称性被打破, 时间对称性受到保护, 产生Kramer简并, K谷与K' 谷出现自旋分裂且带边自旋恰好相反. 与价带极高的自旋轨道分裂能不同, 导带带边主要由磁量子数m = 0的轨道组成, 自旋轨道分裂能仅在10 meV量级左右. 价带的强自旋分裂引起了能谷自旋间的耦合, 即能谷序数与自旋序数的锁定. K谷价带顶电子自旋方向与K' 谷相反, 由于K(K' )能谷的圆偏光二向色性, 特定频率的左旋或右旋光会激发特定自旋的K谷或K' 谷电子. 能谷自旋耦合也使得能谷极化可以通过自旋注入实现, 这对能谷器件的构建有着重要意义. 另一方面, 单层TMDCs材料的自旋轨道耦合与通常Rashba自旋轨道耦合的等效磁场不同, 其磁场方向在能谷周围都是垂直于样品表面, 且大小高达几百特斯拉. 在此大磁场下, 电子自旋方向被钉扎在面外, 面内磁场难以改变自旋方向, 有利于实现伊辛超导. 因而TMDCs独特的能谷性质在超导领域也有着卓越的表现^[43].
设计能谷器件首先需要构建“0”, “1”开关态. 能谷是电子和空穴在倒空间离散的内禀自由度, 因此可以将能谷自由度类比自旋自由度, 使载流子在动量空间中离散的占据位置作为能谷的赝自旋, 通过能谷间不同的占据状态编码“0”, “1”信息态. 相比于此编码方式, “0”, “1”态也可以通过材料的贝里曲率、能谷轨道磁矩的有无来实现, 其基础就是材料能带结构的变化, 例如石墨烯对称性通过外加栅压的改变.
外加应力就是一种极为常见且有效的能带调控手段. 单层MoS₂中K谷是直接带隙并且具有能谷性质. 通过外加应力的手段改变单层MoS₂的能带结构, 使材料变为间接带隙半导体就可以有效地改变其复合路径, 减弱能谷复合的圆二向色性. 同时单层MoS₂材料由于原子层厚度的优势, 在柔性光电子器件领域也有着很好的应用前景^[44,45], 因此应力环境下材料能带结构的变化在谷电子学和光电器件领域都有着重要的研究意义. 理论计算结果表明, 在足够的张应变或者压应变下, 单层MoS₂的能带结构会由直接带隙转变为间接带隙. 不同的是, 张应变下能带结构的转变是由价带顶从K谷转变为${{\varGamma }}$谷造成的, 而压应变下则是由导带底从K谷转变为Λ谷造成的^[46]. 在实验方面, 研究人员通过对单层MoS₂施加单轴应变的方式证明了直接带隙向间接带隙的转变^[47], 而通过流体静压力实验则发现单层MoS₂直接间接带隙转变的具体成因是由于导带底从K谷向Λ谷的移动^[48], 移动则是由于S—Mo—S键角会随外加压力的增大而增大^[49]. 如上所述, 应力可以有效改变材料的能带结构, 这一变化为能谷器件的研制提供了新的可尝试实现途径.

单层TMDCs材料一般难以通过电学手段调控能谷效应的“有”“无”, 多层材料则可以通过外加栅压的方式打破空间反演对称性, 从而诱导出能谷效应. 正如第2节所述, 外加人为手段可以打破石墨烯的空间反演对称性, 使其无质量的狄拉克费米子消失, 能带的贝里曲率非零, 出现能谷圆偏振光选择定则和谷霍尔效应^[6,7]. 在此背景下, 很多研究组都在实验上验证了能隙石墨烯中的能谷输运与可调控的谷霍尔效应^[50-53].
2015年东京大学的研究团队^[52]利用栅极电场打破双层石墨烯的空间反演对称, 成功实现了纯能谷流的产生与检测. 实验在器件一侧沟道中接入恒流源, 由于谷霍尔效应, 不同谷序数的电子在纵向沟道中向相反方向运动, 能谷流不为零而电荷流为零. 类比自旋霍尔效应与其逆效应^[54], 能谷流由于逆谷霍尔效应会在另一侧的横向沟道中积累电荷引起电势差. 非局域霍尔器件结构既可以作为能谷流的源来使用, 同时受栅极调控的电压输出也可构建逻辑功能.
相比于石墨烯, TMDCs材料具有较大的带隙^[41,42]及较强的自旋轨道耦合^[55,56], 更适合作为能谷器件的材料. 与石墨烯材料的可调控能谷效应类似, 在双层或者多层TMDCs材料中也可通过人为调控实现能谷效应.
2013年, TMDCs材料能谷自由度成功通过电学手段实现调控, 在双层MoS₂场效应晶体管中, PL谱圆偏振极化度会随着外加栅压的变化而变化^[57]. 2014年复旦大学的研究团队通过对单层MoS₂进行“折叠”, 人为制造了空间反演破缺的双层MoS₂材料, 诱导出非零的贝里曲率与轨道磁矩并观测到了受结构对称性影响的能谷极化^[58]. 2016年, 双层MoS₂中的谷霍尔效应利用背栅电压成功诱导出现^[23]. 实验利用Kerr转角测量的方法在输运沟道两侧探测到了极化相反的信号. Kerr转角在传统半导体例如GaAs等材料中是测量自旋极化的重要手段, 其正比于自旋磁化强度^[59,60], 而在此实验中则是与能谷轨道磁矩相关. 实验结果证实谷霍尔电导率受到栅极电压的连续调控, 相比于单层材料, 上述双层材料具有的能谷效应可操控性更符合谷电子学器件的需求.
但单层及少层的TMDCs材料中费米能级钉扎效应明显, 采用传统的蒸镀工艺方法制作欧姆接触极其困难^[61-63]. 相比之下, 多层TMDCs材料的加工会容易很多, 同时多层材料相比于单层材料其电导率等电学性质更好, 上述的优点使得能谷器件的研究也围绕多层TMDCs材料开展. 2013年, 多层WSe₂材料体系首次通过外加离子液体栅引入电场的手段打破自身空间反演对称, 探测到了类塞曼型自旋轨道耦合劈裂^[64]. 实验通过电学输运手段测量到了K(K' )谷空穴弱局域化磁阻信号向弱反局域化信号的转变, 并用第一性原理计算得到自旋轨道耦合分裂能可以达到300 meV. 多层TMDCs材料为间接带隙, 直接通过光学手段例如复合圆偏发光信号很难获取能谷信息, 因此可以采用圆偏光电流效应(circular photogalvanic effect, CPGE)测量诱导出现的能谷自由度. 在传统半导体中CPGE来源于自旋轨道耦合导致的k空间能带劈裂, 而TMDCs材料中CPGE的起源与其有所区别. 在空间反演对称性破缺的TMDCs材料中, 圆偏振光会选择性激发K谷或者K' 谷, 而K谷或者K' 谷存在依赖于动量的非对称光吸收过程^[65]. 在圆偏振光激发后, 3个K或K' 谷处会出现载流子在动量空间的非平衡分布, 引起的CPGE电流在受激发的3个等价能谷都是沿着垂直于入射光方向, 因此总电流不会因为对布里渊区求和而抵消. 但K和K' 谷两者贡献的总CPGE电流恰好相反, 因此只有在材料具有圆偏振选择定则的前提下, CPGE电流信号才能测量到. 2015年在实验中观察到了单层MoS₂的CPGE现象^[66], 通过栅压打破对称性也同样测量到了多层WSe₂的CPGE信号^[67], 但是此多层光电流信号来源于导带Λ谷的带内跃迁, 并非K(K' )谷的信号. 2017年, 多层MoS₂材料中K(K' )的CPGE信号被观测到^[68]. 实验利用与A激子共振的圆偏振激光激发多层MoS₂材料, 在没有离子液体栅的情况下, 由于多层MoS₂材料具有空间反演对称性, CPGE信号消失, 如图7(a)所示. 加上离子液体栅后沟道内出现明显的CPGE电流, 如图7(b)所示^[68]. 结果表明离子液体栅打破多层MoS₂的空间反演对称性后, 体系产生非零贝里曲率, K(K' )谷出现圆偏振二向色性.
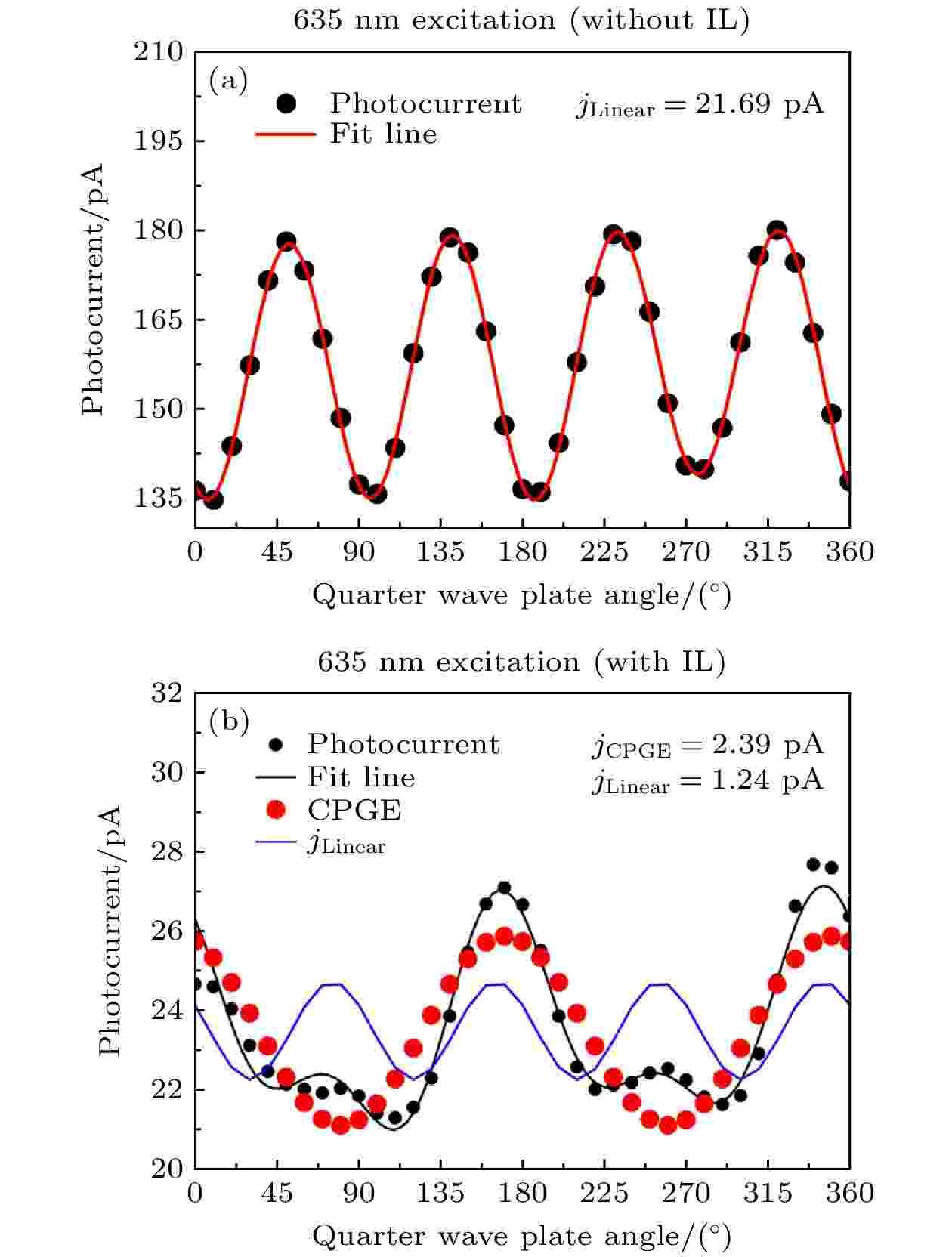图 7 635 nm激发下多层MoS₂中光电流与1/4波片角的函数关系　(a)不加离子液体; (b)有离子液体^[68]
Figure7. Photocurrent as a function of the quarter-wave-plate angle in multilayer MoS₂ under 635 nm excitation: (a) Without the application of ionic liquid; (b) with the application of ionic liquid^[68].

在多层体系中除了外加电场的方法打破空间对称性, 控制TMDCs晶体生长为3R相同样会产生能谷效应^[69]. 3R相的MoS₂单晶空间群为R_3m, 晶体本身空间反演对称性破缺, 能谷电子会解除自旋简并, 光学激发的极化能谷在层间的弛豫会受到极大地抑制^[69]. 而在设计多层材料能谷器件中, 实现K谷与K' 谷在空间上的分离也是重要的一步, 最直接的方法就是实现谷霍尔效应. 2019年, 多层WSe₂材料通过外加离子液体栅诱导产生了谷霍尔效应, 实验实现了多层TMDCs体系中K和K'谷载流子的极化与空间上的分离, 进一步扩展了谷电子学的研究体系^[70].
总之, 无论是双层还是多层TMDCs材料, 都可以通过人为手段在体系中引入非零贝里曲率. 研究结果进一步说明多层TMDCs材料能谷效应可以被人为手段调控, 有希望用于谷电子学器件.

能谷中载流子的极化在谷电子学器件应用中十分重要. 在单层TMDCs材料中自旋与能谷之间的强耦合提供了一个操纵能谷自由度的方法, 即利用光电手段直接注入自旋极化载流子实现能谷的注入. 而能谷极化也可以通过打破K谷与K' 谷之间的简并实现, 最常见的手段就是加入磁场产生塞曼分裂, 分裂大小可以通过掺杂铁磁原子, 利用铁磁近邻效应等方法增强.
谷注入最直接的方法就是利用能谷圆偏光选择定则实现光学注入. 2016年香港大学的崔晓冬研究组^[9]利用圆偏振光在WS₂场效应晶体管中激发产生了与能谷序数相耦合的自旋电流. 在圆偏振光选择定则的制约下, 相同激发波长下的左旋光与右旋光将分别激发K谷与K' 谷的电子. 实验器件两端由隧穿绝缘层和铁磁金属组成了自旋阀的结构, 在电极磁化时, 左旋与右旋光在沟道中产生的电流大小不同, 实现了沟道高低电阻态之间的转化, 验证了沟道中能谷的光学注入. 但上述的光学激发手段在集成电路中无法实现, 因而利用电学方法注入自旋实现能谷极化是谷电子学器件研究的重点. 2016年, 加州大学伯克利分校的张翔研究组和半导体所的赵建华研究组合作, 利用p型导电的稀磁半导体(Ga, Mn)As向单层WS₂注入自旋极化的空穴, 首次实现了对能谷自由度的电磁操控^[10]. 利用p型衬底的原因是单层TMDCs价带的自旋劈裂要远大于其导带. 单层WS₂的价带自旋劈裂达到400 meV, 较大的劈裂抑制了空穴注入另一高能级的能谷, 更容易实现能谷极化. 通过测量圆偏振的电致发光, 在不同磁化方向时由于注入空穴自旋方向相反, 出射光的极化度也相反. 器件电致发光的极化率仅在15%左右, 这需要考虑谷间弛豫及(Ga, Mn)As表面氧化层造成的影响. 与此方法类似, Ni/Fe铁磁金属也可向p型WSe₂注入极化空穴实现能谷极化^[71].
除了上述直接注入极化自旋的方法, 通过外加磁场打破材料体系时间反演对称性, 解除K谷与K' 谷之间的能量简并也可实现能谷的注入. 具体来讲, 外加磁场会导致能谷出现塞曼分裂, 在能量劈裂较大时通过控制材料掺杂进而调节费米能级使其位于K谷与K' 谷导带底或价带顶之间, 即可成功实现能谷极化. 单层MoSe₂和单层WSe₂通过圆偏振荧光的方法测量了带隙光学辐射频率与磁场的依赖关系, 探测到了能谷的塞曼分裂效应^[72,73], 但是这样的分裂只能在低温和极高的磁场下观测, 无法应用到实际器件当中.
将单层TMDCs材料与铁磁材料结合, 利用界面处的磁近邻效应提升g因子, 有望实现可观的能谷分裂. 通过第一性原理计算, 单层2H相的MoTe₂与铁磁绝缘体EuO结合, 可以产生高达300 meV的能谷分裂^[74]. 基于反铁磁绝缘体衬底^[75]、铁磁金属Co, Ni衬底^[76]、半休氏勒合金(half-Heusler)衬底^[77], TMDCs的能谷理论上同样会有较大的能谷简并分裂.
2017年, 磁近邻效应导致的能谷塞曼分裂增大现象被观测到^[78]. 在相同大小的磁场下, EuS衬底上的WSe₂的能谷分裂明显要强于传统的Si/SiO₂衬底上的WSe₂^[78]. 与理论的塞曼分裂相比, 实验上测量到的结果较小, 这是由于EuS与WSe₂的界面并不理想, 并且材料间的晶格失配也会减弱能谷分裂^[79]. 而后实验组又证实了EuS衬底上的WS₂会产生16 meV/T的能谷激子能量分裂, 并探讨了铁磁衬底界面末端原子种类(Eu-或S-)对能谷塞曼分裂的影响^[80].
近年来, 二维磁性半导体发展迅速^[81-83], 其中一些材料也被用于磁近邻效应的衬底材料. 2018年, WSe₂/CrI₃体系中发现了二维磁性材料诱导的能谷塞曼分裂的增强^[84]. 在1—2 T的外加磁场下, 材料出现了较强的能谷分裂. 相比于传统体相铁磁材料, 二维磁性半导体与TMDCs材料之间具有界面平整的优势, 范德瓦耳斯相互作用结合有助于形成更高质量的界面. 另外, 完全由二维材料制成的异质结构也更容易在制作能谷器件中实现集成^[85]. 这些优点促使科研人员对TMDCs/CrI₃异质结构的磁近邻效应做了进一步的理论计算研究, 具体探讨了磁近邻效应对能谷的操控, 以及转角、栅压等条件对磁近邻效应的影响^[86,87]. 但是二维磁性半导体一般在空气中并不稳定, 并且无论是EuS还是CrI₃其居里温度都远小于室温, T_C-EuS = 16 K, T_C-CrI3 = 61 K, 现阶段无法利用其实现器件功能. 居里温度高于室温的钇铁石榴石曾作为铁磁衬底与TMDCs材料结合, 但是实验没有发现明显的塞曼分裂^[88]. 而居里温度高达768 K的单层h-VN铁磁半金属作为铁磁衬底理论计算证明可以使单层WS₂能谷价带分裂达到376 meV, 等效为2703 T的磁场^[89], 极为有利于能谷极化的实现, 但这一结果有待实验验证. 综上, 寻找居里温度较高且可在实验中提供有效磁近邻作用的铁磁材料衬底是需要科研人员亟待解决的问题.
多种原子调控手段也被证实可以打破K谷与K' 谷之间的能量简并, 例如利用磁性原子掺杂^[90,91]. 最近新加坡南洋理工大学的研究团队在单层MoS₂中掺杂了不同浓度的Co, 产生了局域的磁场, 使能谷分裂和g因子得到了增强^[92]. 而在单层MoS₂中掺杂一定浓度的Fe, 由于海森伯交换相互作用能谷塞曼分裂同样获得了增强^[93]. 通过给材料施加应变也可打破能谷简并^[94], 在材料中引入磁性. 单层MoS₂中缺陷的研究证实, S空位缺陷束缚激子大的有效质量及Mo元素d轨道磁矩的影响都会引起有效g因子的增强^[95]. 但是上述的调控结果都表明能谷分裂较小, 无法达到器件应用的要求, 并且无论是掺杂、应变还是缺陷都有可能会对单层TMDCs材料本征属性例如载流子浓度及禁带宽度等性质造成影响.

由于K与K' 谷在动量空间的分离与能谷中自旋轨道耦合作用, 不同能谷电子的量子坐标将受到保护, 因此能谷可以作为量子比特应用在量子计算当中. 研究人员提出基于石墨烯的能谷比特器件模型^[96]. 器件由两个量子点组成, 在量子点中能谷赝自旋处于单态或者三重态, 面内的电场可以调整能谷赝自旋的方向, 同时量子点之间的栅极也可以调控量子点间相互的耦合作用.
最早在石墨烯的研究中提出利用二维原子层材料的能谷性质实现传统光学电学器件的理论设想. 锯齿状边缘(zigzag)的弹道点接触石墨烯纳米带可以作为能谷态选择阀门和特定能谷过滤器, 其生成的谷极化电流可以通过栅压调控^[97]. Yao等^[7]利用此模型提出了能谷发光二极管(light emitting diode, LED)的设想. 利用锯齿边缘的石墨烯纳米带作为能谷过滤器, n区的电子与p区的空穴会分别通过过滤器注入到中间的本征石墨烯中. 当调控过滤器使电子空穴处于同一能谷时, 器件将出射圆偏振光, 类似于自旋LED器件^[98]. 2012年Lee等^[99]设计了一种基于扶手椅型石墨烯纳米带(armchair graphene nanoribbons)的能谷场效应晶体管, 该晶体管调控方式类似于Datta-Das模型的自旋场效应晶体管^[100]. 器件以扶手椅型石墨烯纳米带作为铁磁源极和漏极, K谷与K' 谷等效成自旋向上和向下两个态, 使能谷轨道耦合作用代替Rashba自旋轨道耦合作用^[101,102], 通过在准一维石墨烯沟道中调控注入电子态K谷与K' 谷之间的相位差, 实现电子态在能谷希尔伯特空间Bloch球上态的转动, 从而构建器件开关的功能.
除了石墨烯, 近年来二维TMDCs材料中也涌现出很多谷电子学器件研究. 二维TMDCs材料具有很强的光学响应特性, 以能谷圆偏振光选择定则为基础, 能谷LED在TMDCs材料中成功实现^[103-107]. 能谷LED圆偏振光的出射来源于六角晶格TMDCs材料在倒空间高对称点附近能量色散各向异性^[103]. 在外界电场作用下, LED器件p-n结交界处K谷与K' 谷过剩电子空穴之间交叠大小不同, 因此复合发光强度不同, 进而产生极化旋光出射. 通过调控器件沟道中电场的方向可以实现出射光左旋至右旋的改变^[104-107].
与上述扶手椅型石墨烯纳米带中能谷态类似, TMDCs材料在线偏振光激发下, 也可产生激子能谷的相干态^[108], 相干时间小于1 ps^[109,110]. 激子能谷相干态在Bloch球上的转动可以通过打破K谷与K' 谷之间的简并实现, 转动速率正比于谷间能量的劈裂大小. 由于TMDCs材料本身塞曼分裂较小, 要使得在能谷相干时间内态转动角度适合器件应用, 需要外界调控手段例如磁近邻作用增强塞曼分裂. 在器件设计中除了相干时间, 另一个重要指标就是能谷间弛豫时间. 二维TMDCs材料中电子、空穴、激子都可以携带能谷信息, 但三者能谷寿命有所区别. 一般来讲, 价带自旋分裂能量在300—400 meV, 能谷极化的空穴无法在谷间保持自旋不变的情况下弛豫, 只有同时改变能谷与自旋坐标才能发生谷间散射, 这需要原子尺度的磁散射, 因此空穴能谷寿命最长; 而激子存在相互交换作用, 能谷寿命最短^[111]. 近年来, 科研人员发现通过人为手段有序堆垛二维材料, 可以实现激子超长的能谷寿命^[112-114]. 在范德瓦耳斯异质结构中, 激子的电子空穴空间上分离, 交换作用减弱同时谷间弛豫受到抑制, 实验测得的能谷弛豫时间大大提升^[112-114], 更有利于制作能谷器件. TMDCs材料激子具有很强的光学响应性质, 如果结合谷激子转移^[115], 能谷光电器件的写入与读取信号的功能就能以此实现. 最近, 研究人员通过将纳米线波导与TMDCs材料结合, 利用近场光学手段实现了芯片上的能谷信息写入^[116].
除了新型能谷光电器件的研究, 以能谷自由度实现逻辑电路晶体管近期也有所进展. 晶体管器件依托于载流子的输运, 幸运的是相比于单层TMDCs中谷间弛豫更快的激子, 载流子具有更长的能谷寿命. 2019年, 实验人员在高晶体质量的单层MoS₂中测到了非局域能谷霍尔信号^[26,27], 证明了电子能谷在微米尺度上的迁移. 近期, 南京大学的研究团队^[117]成功研制了一种在常温下实现能谷极化电子产生, 转移输运, 探测的能谷晶体管. 器件利用新月形的不对称等离激元纳米天线在空间上分离不同手性的光子^[118], 结合源极漏极与天线不同的对准方式, 实现在电极与沟道接触的肖特基结上选择性注入能谷电子的功能. 器件栅压通过调节MoS₂的费米能级来改变注入的能谷极化电子浓度, 实现器件的开关态. 能谷极化电子由于贝里曲率会在沟道横向的两个电极产生电势差, 实现光信号向能谷电信号的转变. 实验证实在源漏偏压为零时, 能谷极化的电子会沿浓度梯度方向扩散, 同样会产生横向的输出信号.
而逻辑电路能谷器件的实现也不仅局限在单层材料中, 正如我们在第4节介绍的, 具有空间反演对称性的二维原子层材料可以通过外加电场诱导能谷效应. 最近研究人员提出在1T'相或双层2H相TMDCs材料中, 塞曼型自旋分裂可以通过外加电场诱导出现, 并可利用其调控沟道内自旋与能谷坐标间的耦合, 从而实现能谷—自旋锁定的逻辑门器件^[119,120]. 二维TMDCs材料中能谷与自旋量子坐标之间的强耦合同样也有助于自旋电子学器件中自旋调控与检测的实现^[121,122]. 2017年, TMDCs材料成功与石墨烯相结合构建了自旋阀器件. 器件结合了石墨烯超长的自旋弛豫长度与TMDCs中能谷选择性激发的优点^[121,122], 利用圆偏振光激发TMDCs特定能谷从而实现自旋极化, 扩散到石墨烯中的极化载流子在微米尺度上测量到了非局域自旋阀信号. 实验所实现的能谷极化载流子层间转移也可进一步发展优化能谷器件. 能谷与自旋间的耦合同样被理论证明可以用于产生能谷极化自旋流(valley polarized spin current)^[123]. 通过将铁磁绝缘体与单层TMDCs材料结合, 铁磁绝缘体中受到微波辐射而进动的局域自旋将选择性地激发TMDCs中的自旋, 从而产生能谷极化的自旋流. 由于单层TMDCs材料中非零的贝里曲率作用, 沟道内会出现自旋流的霍尔效应. 这种依赖于谷的自旋流可用于实现纯能谷自旋输运的低功耗逻辑器件.
近期, 科研人员提出在单层TiSiCo材料中可以通过调控能谷与材料空间层之间的耦合(valley-layer coupling, VLC)来实现能谷器件^[124]. 这一设想不同于TMDCs材料体系中以时间反演联系的K(K' )谷作为信息比特, VLC理论上利用的是TiSiCo材料正方形布里渊区中X(X' )能谷的性质. 而以VLC作用构建能谷研究蓝图最重要的一点在于其提供了能谷与外界栅极电场直接的联系, 而这一点是时间反演对称性保护下的K(K' )谷不具有的. 此外, 科研人员发现带有VLC的系统还可以表现出其他有趣的物理现象, 如能谷相关的线性光二色性、能谷的光学选择定则及层间激子的电极化. 总之, 以贝里曲率和轨道磁矩为框架的能谷研究取得了丰硕的成果, 而能谷与层耦合作用的研究蓝图为二维原子层材料谷电子学提供了一个新的探究方向.

迄今为止, 谷电子学在材料物性研究和器件研制方面涌现出大量的研究成果. 为了进一步实现高性能的谷电子学器件, 能谷极化的电学操控、能谷弛豫与相干时间的可控延长、利用原子层状材料的结构调控材料的能谷效应并构建器件都是重要的研究方向. 范德瓦耳斯异质结构、摩尔超晶格, VLC作用也为能谷器件的设计提供了新的维度. 此外, 拓展能谷材料的选择, 将能谷效应推广到三维材料也是一种可能途径. 总之, 实现高性能的谷电子学器件这一目标仍需要能谷材料性质的深入探索和器件性能的进一步优化. 期待在不远的将来, 谷电子学材料和器件研究会涌现出更多突破性的成果.