全文HTML
--> --> -->随着应用设备朝着集成化、便携化的方向发展, 人们对MPA的要求也随之增加, 不仅要求MPA在不同的光频有高吸收效率, 而且还要求能控制MPA的吸收波长和吸收效率. 之前已经有许多课题组提出不同的方法实现吸收波长、吸收效率的控制, 不过这些方法都是通过改变MPA的结构或者改变MPA周围介质材料来实现MPA吸收效率和吸收波长的控制. 如将液晶材料、微流体置于MPA上[9,10], 或利用微机械系统改变MPA的结构[11]. 但是通过液晶或者微机械系统等方法实现MPA吸收特性控制, 在增加器件制备难度的同时还会增大MPA的体积.
近几年, 由于二氧化钒(VO2)光学、电学性能突出, 并且可通过热致相变、电致相变等激励手段实现其半导体与金属之间的可逆相变, 因此逐渐引起人们的关注. 经测试发现VO2的相变温度在68 ℃, 相变后其会从高透射率的半导体状态变为高反射率的金属状态, 电阻率也会从高电阻率变为低电阻率[12,13]. 因为VO2具有上述这些相变特性, 因此逐渐地被用于MPA当中以实现MPA吸收效率的控制. Naorem等[14]设计并制备出由铝纳米阵列、硫化锌、VO2、金属衬底构成的MPA, 经测试发现, VO2温度在21—90 ℃之间变化过程中, MPA吸收效率的调制深度达到了57%. Liu等[15]利用金属钨、VO2、二氧化硅设计并制备出在近红外波段可实现吸收效率控制的MPA, 通过调节VO2温度, 该MPA吸收效率差值可达89.74%. 上述研究虽然可实现MPA吸收效率的控制, 不过并没有实现MPA吸收波长的控制.
与此同时, 人们发现将石墨烯与MPA集成后, 可不通过改变器件结构, 只需改变石墨烯的化学掺杂或两端电压就可实现MPA吸收波长的控制. 经过研究发现, 通过外接电压或者化学掺杂可动态的调制石墨烯的化学势, 而石墨烯的电导率则是由其化学势调控, 这一特性使MPA吸收波长实现调控成为可能[16,17]. Yao等[18]利用椭圆形石墨烯、二氧化硅介质层和金衬底构成MPA, 经计算发现该MPA在近红外波段具有双吸收峰, 另外可以发现随着石墨烯化学势的下降, MPA两吸收波长都实现了不同程度的红移; 范春珍等[19]提出了由十字形的石墨烯层、二氧化硅介质层、金衬底构成的MPA, 经模拟计算发现该MPA在太赫兹波段具有两个高吸收峰, 并且通过增加石墨烯的化学势, MPA的两个吸收波长都实现了蓝移.
虽然借助VO2和石墨烯在不增加器件体积和工艺难度等的情况下, 可分别实现MPA吸收效率和吸收波长的控制, 不过目前它们大多是单独实现吸收效率或吸收波长的控制, 并没有在一个MPA上同时实现吸收效率和吸收波长的控制. 但是目前在光通信、探测、光谱分析等应用中[20,21], 对于能同时实现吸收波长和吸收效率控制的MPA极为迫切, 因此需设计出结构简单、工艺制备难度低, 且能同时实现吸收波长和吸收效率控制的MPA来满足当前应用要求.
本文基于时域有限差分法(finite difference time domain method, FDTD)软件利用石墨烯和VO2材料设计了可同时控制吸收效率和吸收波长的MPA, 经过模拟分析发现, 在化学势从0.1 eV增加到3.0 eV的过程中, 该MPA的吸收波长实现了3.2 μm的调谐, 并且吸收效率均在90%以上. 而且通过改变VO2温度, 在其从半导体态相变到金属态的过程中, MPA的吸收效率调制深度达到了97.08%. 通过本文的研究, 能够为下一代的近红外无线通信、近红外材料探测、生物探测提供高质量吸收特性可控的MPA.
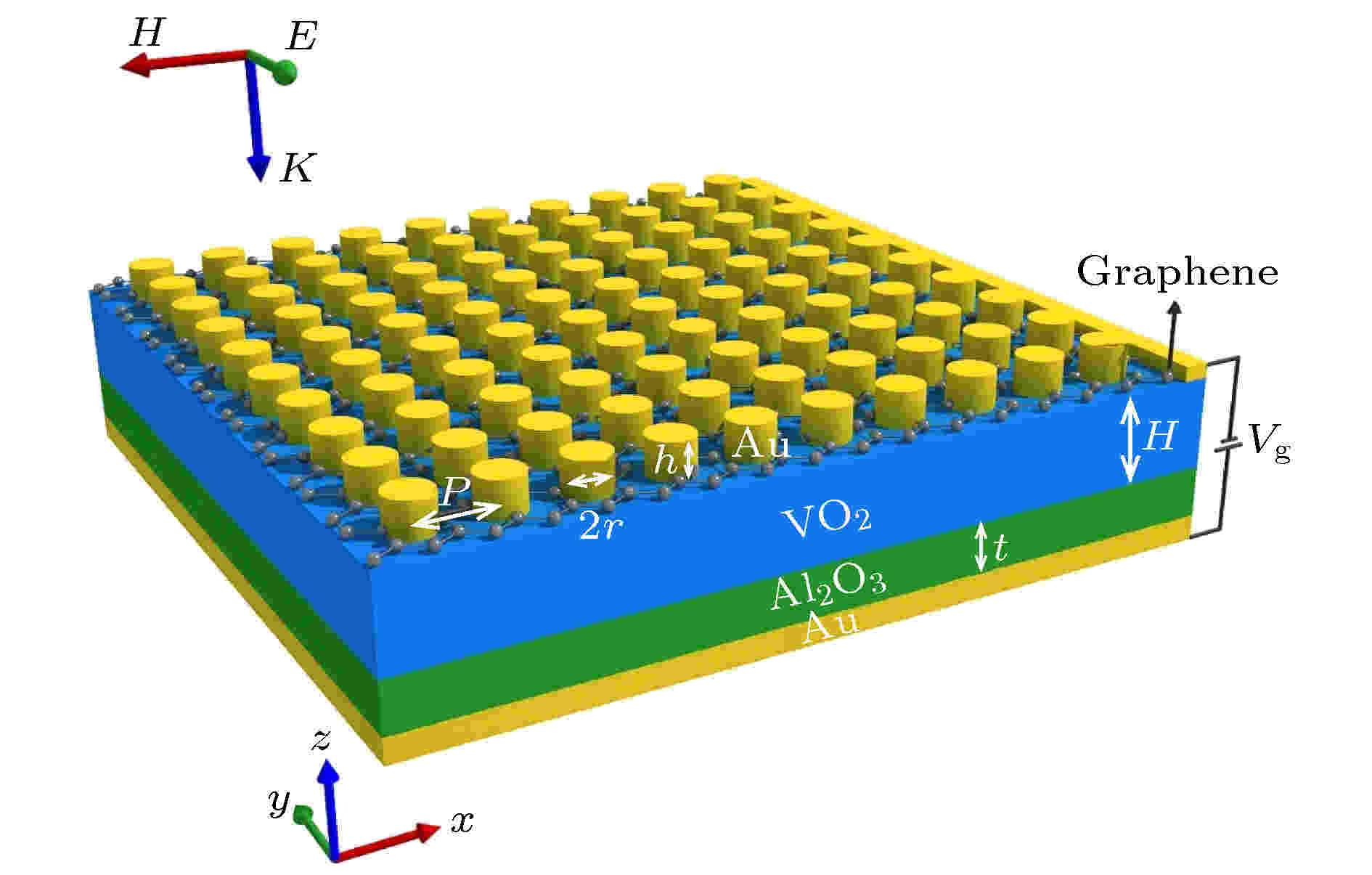图 1 吸收特性可控的MPA结构图Figure1. MPA structure diagram with controllable absorption characteristics.
在具体实验中, 以Al2O3为衬底, 利用磁控溅射方法在Al2O3衬底上获得高质量VO2薄膜, 磁控溅射方法生长的VO2具有薄膜均匀性好、可大面积制备等优点[22]. 本文中Al2O3折射率和消光系数由文献[23]获得. Au的介电常数
石墨烯的电导率δg由两部分构成[25], 分别是带内跃迁电导率δintra和带间跃迁电导率δinter, 具体关系是δg = δintra + δinter. 因为本文中MPA吸收波长在红外波段, 而对于石墨烯, 当处在红外或太赫兹波段时, 其电导率主要由δintra所决定[26,27], 所以在本文中石墨烯的δg可由(2)式表示:
从(2)式可以发现, 石墨烯的电导率δg将会被化学势Ef所影响. 而根据(3)式—(5)式可知, Ef又受外部电压Vg控制.
3.1.MPA吸收效率的控制
利用FDTD方法首先研究了VO2处在相变前后MPA的吸收效率, 具体如图2所示, 在利用FDTD方法模拟计算时, 先建立一个超材料单元, 然后在x, y方向添加周期边界(periodic), 在z方向添加完美匹配层边界条件(perfectly matched layer, PML), 网格类型选用auto non-uniform形式, 精度设为5. 从图2中可以发现, 温度TV = 5 ℃时, 以VO2为材料的MPA在波长λ = 9.66 μm时的吸收效率可达96%, 而当TV达到VO2的相变温度68 ℃时, MPA的吸收效率仅有2.8%. VO2相变前后的吸收效率调制深度(ΔA = (Amax–Amin)/Amax)可达97.08%, 相比于文献[3,14,15]有了较大的提升. 在VO2温度从5 ℃升到68 ℃过程中, 其温度会传导给石墨烯, 但石墨烯的电导率并不会产生明显变化[29]. 此时, P = 0.8 μm, h = 0.05 μm, r = 0.38 μm, H = 0.3 μm, t = 0.05 μm, Ef = 0.1 eV, 入射光为TM偏振. 由图2可知通过改变VO2的温度, 成功实现了MPA吸收效率的控制. 本文中通过外部热源实现对VO2的温度调制, 石墨烯的化学势Ef受外部电压Vg控制, 因此VO2的温度石墨烯电导率影响较小, 另外根据文献[30]可知, 利用电压将石墨烯化学势从0.1 eV调制到3.0 eV, 对二氧化钒影响也较小, 所以可知石墨烯和VO2的两种调制方式互不干扰.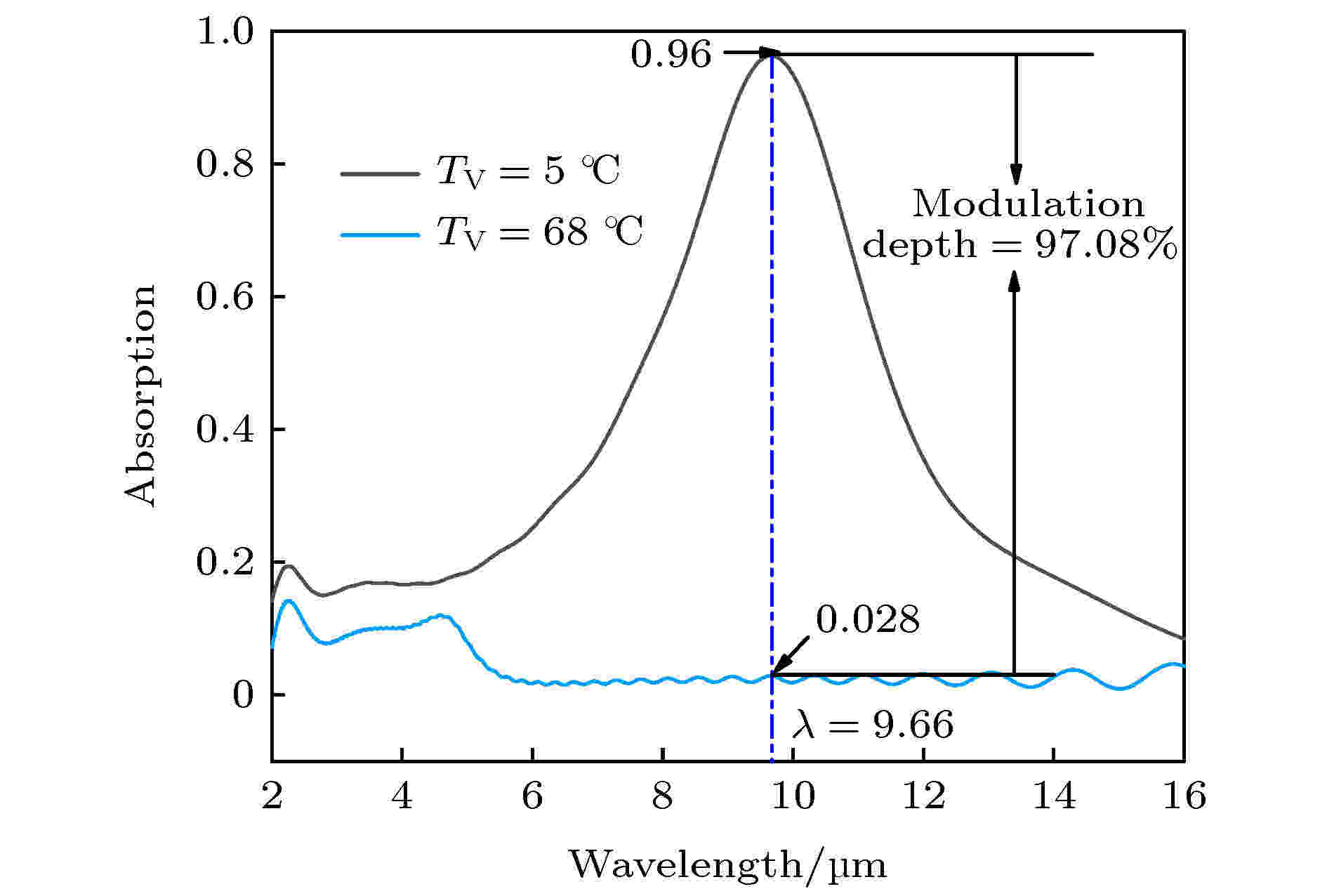
图 2 VO2不同温度下MPA的吸收效率Figure2. Absorption efficiency of MPA at different temperature of VO2.
为了探寻MPA在VO2相变前后吸收效率能实现高调制深度的原因, 我们计算了MPA在TV分别为5 ℃和68 ℃时的磁场分布(入射波长λ = 9.66 μm), 具体如图3所示. 图3(a)是TV = 5 ℃时, MPA的磁场分布, 可以看到大部分能量都聚集在Al2O3和VO2上, 这说明入射光大部分被MPA所吸收. 另外从图3(a)可以知道, 在VO2相变前MPA之所以有高吸收效率, 是因为MPA整体结构形成了法布里-帕罗干涉 (Fabry-Pérot, FP)腔共振, 即入射光在Au衬底-Al2O3/VO2-石墨烯/Au纳米阵列之间形成了干涉增强吸收.
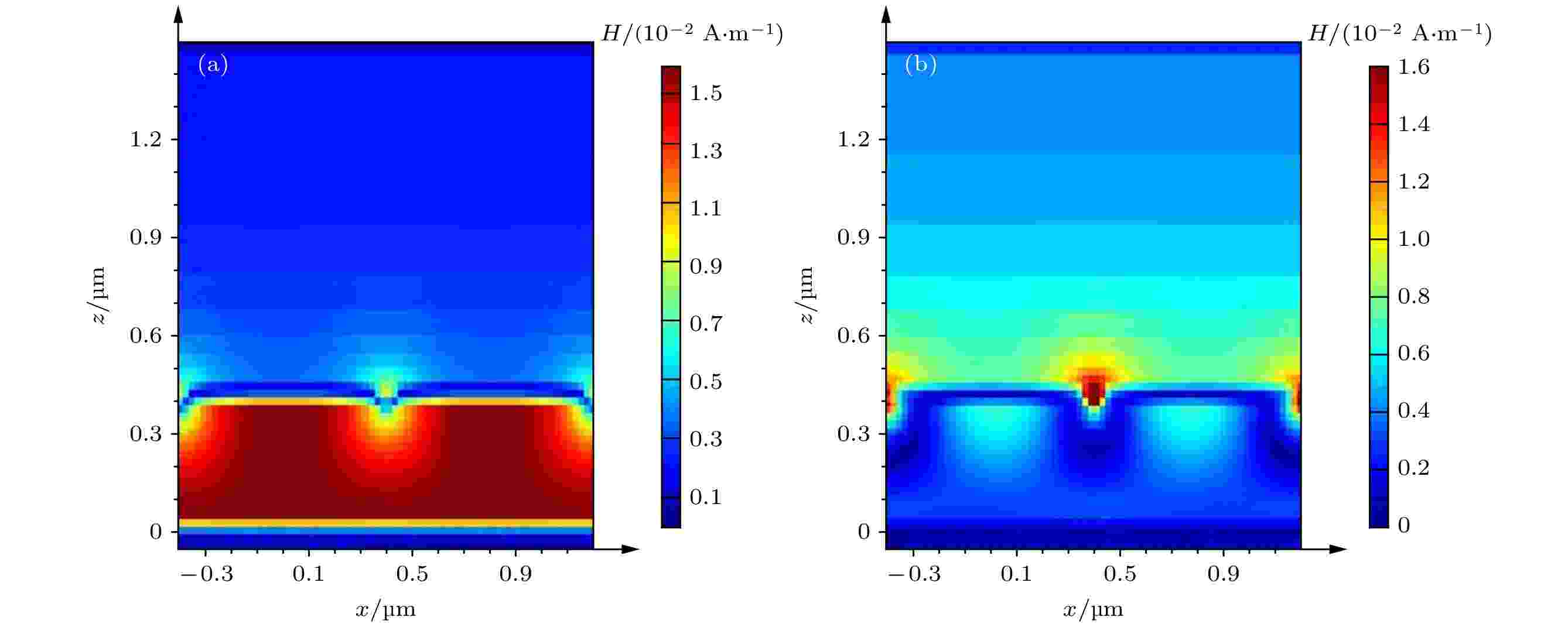图 3 VO2不同温度下MPA磁场分布 (a) TV = 5 ℃; (b) TV = 68 ℃Figure3. Magnetic field distribution of MPA at different temperature of VO2: (a) TV = 5 ℃; (b) TV = 68 ℃.
图3(b)是TV = 68 ℃时MPA的磁场分布, 可以发现因为温度升高, 使VO2产生了相变, 变成了具有金属特性的金属层, 所以当入射光照射到MPA后, 入射光的大部分能量被反射到空气当中, 而在Al2O3和VO2上的能量非常稀少, 从而导致MPA的吸收效率下降到2.8%.
在VO2相变温度68 ℃以下时, MPA能形成FP腔共振吸收, 实现高吸收效率, 是因为在达到相变温度前, VO2都是保持高透射的半导体状态. 而且在相变前VO2的折射率n和消光系数k随温度变化幅度都比较小, 当TV从5 ℃增加到40 ℃过程中, n只增加了0.5左右, 而k只增加了0.05左右, 具体如图4所示. 但是当TV突然增加到了相变温度68 ℃时, VO2的k相比于TV = 5 ℃时突然增加了0.3左右, n增加了6左右, 这就明显变成了高反射的金属状态[31], 所以当TV达到相变温度时, MPA会将入射光几乎全部反射到空气当中, MPA的吸收效率显著下降. 图4中VO2在不同温度下的折射率和消光系数由Material Studio获得, 它是一种具有多种先进算法的的综合性模拟工具, 可对晶体材料的性质进行模拟分析.
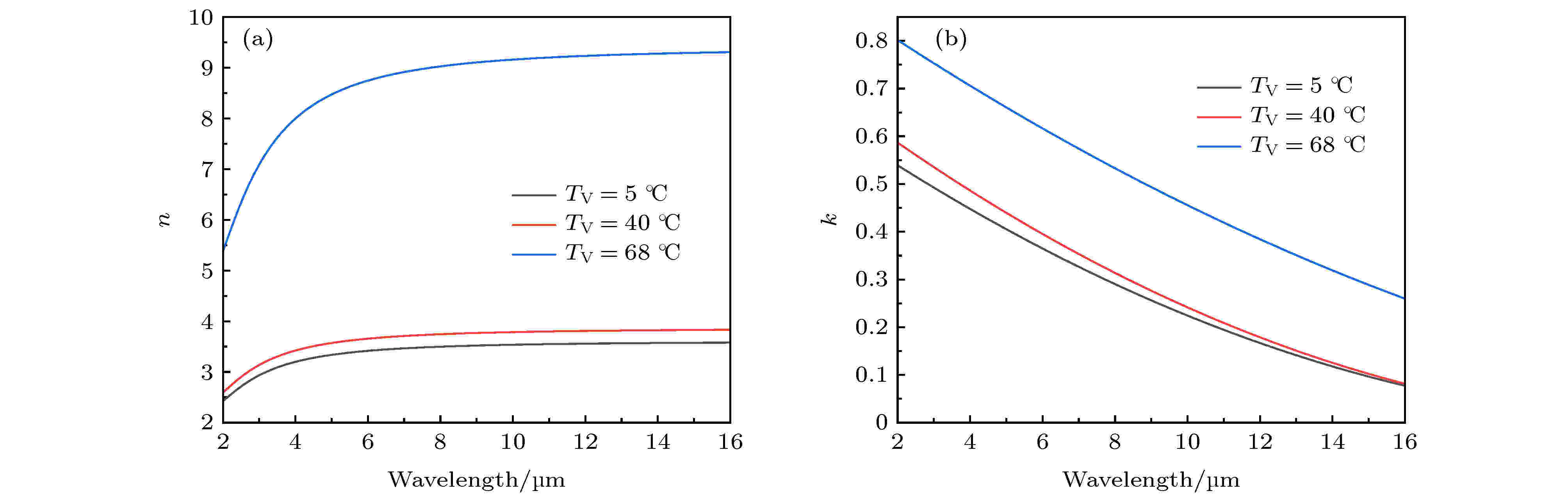图 4 温度对VO2折射率和消光系数的影响 (a) 折射率n; (b)消光系数kFigure4. The influence of temperature on the refractive index and the extinction coefficient of VO2: (a) Refractive index n; (b) extinction coefficient k.
2
3.2.MPA吸收波长的控制
利用FDTD方法研究了石墨烯化学势Ef对MPA吸收波长的影响, 具体结果如图5所示. 可以看到, 当Ef = 0.1 eV时, MPA的吸收波长为9.66 μm, 而当Ef = 3 eV时, MPA的吸收波长为6.46 μm, 吸收波长蓝移了3.2 μm. 因此利用石墨烯实现了对MPA吸收波长的控制. 此时, P = 0.8 μm, h = 0.05 μm, r = 0.38 μm, H = 0.3 μm, t = 0.05 μm, TV = 5 ℃, 入射光为TM偏振. 另外从图5中可以发现, 当Ef = 1 eV时, MPA吸收率最高, 可达99.1%.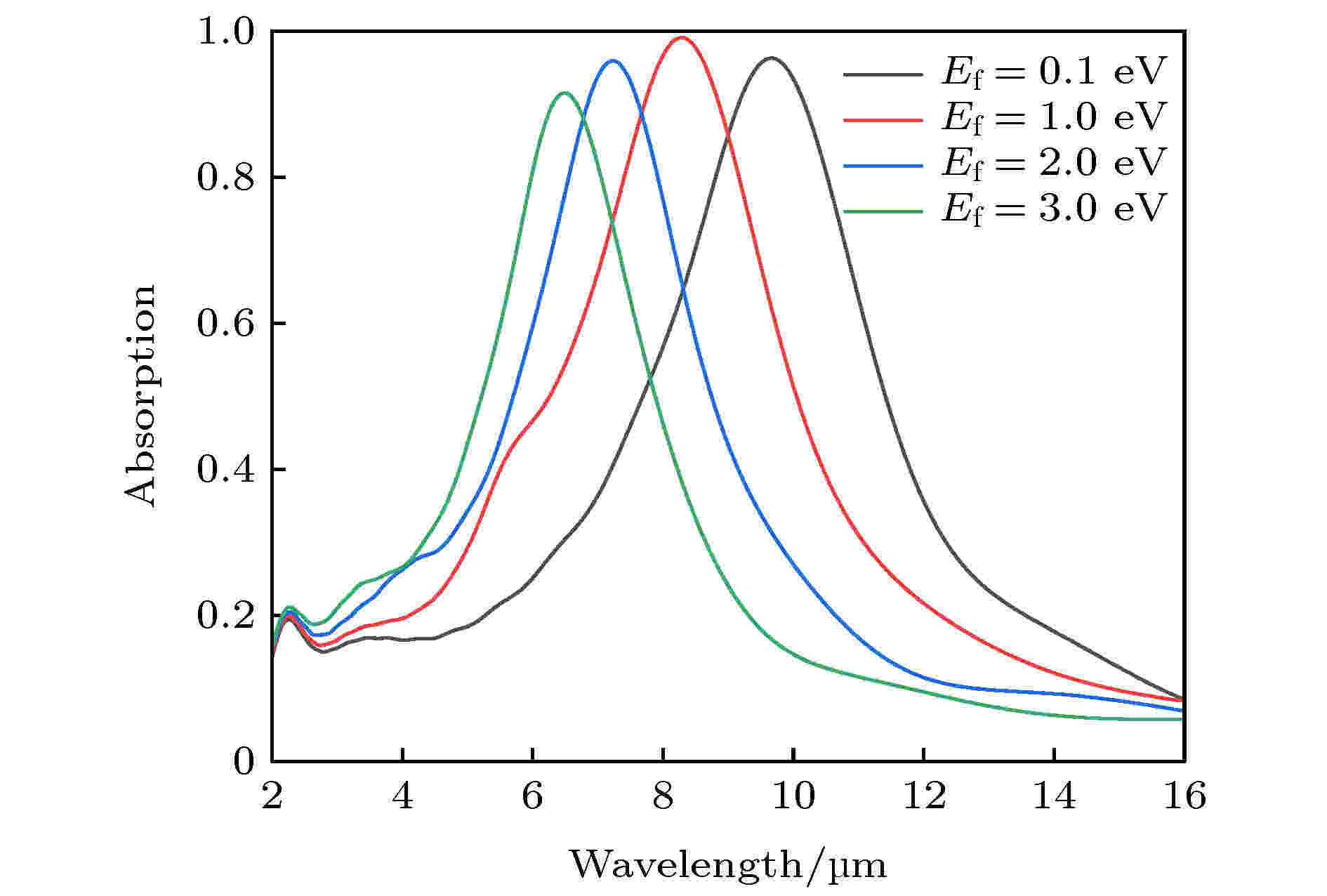
图 5 石墨烯化学势对MPA吸收波长的影响Figure5. The effect of graphene chemical potential on the absorption wavelength of MPA.
随着Ef增加, MPA吸收波长之所以会产生蓝移现象, 是因为石墨烯共振波长λre与石墨烯等效折射率有关, 具体关系为λre = α + β·neff, 其中α, β是与结构参数、周围介电常数有关的常数[32]. 根据(2)式、(6)式和图6可知, 当Ef增加时, neff会逐渐下降, 从而导致石墨烯共振波长λre逐渐减小, 进而影响了MPA的吸收波长[19,31]. 根据(3)式—(5)式可知, 对于石墨烯Ef的控制, 只需通过改变外接电压Vg就可实现MPA吸收波长的控制.
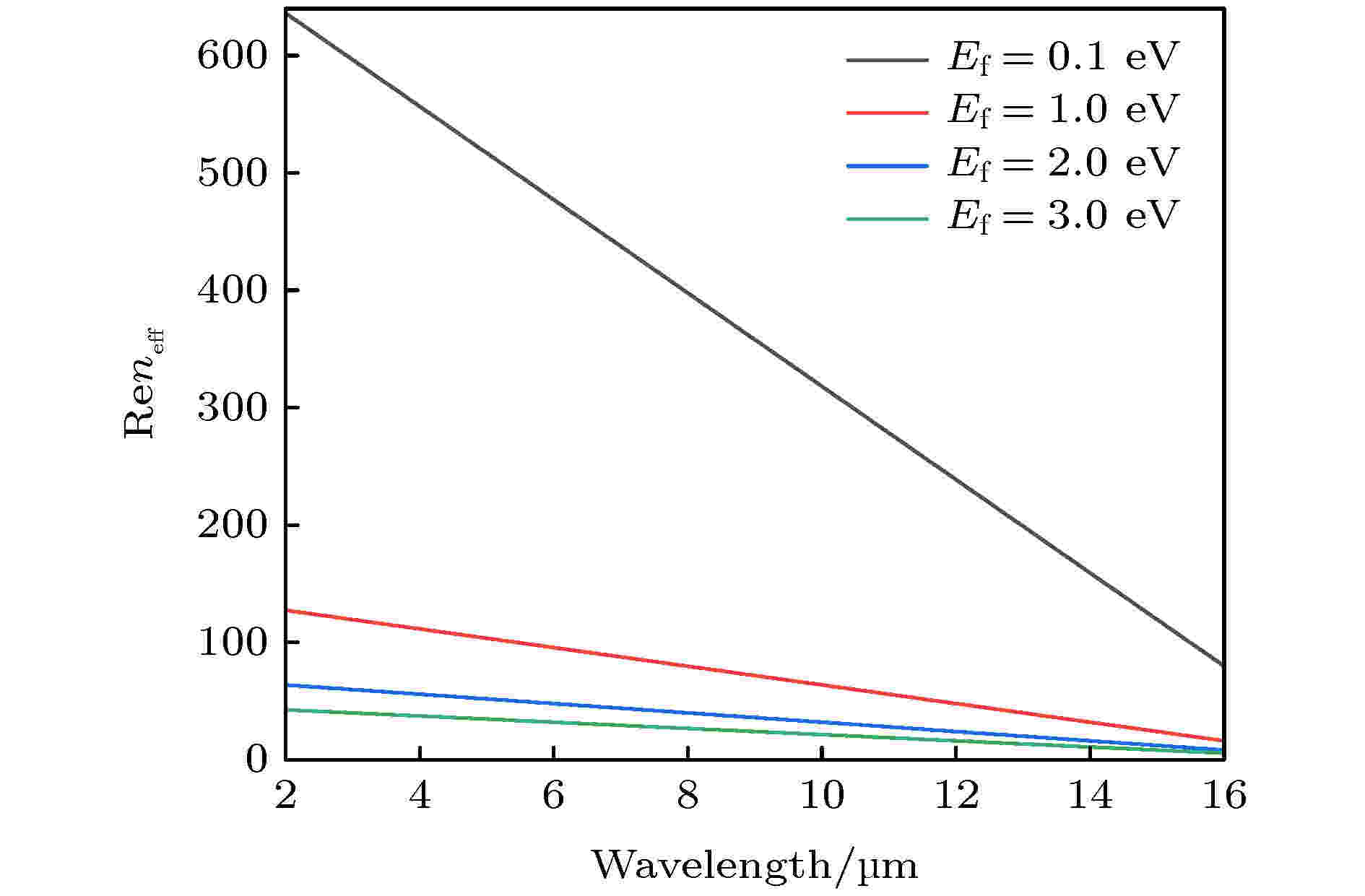图 6 石墨烯化学势对石墨烯等效折射率的影响Figure6. The effect of graphene chemical potential on the equivalent refractive index of graphene.
石墨烯电导率δg与其等效折射率neff的关系为
通过(2)式和(6)式, 计算了不同Ef下石墨烯等效折射率实部的变化趋势, 具体结果如图6所示. 从图中可知, 随着石墨烯化学势Ef升高, 石墨烯等效折射率neff却逐渐减小. 另外从图6可知, 在相同化学势Ef下, 随着波长红移, 石墨烯等效折射率neff也会逐渐减小.
2
3.3.结构参数对MPA吸收特性的影响
为了能够充分掌握MPA结构参数对其吸收特性的影响规律, 本文基于FDTD方法详细地分析了MPA结构参数对其吸收特性地影响, 此时P = 0.8 μm, t = 0.05 μm, TV = 5 ℃, Ef = 0.1 eV. 图7是周期纳米柱半径r对MPA吸收特性的影响, H = 0.3 μm, h = 0.05 μm. 从图7可以发现, 随着r的增加, MPA吸收波长会逐渐红移, 当r从0.32 μm增加到0.38 μm, 吸收波长从7.43 μm增加到了9.66 μm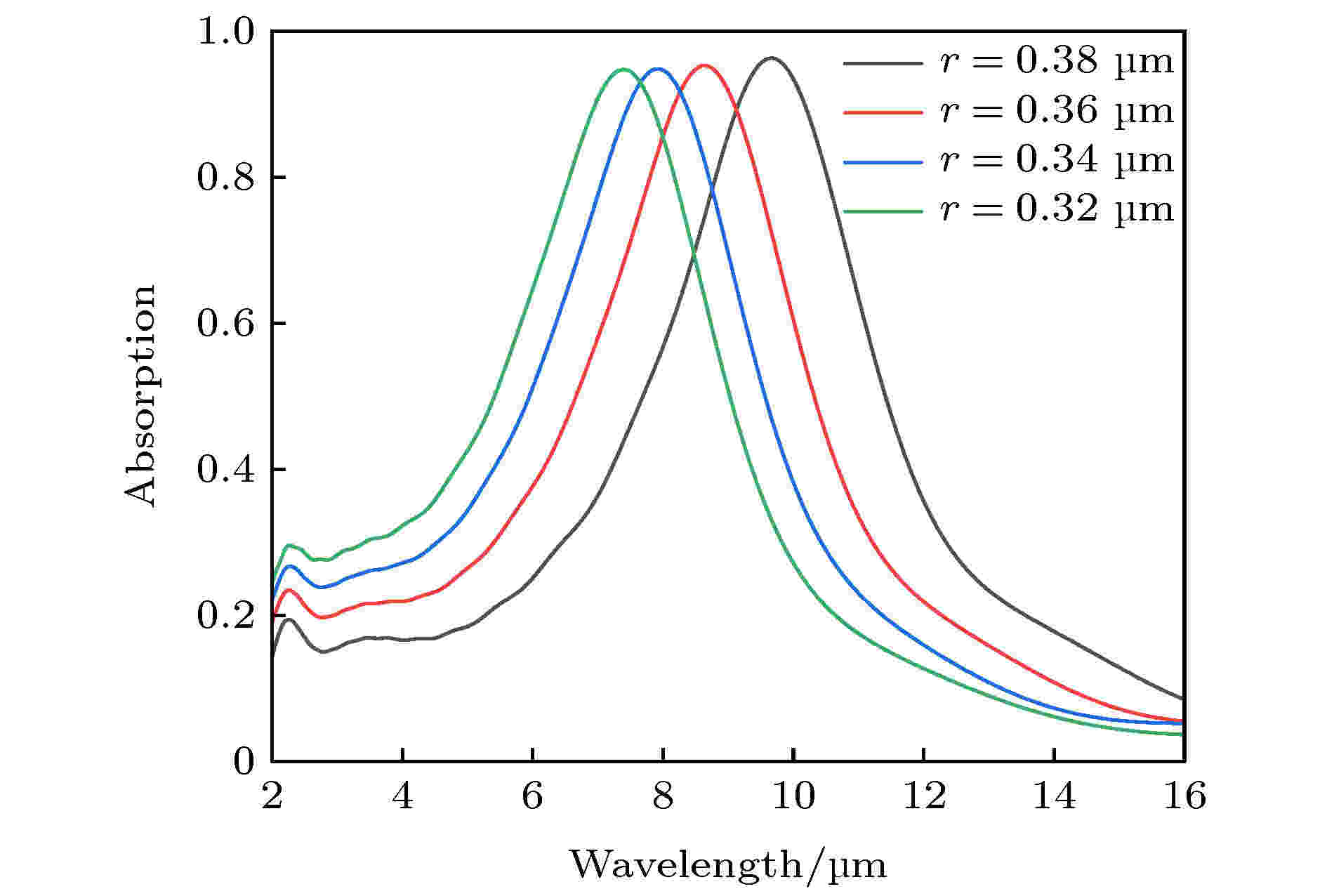
图 7 纳米柱半径对MPA吸收特性的影响Figure7. The influence of nano column radius on the absorption characteristics of MPA.
对于纳米柱半径r能够对MPA吸收波长产生影响的原因, 需要从MPA内部的FP腔共振中探索. 由图3(a)知道, 图1的MPA在VO2相变之前, 能在红外波段产生高吸收效率, 是因为FP腔共振引起的, 而FP腔共振波长λFP是与谐振腔等效折射率nq、共振腔长d有关, 具体关系可表示为λFP = 2nqd/m, 其中m是整数. 谐振腔等效折射率nq由纳米柱阵列等效折射率nTM、VO2折射率、Al2O3折射率、Au衬底折射率所决定. 当纳米柱半径r增加, 纳米柱阵列的占空比f = 2r/P增加, 根据等效介质理论可知, 当f增加, 纳米柱阵列对于TM偏振光的等效折射率nTM会增加. 由此可知, r增加会导致nTM增加, 从而引起nq增加, 最终使FP腔共振波长的红移[25], 如图8所示. 图8利用FDTD方法计算得到, 图中显示的是在波长7 μm和10 μm入射条件下, 不同纳米柱半径r对应的MPA等效折射率nq, 从图8可以看到, 当r从0.3 μm增加到0.38 μm, MPA的等效折射率也相应逐渐变大, 另外不同波长下, MPA对应的等效折射率相差并不是很明显.
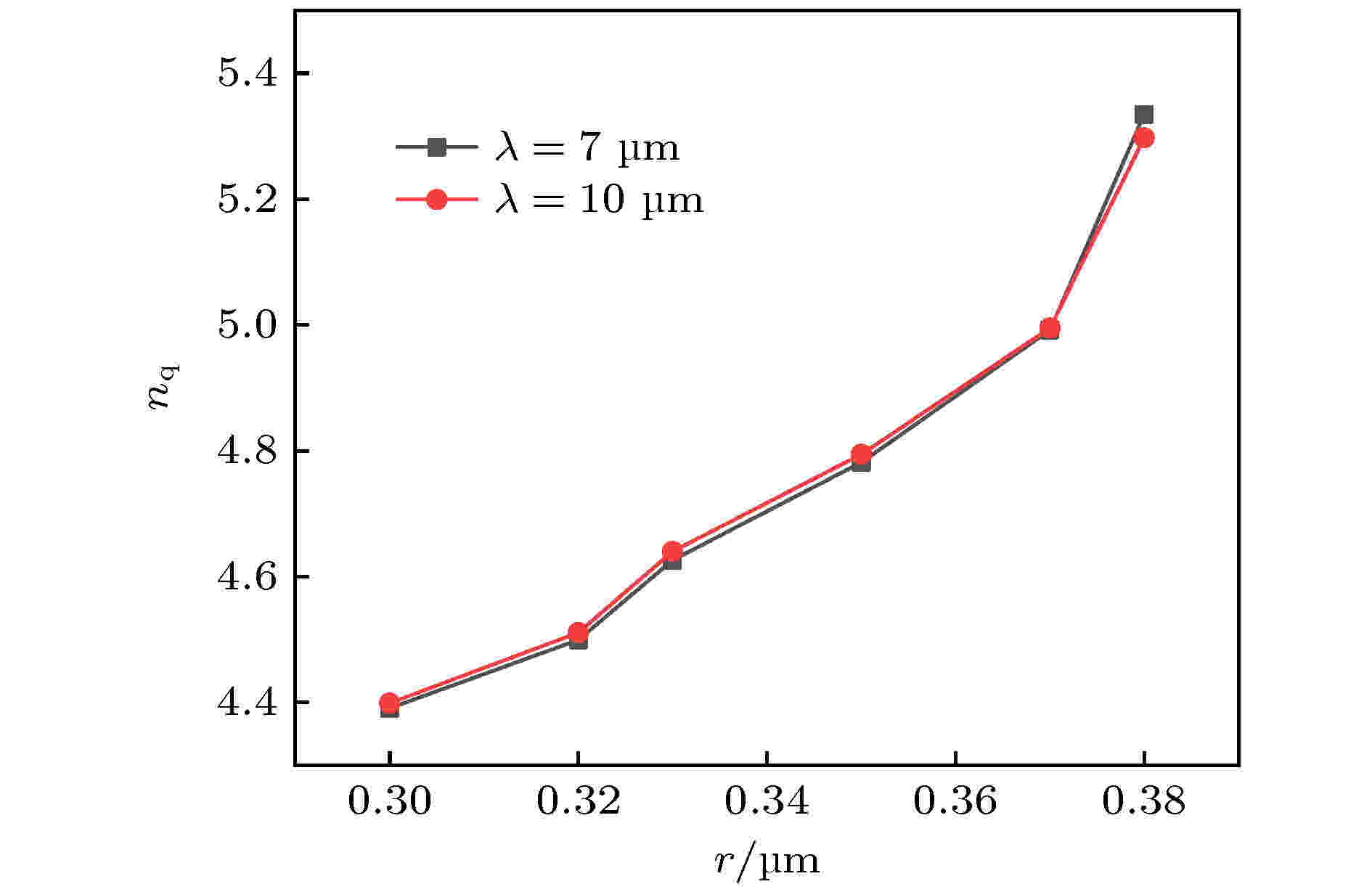图 8 纳米柱半径对MPA结构等效折射率nq的影响Figure8. The influence of nano column radius on the equivalent refractive nq of MPA.
FP腔的共振腔长d主要由Al2O3的厚度H和VO2的厚度t所决定, 但是从图3中可以发现, 其实还有一部分的光会渗透进纳米柱阵列当中, 所以共振腔长d还需将渗透进纳米柱阵列中的一部分厚度Δh考虑进去, 因此共振腔长d可以表示为d = H + t + Δh. 故纳米柱厚度h增加会使d增加, 会使FP腔共振波长λFP增加, 如图9所示, r = 0.38 μm, H = 0.3 μm. 图9是纳米柱厚度对MPA吸收特性的影响, 当h = 0.05 μm时, MPA吸收波长为9.66 μm, 而当h = 0.15 μm时, MPA吸收波长则为10.34 μm. h从0.05 μm增加到0.15 μm, MPA的吸收波长实现了0.68 μm的红移.
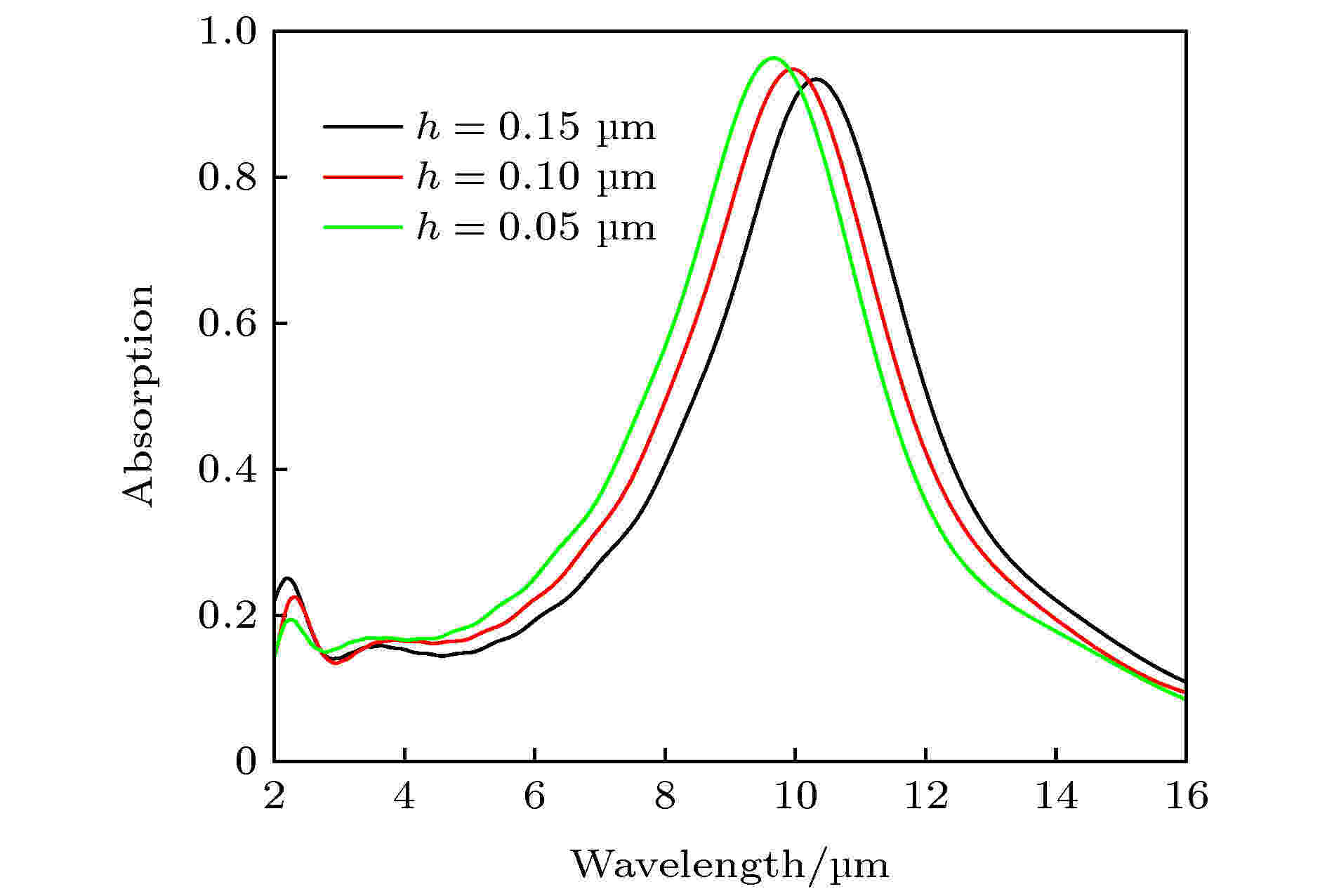图 9 纳米柱厚度对MPA吸收特性的影响Figure9. The influence of nano column thickness on the absorption characteristics of MPA.
图10是在VO2相变前其厚度H对MPA吸收波长的影响, r = 0.38 μm, h = 0.05 μm. 从图10可发现, H从0.2 μm增加到0.4 μm, MPA吸收波长将从8.06 μm增加到11.09 μm. 相比于h对MPA吸收波长的影响, H更为显著, h每增加0.1 μm, 吸收波长增加0.68 μm, 但是H增加0.1 μm, 吸收波长增加1.515 μm, 这主要是因为H是全部包含在共振腔长d中, 但是h只有一小部分厚度Δh是包含在共振腔长d中. 另外从图10可以发现, 随着H的增加, MPA吸收效率将会明显下降.
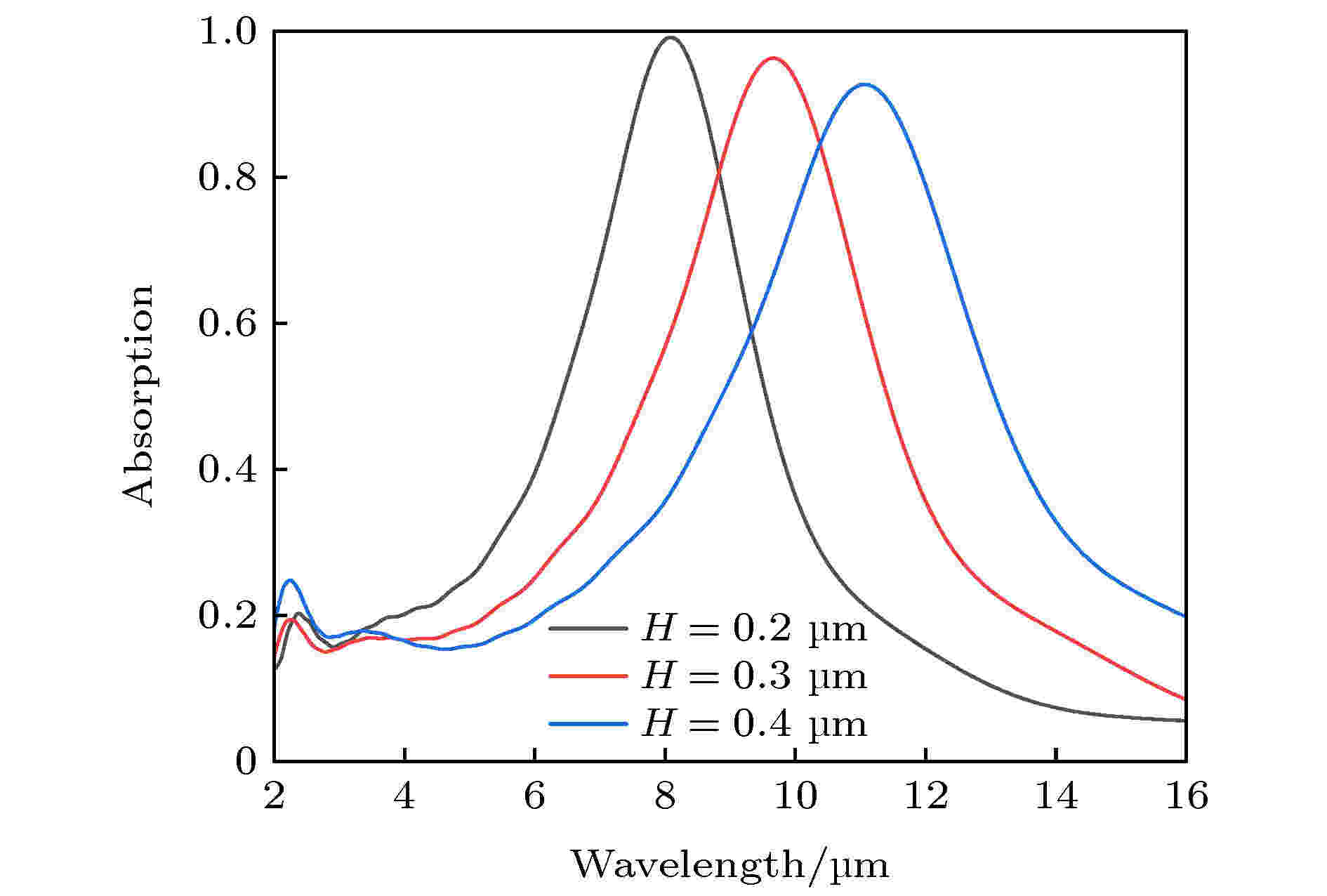图 10 VO2厚度对MPA吸收特性的影响Figure10. The influence of VO2 thickness on the absorption characteristics of MPA.
