摘要:h-LuFeO₃是一种窄带隙铁电半导体材料, 已被证明在铁电光伏领域有较好的应用前景. 然而, 较低的极化强度使光生电子-空穴对复合率大, 限制了h-LuFeO₃基铁电光伏电池效率的提高. 为改善h-LuFeO₃的极化强度, 提高光吸收性质, 本文利用第一性原理计算方法研究了In原子在h-LuFeO₃不同位置的掺杂形成能, 得到最稳定的掺杂位置, 比较了h-Lu_1–xIn_xFeO₃ (x = 0, 0.167, 0.333, 0.667)的带隙、光吸收性能及极化强度等性质. 计算结果表明, 随着In掺杂比例的增加, h-LuFeO₃的晶格常数c/a比不断增大, 铁电极化强度得到提高. 当In∶Lu = 2∶1时, 材料杂质能级出现, Fe-O轨道杂化得到增强, 提高了h-LuFeO₃的光吸收性能. 此工作证明了In掺杂是改善h-LuFeO₃极化强度和光吸收系数的有效方法, 对铁电光伏性能的提高提供一种新途径.
关键词: h-LuFeO₃/
掺杂/
光学性质/
极化强度/
第一性原理

English Abstract

全文HTML

--> --> -->

铁电材料中的铁电极化可作为内建电场促进光生载流子的分离, 使铁电光伏电池能够实现光学带隙以上的开路电压^[1-4]. 这种特殊的铁电光伏效应, 为突破传统p-n结型光伏电池的理论转换效率瓶颈提供了全新的方法, 在新能源领域表现出巨大的应用潜力^[5]. 研究人员对众多铁电材料, 例如钛酸钡(BaTiO₃)、锆钛酸铅(Pb(Zr_xTi_1–x)O₃)、铌酸锂(LiNiO₃)等的光伏性质进行了大量研究^[6-8], 然而, 较大的带隙使得大部分太阳光能量无法被吸收(太阳光能量范围约为0.4—4 eV)^[9]. h-LuFeO₃是一种新型多铁材料, 光学带隙在2.0 eV左右^[10], 在铁电光伏领域有较好的应用前景. 由于本征h-LuFeO₃较低的极化强度(仅为4.7 μC·cm^–2)^[11], 使得h-LuFeO₃基铁电光伏电池的光生载流子复合率较大, 不利于电池光电转换效率的提高. 目前实验上制备的h-LuFeO₃基铁电光伏电池的光电转化效率在0.001%左右^[12]. 先前的研究表明, 提高h-LuFeO₃的极化强度能够有效降低光生载流子的复合率, 增加电池的开路电压^[5], 改善其光吸收性质, 提高h-LuFeO₃基铁电光伏电池的性能.
室温条件下h-LuFeO₃的铁电性不稳定, 可以通过应力使其稳定存在^[13,14]. 然而采用外延应力调控h-LuFeO₃铁电性能对实验条件的要求十分苛刻^[15], 极大地限制了应力对h-LuFeO₃的调控效果. 研究发现, 采用掺杂的方法不仅能对h-LuFeO₃性能进行调控, 且能制备出铁电性在室温下稳定存在的h-LuFeO₃^[16-18]. 该方法对实验条件依赖小, 能够增强材料的铁电光伏相关性能. 在Lu位置置换离子半径较小的离子, 是获得稳定六角结构LuFeO₃的一种重要方法. Lin等^[16]通过第一性原理计算表明, Sc掺杂可以使LuFeO₃更稳定, 而其多铁性不受影响. 但In离子半径比Lu和Sc都要小, 理论上InFeO₃也是六角结构. Liu等^[17]利用In掺杂h-LuFeO₃能得到六角结构的h-Lu_1–xIn_xFeO₃ 材料, X射线全谱拟合结果表明, 随着In含量的增加, 材料结构逐渐由极性的P?6₃cm (x = 0.4—0.6)转变为非极性的P?6₃/mmc (x = 0.75), 即顺电相. 而目前并未深入研究In掺杂对h-LuFeO₃光学性能的影响. 本文基于密度泛函理论(density functional theory, DFT)的第一性原理计算方法对h-Lu_1–xIn_xFeO₃ (x = 0, 0.167, 0.333, 0.667)的磁结构、带隙、光吸收系数及自发极化等性质进行了研究, 揭示In掺杂对h-LuFeO₃的极化性质及光学性质的影响, 为提高h-LuFeO₃的铁电光伏性能提供可靠的理论依据.

使用的第一性原理计算方法均基于Materials Studio软件的CASTEP模块^[10], 采用广义梯度近似(generalized gradient approximation, GGA)和平面赝势波的方法处理电子与离子间的相互作用, 利用GGA下的Perdew-Burke-Ernzerhof (PBE)泛函作为交换关联泛函^[19]. 赝势选取Ultrasolft, 截断能为572 eV, 计算中所有晶胞和原子都进行弛豫, 以达到最稳定状态. 电子自洽精度为 10^–5 eV/atom, 原子受力小于0.05 eV/?, 晶胞结构优化时第一布里渊区的k点采用4 × 4 × 2, 电子结构优化时k点采用6 × 6 × 3. 对于磁性元素Fe采用GGA+U的方法来处理, 其中U是位库仑势. 参考先前的报道, U值选择为4.5^[20].

2

-->

3.1.晶体结构

In在h-LuFeO₃的掺杂位置有两种, 分别记为P1和P2^[21], 如图1(a)所示. 在包含30个原子的晶胞模型中, 有4个P1位原子和2个P2位原子, 首先讨论h-Lu_1–xFe_xO₃最稳定的磁序. 采用A型、C型、G型三种反铁磁结构和铁磁结构对相同的晶胞模型进行优化. 为了得到最稳定的晶胞结构, 以G型反铁磁序h-Lu_0.833In_0.167FeO₃能量为基准, 比较了不同掺杂位置的In原子替换单个Lu原子对h-LuFeO₃磁序的影响, 并比较了相对总能量, 结果如表1所列. 结果表明, 四种磁序中非线性G型反铁磁序的h-Lu_0.833In_0.167FeO₃能量最低, 这与先前报道的计算结论一致^[22], 且无论是P1位掺杂还是P2位掺杂均没有改变磁序. 利用(1)式计算了不同掺杂位置的掺杂形成能: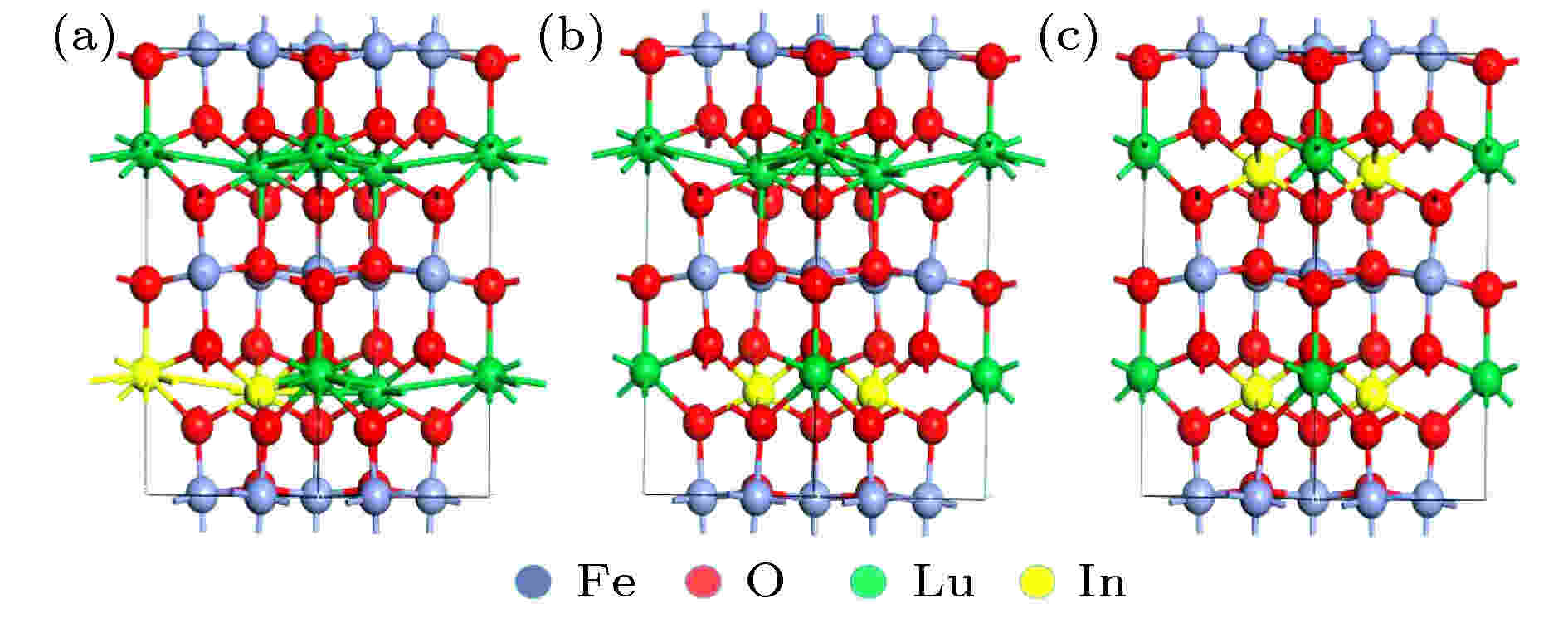
图 1 h-Lu_1–xIn_xFeO₃的球棍结构模型图　(a) P1, P2位置; (b) h-Lu_0.667In_0.333FeO₃; (c) h-Lu_0.333In_0.667FeO₃
Figure1. Model of the ball-and-stick structure of h-Lu_1–xIn_xFeO₃: (a) P1, P2 position; (b) h-Lu_0.667In_0.333FeO₃; (c) h-Lu_0.333In_0.667FeO₃

${E_{\rm{f}}} = E{}_{{\rm{doped}}} - {E_{{\rm{pristine}}}} - {\mu _{{\rm{Lu}}}} + {\mu _{{\rm{In}}}},$

其中E_f为In掺杂形成能, E_doped和E_pristine分别代表掺杂后和掺杂前的h-LuFeO₃总能, μ_Lu和μ_In分别为Lu和In的化学势. 形成能反映了掺杂的难易程度, 形成能越小越容易掺杂. 通过计算发现, P1位置的掺杂形成能为5.426 eV, P2位置的掺杂形成能为5.581 eV, 表明P1位置相对P2位置更容易掺杂.

掺杂位置	G型/eV	C型/eV	A型/eV	铁磁型/eV
未掺	0	0.01	1.37	0.01
P1 位置	0	10.38	3.14	12.51
P2 位置	0	0.03	0.25	1.41

表1不同磁序下不同位置的In掺杂相对能量变化
Table1.Relative energy changes of In doping at different positions under different magnetic orders.

由于本征InFeO₃稳定相是顺电相P?6₃/mmc, 计算时控制了In∶Lu最高为2∶1. h-LuFeO₃的P1位置比P2位置更容易掺杂, 故均选择In原子替换P1位原子, In∶Lu分别为1∶2和2∶1时, 对应的晶胞优化结果如图1(b)和图1(c)所示. 以非线性G型反铁磁序的h-Lu_0.833In_0.167FeO₃能量为基准, 比较了不同磁序的晶胞结构优化后相对能量的变化, 结果如表2所列. 随着掺杂浓度的提高, h-Lu_1–xIn_xFeO₃ (x = 0.333, 0.667)磁序未发生变化, 非线性G型反铁磁序的h-Lu_0.833In_0.167FeO₃能量最低.

材料	G型/eV	C型/eV	A型/eV	铁磁型/eV
h-Lu2/3In1/3FeO3	0	0.0126	0.8604	0.8604
h-Lu1/3In2/3FeO3	0	0.0096	0.8952	0.9487

表2In∶Lu为1∶2和2∶1时h-Lu_1–xIn_xO₃不同磁序的相对能量
Table2.Relative energy of h-Lu_1–xIn_xO₃ with different magnetic sequencewhen In∶Lu is 1∶2 and 2∶1.

确定了最稳定的磁序后, 计算P1位的In掺杂对h-LuFeO₃晶格参数的影响, 与先前实验报道的h-LuFeO₃晶格参数进行对比, 结果如表3所列, 表明非线性G型反铁磁序h-Lu_0.833In_0.167FeO₃结构优化结果与实验值符合较好. 随着In原子含量的提高, h-Lu_1–xIn_xFeO₃晶胞沿c轴拉伸, c/a比从1.94增加到2.04, 这有利于材料自发极化率的增强. 而晶胞略微缩小, 我们猜测可能是由于In的离子半径比Lu离子半径小造成的.

材料	晶格常数/?			体积/?3	轴角/(°)
	a	b	c		α	β	γ
(h-LuFeO3)[15]	5.965	5.965	11.702
(h-LuFeO3)[23]	5.985	5.985	11.770
h-LuFeO3	6.067	6.067	11.756	374.926	90.000	90.000	119.993
h-Lu0.833In0.167FeO3	6.042	6.042	11.880	374.770	90.047	90.004	120.214
h-Lu0.667In0.333FeO3	6.005	6.007	11.935	372.221	90.014	90.033	120.166
h-Lu0.333In0.667FeO3	5.922	5.923	12.119	367.516	89.999	90.001	120.173

表3h-Lu_1–xIn_xO₃的结构优化结果
Table3.Structure optimization results of h-Lu_1–xIn_xO₃.

2 -->

3.2.电子结构

h-Lu_0.833In_0.167FeO₃, h-Lu_0.667In_0.333FeO₃以及h-Lu_0.333In_0.667FeO₃的能带图见图2. 从图2(a)可知, h-Lu_0.833In_0.167FeO₃的带隙大小为1.16 eV, 小于实验值(2.0 eV)^[24], 与先前文献中利用了Local Density Approximation (LDA), Perdew-Burke-Ernzerhof for solid (PBEsol)等方法计算的h-LuFeO₃带隙对比如表4所列. 带隙偏小是因为利用DFT方法会低估材料带隙, 然而掺杂计算的主要目的是为了预测相对变化趋势, 而非研究绝对值的大小, 因此选取DFT方法并不影响最终结论.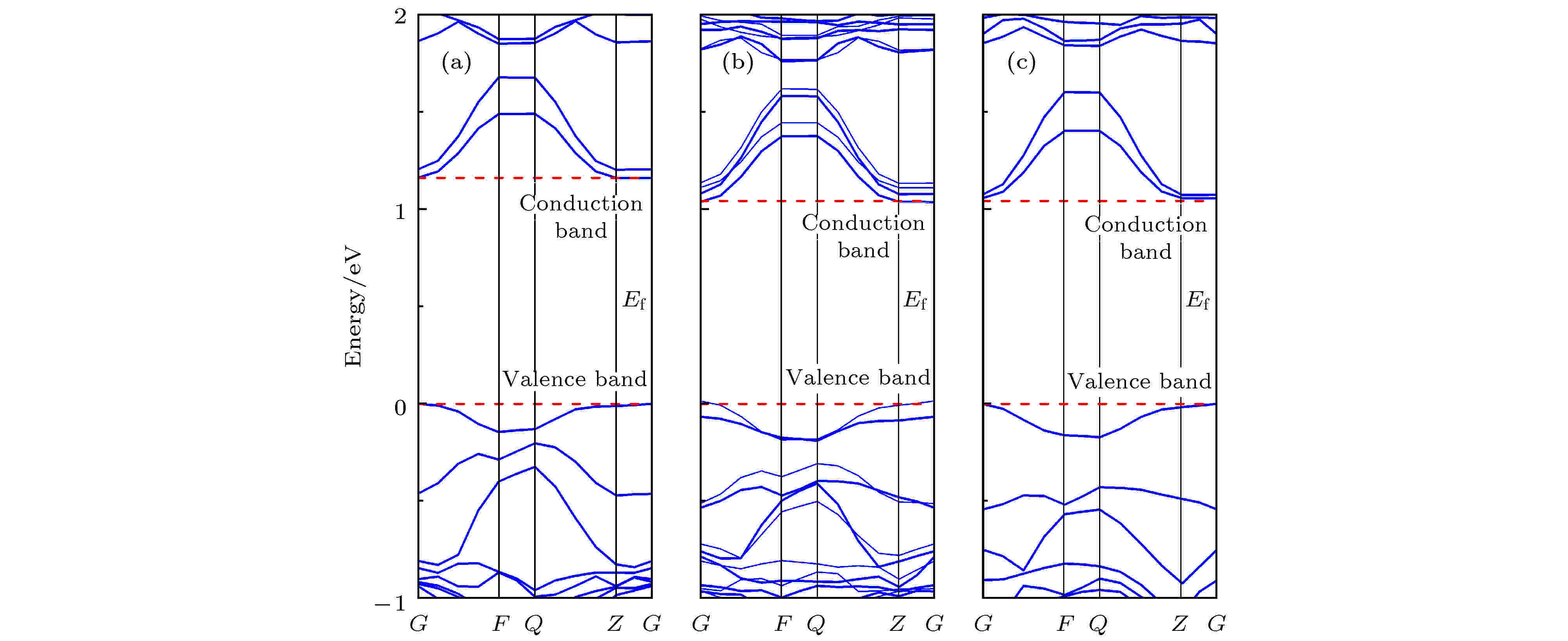
图 2 h-Lu_1–xFe_xO₃的能带图　(a) h-Lu_0.833In_0.167FeO₃; (b) h-Lu_0.667In_0.333FeO₃; (c) h-Lu_0.333In_0.667FeO₃
Figure2. Energy band diagrams of h-Lu_1–xFe_xO₃: (a) h-Lu_0.833In_0.167FeO₃; (b) h-Lu_0.667In_0.333FeO₃; (c) h-Lu_0.333In_0.667FeO₃

	CASTEP[22]	WIEN2K[24]	VASP[25]	本工作
交换关 联泛函	LDA	GGA- PBE	GGA- PBEsol	GGA- PBE
U值	3	4.5	4.61	4.5
带隙/eV	0.54	1.1	1.35	1.16

表4本工作带隙计算结果与已发表结果对比
Table4.Comparison of calculated band gap results with published results.

三种计算模型的h-Lu_1–xIn_xFeO₃导带底和价带顶均在G点, 表明h-Lu_1–xIn_xFeO₃为直接带隙半导体材料. 如图2(b)所示, 当In∶Lu = 1∶2时, 即In占据晶胞中两个P1位置时, 带隙减小到1.05 eV, 表明In原子的替换可减小材料的带隙. 由图2(c)可知, 当In∶Lu = 2∶1时, In完全占据4个P1位置, 带隙的变化并不明显, 仅下降了0.01 eV; 但此时导带底(1—2 eV范围内)杂质能级的增多有利于提升材料的光吸收系数.
为了深入研究In掺杂对h-LuFeO₃带隙两端电子跃迁的影响, 分析了未掺杂h-LuFeO₃和h-Lu_0.333In_0.667FeO₃在带隙附近, 即能量在–2— 2 eV间的态密度图, 如图3所示. 由图3(a)可知, 未掺杂h-LuFeO₃的导带底(1—2 eV范围内)大部分由Fe 3d轨道占据, 小部分由O 2p轨道占据; 价带顶(–1—0 eV范围内)主要是O 2p轨道占据, 而Lu对价带顶和导带底的贡献有限, 从主要占据价带顶的O 2p轨道电子转变为主要占据导带底的Fe 3d轨道电子, 表现出Fe 3d轨道与O 2p轨道的高度杂化. 因此调控Fe 3d轨道与O 2p轨道杂化程度可以影响材料的光吸收性能.
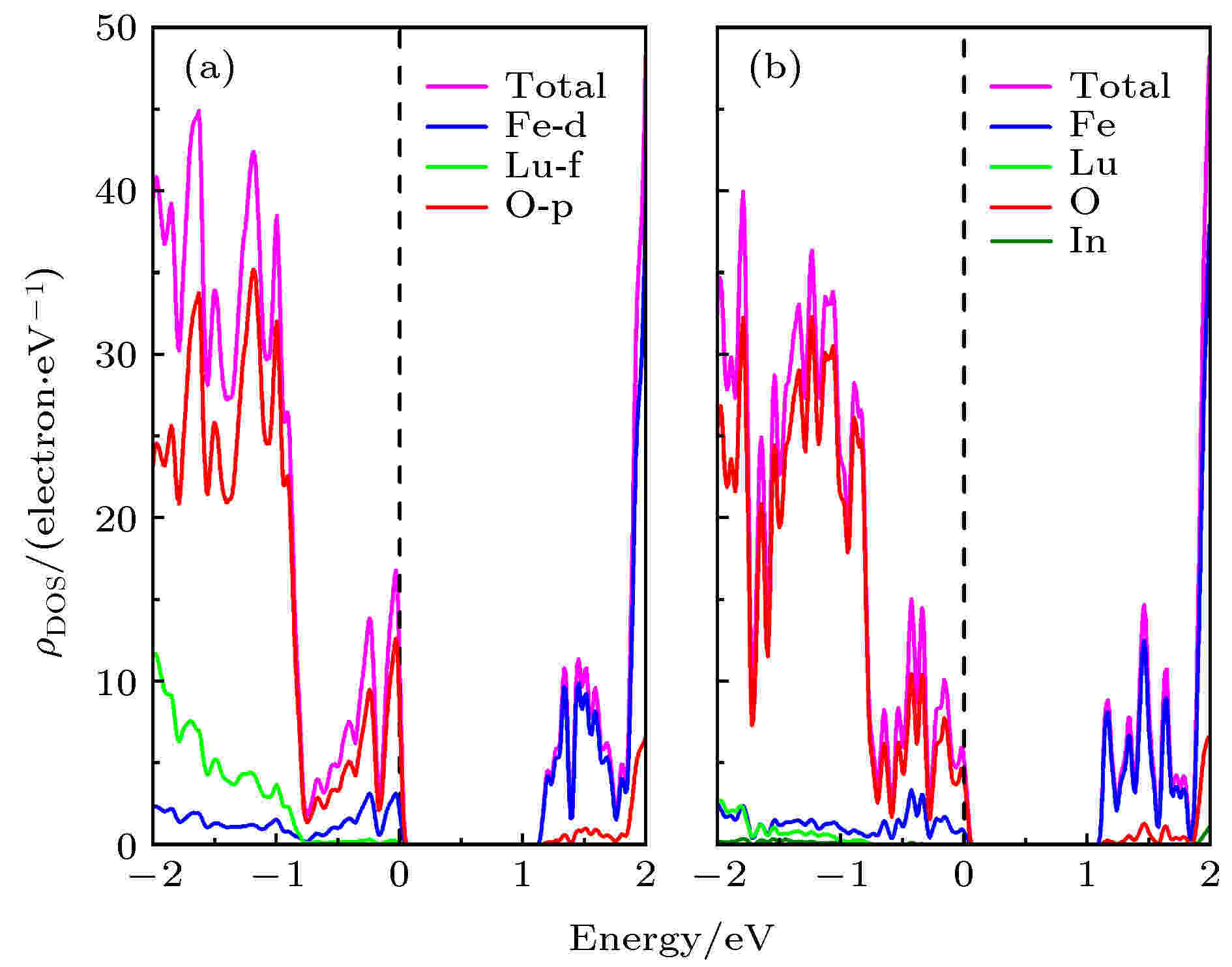图 3 分布态密度图　(a) 未掺杂的h-LuFeO₃; (b) h-Lu_0.333In_0.667FeO₃
Figure3. Distribution density of states: (a) Undoped h-LuFeO₃; (b) h-Lu_0.333In_0.667FeO₃.

图3(b)为h-Lu_0.333In_0.667FeO₃的态密度图, 导带底(1—2 eV范围内)大部分由Fe 3d轨道占据, 小部分由O 2p轨道及In 4s轨道占据; 价带顶(–1—0 eV范围内)主要由O 2p轨道占据. 相对未掺杂的h-LuFeO₃, h-Lu_0.333In_0.667FeO₃杂质能级的出现及导带底Fe 3d轨道赝势峰强度的增大, 使材料带隙缩小, 接收价带电子的能力增强. 分析结果表明, In掺杂影响了材料Fe-O间的轨道杂化, 提高了h-Lu_0.333In_0.667FeO₃的光吸收系数.
2 -->

3.3.光吸收性能及铁电极化强度

图4为光沿c轴入射h-Lu_1–xIn_xFeO₃的光吸收系数变化情况, 发现在1.64—2.4 eV范围内, 掺杂后的光吸收系数比未掺杂的h-LuFeO₃略微减小. 但在能量大于2.4 eV区域, 材料光吸收系数随着In/Lu比值的增大而增大, 表明In掺杂能够有效提高h-LuFeO₃在太阳光能量范围内的光吸收效率.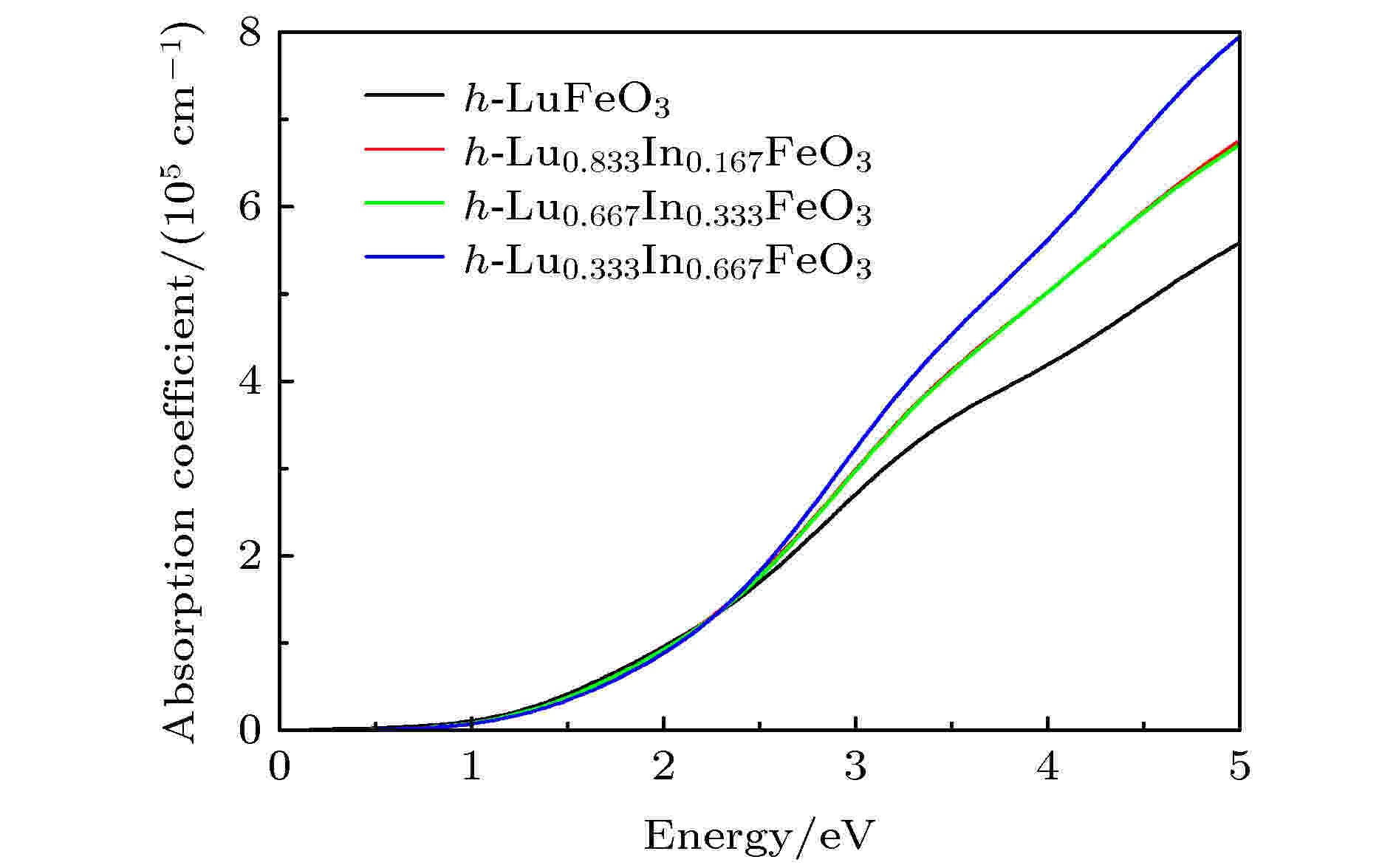
图 4 In掺杂前后h-LuFeO₃光学吸收系数随入射光子能量的变化
Figure4. Change of optical absorption coefficient of h-LuFeO₃ with incident photon energy before and after In doping.

铁电极化是影响铁电光伏性能的另一个重要性质. 铁电光伏材料以自身铁电极化为内建电场, 增大铁电极化能够减少载流子复合概率^[26], 因此缩小带隙和增大铁电极化强度是提高铁电光伏材料性能的两大研究方向. 根据伯恩有效电荷定性计算自发极化强度计算公式为^[27]

$\Delta {P_\alpha } \cong \sum\limits_{j\beta } {\frac{{\partial {P_\alpha }}}{{\partial {u_{j\beta }}}}} \left( {{u_{j\beta }} - {u_{0j\beta }}} \right) = \frac{e}{\varOmega }\sum\limits_{j\beta } {Z_{_{j\alpha \beta }}^{^{\rm{*}}}} \Delta {u_{j\beta }},$

其中e表示电子电荷量, $Z_{_{j\alpha \beta }}^{^{\rm{*}}}$表示伯恩有效电荷, Δu_jβ表示原子相对位移, Ω表示晶胞总体积. 将h-Lu_1–xIn_xFeO₃沿c轴的伯恩有效电荷代入(2)式, 计算得到h-LuFeO₃, h-Lu_0.833In_0.167FeO₃, h-Lu_0.667In_0.333FeO₃及h-Lu_0.333In_0.667FeO₃沿c轴的铁电极化强度, 分别为3.93, 5.91, 7.92和11.02 μC·cm^–2, 如图5中红色曲线所示. 图5中蓝色曲线表示随In/Lu比的增大, h-Lu_1–xIn_xFeO₃晶胞的晶格参数c/a比值的变化. 可见材料的极化值与c/a比有相同的变化趋势, 结果表明在保持铁电相的前提下, 提高材料的c/a比可提高材料的极化强度. 对铁电光伏材料而言, 极化强度的增大能够得到更高的光生电压及光生电流^[11]. 此外, 改变c/a比相当于材料受力沿c轴产生拉应变, 而拉应变能够减小六角铁酸盐类多铁材料的带隙并增强光吸收性质^[13].
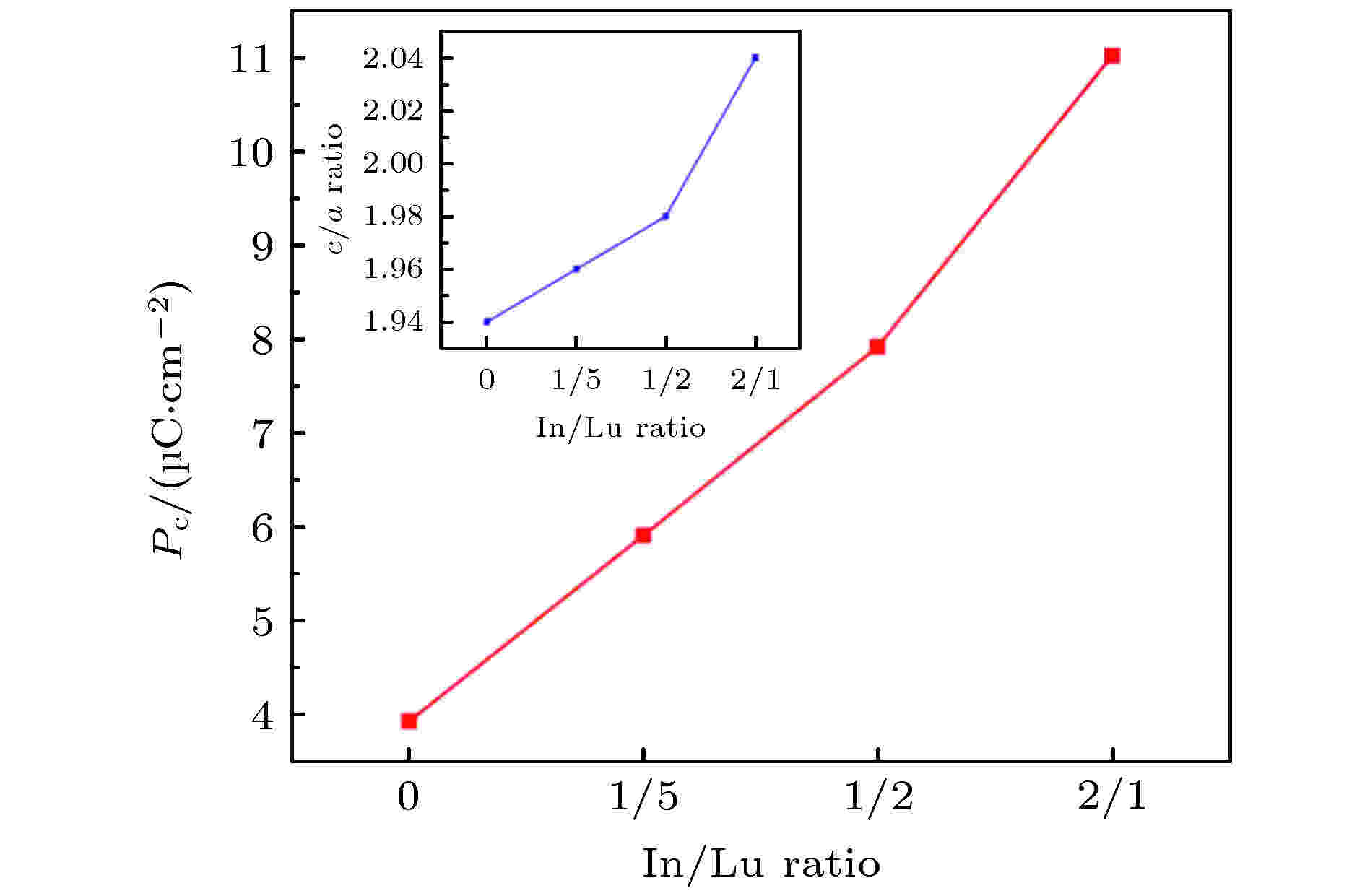图 5 不同In/Lu比的h-Lu_1–xIn_xFeO₃极化值(红色曲线)和晶格常数c/a比(蓝色曲线)
Figure5. Polarization values (red curve) and lattice constant c/a ratios (blue curve) of h-Lu_1–xIn_xFeO₃ with different In/Lu ratios.

本文基于DFT的第一性原理计算方法, 研究了h-Lu_1–xIn_xFeO₃ (x = 0, 0.167, 0.333, 0.667)的带隙、极化强度及光吸收性质. 研究结果表明, In原子在h-LuFeO₃晶胞中会优先替换P1位置, 随着In掺杂量的增加, h-Lu_1–xIn_xFeO₃的晶胞沿c轴拉伸. 当x达到0.667时, 晶格常数c/a比从1.94增大至2.04. 通过分析h-LuFeO₃及h-Lu_0.333In_0.667FeO₃的分态密度可知, c/a比的增大能够增强h-Lu_0.333In_0.667FeO₃层间的Fe-O轨道杂化程度, 提高在太阳光范围内的光吸收系数. 利用伯恩有效电荷定性地计算h-In_1–xLu_xFeO₃的极化强度, 发现In掺杂能够提高材料沿c轴的极化强度, 且极化值的变化趋势与晶格常数c/a比的变化趋势相同. 因此, In掺杂能够有效提高h-LuFeO₃的光吸收系数及铁电极化强度, 为提高铁电光伏性能提供重要理论指导.