删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

原子尺度构建二维材料的第一性原理计算研究

本站小编 Free考研考试/2021-12-29
摘要:随着信息技术的不断进步, 核心元器件朝着运行速度更快、能耗更低、尺寸更小的方向快速发展. 尺寸不断减小导致的量子尺寸效应使得材料和器件呈现出许多与传统三维体系不同的新奇物性. 从原子结构出发, 预测低维材料物性、精准合成、表征、调控并制造性能良好的电子器件, 对未来电子器件的发展及相关应用具有至关重要的意义. 理论计算能在保持原子级准确度的情况下高效、低耗地预测材料结构、物性、界面效应等, 是原子制造技术中不可或缺的重要研究手段. 本综述从第一性原理计算角度出发, 回顾了近年来其在二维材料结构探索、物性研究和异质结构造等方面的应用及取得的重要进展, 并展望了在原子尺度制造背景下二维材料的发展前景.
关键词: 原子制造/
二维材料/
第一性原理计算

English Abstract


全文HTML

--> --> -->
1.引　言
原子制造技术是目前最前沿、最极限的材料和器件制造技术, 是未来高性能器件向运行速度更快、能耗更低、尺寸更小方向进一步发展的关键技术. 功能导向的低维材料结构和物性的预测是原子制造技术上游最重要的部分之一. 二维材料是指材料在两个维度方向上具有较大尺寸而在另外一个维度上仅存在有限尺寸厚度, 是低维纳米材料家族中的重要成员.
关于二维材料的研究可以追溯到2004年, 单层自由状态的石墨烯首次在实验上成功剥离出来[1], 推翻了热涨落条件下不允许任何二维介质在有限温度下存在的认知误区. 在此基础上, 研究人员提出了二维材料的概念. 二维材料中载流子迁移、热量扩散均限制在二维平面内, 材料中受限电子、光子等呈现出许多与三维结构中不同的、物理内涵十分丰富的新奇量子现象[2]和效应. 与传统三维材料不同, 二维材料能极大减弱与基底间的耦合, 为电场调控、化学修饰、异质结构建等提供了极大的便利; 二维材料通常是机械易弯曲的, 是发展柔性器件[3]的理想材料; 二维材料由于其超薄的厚度在未来原子层厚度的高集成度光、电、磁性器件等领域具有广泛的应用前景; 另外, 二维材料具有极大的比表面积, 也为催化、超级电容器等研究注入新的活力.
二维材料研究由最初的石墨烯一枝独秀到目前形形色色的二维材料百花齐放. 除了石墨烯, 一系列的二维材料被相继报道[4], 如硅烯[5-11]、锗烯[12,13]、锡烯[14,15]、黑磷[16,17]、金属硫族化合物[18,19]、MXene [20,21]等. 尤其是最近三年, 研究人员通过高通量方法从材料数据库中搜索出数十个家族、总量上千种的新型二维材料, 并构建了二维晶体材料数据库, 是二维材料研究领域新的里程碑. 这些二维材料具有多样的电子结构[22], 覆盖金属、半导体、绝缘体、半金属和超导体等类型, 同时很多材料具有非常优异的力学、磁学和光学性质.
现阶段二维材料的研究主要集中在材料制备、表征、物性研究、修饰改性和应用探索等方面. 得益于理论计算方法和高性能超级计算机的快速发展, 理论计算在目前二维材料研究的快速发展中起到了举足轻重的作用. 理论计算不但能够高效、准确地预测二维材料的结构稳定性以及电子学、力学、光学、磁学等物性, 而且对实验现象也能进行充分的理论解释. 因此, 几乎每一个二维材料领域中的重要成果中均能看到理论计算的身影.
尽管已有一些二维材料的研究综述, 但近年来二维材料的发展日新月异. 在高通量材料计算和二维材料数据库的推动下, 一系列的新型二维材料、二维材料中的新奇物性不断涌现, 关于二维材料研究的报道逐年递增, 如图1所示. 因此, 本综述将从理论计算角度出发梳理二维材料的研究脉络, 回顾近年来发表的一些具有影响力的工作. 在第2节中, 将简要介绍基于密度泛函理论的计算方法. 在第3节中, 将从层状二维材料、非层状二维材料、二维材料异质结三个方面介绍二维材料的研究进展. 在第4节中, 将对理论计算在二维材料研究领域的应用作一个简单的展望.
图 1 截止到2020年9月以“Two-dimensional materials”为关键词, 从Web of Science网站查询到的近十年的论文发表数
Figure1. Number of publications on two-dimensional materials per year over the last decade. The data is from ISI Web of Science website by September 2020, and the searching keyword is “two-dimensional materials”.

2.理论计算方法
2
2.1.密度泛函理论
-->

2.1.密度泛函理论

20世纪60年代发展起来的密度泛函理论, 是一种将多电子体系近似转化为单电子问题的方法. 基于此理论的第一性原理计算, 已经在多门学科的研究中取得了大量辉煌的成果. 密度泛函理论的奠基人之一沃尔特·科恩(Walter Kohn)也因此于1998年获得了诺贝尔化学奖. 下面简要介绍本文涉及的密度泛函理论的基本内容.
3
2.1.1.绝热近似
-->
2.1.1.绝热近似
晶体属于复杂的多粒子体系, 其定态薛定谔方程可以写作:
$ { H}\varPsi \left({{r}},{R}\right)=E\varPsi \left({{r}},{R}\right), $
其中${ H}$代表哈密顿量的算符; $ E $代表能量; $\varPsi$代表波函数; $ {{r}} $与$ {R} $分别代表所有电子坐标$\left\{ { r } \right\}$与所有原子核坐标$\left\{ { R } \right\}$的集合. 如果没有外场的作用, 哈密顿量$ {H}$包括固体内的电子之间、原子核之间、电子与原子核之间的哈密顿量${ {H}}_{\mathrm{e}}, {{H}}_{\mathrm{n}}, {{H}}_{\mathrm{n}\mathrm{e}}$总和. 因此哈密顿量可写作:
$ {H}={{H}}_{\mathrm{e}}+{{H}}_{\mathrm{n}}+{{H}}_{\mathrm{n}\mathrm{e}}={{T}}_{\mathrm{e}}+{{U}}_{\mathrm{e}\mathrm{e}}+{{T}}_{\mathrm{n}}+{{U}}_{\mathrm{n}\mathrm{n}}+{{U}}_{\mathrm{n}\mathrm{e}}, $
其中${{T}}_{\mathrm{e}}$为电子动能; ${{U}}_{\mathrm{e}\mathrm{e}}$为电子之间的势能; ${{T}}_{\mathrm{n}}$为原子核动能; ${{U}}_{\mathrm{n}\mathrm{n}}$为原子核之间的势能; ${{U}}_{\mathrm{n}\mathrm{e}}$为原子核与电子之间的势能. 求解该薛定谔方程十分困难, 需采取近似方法单独考虑电子的运动与原子核的运动. 由于电子的质量远远小于原子核的质量, 若受到相同的作用力电子的运动速度远远大于原子核的运动速度. 对于原子核的任何移动电子都能瞬间产生响应, 因此可以认为原子核相对于电子是不动的, 这就是玻恩-奥本海默近似, 又称为绝热近似. 按照绝热近似, 原子核的动能和原子核之间的势能可以通过经典力学的方法来处理, 需要用量子力学来描述的只是与电子相关的作用, 因此体系的哈密度量${H}$可以改写为
$ {H}={{T}}_{\mathrm{e}}+{{U}}_{\mathrm{e}\mathrm{e}}+{{V}}_{\mathrm{e}\mathrm{x}\mathrm{t}}, $
其中${{T}}_{\mathrm{e}}$为电子动能; ${{U}}_{\mathrm{e}\mathrm{e}}$为电子相互作用; ${{V}}_{\mathrm{e}\mathrm{x}\mathrm{t}}$为电子所处的外势. 则薛定谔方程为
$ \left[-\frac{{\mathrm{\hslash }}^{2}}{2m}{\nabla }^{2}+\mathrm{V}\left({{r}}\right)\right]\psi \left({{r}}\right)=E\psi \left({{r}}\right), $
其中${\mathrm{\hslash }}^{2}=\dfrac{h}{2\mathrm{\pi }},\; h$是普朗克常数; $ m $代表质量; $ E $代表能量; V代表势能; $ {\nabla }^{2} $代表拉普拉斯算符. 但由于该体系仍然是一个复杂的多电子体系, 还需进一步简化.
3
2.1.2.Hohenberg-Kohn定理
-->
2.1.2.Hohenberg-Kohn定理
与量子力学中将波函数Ψ作为基本变量不同的是, 密度泛函理论是将电子密度函数作为核心变量去描述多电子体系基态的各种性质. 1964年, Hohenberg和Kohn提出两个基本定理.
定理一　作用于多电子体系的外势$ V\left({{r}}\right) $与体系的基态电子密度$ n\left({{r}}\right) $一一对应, 即电子密度函数$ n\left({{r}}\right) $唯一对应$ V({{r}} )$, 就可以唯一确定哈密顿量与体系基态, 体系基态能量$ E\left[n\right] $是$ n\left({{r}}\right) $的唯一泛函.
定理二　在粒子数不变的情况下, 能量泛函$ E\left[n\left({{r}}\right)\right] $当$ n\left({{r}}\right) $取正确密度函数时为极小并且等于基态能量.
根据上述定理, 基态能量可写成泛函形式:
$ \begin{split}E\left[n\right]=\;&\left\langle {\psi \left[n\right]\left|T+U+V\left({{r}}\right)\right|\psi \left[n\right]} \right\rangle \\=\;&F\left[n\right]+\int \mathrm{d}{{r}}V\left(\mathrm{d}{{r}}\right)n\left(\mathrm{d}{{r}}\right), \end{split}$
其中$ F\left[n\right] $代表一个普适的密度泛函, 与$ V\left({{r}}\right) $无关; $ T{\text{和}}U$分别代表多电子体系的动能和内部相互作用势能. 因此, 解决多电子薛定谔方程的问题被绕过了, 现在的目标是使密度泛函最小化.
3
2.1.3.Kohn-Sham方程[23]
-->
2.1.3.Kohn-Sham方程[23]
$ F\left[n\right] $函数形式我们是不知道的, 不过形式上可以写为
$\begin{split}F\left[n\right]=\;&\left\langle {\psi \left[n\right]\left|T+U\right|\psi \left[n\right]} \right\rangle \!=\!T\left[n\right]+\left\langle {\psi \left[n\right]\left|U\right|\psi \left[n\right]} \right\rangle \\ =\;&T[n]\!+\! \frac{{\mathrm{e}}^{2}}{8\mathrm{\pi }{\varepsilon }_{0}}\!\int\! {\rm{d}}{{r}}{\rm{d}}{{{r}}}'\frac{n\left({{r}}\right)n({{{r}}}')}{|{{r}}-{{{r}}}'|} \!+\! {E}_{\mathrm{x}\mathrm{c}}[n],\\[-15pt] \end{split}$
$ {E}_{\mathrm{xc}}\left[n\right]$ 是交换关联能. Kohn与Sham提出了采用单电子的波函数来表示电子密度:
$ n\left({{r}}\right)=\sum _{i}{\left|{\varPsi }_{i}\left({{r}}\right)\right|}^{2}, $
其中动能可以表示为 $T[n]=-\dfrac{\hslash^2}{2m} \sum\nolimits_i \int {\rm d}{ r} \psi_i^* ({ r}) \times \nabla^2 \psi_i ( r)$, $ \psi_i^*({ r}){\text{是}}{\psi }_{i}({ r})$的共轭复数.
则
$F\left[n\right]=T\left[n\right]+\frac{{\mathrm{e}}^{2}}{8\mathrm{\pi }{\varepsilon }_{0}}\int {\rm{d}}{{r}}{\rm{d}}{{{r}}}'\frac{n\left({{r}}\right)n\left({{{r}}}'\right)}{\left|{{r}}-{{{r}}}'\right|}+{E}_{\mathrm{x}\mathrm{c}}\left[n\right] .$
根据变分原理可得到Kohn-Sham方程:
$\left[-\frac{{\mathrm{\hslash }}^{2}}{2m}{\nabla }^{2}+{V}_{\mathrm{e}\mathrm{f}\mathrm{f}}\left({{r}}\right)\right]{\psi }_{i}\left({{r}}\right)={E}_{i}{\psi }_{i}\left({{r}}\right),$
${V}_{\mathrm{eff}}\left({{r}}\right)$代表有效势能,
${V}_{\mathrm{e}\mathrm{f}\mathrm{f}}\left({{r}}\right)=V\left({{r}}\right)+ \dfrac{{\mathrm{e}}^{2}}{4\pi {\varepsilon }_{0}} \displaystyle\int {\rm{d}}{{{r}}}'\dfrac{n\left({{r}}\right)}{\left|{{r}}-{{{r}}}'\right|}+\dfrac{\delta {E}_{\rm xc}\left[n\right]}{\delta n\left({{r}}\right)},$
最后一项$\dfrac{\delta {E}_{\mathrm{x}\mathrm{c}}\left[n\right]}{\delta n\left({{r}}\right)} = {V}_{\mathrm{x}\mathrm{c}}\left({{r}}\right)$是交换关联势.
Kohn-Sham方程的重要之处在于: 在形式上能够将多电子体系的基态问题转变成单电子在有效势场中运动的问题, 其中电子之间复杂的相互作用都包含在泛函项$ {E}_{\mathrm{x}\mathrm{c}}\left[n\right] $里面. 所以Kohn-Sham方程的关键点就在于通过符合常理的近似来找出${E}_{\rm xc}\left[n\right]$的易于分析的简单形式.
3
2.1.4.交换关联泛函
-->
2.1.4.交换关联泛函
局域密度近似(LDA)[24]是一种广泛使用的近似, 在此近似下交换关联泛函可以表示为${E}_{\mathrm{x}\mathrm{c}}\left[n\right]= \displaystyle\int {\rm d}{{r}}n\left({{r}}\right){\varepsilon }_{\rm xc}(n\left({{r}}\right) )$, $ {\varepsilon }_{\mathrm{x}\mathrm{c}}(n\left({{r}}\right)$代表均匀电子气中每一个粒子的交换关联能. 此时Kohn-Sham方程中的的交换关联能可以看作${V}_{\mathrm{x}\mathrm{c}}\left({{r}}\right)= \dfrac{\delta {E}_{\mathrm{x}\mathrm{c}}\left[n\right]}{\delta n\left({{r}}\right)}=\dfrac{\mathrm{d}}{\mathrm{d}n\left({{r}}\right)}\left[n\left({{r}}\right){\varepsilon }_{\mathrm{x}\mathrm{c}}\left(n\left({{r}}\right)\right)\right]$. ${\varepsilon }_{\mathrm{x}\mathrm{c}}(n({{r}})$分为交换能${\varepsilon }_{x}(n({{r}})$和关联能${\varepsilon }_{\mathrm{c}}(n({{r}}))$, 如果得到$ {\varepsilon }_{\mathrm{x}\mathrm{c}}\left(n\left({{r}}\right)\right) $, 这样一来就可以得到具体地求解Kohn-Sham方程.
广义梯度近似(GGA)[25,26] 则引入电子密度和梯度函数再加入自旋, 交换关联泛函可以表示为${E}_{\mathrm{x}\mathrm{c}}[{n}_{\uparrow }, {n}_{\downarrow }] = \displaystyle\int\! {\mathrm{d}}^{3}r{\varepsilon }_{\mathrm{x}\mathrm{c}}({n}_{\uparrow }({{r}}){n}_{\downarrow }({{r}})\nabla {n}_{\uparrow }({{r}})\nabla {n}_{\downarrow }({{r}})).$ Meta-GGA[27] 则又加入自旋密度或动能密度的拉普拉斯算子, 交换关联泛函可以表示为
$ \begin{split}{E}_{\mathrm{x}\mathrm{c}}\left[{n}_{\uparrow },{n}_{\downarrow }\right]=\;&\int {\mathrm{d}}^{3}r{\varepsilon }_{\mathrm{x}\mathrm{c}} \Big({n}_{\uparrow }\left({{r}}\right){n}_{\downarrow }\left({{r}}\right)\nabla {n}_{\uparrow }\left({{r}}\right){n}_{\downarrow }\left({{r}}\right),\\&{\nabla }^{2}{n}_{\uparrow }\left({{r}}\right){\nabla }^{2}{n}_{\downarrow }\left({{r}}\right){\tau }_{\uparrow }\left({{r}}\right){\tau }_{\downarrow }\left({{r}}\right)\Big),\\[-12pt]\end{split}$
其中动能密度$\tau \left({{r}}\right)=\dfrac{1}{2}\displaystyle\sum\nolimits_{i}{\left|{\nabla \varPsi }_{i}\left({{r}}\right)\right|}^{2}$. 除了LDA, GGA和Meta-GGA, 对于更广泛的体系计算还有杂化密度泛函, 它是将精确的Hatree-Fock交换作用与交换关联项杂化在一起, 例如PBE0[28], B3LYP[29] 等.
3
2.1.5.赝势方法
-->
2.1.5.赝势方法
因为原子核区域内的势场发散并十分复杂, 价电子的波函数需要许多平面波基矢展开. 而在离原子核较远的区域, 其势场比较平滑, 价电子的波函数类似平面波函数. 赝势[30]方法就是利用价电子的波函数没有急剧震荡的特性, 有效地减小了波函数展开需要的平面波基矢, 极大地提高了计算效率.
2
2.2.材料稳定性分析
-->

2.2.材料稳定性分析

对于理论预言的新材料, 需要分析其结构是否稳定、有限温度下结构是否发生相变或者被破坏、实验合成潜力等.
3
2.2.1.动力学稳定性计算
-->
2.2.1.动力学稳定性计算
声子谱是表示组成材料原子的集体振动模式. 对于一个包含n个原子的原胞, 声子谱总共有3n支声子, 其中有3条声学支, 3n – 3条光学支. 声学支表示原胞的整体振动, 光学支表示原胞内原子间的相对振动. 材料的振动频率可表示为
$ \omega \propto \sqrt{\frac{\beta }{m}}=\sqrt{\frac{1}{m}\frac{{\partial }^{2}E\left(x\right)}{\partial {x}^{2}}}, $
其中ω为振动频率; β可理解为弹性常量; $ E\left(x\right) $表示原子间相互作用能; x表示原子偏离平衡位置的位移; m为原子质量. 当ω为虚频时,
$ \frac{{\partial }^{2}E\left(x\right)}{\partial {x}^{2}} < 0. $
意味着原子平衡位置处于能量的极大值, 因此该平衡位置的原子是不稳定的. 反之, 声子谱无虚频则表示材料动力学稳定.
3
2.2.2.热稳定性计算
-->
2.2.2.热稳定性计算
通过声子谱判断材料稳定之后, 便可通过分析分子动力学进一步判断材料在一定温度下的稳定性[31]. 分子动力学方法: 首先构建超胞, 然后施加一定温度, 运行一段时间之后观察原胞结构是否遭到破坏来判断该材料能否在该温度下稳定存在. 通过吉布斯自由能计算, 可以比较不同构型在不同温度下的稳定性, 判断材料是否会在一定温度下发生相变.
3
2.2.3.热力学稳定性计算
-->
2.2.3.热力学稳定性计算
形成能是指由相应单质合成化合物所释放的能量. 以二元化合物AxBy为例, 其形成能$ {E}_{\mathrm{f}} $可表示为
$ {E}_{\mathrm{f}}=\frac{E\left({\rm A}_{x}{\rm B}_{y}\right)-xE\left({\rm A}\right)-yE\left({\rm B}\right)}{x+y}, $
其中, $E\left({\rm A}_{x}{\rm B}_{y}\right)$为该二元化学物的总能; $E\left(\rm A\right)$和$E\left(\rm B\right)$分别为基态的A, B单质的化学势.
如果需要判断材料处于稳态还是亚稳态, 可以分析该材料的凸包图(convex hull能量). 如图2所示, 红色虚线是计算稳态AxBy的形成能得到的凸包图, 其纵轴是形成能, 横轴是元素B在AxBy中的占比. 若化合物在红色虚线上方例如插图中的D, 那么它可能分解为A和B, 或者是声子谱没有虚频的亚稳态; 若化合物在红色虚线下方例如插图中的C, 那么它是稳定态.
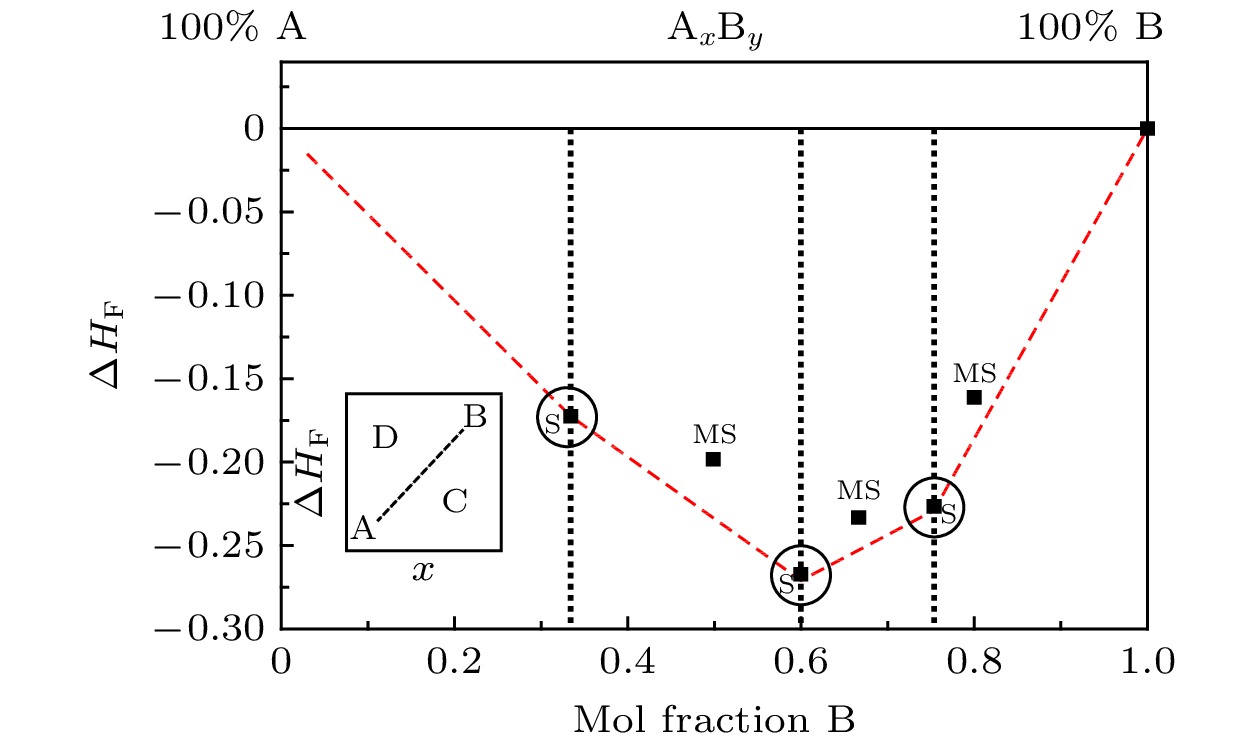图 2 凸包图, 用于判断材料稳态和亚稳态[32]
Figure2. Convex hull diagram is used to estimate the ground state and metastable state of a material[32].

3.讨　论
2
3.1.层状二维原子晶体材料
-->

3.1.层状二维原子晶体材料

在2017年以前, 人们对二维材料的研究主要集中在石墨烯、过渡金属硫族化合物、黑磷等少部分具有层状块体结构的材料上. 尽管它们中的很多材料在某些方面具有优异性能, 但一些三维体系中存在的物性还未在二维材料中发现, 一个非常重要的原因是已经发现和研究的二维材料种类太少. 如何广泛研究并快速扩充二维材料种类是整个二维材料研究领域亟待解决的问题. 基于密度泛函理论的高通量计算是一种非常高效的材料预测手段, 例如高通量计算方法已成功应用于寻找锂空气电池和锂离子电池材料[33,34]、储氢材料[35]、闪烁体材料[36]、电催化剂[37]和光伏材料[38]等. 通过从ICSD (inorganic crystal structure database), COD (crystallography open database)等体相材料数据库中筛选出的层状材料进行第一性原理高通量计算就可以很好地去理解和预测一些潜在的二维材料及其性质.
2017年, Choudhary等[39]基于高通量计算提出了一种从体相材料中识别二维材料的方法. 由于PBE计算晶格常数通常数值会偏高, 尤其是在仅有范德华(van der Waals, vdW)相互作用的方向上. 文章于是利用这一特点作为筛选二维材料的有效判据. 具体来说就是将一种材料在ICSD中实验上测得的晶格常数和在Materials-Project中基于密度泛函理论(DFT)计算的a, b, c三个方向上的晶格常数作比较, 如果两个晶格常数之间相对误差$ \delta $大于等于5％, $(\delta =(l_{\rm PBE} - l_{\rm ICSD})/ l_{\rm ICSD})$那么这种材料可能是层状材料, 并有可能剥离出单层结构. 他们从Materials-Project数据库中识别出1356种满足上述条件的二维材料, 并构建了一个包含体相和单层结构、能量、电子结构和力学性质的二维材料数据库JARVIS-DFT, 它们分类的总体情况如图3所示. 图3(a)显示了所有晶格常数及其组合都存在相对误差. 其中, 有868种二维材料晶格常数a的相对误差大于等于5％, 679种二维材料晶格常数b的相对误差大于等于5％, 651种二维材料晶格常数c的相对误差大于等于5％, 260种二维材料晶格常数a, b, c的相对误差均大于等于5％. 如图3(b)所示, 二维材料不仅可以是过渡金属硫族化合物, 还可以是卤化物、磷化物及其他组合. 图3(c)显示了数据库中材料的结构化学计量比分布, 常见二维材料包括AB2, AB, ABC, ABC2和AB3等结构. 图3(d)显示了数据库中层状材料的空间群分布, $ P\bar6 m2, P\bar3 m1 $和$ P2_1/m $空间群通常称为2H, 1T和1T'相结构, 2H和1T结构是研究报道中的常见结构. 近年来, 实验上也制造了许多具有除2H和1T结构之外的二维晶体材料, 如具有半金属性的WTe2, 其空间群是Pmn21[40,41]. 图3(e)显示了数据库中层状材料的晶系分布, 大多数层状材料属于正交晶系, 其次是单斜晶系和四方晶系. 目前在实验上合成的大部单层材料为六角形蜂窝状结构, 但数据库中新发现的材料表明层状材料也可以是其他晶系. 图3(f)显示了数据库中预测大多数的层状材料是二元和三元化合物.
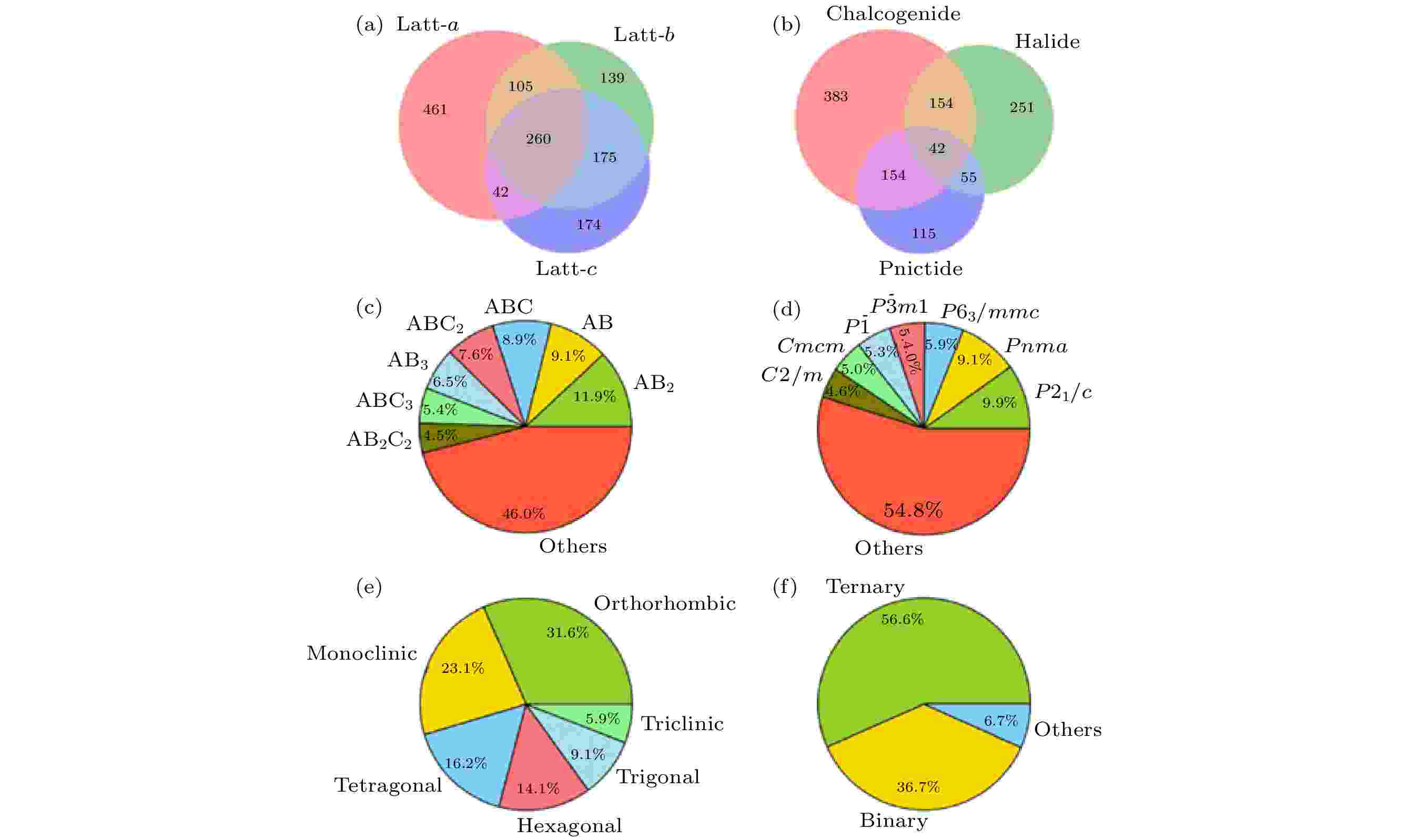图 3 预测的层状材料结构、成分等信息统计　(a) 晶格常数的相对误差; (b) 化学元素组成; (c) 晶体类型; (d) 晶体空间群; (e) 晶系; (f) 元素种类[39]
Figure3. Classification of predicted layered materials in term of (a) relative error in lattice constants; (b) chemical compositions; (c) crystal prototypes; (d) crystal space groups; (e) crystal systems; (f) number of distinct chemical constituents[39].

2018年, Mounet等[42]通过不同的原子几何结构算法识别潜在的二维层状材料, 并通过高通量计算搜索了其中机械易剥离的材料. 他们通过对比ICSD和COD结构数据库中108423种实验已知的结构的原子间距和原子共价键长, 识别出5619种具有层状结构的材料, 再使用考虑范德瓦耳斯修正的密度泛函理论计算研究了这些层状材料的层间结合能, 发现一共有1825种材料可能剥离出二维的单层结构, 其中易剥离的材料有1036种, 潜在可剥离的材料有789种, 如表1所列. 文章还描述了易剥离的材料中比较有研究潜力的、具有较小原胞的258种化合物的声子谱、电子结构、磁性和拓扑性质, 其中表2列出了这258种化合物中有56种化合物具有磁性, 包括37种铁磁体和19种反铁磁体.
Unique to the ICSDUnique to the COD Common to bothTotal sum
Experimental data
CIF inputs9921287070186282
Unique 3D structures (set A)345486035413521108423
Layered 3D structures (set B)3257118011825619
DFT calculations
Layered 3D, relaxed (set C)21651758703210
Binding
energies (set D)		17951267412662
2D easily
exfoliable (EE)		663792941036
2D potentially exfoliable (PE)52434231789
Total11871135251825


表1数据库统计[42]
Table1.Database statistics[42].

FerromagneticAntiferromagnetic
MetalsCo(OH)2, CoO2, ErHCl, ErSeI, EuOBr, EuOI, FeBr2, FeI2,
FeTe, LaCl, NdOBr, PrOBr, ScCl, SmOBr, SmSI, TbBr,
TmI2, TmOI, VS2, VSe2, VTe2, YCl, YbOBr, YbOCl		CoI2, CrSe2, FeO2, FeOCl, FeSe, PrOI, VOBr
SemiconductorsCdOCl, CoBr2, CoCl2, CrOBr, CrOCl, CrSBr, CuCl2,
ErSCl, HoSI, LaBr2, NiBr2, NiCl2, NiI2		CrBr2, CrI2, LaBr, Mn(OH)2, MnBr2, MnCl2,
MnI2, VBr2, VCl2, VI2, VOBr2, VOCl2


表2易剥落的磁性化合物[42]
Table2.Easily exfoliable magnetic compounds[42].

C2DB[43]是一个基于高通量计算的开放式二维材料数据库, 该数据库包含30多种不同晶体结构家族的共1500余种二维材料的电子结构、热力学、力学、磁学和光学性质. 数据库中常见二维材料结构类型如图4所示, 这些丰富多彩的结构类型也表明二维材料家族还有巨大的潜力值得挖掘. 特别强调的是计算电子能带使用了杂化密度泛函(HSE06)和多体微扰理论(G0W0). C2DB数据库的筛选流程是首先通过结构识别算法从体相材料中识别出层状材料及其单层结构和成分信息. 通过元素替换方式构成可能的其他初始理论晶格结构模型, 再按照图5所示的流程计算新二维材料的结构和性质. 此外, 目前已经创建的二维材料数据库还有materials web[44]和2D materials encyclo-pedia[45]等.
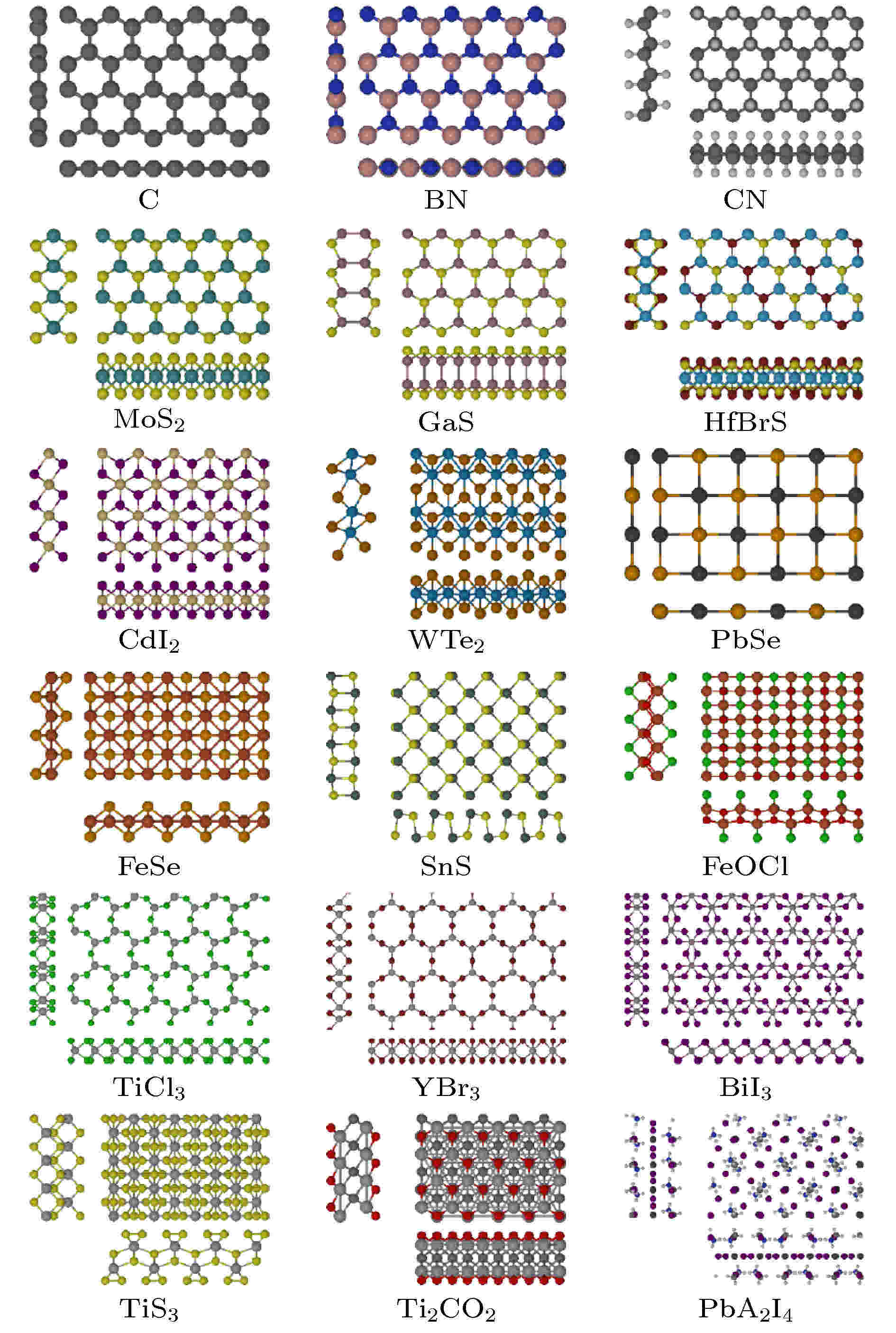图 4 C2DB数据库中典型的二维材料[43]
Figure4. Example of two dimensional materials prototypes in the C2DB[43].

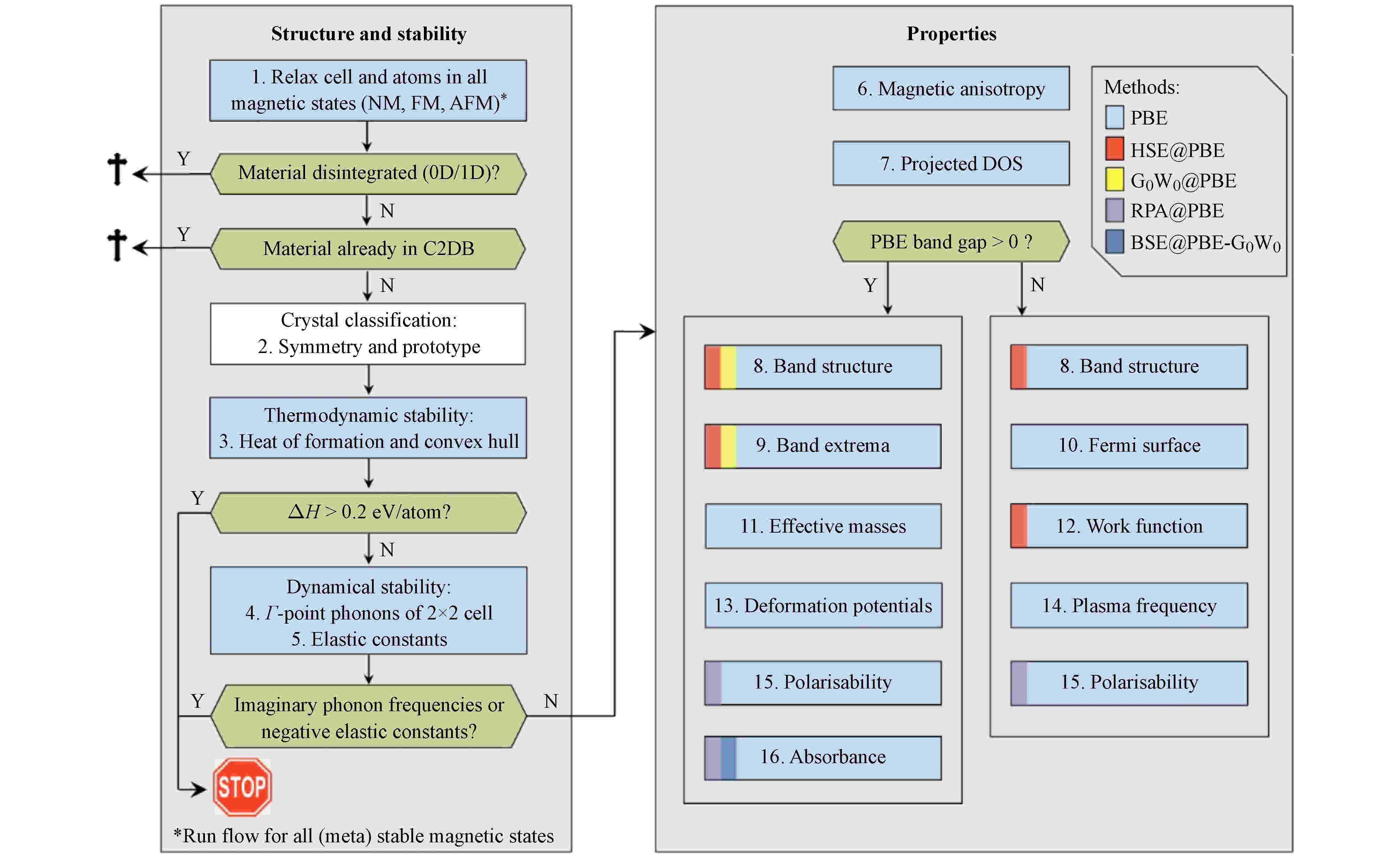图 5 C2DB数据库的工作流程图[43]
Figure5. The workflow of producing data of C2DB[43].

2
3.2.非层状二维原子晶体材料
-->

3.2.非层状二维原子晶体材料

对于体相为层状结构的二维材料, 机械剥离是得到高质量二维单层结构的有效方法. 随着分子束外延等自下而上的制备手段的发展, 一些体相为非层状结构的二维单层结构也被实验合成出来, 并展现出许多新奇的物性. 硅烯和锗烯是这一类二维材料中最早研究的材料. 在剥离出石墨烯之前, 就有理论预测[5]: 单层Si和Ge与石墨烯的平面蜂窝状晶格结构不同, 是翘曲的蜂窝状结构, 并能导致发生量子自旋霍尔效应[46,47]. 受到硅烯、锗烯研究工作的启发, 其他二维单层非层状材料也取得了一系列进展.
3
3.2.1.As和Sb
-->
3.2.1.As和Sb
2015年以前, 大多数报道的二维半导体都具有较小的带隙, 极大地限制了它们在蓝光、紫外光光电器件中的应用. 2015年, Zhang等[48]基于第一性原理计算预测了具有宽带隙和高稳定性的新型二维单元素的半导体砷烯和锑烯. 其中, 体相和单层的As和Sb结构具有与硅烯和锗烯类似的翘曲蜂窝状晶格结构, 体相砷和单层砷烯的结构如图6所示, 体相砷层间距离、键长和键角分别是2.04 ?, 2.49 ?和97.28°. 相比之下, 在砷烯中由于晶格畸变, 键长和键角变化为2.45 ?和92.548°. 体相锑的层间距离、键长和键角分别是1.84 ?, 2.84 ?和93.28°, 锑烯中键长和键角分别为2.45 ?和92.548°. 为了判断这两种新型二维晶体的稳定性, 文章计算了砷烯和锑烯的声子谱如图7所示, 结果显示两种材料的声子谱中均没有虚频, 表明砷烯和锑烯动力学稳定. 2017年Wu等[49]在PdTe2衬底上生长了锑烯, 2018年Shao等[50]也在Ag(111)衬底上成功合成了高质量的锑烯. 体相As和Sb通常是半金属, 而它们的单层结构是带隙为2.49 eV和2.28 eV的间接带隙半导体. 这种电子结构有望在未来具有高开关比的晶体管、蓝光或紫外光光电器件以及机械传感器等方面具有潜在的应用. 另外, 砷烯和锑烯在双轴应变下都能够转变成直接带隙半导体, 在纳米电子和光电器件等领域同样具有潜在的应用.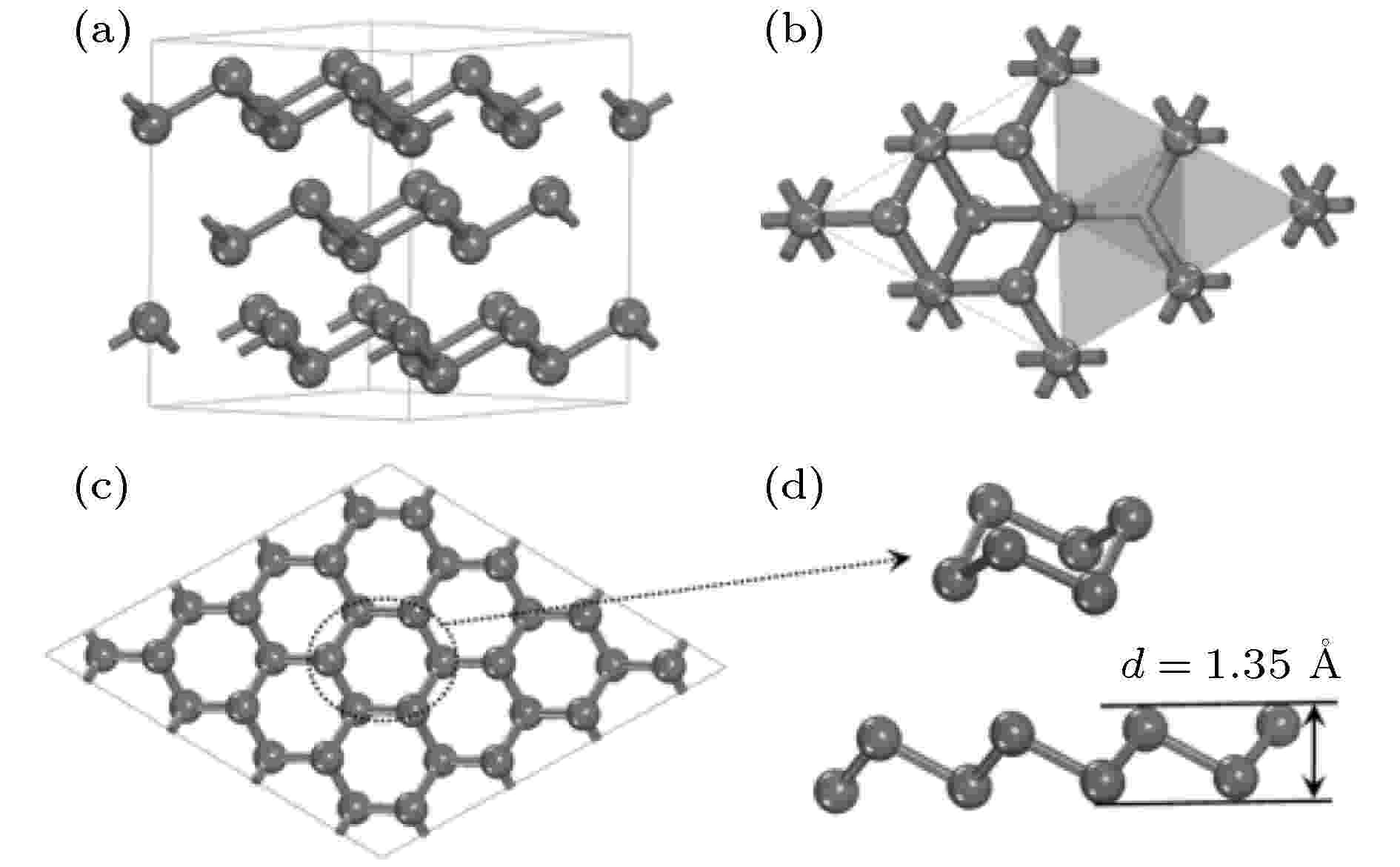
图 6 体相砷的　(a) 俯视图和(b) 顶视图; 翘曲单层砷烯的(c) 俯视图和(d) 侧视图[48]
Figure6. (a) Side view and (b) top view of the structure of arsenic; (c) top view and (d) side view of a buckled As monolayer (arsenene)[48].

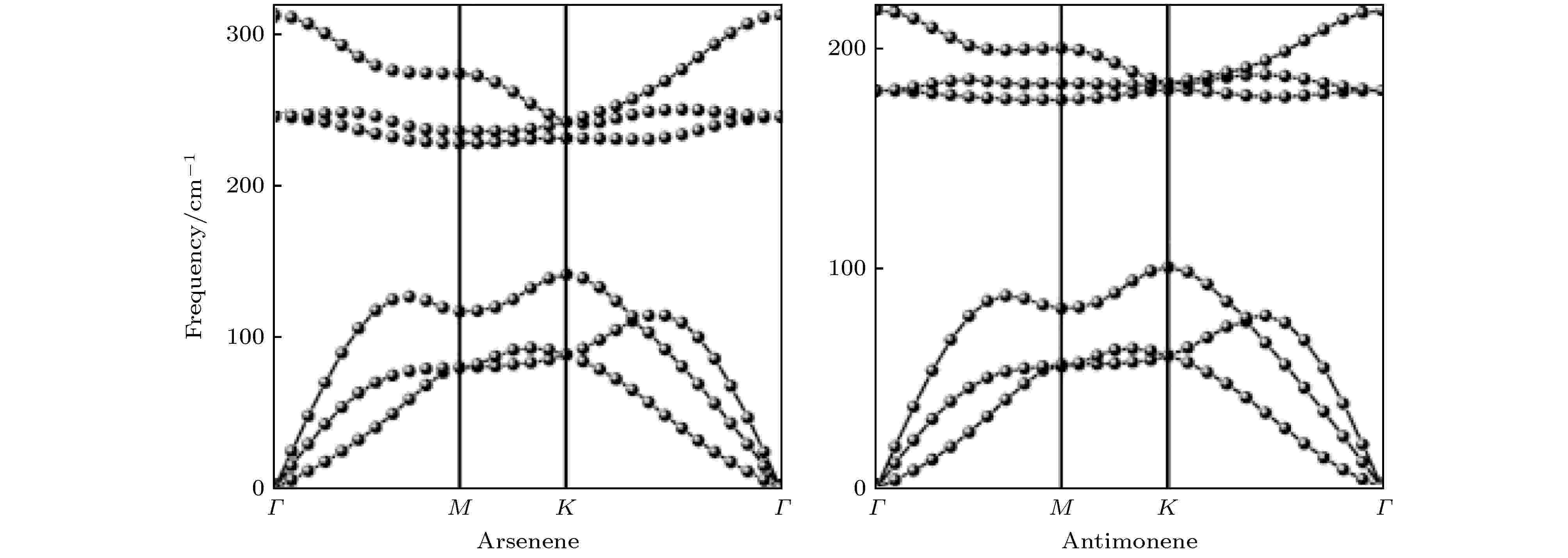图 7 层砷烯和层锑烯的声子谱图[48]
Figure7. Phonon dispersions of arsenene and antimonene[48].

3
3.2.2.单层CuSe
-->
3.2.2.单层CuSe
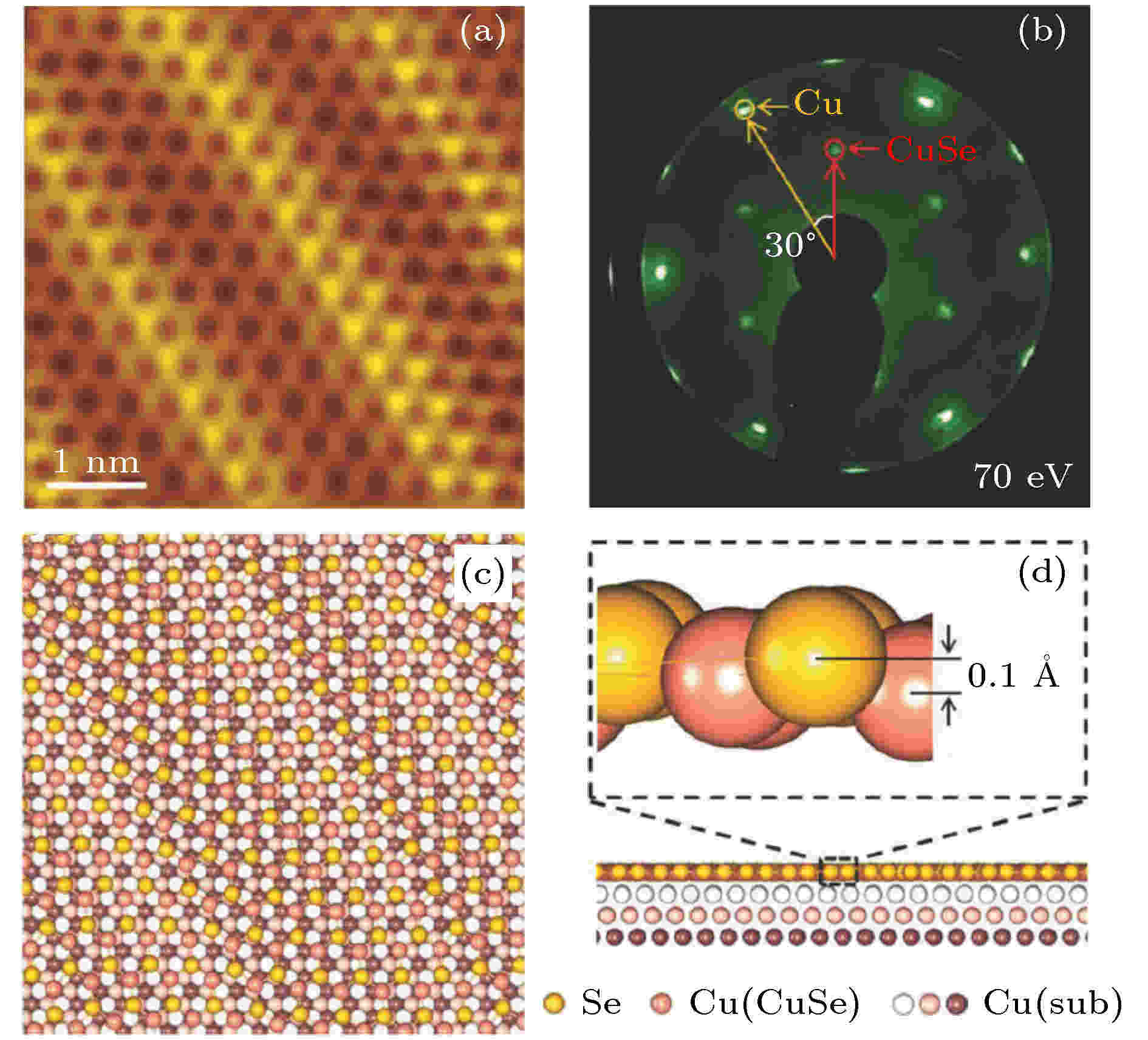2018年, Gao等[51]报道了通过直接硒化Cu(111)表面的方法可以成功制备出具有一维摩尔图案的单层CuSe. 高分辨率扫描隧道显微镜(STM)和低能电子衍射谱(LEED)的测量结果表明CuSe具有六角蜂窝状结构. 通过第一性原理计算进一步确定样品是Cu(111)衬底上生长的具有翘曲的蜂窝状晶格单层CuSe. 图8(a)是Cu(111)衬底上单层CuSe的高分辨率STM图像, 可以清楚地观察到一维摩尔图案. 图8(b)是Cu(111)衬底上单层CuSe的低能电子衍射(LEED)图案, 红色和黄色圆圈分别表示单层CuSe和Cu(111)晶格的衍射斑点, 可以看出单层CuSe与Cu(111)表面之间有30°的旋转. 为了研究Cu(111)表面上单层CuSe的原子构型, 文章构建了 ($ \sqrt{3} \;×\; 9\sqrt{3} $)的三层Cu(111)衬底表面吸附(1 × 10)的单层CuSe的超胞模型. 图8(c)和图8(d)是Cu(111)上单层CuSe优化后的原子结构模型的俯视图和侧视图. 第一性原理计算结果显示该超胞结构具有一维摩尔条纹图8(c)与图8(a)的STM图案非常吻合. 理论计算得到Cu(111)表面上单层CuSe的最大翘曲高度为0.1 ?, 与STM形貌图像中的高度差也是一致的.
图 8 Cu(111)上单层CuSe的(a) 高分辨率STM图像, (b) LEED图; Cu(111)上单层CuSe优化原子结构模型的(c) 俯视图, (d) 侧视图[51]
Figure8. Monolayer CuSe on Cu(111): (a) High-resolution STM image, (b) LEED pattern; optimized atomic structure of monolayer CuSe on Cu(111): (c) top view, (d) side view[51].

通过考虑自旋-轨道耦合(SOC)效应的第一性原理计算对CuSe/Cu(111)电子结构进行理论模拟, 如图9(a)所示: 在能量低于–2.0 eV区域有非常大的电子态密度, 这主要是由Cu(111)基底贡献的; 而在–2.0 eV以上能带主要由CuSe单层贡献, 并有两个孔状带. 实验上ARPES对样品测量结果如图9(b)所示, 与理论计算结果十分吻合, 进一步表明单层CuSe结构稳定并能在实验上成功制备. 另外, 第一性原理计算还研究了单层自由状态下CuSe的电子结构, 发现单层CuSe具有狄拉克节点线费米子(DNLF), 其受到镜面对称性的保护. 这种DNLF存在于自旋-轨道耦合带隙内的拓扑非平庸边缘态上. 如果在弱耦合衬底(例如石墨烯)上合成CuSe, 则可以使用ARPES直接观察到有趣的DNLF特性.
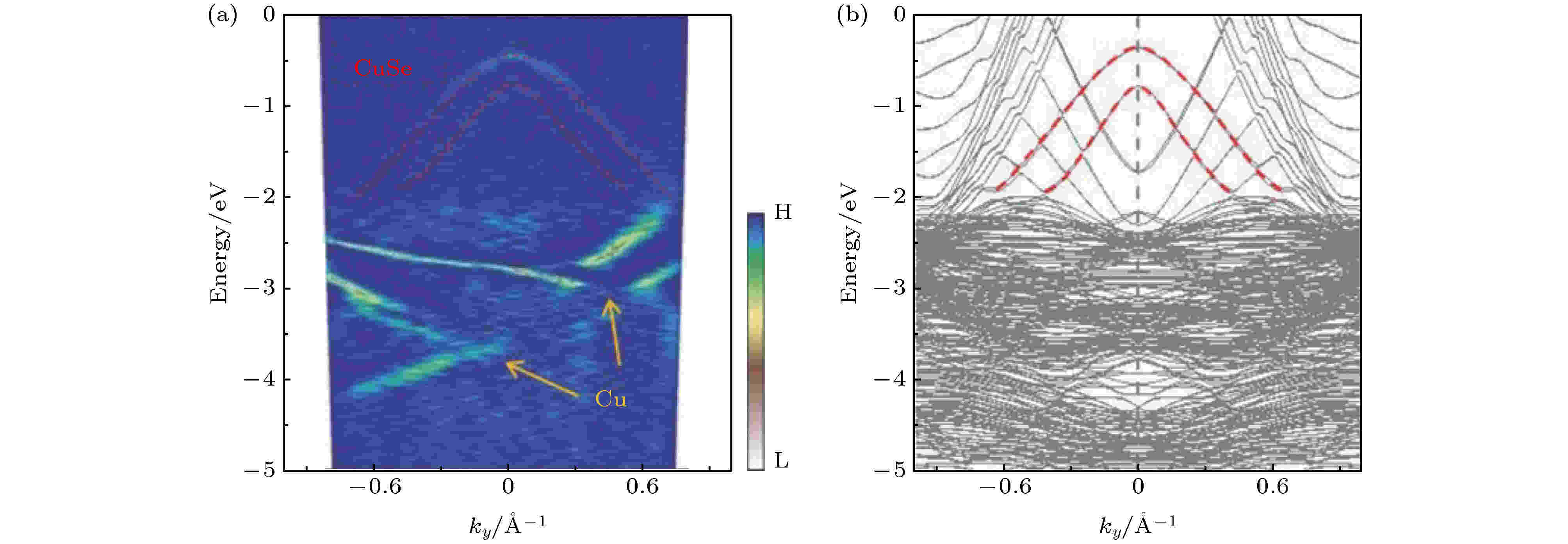图 9 Cu(111)上单层CuSe　(a) 沿K–Γ–K方向测量的ARPES图; (b) 理论计算的能带图[51]
Figure9. Monolayer CuSe on Cu(111): (a) ARPES intensity plots measured along the K–Γ–K direction; (b) calculated band structure [51]

2
3.3.二维材料异质结
-->

3.3.二维材料异质结

范德瓦耳斯异质结构是在一种或两种以上的二维材料上堆垛另一种二维材料, 层与层之间通过范德瓦耳斯力相结合[52]. 强大的层内共价键让二维材料具有很高的面内稳定性, 而相对较弱的范德瓦耳斯力也足以让堆垛在一起的二维材料紧密结合. 随着二维晶体家族的范围逐渐扩展, 在原子精度上可以创建大量的范德瓦耳斯异质结构, 但是受限于实验合成效率问题仅研究了一部分的二维材料异质结. 通过理论计算可以高效模拟大批量异质结物性. 最近, 理论报道了许多不同类型的范德瓦耳斯异质结构中的电、光和磁等性能.
根据能带排列方式, 半导体二维材料组成的异质结一般分为三种类型[53], 分别为I型、II型和III型. I型异质结是指异质结中能隙较小的材料同时具有导带的最小值和价带的最大值, 如图10(a)和图10(b)所示. 能隙较大的材料中激发的电子和空穴可以按照箭头指示方向转移到能隙较小的材料中, 而能隙较小的材料中激发的载流子不能转移到能隙较大的材料中. I型异质结在光学器件中有着非常广泛的应用, 例如发光二极管(LED)[54]和激光器. II型异质结是指导带的最小值和价带的最大值分别位于不同的材料中, 如图10(c)和图10(d)所示. 能隙较大的材料激发的电子可以转移到能隙较窄的材料中, 空穴不可以转移; 而能隙较窄的材料激发的空穴可以转移到能隙较宽的材料中, 电子不可以转移. III型异质结是指一种材料价带的最大值仍然小于另一种材料导带的最小值, 这种异质结构并不常见. 总结来说, 当材料A和材料B构成异质结, 若CBMA > CBMB > VBMB > VBMA, 则为I型异质结; 若CBMB > CBMA > VBMB > VBMA, 则为II型异质结; 若 CBMB > VBMB > CBMA> VBMA, 则为III型异质结, 其中CBM代表导带底, VBM代表价带顶.
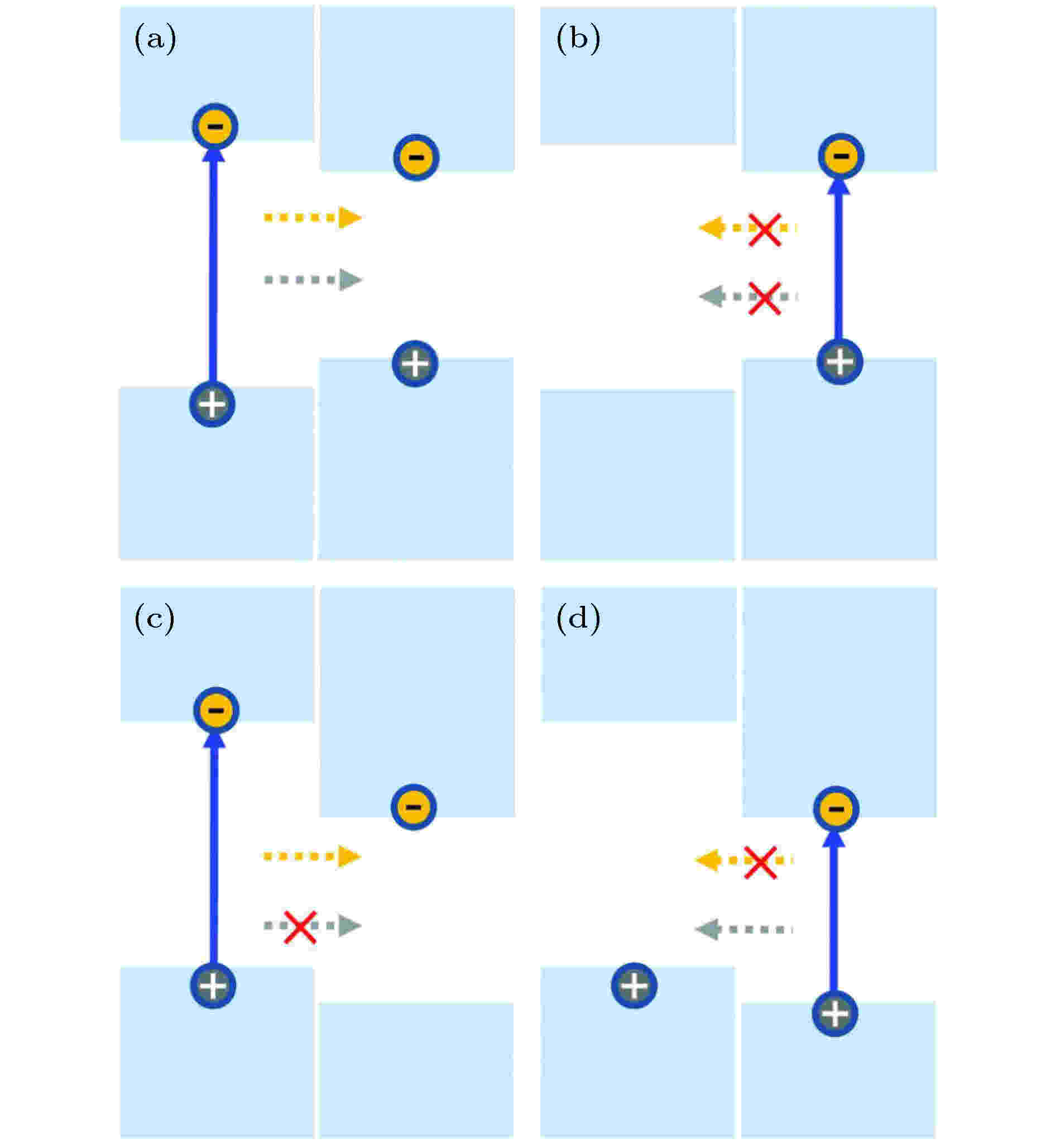图 10 电荷转移示意图　(a), (b) I型异型结; (c), (d) II型异型结[53]
Figure10. Schematic of allowed charge transfer: (a), (b) Type-I heterostructures; (c), (d) type-II heterostructures[53].

2016年, ?z?elik等[55]研究了常见二维半导体材料的能带结构, 其中包括IV和III-V族化合物的单层材料、V族元素的单层材料、过渡金属二卤化物(TMD)和过渡金属三卤化物(TMT). 利用基于密度泛函理论的第一性原理计算, 作者研究了903种不同组合的异质结类型, 建立了异质结周期表, 如图11所示, 其中绿色、红色和蓝色框分别代表I型、II型和III型异质结, 对角线分开的左下区域和右上区域分别是PBE和HSE06的计算结果. 这种预测为未来的实验与理论研究提供了有价值的参考.
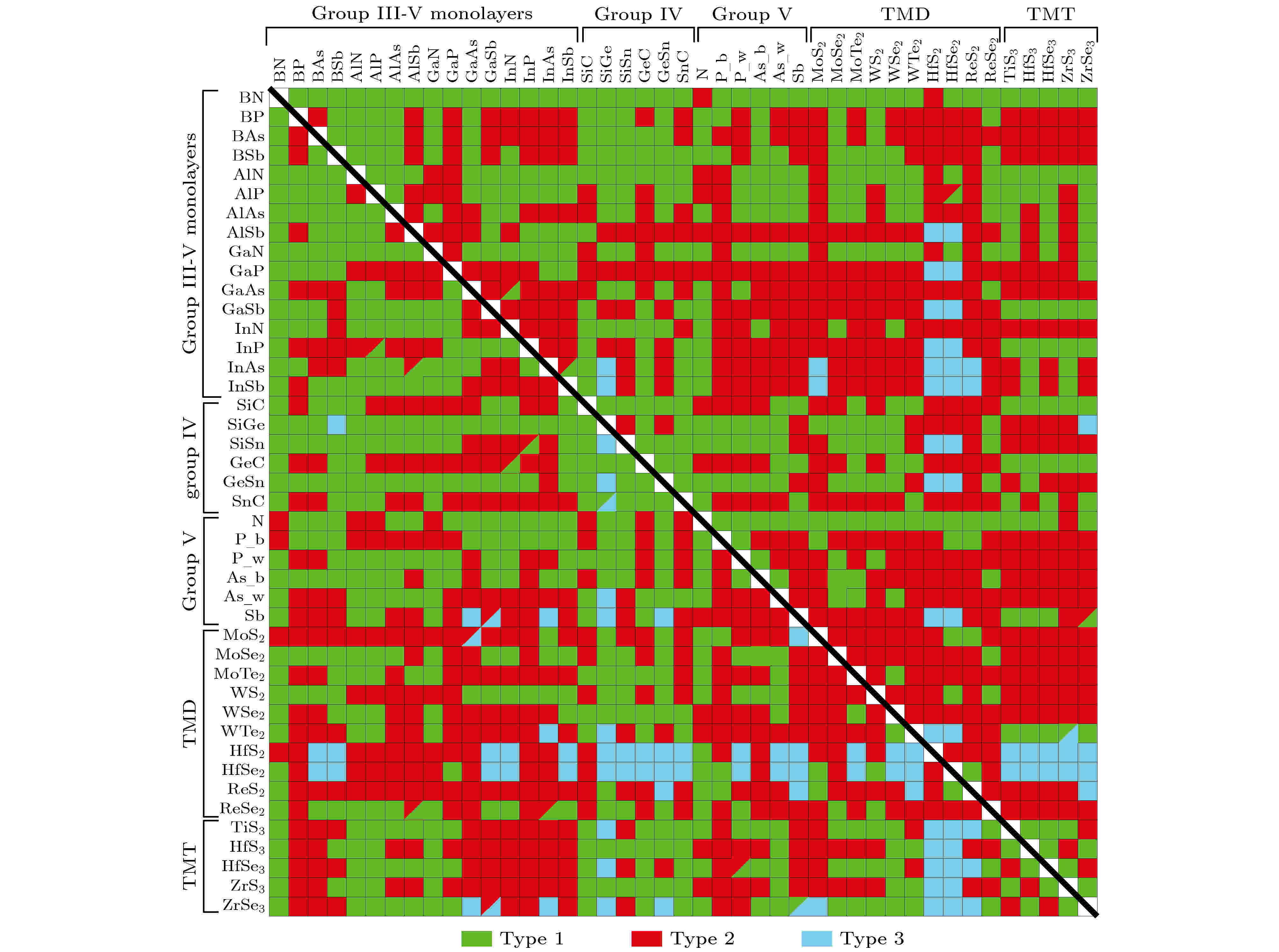图 11 异质结周期表[55]
Figure11. Periodic table of heterostructures[55].

单层的过渡金属二卤化物(TMDs)具有良好的光学性能, 若两个TMD单层组成范德瓦耳斯异质结, 则层内激子和层间激子将会同时存在. 层内激子是指激发的电子和空穴在同一层中, 层间激子[56-59]是指电子和空穴在不同层中. 这样的TMD双层异质结在超快电荷转移、超快层间热激子形成等领域有着潜在的应用. 由较典型的MoS2, MoSe2, WS2和WSe2这4种材料组成的MoSe2/MoSe2[60], MoS2/WS2[61-65], MoS2/WSe2[66-72], MoSe2/WSe2[73], MoSe2/WSe2[74]和WS2/WSe2[75]这6种范德瓦耳斯异质结均为II型异质结, 并且它们具有相似的电子和光学性质.
2018年, Torun等[76]对MoS2/WS2异质结进行第一性原理计算. MoS2/WS2异质结的激子效应光谱如图12(a)所示, 其中蓝色、红色、绿色分别是MoS2, WS2和MoS2/WS2的吸收光谱. 在MoS2/WS2中, X1激子是层间激子, 其能量比MoS2层中层内激子X2和WS2层中层内激子X3低. 投影能带结构如图12(b)所示, 激子在K点处从价带的最大值跃迁到导带的最小值. 具有激子效应异质结的能带排列如图12(c)所示, MoS2/WS2的层间激子X1的结合能为0.43 eV, 比MoS2层和WS2层的层内激子X2, X3的结合能数值小70 meV. 这是因为电荷载流子在空间上的分离降低了层间激子结合能, 层间较弱的库仑作用使层间激子的结合能远小于层内激子的结合能, 导致层间激子是最低能级, 任一层中的层内激子都是激发态. 突出的激子效应在超薄材料的载流子动力学领域有着重要的应用.
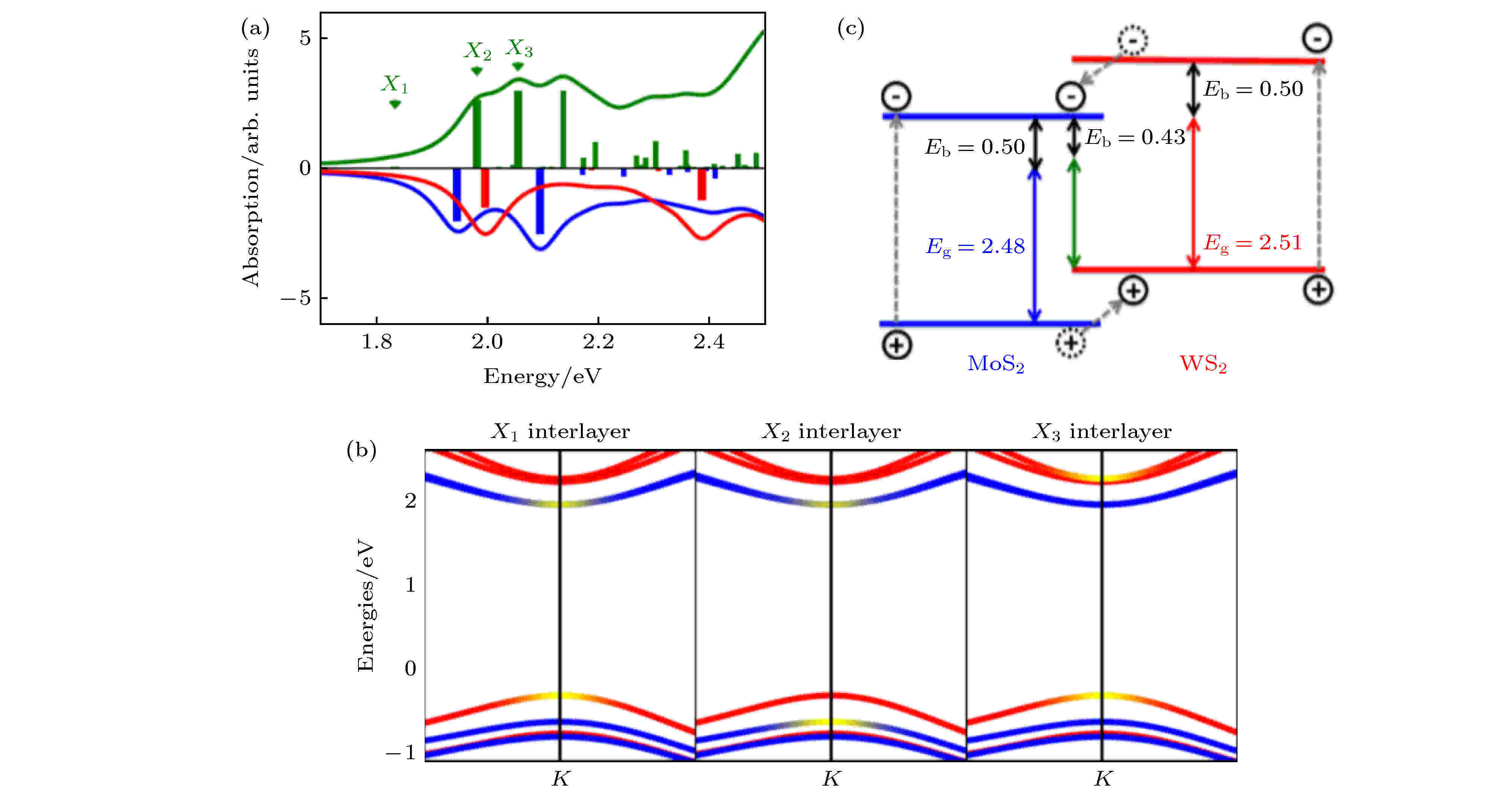图 12 (a) MoS2, WS2和MoS2/WS2的吸收光谱图; (b) 布里渊区K点附近的电子能带; (c) 异质结的能带排列[76]
Figure12. (a) Absorption spectra of MoS2, WS2 and MoS2/WS2; (b) electron band near the K point in the Brillouin zone; (c) band arrangement of heterostructures[76].

2018年, Gillen和Maultzsch等[77]对三种不同堆垛结构的MoSe2/WSe2异质结进行第一性原理计算. 三种不同的堆垛结构均保持六角晶格对称性, 其中, AA堆垛是WSe2层相对于MoSe2层的零度旋转; AA' 堆垛是WSe2层相对于MoSe2层旋转180°, 这种堆垛方式对应的结构是最稳定的; AB堆垛是在AA堆垛基础上将WSe2层平移$a/\sqrt{3}$, 其中a是面内晶格常数. 优化后的三种异质结构如图13所示, 不同的堆垛结构对面内晶格??常数仅有非常小的影响, 变化仅为0.1%, 但是层间距会有非常明显的变化. 电子能带图中也可以看出不同堆垛方式对能带带边位置、带隙均有影响, 但是堆垛结构不会影响异质结的种类, 这三种结构均是II型异质结. 这篇文章还预测了MoSe2/WSe2异质结在K点处的激子跃迁行为, 电子和空穴在空间中是电荷分离的, 电子限制在MoSe2层中而空穴限制在WSe2层. 对于最低能量的层间激子, 它们的激子结合能是250 meV. 同时, 堆垛结构对层间激子的峰值能量和易振荡的强度也会有很大程度的影响.
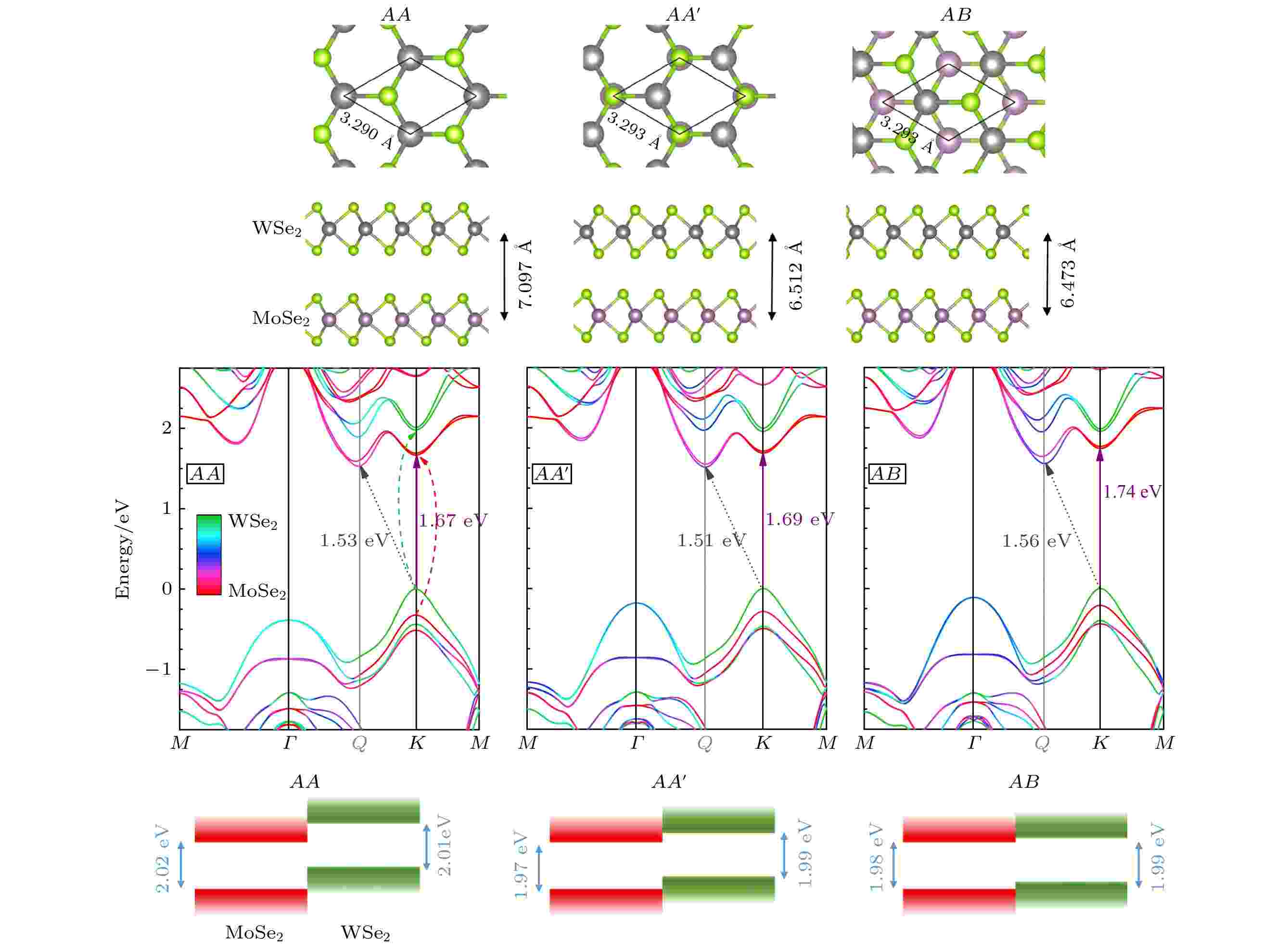图 13 AA, AA', AB型MoSe2/WSe2异质结的结构及能带[77]
Figure13. Structure and energy band of AA, AA', AB MoSe2/WSe2 heterostructures[77].

4.总结和展望
二维原子晶体材料的研究是近年来凝聚态物理和材料科学等领域中非常热门的研究方向. 尽管人们已经发展出了很多种制备二维材料的方法, 但实验上研究新型二维材料耗时长、成本高昂. 基于密度泛函理论的高通量计算可以高效、准确地预测一些实验上还未合成的二维材料的结构及其性质. 近年来materials cloud, C2DB, JARVIS-DFT, 2D materials encyclopedia等层状二维材料计算数据库也在不断发展中. 理论计算还预测了体相为非层状结构的二维单层材料, 如最早预测的硅烯、锗烯, 再到单层砷、单层锑、单层CuSe等, 它们皆展现出许多新奇的物性, 并且能够在实验上成功制备出来. 除此之外, 人们还研究了将不同二维材料堆叠成范德瓦耳斯异质结, 以实现单层材料不具备的性质和潜在应用.
科学家们已经预言了大量新型二维原子晶体材料, 对二维材料几何结构、基态电子结构的研究比较完善, 但其他的性质, 如光学、力学、热电、磁学和拓扑学等方面的性质还有很大的研究空间; 二维材料的应用研究还处在原理器件研究上, 距离找到具有理想性能的二维功能材料并制作出可应用的器件还有较大的差距; 一些基于新原理的新型器件可能在将来也不断涌现; 另外, 对于一些材料或材料的某些性质, 理论计算得到的结果与实验结果不能够很好地吻合, 因此, 发展更完善的理论计算体系、发掘更有效的计算方法, 也是科研人员的重要工作方向.
相关话题/材料 结构 电子 计算 实验
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 二维原子层谷电子学材料和器件
    摘要:人为操控电子的内禀自由度是现代电子器件的核心和关键.如今电子的电荷和自旋自由度已经被广泛地应用于逻辑计算与信息存储.以二维过渡金属硫属化合物为代表的二维原子层材料由于其具有独特的谷自由度和优异的物理性质,成为了新型谷电子学器件研究的优选材料体系.本文介绍了能谷的基本概念、谷材料的基本物理性质、 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 二维材料的转移方法
    摘要:二维材料及其异质结在电子学、光电子学等领域具有潜在应用,是延续摩尔定律的候选电子材料.二维材料的转移对于物性测量与器件构筑至关重要.本文综述了一些具有代表性的转移方法,详细介绍了各个方法的操作步骤,并基于转移后样品表面清洁程度、转移所需时间以及操作难易等方面对各个转移方法进行了对比归纳.经典干 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • Li(Na)AuS体系拓扑绝缘体材料的能带结构
    摘要:在拓扑领域中发现可以通过大数据搜索拓扑绝缘体,使得此领域对材料的探索转变为对材料性质的研究.半Heusler合金体系是非平庸拓扑绝缘体材料的重要载体.通过全势线性缀加平面波方法计算Li(Na)AuS体系拓扑绝缘体材料的能带结构.采用各种关联泛函计算LiAuS的平衡晶格常数,发现得到的能带图均为 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 吸收波长和吸收效率可控的超材料吸收器
    摘要:为了使超材料完美吸收器(metamaterialperfectabsorber,MPA)能够同时实现吸收效率和吸收波长的控制,本文提出利用二氧化钒(VO2)和石墨烯作为MPA的材料,通过对MPA的结构设计,在红外波段实现了高吸收,吸收效率最高可达99%.研究发现通过改变VO2的温度和石墨烯的化 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于二维六方氮化硼材料的光子晶体非对称传输异质结构设计
    摘要:二维六方氮化硼(hexagonalboronnitride,hBN)材料在产生光学稳定的超亮量子单光子光源领域有着潜在应用,有望用于量子计算和信息处理平台,已成为研究热点.而光学非对称传输设备是集成量子计算芯片中的关键器件之一.本文从理论上提出了一种基于hBN材料光子晶体异质结构的纳米光子学非 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 高温超导体电子结构和超导机理的角分辨光电子能谱研究
    摘要:超导是一种奇异的宏观量子现象.100多年来,已发现的超导体主要分为两类:以金属或者合金为代表的常规超导体以及以铜氧化物和铁基高温超导体为代表的非常规超导体.常规超导体的超导机理能被BCS超导理论完美解释,但高温超导体的超导机理至今仍未达成共识,已经成为凝聚态物理领域中长期争论且充满挑战的重大科 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 重费米子超导理论和材料研究进展
    摘要:重费米子超导体是一类典型的强关联和非常规超导系统,超导的产生与量子临界涨落有着紧密的关系.在实际材料中,不同结构体系的重费米子超导体往往表现出非常不同的竞争序和超导性质,表明f电子的行为对材料的结构特征具有敏感依赖性.特别是最近几年的超导实验研究,表明具体材料的实际电子结构对重费米子超导的性质 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 电子型FeSe基高温超导体的磁通束缚态与Majorana零能模
    摘要:作为凝聚态物理中一类新奇准粒子态,Majorana零能模(Majoranazeromode)由于可用来实现拓扑量子计算而成为当前的研究热点.理论预言,Majorana零能模可作为特殊的束缚态出现在一些拓扑超导体的磁通涡旋中.但实际超导体磁通中还可能存在其他低能束缚态或杂质态,这给Majoran ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 中国超导电子学研究及应用进展
    摘要:超导体的发现距今已有近110年了,高温超导体的发现也已经有30多年了.超导材料的电子学应用在最近一二十年取得了突破性进展.高温超导微波器件显示了比传统微波器件更优越的性能,已经在移动通信、雷达和一些特殊通信系统中取得了规模化应用.超导量子干涉器件以其磁场和电流测量的超高灵敏度,成为地质勘探、磁 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 超级质子-质子对撞机中束流热屏的热-结构耦合模拟分析
    摘要:束流热屏(beamscreen)是新一代高能粒子对撞机中的重要部件,用于将束流在管道中运行时产生的热量转移到冷却系统中,同时通过束流热屏上的排气孔将残余气体输送至冷管壁上,维持良好的真空度.然而,在转移热负载的过程中,温度变化产生的形变会影响束流热屏的结构稳定性.如何在保证束流热屏良好传热性能 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.