摘要:由于MnBi₂Te₄电子结构具有对晶格常数的改变相当敏感的特性, 本文采用基于密度泛函理论的第一性原理方法对MnBi₂Te₄反铁磁块体的电子结构施加等体积应变调控. 研究发现体系能带结构在材料等体积拉伸和压缩作用下变化灵敏, 体系出现绝缘体-金属相变. 特别地, 当施加特定应变后导带和价带在Γ处出现交叉, 体系呈零带隙状态. 在此应变下仍可观察到能带反转的现象, 具有非平庸的能带拓扑性质. 根据不同应变下的电荷密度图, 发现等体积应变会影响体系七倍层层间距, 其中等体积压缩和拉伸应变可分别增大和减小Te原子层间距, 表明等体积压缩有利于降低反铁磁层间耦合. 通过等体积压力应变调控, 掌握了MnBi₂Te₄的电子结构的变化规律, 这对本征磁性拓扑绝缘体MnBi₂Te₄的物性研究和实验制备具有重要的指导意义.
关键词: MnBi₂Te₄/
应力应变/
本征磁性拓扑绝缘体/
第一性原理计算

English Abstract

全文HTML

--> --> -->

拓扑绝缘体^[1,2]凭其内部绝缘而表面或界面导电的奇异特性而备受关注, 通过各种手段调控其表面结构可获得许多独具特色的物理性质. 在磁场作用或磁性原子参与情况下, 拓扑绝缘体的时间反演对称性将被打破, 从而产生诸如量子反常霍尔效应^[3-5]、 量子化磁电效应^[6]、马约拉纳费米子^[7]等有趣的物理现象. 尽管磁性与拓扑序相互作用后能产生许多独特的现象, 但由于磁体拓扑材料复杂的磁结构和苛刻的制备条件, 实验上的研究可谓举步维艰. 随即, 稀磁拓扑绝缘体、反铁磁拓扑绝缘体、磁性外尔半金属等大量的本征磁拓扑态材料先后被发现^[8], 又通过密度泛函理论计算得到一种概念上新型的磁性和拓扑绝缘体(magnetic insulator/topological insulator, MI/TI)界面^[9].
值得关注的是, 一种本征磁性拓扑绝缘体材料—MnBi₂Te₄被发现^[8,10,11]. 实验上相继通过各种方法成功合成了MnBi₂Te₄单晶, 如固相反应法^[12,13]、Bi-Te通量法^[14,15]、缓慢冷却法^[16]、熔融和退火方法^[17]、分子束外延技术交替法^[18]等. 与MnBi₂Te₄同构的MnSb₂Te₄也以单晶形式被成功合成了^[19,20]. 可见MnBi₂Te₄的出现再次打破了以往磁性拓扑材料难以实现的障碍. 清华大学物理系徐勇等^[8]还预测了具有层内铁磁和层间反铁磁交换作用的范德瓦耳斯层状MnBi₂Te₄系列材料, 不少专家也研究了天然异质结层状结构MnBi₂Te₄(Bi₂Te₃)_n(n为正整数)^[21-27]. MnBi₂Te₄具有非常丰富的拓扑量子态, 在偶数层和奇数层薄膜中可分别获得本征轴绝缘体和量子反常霍尔绝缘体等等^[8,28]. 作为集拓扑性质和磁学性质于一身的新型材料, 目前业内已探索到的MnBi₂Te₄相关性质如下: 存在量子反常霍尔效应(quantized anomalous Hall effect, QAHE)、量化拓扑磁电效应(topological magnetoelectric effect, TME)的拓扑轴态、最小理想外尔半金属、二维铁磁性性质^[10,11,29], 具有高Chern数特征^[30,31]、有保持反铁磁序的无间隙狄拉克锥^[26,32,33]、存在更接近费米能级的第二狄拉克锥^[32]、磁相变^{[12,22,33,34]}、在反铁磁结构中从轴子绝缘体到Chern绝缘体的量子相变^[34,35]、通过建立异质结能实现反常霍尔态^[31,36,37]等.
最有趣的是, MnBi₂Te₄对晶格常数的改变十分敏感^[10], 在施加应力 (静水压)作用下, 晶格常数、电阻率和载流子浓度会随应力不同而发生改变. 2019年, 中科院物理所程金光研究员课题组^[38]从实验和理论结合出发对MnBi₂Te₄ A型反铁磁构型施加静水压, 发现在12.5 GPa以内体系不发生结构转变, 而奈尔温度T_N会随着压力的增加先稍微变大后逐渐减小, 并在7 GPa完全消失. 他们提出反铁磁(antiferromagnetic, AFM)和铁磁(ferromagnetic, FM)磁组态的竞争机制, 发现由于层间距离的减小, AFM开始增强, 但在大约7—8 GPa时逐渐被抑制直至完全消失, 还通过理论计算, 对MnBi₂Te₄的磁相变进行研究, 对晶格常数进行拟合, 证明对MnBi₂Te₄加静水压应变是可行的. 2020年, 上海科技大学李刚等^[39]同样通过实验和理论对体系进行静水压应变研究, 发现高压会引起结构相变, 但在高压结构相变前仍存在非平庸拓扑态. 最终表明MnBi₂Te₄和MnBi₄Te₇是一种高度可调谐的磁性拓扑绝缘体, 在压缩过程中会出现相变和新的基态. 但是目前对MnBi₂Te₄应力方面的研究仍然不系统. 又由于研究表明A型反铁磁(层内铁磁层间反铁磁)是MnBi₂Te₄的磁基态, 具有约0.2 eV的拓扑非平庸能隙^[10], 并且MnBi₂Te₄反铁磁拓扑绝缘体具有长期探索的表面轴拓扑态, 实验上也证实其具有轴子绝缘体相^[40]. 所以本文对MnBi₂Te₄的反铁磁结构施加等体积应变进行第一性原理计算, 着重关注其能带结构和电荷密度等的变化, 这对实验制备及实际应用等方面都具有重要的指导意义.
应变调控材料性质是探索物质规律很常用的方法之一. 2014年Liu等^[41]通过隧道光谱法和密度泛函理论计算证实Bi₂Se₃表面狄拉克态因面内拉伸应变而增强, 在压缩应变下被破坏. 2016年Inamoto和Takashiri^[42]提出Bi₂Te₃能带结构中的导带底边缘受压缩应变变窄, 即有效质量变小; 并结合实验和理论研究了热电性能受应变的影响. 2018年Hajji等^[43]对Bi₂Te₃施加双轴应变, 发现在3%压力下带隙变大, 而塞贝克系数、热电及电导率降低. 2019年我们通过对磁性掺杂拓扑绝缘体Sb_2–xCr_xTe₃施加静水压应变调控能带结构, 研究表明应变对Bi₂Se₃家族体系的纵向层间距影响较大, 应变可以实现半导体与金属间的相变^[44]. 此外, 应变还被应用在许多方面, 比如, 调制能带结构^[44-46]、分析有效质量^[45]和载流子浓度^[47]. 特别地, 双轴应变可以应用于驱动量子极性相变^[48]、铁电性和拓扑相变的共存^[49,50]、磁性转化^[38,50-52]和新型磁相研究^[53], 还可以用来研究极化特性对电子迁移率的影响^[54]以及调控居里温度^[50,55]等.
显然, 应力应变是外场调控非常典型并且行之有效的研究方法之一, 也是衡量材料韧性的一个关键因素. 尤其是静水压应变机制是比较成熟且经典的应变调控方法, 而我们换个角度采用等体积应变进行研究的根本原因在于等体积应变在三个方向所施加的应力并不相同, 它保证了体积的不变性, 将面内与层间的维度区分开进行研究, 这有利于探讨晶体晶格常数内部动态调整和AFM, FM磁序动态竞争的相关问题. 众所周知, 热力学过程含有等压过程、等温过程及等容过程, 其中等容过程正是体积不变的热力学过程. 等体积应变作为一种新的应变调控方法, 考虑了晶体自身的弹性, 在弹性限度内(未发生结构相变) 有着类似弹性块体一样在某平面受压缩或拉伸可在另一维度自我调适而发生弹性形变的性质, 这对实验和生产应用具有实际意义, 而且可操作性强. 它不仅能赋予材料更多样的变化, 还与实际生产应用息息相关. 而MnBi₂Te₄的应变调控方面的理论研究尚有待进一步拓展, 考虑到MnBi₂Te₄对应力很敏感的特性和反铁磁构型为其基态的事实, 对其进行等体积应变调控, 从而找到应力应变规律, 这是至关重要且合理有效的一个研究课题, 将给实验及实际应用提供理论指导.

2

-->

2.1.模型构建与参数设置

基于密度泛函理论(density functional theory, DFT)的第一性原理计算主要通过维也纳从头算模拟程序包(Vienna ab initio simulation package, VASP)^[56,57]使用投影缀加平面波(projected augmented wave, PAW)^[58]方法实现, 其中平面波截断能选取350 eV. 同时利用Perdew-Burke-Ernzerhof型广义梯度近似(generalized gradient approximation, GGA)的交换关联函数^[59]进行计算, 并用加U方法处理Mn原子的3d轨道, 其中U值取4 eV^[8]. 图1(a)所示为MnBi₂Te₄的晶胞结构, 其传统晶胞属于R$ \bar{3} $m空间群(No. 166), 晶格常数为a = b = 4.36 ?和c = 40.6 ?. 我们计算的反铁磁单胞由红色虚线浅蓝色填充框标出, 并且上下自旋通过箭头表示出来. 包含所有高对称点的第一布里渊区由图1(c)给出.
图 1 (a) MnBi₂Te₄反铁磁结构(上下自旋由不同颜色的箭头标出)及其(b)顶部视图; (c) 包含能带计算过程每个高对称点的第一布里渊区
Figure1. (a) MnBi₂Te₄ antiferromagnetic structure (the upper and lower spins are marked by arrows of different colors) and its (b) top view; (c) the first Brillouin zone containing each high symmetry point in the energy band calculation process.

由于Mn原子具有磁性, 本文采用A型反铁磁(即层内铁磁层间反铁磁)的磁基态构型, 对MnBi₂Te₄反铁磁块体的每个锰加了5 $ {\mu} _{\rm B} $的磁矩. 反铁磁构型由两个铁磁七倍层(Mn-Te-Bi-Te-Te-Bi-Te)组成, 如图1(a)的箭头所示. 用力标准判据进行结构优化, 使其收敛到0.02 eV/?. 计算过程考虑自旋轨道耦合(strong spin-orbit coupling, SOC)作用. 弛豫与自洽采用9 × 9 × 3的Monkhorst-Pack k点网格进行计算, 而能带计算采取的高对称点为${\varGamma}$(0, 0, 0), Z($ \pi, \pi, \pi $), F($ \pi, \pi $, 0), L($ \pi $, 0, 0).
2 -->

2.2.等体积应变方法

所谓等体积应变, 即通过控制晶格常数a (b)同时拉伸或压缩, 并且相应地改变c轴以保证晶胞体积不变. 其六方晶系晶胞体积具体计算表达式如下:

$V = {{a}} \cdot {{b}} \times {{c}} = abc\sin {60^{\circ} }.$

对传统晶胞施加等体积应变后的详细结构参数如表1所列.

拉伸应变 $ \eta$/%	a = b/?	c/?	压缩应变 $ \eta$/%	a = b/?	c/?
0	4.360	40.600	0	4.360	40.600
1	4.404	39.793	–1	4.316	41.432
2	4.447	39.027	–2	4.273	42.270
3	4.491	38.266	–3	4.229	43.154
4	4.534	37.544	–4	4.186	44.045
5	4.578	36.825	–5	4.142	44.986
6	4.622	36.134	–6	4.098	45.948
7	4.665	35.462	–7	4.055	46.942
8	4.709	34.808	–8	4.011	47.968
9	4.752	34.172	–9	3.968	49.028
10	4.800	33.554	–10	3.924	50.123

表1不同等体积应变下体系的晶格常数
Table1.The lattice constants of the system under different isometric strains.

应变$ \eta$由以下表达式给出, 其中$ a_{0} $表示晶胞a轴的初始晶格常数:

$\eta = \left( {\frac{{a - {a_0}}}{{{a_0}}}} \right) \times 100\%. $

首先计算出等体积拉伸和压缩应变下的能带结构演化图^[60], 如图2和图3所示, 其中费米能级用浅蓝色点线表示, 价带顶(valence band maximum, VBM)和导带底(conduction band minimum, CBM)分别用红、蓝颜色的球标注. 由图2可知, 低于5%应变的CBM都在Z点. 由于费米能级附近电子态的竞争, VBM由最初的Z点变为$ {\varGamma} $附近, 并且$ {\varGamma} $-L之间价带上的一点(图中用五角星标注)随着拉伸应变的增加而逐渐升高, 直至$ \eta$ = 6%突破费米能级变为金属. 而这种竞争恰是由应变导致的, 它给反铁磁块体结构实现绝缘体相与金属相间的转变提供了可能, 最近相关研究也表明MnBi₂Te₄可通过加压实现相转变^[38,39].
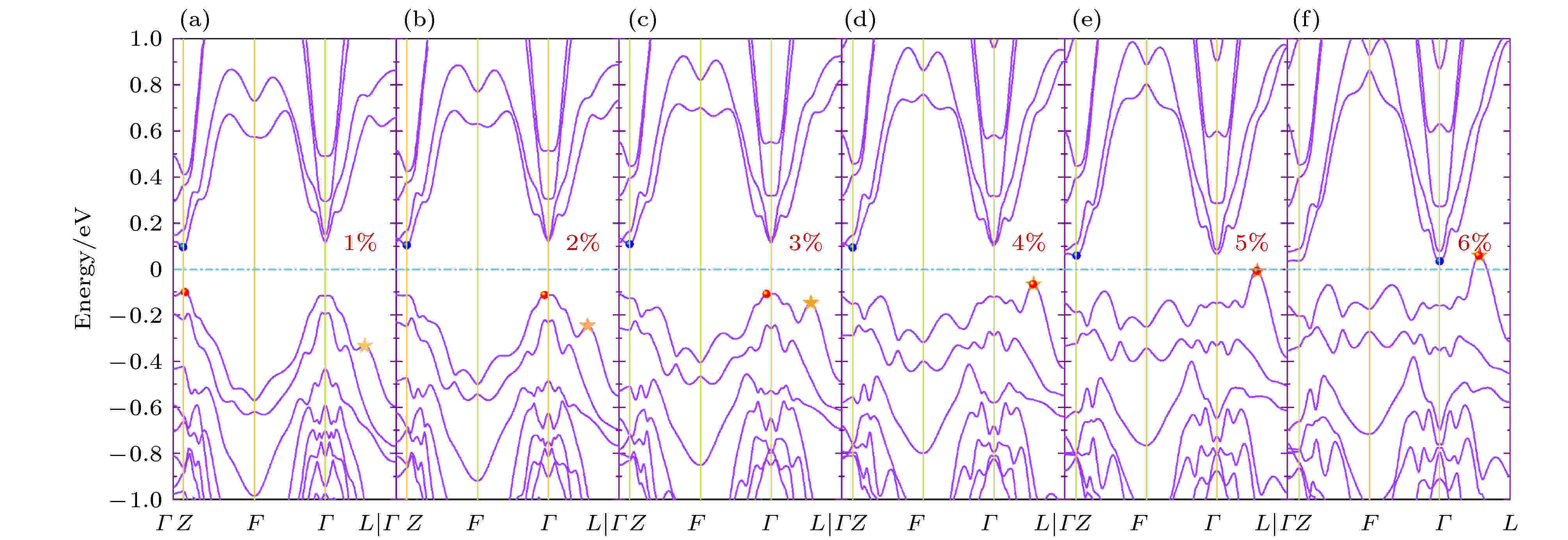图 2 (a)?(f)等体积拉伸应变作用下的能带结构图
Figure2. (a)?(f) The band structure diagram under isometric tensile strains.

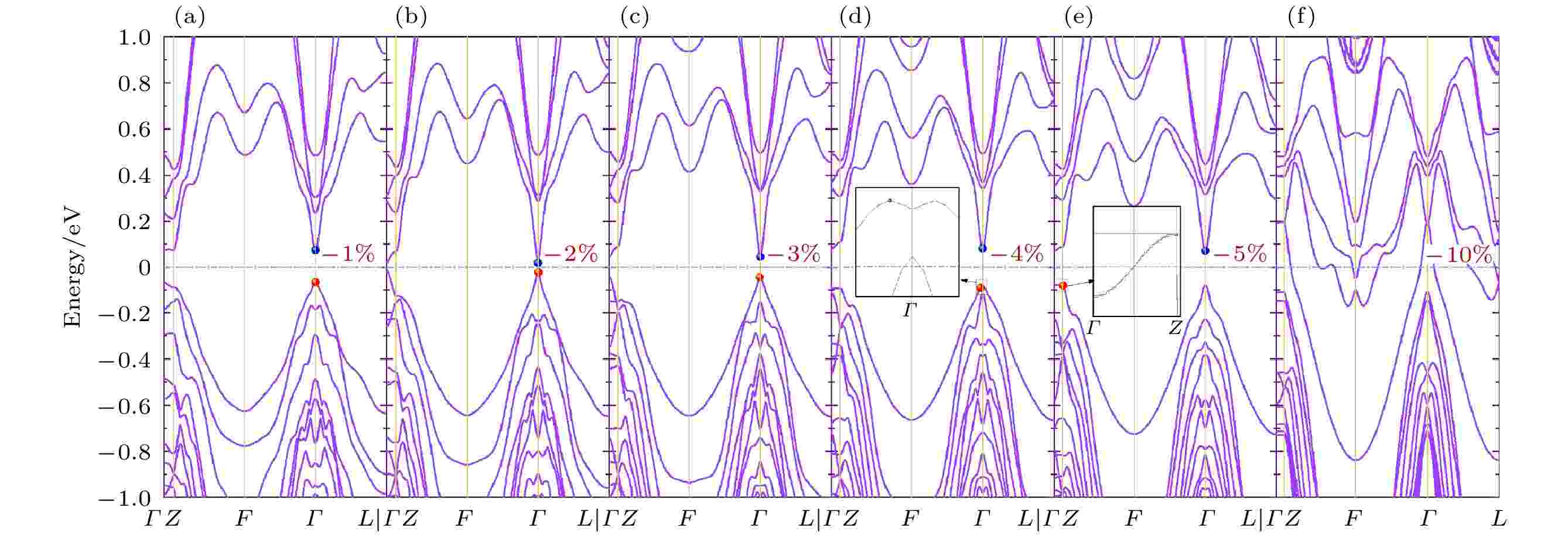图 3 (a)?(f) 等体积压缩应变作用下的能带结构图
Figure3. (a)?(f) The band structure diagram under isometric compression strains.

图3为对体系施加不同程度的等体积压缩应变后得到的能带图. 低程度压缩应变(–3%以内) 体系呈直接带隙(均在${\varGamma}$点), –4%以后VBM开始偏离${\varGamma}$点而变为间接带隙(由图3(d)和图3(e)的嵌入图可明显看到). –6%往后的应变呈现F点导带逐渐下降、${\varGamma}$点处的价带逐渐上升,并先后交于费米能级成为金属, –10% ${\varGamma}$点的导带和价带相交叉如图3(f)所示. 特别值得注意的是, 在–2%时(见图2(b))可发现带隙极小, 于是在其附近进行加压调控, 得到导带与价带交叉的特殊应变值, 具体将在后文讨论. 对图2和图3综合分析发现, 可通过等体积应变调控MnBi₂Te₄的能带结构, 低应变尺度下体系为绝缘体, 其CBM, VBM随应变在${\varGamma}$点与Z点附近变化并分别在拉伸和压缩应变下存在明显的电子态竞争和能带交叉的现象, 实现了应变调控绝缘体-金属间相变的预期目标.
前面介绍了应变调控下的能带结构变化, 现在通过能量和应变的变化曲线来更直观地了解其变化规律. 从图4(a)的应变-能量图可以看出, 无应变体系的能量最低, 但与带交叉的–2.26%相差不多, 约为0.1 eV. 图4(b)给出了结构优化后单胞的晶格常数a(b)及c随应变的变化规律, 呈现线性且此消彼长的趋势也正是所采用的等体积应变的效果. 特别地, 图4(c)和图4(d)清晰表示出体系CBM, VBM和带隙随等体积应变的变化规律. 由图4(c)可见, 拉伸应变能带带隙自无应变后先变大后减小, 在2%左右为最大, 在5%后带隙逐渐缩小并趋于零, 并且在6%应变时费米能级穿过价带顶变为金属(从图2(f)可明显看出). 然而, 等体积压缩应变的能隙呈现先减小后增大, 最后再持续减小的趋势. 结合图4(d)清晰可见, 在–2.26%处CBM与VBM都在$ {\varGamma} $点且刚好相接, 带隙为0 eV.
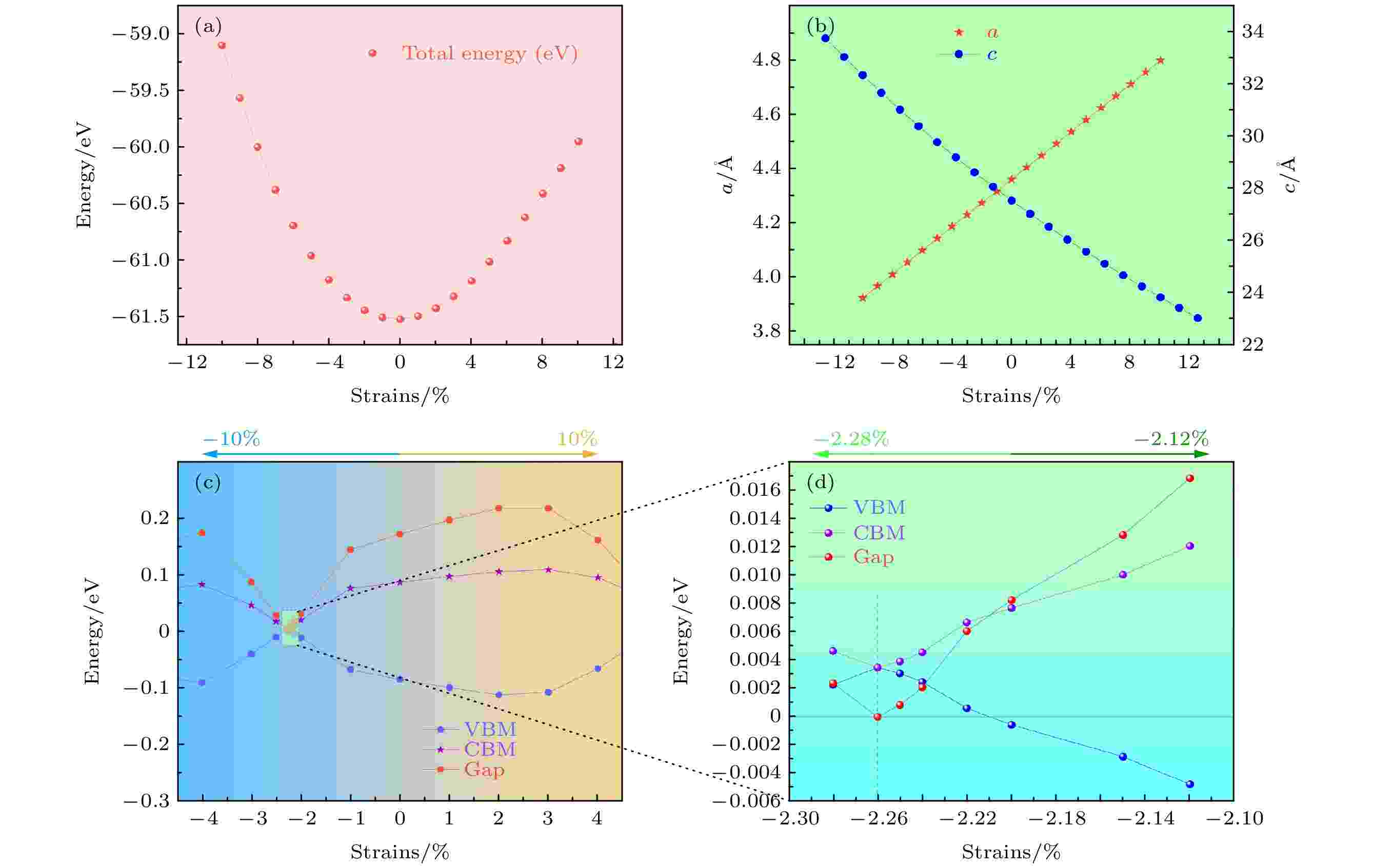图 4 (a) 体系总能随应变的变化趋势; (b)单胞晶格常数随应变的演变规律; (c)等体积应变对带隙的影响; (d)图(c)虚线框处的局部放大图(CBM和VBM随应变的演变趋势也被给出)
Figure4. (a) Variation trend of total energy of the system with strain; (b) evolution regular of unit cell lattice constant with strain; (c) the effect of isometric strain on the band gap; (d) part a enlarged view of the dotted frame in Fig.4 (c). (The evolution trends of the bottom of CBM and VBM with strain are also given)

为了进一步讨论等体积应变对体系原子之间电荷分布情况的影响, 特将$ \pm $5%, $ \pm $10%及无应变体系的电荷密度进行对比, 如图5所示. 分别选择典型的(1$ \bar{1} $0)和(001)晶面进行分析, 图5中对三种原子进行示意, 结构图详见图1(a). MnBi₂Te₄铁磁单胞可看成两个Te-Bi-Te层中间插入一个Mn层的七倍层构成, 七倍层间受范德华力作用. 从电荷密度二维图中发现该体系七倍层内作用较强成离子键, 但七倍层间作用较弱. 由(1$ \bar{1} $0)面还可以看到, 施加等体积拉伸应变使得远离Mn层的两个Te层逐渐靠近(图5中灰色虚线标出), 呈现键上有电荷分布特征, 表示它们之间相互作用增强, 反之压缩应变使二者相互远离, 作用减弱(两Te层在图7(a)用虚线框标注出). 同样, 由图5中(001)晶面也可以发现, 压缩应变使Te与Bi间作用增强, 但拉伸由于七倍层间两Te层靠近反而使其与七倍层内的Bi间作用减弱.
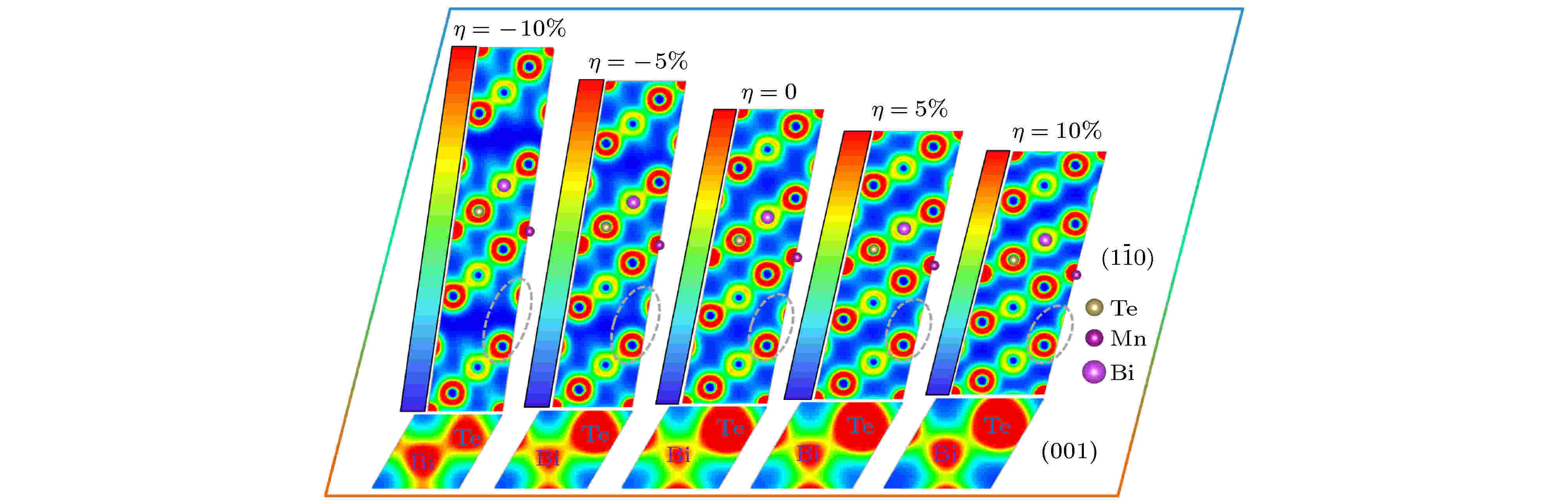图 5 不同等体积应变作用后的电荷密度图　(a) –10%; (b) –5%; (c) 无应变体系; (d) 5%; (e) 10%. Mn, Bi, Te原子的位置用不同颜色的球对应标出; (1$\bar{1}$0)和(001)晶面距离原点所在平面分别为0 $\times \;{d}$及0.41 $\times\;{d}$ (对于饱和度: 红色取13%表示电荷增加, 蓝色取7%代表电荷减少)
Figure5. Charge density diagram after different isometric strains: (a) –10%; (b) –5%; (c) unstrained system; (d) 5%; (e) 10%. The positions of Mn, Bi and Te atoms are correspondingly marked with balls of different colors; The crystal plane (1 $ \bar{1} $ 0) and (001) are 0 $\times\;{d}$ and 0.41 $\times\;{d}$ respectively. For saturation: red takes 13% means charge increase, blue takes 7% means charge decrease

为了进一步解释带隙等费米能级附近电子结构的内在机理, 对费米面附近最高价带的局部电荷密度(本征态波函数的模方), 计算局部电荷密度可以用来说明费米面附近电子结构受等体积应变影响的事实. 图6所示为最高价带的电荷密度受等体积应变的变化演变图, 并且计算了ab平面平均密度曲线(沿着c方向). 从图6可以看到, 等体积应变确实对费米面附近的电子结构有影响. 虽然随着c轴的减小, 最高价带上的局域电荷密度强度有所减弱, 但是Te-Te原子之间成键(平均面电荷密度曲线纵轴5—7 ?位置)的强度相对变大, 并且Te-Te层的面平均密度表现为愈加对称(尤其是5%应变下的结果). 这与上述的二维电荷密度图结果一致, 都揭示了等体积拉伸应变有利于增强Te-Te层之间的耦合的本质结果. 综上所述, 研究结果表明应变对原为范德华力作用的两个Te层影响颇大, 对a (b)轴的拉伸会加强七倍层间耦合, 反之减弱.
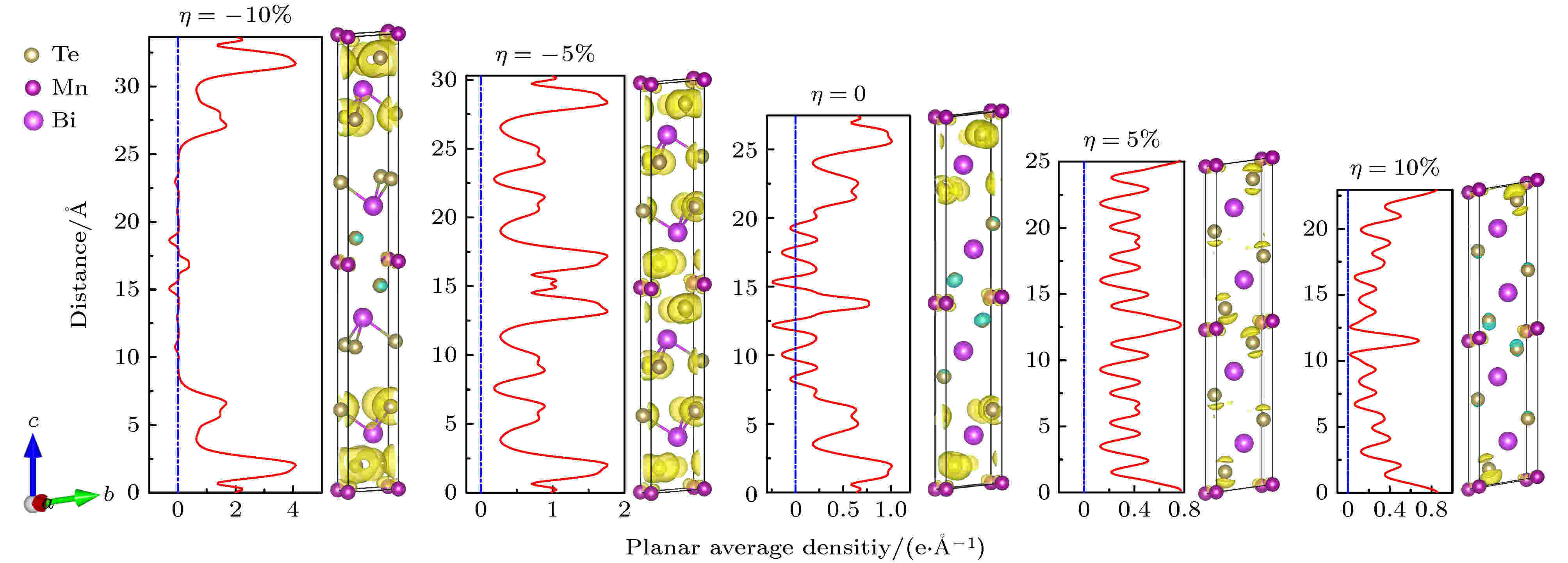图 6 最高价带的局部电荷密度随不同等体积应变的演变图(并相应给出ab平面的平均面电荷密度曲线) (图中三维局部电荷密度的isosurface值均取0.0006 e/bohr³, 黄色代表电荷积累, 蓝色表示电荷减少)
Figure6. The evolution diagram of the local charge density of the highest valence band with different isometric strains and correspondingly give the average surface charge density curve of the ab plane. (The isosurface values of the three-dimensional local charge density in the figure are all 0.0006 e/bohr³. The yellow color represents the accumulation of charge, while the blue color represents the decrease of the charge)

上面提及七倍层层间距随应变发生变化, 下面对层间距进行具体分析, 图7(a)给出了七倍层及其层间距示意图. 图7(b)特别直观地表达出等体积压缩应变使七倍层层间距增大, 并从图7(c)看出压缩应变使Te-Te原子间距也明显增大, 意味着其范德华力作用减弱; 而等体积拉伸应变减小了七倍层层间距, 即使Te-Te距离因为a (b)轴的拉伸而略显变大, 但是层间垂直距离属实明显变小, 故而增强了层间作用.
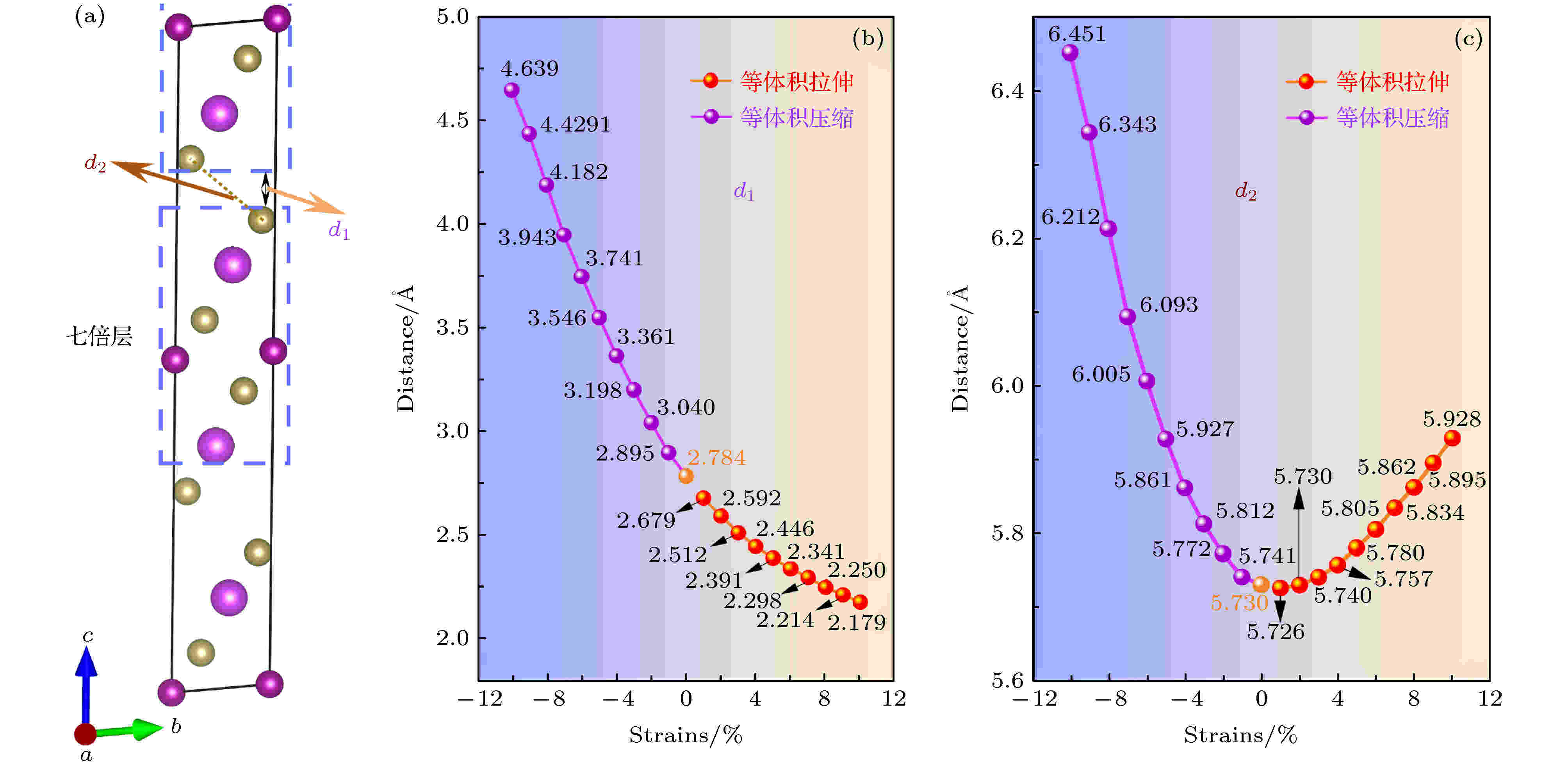图 7 (a)七倍层间距结构示意图; (b)七倍层层间距和(c)Te-Te原子间距随应变的变化规律曲线. 图(b)和图(c)中具体距离也相应标出
Figure7. (a) Schematic diagram of the structure of the sevenfold interval; Variation of the curve of (b) the interval of the sevenfold interval and (c) Te-Te interatomic distance with strain. The specific distance in Fig. (b) and Fig. (c) is also marked accordingly

针对能带出现的一个有趣的零带隙交叉点(应变–2.26%), 现着重对其进行计算分析. 理论上讲, 反铁磁存在时间反演对称性的破缺, 不能形成受Z₂保护的拓扑绝缘体. 然而MnBi₂Te₄却满足$ S = T\tau_{1/2} $对称性^[10], 它同时具有时间反演对称和空间平移对称性质. 由于平移算符的存在, 在其满足S对称性的表面能够形成受拓扑保护的狄拉克锥, 而不受S对称性保护的表面(001)要打开能隙^[10]. 又据近年的Nature文章报道, 已在MnBi₂Te₄中实现磁性打开带隙的反铁磁拓扑绝缘体、底表面和顶表面绝缘^[61,62], 看似已不能在(001)面出现狄拉克锥. 然而, 通过施加等体积应变, 即在ab平面受到2.26%压缩应变后可以在$\varGamma$处实现导带与价带交叉, 此时带隙刚好处于0 eV的临界点, 即可能存在狄拉克锥. 此结果与近期南方科技大学的结论高度一致^[63]. 如图8(a)所示, 我们发现在$\varGamma$处出现交叉(直接带隙), 而从图8(b)看出费米能级附近的态密度主要由Te跟Bi元素贡献. 于是进一步计算了其能带投影和分波态密度, 发现费米能级附近主要由Te及Bi两种元素的p轨道贡献. 结合图8(c)和图8(d)可以看出, 导带主要由Bi-p轨道构成, 价带主要由Te-p轨道贡献, 并且从图8(d)可明显看出发生能带反转. 这种兼具反铁磁序并且能带反转的结果与其他文献一致^[8,61]. 特别地, 从图8(b)和图8(d)两幅态密度图还看到, 价带大约在–0.6 eV附近出现一个尖峰, 表明此时三种元素成键较强, 相互作用明显.
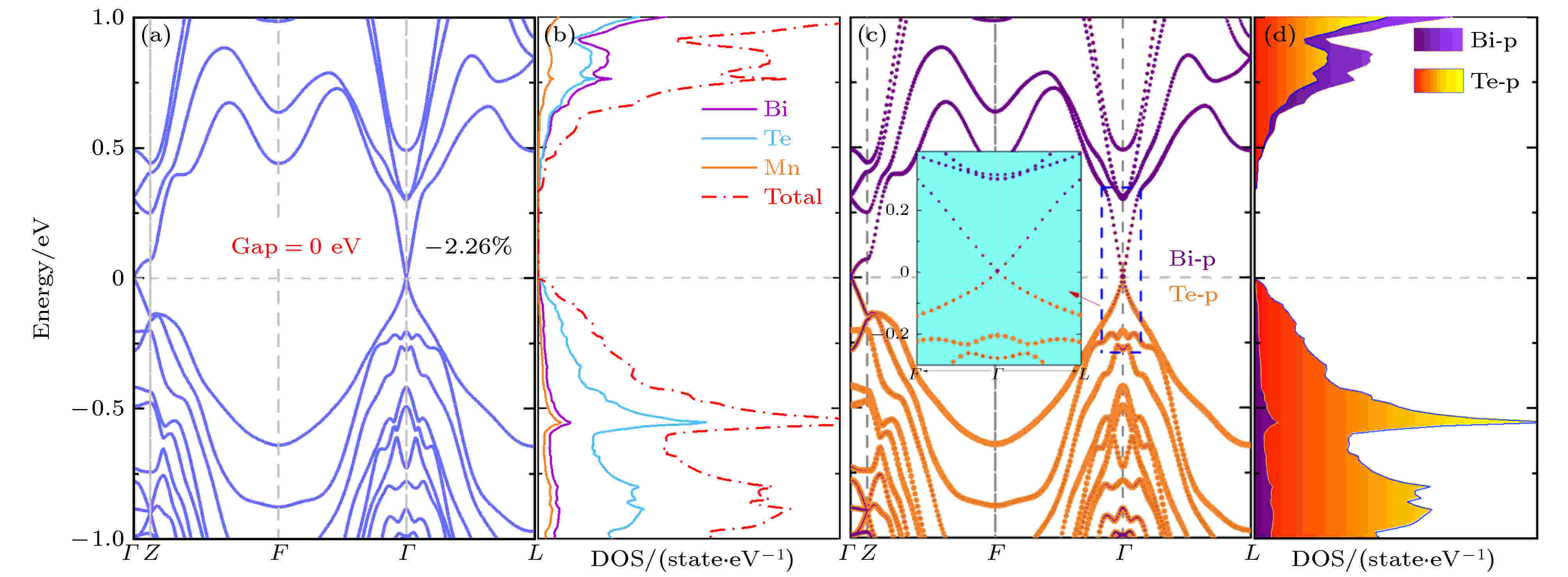图 8 施加2.26%等体积压缩应变时的(a) 总能带结构图, (b) 每类原子的态密度及总态密度, (c) Bi和Te的p轨道能带投影, (d) Bi-p和Te-p轨道分波态密度. 图(c)中含$\varGamma$点费米能级附近的放大图, 由虚线框标出并由箭头指示
Figure8. When 2.26% isometric compressive strain is applied: (a) Structure diagram of the total energy band; (b) state density and total state density of each type of atom; (c) the p orbital energy band projection of Bi and Te; (d) Bi-p and Te-porbit partial wave density. Fig. (c) contains an enlarged view of the $\varGamma$ point near the Fermi level, marked by a dotted frame and indicated by an arrow

最后, 为了比较能带交叉点相应的特殊应变对初始结构的电荷影响, 对–2.26%等体积应变与无应变体系进行差分电荷密度计算, 具体公式为$ \Delta\rho = \rho_{\rm {perfect}}-\rho_{\rm {strain}} $, 图9(a)和图9(b)所示分别为差分电荷密度三维、二维图. 可以看出, 相比–2.26%等体积应变, 无应变体系的Mn原子附近呈纵向得电子而横向失去电子趋势, Te原子在七倍层间得电子, 七倍层内失电子, 说明该等体积压缩应变促使七倍层间的电荷分布减少, 相互作用减弱, 正如前面所述, 这是挤压ab平面而拉伸c轴造成的电荷转移结果, 等体积压缩应变有助于减弱七倍层边界Te原子层的相互作用, 从而与七倍层内Bi原子成键更稳定.
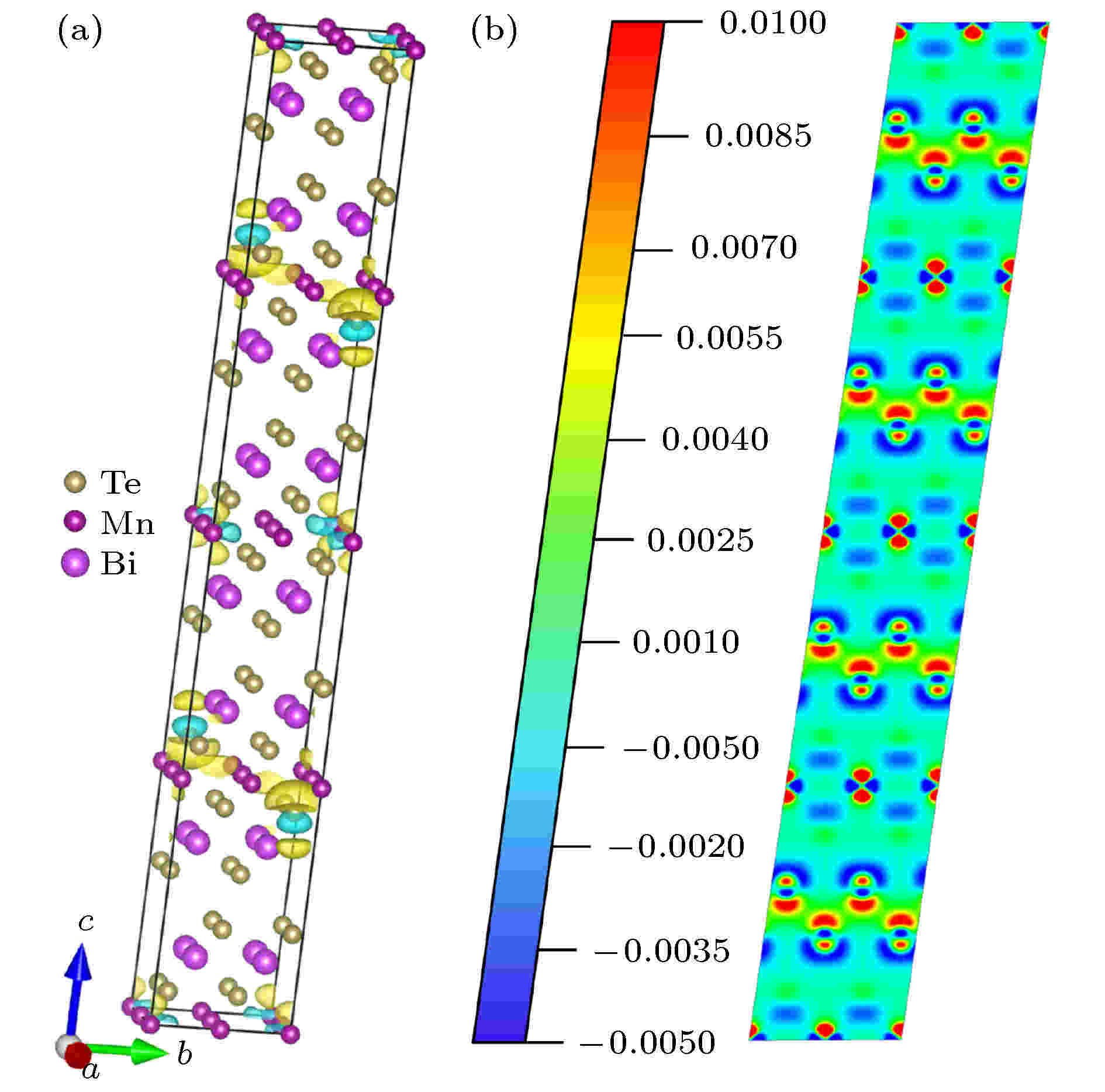图 9 –2.26%等体积应变作用后同无应变体系2 × 2 × 2超胞的差分电荷密度　(a)三维图(黄色表电荷增加, 而蓝色表电荷减少); (b) (100)晶面切面二维图(红色和蓝色分别表示电荷增加及减少, 饱和度的值由图中标尺标出). 图(a)取isosurface = 0.008 e/bohr³, 图(b)的切面取原点所在平面(即0 × d)
Figure9. Differential charge density of –2.26% isometric strain and unstrained system: (a) Three dimensinal graph (yellow color represents charge accumulation and blue color charge depletion); (b) two dimensional drawing of crystal plane (100). (Red and blue indicate charge increase and decrease respectively. The values of saturation are marked on the scale in the figure). Fig. (a) takes isosurface = 0.008 e/bohr³, the cut plane of Fig. (b) takes the plane of the origin (ie 0 $ \times$ d)

本文通过基于DFT的第一性原理计算的方法对本征反铁磁拓扑绝缘体MnBi₂Te₄实施等体积应变研究. 得到的结果主要包括以下三个方面: 第一, 能带结构会随等体积应变呈现一定的演变规律, 并可实现绝缘体-金属间相变的应变调控机制; 第二, 细化调节能带结构发现当应变为–2.26%时导、价带在$\varGamma$点处交叉, 这为当前关于S对称性表面态的相关研究提供了重要的理论依据, 并且从其态密度图中可明显看出存在能带反转的现象; 第三, 从拉伸(压缩)及无应变体系的电荷密度发现该体系具有Mn-Te-Bi-Te:Te-Bi-Te-Mn的七倍层层状结构. 另外, 发现ab平面拉伸而c轴压缩的应变效果, 可增强七倍层边界的Te原子层之间的成键作用; 反之, 则七倍层层间距增加, 反铁磁耦合强度随之降低. 而减小反铁磁的层间耦合作用, 使得在低外磁场下便可产生稳定的铁磁态是当前业内探索QAHE的一个重点目标, 本结论刚好通过施加应力调控其层间相互作用, 为实验上实现QAHE提供有力参考.
本工作的计算在国家超级计算天津中心天河一号执行, 在此表示感谢.