摘要:利用基于密度泛函理论的第一性原理方法, 研究了掺杂铁、钴和镍原子的锯齿型磷烯纳米带(ZPNR)的磁电子学特性. 研究表明, 掺杂和未掺杂ZPNR的结构都是稳定的. 当处于非磁态时, 未掺杂和掺杂钴原子的ZPNR为半导体, 而掺杂铁或者镍原子的ZPNR为金属. 自旋极化计算表明, 未掺杂和掺杂钴原子的ZPNR无磁性, 而掺杂铁或者镍原子的ZPNR有磁性, 但只能表现出铁磁性. 处于铁磁态时, 掺杂铁原子的ZPNR为磁性半导体, 而掺杂镍原子的ZPNR为磁性半金属. 掺杂铁或者镍原子的ZPNR的磁性主要由杂质原子贡献, 产生磁性的原因则是在ZPNR中存在未配对电子. 掺杂位置对ZPNR的磁电子学特性有一定的影响. 该研究对于发展基于磷烯纳米带的纳米电子器件具有重要意义.
关键词: 磷烯纳米带/
掺杂/
电子特性/
磁性

English Abstract

全文HTML

--> --> -->

最近, 实验上通过机械剥落方法从块体黑磷分离出来一种新的二维材料—磷烯^[1,2], 立即受到普遍关注. 研究者从施加应力^[3-6]、引入缺陷^[7,8]、表面吸附^[8-10]和取代掺杂^[10-15]等几个角度出发, 对磷烯进行了广泛地研究. 结果表明, 磷烯具有优越的电子特性, 在未来纳米电子学中具有广阔的应用前景^[16-19]. 通过裁剪二维磷烯, 可以获得准一维的磷烯纳米带(PNR). 根据边缘结构不同, PNR分为锯齿型磷烯纳米带(ZPNR)和扶手椅型磷烯纳米带(APNR). 裸边ZPNR为金属, 且与纳米带的宽度无关; 而裸边APNR为间接带隙半导体, 其带隙随纳米带宽度的增加而减少^[20-22]. 边缘氢饱和后, ZPNR转变为近直接带隙的半导体, APNR转变为直接带隙半导体. 边缘用氢饱和后的ZPNR和APNR的带隙随着宽度的增加而减小^[20-24]. 边缘被F, Cl, O, S, Se, Fe, Co, Ni和 OH等不同原子或基团饱和的PNR的电子特性也被广泛研究^[25-28]. 此外, 如Guo等^[29]发现在边缘氢饱和的APNR中央或边缘掺杂C原子, APNR转变为金属. Zhou等^[30]发现在裸边APNR的中央或边缘掺杂B, N, F和Al原子, APNR仍然是半导体, 而在裸边APNR的中央掺杂C, O, Si, S原子, APNR转变为金属.
目前对磷烯纳米带磁性的研究也有一些报道, 例如, Du等^[31]研究了裸边ZPNR在4种磁构型下的磁性, 这4种磁构型分别为: 铁磁(FM)αα-αα、反铁磁(AFM-1)αα-ββ、反铁磁(AFM-2)αβ-αβ、反铁磁(AFM-3)αβ-αβ, 研究表明裸边ZPNR的FM 态和AFM-1态无磁性, 而AFM-2态有磁性. Zhu等^[32]发现边缘氢饱和的ZPNR没有磁性. Ding等^[33]发现OHO 和 OH钝化的ZPNR和APNR具有磁性. Ren等^[34]发现边缘用OH/NO₂ (或NH₂/NO₂)与O按2∶1比率的饱和ZPNR可实现自旋极化半金属. Zhou等^[30]发现在裸边APNR的边缘掺杂C, O, Si和S原子, APNR有磁性. 然而对磷烯纳米带如何获得半金属, 如何诱发高性能的磁性, 以及诱发磁性的机理等仍需进一步研究.
本文采用基于密度泛函理论(DFT)的第一性原理, 探讨掺杂过渡金属铁(Fe)、钴(Co)和镍(Ni)原子的ZPNR的磁电子学特性, 以及掺杂位置对其影响. 研究表明, 在ZPNR中掺杂不同的杂质表现出不同的特性, 有的有磁性, 有的没有磁性, 提出了在ZPNR中实现半金属的一种新方法, 并且掺杂位置对ZPNR的磁电子学特性有一定的影响. 这些研究结果对于发展基于磷烯的纳米电子器件具有重要意义.

掺杂ZPNR的几何结构如图1所示, 其中图1(a)和图1(b)分别为俯视和侧视图. 图中模型结构为计算选取的超原胞, 纳米带沿图1(a)中Z方向延展. 图中白色、橙色和绿色小球分别表示H, P和Ni原子, n表示ZPNR的带宽, 即沿宽度方向的锯齿型磷原子链的排数, 图中ZPNR的带宽n = 8. 图中的x表示掺杂的位置, 分别用Fe, Co和Ni取代x位置的P原子. 作为例子, 图1(a)和图1(b)中的x位置为Ni原子. 为了叙述方便, 将Fe, Co和Ni原子取代P原子后的ZPNR分别称为Fe-ZPNR, Co-ZPNR和Ni-ZPNR. 为了消除悬挂键, 所有ZPNR边缘用H原子饱和.
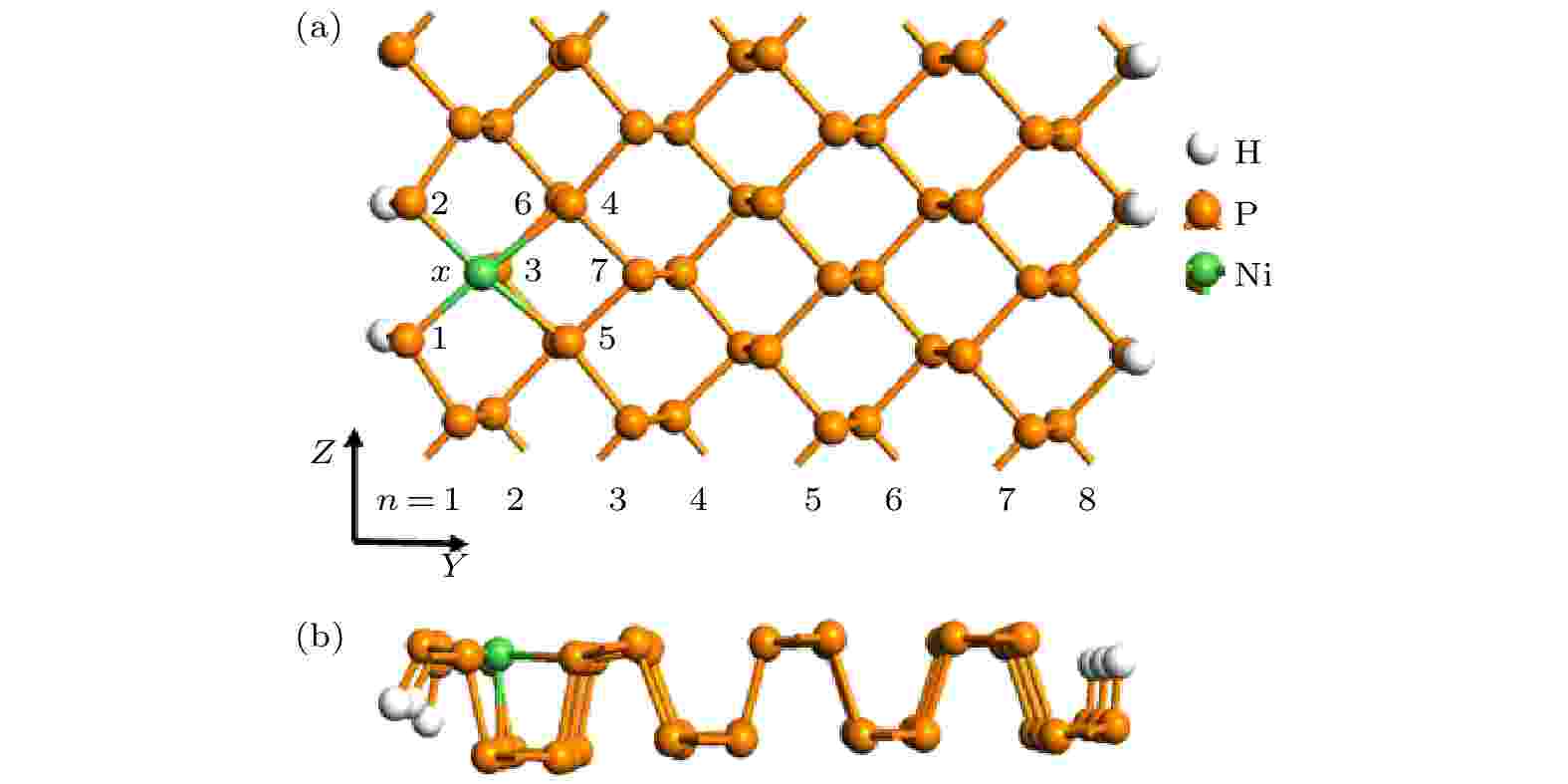图 1 掺杂ZPNR的模型结构
Figure1. The geometric structure of doped ZPNRs.

采用基于密度泛函理论(DFT)的第一性原理的ATK(Atomistix ToolKit)软件包对几何结构进行优化和计算电磁性质, 目前这个软件包已被广泛用于纳米结构的研究中^[35-38]. 模型结构在非磁状态下进行优化. 结构优化收敛的标准是作用在每个原子上的力小于0.01 eV/?. 为了求解Kohn-Sham 方程, 交换关联势采用广义梯度近似(GGA)中的PBE近似, 赝势采用模守恒赝势, 基函数组选用DZP (double$\zeta $+polarized). 在简约布里渊区的k点抽样采用1 × 1 × 30. 能量截断半径(mesh cut-off)采用75 Hartree. 非周期方向, 即超原胞的X和Y方向的真空层设置为20 ?.

2

-->

3.1.结构和稳定性分析

为了便于说明掺杂ZPNR的结构, 在图1(a)中对杂质原子附近的P原子进行了编号, 分别为1—7. 相应的P原子用P_i表示, 其中i = 1, 2, 3, 4, 5, 6, 7. 由图1可见, 取代掺杂后, 杂质原子附近的ZPNR结构发生了一些形变, 最明显的变化就是杂质原子与周边5个P原子(P₁—P₅)成键, 而原始ZPNR的P原子只与相邻3个P原子成键. 杂质原子与周边5个P原子之间的键长如表1所示, 表中d₁—d₅分别为杂质原子与其邻近的5个磷原子P₁—P₅的键长. 作为对比, 表中还列出了未掺杂ZPNR的相关参数. 由表1可见, 未掺杂ZPNR 的d₁, d₂和d₃相等, 都为2.25 ?, 与以前的计算结果一致^[11-13]. 掺杂ZPNR 的键长与未掺杂ZPNR的键长相比略有增减, 但相差不大, 其中Ni-ZPNR 的d₄和d₅增加幅度最大, 大约增加了10%, 而其余键长的增减幅度不足4%. 掺杂后, 杂质原子与P₄, P₅原子成键, 结果导致杂质原子略微向纳米带对称中心移动.

system	d1/?	d2/?	d3/?	d4/?	d5/?	Eb/eV	ENM–EFM/meV
ZPNR	2.25	2.25	2.25	—	—	–5.65	0
Fe-ZPNR	2.27	2.27	2.17	2.32	2.32	–5.69	130.11
Co-ZPNR	2.22	2.22	2.25	2.32	2.32	–5.68	0
Ni-ZPNR	2.26	2.26	2.25	2.50	2.48	–5.65	7.23

表1掺杂和未掺杂ZPNR的键长、结合能和总能差
Table1.The bond lengths, binding energy, and total energy difference of doped and pristine ZPNRs.

为了研究取代掺杂结构的能量稳定性, 分别取各掺杂ZPNR的超原胞计算结合能E_b, 其定义为^[39-41]

${E_{\rm{b}}} = \frac{{{E_{{\rm{dop}}}} - {n_{\rm{P}}}{E_{\rm{P}}} - {n_{\rm{H}}}{E_{\rm{H}}} - {n_{\rm{X}}}{E_{\rm{X}}}}}{{{n_{\rm{P}}} + {n_{\rm{H}}} + {n_{\rm{X}}}}}, $

其中E_dop为掺杂ZPNR超原胞的总能量; E_P, E_H和E_X分别为单个P、H和杂质原子的能量, n_P, n_H和n_X分别为超原胞内P, H和杂质原子的数量, 其中杂质原子分别为Fe, Co和Ni. 计算结果如表1所示, 表中还列出了未掺杂ZPNR的结合能. 由表1可见, 各掺杂和未掺杂ZPNR的结合能都为负值, 说明各掺杂和未掺杂ZPNR的结构都是稳定的.
为了进一步研究取代掺杂结构的能量稳定性, 分别取各掺杂ZPNR的超原胞计算吉布斯自由能E_G, 其定义为^[42]

${E_{\rm{G}}} = {E_{\rm{T}}} - {\chi _{\rm{P}}}{\mu _{\rm{P}}} - {\chi _{\rm{H}}}{\mu _{\rm{H}}} - {\chi _{\rm{i}}}{\mu _{\rm{i}}},$

其中E_T为掺杂ZPNR超原胞的每个原子的能量; χ_P, χ_H和χ_i分别为P、H和杂质原子的摩尔分数; μ_P, μ_H和μ_i 分别为每个P、H和杂质原子的化学势, 其中杂质原子分别为Fe, Co和Ni. μ_P为磷烯中每个原子的能量, μ_H为氢分子中每个原子的能量, μ_i为体态下每个杂质原子的能量. 计算结果显示, Fe-ZPNR, Co-ZPNR和Ni-ZPNR的吉布斯自由能分别为–0.40, –0.41, –0.40 eV. 由此可见, 各掺杂ZPNR的吉布斯自由能都为负值, 说明各掺杂ZPNR的结构都稳定.
为了检验取代掺杂结构的热稳定性, 我们在几何优化后对其进行了Forcite退火分子动力学模拟^[43]. 整个模拟过程使用4个退火循环, 并使用微正则系综. 每个退火循环由初始温度300 K升高至最高温度500 K, 然后冷却至初始温度. 整个模拟过程运行8000步, 总时间为8 ps. 模拟退火后的几何结构如图2所示, 图2(a)—(c)分别为Fe-ZPNR, Co-ZPNR和Ni-ZPNR. 与退火前的ZPNR相比, 杂质原子与周边P原子间的键长略有变化, 但没有产生局部重建. 这表明所有掺杂ZPNR的热稳定性很好.
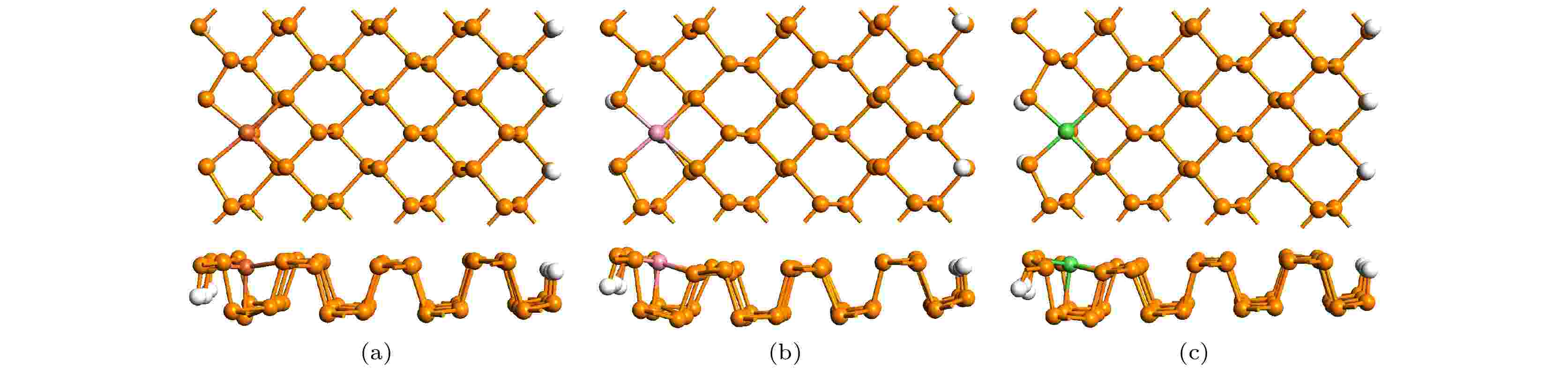图 2 模拟退火后的模型结构　(a) Fe-ZPNR; (b) Co-ZPNR; (c) Ni-ZPNR
Figure2. The geometric structure after anneal simulation: (a) Fe-ZPNR; (b) Co-ZPNR; (c) Ni-ZPNR.

2 -->

3.2.掺杂ZPNR的磁电子学特性

我们首先对掺杂ZPNR进行自旋非极化计算, 其对应的非磁(NM)态的能带结构和态密度(DOS)如图3(a)和图3(b)所示. 图中Fe, Co和Ni分别表示Fe-ZPNR, Co-ZPNR和Ni-ZPNR, 而ZPNR表示未掺杂的ZPNR. 图中虚线表示费米能级, 设为零. 由图3可见, 未掺杂的ZPNR没有能带穿越费米能级, 且在费米能级附近一定能量范围内, ZPNR的DOS为零, 故未掺杂的ZPNR为半导体. 未掺杂的ZPNR的导带底和价带顶都位于Γ点, 故为直接带隙半导体, 其带隙大小为1.51 eV, 这与以前的研究结果是一致的^[20-24]. 由图3(a)可见, 掺杂ZPNR都由于掺杂而引入了两条能带, 图中用a, b进行了标示. Fe-ZPNR和Ni-ZPNR各有一条能带(即能带a)穿越费米能级, 而Co-ZPNR没有能带穿越费米能级. 由图2(b)可见, Fe-ZPNR和Ni-ZPNR的DOS在费米能级处都不为零, 而Co-ZPNR的DOS在费米能级处为零. 故当处于NM态时, Fe-ZPNR和Ni-ZPNR为金属, 而Co-ZPNR依然为半导体. Co-ZPNR为间接带隙半导体, 其带隙大小为1.12 eV, 小于未掺杂的ZPNR的带隙. 由此可见, 掺杂Fe或者Ni原子将ZPNR由半导体转变为金属, 而掺杂Co原子则将ZPNR由直接带隙半导体转变成为间接带隙半导体, 且带隙减小.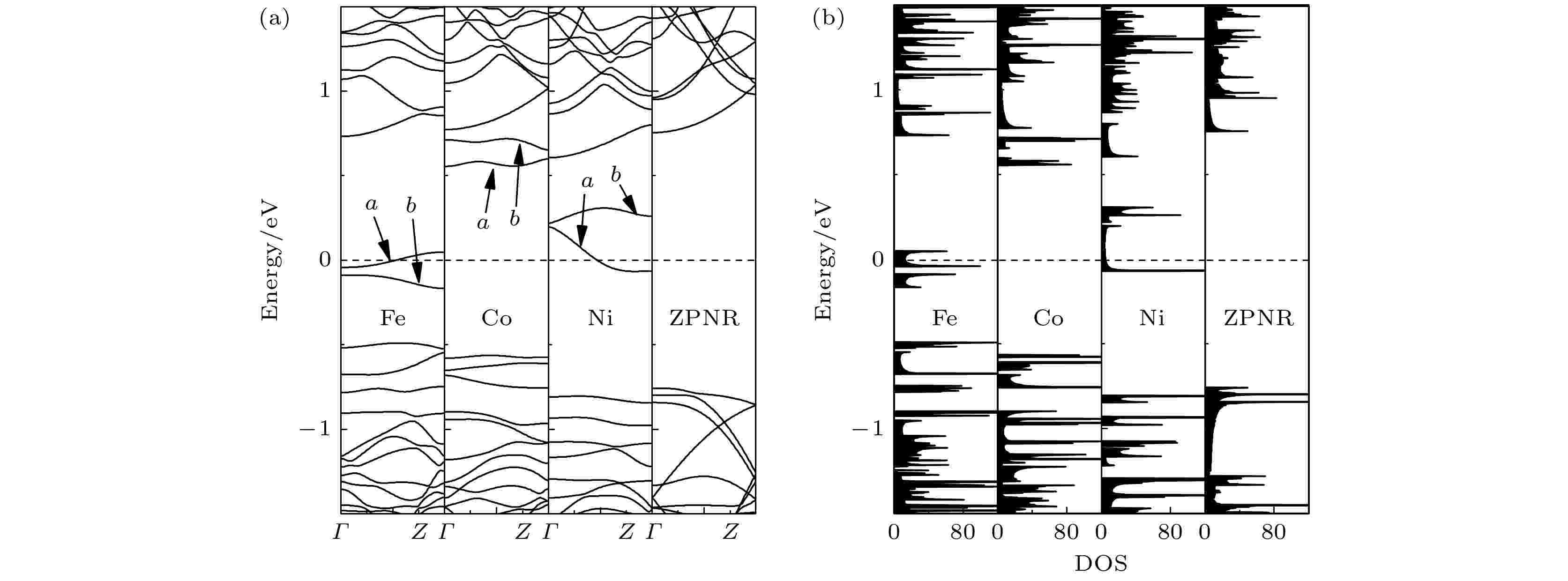
图 3 ZPNR处于NM态的 (a) 能带结构和 (b) 态密度
Figure3. (a) The band structure and (b) density of states of ZPNRs in the nonmagnetic state.

为了更清楚地分析杂质原子对能带结构的影响, 图4绘出了掺杂ZPNR能带结构中能带a的电荷密度图, 图4(a)—(c)分别为Fe-ZPNR, Co-ZPNR和Ni-ZPNR, 等值面取0.3 |e|/?³. 由图4可见, 掺杂ZPNR的能带a由杂质原子起主要作用, 而起次要作用的是杂质原子附近的几个P原子. 由此可见, 能带a正是由于掺杂而引入的杂质能带, 并导致Fe-ZPNR和Ni-ZPNR由半导体转变为金属, 而Co-ZPNR的带隙小于未掺杂的ZPNR的带隙.
图 4 部分能带的电荷密度　(a) Fe-ZPNR; (b) Co-ZPNR; (c) Ni-ZPNR
Figure4. The charge density of partial band: (a) Fe-ZPNR; (b) Co-ZPNR; (c) Ni-ZPNR.

为了更进一步分析杂质原子中哪个轨道的电子起主要作用, 图5绘出了掺杂ZPNR的投影态密度(PDOS)图, 图5(a)—(c)分别为Fe-ZPNR, Co-ZPNR和Ni-ZPNR. 图中的Fe, Co和Ni分别表示投影到Fe, Co和Ni原子的PDOS, 而s, p和d则分别表示投影到相应杂质原子的s, p和d轨道的PDOS. 可见, 杂质原子的PDOS主要由其d轨道的电子贡献, 即掺杂ZPNR的杂质原子对电子特性起主要作用的是d轨道的电子.
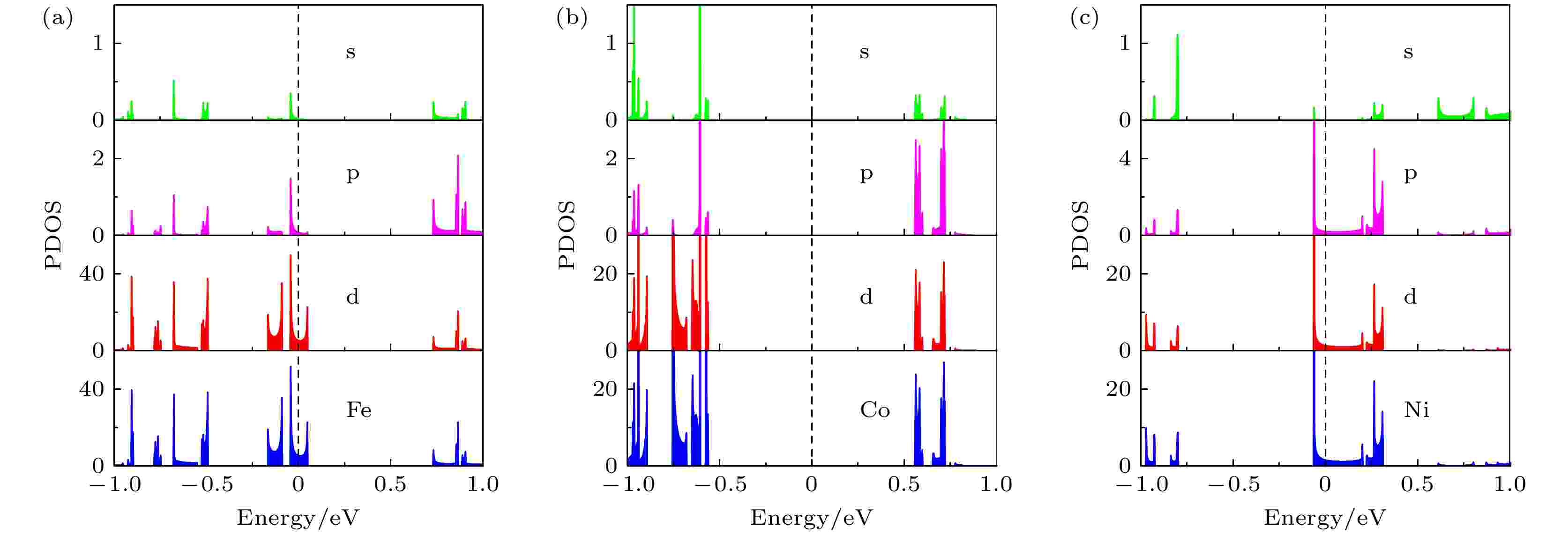图 5 掺杂ZPNRs投影态密度　(a) Fe-ZPNR; (b) Co-ZPNR; (c) Ni-ZPNR
Figure5. The partial density of states of ZPNRs: (a) Fe-ZPNR; (b) Co-ZPNR; (c) Ni-ZPNR.

现在我们对掺杂ZPNR进行自旋极化计算以研究掺杂诱发的磁性. 定义NM态与铁磁(FM)态之间的总能差为$\Delta E = {E_{{\rm{NM}}}} - {E_{{\rm{FM}}}}$, E_NM和E_FM分别为各超原胞在NM态和FM态的总能. 由表1可见, 未掺杂ZPNR和Co-ZPNR的总能差ΔE = 0, 表明未掺杂ZPNR和Co-ZPNR无磁性, 基态即为NM态. Fe-ZPNR和Ni-ZPNR的总能差ΔE > 0, 即E_NM > E_FM, 表明Fe-ZPNR和Ni-ZPNR的基态是FM态.
为了分析掺杂ZPNR的磁电子学特性, 图6展示了掺杂ZPNR处于FM态的能带结构和态密度, 图6(a)—(d)分别为未掺杂ZPNR, Fe-ZPNR, Co-ZPNR和Ni-ZPNR. 图6中蓝色实线和红色实线分别表示α和β自旋(下同). 由图6(a)和图6(c)可见, 未掺杂ZPNR和Co-ZPNR的能带是简并的, 没有能带穿越费米能级, 在费米能级附近一定能量范围内, ZPNR的DOS为零, 故未掺杂ZPNR和Co-ZPNR为半导体, 其带隙大小分别为1.51和1.12 eV. 能带简并这一特性结合总能差ΔE = 0, 进一步表明未掺杂ZPNR和Co-ZPNR没有磁性. 未掺杂ZPNR没有磁性, 这一结果与之前的研究结果^[32]是一致的. 由图6(b)和图6(d)可见, Fe-ZPNR和Ni-ZPNR在费米能级附近的能带都发生了分裂, 表明Fe-ZPNR和Ni-ZPNR具有磁性. Fe-ZPNR的α和β自旋都没有能带穿越费米能级, 且在费米能级处的态密度都为零, 故Fe-ZPNR为自旋半导体, 且为半-半导体. Fe-ZPNR的α和β自旋的导带底和价带顶都位于Γ点, 故都为直接带隙, 其带隙大小分别为0.87和0.13 eV. Ni-ZPNR的β自旋没有能带穿越费米能级, 但α自旋有能带穿越费米能级, 且在费米能级处β自旋的态密度不为零, 而α自旋的态密度为零, 故Ni-ZPNR为半金属. Ni-ZPNR的β自旋为间接带隙, 其带隙大小为0.90 eV. 可见, 掺杂Fe原子可使ZPNR由无磁性半导体转变为磁性半导体, 而掺杂Ni原子可使ZPNR由无磁性半导体转变为磁性半金属.
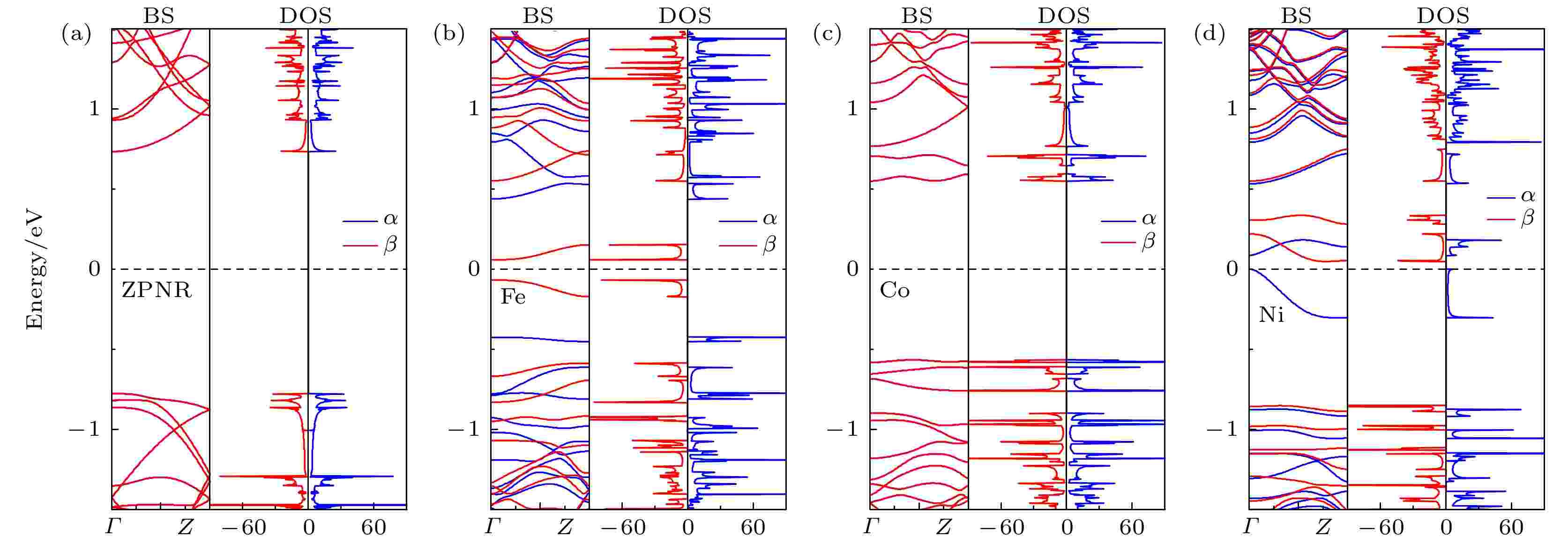图 6 ZPNR处于FM态的能带结构和态密度　(a) ZPNR; (b) Fe-ZPNR; (c) Co-ZPNR; (d) Ni-ZPNR
Figure6. The band structure and density of states of ZPNRs in the ferromagnetic state: (a) ZPNR; (b) Fe-ZPNR; (c) Co-ZPNR; (d) Ni-ZPNR.

为了分析磁性的来源, 图7给出了掺杂ZPNR在FM态的自旋极化电荷密度等值面图, 图7(a)—(c)分别为Fe-ZPNR, Co-ZPNR和Ni-ZPNR. 图7中红色和蓝色分别代表α和β自旋, 等值面取0.02 |e|/?³. 自旋极化电荷密度$\Delta \rho = {\rho _\alpha } - {\rho _\beta }$, 其中${\rho _\alpha }$和${\rho _\beta }$分别表示α和β自旋的电荷密度. 由图7(a)和图7(c)可见, Fe-ZPNR和Ni-ZPNR的自旋极化电荷密度的共同特点是, 在该等值面下, 几乎只见到α自旋电荷, 且自旋电荷主要分布于杂质原子, 其次分布于杂质原子附近的P原子. 因为只在纳米带左边缘掺杂, α自旋的电荷分布在左边缘, 右边缘未见到自旋电荷, 所以Fe-ZPNR和Ni-ZPNR磁性状态都表现为铁磁性, 而且只能表现出FM态, 不会出现反铁磁(AFM)态. 由图7(b)可见, 在该等值面下, Co-ZPNR没有观察到自旋极化电荷. 可见Fe-ZPNR和Ni-ZPNR的磁性主要来源于杂质原子, 而Co-ZPNR无磁性.
图 7 自旋极化电荷密度等值面图　(a) Fe-ZPNR; (b) Co-ZPNR; (c) Ni-ZPNR
Figure7. The isosurface plots of spin polarization charge density in the ferromagnetic state: (a) Fe-ZPNR; (b) Co-ZPNR; (c) Ni-ZPNR

对ZPNR磁矩计算结果表明, 未掺杂ZPNR和Co-ZPNR超原胞的总磁矩为0μ_B, Fe-ZPNR和Ni-ZPNR超原胞的总磁矩分别为1.00μ_B和0.89μ_B, μ_B为玻尔磁子. 磁矩计算结果同样表明, 对Fe-ZPNR和Ni-ZPNR的磁矩贡献最大的是杂质原子. Fe和Ni原子的磁矩分别为0.96μ_B和0.43μ_B, 分别对其超原胞的总磁矩贡献了96.0%和48.3%. 由此可进一步说明掺杂Fe-ZPNR和Ni-ZPNR的磁性主要由杂质原子贡献. 而未掺杂ZPNR和Co-ZPNR超原胞的总磁矩为零, 也进一步表明未掺杂ZPNR和Co-ZPNR没有磁性.
掺杂诱发ZPNR的磁性, 可做如下解释. 由于P原子最外层具有5个价电子, 每个P原子与周边3个P原子成键, 即有3个电子与周边原子的电子配对, 剩余2个电子配对. 按照能量最小原理, 原子内的电子先填充4s层, 再填充3d层. 对于Fe, Co和Ni原子来说, 它们的4s层都填充2个电子, 而3d层填充的电子数量分别为6, 7和8个. 由前面的分析知道, 在掺杂ZPNR中, 杂质原子与周边5个P原子成键, 且杂质原子对电子特性起主要作用的是d轨道的电子. Fe原子的3d层有6个电子, Fe原子与周边5个P原子成键, 剩下1个未配对电子. Co原子的3d层有7个电子, Co原子与周边5个P原子成键, 剩下的两个电子配对. 而Ni原子的3d层有8个电子, Ni原子与周边5个P原子成键, 剩余3个电子, 其中2个电子配对, 剩下1个未配对电子. 正是由于在ZPNR中掺杂Fe和Ni原子出现了未配对电子, 才导致Fe-ZPNR和Ni-ZPNR具有磁性. 而在ZPNR中掺杂Co原子没有出现未配对电子, 因此Co-ZPNR没有磁性.
2 -->

3.3.掺杂位置对磁电子学特性的影响

为了研究掺杂位置对掺杂ZPNR磁电子学特性的影响, 在此以掺杂Ni原子为例进行分析, 其能带结构如图8所示, 图8(a)和图8(b)分别为NM态和FM态, 图8(b)中的插图为费米能级附近能带结构的局部放大图. 为了说明方便, 将Ni原子取代图1(a)中标注x, 6和7的P原子的ZPNR分别用Ni_x-ZPNR, Ni₆-ZPNR和Ni₇-ZPNR表示. 标注x, 6和7的P原子分别位于第1, 第2和第3条P原子链靠纳米带对称中心一侧的中间位置. 图8中的6和7分别代表Ni₆-ZPNR和Ni₇-ZPNR. 结合图3(a)和图8(a)可见, 当处于NM态时, 在ZPNR的3个不同位置掺杂Ni原子, 都在费米能级附近引入了两条杂质能带, 并且有一条穿越费米能级, 故ZPNR属性不变, 都为金属. 结合图6(d)和图8(b)可见, 当处于FM态时, 在ZPNR的3个不同位置掺杂Ni原子, 费米能级附近的能带都发生了分裂, 但呈现出不同的特性. Ni₆-ZPNR的磁电子学特性与Ni_x-ZPNR相同, α自旋有能带穿越费米能级, 但β自旋没有能带穿越费米能级, 即呈现为半金属. Ni₆-ZPNR的β自旋为直接带隙, 其带隙大小为0.74 eV. 但Ni₇-ZPNR的磁电子学特性与Ni_x-ZPNR不同, 此时α和β自旋都没有能带穿越费米能级, 即呈现为磁性半导体. Ni₇-ZPNR的α和β自旋都为间接带隙, 其带隙大小分别为0.16 eV和 0.74 eV. 由此可见, 当处于FM态时, 在靠近纳米带边缘位置掺杂Ni原子, ZPNR表现为磁性半金属, 而在靠近纳米带对称中心位置掺杂Ni原子, ZPNR则表现为磁性半导体.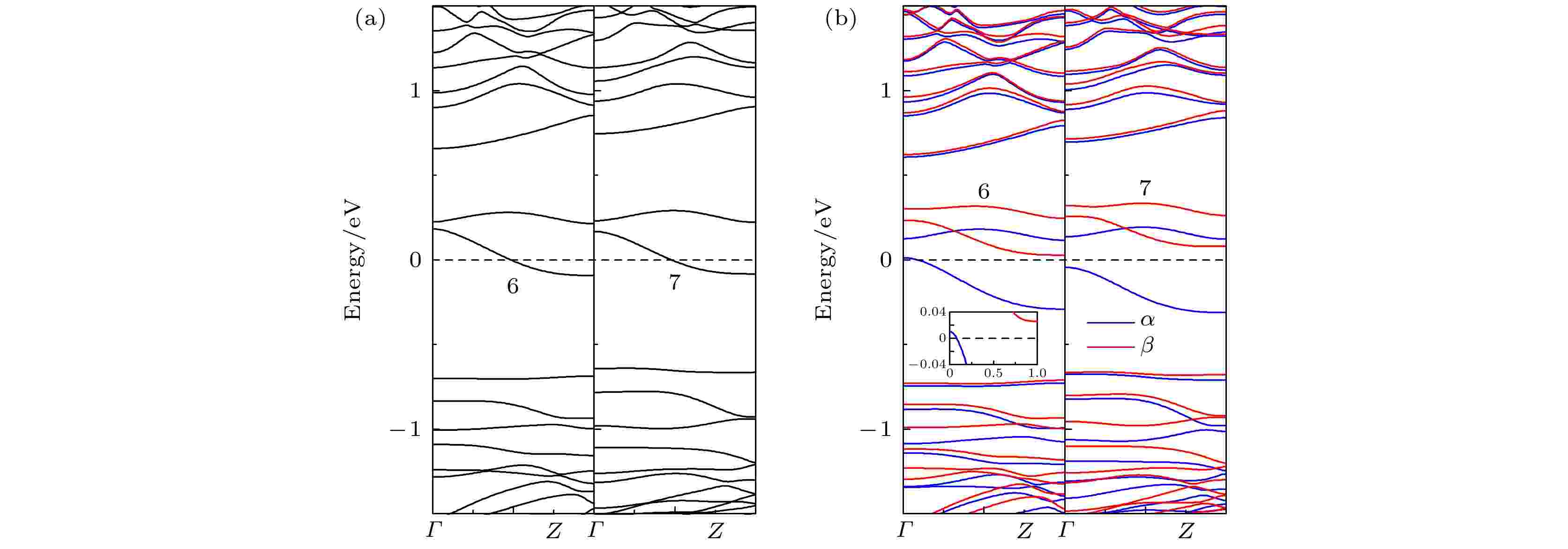
图 8 改变掺杂位置时ZPNR的能带结构　(a) NM; (b) FM
Figure8. The band structure of ZPNRs with different doping position: (a) NM; (b) FM.

利用基于密度泛函理论的第一性原理方法, 研究了掺杂Fe, Co和Ni原子的锯齿形磷烯纳米带的磁电子学特性. 研究表明, 掺杂和未掺杂ZPNR的结构都是稳定的, 未掺杂ZPNR和Co-ZPNR的基态为NM态, 而Fe-ZPNR和Ni-ZPNR的基态是FM态. 当处于NM态时, 掺杂Fe或者Ni原子将ZPNR由半导体转变为金属, 而掺杂Co原子则将ZPNR由直接带隙半导体转变成为间接带隙半导体, 且带隙减小. 发生这种转变是由于掺杂在能带结构中引入了杂质能带. 处于FM态时, 未掺杂ZPNR和Co-ZPNR无磁性, 掺杂Fe原子使ZPNR由无磁性半导体转变为磁性半导体, 而掺杂Ni原子使ZPNR由无磁性半导体转变为磁性半金属. Fe-ZPNR和Ni-ZPNR的磁性主要由杂质原子贡献. Fe-ZPNR和Ni-ZPNR具有磁性, 是由于在ZPNR中掺杂Fe和Ni原子出现了未配对电子. 而Co-ZPNR没有磁性, 则是在ZPNR中掺杂Co原子没有出现未配对电子. 掺杂位置对ZPNR的磁电子学特性有一定的影响, 当处于FM态时, 在靠近纳米带边缘位置掺杂Ni原子, ZPNR表现为半金属, 而在靠近纳米带对称中心位置掺杂Ni原子, ZPNR则表现为磁性半导体. 该研究对于发展基于磷烯纳米带的纳米电子器件具有重要意义.