摘要:193 nm波长浸没式步进扫描投影光刻机是实现45 nm及以下技术节点集成电路制造的核心装备. 增大数值孔径是提高光刻分辨率的有效途径, 而大数值孔径曝光系统的偏振性能严重影响光刻成像质量. 光刻机曝光系统偏振参数的高精度检测是对其进行有效调控的前提. 基于光栅的偏振检测技术能实现浸没式光刻机偏振检测装置的小型化, 满足其快速、高精度在线检测的需求, 该技术中的关键部件是结构紧凑且偏振性能良好的光栅. 本文基于反常偏振效应和双层金属光栅对TE偏振光的透射增强原理, 采用严格耦合波理论和有限时域差分方法, 设计了一种双层金属光栅偏振器. 计算了该偏振器的初始结构参数, 并通过数值仿真得到了其偏振性能关于各光栅参数的变化关系. 仿真结果表明, 中间层高度是影响TE偏振光透射增强的主要因素; 垂直入射时TE偏振光的透过率可达到56.8%, 消光比高达65.6 dB. 与现有同波段金属光栅偏振器相比, 所设计的光栅偏振器在保证高透过率的同时, 消光比提升了四个数量级.
关键词: 双层金属光栅/
偏振检测/
深紫外/
浸没式光刻机

English Abstract

全文HTML

--> --> -->

随着大规模集成电路制造工艺发展到45 nm及以下技术节点, 步进扫描投影光刻机必须使用大数值孔径曝光系统. 大数值孔径条件下, 曝光系统的偏振性能对光刻成像对比度、光刻工艺窗口和掩模误差增强因子等指标的影响不可忽略, 其严重影响光刻成像质量, 且随技术节点的缩减愈加明显^[1-4]. 对曝光系统偏振参数进行有效调控的前提是实现其偏振参数的高精度检测. 通常在光刻机的掩模面或硅片面进行曝光系统的偏振参数检测. 旋转波片法是光刻机曝光系统偏振参数检测的常用方法, 其检测装置主要由光学成像单元、四分之一波片、检偏器和探测器组成^[5-8]. 基于旋转波片法的浸没式光刻机偏振检测系统常用偏振棱镜作为检偏器, 偏振棱镜体积大且需要与后置光学元件距离足够长以实现偏振分束, 难以实现小型化. 在检测过程中, 旋转波片法需要驱动装置控制波片旋转, 这使得整个检测装置结构复杂、体积庞大. 以NA1.35步进扫描投影光刻机曝光系统为例, 其掩模面与照明系统最后一个单元(均匀性校正单元)的纵向距离仅53 mm, 旋转波片法通常需要将照明光束传递至掩模外较大空间以放置偏振检测装置. 此外, 浸没式光刻机偏振检测精度要求DOP(3σ) < 0.3%, 数值计算表明此时要求检偏器的消光比达到30 dB以上. 为满足浸没式光刻机偏振检测系统的小型化和快速、高精度检测需求, 实现插入式偏振检测, 具有优越偏振性能且体积小、易集成的偏振器是其关键.
金属光栅偏振器可在较宽光谱范围内实现高消光比和高透过率, 且具有体积小、易集成化、设计灵活等特点, 已被广泛应用于可见光和红外光学系统^[9-11]. 在深紫外波段, 研究者^[12-14]提出的光栅偏振器的光栅周期均在100 nm甚至更小, 且偏振性能不佳. Honkanen等^[15]发现在金属光栅偏振器的共振域存在反常偏振现象, 即TE偏振光的传输效率高于TM偏振光. Kang等^[16,17]基于亚波长金属光栅的反常偏振效应, 提出深紫外铝-二氧化硅混合光栅, 在196 nm波长下透过率为30%, 消光比为35 dB. 张冲等^[18]提出一种深紫外介质-金属光栅偏振器, 在193 nm波长下透过率为60%, 消光比为180: 1(23 dB). 以上偏振器不能兼具高消光比和高透过率, 无法满足浸没式光刻机曝光系统对偏振检测装置的需求. 而双层金属光栅具有更加优越的偏振性能且其制作方法简单, 工艺容差要求和成本较低, 且对TE偏振光有异常透射作用^[19-21]. 在可见光和红外波段, 研究者利用双层金属光栅中TM偏振光入射时表面等离子体激元耦合共振, 以及双层金属光栅内形成类Fabry-Perot腔谐振增强效果, 实现对TE偏振光透射的增强^[22,23], 但在深紫外波段的设计鲜有报道.
本文针对193 nm波长浸没式光刻机偏振检测装置高精度、小型化和低成本需求, 将金属光栅共振域的反常偏振效应和双层金属光栅对TE偏振光的异常透射特性结合, 基于严格耦合波(rigorous coupled-wave analysis, RCWA)和时域有限差分方法(finite-difference time-domain, FDTD)设计一种透射式双层金属光栅偏振器. 利用TM偏振光入射时在不同金属-介质界面产生的表面等离子体共振效应和双层金属光栅结构中形成的类F-P腔谐振增强机理, 确定光栅的初始结构参数. 分析双层金属光栅占空比、介质层厚度、金属层厚度等结构参数对偏振透过率和消光比的影响, 在此基础上对各结构参数进行优化. 通过在双层金属光栅和基底间添加一定厚度的氟化镁介质层进一步提高该光栅的偏振性能. 不同偏振光入射条件下, 对所设计光栅的截面场分布进行了分析, 以确定该结构偏振性能产生的物理机制.

双层金属光栅偏振器结构如图1所示, 光栅基底材料为熔石英, 金属材料为在深紫外具有反常偏振效应的铝. 光栅主要参数包括: 光栅周期P, 顶层金属栅线宽度w, 占空比w/P, 顶层和底层金属层厚度h, 二氧化硅介质层厚度H和氟化镁介质层厚度h₁. 光源波长为193 nm, 光源从基底沿z轴正方向垂直入射. 入射光分为电场垂直于栅线方向的TM偏振光分量和平行于栅线的TE偏振光分量. 消光比(extinction ratio, ER)定义为$10\log \left({{{{T_{{\rm{TE}}}}} / {{T_{{\rm{TM}}}}}}} \right)$.
图 1 双层金属光栅偏振器结构示意图
Figure1. Schematic diagram of bilayer metallic grating polarizer.

光栅周期是影响光栅偏振性能的关键参数之一. 当光栅周期远小于入射波长时称为亚波长光栅, 此时透射光波中只有零级衍射光波, 其他级次的衍射光波均为倏逝波. 当光栅周期介于入射波长的一半到两倍之间时为光栅的共振域, 共振域光栅会出现瑞利-伍德异常现象^[15], 此时m级衍射光的衍射角达到90°(即沿光栅表面传播), 引起衍射波能量在其他衍射级次上重新分布, 透射光强会呈现尖锐的变化. 该异常发生条件为

$P\left({{n_i}\sin {\theta _i} \pm {n_{\rm{s}}}} \right) = m\lambda ,$

其中P为光栅周期; ${n_i}$为入射介质折射率; ${\theta _i}$为入射角; ${n_{\rm{s}}}$为出射介质折射率; $\lambda $为入射波长.
深紫外波段常用基底材料是熔石英和氟化镁. 波长为193 nm时, 二者折射率分别是${n_{{\rm{SiO}}_2}} = 1.5629{{ + }} 0 i$和${n_{{\rm{MgF}}_2}} = 1.4796{{ + }} 0.0019 i$. 由于氟化镁折射率虚部不为零, 当基底厚度较大时, 基底吸收不可忽略, 导致透过率降低. 为保证高透过率, 光栅基底选择为熔石英. 为得到高衍射效率和高偏振, 要求只存在零级衍射光, 同时根据瑞利-伍德异常条件, 计算光栅周期应小于193 nm.
表面等离子体激元会影响金属光栅TM偏振光的透过率^[24-30]. 反常偏振条件下, 利用表面等离子体共振对TM偏振光透射的强抑制作用, 可获得高消光比光栅. TM偏振光具有垂直于金属表面的电场分量, 使金属产生表面电荷, 当入射光波矢和表面等离子波的波矢相匹配时, 两种电磁波模式发生强烈地耦合激发表面等离子体波, 产生表面等离子体共振. 共振条件为^[31]

${k_0}\sqrt \varepsilon \sin {\theta _i} + m\frac{{2{\rm{\pi }}}}{P} = \pm {k_0}\sqrt {\frac{{{\varepsilon _{\rm{m}}}\varepsilon }}{{{\varepsilon _{\rm{m}}} + \varepsilon }}} ,$

其中$m > 0$取+号, $m < 0$取-号; ${k_0} = {{2{\text{π}}} / \lambda }$为真空中的波数; $\varepsilon $和${\varepsilon _{\rm{m}}}$分别为介质和金属材料介电常数.
当入射波长接近表面等离子体共振波长时, 光栅产生透射异常. 当共振波长为193 nm时, 在铝-空气界面和铝-氟化镁界面产生表面等离子体共振的光栅周期条件分别为: 172 nm和97 nm. 然而表面等离子体共振波长会偏离透射光谱的峰谷位置, 即表面等离子体共振产生异常透射的对应波长存在偏离共振波长的情况^[32]. 此外, 只产生零级衍射光时要求光栅周期小于193 nm, 综合考虑器件的偏振性能需求和制造工艺难度选择光栅周期为180 nm.
对于TM偏振光入射进入底层金属光栅中, 铝-二氧化硅-铝腔形成金属-介质-金属缝隙波导. 当满足波矢匹配条件时, 波导中TM偏振光的光学模式在其界面转化成表面等离子体激元模式. 表面等离子体激元在波导中的色散方程为^[33]

$\frac{{\varepsilon {k_{\rm{m}}}}}{{{\varepsilon _{\rm{m}}}k}} = \frac{{1 - \exp \left({ka} \right)}}{{1 + \exp \left({ka} \right)}},$

$\begin{split} &k = {k_0}\sqrt {{{\left({\frac{{{\beta _{{\rm{spp}}}}}}{{{k_0}}}} \right)}^2} - \varepsilon } \\ &{k_{\rm{m}}} = {k_0}\sqrt {{{\left({\frac{{{\beta _{{\rm{spp}}}}}}{{{k_0}}}} \right)}^2} - {\varepsilon _{\rm{m}}}}, \end{split} $

${n_{{\rm{spp}}}} = {{{\beta _{{\rm{spp}}}}} / {{k_0}}},$

其中, a为介质宽度; ${\left[ {{\rm{Re}} \left(k \right)} \right]^{ - 1}}$和${\left[ {{\rm{Re}} \left({{k_{\rm{m}}}} \right)} \right]^{ - 1}}$分别为表面等离子体在介质和金属中的衰减长度; ${\beta _{{\rm{spp}}}}$为波导模式中电磁波传播常数; ${n_{{\rm{spp}}}}$为波导中有效折射率.
金属-介质-金属波导类似于一个F-P谐振腔, TM偏振光入射到金属表面产生表面等离子体波, 并在腔内产生驻波. 光栅深度调制波导内包含驻波周期的个数, 进而调制其透射光谱产生周期性变化. 当光栅深度为驻波周期的非整数倍时, 出射面金属顶角产生更强的电偶极子, 此时入射面金属的电荷很少, TM偏振光的透过率降低^[34]. 根据类F-P腔谐振条件可以初步确定金属层的厚度, F-P腔谐振公式为^[25-27]

$\frac{{m\lambda }}{{{\rm{Re}} \left({{n_{{\rm{F}} -{\rm{ P}}}}} \right)}} = 2{h_{{\rm{F}} -{\rm{ P}}}} + \Delta ,$

其中${n_{{\rm{F}} -{\rm{ P}}}} = {\beta / {{k_0}}}$, $\beta $为类F-P腔内电磁波传播常数; $ \Delta $为腔内反射产生的附加相移修正项, 反映了入射波长和基底介电常数等对类F-P腔长度的影响, 当腔体结构确定时, $ \Delta $为定值.
TM偏振光入射时, 联立(3)式—(5)式计算底层金属光栅形成的类F-P腔中, 腔内有效折射率为2.25. m = 1时, 忽略修正项, 共振周期为42.8 nm. TE偏振光没有垂直于金属表面的电场分量, 无法满足耦合条件, 不产生表面等离子体激元, 计算m = 1时共振周期为61.7 nm. 为使TE偏振光透射增强, 取金属层高度接近其共振周期; 为使TM偏振光透射被抑制, 取金属层高度接近其共振周期的1.5倍, 故金属层初始高度定为60 nm.
TE偏振光入射时, 介质腔存在截止宽度^[35,36]. 当介质腔宽度小于${\lambda / {2 n}}$时, TE偏振光透射截止(n为腔内折射率). 此外, 在截止宽度附近存在一个介质宽度使TE偏振光透射增强, 且在狭缝附近的能流密度呈现出光学漩涡和其他类型的相位奇异性^[37]. TE偏振光入射, 介质分别为二氧化硅和空气时的金属光栅介质腔截止宽度分别为61.7 nm和96.5 nm. 为保证TE偏振光的高透过率, 取w初始宽度为84 nm, 即占空比为0.47.
根据“膜系统”方法, 可将双层金属光栅的介质-空气中间层等效为一层均匀电介质, 视为一层波导, 计算中间层两相介质的等效折射率公式为

${n_{{\rm{eff}}}} = \sqrt {n_0^2\frac{{n_1^2 + 2n_0^2 + 2{g_1}\left({n_1^2 - n_0^2} \right)}}{{n_1^2 + 2n_0^2 - {g_1}\left({n_1^2 - n_0^2} \right)}}} ,$

其中${n_0}$是模相(主相)折射率; ${n_1}$是嵌入相折射率, ${g_1}$是嵌入相的体积百分比.
将双层金属光栅结构等效成顶层为金属-空气层, 中间层为波导层, 底层为金属-介质层, 将顶层和底层光栅等效成金属层, 视为腔体, 近似形成类F-P谐振腔^[21]. 通过底层光栅传输的光波在顶层光栅处产生部分反射, 并在中间层多次反射后产生干涉. 其中间层高度根据使TE偏振光入射时在该类F-P腔中产生共振增强确定. 当m = 1时, 计算共振周期为78.7 nm, 取初始中间层高度为75 nm, 二氧化硅层高度为中间层高度和金属层高度之和, 其初始高度为135 nm.
由于熔石英基底折射率大于氟化镁, 可在光栅与基底之间添加适当厚度的氟化镁介质层, 起到减反增透的效果, 进一步提高器件透过率^[38]. 当膜层的光学厚度为${\lambda / 4}$时增透效果最好, 故氟化镁介质层初始高度设置为33 nm.
根据瑞利-伍德异常和表面等离子体共振条件, 确定双层金属光栅的周期为180 nm; 根据TE偏振光在介质腔内的截止宽度, 确定初始占空比为0.47; 根据顶层和底层金属光栅层中金属-介质-金属结构形成的类F-P腔谐振, 确定金属层初始厚度为60 nm; 根据将顶层和底层金属光栅间的中间层等效为一层波导, 确定中间层的初始高度为75 nm, 二氧化硅层初始高度为135 nm; 根据增透膜层原理, 确定氟化镁介质层初始高度为33 nm. 根据以上双层金属光栅的初始结构参数, 利用Lumerical FDTD Solutions进行数值仿真, 其中, 在光栅周期性方向上(± x)采用周期性边界条件, 在光束传播方向(± z)上采用完美匹配层边界条件. 结合数值仿真结果对光栅各结构参数进行优化, 并对其偏振透射增强产生的物理机制进行验证与分析.

2

-->

3.1.占空比对光栅偏振性能的影响

根据第2节初始参数设计, 光栅周期为180 nm, 初始金属光栅层高度为60 nm, 二氧化硅层高度为135 nm, 氟化镁层高度为33 nm. 占空比变化对光栅偏振透过率和消光比的影响如图2所示. 图2表明: 随着占空比的增大, TE偏振光透过率先增大后减小, 占空比大于0.8时, 出现正常偏振现象, 即TM偏振光透过率大于TE偏振光透过率; TM偏振光透过率整体较小, 在占空比为0.44处取得极小值, 此时消光比为极大值. 故取占空比为0.44, 对应的顶层金属栅线宽度w为80 nm.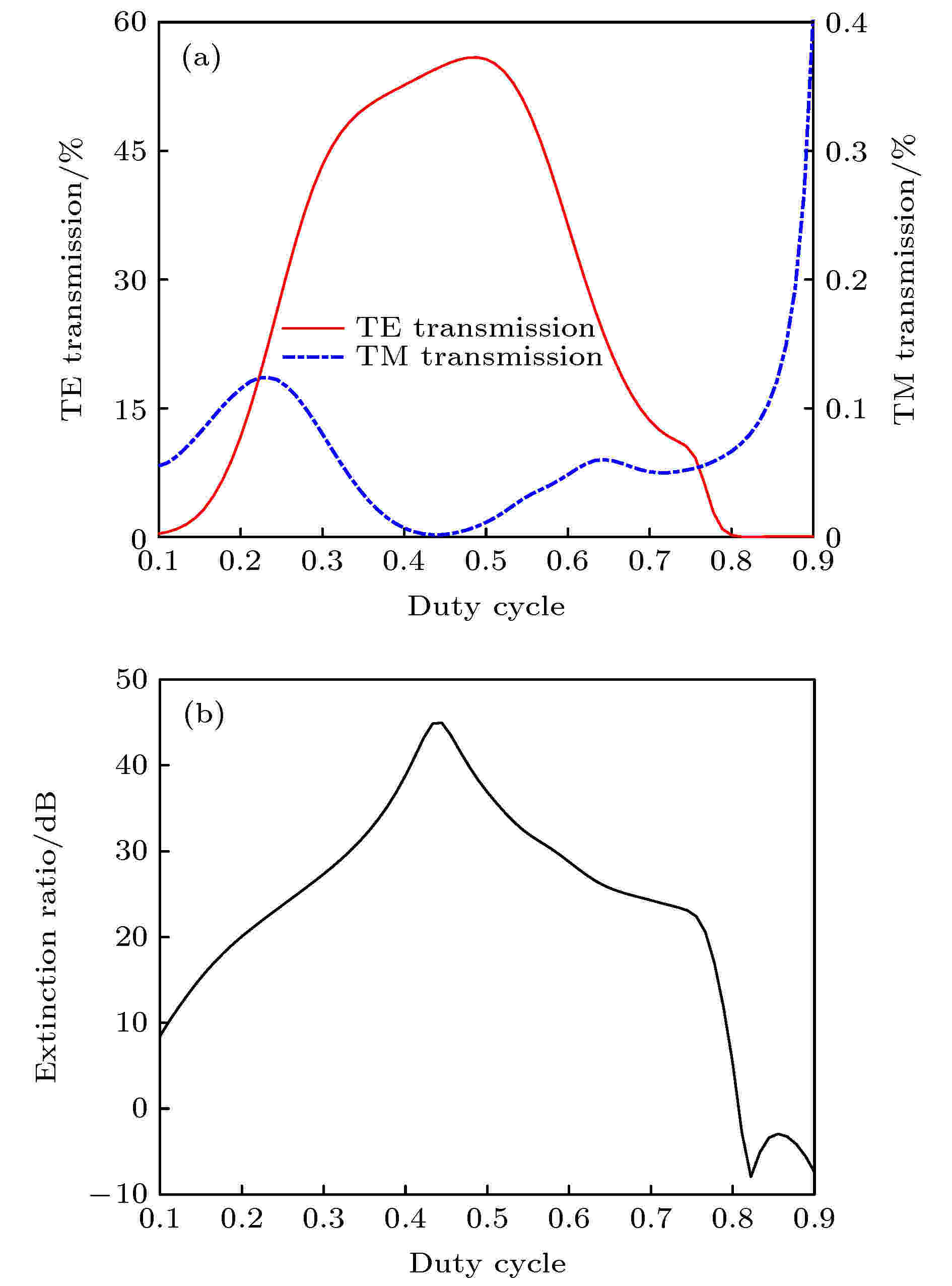
图 2 占空比对光栅偏振性能的影响　(a) 透过率; (b) 消光比
Figure2. Polarization performance of grating as functions of the grating duty cycle: (a) Transmission; (b) extinction ratio.

2 -->

3.2.二氧化硅层高度对光栅偏振性能的影响

将中间层视为一层波导, 顶层和底层光栅的表面电磁波在波导内产生共振, 导致透射异常. 二氧化硅层的高度直接影响波导层的厚度, 是影响透射异常的关键参数之一. 保持光栅周期为180 nm, 占空比为0.44, 金属层高度为60 nm, 氟化镁层高度为33 nm不变, 二氧化硅层高度对光栅偏振透过率和消光比的影响如图3所示. 二氧化硅层高度为130 nm时消光比达到第一个极大值, 同时TE偏振光透过率较高, 确定二氧化硅层厚度为130 nm, 此时中间层高度为70 nm.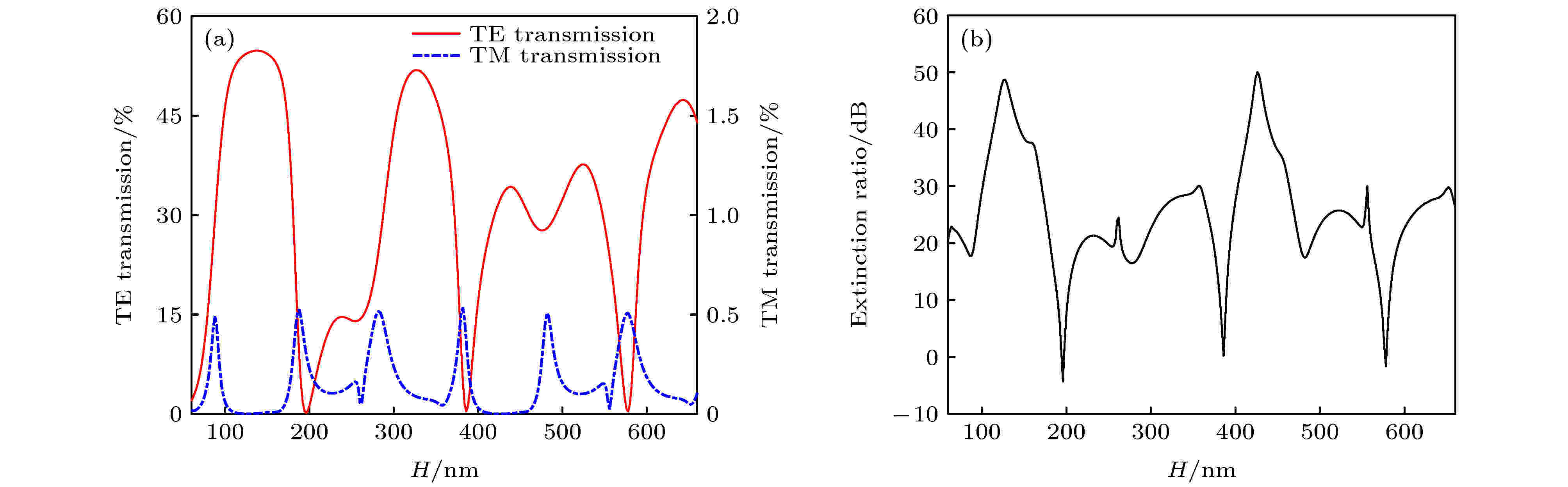
图 3 二氧化硅层高度对光栅偏振性能的影响　(a) 透过率; (b) 消光比
Figure3. Polarization performance of grating as functions of the silica height: (a) Transmission; (b) Extinction ratio.

由图3可知, TE和TM偏振光透过率随二氧化硅层的高度产生周期性振荡, 二者的透过率峰值周期由底层和顶层金属-介质腔与双层光栅构成的类F-P腔组成的复杂腔体共同决定. 二氧化硅层高度对TE偏振光透过率具有较强调制作用, 表明中间层的高度对实现TE偏振光透射增强起决定性作用. 当二氧化硅层高度为626 nm时, TM和TE偏振光入射时的电场分布如图4所示. 图4(a)表明TM偏振光入射时, 金属-介质产生的表面等离子体进入底层金属光栅介质腔中, 发生类F-P共振, 并有少量TM偏振光进入中间层. 在中间层中, 空气腔和二氧化硅腔内的共振周期不相同, TM偏振入射时不能简单将中间层等效成一层介质波导, 其实际的透过率峰值由复杂腔膜效应共同调制. 对于TE偏振光, 由于铝光栅在深紫外波段的反常偏振效应, 入射光被强烈地耦合进光栅介质中, 并在中间层振荡产生共振(图4(b)). 在中间层其共振整体表现为三个周期, 出现两次趋于零的透过率极小, TE偏振光透过率同样由空气腔和二氧化硅腔共同调制. 这也是实际透过率峰值周期与将其简化为类F-P谐振所计算的周期存在差距的原因.
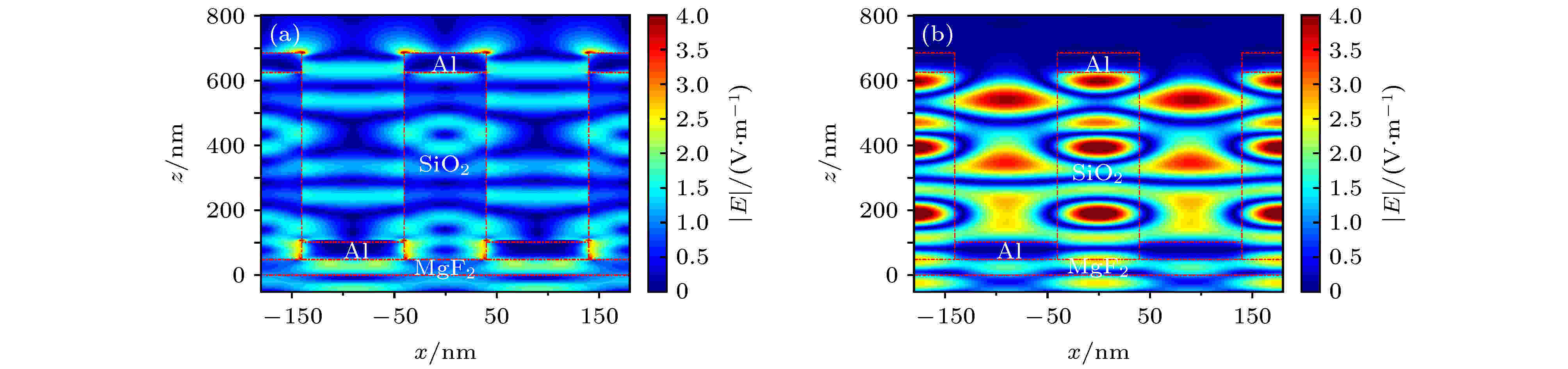图 4 正入射时光栅截面电场分布　(a) TM偏振光; (b) TE偏振光
Figure4. Field distribution of grating cross-section when the light is incident normally: (a) TM-polarized light; (b) TE-polarized light.

2 -->

3.3.金属层高度对光栅偏振性能的影响

将顶层和底层金属光栅视为类F-P谐振腔, 其腔长由金属层高度决定. 腔内介质和入射光波长一定时, 金属层高度影响与之匹配的类F-P腔谐振的模数, 其决定透射峰值周期的个数. 保持光栅周期为180 nm, 占空比为0.44, 中间层高度为70 nm(二氧化硅层高度随金属层高度变化), 氟化镁层厚度为33 nm不变, 金属层高度变化对光栅偏振透过率和消光比的影响如图5所示. 在金属层高度为54 nm处, 消光比达到峰值, 且TE偏振光透过率较大, 故确定金属层高度为54 nm.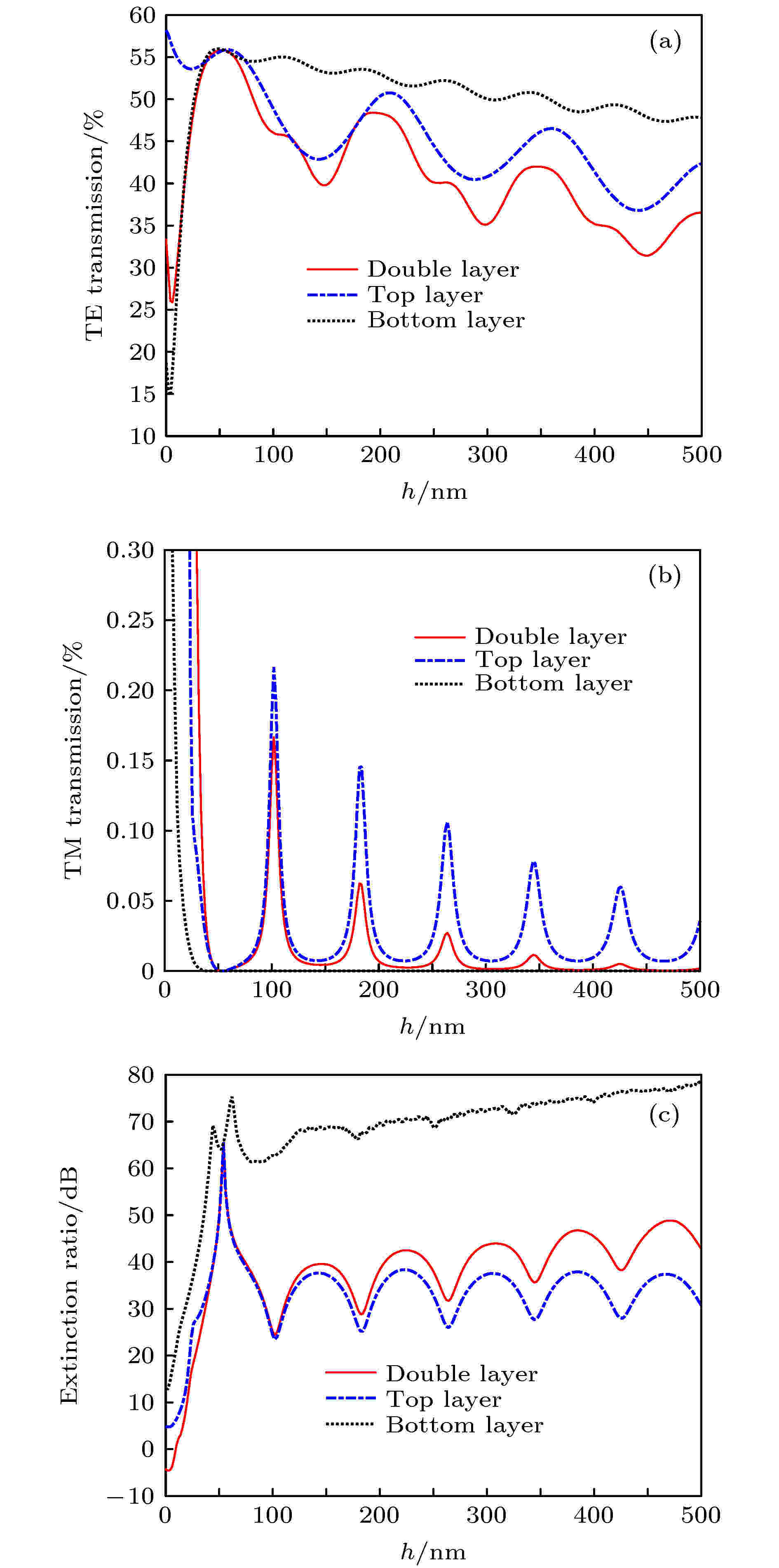
图 5 金属层高度对光栅偏振性能的影响　(a) TE透过率; (b) TM透过率; (c)消光比
Figure5. Polarization performance of grating as functions of the metal layer height: (a) TE transmission; (b) TM transmission; (c) Extinction ratio.

考虑顶层和底层光栅金属高度同时变化、仅顶层光栅金属高度变化和仅底层光栅金属高度变化(保持另一金属高度为54 nm)三种情况. 如图5所示, TE和TM偏振光透过率均呈周期性振荡下降趋势, 且由于金属间介质折射率不同导致振荡周期不同. 其中顶层和底层光栅金属高度同时变化情况下, TE偏振光透过率呈振荡下降趋势, 其振荡周期由底层和顶层光栅随金属高度变化的振荡周期共同调制, 且受顶层光栅影响较大; TM偏振光入射时, 其透过率振荡下降的周期与仅顶层光栅金属高度变化时的振荡周期一致, 均为80 nm. TM偏振光透过率主要由顶层光栅金属层高度调制, 对于顶层金属光栅形成的类F-P腔, 联立(3)式—(6)式计算其腔内有效折射率为${\rm{1}}.{\rm{19}}$, 类F-P共振周期为80.7 nm, 理论计算与数值仿真结果一致.
2 -->

3.4.氟化镁层高度对光栅偏振性能的影响

氟化镁层作为增透膜层, 其厚度直接影响增透效果. 通过上述仿真分析确定光栅周期为180 nm, 占空比为0.44, 金属层高度为54 nm, 中间层高70 nm(二氧化硅层高度为124 nm), 保持以上参数不变, 氟化镁层高度变化对光栅偏振透过率和消光比的影响如图6所示. 氟化镁层高度为48 nm时, TE偏振光透过率为极大值, 同时消光比较高. 因此, 确定氟化镁层高度为48 nm. 未添加氟化镁介质层的TE偏振透过率为53.1%, TM偏振透过率为1.79 × 10^–7, 消光比为54.7 dB; 添加48 nm氟化镁介质层后, TE偏振透过率为56.8%, TM偏振透过率为1.55 × 10^–7, 消光比为65.6 dB. 添加氟化镁层后, TE偏振透过率提高7%, 消光比提高20%. 随着氟化镁层的增高, TE偏振光透过率周期性振荡, TM偏振光透过率在较小的范围内振荡, 且二者振荡的周期与特征不同, 其原因是TE偏振光和TM偏振光在氟化镁介质中的等效折射率不同^[38].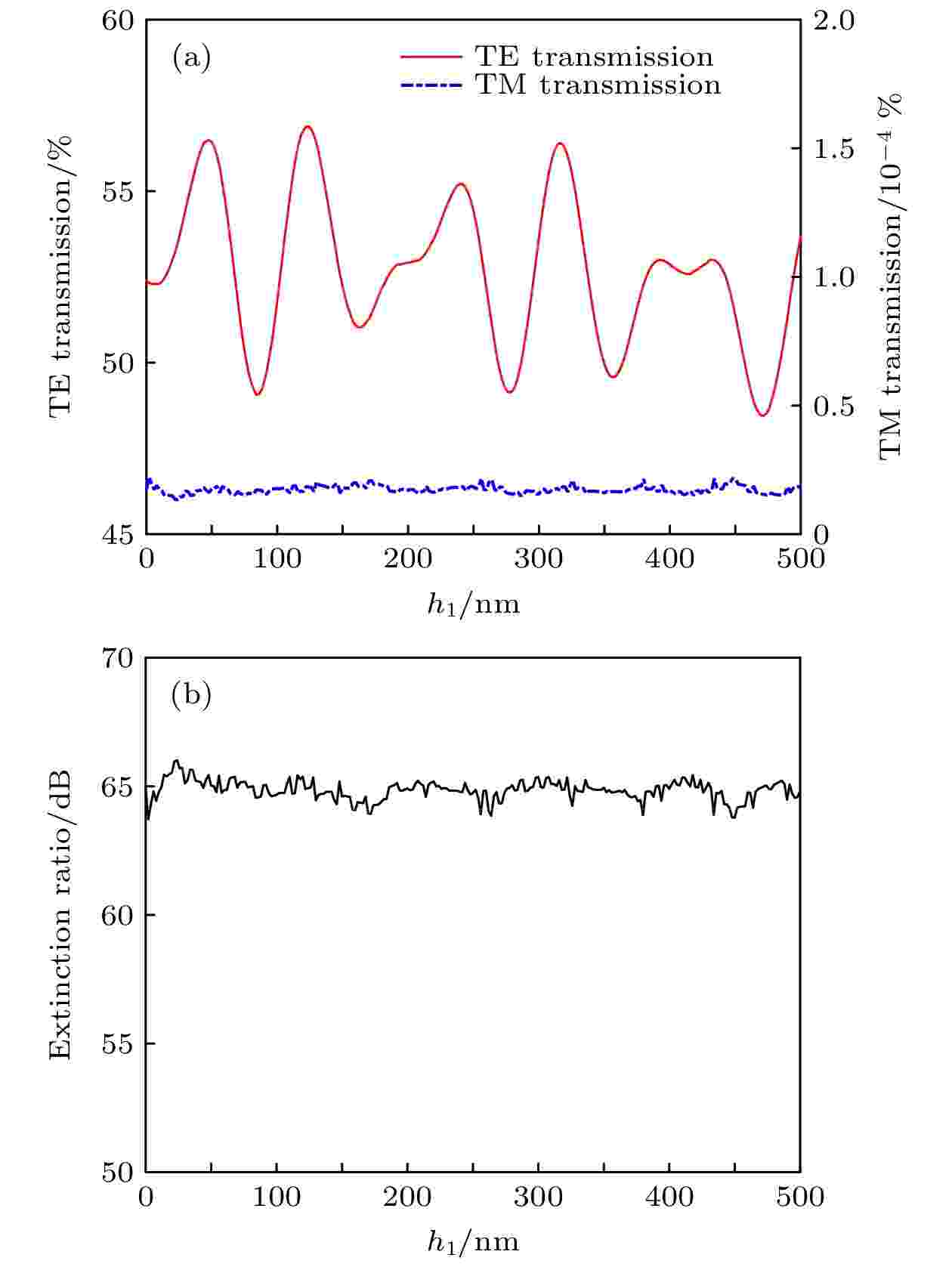
图 6 光栅氟化镁层高度对偏振性能的影响　(a) 透过率; (b) 消光比
Figure6. Polarization performance of grating as functions of Magnesium fluoride height: (a) Transmission; (b) Extinction ratio.

2 -->

3.5.光栅截面场分析

通过以上仿真分析, 确定双层金属光栅周期为180 nm, 占空比为0.44, 二氧化硅光栅层高度为124 nm, 顶层和底层金属层高度为54 nm, 氟化镁层高度为48 nm. 该结构参数下, 双层金属光栅对TE偏振光透射增强, TM偏振光透射被抑制, 消光比高, 为进一步分析该现象出现的机制, 对TE和TM偏振光入射时该光栅结构的电磁场和坡印廷矢量分布进行仿真分析.
TE偏振光入射时, 电场截面分布如图7(a). 光源从基底背向入射, 金属界面的反射光与入射光在铝-氟化镁界面叠加产生驻波. TE偏振光没有垂直金属界面的电场分量, 不产生表面等离子体, 仅引起沿栅线方向的表面电流. 沿入射方向的行波光束与来自顶层金属光栅的反射波在介质腔中形成驻波, 腔内电磁场重新分布, 其中电场能量集中于腔中心, 侧壁上电场很少. 坡印廷矢量分布如图7(b), 可以看出, 当介质腔的宽度大于TE偏振光的截止宽度时, 进入底层介质腔中的辐射模式形成驻波, 包含整数个驻波产生透射增强, 并沿着顶层金属-介质界面泄漏, 泄漏波与表面波耦合并沿着金属-介质界面传播. 顶层介质腔起到光学漏斗的作用, 收集并引导TE偏振光进入腔内, 使TE偏振透射增强^[39,40]. 反常偏振情况下, 在底层光栅金属层上方的介质腔附近, 能流密度出现周期性的相位奇点(图7(b)), 其对应位置上的时间平均坡印廷矢量振幅为零, 能流方向或等效相位不确定. 相位奇点处的坡印廷矢量方向主要表现为光学旋涡(a和b点)或者鞍点(c和d点)两种状态, 其中光学漩涡能引导更多的能量流以漏斗状进入介质腔, 使得TE偏振光透射增强. 当介质宽度略大于截止宽度, 沿对称方向的相位奇点阵列湮灭, 将导致更平滑的功率流场, 相应地TE偏振光传输增强^[37].
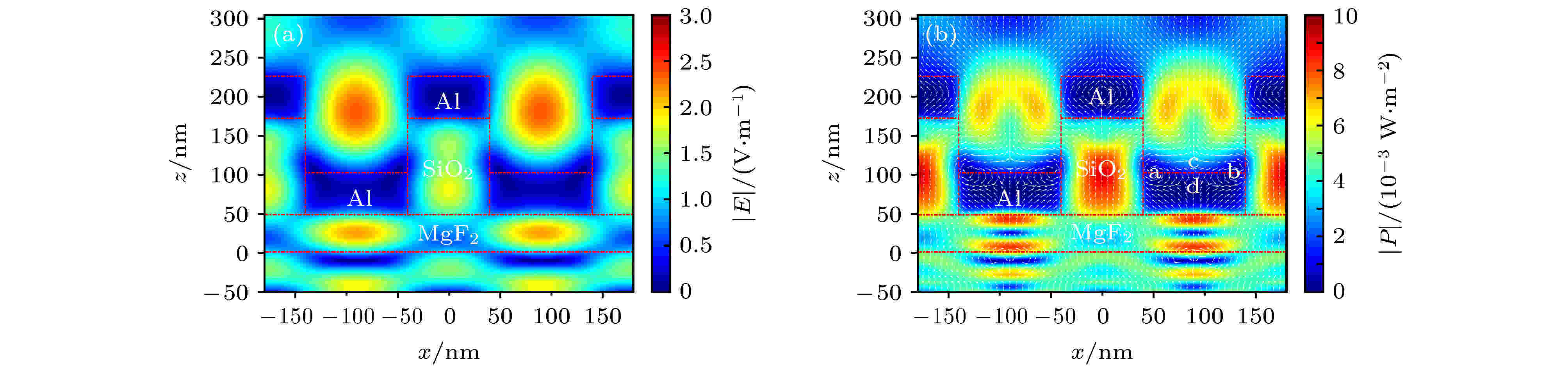图 7 TE偏振光正入射时光栅截面场分布　(a) 电场分布; (b) 坡印廷矢量方向(箭头)和幅度(颜色图)
Figure7. Field distribution of grating cross-section when TE-polarized light is incident normally: (a) Electric field distribution; (b) Poynting vector direction (arrowheads) and magnitude (color map).

TM偏振光入射时, 电场截面分布如图8(a)所示, 光源从基底背向入射, 经底层和顶层光栅连续衰减, 光栅结构上方的微弱电场表明几乎没有TM偏振光通过. 金属界面的反射光与入射光在在铝-氟化镁界面叠加产生驻波. TM偏振光入射时, 垂直于金属-介质界面的电场分量E_x和E_z使金属表面产生表面电荷的集体振荡. 当入射光波矢与表面等离子体波满足波矢匹配条件时, 两电磁波模式强烈耦合, 有效地激发表面等离子体共振. 表面等离子体波沿着界面传播并沿远离界面方向呈指数衰减. 由于电场E_z分量在界面上的不连续性, 移动的表面电荷被栅线边缘阻碍, 在金属栅线顶角处产生积聚电荷振荡, 形成电偶极子. 表面电荷和电流沿z向携带行波光束进入铝-二氧化硅-铝组成的类F-P腔中形成驻波, 腔内电荷和电流重新分布, 并在底层光栅的铝-空气界面顶角处产生更强的电偶极子. 如图8(a)所示, 当正负电荷间以低频模式相互移动时, 在金属栅线的两顶角位置分别积累正电荷和负电荷. 正负电荷间电场线扭曲越小, 集聚在电场中的能量越弱, 从而有效抑制TM偏振透射^[41]. 如图8(b)所示, 耦合进入二氧化硅层的光在接近底层光栅铝-氟化镁界面的位置能流方向内旋与入射光方向相反, TM偏振光被强反射. 此外, 介质腔内的能量流更集中地沿腔壁流动, 并在底层金属光栅的上表面逐渐衰减, 导致TM偏振光透过率低.
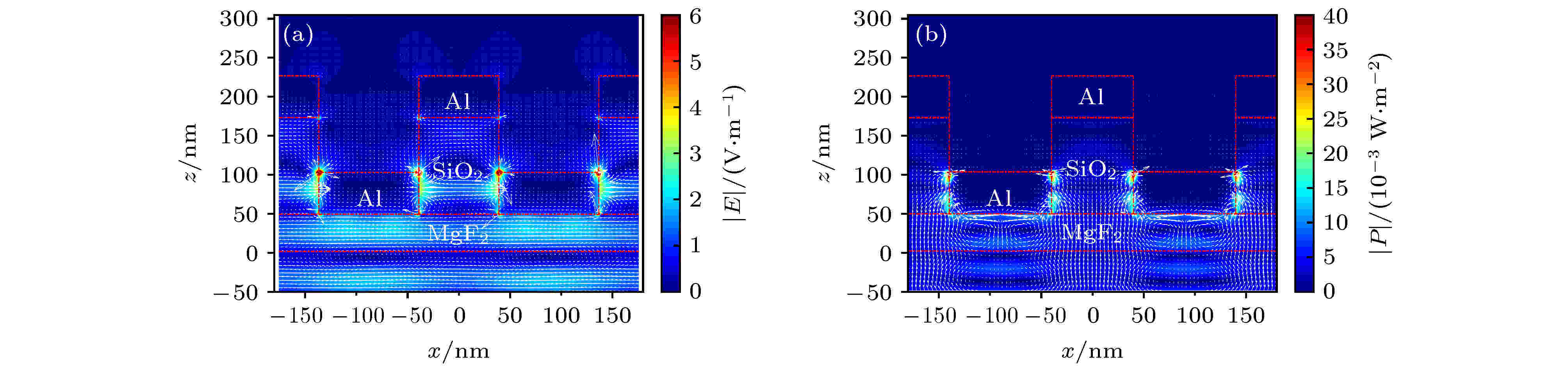图 8 TM偏振光正入射时光栅截面场分布　(a) 瞬时(箭头)和时间平均电场分布; (b) 坡印廷矢量方向(箭头)和幅度(颜色图)
Figure8. Field distribution of grating cross-section when TM-polarized light is incident normally: (a) Instantsneous (arrowheads) and time-averaged (color map) electric field distribution; (b) Poynting vector direction (arrowheads) and magnitude (color map).

光栅制备的工艺误差会使实际光栅的结构参数偏离理论设计值, 并导致光栅透过率和消光比性能与理论计算之间产生差异. 因此, 需要对光栅结构参数的工艺容差进行分析, 以评估所设计光栅偏振器的可加工性. 通过以上仿真分析可知, 双层金属光栅的占空比、金属层高度和中间层高度是影响其偏振性能的主要参数. 图9为光栅偏振性能随占空比(顶层金属栅线宽度w)、金属层高度h和中间层高度(H₁)变化的等高线图. 由图9(a), 图9(c)和图9(e)可知, 在不同结构参数组合变化情况下, TE透过率均在52%—57%范围内, 即TE透过率对结构参数的工艺容差较大. 如图9(b), 图9(d)和图9(f)虚线框所示, 光栅消光比大于40 dB的工艺容差为[w, h, H₁] = [76—87 nm, 49—61 nm, 66—78 nm], 且在整个光栅结构参数变化范围内([w, h, H₁] = [70—90 nm, 44—64 nm, 60—80 nm]), 光栅消光比均达到30 dB以上. 所设计光栅偏振器在较大的工艺误差范围内均具有良好的偏振性能. 对照浸没式光刻机偏振检测精度要求检偏器的消光比为30 dB, 所设计的双层金属光栅在较大的工艺容差范围内均能满足光刻机偏振检测装置对检偏器的性能需求.
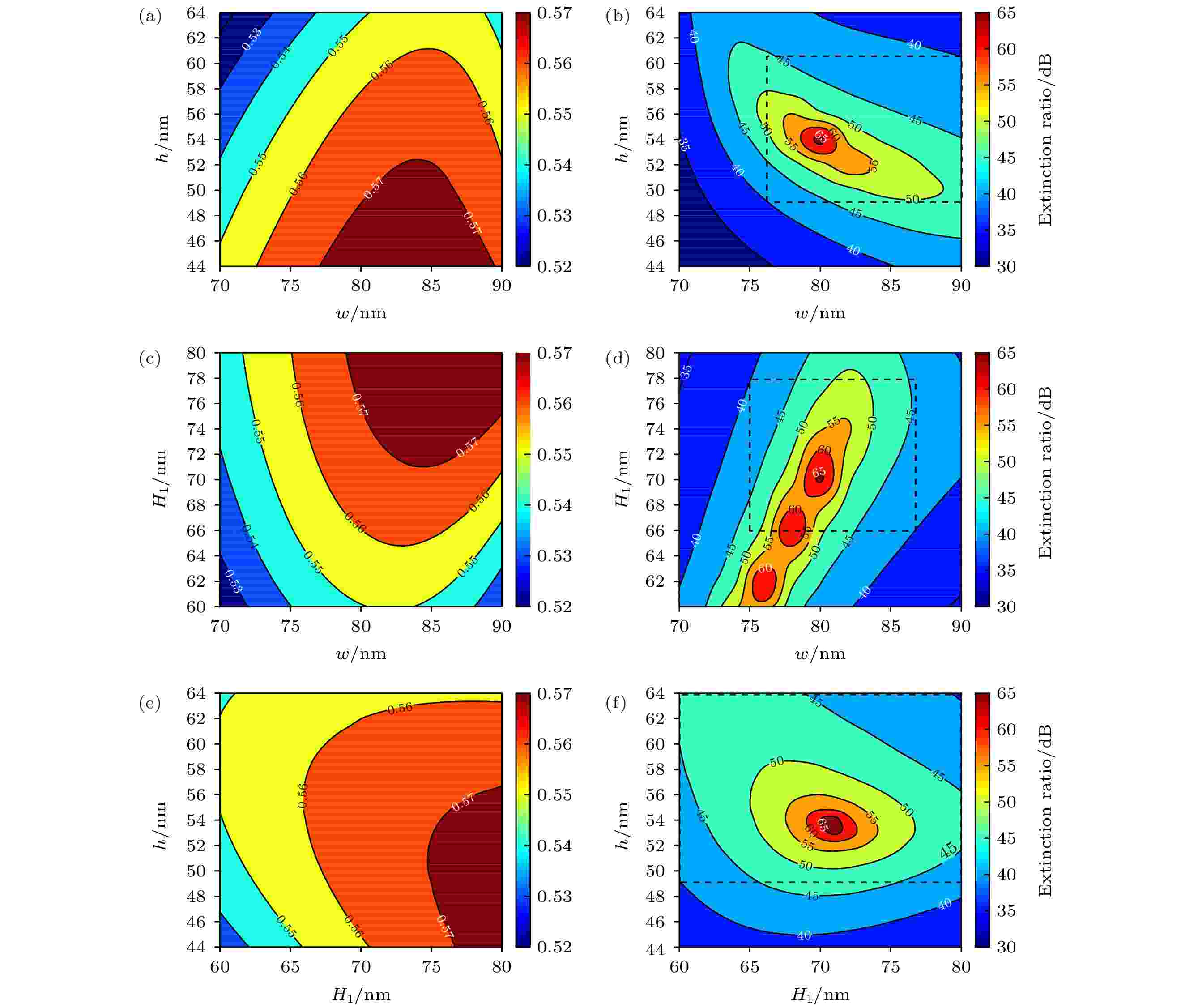图 9 光栅的工艺容差分析　(a), (b)为占空比和金属层高度分别对TE透过率和消光比的影响; (c), (d)为占空比和中间层高度分别对TE透过率和消光比的影响; (e), (f)为金属层和中间层高度分别对TE透过率和消光比的影响
Figure9. Fabrication tolerance analysis of grating: (a) and (b) are TE transmission and extinction ratio as function of the grating duty cycle and metal layer height, respectively; (c) and (d) are TE transmission and extinction ratio as function of the grating duty cycle and middle layer height, respectively; (e) and (f) are TE transmission and extinction ratio as function of the grating metal layer height and middle layer height, respectively.

本文针对193 nm波长浸没式光刻机对偏振检测装置小型化和快速、高精度检测需求, 将双层金属光栅偏振器引入偏振检测系统. 基于共振域光栅的反常偏振效应和双层金属光栅对TE偏振光的透射增强, 采用严格耦合波理论和有限时域差分方法, 利用表面等离子体共振对TM偏振光透射的抑制作用, 同时控制双层金属光栅中形成类F-P谐振腔腔长以实现对TM偏振光的透射抑制和TE偏振光的透射增强, 确定双层金属光栅的初始结构参数. 在此基础上, 分析了各结构参数对该光栅偏振器偏振透过率和消光比的影响, 优化设计了一种工作波长为193 nm的双层金属光栅偏振器. 所设计的双层金属光栅偏振器周期为180 nm, 占空比为0.44, 二氧化硅层高度为124 nm, 金属层高度为54 nm, 氟化镁层高度为48 nm. 数值仿真结果表明, TE偏振光入射到底层光栅介质腔内时形成驻波并产生透射增强, 然后沿着金属-介质界面进入顶层光栅形成的光学漏斗, 其透射光被进一步增强; 而当TM偏振光入射时, 由于激发表面等离子体共振的电荷分布为低频模式, 较弱的电场能量使得TM偏振透射被强抑制, 最后经顶层光栅连续衰减后几乎没有TM偏振光透过; 该偏振器在193 nm波长下的TE偏振光透过率为56.8%, 消光比为65.6 dB. 相比于现有的同波段金属光栅偏振器, 所设计的光栅偏振器可实现在保证高透过率的同时, 消光比提升了四个数量级. 结构参数分析表明, 该光栅偏振器在较大的工艺容差范围内均能满足光刻机偏振检测装置对检偏器的性能需求.