摘要:一维非共轭烷烃链虽不具富电子或少电子特征, 但常存在于单分子器件或多肽、蛋白质等生物分子中, 对电子传输产生重要影响. 为理解这类物质的电子输运特征, 本研究设计了一维线性非共轭(CH₂)_n分子结模型, 并利用密度泛函理论结合非平衡态格林函数的方法, 对(CH₂)_n(n = 1—12)线性分子链与两个石墨烯电极耦合而成的分子结进行了第一性原理计算. 结果表明, CH₂分子链随着n值的变化, 其电导值表现出明显的奇偶振荡现象, 并且随着链长的增加呈指数级的衰减, 这一结果与实验研究取得了很好的一致性, 为理解和设计性能更加优良的单分子器件提供了重要理论依据.
关键词: 亚甲基/
第一性原理/
电子输运/
非平衡格林函数

English Abstract

全文HTML

--> --> -->

近二十年来, 各种纳米级电极制备技术的出现, 促进了单分子电子学领域在实验和理论方面的快速发展^[1]. 石墨烯作为一种优良的电子导体, 在电磁屏蔽^[2]、微型智能传感^[3]及雷达吸波材料^[4]等方面得到了广泛应用. 特别是Guo等^[5-8]利用单层石墨烯作为电极, 构建的“石墨烯-分子-石墨烯(graphene-molecule-graphene, GMG)”异质结, 表现出了结构精确可控、信号可调的特点, 在揭示光开关^[5]、化学/生物传感^[6]、氢键作用^[7]等物质转换规律和生命本征现象方面显示了独特优势, 为将来颠覆性芯片技术和精准分子诊断技术的发展提供了基础^[8]. 尤其是Jia等^[9]将二芳烯作为功能中心, 在石墨烯电极间构建了一个光、电双模式诱导的单分子全可逆光电子器件. 在这一突破性工作中, 为了避免分子与电极接触界面间的耦合, 在功能分子二芳烯的两边各引入了关键性的3个亚甲基(CH₂). 此外, 研究固态分子结中生物分子的电子转移对于理解许多重要的生理过程具有重要意义^[10]. 多肽单分子电子输运的实验^[11]和理论^[12]研究均说明, 多肽分子中处于电子传输方向的主链或分子侧链上的CH₂和CH₃等烷烃基团对于电子的输运都产生了一定的影响. 然而, 如何理解这些烷烃在分子结中的电子输运, 烷烃基团的数量对于电导有什么影响仍未见系统的研究.
近来, 有关一维分子链电子输运的研究引起了人们的广泛关注. Mu等^[13]通过理论方法研究了一维(SiC)_n (n = 1—4)分子链随着n的改变, 其导电性质的变化规律, 阐明了这一分子链的半导体导电特征. Liu等针对(GaAs)_n (n = 1—4)原子链的研究, 发现了n值的不同导致的金属或负微分电阻现象; 而针对Si原子链的电子输运研究却发现了明显的奇偶电导振荡现象^[14]. 此外, 一维富电子有机共轭分子链^[15,16]、点缺陷石墨烯^[17]、石墨烯层数^[18]等不同分子结的导电性质也被研究报道, 证实石墨烯的输运机制主要来源于单层石墨烯的弹道散射或少层石墨烯的声子散射作用.
烷烃分子由于不具有金属或分子导体的导电性质, 同时也不属于富电子的共轭体系, 因此在分子器件的研究中较少被探讨. Malen等^[19]通过实验研究了(CH₂)_n分子结的导电特征, 发现其电导值的衰减与链长之间呈指数的关系, 但并没有详细阐释其电子输运机制. 为进一步理解非共轭烷烃在分子器件中的导电本质, 讨论不同链长烷烃分子结的电子输运特性, 本文将基于密度泛函理论(DFT)和非平衡态格林函数(NEGF)相结合的第一性原理方法, 对石墨烯基线性(CH₂)_n分子结(n = 1—12)的电子输运性质进行了理论研究, 以便为单分子器件的设计提供更多的理论指导.

为研究石墨烯基CH₂分子结的电子输运特性, 我们构建了如图1所示的“石墨烯-分子-石墨烯(GMG)”异质结计算模型. 由于该“GMG”异质结在实验过程中均由含氨基的分子与边缘羧基化的石墨烯电极耦合而得, 因此本文计算模型通过将两头含有氨基的CH₂分子链通过酰胺键偶联到两侧石墨烯电极间, 设计了1个“三明治”模型的双电极电子输运体系. CH₂分子链沿着z轴方向延伸, 且为电子输运的方向, 而x、y方向为周期性结构. 左右石墨烯电极间距随着CH₂基团的数目增加而递增, 但均处于同一平面, 每个电极区各包含10 × 6阵列的60个碳原子. 散射区所有边缘碳原子均使用氢原子饱和. 模拟过程中, 整个分子模型置于长方形盒子中, 石墨烯平面距离盒子y方向上下边界均为6 ?.
图 1 (CH₂)_n分子结(n = 1?12)计算模型示意图(金色球: 碳原子C, 红色球: 氧原子O, 灰色球: 氮原子N, 淡粉色球: 氢原子H)
Figure1. Schematic illustration of (CH₂)_n (n = 1?12) molecule junction (golden ball: carbon atom, red ball, oxygen atom, grey ball: nitrogen atom, light pink ball: hydrogen atom).

本研究基于密度泛函理论(DFT)与非平衡态格林函数(NEGF)相结合的第一性原理计算方法, 采用SIESTA 4.1^[20,21]软件来完成相关计算. 其中, 密度泛函采用基于数值基组的方法来求解Kohn-Shan方程. SIESTA软件包近来被广泛用于各种材料模拟中, 并取得了与实验结果良好的一致性^[22]. 分子结的结构优化过程中, 对电极区原子进行固定, 其余原子自由弛豫到受力小于0.01 eV / ?时达到收敛标准. 计算采用PBE^[23]的广义梯度近似(GGA)方法来描述电子的交换关联作用, 核芯势采用模守恒的Troullier-Martins赝势^[24]. 实空间积分格点截断设置为250 Ry, 体系的电子温度设置为300 K. 电极区使用了单ζ极化基组(SZP), 而其余原子采用了双ζ基组(DZP)对波函数进行展开.
在电子输运计算中(TRANSIESTA程序包^[25]), 使用Monkhorst-Pack采样方法, 选取1 × 1 × 50的k点来计算电子的透射率. 通过(CH₂)_n分子结和2个石墨烯电极的电流可以根据以下Landauer-Buttiker公式来计算.

$I\left( V \right) = \frac{{2e}}{h}\int T \left( {E,V} \right)\left[ {f(E - {\mu _{\rm{L}}}) - f(E - {\mu _{\rm{R}}})} \right]{\rm{d}}E,$

其中: $ {f}{(}{E}-\mu _{\rm{L}}{)} $和$ {f}{(}{E}-\mu _{\rm{R}}{)} $为左右电极的费米-狄拉克分布函数; $ \mu _{\rm{L}} $和$ \mu _{\rm{R}} $为左右电极的化学势; $ {T}\left({E}{, }{}{V}\right) $是电压为V时能量为E的电子从左到右传输的透射系数, 能量积分区间为[$ \mu _{\rm{L}} $, $ \mu _{\rm{R}} $]; 当外电压V = 0 V时, 体系的平衡电导可由零偏压下平衡态的费米能级E_F处的透射值T乘以量子电导G₀ (G₀ = ${{2{e^2}}}/{h}$)得出. 此外, 采用Inelastica软件包^[26]计算了不同分子结的导电通道, 采用 VESTA程序^[27]对所有模型结构进行了可视化.

2

-->

3.1.结构优化

为了更好地模拟亚甲基分子链的电子传输特性, 在“石墨烯-(CH₂)_n-石墨烯”分子结模型中, 我们参考游离烷烃分子中C—C键和C—N键的键长, 首先对两头连接有氨基的(CH₂)_n分子链进行了结构优化, 然后根据优化的N-N之间的距离设置了石墨烯两侧耦合点的间距, 最后将含有氨基的亚甲基分子链通过酰胺键连接于两侧羧基化的石墨烯电极间, 并再次进行结构优化, 得到如图2所示的n从1到12的一维线性非共轭亚甲基分子结稳定构型. 进一步地, 我们依据公式ΔE = E [GMG] – E [石墨烯电极]– E [分子链], 计算了这些分子结的结合能并列于表1中, 结果发现, 其结合能在数值上非常接近, 均介于–10.90 eV到–11.72 eV之间, 说明优化得到的这些一维非共轭(CH₂)_n分子结为稳定的平衡结构.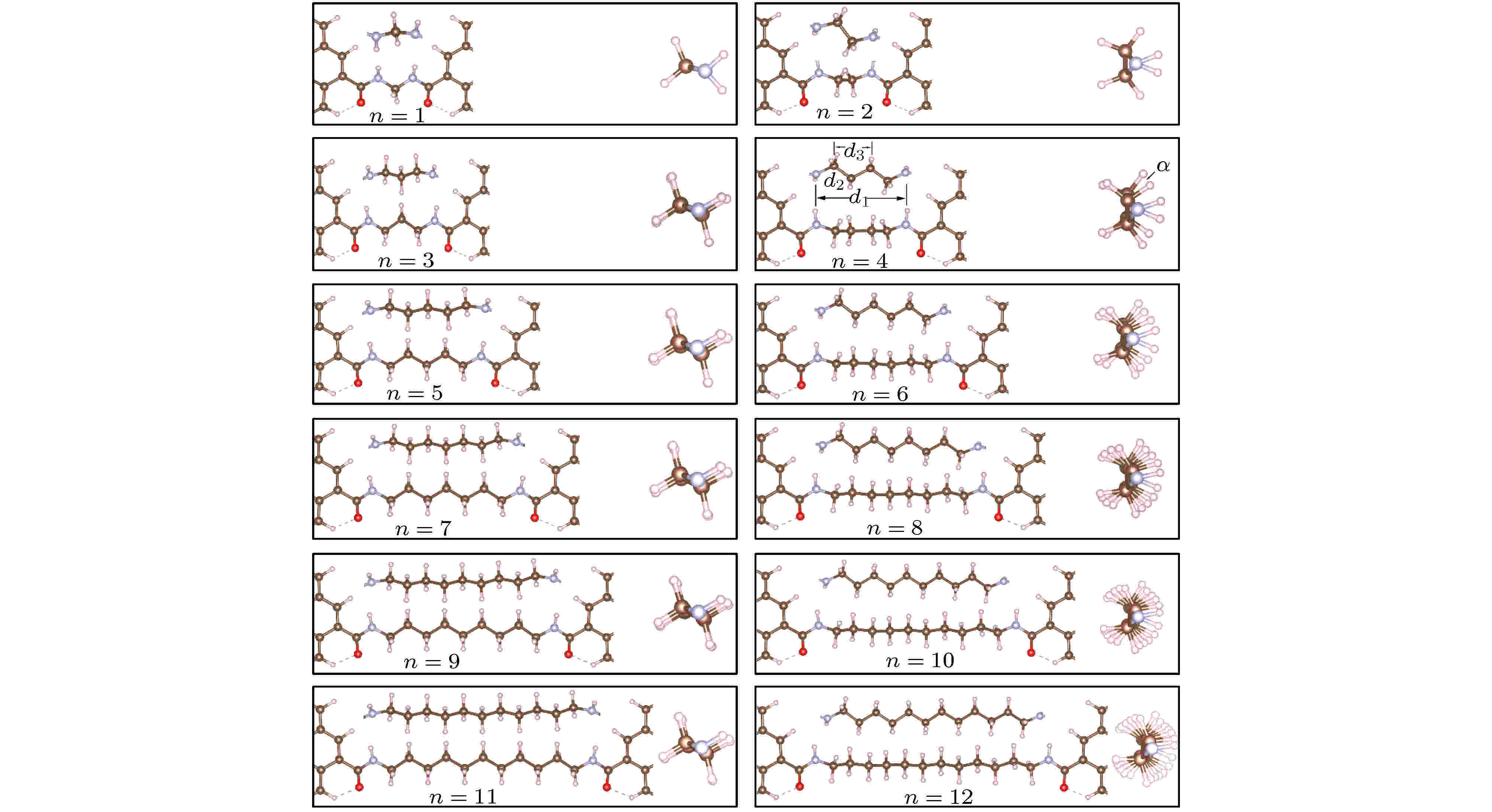
图 2 (CH₂)_n分子结(n = 1?12)稳定结构图(每个图中下方为沿y轴方向的俯视图, 上方和右方插图分别为沿x和z轴方向的侧视图, 坐标方向和小球颜色说明见图1)
Figure2. The stable structure of (CH₂)_n (n = 1?12) molecule junction (on each diagram, the bottom figure is a top view along y axis, the upper and right side inset is a side view along x and z axis, respectively. Coordinate direction and color description of the ball are shown in Fig. 1).

n	d1N—N /?	d2C—C /?	d3C—C /?	α/(°)	ΔE/eV
1	2.44	—	—	—	–10.90
2	3.67	1.55	—	—	–11.04
3	5.10	1.55	2.54	2.25	–11.12
4	6.22	1.53	2.55	18.81	–11.45
5	7.71	1.55	2.63	0.91	–11.52
6	8.91	1.54	2.59	15.12	–11.55
7	10.30	1.55	2.62	0.41	–11.66
8	11.51	1.54	2.60	14.61	–11.57
9	12.90	1.55	2.62	0.80	–11.69
10	14.11	1.54	2.61	14.93	–11.60
11	15.51	1.55	2.62	1.85	–11.72
12	16.71	1.54	2.61	14.19	–11.60

表1(CH₂)_n分子结(n = 1—12)的平均键长、键角和结合能(d₁, d₂, d₃, α如图2所示)
Table1.The average bond length, bond angle and binding energy in (CH₂)_n (n = 1–12) molecule junction (the bond length of d₁, d₂, d₃ and the bond angle α are shown in Fig. 2).

分析图2中优化得到的不同n值时分子结的稳定构型, 可以发现, 当n为奇数时, 亚甲基分子链中碳原子基本都处于石墨烯的电极平面内(xy平面), 并以“之”字形沿着分子链方向(z轴)左右排列, 而n为偶数时, 碳原子虽仍为“之”字形排列, 但均在石墨烯电极平面上下波动. 同时, 从图2右侧的插图中, 还可以看出, 电极间存在奇数个CH₂基团时, 分布于“之”字形左右的数个CH₂几乎重叠, 而为偶数个CH₂基团时, “之”字形分布的CH₂在电极平面上下沿z轴方向以一定角度扭转延伸, 并随着n值的增加, 这一扭转角α逐渐变小(见表1中α值). 此外, 表1中列出了不同n值时, 分子结的键长、键角数值. d₁代表了分子结中(CH₂)_n分子链上两端N原子之间的距离. 从表中这一数值变化中可以发现, n值由奇数增加为偶数时, d₁的值增加了约1.40 ?, 而由偶数增加为奇数时, d₁值却只增加了约1.20 ?. 这些变化充分说明一维石墨烯基(CH₂)_n分子结在结构上有明显的奇偶特征. 其余代表烷烃分子中C—C键长的d₂, 以及代表烷烃分子中间位C—C键的键长d₃并没有随着n的增加而产生明显的差异.
2 -->

3.2.透射谱

根据优化得到的(CH₂)_n分子结(n = 1—12)平衡结构, 本文计算了零偏压时, 各(CH₂)_n分子链的透射谱. 结果如图3所示, 所有分子结的透射谱表现出了类似的峰形特征, 并且由于亚甲基的非共轭结构, 使得透射谱在费米能级附近没有明显的隧穿共振峰, 从而导致了这一分子链较差的导电性质. 同时, 随着分子链n值的增加, 这一分子结的透射系数明显地降低. 尤其值得注意的是, 比较图3(a)奇数分子链和图3(b)偶数分子链的透射谱, 能够发现, 偶数个CH₂基团的分子链导电性明显差于奇数分子链, 并且由于结构上的奇偶性, 这一分子结的电导值也表现出明显的振荡衰减(见图3(a)中插图), 这一现象在Si^[14], C^[28]等原子链的电子输运研究中也被发现, 但Si原子链的电导振荡现象会随着原子数的增加而逐渐减弱, 而在CH₂分子链中却并没有发现这一趋势.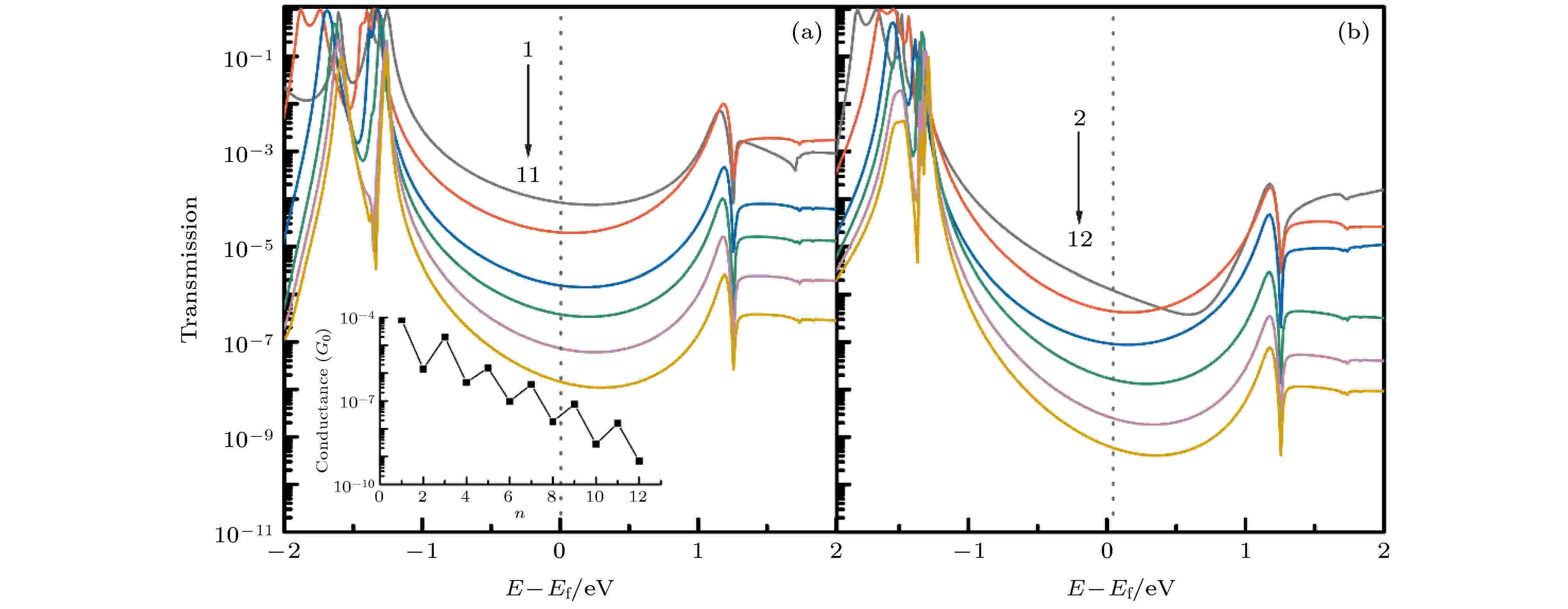
图 3 奇数　(a)和偶数(b) (CH₂)_n分子结在零偏压下的透射谱图
Figure3. Transmission coefficient as a function of energy for odd (a) and even (b) (CH₂)_n molecule junction under zero external bias.

2 -->

3.3.平衡电导与分子链长度的关系

电荷输运的机理有两种: 不依赖温度的连续隧穿和依赖于温度的非连续性跳跃. 连续隧穿机理认为, 分子链的长度决定了电子从左电极到右电极传输的距离, 成为影响单分子电子器件导电性质的一个关键因素. 通常情况下, 分子器件的电导将随着长度呈指数性衰减, 其关系可用如(2)式表示^[1]: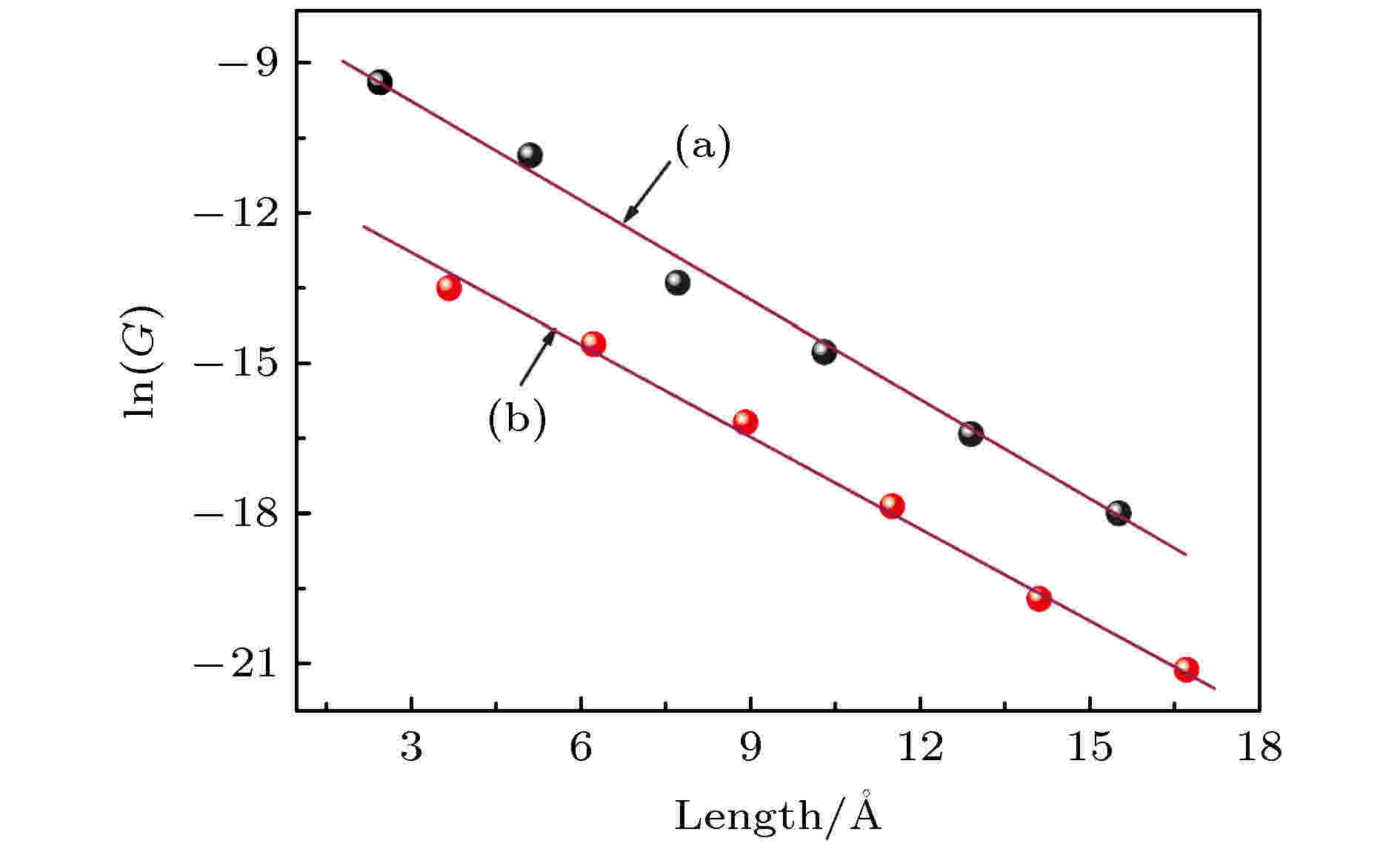

$G = {G_0}{\rm{exp}}( - \beta L),$

其中: G为分子电导, G₀为量子电导常数, L是分子的长度, β为衰减常数. 因此, 本文根据零偏压下(CH₂)_n分子结在费米能级处的透射系数得到了n从1到12的不同分子链导电值, 并将分子链中N-N键的键长d₁作为分子的长度, 总结了(CH₂)_n分子链的电导和长度之间的关系, 结果如图4所示. 由于该分子链随着长度的增加, 其电导表现出了明显的振荡现象. 因此, 从图4可以看出, 奇数或偶数分子链的电导均随分子长度变化呈指数性衰减的趋势, 并且其线性方程分别为: ln(G) = –0.67L – 7.78 (图4中奇数a, 线性相关系数r = 0.9966)和ln(G) = –0.60L –11.00 (图4中偶数b, 线性相关系数r = 0.9978). 根据线性方程, 可知奇数和偶数(CH₂)_n分子链的衰减常数基本一致, 分别为0.67和0.60, 相比较于实验报道的衰减常数0.94而言^[19], 尽管β值要小一些, 但实验中使用的电极为金电极. 相关研究也证实, β值也将会因耦合基团、溶剂环境等测试条件的改变而改变^[1].
图 4 奇数　(a)和偶数(b) (CH₂)_n分子结零偏压电导与分子链长度关系图
Figure4. The plot of conductance versus chain length for odd (a) and even (b) molecular junction of (CH₂)_n at the bias of 0 V.

为了更好地理解(CH₂)_n奇偶分子链导电性质的差异和振荡现象, 本文分别以n为11和12的分子结为例, 计算了这个一维非共轭体系的导电本征通道(图5). 从图5可以看出, 不论是奇数还是偶数分子链, 其导电作用主要都是通过C—C键之间的定域σ电子进行电荷传输, 相对于π键的共轭体系, 导电性质要更差一些, 因而, 计算得到的衰减常数β值也要更大(一般来说, β值越小, 共轭体系越明显, 导电性也更好). 此外, 通过比较图5(a)和图5(b), 可以发现两者最大的区别是奇数分子链中, 每个CH₂基团及对应的σ键与石墨烯电极基本处于同一平面, 因而也更有利于电子传输, 而偶数分子链中, 两者正好为垂直关系. 这充分说明了一维非共轭(CH₂)_n分子结出现电导奇偶振荡的本质原因. 进一步分析其电子输运的本质, n为奇数时, 应该是以声子散射机制为主; n为偶数时, 应该以定程跳跃散射为主. 因此, 表现出的奇数电导比偶数电导大1个数量级以上^[29].
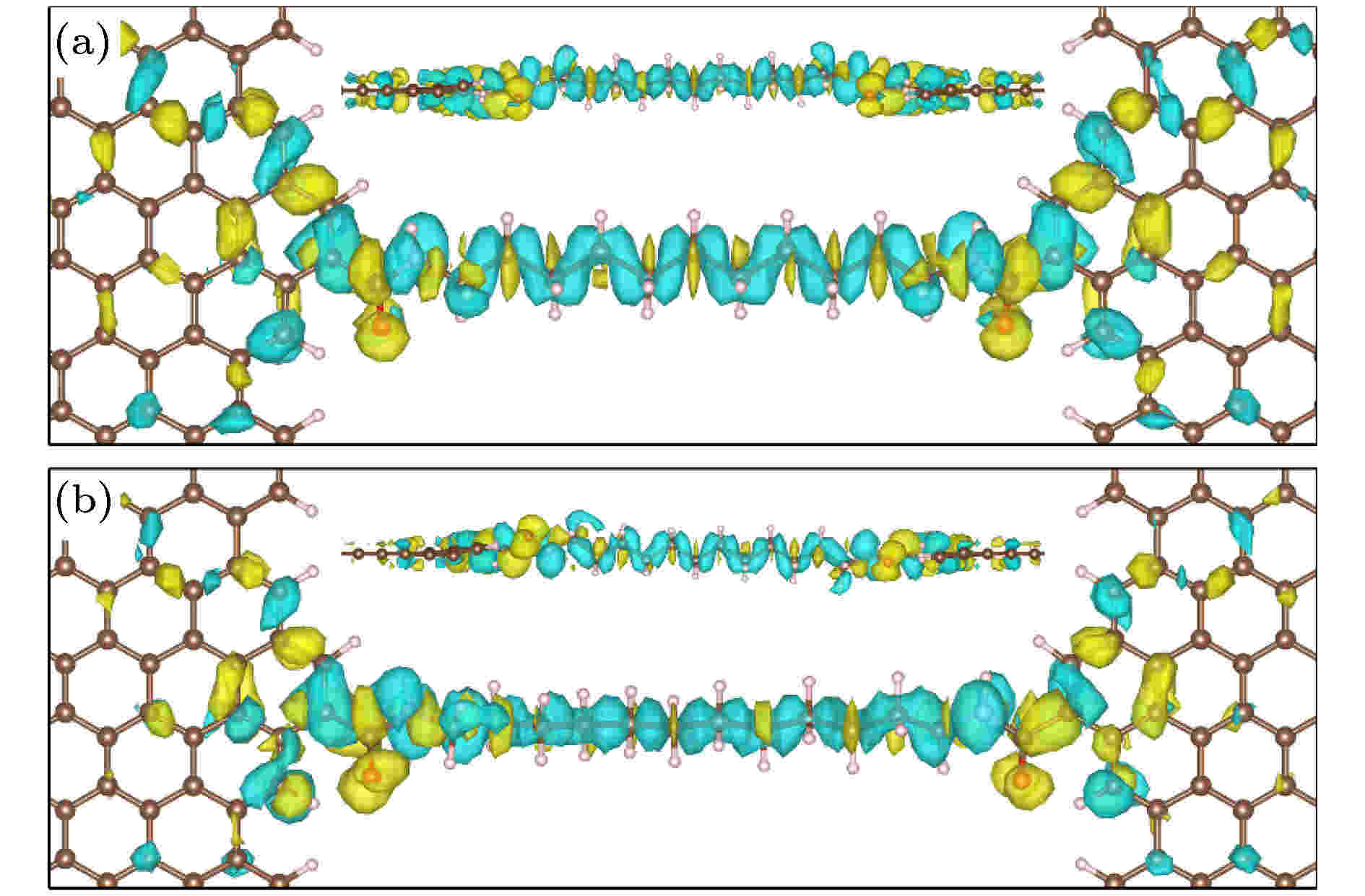图 5 奇数　(a)和偶数(b) (CH₂)_n分子结导电通道图(上方插图为沿x轴的侧视图, 蓝色和黄色区域分别代表得失电荷密度)
Figure5. The eigenchannels of odd (a) and even (b) molecular junction of (CH₂)_n (The upper inset is a side view along x axis, blue and yellow areas denote the gain and loss of electron density)

2 -->

3.4.电流电压关系

外偏压也是影响单分子器件导电性质的一个重要因素. 本文进一步计算了不同链长(CH₂)_n分子结在外偏压为0—2.0 V范围内不同电压下的电流值, 结果如图6所示. 可以看出, (CH₂)_n分子结的I-V曲线与文献报道的石墨二炔纳米带的I-V曲线特征相似, 具有半导体特征^[30], 尽管奇数分子链相较偶数分子链的电流值要大10倍以上, 但由于烷烃链的导电性较差, 导致该分子链整体电流值均较小, 仅为几到几十nA的数量级. 此外, 从图中还可以看出, 奇数分子链的导通电压约为1.0 V(图6(a)), 而偶数分子链约为1.5 V (图6(b)). 这一偶数分子链较差的导电特性也与之前对导电通道的分析相吻合. 值得注意的是, 当分子链长度为n = 4, 外电压大于1.6 V时, 其电流值超过n = 2的分子链电流值, 根据Landauer-Buttiker公式, 分析其原因为偏压窗口增大后, n = 4的分子链积分计算所得到的透射率增大, 导致了电流的增加^[31].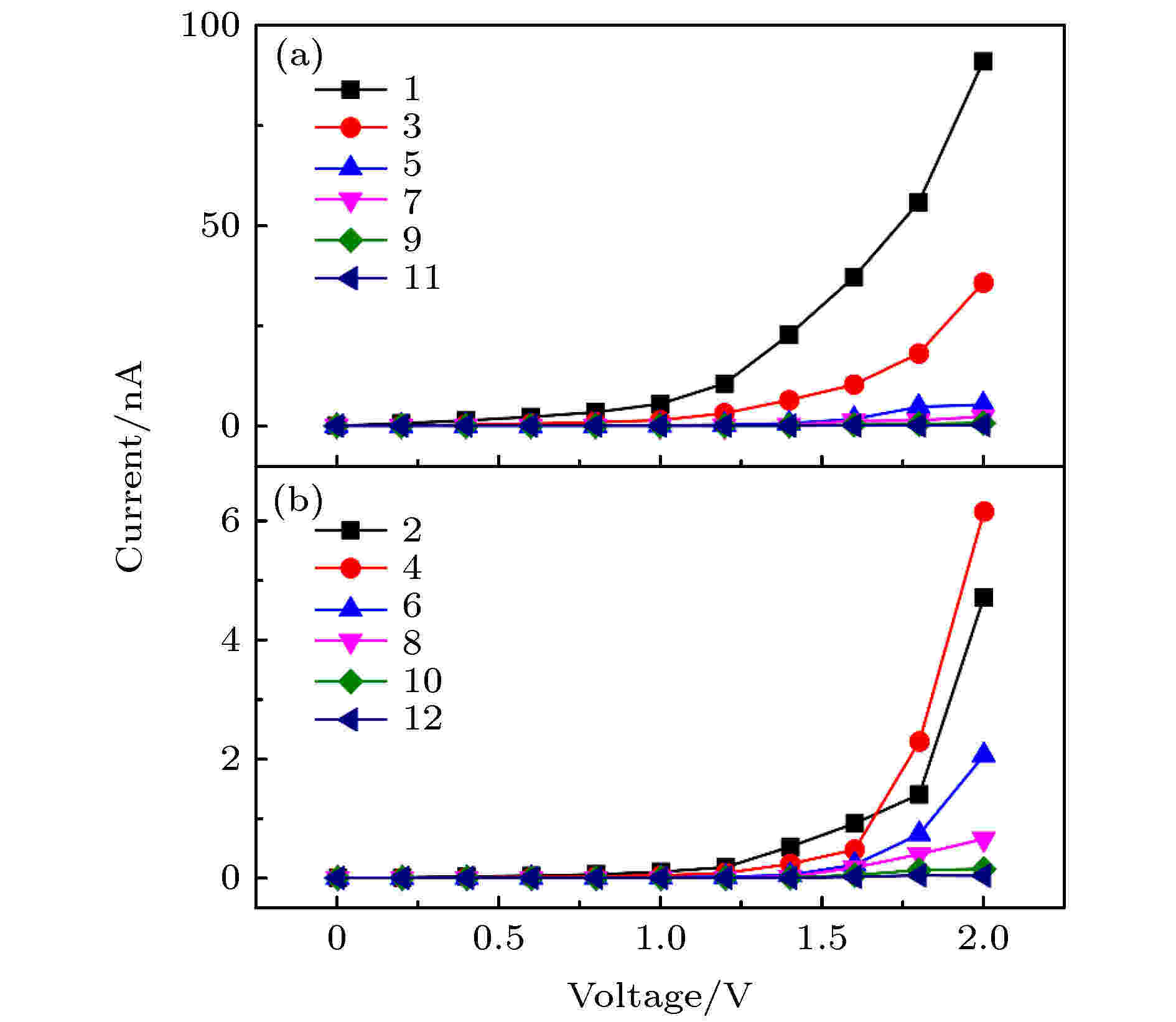
图 6 奇数　(a)和偶数(b) (CH₂)_n分子结在不同电压下的电流图
Figure6. The current of odd (a) and even (b) (CH₂)_n molecular junction under different external bias.

石墨烯基单分子器件中, 线性非共轭 (CH₂)_n基团的引入可以避免功能分子与电极的耦合, 对电子输运性质有着重要影响. 本文针对这一问题, 通过密度泛函理论与非平衡态格林函数相结合的方法, 对(CH₂)_n (n = 1—12)线性分子链与石墨烯半无限电极耦合构成的“石墨烯-(CH₂)_n-石墨烯”分子结的电子输运行为进行了模拟研究. 通过对12个不同链长的分子结稳定结构的优化, 发现奇数个(CH₂)_n基团的分子链沿着石墨烯平面从左电极向着右电极延伸, 而偶数分子链中CH₂基团却在石墨烯平面上下分布且以一定的旋转角向右延伸. 这种结构上的差异也导致了透射谱的相应变化和电导的奇偶振荡. 进一步地, 我们还通过研究不同分子链在零偏压时的电导与链长之间的关系, 分析了此一维线性非共轭分子链的电子传输机理. 结果发现, (CH₂)_n分子链的电子传输符合连续隧穿的电子输运机制, 并且计算得到其电导随分子链指数性衰减的常数β值约为0.67, 与文献报道的实验结果基本一致. 通过I-V曲线, 也可以发现这个分子链半导体的导电特征和电流的奇偶变化依赖性. 此外, 我们还计算了奇、偶不同分子链的导电本征通道, 从而进一步佐证了这一分子链的导电特性, 并解释了该研究模型中奇偶振荡现象的本质. 希望本文的研究结果能为单分子纳米器件的设计与开发提供重要理论参考.