摘要:通过第一性原理计算探讨了蓝磷烯与过渡金属硫化物MoTe₂/WTe₂形成范德瓦耳斯异质结的电子结构和光学性质, 以及施加双轴应力对相关性质的影响. 计算结果表明, 形成BlueP/X Te₂ (X = Mo, W)异质结, 二者能带排列为间接带隙type-II并有较强的红外光吸收, 同时屏蔽特性增强. 随压缩应力增加, BlueP/X Te₂转变为直接带隙type-II能带排列最后转变为金属性; 随拉伸应力增加, 异质结转变为间接带隙type-I能带排列. 外加应力也能有效调控异质结的光吸收性质, 随压缩应力增加吸收边红移, 光吸收响应拓展至中红外光谱区且吸收系数增大; BlueP/MoTe₂较BlueP/WTe₂在中红外至红外光区间表现出更强的光吸收响应; 静态介电常数ε₁(0)大幅增加. 结果表明, 压缩应力对BlueP/MoTe₂和BlueP/WTe₂能带排列、光吸收特性均有显著的调控作用, 其中BlueP/MoTe₂对调控更敏感, 这些特性也使BlueP/X Te₂异质结在窄禁带中红外半导体材料及光电器件具有令人期待的应用价值.
关键词: BlueP/X Te₂ (X = Mo, W)异质结/
电子结构/
光学性质/
应力

English Abstract

全文HTML

--> --> -->

石墨烯的成功制备改变了原有单原子材料在非绝对零度下不能稳定存在的传统认识^[1], 也激发了国内外学术界对二维层状材料的重点关注. 其中, 二维过渡金属硫族化合物(TMDs) MX₂ (M = Mo, W, X = S, Se, Te)^[2-4]及其与其他二维材料堆叠构成范德瓦耳斯异质结的研究工作获得了大量成果^[5-10].
科学家们已成功制备了二维单层TMDs如MoTe₂和MoSe₂等^[11,12], 为进一步实验研究奠定了基础. 具有代表性的TMDs材料MoTe₂, 通常有三种晶体结构^[13,14], 即2H-MoTe₂, 1T′-MoTe₂, T_d-MoTe₂. 其中, 2H-MoTe₂具有半导体属性, 属六方晶系, 空间群为P6₃/mmc. 体材料MoTe₂为间接带隙半导体(约0.93 eV), 载流子迁移率可高达4000 cm²·V^–1·s^–1[15]. 单层MoTe₂则为直接带隙(约1.1 eV), 在近红外区域表现出其特有的光学性质. Qiao等^[16]制备出薄层MoTe₂纳米片, 实验发现其析氢效率优于厚层MoTe₂材料. 有研究者还预测单层MoTe₂和单层WTe₂为二维拓扑绝缘体^[14,17], 由此更增加了科研工作者对MoTe₂和WTe₂等TMDs的研究兴趣. 此外, 磷烯是具有较宽带隙和较高载流子迁移率的半导体材料^[18,19], 其中有两种同素异形体蓝磷和黑磷受到研究者们的诸多关注. 二维层状蓝磷(BlueP)与黑磷不同, BlueP是结构类似于TMDs六方晶体结构的间接带隙半导体(≈ 2 eV), 而黑磷为正交结构的直接带隙半导体(≈ 1.03 eV). 近期Zhang等^[20]采用外延生长已成功制备了六方结构的单层BlueP, 室温下BlueP具有高稳定性、快速的载流子迁移率等特性(μ_e～466, μ_h～1711 cm²·V^–1·s^–1), 预示着蓝磷烯在电子和光电子领域的应用前景^[21,22].
关注二维层状材料的同时, 由单层或少层不同二维材料堆叠构成的范德瓦耳斯异质结也成为了研究热点. 因构成范德瓦耳斯异质结二维材料的带隙不同, 可通过合理设计将其进行合适的组合, 异质结两侧材料导带底和价带顶形成不连续的台阶, 从而可形成type-I, type-II或type-III能带排列. Zhang 等^[23]成功制备MoS₂/MoTe₂ type-II异质结, 探测到1550 nm的红外光响应, Wu等^[24]制备的MoTe₂/MoS₂异质结晶体管具有几毫安的开态电流, 开关比达10⁵. 研究人员也对基于蓝磷烯的BlueP/BP^[25], BlueP/TMDs^[26-28], BlueP/g-GaN^[29], BlueP/G^[30]等范德瓦耳斯异质结的结构和电子特性展开理论研究. 这些研究成果表明二维层状材料形成异质结后不仅保持了其本征性质, 还表现出新的功能, 使其在电子、光电子器件的应用备受期待^[2,3,31,32], 可能实现下一代超薄器件^[33-35].
为了设计和制造相关器件, 深入了解异质结能带排列及界面特性至关重要. 为此, 需要深入探究构成异质结材料的电子、光学和输运等特性, 以及能带结构和能带排列的调控规律, 以便能够寻找到更多将新材料应用于实际器件中的方法. 传统半导体材料制备中广泛采用化学掺杂、表面改性和应力工程来实现能带结构调控, 其中应力工程被认为是较稳定、可控的调控方法. 对于二维材料, 通过改变材料层数、外加电场、材料应力等方式可实现其带隙的调控^[36-39]. 实验研究表明, 通过应力工程能有效调控二维材料的电子结构, 并提升异质结界面处电荷输运的性能^[40,41], 因此应力工程在二维材料及其异质结的研究和实际应用中会成为重要关注点之一. 由于晶胞内原子结构为六方晶系的2H-X Te₂ (X = Mo, W)与BlueP晶体结构相似, 晶格匹配度高. 本文以二维2H-X Te₂与单层BlueP构建范德瓦耳斯异质结模型, 采用第一性原理探究异质结层间相互作用引发的新的物理效应, 以及施加双轴应力对异质结能带结构、能带排列、电子及光学等相关性质的调控作用, 以期为二维异质结的合理设计、成功构建、有效调控和成功制备提供有益的参考.

本文采用基于密度泛函理论(DFT)的VASP(Vienna ab initio simulation package)^[42]软件包进行第一性原理计算. 采用广义梯度近似的Perdew-Burke-Ernzerhof ^[43]泛函描述电子交换和关联作用, 通过投影缀加波^[44]方法描述离子实和价带子间相互作用, 采用optB86修正的DFT方法^[45]以准确描述层状结构材料中范德瓦耳斯相互作用力. 布里渊区取样采用Monkhorst-Pack^[44]方法产生15 × 15 × 1 k点网格进行几何优化, 自洽场收敛标准为10^–6 eV, 截止能量为500 eV, 能量收敛标准为10^–5 eV/atom, 以每个原子上力小于0.01 eV/ ?来判定力的收敛. 取xy平面为二维材料平面方向, 设置大于20 ?的真空层作为隔离, 以进一步消除可能产生的相互作用.
为构建合理的BlueP/X Te₂ (X = Mo, W)范德瓦耳斯异质结模型, 首先计算了单层BlueP与X Te₂的能带结构和晶格参数, 计算结果列于表1中. 结构优化后的BlueP, MoTe₂, WTe₂的晶格参数分别为3.28, 3.55, 3.55 ?. 图1(a)—(c)分别为单层BlueP和X Te₂的能带结构图和分态密度图. 可以看出, 单层BlueP为1.94 eV的间接带隙, 导带最小值(CBM)位于G点与M点之间, 价带最大值(VBM)位于K点与G点之间; X Te₂为CBM与VBM均位于K点上的直接带隙, 禁带宽度分别为1.11 eV (MoTe₂)和1.08 eV (WTe₂), 二者态密度的VBM分别由Mo原子和W原子的d轨道及部分Te原子5p轨道主导, CBM则分别由Mo原子和W原子的d轨道主导. 上述计算结果与理论值^[21,46]和实验值^[47,48]相符, 也说明本文计算方法的准确性和可靠性. 如图2所示, 构建了六种高对称模型, 为能更好地实现晶格匹配, 建模选择在3 × 3 × 1的X Te₂上方堆叠3 × 3 × 1的BlueP, 来构建图2(a) BlueP/MoTe₂与图2(d) BlueP/WTe₂模型, 再将BlueP层沿y方向平移, 分别构建图2(b)、图2(e)和图2(c)、图2(f)模型. 结构优化后选取结构最稳定的堆垛方式图2(a)与图2(d)为研究用模型, 它们之间的晶格失配度σ分别为3.6% (BlueP/MoTe₂)和3.9% (BlueP/WTe₂), 均小于5%^[42], 说明了实验形成BlueP/X Te₂异质结的可行性.

	a/?	Eg/eV	σ/%	d0/?
BlueP	3.28	1.94 (间)	—	—
MoTe2	3.55	1.11 (直)	—	—
WTe2	3.55	1.08 (直)	—	—
BlueP/MoTe2	3.39	0.6 (间)	3.6	3.3
BlueP/WTe2	3.43	0.713 (间)	3.9	3.4

表1单层BlueP, MoTe₂和WTe₂及异质结BlueP/X Te₂的晶格常数、带隙、晶格失配度, 以及异质结BlueP/X Te₂的层间距
Table1.Lattice constants a, band gaps E_g, lattice mismatch σ of BlueP, MoTe₂ and WTe₂ monolayers and BlueP/X Te₂ heterostructures, and interlayer distance d₀ of BlueP/X Te₂ heterostructures.

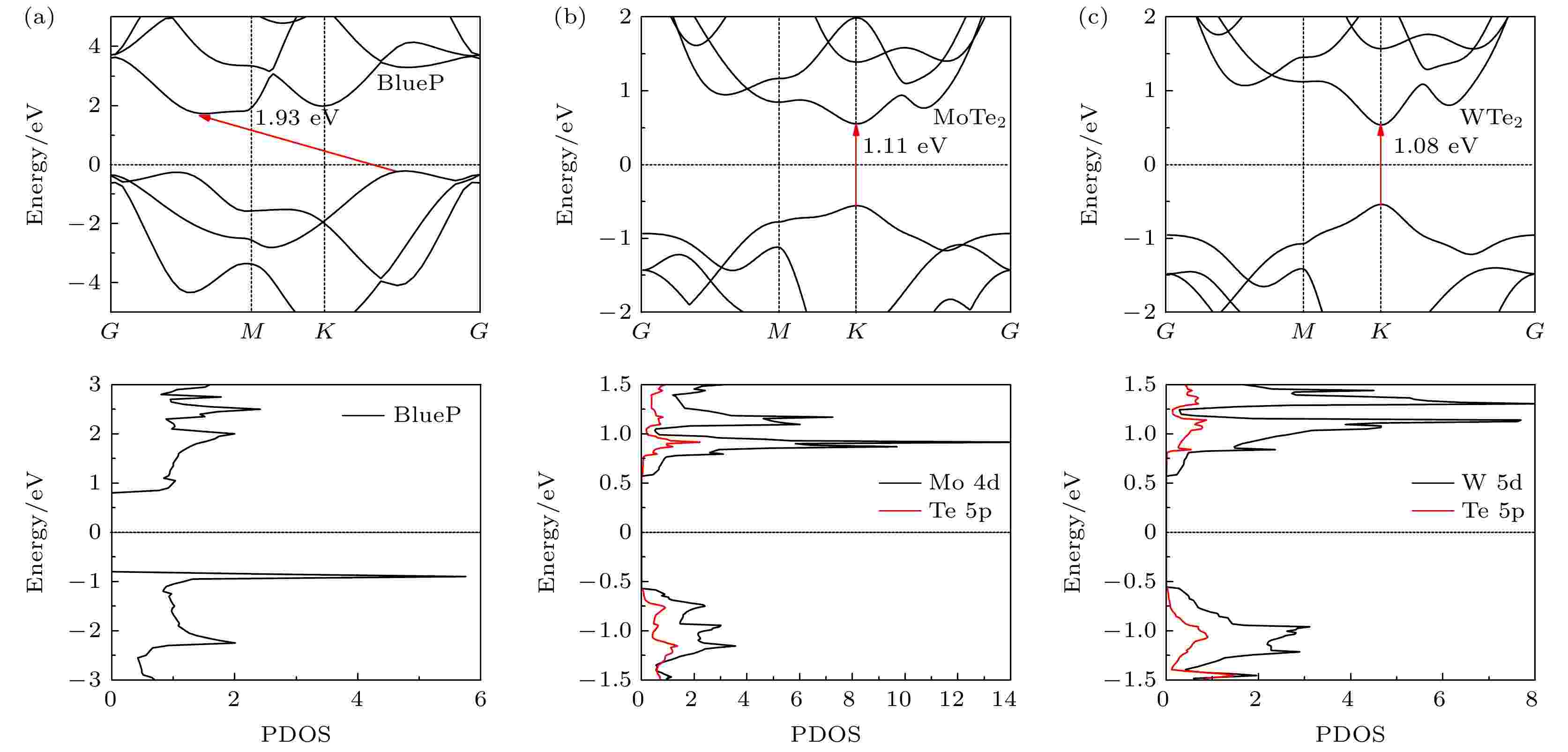图 1 单层BlueP与X Te₂的能带结构图和态密度图　(a) BlueP; (b) MoTe₂; (c) WTe₂
Figure1. Energy band structures and density of states of BlueP and X Te₂ monolayer: (a) BlueP; (b) MoTe₂; (c) WTe₂.

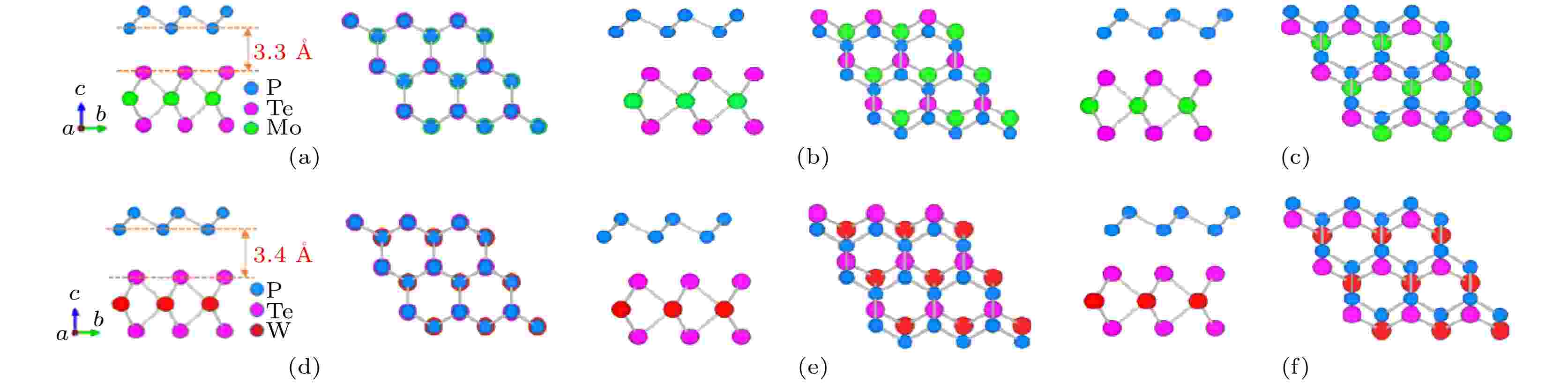图 2 BlueP/X Te₂异质结模型的侧视图和俯视图　(a), (b), (c) BlueP/MoTe₂; (d), (e), (f) BlueP/WTe₂
Figure2. Side and top view of BlueP/X Te₂ van der Waals heterostructures: (a), (b), (c) BlueP/MoTe₂; (d), (e), (f) BlueP/WTe₂

2

-->

3.1.BlueP/X Te₂异质结结构稳定性

异质结界面间结合能(E_b)能够定量表征异质结的相对稳定性, 结合能绝对值越大, 说明体系越稳定. 本文计算结构弛豫后BlueP/X Te₂异质结界面结合能E_b随层间距(d₀)的变化关系, 以确定异质结最佳d₀. 异质结界面E_b由下式给出^[38,39,49]:

${E_{{\rm{b}}}} = \left[ {{E_{{\rm{BlueP}}/X{\rm{T}}{{\rm{e}}_2}}} - \left( {{E_{X{\rm{T}}{{\rm{e}}_2}}} + {E_{{\rm{BlueP}}}}} \right)} \right]/N,$

式中$ {E}_{{\rm{BlueP}}/{X{\rm{Te}}}_{2}} $, $ {E}_{{X{\rm{Te}}}_{2}}, {E}_{{\rm{BlueP}}} $分别为异质结BlueP/X Te₂、单层X Te₂和BlueP的总能; N为BlueP单位晶胞数. 负值E_b表示形成了稳定的界面结合. 图3为BlueP/X Te₂异质结结合能随层间距的变化. 计算结果表明, BlueP/X Te₂异质结层间距为3.30 ? (BlueP/MoTe₂)和3.40 ? (BlueP/WTe₂)时, 二者分别具有最低结合能–29 meV/unit-cell (BlueP/MoTe₂)和–108 meV/unit-cell (BlueP/WTe₂), 均能形成最稳定的界面结合, 而BlueP/WTe₂较BlueP/MoTe₂能够形成更稳定的异质结. 上述结果分别与异质结^[50-54]体系结合能量级相同, 表明BlueP/X Te₂异质结层间形成了弱的范德瓦耳斯力, 具有能量稳定性且实验制备可行. 本文后续的结果与讨论均基于上述层间距对应的稳定结构模型.
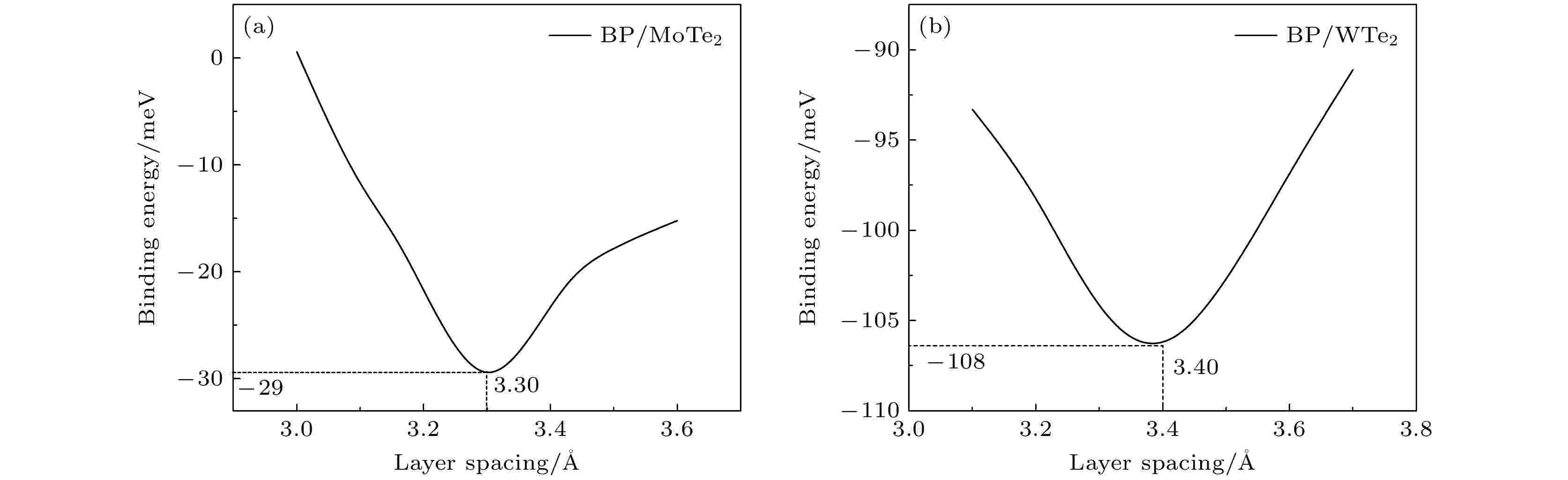图 3 BlueP/X Te₂异质结结合能E_b随层间距d₀的变化　(a) BlueP/MoTe₂; (b) BlueP/WTe₂
Figure3. Binding energy of the BlueP/X Te₂ van der Waals heterostructures as a function of the distance d₀ between the BlueP and X Te₂ monolayers: (a) BlueP/MoTe₂; (b) BlueP/WTe₂.

2 -->

3.2.BlueP/X Te₂异质结电子结构

图4为BlueP/XTe₂异质结的能带结构、总态密度、能带排列及CBM和VBM分解电荷密度图. 由于蓝磷层为间接能带结构, 其对异质结的层间耦合作用使得BlueP/X Te₂均为间接带隙半导体. 如图4(a)和图4(e)能带结构图所示, 二者的CBM和VBM均分别位于M点和G点, 带隙宽度分别为0.60 eV (BlueP/MoTe₂)和0.713 eV (BlueP/WTe₂). 这是由于形成异质结后, 提高了G点价带的能级, 降低了M点导带的能级, 且BlueP表现出比MoTe₂ (WTe₂)更低的导带能级, 使BlueP与MoTe₂ (WTe₂)的价带和导带间产生弱相互作用. 因此, 二者能带结构的CBM主要表现为BlueP在G点与M点间的特征, 而VBM均表现出单层MoTe₂和WTe₂的特征. 如图4(b)和图4(f)态密度图所示, 与单层X Te₂态密度相比, 形成异质结后X Te₂的态密度向低能态移动, 体系的CBM均主要源于BlueP的贡献, 而VBM分别主要源于MoTe₂和WTe₂. 综上所述, 在BlueP/MoTe₂和BlueP/WTe₂体系均形成了间接带隙的type-II能带排列, 其CBM均位于M点的BlueP, VBM位于G点的X Te₂中, 仅BlueP/MoTe₂的带隙值略小于BlueP/WTe₂, 能带排列如图4(c)和图4(g)所示. 图4(d)和图4(h)给出了BlueP/X Te₂的CBM和VBM的分解电荷密度图, 图示结果更直观地说明BlueP/X Te₂异质结是CBM源于BuleP, 而VBM源于X Te₂的type-II能带排列. 由于BlueP与X Te₂价带和导带的相对独立, 及其层间强耦合作用缩短了异质结区的能量差, 使异质结比单层材料具有更长的波长响应能力. 若异质结处于光激发状态, 光生电子通过X Te₂价带到BlueP导带的直接跃迁, 缩短了带间跃迁的能量差(带间能量差分别为BlueP/MoTe₂～0.60 eV, BlueP/WTe₂～0.713 eV). 相较于单层BlueP与X Te₂, 异质结拓宽了光谱响应范围. 同时, 由于BlueP与X Te₂费米能级的差异, 在异质结界面处产生接触电势差, 驱动电荷转移并形成空间电荷区, 产生内建电场, 使得光生电子和空穴分别快速转移至BlueP层的CBM和X Te₂层VBM, 从而自发地在空间上实现光生电子和空穴的分离与收集, 极大地促进光生载流子的生成, 进而能够提升异质结的光电特性, 因此二者作为设计和制造新型光电器件的新型材料具有令人期待的应用前景.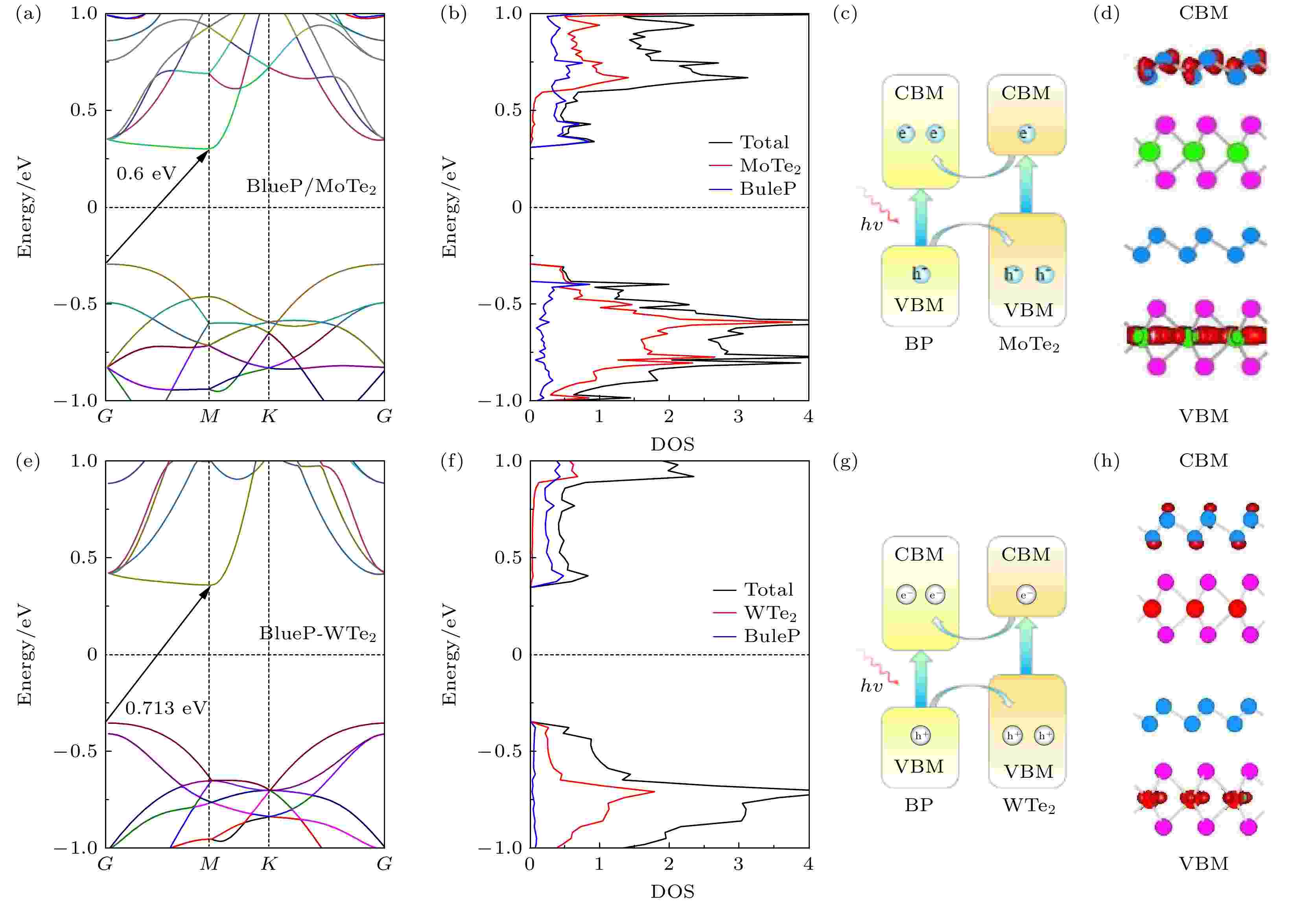
图 4 BlueP/X Te₂异质结能带结构、分态密度、能带排列及异质结中CBM和VBM分解电荷密度图　(a)?(d) BlueP/MoTe₂; (e)?(h) BlueP/WTe₂
Figure4. Energy band structures, partial density of states (PDOS), band alignment and the band decomposed charge density of CBM and VBM in heterostructures: (a)?(d) BlueP/MoTe₂; (e)?(h) BlueP/WTe₂.

2 -->

3.3.BlueP/X Te₂异质结应力调控研究

对BlueP/X Te₂异质结沿a和b轴方向施加双轴应力, 施加的应力与应变间存在对应关系为$\varepsilon = {\left(a-{a}_{0}\right)}/{{a}_{0}}\times 100{\text{%}}$, 式中$ {a}_{0} $为结构优化后体系未施加应力时晶格常数, $\varepsilon > 0\; (\varepsilon < 0)$表示体系施加拉伸(压缩)应力. 图5为BlueP/X Te₂异质结体系总能与双轴应变关系图, $ \Delta E={E}_{\rm{\varepsilon }}-{E}_{0} $^[55], 式中$ {E}_{0} $与$ {E}_{\rm{\varepsilon }} $分别为施加应力前后体系的总能. 若$ \Delta E>0 $, 则表明异质结施加应力后体系仍处于稳定状态. 如图5所示, 应力在从–8%到+8%的压缩和拉伸变化区间内BlueP/X Te₂体系的$ \Delta E>0 $, 且随着应力的增加$ \Delta E $值逐渐增大, 并均未出现能量突变点, 说明BlueP/X Te₂体系施加应力后晶格有序性未受到破坏, 体系仍处于稳定状态.
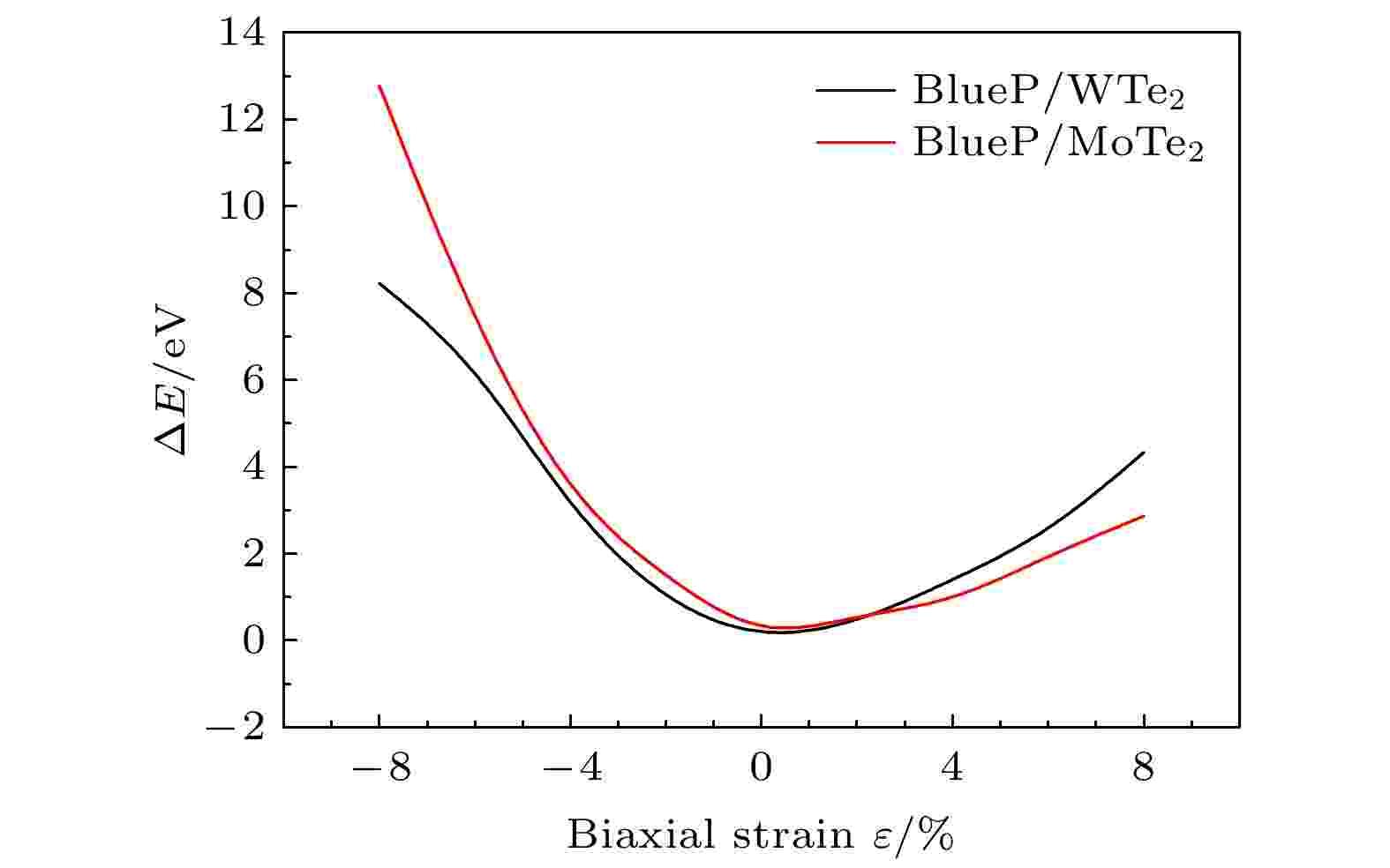图 5 BlueP/X Te₂异质结体系总能与双轴应变关系图
Figure5. Total energy of the BlueP/X Te₂ van der Waals heterostructures as a function of the biaxial strain ε

图6为不同应力下BlueP/X Te₂异质结能带结构图. 如图6(a)所示, 当施加压缩应力–2% < $ \varepsilon $ < –4%时, BlueP/MoTe₂的VBM位置的动量空间产生移动, 由未施加应力时的G点移至M点, 此时体系CBM和VBM位置均位于动量空间M点, 实现动量匹配, 使间接带隙转变为直接带隙, 且随着应力的增加带隙由0.43 eV减小至0.207 eV; 压缩应力增加至–6%和–8%时, 体系费米能级(E_F)穿过价带和导带, 带隙减小为零, 异质结转变为金属性. 施加拉伸应力+2% < $ \varepsilon $ < +6%时, BlueP/MoTe₂保持间接带隙结构, 随着应力的增加VBM向E_F移动, 带隙由0.52 eV逐渐减小至0.35 eV. 拉伸应力增至+8%, 体系动量空间产生移动, VBM由G点移至G和M点之间, CBM则由M点移至G点, 带隙减小至0.27 eV. 与BlueP/MoTe₂体系相似, 如图6(b)所示施加压缩应力–2% < $ \varepsilon $ < –6%, BlueP/WTe₂的VBM由间接带隙时G点移至M点, 体系转变为直接带隙, 且随着应力的增加带隙由0.577 eV逐渐减小至0.286 eV; 与BlueP/MoTe₂异质结不同, 当压缩应力增加至–8%时, BlueP/WTe₂的E_F穿过导带, 带隙减小为零, 异质结转变为金属性. 施加拉伸应力+2% < $ \varepsilon $ < +8%, BlueP/WTe₂亦保持间接带隙结构, 随着应力的增加VBM向E_F移动, 带隙由0.435 eV逐渐减小至0.158 eV. 在上述变化的同时, 当应力增加至+6%和+8%时, 动量空间产生移动, 体系的VBM由G点移至G与M点之间后, CBM又由M点移至G点.
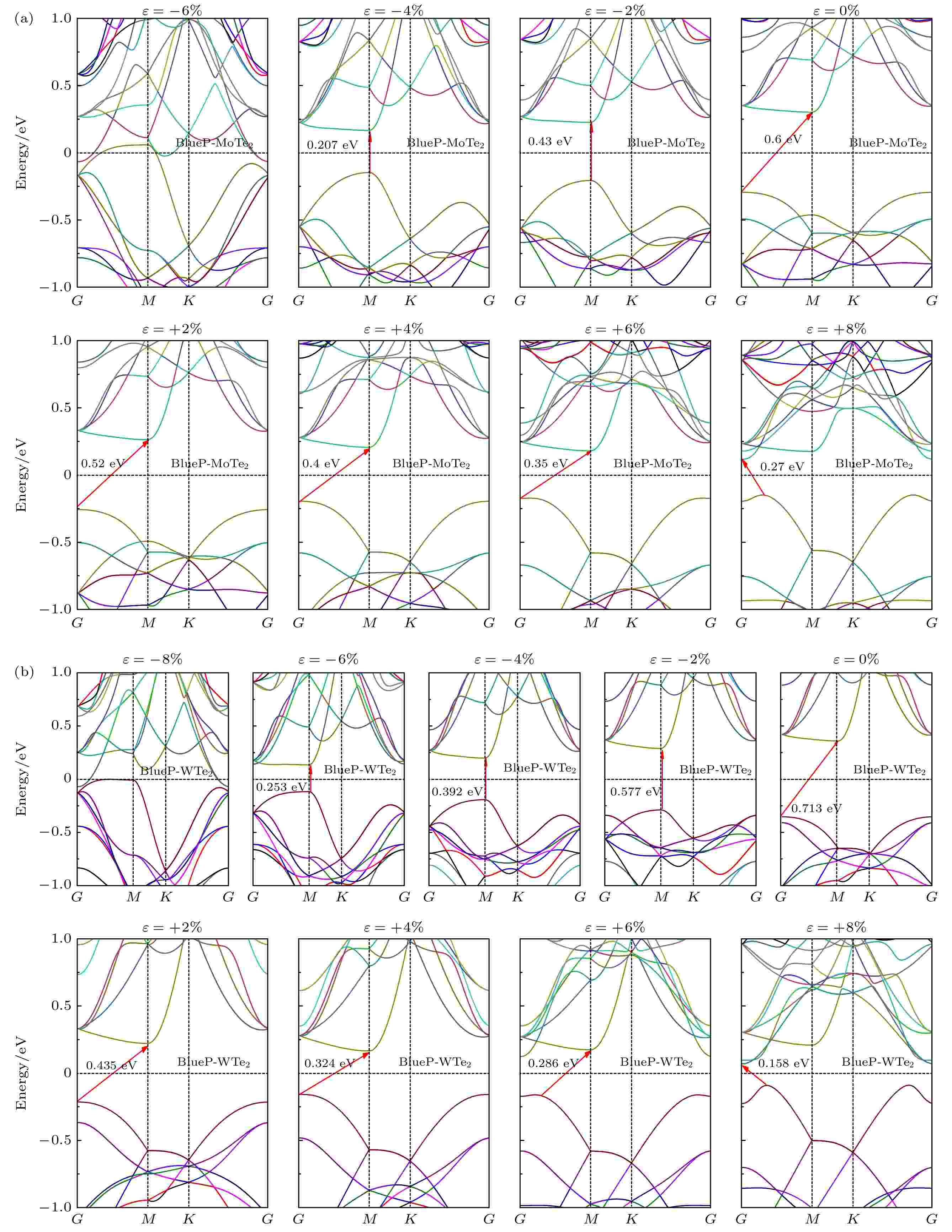图 6 施加不同应力下(a) BlueP/MoTe₂和(b) BlueP/WTe₂异质结能带图, 其中ε > 0 (ε < 0)表示体系施加拉伸(压缩)应力
Figure6. Energy band structures under different biaxial strains for (a) BlueP/MoTe₂ and (b) BlueP/WTe₂, where $ \varepsilon >0\;(\varepsilon <0) $ represents the tensile strain (compressive strain).

图7为不同应力下BlueP/X Te₂异质结分态密度图. 如图7(a)所示, 在应力从–6%到+8%的压缩和拉伸变化区间内, 随着应力的增加BlueP/MoTe₂体系价带和导带逐渐延展, 且电子态密度均向低能态移动. 不同之处在于, 随着压缩应力的增加Mo的d态较Te和P的p态移动速度更快, 导致能带结构带隙逐渐减小直至转变为金属; 而随着拉伸应力的增加, BlueP的导带和价带向E_F移动, 导致异质结带隙逐渐减小. BlueP/MoTe₂施加压缩应力为–2% < ε < –4%时, 体系态密度仍表现为CBM主要源于BlueP, VBM源于MoTe₂贡献的type-II能带排列. 但施加应力使动量空间发生移动, 异质结由间接带隙type-II转变为直接带隙的type-II能带排列. BlueP/MoTe₂施加拉伸应力为+2% < ε < +8%时, 体系态密度CBM和VBM均主要源于BlueP, 异质结由type-II转变为type-I型能带排列. 结合前述能带结构分析, 体系施加拉伸应力没有实现动量空间匹配, 异质结转变为间接带隙的type-I能带排列. 如图7(b)所示, 在应力从–8%到+8%的变化区间内, 随应力的增加BlueP/WTe₂价带和导带表现出的延展性、电子态密度均向低能态移动、带隙的减小, 以及施加压缩和拉伸应力时异质结能带排列的演化等特征均与BlueP/MoTe₂异质结的变化过程相似, 仅当压缩应力增至–8%时, 带隙减小为零转变为金属.
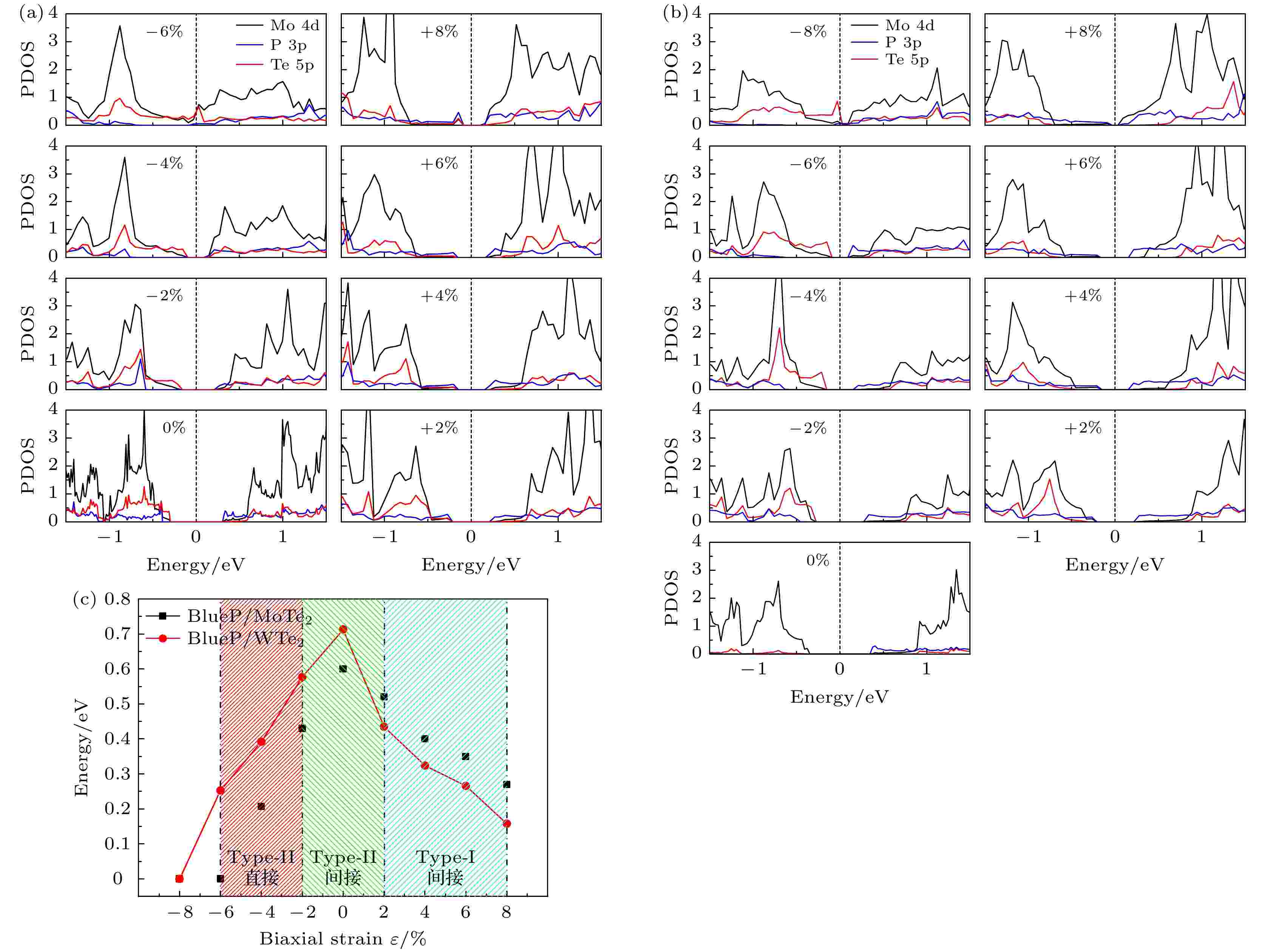图 7 施加不同应力下(a) BlueP/MoTe₂和(b) BlueP/WTe₂异质结分态密度图; (c) BlueP/X Te₂带隙与应力变化关系图; ε > 0 (ε < 0)表示体系施加拉伸(压缩)应力
Figure7. Partial density of states under different biaxial strains for (a) BlueP/MoTe₂ and (b) BlueP/WTe₂; (c) the band gap as a function of biaxial strains in BlueP/X Te₂ van der Waals heterostructures; ε > 0 (ε < 0) represents the tensile strain (compressive strain).

图7(c)更直观说明了施加应力对BlueP/X Te₂异质结能带结构调控的演变过程. BlueP与X Te₂构成的异质结同为间接带隙type-II能带排列, 施加应力改变了BlueP/X Te₂异质结带隙宽度和能带排列类型. 可以看出, 施加压缩应力使动量空间移动, BlueP/X Te₂由间接带隙type-II转变为直接带隙type-II能带排列; 施加拉伸应力BlueP/X Te₂由间接带隙type-II转变为间接带隙type-I能带排列. 此外, 两异质结带隙宽度均随应力增大而减小, 当施加压缩应力时, 二者带隙宽度的变化率相同, 但由于二者晶格失配度有差异, BlueP/MoTe₂在–6%时带隙变为零, 而BlueP/WTe₂在压缩应力增至–8%时带隙才变为零; 当施加拉伸应力时, BlueP/WTe₂带隙减小的速率较BlueP/MoTe₂快. 综合比较压力调控的变化可知, BlueP/MoTe₂对压缩应力调控更敏感, 而BlueP/WTe₂对拉伸应力调控更敏感. 综上所述, 压缩应力调控将异质结转变为直接带隙type-II能带排列, 改变了原间接带隙光吸收弱的情况, 大幅提升了异质结光电性能; 拉伸应力调控将异质结转变为间接带隙type-I能带排列, I型异质结可实现电子和空穴在空间上被束缚在同一种半导体材料中, 有利于电子和空穴的收集和应用, 从而更高效地实现辐射复合. 应力调控能带排列类型同时使异质结带隙宽度减小, 将异质结光谱响应范围由单层材料的近红外光谱拓宽至中红外光谱区(如图6和图7所示), 使其在窄禁带中远红外半导体材料及光电器件具有令人期待的应用价值.
2 -->

3.4.BlueP/X Te₂异质结光学性质研究

介电函数ε(ω)材料的电子结构密切相关, 其表达式ε(ω) = ε₁(ω) + iε₂(ω)宏观光学性质与微观电子结构联系起来, 反映了固体能带结构及各种光谱的信息^[56]. 由介电函数的实部ε₁(ω)推知入射光在固体材料中的传播特性. ε₁(0)静态介电常数, 其决定了材料的屏蔽特性, ε₁(0)值越大说明材料的屏蔽特性越强; 若在某一入射光频率范围内ε₁(ω) < 0, 则说明该频率的入射光在此材料中无法传播. 图8为不同应力下BlueP/X Te₂异质结介电函数实部ε₁(ω)的谱图. 如图8(a)和图8(b)所示, 单层BlueP和X Te₂的ε₁(0)分别为2.19 (BlueP), 5.43 (MoTe₂), 5.24 (WTe₂). 形成异质结后, 该值分别增加为6.93 (BlueP/MoTe₂)和6.53 (BlueP/WTe₂), 前者略高于后者, 均表现出很好的屏蔽特性. 如图8(c)、图8(d)和图8(e)、图8(f)所示, 施加压缩应力异质结BlueP/X Te₂的静态介电常数ε₁(0)随着应力的增大而大幅增加(如图8(c)中插图所示), 说明施加压缩应力使材料的屏蔽特性增强; 施加拉伸应力时异质结的$ \varepsilon _{1}\left({0}\right) $随应力增加略有减小. 对于直接带隙半导体材料, 静态介电常数与带隙间存在如下关系^[57]:
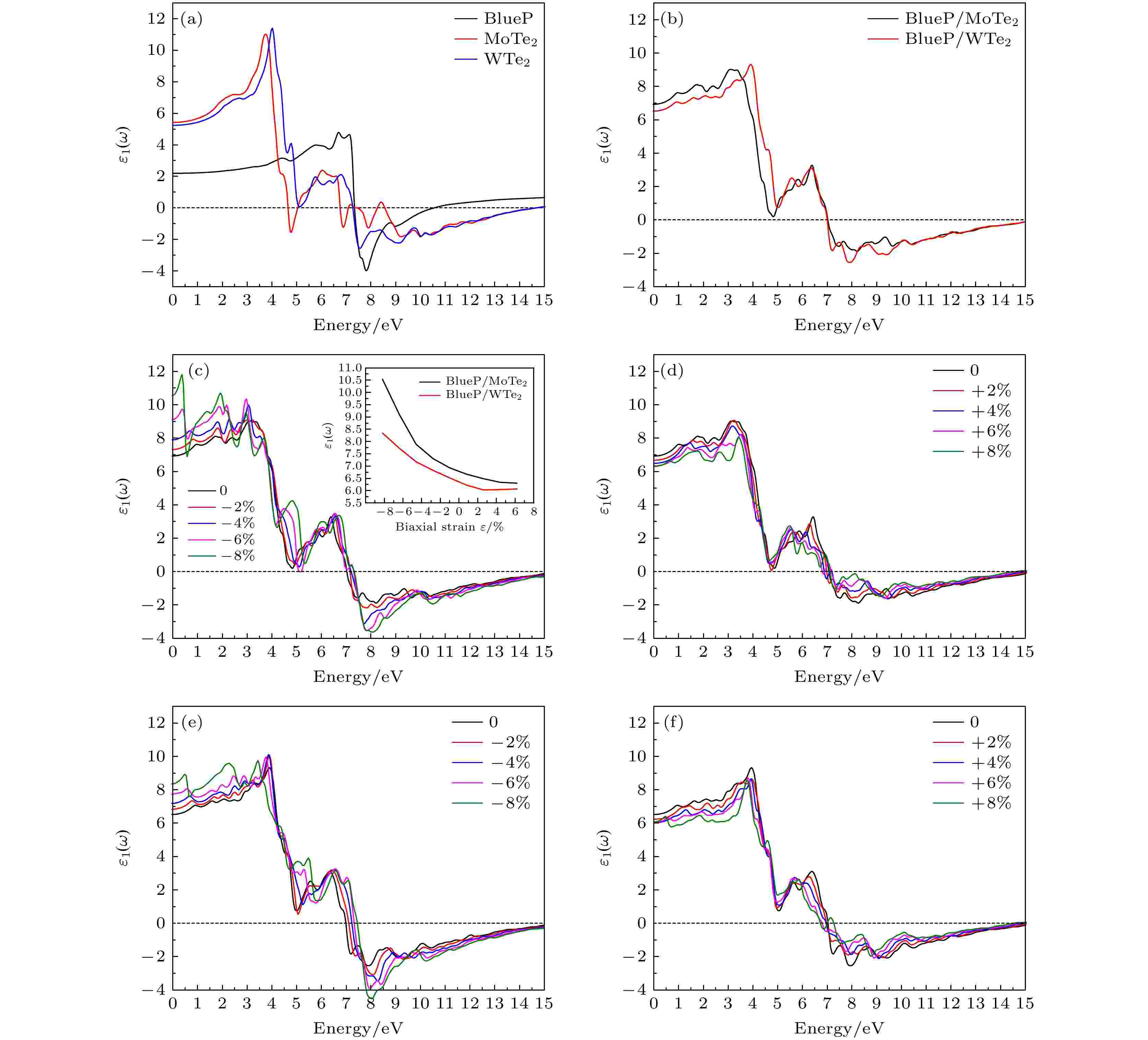图 8 单层BlueP与X Te₂及施加不同应力下BlueP/X Te₂异质结介电函数实部ε₁(ω)谱图　(a)单层BlueP与X Te₂; (b) BlueP/X Te₂异质结; (c), (e) BlueP/MoTe₂, BlueP/WTe₂, ε < 0; (d), (f) BlueP/MoTe₂, BlueP/WTe₂, ε > 0; ε > 0 (ε < 0)表示体系施加拉伸(压缩)应力
Figure8. Real part of the dielectric function of BlueP and X Te₂ monolayer, and BlueP/X Te₂ heterostructures under different biaxial strains: (a) BlueP and X Te₂ monolayer; (b) BlueP/X Te₂; (c), (e) BlueP/MoTe₂, BlueP/WTe₂, ε < 0; (d), (f) BlueP/MoTe₂, BlueP/WTe₂, ε > 0; ε > 0 (ε < 0) represents the tensile strain (compressive strain).

${\varepsilon _1}\left( 0 \right) \approx 1 + {\left( {\frac{{\hbar {\omega _{\rm{p}}}}}{{{E_{\rm{g}}}}}} \right)^2},$

式中, $\hbar $ω_p为等离子体能量, E_g为带隙. 因此, 由图8(c)中插图所示ε₁(0)随压缩应力增加而增大的变化趋势可推断异质结BlueP/X Te₂的带隙是随应力增加而减小的, 这与图6中带隙随压缩应力增加而减小的结果一致. 对于间接带隙半导体, 电子跃迁发生在不同的动量空间, 其光学性质与体系电子结构的关系较复杂, 故不适用上述关系式. 此外, 单层BlueP和WTe₂的介电函数实部分别在7.34—10.56 eV和7.34—15 eV光能区间ε₁(ω) < 0, 而单层MoTe₂则在4.6—15 eV的光能区间有多个频段ε₁(ω) < 0, 形成异质结后的介电函数实部在7.0—15 eV光能区间附近时ε₁(ω) < 0, 说明上述能量区间的光不能在这些材料中传播.
图9为不同应力下BlueP/X Te₂异质结的光吸收谱. 如图9(a)和图9(b)所示, 单层BlueP对可见光吸收弱, 在紫外光区吸收较强; 单层MoTe₂与WTe₂在红外光均有较强的吸收边(～1 eV), 且在红外到紫外光区间吸收系数均大于单层BlueP, 这源于二者均为直接带隙, 计算结果与文献[26]相符; 形成异质结后, BlueP/X Te₂的光吸收谱均发生红移, 且有较强的的光吸收, 光吸收系数达10^–5 cm^–1, 两异质结分别在大约0.6—0.7 eV附近有吸收边. 单层材料和异质结的光吸收特性与图6中能带结构的计算结果相符. 如图9(a)插图所示, 从吸收边至紫外光的4.5 eV区间异质结BlueP/MoTe₂比BlueP/WTe₂有更强的光吸收, 在光子能量大于4.5 eV后BlueP/WTe₂的光吸收系数较大. 图9(c)和图9(d)分别为BlueP/X Te₂在施加应力下的光吸收谱. 如图9(c)所示, 与未施加应力相比, 随压缩应力增加, BlueP/MoTe₂吸收边发生红移, 光吸收响应拓展至中红外光谱区且吸收系数增加; 随着拉伸应力增加, BlueP/MoTe₂的光吸收系数较未施加应力时在吸收边至1.25 eV区间降低, 在1.25—1.8 eV的光能区间略有增加, 在1.8—2.0 eV光能区间开始减小. 如图9(d)所示, 异质结BlueP/WTe₂光吸收谱特性随施加应力的变化过程与BlueP/MoTe₂类似, 仅在施加压缩应力时, BlueP/MoTe₂在中红外至红外光区间的光吸收系数较BlueP/WTe₂大. 如图9(c)—(d)插图所示, 施加压缩和拉伸应力, 两异质结光吸收谱中位于4.5 eV和7.5 eV附近的吸收峰均发生红移. 较未施加应力时, 施加压缩应力且随着应力增加, 两异质结的光吸收谱发生红移, 光吸收系数增大. 这主要源于施加压缩应力使异质结能带结构由间接带隙转变为直接带隙, 因此光吸收增强; 另随应力增加带隙减小, 因此表现出光吸收红移.
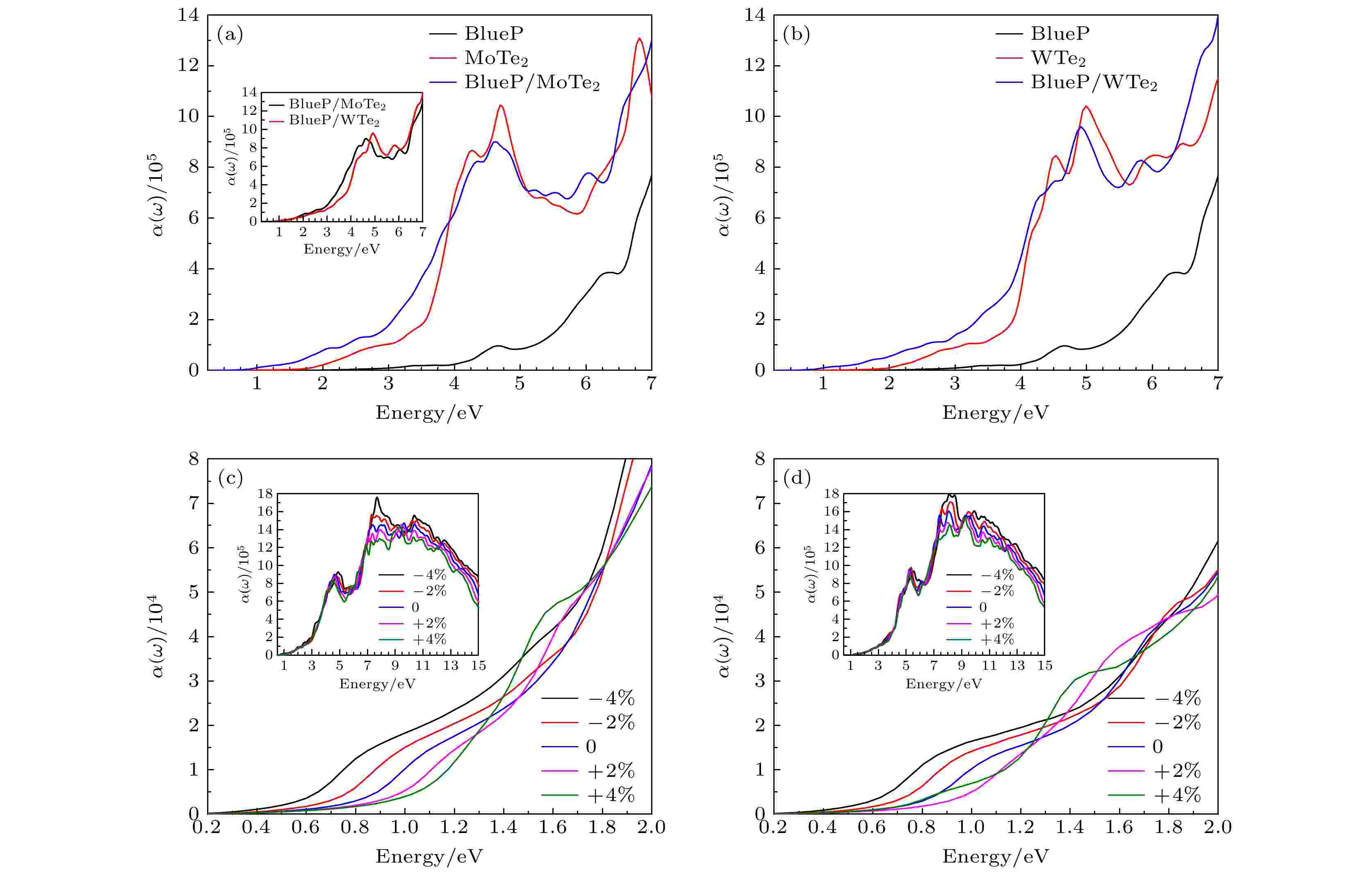图 9 单层BlueP与X Te₂及施加不同应力下BlueP/X Te₂异质结光吸收谱　(a)单层BlueP, MoTe₂与BlueP/MoTe₂; (b)单层BlueP, WTe₂与BlueP/WTe₂; (c), (d) BlueP/MoTe₂, BlueP/WTe₂, 施加应力区间为–4%–+4%
Figure9. Absorption coefficient of BlueP and X Te₂ monolayer, and BlueP/XTe₂ heterostructures under different biaxial strains: (a) BlueP, MoTe₂ monolayer and BlueP/MoTe₂; (b) BlueP, WTe₂ monolayer and BlueP/WTe₂; (c) and (d) for BlueP/MoTe₂ and BlueP/WTe₂ within the biaxial strains –4%–+4%, respectively.

采用第一性原理计算探讨了蓝磷烯与过渡金属硫化物MoTe₂/WTe₂形成范德瓦耳斯异质结的电子结构和光学性质. 计算结果表明, 单层BlueP与X Te₂均形成间接带隙的type-II能带排列. 在光激发下异质结自发地在空间上实现光生电子和空穴的分离与收集, 提升了异质结的光电特性. 光吸收谱的分析表明, 较单层材料异质结, 吸收谱发生红移且有较强的光吸收, 同时屏蔽特性也增强. BlueP/X Te₂异质结的能带结构、能带排列类型及光学性质表现出显著地应力可调控性. 施加压缩应力, BlueP/X Te₂转变为直接带隙type-II能带排列, 随应力继续增加其转变为金属性; 施加拉伸应力, 异质结转变为间接带隙type-I能带排列. BlueP/X Te₂的光学性质, 随压缩应力增加吸收边发生红移, 光吸收响应拓展至中红外光谱区且吸收系数增大, 其中BlueP/MoTe₂较BlueP/WTe₂在中红外至红外光区间表现出更强的光吸收响应. 同时, 随压缩应力增大BlueP/X Te₂的静态介电常数$ {\varepsilon }_{1}\left(0\right) $大幅增加, 屏蔽特性增强. 综上所述, 蓝磷烯与MoTe₂/WTe₂形成稳定的范德瓦耳斯异质结, 压缩应力对BlueP/MoTe₂和BlueP/WTe₂均有显著的调控作用, 而BlueP/MoTe₂对调控更敏感. 外加应力的调控作用影响了BlueP/X Te₂异质结的能带结构, 从而影响其光学性质, 反之, 外加应力使异质结的光学性质发生变化, 反映了其能带结构、能带排列、界面耦合作用的变化, 能够帮助我们深入认识和理解二维层状材料构成的范德瓦耳斯异质结的相关变化规律, 并探讨其更多新的应用. BlueP/X Te₂异质结在应力调控下所表现出的能带排列演化及光谱响应范围的拓宽等特性, 使其在窄禁带中红外半导体材料及光电器件具有潜在的应用价值.