全文HTML
--> --> -->众所周知, 从实验上直接观测材料变形过程中结构演化的细节与规律的成本高昂, 且会受到现代电子和光学显微等技术的限制, 所以人们开始探索新的途径. 得益于计算机技术的飞快发展, 分子动力学(molecular dynamics, MD)模拟在新材料的设计和研发中发挥着越来越重要的作用[11-14]. 通过MD模拟方法揭示石墨烯/金属基复合材料中潜在的变形机理和原子微观结构的演化规律, 对于进一步设计高强高韧的复合材料起着关键作用[15]. Weng等[16]采用MD模拟方法研究了层厚度对石墨烯/铜基复合材料力学性能的影响, 结果表明石墨烯由于极高的面内强度能有效阻碍位错的滑移, 且石墨烯/铜界面的协同作用可以明显增强复合材料的平均流动应力. Shuang和Aifantis[17]通过MD模拟方法发现位错连续传递到石墨烯上会导致石墨烯发生局部变形, 进而提出了滑移、透射和反射三种石墨烯与位错之间的相互作用机制. 当前, 虽然对石墨烯/金属基复合材料力学性能的研究已经取得了初步成果, 然而位错与不同位向石墨烯的相互作用机制仍有待进一步揭示. 本文通过MD模拟方法研究了石墨烯/铝基(Gr/Al)复合材料的纳米压痕过程, 分析了90°, 45°和0°三种不同位向的石墨烯与位错之间的相互作用机制, 揭示了其对Gr/Al复合材料塑性区的影响. 本文的研究结果为进一步设计高性能的石墨烯/金属基复合材料提供了一定的理论依据.
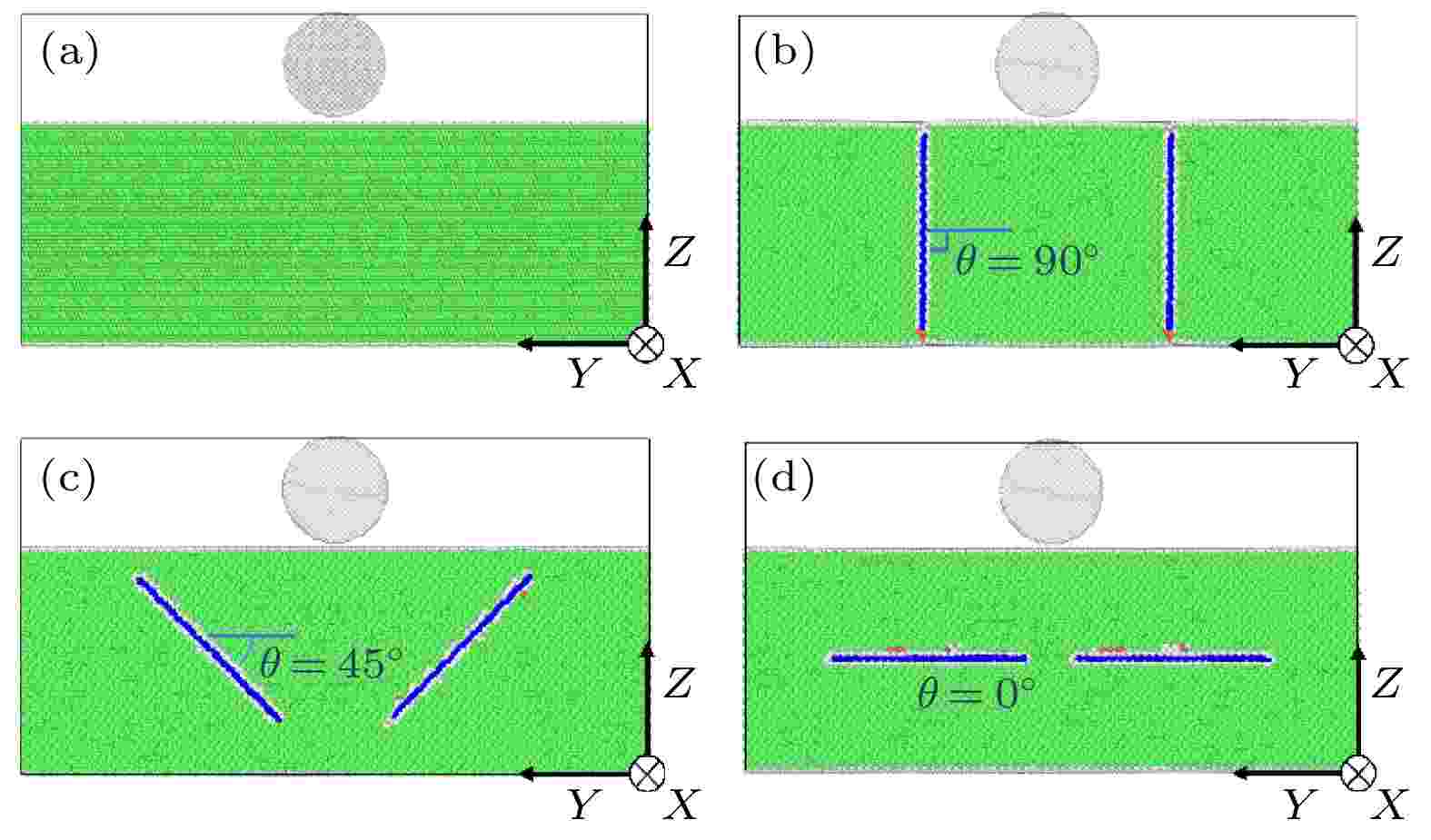图 1 (a)纯铝的初始模型; 石墨烯的嵌入方位分别为(b) 90°, (c) 45°和(d) 0°的Gr/Al复合材料的初始模型, 其中蓝色原子为对称的石墨烯片, 绿色原子为铝基体Figure1. (a) Initial model of the pure Al; initial model of the Gr/Al composites with graphene orientations of (b) 90°, (c) 45°, and (d) 0°, where blue atoms represent symmetrical graphene sheets and green atoms are Al matrix.
势函数的正确选择是保证MD模拟结果准确性和可靠性的关键. 本文采用组合势, 铝原子之间的相互作用采用Mishin等[21]提出的嵌入原子势描述, 碳原子之间的相互作用采用AIREBO势[22]描述. 此外, 用Lennard-Jones (L-J)势描述碳原子与铝原子之间的相互作用, 其中参数取值分别为ε = 0.035078 eV和σ = 0.30135 nm. 该L-J势函数已经广泛用于研究石墨烯/金属基复合材料的力学性能和变形机制[23,24]. 本文采用可视化工具(OVITO)[25]分析压痕过程中微观结构的演化规律, 利用公共近邻分析法(common neighbor analysis, CNA)[26]分析局部原子晶体结构, 采用位错提取法(dislocation extraction algorithm, DXA)[27]识别位错的类型.
3.1.纯铝和石墨烯/铝基复合材料在加载阶段的变形行为
为了研究在加载阶段, 石墨烯嵌入方位对Gr/Al复合材料力学行为的影响, 图2给出了Gr/Al-90°, Gr/Al-45°, Gr/Al-0°复合材料和纯铝4个模型的压痕力与压痕深度之间的关系曲线. 在模拟中, 压痕力等于压痕过程中基体原子对压头原子反作用力之和[28]. 从图2可以观察到, 不同石墨烯位向的Gr/Al复合材料和纯铝的压痕力整体上均随压痕深度增加而增大, 其中a—f这6个特征点将加载阶段分成I—V五部分. 此外, 从图2可知, 压痕力在变形后期出现了明显的波动现象, 这主要是由于压头在加载过程中积累的能量随着位错的滑移不断地释放. 应该注意的是, 由于不同模型在压痕载荷下的变形行为有差异, 所以本文提供的6个点为近似特征点. 在a点(曲线上压痕力等于0的点)之前, 所有模型的压痕力从负值缓慢增加到0, 这是因为压头原子与基体原子之间存在黏附力. 随着压痕深度增加, 进入碳原子与铝原子短程力的作用范围, 该研究与Jiao等[29]的模拟结果一致.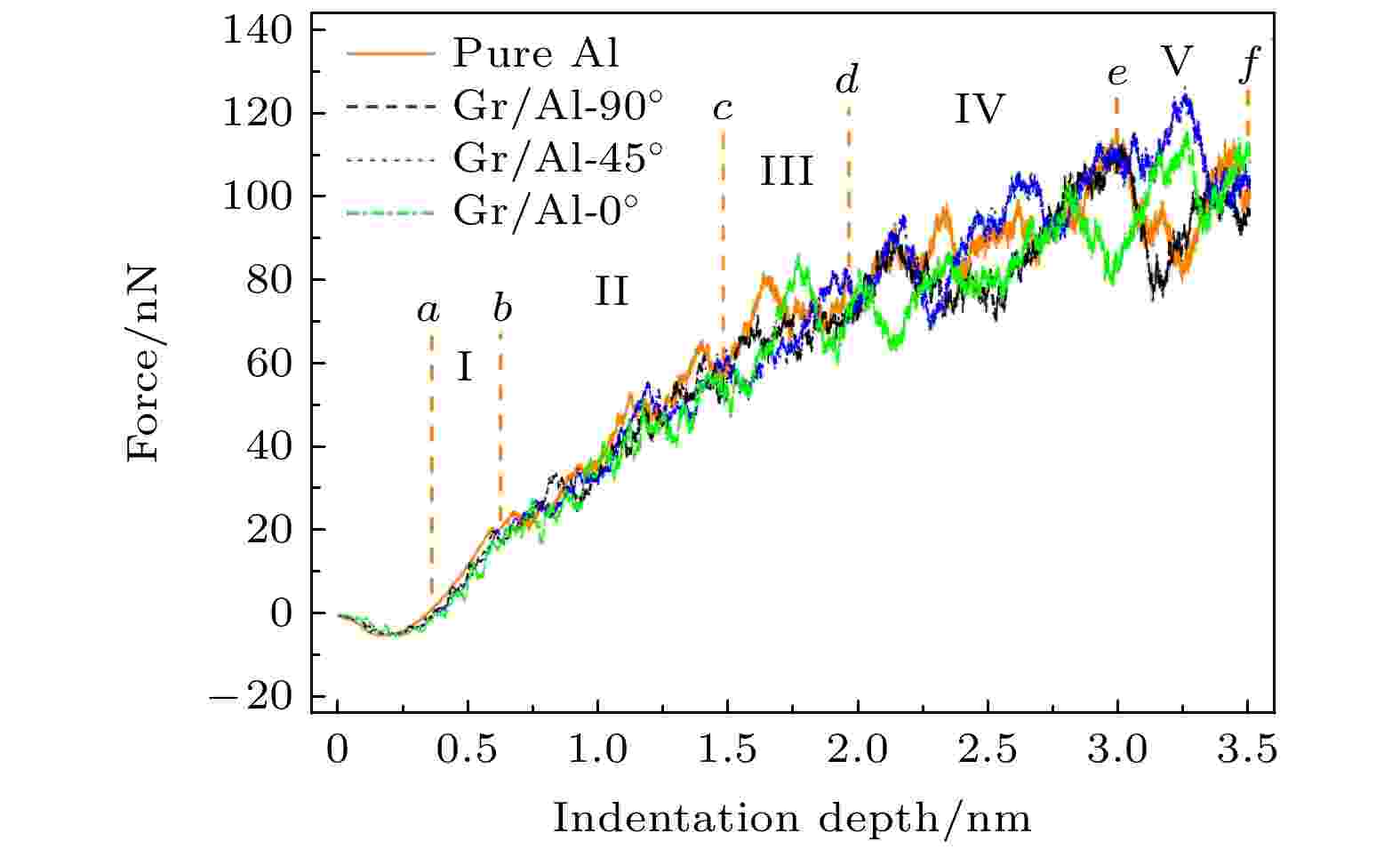
图 2 加载过程中, 纯铝和Gr/Al复合材料的压痕力与压痕深度的关系Figure2. Relationship between indentation force and indentation depth of the pure Al and the Gr/Al composites during the loading stage.
为了研究Gr/Al复合材料中位错与石墨烯的相互作用机理, 图3运用DXA法描述了纯铝和Gr/Al复合材料在b—f这5个特征点的位错线分布图. 图2所示的I区域为弹性阶段, 在这个阶段纯铝和Gr/Al复合材料内部均没有新的位错产生. 纯铝在b点出现压痕力下降的现象, 观察图3中b点对应的位错线分布图可以看出, 肖克利不全位错在接触表面下方的压痕轴两侧开始形核, 位错的形核和滑移释放了局部集中的应力从而导致了压痕力的下降, 该研究与Lee等[20]的研究结果是一致的. 从图3可以看出, 所有Gr/Al复合材料的成核位点都位于压痕轴两侧. 研究表明, Gr/Al-90°, Gr/Al-45°和Gr/Al-0°复合材料分别在压痕深度为0.60, 0.60和0.64 nm时位错开始形核. 对于Gr/Al-0°复合材料, 垂直于加载方向的石墨烯降低了压痕方向刚度, 导致位错成核在更大压痕深度处发生[30]. 在区域II, 对于纯铝模型, 基体内肖克利不全位错在压头下方的{111}滑移面内滑移, 形成了图3中c点红色箭头所示的胚胎棱柱形位错环, 这与图2中压痕力下降的现象是相对应的. 对于Gr/Al复合材料, 随着压痕深度的增加, 肖克利不全位错向着石墨烯方向滑移, 压头下方的位错网络迅速扩展. 对于Gr/Al-45°复合材料, 在压痕深度为1.27 nm处, 胚胎棱柱形位错环脱离压头下方形成棱柱形位错环, 随着压痕深度增加, 石墨烯阻碍了位错环的运动. 然而, 对于Gr/Al-90°和Gr/Al-0°复合材料, 位错环没有脱离压头, 压头下方的位错网络之间通过肖克利不全位错与石墨烯连接. 在区域III, 对于纯铝模型, 在压头下方的位错网络形成多个胚胎棱柱形位错环, 这些胚胎棱柱形位错环竞争生长, 导致曲线高度振荡. 如图3中d点红色箭头处所示, 当压痕深度增加到1.96 nm时, 胚胎棱柱形位错环从压头下方的位错网络中脱离出来形成棱柱形位错环向基体底部滑移. 从Gr/Al复合材料的位错线分布也可以观察到, 多个胚胎棱柱形位错环竞争生长, 如图3中d点所示. 棱柱形位错环滑移分为两种, 第一种是沿基体表面滑移, 这是因为在X和Y方向上存在周期性; 第二种是在基体内部向下运动, 棱柱形位错环运动到底端附近时, 由于受到固定层的影响在底端附近滑移. 在区域IV, 对于纯铝, 压头下方的位错网络中的胚胎棱柱形位错环继续生长, 棱柱形位错环沿着基体表面滑移或基体内部向下滑移. 然而, 在Gr/Al复合材料中, 石墨烯可以有效阻挡位错环在基体内部的滑移, 其中在Gr/Al-45°和Gr/Al-0°复合材料中观察到位错环可以在两片对称石墨烯之间的空隙处向下扩展, 如图3中e点Gr/Al中位错线分布图所示. 当达到最大压痕深度f点时, Gr/Al复合材料中位错与石墨烯的相互作用影响了压头下方的位错线分布, 特别是Gr/Al-0°复合材料, 在石墨烯与压头下方之间形成位错网络. 基于以上研究可以发现, 石墨烯嵌入方位在纳米压痕过程中对基体内塑性变形过程会产生显著影响.
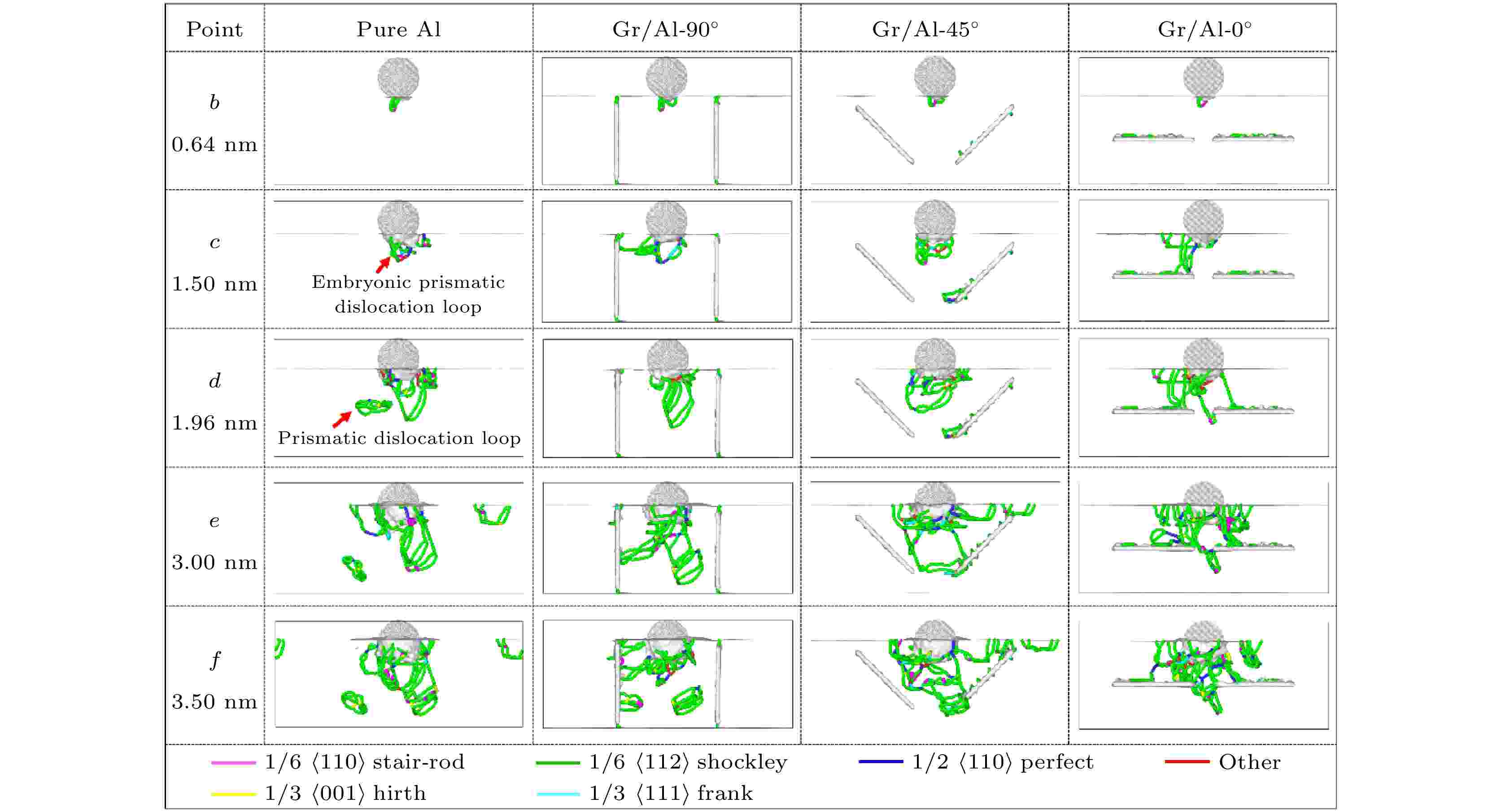图 3 加载过程中, 纯铝和Gr/Al复合材料在特征点b—f的位错线分布图Figure3. Dislocation line distribution diagram of the pure Al and the Gr/Al composites at the characteristic points b–f during the loading stage.
为了研究位错环与不同位向石墨烯之间的相互作用, 图4(a)给出了由{111}型滑移面组成的棱柱形位错环的详细结构图. 从图4(a)可以看出, 棱柱形位错环均由堆垛层错与伯氏矢量不同的肖克利不全位错组成. 研究该结构在材料的塑性变形过程中具有重要意义, 因为随着棱柱形位错环在基体内部或表面滑移, 可以扩大基体内部的塑性区. 与纯铝相比, Gr/Al复合材料中石墨烯的嵌入影响了基体内部位错环的生长和滑移. 图4(b)—(d)所示为利用DXA和位移矢量法描述的Gr/Al-90°, Gr/Al-45°和Gr/Al-0°这3个模型在压痕深度分别为1.75, 1.59和1.59 nm (即图2中位于III区域)时, 基体中位错线瞬态图和石墨烯面内原子起伏图, 其中位移矢量法利用相对位移大小进行着色. 对于Gr/Al-90°复合材料, 从图4(b)可以看出石墨烯阻碍了沿表面滑移的棱柱形位错环. 在Gr/Al-45°复合材料中, 棱柱形位错环向下滑移的过程中遇到石墨烯, 棱柱形位错环一端肖克利不全位错湮灭, 另一端固定在石墨烯表面, 如图4(c)所示. 对于Gr/Al-0°复合材料, 胚胎棱柱形位错环扩展到石墨烯表面, 在压头下方与石墨烯之间形成肖克利不全位错组成的连接, 如图4(d)所示. 以上研究表明, 石墨烯的嵌入方位对位错的阻碍方式会有明显的影响. 此外, 从图4(b)—(d)石墨烯面内碳原子位移标色可以观察到位错与石墨烯之间相互作用的位置. 位错环滑移到Gr/Al界面处, 由于界面处没有连续的滑移面, 石墨烯面内的碳原子沿着位错环的方向发生弹性变形. 不难发现, 石墨烯在位错传播过程中起到了屏障的作用. 这是因为石墨烯面内弹性模量高达1 TPa[31], 位错环与石墨烯发生相互作用, 石墨烯面内碳原子位移在弹性范围内, 不会导致碳—碳键断裂. 又由于石墨烯弯曲刚度低, 所以会沿位错环的方向发生弹性变形, 这与Chang等[30]在石墨烯/镍基复合材料中发现的结果是一致的. 以上研究表明, Gr/Al复合材料在纳米压痕过程中, 随着压痕深度增加, 位错环在滑移过程中被石墨烯阻挡, 改变了塑性区的扩展趋势.
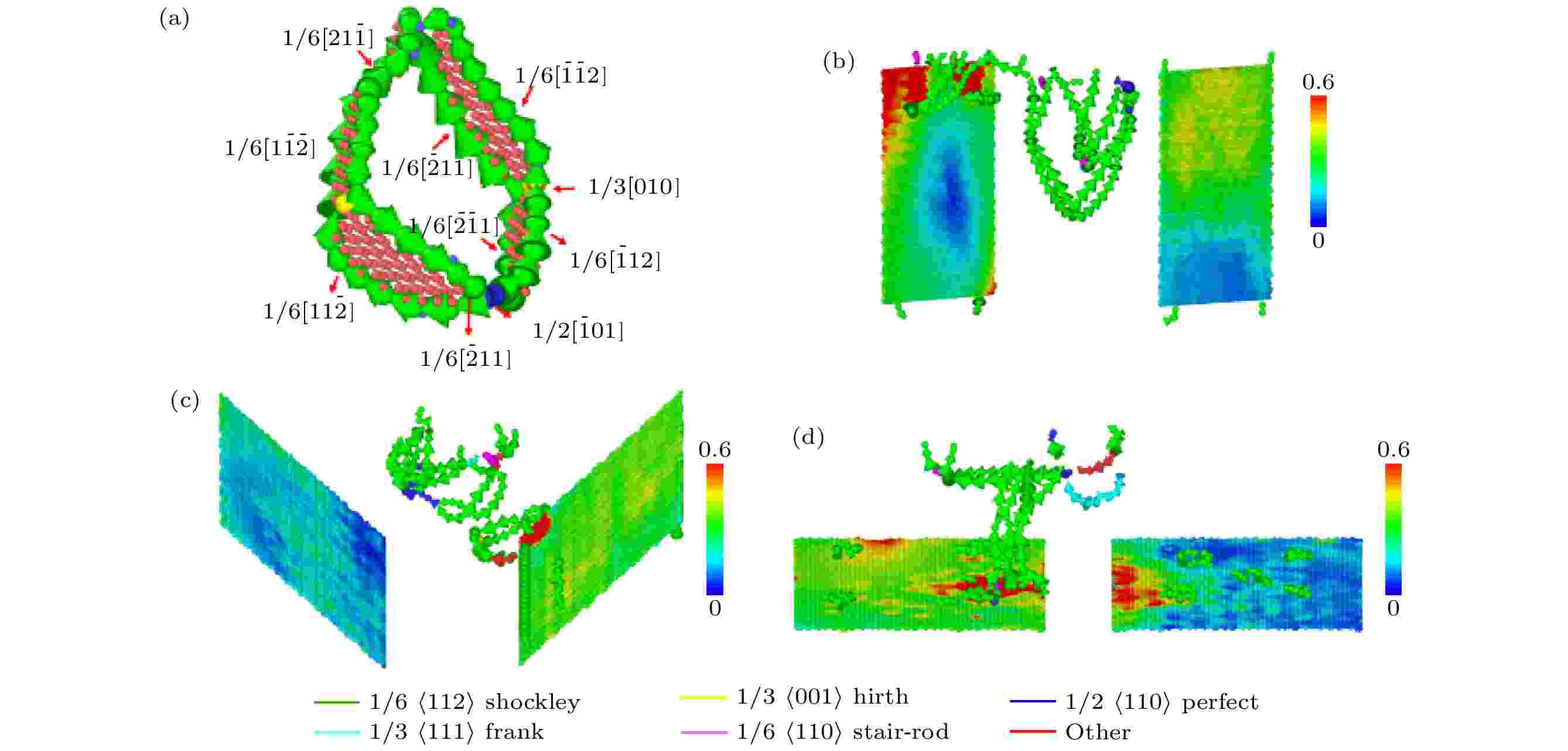图 4 (a)棱柱形位错环的原子结构图; (b)—(d) Gr/Al复合材料在石墨烯嵌入位向分别为(b) 90°, (c) 45°和(d) 0°, 压痕深度分别为(b) 1.75 nm, (c) 1.59 nm和(d) 1.59 nm时的位错线分布和石墨烯的表面起伏情况Figure4. (a) Atomic snapshot of prismatic dislocation loop; (b)–(d) dislocation line distribution of Gr/Al composites and in-plane height profile of graphene at the indentation depth of (b) 1.75 nm, (c) 1.59 nm, and (d) 1.59 nm, with graphene orientations of (b) 90°, (c) 45°, and (d) 0°.
2
3.2.纯铝和石墨烯/铝基复合材料在卸载阶段的变形行为
为了研究在卸载阶段, 石墨烯嵌入方位对Gr/Al复合材料力学行为的影响, 图5(a)给出了Gr/Al复合材料和纯铝4个模型的压痕力与压痕深度之间的关系曲线. 从图5(a)可以看出, 压痕力从正值逐渐减小, 这是由于压头与基体之间的距离增大, 排斥力减弱. 随着压头继续抬升至3.0 nm左右, 施加在压头上的力变为负值, 这是由于压头原子与基体原子之间存在黏附力. 随着压头继续抬升至1.2 nm左右, 压痕力变为0, 压头与压痕区域表面原子的距离超过了远程力的作用范围. 为了研究不同位向石墨烯对卸载阶段位错演化的影响, 图5(b)给出了纯铝和Gr/Al复合材料的总位错线长度演化曲线. 从图5(b)可以看出, 随着压头回升, 所有模型的位错线长度减小, 在压痕深度2.75—2.50 nm之间位错线长度骤然下跌, 之后达到一个平稳值. Gr/Al-90°, Gr/Al-0°, Gr/Al-45°复合材料和纯铝的位错线总长度的平稳值分别为45.36, 160.69, 219.73和136.53 nm. 4个模型在卸载过程中位错线总长度值分别下跌了84.14%, 55.55%, 37.95%和55.14%. 基体内总位错线长度演化规律与压头下方形成的位错网络紧密相关.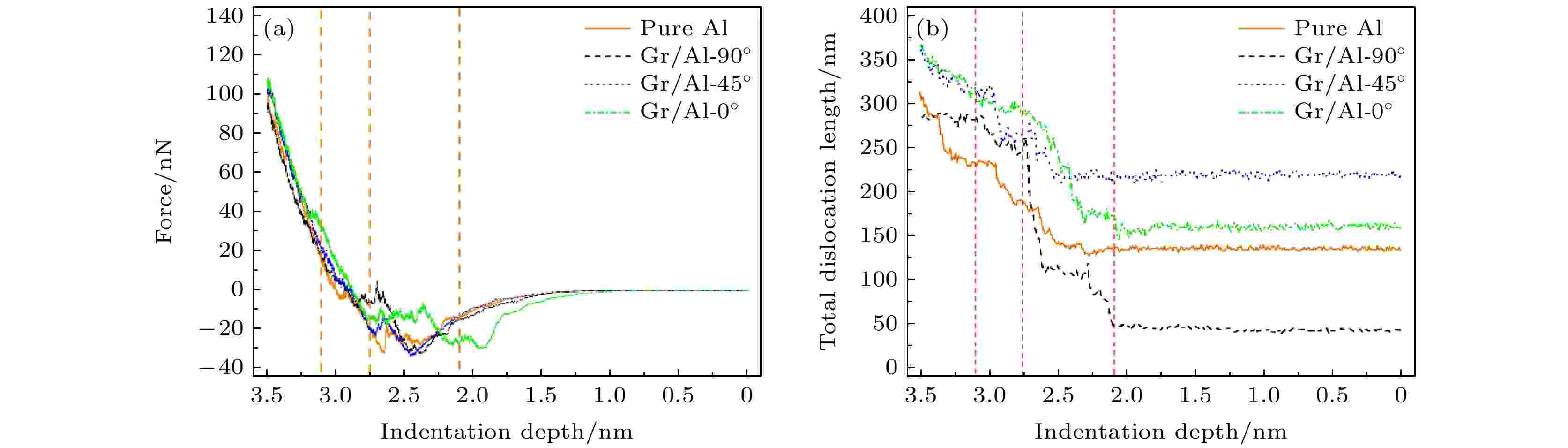
图 5 (a)卸载过程中, 纯铝和Gr/Al复合材料的压痕力与压痕深度的关系; (b) 卸载过程中, 纯铝和Gr/Al复合材料的总位错线长度的演化Figure5. (a) Relationship between indentation force and indentation depth of the pure Al and the Gr/Al composites during the unloading stage; (b) evolution of total dislocation length of the pure Al and the Gr/Al composites during the unloading stage.
为了进一步分析纯铝和Gr/Al复合材料在卸载过程中铝基体内的位错演化行为, 图6利用DXA法给出了纯铝和Gr/Al复合材料在压痕深度为3.11, 2.76和2.09 nm时的位错线分布图. 对于纯铝, 在压头逐渐抬升的过程中, 塑性区内的位错逐渐向反方向运动, 棱柱形位错环与压头下方的位错网络重新组合, 基体内部的位错缺陷逐渐湮灭. 在Gr/Al-90°复合材料中, 位错环沿着石墨烯表面向上滑移, 与压头下方的位错网络重新组合, 在连接处形成压杆位错, 但是随着压头继续回升, 肖克利不全位错不断合成和分解, 从可视化结果看出基体内大部分位错湮灭. 从图6(b)和图6(c)可以明显看出, 在石墨烯之间的间隙处穿过的位错, 随着压头回升, 位错与石墨烯的两端产生较强的相互作用, 阻碍了位错的运动. 因此, 在Gr/Al-45°和Gr/Al-0°的铝晶体中留下了较多的位错.
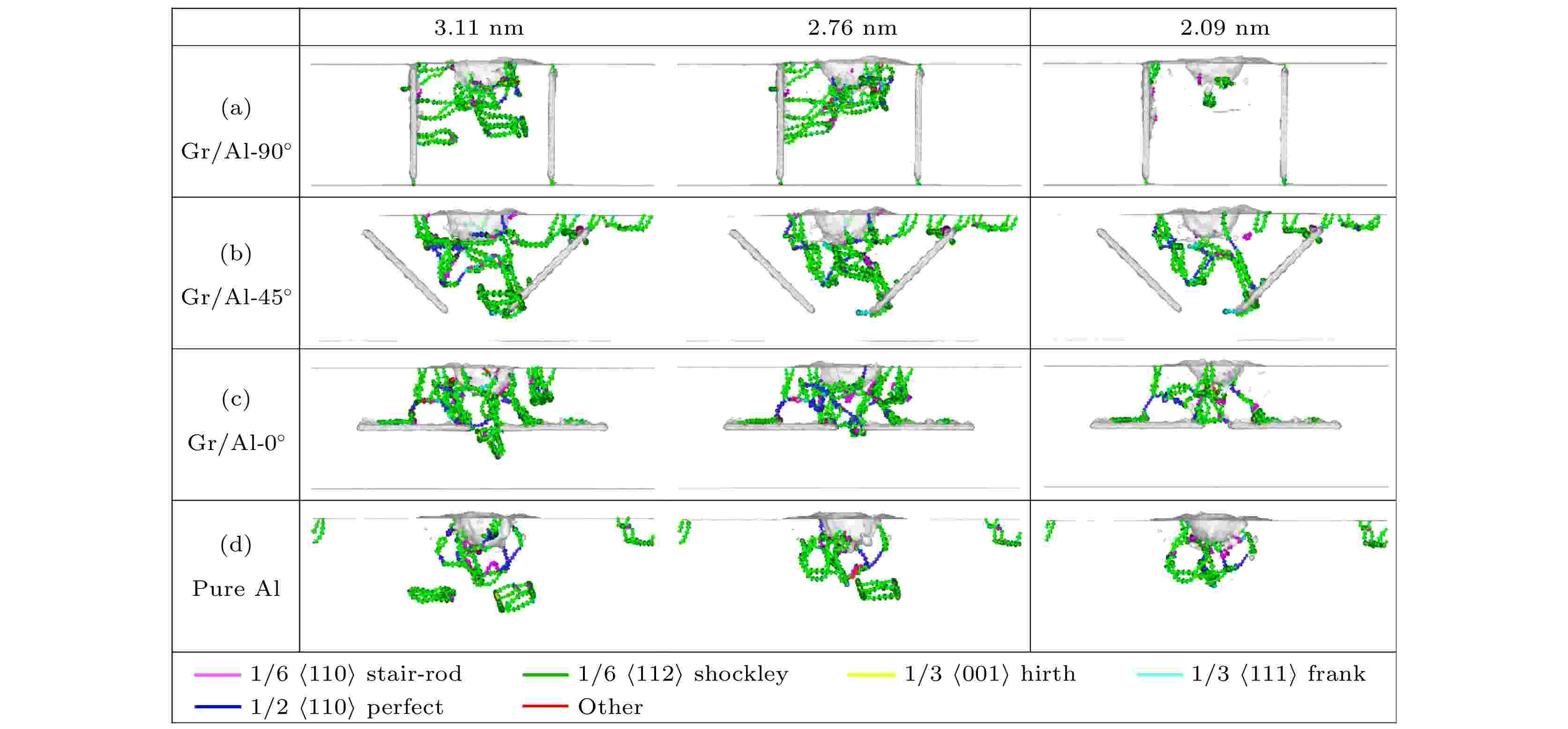图 6 卸载过程中, 纯铝和Gr/Al复合材料在不同压痕深度的位错线分布图Figure6. Dislocation line distribution diagram of the pure Al and the Gr/Al composites at various depths during the unloading stage.
2
3.3.石墨烯嵌入方位对Gr/Al复合材料塑性区的影响
为了分析石墨烯嵌入方位对Gr/Al复合材料塑性区的影响, 图7给出了加载阶段压痕深度为3.50 nm和卸载阶段压痕深度为0.00 nm时, 利用CNA法描述的原子结构图, 其中蓝色虚线是依据Gao等[32]提出的塑性区定义给出的大致轮廓. 为了方便观测, 其中具有面心立方结构的原子均被去除. Gao等[32]指出塑性区中的位错可以分为两类: 压头下方附近的位错和远离压头下方附近的位错, 并且给出纯铝内半球形塑性区半径的定义为, 压头下方附近的位错网络到压头的最大距离. 从图7可以看出, 对于Gr/Al-90°和Gr/Al-0°复合材料, 嵌入的石墨烯分别限制了宽度和深度方向的位错扩展, 改变了半球形塑性区内位错的分布. 而对于Gr/Al-45°复合材料来说, 由于石墨烯对位错滑移的阻碍作用, 石墨烯与塑性区相切, 减小了半球形塑性区的体积. 以上研究还表明, 石墨烯在铝基体内的嵌入方位不同, 在塑性变形过程中产生的塑性应变梯度就不同. 也就是说, 不同位向的石墨烯对位错阻碍的强度不同, 对基体内塑性区的大小影响不同, 这与Shuang和Aifantis[17]的研究结果一致. 完全卸载后, 与f (即压痕深度为3.5 nm)点的塑性区相比, 不同模型的塑性区的收缩大小不同. 从可视化结果计算Gr/Al-90°, Gr/Al-0°和Gr/Al-45°复合材料和纯铝卸载前后塑性区的收缩大小分别为75.68%, 53.89%, 31.92%和56.03%. 从3.3节的研究发现, Gr/Al-90°复合材料的塑性区明显收缩, 值得注意的是, 该模型位错线长度值达到平稳后最低. 这也再次证明了石墨烯与位错的相互作用, 与塑性区变形趋势紧密相关.
图 7 纯铝和Gr/Al复合材料在压痕深度3.50和0.00 nm时的微结构, 蓝色虚线表示塑性区Figure7. Microstructures of the pure Al and the Gr/Al composites at indentation depth 3.50 and 0.00 nm, where the blue dotted line indicates the plastic zone.
2
3.4.石墨烯嵌入方位对Gr/Al复合材料硬度的影响
为了定量评估石墨烯嵌入方位对Gr/Al复合材料力学性能的影响, 图8给出了Gr/Al复合材料的硬度与石墨烯嵌入方位的关系曲线. 在这儿, 复合材料的硬度用压痕深度在1.96 (即图2中的 d点)—3.50 nm (即图2中的f点)之间接触压力的平均值进行定量描述, 其中接触压力由压痕力除以投影到平面的接触面积计算得到[33]. 选取该范围内的接触压力, 是因为位错环的演变过程是衡量压头下方的塑性变形强弱程度的重要依据和远离压头区域的内部缺陷演化的内在表现. 从图8可知, Gr/Al-45°复合材料的硬度3.75 GPa较纯铝的硬度3.59 GPa提高4.46%, Gr/Al-90°和Gr/Al-0°复合材料的硬度分别为3.44和3.41 GPa, 与纯铝的硬度相比分别减小了4.18%和5.01%. 泰勒模型[34,35]指出了塑性区内位错密度与硬度之间存在一定的关联, 位错密度越大, 硬度越大. 为了揭示图8所示的硬度随石墨烯嵌入方位的变化行为, 计算了加载阶段位错线总长度随压痕深度的变化, 发现Gr/Al-45°和Gr/Al-0°复合材料的总位错线长度值大于Gr/Al-90°和纯铝的总位错线长度. 因此, Gr/Al-90°复合材料的硬度较低. 在Gr/Al-45°复合材料中, 45°的石墨烯片与位错相互作用, 减小了塑性区的体积, 并且增大了塑性区中存储的位错数量, 进而提高了复合材料的硬度. 与Gr/Al-45°复合材料不同, 在Gr/Al-0°复合材料中, 压头与石墨烯之间肖克利不全位错构成的位错网络增大了塑性区内的位错数量, 但是大量位错与石墨烯相互作用, 导致石墨烯面内产生大范围的弹性变形, 削弱了压头附近的接触压力, 从而导致了硬度的降低, 这与Vardanyan和Urbassek[36]的研究结果一致.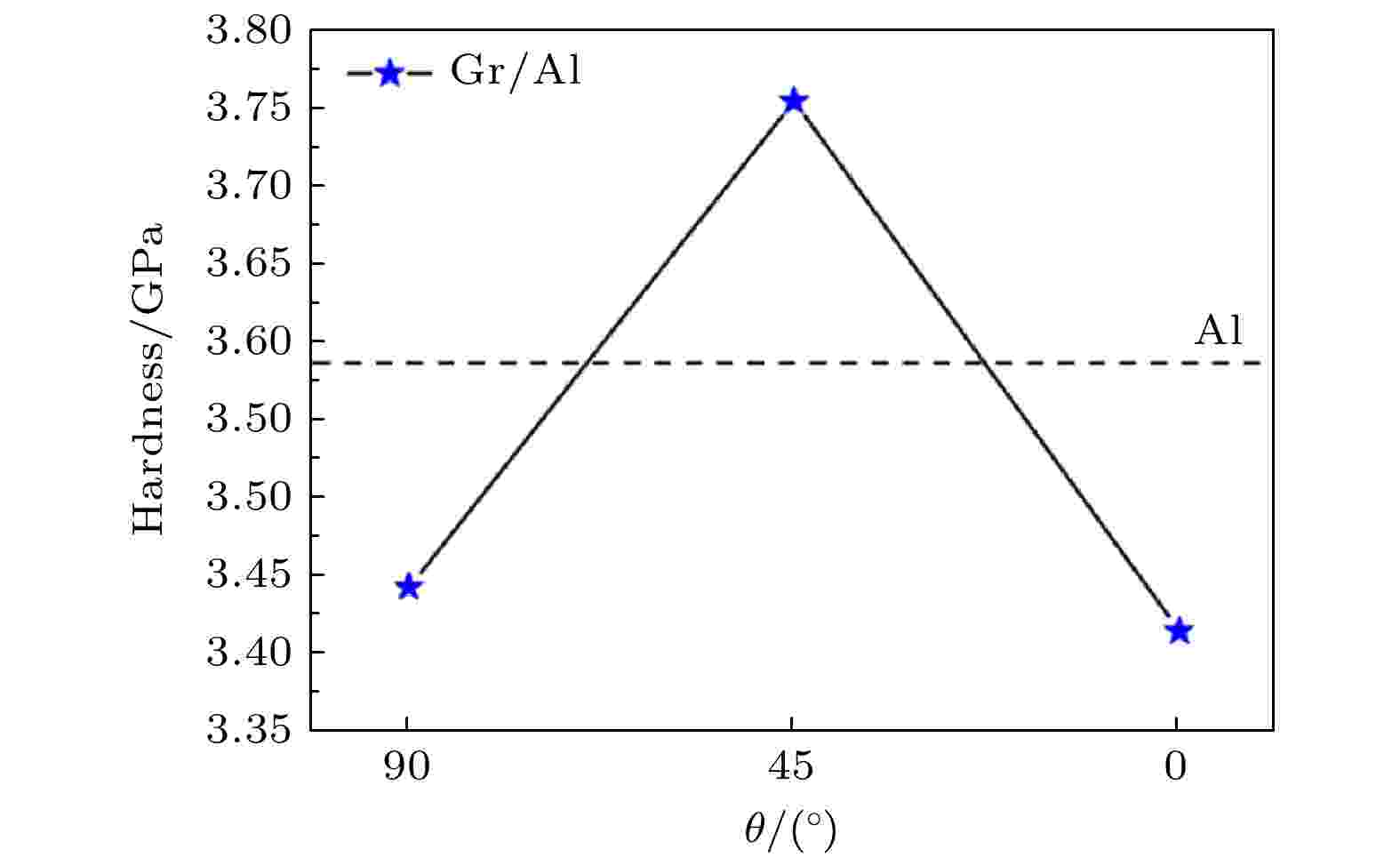
图 8 Gr/Al复合材料的硬度随石墨烯嵌入方位的变化Figure8. Relationship between the hardness of Gr/Al composites and different orientations of graphene.
