删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于忆容器件的神经形态计算研究进展

本站小编 Free考研考试/2021-12-29
摘要:人工智能的快速发展需要人工智能专用硬件的快速发展, 受人脑存算一体、并行处理启发而构建的包含突触与神经元的神经形态计算架构, 可以有效地降低人工智能中计算工作的能耗. 记忆元件在神经形态计算的硬件实现中展现出巨大的应用价值; 相比传统器件, 用忆阻器构建突触、神经元能极大地降低计算能耗, 然而在基于忆阻器构建的神经网络中, 更新、读取等操作存在由忆阻电压电流造成的系统性能量损失. 忆容器作为忆阻器衍生器件, 被认为是实现低耗能神经网络的潜在器件, 引起国内外研究者关注. 本文综述了实物/仿真忆容器件及其在神经形态计算中的最新进展, 主要包括目: 前实物/仿真忆容器原理与特性, 代表性的忆容突触、神经元及神经形态计算架构, 并通过总结近年来忆容器研究所取得的成果, 对当前该领域面临的挑战及未来忆容神经网络发展的重点进行总结与展望.
关键词: 忆容器/
忆容机理/
突触/
神经网络

English Abstract


全文HTML

--> --> -->
1.引　言
近年来, 随着大数据的应用与神经网络训练算法的突破, 人工神经网络(ANN)取得了长足的进展, 对医疗诊断、环境科学、智能机器、物联网和安全等多个领域产生了深远的影响[1]. 虽然ANN能够实现比传统方法更节能的算法, 但它们通常使用传统的冯诺依曼计算架构来实现, 在这种架构下, 物理上独立的逻辑和内存块之间的数据传输会导致处理瓶颈和不必要的电能消耗. 受人脑的存算一体、并行处理启发而构建的包含突触与神经元的神经形态计算架构, 被认为是突破冯诺依曼瓶颈、降低电能消耗的有效途径[2]. 神经形态计算的早期成功很大程度上依赖于传统的电子器件, 特别是硅基互补金属-氧化物-半导体(CMOS)晶体管的脉冲神经网络[2-4], 如IBM的TrueNorth芯片[3]和欧盟人脑计划的SpiNNaker项目[4]. 与传统的电子器件相比, 新兴电子器件如忆阻器[5,6], 在神经元构建[7-9]、非易失性储存[10,11]等方面有着巨大优势, 2020年, 清华大学先后实现用1M1T结构阵列完成卷积神经网络计算[12], 以及低能耗的全忆阻神经元[13]. 然而, 目前基于忆阻器实现的神经网络架构中, 通常使用电导表示权重, 其用施加电压、检测电流的方式来更新和读取权重的过程存在不可避免的电能损耗. 优化权重表示方法、改变权重更新读取方式, 被认为是降低系统性电能损耗的有效途径. 作为忆阻器衍生器件而提出的忆容器[14]被认为是实现低耗能神经网络的潜在器件[15-22], 引起国内外研究者关注.
早在2009年, Ventra与Pershin 就联合“忆阻器之父”蔡少棠教授在Proceedings of the IEEE上将忆阻器的概念和理论拓展到了电容型器件和电感型器件领域, 并据此提出了忆容系统和忆感系统. 类似于忆阻系统, 忆容系统可分为电压控制型和电荷控制型, 对于电压控制型的忆容系统, 有[14]
$ q\left(t\right)=C\left(x,{V}_{\rm{C}},t\right){V}_{\rm{C}}\left(t\right){,} $
$ \dot{x}=f(x,{V}_{\rm{C}},t){,} $
其中: $ q\left(t\right) $表示t时刻整个系统存储电荷的值; $ {V}_{\rm{C}}\left(t\right) $表示系统两个端口间的电压; C表示系统的瞬时忆容值, 该瞬时值由系统内部的一个变量决定; x为状态变量.
相应的, 电荷控制型的忆容系统被定义为:
$ {V}_{\rm{C}}\left(t\right)={C}^{-1}\left(x,q,t\right)q\left(t\right){,} $
$ \dot{x}=f(x,q,t){,} $
其中, $ {C}^{-1} $为忆容值的倒数.
理想压控/荷控忆容器作为忆容系统的子类, 忆容值可以简化为只与流经系统电压/电荷的历史有关, 理想压控忆容器的数学表达为
$ C=C\left({\int }_{{t}_{0}}^{t}{V}_{\rm{C}}\left(\tau \right){\rm{d}}\tau \right){. } $
理想荷控忆容器表达为
$ C=C\left({\int }_{{t}_{0}}^{t}q\left(\tau \right){\rm{d}}\tau \right){. } $
理想忆容器的定义建立了电荷q与电压V之间的状态依赖关系, 同时模型还对忆容器的捏滞曲线提出了关于原点对称、随频率变化等要求, 并将 q-V域过原点的奇对称捏滞曲线作为忆容器的判定标志, 如图1所示[14]. 由于忆容器理论自身还在不断完善, 实际研究中的忆容器往往不符合2009年提出的理想忆容器数学模型. 2015年, 蔡少棠教授[23]提出广义忆阻器的概念, 定义广义忆阻器的忆阻由输入电流(或电压)和一个或更多状态变量同时决定. 我们根据广义忆阻器的概念可以提出类似的广义忆容器的概念, 即广义忆容器的忆容由输入电压(或电荷)和一个或更多状态变量同时决定, 因此其q-V捏滞曲线也不需要关于原点对称, 目前大多数报道的忆容器件[20,24-38]及其仿真模型[39-54]都属于这类广义忆容器. 与忆阻器的R-V特性类似, 忆容器的C-V特性使高效低耗能的容性神经形态计算[55]成为可能.
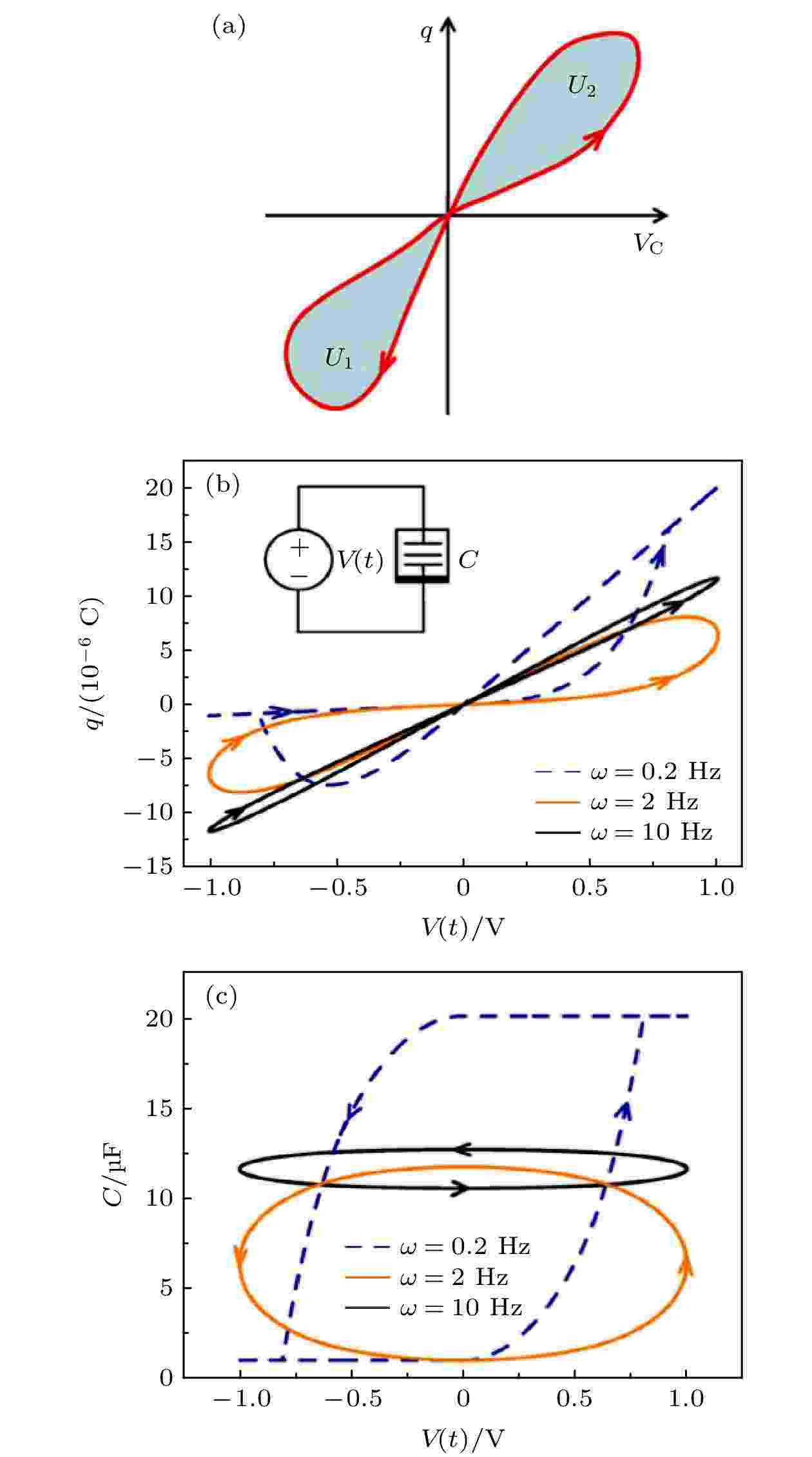图 1 (a)忆容系统的捏滞曲线[14]; (b)仿真的压控忆容器q-V曲线[14]; (c) 仿真的压控忆容器C-V曲线[14]
Figure1. (a) Schematics of a pinched hysteresis loop of a memcapacitive system[14]; (b) q-V curve of a simulated voltage-controlled memcapacitor[14]; (c) C-V curve of a simulated voltage-controlled memcapacitor[14].

如图2所示, 基于忆容器的神经形态计算研究可分为3个层次: 1)基础忆容器件; 2)基于基础忆容器件的突触、神经元; 3)由突触、神经元构成的忆容神经网络及相应网络的特征算法. 由于电容器本身的能量存储、电压保持等性质及忆容器的非易失电容积分、脉冲电压阈值激发等特性, 基于忆容突触、神经元[16,21]的输入电压/电荷-检测电压/电荷方式相比基于忆阻突触、神经元的输入电压-检测电流方式, 在降低网络能耗方面有着巨大的优势; 但实物器件方面, 目前实现的忆容神经元相比理想忆容神经元在能耗及性能上还存在差距[20,27,56].
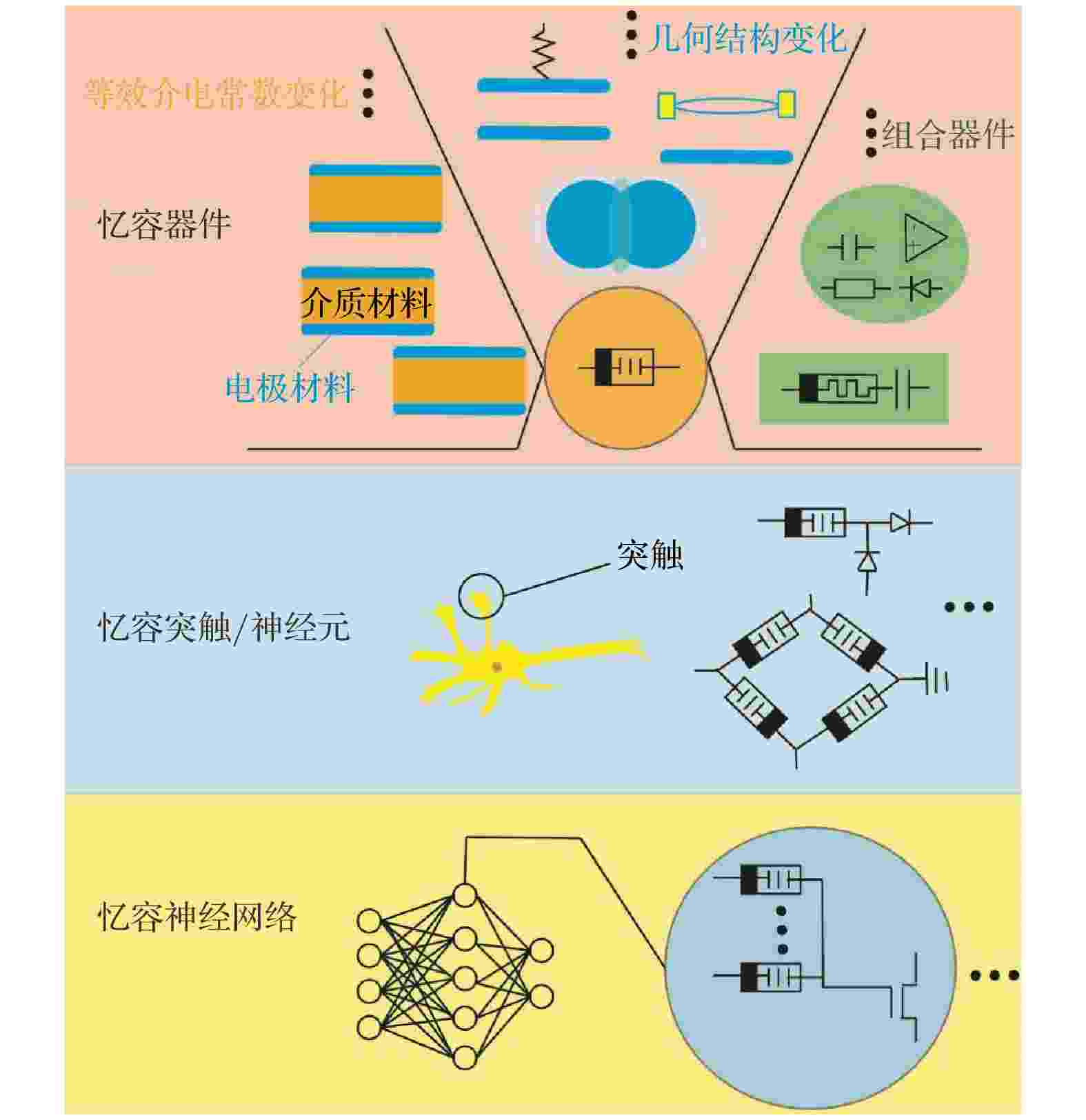图 2 基于忆容的神经形态计算
Figure2. Neuromorphic computation based on memcapacitors.

本文概述了基于忆容神经形态计算的最新进展. 主要包括目前实物/仿真忆容器原理与特性、代表性的忆容突触、神经元及神经形态计算架构, 并在文章最后对当前该领域面临的挑战及未来忆容神经网络发展的重点进行总结与展望.
2.实物忆容器件
现阶段忆容器的实现原理可分为3类: 1)整体等效介电常数变化. 偏置电压的作用使器件整体的等效介电常数展现出随偏置电压非线性变化的忆容效应. 2)几何结构变化. 偏置电压改变电容电极形状、电极间距等几何结构以实现可控变容, 如弹簧电极结构、双球电极结构、弹性薄膜电极结构等[30,31,57]. 3)多器件组合. 将不同器件组合使整体对外输入输出表现出忆容特性, 如伪忆容将忆阻器与大电容串联[20,58]及由电阻、电容、放大器等器件构成的忆容电路[40,42,49,51,52].
2
2.1.基于整体等效介电常数变化的忆容
-->

2.1.基于整体等效介电常数变化的忆容

研究人员在一些含单/复合金属氧化物层[24,32-36,59]及一些含有机聚/络合物层[25-27,60]的三明治结构器件中发现忆容效应, 目前所提出的忆容机理包括导电纳米丝的产生与湮灭[35,38]、界面肖特基势垒调制[24,36,37]、离子/离子团迁移[26,61]、分子群极化[27]、氧化/还原TiOx活性层[59]、氧空位迁移时氧化物介电常数变化[33,62]、电荷歧化[25]、有机介质材料导电性转变[60]、形成空间绝缘层[28]等.
目前提出的含单/复合金属氧化物层介质材料的忆容器结构包括: Au/Pr0.7Ca0.3MnO3(PCMO)/YBCO/LAO结构[28], Au/Ti–HfO2-InP/InGaAs结构[37], Pt/LaAlO3/Nb:SrTiO3/Pt结构[38], Pt/TiOx/TiO2/Pt结构[35,59], Ag/MoOx/MoS2/Ag结构[24], Ti/Al2O3/Nb2O5/Ti结构[36], ITO/HfOx/p-Si结构[33], Pt/LSMCO/NSTO(Nb:SrTiO3)结构[34]等. 偏压会使这些器件的电极与介质材料之间或同/不同介质材料层之间发生氧空位迁移. 下面将以HfOx为介质材料的忆容器为例, 简要介绍氧空位迁移对忆容器件的调控机理.
ITO/HfOx/p-Si结构的忆容性质如图3所示[33], 当施加正向偏置电压时, HfOx层的氧离子向ITO电极进行迁移, HfOx层材料介电常数降低, 电容下降; 当偏置电压方向改变时, 氧离子迁移回HfOx层, 电容上升. Pt/HfOx/n-IGZO结构忆容器同理[62], 不同方向的偏压使HfOx层与n-IGZO层发生氧离子迁移, 导致显著忆容现象. 然而, 利用氧空位迁移时氧化物介电常数变化进行调控有一个明显缺点, 施加偏置电压时, HfOx层形成的氧空位产生的电场会吸引氧离子重新组合, 使这类器件重复加压循环后, 保持性与稳定性受到影响.
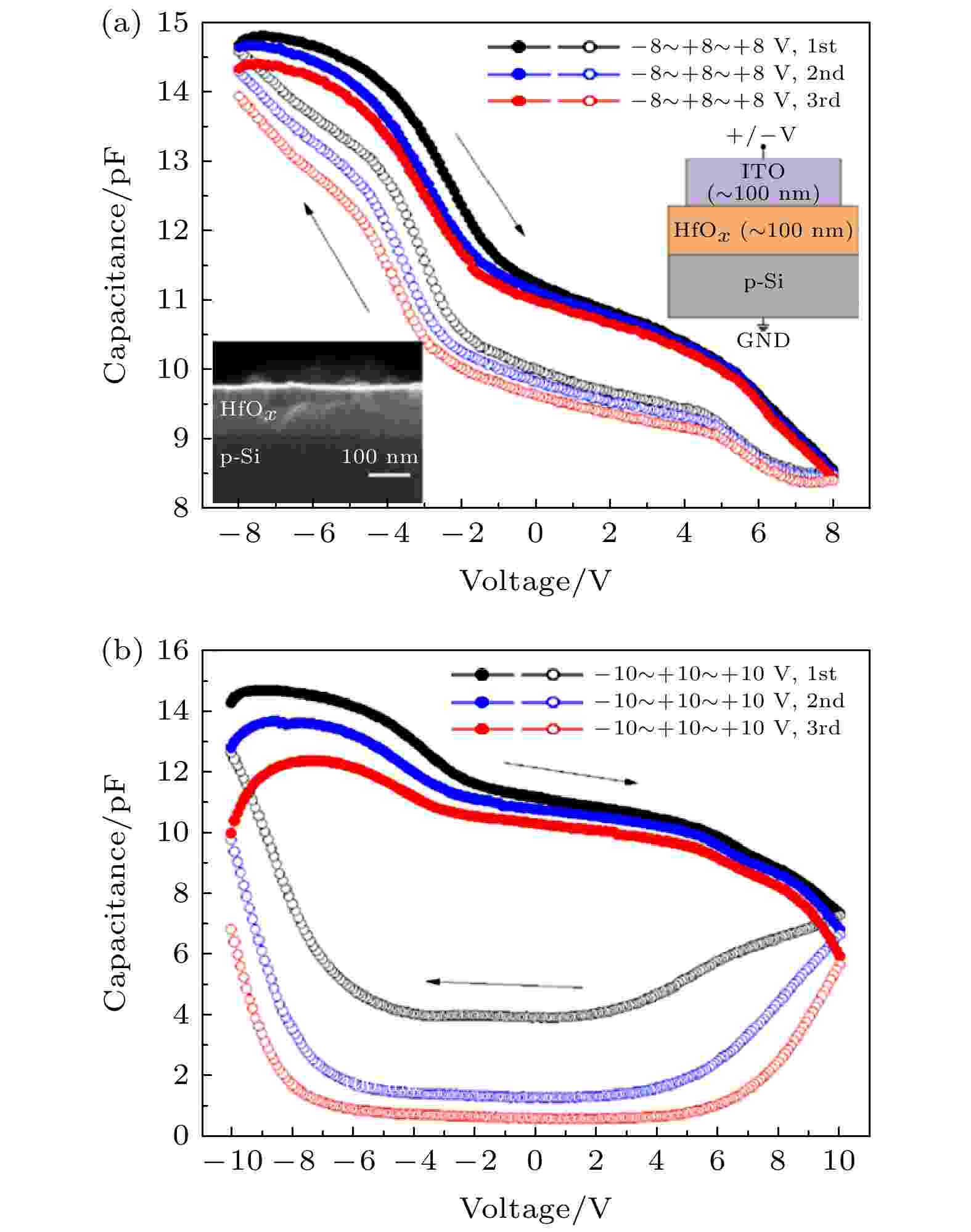图 3 ITO (In-Sn-O)/HfOx/p-Si结构忆容器及C-V曲线[33]
Figure3. Structure of ITO (In-Sn-O)/HfOx/p-S memcapacitor and its C-V curves[33].

图4为Au/Ti/HfOx/InP结构忆容器[37], 与前两种以HfOx为介质材料的忆容原理不同, 器件的HfOx/InP界面处形成了一个电荷积累层, 器件能带图如图4(b)所示, 电容-电压与电阻-电压曲线如图4(c)和图4(d)所示. Pt/Pr0.7Ca0.3MnO3(PCMO)/YBCO/LAO结构的忆容现象源于电荷绝缘层, 忆容性质如图5(a)所示[28], 当加正负脉冲时, 电容容值随脉冲方向不断跳变. 在PCMO中, 导电机理一般被认为是由小极化子组成的载流子, 沿着Mn-O-Mn-O链即Mn的d电子态与O的p电子态杂化运动; 而氧空位会降低甚至破坏这一杂化, 使电阻增大电子堆积, 在PCMO薄膜中形成空间电荷绝缘层. 电容开关效应随频率变化如图5(c)所示, 器件电容呈串联效应, 故当施加负脉冲时, 氧空位在顶部堆积, 使器件顶部形成空间电荷绝缘区, 顶部串联的电阻、电容增大导致器件整体的电容、电阻增大; 当施加正脉冲时, 局部空穴减少, 顶部电阻、电容减小, 器件整体电阻、电容减小.
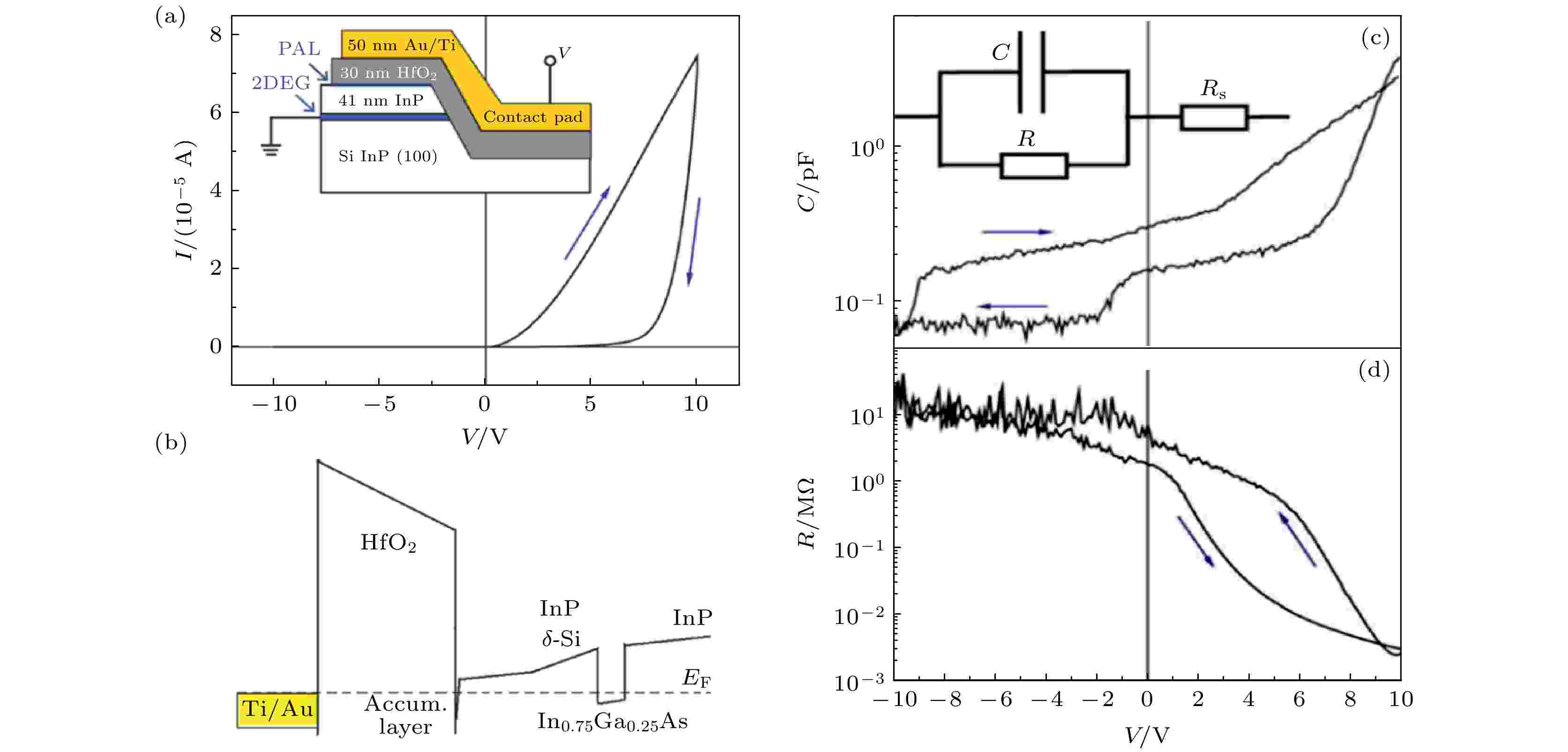图 4 Au/Ti/HfOx/InP结构忆容器[37]　(a) 器件结构及总I-V曲线; (b) 零偏压下器件能带结构; (c) 器件$ {\rm{R}}{\rm{C}} $等效电路及C-V曲线; (d) 器件R-V曲线
Figure4. Structure of Au/Ti/HfOx/InP memcapacitor[37]: (a) device structure and total I-V curves; (b) schematics for the band diagram of the metal HfO2-semiconductordiode at zero bias; (c) equivalent circuit of device and its C-V curves; (d) R-V curves.

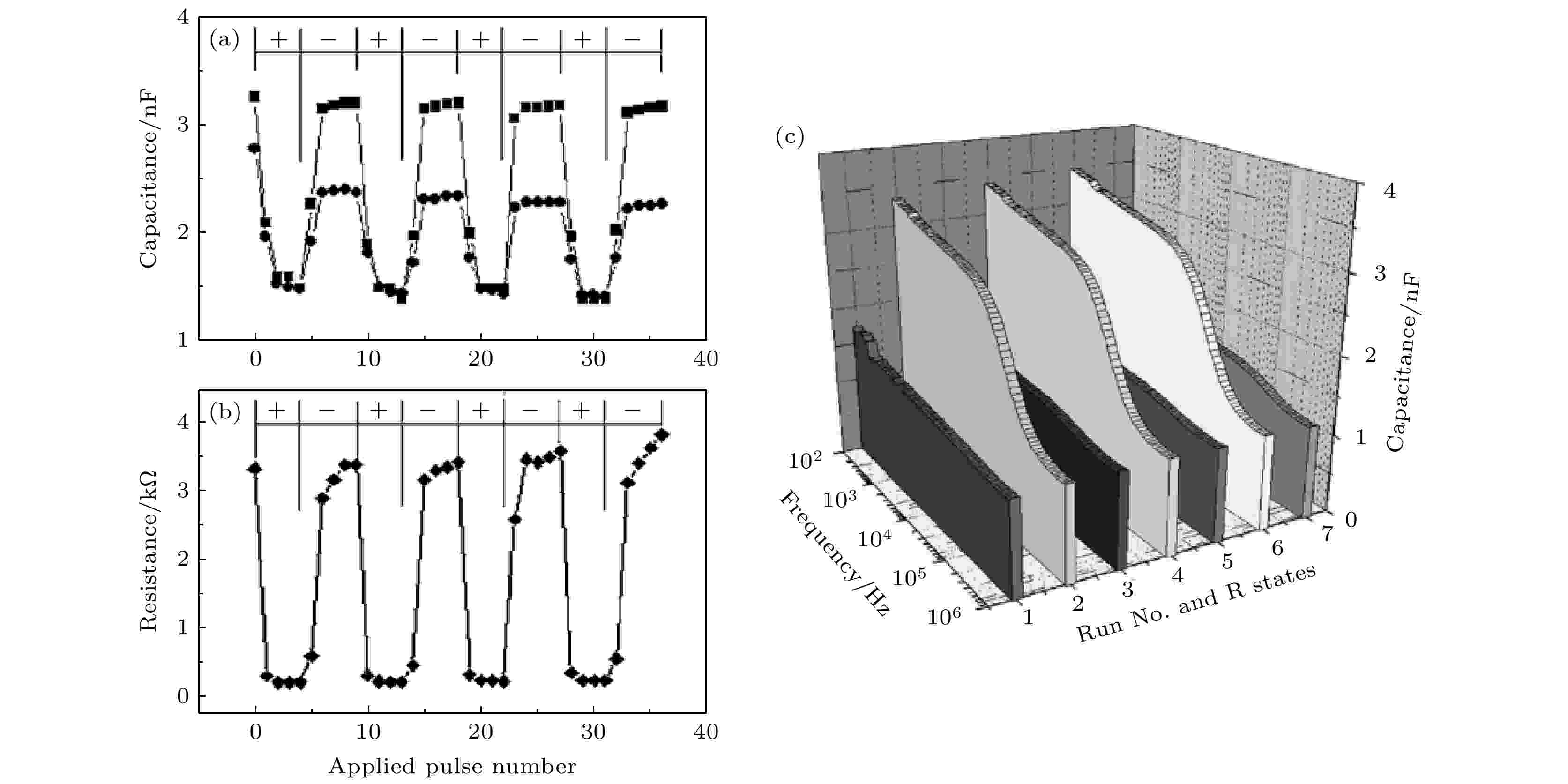图 5 室温下Pt/Pr0.7Ca0.3MnO3(PCMO)/YBCO/LAO结构忆容器性质[28]　(a) 非易失电容随脉冲电压数的变化; (b) 非易失电阻随脉冲电压数的变化; (c) 非易失电容随测试电压频率的变化
Figure5. Nonvolatile capacitance and resistance changes for Au/PCMO/YBCO/LAO structure sample at room temperature[28]: (a) Nonvolatile capacitance changes with applied pulse numbers; (b) nonvolatile resistance changes with applied pulse numbers; (c) nonvolatile capacitance changes with frequency.

界面肖特基势垒也可以对器件电容进行调制. Ag(TE)/MoOx/MoS2/Ag(BE)器件结构如图6(a)所示[24], Ag(TE)与MoOx界面形成肖特基结. 未施加偏压时, Ag器件MoOx层Mo6+(MoO3)与Mo5+(MoOxSy)的分布含量随深度的关系如图6(b)所示, 随着深度增加Mo6+含量不断降低. 当对器件施加偏置电压时, MoOx层发生氧空位迁移, Ag(TE)/MoOx界面附近的Mo6+与Mo5+分布含量改变, 对Ag(TE)与MoOx界面形成的肖特基势垒进行调制, 出现的忆容、忆阻现象如图6(c)所示. 肖特基势垒调制机制也出现在Pt/LaAlO3/Nb:SrTiO3结构[34]、Ti/Al2O3/Nb2O5/Ti结构[36]等忆容器件中, 偏压使与电极形成肖特基结的介质材料层发生氧空位迁移, 调制肖特基势垒, 可出现忆容现象.
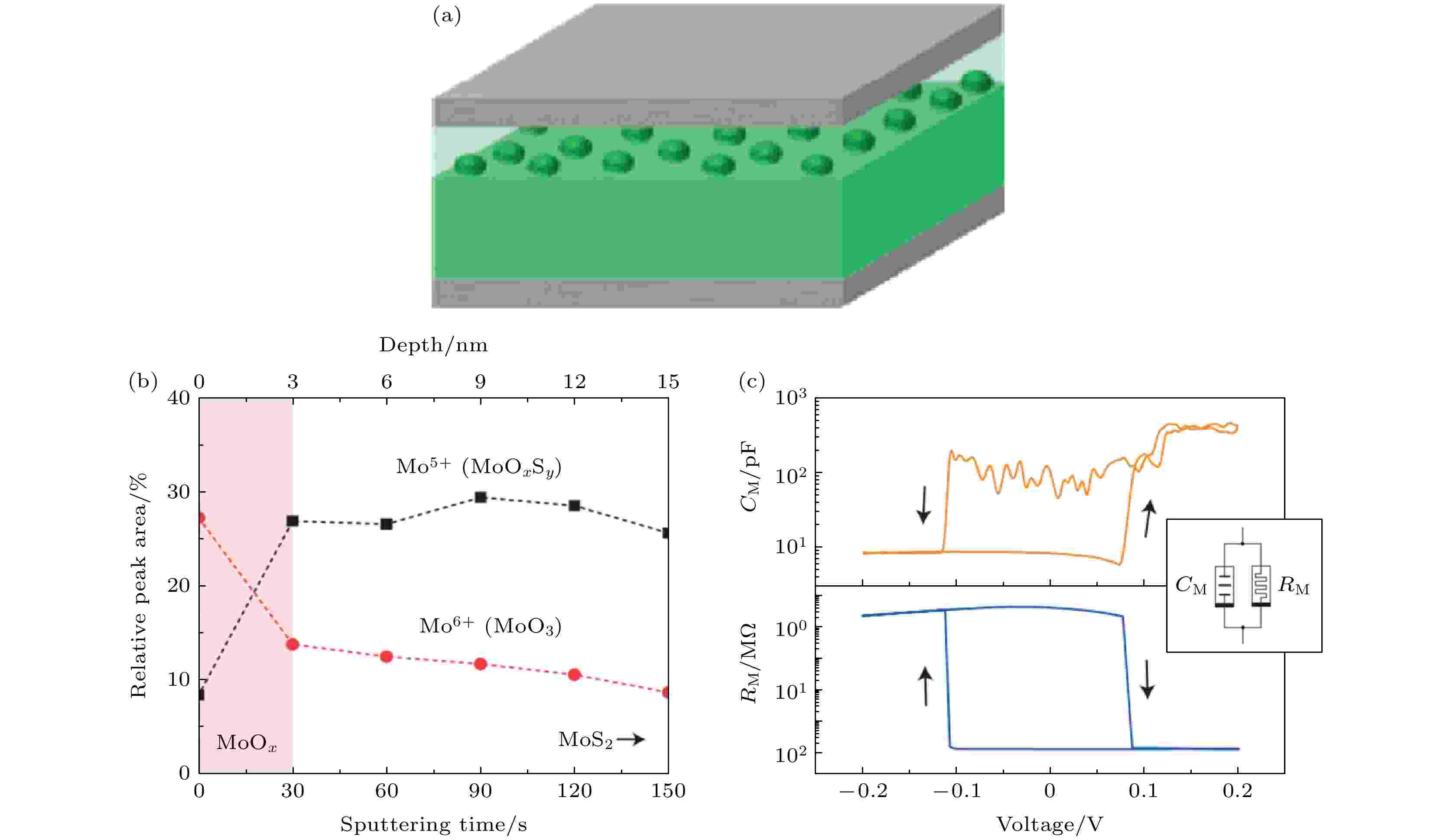图 6 (a) Ag(TE)/MoOx/MoS2/Ag(BE)忆容器件结构[24]; (b)钼氧化态MoOx/MoS2样品在200 ℃持续3 h退火后的XPS剖面; 填充区域代表一个Mo6 +丰富的区域[24]; (c)电阻、电容开关性质[24]
Figure6. [24](a) Ag(TE)/MoOx/MoS2/Ag(BE) structure memcapacitor[24]; (b) Molybdenum oxidation-state XPS profile of the MoOx/MoS2 sample annealed at 200 ℃ for 3 h; the filled area represents a Mo6+ -rich region[24]; (c) capacitance and resistance switch characteristics[24].

以上器件有诸多相似特征. 首先, 这些器件的忆容性质都是器件内部发生氧空位迁移导致的, 他们的电容比一般大于10, 这使得可以在计算中代表0与1. 相较来说, 用二维材料MoOx/MoS2基于肖特基势垒调制机理的忆容器件开关电压低, 鲁棒性好; 基于HfOx材料介电常数变化的忆容器高/低电容稳定, 但鲁棒性不好. 另一方面, 目前大部分基于单/复合金属氧化物层的忆容器并非绝缘体, 相对于不超过10 nF的最大电容态, 其器件的电阻过小, 所产生的漏电效应显著, 距理想忆容的数学模型及实际应用还有不小距离.
除了基于氧空位迁移的无机单/复合金属氧化物忆容, 研究人员在含有机聚/络合物层的三明治结构中发现良好的忆容效应. 2009年惠普实验室将MEH-PPV(2-methoxy-5-(2'-ethylhexyloxy)-p-phenylene vinylene)有机聚合物层加入含RbAg4I5离子导体层的Al/Ti/RbAg4I5/MEH-PPV/SiO2/p-Si/Al结构中, 如图7(a)所示[26]. 无偏压时, Ag+离子扩散到聚合物层, I–离子不显著扩散; 当施加负偏压时, 离子导体层的I–离子向聚合物层逐渐扩散并形成${\rm{I}}_3^-$离子团, ${\rm{I}}_3^- $离子团与Ag+离子形成离子偶极子固定在聚合物层, 使有MEH-PPV层介电常数增大; 当去除偏压时, Ag+由于受I–离子在聚合物中的电场的吸引, 介电常数基本保持不变; 当施加正偏置电压到一定值时, I–离子漂移回离子导体层, MEH-PPV层介电常数降低. 器件的电容一定程度上取决于离子迁移的程度, 使得器件的保持性受外界条件影响较大; 同时离子迁移对MEH-PPV层的破坏在一定程度上会影响器件鲁棒性. 2019年, 苏州大学研究团队在ITO/MASnBr3 (MA = methylammonium)/Au结构器件中发现高电容、多电容态的忆容效应, 忆容器结构、忆容原理与忆容特性如图7(b)、图7(c)、图7(d)所示, 该器件的忆容效应被认为来自于介质层中Br–离子迁移触发的p-i-n结电容调制[61]. 同年, 苏州大学王穗东课题组[60]提出Cu/并五苯(pentacene) /聚苯乙烯(polystyrene) (PS)/SiO2/Si结构器件, 如图7(e)所示. 在高的负偏压下, Cu电极很难将电子注入并五苯层, 并五苯层表现为空穴耗尽的介电层, Cmin反映为并五苯层、PS层和SiO2介电层的总串联电容; 高正偏置的情况下, 并五苯层易被空穴注入, 表现为空穴累加, 使得Cmax仅反映PS层和SiO2介电层的总串联电容.
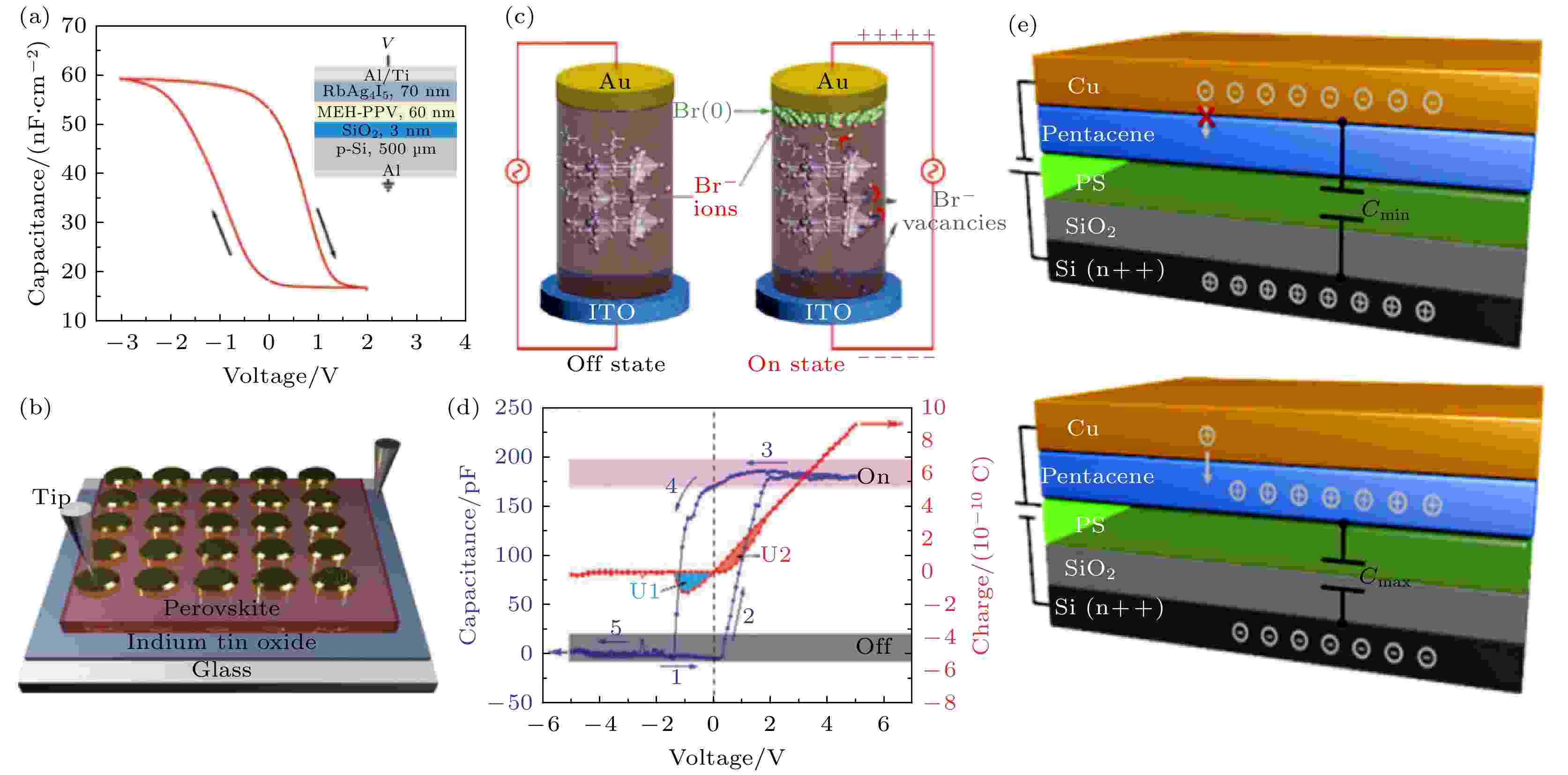图 7 (a)Al/Ti/RbAg4I5 /MEH-PPV/SiO2 /p-Si/Al忆容器结构及其特性曲线[26]; (b) ITO/MASnBr3/Au结构图[61]; (c) ITO/MASnBr3/Au原理图[61]; (d) ITO/MASnBr3/Au结构的忆容特性(1 MHz下的C-V与Q-V特性)[61]; (e) 硅底电极保持接地的有机薄膜记忆电容的器件结构和正负偏压下的电荷积累方案[60]
Figure7. (a) A memory capacitor with an Al/Ti/RbAg4I5 /MEH-PPV/SiO2 /p-Si/Al structure (inset) and its characteristic curve[26]; (b) schematic diagram of the ITO/MASnBr3/Au structure[61]; (c) mechanism of the ITO/MASnBr3/Au structure[61]; (d) memcapacitive characteristics of the ITO/MASnBr3/Au device(C-V hysteresis and Q-V loops detected at 1 MHz); (e) device structure and charge accumulation scheme under negative (top) and positive (bottom) biases of an organic thin film memcapacitor, where the Si bottom electrode is kept grounded[60].

2020年南京大学与聊城大学团队用Al/copolymer/ITO结构忆容器实现short\long-term plasticity (SLTP), paired pulse facilitation (PPF)等神经突触功能, 且开关电压仅0.5 V, 如图8所示[27]. 器件电容的改变主要源于共聚物膜的极化特性, 极化与去极化分别对应着器件的高容态与低容态, 极化与去极化的过程需要时间, 故会有电容的脉冲渐变性质. 同年, 新加坡国立大学研究团队在nature nanotechnology期刊上报导含金属有机络合物层的Au(flat)/[Ru(L)2](PF6)2/Au nanodiscs/ ITO/YSZ结构器件出现忆容、忆阻开关效应, 如图9所示[25]. 文献认为, 外加电场会诱导材料发生电荷歧化, 使材料中电子的对称性破缺, 进而出现忆容、忆阻开关效应. 相比之前提出的有机忆容器件, 该器件将有机层厚度限制在纳米级的同时, 还具有高度的可复制性和鲁棒性, 为忆容器、忆阻器的构建提供了一种新思路.
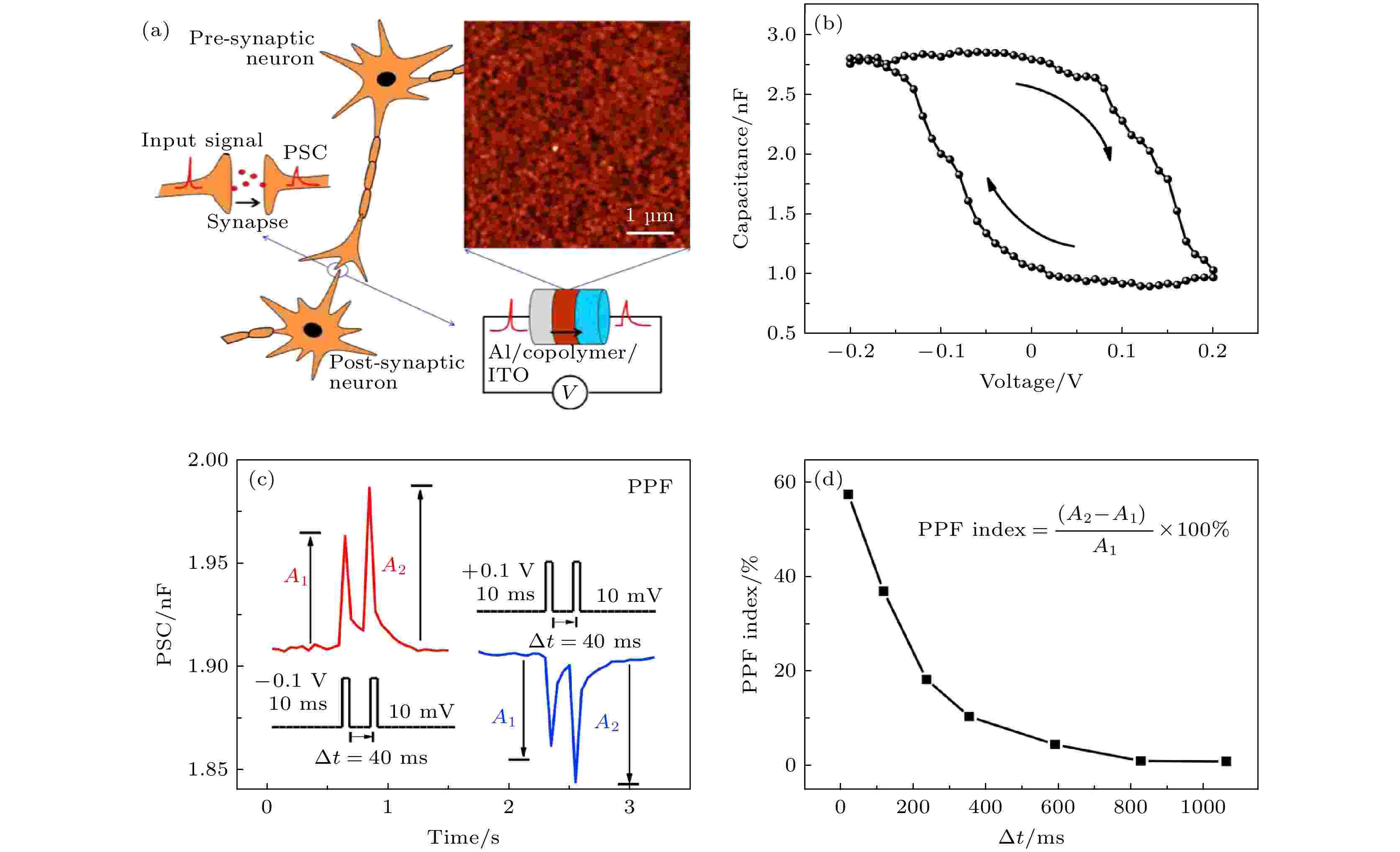图 8 基于记忆电容的人工突触短期塑性模拟[27]　(a) 生物突触和Al/共聚物/ITO人工突触装置信号传输示意图, 共聚物薄膜的AFM图像; (b) C-V曲线; (c) 器件的PPF行为, A1和A2分别代表第一个和第二个突触前突起的PSC, 红色和蓝色曲线分别代表正、负电压下的兴奋性PSC和抑制性PSC; (d) PPF指数被绘制成时间间隔的函数
Figure8. Short-term plasticity emulated in artificial synapse based on memory capacitance[27]: (a) Schematic illustrations of the signal transmission in biological synapse and the Al/copolymer/ITO artificial synaptic device. AFM image of copolymer film; (b) the C-V curves; (c) PPF behaviors of the device. A1 and A2 represent the PSC of the first and second presynaptic spike, respectively. The red and blue curves represent the excitatory and inhibitory PSC under negative and positive voltage, respectively. The inset shows schematic of pulse application; (d)PPF index plotted as a function of the time interval.

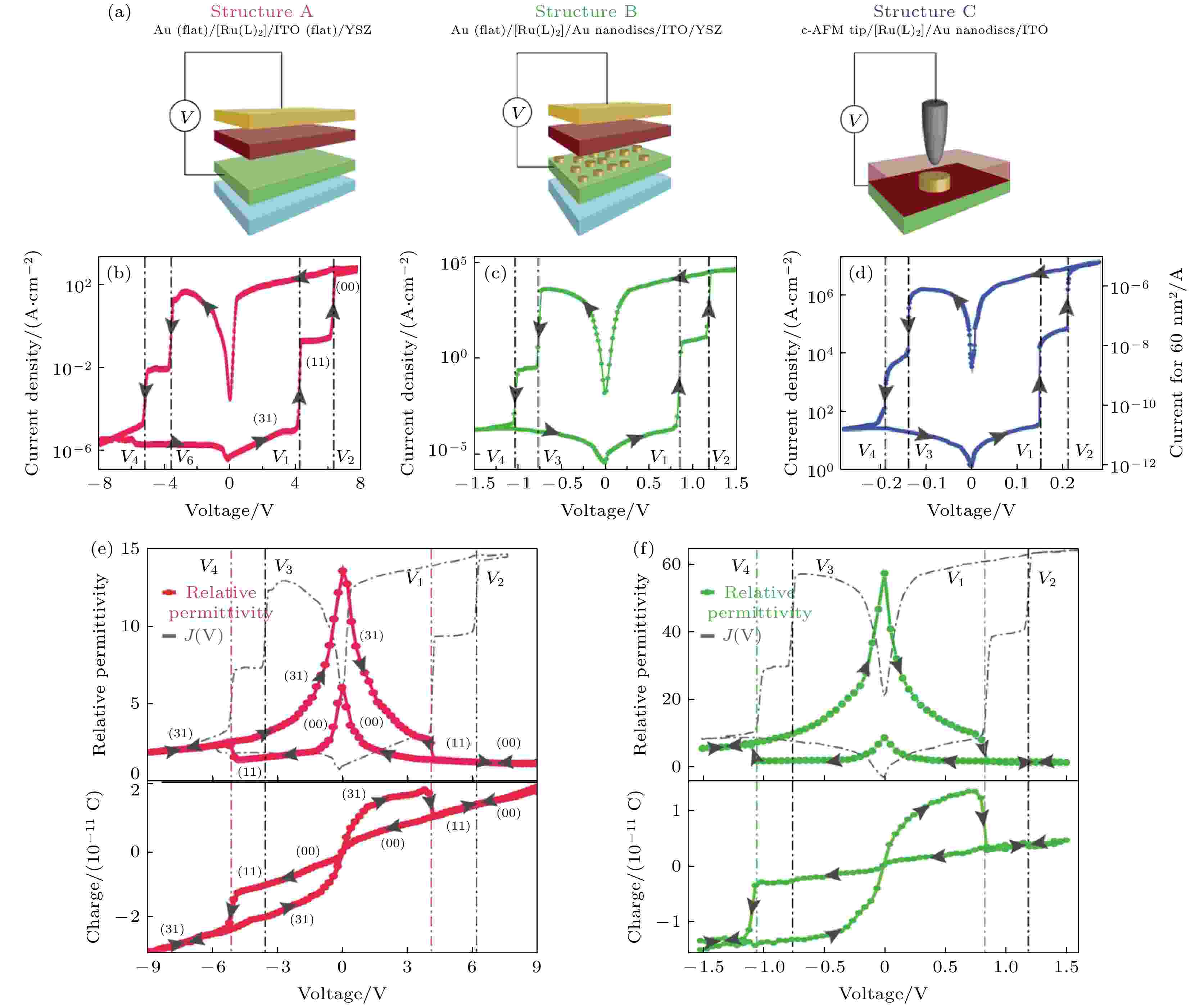图 9 带[Ru(L)2](PF6)2层器件的测试结构及电学特性[25]　(a) 3种结构的示意图; (b)—(d) A(b), B (c)和C (d)结构电流密度对电压J(V)的特性; (e)—(f) 顶部面板显示了结构A(e)和B(f)的相对介电常数与电压的特性, 并覆盖了相应结构的J(V)曲线; 底部的面板显示了结构A(e)和B(f)对应的电荷和电压曲线
Figure9. Test structures and electrical characterizations of devices with [Ru(L)2](PF6)[25]: (a) Schematic illustration of the three structures; (b)–(d) the current density versus voltage J(V) characteristics of structures A(b), B(c) and C(d); (e)–(f) the top panels show the relative permittivity versus voltage characteristics of structures A(e) and B(f), overlaid with the J(V) curves of the corresponding structures. The bottom panels show the corresponding charge versus voltage profiles for structures A(e) and B(f).

有机聚合物相对较大的电阻率, 能有效地减缓忆容器中电荷的泄漏速度, 使器件具备应用于人工神经网络的基础, 但如何进一步减小器件面积、提高器件电容变化速度, 是需要进一步解决的问题.
还有一些关于微型忆容器结构的设想, 比如Martinez-Rincon等[29]于2010年提出, 在平板电容器内插入多层金属和绝缘材料层, 通过金属板间电子隧穿实现忆容效应. 结构如图10所示, 插入的金属板之间距离非常短, 与电容外部电极板距离较远. 该结构使得内部金属板与电极板之间不会传递电荷, 而内部金属板间由于距离非常小, 电极板的偏压使金属板间发生电子隧穿, 电荷在金属板间转移, 影响整体等效的介电常数, 进而出现忆容效应.
图 10 电子隧穿忆容模型[29]
Figure10. Scheme of an electron tunneling memcapacitor[29].

2
2.2.几何效应忆容
-->

2.2.几何效应忆容

与基于整体等效介电常数变化的忆容不同, 几何效应忆容通过改变器件的几何结构以达到改变电容值的目的, 目前主要有基于微/纳机电(MEMS/NEMS)系统的忆容[31]与基于生物模拟系统的忆容[30]. 其忆容特性源于微纳尺度下系统机械和电气性能的相互作用.
图11(a)和图11(b)是由MEMS技术搭建的忆容系统[31]与相应电压电容曲线. 该系统电容的改变来源于外加电压导致的极板间距离变动. 与之相似的, 图11(c)为提出的理想弹性电极忆容, 上极板由弹簧悬挂, 电压改变极板上电荷进而改变受力使上下极板间距离变动, 达到电压控制电容的目的. 这样的忆容系统也可由弹性薄膜作为电极实现[57,63], 只用将之前的弹簧与上极板用弹性薄膜代替.
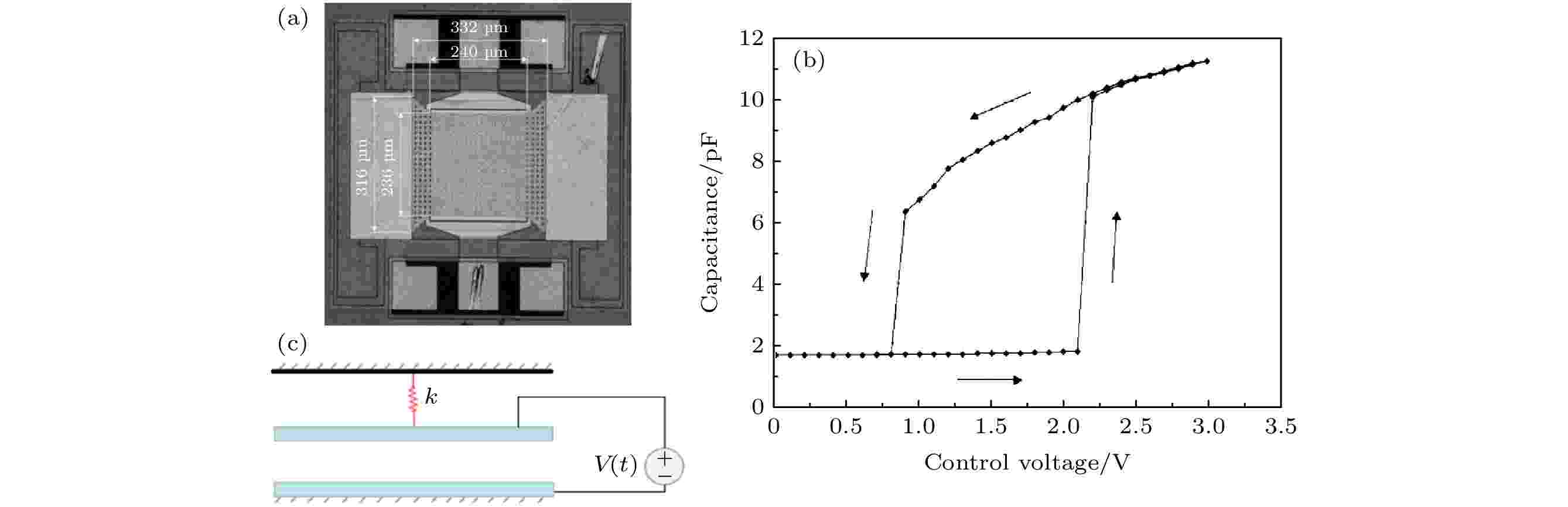图 11 (a) 双状态MEM忆容[31]; (b) 忆容的电容-电压曲线[31]; (c) 弹性电极忆容
Figure11. (a) Photograph of a two-state MEM capacitor[31]; (b) measured capacitance as a function of voltage of the two-state capacitor[31]; (c) elastic poles memcapacitor.

图12展示的BMC(biomolecular memcapacitor)是一个由仿生膜组装而成的忆容器[30]. 在有机溶剂中, 磷脂单分子层膜包裹的两个油滴在接触处形成椭圆形磷脂双分子层容性界面膜, 构成器件. 器件忆容方程可表达为
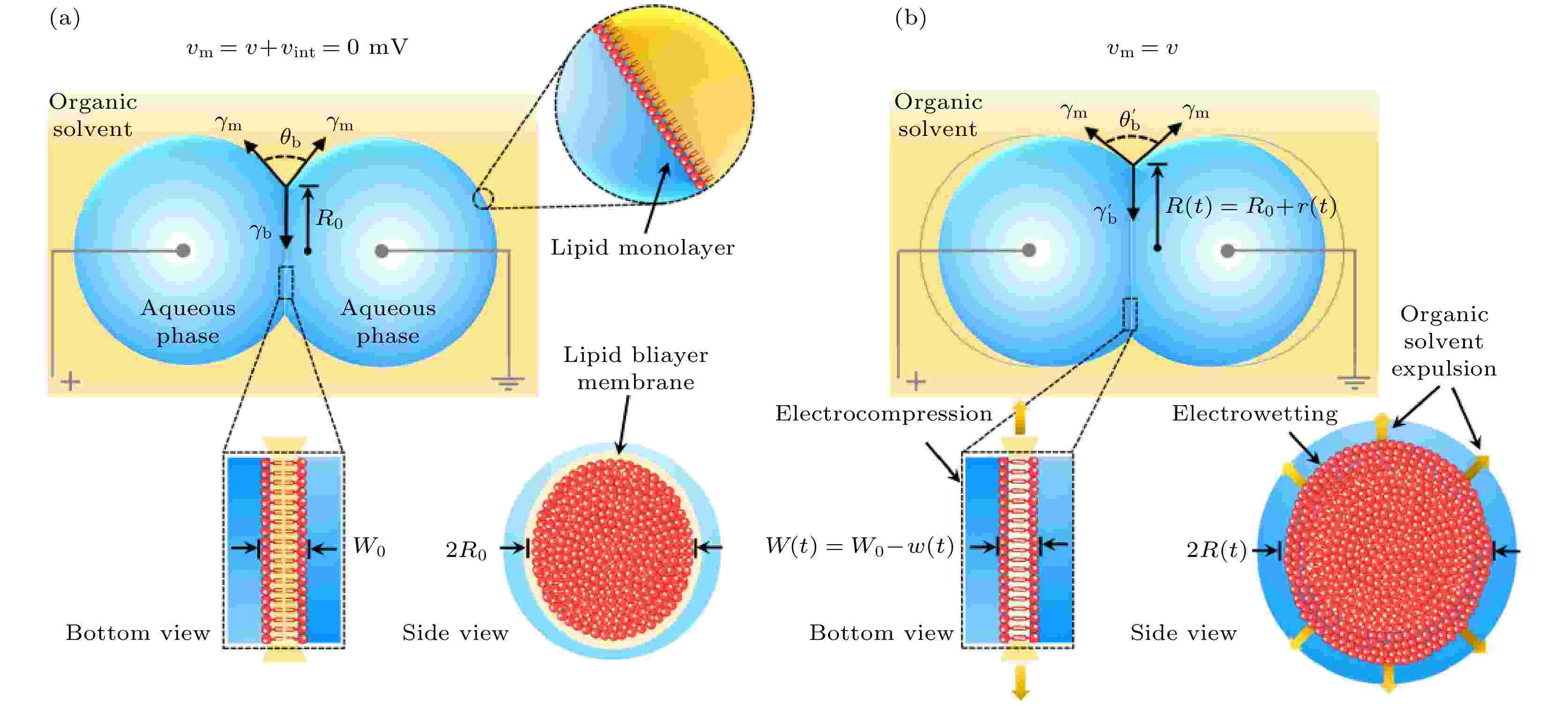图 12 生物忆容器仿生膜组装与电行为[30]　(a) 一种模拟生物膜结构的电容平面脂质双分子层, 在脂质包被的微滴之间接触并排除多余油脂后自发形成; (b) 由静膜电压v(t)引起的几何变化示意图
Figure12. Biomimetic membrane assembly and electromechanical behaviours[30]: (a) A capacitive planar lipid bilayer that mimics the structure of a biological membrane forms spontaneously upon contact between lipid-coated droplets and exclusion of excess oil; (b) a schematic describing the geometrical changes caused by a net membrane voltage, v(t).

$ Q=C(W,R)V{,} $
其中, Q为电容上电荷, W为器件磷脂双分子层容性界面膜厚度, R为膜半径. 其带曲率平行板电容可表达为
$ C=\frac{\varepsilon {\varepsilon }_{0}\left(a{\rm{\pi }}R\right(t{)}^{2})}{W\left(t\right)}{,} $
其中, a为平面椭圆度. 当器件两端施加偏置电压时, 离子在膜两端迅速积累, 离子积累产生的张力使得界面膜排出或吸收膜间夹的葵烷分子, 使得界面膜的形状及双分子层疏水层厚度改变, 动力学方程为
$ \frac{{{\rm{d}}R\left( t \right)}}{{{\rm{d}}t}} = \frac{1}{{{\xi _{{\rm{ew}}}}}}\left( {\frac{{a\varepsilon {\varepsilon _0}}}{{2W\left( t \right)}}v{{\left( t \right)}^2} - {k_{{\rm{ew}}}}(R(t) - {R_0})} \right), $
$ \frac{{{\rm{d}}W\left( t \right)}}{{{\rm{d}}t}}=\frac{1}{{{\xi _{{\rm{ec}}}}}}\left({ - \frac{{a\varepsilon {\varepsilon _0}\pi R{{(t)}^2}}}{{2W\left(t \right)}}v{{(t)}^2}+{k_{{\rm{ec}}}}({W_0}-W(t))}\right), $
其中, ξ与k为有效阻尼与刚度, v为外加偏压. 器件有效电压频率在10 Hz内, 该频率下该器件电容的相对变化通常160%到200%.
目前, 相较于整体等效介电常数变化的忆容, 改变器件几何结构实现的忆容在电容开关比、电容大小、响应速度等方面不如前者. 由于需要改变器件几何结构, 电压频率也有所限制, 但基于几何结构变化的忆容电极之间可以做到近乎绝缘, 无泄漏电流问题.
2
2.3.多器件组合忆容
-->

2.3.多器件组合忆容

伪忆容结构在2012年首次被提出[15], 其模型经过不断完善[45], 2018年被实物实现. 伪忆容实物与等效电路及忆容性质如图13所示[20], 由Pt/ Ag/SiOx:Ag/Ag/Pt结构的忆阻器与Pt/Ta2O5/ TaOx/Pt结构电容器串联构成. 忆阻器的寄生电容是小电容, 与忆阻器串联的电容是大电容, 当施加高电压, 忆阻器由高阻态转为低阻态, 此时忆阻的寄生电容效应可忽略, 于是有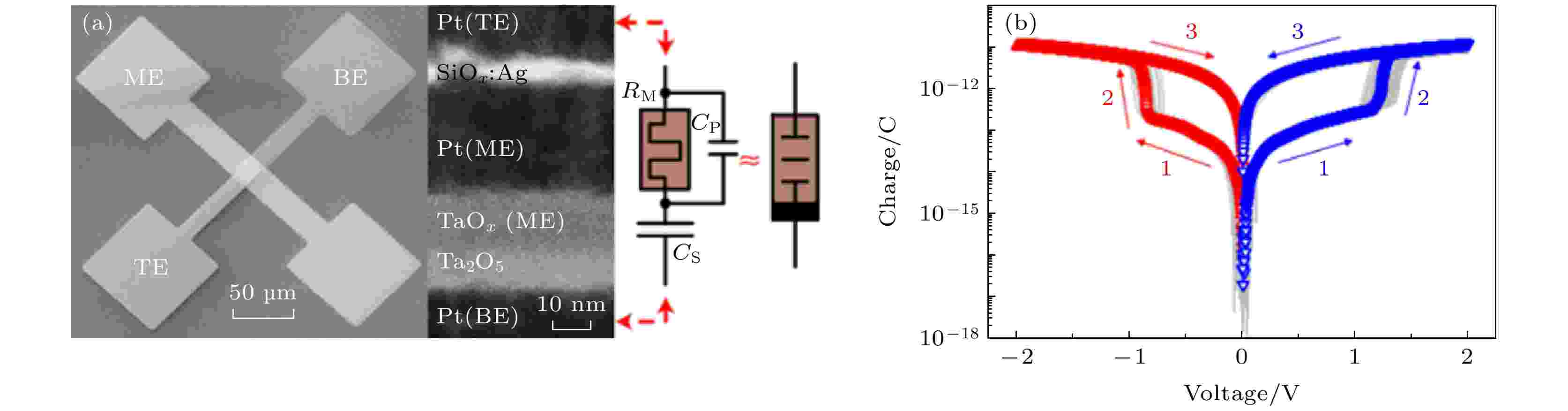
图 13 伪忆容[20]　(a) 伪忆容的扫描电子显微图的平面视图和透射电子显微图的截面图; (b)集成伪忆容的电荷-电压关系
Figure13. Dynamic pseudo-memcapacitor(DPM)[20]: (a) a scanning electron micrograph of the plan view of the integrated DPM, and a transmission electron micrograph of the cross-section; (b) charge-voltage relationship of the integrated DPM.

$ {C}_{{\rm{z}}}={C}_{\rm{S}}{,} $
其中:
当施加反向电压时, 忆阻转为高阻态, Rm相当于断路, 忆阻寄生电容显现与外加电容串联有
$ {C}_{\rm{Z}}=\frac{{C}_{\rm{P}}{C}_{\rm{S}}}{{C}_{\rm{P}}+{C}_{\rm{S}}}{,} $
由$ {C}_{\rm{P}}\ll {C}_{\rm{S}} $得
$ {C}_{\rm{Z}}\approx {C}_{\rm{P}}{. } $
故通过控制忆阻器两端的电压可以控制器件的总忆容. 与基于其他的单一忆容相比, 伪忆容能实现理想的电容切换, 可直接用于忆容神经网络的构建; 但相应的, 伪忆容的容值切换源于忆阻的电阻切换, 故开关能耗相比理想忆容器件更大; 由于需要串联一个很大的电容, 大电容的充电放电时间与忆阻的高低电阻切换速度也在一定程度上限制伪忆容的应用范围.
用更多器件组合而成的忆容如图14所示, 图14(a)中是一个基于米勒效应的忆容[49], 我们可以很容易的得到
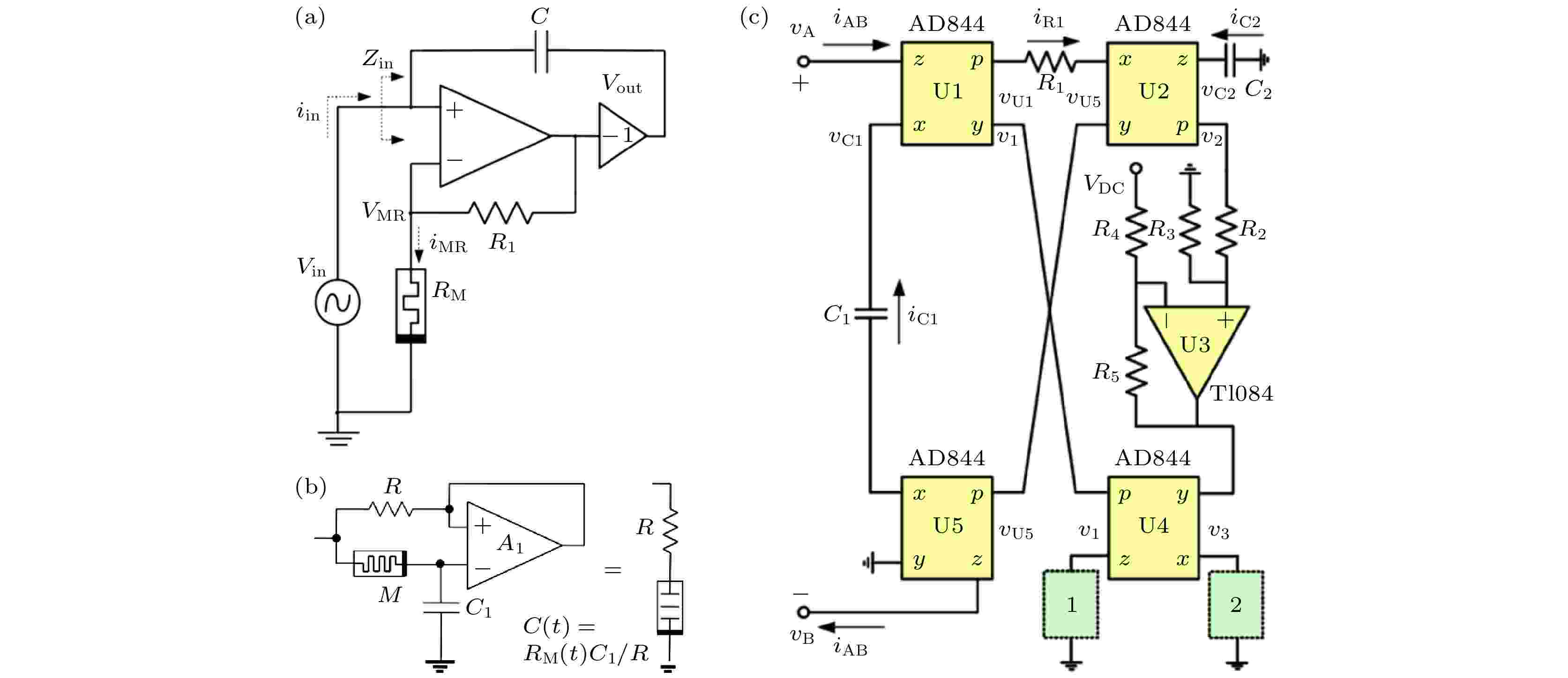图 14 忆容仿真电路原理图　(a) 基于密勒效应的忆容仿真电路[49]; (b) 忆容-电阻串联电路[47]; (c) 提出的多功能电路[51]
Figure14. Schematic of the memcapacitor emulator: (a) Schematic of the memcapacitor emulator based on the Miller effect[49]; (b) memcapacitor-resistor series circuit[47]; (c) the proposed mutator circuit[51].

$ {{C}_{\rm{M}}}=C\cdot \left( 2+{}{{{R}_{1}}}/{{{R}_{\rm{M}}}}\; \right), $
忆阻RM的阻值随输入电压变化, 故输入电容随输入电压变化.
图14(b)是一个等效的电阻串联忆容电路[47], 得输入阻抗表达式为
$Z=\frac{{{R}_{1}}{{R}_{\rm{M}}}}{{{R}_{1}}+{{R}_{\rm{M}}}}+\frac{1}{{\rm{j}}\omega \left( C\left( 1+ {{{R}_{1}}}/{{{R}_{\rm{M}}}}\; \right) \right)}.$
由(15)式得串联忆容为
${{C}_{\rm{M}}}=C\cdot \left( 1+ {{{R}_{1}}}/{{{R}_{\rm{M}}}}\; \right).$
图14(c)给出一个广义忆系列模型[51], 绿框部分为忆系列元件的通用接口, 可以通过改变接口元件实现忆容-忆阻-忆感的切换. 当1处取电阻, 2处取变容二极管时, 电路输入输出为忆容器, 忆容大小可表示为
$ {C}_{{\rm{A}}{\rm{B}}}=a{{\phi }_{{\rm{A}}{\rm{B}}}}^{2}+\beta {\phi }_{{\rm{A}}{\rm{B}}}+\lambda {. } $
其中: α, β, λ都为电路相关常数; $ {\phi }_{{\rm{A}}{\rm{B}}} $为.
还有很多类似的忆容电路, 但目前为止提出的组合忆容电路都较复杂[40,50,52,53]. 组合器件模拟的忆容, 能很好地模拟忆容的电容变化等特性, 可用于仿真、电路设计等方面[64-66], 但能耗、规模、响应速度等方面不具备参考性.
3.基于忆容的突触及神经元
人们提出的神经元模型有很多, 其中最早提出且影响最大的是1943年心理学家McCulloch和数学家Pitts在分析总结神经元基本特性的基础上提出的MP神经元模型[67], 指出了神经元的形式化数学描述和网络结构方法. MP模型中, 单个神经元结构如图15所示, 神经元的细胞体将树突中突触连接所提供的电荷收集并累加, 直到总电荷达到阈值, 然后神经元沿着轴突发射一个峰值, 由此产生的脉冲传递到通过突触连接的其他神经元, 这些神经元可以根据突触的权重加强或抑制信号.
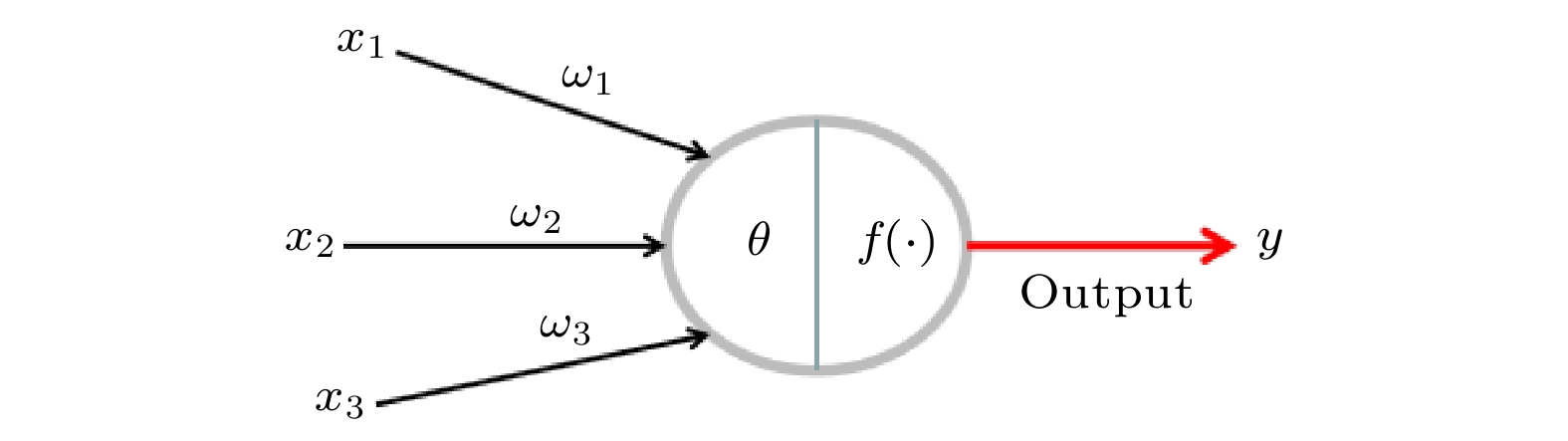图 15 MP神经元模型
Figure15. MP-neuron mode.

数学上描述为
$ y=f\bigg(\sum _{i=1}^{n}{\omega }_{i}{x}_{i}-\theta \bigg), $
其中, y为神经元的信号输出, x为上一个神经元的信号输入, ω为突触的权值, θ为神经元胞体的阈值; 函数f为激活函数, 通常用非线性函数如sigmoid函数, 或线性函数如斜面函数、阈值函数等.
1952年, 人们提出了生理学上更准确的Hodgkin-Huxley神经元模型[68], 涉及K+, Ca2+离子浓度等的超过20个参数的耦合微分方程, 为神经元近似模拟研究提供参考[69]. 后来神经科学研究将重点转移到神经元群体的学习、认知和行为等更高层次的概念上, 由此产生的模型如Hopfield网络、Hebbian学习等, 成为人工神经网络架构和学习规则的基础[70,71]. 目前用于神经形态计算的人工神经网络可分为脉冲神经网络和非脉冲神经网络(卷积神经网络等), 这些网络一般由大量神经元组成, 神经元之间依靠突触连接[19,21,22].
脉冲神经网络与非脉冲神经网络中的突触可以共用, 这些突触包含两个功能—权重存储的功能和根据脉冲触发修改权重的功能. 不同类型网络的神经元功能差别很大, 但结构都可以概括为两部分, 突触信号接收部分与信号加工输出部分. 目前代表性基于忆容构建的神经突触有: 单忆容突触[27]、四忆容桥式突触[16]、电压源\电流源\忆容器混合突触[18]. 代表性神经元结构有: N忆容单MOS管结构神经元(N为大于1的整数)[21]、带二极管脉冲神经元[17]及伪忆容脉冲神经元[20]等. 由于目前实物忆容器件的限制, 规模较大的忆容神经形态计算网络多以仿真形式进行.
2
3.1.基于忆容的人工神经突触
-->

3.1.基于忆容的人工神经突触

阈值电压型忆容器本身可以作为一个突触, 用电容值代表存储的权重, 低于阈值的脉冲电压读取权重, 高于阈值的脉冲电压修改权重, 如上文忆容器件部分的Al/copolymer/ITO结构忆容器[27], 可以作为独立的突触应用于人工神经网络中.
图16所示为基于4个全同忆容器的突触电路[16], 令D为电容的倒数, 有
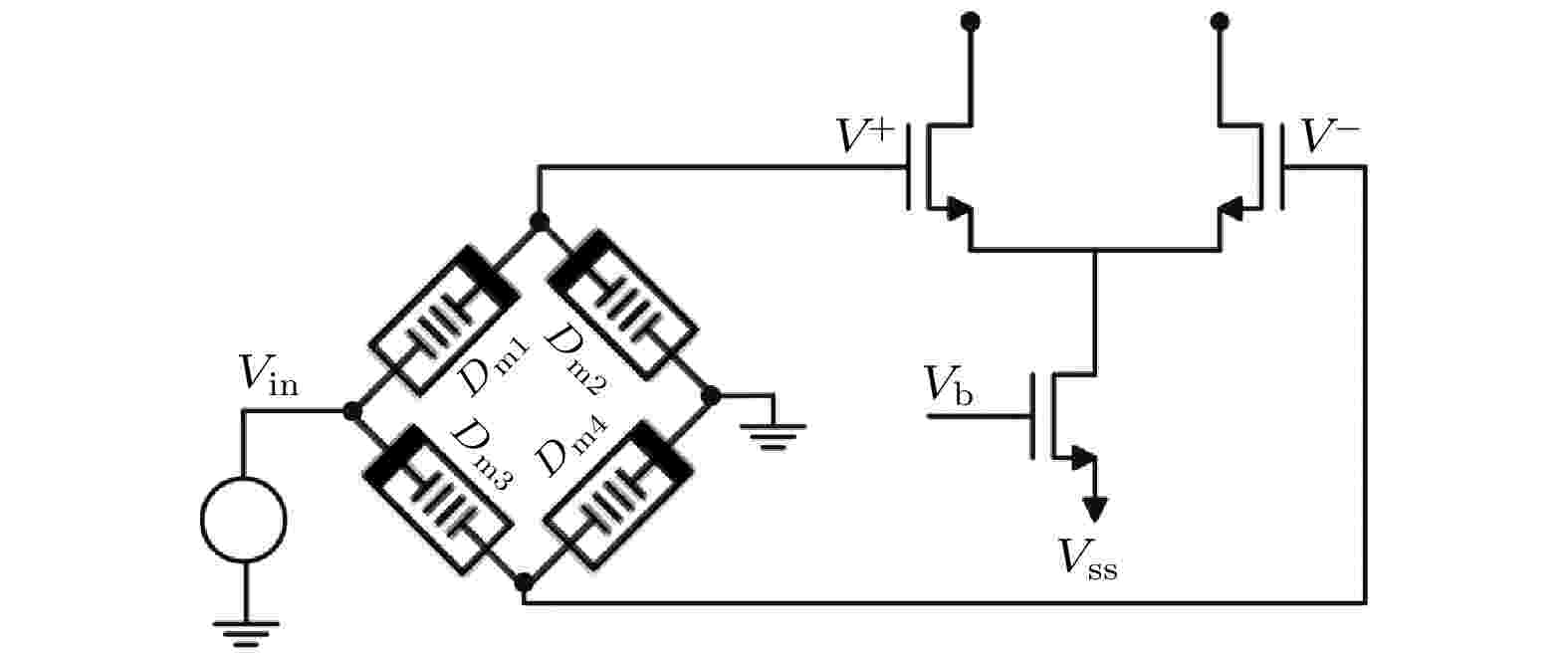图 16 忆容桥式突触电路[16]
Figure16. Memcapacitor bridge synaptic circuit[16].

$ {D}_{a}={D}_{2}={D}_{3},~~{D}_{b}={D}_{1}={D}_{4}{,} $
上下两路总电容相同, 故加压时通过上下两路的电荷总量q相同, 由忆容的性质
$ D=f\left(\int q{\rm{d}}t\right){,} $
得
$ {D}_{\rm{a}}+{D}_{\rm{b}}=c, $
其中, c为一常数. 由基尔霍夫定律知, 输入输出电压
${{V}_{\rm{out}}}=\varPsi {{V}_{\rm{in}}}, $
$\varPsi = {\left( {{D}_{\rm{a}}}-{{D}_{\rm{b}}} \right)}/{\left( {{D}_{\rm{a}}}+{{D}_{\rm{b}}} \right)}\;,$
其中, Ψ为权重, 具有权重存储的目的, 当施加超过阈值的电压脉冲时, Ψ可在一定范围内变化, 可达到权重更新的目的.
2
3.2.基于忆容的脉冲网络神经元
-->

3.2.基于忆容的脉冲网络神经元

如图17(a)所示为带二极管的脉冲神经元结构[17], C1, C2, ···, Cn为忆容突触, 绿色方框内的Nj为神经元的胞体, S为受控开关. 当胞体的输出电压Vout大于设定的阈值时, 开关S闭合, 使胞体内的电容C电压归零, 同时神经元向下一个突触发出一个电压脉冲. 神经元实现的STDP特性如图17(b)所示, 突触不同权重对神经元输出脉冲间隔的调制如图17(c)所示.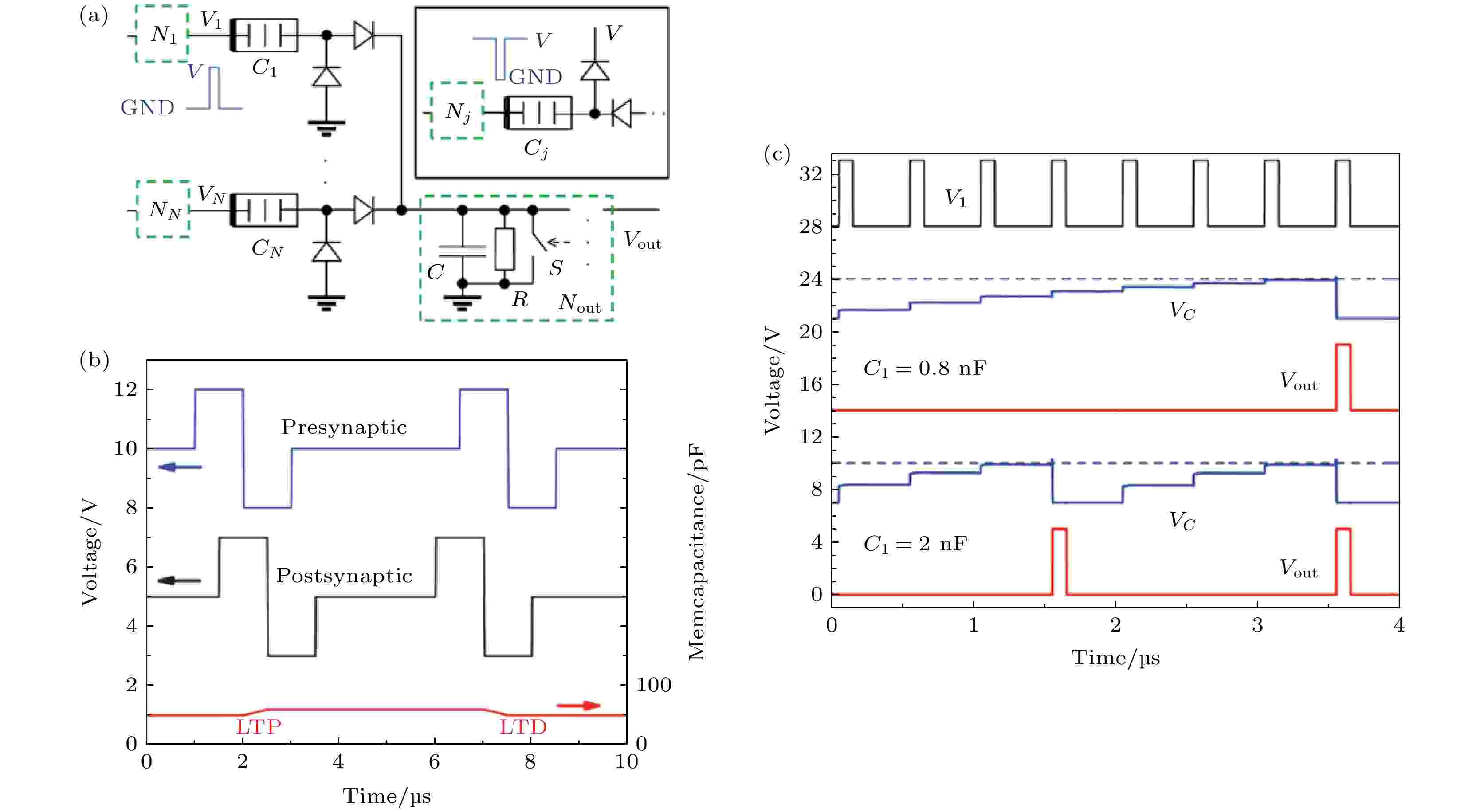
图 17 忆容记忆突触[17]　(a) 集成神经网络中的忆容突触; (b) 忆容突触实现STDP; (c) 单个突触的集成忆容神经元点火仿真
Figure17. Memcapacitive synapses[17] (a) Memcapacitive synapses in integrate-and-fire neural network; (b) STDP with memcapacitive synapses; (c) simulation of integrate-and-fire memcapacitive network with only one spiking neuron.

如图18所示, 为一个伪忆容脉冲神经元的结构与动作过程[20]. 图18(b)为突触动作过程: t1时刻, 当输入端输入电压脉冲时, 伪忆容内部的忆阻进行脉冲积累; t2时刻, 当输入脉冲积分超过阈值时, 伪忆容内部的忆阻开启, 大电容快速充电, 输出电压突增; t3时刻, 之后当输入脉冲电压到的脉冲底电压时, 内部忆阻器由电容作用的反向偏压而关闭, 恢复到初始状态. 输入输出电压脉冲曲线如图18(d)所示, 当输入脉冲数达到一定数量时, 出现输出脉冲.
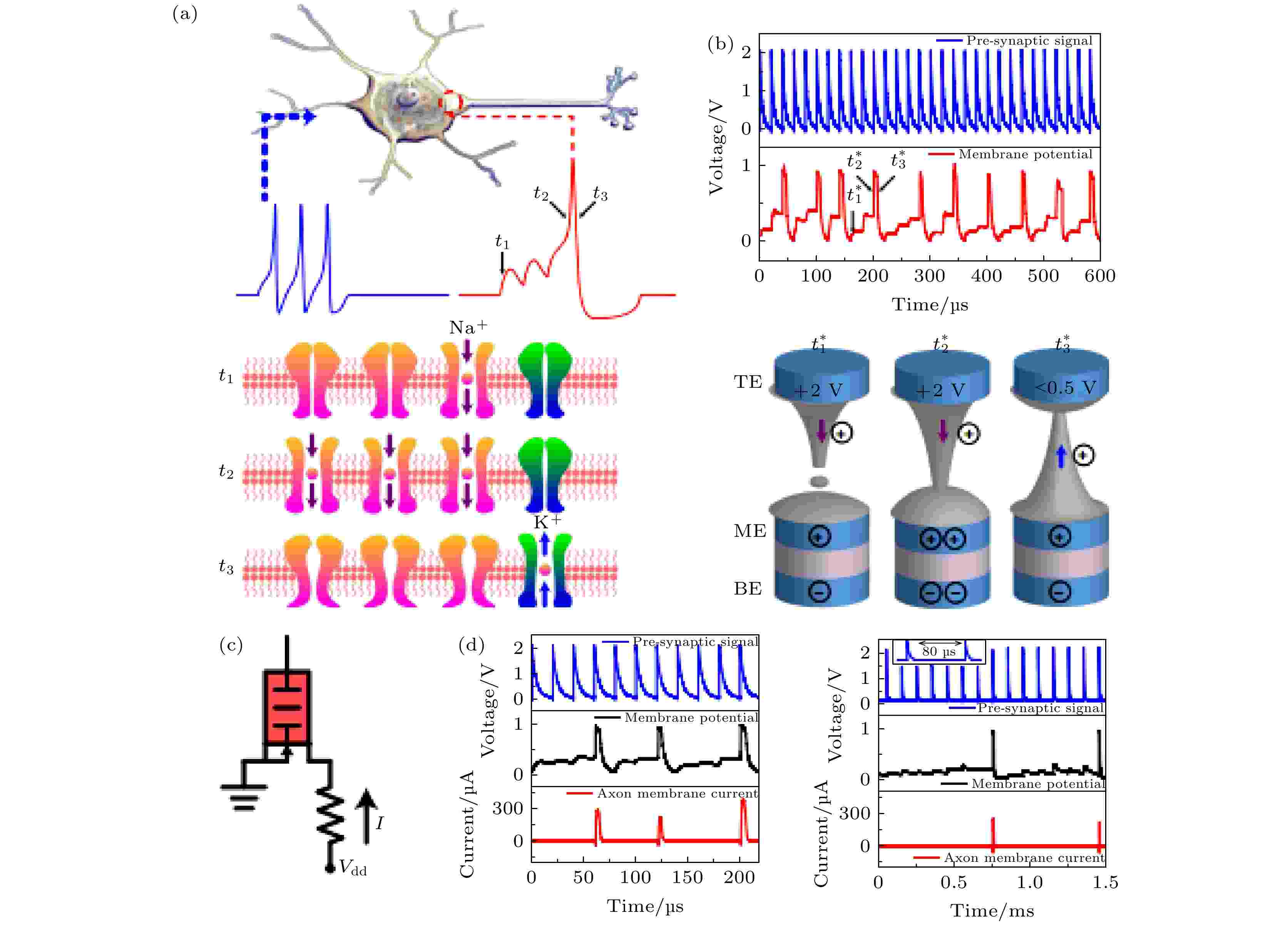图 18 伪忆容突触[20]　(a) 生物神经元接受高频突触后输入后产生动作电位的示意图; (b) 伪忆容的集成和触发过程; (c) 电子神经元晶体管的原理图; (d) 电子神经元-晶体管集成-点火过程的动力学
Figure18. Pseudo-memcapacitor synapse[20]: (a) Schematic representation of a biological neuron generating an action potential after receiving high-frequency post-synaptic inputs; (b) the integrate-and-fire process of a pseudo-memcapacitor synapse; (c) schematic of the synapse-transistor; (d) dynamics of the synapse-transistor integrate-and-fire process.

2
3.3.基于忆容的非脉冲网络神经元
-->

3.3.基于忆容的非脉冲网络神经元

图19为忆容-MOC耦合神经元接收突触信号的部分[21], 由MOS管连接多个忆容突触, 并接收忆容突触的信号. 其中V1, ···, Vm为输入电压信号, C0为MOS管的等效耦合电容, C1,···, Cm为忆容突触的电容值(权重). 使V0 = 0接地, 有输出电压: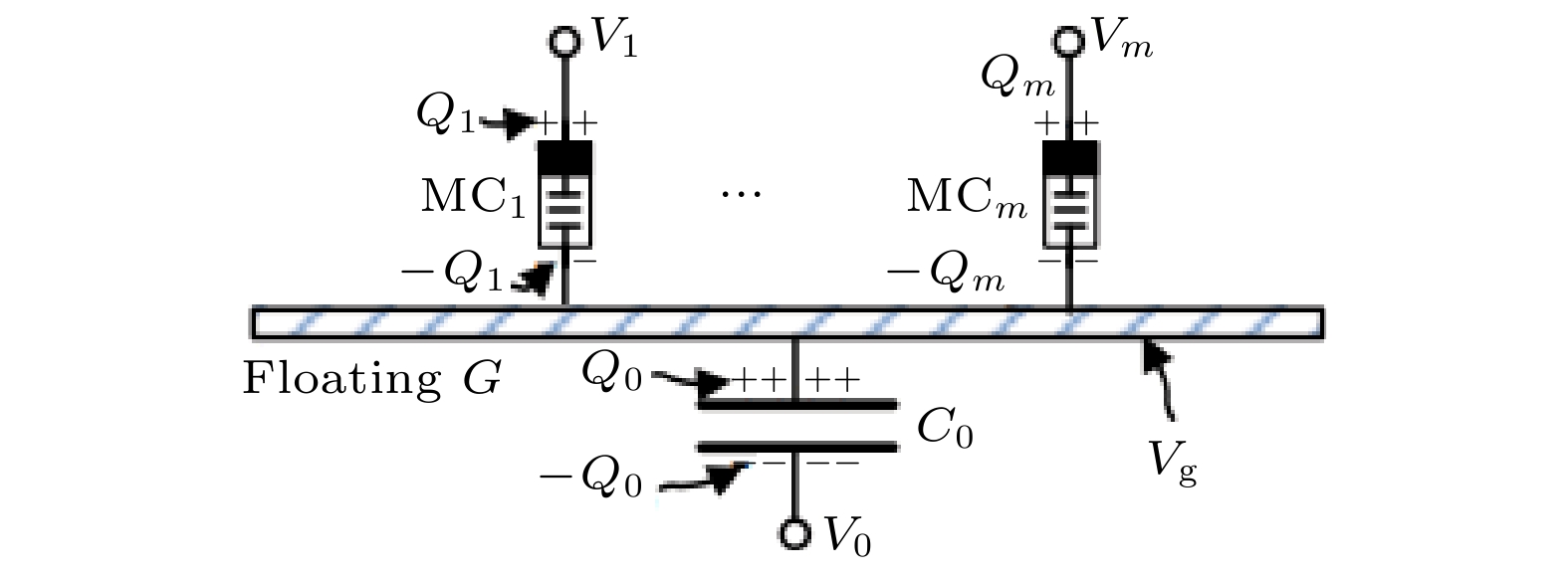
图 19 忆容-MOS耦合神经元胞体[21]
Figure19. Neuron-MOS transistor couples the memcapacitor cells[21].

$ {V_{\rm{g}}} = \sum _{i = 1}^m\frac{{{C_i}}}{{{C_{{\rm{Tot}}}}}} \cdot {V_i}, $
其中
$ {C_{{\rm{Tot}}}} = \sum _{i = 0}^m{C_i}. $
Vg即为接收到的突触信号.
图20(a)为含n个忆容-MOS耦合神经元的网络结构. 图20(b)和图20(d)为忆容-MOC耦合神经元的信号加工输出部分, 功能为将sigmoid函数或线性函数作用到所接收的突触信号上, 并输出给下一个神经元. sigmoid函数电路输出表达式为
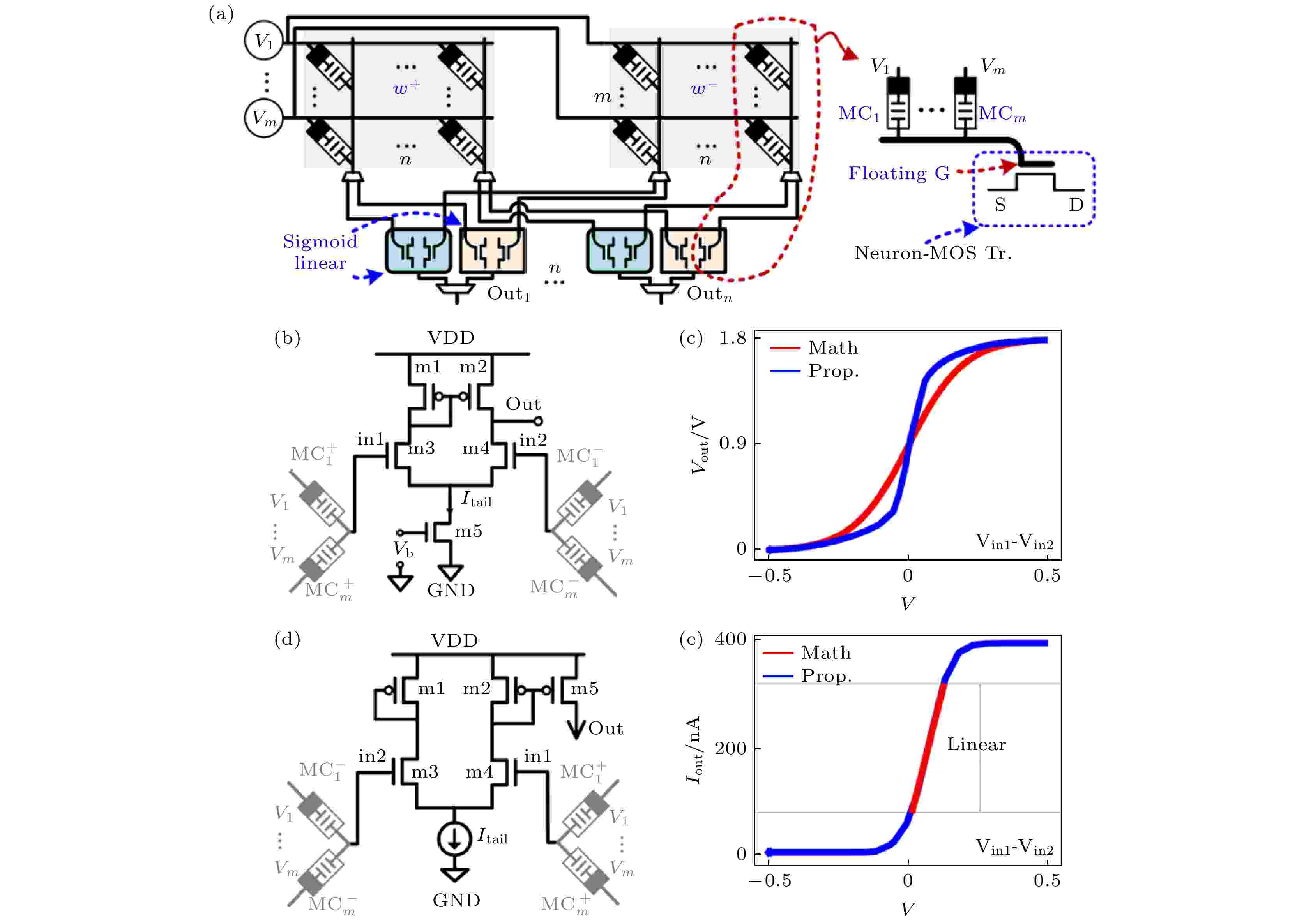图 20 MC-ACU[21]　(a) 全结构电路图; (b) sigmoid神经元电路; (c) 在HSPICE中的仿真曲线(蓝)与理论数学曲线(红)对比; (d) 线性神经元电路; (e)在HSPICE中的仿真曲线(蓝)与理论数学曲线(红)对比
Figure20. MC-ACU[21]: (a) Overall architecture; (b) sigmoid neuron circuit; (c) simulation results in HSPICE (blue) compared with the mathematical sigmoid(red); (d) linear neuron circuit; (e) simulation results in HSPICE (blue) compared with the mathematical linear (red).

$ {V_{{\rm{out}}}} = {V_{{\rm{DD}}}} - {I_{{\rm{Tail}}}} \cdot {a_0} \cdot {r_0} \cdot \dfrac{1}{{1 + {\rm{exp}}\left( {\dfrac{{{V_{{\rm{in}}1}} - {V_{{\rm{in}}2}}}}{{{V_{\rm{T}}}}}} \right)}},$
其中, VDD为图示的电压源电压, Vin1和Vin2分别为in1和in2处的电位. 其他均为一些固定参数, 其与sigmoid函数比较的曲线如图20(c)所示.
图20(d)所示的线性函数电路输出表达式为
$\begin{split}{V_{{\rm{out}}}} =\;& \dfrac{{{a_{\rm{F}}} \cdot {I_{{\rm{Tail}}}}}}{{1 + {\rm{exp}}\left( {\frac{{{V_{{\rm{in}}1}} - {V_{{\rm{in}}2}}}}{{{V_{\rm{T}}}}}} \right)}} \\\approx\;& \frac{{{a_{\rm{F}}} \cdot {I_{{\rm{Tail}}}}}}{2} \cdot \left( {1 + \dfrac{{{V_{{\rm{in}}1}} - {V_{{\rm{in}}2}}}}{{{V_{\rm{T}}}}}} \right). \end{split}$
仿真曲线如图20(e).
4.基于忆容的神经形态计算
McCulloch与Pitts证明, 在神经元相互连接且同步的情况下, 网络能计算任何已知函数[67]. 只需更改神经元的连接方式, 即可构成不同应用下所需的神经网络. 2018年Wang等[20]用伪忆容神经元模拟联想学习—巴普诺夫的狗实验. 2019年Tran等[22]提出用忆容进行储层运算的架构.
Hebbian规则是突触权重调节最重要的细胞机制之一[72], 揭示了突触前后膜相关信号与突触权重变化之间的关系. 图21为用伪忆容网络基于类Hebbian规则实现的联想学习实验[20]. 两个突触前电压脉冲信号分别模拟看到食物和听到铃声, 突触后神经元模拟狗的流涎; 与“食物”突触前神经元连接的突触的初始重量较大, 而与“铃声”突触前神经元连接的突触的初始重量较小. 经过一系列“铃声”与“食物”的联合刺激后, 成功实现只有“铃声”刺激的情况下, 突触后神经元兴奋, 即“狗流涎”.
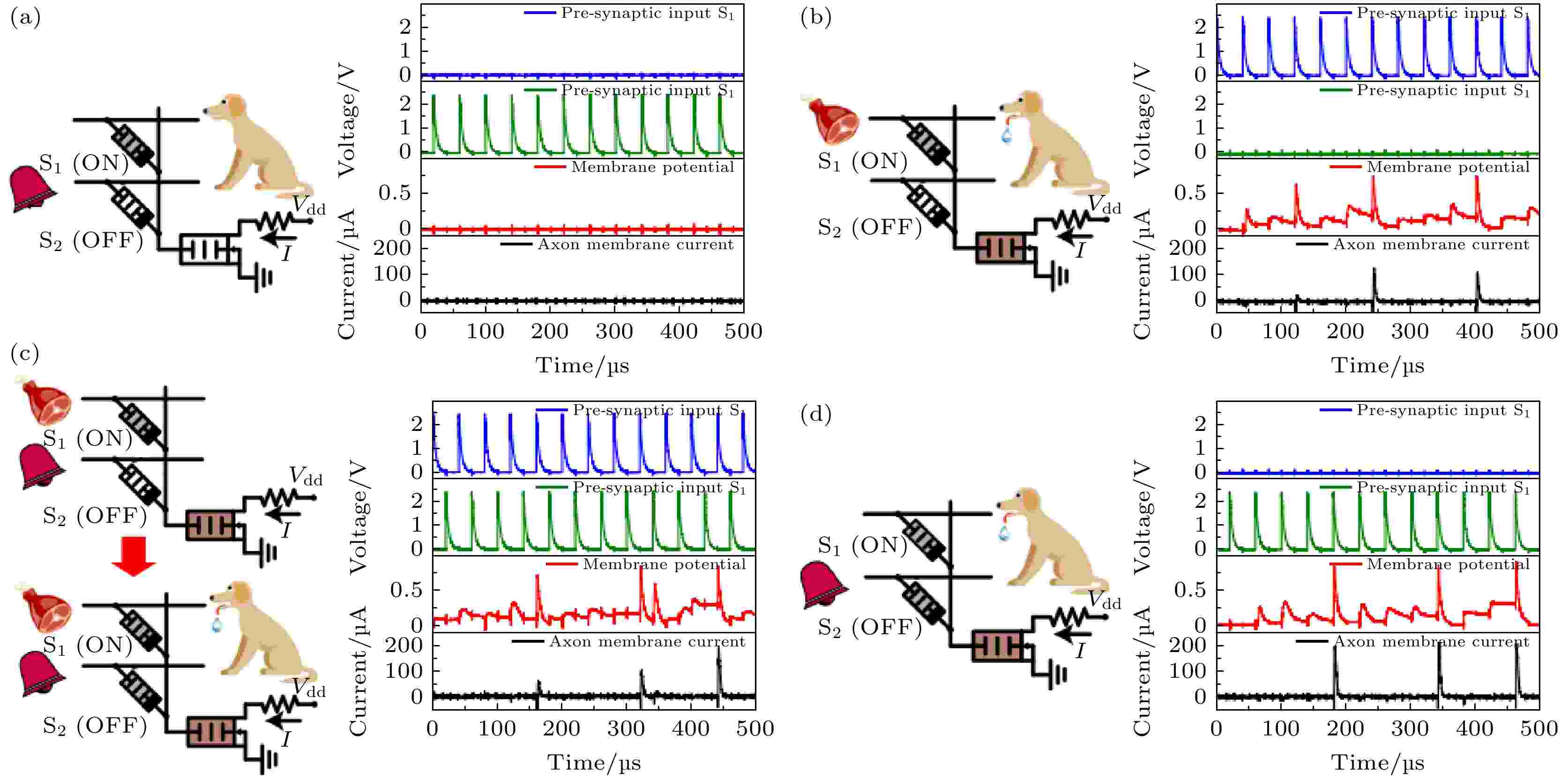图 21 基于电容式网络的联想学习机制[20]. 两个突触前信号分别模拟食物的视觉和铃声. 突触后神经元模拟狗的唾液分泌. 与“食物”突触前神经元连接的突触的初始权重较大, 而与“钟”突触前神经元连接的突触的初始权重较小
Figure21. Capacitive network for associative learning based on the Hebbian-like mechanism[20]. Two pre-synaptic signals model the sight of food and the sound of a bell, respectively. The post-synaptic neuron models the salivation of a dog. The initial weight of the synapse interfacing with the “food” pre-synaptic neuron was large, while that of the synapse connected to the “bell” pre-synaptic neuron was small

储层计算是一种相对较新的神经形态计算结构, 与传统递归神经网络(RNN)相比, 期避免训练大规模节点, 大大提高计算效率, 可用于火焰模拟、股票预测等多种混沌预测场合. 基于忆容的储层计算结构如图22所示[22], 该结构将忆容网络作为储层(reservoir), 储层的忆容器之间用纳米线随机连接, 网络中的节点电压矩阵x(t)为储层向读出层(readout layer)提供的状态变量, Wres(t)为包含储层每一个忆容容值的矩阵定义为
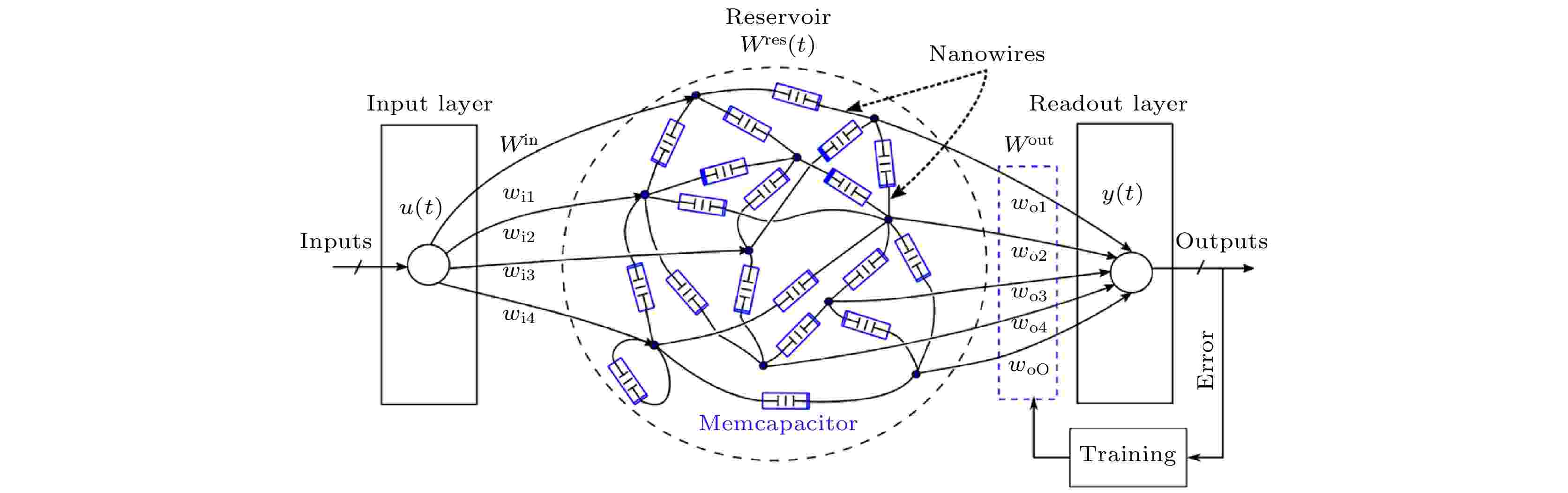图 22 忆容储层计算网络[22]
Figure22. A memcapacitive reservoir network[22].

$ {{{\mathit{\boldsymbol{W}}}}^{{\rm{res}}}}\left( {{\mathit{\boldsymbol{t}}}} \right) = [{\rm{M}}{{\rm{C}}_1},{\rm{M}}{{\rm{C}}_2},{\rm{M}}{{\rm{C}}_3}, \cdots ,{\rm{M}}{{\rm{C}}_n}]{{.}}$
网络运行, 输入信号u(t)通过固定矩阵W in向储层提供刺激, 此时节点电压矩阵x(t)随网络容值与时间变化, x(t)被定义为
$ {{\mathit{\boldsymbol{x}}}}({{\mathit{\boldsymbol{t}}}}+{\bf{1}})=f\left[{{{\mathit{\boldsymbol{W}}}}}^{{\rm{r}}{\rm{e}}{\rm{s}}}\right({{\mathit{\boldsymbol{t}}}}\left){{\mathit{\boldsymbol{x}}}}\right({{\mathit{\boldsymbol{t}}}})+{{{\mathit{\boldsymbol{W}}}}}^{{\rm{i}}{\rm{n}}}{{\mathit{\boldsymbol{u}}}}({{\mathit{\boldsymbol{t}}}}\left)\right]{.} $
其中, f为节点传递函数. 输出y(t)为
$ {{\mathit{\boldsymbol{y}}}}\left({{\mathit{\boldsymbol{t}}}}\right)={{\mathit{\boldsymbol{x}}}}\left({{\mathit{\boldsymbol{t}}}}\right){{{\mathit{\boldsymbol{W}}}}}^{\rm{out}} $
其中, Wout为固定输出矩阵, 匹配矩阵维数.
每次运算后将储层状态x(t)记录, 用记录的x(t)与y(t)对Wout用梯度下降法进行训练, 输出层训练完成后, 总训练过程结束. 之后该网络即可用于预测信号或模拟信号.
5.总结与展望
忆容器作为新型非线性无源器件, 其容值与输入电压/电荷的历史相关, 是与忆阻器等共同构建超低能耗神经网络的理想器件. 自2009年忆容被提出, 国内外研究者们在提升实物忆容器的综合性能、构建低耗能忆容神经形态计算网络等方面取得了较大的突破, 但由于发展时间较短, 实物忆容器的综合性能与实际应用要求的忆容器性能相比存在一定的距离, 因此, 还需要在忆容机理、忆容材料、忆容综合应用电路设计等方向继续探索.
对于基于整体等效介电常数变化的忆容器而言, 器件尺寸的缩减会伴随着器件漏电流增大、击穿电压降低的现象; 当忆容介质层的厚度减小到一定程度时会导致器件电导激增, 电容值下降. 在大规模集成方面, 这是忆容器与忆阻器、CMOS晶体管等器件相比的不足之处, 这将影响忆容器的实际应用. 如何获得同时具有微纳尺寸与高绝缘性的忆容器仍然是未来研究的难点与重点之一.
另外, 理论上, 相比基于忆阻的神经形态计算, 基于忆容的神经形态计算在神经元接收与发射信号上消耗的能量更少, 但检测信号所需外围电路的能量开销及对检测器件的精度要求难以估计. 结合忆阻器与忆容器等器件自身的特点, 最大程度的利用忆阻器、忆容器、晶体管等器件的优势组合设计神经形态计算电路是未来的必然趋势.
理论方面, 相较于CMOS晶体管、忆阻器等元器件, 目前对忆容的容变机理还没有成体系的解释, 无法通过理论模拟定量预测、仿真忆容现象, 建立更多切合实际的忆容实物器件模型; 而CMOS晶体管、忆阻器等器件的工作机理相对明确, 有较为成熟的实物器件模型及较为清晰的技术发展路线. 未来需要对忆容机理进一步探索, 为实物忆容器件制造与性能提升奠定理论基础. 此外, 拓展新型非压控/荷控忆容器件比如光控、声控、温控忆容等, 也将极大促进忆容器应用的发展.
相关话题/电压 结构 计算 神经 网络
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 不同周期结构硅锗超晶格导热性能研究
    摘要:构造了均匀、梯度、随机3种不同周期分布的硅/锗(Si/Ge)超晶格结构.采用非平衡分子动力学(NEMD)方法模拟了硅/锗超晶格在3种不同周期分布下的热导率,并研究了样本总长度和温度对热导率的影响.模拟结果表明:梯度和随机周期Si/Ge超晶格的热导率明显低于均匀周期结构超晶格;在不同的周期结构下 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 温稠密物质中不同价态离子分布对X-射线弹性散射光谱计算的影响
    摘要:在天体物理和惯性约束聚变研究中涉及到的温稠密物质通常包含多种元素的混合,并且每种元素还被电离成多种离子价态,不同价态离子结构及其丰度将直接影响温稠密物质的诊断及其物理性质.同时,从电子结构计算出发来研究宏观物理性质时,还需要考虑温度、密度效应对离子结构的影响.本文从不同价态离子的电子结构计算出 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 相变材料与超表面复合结构太赫兹移相器
    摘要:利用相变材料嵌入超表面组成复合结构实现太赫兹移相器,该器件自上而下依次为二氧化钒嵌入金属层、液晶、二氧化钒嵌入金属层、二氧化硅层.通过二氧化钒的相变特性和液晶的双折率特性同时作用实现对器件相位调控.随着外加温度变化二氧化钒电导率发生改变,器件的相位随之产生移动,同样的对液晶层施加不同的电压导致 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于表面等离子体共振的新型超宽带微结构光纤传感器研究
    摘要:基于表面等离子体共振的微结构光纤传感器具有高灵敏、免标记和实时监控等优点.如今,由于此类传感器广泛应用于食品安全控制、环境检测、生物分子分析物检测等诸多领域而受到大量研究.然而,目前所报道的绝大多数此类传感器只能应用于可见光或近中红外传感.因此,对可应用于中红外传感的表面等离子体共振微结构光纤 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 晶格匹配InAlN/GaN异质结肖特基接触反向电流的电压与温度依赖关系
    摘要:测量了晶格匹配InAlN/GaN异质结肖特基接触的反向变温电流-电压特性曲线,研究了反向漏电流的偏压与温度依赖关系.结果表明:1)电流是电压和温度的强函数,饱和电流远大于理论值,无法采用经典热发射模型解释;2)在低偏压区,数据满足$\ln(I/E)\text{-}E^{1/2}$线性依赖关系, ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 垂直各向异性Ho<sub>3</sub>Fe<sub>5</sub>O<sub>12</sub>薄膜的外延生长与其异质结构的自旋
    摘要:垂直磁各向异性稀土-铁-石榴石纳米薄膜在自旋电子学中具有重要应用前景.本文使用溅射方法在(111)取向掺杂钇钪的钆镓石榴石(Gd0.63Y2.37Sc2Ga3O12,GYSGG)单晶衬底上外延生长了2—100nm厚的钬铁石榴石(Ho3Fe5O12,HoIG)薄膜,并进一步在HoIG上沉积了3n ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于通信序列熵的复杂网络传输容量
    摘要:网络的传输性能在一定程度上依赖于网络的拓扑结构.本文从结构信息的角度分析复杂网络的传输动力学行为,寻找影响网络传输容量的信息结构测度指标.通信序列熵可以有效地量化网络的整体结构信息,为了表征网络整体传输能力,把通信序列熵引入到复杂网络传输动力学分析中,研究网络的通信序列熵与传输性能之间的关联特 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于格兰杰因果网络的中美贸易战对上证行业冲击的研究
    摘要:中美贸易战对行业冲击是普遍关注的问题,本文选取2016年8月—2019年10月的上证行业指数,构建了格兰杰因果关系网络,然后结合事件分析法对风险传播模型的参数进行估计,最后利用蒙特卡罗算法模拟行业受到贸易战冲击后金融风险传播情况,并计算贸易战发生前后的上证股市金融网络风险传播的基本再生数.研究 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 原子尺度材料三维结构、磁性及动态演变的透射电子显微学表征
    摘要:原子表征与操控是实现原子制造必须突破的物理瓶颈之一.像差校正电子显微学方法因其优异的空间分辨率,为实现原子精细制造提供了有力的表征手段.因此,利用电子显微学手段,在原子尺度对原子制造的材料及器件进行三维结构和性能的协同表征,对于深入理解原子水平材料操控的物理机理具有非常重要的意义.纳米团簇及纳 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • DNA折纸结构介导的多尺度纳米结构精准制造
    摘要:原子及近原子尺度制造在近年来一直是物质科学领域被广泛探讨的前沿问题.当制造和加工的尺度从微米、纳米逐渐走向原子级别时,材料在常规尺度下所具备的性质已无法通过经典理论进行解释,相反地,会在这一尺度下展现出一系列新奇的特性.因而对材料极限制造尺度和颠覆性物性的不断追求始终是科学界共同关注的重点领域 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.