摘要:在天体物理和惯性约束聚变研究中涉及到的温稠密物质通常包含多种元素的混合, 并且每种元素还被电离成多种离子价态, 不同价态离子结构及其丰度将直接影响温稠密物质的诊断及其物理性质. 同时, 从电子结构计算出发来研究宏观物理性质时, 还需要考虑温度、密度效应对离子结构的影响. 本文从不同价态离子的电子结构计算出发, 采用考虑了离子间相互作用的Saha方程获得了稠密环境下的离子丰度, 并使用超网链(hypernetted-chain)近似对铝、金以及碳-氢混合物的径向分布函数进行了计算, 结合离子周围电子的密度分布, 最后获得X-射线汤姆逊散射的弹性散射谱. 在X-射线散射谱计算中, 计算了温稠密物质中同时存在不同离子价态时的电子结构和径向分布函数, 发现在相同的等离子体环境下不同价态离子的径向分布函数和电子结构差别较大. 这将对依赖于微观统计过程的物理性质, 比如散射光谱, 将产生较大的影响.
关键词: 温稠密物质/
径向分布函数/
超网链近似/
弹性散射

English Abstract

全文HTML

--> --> -->

过去几十年, 由于激光技术的发展, 强激光不仅能够在实验室中产生温稠密物质, 而且还可以产生X-射线为诊断温稠密物质结构提供了手段, 使得高能量密度物理的研究得到快速发展. X-射线弹性散射谱能够反映出温稠密物质中的离子结构, 而离子结构的信息在计算中直接取决于离子的径向分布函数和电子分布. 同时, 径向分布函数也能够反映出等离子体中离子间的关联效应^[1-3]. 另外, 通过离子结构的计算结果还可以直接获得宏观物理性质, 比如, 物态方程和离子输运性质^[4,5]. 所以, 离子结构的精确计算对天体物理和惯性约束聚变^[1]中所涉及到基本物理参数的研究有着重要应用价值.
在波恩-奥本海默近似下, 量子分子动力学(quantum molecular dynamics, QMD)^[6-8]是在含温密度泛函理论框架下计算电子结构, 通过能量变分获得离子间的受力, 进而通过求解离子运动的牛顿方程可以很好地描述温稠密物质中的电子、离子结构, 并能够得到合理的宏观物理性质. 但在较高温度、密度状态下, 由于模拟系统中的高能量电子的描述需要更宽能量状态区域, 这将使得计算量大大增加, 限制了高温状态下模拟系统中包含更多离子的可能性. 为了快速的获得温稠密状态下电子密度的空间分布, 人们使用Thomas-Fermi(TF)近似^[9]直接计算离子周围电子密度分布, 发展了无轨道的分子动力学(orbital free molecular dynamics, OFMD)^[10]来计算高温稠密物质的性质, 但对于束缚轨道的计算将带来较大的误差. 在温稠密状态下, 由于温度和密度的效应, 物质将会被电离成不同价态的离子, QMD和OFMD都不能有效的提取不同离子价态分布信息. 对于传统低密度等离子体中离子结构的计算, 通常忽略离子间的相互作用, 采用自由离子模型来计算离子的结构. 但对于温稠密物质, 离子间的耦合较强, 忽略稠密环境效应将会对离子结构计算产生较大影响. 本课题组已经发展了多离子的分子动力学模型^[11], 考虑了稠密环境下离子间相互作用对离子丰度影响, 采用分子动力学模拟给出离子的输运性质. 但在较高温度下, 由于离子丰度分布较宽, 需要同时模拟更多的离子或者模拟更久的时间才能给出合理的计算结果, 大大增加了计算量. 在已知粒子间相互作用势的情况下, 为了能够快速准确的获得离子间的径向分布函数, 通过耦合Ornstein-Zernike方程, 超网链(hypernetted-chain, HNC)近似^[12-14]可以给出合理的描述.
本文将首先使用计算原子结构的相对论程序FAC(flexible atomic code)^[15]获得不同价态离子的电子结构; 然后采用考虑了离子间相互作用的Saha方程给出离子价态分布^[14,16], 使用超网链近似来计算不同价离子间的径向分布; 最后结合不同价离子的径向分布函数以及离子周围的电子分布, 给出X-射线弹性散射谱随角度变化关系. 在此基础上, 通过比较温稠密区域不同价离子的径向分布函数和X-射线的弹性散射谱, 本文讨论了随着等离子体温度密度变化, 离子丰度对径向分布函数的影响, 并与平均原子计算结果进行了对比, 研究不同统计过程对离子结构以及X-射线弹性散射谱的影响.

2

-->

2.1.径向分布函数

径向分布函数在确定气体、等离子体、流体等多粒子系统结构特性的研究中扮演了重要角色, 它是用统计方法来描述系统中粒子间相对位置变化. 在类流体的描述中, 径向分布函数和其他的关联函数只依赖粒子之间的相对位置($r = |{r_1} - {r_2}|$), 对于多种粒子组成的系统中两个粒子之间的径向分布函数可以表示为

${g_{ab}}({r_1},{r_2}) = \frac{1}{{{n_a}{n_b}}}\left\langle {\sum\limits_{\begin{subarray}{l} i = 1 \\ i \ne j \end{subarray}} ^{{N_a}} {\sum\limits_{\begin{subarray}{l} j = 1 \\ \forall a = b \end{subarray}} ^{{N_b}} {\delta ({r_1} - {r_i})\delta ({r_2} - {r_j})} } } \right\rangle , $

其中, r_i, r_j表示粒子的位置, $\left\langle {\;} \right\rangle$表示正则系综的平均. ${n_a}$, ${n_b}$和${N_a}$, ${N_b}$分别表示a, b类粒子数密度和粒子数. 总关联函数可以用径向分布函数表示为${h_{ab}} = {g_{ab}} - 1$. 通过对总关联函数的傅里叶变换, 还可以获得多组分混合物质的静态结构因子:

$S{}_{ab}(k) = {\delta _{ab}} + \sqrt {{n_a}{n_b}} \int {{h_{ab}}\exp ({\rm{i}}kr){\rm{d}}r} ,$

${\delta _{ab}}$在a, b为同类离子时为${\delta _{ab}}= 1$, a, b为不同种类离子时为${\delta _{ab}} = 0$.
在实际的数值计算中, 已知粒子间的相互作用时, 可以通过不同的方式获得粒子的径向分布函数, 比如分子动力学^[10]、蒙特卡洛方法^[17]以及HNC近似^[12-14]. 为了快速获得混合等离子体中的离子间径向分布函数, 本文采用HNC近似来计算温稠密物质中离子间的关联函数, 如下式:

${h_{ab}}(r) = \exp[ - \beta {V_{ab}}(r) + {h_{ab}}(r) - {c_{ab}}(r)] - 1,$

其中, ${h_{ab}}$, ${c_{ab}}$分别为总关联函数和直接关联函数, ${V_{ab}}$为a粒子和b粒子之间的势能. 在关联函数的计算过程中, 还需要Ornstein-Zernike方程形成闭合关系, 从而进行自洽迭代来求解. Ornstein-Zernike方程表示如下:

$ {h}_{ab}={c}_{ab}+{\displaystyle \sum _{c}{n}_{c}}{\displaystyle \int {\rm{d}}{\mathit{\boldsymbol{r}}}}{c}_{ac}({\mathit{\boldsymbol{r}}}){h}_{cb}(r-{\mathit{\boldsymbol{r}}}), $

其中${n_c}$表示c类粒子的离子数密度.
采用HNC近似来计算粒子间的径向分布函数, 首先需要获得粒子间的相互作用势. 从头计算粒子间的相互作用势需要求解多体问题, 是非常困难的. 人们通常建立不同的计算模型来描述离子间的相互作用, 比如Yukawa模型、Deutsch模型^[18]、Klimontovich 和Kraeft(KK)模型^[19]以及Kelbg模型^[20]等. 这些模型都是针对不同条件下提出计算离子间相互作用的模型, 都有一定的适用范围. 在温稠密物质中, 考虑到存在不同价离子和自由电子, 以及电子、离子间的库伦屏蔽效应, 在计算离子间的径向分布函数时采用Yukawa势来描述离子间的相互作用:

${V_{ab}}(r) = \frac{{{z_a}{z_b}{e^2}}}{r}\exp ( - {k_{\rm{D}}}r), $

其中${k_{\rm{D}}}$为屏蔽系数, 是屏蔽长度的倒数. 考虑到在温稠密物质中离子间的相互作用势主要被自由电子屏蔽, 所以, 在计算中屏蔽系数时只考虑自由电子对屏蔽的贡献, 由公式:

$k_{\rm{e}}^2 = \frac{{4{{\rm{e}}^2}{m_e}}}{{{\rm{\pi }}{\hbar ^3}}}\int_0^\infty {{\rm{d}}p{f_{\rm{e}}}} (p), $

计算得到. 其中${f_{\rm{e}}}(p) = \dfrac{{\rm{1}}}{{{{1 + \exp[(}}{{{p^2}} / {2 m - \mu )/T]}}}}$为电子的费米-狄拉克分布函数.
2 -->

2.2.X-射线弹性散射光谱计算

在温稠密物质的X-射线散射中, 将一束已知光谱强度的X-射线照射在温稠密物质上, 在不同角度探测被散射的X-射线的光谱就可以获取温稠密物质的温度、密度以及平均电离度的信息. 散射X-射线的转移动量依赖于散射角度:

$k{{ = 2}}{k_{\rm{0}}}\sin \frac{\theta }{{\rm{2}}}$

其中, k表示在不同散射角上收集到X-射线动量和初始动量k₀的差. 散射谱的测量和物质的动态结构因子$ S\left(k, \omega \right) $直接相关, 其中$ \omega $表示X-射线转移到电子上的能量. 根据Chihara公式^[21], 可以将动态结构因子近似分成弹性散射、非弹性散射部分, 其中非弹性散射又可以简单分为伴随动量反冲或动能交换的自由电子散射和伴随激发或者电离的束缚电子的散射. 弹性散射部分是原子核以及随原子核一起运动的电子对X-射线的散射, 对这部分散射可以忽略X-射线的能量损失, 弹性散射可以给出离子的结构信息. 由于温稠密物质中存在不同价态的离子, 所以在计算X-射线散射谱时需要考虑多种离子价态的贡献. 动态结构因子中弹性散射部分可以表示为形状因子与静态结构因子的乘积^[22,23], 也被称为Rayleigh峰, 其在动量空间可以表达为

$\begin{split}&{W_R}(k) =\\& \sum\limits_{i,j} {\sqrt {{x_i}{x_j}} } [ {f_i}(k) + {q_i}(k) ]\left[ {{f_j}(k) + {q_j}(k)} \right]{S_{ij}}(k), \end{split}$

其中静态结构因子由多组分的超网链近似获得; 形状因子由每价离子周围分布的自由电子和束缚电子贡献, 在傅里叶空间可以将形状因子表示为

${f_I}(k) + {q_I}(k) = \frac{{4{\rm{\pi }}}}{k}\int_0^{{r_b}} [ {\rho _b}(r) + {\rho _f}(r) ] r\sin (kr){\rm{d}}r, $

其中${\rho _b}(r)$为束缚电子密度, 根据组态的占据数乘上波函数模方求和得到:

${\rho _b}(r){{ = }}\frac{{\rm{1}}}{{{\rm{4\pi }}{r^2}}}\sum\limits_n {{w_n}\left| {P_n^2(r) + Q_n^2(r)} \right|} , $

其中${P_n}$, ${Q_n}$是求解Dirac方程得到波函数的大、小分量, ${w_n}$表示束缚轨道上的占据电子数目. 自由电子密度由Thomas-Fermi近似得到如下式所示:

$ \begin{split}&{\rho }_{\rm{f}}(r)=\frac{\rm{1}}{{\rm{\pi}}^{\rm{2}}}\displaystyle {\int }_{{p}_{0(r)}}^{\infty }{\rm{d}}p \\&\cdot\frac{{p}^{2}}{{\rm{exp}}\big\{\big[\sqrt{{p}^{2}{c}^{2}+{c}^{4}}-{c}^{2}-V(r)-\mu \big]/{k}_{B}T \big\}+1},\end{split} $

其中${p_0}(r) = {{[2 V(r){c^2} + {V^2}(r)]} / c}$, $\mu $为化学势, 由电中性条件得到, c为光速.

在温稠密物质中由于多种价态离子同时存在, 并且每一种价态离子所形成的势场不同, 从而影响该离子周围的其他离子分布, 径向分布函数可以对离子的分布给出很好的描述. 首先在温度为10⁴ K、离子数密度为n = 10²⁴ cm^–3的条件下, 使用HNC近似计算了金元素二价和一价等粒子数混合情况下的径向分布函数, 如图1所示, 不同价离子间的相互作用势都采用Yukawa对势形式进行计算. 在图中, 将计算结果与Wünsch等^[22]已发表的结果^[2]进行了比较. 因为在计算中都使用了Yukawa势函数, 并且都是使用HNC近似方法计算得到的计算结果, 所以, 可以看出本文的计算结果和Wünsch等^[22]结果基本上是重合的. 从而也说明了, 发展的HNC程序在计算不同价离子的关联函数时是没有问题的. 为了进一步比较不同统计过程对径向分布函数的影响, 首先按照离子丰度将不同价离子平均成一种价态(A = 1.5), 然后按照单组分形式可以给出一种平均离子的径向分布函数(图中OCP标记的计算结果); 也采用了多组分HNC计算得到的不同价离子的径向分布函数, 然后再根据丰度进行平均(图中average标记的计算结果). 可以看出, 虽然都采用Yukawa形式的势函数, 但两种统计的先后顺序差异对计算结果产生了差别. 这也说明了从微观电子结构计算出发来获得温稠密物质的宏观性质时, 不同的统计过程将影响所计算的宏观物理性质.
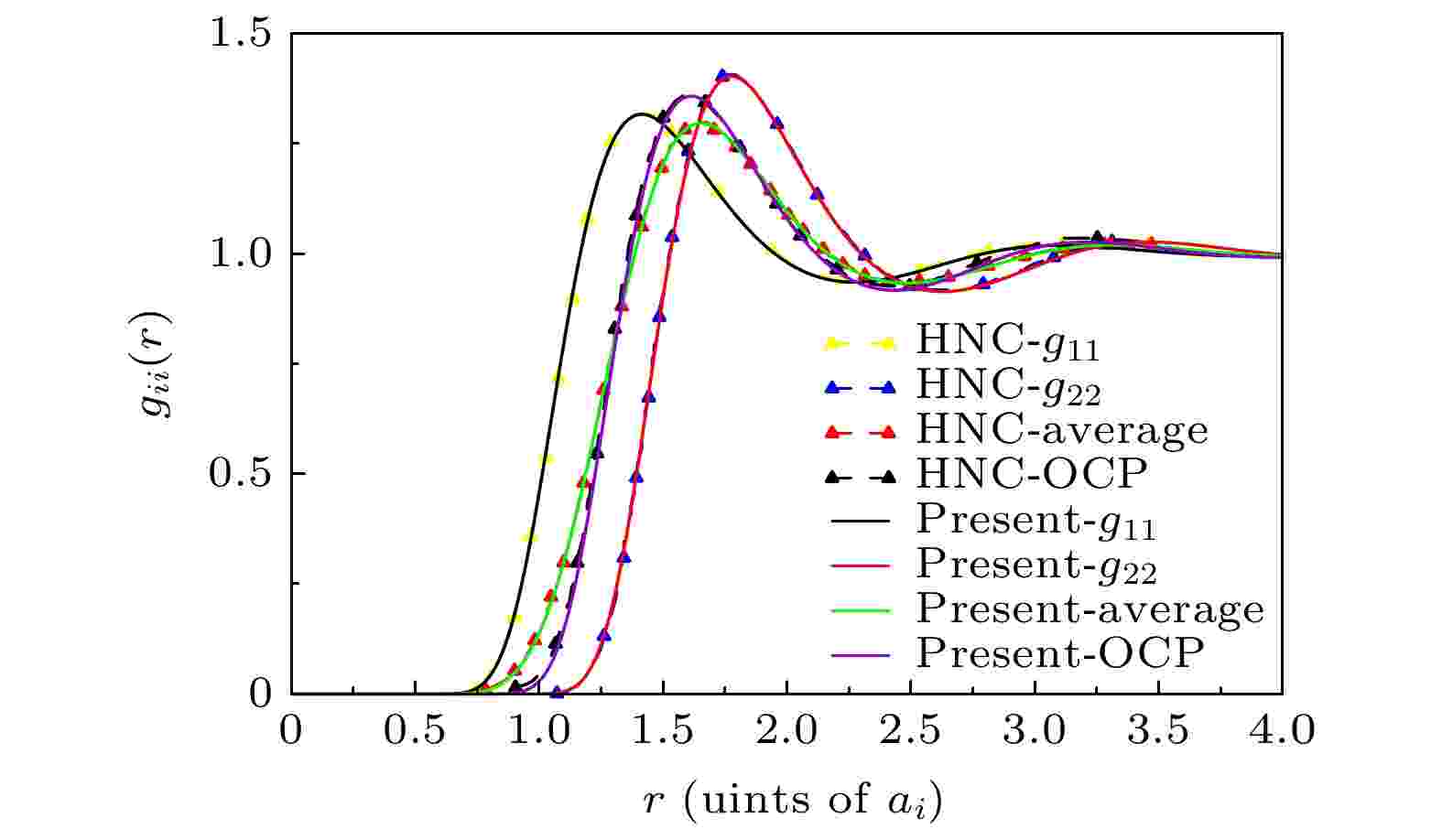图 1 在温度为10⁴ K、离子数密度为10²⁴ cm^–3时, Au¹⁺和Au²⁺混合离子价态的径向分布函数. Present表示本文工作的计算结果(实线); HNC表示文献[2]中采用HNC近似计算的结果(虚线 + 上三角); OCP表示平均成一种价态离子的径向分布函数; average表示各价离子的径向分布函数的算数平均
Figure1. The radial distribution function of Au¹⁺, Au²⁺ in gold plasma with ion number density of 10²⁴ cm^–3 and temperature of 10⁴ K. Present represents the result of the present paper (solid line); HNC represents the result of HNC approximation in the Ref. [2] (dotted line + upper triangle); OCP is the radial distribution function of mean charge-state ion; average labels the average results of the radial distribution function of different charge-state ions.

为了进一步测试HNC计算程序对于混合物质的计算, 在当前的理论框架下, 又计算了在温度为2.0 × 10⁴ K、密度为2.5 × 10²³ cm^–3CH混合物质的径向分布函数, 其中C⁴⁺和H⁺离子数密度比为1∶1. 将计算结果和Wünsch等^[22]已发表的结果^[2]进行比较, 如图2所示. 从图中可以看出, 计算的结果和Wünsch等^[22]结果基本一样. 从而进一步说明, 本文的HNC程序能够实现不同元素、同种元素不同价离子的径向分布函数的计算.
图 2 在离子数密度为n_H = n_C = 2.5 × 10²³ cm^–3、温度为T = 2 × 10⁴ K时, 碳-氢混合等离子体中C⁴⁺和H⁺的径向分布函数; Present是本文计算结果(实线), HNC是文献[2]中用HNC近似的计算结果(虚线 + 上三角)
Figure2. The radial distribution function of C⁴⁺ and H⁺ in the CH mixture plasma at number density, n_H = n_C = 2.5 × 10²³ cm^–3, and the temperature, T = 2 × 10⁴ K. And solid lines label the present results; and dashed lines with upper triangles are the results of Ref. [2].

在计算离子间的相互作用势时, 按照方程(5)的方式考虑了自由电子屏蔽效应, 构造了离子间的Yukawa势, 然后使用考虑了离子关联效应的Saha方程^[10]计算了密度为8.1 g/cm³、不同温度(10, 20, 40和100 eV)下温稠密铝等离子体中离子丰度, 如表1所示. 从表中可以看出, 由于压致电离效应, 在温度为10 eV时等离子体中只有3种离子价态, 并且2价、4价离子的丰度很小, 主要是3价离子, 这和常态下金属铝有3个自由电子也相吻合. 随着温度的升高, 2p壳层被打开, 同时更多的电子电离导致离子周围的势阱变深, 不同价离子的能量差别越来越小, 所以, 即使在3倍的固体密度下铝等离子体中也同时存在更多价态的离子.

100 eV价态	A = 7.196丰度		40 eV价态	A = 4.28丰度		20 eV价态	A = 3.27丰度		10 eV价态	A = 3.007丰度
4	0.016		2	0.001		2	0.003		2	0.001
5	0.081		3	0.175		3	0.735		3	0.991
6	0.212		4	0.438		4	0.251		4	0.008
7	0.247		5	0.315		5	0.011
8	0.290		6	0.067
9	0.132		7	0.004
10	0.021

表1在密度为8.1 g/cm³、不同温度下温稠密铝的离子丰度, A表示平均电离度
Table1.Charge-state fractions of Al at density, 8.1 g/cm³, A is average charge state.

获得了离子丰度和相互作用势后, 就可以使用多组分的HNC计算程序计算不同价态离子间的径向分布函数. 为了比较不同统计过程的计算结果, 也采用了平均原子模型+超网链近似的方法(AAHNC)^[3]计算了平均离子的径向分布函数. AAHNC模型是首先将等离子体中的不同价态离子平均成一种价态, 在离子球里自洽计算电子的结构时考虑离子间的关联效应, 其中的关联函数也是由HNC近似给出, 离子间的相互作用势由修正的Gordon-Kim方法计算. 在计算不同价态离子的径向分布函数时, 按照表1给出的离子丰度, 在图3中给出了铝在密度为8.1 g/cm³、温度分别为10, 20, 40和100 eV时离子径向分布函数的计算结果. 图中黄色实线是AAHNC模型的计算结果, 不同颜色的虚线依次表示由多组分的HNC近似得到的不同价态离子的径向分布函数. 从图3中可以看出, AAHNC计算得到径向分布函数都是位于各种不同价态离子计算结果的中间, 但由于平均电离度并不等于某个整数价态离子, 比如20、40和100 eV的计算结果中, 它和中间价态离子的计算结果还是有差别的. 另一方面, 即使在10 eV时, AAHNC模型给出的平均电离度也是3价, 但和直接采用多组分HNC的计算的径向分布函数也是有差别的, 这就说明从不同的统计方法将会对离子结构的计算结果带来影响. 随着温度的升高, 平均电离度越来越大, 由于更多自由电子屏蔽, 相邻价态离子的径向分布函数差别越来越小. 但由于离子价态分布范围越来越宽, 平均价态离子计算结果和最高价、最低价离子计算结果的差别也越来越大. 在这样物理条件下, 一些非常依赖于微观离子结构的宏观物理性质, 比如光谱以及光谱的散射性质, 当从微观离子结构计算出发, 使用不同统计过程将对计算结果产生较大影响.
图 3 在密度为8.1 g/cm³、不同温度下温稠密铝中, 采用多组分HNC近似给出不同价态离子(虚线)的径向分布与AAHNC模型(实线)计算结果的比较
Figure3. Different ion species pair distribution functions (dashed lines) of Al at density, 8.1 g/cm³, and different temperatures calculated by HNC approximation, comparing with that of AAHNC model (orange solid lines).

从电子结构计算出发来研究温稠密物质体中的离子结构, 除了依赖于离子的空间分布, 还依赖于离子周围的电子密度分布. 所以, 在获得了不同价离子丰度及径向分布函数的基础上, 还需要按照式(9)计算形状因子(form factor). 在温稠密物质环境中, 由于离子间的强耦合以及电子简并效应使得离子的高激发态较少, 因此在使用FAC程序计算电子时, 只考虑了不同价态离子的基态电子结构^[14]. 与图3一样, 在图4中比较了不同价态离子和AAHNC模型计算得到的形状因子. 由于不同价离子的中心对称势函数不同, 周围电子密度分布的差异导致了不同价态离子的形状因子差别, 特别对低k区域, 也就是外层电子的分布在小角度散射情况下对离子价态的依赖非常明显. 与径向分布函数的计算结果类似, 虽然AAHNC模型计算的形状因子都是从不同价态离子的计算结果中间穿过, 但随着温度的升高, 温稠密物质中出现越来越多的不同价态离子, 特别对于100 eV的计算结果, 由于很宽的离子价态分布导致最高价态、最低价态的计算结果差别很大.
图 4 密度为8.1 g/cm³、不同温度下温稠密铝等离子体中, 不同价态离子(虚线)、AAHNC模型计算(实线)的形状结构因子随着散射角度的变化.
Figure4. Form factor of different ion species (dashed lines) of Al at density, 8.1 g/cm³, and different temperatures, comparing with that of AAHNC (orange solid lines).

为了更好地和实验以及其他理论计算结果进行比较, 在获得不同价离子的径向分布和形状因子基础上, 通过方程(8)计算了温度为10 eV、密度为8.1 g/cm³温稠密铝等离子体X-射线弹性散射随不同散射角变化, 如图5所示. 图中的Multi-ion是表示本文使用的方法给出的计算结果. AAHNC是表示由一种平均价态离子的结构直接计算得到的结果. 图中的HNC和AAHNC方法类似, 都是采用超网链近似获得离子间的关联函数, 只是在计算电子-离子、离子-离子间的相互作用势时采用了无规相近似(random-phase approximation, RPA)的方法. QMD表示的量子分子动力学模拟的计算结果. 从图上可以看出, 除了在低k区域外, 考虑了多价态离子的计算结果和其他理论模型吻合都比较好. 在低k区域的差别, 主要是由于在计算过程只考虑了离子对势而忽略了离子的长程相互作用. 对于稠密物质中, 由于自由电子的屏蔽, 忽略长程库伦相互作用也是合理的近似. 因此可以看出, 本文发展的多价态离子结果计算方法可以对温稠密物质给出合理的描述. 除了最高的两个点外, 理论计算结果和实验吻合的都很好. 在已发表的工作^[27,28]中已经讨论过, 如果认为该实验测量对应的物质状态处于非平衡状态, 在理论模拟中考虑到电子、离子具有不同的温度后, 可以得到了和实验较吻合的结果.
图 5 在密度为8.1 g/cm³、温度10 eV下温稠密铝等离子体中, 离子结构随不同散射角的变化关系. Multi-ion表示本文使用的方法给出的计算结果(虚线); AAHNC表示AAHNC模型的计算结果(实线)^[3]; QMD表示量子分子动力学计算结果(点-虚线)^[24]; HNC表示文献^[25]中采用HNC近似计算离子结构的结果(点线); 带有误差范围的点表示实验结果^[26]
Figure5. Ion feature for Al as function of k at a temperature of 10 eV and a density of 8.1 g/cm³: Multi-ion (dashed line), AAHNC (solid line)^[3], QMD (dot-dashed line)^[24], HNC (dot line)^[25] and experimental data (points with error bars)^[26].

本文从原子结构计算出发, 使用FAC程序求解Dirac方程获得不同价态离子的电子结构及其能量; 根据自由电子分布, 采用Yukawa模型构造了温稠密物质中离子间相互作用势函数; 在此基础上, 通过考虑了离子间相互作用的Saha方程计算了离子的丰度分布, 进而采用混合组分的超网链(HNC)近似计算温稠密Au, Al和CH混合物质中不同价态离子径向分布函数. 计算结果与平均原子的计算结果进行比较, 发现统计的先后顺序差异对离子结构及其电子分布的影响. 基于不同价态的径向分布函数及其周围的电子分布, 按照Chihara公式, 又计算了温稠密Al等离子体的 X-射线弹性散射谱, 虽然计算结果与其他理论和实验结果吻合较好, 但不同价态离子的径向分布函数和形状因子差别较大, 进一步说明在温稠密物质中考虑不同价态离子结构对宏观物理性质的影响.