摘要:高能质子在散裂靶中的能量沉积是散裂靶中子学研究的重要内容之一, 准确掌握高能质子在散裂靶中引起的能量沉积分布与瞬态变化是开展散裂靶热工流体设计的重要前提. 本文采用MCNPX, PHITS与FLUKA三种蒙特卡罗模拟程序, 计算并比较了高能质子入射重金属铅靶、钨靶的能量沉积分布及不同粒子对总能量沉积的占比贡献; 针对高能质子入射金属钨靶的能量沉积实验数据空白, 采用热释光探测器阵列测量了250 MeV质子束入射厚钨靶的能量沉积分布, 实验结果表明蒙特卡罗模拟程序在散裂靶中能量沉积的计算结果具有较高的可靠性.
关键词: 能量沉积/
高能质子/
散裂靶/
蒙特卡罗程序

English Abstract

全文HTML

--> --> -->

近年来, 我国先后启动了中国散裂中子源(China Spallation Neutron Source, CSNS)项目^[1], 以及未来先进核裂变能-加速器驱动次临界系统 (accelerator driven sub-critical system, ADS)项目^[2]. CSNS项目采用1.6 GeV的高能质子束流轰击钽包钨靶^[3], 在靶上发生散裂反应并产生大量中子, 为中子散射及相关领域提供科学研究与实验平台; 在ADS项目中, 高能质子轰击重金属靶, 为ADS次临界反应堆提供持续中子外源. 在散裂靶中, 高能质子主要通过与靶原子的激发电离过程, 以及与靶核发生散裂反应过程损失能量. 掌握高能质子在散裂靶中能量沉积的产生机制, 分析热量沉积的空间分布与瞬态变化, 是开展散裂靶热工流体设计的重要前提.
目前, 高能质子束在散裂靶中的能量沉积数据主要通过MCNPX^[4], PHITS^[5], FLUKA^[6]等蒙特卡罗粒子输运程序计算获得, 模拟计算的准确度依赖于程序中物理模型对各个能量沉积途径的处理及采用的计算方法. MCNPX程序中的核子级联模型包括BERTINI, ISABEL, CEM2K和INCL4, 各个模型的主要区别在于对级联相互作用过程与对核密度等的近似处理; PHITS采用JAM模型作为强子级联模型, 在低能端采用JENDL核数据; FLUKA采用PEANUT模型与ENDF核数据进行相关计算.
受实验条件如束流能量、束流时间等的限制, 高能质子在散裂靶中的能量沉积测量数据非常有限. 国际上采用量热法进行靶内能量沉积测量^[7-12], 即通过测量靶内各处由于能量沉积导致的温度变化而获得能量沉积分布, 但是只有束流较强时才能使靶体温度上升到可准确测量的范围. 文献[13]表明在较低束流强度条件下, 在散裂靶内布置热释光探测器(thermoluminescence detector, TLD), 通过测量TLD的剂量分布可以分析散裂靶内的能量沉积. 本文采用MCNPX, PHITS与FLUKA三种蒙特卡罗程序, 首先计算了不同能量高能质子入射重金属铅靶、钨靶的总能量沉积及其在入射深度的分布, 并通过与已有的测量数据进行比较, 评估不同级联模型的计算结果; 其后计算了不同能量的质子在散裂靶中产生的不同类型粒子, 并获得各种粒子对总能量沉积的占比贡献; 最后利用兰州重离子加速器^[14]提供的250 MeV质子束流, 采用TLD阵列测量250 MeV质子束入射钨靶的能量沉积分布, 测量结果验证了蒙特卡罗程序计算质子入射散裂靶能量沉积的可靠性.

2

-->

2.1.计算方法

高能质子在散裂靶中的能量沉积计算分别采用MCNPX, PHITS和FLUKA三种粒子输运程序开展. 在采用MCNPX程序进行计算时, 分别采用了BERTINI模型、ISABEL模型、CEM2K模型与INCL4模型作为级联模型. 在采用PHITS程序和FLUKA程序进行计算时, 则分别采用了JAM级联模型与PEANUT模型. 计算所选用的散裂靶模型为直径为20 cm, 长度为50 cm的圆柱体. 铅的密度为11.3 g/cm³, 同位素²⁰⁴Pb, ²⁰⁶Pb, ²⁰⁷Pb和²⁰⁸Pb的质量丰度分别为1.4%, 24.1%, 22.1%和52.4%; 钨的密度为19.0 g/cm³, 同位素¹⁸⁰W, ¹⁸²W, ¹⁸³W, ¹⁸⁴W和¹⁸⁶W的质量丰度分别为0.12%, 26.5%, 14.31%, 30.64%和28.43%. 为了对比于国际上已有的实验数据, 验证模拟计算方法的可靠性, 质子能量分别为800, 1000, 1200 MeV, 从圆柱体靶端面垂直入射, 质子在入射横截面上的抽样概率服从二维高斯分布, 半高宽均为2.4 cm.
2 -->

2.2.质子入射铅靶的能量沉积计算结果

图1(a)给出了MCNPX, PHITS与FLUKA三种粒子输运程序对入射能量为800, 1000, 1200 MeV的质子入射铅靶的总能量沉积. 同时, 图1(a)还给出了Belyakov-Bodin等^[7]采用热电偶法在铅靶中测量到的能量沉积实验值. 可以看出, 三种粒子输运程序的计算结果相对于实验值整体偏大; 与MCNPX相比, PHITS与FLUKA的计算结果更大; 即使采用MCNPX程序进行计算, 不同的级联模型所对应的模拟结果也各不相同: 采用ISABEL模型的计算值较大, INCL4与BERTINI模型次之, CEM2K模型的计算结果最小. 对1000 MeV的质子入射能量而言, PHITS的模拟值比测量值高约16.1%, FLUKA的模拟值比测量值高15.6%, MCNPX-CEM2K的模拟值比测量值高约9%, 采用CEM2K级联模型获得的能量沉积值最接近实验测量值, 计算结果的统计误差可忽略不计.
图 1 (a)不同模拟程序对铅靶总能量沉积计算的对比; (b) 铅靶中能量沉积线性密度的轴向分布
Figure1. (a) Comparison of total energy deposition in lead target calculated by different Monte Carlo codes; (b) axial distribution of linear density of energy deposition in lead target.

散裂靶单位长度中的能量沉积值被称为能量沉积线性密度. 图1(b)给出了采用MCNPX-CEM2K模型计算出的能量沉积线性密度在铅靶中的分布. 通过与文献[7]中的测量数据进行比较, 可以看出, 高能质子在铅靶长度方向的能量沉积线性密度计算结果与测量结果在整体上能较好符合; 随着质子入射深度的增加, 能量沉积线性密度计算值的偏差略有增大.
另外, 我们采用MCNPX程序中的CEM2K级联模型计算得到了不同能量质子入射铅靶时, 不同粒子对总能量沉积值的占比贡献, 如表1所示. 计算数据表明, 质子作为入射粒子, 通过与靶核外电子的电离、激发过程及与靶核的散裂反应过程损失能量, 对总能量沉积的贡献最大; 铅是原子序数较高的材料, 对光子的阻止本领很强, 这导致了质子与散裂靶相互作用产生的光子在靶中的能量沉积较大; 随着入射质子能量的增大, 散裂反应产生的次级带电粒子增多, 预平衡与蒸发过程的剩余核会达到更高的自旋和激发态, 这导致了质子对总能量沉积的占比逐渐减小, 轻带电粒子与光子的占比贡献逐步增大.

粒子	800 MeV			1000 MeV			1200 MeV
	沉积能 量/MeV	对总能量沉积值 的占比/%		沉积能 量/MeV	对总能量沉积值 的占比/%		沉积能 量/MeV	对总能量沉积值 的占比/%
全部粒子	497.9	100		572.0	100		648.7	100
质子	413.9	83.13		435.6	76.15		455.0	70.15
光子	47.5	9.54		74.8	13.08		104.0	16.03
π0	0.2	0.04		0.4	0.06		0.5	0.08
带电π介子(± π)	6.6	1.33		13.7	2.39		21.9	3.37
氘	13.7	2.75		21.2	3.71		29.0	4.47
氚	5.0	1.01		8.5	1.48		12.3	1.90
氦–3	2.8	0.57		5.1	0.90		8.0	1.23
α粒子	6.1	1.23		10.1	1.77		14.6	2.26
中子	2.0	0.40		2.7	0.47		3.3	0.51
初级质子 电离作用	268.8	52.73		247.9	48.63		233.1	45.72

表1CEM2K级联模型计算质子入射铅靶产生的不同粒子对总能量沉积的占比贡献
Table1.The calculated contribution of different particles to the total energy deposition in lead target by CEM2K-Cascade-Mode

为了对比不同级联模型的次级粒子计算结果, 我们还采用MCNPX中的BERTINI, ISABEL, INCL4级联模型分别对1000 MeV质子进行了模拟, 计算结果如表2. 从表2可以看出, 4种级联模型对初级质子电离作用的能量沉积计算结果几乎相等, 这是因为初级质子的电离作用仅受到入射粒子和散裂靶的影响, 与级联过程无关; 相对其他两种级联模型, CEM2K对次级质子沉积能量计算值最小, 对光子、氘、氚、氦-3的能量沉积计算值最大, 这是因为CEM2K融合了DUBNA级联模型、Exciton激子模型、GEM蒸发模型、RAL裂变模型、Fermi-breakup模型及光核反应模型等, 在计算剩余核、裂变产物、轻核产生及碰撞-反弹过程时更为准确^[15].

粒子	BERTINI			ISABEL			CEM2 K			INCL4
	沉积能 量/MeV	对总能量沉积值 的占比/%		沉积能 量/MeV	对总能量沉积值 的占比/%		沉积能 量/MeV	对总能量沉积值 的占比/%		沉积能 量/MeV	对总能量沉积值 的占比/%
全部粒子	580.3	100		603.0	100		572.0	100.00		594.5	100
质子	474.0	81.67		493.0	81.76		435.6	76.15		500.6	84.20
光子	63.7	10.98		76.2	12.64		74.8	13.08		60.7	10.21
π0	0.3	0.05		0.3	0.05		0.3	0.06		0.3	0.04
带电π介 子(± π)	14.9	2.56		13.9	2.31		13.7	2.39		15.5	2.60
氘	6.4	1.10		3.7	0.62		21.2	3.71		4.0	0.67
氚	3.0	0.52		1.9	0.32		8.5	1.48		1.8	0.30
氦–3	0.4	0.06		0.1	0.02		5.1	0.90		0.2	0.03
α粒子	14.8	2.56		11.8	1.96		10.1	1.77		9.1	1.53
中子	2.9	0.49		1.9	0.32		2.7	0.47		2.5	0.42
初级质子电 离作用	245.1	48.06		243.6	47.79		247.9	48.63		245.0	48.06

表2BERTINI, ISABEL, CEM2K与INCL4级联模型计算1000 MeV质子入射铅靶产生的不同粒子对总能量沉积值的占比贡献
Table2.The calculated contribution of different particles to the total energy deposition in lead target by 1000 MeV protons with BERTINI, ISABEL, CEM2K, and INCL4 cascade mode.

2 -->

2.3.质子入射钨靶的能量沉积计算结果

同样, 对不同能量的质子入射钨靶产生的能量沉积进行计算, 图2(a)为采用不同计算模型获得的总能量沉积随入射质子能量的变化. 与铅靶的情况类似, PHITS与FLUKA的计算结果相对于MCNPX各个级联模型偏大. 图2(b)为采用MCNPX-CEM2K模型计算的能量沉积线性密度分布. 在现阶段, CSNS项目采用了钽包钨作为散裂靶, ADS项目则采用钨镍合金靶, 然而, 由于国内外尚无高能质子入射钨靶产生的能量沉积实验数据, CSNS与ADS的热工流体设计只能根据计算数据开展. 对于中高能质子入射钨靶的能量沉积计算亟需实验数据验证和可靠程度评估.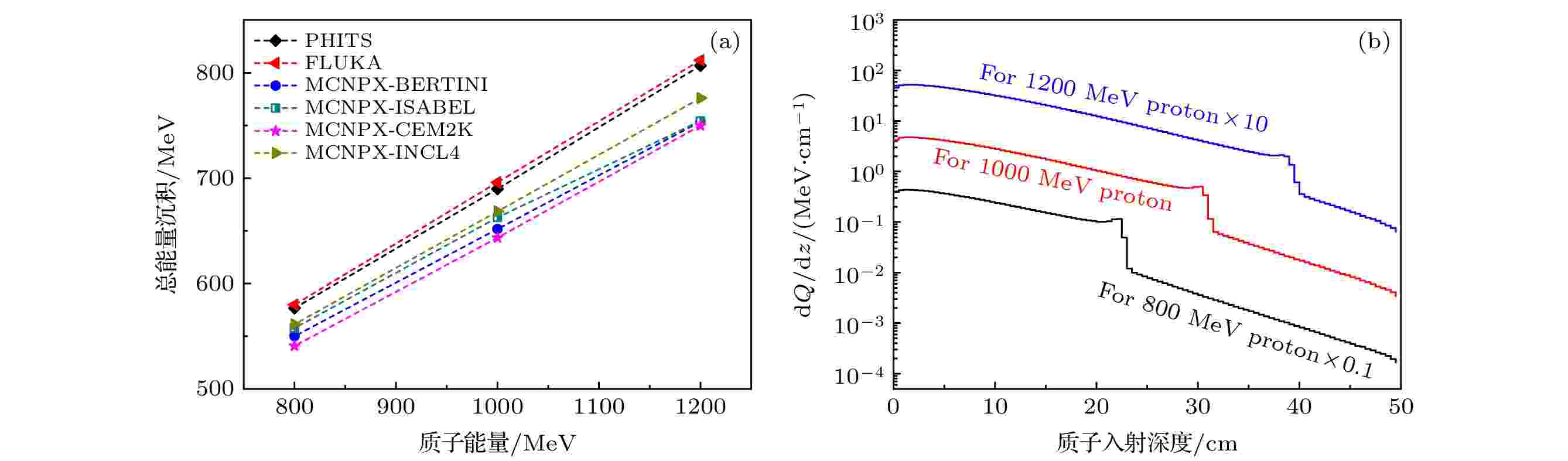
图 2 (a)不同模拟程序对钨靶总能量沉积计算的对比; (b)钨靶中能量沉积线性密度分布
Figure2. (a) Comparison of total energy deposition in tungsten target calculated by different Monte Carlo code; (b) axial distribution of linear density of energy deposition in tungsten target.

2

-->

3.1.实　验

目前, 国内仅有兰州重离子加速器国家实验室的高能质子实验平台可提供能量为250 MeV的质子束流, 流强约为10⁷ proton/s. 由于束流强度偏低, 我们采用TLD^[13,16]的测量方法, 通过测量钨靶中TLD的剂量分布, 从而获得能量沉积数据, 并与模拟计算的结果进行对比.
质子在钨靶中的能量沉积的验证实验示意图如图3所示. 整个钨靶厚度为4 cm, 由厚度分别为1.0, 1.0, 0.5, 0.5, 0.5, 0.5 cm的几个靶块组成. 实验使用的TLD是由防化研究院生产的GR100系列, 其主要成分是LiF(Mg, Ti). 在钨靶的质子入射端面放置了一层TLD, 用于分析质子束流强度与分布. 在钨靶靶块之间布置了若干TLD, 用于分析钨靶不同深度处的能量沉积分布. 为了固定TLD的位置, 加工制作了1 mm厚的硬铝支架, 2个TLD的间距是3 mm. 置于钨靶内部的TLD大多数采用“十”字分布. 为了降低加速器输出质子脉冲稳定性和重复性影响, 实验仅接受了1个质子脉冲束团的辐照, 这也能确保所有TLD都能工作在剂量线性响应区域.
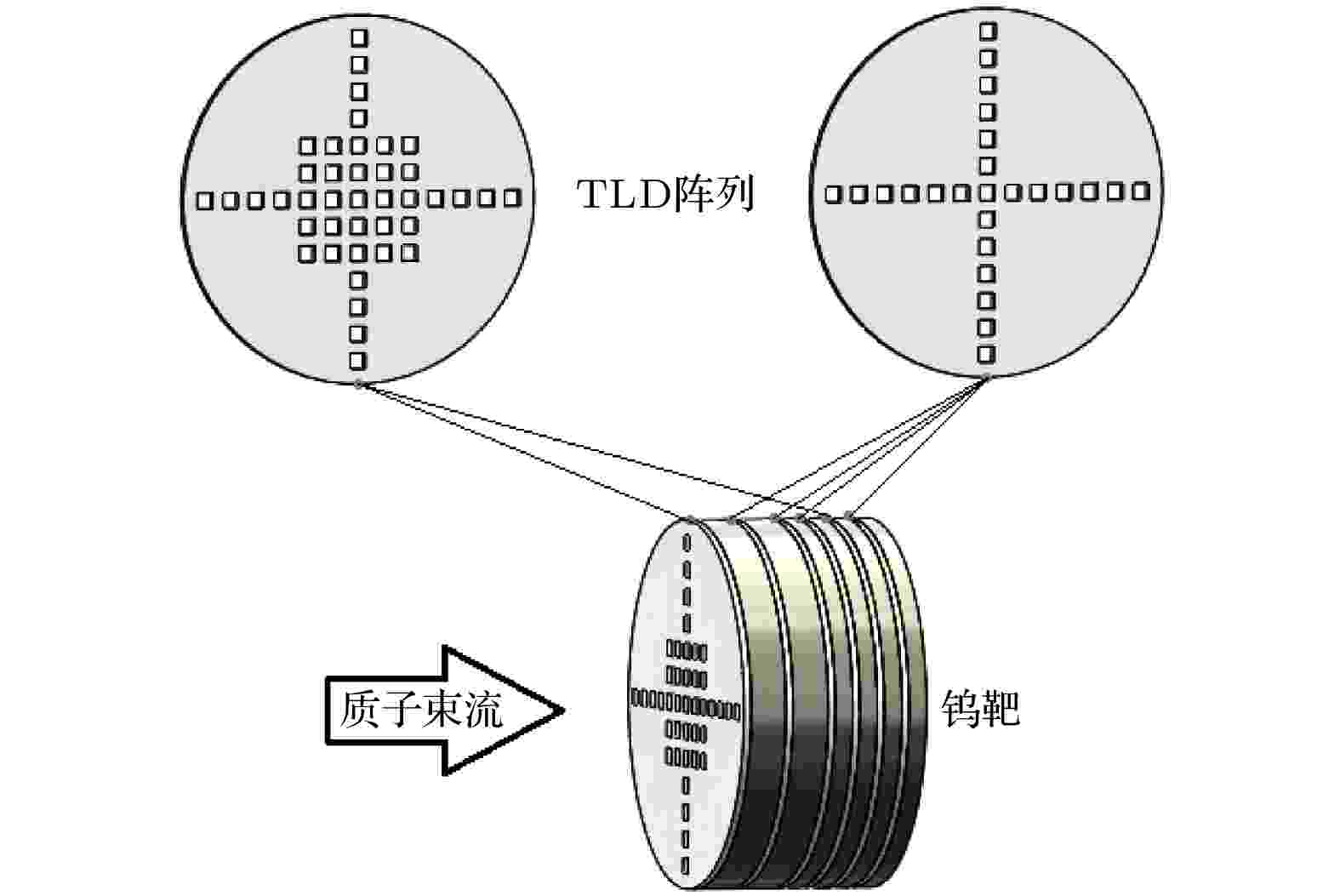图 3 质子在钨靶中的能量沉积测量示意图
Figure3. Schematic of the energy deposition measurement in a tungsten target incident by protons.

经过辐照的TLD采用RGD6型热释光仪^[17]进行数据读出. RGD6型热释光仪通过测量TLD的积分光产额并与标准⁶⁰Co伽玛源剂量的标定光产额进行对比, 其输出量的单位是μGy. 第一层TLD的剂量读出结果如图4所示. 可以看出, 在钨靶几何中心水平面偏左下方区域的TLD剂量读数值较大, 这个区域对应着加速器输出质子束流的直接照射位置. 根据第一层TLD测得的质子直射区域, 结合图3的实验布置, 可以看出仅有 (0, –1) 位置的TLD在质子入射深度的各层对应位置有测量点. 我们采用MCNPX对单个能量为250 MeV的质子直射TLD时的总能量沉积开展了模拟计算. 具有不同线性能量转移值(linear energy transfer, LET)的带电粒子对TLD照射相同剂量后, 相对于等同剂量的⁶⁰Co伽玛源射线照射, TLD的积分发光量会发生变化, 这被称为TLD的相对发光效率^[18]. 第一层TLD被能量为250 MeV的质子直接入射, 对应相对发光效率值^[19]约为1.02. TLD测量值的单位是μGy, 计算值的单位是MeV/g, 通过单位转换与发光效率修正, 对比得到在本次实验中单个质子脉冲辐照钨靶时, 到达(0, –1)位置TLD有效面积上的质子数目约为4.74 × 10⁶个.
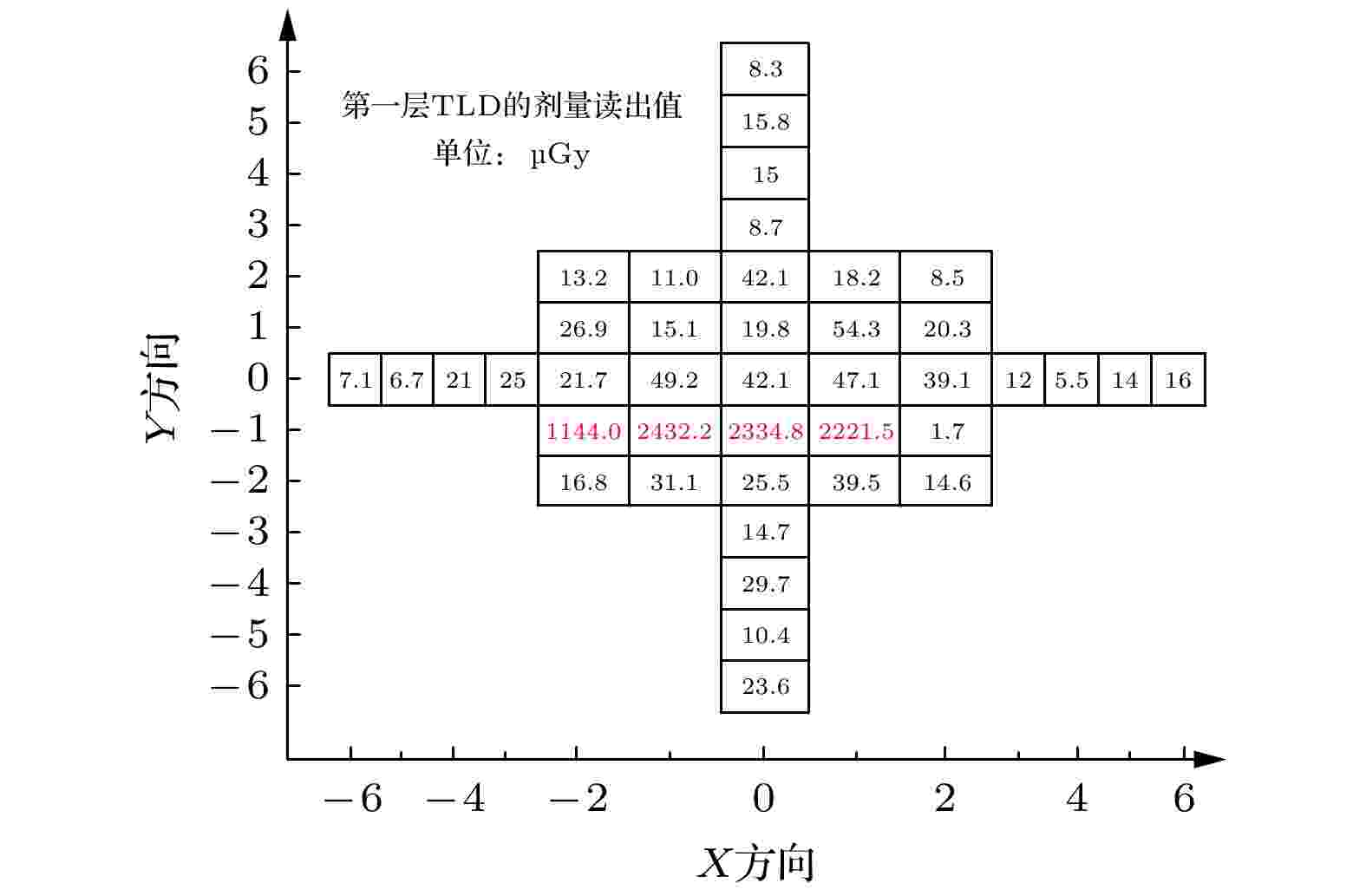图 4 第一层TLD的剂量读出值
Figure4. TLD dose readouts at the first layer.

2 -->

3.2.实验结果分析

为了获得不同深度位置TLD的相对发光效率值, 利用SRIM^[20]程序计算了质子在穿透不同厚度的钨靶后的剩余能量, 并转换为等效水LET值如图5所示. 根据文献[19], 当入射粒子的等效水LET值在0.4—1.2 keV/μm范围时, LiF(Mg, Ti)相对发光效率约为1.02.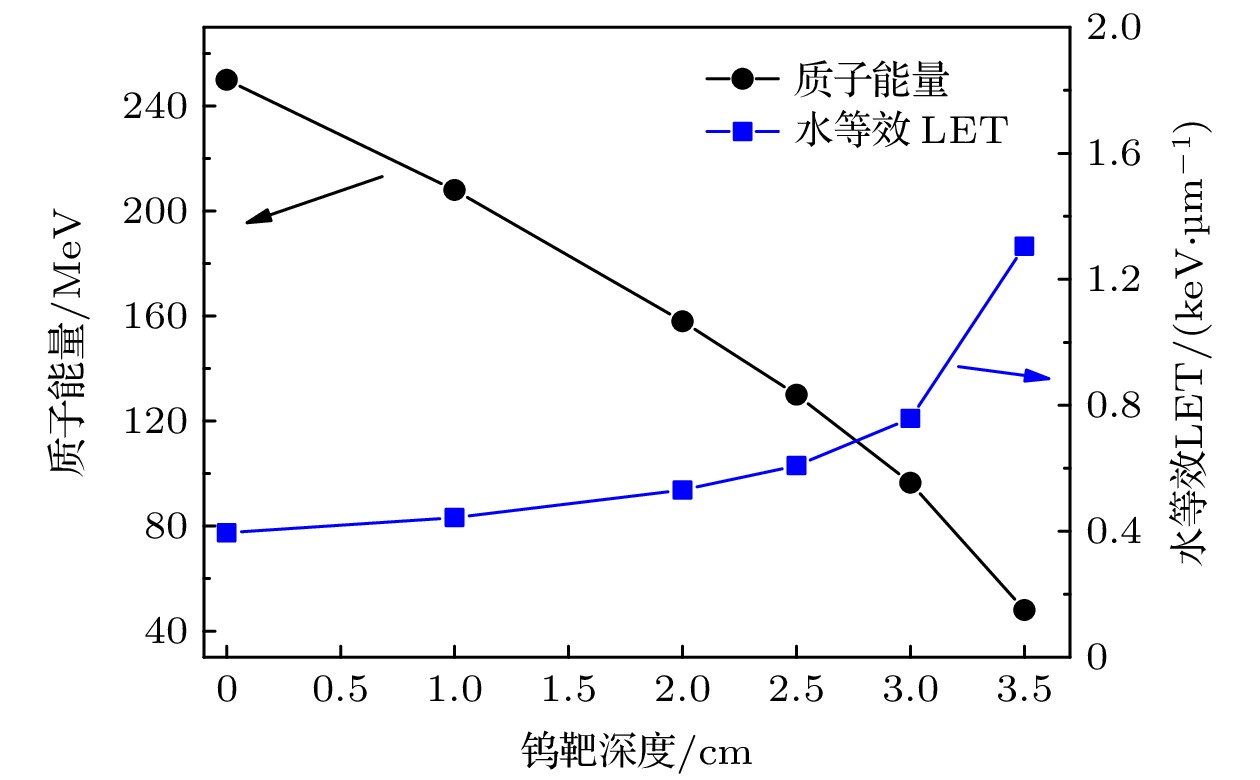
图 5 不同深度的钨靶中质子的平均能量与水等效LET值
Figure5. Average proton energy in the tungsten target and equivalent LET in water.

由于质子是重金属钨靶中能量沉积的主要贡献者, 结合TLD有效面积接受的入射质子数目与相对发光效率, 可以将TLD剂量测量值μGy进行单位转换, 得到单个质子在TLD中引起的能量沉积值, 即MeV/(g·proton).
我们选用MCNPX-CEM2K级联模型对 (0, –1) 位置不同质子入射深度的TLD进行了模拟计算. 首先, 根据图3中测量实验布置的几何条件建立计算模型; 然后, 利用程序中的能量沉积记录卡对分布在钨靶内部不同质子入射深度的TLD中总能量沉积进行了记录. TLD能量沉积模拟计算值与实验测量值, 以及其二者的比较如图6所示.
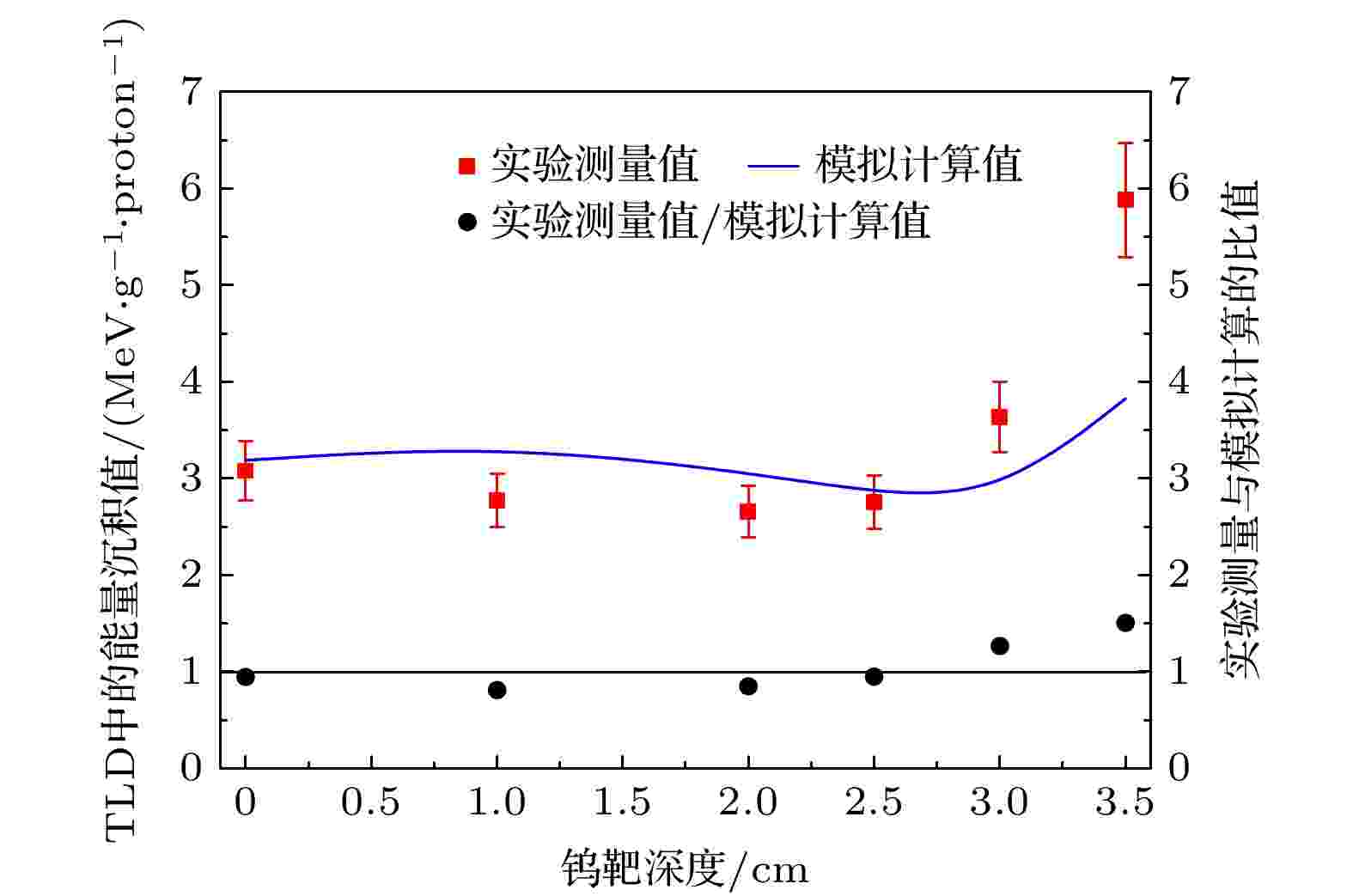图 6 钨靶中TLD的能量沉积测量值与计算值
Figure6. Energy deposition comparison between measurement and calculation of TLD in tungsten target.

可以看出, 总的说来, MCNPX-CEM2K模型能够较好地模拟钨靶中热量沉积的结果. 通过细致地对比可以发现, 在钨靶较浅位置, 实验测量值比模拟计算值略小; 随着钨靶深度的增加, 测量值与模拟值的偏差逐步增大; 在质子射程末端位置, 二者相差最大. 出现较大差别的原因有以下几点: 首先, TLD的有效面积较小, 入射质子束细微的非垂直入射会对较深钨靶位置的测量值带来较大影响; 第二, 随着钨靶深度的增加, 较高LET的次级带电粒子对总能量沉积的占比贡献增大, 质子对总能量沉积的贡献份额减小, 这就需要对TLD的相对发光效率进行更细致的修正. 实验测量数据的误差为10%, 主要来源于质子束斑的不规则、同批次TLD出厂性能的差异、剂量读出设备的系统误差等.

本文分别采用MCNPX, PHITS和FLUKA三种蒙特卡罗粒子输运程序计算了高能质子在金属散裂靶中的能量沉积分布, 通过与已有实验测量结果的比较, 表明这三种蒙特卡罗程序能够对铅靶的能量沉积进行较准确的模拟计算, 相对于实验测量值, 模拟计算的结果高约10%—15%, 即蒙特卡罗程序的模拟计算结果能够比较保守地估计铅靶中的热量沉积. 对3个不同模拟程序及同一模拟程序的不同级联模型的计算结果进行比较, 表明MCNPX程序中的CEM2K级联模型的计算结果最接近实验测量值. 由于迄今国内外尚无高能质子在钨靶中的能量沉积测量数据, 我们利用热释光探测器LiF(Mg, Ti), 测量了能量为250 MeV的质子束在钨靶中的能量沉积分布, 结果表明除了在质子射程末端有较大的差异外, 能量沉积的实验测量结果与MCNPX的计算值有较好的吻合. 通过与实验数据的比较, 验证了蒙特卡罗模拟程序对能量沉积计算具有较高的可靠性.