摘要:基于固体边缘效应, 对碳化硅(SiC)表面激光加工圆环形沟槽的润湿特性进行实验研究, 通过分析去离子水在圆环槽上的润湿性能及其在边缘处的铺展行为, 获得了环槽深度与环槽宽度对液滴在边缘处最大表观接触角的影响规律. 结果表明, SiC圆环槽阻碍液滴铺展, 光滑基体表面上接触角为70°, 激光加工圆环槽深度为290 μm, 宽度为1 mm时, 接触角可达138.5°. 随槽深的增大, 接触角呈现先增大后趋于稳定的趋势, 临界槽深为80 μm. 当槽深小于该极值时, 接触角随槽深的增大而线性增大; 当槽深大于该极值时, 液滴处于稳定钉扎状态, 接触角趋于稳定, 其稳定值符合Gibbs不等式. 环槽宽度存在一临界值40 μm. 当槽宽低于该值时, 液滴接触环槽外缘后越过沟槽继续在平面上铺展; 当槽宽大于该值时, 接触角趋于稳定, 液滴沿边缘铺展.
关键词: SiC/
圆环槽/
液滴铺展/
边缘效应

English Abstract

全文HTML

--> --> -->

表面几何边缘处, 存在液体在毛细力作用下也不能移动的钉扎现象, 这阻碍了液体的铺展, 使接触角增大, 形成固体边缘效应^[1-3]. 基于边缘效应的研究表明^[4-8], 通过合理的表面形貌设计, 可实现对表面液滴铺展的有效限制, 这一结果已广泛应用于微芯片组装的对准^[9]、液滴失稳防护^[10]、各向异性织构制备^[11]、毛细管制备^[12]及微流控装置的防漏^[13]、机身表面冷凝除水^[14]等场合, 也为轴承、密封等工程表面润滑流体的流失控制提供了潜在应用途径.
Gibbs等^[15]首先提出Gibbs方程式, 在几何角度上探讨了边缘处表观接触角与边缘倾角和前进接触角之间的关系. Du等^[16]和Qiao等^[17]针对液滴在不同结构表面上的形态研究表明表面能量势垒对液滴形态起到至关重要的作用. Kim等^[18]的研究表明, 液滴形态和钉扎点位置受重力的影响. Wang等^[19]实验研究了不规则结构的边缘效应, 结果表明锐边对接触线有很强的钉扎作用, 能显著改变接触角及其润湿状态. 通过合理的设计边缘处的形状、尺寸及结构等参数, 可利用边缘效应实现液滴的稳定钉扎, 减缓液滴铺展. Ma等^[20]和Tóth等^[21]对比分析了方形和圆柱形结构边缘处的润湿状态, 结果表明相同表面面积, 圆柱形结构能钉扎更大的液滴.
为更好地理解圆柱形槽边缘效应对液滴铺展行为的影响规律, 已有****开展了材料属性^[22]、倾角^[2,22-24]、侧壁表面粗糙度^[24,25]、侧壁高度^[9,24,26]等参数的影响研究, 结果表明上述参数均影响固体的边缘效应, 通过改善边缘尺寸、选取合适材料等方法, 可有效提高边缘处的最大接触角. Chang等^[9]对液滴在不同侧壁高度微芯片上边缘效应的研究表明, 侧壁高度对接触线钉扎和自定线过程均有影响, 侧壁高度大于280 nm可实现液滴的稳定钉扎. Oliver等^[22]研究了铝盘表面上液滴的铺展行为, 证实了液滴在边缘处钉扎时的Gibbs条件, 发现液滴在侧壁同一高度处达到一固定的临界接触角; 然而, 在90°侧壁倾角的蓝宝石表面并不存在这一现象. Kalinin等^[24]采用微加工技术加工圆柱凸台, 结果表明微加工表面可大大提高液滴在边缘处的最大接触角: 当环高大于2 μm时边缘效应显著, 且最大接触角不再随高度变化; 环高小于2 μm, 最大接触角随环高的减小而减小; 研究结果同时表明, 最大接触角的大小与环宽无关. Muller等^[26]实验研究了液滴在高为200 nm—31.8 μm的圆柱形硅片上的边缘效应, 表明高度在630 nm以内, 柱面存在对接触角无影响; 小于7.2 μm时, 最大接触角随高度的增大呈线性增大; 高于7.2 μm后, 接触线钉扎基本稳定. 研究同时表明, 柱面半径、进样速度及湿度等参数不影响边缘处的最大接触角及其润湿性转变. Wang等^[27]对沟槽织构上液滴的各向异性研究表明, 液滴在垂直于沟槽方向上的铺展行为受沟槽尺寸的影响显著. 随沟槽宽度的增大, 液滴接触角呈先增大后减小的趋势, 当槽宽为128 μm时接触角存在最大值. 基于侧壁粗糙度对边缘效应的影响研究表明^[23,28], 不光滑的侧面使得表面粗糙度与宏观几何形貌之间的关系更加复杂. 相较于上述微观结构的研究, 密封端面上宏观结构对承载能力和密封性能的影响显著. 润湿界面对润滑油膜厚度有显著影响^[29], 因此研究固体边缘效应对液滴铺展特性的影响对于探讨密封设计与优化具有十分重要的意义.
目前, 针对SiC基体的边缘效应, 尤其是结构参数的影响规律研究较为欠缺. 本文选取密封常用材料SiC为研究对象, 采用激光加工工艺在基体上制备不同槽深和槽宽的圆环槽, 分别探讨了去离子水在圆环槽上的铺展特性、边缘处的钉扎效应等现象, 在此基础上研究了槽深和槽宽对最大表观接触角影响规律, 并探讨其影响机理, 以期为可控流体流失的密封端面设计提供设计参考.

2

-->

2.1.实验方案

图1所示为本实验原理图, 首先将试件置于水平载物台上, 载物台通过水平仪调平, 以防止由于表面不平引起的液滴侧向运动. 采用微量进样器以0.2 μL/s的速度补充液体, 通过在水平和竖直方向配置显微镜头的CCD相机观测液滴在SiC圆环槽表面上的润湿及铺展行为, 抓取30帧/s的液滴运动视频及铺展俯视图, 记录液滴形状及接触角随液滴体积的变化规律, 所得实验数据储存于计算机中并进行后续处理.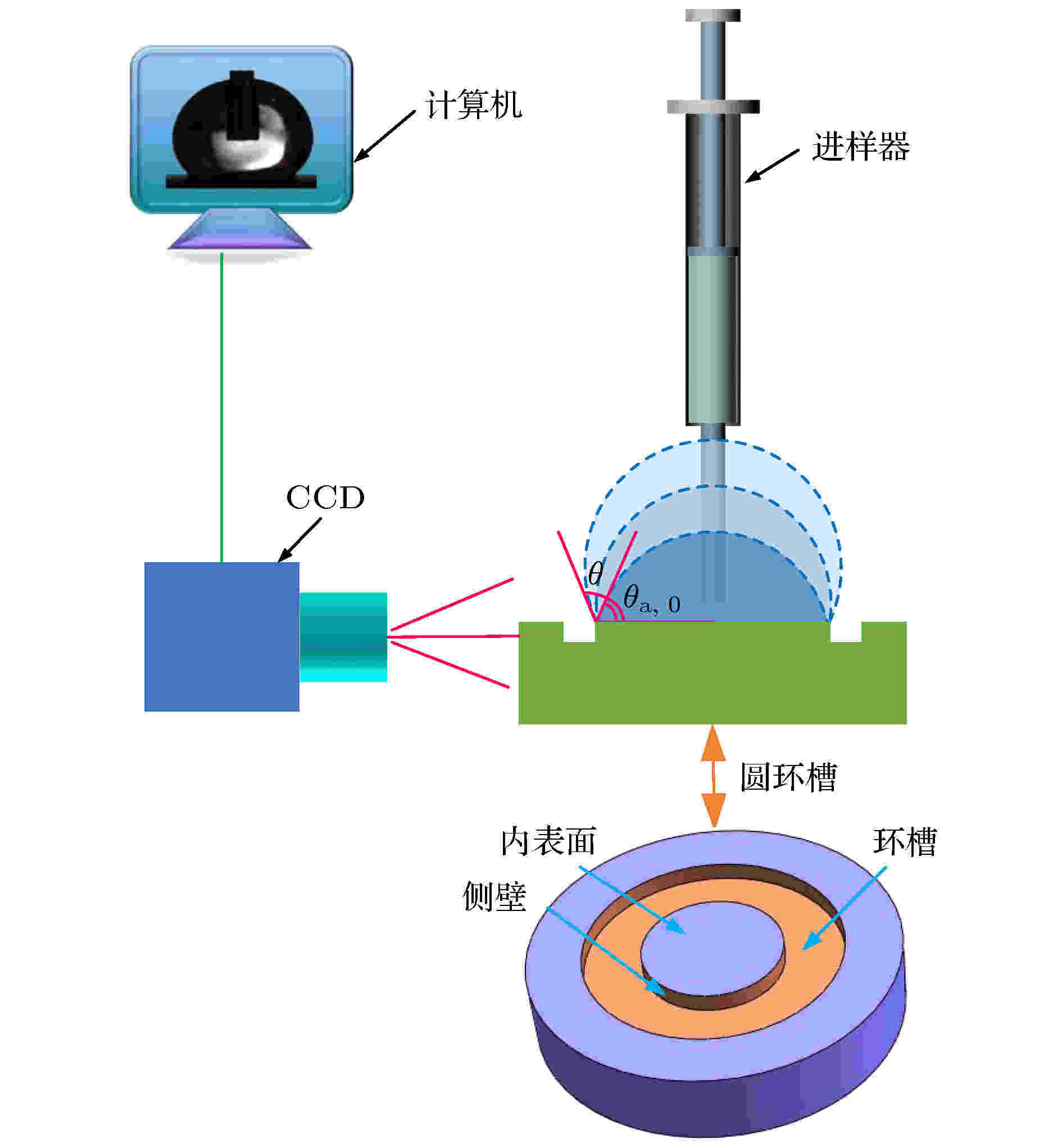
图 1 实验装置原理图
Figure1. Schematic diagram of experiment device.

采用五点拟合法进行接触角的测量, 选取去离子水进行润湿性及铺展特性的研究, 其表面张力γ = 0.072 N/m, 动力黏度η = 8.9 × 10^–4 Pa·s, 密度ρ = 10³ kg/m³; 实验环境温度为25 ℃, 空气湿度为40%, 每组试验重复5次.
2 -->

2.2.形貌设计

Young^[30]给出光滑表面上液滴的润湿性模型: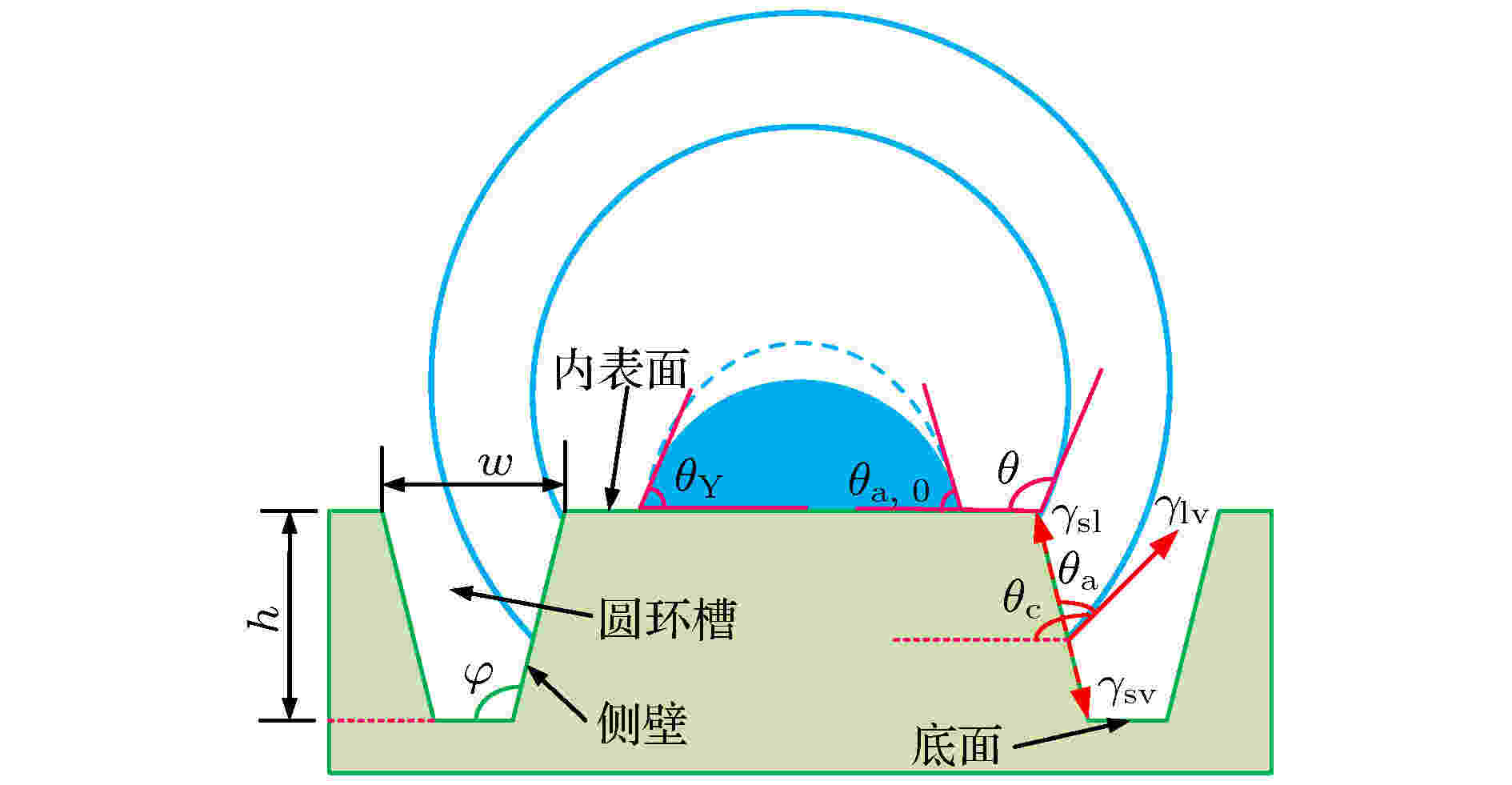

${\gamma _{{\rm{lv}}}} \cdot \cos {\theta _{\rm{Y}}} + {\gamma _{{\rm{sl}}}} - \gamma {}_{{\rm{sv}}} = 0,$

其中, γ_lv, γ_sl, γ_sv分别为液-气、固-液、固-气的表面张力, θ_Y为固有接触角. 式(1)表明在绝对光滑表面上, 液滴的接触角仅与表面张力有关. 而实际工程表面上, 必然存在表面缺陷, 液滴越过表面缺陷时, 需克服表面缺陷产生的能量势垒作用. 液滴在圆环形槽表面上的铺展原理图如图2所示.
图 2 液滴在圆环形槽表面铺展原理图
Figure2. Schematic diagram of droplet spreading on ring-grooved structures.

液滴在光滑内表面的固有接触角为θ_Y, 随着液体的不断注入, 接触角变为前进接触角θ_{a, 0}时, 接触线开始沿着内表面向边缘处移动, 到达边缘处产生钉扎, 边缘处的表观接触角为θ. 随着液体的继续补充, 液滴沿侧壁移动一段距离, 达到临界接触角θ_C后产生坍塌. 临界接触角θ_C首先由Gibbs^[15]提出, 以说明两光滑表面边缘处的钉扎效应, 其表达式为

${\theta _{\rm{C}}} = {\theta _{{\rm{a,0}}}} + {\rm{(180}}^\circ -\phi {\rm{)}},$

其中, θ_C为边缘处的临界接触角, φ为侧壁倾斜角. 可以看出, 表观接触角主要与前进接触角和侧壁倾斜角有关, 对特定结构的材料而言, 表观接触角的变化最终受限于前进接触角. 对于实际表面, 表观接触角通常由Gibbs不等式来表征^[2,25,28]:

$\theta _{\rm{a}} < \theta < {\rm{(180}}^\circ -\phi {\rm{)}} + \theta_ {\rm{a}},$

其中, θ为表观接触角, 即液滴切线与水平方向之间的夹角, θ_a为液滴在侧壁上的前进接触角. 对于光滑表面φ = 180°, 当表面存在一固体边缘时φ < 180°, 因此边缘处产生的钉扎效应可提高接触角.
Oliver^[22]进一步给出了液滴稳定条件:

$\phi _{\rm{c}} = \theta _{\rm{a}} + 2{\tan ^{ - 1}}\left(\frac{1}{2}\cot \theta _{\rm{a}}\right),$

其中, φ_c为Oliver给出的液滴稳定时侧壁倾斜角的临界值. 当φ > φ_c时, 随液滴体积的增加, 液滴越过边缘后, 处于稳定状态, 并最终在重力作用下产生破裂; θ_a < φ < φ_c时, 液滴越过边缘后呈现不稳定状态, 接触线产生突然跳跃, 并沿着侧壁产生扩散^[2,22].
液滴在表面上受到惯性力、表面张力、黏性力和重力作用. 本实验中, 选取去离子水为研究对象, 其毛细长度l_c^[1]为

$l_{\rm{c}} = \sqrt {\frac{\gamma }{{\rho g}}} = {2.7\;{\rm{mm}}},$

其中, γ为液体的表面张力, ρ为液体密度, g为重力加速度. 实验中圆环槽内半径r_i = 1.5 mm < l_c, 因此可忽略重力效应的影响.
通常采用We数表征惯性力与表面张力之间的关系^[1,31], 有:

$We = \frac{{\rho R \cdot {\nu ^2}}}{\gamma },$

其中, R为液体的特征长度, 取为R = 1.5 mm, v为液体的进样速度v = 0.2 μL/s, 求得We < 0.02, 此时惯性力可忽略.
采用Ca数表征黏性力与表面张力之间的作用关系, 有:

$Ca = {{\mu \cdot \nu }}/{\gamma },$

其中, μ为液体黏度, 求得Ca < 10^–5, 可认为液滴在表面上的运动处于准静态过程.
2 -->

2.3.试件制备

实验选取SiC作为基体材料, 采用光纤激光打标机在SiC基体上加工环形沟槽, 并进行二次抛光, 使用去离子水和丙酮清洗, 烘干后进行液滴的铺展实验. 图3以深100 μm, 宽1 mm的圆环形沟槽为例, 给出采用DektakXT台阶仪获得的表面形貌图及其二维轮廓图.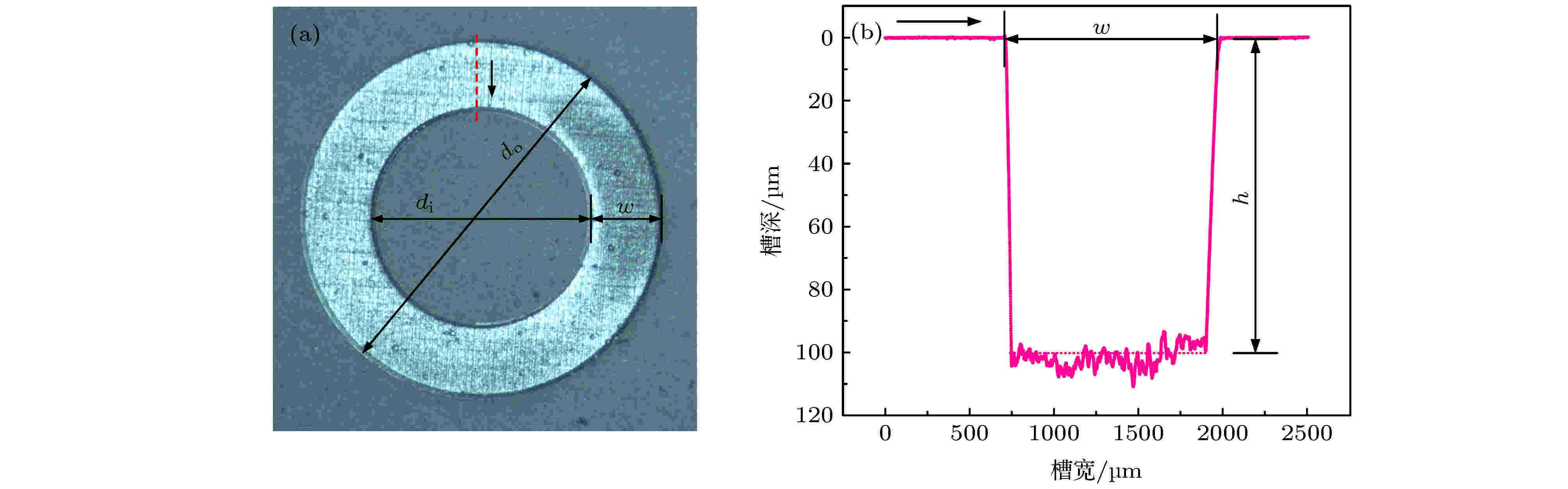
图 3 圆环槽形貌示意图　(a) 表面形貌图; (b) 二维轮廓图(d_i = 3 mm, h = 100 μm, w = 1 mm)
Figure3. Schematic diagram of ring groove topography: (a) Surface topography; (b) 2D contour map (d_i = 3 mm, h = 100 μm, w = 1 mm).

由图可见, 环槽内表面为抛光平面, 测得表面粗糙度R_a为0.1 μm. 环槽内径为d_i, 激光加工圆环形沟槽外径为d_o, 槽深为h, 环槽内壁倾角φ为94°, 符合方程(4)的稳定性条件. 为表征方便, 定义环槽宽度w = (d_o–d_i)/2.
图4给出去离子水在光滑SiC基体和激光织构SiC基体上的润湿性能. 光滑表面上的固有接触角θ_Y = 70°(图4(a)), 其前进接触角θ_{a, 0} = 76.5°, 见图4(b). 激光加工后, 表面粗糙度增加(R_a为0.8 μm), 其亲水性增强, 固有接触角θ₁ = 50°(图4(c)), 织构表面上的前进接触角为θ_a = 54°(图4(d)).
图 4 SiC圆环槽表面接触角　(a) 光滑平面固态接触角; (b) 光滑表面前进接触角; (c) 织构表面固有接触角; (d) 织构表面前进接触角
Figure4. SiC ring groove surface contact angle: (a)Smooth plane static contact angle; (b) smooth surface advancing contact angle; (c) static contact angle of textured surface; (d) advancing contact angle of textured surface.

前进接触角θ_a大于固有接触角θ₁, 主要是由于表面是不均匀的, 结构的不均匀性必然会导致表面能障的存在, 阻止接触线的移动, 导致表观接触角增大. 固体边缘的存在, 同样会产生能量势垒, 引起接触角变化, 为更好的描述边缘效应的影响, 后续涉及到的接触角均为侧壁处前进接触角θ_a = 54°.
相关研究表明, 内表面半径、进样速度等不影响边缘处的最大接触角^[26]. 考虑激光加工特点, 固定内径d_i = 3 mm, 改变槽深和槽宽进行实验设计. 实验用圆环槽的几何参数见表1.

序号	内径di/ mm	槽深h/μm	槽宽w/μm	序号	内径di/mm	槽深h/μm	槽宽w/μm
1	3	20	1000	2	3	100	20
		50					40
		80					60
		100					80
		200					100
		290					200
		480
		620

表1SiC圆环槽几何参数表
Table1.Structural parameters of ring grooved on SiC surface.

2

-->

3.1.液滴的铺展行为

图5所示为液滴在h = 290 μm, w = 1 mm圆环槽上的铺展行为. 由图可见, 液滴在圆环槽上的铺展分为4个阶段: 1)液滴体积逐渐增大, 液滴以前进接触角θ_{a, 0}为76.5°沿着光滑内表面向边缘处运动(图5(a)); 2)液滴接触线与边缘接触, 此时接触角θ₀维持为76.5°(图5(b)); 3)液滴在边缘处产生钉扎(图5(c)), 随着体积增大, 接触角增大, 破裂前达到最大θ_max; 4)液滴失稳, 迅速的沿侧壁铺展, 浸润环槽后在外径处继续铺展, 直到接触角稳定在θ^'为68.5°(图5(d)).
图 5 液滴在SiC圆环槽的铺展行为　(a)内表面前进液滴; (b) 内边缘前进液滴; (c) 内边缘临界液滴; (d) 破裂液滴
Figure5. Spreading behavior of liquid drop in SiC ring groove: (a) Advancing drop on the inner surface; (b) advancing drop on inner edge; (c) inner edge critical drop; (d) breaking up.

由阶段1)到2), 液滴接触角始终是恒定的, 即抛光的光滑SiC表面可视为各向同性结构, 进样速度不高时, 液滴以恒定前进接触角向边缘移动. 由阶段2)到3)运动时, 液滴接触线钉扎在边缘处, 随体积增大, 接触角增大, 直至达到最大接触角138.5°, 同时对照俯视图可见, 液滴始终钉扎在内径边缘处. 由阶段3)到4)的俯视图可以看出, 液滴接触角达到最大值后继续补充液体, 液滴失稳, 其越过环槽外径继续铺展, 并最终达到稳定.
由图5(c)可见, 液滴在边缘处的最大接触角为138.5°, 小于Gibbs方程式所求得的140°. 产生这种现象, 可能是由于液滴振动造成的, 也可能是由于表面粗糙度等因素产生的^[23,32].
2 -->

3.2.边缘处的钉扎效应

图6所示为去离子水在SiC圆环槽内表面的接触角示意图. 液滴刚到达边缘时, 接触角与光滑表面上的前进接触角一致, 为76.5°(图6(a)). 随着液体的持续补充, 液滴体积增大, 接触线尺寸基本不变或沿侧壁产生缓慢移动, 必然导致接触角增大, 如图6(b)—6(g)所示, 液滴表观接触角由图6(b)所示的93.4°增大至图6(g)所示的133.3°. 继续补充液体, 到达图6(h)时, 液滴有最大体积28.2 μL, 对应有最大表观接触角138.5°. 可见, 随液滴体积增大, 在边缘处接触角呈现增加的趋势. 这一结果与方程式(2)相符, 圆环槽边缘的存在使钉扎效应增强, 接触角增大.
图 6 液滴在SiC圆环形槽内表面边缘处的接触角(h = 290 μm, w = 1 mm)
Figure6. Contact angle of the droplet at the edge of the inner surface of the SiC circular groove (h = 290 μm, w = 1 mm).

产生这种现象主要是由于边缘的存在产生能量势垒, 阻碍液滴的进一步铺展, 为适应液滴额外增加的体积, 必然导致液滴接触角的增大.
2 -->

3.3.槽深对液滴铺展性能的影响

图7给出液滴在圆环槽(d_i = 3 mm, w = 1 mm)基体上, 最大表观接触角θ_max随槽深的变化曲线, 试验所选参数见表1. 由图可见, 随槽深增大, 接触角呈现先增大后趋于稳定的趋势. 槽深h为20 μm时, θ_max为115.5°; 当h增大到80 μm, θ_max几乎呈线性增大到138°, 随后θ_max基本保持不变, 这一结果与Oliver等^[22]、Kalinin等^[24]、Muller等^[26]的结果一致. 同时, 也与方程(2)的理论分析一致, 即初始达到θ_max时从几何关系上对应着一稳定的槽深值. 宏观上分析这一现象产生的原因, 可能是由于黏性效应或机械振动导致随θ_max增大液滴在侧壁上的滑移长度增大. 当滑移长度小于槽深时, 液滴处于稳定状态, 随液滴体积的持续增大, 达到临界值后产生坍塌. 当滑移长度大于槽深时, 出现液滴与槽底的接触, 此时液滴处于亚稳态, 微小的外力作用(如机械运动)即可导致液滴破裂, 若继续增加液体, 将导致液滴在表面张力作用下产生坍塌.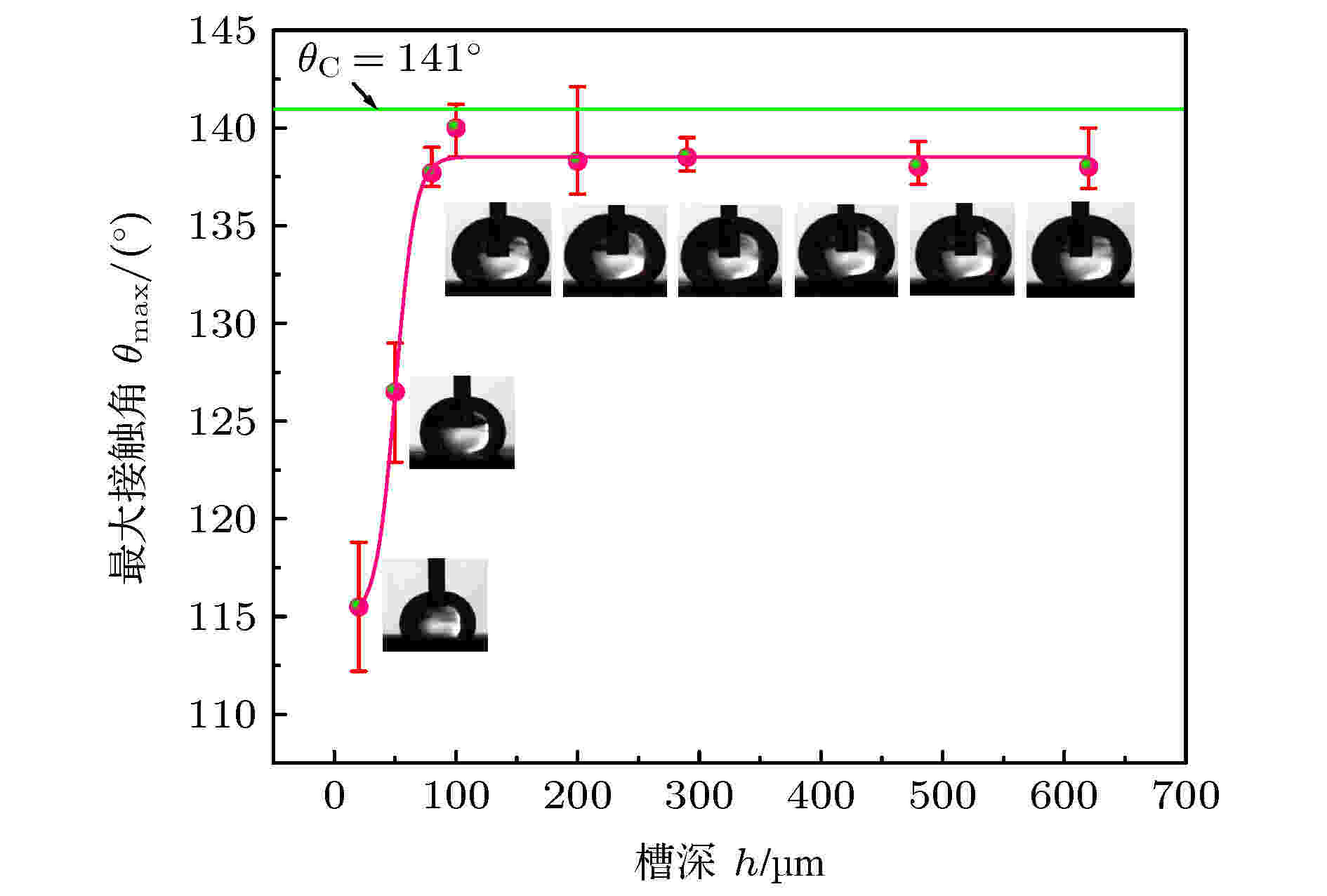
图 7 最大接触角随槽深的变化曲线(d_i =3 mm, w = 1 mm)
Figure7. Variation curve of maximum contact angle with groove depth(d_i = 3 mm, w = 1 mm).

可以认为, 液滴在圆环形槽边缘处存在一临界槽深h_c, 即达到θ_max时对应的最小槽深值, 使液滴由稳定状态向亚稳态转变. 当h > h_c时, 液滴在边缘处于稳定钉扎状态, θ_max不随槽深的变化而变化, 随着液滴体积的持续增加, 当达到临界体积后产生液滴坍塌. 当h ≤ h_c时, 液滴处于亚稳态, θ_max随槽深的减小而显著减小, 当表观接触角达到θ_max时, 继续增加液体, 使液滴在表面张力作用下产生坍塌. 对于激光加工圆环槽的SiC基体, h_c为80 μm.
图7中当h = 100 μm时存在一较其它组略大的θ_max, 可能是由于侧壁表面粗糙度或表面污染等原因造成的.
当前, 针对液滴在接触线处的钉扎及其沿侧壁的润湿铺展过程有两种主要观点: 1)液滴接触角在内表面首先增大到θ_max, 然后沿侧壁开始产生滑移^[15]; 2)液滴在边缘处接触角增大的同时, 并没有固定在边缘上, 而是同时产生侧壁上的润湿^[10,26]. 实验中当h < h_c时, 随深度减小, θ_max呈线性减小, 因此认为液滴的接触角增大与沿侧壁的润湿同时发生; 否则在所有环槽表面上, 接触角都应同时达到最大值之后, 再产生铺展运动.
2 -->

3.4.槽宽对液滴铺展性能的影响

对于d_i = 3 mm, h = 100 μm, 改变槽宽w, 可得到θ_max随w的变化曲线如图8所示.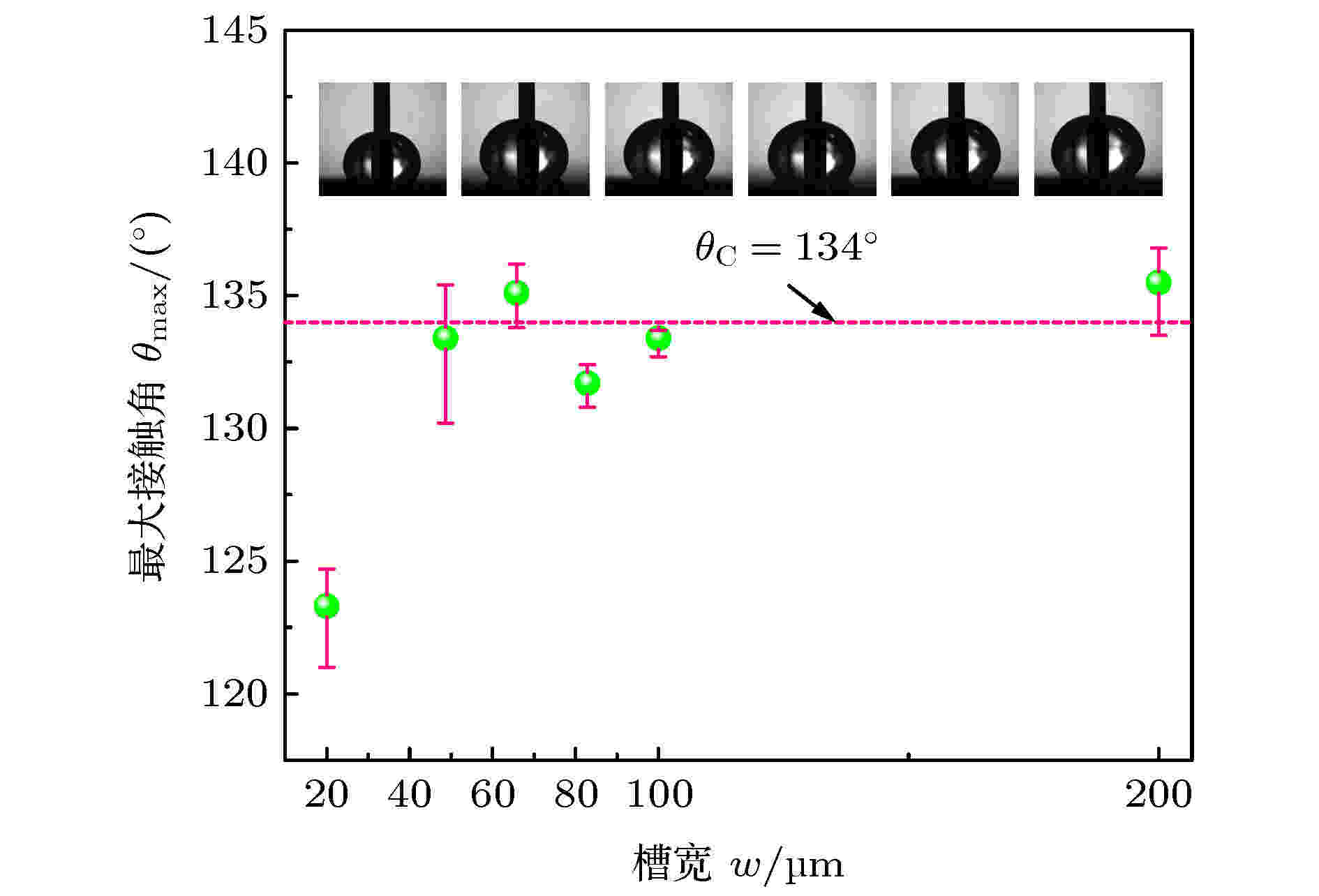
图 8 最大接触角随槽宽的变化曲线
Figure8. Variation curve of maximum contact angle with groove width.

由图可见, 当w = 20 μm时, θ_max = 123.3°; 当w > 40 μm时, θ_max为134° ± 3°. 即, 对于h = 100 μm处于稳定钉扎状态的圆环槽, 存在一临界槽宽w_c = 40 μm, 当w < w_c时, θ_max随w的增大而增大; 当w ≥ w_c时, θ_max随槽宽的增大不再产生变化. 这一结果与Wang等^[27]液滴接触角随沟槽尺寸的变化规律一致. 采用极限分析法, 当槽宽为无穷小时表面可视为光滑表面, 此时接触角较小为光滑表面接触角^[27]; 当槽宽为无穷大时表面可视为圆形凸台, 理想条件下接触角应稳定在Gibbs临界接触角.
考虑液滴的运动特性分析产生这种现象的原因, 主要是由于当槽深h > h_c、槽宽w ≤ w_c时, 液滴在侧壁上的前进接触角为54°, 由θ_a, h, w之间的几何关系可知, 液滴在接触圆环槽底部之前先接触圆环槽的外径边缘, 阻碍液滴运动的能量势垒减小, 更易导致液滴的失稳和铺展润湿. 因此w越小, θ_max越小; 当w ≥ w_c时, θ_max基本趋于稳定. 对于激光加工圆环槽的SiC基体, w_c为40 μm.
综上可知, 当w ≥ w_c, h > h_c时, 液滴在边缘处产生稳定钉扎, θ_max与槽深和槽宽无关. 当w ≥ w_c, h ≤ h_c时, 液滴体积增大, 使边缘处接触角增大, 同时, 液滴开始沿侧壁运动; 当液滴接触线触到槽底时, 液滴处于不稳定状态, 继续增加液体, 微小外力作用使液滴坍塌; 此时, 随槽深减小, θ_max呈线性迅速减小. 对于h > h_c处于稳定钉扎的环槽, 当w < w_c时, 液滴轮廓线在接触槽底之前先接触圆环槽外边缘, 此时液滴运动的能量势垒降低, 因此θ_max随槽宽减小而减小.

对SiC表面激光加工圆环槽阻碍液体铺展作用的边缘效应进行了研究, 重点分析了圆环槽深度和宽度对边缘润湿现象的影响规律. 结果表明:
1)环槽内表面处边缘效应可导致表观接触角的增大, 通过合理的参数设计可使SiC表面液滴的表观接触角由70°增大为138.5°, 从而可实现表面液体铺展运动的主动控制.
2)边缘处液滴接触角增大的同时伴随着沿环槽侧壁的滑移, 滑移距离存在一极值, 即存在一临界槽深h_c. 当h ≤ h_c时, θ_max随h的增大呈线性增大; 当环槽深度h > h_c时, 液滴在边缘处产生稳定钉扎, θ_max基本不变. 对SiC圆环槽而言, 其临界深度为80 μm.
3)圆环槽宽度影响边缘的阻碍作用, 宽度增大时, 液滴跨越沟槽的能量壁垒增大. 本研究中, 槽宽在40 μm范围内影响圆环槽对液体铺展的阻碍作用, 槽宽大于40 μm后液滴在边缘产生稳定钉扎.