全文HTML
--> --> -->材料显微组织对材料性能有重要影响. 开展微观组织演变模拟对于深入理解晶粒形核和长大/粗化过程, 有效控制合金凝固组织具有重要意义. 在合金微观组织模拟方面, 目前采用的方法主要有: 相场法(PF)[11-13]和元胞自动机法(CA)[14,15]. 其中, CA方法能够充分地考虑影响枝晶生长的各种物理机理, 与具有明确物理意义的参数相结合, 算法简单, 计算效率较高. 1994年, Gandin和Rappaz [16]首先建立了研究凝固组织形成过程的二维CA模型, 计算了晶粒在模具壁或熔体内部的异质形核, 再现了柱状晶向等轴晶的转变(CET)以及柱状晶的竞争生长, 但该模型只适用于模拟纯金属等温凝固过程. 此后, CA模拟方法得到了迅速的发展. 2001年, Zhu和Hong[17]在考虑固、液相之间溶质再分配的基础上提出了改进的CA模型, 模拟了Al-Cu合金凝固过程中柱状晶和等轴晶的形貌演变. 石玉峰等[18]建立了适用于三元铝合金枝晶生长的CA模型, 模拟了Al-Si-Mg合金的枝晶组织演变. 随后, 潘诗琰和朱鸣芳[19]又将CA模型从二维扩展到了三维. 张显飞等[20]建立了模拟合金树枝晶生长的三维元胞自动机模型, 考虑了合金元素之间相互作用对溶质扩散的影响, 给出了耦合枝晶生长动力学和合金凝固热力学计算模拟凝固组织形成过程的方法, 并用所建模型模拟了二元Al-Cu合金和三元Al-Cu-Mg合金的枝晶生长过程. 迄今为止, CA模型的发展经历了从二维到三维、从纯金属到合金的过程, 并逐渐引入温度场、浓度场等对晶粒微观组织形貌演变的影响, 能够很好地呈现界面处溶质再分配、成分过冷等对生长的影响. 然而, 以往的CA模型通常依据实验结果来推测合金凝固时的形核过程, 不能真正地实现晶粒形核与枝晶生长过程的耦合模拟.
本文在耦合合金热力学计算的基础上, 基于群体动力学方法描述α-Al形核过程及球形生长过程, 基于CA方法描述α-Al晶粒枝晶生长. 实现了晶粒形核与枝晶生长过程的耦合计算. 通过与实验结果比较, 验证了该模型的准确性. 利用所建模型研究了不同凝固条件下Al-5Ti-1B中间合金细化处理工业纯铝过程中的凝固组织演变行为.
2
2.1.α-Al形核及晶粒球形长大的群体动力学模型
定义函数f (r, t)来描述α-Al晶粒的尺寸分布. 则t时刻, 熔体内半径处于r — r + dr范围内α-Al晶粒的数量密度为f (r, t)dr. α-Al晶粒的数量密度n, 平均半径
当Al熔体中有充足数量的有效异质形核粒子时, α-Al的形核率通过经典形核理论计算[23]:
当熔体中有效异质形核粒子数量不足时, 在t—t + ?t时间段内, α-Al晶粒形核过程受该时间间隔内熔体中有效异质形核粒子数量密度ΔN(t)的限制, 该时间段内, α-Al的形核率表示为
2
2.2.α-Al枝晶生长的CA模型
当晶粒不能维持球形生长形态时, 会转变为树枝状的形貌继续长大. 在枝晶生长过程中, 液相中溶质扩散的浓度场控制方程为[17]
在Δt时间内, 界面元胞固相分数的增量Δfs通过下式计算[20]:
基于固液界面处溶质守恒原则, 界面的法向生长速度vn为[24]
枝晶生长过程中, 枝晶表面的过冷度ΔT可以表示为[18]
2
2.3.合金热力学计算
基于置换溶液模型, 合金体系的吉布斯自由能由下式计算[26]:
Al熔体与α-Al之间的界面能σS/L可以通过下式计算[28]:
ΔSf, m可以通过热力学第二定律导出式计算[29]:
ΔHf, m通过下式计算[29]:
2
2.4.温度场控制方程
凝固过程中, 合金熔体的温度变化通过下式计算:| Element | Liquidus slope, m | Partition coefficient, k | Solute composition/% (weight percent) | Q |
| Fe | –2.925 | 0.030 | 0.0825 | 0.234 |
| Si | –6.62 | 0.120 | 0.0475 | 0.276 |
| Ga | –2.52 | 0.140 | 0.0125 | 0.028 |
| Ni | –3.50 | 0.004 | 0.0051 | 0.018 |
| V | 9.71 | 3.330 | 0.0079 | 0.167 |
| Ti | 25.63 | 7.000 | 0.0042 | 0.63 |
| Na | –7.84 | 0.013 | 0.0015 | 0.012 |
表1工业纯铝成分[30]
Table1.The composition of solute in the CP-Al alloys used by Greer et al.[30].
| Parameter | Value |
| Cooling rate of the CP-Al melt/(K·s–1) | 3.5 |
| Strength of the anisotropy of the interfacial energy, ε | 0.04 |
| Gibbs-Thomson coefficient, $\varGamma $/mK | 1.42 × 107 |
| Heat capacity of Al melt, CP/(J·K–1·m3) | 2.58 × 106 |
| Average jump distance of Al atoms in Al melt, δ/m | 2.87 × 10–10 |
| Boltzmann’s constant, kB | 1.38 × 10–23 |
表2模拟使用的工业纯铝参数[22,30,32]
Table2.The parameters of CP-Al alloys used in the simulations[22,30,32].
加入熔体中的TiB2粒子尺寸分布通过下式描述:
2
3.1.细化处理条件下铝合金凝固微观组织演变
通过拟合计算确定α-Al与TiB2粒子之间的接触角θ. 即取不同的接触角θ, 模拟0.3%的Al-5Ti-1B中间合金添加到工业纯铝熔体中, 并以3.5 K/s的冷却速度凝固后工业纯铝的最终凝固组织及晶粒尺寸. 对比模拟结果与实验结果, 确定θ为4.8°.图1为添加0.01% Al-5Ti-1B中间合金后, 熔体以3.5 K/s的速度冷却时, 工业纯铝凝固过程中熔体的过饱和度、液-固相变的形核驱动力以及α-Al形核率与凝固时间的关系. 随着熔体温度的降低, 熔体逐渐变为过饱和状态. 熔体的过饱和度和形核驱动力随着熔体冷却时间的延长逐渐增大. 当熔体的温度降低到某一临界温度时, α-Al在Al熔体中开始形核. 形核过程非常短暂, 大约为0.07 s. 由于受到有效TiB2粒子数量的影响, α-Al的形核过程可分为两个阶段: 阶段I为形核刚开始发生时, 熔体中有效TiB2粒子数量充足, α-Al形核率由(6)式确定; 阶段II为随着熔体过饱和度、α-Al形核驱动力的增大, 有效TiB2粒子数量增加速度不能满足熔体形核时, 有效TiB2粒子数目将限制熔体中α-Al的形核(图1中阶段II). 熔体冷却过程中, 晶粒形核和长大释放凝固潜热趋向于降低熔体过冷度, 熔体与外界热交换引起的熔体温度降低将增加熔体过冷度. 在凝固的初始阶段, 熔体中α-Al晶粒的形核率及数量比较低, 因此熔体过冷度随着凝固时间的增加逐渐增加. 高的过冷度使得熔体内部晶核形核率增加, 形成较多新的α-Al晶粒. 当凝固潜热释放的速度超过熔体与外界换热速度时, 再辉发生, 熔体过冷度减小, 不能进一步提供新的有效异质核心, 形核过程停止.
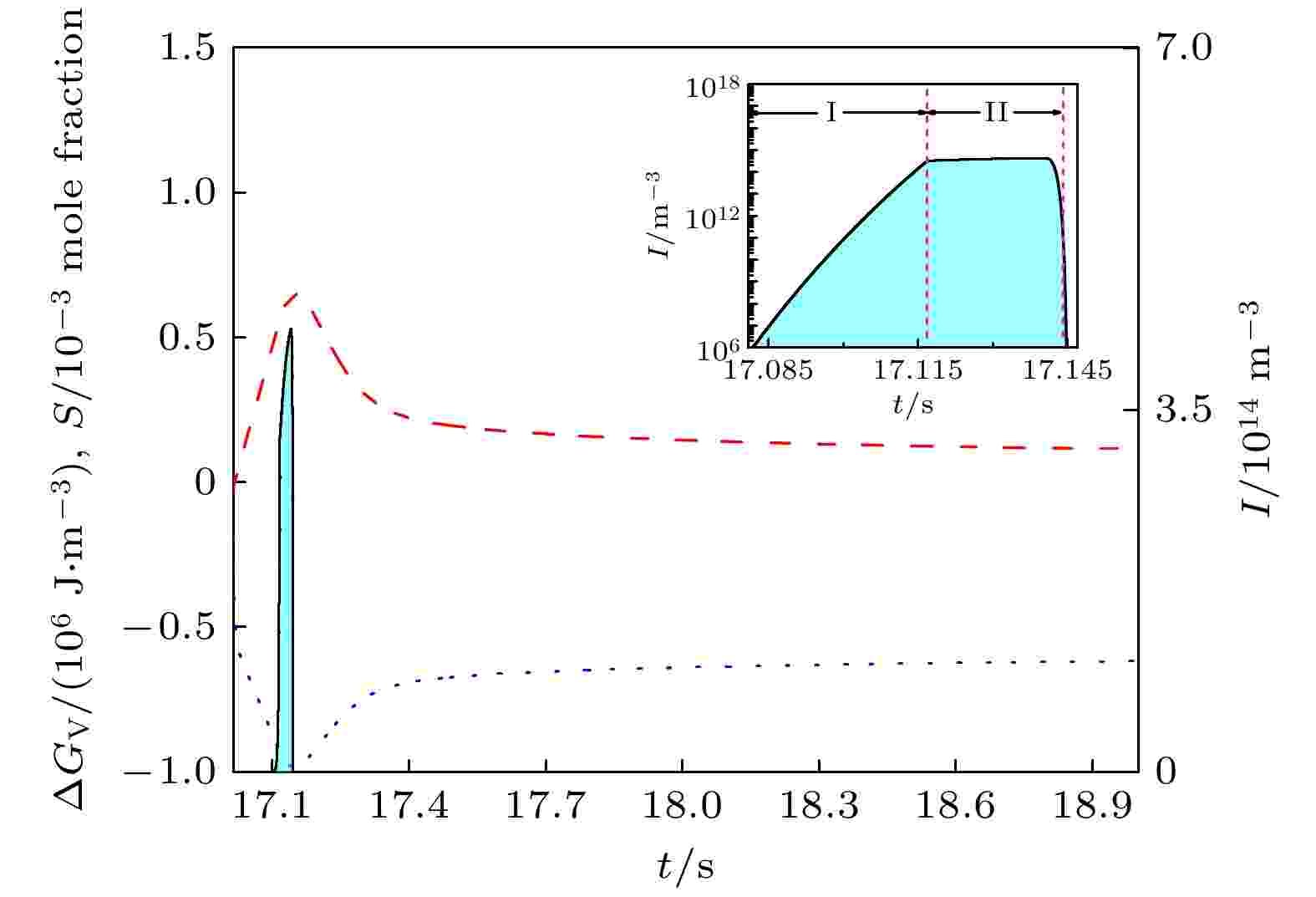图 1 0.01% Al-5Ti-1B中间合金细化处理工业纯铝凝固过程中, 熔体过饱和度S = Cl – Ce, α-Al形核驱动力ΔGV, 异质形核率I随时间的变化. 熔体冷速为3.5 K/sFigure1. The supersaturation of the melt S = Cl – Ce (dash line), the driving force of nucleation ΔGV (dot line) and the heterogeneous nucleation rate I (solid line) of α-Al during cooling the CP-Al melt inoculated by 0.01% Al-5Ti-1B master alloy at the cooling rate of 3.5 K/s.
α-Al异质形核期间, 晶粒数量随着凝固时间增加逐渐增加, 尺寸分布变宽(如图2所示). 形成的α-Al晶粒在形核早期以球状方式快速生长, 当晶粒半径超过球状生长的临界值(
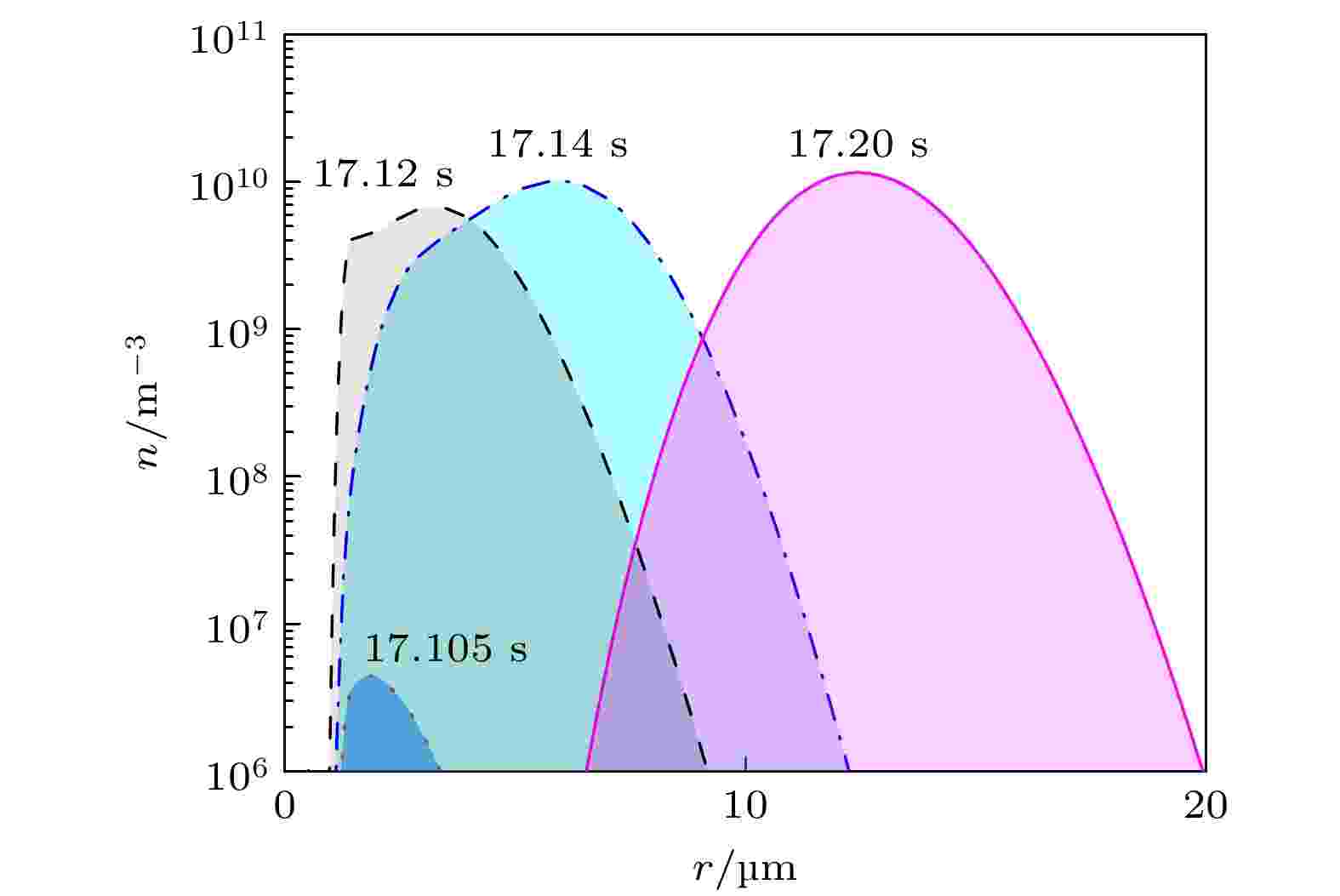图 2 0.01% Al-5Ti-1B中间合金细化处理工业纯铝凝固过程中, α-Al晶核半径r分布随时间的变化. 熔体冷速为3.5 K/sFigure2. The radius distribution of α-Al nucleus at different time during cooling the CP-Al melt inoculated by 0.01% Al-5Ti-1B master alloy at the cooling rate of 3.5 K/s.
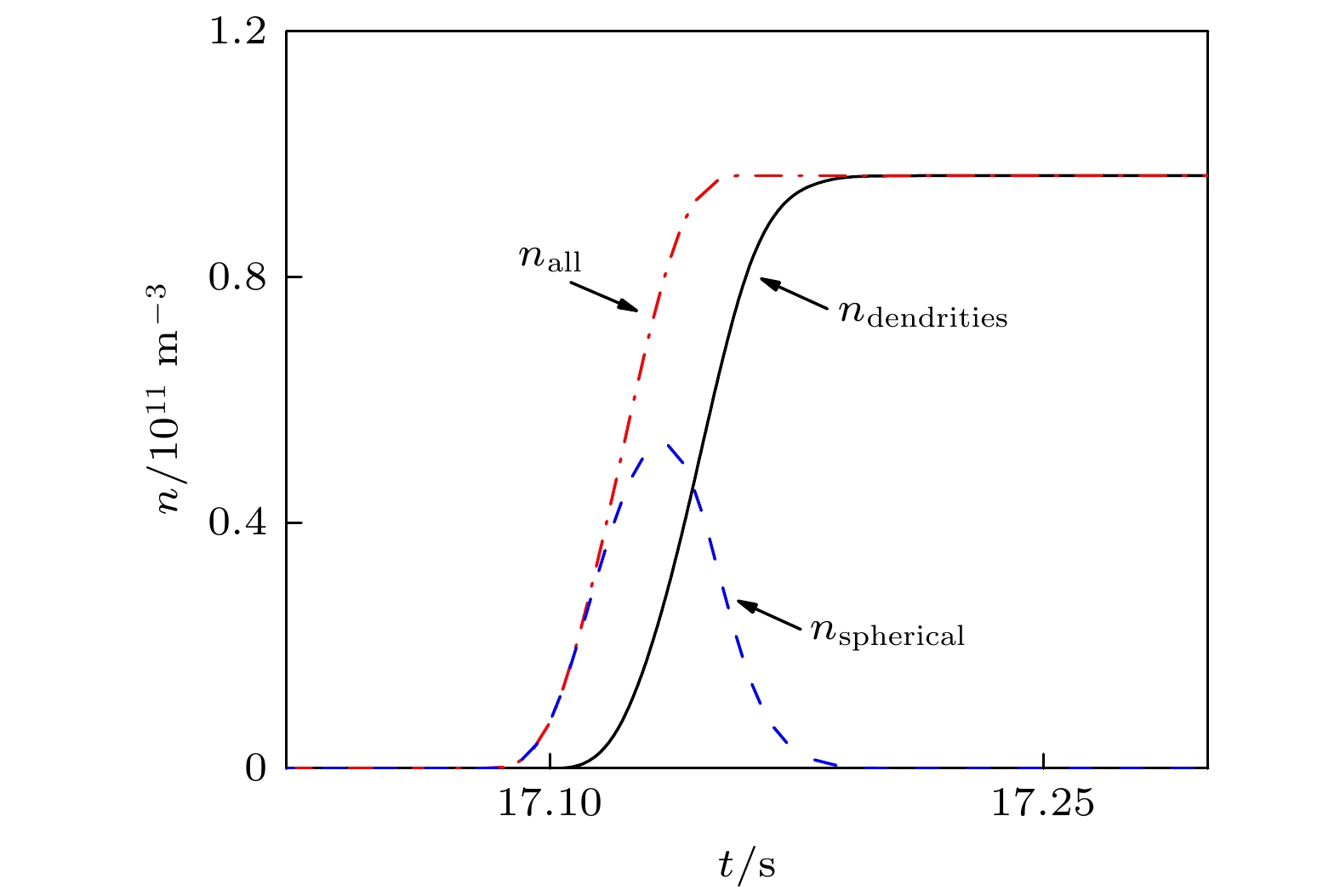图 3 0.01% Al-5Ti-1B中间合金细化处理工业纯铝凝固过程中, α-Al晶核总数量nall, 球状晶nspherical以及树枝晶数目ndendrities随时间的变化. 熔体冷速为3.5 K/sFigure3. The number density of all nucleus nall in the Al melt, the number density of spherical nucleus nspherical and the number density of dendrities ndendrities during cooling the CP-Al melt inoculated by 0.01% Al-5Ti-1B master alloy at the cooling rate of 3.5 K/s.
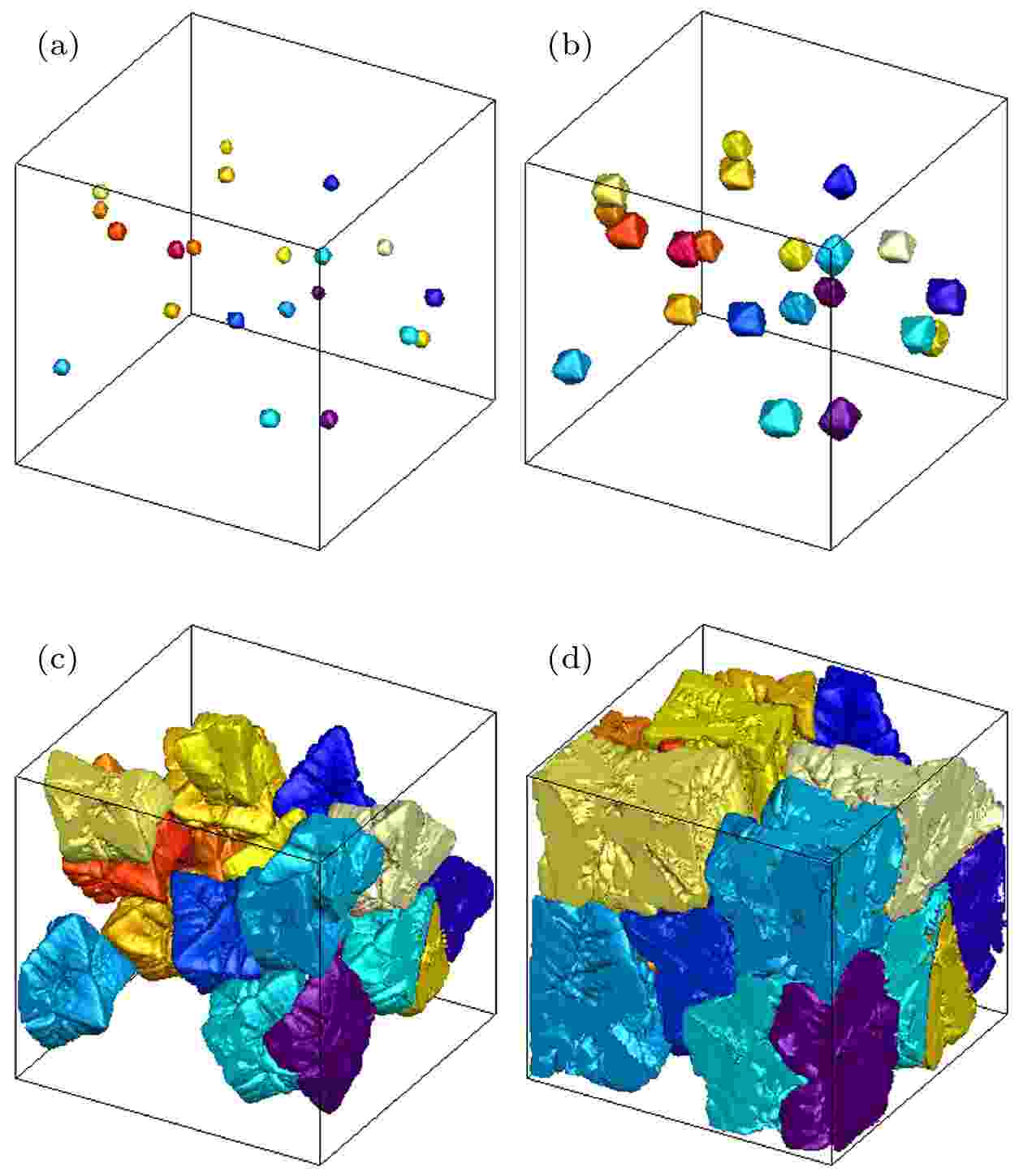图 4 0.01% Al-5Ti-1B中间合金细化处理工业纯铝凝固微观组织演变过程 (a) 固相分数 = 0.1%; (b) 固相分数 = 1.0%; (c) 固相分数 = 25.0%; (d) 固相分数 = 70.0%. 熔体冷速为3.5 K/s. 计算区域尺寸为600 μm × 600 μm × 600 μmFigure4. Solidification microstructure evolution during cooling the CP-Al melt inoculated by 0.01% Al-5Ti-1B master alloy at a cooling rate of 3.5 K/s: (a) Solid fraction = 0.1%; (b) solid fraction = 1.0%; (c) solid fraction = 25.0%; (d) solid fraction = 70.0%. The size of computational domain is 600 μm × 600 μm × 600 μm.
2
3.2.中间合金添加量对铝合金凝固过程的影响
图5为工业纯铝熔体中添加不同数量Al-5Ti-1B中间合金凝固时, α-Al异质形核率与熔体过冷度随时间的变化关系. 可以看出, 当Al-5Ti-1B中间合金加入量为0.01%时, α-Al在熔体过冷度约为0.4 K时开始形核. 形核过程中, 阶段I的形核主要受熔体过冷度的控制, 形核率随熔体过冷度的增大不断增加. 异质形核过程进入阶段II时, 熔体中有效TiB2粒子数量不足, α-Al形核受到熔体中有效TiB2粒子数量限制. 随着凝固潜热释放速度的增加, 熔体过冷度开始降低, 再辉发生, 形核过程停止. 形核过程中阶段I和II持续时间分别占总形核时间的50%左右. 当Al-5Ti-1B加入量为0.4%和1.0%时, 由于Al-Ti合金体系富铝角液相线斜率为正值, 额外的溶质Ti含量的增加使液相线温度提高, 因此熔体形核时达到的最大形核过冷度较大, 熔体中有效TiB2粒子数量随之增加. 当熔体过冷度分别约为0.6和1.0 K时, α-Al开始形核. 形核过程中, 阶段I发生的时间占整个形核过程的90%左右. 阶段II发生较短时间后, 熔体中形核及晶粒生长带来的固相分数增加释放凝固潜热速率足够快, 熔体过冷度开始降低, 再辉发生, 形核过程停止.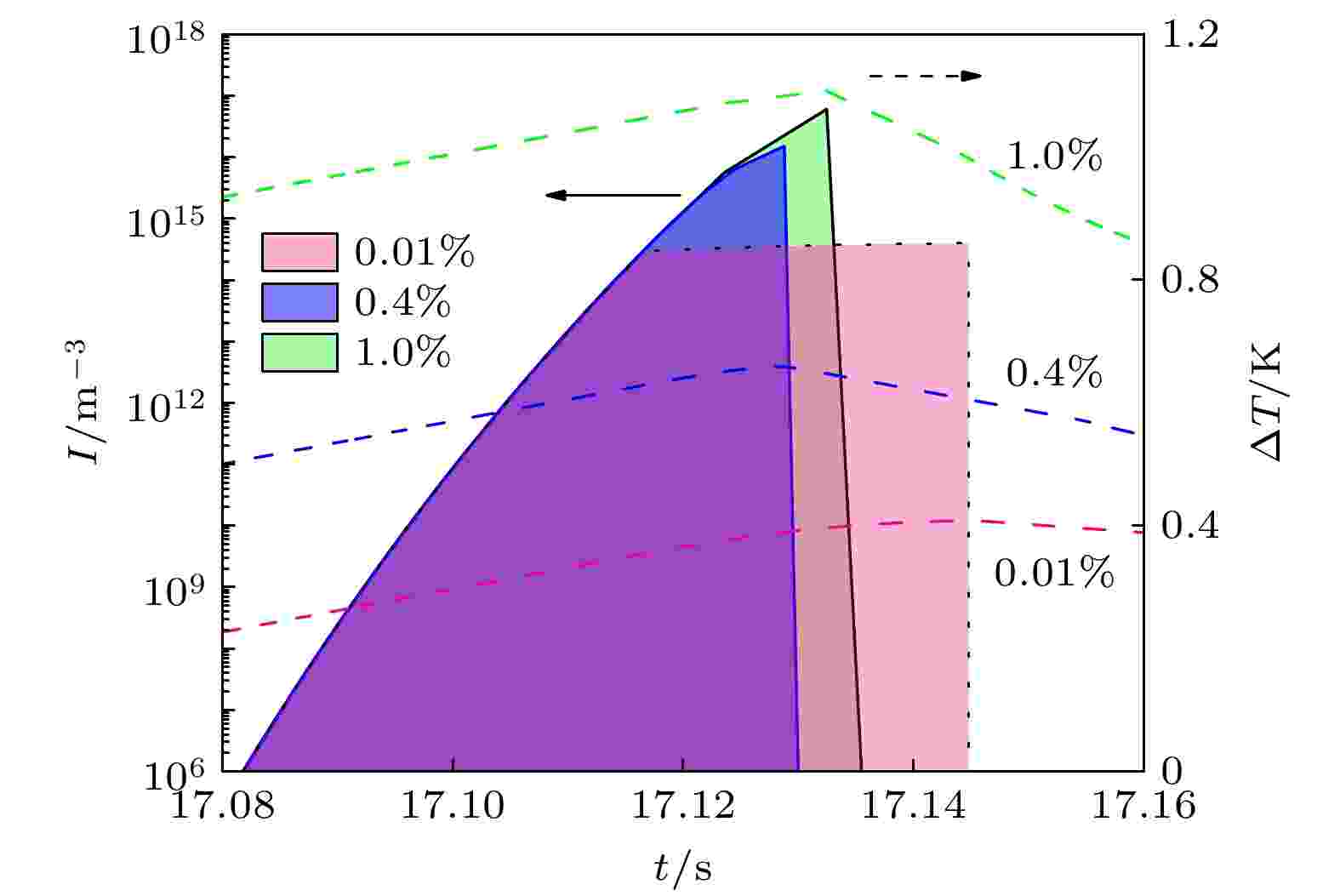
图 5 不同数量Al-5Ti-1B中间合金细化工业纯铝凝固时异质形核率I, 熔体过冷度ΔT随时间的变化. 熔体冷速为3.5 K/sFigure5. Calculated heterogeneous nucleation rate I of α-Al and the undercooling of the melt ΔT for the CP-Al inoculated by different amount of Al-5Ti-1B master alloy at a cooling rate of 3.5 K/s.
图6为模拟计算的工业纯铝最终凝固组织. 可以看到, 随着中间合金添加量的增加, 凝固组织中含有的晶粒数目逐渐增多, 晶粒尺寸逐渐减少. 当凝固组织晶粒尺寸较大时, 枝晶的枝晶臂均较发达, 晶粒大小分布较分散. 这类凝固组织通常具有较差力学能与后续加工性能. 随着晶粒尺寸的降低, 枝晶臂的生长受到限制, 凝固组织主要以均匀细小的等轴晶粒组成. 图7给出了不同数量细化剂细化工业纯铝晶粒尺寸的预测值与实验值. 可以发现, 模拟结果与实验结果符合得较好.
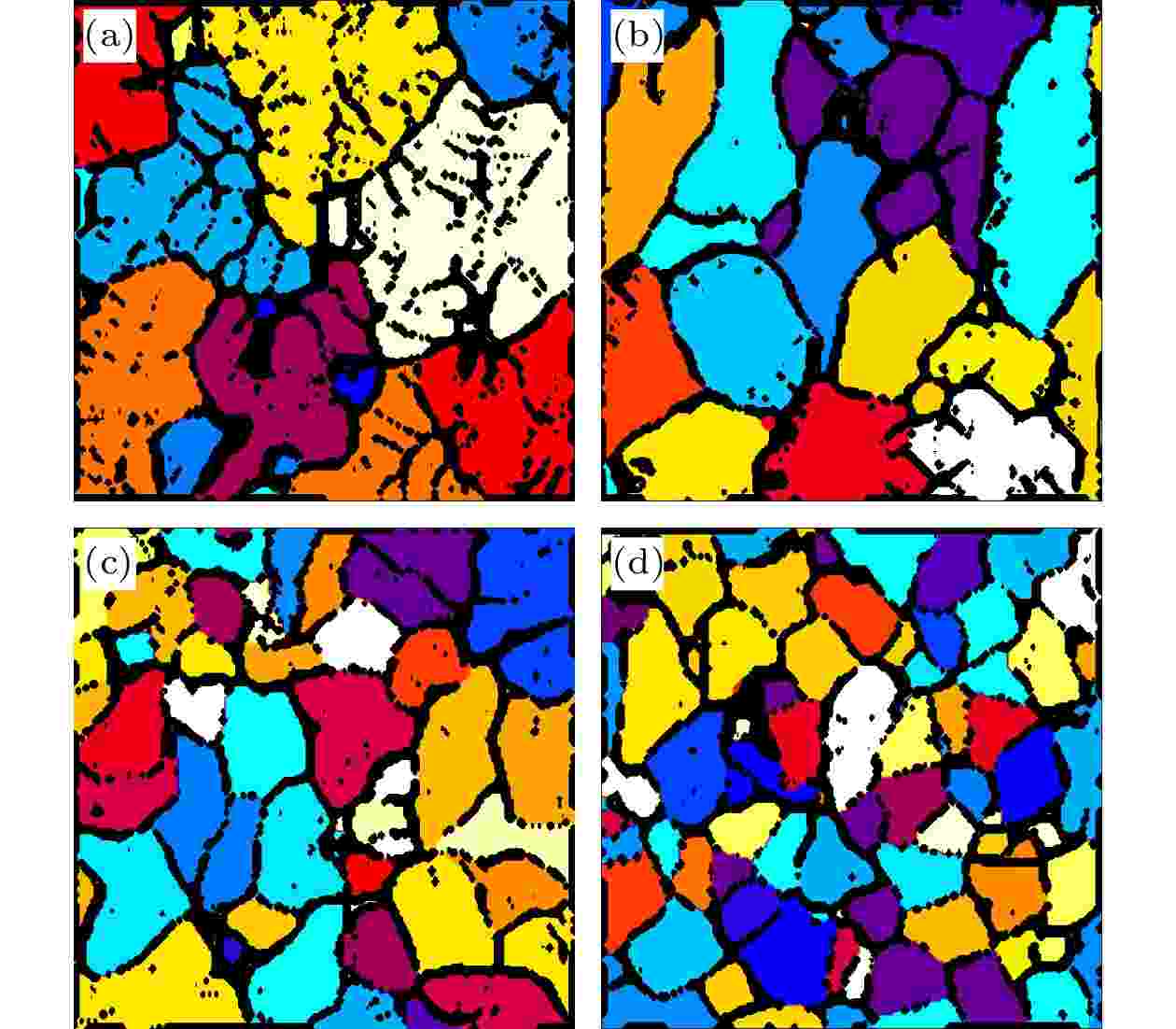图 6 不同数量Al-5Ti-1B中间合金细化工业纯铝凝固组织模拟结果 (a) 0.005%; (b) 0.01%; (c) 0.4%; (d) 1.0%. 熔体冷速为3.5 K/s. 计算区域尺寸为900 μm × 900 μm × 900 μmFigure6. Simulated solidification microstructure for the CP-Al melt inoculated by different amount of Al-5Ti-1B master alloy at a cooling rate of 3.5 K/s: (a) 0.005%; (b) 0.01%; (c) 0.4%; (d) 1.0%. The size of computational domain is 900 μm × 900 μm × 900 μm.
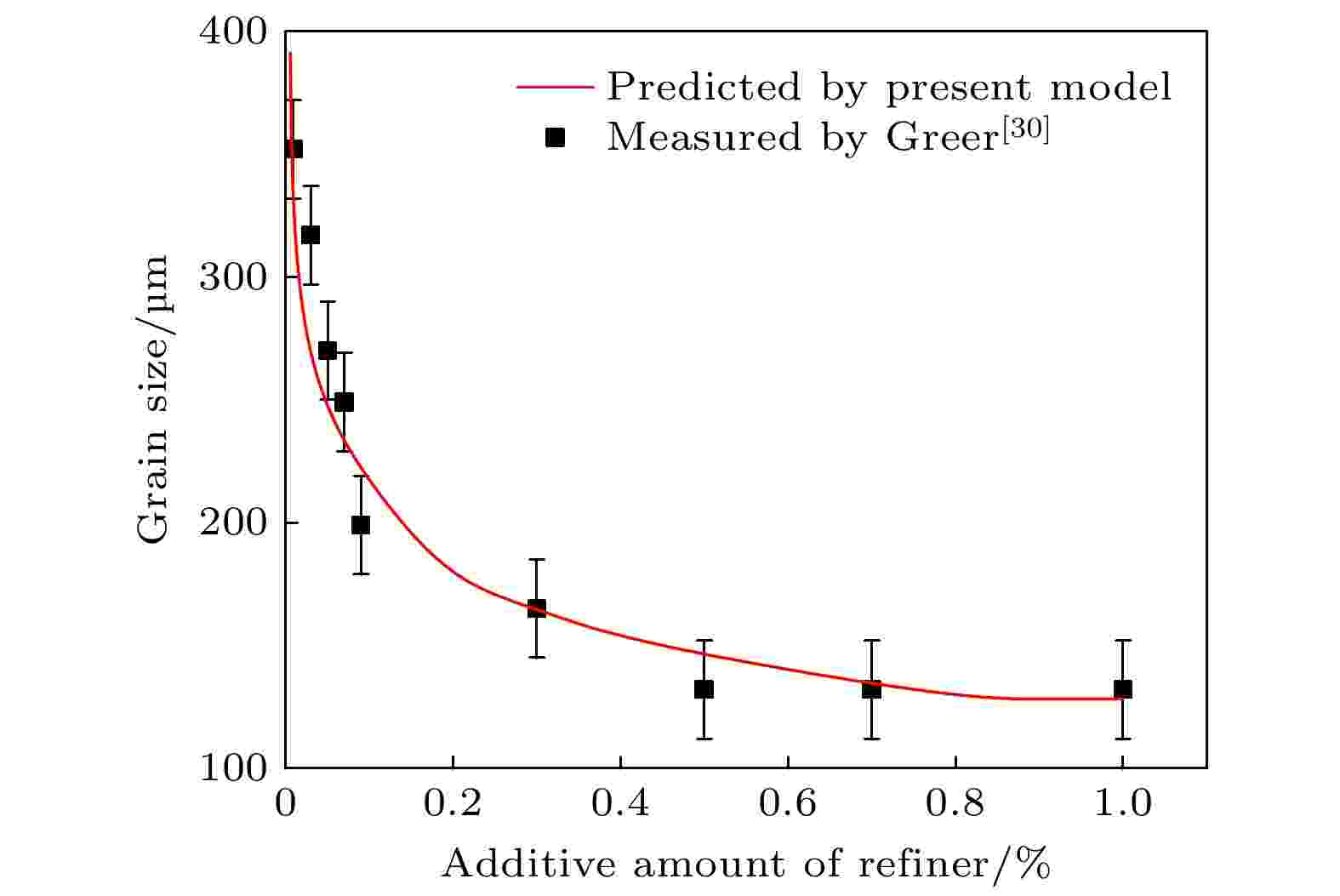图 7 不同数量Al-5Ti-1B中间合金细化工业纯铝晶粒尺寸预测结果与实验结果. 熔体冷速为3.5 K/s. 误差棒为标准偏差Figure7. Predicted and measured grains size vs. the additive amount of Al-5Ti-1B master alloy for the inoculated CP-Al at a cooling rate of 3.5 K/s. The error bars represent the standard deviations.
2
3.3.冷却速度对细化处理条件下铝合金凝固过程的影响
图8给出了不同冷速条件下α-Al异质形核率随时间的变化. 可以看出, 当熔体的冷却速度为1.0, 2.0和5.5 K/s时, 第I阶段形核占据了α-Al异质形核的大部分, 第II阶段形核只持续很短的时间后, 再辉发生, 形核停止(如图8(a)—图8(c)). 当熔体的冷却速度为10 K/s时, 形核阶段I持续时间所占比例降低, 之后阶段II的形核过程受熔体中异质核心粒子数量的限制, 直到再辉发生, 形核停止, 如图8(d).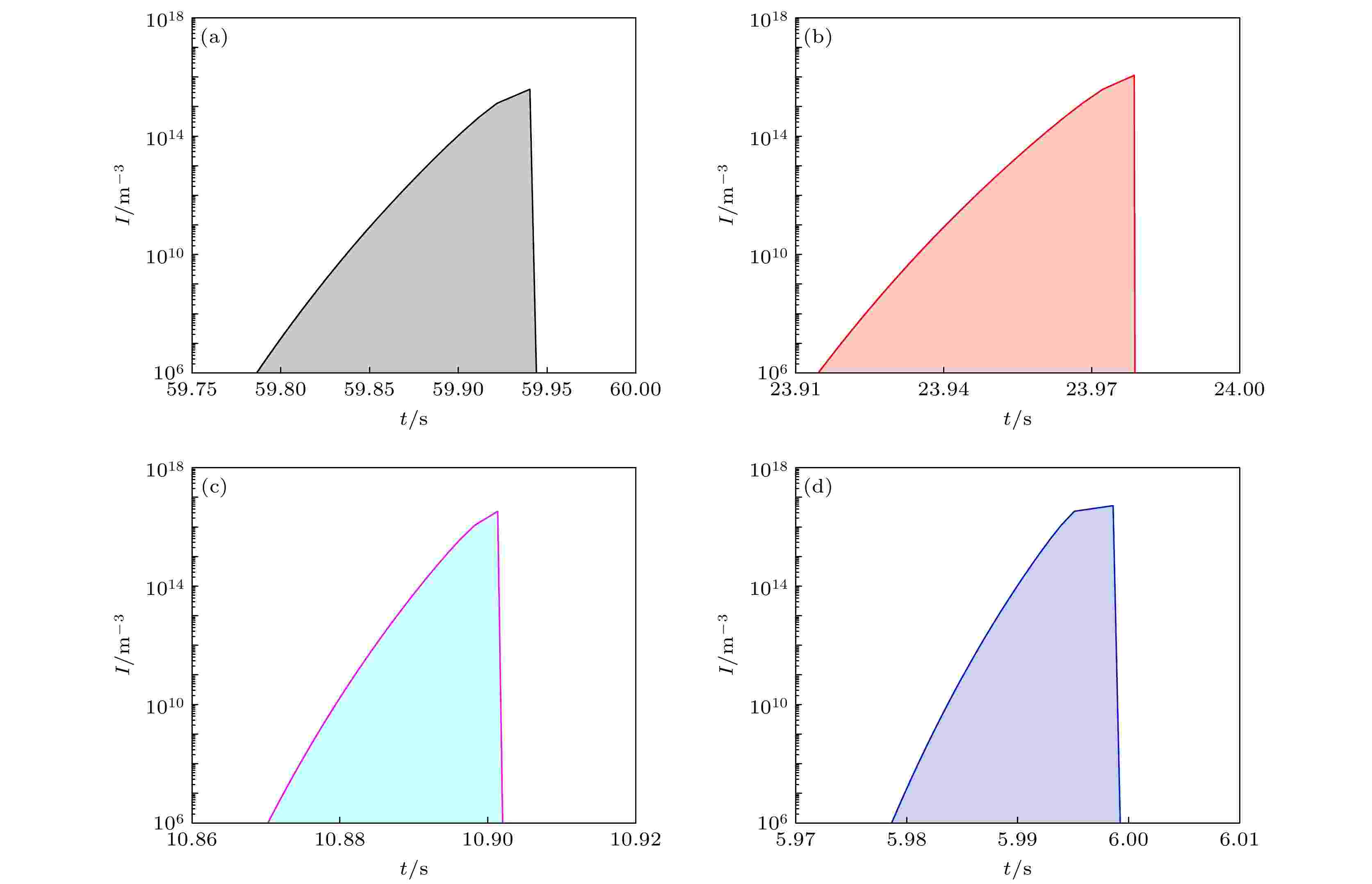
图 8 不同冷却速度下经0.5% Al-5Ti-1B中间合金细化处理, 工业纯铝凝固时α-Al形核率随时间的变化 (a) 1.0 K/s; (b) 2.0 K/s; (c) 5.5 K/s; (d) 10.0 K/sFigure8. Calculated heterogeneous nucleation rate of α-Al during cooling the CP-Al inoculated by 0.5% Al-5Ti-1B master alloy at the different rate: (a) 1.0 K/s; (b) 2.0 K/s; (c) 5.5 K/s; (d) 10.0 K/s.
图9为不同冷速条件下, 0.5% Al-5Ti-1B中间合金细化处理工业纯铝凝固组织的模拟结果. 可以看到, 随着熔体冷却速度的增加, 凝固组织中含有的晶粒数目逐渐增多, 晶粒尺寸逐渐减少. 当熔体冷却速度较低时, 凝固过程中形核数目较少, 凝固组织晶粒较大. 当熔体冷却速度较高时, 凝固过程中短时间内产生的晶核数目较多, 晶粒没有充足的时间长大, 枝晶的枝晶臂生长受到周围晶粒的阻碍, 合金最终凝固组织主要以均匀细小的等轴晶粒组成. 图10给出了不同冷速条件下经0.5% Al-5Ti-1B中间合金细化, 工业纯铝晶粒尺寸的预测值与实验值. 可以发现, 模拟结果与实验结果符合得较好.
图 9 0.5%Al-5Ti-1B中间合金细化工业纯铝, 在不同冷却速度凝固后凝固组织的模拟结果 (a) 1.0 K/s; (b) 2.0 K/s; (c) 5.5 K/s; (d) 10 K/s. 计算区域尺寸为900 μm × 900 μm × 900 μmFigure9. Simulated solidification microstructure for the CP-Al melt inoculated by 0.5% Al-5Ti-1B master alloy at the different cooling rate of the melt: (a) 1.0 K/s; (b) 2.0 K/s; (c) 5.5 K/s; (d) 10 K/s. The size of computational domain is 900 μm × 900 μm × 900 μm.
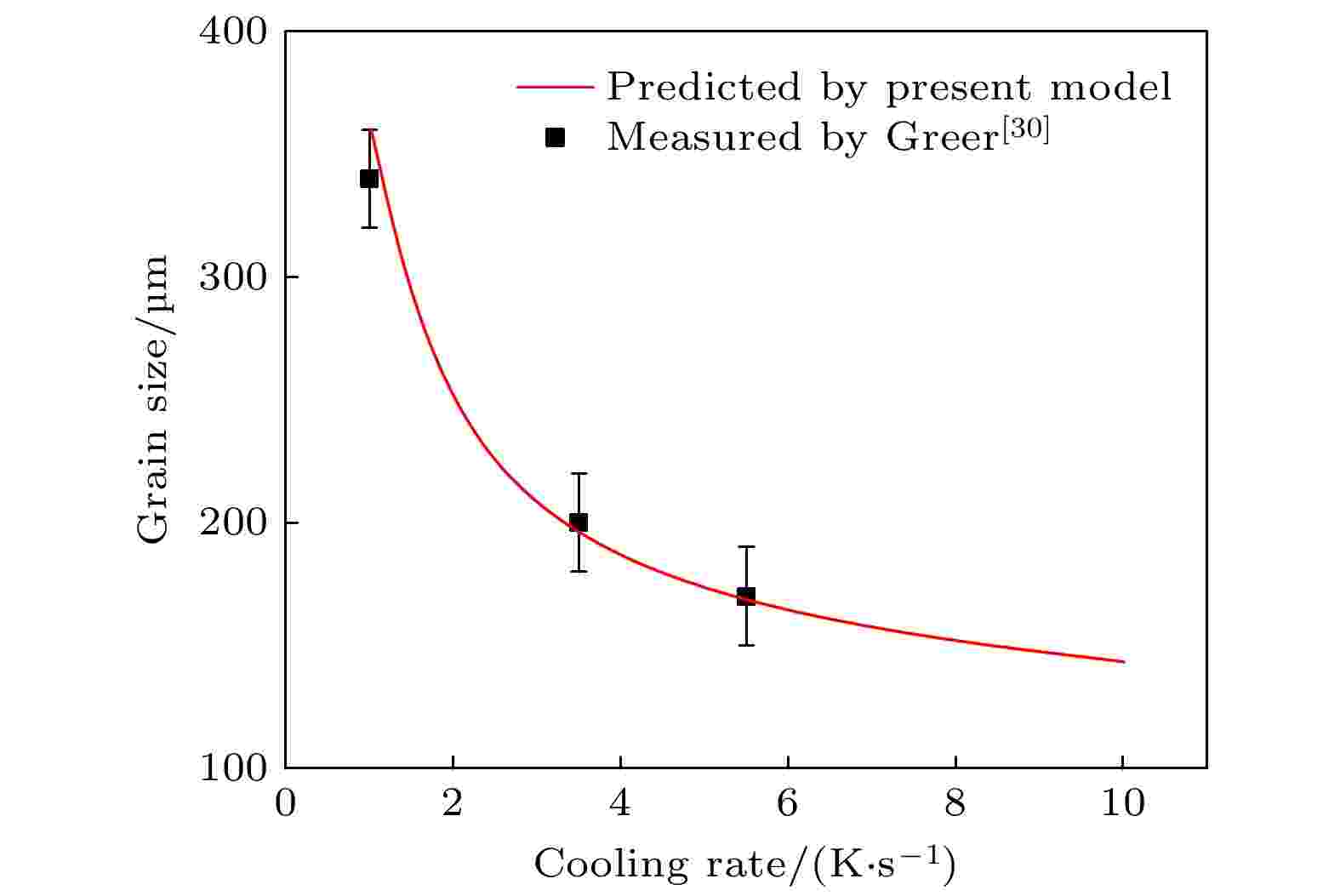图 10 0.5%Al-5Ti-1B中间合金细化工业纯铝, 在不同冷却速度下凝固后晶粒尺寸预测结果与实验结果. 误差棒为标准偏差Figure10. Predicted and measured grains size vs. the cooling rate of the melt for the CP-Al inoculated by 0.5%Al-5Ti-1B master alloy. The error bars represent the standard deviations.
