摘要: 利用线性稳定性方法研究了外加磁场对二元合金凝固过程中糊状层稳定性的影响, 且模型同时考虑了温度场、浓度场和流动的耦合作用. 利用计算得出的色散关系式分析了磁场对糊状层稳定性的影响, 其中包括直接模式和振荡模式. 给出了不同情况下外加磁场对糊状层稳定性的影响, 发现磁洛伦兹力可以减小由浮力引起的失稳效应. 振荡模式下外加磁场对糊状层产生稳定作用, 但直接模式下外加磁场对糊状层的稳定作用具有不确定性. 本文所给出结果为工业中利用外加磁场改善产品的质量提供了重要的理论参考.
关键词: 糊状层 /
磁流体动力学 /
稳定性 English Abstract Effect of magnetic field on stability in mushy layer during binary alloy solidification Fan Hai-Long Chen Ming-Wen School of Mathematics and Physics, University of Science and Technology Beijing, Beijing 100083, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11401021, 51971031)Received Date: 21 October 2020Accepted Date: 16 November 2020Available Online: 12 March 2021Published Online: 20 March 2021Abstract: During directional solidification of binary alloy mixtures, instability in the solid/liquid interface appears due to constitutional undercooling. As a result of this instability, a reactive porous medium, namely mushy layer, is formed, and it separates the liquid phase from the solid phase completely. The intrinsic structure of the mushy layer is of fine-scale dendritic crystal that shelters solute in the interstitial fluid. In a gravitational field, the rejection of lighter solute components from an advancing solidification front brings about unstable density gradient. Ensuing convective motions in the mush are driven by a density difference. The convection can change the solid matrix of the mushy layer. Hence, the dynamic response of the mushy layer is driven by interaction among heat transfer, solute transport and convection. As a contactless control tool, external magnetic field can change the heat and solute transport, which has a significant effect on the phase change process. Therefore, when magnetic field, thermal diffusion, solute transport and buoyancy convection are considered simultaneously in the phase transformation process, the mechanism of mushy region will become more complex and interesting. In this paper, the effect of external magnetic field on the stability of mushy layer during binary alloy solidification is studied. The coupling effects of magnetic field, temperature field, concentration field and convection are considered in the model. Including the direct mode and the oscillation mode, the resulting dispersion relation reveals the influence of magnetic field on the stability of mushy layer through linear stability analysis. It is found that the Lorentz force can reduce the instability effect which is caused by buoyancy convection. In the oscillation mode, an external magnetic field brings about a stabilizing effect on the mushy layer, but in the direct mode, the effect of external magnetic field on stability of the mushy layer is uncertain. In conclusion, the finding in this paper provides an important theoretical reference for improving products quality by applying an external magnetic field in the metals processing industry.Keywords: mushy layer /magnetohydrodynamics /stability 全文HTML --> --> --> 1.引 言 在合金的凝固过程中由于成分过冷(constitutional supercooling)的存在, 界面会出现不稳定性[1 ,2 ] . 这种不稳定性的进一步演化导致在固相和液相之间出现一种新的形态, 即糊状区[3 ] . 糊状区可以理解为是由树枝状晶体、柱状晶体和液体组成的一种反应多孔区域(reactive porous regions)[4 ] . 研究糊状层的稳定性对于凝固问题有着重要的意义. 在重力场中由于不同成分之间密度差的存在导致流动的产生, 这使得糊状区同时受到温度场、浓度场以及流动的耦合作用. 已有一些研究者研究了这些耦合作用下糊状区的稳定性问题. 例如Anderson和Worster[5 ] 分析了二元合金凝固过程中糊状层的稳定性, 给出了识别振荡对流不稳定性的方法. Guba和Anderson[6 ] 分析了三元合金定向凝固过程中糊状层的稳定性. 该模型包括热输运、溶质扩散和对流输运, 并确定了新的对流不稳定性, 包括直接模式和振荡模式.[7 -10 ] 、改善铸件的凝固组织[11 ,12 ] 、减少产品的表面缺陷[13 ] 等. 磁场的存在改变了热输运和溶质输运, 对凝固过程有着重要的影响. 因此研究磁场作用下糊状区的动力学行为就显得至关重要. 例如, Riahi[14 ] 研究了垂直磁场对糊状层中对流的影响. 发现外加磁场可以减弱烟囱(chimney)中的流动, 从而减少产品的雀斑缺陷. Muddamallappa等[15 ] 利用数值方法研究了二元合金在磁场中的凝固问题. 结果表明Chandrasekhar数的增大对凝固有稳定作用, 且临界瑞利数随着Chandrasekhar数的增大而增大. Kao等[16 ] 通过数值方法模拟了横向磁场对树枝状晶体尺寸和间距的影响. 研究结果发现由于洛伦兹力使得枝晶间的区域产生了流动, 从而改变了溶质的输运过程并影响了枝晶的生长. Sarkar等[17 ] 研究了二元合金凝固过程中糊状层的磁流体动力学, 结果表明外加磁场增强了糊状层的稳定性, 但在其模型中没有考虑溶质输运. 值得指出的是当在相变过程中同时考虑热扩散、溶质输运和浮力对流时, 问题将变得更加复杂和有趣[18 -20 ] .2.数学模型 22.1.控制方程 2.1.控制方程 考虑二元合金在磁场中的凝固问题, 认定糊状层的上下边界是等温的、不变形的和不渗透的. 这使得糊状层与系统的其他部分动态隔离, 具体描述见图1 . 假定系统以恒定速率${V^*}$ 向上凝固, 在$0 < z^* < {H^*}$ 的区域内存在一个厚度为${H^*}$ 的糊状层. 糊状层顶部和底部的温度及浓度分别为$T_{{\rm{top}}}^{{*}}$ , $T_{{\rm{bot}}}^{{*}}$ , $C_{{\rm{top}}}^{{*}}$ , $C_{{\rm{bot}}}^{{*}}$ , 同时假设它们为常数. 为了便于分析, 假设固相和液相的比热和热导率相同.图 1 以恒定速度${V^*}$ 凝固的糊状层示意图Figure1. Schematic representation of mushy layer system, which advancing upwards with a constant solidification speed ${V^*}$ .B B ${z^*}$ 轴垂直向上. 此外, 认定在糊状层具有恒定的导电率${\sigma _{\rm{e}}}$ , 且黏性耗散和焦(耳)热效应对传热的影响可以忽略不计. 认定糊状层受到磁场诱导洛伦兹力的影响[21 ] , 洛伦兹力表达式如下:J ${{J}} = {\rho _{\rm{e}}}{{{u}}^*} + {\sigma _{\rm{e}}}({{E}} + {{{u}}^*} \times {{B}})$ [21 ] , 其中${{{u}}^*}$ 表示流体速度, E ${\rho _{\rm{e}}}$ 表示电荷密度. 类似于文献[17 ]中的讨论, 本文忽略电场E ${\rho _{\rm{e}}}{{{u}}^*} \approx 0$ . 因此, 洛伦兹力方程可以重写为${{F}} = {\sigma _{\rm{e}}}({{{u}}^*} \times {{B}}) \times {{B}}$ .${T^*}$ 表示液相温度; ${C^*}$ 表示液相浓度; $\phi $ 为糊状区固体体积分数; ${p^*}$ 表示降低的压力(即动态压力和静水部分的和, ${p^*} = {p_{{\rm{dyn}}}} + \rho _{{\rm{top}}}^{{*}}{g^*}{z^*}$ ); ${{{u}}^*}$ 为达西速度; ${c^*}$ 是比热; ${k^*}$ 是热导率; $L_{\rm{v}}^{{*}}$ 是潜热; ${D^*}$ 表示溶质扩散系数; ${k_1}$ 表示偏析系数; ${m^*}$ 是液相线斜率; ${\varPi ^*}(\phi )$ 表示糊状层的渗透率; ${\mu ^*}$ 是流体的动态黏度; g 是重力加速度; $\hat{{k}}$ 表示向上的单位矢量; ${\rho ^*} = \rho _{{\rm{top}}}^*[1 - {\alpha ^*}({T^*} - T_{{\rm{top}}}^{{*}}) - \alpha _1^*({C^*} - C_{{\rm{top}}}^{{*}})]$ , 其物理含义是糊状层中的对流运动是由密度差驱动的, 同时假定密度与温度、浓度呈线性关系[6 ] , 其中$\rho _{{\rm{top}}}^{{*}}$ 表示糊状层顶部的密度, ${\alpha ^*}$ 和$\alpha _1^*$ 为常数.$ {z^*} = {H^*}$ 时,$ {z^*} = 0$ 时,2.2.无量纲化 -->2.2.无量纲化 采用类似于文献[6 ]的无量纲化方案, 选择凝固速率${V^*}$ 作为速度尺度, 长度尺度为${{{\kappa ^*}}}/{{{V^*}}}$ , 时间尺度为${{{\kappa ^*}}}/{{{V^*}^2}}$ , 压力尺度为$\dfrac{{{\mu ^*}{\kappa ^*}}}{{{\varPi ^*}({\phi _0})}}$ , 密度尺度为$\dfrac{{{\mu ^*}{V^*}}}{{{g^*}{\varPi ^*}({\phi _0})}}\;$ , 温度和浓度为$\;T = \dfrac{{{T^*} - T_{{\rm{top}}}^*}}{{\Delta {T^*}}}$ , $\;C = $ $ \dfrac{{{C^*} - C_{{\rm{top}}}^*}}{{\Delta {C^*}}}$ , 其中, $\Delta {T^*} = T_{{\rm{top}}}^* - T_{{\rm{bot}}}^{{*}}$ , $\Delta {C^*} = C_{{\rm{top}}}^{{*}} - $ $ C_{{\rm{bot}}}^{{*}}$ . 这里${\kappa ^*} = {{{k^*}}}/{{{c^*}}}$ 表示热扩散系数, ${\varPi ^*}({\phi _0})$ 为渗透率尺度.$ z = \delta $ 时,$ z = 0$ 时,2.3.重标度 -->2.3.重标度 通过限制糊状层的厚度是薄的$\delta \ll 1$ , 使得模型是渐近减小的. 其物理含义是糊状层的厚度远小于热扩散长度, 或者等效地认为凝固速率远小于热传导穿过糊状层的传热速率. 下面重新标度系统, 令${C^{{\rm{bot}}}} = \dfrac{{{{\bar C}^{{\rm{bot}}}}}}{{{\delta ^2}}}$ , $S = \dfrac{{\bar S}}{{{\delta ^2}}}$ , $(x, z) = \delta (\bar x, \bar z)$ , $t = {\delta ^2}\bar t$ , $Ra = \dfrac{1}{\delta }\overline {Ra}$ , $R{a_1} = \dfrac{1}{\delta }\overline {R{a_1}}$ , 则系统的控制方程变为3.稳定性分析 为了研究系统的稳定性, 可做如下分解:$\tilde T(\bar z)$ , $\tilde C(\bar z)$ , $\tilde \phi (\bar z)$ , $\tilde p(\bar z)$ 表示无流动的基态解; $\hat T(\bar z)$ , $\hat C(\bar z)$ , $\hat \phi (\bar z)$ , $\hat{{u}}(\bar z)$ , $\hat p(\bar z)$ 表示扰动态; $\hat{{u}} = $ $ [\hat u(z), \hat v(z), \hat w(z)]$ , $\sigma = {\sigma _{\rm{R}}} + {\rm{i}}{\sigma _{\rm{I}}}$ 表示复的增长率, k 表示水平波数.3.1.稳态解 3.1.稳态解 类似于文献[6 ]容易求得系统的稳态解为3.2.线性扰动方程 -->3.2.线性扰动方程 为便于分析, 对(19 )式应用两次旋度可以消去压力p 且化简为$D = \dfrac{{\rm{d}}}{{{\rm{d}}\bar z}}.$ 25 )—(28 )具有如下形式的渐近解:$O({\delta ^0})$ 阶的控制方程为6 ]可解的$J = {n^2}{{\text{π}}^2} + {k^2}$ . 需要指出的是${\sigma _1}$ 出现在(39 )式${\phi ^0}$ 的解中, 而${\sigma _1}$ 却是未知的. 这就需要通过下面$O({\delta ^1})$ 阶的可解性条件来确定. $O({\delta ^1})$ 阶的控制方程为41 )式和(42 )式的可解性条件得43 )表征了糊状层凝固系统中的各种物理效应, 将在第4 节进行讨论.4.讨 论 在稳定性分析中, 为了清楚地分析驱动不稳定性的物理机制, 将结果简化为下面的两种情况: $\overline {Ra} = 0$ , $\overline {R{a_1}} \ne 0$ 和$\overline {Ra} \ne 0$ , $\overline {R{a_1}} = 0$ . 本文重点讨论$\overline {Ra} = 0$ , $\overline {R{a_1}} \ne 0$ 的情况, 即认为系统只有溶质C 对浮力有贡献. 对于$\overline {Ra} \ne 0$ , $\overline {R{a_1}} = 0$ (即浮力是由温度T 驱动的情况), 可以利用同样的方法进行讨论.C 对浮力有贡献情况下, 下面主要给出中性稳定性的结果.4.1.直接模式(direct modes) 4.1.直接模式(direct modes) 对于中性稳定的直接模式($\sigma _R^1 = 0$ , $\sigma _I^1 = 0$ ), 由(43 )式可得中性稳定性的Rayleigh数为45 )式可以看出在$(\overline {R{a_1}}, k)$ 平面上的中性曲线可以位于静态不稳定区域($\overline {R{a_1}} < 0$ )或静态稳定($\overline {R{a_1}} > 0$ )区域, 这取决于${\varOmega _1} + {\hat \varOmega _1}$ 的符号.$\sigma _{\rm{R}}^1 < 0$ )和不稳定区域($\sigma _{\rm{R}}^{\rm{1}} > 0$ ), 对$\overline {R{a_1}} $ 求导有45 )式和(46 )式可看出, 可将直接模式的中性稳定性曲线分为下面4种情况:${\varOmega _1} + {\hat \varOmega _1} > 0$ , ${c_1} > 0$ , ${d_1} < 0$ ;${\varOmega _1} + {\hat \varOmega _1} > 0$ , ${c_1} < 0$ , ${d_1} > 0$ ;${\varOmega _1} + {\hat \varOmega _1} < 0$ , ${c_1} > 0$ , ${d_1} < 0$ ;${\varOmega _1} + {\hat \varOmega _1} < 0$ , ${c_1} < 0$ , ${d_1} > 0$ .图2 给出了在$(\overline {R{a_1}}, k)$ 平面上这些情况下的中性稳定性图. 情况1): 在${\rm{Ham}} = 0$ 时与文献[6 ]附录C中通过数值方法研究的结论是一致的. 当${\rm{Ham}} = 5$ 时可以看出不稳定区域减小, 这说明磁场对糊状区的凝固有稳定的作用. 情况2): 由图2 可以看出外加磁场对糊状层产生了不稳定的作用. 情况3): 在物理上是不可能发生的[6 ] . 情况4): 即当$\overline {R{a_1}} > 0$ 时, 由图2 可以看出施加的磁场对糊状层有稳定作用. 这一结果与文献[15 ]利用数值方法研究磁场对糊状区影响的结果是一致的.图 2 直接模式的中性稳定性曲线和不稳定区域(阴影部分)示意图 (a)情况1; (b)情况2; (c)情况3; (d)情况4Figure2. Schematic representation of the neutral-stability curves and the regions of instability (shaded) for direct modes: (a) Situation 1; (b) situation 2; (c) situation 3; (d) situation 4.4.2.振荡模式(oscillatory modes) -->4.2.振荡模式(oscillatory modes) 对于中性稳定的振荡模式($\sigma _{\rm{R}}^1 = 0$ , $\sigma _{\rm{I}}^{\rm{1}} \ne 0$ ), 由(43 )式可得中性稳定性的Rayleigh数为47 )式中频率$\sigma _{\rm{I}}^{\rm{1}}$ 是(48 )式的实非零解.47 )式和(48 )式可以看出, ${Q_1} = \dfrac{{{d_1}}}{{{c_1}}}$ 对振荡不稳定性有着重要的影响, 且当${Q_1} > \dfrac{{{{\text{π}}^2}}}{{4({{\text{π}}^2} + {k^2})}}$ 时出现振荡模式. 类似于直接模式, 将振荡模式的中性稳定性曲线分为以下4种情况:${\varOmega _1} + {\hat \varOmega _1} > 0$ , ${c_1} > 0$ , ${d_1} > 0$ ;${\varOmega _1} + {\hat \varOmega _1} > 0$ , ${c_1} < 0$ , ${d_1} < 0$ ;$ {\varOmega _1} + {\hat \varOmega _1} < 0 $ , ${c_1} > 0$ , ${d_1} > 0$ ;$ {\varOmega _1} + {\hat \varOmega _1} < 0 $ , ${c_1} < 0$ , ${d_1} < 0$ .图3 给出了在$(\overline {R{a_1}}, k)$ 平面上这些情况下的中性稳定性图. 情况1), 2), 4)的图示表明磁场对糊状区的凝固有稳定的作用. 情况3): 在物理上是不可能发生的[6 ] . 也就是说, 外部施加的磁场对振荡模式下的糊状层产生稳定作用, 这一结果与文献[17 ]的研究成果是一致的.图 3 振荡模式的中性稳定性曲线示意图(振荡模式的不稳定性区域为图中实线(黑色)和点划线(红色)之间的部分) (a)情况1; (b)情况2; (c)情况3; (d)情况4Figure3. Schematic representation of the neutral-stability curves for the oscillatory modes: (a) Situation 1; (b) situation 2; (c) situation 3; (d) situation 4. The instability region of oscillation mode is the part between solid line (black) and dashed line (red).5.结 论 本文将Guba和Anderson[6 ] 给出的糊状层凝固模型推广到了包含外加磁场作用的情况. 分析了磁场对糊状层稳定性的影响, 其中包括直接模式和振荡模式. 通过分析振荡模式下的中性稳定性发现磁洛伦兹力总是起稳定作用, 这一发现与文献[17 ]的结论是一致的. 但在对直接模式下中性稳定性的分析中发现外加磁场并非总是起稳定作用. 实际上我们可以理解为糊状层的稳定性是热扩散、溶质扩散、流动和洛伦兹力耦合作用的结果. 总之, 本文的结论为冶金工业中利用磁场来提高产品的质量提供了重要的理论参考. 






 图 1 以恒定速度
图 1 以恒定速度




















































































































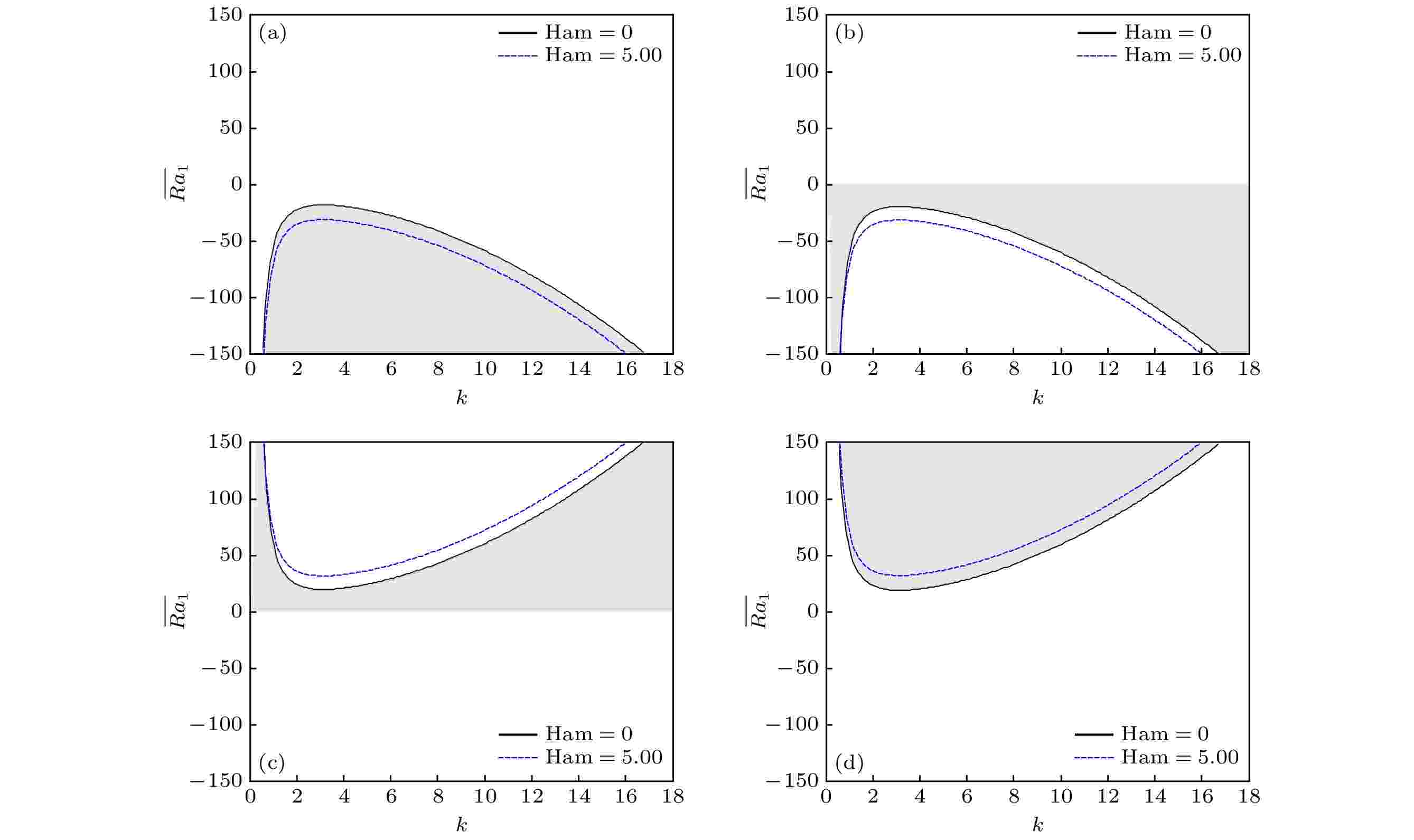 图 2 直接模式的中性稳定性曲线和不稳定区域(阴影部分)示意图 (a)情况1; (b)情况2; (c)情况3; (d)情况4
图 2 直接模式的中性稳定性曲线和不稳定区域(阴影部分)示意图 (a)情况1; (b)情况2; (c)情况3; (d)情况4

















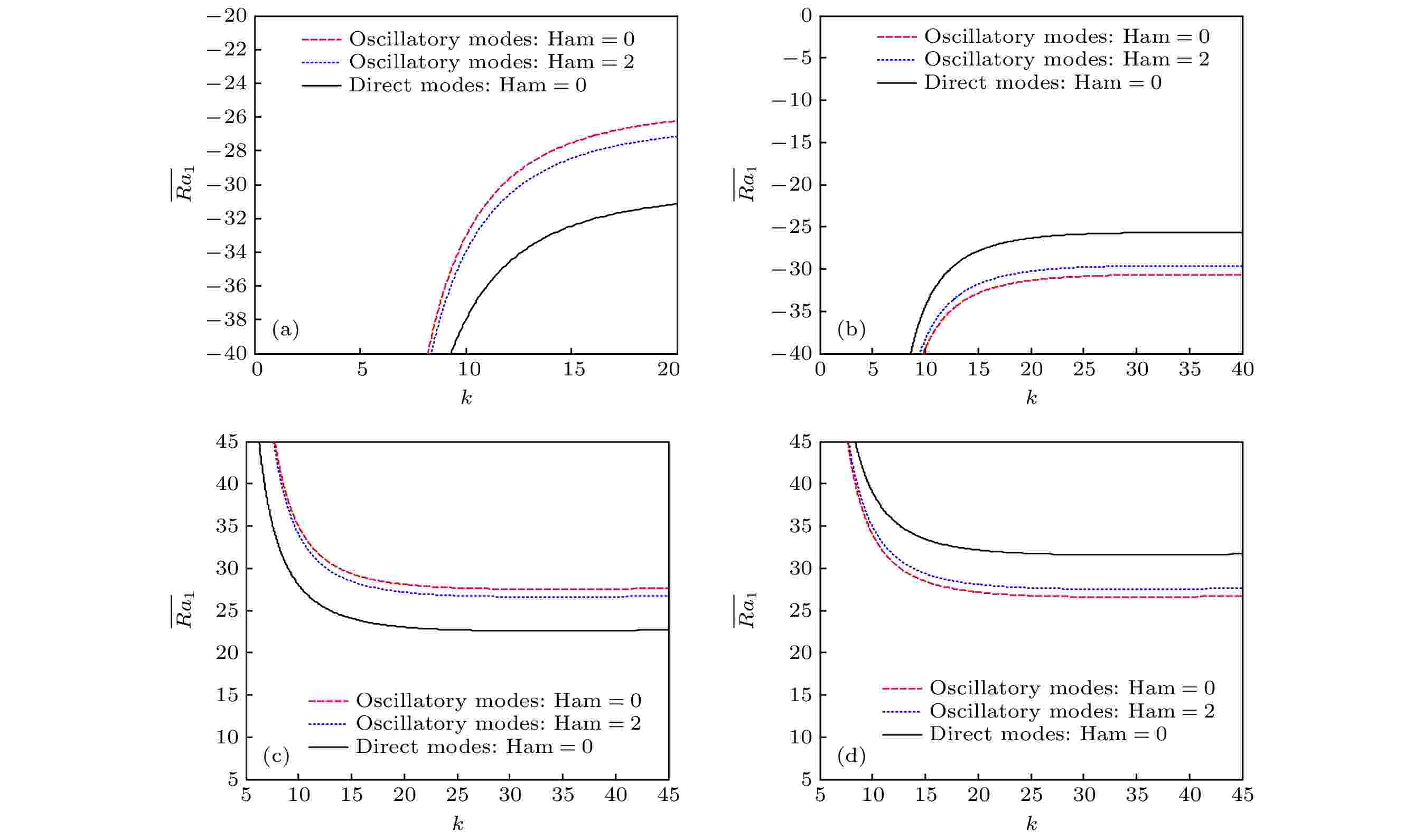 图 3 振荡模式的中性稳定性曲线示意图(振荡模式的不稳定性区域为图中实线(黑色)和点划线(红色)之间的部分) (a)情况1; (b)情况2; (c)情况3; (d)情况4
图 3 振荡模式的中性稳定性曲线示意图(振荡模式的不稳定性区域为图中实线(黑色)和点划线(红色)之间的部分) (a)情况1; (b)情况2; (c)情况3; (d)情况4