摘要: 非线性动力系统极易发生共振, 在多频激励下可能发生联合共振或组合共振, 目前关于非线性系统的主-超谐联合共振的研究少见报道. 本文以Duffing系统为对象, 研究系统在主-超谐联合共振时的周期运动和通往混沌的道路. 应用多尺度法得到系统的近似解析解, 并利用数值方法对解析解进行验证, 结果吻合良好. 基于Lyapunov第一方法得到稳态周期解的稳定性条件, 并分析了非线性刚度对稳态周期解的幅值和稳定性的影响. 此外, 由于近似解只能描述周期运动, 不足以描述系统的全局特性, 因而应用Melnikov方法对系统进行全局分析, 得到系统进入Smale马蹄意义下混沌的条件, 依据该条件以及主-超谐联合共振的条件选取一组参数进行数值仿真. 分岔图和最大Lyapunov指数显示出两个临界值: 当激励幅值通过第一个临界值时, 异宿轨道破裂, 混沌吸引子突然出现, 系统以激变方式进入混沌; 激励幅值通过第二个临界值时, 系统在混沌态下再次发生激变, 进入另一种混沌态. 利用Melnikov方法考察了第一个临界值在多种频率组合下的变化趋势, 并用数值仿真验证了解析结果的正确性.
关键词: Duffing系统 /
联合共振 /
非线性动力系统 /
混沌 English Abstract Simultaneous primary and super-harmonic resonance of Duffing oscillator Li Hang 1,2 ,Shen Yong-Jun 1,2 ,Yang Shao-Pu 1 ,Peng Meng-Fei 2 ,Han Yan-Jun 2 1.State Key Laboratory of Mechanical Behavior and System Safety of Traffic Engineering Structures, Shijiazhuang Tiedao University, Shijiazhuang 050043, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. U1934201, 11772206)Received Date: 03 July 2020Accepted Date: 07 September 2020Available Online: 02 February 2021Published Online: 20 February 2021Abstract: There are many resonance phenomena in a nonlinear dynamical system subjected to forced excitation, especially the excitation with multiple frequencies. Duffing oscillator subjected to the excitation with multiple frequencies may exhibit some complex resonance phenomena, such as simultaneous resonance and combination resonance. In this paper, the simultaneous primary and super-harmonic resonance of Duffing oscillator is studied, and it is analyzed in periodic motion and chaotic motion. Firstly, the approximate analytical solution is obtained by the method of multiple scales, and the correctness and accuracy of the analytical solution are verified through numerical simulation. Furthermore, the amplitude-frequency equation and phase-frequency equation of the steady-state response are derived from the approximate solution, and the stability of the steady-state response is analyzed based on Lyapunov’s first method. It is found that there are at most two stable periodic solutions and one unstable periodic solution. The effects of nonlinear stiffness on steady-state response is also analyzed through numerical simulation. However, the approximate solution obtained by the singular perturbation method is not sufficient to describe the global characteristics of the system, therefore, the necessary condition for the chaos in the sense of Smale horseshoes is derived based on the Melnikov method. Finally, one-demonstrational system that meets the condition of simultaneous resonance is analyzed through numerical simulation, and the bifurcation diagram shows the two thresholds of the demonstration system. At the first threshold, the heteroclinic orbit of the system breaks, and the system goes to chaos in crisis way. At the second threshold, the crisis reappears and the new strange attractor appears. The variation of the first critical value under various frequency combinations is investigated based on the Melnikov method, and the results are compared with the results of numerical simulation. The analytical and numerical results are qualitatively the same although there is a quantitative difference between them.Keywords: Duffing system /simultaneous resonance /nonlinear dynamical system /chaos 全文HTML --> --> --> 1.引 言 Duffing系统是经典的非线性动力系统, 能够描述转子系统[1 -2 ] 、船舶横摇[3 -4 ] 和受电弓弓头悬挂系统的垂向振动[5 -6 ] 等多种动力学问题, 在微弱信号检测[7 -9 ] 和能量采集[10 -11 ] 领域也有应用. 目前在对Duffing振子的研究中, 系统的周期振动解及其稳定性受到****关注. Shen等[12 ,13 ] 研究了分数阶Duffing系统的主共振, 利用平均法得到系统的近似解, 分析了分数阶项对系统稳态响应的影响, 提出等效线性刚度和等效线性阻尼的概念. Agarwal等[14 ] 研究了高斯白噪声激励下刚度软化Duffing系统的频响特性, 并通过实验分析了噪声幅值对系统跳跃现象的影响, 发现噪声可以破坏无噪声系统中的迟滞特性. 温少芳等[15 ] 研究了一类含分数阶时滞耦合反馈的Duffing系统, 利用平均法得到系统的一阶近似解, 并分析了反馈系数和分数阶项对系统动力学特性的影响, 发现分数阶时滞耦合反馈同时具有速度时滞反馈和位移时滞反馈的作用.[16 ] 研究了有界噪声与周期激励下Duffing系统的混沌运动, 基于Melnikov方法得到了系统进入混沌运动的必要条件, 讨论了噪声对系统混沌阈值的影响. 马少娟等[17 ] 和吴存利等[18 ] 研究了含随机参数的Duffing系统, 利用多项式逼近方法将随机系统等效为确定性系统, 用确定性系统的方法研究了随机系统的混沌运动. Niu等[19 ] 研究了一类分数阶Duffing系统的混沌运动, 利用谐波平衡法得到了原系统的等效整数阶系统, 基于Melnikov方法得到系统进入混沌的条件. 在对Duffing系统周期振动解和混沌运动的研究中也发展了一些新的研究方法. Liu等[20 ] 提出推广的广义胞映射法可用于分数阶Duffing系统的全局分析. Shen等[21 ] 和Niu等[22 ] 对增量谐波平衡法的推广可用于分数阶系统和强非线性系统的高阶近似分析.[23 ] 、亚谐共振[24 ] 等, 受多频激励的非线性系统还可能发生组合共振[25 ] 或者联合共振[26 ,27 ] . 尤其在联合共振下, Duffing系统的稳态周期解可多达7个分支, 其中包括4个稳定分支, 系统的响应在稳定分支间的跳跃现象更为复杂. 此外, 在多个激励频率不可公约时, Duffing系统将产生概周期响应[28 ] , 并且随着系统参数改变, 概周期响应容易失稳进入混沌[29 ] . 毕勤胜等[30 ] 研究了一类受两个简谐激励且频率不可公约的Duffing系统, 对系统在非共振情况下通往混沌的道路进行研究, 发现随着激励幅值改变, 概周期响应的某一周期分量或某一组合频率成分将发生倍化分岔导致混沌. 在实际问题中, 动力系统往往受到多个激励源的作用, 因此对多频激励的非线性系统进行研究是有必要的. 鉴于针对非线性系统在主-超谐联合共振情况下的研究极为少见, 本文以多频激励Duffing系统为对象, 考察系统在主-超谐联合共振时的周期运动与混沌运动. 通过多尺度法得到系统的近似解析解, 研究周期运动在Lyapunov意义下的稳定性. 基于Melnikov方法分析系统的全局动力学特性, 研究Duffing系统在主-超谐联合共振时通往混沌的道路.2.Duffing系统的主-超谐联合共振的一次近似解 研究受两个简谐激励的Duffing系统:$m$ , $c$ , $k$ , ${\alpha _1}$ , ${F_i}$ 和${\omega _i}$ ($i = 1, 2$ )分别为系统的质量、线性阻尼系数、线性刚度系数、非线性刚度系数、激励幅值和激励频率.$\varepsilon $ 为小参数, 满足$0 < \varepsilon \ll 1$ , ${\omega _0}$ 为系统的固有频率.1 )式可以等价地写成${\omega _1} \approx {\omega _0}$ , ${\omega _2} \approx \dfrac{1}{3}{\omega _0}$ , 且${f_1}$ 为小量, 即${\sigma _1}$ 和${\sigma _2}$ 为引入的调谐因子, 从而(2 )式成为[27 ] 研究系统的一次近似解. 引入两个时间尺度${T_0} = t$ , ${T_1} = \varepsilon t$ , 并假设(3 )式的解具有如下形式:4 )式代入(3 )式, 比较$\varepsilon $ 的同次幂, 得到一组偏微分方程:5a )式的解为$a\left( {{T_1}} \right)$ 和$\beta \left( {{T_1}} \right)$ 分别为慢变振幅和相位.6 )式可写成复数形式:$A\left( {{T_1}} \right) = \dfrac{{a\left( {{T_1}} \right)}}{2}{{\rm{e}}^{{\rm{j}}\beta \left( {{T_1}} \right)}}$ , $B = \dfrac{{9{f_2}}}{{16\, \omega _0^2}}$ , ${\rm{cc}}$ 为前述所有项的共轭.7 )式代入(5b )式得到:$A\left( {{T_1}} \right) = \dfrac{{a\left( {{T_1}} \right)}}{2}{{\rm{e}}^{{\rm{j}}\beta \left( {{T_1}} \right)}}$ 代入(9 )式, 分离实部和虚部可以得到慢变振幅$a\left( {{T_1}} \right)$ 和慢变相位$\beta \left( {{T_1}} \right)$ 满足的微分方程组:1 )在主-超谐联合共振下的一次近似解可以表示为$a$ 和$\beta $ 是${T_1}$ 的函数, 由(10 )式确定.3.周期运动的稳定性 23.1.Lyapunov意义下的稳定性条件 3.1.Lyapunov意义下的稳定性条件 相比瞬态响应, 稳态响应的稳定性更值得关注. 观察(10 )式可以发现, 定常解存在, 即${D_1}a = 0$ 和${D_1}\beta = 0$ 有解的必要条件是$\beta - {\sigma _1}{T_1}$ 和$\beta - 3{\sigma _2}{T_1}$ 是常数, 这时有${D_1}\beta = {\sigma _1} = 3{\sigma _2}$ . 进一步可以得到${\omega _1} = 3{\omega _2}$ , 即只有当两个激励频率满足此倍数关系时, 才能通过解析方法求得主-超谐联合共振的定常解.$\sigma = {\sigma _1} = 3{\sigma _2}$ , 再令$\beta - \sigma {T_1} = \varphi $ , (10 )式可以写成自治的形式:$a$ 和$\varphi $ 是${T_1}$ 的函数, 由(12 )式确定.13 )式的正确性, 利用变步长四阶五级Runge-Kutta法对系统(1 )进行数值仿真并和一次近似解对比, 取系统参数$m \!=\! 1,\; c = 0.02,\; k = 4,\; {\alpha _1} = 0.4,\; {F_1} = 0.1,\; {F_2} \!=\! 2, {\omega _2} = {\omega _1}/3$ . 首先对比稳态响应的幅频曲线, 仿真时长$t = 1000$ , 取后$20\% $ 响应的最大值为稳态幅值$\bar u$ , 得到解析解与数值解的幅频曲线对比结果如图1 所示. 然后对比位移时间历程, 取激励频率${\omega _1} \!=\! 2.2$ , ${\omega _2} \!=\! {\omega _1}/3$ , 解析解初值取$( {{a_0}, {\varphi _0}} ) =( {0.1, 0} )$ , 对应的数值解初值由(13 )式计算, 仿真得到解析解与数值解的位移时间历程对比结果如图2 所示.图 1 幅频曲线对比Figure1. Comparisons of amplitude-frequency curves.图 2 位移时间历程对比 (a) 瞬态响应; (b) 稳态响应Figure2. Comparisons of displacement time histories: (a) Transient response; (b) steady-state response.图1 和图2 中可见, 解析解和数值解在较宽的频率范围内吻合良好, 即使是瞬态响应也能够较为精确地描述. 此外, 从图1 中可以看到系统的稳态响应在一定频率范围内具有多值性, 事实上, 系统的多值性和稳定性都由近似解中的第一部分, 即$a\cos \left( {{\omega _1}t + \varphi } \right)$ 支配. 因此, 在系统周期运动的稳定性分析中只需考察这一部分.12 )式中的${D_1}a = 0$ , ${D_1}\varphi = 0$ , 可以得到定常解的振幅$\bar a$ 和相位$\bar \varphi $ 满足的方程组:14 )式导出定常解的幅频响应方程和相频响应方程分别为${{V}} = {\left[ {a, \varphi } \right]^{\rm{T}}}$ , 构造向量函数:$\left( {\bar a, \bar \varphi } \right)$ 处, $F\left( {{V}} \right)$ 的Jacobi矩阵和特征方程分别为$P = {\rm{tr}}{{J}}$ , $Q = \det \left[ {{J}} \right]$ .[31 ] , 系统在定常解$\left( {\bar a, \bar \varphi } \right)$ 处渐近稳定的条件是$P < 0$ 且$Q > 0$ . 对于阻尼系统, 总有$P < 0$ , 因此系统的稳态周期运动在Lyapunov意义下的稳定性条件为3.2.数值仿真 -->3.2.数值仿真 仍取参数$m = 1$ , $c = 0.02$ , $k = 4$ , ${F_1} = 0.1$ , ${F_2} = 2$ , ${\omega _2} = {\omega _1}/3$ . 由(15 )式计算定常解的幅频特性和相频特性, 再由(18 )式判断对应解支的稳定性, 得到${\alpha _1} = 0.4$ 和${\alpha _1} = - 0.4$ 时定常解的幅频曲线和相频曲线分别如图3 和图4 所示. 从图3 和图4 可见, 系统最多存在2个稳定解支和1个不稳定解支, 且图3(b) 的多值区域与图1 吻合. 如前所述, 许多工程振动问题都可以由Duffing系统描述. 转子系统在启停过程中可能经过共振区, 这时系统的响应将会在多个稳定解支之间切换, 振幅突然增大或减小, 称为跳跃现象. Wang等[11 ] 基于Duffing系统设计了一种能量采集装置, 在能量采集实验中观察到这种跳跃现象.图 3 定常解的幅频曲线 (a) ${\alpha _1} \!=\! - 0.4$ , 刚度软化; (b) ${\alpha _1} \!=\! 0.4$ , 刚度硬化 (圆表示稳定解支, 星号表示不稳定解支)Figure3. Amplitude-frequency curves of steady-state response: (a) ${\alpha _1} = - 0.4$ , stiffness softening; (b) ${\alpha _1} = 0.4$ , stiffness hardening (the circles for stable solution and the asterisks for unstable one).图 4 定常解的相频曲线 (a) ${\alpha _1} \!=\! - 0.4$ , 刚度软化; (b) ${\alpha _1} \!= 0.4$ , 刚度硬化(圆表示稳定解支, 星号表示不稳定解支)Figure4. Phase-frequency curves of steady-state response: (a) ${\alpha _1} = - 0.4$ , stiffness softening; (b) ${\alpha _1} = 0.4$ , stiffness hardening (the circles for stable solution and the asterisks for unstable one).15 )式和(18 )式仿真得到非线性刚度系数${\alpha _1}$ 对系统的影响如图5 所示. 对于刚度软化系统, 随着系统刚度逐渐软化, 共振峰逐渐降低, 多解区域扩大; 对于刚度硬化系统, 随着系统逐渐硬化, 共振峰也逐渐降低, 但对多解区域影响不大.图 5 非线性系数${\alpha _1}$ 的影响 (a) 刚度软化; (b) 刚度硬化 (圆表示稳定解支, 星号表示不稳定解支)Figure5. Effects of the nonlinear coefficient ${\alpha _1}$ : (a) Stiffness softening; (b) stiffness hardening (the circles for stable solution and the asterisks for unstable one).4.混沌运动分析 24.1.系统的混沌阈值 4.1.系统的混沌阈值 摄动理论得到的近似解具有一定局限性. 由于系统在一定条件下可能进入混沌, 此时近似解无法描述系统的响应, 因而需对系统进行全局分析, 确定系统的混沌阈值. Melnikov方法是检测动力系统混沌阈值的常用解析方法, 通过考察过鞍点的稳定流形和不稳定流形之间的距离, 得到系统的同宿轨道或异宿轨道发生横截相交的数学条件, 从而可以判断系统是否进入Smale马蹄意义下的混沌.1 )刚度软化(即${\alpha _1} < 0$ )的情况, 对(1 )式进行如下坐标变换$\varsigma $ 为小参数. 从而(1 )式可以写成:19 )式写成状态方程形式:$\varsigma = 0$ 时, 未扰系统为Hamilton系统:21 )有三个平衡点$\left( {0, 0} \right)$ , $\left( { - \dfrac{{{\omega _0}}}{{\sqrt \gamma }}, 0} \right)$ , $\left( {\dfrac{{{\omega _0}}}{{\sqrt \gamma }}, 0} \right)$ .$\left( {0, 0} \right)$ 是中心, $\left( { \pm \dfrac{{{\omega _0}}}{{\sqrt \gamma }}, 0} \right)$ 是鞍点. 连接鞍点的异宿轨道可以由下式求解:$t = 0$ 时, ${u_1}\left( 0 \right) = 0$ , 由(25a )式可以得到${u_2}\left( 0 \right) = \dfrac{{\omega _0^2}}{{\sqrt {2\gamma } }}$ 或${u_2}\left( 0 \right) = - \dfrac{{\omega _0^2}}{{\sqrt {2\gamma } }}$ . 从而可以由(25 )式解得${u_1}$ 和${u_2}$ 满足:19 )式写成向量函数形式:19 )的Melnikov函数为1 )出现异宿轨道横截相交的必要条件是:4.2.数值仿真 -->4.2.数值仿真 由(30 )式可知, 对于刚度软化的系统(1 ), 激励${F_i}$ 越强、阻尼$c$ 越小和非线性刚度${\alpha _1}$ 越软, 易于使系统的异宿轨道发生横截相交, 从而系统(1 )进入Smale马蹄意义下的混沌. 由于激励幅值${F_1}$ 已限制为小量, 而${F_2}$ 的选取较为自由, 因而考察${F_2}$ 对系统动力学特性的影响. 取系统参数$m = 1$ , $c = 0.3$ , $k = 1$ , ${\alpha _1} = - 1$ , ${F_1} = 0.2$ , ${\omega _1} = 1.1$ , ${\omega _2} = {\omega _1}/3$ , 代入(30 )式得到${F_2} > {\rm{0}}{\rm{.0623}}$ . 即在上述的参数下, 当${F_2} > {\rm{0}}{\rm{.0623}}$ 时系统(1 )可能出现异宿轨道横截相交, 并且${F_2}$ 越大于此值, 系统越可能进入混沌. 但该条件仅为系统进入混沌的必要条件, 还需进一步通过数值仿真才能得到系统进入混沌的临界值.${F_2}$ 下利用自由插值的梯形方法[32 ,33 ] 对系统(1 )进行数值仿真, ${F_2}$ 的起始值为$0.0600$ , 初值为$\left( {{u_{01}}, {{\dot u}_{01}}} \right)$ = ( 0.208010172501537, 0.326464098793873), 仿真时长为$t = 200{\text{π}}/{\omega _2}$ , 步长为$2 \times {10^{ - 4}}{\text{π}}/{\omega _2}$ . 仿真得到系统的分岔图如图6 所示. 奇怪吸引子的相轨迹线在局部上总是以指数速率分离的, Lyapunov指数通过度量相邻相轨迹线分离或收敛的平均变化率判断系统是否进入混沌, 是一种可靠的定量分析方法. 利用Jacobian法[34 ] 计算得到这组参数下系统的最大Lyapunov指数随${F_2}$ 变化的趋势如图7 所示.图 6 系统(1 )随${F_2}$ 变化的分岔图 (a) 整体图; (b) 局部放大图Figure6. Bifurcation diagram of Eq. (1 ) changing with ${F_2}$ : (a) Panoramic view; (b) local enlarged view.图 7 系统(1 )的最大Lyapunov指数随${F_2}$ 变化的趋势 (a) 整体图; (b) 局部放大图Figure7. The trend of the largest Lyapunov exponent of Eq. (1 ) changing with ${F_2}$ : (a) Panoramic view; (b) Local enlarged view.图6 可见, 当${F_2} > 0.259$ 时, 系统发生激变进入混沌态, 与图7 中${F_2} > 0.259$ 时最大Lyapunov指数的骤增吻合. 取${F_2} = 0.259$ , 初值为$\left( {{u_{02}}, {{\dot u}_{02}}} \right)$ = ( 0.110106001335058, 0.248137954024669) , 得到系统的周期轨道如图8 . 取${F_2} = 0.2595$ , 初值为$( {u_{03}}, {{\dot u}_{03}} )$ = ( 0.091801856843936, 0.382525085869613), 仿真得到系统的位移时间历程、相轨迹和Poincare截面如图9 所示. 从图8 和图9 可见, 激励幅值${F_2}$ 从$0.259$ 增加到$0.2595$ 时异宿轨道破裂, 周期轨道发展成为混沌吸引子, 系统的相轨迹受到左侧鞍点吸引. 此外, 从图6 可见系统在${F_2} > 0.268$ 时再次发生激变, 进入另一种混沌态. 取${F_2} = 0.268$ , 初值为$( {u_{04}}, {{\dot u}_{04}} )$ = (0.144691373245013, 0.202712823433900), 仿真得到系统的位移时间历程和相轨迹如图10 所示, 这时系统的相轨迹被左右两个鞍点吸引, 出现新的混沌吸引子.图 8 ${F_2} = 0.259$ 时的周期轨道Figure8. Periodic orbits for ${F_2} = 0.259$ .图 9 ${F_2} = 0.2595$ 时的混沌状态 (a) Poincare截面; (b) 位移时间历程; (c) 相轨迹Figure9. Chaotic state for ${F_2} = 0.2595$ : (a) Poincare map; (b) displacement time histories; (c) phase trajectory.图 10 ${F_2} = 0.268$ 时的混沌状态 (a) 位移时间历程; (b) 相轨迹Figure10. Chaotic state for ${F_2} = 0.268$ : (a) Displacement time histories; (b) phase trajectory.4.3.解析结果与数值仿真结果的关系 -->4.3.解析结果与数值仿真结果的关系 在前述的系统参数下, 通过Melnikov方法解析得到激励幅值${F_2}$ 的临界值为$0.0623$ , 通过数值仿真得到系统首次出现混沌的临界值为$0.259$ . 为进一步研究解析与数值仿真得到的临界值的关系, 仍取系统参数$m = 1$ , $c = 0.3$ , $k = 1$ , ${\alpha _1} = - 1$ , ${F_1} = 0.2$ , 并且激励频率保持严格的倍数关系${\omega _1} = 3{\omega _2}$ , 分别利用数值仿真和Melnikov方法解析求解不同的频率组合下${F_2}$ 的临界值, 得到仿真结果与解析结果的对比如图11(a) 所示.图 11 临界激励幅值${F_2}$ 的解析结果与数值仿真结果对比 (a) ${\omega _1} = 3{\omega _2}$ ; (b) ${\omega _1} = 1.1$ ; (c) ${\omega _2} = 0.3667$ (星号代表解析结果, 圆代表数值仿真结果)Figure11. Comparisons of analytical results and numerical simulation results of critical excitation amplitude ${F_2}$ : (a) ${\omega _1} = 3{\omega _2}$ ; (b) ${\omega _1} = 1.1$ ; (c) ${\omega _2} = 0.3667$ (the asterisks for analytical results and the circles for numerical simulation results).${\omega _1} \approx 3{\omega _2}$ 的情况. 其他参数不变, 并且固定${\omega _1} = 1.1$ , 求解不同的激励频率${\omega _2}$ 下系统出现混沌的临界激励幅值${F_2}$ , 得到解析与数值仿真结果对比如图11(b) 所示. 再固定${\omega _2} = 0.3667$ , 求解不同的激励频率${\omega _1}$ 下系统出现混沌的临界激励幅值${F_2}$ , 得到结果如图11(c) 所示.图11 可见, 解析结果能够大致反映${F_2}$ 的临界值的趋势, 与仿真结果仅在数值上存在差异, 原因是Melnikov方法解析得到的临界值仅为系统进入混沌的必要条件, 系统的激励幅值${F_2}$ 需大于该临界值到一定程度才能首次进入混沌. 此外, 从图11(a) 和图11(c) 可见, 系统在激励频率满足严格的倍数关系和近似的倍数关系这两种情况下, 临界值的变化趋势大致相同.5.结 论 应用多尺度法得到Duffing系统的主-超谐联合共振的近似解析解, 并用数值方法进行验证, 解析解的瞬态过程和稳态过程都具有较高精度. 基于Lyapunov第一方法研究了系统稳态周期运动的稳定性, 发现系统最多存在2个稳定解支和1个不稳定解支. 讨论了非线性刚度对稳态周期运动的幅频响应的影响, 结果表明非线性刚度硬化和软化均能够降低响应的幅值, 并且刚度软化能够进一步影响响应的多值性. 基于Melnikov方法对刚度软化系统进行全局分析, 得到系统的异宿轨道横截相交的必要条件, 发现较大的激励幅值、小阻尼和刚度软化容易使系统进入混沌. 选取一组符合主-超谐联合共振条件的参数进行数值仿真, 发现两个临界值. 当激励幅值通过第一个临界值时, 系统的异宿轨道破裂, 以激变方式进入混沌态; 激励幅值通过第二个临界值时, 系统再次发生激变, 出现新的混沌吸引子. 对多种频率组合的参数分别利用数值仿真和Melnikov方法解析得到系统首次进入混沌的临界值, 对两种方法所得结果进行了对比, 解析结果在一定程度上能够真实反映系统的临界值变化的趋势, 数值仿真的结果也验证了解析结果的正确性. 














































 图 1 幅频曲线对比
图 1 幅频曲线对比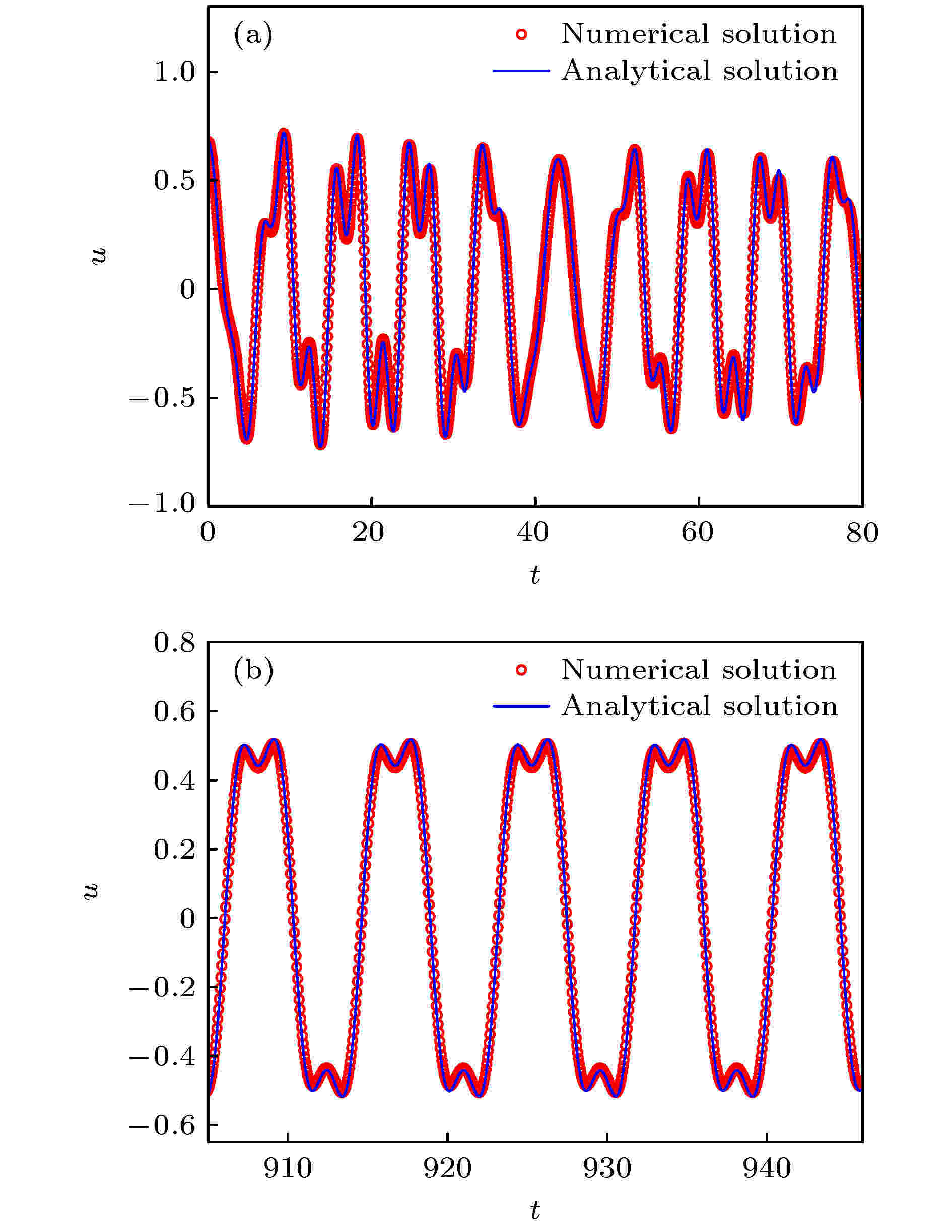 图 2 位移时间历程对比 (a) 瞬态响应; (b) 稳态响应
图 2 位移时间历程对比 (a) 瞬态响应; (b) 稳态响应























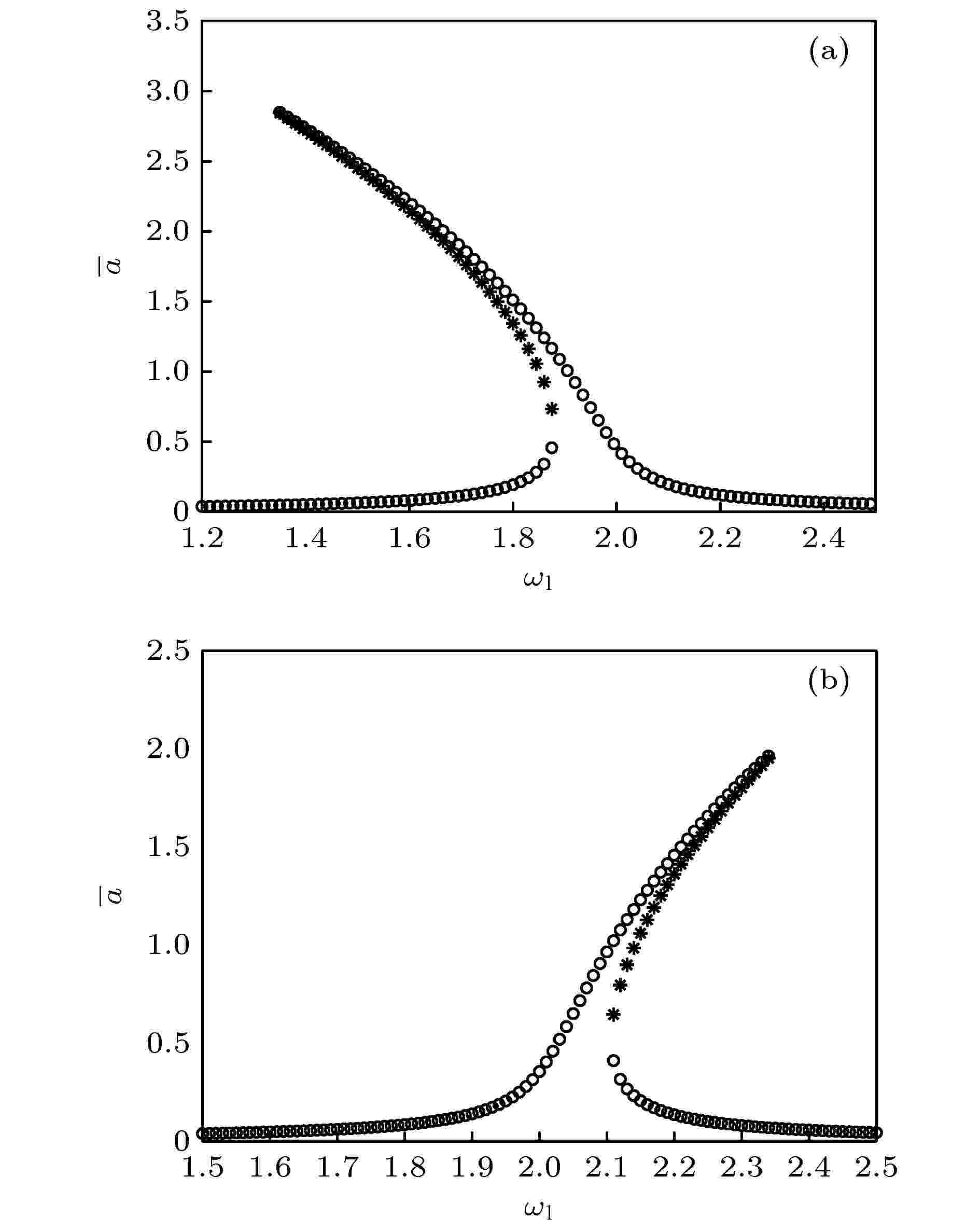 图 3 定常解的幅频曲线 (a)
图 3 定常解的幅频曲线 (a) 



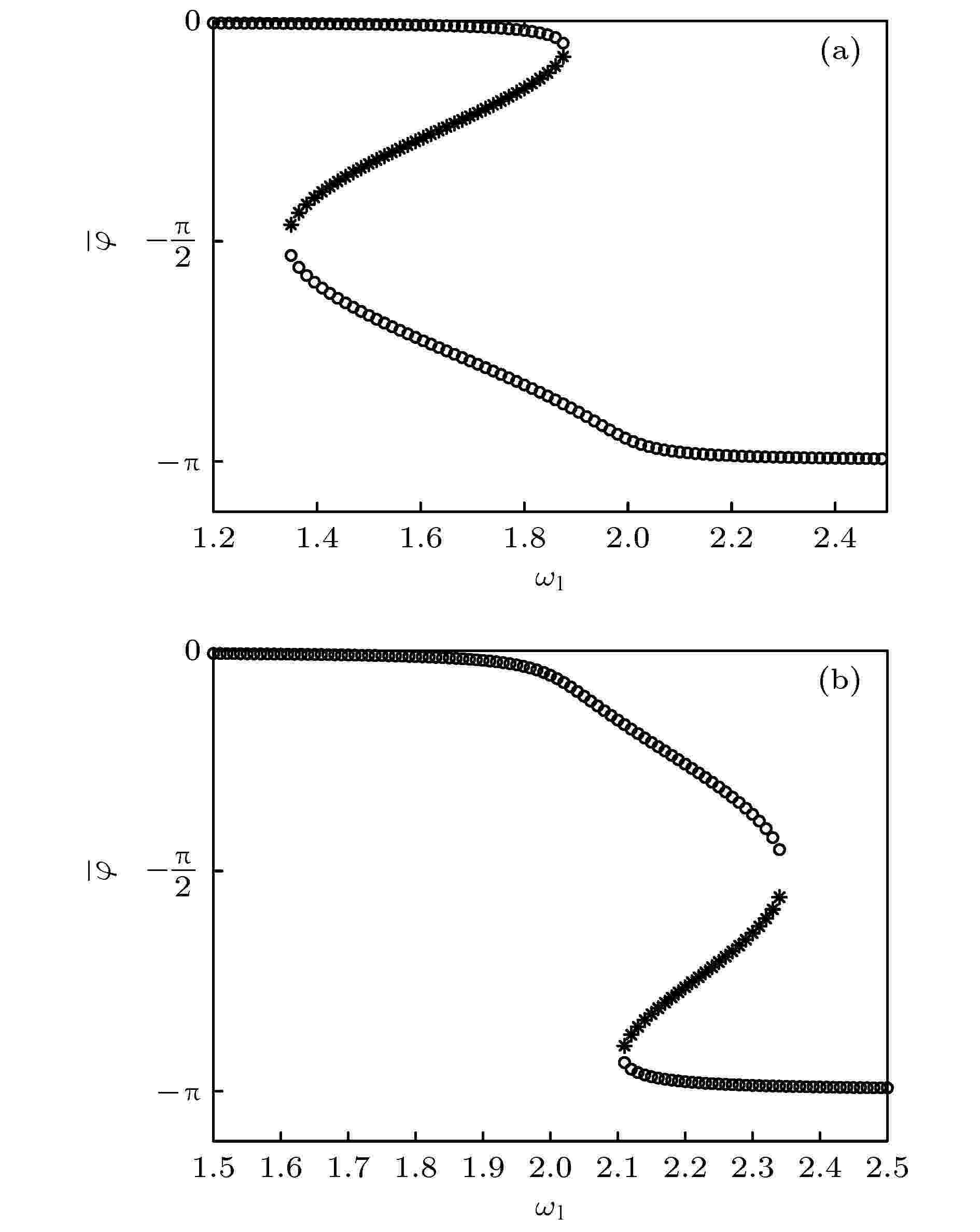 图 4 定常解的相频曲线 (a)
图 4 定常解的相频曲线 (a) 




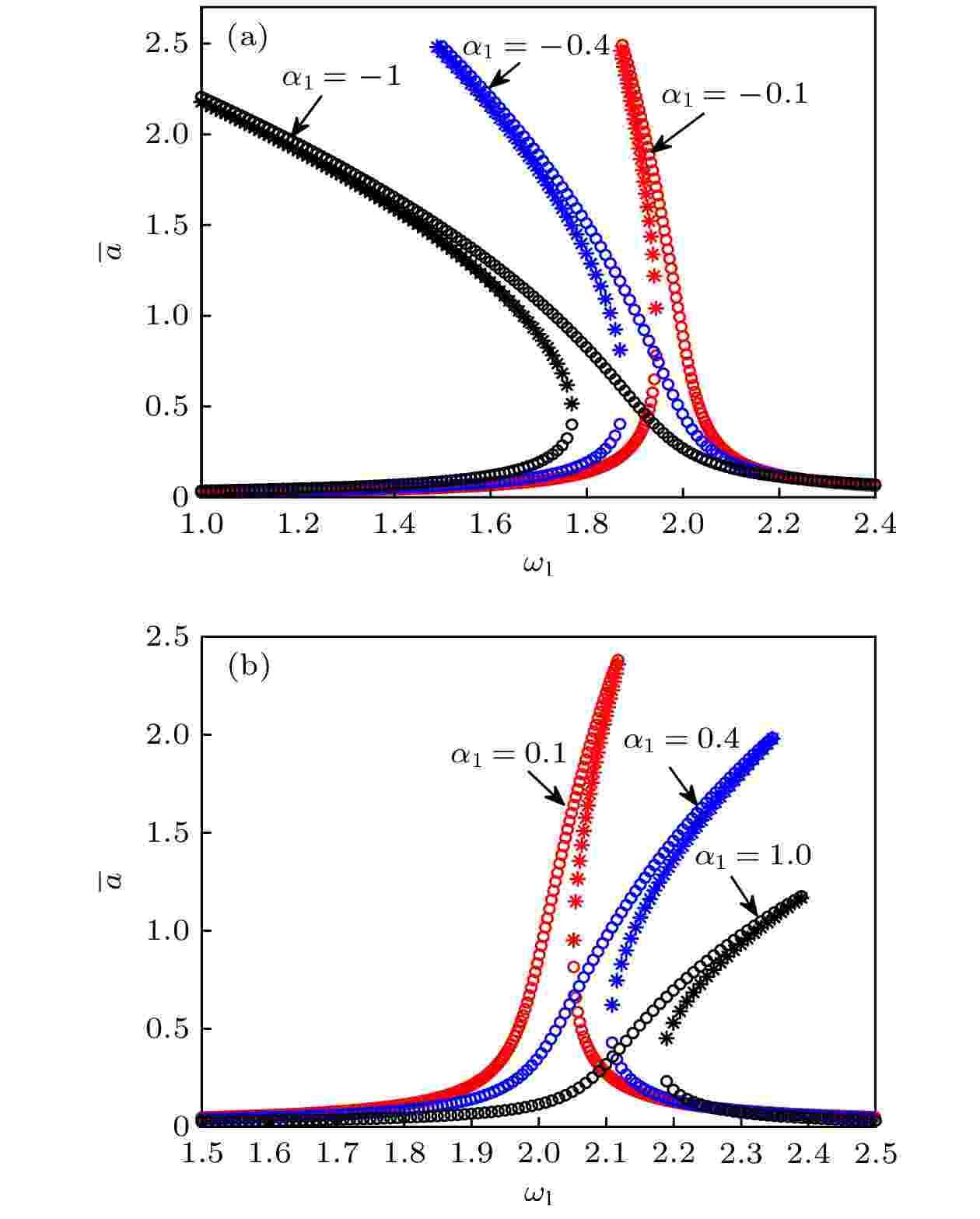 图 5 非线性系数
图 5 非线性系数




















































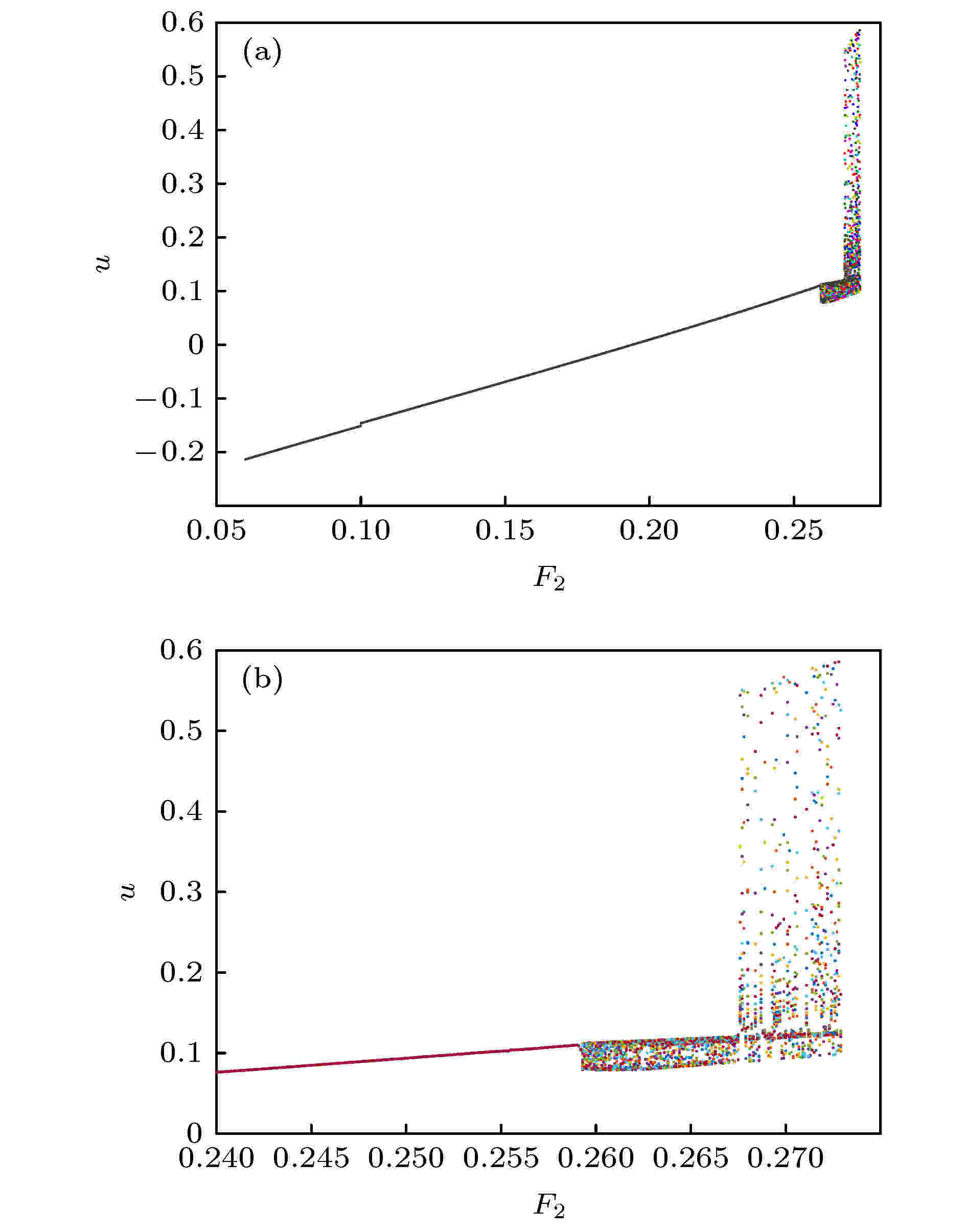 图 6 系统(1)随
图 6 系统(1)随

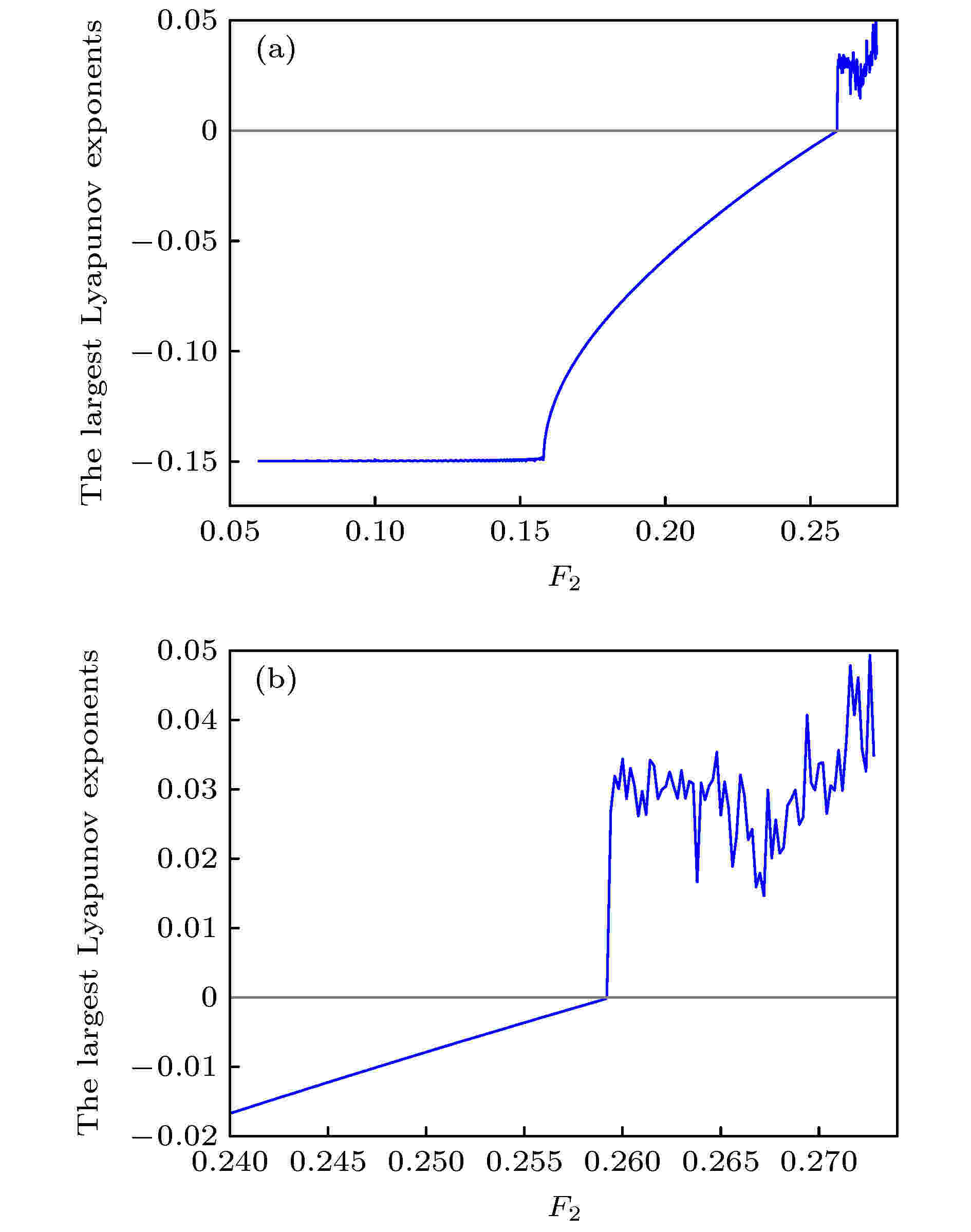 图 7 系统(1)的最大Lyapunov指数随
图 7 系统(1)的最大Lyapunov指数随















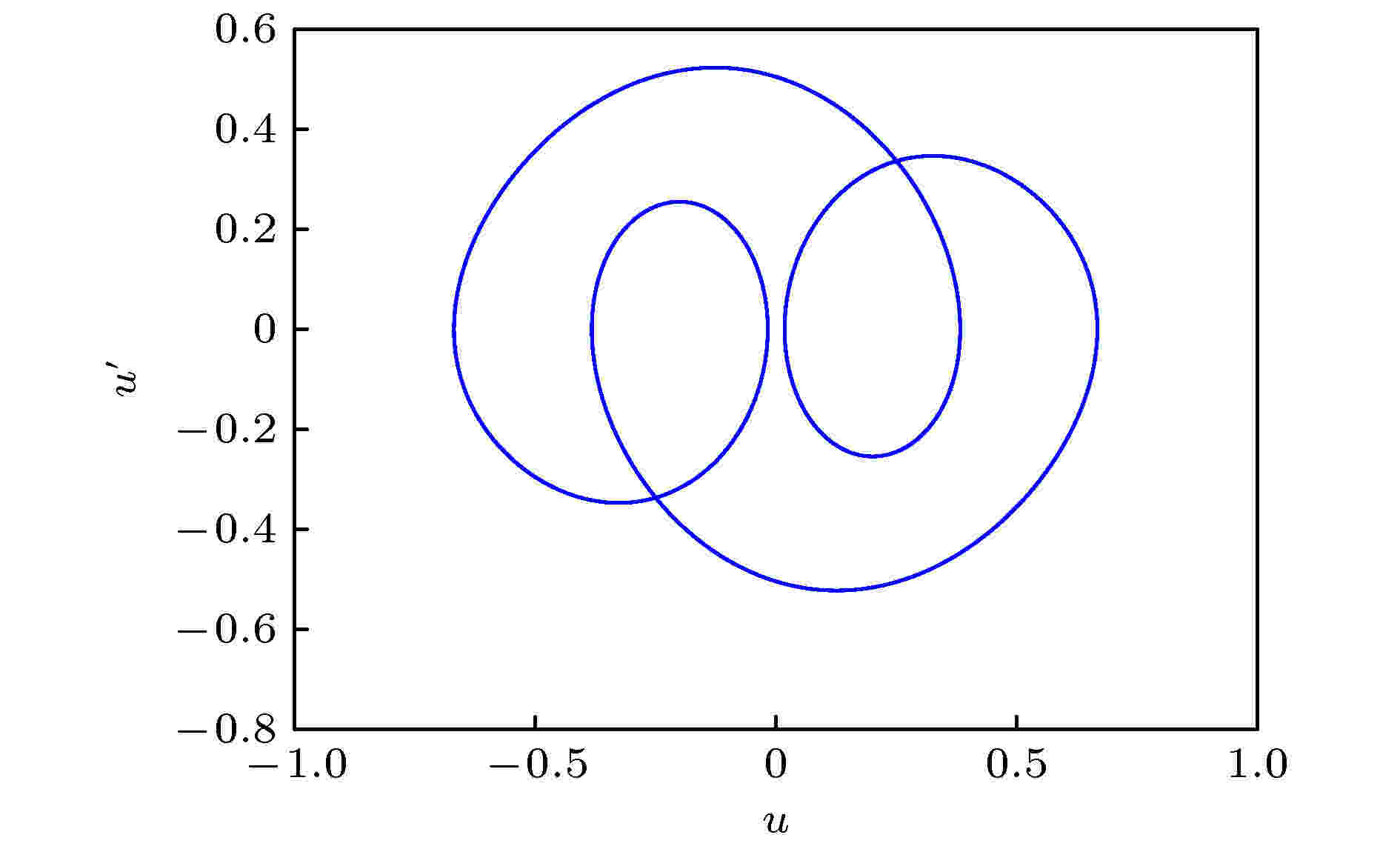 图 8
图 8 

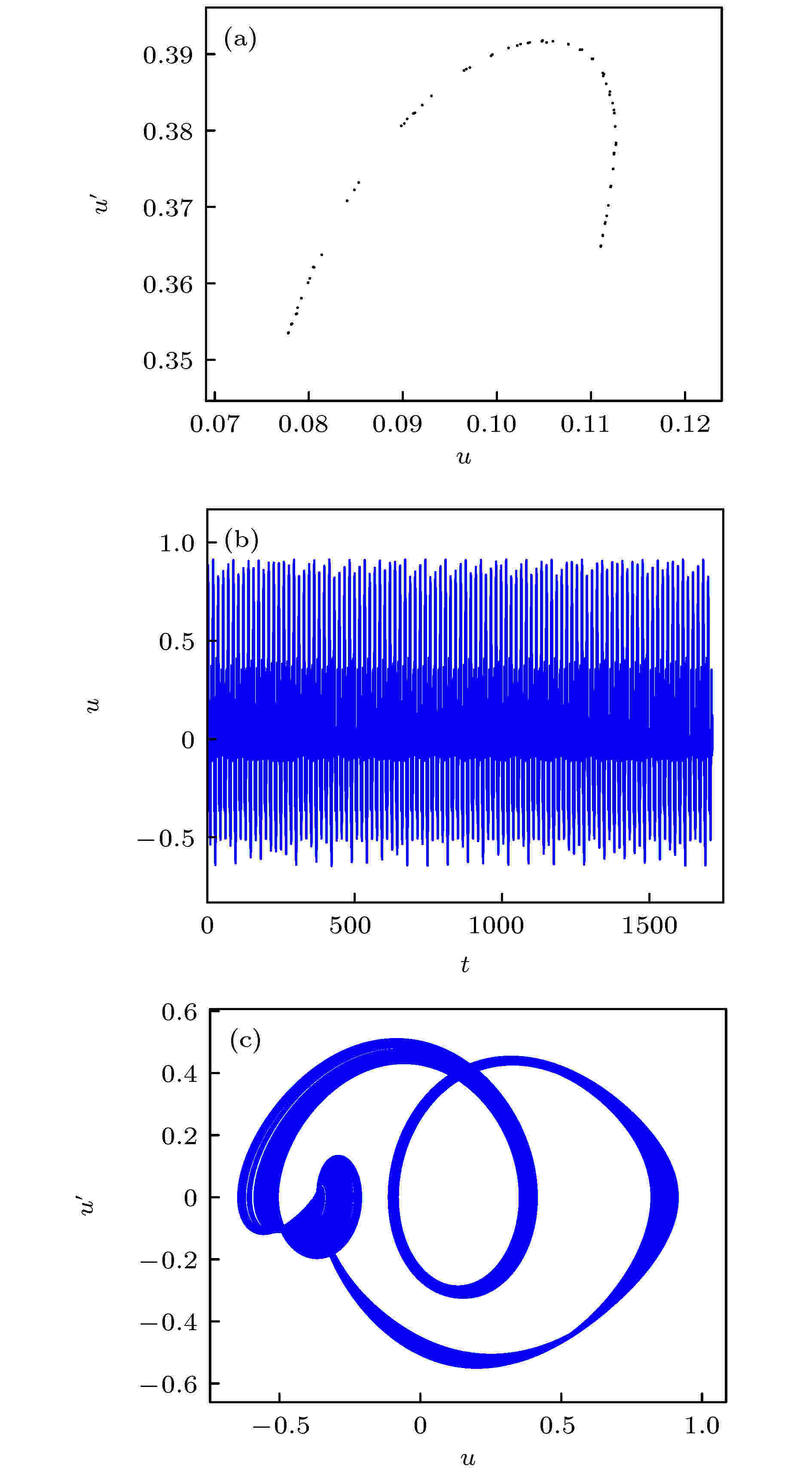 图 9
图 9 

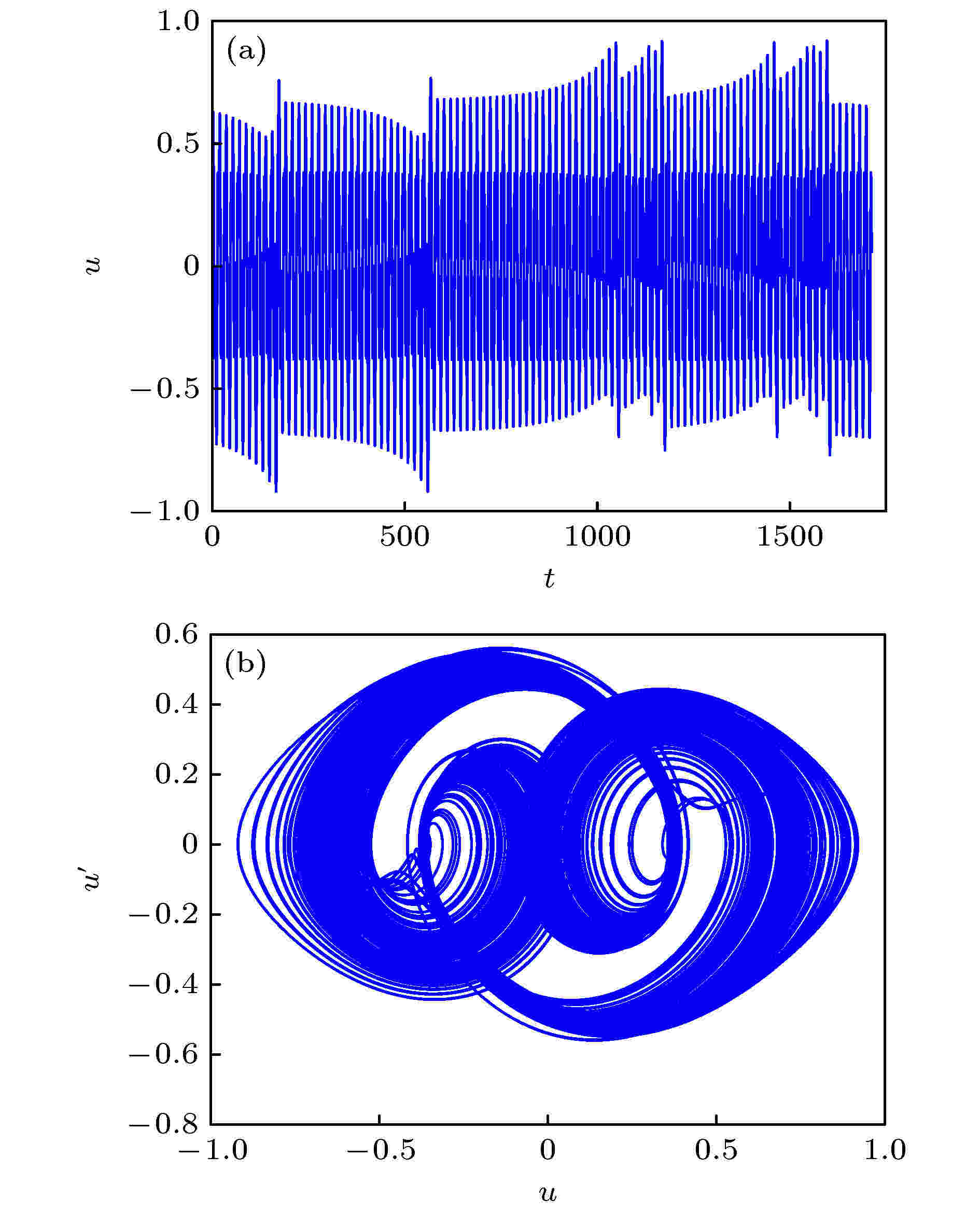 图 10
图 10 













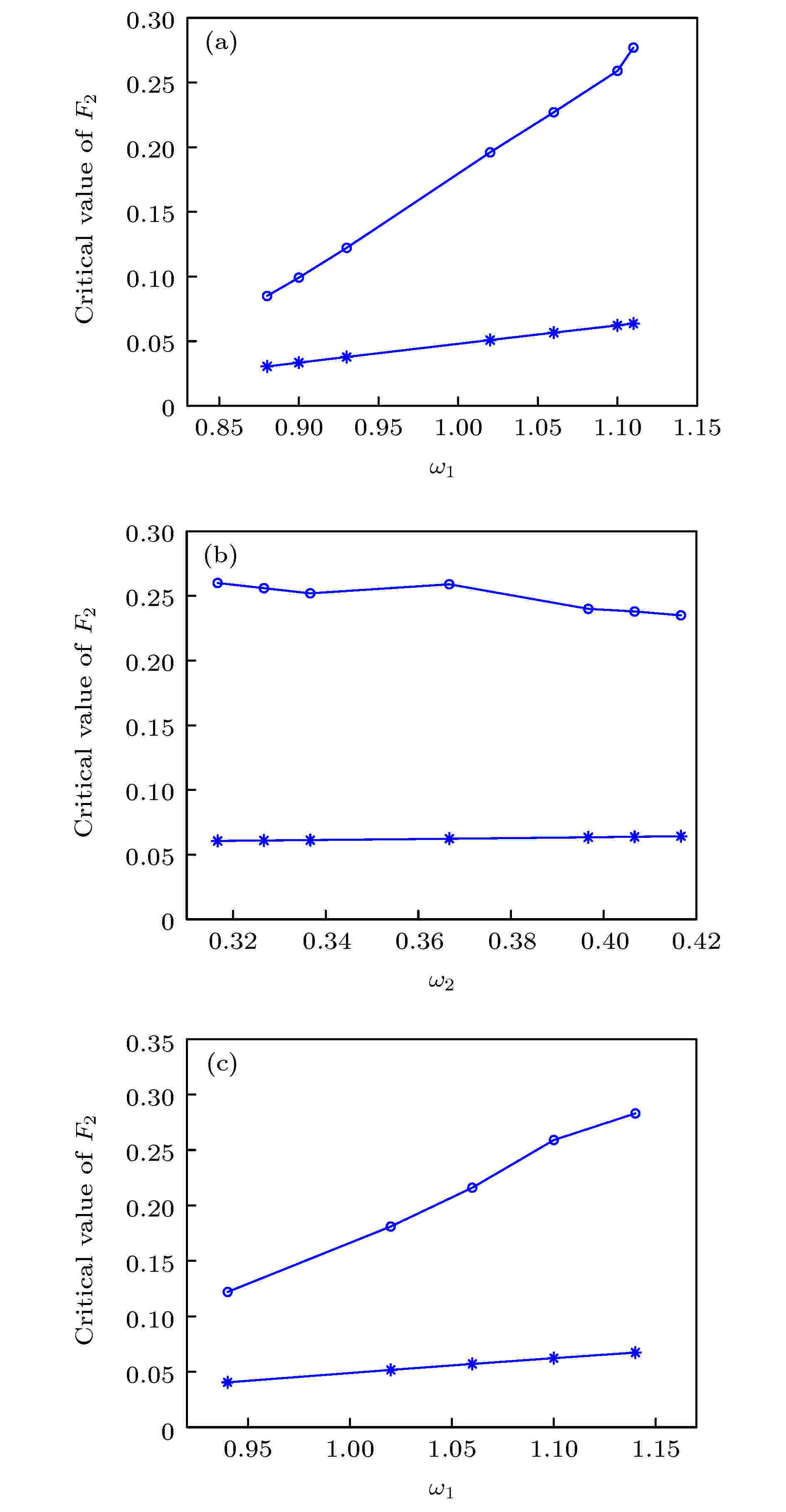 图 11 临界激励幅值
图 11 临界激励幅值




















