摘要: 钙、钾、钠等离子在细胞内连续泵送和传输时产生的时变电场不仅会影响神经元的放电活动, 而且会诱导时变磁场去进一步调节细胞内离子的传播. 根据麦克斯韦电磁场理论, 时变的电场和磁场在细胞内外的电生理环境中会相互激发而产生电磁场. 为了探究电磁场影响下的神经元放电节律转迁, 本文在三维Hindmarsh-Rose (HR)神经元模型的基础上, 引入磁通变量和电场变量, 建立了一个五维HR神经元模型(简称EMFN模型). 首先, 结合Matcont软件分析了EMFN模型的平衡点分布与全局分岔性质, 发现并分析了该模型存在的亚临界Hopf分岔、隐藏放电及其周期放电与静息态共存等现象. 其次, 利用双参数及单参数分岔、ISI 分岔和最大Lyapunov指数等工具进行数值仿真, 详细分析了EMFN模型存在的伴有混沌及无混沌的加周期分岔结构、混合模式放电和共存模式放电等现象, 同时揭示了电场和磁场强度影响其放电节律的转迁规律. 最后, 利用Washout控制器将EMFN模型的亚临界Hopf分岔转化为超临界Hopf分岔, 使其在分岔点附近的拓扑结构发生改变, 由此达到消除其隐藏放电的目的. 本文的研究结果证实了新建神经元模型具有丰富的放电节律, 将影响神经元的信息传递和编码, 为完善神经元模型, 揭示电磁场对生物神经系统的影响, 以及探求一些神经性疾病的致病机理提供了思路.
关键词: 电磁场 /
Hopf分岔分析 /
隐藏吸引子 /
双参数分岔 /
混合模式放电 English Abstract Dynamic response and control of neuros based on electromagnetic field theory An Xin-Lei 1,2 ,Qiao Shuai 1 ,Zhang Li 3 1.School of Mathematics and Physics, Lanzhou Jiaotong University, Lanzhou 730070, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 11962012) and the China Postdoctoral Science Foundation (Grant No. 2018M633649XB)Received Date: 16 August 2020Accepted Date: 16 September 2020Available Online: 26 February 2021Published Online: 05 March 2021Abstract: The time-varying electric fields generated by continuously pumping and transmitting calcium, potassium and sodium ions in cells not only affect the discharge activity of neurons, but also induce time-varying magnetic fields to further regulate the fluctuation of ions. According to the Maxwell's electromagnetic field theory, time-varying electric field and magnetic field can stimulate each other in the electrophysiological environment inside and outside the cells to produce electromagnetic field. In order to explore the discharge rhythm transition of neurons under the influence of electromagnetic fields, a five-dimensional (5D) HR neuron model (EMFN model for short) is established by introducing magnetic flux variable and electric field variable into a three-dimensional (3D) Hindmarsh-Rose (HR) neuron model. Firstly, the equilibrium distribution and global bifurcation properties of EMFN model are analyzed by Matcont software, then the existence of subcritical Hopf bifurcation, hidden discharge, coexistence of periodic discharge and resting state are found and analyzed. Secondly, by using the tools of two-parameter and one-parameter bifurcation, ISI bifurcation and the maximum Lyapunov exponent for numerical simulation, the period-adding bifurcation with and without chaos, mixed mode discharge and coexistence mode discharge in the EMFN model are analyzed in detail. At the same time, the transition law of discharge rhythm with the influence of electric field and magnetic field intensity is revealed. Finally, the Washout controller is used to convert the subcritical Hopf bifurcation into supercritical Hopf bifurcation, so the topological structure of EMFN model near the bifurcation point is changed for eliminating the hidden discharge. The research results of this paper confirm that the novel neuron model has rich discharge rhythm, which will affect the information transmission and coding, and provide some ideas for improving the neuron models, revealing the influence of electromagnetic field on biological nervous system, and exploring the pathogenic mechanism of some neurological diseases.Keywords: electromagnetic fields /Hopf bifurcation analysis /hidden attractor /two-parameter bifurcation /mixed mode discharge 全文HTML --> --> --> 1.引 言 神经系统是生物体内起主导作用的系统, 支配着感觉、运动和记忆等功能. 生物神经系统的基本结构和功能单位是神经元, 神经元通过复杂的放电活动来实现非线性功能. 神经元的放电活动具有一定的节律性, 这与神经信息的产生、转递和解码密切相关, 因此, 研究神经元的放电活动的动力学特性具有重要的生理学和神经工程意义[1 -4 ] . 神经元模型的建立为定量分析神经元放电活动的规律奠定了基础, 同时也极大地促进了神经科学的发展[5 -8 ] . 实际上, 神经元模型可以分为两大类: 一类是基于电导依赖或生物物理学模型, 它强调了各离子通道对神经元膜电位的影响, 其中典型的模型有Hodgkin-Huxley(HH)模型[9 ] 、Morris-Lecar(ML)模型[10 ] 、Chay模型[11 ] 和Hindmarsh-Rose (HR)模型[12 ] 等, 通常情况下, 这类模型的维数较高并且数值分析困难, 不适合应用于耦合系统和神经元网络的研究; 另一类是现象学或者非电导依赖模型, 这类模型注重神经元的输入和输出关系, 并不考虑具体的生理机制对膜电压的影响, 例如Izhikevich模型[13 ] 、Fitzhugh-Nagumo(FHN)模型[14 ] 和True-North模型[15 ] 等, 这类模型结构简单并且计算简便, 从而被广泛应用于神经元动力学分析及其网络仿真的研究[16 -18 ] .[19 ] 提出了一种具有阈值切换机制的新型忆阻器仿真器, 并建立了一个能够产生峰和簇放电行为的神经元电路. Bao等[20 ] 报道了一种带有忆阻器的三维HR神经元模型, 该模型不存在任何平衡点, 却存在周期吸引子与混沌吸引子共存的隐藏动力学现象, 并且基于电路实验进行了数值模拟验证. Usha和Subha[21 ] 分析了带有磁通变量的HR神经元模型分岔模式, 并研究了电突触和化学突触耦合下同步、去同步和尖峰放电态与静息态共存振荡行为. Zhao等[22 ] 讨论了具有磁通耦合的扩展HR神经元的相位同步问题, 发现在相同的激励电流下, 随着耦合相位的增大, 耦合强度达到相位同步的阈值逐渐变小. Pham等[23 ] 研究了具有记忆性突触权值的神经网络, 它可以在不存在平衡点的情况下产生超混沌隐藏吸引子.[24 -28 ] . Ma和Tang[24 ] 开创性地考虑在离子穿越细胞膜或持续的电磁辐射刺激下, 细胞膜内外会产生电磁感应而改变细胞膜上的磁通量, 进而在HR神经元模型中引入磁通量去描述上述电磁感应现象, 并对其进行新角度下的放电行为初探. 随后, Lü等[25 ] 讨论了考虑磁通量的神经元模型的动力学特性, 通过改变初始状态, 可以观察到多种模式的放电活动, 反映了该神经元的记忆效应. Wu等[26 ] 通过对上述神经元施加加性相位噪声来检测神经元在膜态中的动态响应和相变, 对电活动的动力学特性进行了检测和讨论, 并观察到双相干共振行为. 此外, 在神经元模型的膜电位采样时间序列中可以观察到多种模式的电活动. Kafraja等[27 ] 提出了一个三变量具有记忆性的Izhikevich模型来描述神经元在电磁感应和噪声作用下的动力学行为, 该模型可以描述内外磁场对神经元的影响. An和Zhang[28 ] 基于双参数数值仿真发现了考虑磁通量的神经元模型具有丰富的分岔结构, 例如混合模式振荡和加周期分岔, 并设计一个Hamilton能量反馈控制器, 将其控制到不同的周期簇放电状态. 上述文献的研究表明, 电磁感应现象的引入, 使原有的神经元模型更具有现实和物理意义, 同时也能展现出更丰富的放电模式. 此外, 这些模型也可用于进一步对电磁辐射影响下的生物神经系统的研究.[29 ] 考虑电荷分布和极化变化引起的电场效应, 在HR神经元的基础上, 建立了一个具有感应电场的神经元模型, 并对其电活动的动力学行为进行了分析和讨论, 证实了在不同的电场作用下, 神经元的电活动会发生不同的模态跃迁. Du等[30 ] 研究了感应电场作用下正弦IEF和随机相位对单个神经元和神经元网络信息编码和传输的联合作用机制, 得到了单个神经元放电模式的跃迁状态, 包括簇放电、峰放电和阈下振荡, 并提出应该采用多种方法改进或重建神经元系统电磁感应模型. 另外, 通过电容器耦合, 非线性电路之间也可以建立时变的电场. Wang等[31 ] 综述了忆阻器在神经动力学、时延、同步模式, 特别是电磁感应与辐射、场效应下神经元模型的建立、场耦合对非线性电路间信号传播的影响. 同时指出, 两个电路的输出可以通过在极板上连续充电和放电, 激活耦合电容器中的时变电场. Oliveira等[32 ] 讨论了两个电容耦合Van der Pol振荡器的同步问题, 并通过数值仿真和理论分析指出此耦合方式不会增加额外的噪声源和电力消耗. Xu等[33 ] 指出, 通过电容耦合的两个非线性电路被激活时, 可以产生一个时变电场, 耦合电容器的能量流传播可进一步调节输出和动力学耦合电路. 电场和电容器耦合为神经元之间的信号编码提供了新的认识, 即使在突触耦合被抑制或未激活的情况下, 电场效应也有利于神经元之间的信号传播.2.模型描述 马军研究组[24 ,25 ] 认为神经元膜电位的持续波动或者改变将会在细胞周围产生磁场, 由此通过忆阻器引入磁通变量来模拟磁场与膜电位之间的相互作用, 建立了一个四变量的HR神经元模型:$x, \;y, \;z, \;\phi, \;I$ 分别表示膜电位、与钠离子和钾离子相关的恢复快电流、与钙离子相关的自适应慢电流、磁通变量和外界刺激电流; $a, \;b, \;c, \;d, \;r, \;s, \;{\chi _0}$ 是模型重要的参数; ${I_{\rm{e}}}$ 表示磁场产生的电磁感应电流, 其数学表达式为${I_{\rm{e}}} = - {k_0}W(\phi )x = - {k_0}(\alpha + 3\beta {\phi ^2})x$ , $W(\phi )$ 为磁控忆阻器, 参数${k_0}$ 调节膜电位和磁通之间的相互作用, 可视为磁场的反馈强度. 由于该模型引入了磁通变量, 使该模型具有更多的分岔参数, 并且膜电位的放电模式将更加丰富, 从而被广泛应用于神经元的分岔分析、膜电位的迁移控制和场耦合下神经网络的同步行为研究[34 ,35 ] . 众所周知, 神经元的放电活动会受各离子通道作用的影响, 离子通道能改变细胞内外离子浓度的分布, 同时也决定了细胞的动作电位. Ma等[29 ] 认为外电场参与了细胞内各离子的传输和交换, 从而引起膜电位的变化, 通过引入电场变量, 详细研究了电场作用下HR神经元模型的放电特性.2 )式中的变量和参数与(1 )式中相同. 变量$E$ 表示感应电场, 考虑到与自适应慢电流$z$ 相比, 快电流$y$ 对电场的变化更敏感, 由此通过对变量$y$ 施加${k_1}E$ 来描述电场的影响, ${k_1}$ 用来调节电场和快电流之间的相互作用, 可视为电场的反馈强度. 对于神经元系统而言, 参数${k_1}, \;{k_2}, \;{k_4}$ 的取值很大程度上取决于神经元的固有的兴奋特性. 此外$ - {k_3}\phi $ 和$ - {k_5}E$ 分别表示神经元对磁场和电场的自适应调节项. 最初的HR模型是一个无量纲的模型, 因此, 模型(2 )的参数均为无量纲参数. 这里, 部分参数取Hindmarsh和Rose在1984年建立HR神经元模型时设定的基准值: $a = 1.0$ , $b = 3.0$ , $c = 1.0$ , $d = 5.0$ , $s = 4.0$ , $r = 0.006$ , ${\chi _0} = - 1.61$ . $I$ 一般在$[ - 10, 10]$ 内取值, 本文取$I = 3$ . 其余参数取为: $\alpha = 0.2$ , $\beta = 0.0{\rm{3}}$ , ${k_0} = 0.1$ , ${k_1} = 0.{\rm{1}}$ , ${k_2} = 0.{\rm{3}}$ , ${k_3} = 0.{\rm{5}}$ , ${k_4} = 0.{\rm{2}}$ , ${k_5} = 0.{\rm{3}}$ . EMFN模型在神经元模型(1 )的基础上引入电场作为第五个变量去描述神经元内部的电场效应, 以此来研究神经元内部电场和磁场相互激发而形成的电磁场对神经系统的影响.3.分岔分析与隐藏放电 23.1.平衡点稳定性与Hopf分岔分析 3.1.平衡点稳定性与Hopf分岔分析 考虑电场和磁场效应的EMFN模型(2 )将具有更加丰富的动力学特性, 为了探索其放电和分岔模式, 首先需要分析其平衡点的分布及其稳定性. 由模型(2 )的动力学方程可得零线方程组:3 )的实数解$({x_0}, {y_0}, {z_0}, {\phi _0}, {z_0})$ , 可获得模型(2 )平衡点为${{{P}}_0} = ({x_0}, {y_0}, {z_0}, {\phi _0}, {z_0})$ , 并且由方程组(3 )可得4 )的根依赖于$I$ 和${k_i}\;(i = 1, 2, 3, 4, 5)$ 的取值, 并且其实数根就是平衡点处的${x_0}$ . 由方程组(3 )可确定平衡点处其余的坐标:2 )在平衡点${{{P}}_0}$ 的稳定性是由相应线性化矩阵${{A}}$ 的特征根所决定:图1 所示的EMFN模型(2 )关于参数$I$ 和膜电压$x$ 的全局分岔图(图中黑色曲线为平衡点处的${x_0}$ , 红色星点为Hopf分岔点$H$ , 绿色区域为稳定的静息态, 红色区域为周期2簇放电态, 黄色区域为周期1尖峰放电态, 浅蓝色区域为小振幅振荡发散态), 并且在Hopf分岔点$H$ 处的位置和相应的特征根为图 1 EMFN模型(2 )在$x \in [ - 20, 20]$ 时的吸引域Figure1. The attractive basins of EMFN model (2 ) when $x \in [ - 20, 20]$ .${L_H} = 0.000{\rm{24971}} > 0$ . 由此可知, EMFN模型(2 )在分岔点$H$ 发生亚临界Hopf分岔, 其分岔的方向为参数$I$ 减小的方向. 通过观察图1 可知, EMFN模型(2 )在Hopf分岔点$H$ 分岔前后都存在放电模式不同的吸引域, 即在分岔点$H$ 附近, 模型(2 )的放电模式不仅与参数$I$ 取值相关, 而且与初值$x$ 也密切相关. 因此, 揭示神经元模型(2 )在分岔点$H$ 附近的放电规律, 可为对神经元异常放电行为的探讨提供参考.3.2.共存放电 -->3.2.共存放电 在非线性系统参数不变的情况下, 改变初始状态, 系统运行可能渐近趋向的定点、混沌或周期、准周期等不同稳定状态的现象称为多稳定性或共存吸引子[36 ,37 ] , 多稳定性表现出非线性动力系统丰富的稳定状态多样性, 并为系统提供了很大的灵活性. 本文所设计的EMFN模型(2 )具有丰富的共存放电现象.$I = {I_1} = {\rm{1}}{\rm{.172 > }}{I_H}$ , 相应的平衡点为6 )对应的特征根为${{{P}}_1}$ 为不稳定的焦结点. 若${I_1}$ 不变, 取初值为2 )的放电波形图如图2(a) 中蓝色曲线所示, 图2(b) 为图2(a) 中蓝色曲线的放大. 易知, 模型(2 )在6000个时间单位内处于发散趋势的小振幅振荡态(经过更长的时间仿真, 此发散趋势的振荡态将趋于周期2簇放电态, 这里将不再展示). 其原因是平衡点${{{P}}_1}$ 的特征根$0 < {\rm{Re}} (\lambda _{{I_1}}^{1, 2}) \ll 1$ , 故当初值在${{{P}}_1}$ 附近取值时, 神经元呈现出图2(b) 所示的发散态. 明显地, 神经元模型(2 )在平衡点${{{P}}_1}$ 附近的小振幅振荡区域比较小, 而周期2簇放电区域比较大.图 2 EMFN模型(2 )的时间响应图和吸引子 (a) ${P_1}$ 附近的共存振荡; (b) 图(a)中蓝色放大图; (c)${P_1}$ 附近的周期2极限环; (d) ${P_2}$ 附近的共存振荡; (e) 图(d)中蓝色放大图; (f) ${P_2}$ 附近的周期2极限环; (g)${P_3}$ 附近的共存振荡; (h) 图(g)中蓝色放大图; (i)${P_3}$ 附近的周期1极限环Figure2. Time responses and attractors of EMFN model (2 ): (a) Coexistence oscillation near ${P_1}$ ; (b) enlargement of the blue in (a); (c) limit cycle with period-2 near ${P_1}$ ; (d) coexistence oscillation near ${P_2}$ ; (e) enlargement of the blue in (d); (f) limit cycle with period-2 near ${P_2}$ ; (g) coexistence oscillation near ${P_3}$ ; (h) enlargement of the blue in (g); (i) limit cycle with period-1 near ${P_3}$ .${{{P}}_1}$ 较远处取值时, 如2 )的放电波形图如图2(a) 中红色曲线所示的周期2簇放电状态, 其振荡幅度远大于处在发散趋势的蓝色曲线所示的振荡幅度, 图2(c) 为对应的极限环吸引子.$I = {I_2} = 1.{\rm{152}} < {I_H}$ 6 )对应的特征根为${{{P}}_2}$ 为稳定的焦结点. 若${I_2}$ 不变, 取2 )的放电波形图如图2(d) , (e) 中蓝色曲线所示, 图2(e) 为图2(d) 中蓝色曲线的放大. 易知, 神经元模型此时处于收敛趋势的小振幅振荡态. 其原因是平衡点${{{P}}_2}$ 的特征根$ {\rm{Re}} (\lambda _{{I_2}}^{1, 2})<0 $ , 故当初值在${{{P}}_2}$ 附近取值时, 模型(2 )呈现出如图2(d) , (e) 中所示的静息态.${{{P}}_2}$ 较远处取值时, 模型(2 )也表现出初值敏感特性:2 )的放电波形图如图2(d) 中红色曲线所示的周期2簇放电状态, 其相轨迹为稳定的周期2极限环吸引子, 如图2(f) 所示. 明显地, 模型(2 )在两组初值下呈现小振幅振荡和周期2簇放电的共存状态.$I = {I_3} = 1.{\rm{086}} < {I_{\rm{2}}}$ 6 )对应的特征根为${{{P}}_3}$ 为稳定的焦结点. 若${I_3}$ 不变, 取初值2 )的放电波形图如图2(g) 和图2(h) 中蓝色曲线所示, 图2(h) 为图2(g) 中蓝色曲线的放大. 可以看出, 模型(2 )此时处于静息态. 对比图2(e) 和图2(h) 可知, $I = {I_{\rm{3}}}$ 时的膜电压的收敛速度远比$I = {I_2}$ 时要快, 其原因是平衡点${{{P}}_3}$ 距离亚临界Hopf分岔点$H$ 比平衡点${{{P}}_2}$ 较远, 并且$ {\rm{Re}} (\lambda _{{I_3}}^{1, 2}) < {\rm{Re}} (\lambda _{{I_2}}^{1, 2})< 0 $ .2 )的放电波形图呈现如图2(g) 中红色曲线所示的周期1峰放电状态, 其相轨迹为稳定的周期1极限环吸引子, 如图2(i) 所示. 此时, 神经元的双稳态吸引域如图3(e) 和图3(f) 所示(红色区域为周期2簇放电, 黄色区域为周期1峰放电, 浅蓝色区域为具有收敛趋势的小振幅振荡, 绿色区域为静息态, 黑色红星为平衡点), 相比图3(c) 和图3(d) 所示的吸引域, 其拓扑结构发生了显著的变化, 即代表静息态的绿色区域变大, 而代表周期1峰放电态的黄色区域比处于周期2簇放电的红色区域小. 明显地, EMFN模型(2 )在两组初值下呈现静息态和周期1峰放电的共存状态.图 3 EMFN模型(2 )的吸引域 (a), (c)和(e)是外界刺激电流分别取${I_{\rm{1}}}, \;{I_2}, \;{I_3}$ 时x -y 上的吸引域; (b), (d)和(f)是外界刺激电流分别取${I_{\rm{1}}}, \;{I_2}, \;{I_3}$ 时x -? 上的吸引域Figure3. The attractive basins of EMFN model (2 ): (a), (c) and (e) are the attractive basins in x -y plane under ${I_{\rm{1}}}, \;{I_2}, \;{I_3}$ , respectively; (b), (d) and (f) are the attractive basins in x -? plane under ${I_{\rm{1}}}, \;{I_2}, \;{I_3}$ , respectively.2 )在不同的初始状态下发现不同吸引子共存的现象, 说明该系统对初始状态具有很强的敏感性, 这与磁控忆阻器的引入而导致的神经元模型非线性加强有关.3.3.隐藏振荡 -->3.3.隐藏振荡 从上述讨论可知, 当外界刺激电流取不同的值时, EMFN模型(2 )在不同的初始状态下展现不同的放电状态, 如静息态、周期1放电和周期2放电等共存的现象. 另外, 还可以发现EMFN模型(2 )具有另一个有趣的现象, 即隐藏吸引子. 隐藏吸引子的吸引域不包含平衡点的邻域[38 ] (无平衡点或者仅有稳定平衡点的动力系统产生的吸引子都属于隐藏吸引子).$I = {I_1}$ 时, 通过分析发现EMFN模型(2 )在其对应的不稳定平衡点${{{P}}_1}$ 的自激振荡作用下产生周期2的簇放电现象. 从图3(a) 和图3(b) 的红色区域可以看出, 周期2簇放电的吸引域与平衡点的小领域不相交. 明显地, 此时的周期2簇放电属于隐藏放电范畴.$I = {I_2}$ 和${I_3}$ 时, EMFN模型(2 )对应的平衡点为稳定的焦结点, 产生的周期2簇放电现象则属于隐藏放电范畴. 其机制为模型(2 )在分岔点$H$ 处发生了亚临界Hopf分岔, 相应的平衡点的稳定性由不稳定的放电状态变为稳定的放电状态, 并产生了不稳定的极限环, 同时, 在这个不稳定的极限环外存在一个稳定的周期2极限环吸引子. 因此, 当参数取值不变, 在稳定的周期2极限环所产生吸引域内取值时, 模型(2 )处于周期为2的簇放电状态, 如图3(c) ,(d) 直观所示, 在x- y 和x- ? 平面上的吸引域上都存在着大范围的隐藏周期2放电区域.4.基于双参数的分岔分析 24.1.伴有混沌和无混沌的加周期分岔 4.1.伴有混沌和无混沌的加周期分岔 EMFN模型(2 )能比较精确地描述电磁场下神经元的放电活动, 并且具有更多的分岔参数. 当外界电磁场变化时, 很难保持新系统的各参数取值不变, 因此, 研究多个参数同时变化下神经元模型的放电节律转迁更具有实际参考价值. 本节通过计算双参数分岔图、单参数分岔图、最大Lyapunov指数和时间响应图等来模拟EMFN模型(2 )随各参数组合下的分岔结构. 此外, 在数值模拟过程中, 采用四阶龙格-库塔算法, 初值固定为5 次迭代, 用后续的3 × 107 步计算最大Lyapunov指数. 随后继续进行20 × 105 步的迭代, 并且记录迭代过程中膜电压x 存在的极值(最大值或最小值), 可通过判断各组脉冲是否重复, 由此获得周期态或者混沌态[39 -41 ] . EMFN模型(2 )的膜电压x 在双参数平面中的分岔图如图4 所示, 其仿真图采用了$500 \times 500$ 等距参数点覆盖, 此外, 用不同的颜色绘制膜电压的不同放电状态, 并且图右侧的颜色应运用相应的数字进行标记. 需要说明的是, 当膜电压x 的周期大于等于20时, 统一运用白色区域表示. 图4(a) —(f) 展示了EMFN模型(2 )存在的“梳”状混沌结构. 如图4(a) 所示, 在参数$I \in [2.1, 4.1], \;b \in [2.8, 3.5]$ 的参数平面上, 模型(2 )存在丰富的周期放电和混沌放电状态. 观察图4(a) 中最大的颜色区域(即黄色区域), 膜电压x 处于周期1尖峰放电态, 并且通过倍周期分岔结构与混沌区域相连接. 类似地, 其余周期区域也存在倍周期分岔结构, 并且以“舌形”嵌入混沌区域中[41 ] . 此外, 通过观察发现许多自相似和递归性的分岔模式. 当保持参数$b = - 0.3485 I + 4.2318$ 不变, 参数$I \in [2.1, 4.1]$ 时(沿着图4(a) 中黑色直线所示的方向), 模型(2 )的峰峰间期(ISI)分岔图和膜电压x 的最大值分岔图分别如图5(a) 和图5(b) 所示, 图6 为图5 相应的最大Lyapunov指数. 因此, EMFN模型(2 )表现出伴有混沌的加周期分岔模式, 即周期1$ \to $ 周期2$ \to $ 周期4$ \to \cdots \to $ 首次出现混沌窗口$ \to $ 周期2$ \to $ 周期4$ \to $ 周期8$ \to \cdots \to $ 再次出现混沌窗口$ \to $ 周期3$ \to $ 周期6$ \to $ 周期12$ \to \cdots $ . 模型(2 )按照上述的加周期分岔和混沌交替模式, 并且每经过一次混沌放电后的周期数要比之前相应的周期数大1, 最终进入混沌放电态或者更高周期的簇放电态. 在图4(a) 中, $A$ 点所对应的参数点为$A(I, b) = (2.389, 3.293)$ , 此时的模型(2 )处于周期3簇放电状态, 其膜电压x 的时间响应如图7(a) 所示. 此外, 在图4(a) 中的B , C 和 D 点, 相应的参数取值分别为图 4 EMFN模型(2 )关于x 的双参数分岔图 (a) $I$ 和$b$ 对应的分岔图; (b) $I$ 和$d$ 对应的分岔图; (c) $c$ 和$d$ 对应的分岔图; (d) $I$ 和$r$ 对应的分岔图; (e) $s$ 和$r$ 对应的分岔图; (f) ${\chi _0}$ 和$r$ 对应的分岔图; (g) $I$ 和${k_1}$ 对应的分岔图; (h) $I$ 和${\chi _0}$ 对应的分岔图; (i) $I$ 和$s$ 对应的分岔图Figure4. Two-parameter bifurcation diagrams of EMFN model (2 ) versus x : (a) Bifurcation diagram versus $I$ and $b$ ; (b) bifurcation diagram versus $I$ and $d$ ; (c) bifurcation diagram versus $c$ and $d$ ; (d) bifurcation diagram versus $I$ and $r$ ; (e) bifurcation diagram versus $s$ and $r$ ; (f) bifurcation diagram versus ${\chi _0}$ and $r$ ; (g) bifurcation diagram versus $I$ and ${k_1}$ ; (h) bifurcation diagram versus $I$ and ${\chi _0}$ ; (i) bifurcation diagram versus $I$ and $s$ .图 5 关于$I$ 的ISI分岔图和单参分岔图 (a) ISI 分岔图; (b) 单参分岔图Figure5. ISI bifurcation and one-parameter bifurcation versus I : (a) ISI bifurcation; (b) one-parameter bifurcation.图 6 对应于图5 的最大 Lyapunov 指数图Figure6. The largest Lyapunov diagram corresponding to Fig.5 .图 7 EMFN模型(2 )关于$I$ 和$b$ 的时间响应图 (a) $I = 2.389, b = 3.239$ 时的周期3簇放电; (b) $I = 2.577, b = 3.173$ 时的周期4簇放电; (c) $I = 2.733, b = 3.134$ 时的周期5簇放电; (d) $I = 2.898, b = 3.093$ 时的周期6簇放电Figure7. Time response diagram of EMFN model (2 ) versus $I$ and $b$ : (a) Bursting with period-3 when $I = 2.389, b = 3.239$ ; (b) bursting with period-4 when $I = 2.577, b = 3.173$ ; (c) bursting with period-5 when $I = 2.733, b = 3.134$ ; (d) bursting with period-6 when $I = 2.898, b = 3.093$ .x 相应的时间响应分别如图7(b) —(d) 所示. 图4(b) —(f) 也存在类似的伴有混沌的加周期分岔结构, 本节不再详细描述.图4(g) —(i) 显示了EMFN模型(2 )的无混沌加周期分岔结构, 即通过加周期分岔模式从某种周期状态直接进入相邻的周期状态. 当参数$I \in [1.5, 3],\; {k_1} \in [0, 0.28]$ 时, 如图4(g) 所示, 沿着左下到右上的方向, 模型(2 )的分岔模式为周期1$ \to $ 周期2$ \to $ 周期3$ \to \cdots \to $ 周期18$ \to $ 更高的加周期分岔模式. 此外, 还可以观察到这些周期区域呈现带条状分布, 并且随着周期数逐渐增大, 相应的颜色带逐渐减小(例如, 周期2的颜色带明显比周期3的颜色带宽). 类似地, 在图4(h) 和图4(i) 所示的参数平面上, 模型(2 )也存在无混沌加周期分岔结构.2 )在不同的参数区域内存在不同的加周期分岔. 神经元的节律模式与控制参数呈现出明显的对应关系, 因此, 在图4(a) —(f) 中的参数变化区域内出现伴有混沌的加周期分岔现象的产生机理是模型(2 )在此组参数的变化下具有更高的兴奋性和更强的节律性, 进而引起了激变现象, 即簇放电经合并激变进入混沌放电, 再经边界激变进入更高周期的簇放电, 同时伴有内部激变现象. 在图4(g) —(i) 中的参数变化区域内, 新建模型仅存在加周期分岔现象, 未见混沌放电存在, 呈现出比较规则的加周期分岔转迁模式.4.2.混合模式放电 -->4.2.混合模式放电 混合模式振荡是一类大振幅与小振幅交替出现复杂的动力学现象, 能够产生混合模式振荡的模型通常是包含了多重时间尺度的非线性微分方程组[42 ] , 并且在电子电路、化学反应和生物数学等领域都有发现[43 ,44 ] . 神经元模型属于多时间尺度的动力系统, 它不仅能产生${L^0}$ 型簇放电(即周期为$L$ 的簇放电模式), 也能够产生${L^S}$ 型混合模式放电(其中$L, S$ 分别表示一个振荡周期内大振幅与小振幅振荡出现的次数). 考虑到EMFN模型(2 )具有更多的分岔参数, 因此该模型存在丰富的簇放电模式和分岔结构. 如图8 所示, 在参数${k_0} \in [0, 1.2], \;d \in [4.2, 5.4]$ 平面上, 模型(2 )存在大量的带状周期区域和一些无规则的混合窗口, 并且相应的周期都是通过倍周期分岔结构与混沌区域相连接. 此外, 对于连续系统(2 )而言, 在图中右侧区域的周期颜色带存在不连续的情况, 这些异常的分岔结构往往是由于系统分岔类型发生了突变, 并且常伴随着共存吸引子的产生[39 ,41 ] . 能够产生混合模式放电的最小神经元模型是包含多重时间尺度的三维非线性方程组, 对于高维的动力系统, 由于产生机理的相关理论仍不完备, 于是采用数值方法对模型产生的混合模式放电进行分析[45 ] .图 8 EMFN模型(2 )关于${k_0}$ 和$d$ 的双参数分岔图Figure8. Two-parameter bifurcation diagram of EMFN model (2 ) corresponding to ${k_0}$ and $d$ .2 )在图8 中左侧的周期区域处于周期簇放电状态, 但在右侧区域处于混合模式放电状态, 而在周期不连续区域, 模型(2 )处于周期簇放电与相应的混合模式放电共存状态. 例如, 若参数$({k_0}, d) = (0.6587, 4.2596)$ 保持不变, 当初值分别为${\rm{(9}}{\rm{.0, 0}}{\rm{.1, 0}}{\rm{.1, 0}}{\rm{.1, 0}}{\rm{.1)}}$ 和${\rm{( - 9}}{\rm{.0, 0}}{\rm{.1, 0}}{\rm{.1, 0}}{\rm{.1, 0}}{\rm{.1)}}$ 时, 模型(2 ) 分别处于周期2簇放电和${2^1}$ 型混合模式放电, 其相应的时间响应图分别如图9(a) 和图9(b) 所示. 图10(a) 和图10(b) 展示的是x -? 和y -E 平面上的吸引域, 其中黄色区域为周期2簇放电, 红色区域为${2^1}$ 型混合模式放电. 由此可知, 模型(2 )的放电模式不仅与其参数取值相关, 而且也与初值密切相关. 通过观察图9(a) 和图9(b) , 可以发现混合模式放电的大振幅周期数与簇放电的周期数相同, 即模型(2 )可以通过初值的改变产生小振幅放电, 并且与原簇放电模式结合而形成新的混合放电模式. 类似地, 当${k_0}$ 和$d$ 分别取值${\rm{(0}}{\rm{.7032, 4}}{\rm{.3758)}}$ 和${\rm{(0}}{\rm{.7123, 4}}{\rm{.5032)}}$ 时, 模型(2 )分别处于周期3簇放电与周期${{\rm{3}}^1}$ 共存模式放电状态和周期4簇放电与周期${{\rm{4}}^2}$ 共存模式放电状态, 图10(c) —(f) 为相应平面上的吸引域(红色区域表示周期簇放电, 黄色区域表示混合模式放电). 此外, 在图8 中不连续的分岔区域还存在着大量的共存模式放电, 这些区域对初值十分敏感, 对机体神经系统来说将可能会引起突发的心率失调, 因此在相关生物实验中应尽量避免这些区域, 我们可以通过调节电磁反馈项${k_0}$ , 使神经元趋于稳定的周期簇放电状态.图 9 EMFN模型(2 )的时间响应图 (a) 周期2放电; (b) 周期${2^1}$ 放电; (c) 周期3放电; (d) 周期${3^1}$ 放电; (e) 周期4放电; (f) 周期${{\rm{4}}^{\rm{2}}}$ 放电Figure9. Time response diagrams of EMFN model (2 ): (a) Discharge with period-2; (b) discharge with period-${2^1}$ ; (c) discharge with period-3; (d) discharge with period-${3^1}$ ; (e) discharge with period-4; (f) discharge with period-${4^2}$ .图 10 EMFN模型(2 )的共存吸引域 (a)$({k_0}, d) = (0.6587, 4.2596)$ 时关于x -? 的吸引域; (b)$({k_0}, d) = (0.6587, 4.2596)$ 时关于x -E 的吸引域; (c)$({k_0}, d) = (0.7032, 4.3758)$ 时关于x -? 的吸引域; (d)$({k_0}, d) = (0.7032, 4.3758)$ 时关x -E 于的吸引域; (e) $({k_0}, d) = (0.7{\rm{123}}, 4.{\rm{5032}})$ 时关于x -? 的吸引域; (f) $({k_0}, d) = (0.7{\rm{123}}, 4.{\rm{5032}})$ 时关于x -E 的吸引域Figure10. The coexisting attraction domains of EMFN model (2 ): (a) Attractive basins of x -? plane when $({k_0}, d) = (0.6587, 4.2596)$ ; (b) attractive basins of x -E plane when $({k_0}, d) = (0.6587, 4.2596)$ ; (c) attractive basins of x -? plane when $({k_0}, d) = (0.7032, 4.3758)$ ; (d) attractive basins of x -E plane when $({k_0}, d) = (0.7032, 4.3758)$ ; (e) attractive basins of x -? plane when $({k_0}, d) = (0.7123, 4.5032)$ ; (f) attractive basins of x -E plane when $({k_0}, d) = (0.7123, 4.5032)$ .$d = 1.9967{k_0} - 4.2091$ 不变, 并且${k_0} \in [0, 0.6]$ 时, 即沿着图8 中黑线所示的分岔方向, EMFN模型(2 )的ISI分岔图和关于膜电压$x$ 的分岔图分别如图11(a) 和图11(b) 直观所示. 模型(2 )首先进行伴有混沌的加周期分岔模式: 周期2$ \to $ 混沌$ \to $ 周期3$ \to $ 混沌$ \to $ 周期4$ \to $ 混沌$ \to $ 周期5$ \to $ 混沌, 此后混沌窗口消失, 进入无混沌加周期分岔模式: 周期6$ \to $ 周期7$\to \cdots \to$ 周期14$ \to $ 更高的簇放电状态. 图12 展示了相应的最大Lyapunov指数, 很好地吻合了图11 所示的分岔图. 此外, 在图8 右侧混合模式放电趋于白线所示的分岔方向, 即当参数$d = 2.9851{k_0} - 1.8119, {k_0} \in [0.8, 1.2]$ 时膜电压$x$ 的发放数[43 ,44 ] (在一个混合模式放电周期内, 小振幅数占总振幅数的比例)的变化如图13 所示. 明显地, 膜电压$x$ 的发放数呈现阶梯状分布, 其变化规律为: 周期${1^2}$ $ \to $ 周期${2^2}$ $ \to $ 周期${3^2}$ $ \to $ 周期${4^2}$ $ \to $ 周期${4^3}$ $ \to $ 周期${5^3}$ $ \to $ 周期${6^3}$ $ \to $ 周期${7^3}$ $ \to $ 周期${8^3}$ $ \to $ 周期${8^4}$ $ \to $ 周期${9^4}$ $ \to $ 周期${10^4}$ $ \to $ 周期${11^4}$ $ \to $ 周期${12^4}$ $ \to $ 周期${13^4}$ $ \to $ 周期${13^5}$ $ \to $ 周期${14^5}$ $ \to $ 周期${16^5}$ $ \to $ 周期${17^5}$ . 虽然模型(2 )的混合模式放电周期较高并且比较复杂, 但其变化具有一定的自相似规律, 即随着${k_0}$ 的增加, 大振幅和小振幅都会随之逐渐增加, 如图13 所示的发放数呈现“四阶梯”状分布.图 11 关于${k_0}$ 的ISI分岔图和单参分岔图 (a) ISI 分岔图; (b) 单参分岔图Figure11. ISI bifurcation and one-parameter bifurcation versus ${k_0}$ : (a) ISI bifurcation; (b) one-parameter bifurcation.图 12 对应于图11 的最大 Lyapunov 指数图Figure12. The largest Lyapunov diagram corresponding to Fig.11 .图 13 膜电压的发放数关于参数${k_0}$ 变化图Figure13. The change of spike count of membrane voltage versus parameter ${k_0}$ .2 )普遍存在丰富且复杂的混合模式放电和共存模式放电, 这是由于高维系统的复杂性引起的, 本节的研究结果揭示了其分岔规律, 这将为神经元相关疾病的治疗和控制提供有益的探讨.4.3.电场和磁场强度影响下的混合模式放电 -->4.3.电场和磁场强度影响下的混合模式放电 与双参数$({k_0}, d)$ 影响下的动力学类似, 电场和磁场强度$({k_1}, {k_0})$ 对EMFN模型(2 )也有很大的影响, 尤其是周期簇放电的产生与转迁, 图14 展示了${k_1} \in (0, 0.25), {k_0} \in (0, 1.2)$ 时的双参分岔图. 明显地, 模型(2 )在此组参数下存在大量的带状周期区域和一些无规则的混合窗口, 并且相应的周期也均是通过倍周期分岔结构与混沌区域相连接.图 14 EMFN模型(2 )关于${k_0}$ 和${k_1}$ 的双参数分岔图Figure14. Two-parameter bifurcation diagram of EMFN model (2 ) corresponding to ${k_0}$ and ${k_1}$ .2 )的初值$(0.1, 0.1, 0.1, 0.1, 0.1)$ 保持不变, 参数为$({k_1}, {k_0}) = (0.01403, 0.7214)$ 和$({k_1}, {k_0}) = (0.01603, 0.7743)$ 时, 模型(2 )分别处于如图15(a) 和图15(b) 所示的周期6和周期${6^3}$ 的混合模式放电状态. 类似地, 当$({k_1}, {k_0})$ 分别取值$(0.03808, 0.7599)$ 和$(0.0{\rm{3809}}, 0.{\rm{8056}})$ 时, 模型(2 )分别处于如图15(c) 和图15(d) 所示的周期7簇放电与周期${{\rm{7}}^3}$ 的混合模式放电状态. 当$({k_1}, {k_0})$ 分别取值$(0.06112, 0.7841)$ 和$(0.05912, 0.8441)$ 时, 模型(2 )分别处于如图15(e) 和图15(f) 所示周期8簇放电与周期${{\rm{8}}^3}$ 的混合模式放电状态.图 15 EMFN模型(2 )的时间响应图 (a) 周期6放电; (b) 周期${6^3}$ 放电; (c) 周期7放电; (d) 周期${7^3}$ 放电; (e) 周期8放电; (f) 周期${8^3}$ 放电Figure15. Time response diagrams of EMFN model (2 ): (a) Discharge with period-6; (b) discharge with period-${6^3}$ ; (c) discharge with period-7; (d) discharge with period-${7^3}$ ; (e) discharge with period-8; (f) discharge with period-${8^3}$ .图15 可以发现, 混合模式放电的大振幅周期数与簇放电的周期数相同, 即可以通过微调电场和磁场强度使模型(2 )产生小振幅放电, 并且与原簇放电模式结合而形成新的混合放电模式.${k_1} = 0.8333{k_0} - 0.3333$ 不变, 并且${k_0} \in [0.4, 0.7]$ 时, EMFN模型(2 )的ISI分岔图和关于膜电压$x$ 的分岔图分别如图16(a) 和图16(b) 直观所示. 模型(2 )展现出无混沌的加周期分岔模式: 周期5$ \to $ 周期6$ \to $ 周期7$ \to $ 周期8$ \to $ 周期9$\to \cdots$ . 此外, 在图14 右侧混合模式放电区域, 即当参数$ {k_1} = 0.4762{k_0} - 0.3714\;(0.8 \leqslant {k_0} \leqslant 1.2) $ 时膜电压$x$ 的发放数变化如图17 所示. 明显地, 膜电压$x$ 的发放数呈现阶梯状分布, 其变化规律为: 周期${6^3}$ $ \to $ 周期${7^3}$ $ \to $ 周期${8^3}$ $ \to $ 周期${9^3}$ $ \to $ 周期${10^3}$ $ \to $ 周期${11^3}$ $ \to $ 周期${11^4}$ $ \to $ 周期${12^4}$ $ \to $ 周期${13^4}$ $ \to $ 周期${14^4}$ $ \to $ 周期${15^4}$ $ \to $ 周期${16^4}$ .图 16 关于${k_0}$ 的 ISI 分岔图和单参分岔图Figure16. ISI bifurcation and one-parameter bifurcation versus ${k_0}$ .图 17 膜电压的发放数关于参数${k_0}$ 变化图Figure17. The change of spike count of membrane voltage versus parameter ${k_0}$ .${k_0}$ 的增加, 大振幅和小振幅都会随之逐渐增加, 如图17 所示的发放数呈现“双阶梯”状分布. 本节揭示了电场和磁场影响下EMFN模型(2 )中的混合模式放电节律转迁规律, 以期有助于探寻电磁场对生物系统兴奋性的影响机理.4.4.电场方程对EMFN模型(2 )的影响 -->4.4.电场方程对EMFN模型(2 )的影响 本文将第五维电场变量引入文献[24 ]中考虑磁场时的神经元模型, (2 )式中${k_4}$ 和${k_5}$ 是两个关键参数, 体现了外界刺激电流对神经元内部电场的感应和反馈效应. 图18 描述了EMFN模型(2 )关于$I$ 和${k_4}, \;\;{k_5}$ 的双参数分岔图.图 18 EMFN模型(2 )关于I 和${k_4}, \;{k_5}$ 的双参数分岔图Figure18. Two-parameter bifurcation diagram of EMFN model (2 ) corresponding to I and ${k_4}, \;{k_5}$ .图18 中可以看出, 在参数$I \in [1, 4],\; {k_4} \in [0, 1]$ 平面上, EMFN模型(2 )存在周期和混沌振荡区域. 其中, 周期振荡区域呈现“条状”分布, 相应的周期数越大, 其“条形”区域越窄. 此外, 在每个“条状”周期的末端将通过倍周期分岔结构与混沌区域相连接, 并且, 图中右上角存在大范围白色区域, 说明该系统在此参数区域内存在高周期簇放电状态或者混沌态. 类似地, 在参数$I \in [1, 4], {k_5} \in [0, 1]$ 平面上, EMFN模型(2 )呈现出有规律的周期分布, 即: 沿着由左上到右下的方向, 该模型将由静息态$ \to $ 周期1$ \to $ 周期2$ \to \cdots$ , 到高周期的簇放电态或混沌态. 此外, 与混沌相接的周期区域呈现出“舌状”分布, 并且具有明显的倍周期分岔结构. 图19 和图20 描述了EMFN模型(2 ) 关于$I$ 和${k_4}, \;{k_5}$ 的 ISI 分岔图和单参数分岔图.图 19 当$I \in [3.1, \;4], \;{k_4} = 0.4556 I - 1.4122\;$ 时, EMFN模型(2 )的 ISI 分岔图(a)和单参分岔图(b)Figure19. (a) ISI bifurcation and (b) one-parameter bifurcation of EMFN model (2 ) when $I \in [3.1, \;4], \;{k_4} = 0.4556 I - 1.4122$ .图 20 当$I \in [2.9, \;3.7], \;{k_5} = - 0.9659 I + 3.7897$ 时, EMFN模型(2 )的 ISI 分岔图(a)和单参分岔图(b)Figure20. (a) ISI bifurcation and (b) one-parameter bifurcation of EMFN model (2 ) when $I \in [2.9, \;3.7], \;{k_5} = - 0.9659 I + 3.7897$ .5.隐藏动力学控制 隐藏吸引子的存在可能导致突发混沌或周期大幅度跃迁, 将会影响系统的正常运行而带来灾难性的后果[38 ,46 ] . 因此, 如何有效地抑制神经元系统中的隐藏放电具有重要的理论和现实意义. 由于EMFN模型(2 )在分岔点$H$ 处发生亚临界Hopf分岔, 并且在其附近发现周期1和周期2的隐藏极限环吸引子. 为了有效消除隐藏放电现象, 本节基于Washout控制器, 对分岔点$H$ 的Hopf分岔类型进行控制, 在不改变平衡点位置的前提下, 使其亚临界Hopf分岔转化为超临界Hopf分岔, 从而使EMFN模型(2 )在分岔点$H$ 处附近的拓扑结构发生改变, 由此达到消除其隐藏放电的目的. 施加控制后的模型为$v$ 为Washout滤波器的状态变量,$m$ 为控制器的反馈增益, $\xi $ 为滤波器时间常数的倒数, 本文选取参数$\xi = 0.0{\rm{7}}$ , 其余的参数与EMFN模型(2 )的基准参数取值相同.7 )写出矩阵形式, 即8 )式中有7 )关于外界刺激电流$I$ 分岔的位置是不变的, 即当参数$I = {I_H}$ 时, 受控系统也发生亚临界Hopf分岔, 此时相应的平衡点为7 )在平衡点${{{P}}_{\rm{c}}}$ 处的线性化矩阵${{{A}}_{\rm{c}}}$ 为${{{A}}_{\rm{c}}}$ 的特征根为7 )在平衡点${{{P}}_{\rm{c}}}$ 处存在一对实部为零的共轭特征根, 即该系统发生了Hopf分岔, 下面分析系统(7 )在平衡点${{{P}}_{\rm{c}}}$ 处关于参数$m$ 的Hopf分岔类型.7 )中的线性项与非线性项分开表示为8 )式中$G({{X}}) = F({{X}}) - {{{A}}_{\rm{c}}}{{X}}$ 为非线性项, 对系统(8 )做线性变换${{X}} = {{BY}} + {{{P'}}_{\rm{c}}}$ , 其中${{{P'}}_{\rm{c}}}$ 是${{{P}}_{\rm{c}}}$ 的转置矩阵. 矩阵${{B}} = [{\rm{Re}} ({{{\mu }}_1}), {\rm{Im}} ({{{\mu }}_1}), {{{\mu }}_3}, {{{\mu }}_4}, {{{\mu }}_5}, {{{\mu }}_6}]$ 的前两列分别为特征根${\lambda _1} = {\omega _0}{\rm{i}} = 0.{\rm{03230434 i}}$ 对应的特征向量${{{\mu }}_1}$ 的实部和虚部, 第三列为特征根${\lambda _3}$ 对应的特征向量${{{\mu }}_3}$ , 第四列为特征根${\lambda _4}$ 对应的特征向量${{{\mu }}_4}$ , 第五列为特征根${\lambda _5}$ 对应的特征向量${{{\mu }}_5}$ , 第六列为特征根${\lambda _6}$ 对应的特征向量${{{\mu }}_6}$ . 由此经计算可得矩阵${{B}}$ 及其逆矩阵${{{B}}^{ - 1}}$ 分别为8 )如下:10 )式中${{J}} = {{{B}}^{ - 1}}{{{A}}_{\rm{c}}}{{B}}$ 是系统的Jordan矩阵, ${\bar{ F}} = {{{B}}^{ - 1}}{{F}}({{BY}} + {{{P'}}_{\rm{c}}}) - {{{B}}^{ - 1}}{{{A}}_{\rm{c}}}{{BY}}$ 为非线性项, 其分量形式为$\eta $ 表达式为$\eta $ 决定Hopf分岔周期解的稳定性, 当$\eta < 0$ 时, 受控系统(10 )分岔产生的极限环是稳定的, 即系统发生超临界Hopf分岔; 当$\eta > 0$ 时, 受控系统(10 )分岔产生的极限环是不稳定的, 即系统发生亚临界Hopf分岔, 其判别式(11 )中各特征量计算表达式分别为$\eta = 0.0000{\rm{7054}}m + 0.0024971{\rm{2}}$ , 当$\eta < 0$ 时, 即当控制参数$m < {m_0} = - {\rm{35}}{\rm{.40005671}}$ 时, 受控系统(7 )在平衡点${{{P}}_{\rm{c}}}$ 处发生超临界Hopf分岔. 由此可以通过调节反馈增益$m$ 值的大小, 使得EMFN模型(2 )分岔点$H$ 处发生超临界Hopf分岔, 继而导致隐藏放电行为的改变.3.3 节可知, 当外界刺激电流$I < {I_{\rm{H}}}$ 时(例如$I = {I_2}$ 和${I_3}$ ), 模型(2 )存在隐藏放电现象. 为了验证Washout控制器的有效性, 本节主要分析外界刺激电流为$I = {I_2}\;({I_3})$ 时, 受控系统(7 )隐藏放电的变化情况. 当外界刺激电流$I = {I_{\rm{2}}}$ 时, 受控系统(7 )的平衡点为$m$ 对受控系统(7 )放电模式的影响如图21(a) 所示(红色区域表示周期2的隐藏放电, 黄色区域表示周期1的隐藏放电, 绿色区域表示稳定平衡点的吸引域, 黑色星点分别表示平衡点${{{P}}_{{\rm{c1}}}}$ 和${{{P}}_{{\rm{c2}}}}$ ). 当膜电压$x \in [ - 20, 20]$ , 反馈增益$m < {m_1} = - 6.846$ 时, 受控系统(7 )的周期2隐藏放电行为完全消失. 类似地, 当刺激电流$I = {I_{\rm{3}}}$ 时, 受控系统(7 )的平衡点为图 21 反馈增益$m$ 对受控系统(7 )的放电影响 (a) 当$I = {I_2}$ 时, 受控系统(7 )放电演化图; (b) 当$I = {I_3}$ 时, 受控系统(7 )放电演化图Figure21. The discharge influence of feedback gain $m$ to controlled system (7 ): (a) Discharge evolution of the controlled system (7 ) when $I = {I_2}$ ; (b) Discharge evolution of the controlled system (7 ) when $I = {I_3}$ .$m$ 对受控系统(7 )的放电模式的影响如图21(b) 所示. 通过数值仿真发现, 当反馈增益$m < {m_2} = - 1.149$ 时, 无论膜电压$x$ 取任何初值, 受控系统(7 )的周期1隐藏放电行为也完全消失.6.结 论 在神经细胞中, 穿过细胞膜的离子浓度的波动会产生时变的感应电场和感应磁场, 本文基于麦克斯韦电磁场理论, 讨论了电磁场影响下的HR神经元模型的放电节律转迁及其隐藏放电控制. 主要工作为: 1) 发现EMFN模型存在亚临界Hopf分岔、隐藏放电及其周期放电与静息态共存的现象; 2) 通过分析EMFN模型的双参数及单参数分岔、ISI 分岔和最大Lyapunov指数, 揭示其伴有混沌及无混沌的加周期分岔结构、混合模式放电和共存模式放电等现象, 分析了电场和磁场强度影响其放电节律的转迁规律; 3) 利用Washout控制器对EMFN模型进行控制, 通过改变其亚临界Hopf分岔, 消除不期望的隐藏放电现象.1 )具有更丰富的放电现象, 如加周期模式、混合模式、共存模式和隐藏模式等放电现象. 由此可见, 新模型在外部刺激下可以体现电磁场的感应现象及其反馈功能, 也可以利用电场和磁通变量作为接收外部电磁辐射的桥梁, 进而研究电磁辐射对神经元的影响, 这将是本文的后续研究工作. 
















































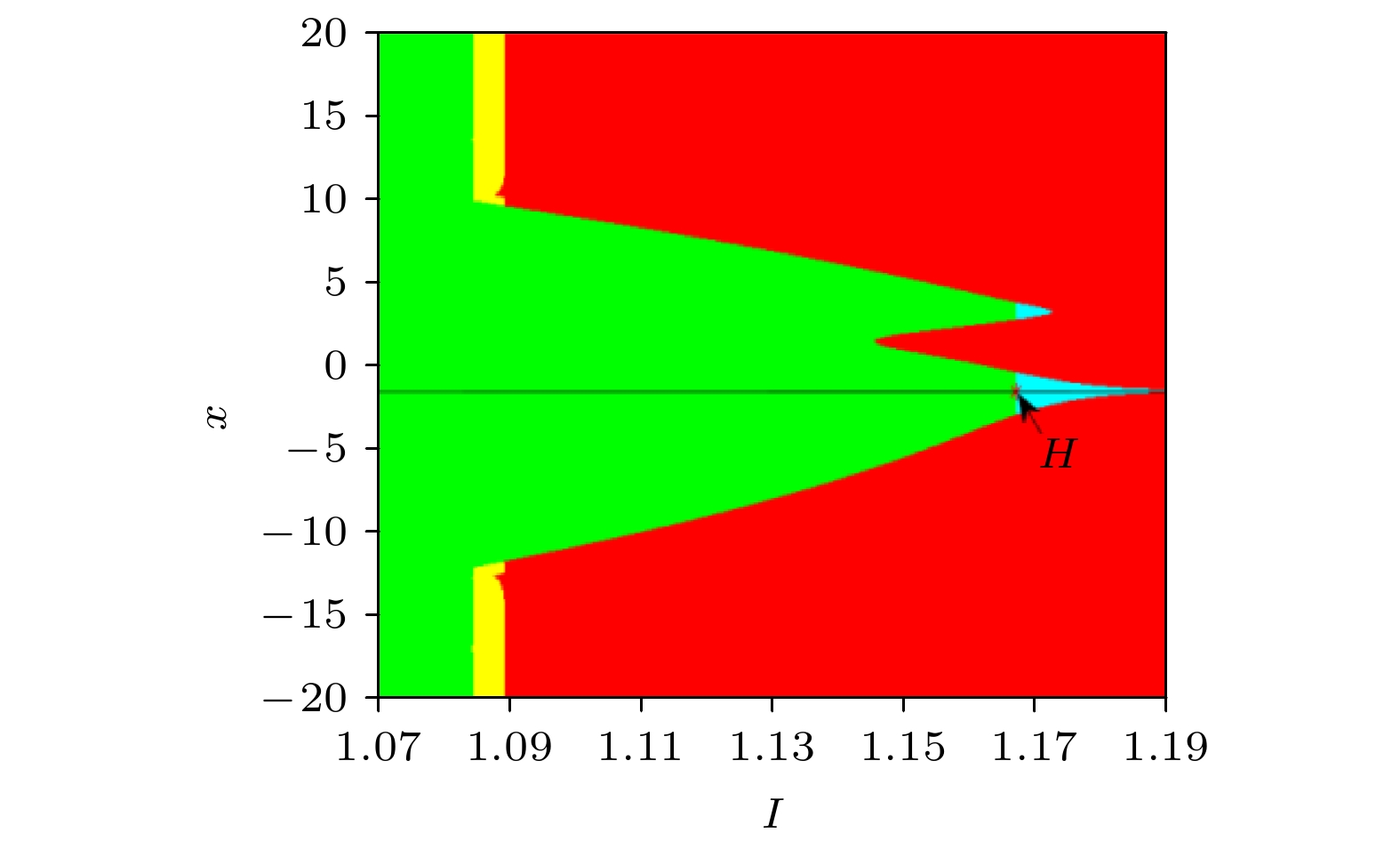 图 1 EMFN模型(2)在
图 1 EMFN模型(2)在




































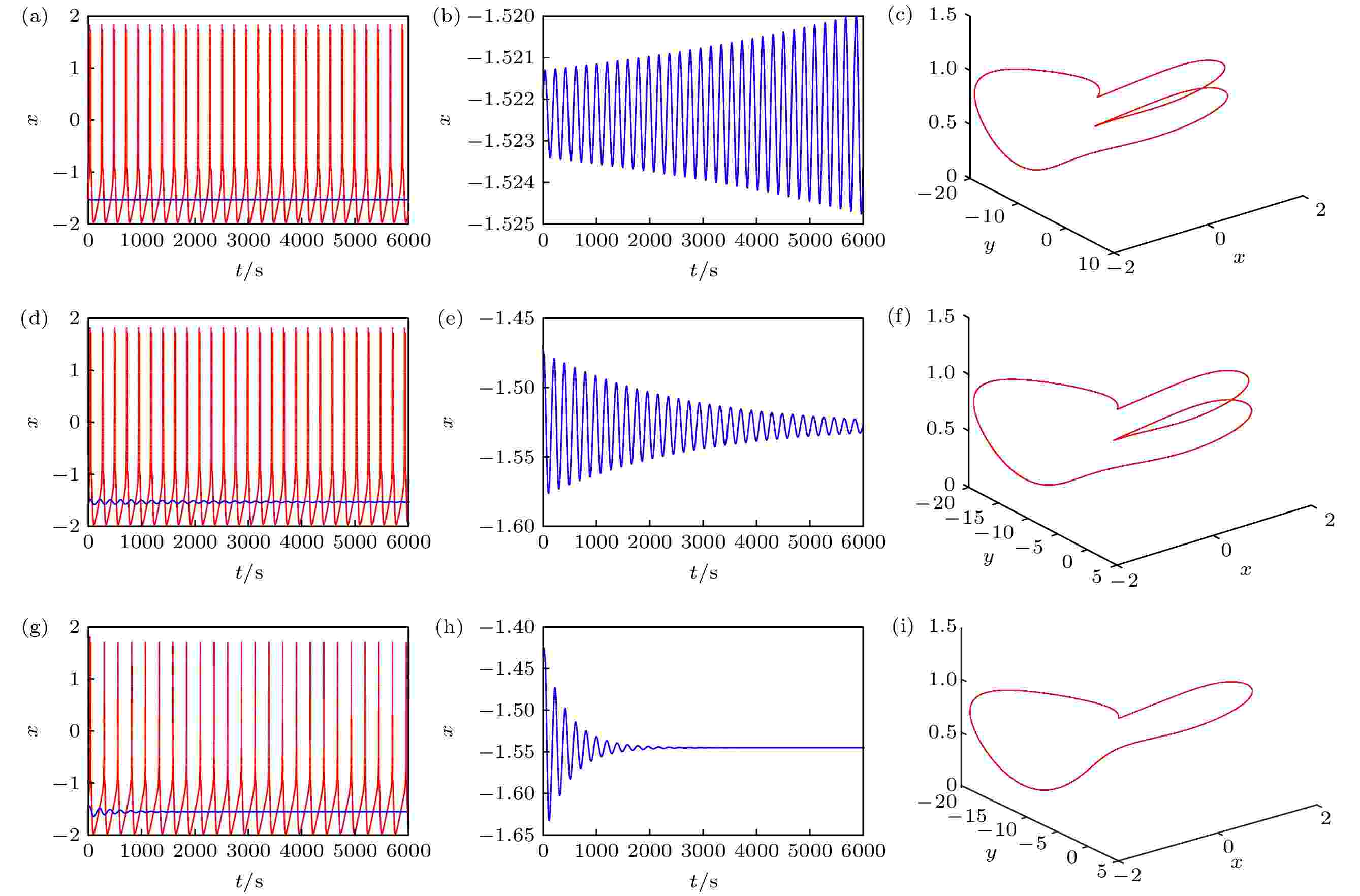 图 2 EMFN模型(2)的时间响应图和吸引子 (a)
图 2 EMFN模型(2)的时间响应图和吸引子 (a) 










































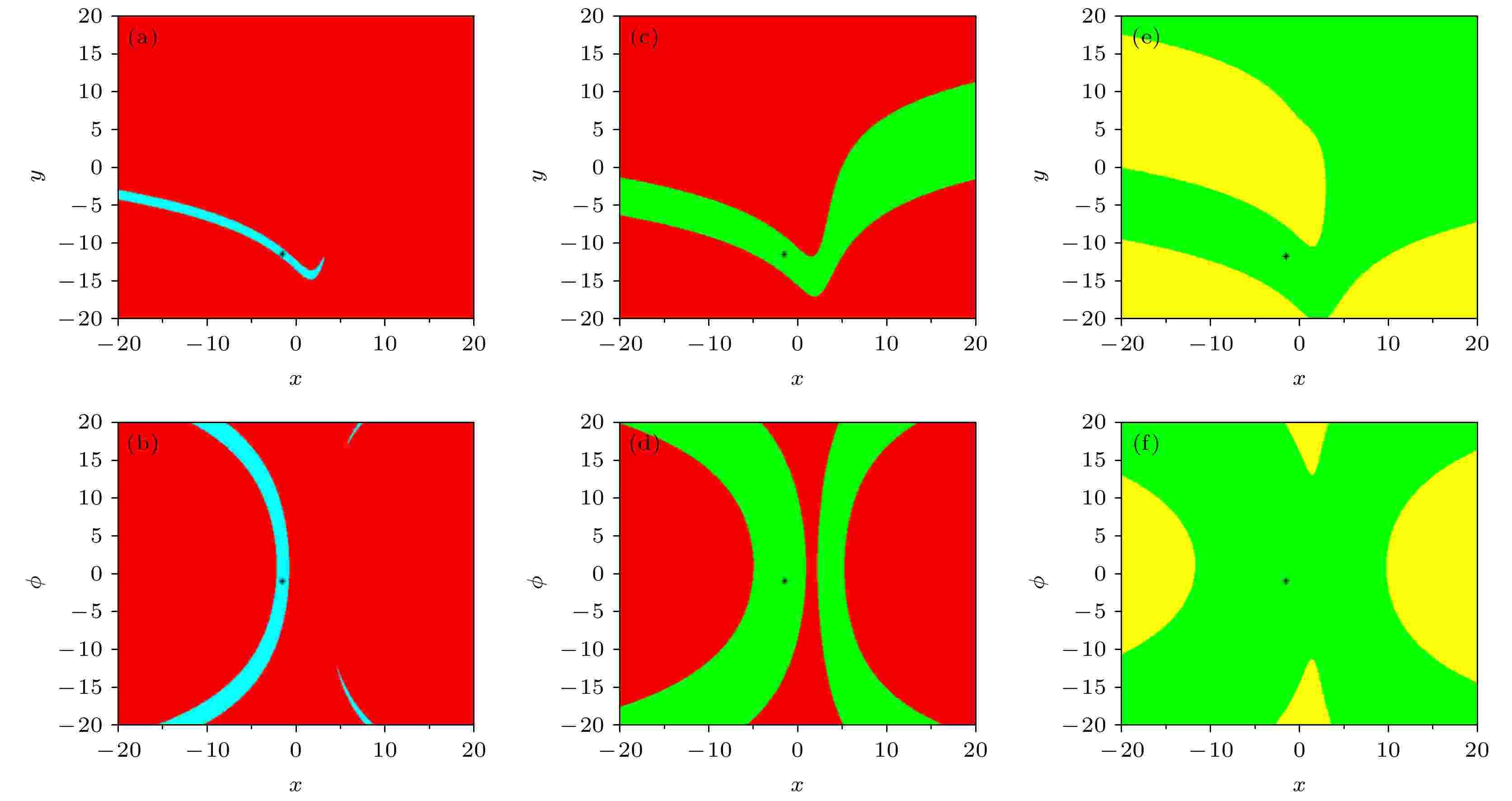 图 3 EMFN模型(2)的吸引域 (a), (c)和(e)是外界刺激电流分别取
图 3 EMFN模型(2)的吸引域 (a), (c)和(e)是外界刺激电流分别取























































































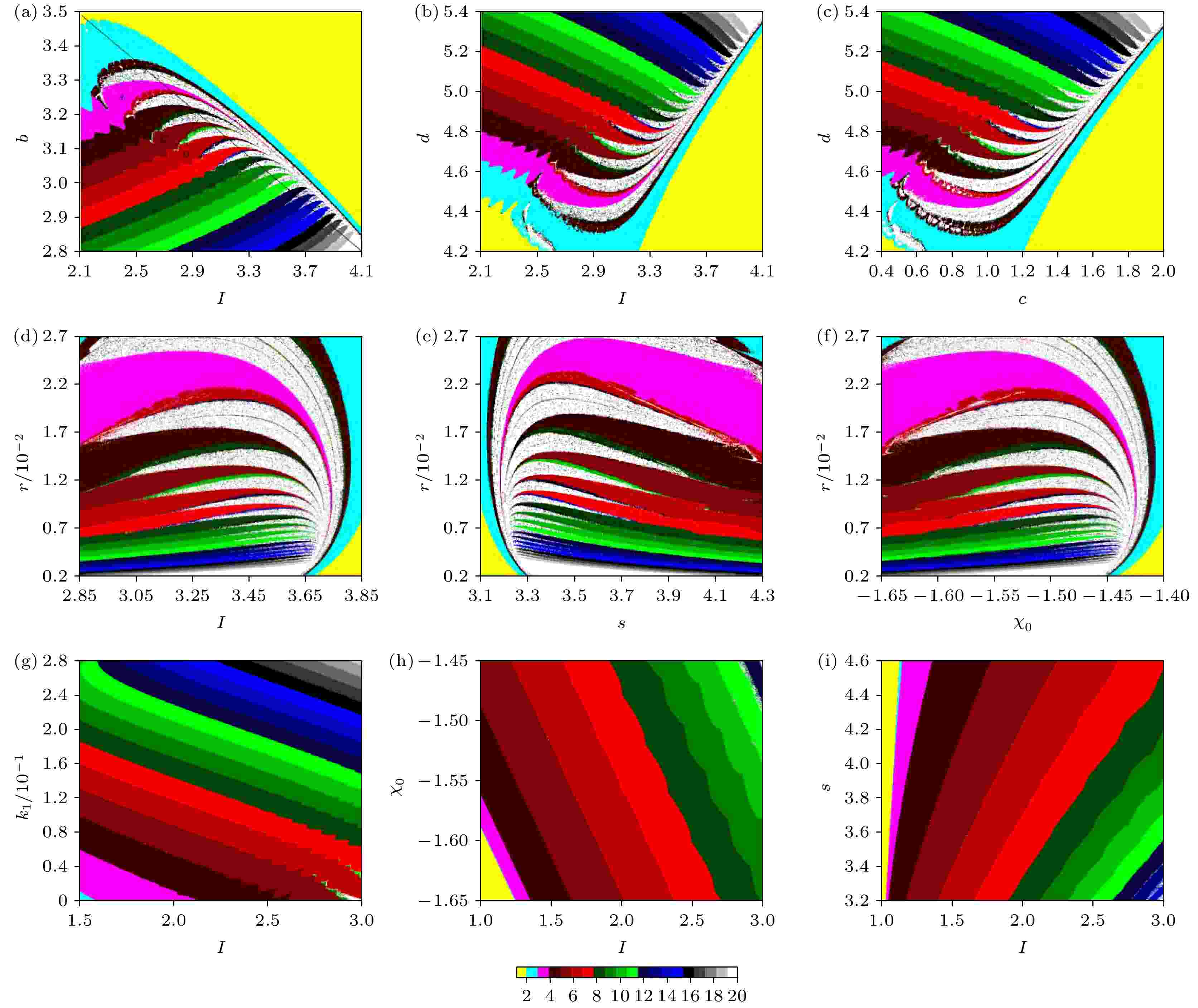 图 4 EMFN模型(2)关于x的双参数分岔图 (a)
图 4 EMFN模型(2)关于x的双参数分岔图 (a) 























































































































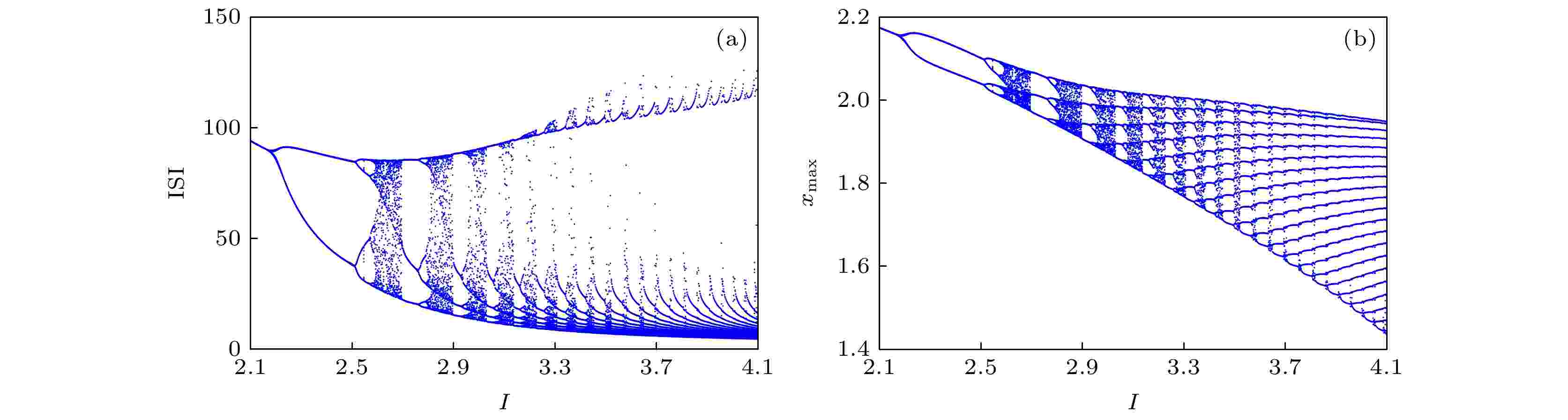 图 5 关于
图 5 关于
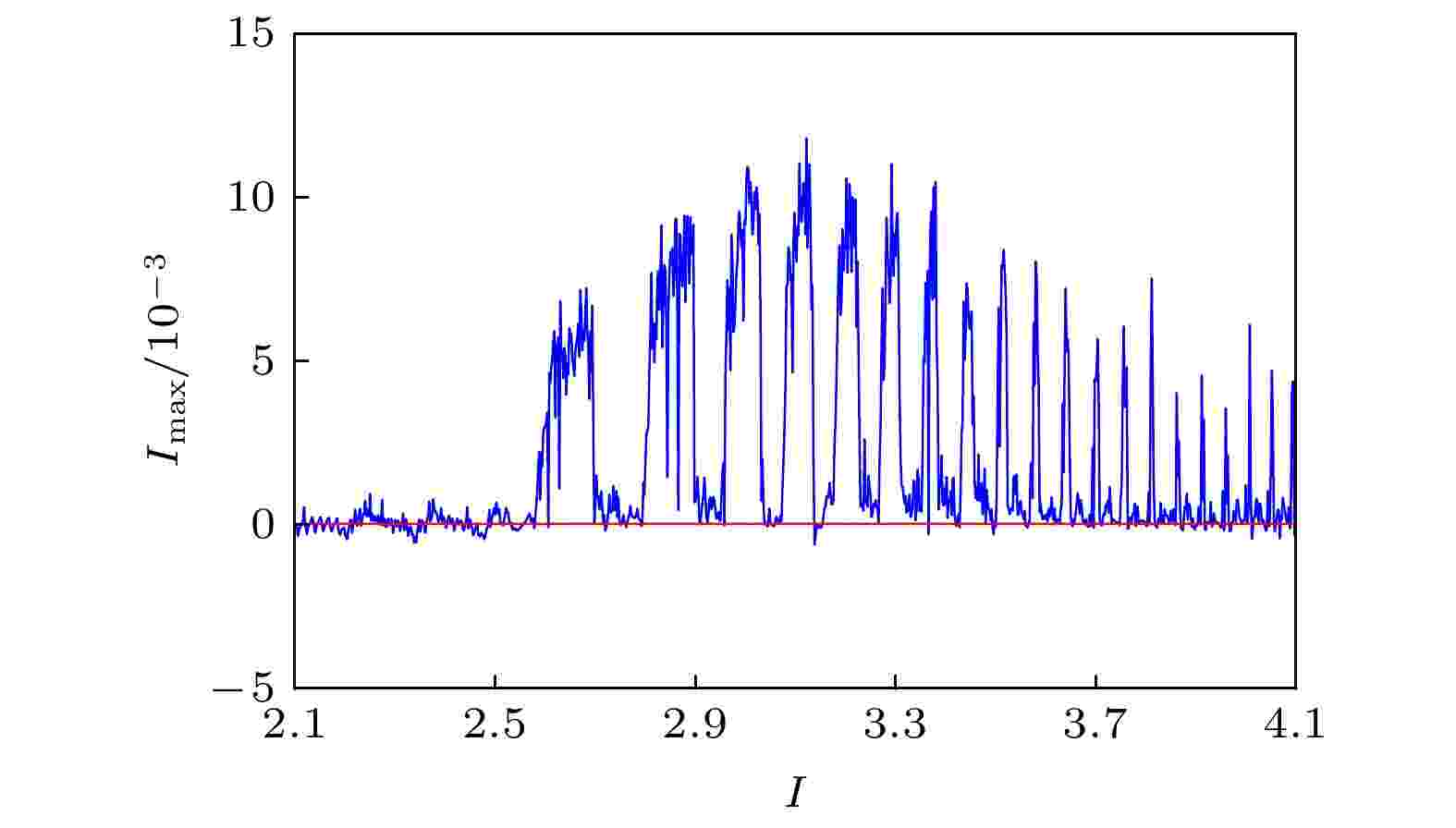 图 6 对应于图5的最大 Lyapunov 指数图
图 6 对应于图5的最大 Lyapunov 指数图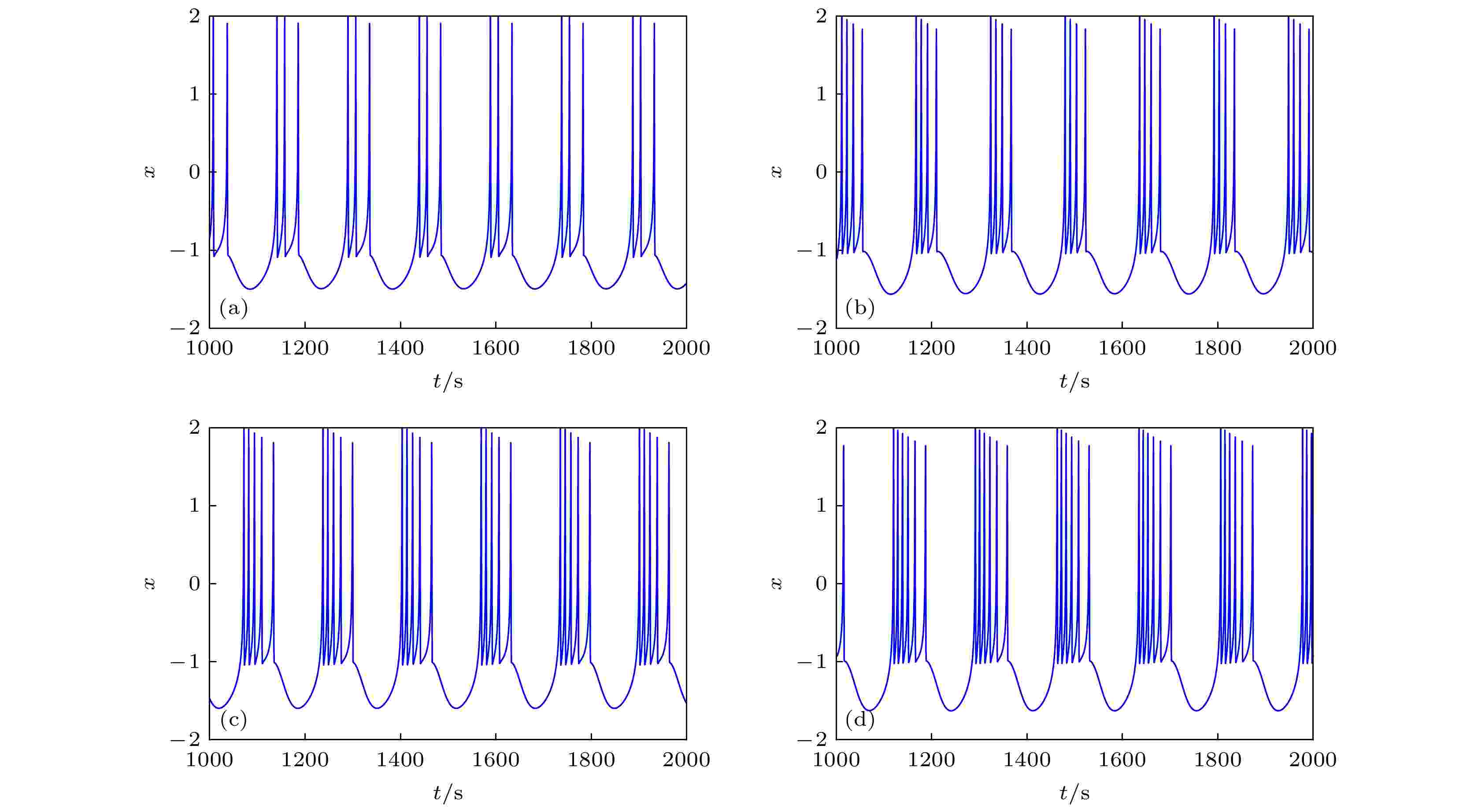 图 7 EMFN模型(2)关于
图 7 EMFN模型(2)关于



























 图 8 EMFN模型(2)关于
图 8 EMFN模型(2)关于



















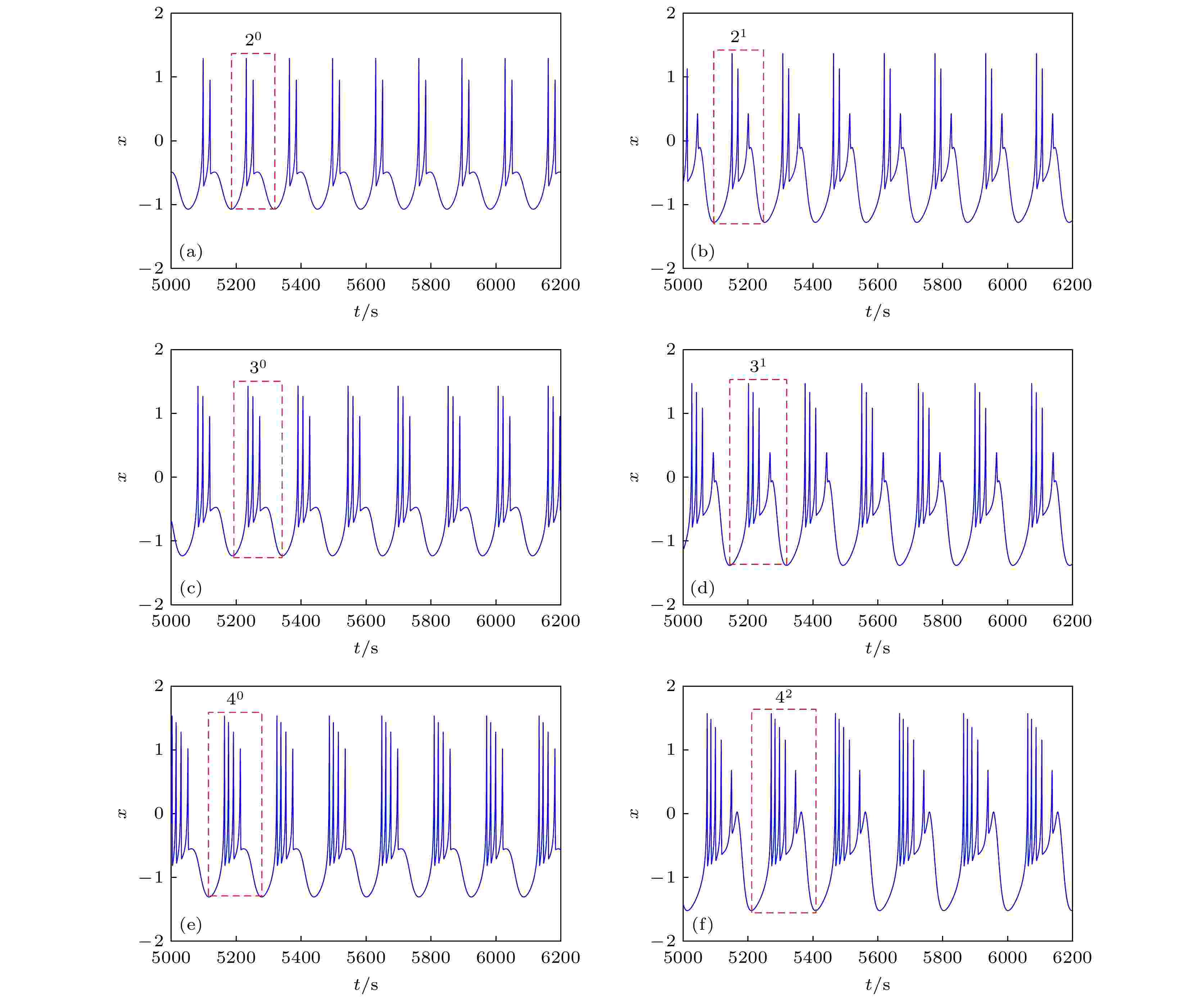 图 9 EMFN模型(2)的时间响应图 (a) 周期2放电; (b) 周期
图 9 EMFN模型(2)的时间响应图 (a) 周期2放电; (b) 周期





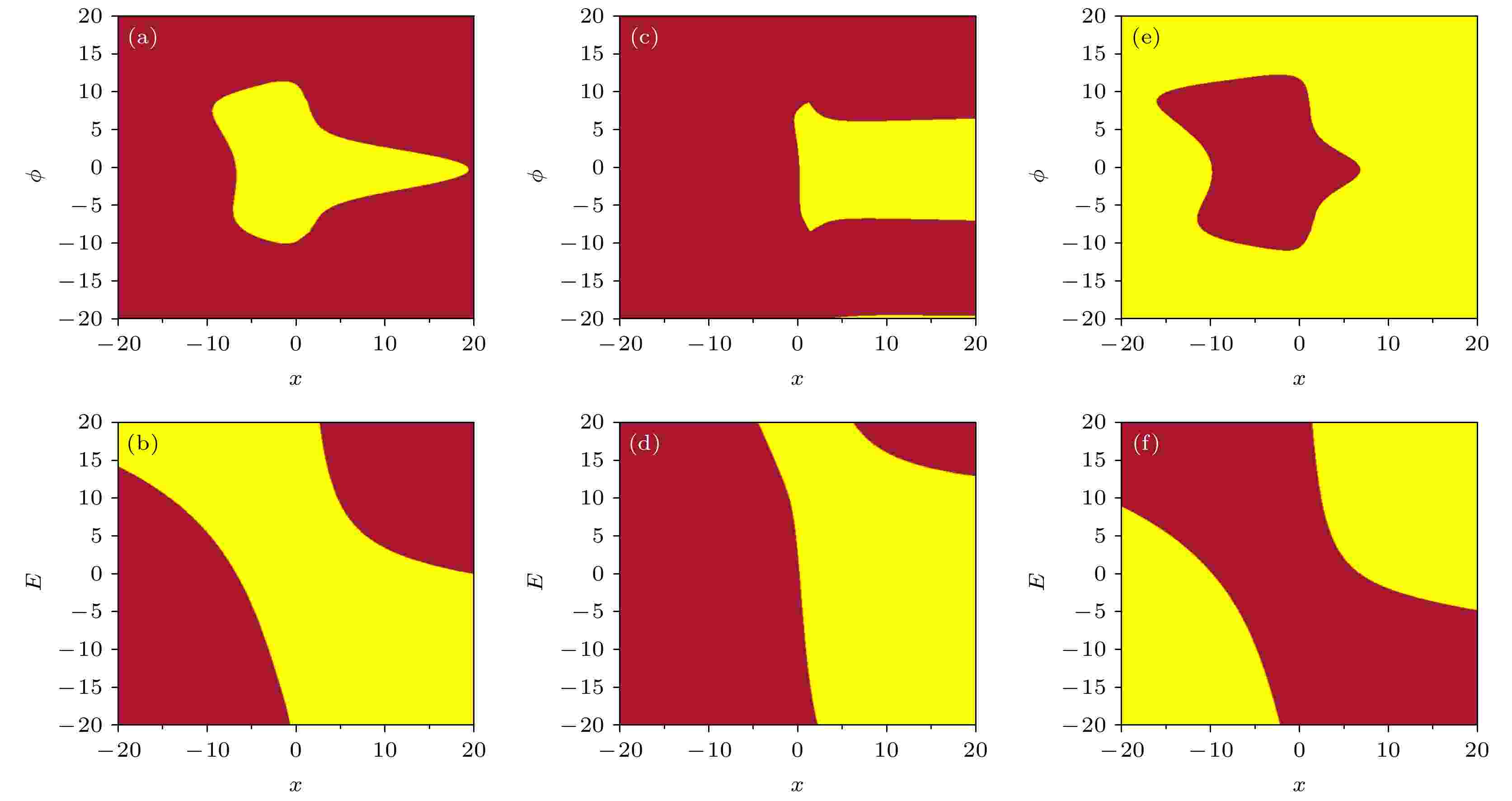 图 10 EMFN模型(2)的共存吸引域 (a)
图 10 EMFN模型(2)的共存吸引域 (a)













































































































































































































































































































































































































































































































































































































































































































































































































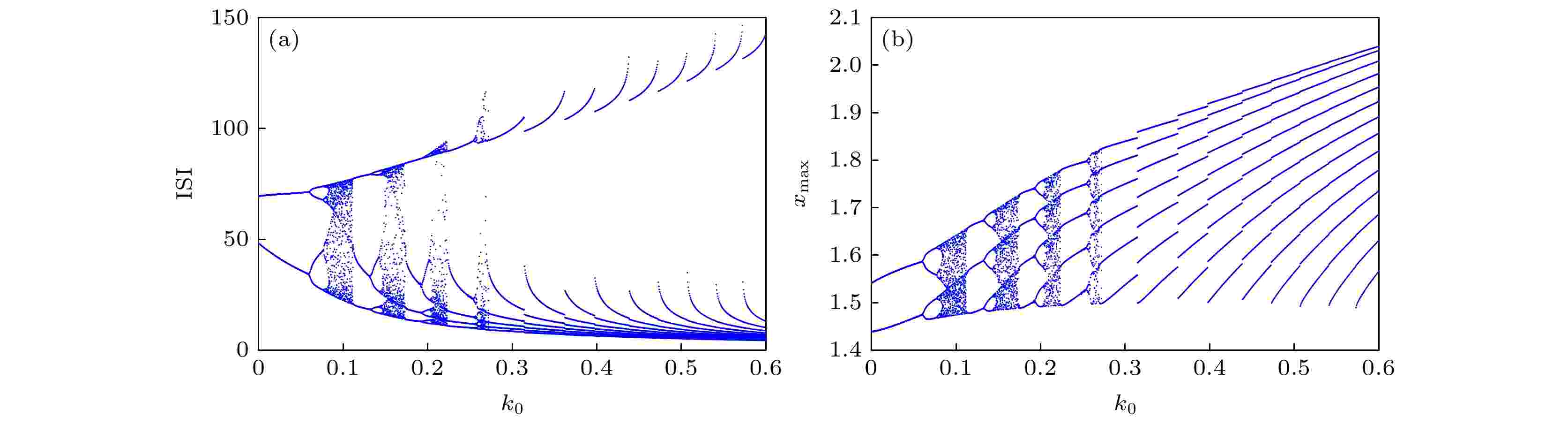 图 11 关于
图 11 关于

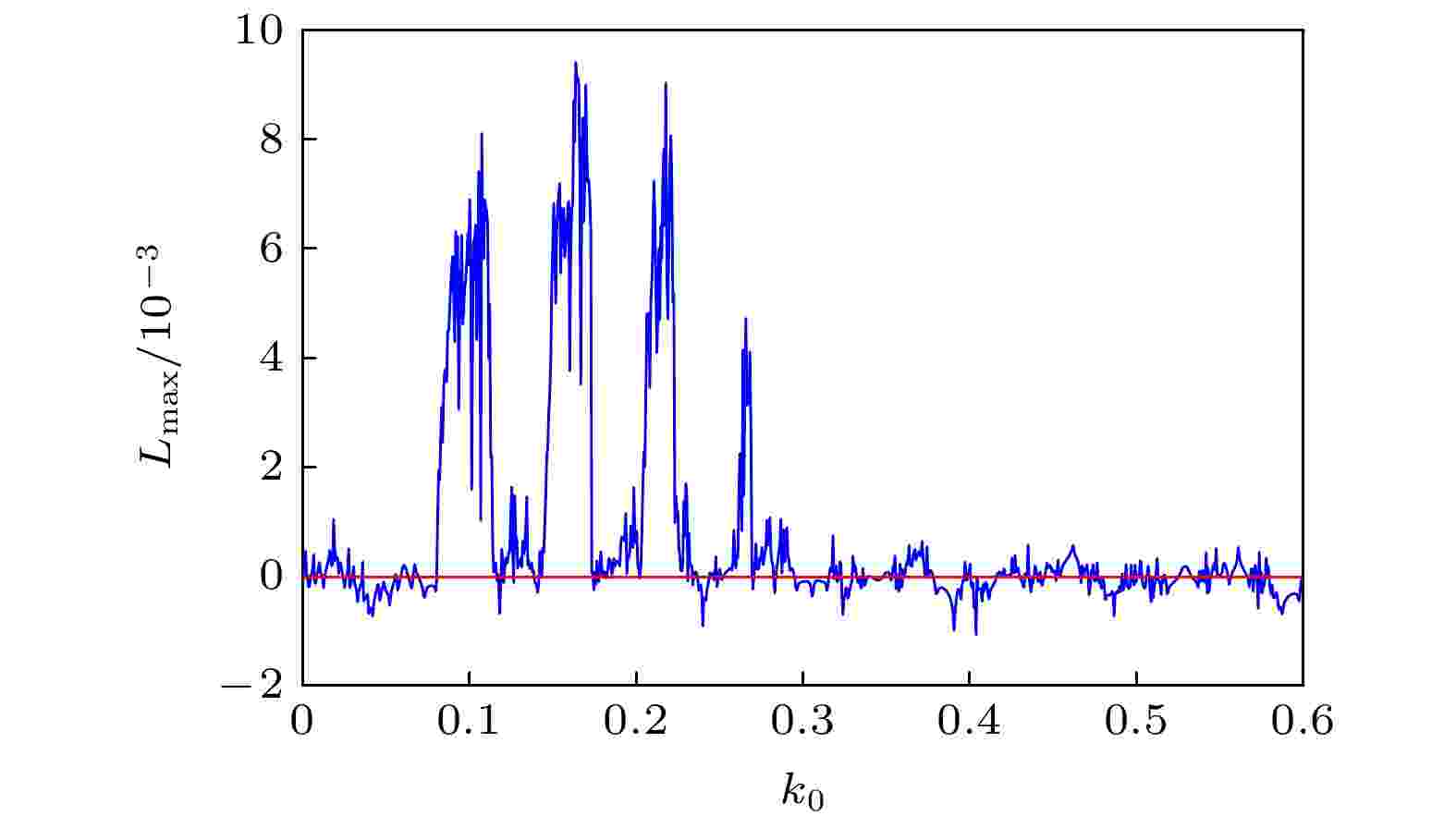 图 12 对应于图11的最大 Lyapunov 指数图
图 12 对应于图11的最大 Lyapunov 指数图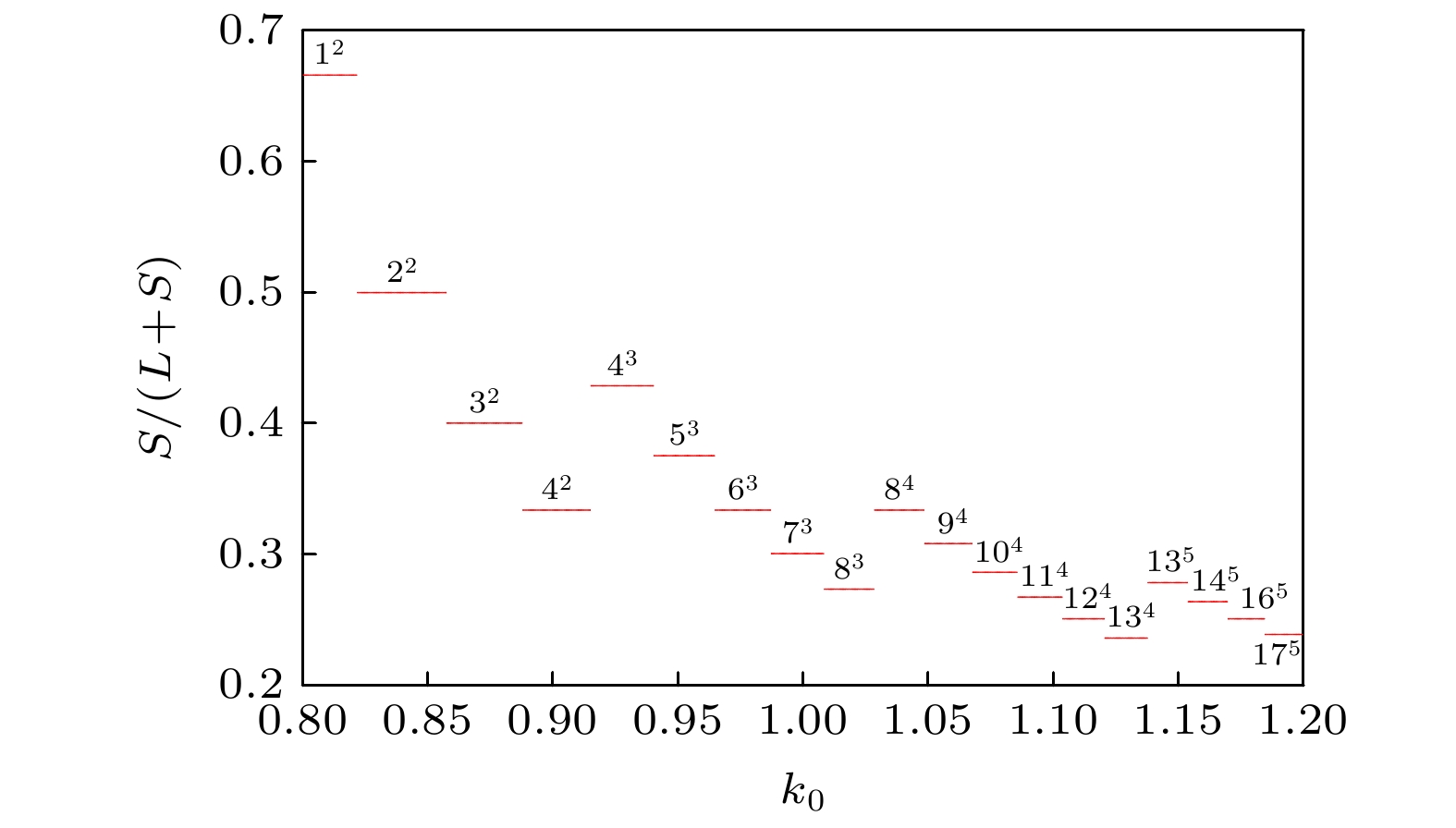 图 13 膜电压的发放数关于参数
图 13 膜电压的发放数关于参数




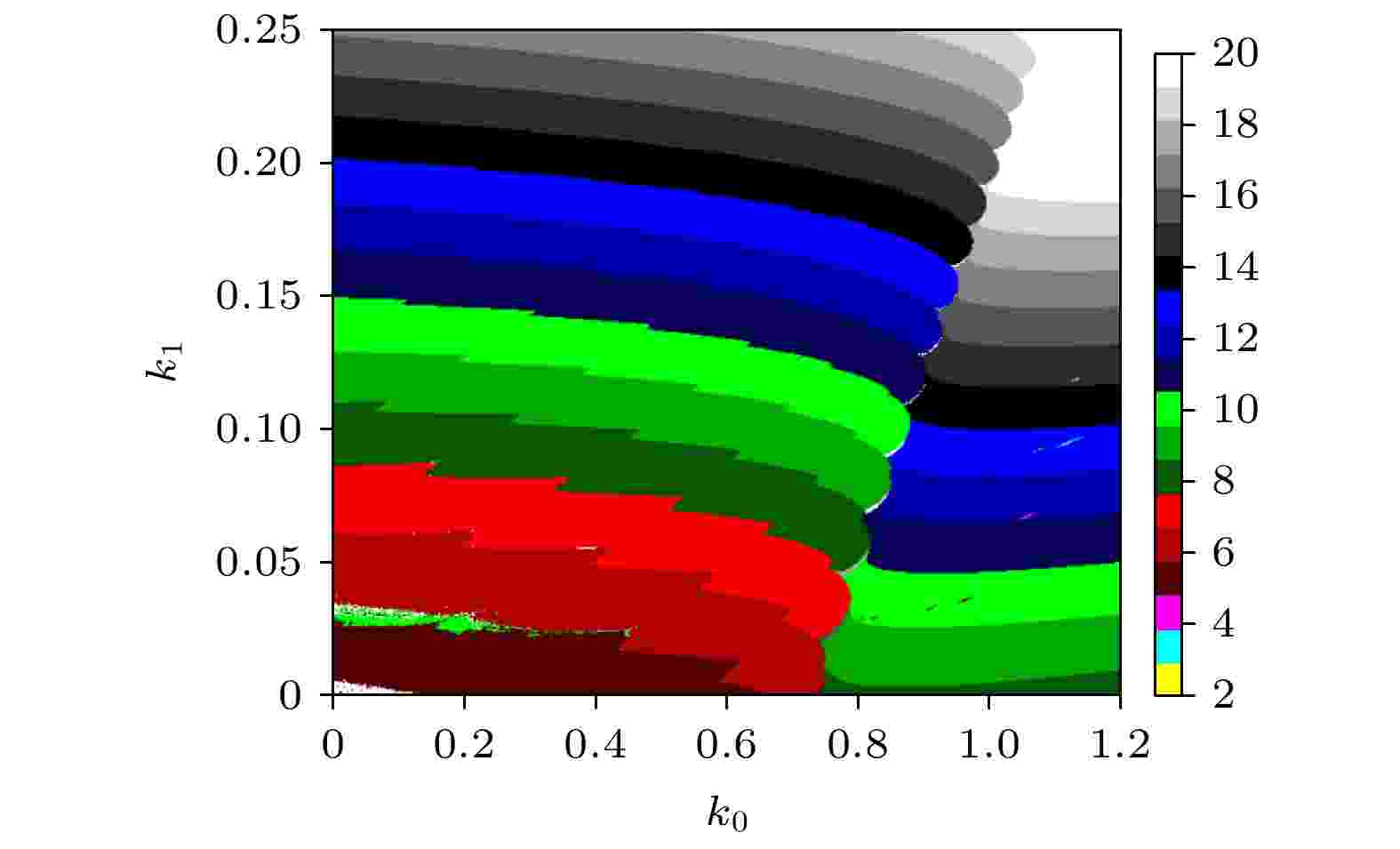 图 14 EMFN模型(2)关于
图 14 EMFN模型(2)关于

















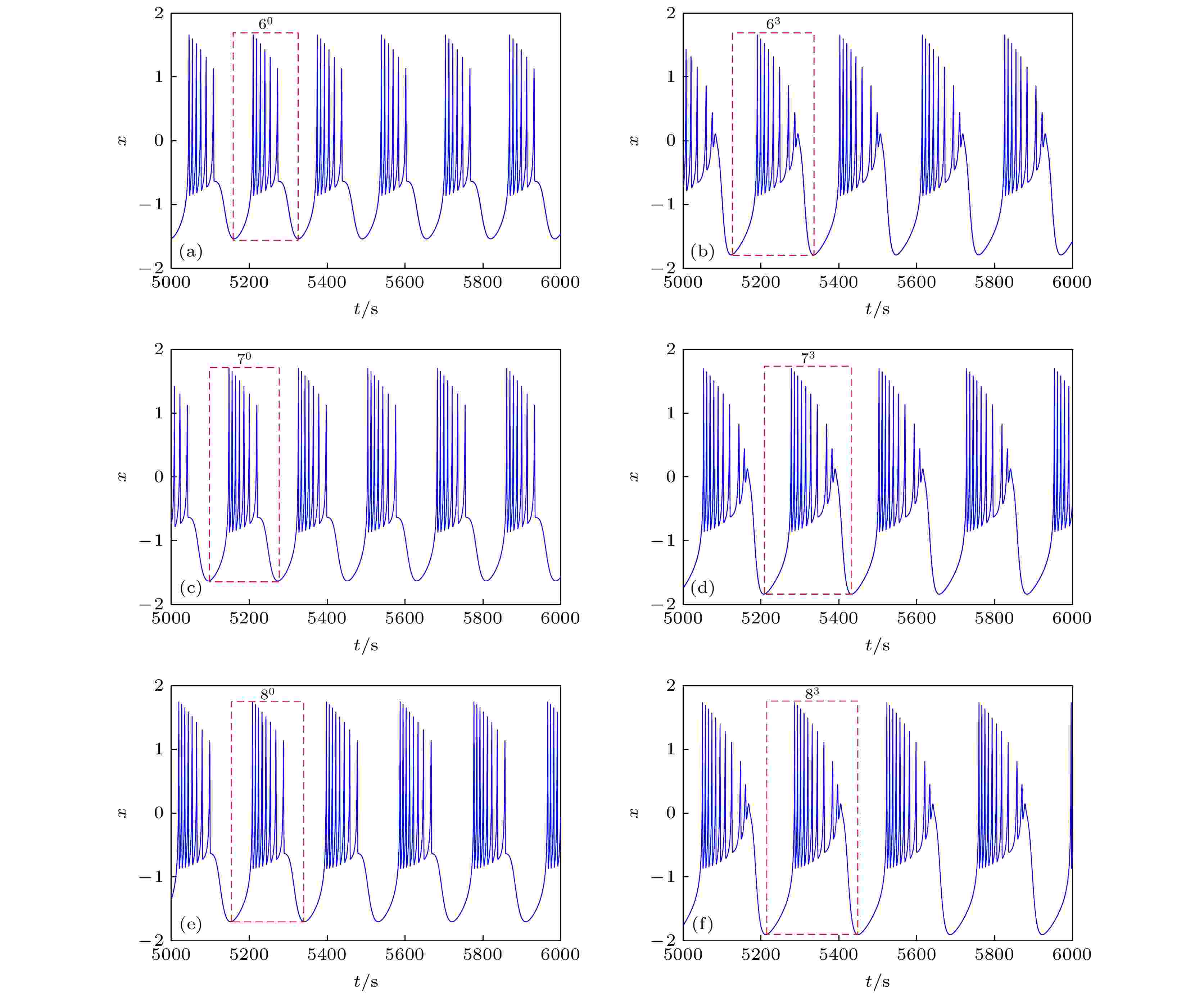 图 15 EMFN模型(2)的时间响应图 (a) 周期6放电; (b) 周期
图 15 EMFN模型(2)的时间响应图 (a) 周期6放电; (b) 周期































































































































































































































































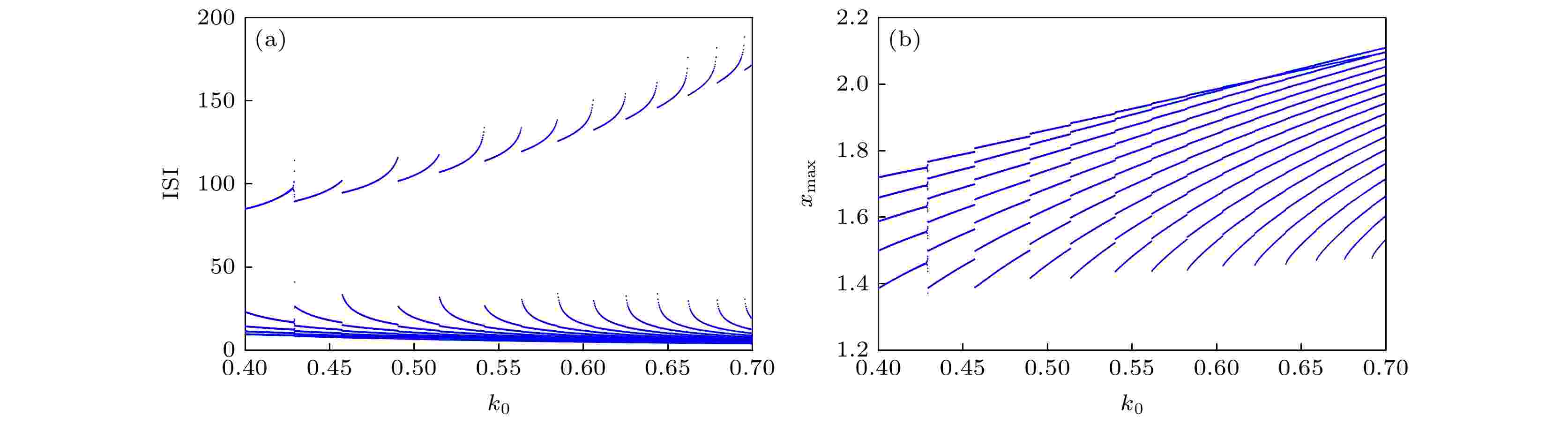 图 16 关于
图 16 关于

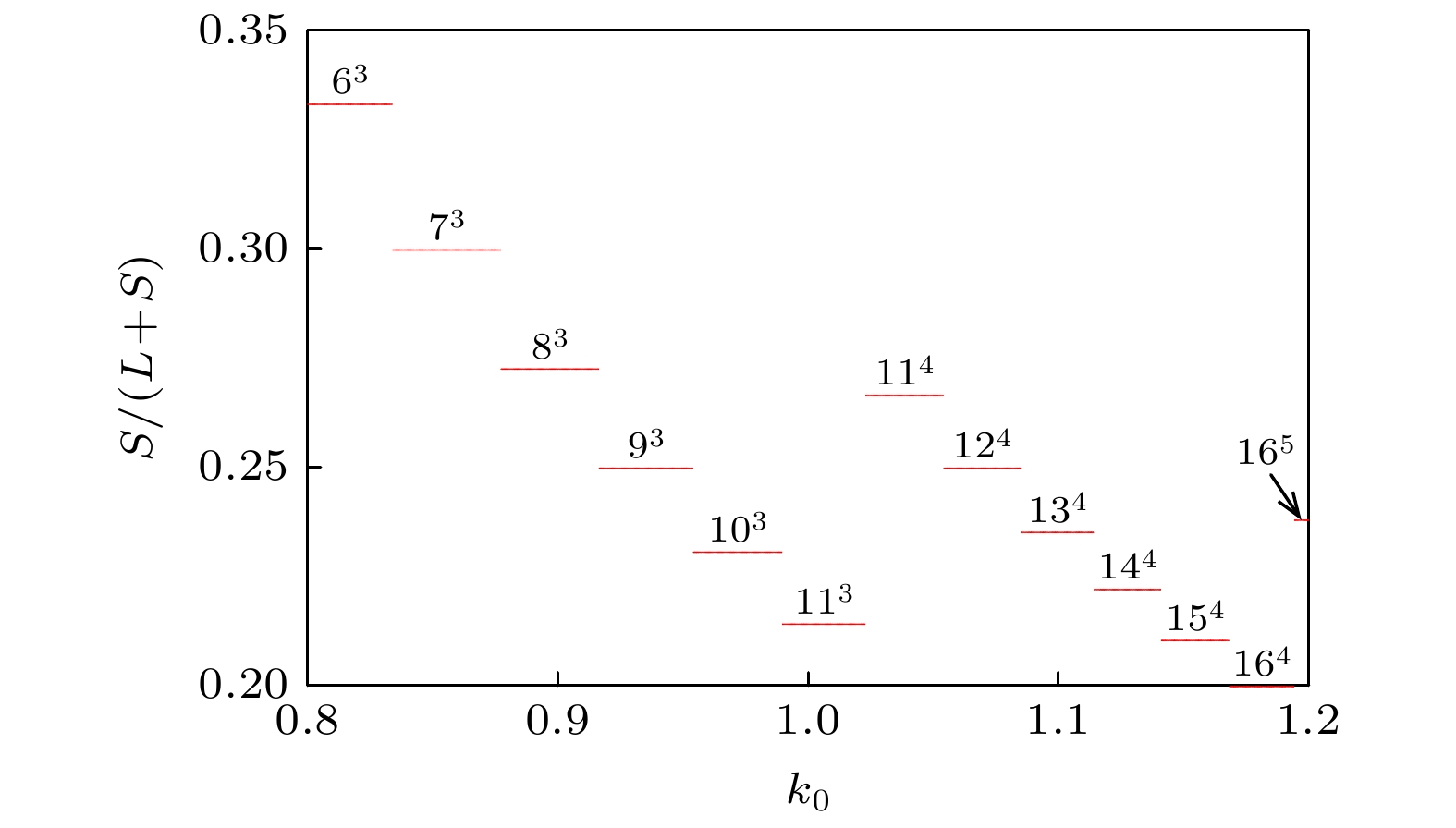 图 17 膜电压的发放数关于参数
图 17 膜电压的发放数关于参数






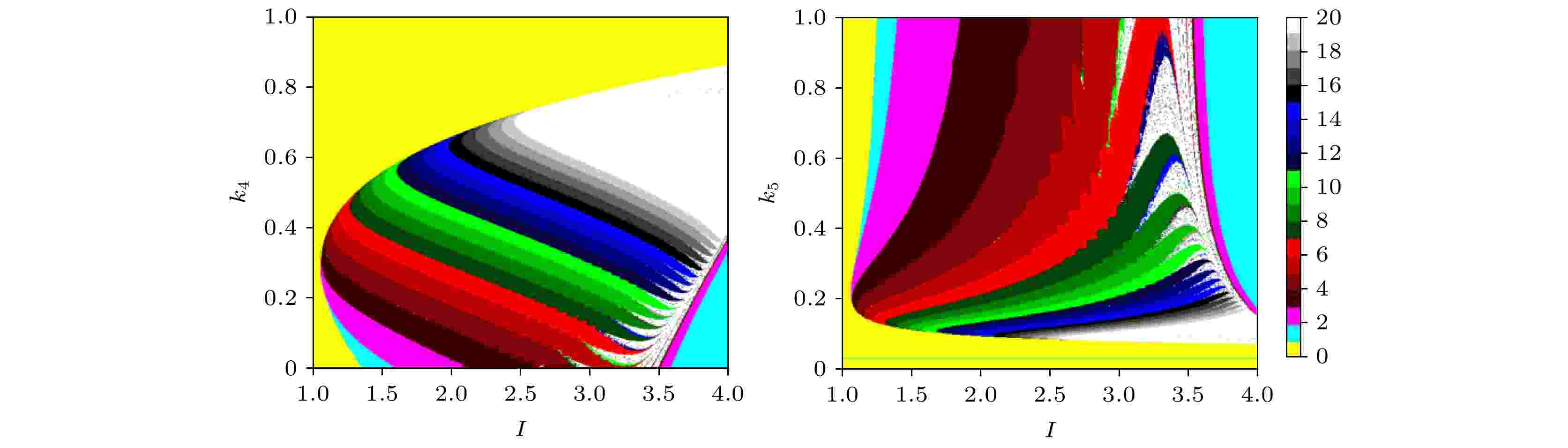 图 18 EMFN模型(2)关于I和
图 18 EMFN模型(2)关于I和










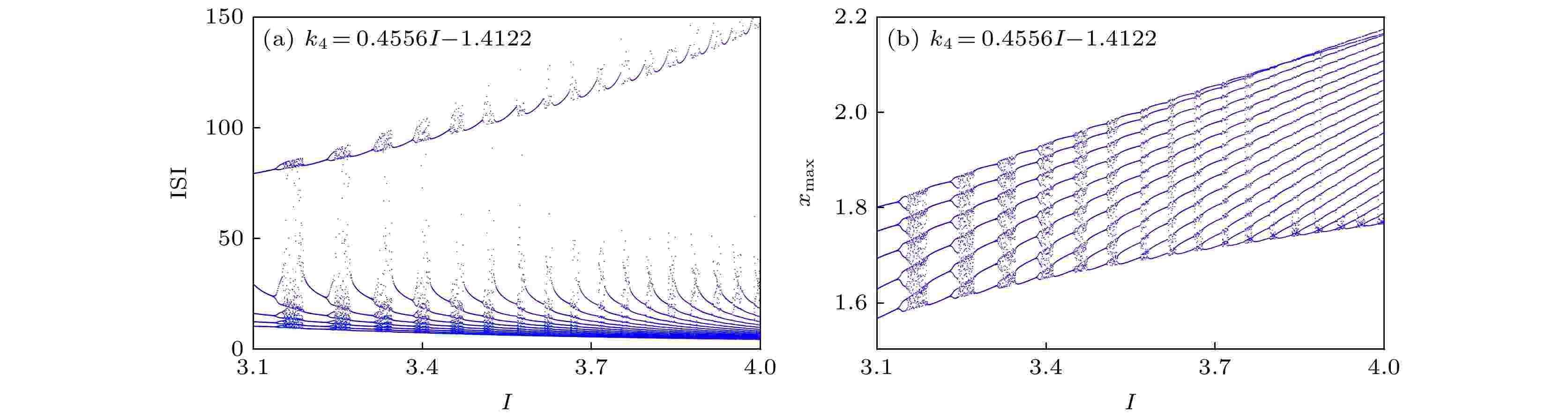 图 19 当
图 19 当

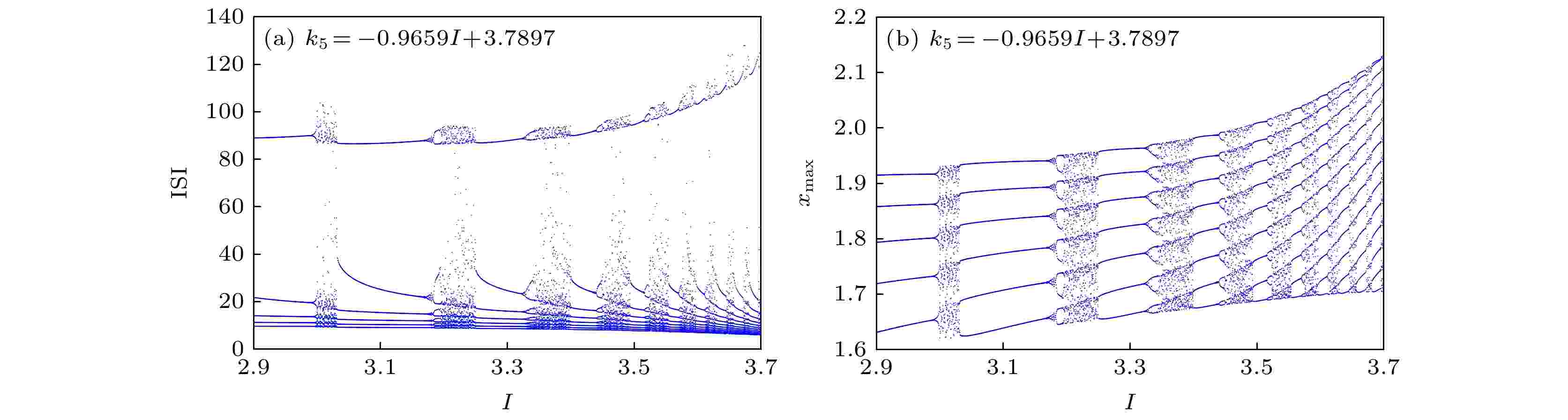 图 20 当
图 20 当
































































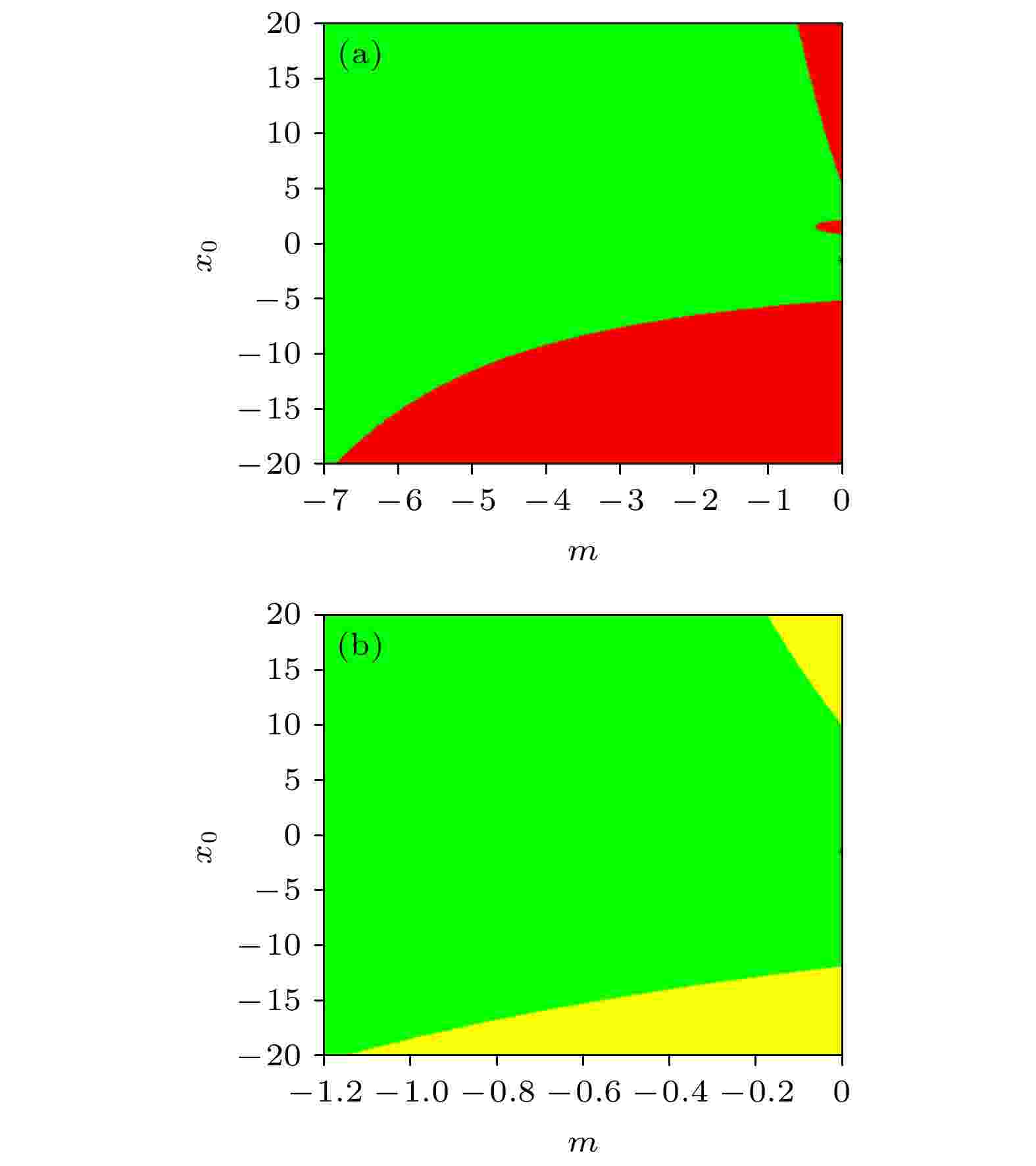 图 21 反馈增益
图 21 反馈增益








