全文HTML
--> --> -->目前大多数的超表面仅能在特定波长实现全息显示[17-19], 因此在不同设定波长下实现波长复用全息显示有迫切需求. 已有许多文献运用超表面对2—3个波长的独立调控, 从而实现多波长复用全息显示. 主要分成两大类: 在超表面中每个像素单元上填充多个微元结构; 超表面中每个像素单元采用单一微元结构.
通过在超表面中每个像素单元中填充多个微元结构, 并且设定像素单元中每个微元结构对特定波长响应调制, 实现多波长复用显示. Wang等[20]提出了基于4个硅矩形柱构成超表面微元的超表面结构, 实现了红绿蓝三色圆偏振光复用的全息显示. 该超表面微元由三种尺寸的硅矩形柱组成, 每种尺寸矩形柱对应红绿蓝三色光的左右旋圆偏振光的透射偏振转化效率不同, 结合Multiwavelength Gerchberg-Saxton(MWGS)相位恢复算法, 实现了红绿蓝三色光和左旋偏振、右旋偏振光复用的全息显示, 其中红绿蓝三色光的衍射效率分别为18.0%, 5.2%, 3.6%. 由于超表面中每个像素单元填充多个微元结构, 增加了每个像素点的尺寸, 从而减低了显示分辨率[21], 并且限制了各波长的衍射效率.
为了不降低显示分辨率, 超表面中每个像素单元采用单个结构的微元, 通过对振幅和相位的同时调控实现多波长复用全息显示. Huang等[22]提出了一种铝金属注射成形 (metal injection molding, MIM) 三层结构反射式超表面, 实现了红绿蓝三色波长复用全息显示. Qin等[23]提出铝椭圆孔洞结构超表面, 实现了透射式全彩全息显示. Wan等[24]采用铝椭圆孔洞结构超表面, 将红绿蓝三色波长对应的全息图添加相位偏移量, 从而实现了红绿蓝三色波长复用全息显示. 由于上述三种超表面中每个微元结构对不同波长具有相同的相位, 进而导致波长串扰. 各向异性超表面微元对不同波长具有不同的相位, 可以用于设计多功能超表面, 特别是双波长超表面[25-27], 能够降低波长串扰并且提升衍射效率.
因此, 本文提出实现波长和线偏振态同时复用的全息显示的单一结构超表面, 并对其进行优化设计, 可以有效降低波长串扰.
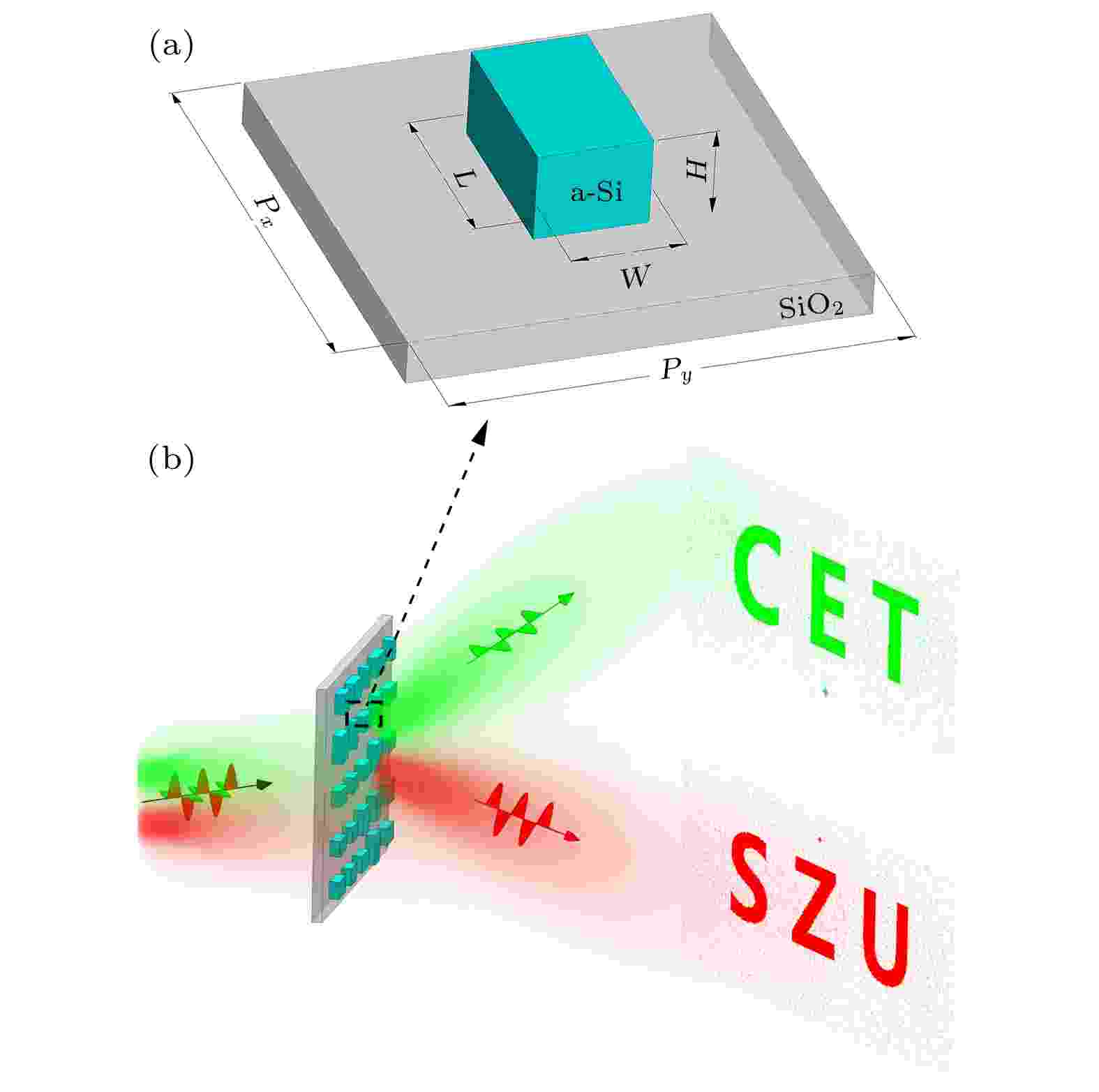图 1 (a) 超表面微元结构示意图; (b) 超表面在532 nm波长和633 nm波长、正交线偏振态下, 全息显示示意图Figure1. (a) Schematic of unit cell structure consisting of Si nanobrick on the SiO2 substrate; (b) schematic of hologram metasurface at wavelength of 532 nm and 633 nm with orthogonal linear polarizations.
超表面的微元结构为矩形柱, 如图1(a)所示, 高度H为270 nm的微元, 在x方向上的周期为Px = 260 nm, 在y方向上的周期为Py = 310 nm. L, W分别为矩形柱在x, y方向上的尺寸. 非晶硅(a-Si)由于其在可见光和近红外波段折射率高, 被广泛应用于可见光超表面全息[6,10,28]和近红外超表面全息[18,29]. 本文选取非晶硅作为微元材料, 其在波长为532 nm和波长为633 nm处的折射率分别为4.03 + 0.093i和3.78 + 0.026i, SiO2作为基底材料, 其折射率为
为了获得在不同入射条件下, 矩形微元结构尺寸参数与透过相位之间的映射关系, 应用商用FDTD软件模拟计算出在532 nm波长、x线偏振光、633 nm波长、y线偏振光垂直入射下, 透射光的相位和透过效率随矩形柱的尺寸参数(L, W)变化时的分布, 如图2所示. 由图2可知, 当532 nm波长、x线偏振光入射时, 透射光的相位和透过效率主要受矩形柱的L参数调控, W参数所起的作用相对较小. 而当633 nm波长、y线偏振光入射时, 透射光的相位和透过效率主要受矩形柱的W调控[18,29].
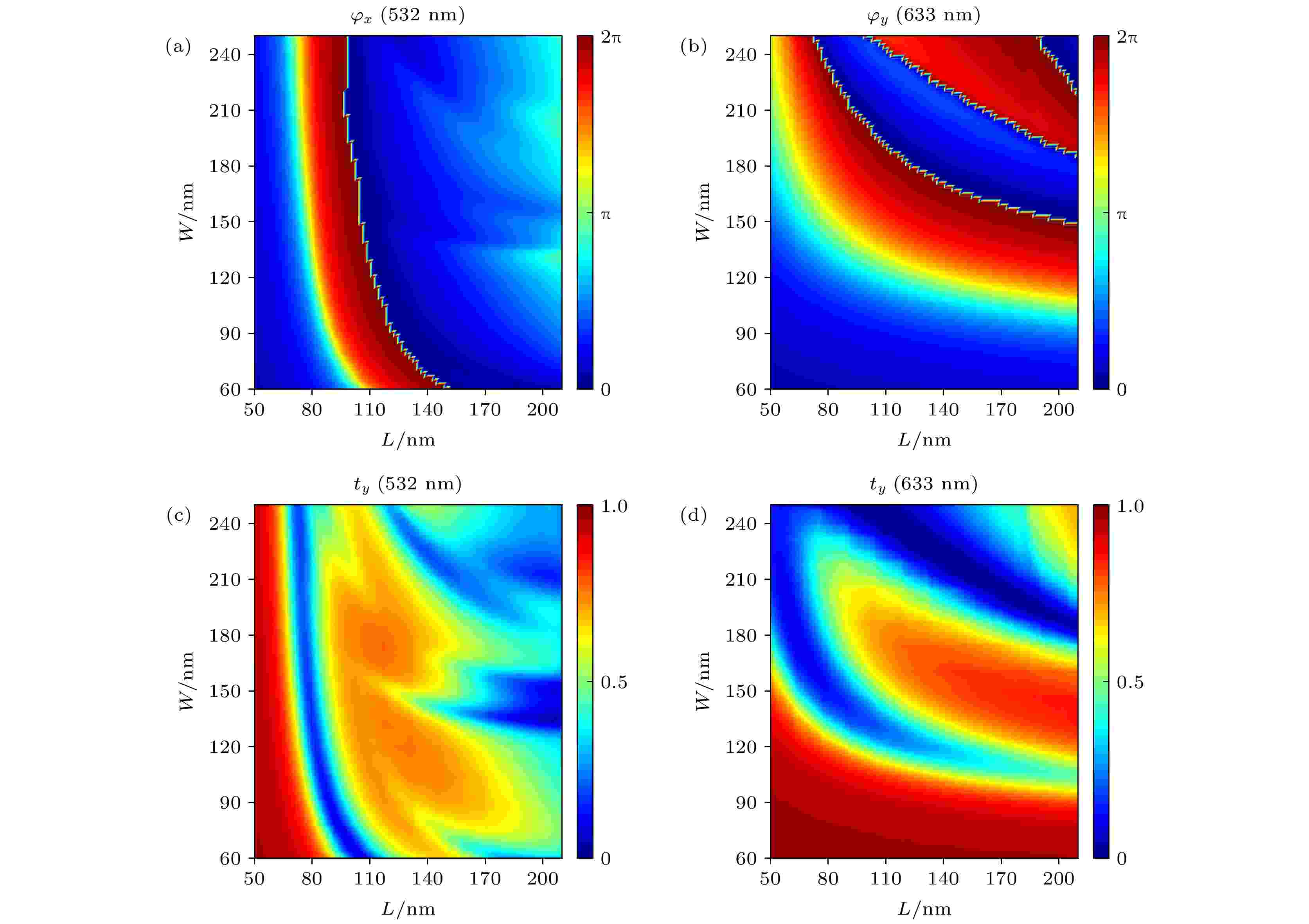图 2 超表面微元相位分布 (a) 532 nm波长、x线偏振态, (b) 633 nm波长、y线偏振态; 超表面微元透过效率分布 (c) 532 nm波长、x线偏振态, (d) 633 nm波长、y线偏振态Figure2. Phase of the metasurface (a) at 532 nm for x-polarization light and (b) at 633 nm for y-polarization light. Transmission of the metasurface (c) at 532 nm for x-polarization light and (d) at 633 nm for y-polarization light.
利用GS算法计算532 nm波长显示CET字符的全息图, 经八阶量化后其相位分布为φ1(x, y), 633 nm波长显示SZU字符的全息图, 经八阶量化后其相位分布为φ2(x, y), 其中x, y为全息图中像素点的坐标. 经八阶量化后CET字符和SZU字符的相位分布如图3所示.
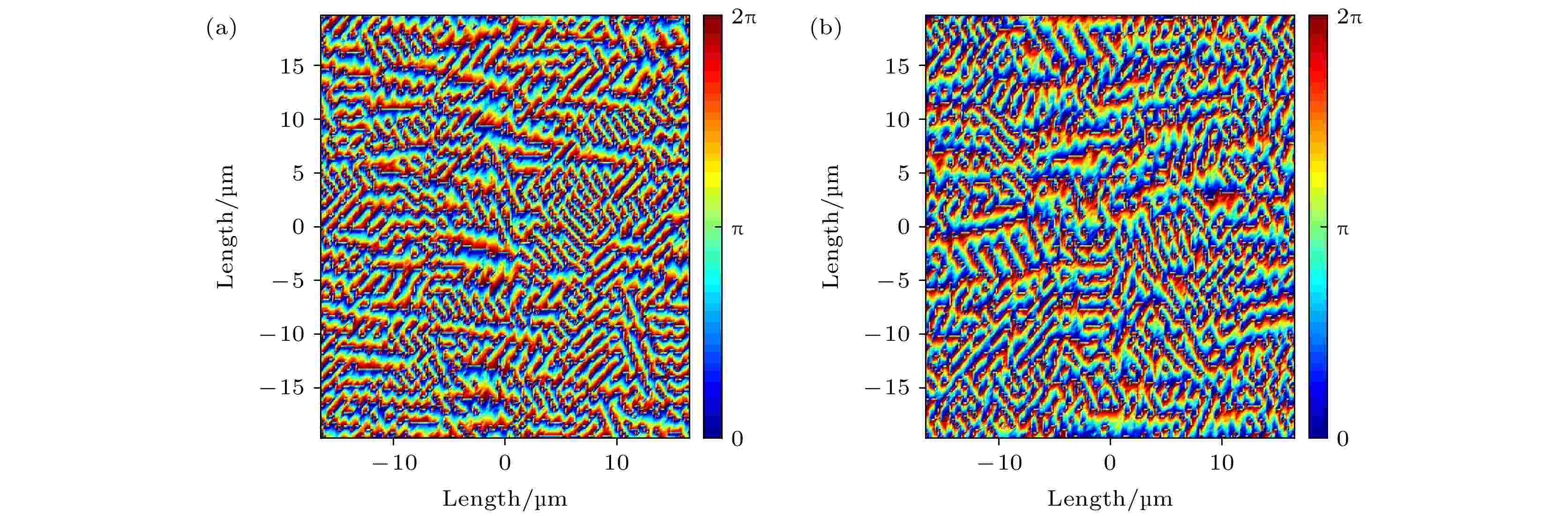图 3 GS算法计算得到的经八阶量化后目标字符的相位分布 (a) CET字符; (b) SZU字符Figure3. The phase distribution of the images using GS algorithm with eight-step: (a) Image“CET”; (b) image“SZU”.
为了从图2中优化得到合适的矩形微元尺寸参数, 使(x, y)处的矩形微元能够同时表示两幅全息图对应位置上的相位φ1(x, y)和φ2(x, y), 并且能同时保证透过效率相对较大. 本文建立了科学的评价函数Δ(x, y)来辅助选取, 评价函数如(2)式所示:
字符CET和SZU对应的全息图八阶量化后各像素点的相位有8种值, φ1(n), φ2(m)(n = 1, 2,···, 8; m = 1, 2,···, 8), 由于要应用一个微元表示不同入射条件下的两种相位, 并且同一位置的像素点上对应的两种相位组合最多有64个(φ1(n), φ2(m)), 那么根据(2)式和图2所示的透过相位与微元尺寸之间的关系, 搜索出这64个组合所对应64个最优的硅矩形柱几何参数L(n, m), W(n, m). 硅矩形柱几何参数L(n, m), W(n, m)对应的在532 nm 波长x偏振光入射下的透过相位为φx(n, m), 透过效率为tx(n, m), 而在633 nm波长、y偏振光入射下的透过相位为φy(n, m), 透过效率为ty(n, m). 图4(a),(b)为筛选得出的64种硅矩形柱对应的透过相位与64种理想组合相位的差值. 图4(c),(d)为筛选得出的64种硅矩形柱对应的透过效率. 由图4(a),(b)可知, 相位差值基本都小于π/8, 绝大部分都接近于0. 由图4(c),(d)可知, 硅矩形柱几何参数对应的透过效率变化较大, 根据图2, 为了满足相位差值尽量小, 所筛选的硅矩形柱几何参数无法避开透过效率过低的区间.
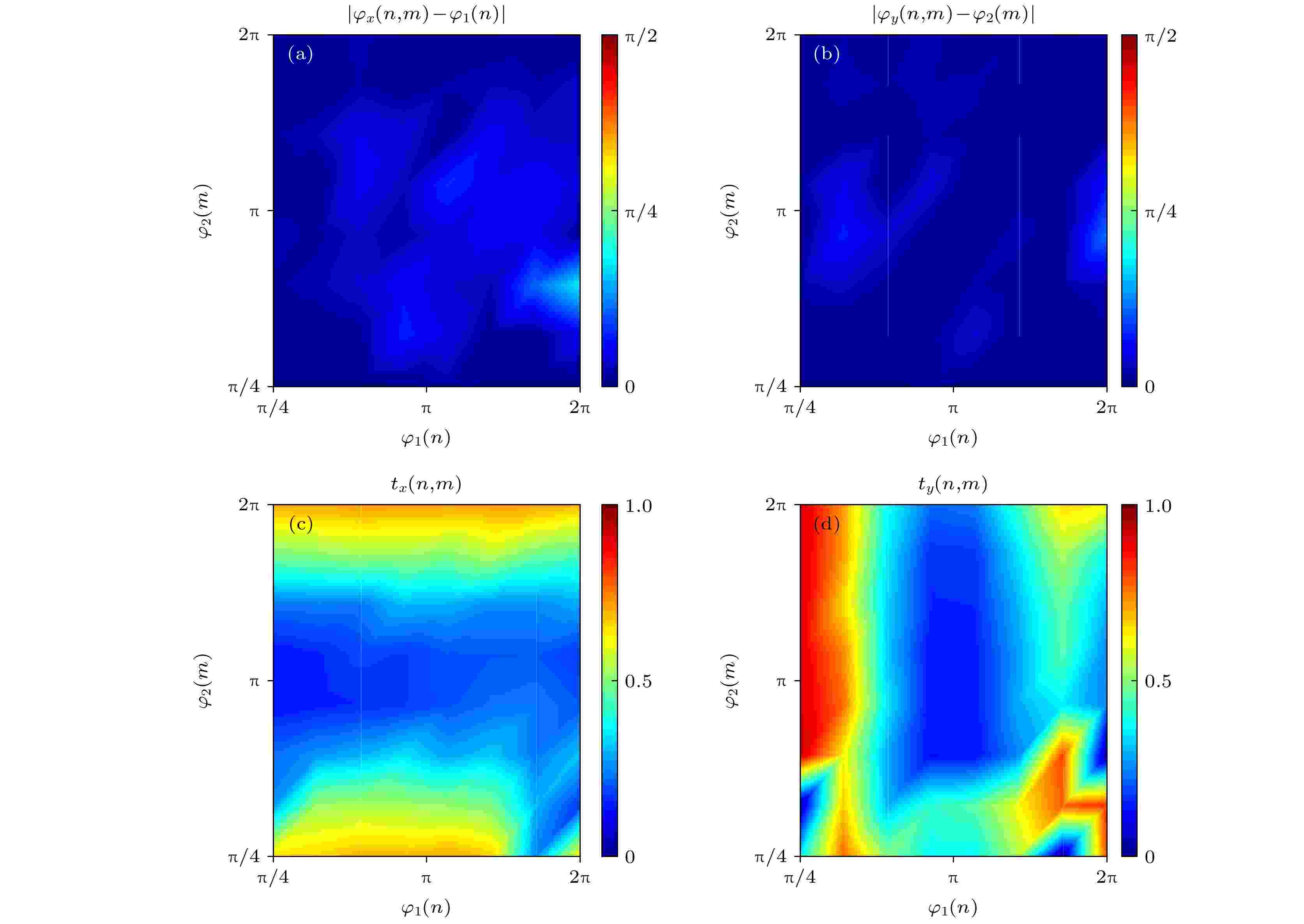图 4 64种硅矩形柱对应的透过相位与理想组合相位的差值 (a) 532 nm波长、x线偏振态, (b) 633 nm波长、y线偏振态; 64种硅矩形柱对应的透过效率 (c) 532 nm波长、x线偏振态, (d) 633 nm波长、y线偏振态Figure4. The deviation plot between the designed and ideal phase (a) at 532 nm for x-polarization light and (b) at 633 nm for y-polarization light. The transmission of the designed metasuface nanoblock (c) at 532 nm for x-polarization light and (d) at 633 nm for y-polarization light.
根据字符全息图的相位分布, 获得全息图上所有像素点对应的矩形柱尺寸L(x, y)和W(x, y), 组成双波长、线偏振复用全息显示的超表面. 其示意图如图5(a)所示. 图5(b)为根据超表面3 × 3 像素点内硅矩形柱几何参数的尺寸L(n, m), W(n, m), 计算得到的532 nm波长、x偏振光和633 nm波长、y偏振光对应的透过相位值和透过效率.
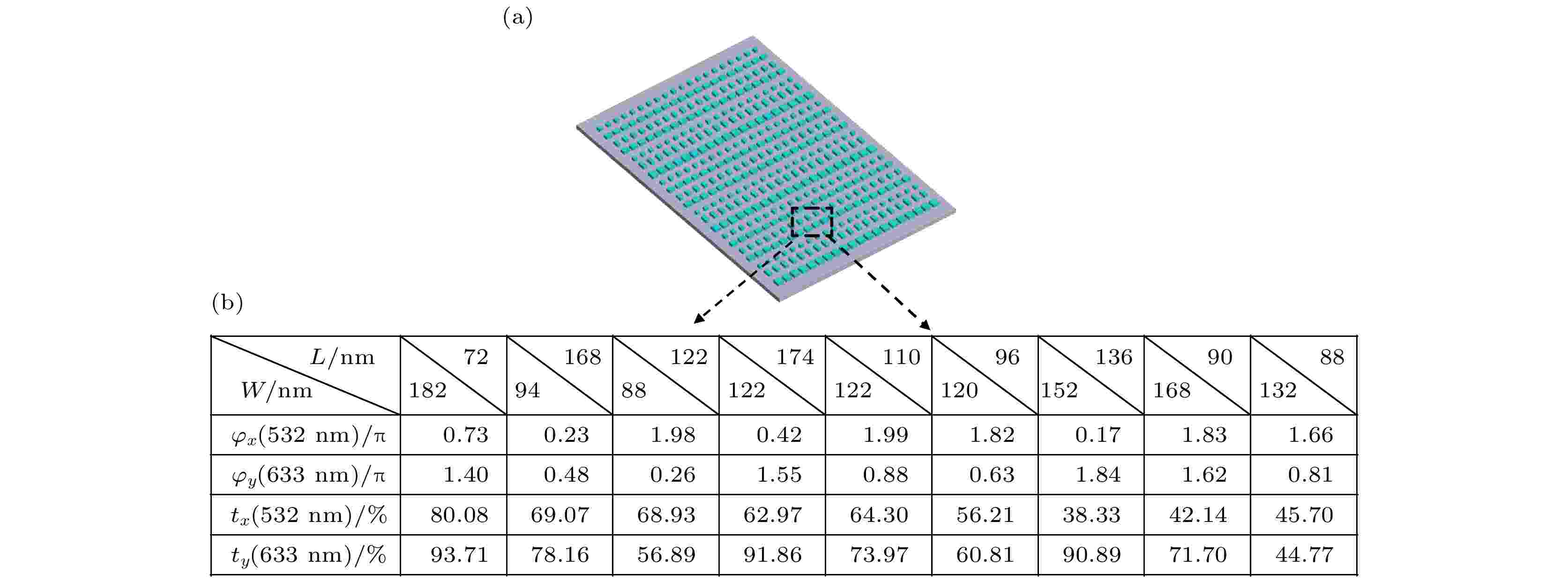图 5 (a) 超表面结构示意图; (b) 超表面3 × 3 像素点内硅矩形柱几何参数的尺寸L(n, m), W(n, m), 分别在532 nm波长、x偏振光和633 nm波长、y偏振光入射下对应的透过相位值和透过效率Figure5. (a) Schematic of metasurface; (b) phase matrix, transmission matrix, length of rectangular unit cell matrix and width of rectangular unit cell matrix. This is shown for 3 × 3 pixel subsection of the metasurface.
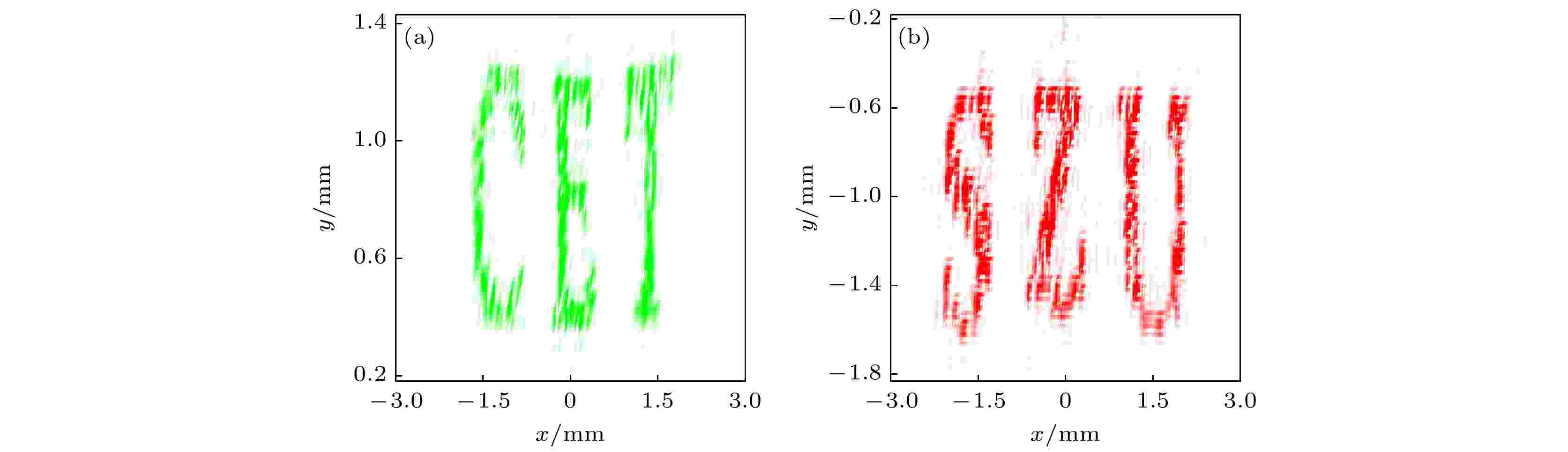图 6 仿真得到的字符的全息再现像 (a) 532 nm波长、x线偏振态; (b) 633 nm波长、y线偏振态Figure6. Simulated recovered image from the phase map of metasureface: (a) For x-polarization at 532 nm; (b) for y-polarization at 632 nm illumination.
全息超表面总衍射效率等于超表面的透过效率与全息衍射效率的乘积. 其中全息衍射效率定义为重建图像的光强与超表面的透过光强的比值. 由于超表面上每个点的微元尺寸不同, 每个点的透过效率也不相同, 因此整个超表面的透过效率定义为超表面上所有微元的透过效率的平均值[32,33]. 根据FDTD计算, 532 nm 波长、x偏振光入射时, 透射效率为36.7%, 总的衍射效率为12.8%; 当633 nm波长、y偏振光入射时, 透过效率为36.8%, 总的衍射效率为11.4%. 由于仿真中超表面微元个数较少, 因此全息再现像质量不高, 衍射效率相对较低, 实际制作中可通过提高微元数量来提升成像质量和衍射效率.
通过仿真结果与期望输出的目标字符比较可知, 本文提出的单一的矩形结构超表面可实现532 nm、632 nm波长和x偏振、y偏振复用的全息显示, 能够使用现有的互补金属氧化物半导体(complementary metal oxide semiconductor, CMOS)加工工艺制作, 降低了加工制作难度, 降低了波长间的串扰, 并具有较高的衍射效率, 具有重要的学术意义和应用价值.
