删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于铌酸锂双折射晶体的皮秒拍瓦激光系统光谱整形

本站小编 Free考研考试/2021-12-29
摘要:为补偿皮秒拍瓦激光系统中钕玻璃宽带放大引起的增益窄化, 提出了一种基于铌酸锂双折射晶体的高能量光谱整形方法. 在相同强度调制下, 对比了BBO、铌酸锂和石英3种晶体, 针对1053 nm激光, 选用了高双折射率、大口径且不易潮解的铌酸锂作为整形晶体. 理论分析了晶体厚度、倾斜角、面内旋转角对强度调制的影响, 发现它们分别决定调制的带宽、中心波长及深度. 并对整形过程中晶体引入的光谱相位进行了分析, 发现各阶色散量随晶体厚度、倾斜角、面内旋转角变化的规律, 因此可通过上述参数控制各阶色散量. 在此基础上, 开展了中心波长为1053 nm、带宽为10 nm、调制深度为80%的光谱整形实验和相位测量实验, 实验与理论分析相一致. 针对神光Ⅱ皮秒拍瓦激光系统, 利用上述整形方案, 国内首次实现了1700 J, 6 nm (FWHM)的高能宽带激光输出, 有效补偿了增益窄化. 研究结果对国内基于钕玻璃放大系统的宽频带激光装置的工程研制具有重要意义.
关键词: 高能光谱整形/
双折射晶体/
光谱相位/
高能拍瓦激光系统

English Abstract


全文HTML

--> --> -->
1.引　言
啁啾脉冲放大技术(chirped pulse amplification, CPA)[1-3]的提出, 为超强、超短激光[4]发展注入了活力, 激光系统在高能量、宽频带、高功率方面不断迈上新的台阶. 在以增益介质为基础的啁啾脉冲放大过程中, 由于介质的增益线型限制, 脉冲中心频率的增益大于边缘频率, 因此, 脉冲经增益介质放大时光谱不断变窄, 这种现象被称为增益窄化效应[5-7]. 它会对激光系统带来一系列不利影响, 一方面, 啁啾脉冲光谱窄化对应着时间窄化, 时间窄化后的啁啾脉冲对后续增益链的损伤阈值将提出更高要求[8], 同时会带来更高B积分累积; 另一方面, 在傅里叶变换极限(Fourier transform limit, FTL)下, 光谱宽度和脉冲宽度的乘积是一个常数[9], 光谱的窄化将限制后期的脉冲压缩, 不利于获得更短激光脉冲输出. 因此, 补偿放大过程中的增益窄化效应, 进行光谱整形具有重要意义.
目前, 常用的光谱整形技术有: 空间光调制器(spatial light modulator, SLM)[10,11]、声光可编程色散滤波器(acouto-optic programmable dispersive filter, AOPDF)[12]、抽运光整形[13]和双折射晶体整形[14]等. 由于SLM和AOPDF损伤阈值较低, 两者仅能支持小能量的光谱整形; 而在光参量啁啾脉冲放大(optical parametric chirped pulse amplification, OPCPA)中, 通过抽运光间接整形, 虽然可以支持高能量输出, 但增加了抽运光的制备难度, 同时会使OPCPA效率降低; 因此, 具备损伤阈值高、插入损耗小、使用方便等特点的双折射晶体, 被广泛应用于光谱整形中. 针对800 nm激光, 使用石英双折射晶体抑制增益窄化的光谱整形已趋于成熟, 例如: 1996年Bart等[15]将石英平板插入钛宝石再生放大器中, 将光谱半高全宽(full width at half maximum, FWHM)从32 nm展宽到45 nm; 类似地, 2007年陆效明等[16]利用761 μm厚石英平板, 将光谱从28 nm展宽到62 nm. 相对于钛宝石, 易获得大口径、高光学质量的钕玻璃(中心波长1053 nm)更适合于高能量输出, 但是, 它的受激发射截面带宽仅为20 nm[17], 增益窄化效应更为严重, 更难补偿. 近来, 针对1053 nm的双折射光谱整形报道较少, 美国NIF装置[18,19]于2012年对钕玻璃作为增益介质的再生放大器, 使用石英晶体将光谱从3 nm(FWHM)展宽到5 nm; 2003年国内朱鹏飞等[20]使用12 mm厚石英对钕玻璃增益窄化进行补偿, 将光谱从13 nm(FWHM)展宽到15 nm, 展宽效果不明显. 上述报道中, 无论是针对钛宝石还是钕玻璃的双折射晶体光谱整形, 均未对整形过程中晶体引入的光谱相位[21]进行分析. 随着脉冲压缩、相干组束、高信噪比输出等对光谱相位的要求越来越高, 对晶体引入的光谱相位进行分析具有重要意义. 此外, 国内高能拍瓦激光系统为获得更高能量、更短脉宽的高功率输出, 也急需开展针对1053 nm抑制钕玻璃增益窄化的光谱整形工作.
本文针对高能拍瓦激光系统中钕玻璃的增益窄化, 提出了一种基于铌酸锂双折射晶体的高能量光谱整形方法. 在理论上, 从双折射晶体严格琼斯矩阵[22]出发, 研究了晶体厚度、倾斜角、面内旋转角对光谱强度调制和晶体引入相位的影响, 首次模拟了晶体引入的各阶色散量随晶体厚度、倾斜角、面内旋转角的变化情况, 发现通过上述参数可对晶体引入的各阶色散量进行控制. 在此基础上, 搭建了光谱整形模块, 利用神光Ⅱ高能拍瓦激光系统, 有效补偿了钕玻璃放大的增益窄化效应, 在国内首次实现了1700 J, 6 nm (FWHM)的高能宽带激光输出, 是未整形时3.2 nm的2倍. 并开展实验对晶体引入的光谱相位进行测量, 实验与理论模拟相一致. 本文结果将为双折射晶体光谱整形中晶体的参数设计, 材料选择及后续光谱相位补偿提供依据, 也可为高能拍瓦激光系统信噪比的提升提供参考.
2.原理和分析
当晶体光轴在晶体表面时, 倾斜双折射平板的严格琼斯变换矩阵[22]为

$\begin{split} &{{M}}(\theta,\phi ) = {(n_{\rm{o}}^2 - {\cos ^2}\phi {\cos ^2}\theta )^{ - 1}} \\&\times \left[ {\begin{array}{*{20}{c}} {\exp ({\rm{i}}{\delta _{\rm{e}}})(n_{\rm{o}}^2 - {{\cos }^2}\theta ){{\cos }^2}\phi + \exp ({\rm{i}}{\delta _{\rm{o}}})n_{\rm{o}}^2{{\sin }^2}\phi }&{\left[ {\exp ({\rm{i}}{\delta _{\rm{e}}}) - \exp ({\rm{i}}{\delta _{\rm{o}}})} \right]{n_{\rm{o}}}\sin \phi \cos \phi {{\left( {n_{\rm{o}}^2{{\cos }^2}\theta } \right)}^{1/2}}} \\ {\left[ {\exp ({\rm{i}}{\delta _{\rm{e}}}) - \exp ({\rm{i}}{\delta _{\rm{o}}})} \right]{n_{\rm{o}}}\sin \phi \cos \phi {{\left( {n_{\rm{o}}^2{{\cos }^2}\theta } \right)}^{1/2}}}&{\exp ({\rm{i}}{\delta _{\rm{e}}})n_o^2{{\sin }^2}\phi + \exp ({\rm{i}}{\delta _{\rm{o}}})(n_{\rm{o}}^2 - {{\cos }^2}\theta ){{\cos }^2}\phi } \end{array}} \right] \end{split} ,$

式中δo, δe分别为o光、e光通过双折射晶体后的相位改变量, 由下式表示:
$\begin{split}& {\delta _{\rm{e}}}\left( {\theta,\phi } \right) = \\& \frac{{2{\rm{\pi }}}}{\lambda }{n_{\rm{e}}}t\left[ {\dfrac{{1 + \dfrac{{{{\cos }^2}\theta {{\cos }^2}\phi }}{{n_{\rm{e}}^{\rm{2}}}} - \dfrac{{{{\cos }^2}\theta {{\cos }^2}\phi }}{{n_{\rm{o}}^2}}}}{{{{\left( {1 - \dfrac{{{{\cos }^2}\theta {{\sin }^2}\phi }}{{n_{\rm{e}}^{\rm{2}}}} - \dfrac{{{{\cos }^2}\theta {{\cos }^2}\phi }}{{n_{\rm{o}}^{\rm{2}}}}} \right)}^{1/2}}}}} \right],\end{split}$
${\delta _{\rm{o}}}\left( {\theta,\phi } \right) = \frac{{2{\rm{\pi }}{n_{\rm{o}}}t}}{{\lambda {{\left[ {1 - {{{{\cos }^2}\theta }}/{{n_{\rm{o}}^{\rm{2}}}}} \right]}^{1/2}}}},$
式中: no, ne为晶体主折射率; λ为入射脉冲中心波长; t为晶体厚度; θ为入射光线和晶体表面的夹角, 记作倾斜角; ?为晶体光轴和入射面的夹角, 记作面内旋转角. 由于双折射分裂相对于光斑半径较小, 此处予以忽略. 倾斜双折射平板的厚度t、倾斜角θ和面内旋转角?如图1所示.
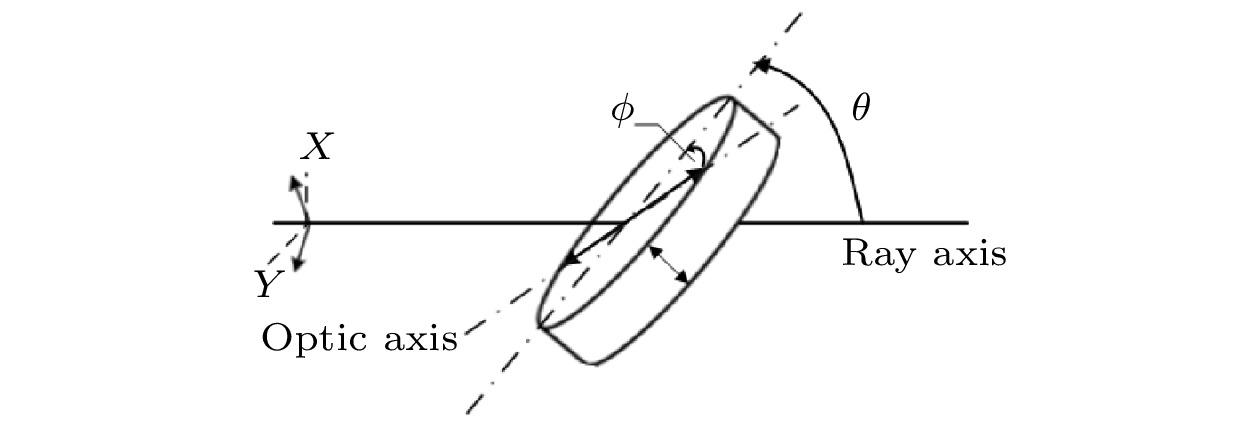图 1 倾斜双折射平板的厚度t、倾斜角θ和面内旋转角?示意图[14]
Figure1. Schematic diagram of the thickness t, tilt angle θ, and in-plane rotation angle ? of the tilted birefringent plate[14].

双折射晶体作为滤波元件, 要求入射光为TM (transverse magnetic mode, TM)偏振, 对于单位振幅入射光, 平板后表面的透射光为
$\left[ {\begin{array}{*{20}{c}} {{E_{{\rm{TE}}}}} \\ {{E_{{\rm{TM}}}}} \end{array}} \right] = {{M}}\left( {\theta,\phi } \right)\left[ {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right],$
由(1)式和(4)式可得透射光电场复振幅[14]为
$\begin{split} {E_{{\rm{TM}}}} =\;& {\left[ {n_{\rm{o}}^2 - {{\cos }^2}\phi {{\cos }^2}\theta } \right]^{ - 1}} \big[ \exp \left( {{\rm{i}}{\delta _{\rm{e}}}} \right)n_{\rm{o}}^{\rm{2}}{{\sin }^2}\phi \\ & + \exp \left( {{\rm{i}}{\delta _{\rm{o}}}} \right)\left( {n_{\rm{o}}^{\rm{2}} - {{\cos }^2}\theta } \right){{\cos }^2}\phi \big], \end{split} $
将(5)式代入δo, δe, 可得双折射平板透过率函数:
$\begin{split} & {I_{{\rm{TM}}}} = {E_{{\rm{TM}}}}E_{{\rm{TM}}}^{{*}}= \\ & 1 - {\sin ^2}\left( {2\phi } \right)\frac{{\left( {n_{\rm{o}}^4 - n_{\rm{o}}^{\rm{2}}{{\cos }^2}\theta } \right)}}{{{{\left( {n_{\rm{o}}^2 - {{\cos }^2}\phi {{\cos }^2}\theta } \right)}^2}}} \\ &\times {\sin ^2}\Bigg\{ \frac{{{\rm{\pi }}t}}{\lambda }\Bigg[ \frac{{{n_{\rm{e}}}\left( {1 + {{{{\cos }^2}\theta {{\cos }^2}\phi } / {n_{\rm{e}}^{\rm{2}} - {{{{\cos }^2}\theta {{\cos }^2}\phi } / {n_{\rm{o}}^2}}}}} \right)}}{{{{\left( {1 - {{{{\cos }^2}\theta {{\sin }^2}\phi } / {n_{\rm{e}}^{\rm{2}} - {{{{\cos }^2}\theta {{\cos }^2}\phi } / {n_{\rm{o}}^{\rm{2}}}}}}} \right)}^{1/2}}}}\\&- \frac{{n_{\rm{o}}^{\rm{2}}}}{{{{\left( {1 - {{{{\cos }^2}\theta } / {n_{\rm{o}}^{\rm{2}}}}} \right)}^{{1 / 2}}}}} \Bigg] \Bigg\},\\[-20pt] \end{split} $
双折射平板引入的光谱相位:
$\begin{split} & \varphi \left( \omega \right)= - {\rm{ta}}{{\rm{n}}^{ - 1}}\left[ {\frac{{{\rm{Im}} \left( {{E_{{\rm{TM}}}}} \right)}}{{{\rm{Re}} \left( {{E_{{\rm{TM}}}}} \right)}}} \right]= \\ & - {\rm{ta}}{{\rm{n}}^{ - 1}}\!\!\left[ {\frac{{n_{\rm{o}}^{\rm{2}}\sin {\delta _{\rm{e}}}{{\sin }^2}\phi \!+\! \left( {n_{\rm{o}}^{\rm{2}} - {{\cos }^2}\theta } \right)\sin {\delta _{\rm{o}}}{{\cos }^2}\phi }}{{n_{\rm{o}}^{\rm{2}}\cos {\delta _{\rm{e}}}{{\sin }^2}\phi \!+\! \left( {n_{\rm{o}}^{\rm{2}} - {{\cos }^2}\theta } \right)\cos {\delta _{\rm{o}}}{{\cos }^2}\phi }}} \right], \end{split} $
式中: ω为激光圆频率, $\omega = {{2{\text{π}}c}}/{\lambda }$; c为真空中光速. 结合(2)式和(3)式可以看出, 厚度t通过影响e光、o光的相位延迟量δe, δo来影响光谱总相位. 此外, (7)式仅特定情况下(θ = 90°, ? = 0°或90°)具有解析表达式, 因此本文使用数值模拟的形式分析了参数t, θ和?对光谱相位的影响.
将(7)式光谱相位在中心频率ω0处泰勒展开为
$\begin{split} \;& \varphi ( \omega )={\varphi _0} + \varphi ' ( \omega - {\omega _0} )+\frac{{\rm{1}}}{{\rm{2}}}\varphi ''{( {\omega - {\omega _0}} )^2}\\&~~+\frac{{\rm{1}}}{{\rm{6}}}\varphi '''{( {\omega - {\omega _0}} )^3} \!+\! \frac{{\rm{1}}}{{{\rm{24}}}}\varphi ''''{({\omega - {\omega _0}} )^{\rm{4}}} \!+\! \cdots ,\end{split} $
式中, ${\varphi _0}$为绝对相位, $\varphi '$为群速度延迟(group velocity delay, GVD), $\varphi ''$为群延迟色散(group delay dispersion, GDD), $\varphi '''$和$\varphi ''''$分别为三阶色散(third-order dispersion, TOD)和四阶色散(fourth-order fispersion, FOD). 考虑到目前的AOPDF仅能补偿到四阶, 与之相对照, 本文的分析中也只考虑到四阶色散.
2
2.1.光谱整形的强度和相位调制分析
-->

2.1.光谱整形的强度和相位调制分析

双折射晶体通过在放大介质增益中心波长处增加损耗来抑制增益窄化效应, 即双折射晶体透过率函数在放大介质增益线型的中心波长处透过率低, 在中心波长两侧, 增益相对较小处透过率高, 以此来补偿放大过程中的增益窄化.
从(6)式可以看出, 透过率函数除了与晶体厚度t、倾斜角θ、面内旋转角?有关外, 还与晶体主折射no和ne有关, 因此, 本文对BBO、铌酸锂(LiNbO3)和石英(quartz) 3种不同双折射晶体进行了对比. 三者的双折射率如图2(a)所示, 双折射率由大到小依次为BBO、铌酸锂、石英. 在实现如图2(b)的强度调制时, BBO、铌酸锂、石英的厚度t依次为1.0, 1.5, 13.5 mm. 由此可见, 当强度调制相同时, 晶体双折射率越高, 所需厚度越小.
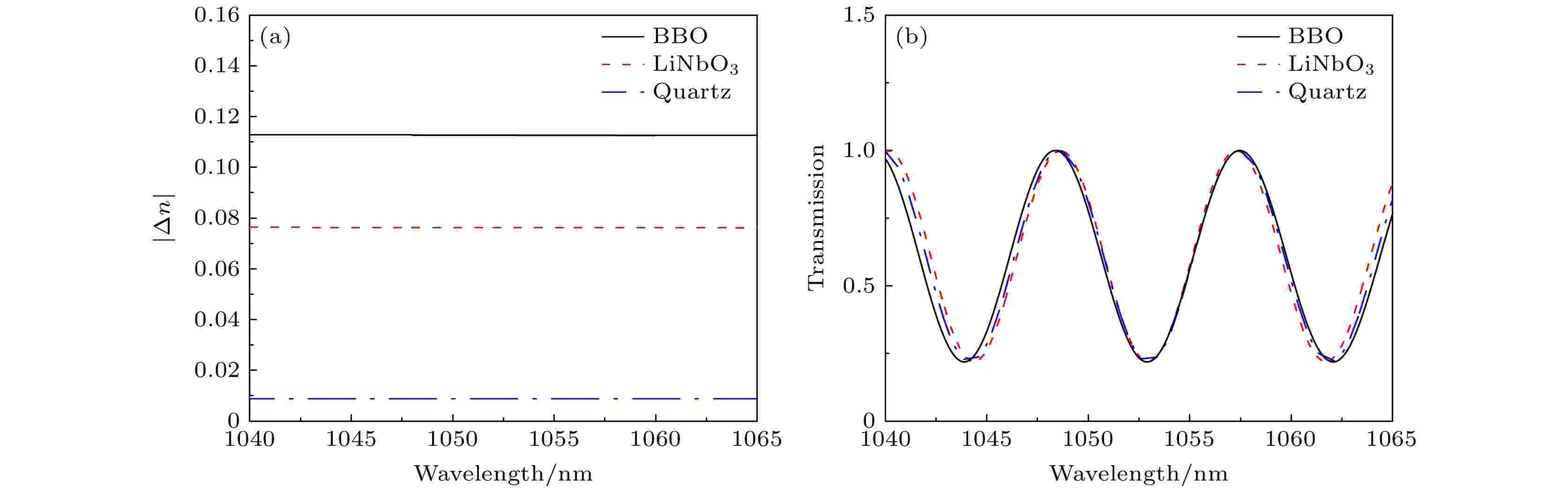图 2 BBO、铌酸锂(LiNbO3)和石英(quartz) 3种晶体的对比图　(a) 3种晶体的双折射率曲线; (b) 3种晶体实现相同强度调制的透过率曲线
Figure2. Comparison graph of three crystals of BBO, LiNbO3, and quartz: (a) The birefringence curves of three crystals; (b) the transmittance curves of the three kinds of crystals achieve the same intensity modulation.

针对1053 nm激光脉冲, 本文选用了双折射率大于石英的铌酸锂作为分析和实验材料, 相对BBO晶体, 铌酸锂易大口径生长且不易潮解. 本文数值模拟了晶体透过率函数随厚度t、倾斜角θ、面内旋转角?的变化情况, 并同时分析了各参数对晶体引入的光谱相位的影响.
透过率函数和晶体引入的光谱总相位随厚度t变化的曲线如图3(a)所示, 可见, 晶体厚度对透过率函数的调制中心位置及调制带宽均影响明显, 但对调制深度无明显影响. 同时, 随着t的增大, 晶体引入的光谱总相位变大. 为进一步分析总相位中各阶相位的变化规律, 运用(8)式进一步计算了GVD, GDD, TOD, FOD随t变化的曲线. 如图3(b)所示, GVD随厚度在104 fs量级变化, 其余各阶色散随厚度t高频率振荡, 且振荡幅值随厚度t增大. 在厚度为1.5 mm附近时, GDD, TOD, FOD分别在 ± 105 fs2, ± 108 fs3, ± 1011 fs4区间内振荡.
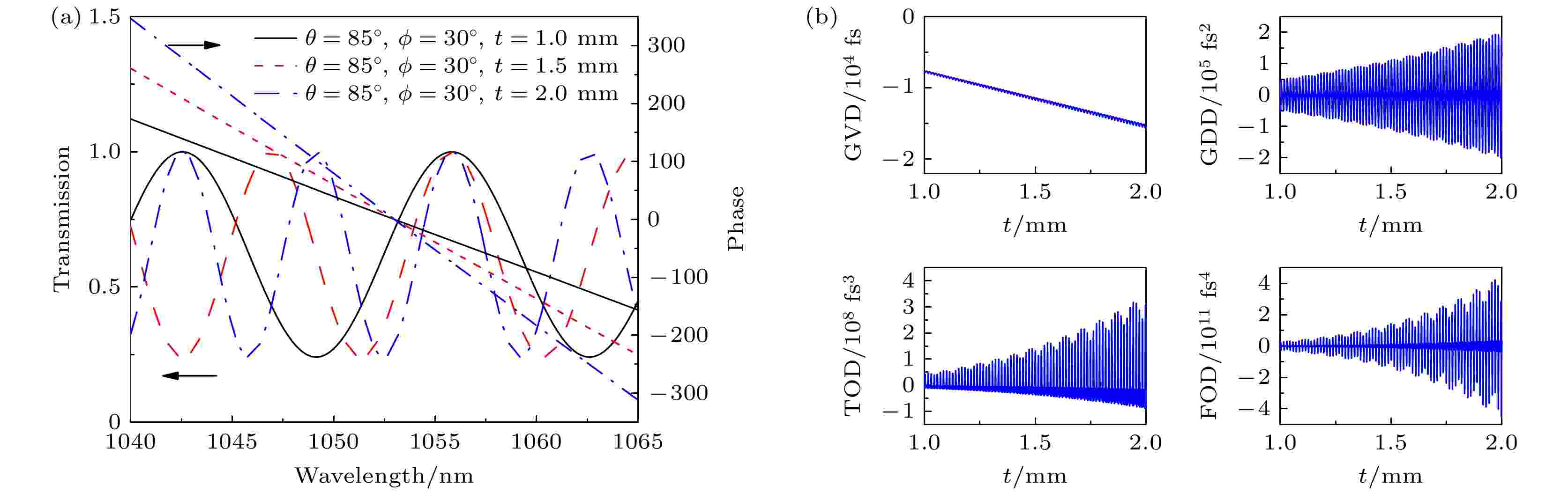图 3 当θ = 85°, ? = 30°, t = 1.0, 1.5, 2.0 mm时, 透过率函数、晶体引入的光谱总相位及各阶色散的变化曲线　(a) t = 1.0, 1.5, 2.0 mm时, 透过率函数、光谱总相位随波长的变化曲线; (b) GVD, GDD, TOD, FOD随厚度t的变化
Figure3. The curve of transmittance function, total phase of the spectrum, and each order dispersion introduced by the crystal with θ = 85°, ? = 30°, t = 1.0, 1.5, 2.0 mm: (a) The transmittance function and total phase of spectrum changes with wavelength; (b) GVD, GDD, TOD, FOD changes with thickness t.

类似地, 倾斜角θ对透过率函数和晶体引入光谱总相位的影响如图4(a)所示, 可见, 透过率函数的衰减中心位置随θ变化明显, 但调制深度及带宽无明显变化. 此外, 晶体引入的光谱总相位随倾斜角θ变化不明显, 这主要是由于GVD的影响. 为了进一步研究θ对高阶相位的影响, 对光谱总相位进行泰勒展开, 得到高阶色散随θ变化情况, 如图4(b)所示, 各级色散随θ周期振荡, GDD, TOD, FOD的振荡范围分别为 ± 105, ± 107, ± 1011 fs4.
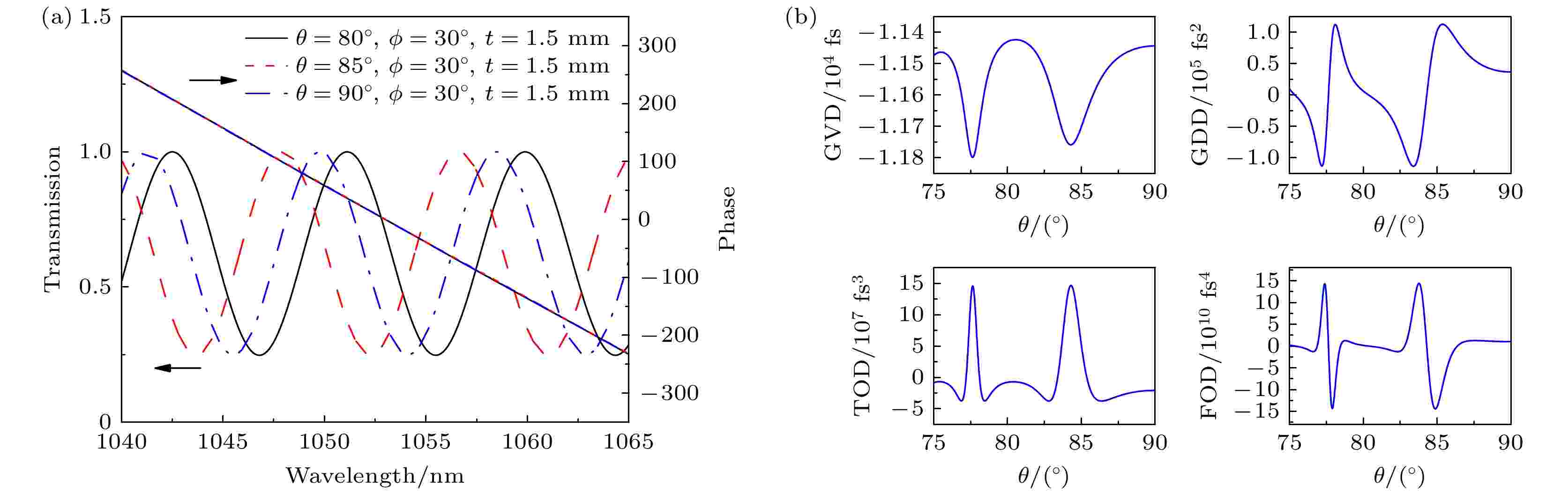图 4 当? = 30°, t = 1.5 mm, θ = 80°, 85°, 90°时, 透过率函数、晶体引入的光谱总相位及各阶色散的变化曲线　(a) 透过率函数、光谱总相位随波长的变化曲线; (b) GVD, GDD, TOD, FOD随厚度θ的变化
Figure4. The curve of transmittance function, total phase of the spectrum and each order dispersion introduced by the crystal with ? = 30°, t = 1.5 mm, θ = 80°, 85°, 90°: (a) The transmittance function and total phase of spectrum changes with wavelength; (b) GVD, GDD, TOD, FOD changes with thickness θ.

同样地, 透过率函数与晶体引入的光谱总相位随参数?的变化曲线如图5(a)所示, 可以看出, 随着?的变化透过率函数的调制深度发生明显变化, 衰减中心、调制带宽变化不明显, 由?取不同值时引入光谱总相位的对比可以看出, 光谱总相位随?变化不明显, 这同样是由于GVD的影响. 如图5(b)所示, 各阶色散量随?的变化, 起伏较为平缓, 如在?从25°变化到35°的过程中, FOD变化了3 × 1011 fs4.
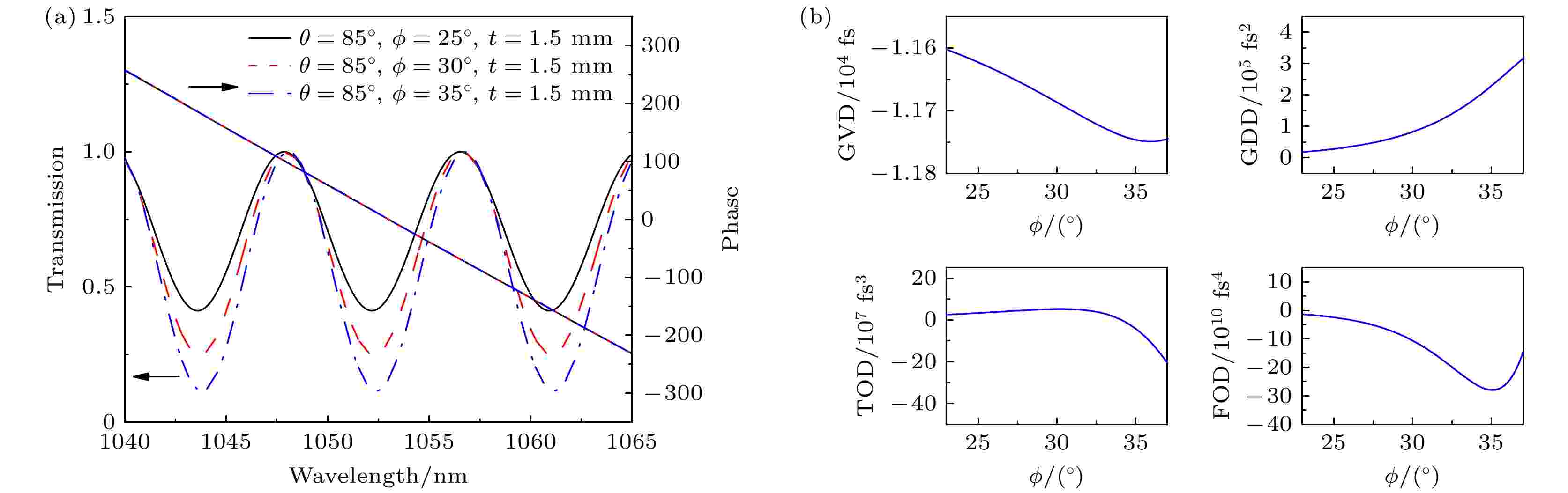图 5 当θ = 85°, t = 1.5 mm, ? = 25°, 30°, 35°时, 透过率函数、晶体引入的光谱总相位及各阶色散的变化曲线　(a) 透过率函数、光谱总相位随波长的变化曲线; (b) GVD, GDD, TOD, FOD随厚度?的变化
Figure5. The curve of transmittance function, total phase of the spectrum, and each order dispersion introduced by the crystal with θ = 85°, t = 1.5 mm, ? = 25°, 30°, 35°: (a) The transmittance function and total phase of spectrum changes with wavelength; (b) GVD, GDD, TOD, FOD changes with thickness ?.

综上所述, 透过率函数的调制深度受面内旋转角?影响, 衰减中心的位置由倾斜角θ控制, 调制带宽由厚度t决定. 引入的光谱总相位随晶体厚度变化显著, 且厚度越大引入的总相位越大, 倾斜角θ、面内旋转角?对光谱总相位影响不明显. 此外, 高阶色散均可由厚度t、倾斜角θ、面内旋转角?进行控制, 其中对厚度t的变化最敏感.
2
2.2.相位调制对时域脉冲的影响分析
-->

2.2.相位调制对时域脉冲的影响分析

由上述分析可以看出, 在激光放大链路中插入双折射晶体, 对光谱强度进行整形的同时, 还会产生附加相位调制. 随着各阶相位的引入, 对光束的脉宽、信噪比等均可能产生影响. 本文对光谱整形过程中双折射晶体引入的光谱相位对时域脉冲的影响进行了模拟分析.
以理想高斯信号为例, 在频域加入双折射晶体引入的各阶光谱相位:
${E_{{\rm{out}}}}\left( \omega \right) = E\left( \omega \right)\exp \left[ {{\rm{i}}{\varphi _j}\left( \omega \right)} \right],$
之后将高斯信号变换到时域:
${E_{{\rm{out}}}}\left( t \right) = \frac{1}{{\sqrt {2{\rm{\pi }}} }}\int_{ - \infty }^{ + \infty } {E\left( \omega \right)} \exp \left[ {{\rm{i}}\varphi \left( \omega \right)} \right]\exp \left( {{\rm{i}}\omega t} \right){\rm{d}}\omega ,$
考虑到一阶相位产生的延时, 以及二阶相位对脉宽的调制在光束延迟和压缩调节中可以补偿, 而更高阶相位影响较小, 本文主要对三、四阶相位进行了分析.
根据2.1节中各阶色散随晶体各参数的变化情况, 在晶体厚度为1.5 mm附近调节晶体各参数, 控制晶体引入的四阶色散分别取正最大1.4 × 1011 fs4、负最大–1.4 × 1011 fs4及0 fs4, 3种情况下, 晶体引入的三、四阶相位如图6所示.
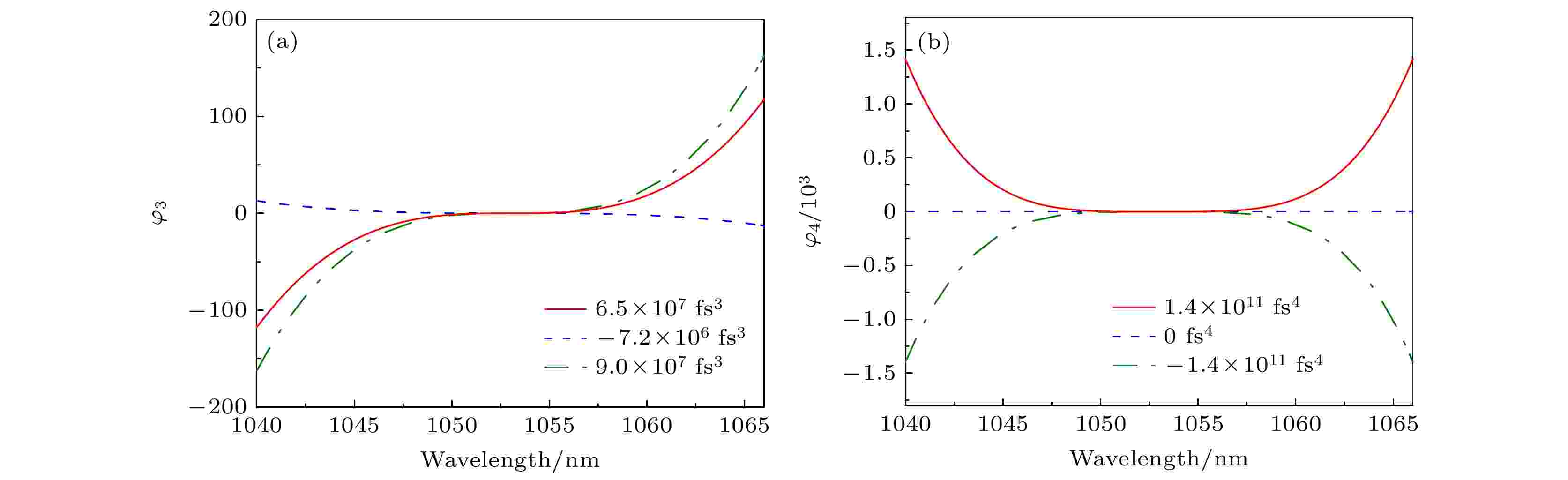图 6 双折射晶体引入的三、四阶相位　(a) 三阶相位; (b) 四阶相位
Figure6. Third and fourth order phase introduced by birefringent crystal: (a) Third order phase; (b) fourth order phase.

运用(9)式分别将图6中的三阶、四阶相位之和加入到中心波长为1053 nm、脉宽为230 fs、光谱宽度为6.5 nm (FWHM)的高斯信号中, 对时域脉冲的影响结果如图7所示.
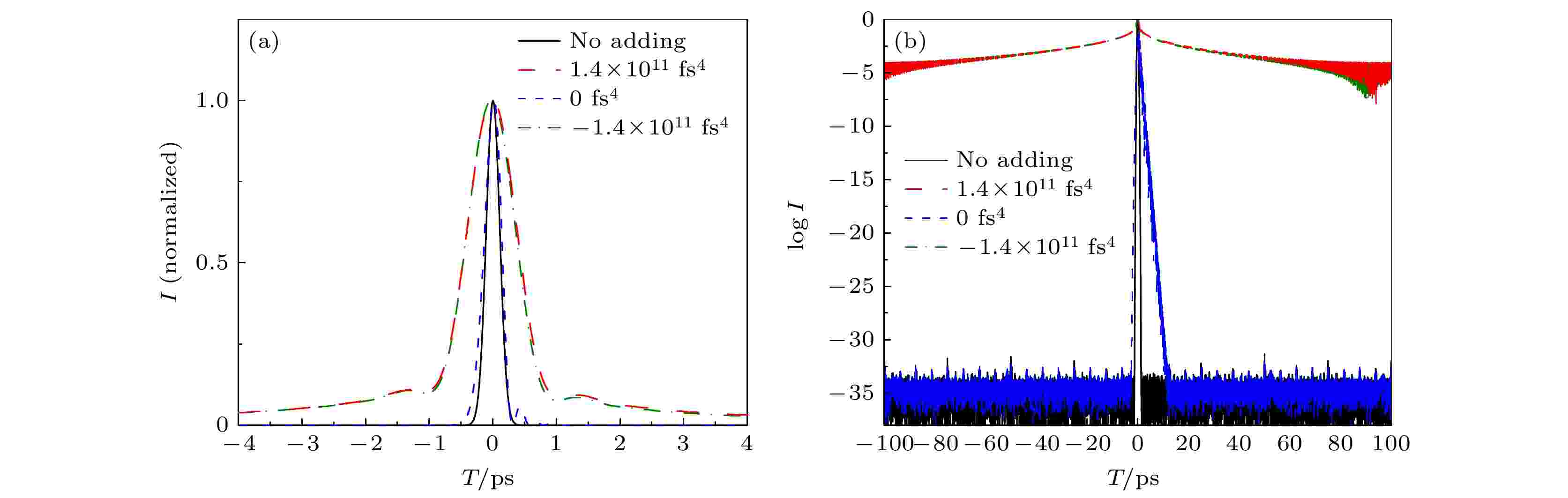图 7 在高斯信号中加入三、四阶相位后的时域脉冲图　(a) 线性坐标时域图; (b)对数坐标时域图
Figure7. Time-domain pulse diagram of third and fourth order phase added to Gaussian signal: (a) Linear coordinate time domain diagram; (b) logarithmic coordinate time domain diagram.

可以看出, 当四阶色散取正最大值和负最大值时, 对脉冲有明显的调制作用, 并使脉冲信噪比下降到10–5量级; 当四阶色散取零时, 三阶色散的影响得以显现, 使信噪比成不对称性下降; 此外, 四阶色散正最大与负最大对脉冲信噪比的影响几乎相同.
在神光Ⅱ高能拍瓦激光系统中, 由于钕玻璃放大过程中的B积分累积, 将系统信噪比限制在10–9量级; 展宽器、压缩器引起的光谱剪切, 将信噪比限制在10–11量级[23]; 展宽器、压缩器光栅带来的散射噪声和OPCPA的参量荧光会将数十皮秒外的信噪比限制在10–8量级. 此外, 展宽器和压缩器的剩余三、四阶色散量分别在107 fs3, 109 fs4量级, 其他材料引入的各阶色散在105量级以下[24], 由上述模拟计算得到, 1.5 mm厚的铌酸锂晶体, 引入的三、四阶色散量极值分别在108 fs3, 1011 fs4量级, 由此可以看出, 当双折射晶体处于高阶色散量极值状态时, 将成为影响系统脉冲信噪比的限制因素. 因此, 在整形过程中, 需要通过调节参数来控制晶体引入的高阶色散, 以减小双折射晶体对系统信噪比的影响.
3.实验与数据
依据理论分析, 设计了光谱整形模块, 并对神光Ⅱ高能拍瓦激光系统中钕玻璃宽带放大引起的增益窄化进行了补偿. 神光Ⅱ高能拍瓦激光系统装置框图如图8(a)所示, 振荡器输出的230 fs, 6.5 nm (FWHM)种子光经展宽器展宽为3.2 ns, 由OPCPA放大后, 脉冲能量为50 mJ, 光谱宽度为10 nm (FWHM), 后通过由2个Φ40 mm、2个Φ70 mm棒状放大器, 以及2个Φ100 mm、3个Φ200 mm和4个Φ320 mm片状放大器组成的钕玻璃放大系统, 脉冲能量被放大到1700 J, 之后通过可变形镜对像差和畸变修正后送入压缩器压缩到1 ps, 最后经过离轴抛面镜聚焦, 得到能量1 kJ, 50%能量集中在直径25 μm内[23]. 如图8(a)所示, 本文设计的光谱整形模块放置在OPCPA后, 钕玻璃放大系统前的链路中, 对钕玻璃宽带放大引起的增益窄化效应进行预补偿.
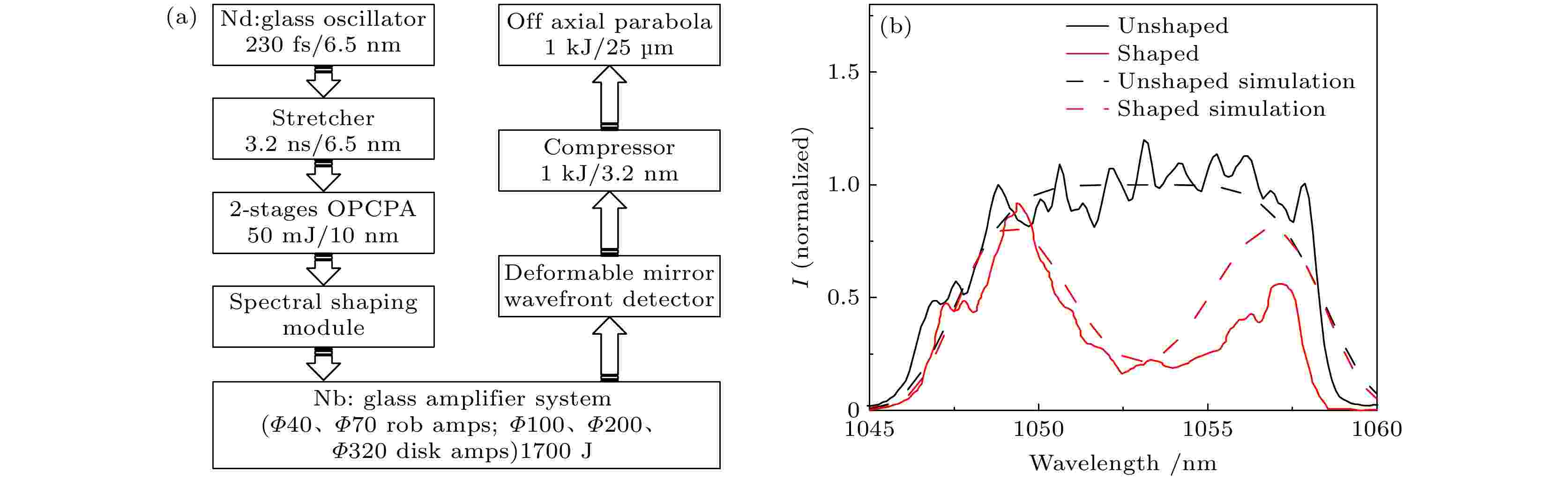图 8 皮秒拍瓦激光系统装置框图及注入钕玻璃放大系统前的预补偿光谱图　(a) 神光Ⅱ高能拍瓦激光系统装置框图[23]; (b) 强度调制前后注入钕玻璃放大系统前的预补偿光谱实验和模拟图
Figure8. Block diagram of picosecond petawatt laser system and pre-compensation spectrum before injection of Nb:glass amplifier system: (a) Block diagram of ShenguangⅡhigh-energy petawatt laser system[23]; (b) pre-compensation spectrum experiment and simulation diagram before and after intensity modulation before injection of Nb:glass amplifier system.

如图9(a)中的光谱整形模块, 由偏振片P1, P2及铌酸锂晶体组成, 其中偏振片P1, P2透过偏振均为TM偏振. 根据强度调制的理论分析, 设置铌酸锂晶体参数为t = 1.5 mm, θ = 86°, ? = 31°, 开展了中心波长为1053 nm、调制带宽10 nm、调制深度80%的光谱整形实验. 脉冲由OPCPA输出后, 经光谱整形模块得到的预补偿光谱如图8(b)所示, 其中黑色实线是未经整形的实验测量值, 黑色虚线是对应的模拟值, 红色实线是整形后的实验测量值, 红色虚线为模拟值, 与补偿前相比, 在中心波长处形成深度80%的调制, 且实验与模拟结果拟合良好.
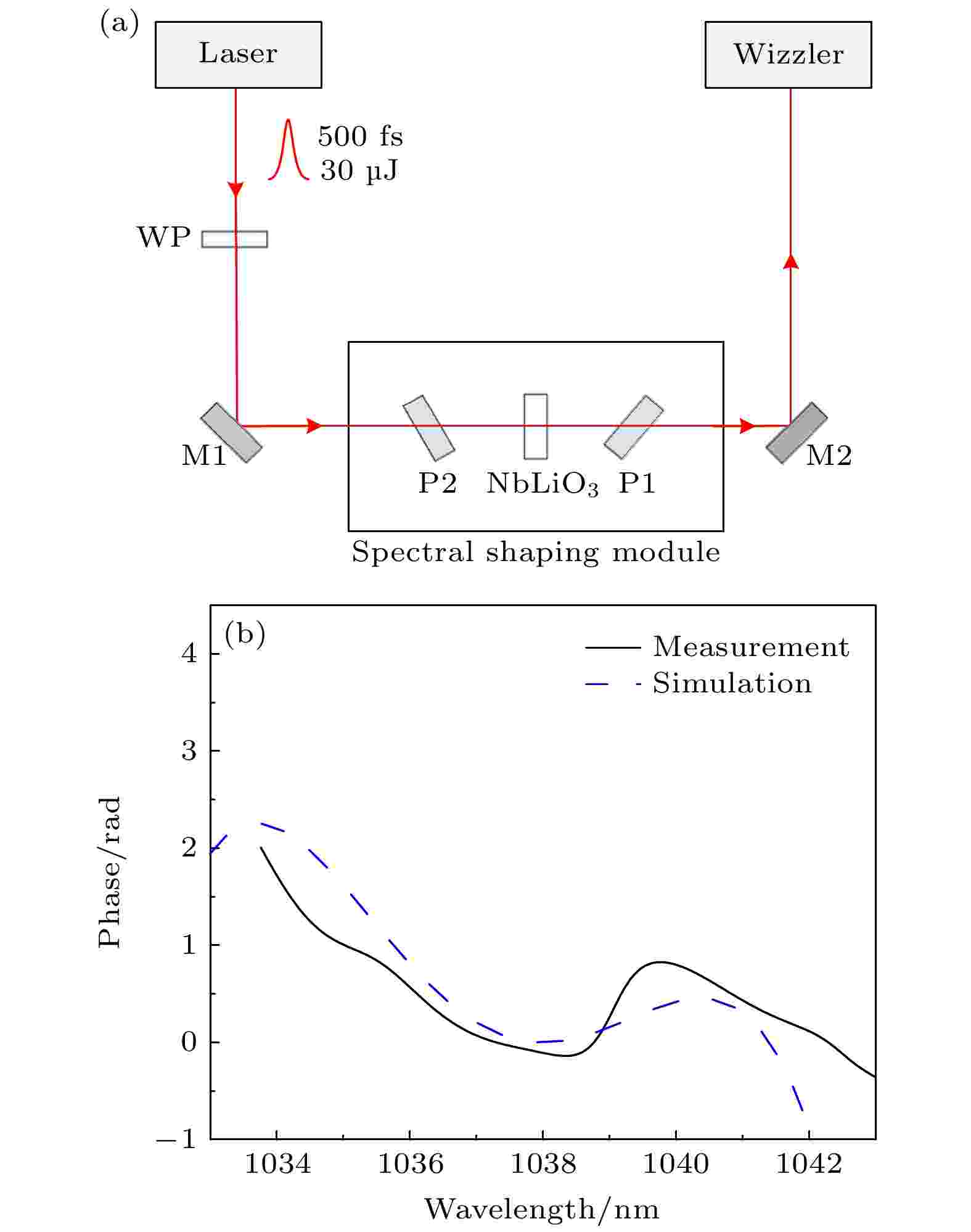图 9 相位测量实验光路图及相位测量结果　(a) 相位测量实验光路图; (b)晶体引入相位的实验测量与模拟图
Figure9. Beam path diagram of phase measurement experiment and phase measurement results: (a) Beam path diagram of phase measurement experiment; (b) experimental measurement and simulation diagram of the phase introduced by the crystal.

同时为进一步研究整形过程中晶体引入的光谱相位, 本文设计实验使用Wizzler对光谱相位进行了测量. 光路如图9(a)所示, 激光脉冲由500 fs, 30 μJ, 1038 nm激光器输出后, 经过波片WP (wave plate, WP)、反射镜M1进入光谱整形模块, 后经反射镜M2进入Wizzler进行光谱相位测量, 其中波片WP用于控制进入Wizzler的脉冲能量. 本文分别对不放入晶体及晶体处于上述强度整形状态时的各阶光谱相位进行测量, 两种状态所测数值做差, 进而得到晶体自身引入的各阶光谱相位, 其中光谱相位测量值如图9(b)实线所示. 实验中晶体实际厚度为1.5018 mm, θ = 86°, ? = 31°. 为了更好地分析实验测量相位, 拟合中保留至五阶色散, 模拟结果如图9(b)所示, 可以看出, 模拟值与实验测量值变化趋势相同, 远离中心波长的偏差主要是由于相位拟合过程中忽略了高阶项引起的. 该实验验证了本文中对双折射晶体引入的相位及各阶色散计算方法的准确性.
针对神光Ⅱ高能拍瓦激光系统, 光谱整形模块插入前后经钕玻璃放大系统输出的光谱如图10(a)所示, 其中黑色实线是整形前的输出光谱图, 红色虚线是整形后的输出光谱图, 通过两者对比可以看出, 整形后光谱展宽2倍, 该实验在国内首次实现了1700 J, 6 nm (FWHM)激光输出. 图9(b)为输出光谱所能支持的傅里叶变换极限脉冲比较图, 可见, 补偿增益窄化后时域脉冲傅里叶变换极限由800 fs (FWHM)减小到400 fs, 这将使聚焦功率密度增加1倍, 在技术上解决压缩光栅的能量受限问题之后, 将对神光Ⅱ高能拍瓦激光系统的性能提升具有重要意义.
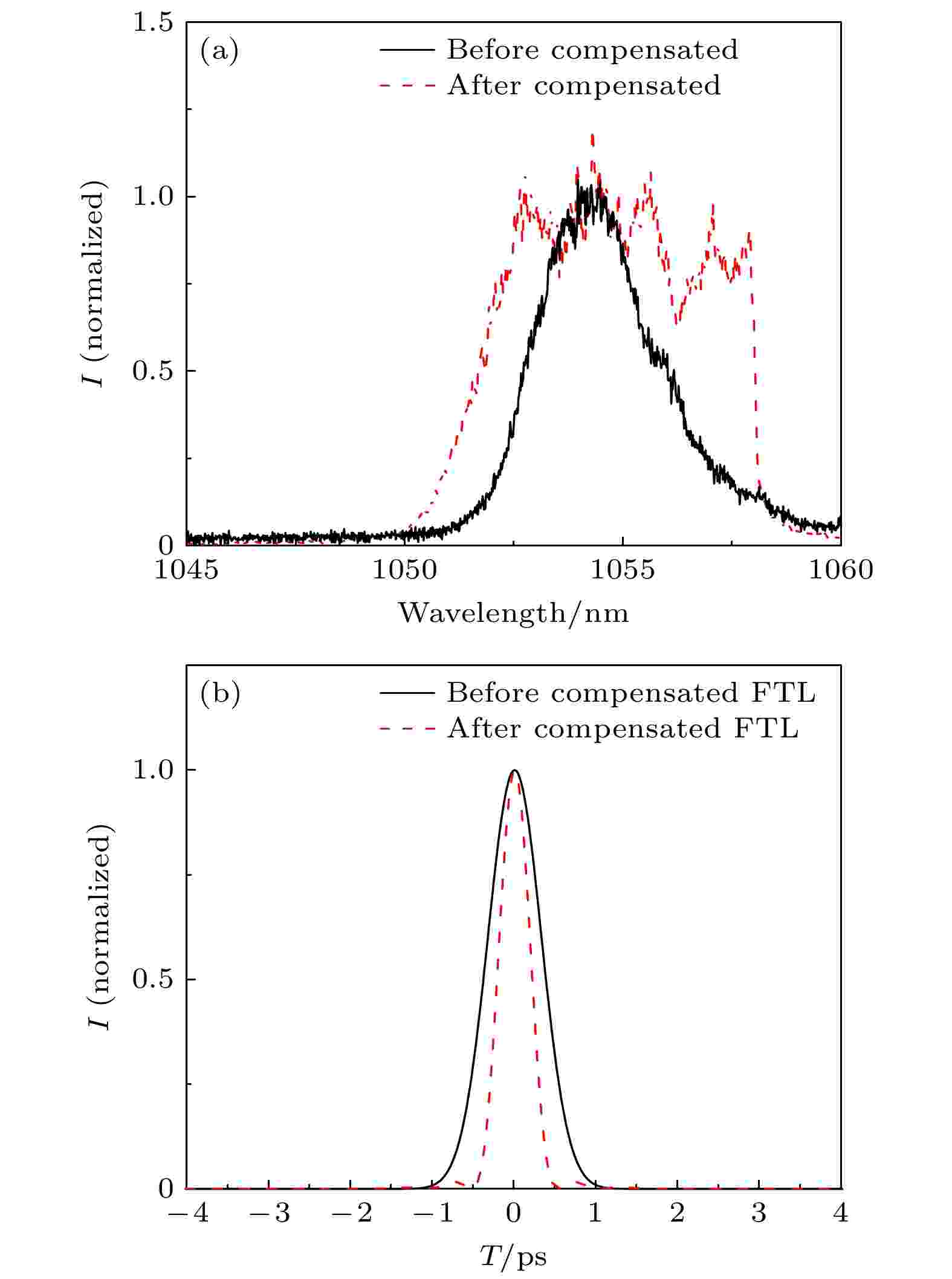图 10 补偿增益窄化前后的输出光谱图与傅里叶变换极限脉冲比较图　(a) 补偿增益窄化与未补偿增益窄化的输出光谱实验图; (b) 补偿增益窄化与未补偿增益窄化的傅里叶变换极限脉冲
Figure10. Comparison of output spectrum and Fourier transform limit pulse before and after compensation gain narrowing: (a) Experimental graphs of output spectra of compensated gain narrowing and uncompensated gain narrowing; (b) the Fourier transform limit pulse with compensated gain narrowing and uncompensated gain narrowing.

4.结　论
提出了一种基于铌酸锂双折射晶体的高能量光谱整形方法, 解决了钕玻璃放大过程中光谱窄化的问题. 首先, 对比了BBO、铌酸锂、石英3种双折射晶体, 确定了选用铌酸锂作为整形晶体; 通过控制晶体厚度t、倾斜角θ、面内旋转角?, 实现了对光谱强度调制的调制带宽、中心波长和调制深度的控制; 首次分析了整形过程中晶体引入的光谱相位及各阶色散, 数值模拟了各阶色散随晶体厚度t、倾斜角θ、面内旋转角?的变化曲线. 其次, 在理论分析的基础上, 搭建光谱整形模块, 实验测量了晶体引入的相位, 验证了理论分析的准确性. 最后, 利用神光Ⅱ高能拍瓦激光系统, 使用上述光谱整形模块, 有效补偿了钕玻璃的增益窄化效应, 在国内首次实现了1700 J, 6 nm (FWHM)的高能宽带激光输出.
本文成功补偿了皮秒拍瓦激光系统中钕玻璃宽带放大引起的增益窄化效应, 实现了高能宽带激光输出, 并首次从相位角度对双折射晶体光谱整形进行了分析, 可以为高能激光的同步、相干组束、高信噪比输出等对光谱相位要求较高的研究领域提供指导, 对国内基于钕玻璃放大的高能拍瓦激光系统的工程研制具有重要意义. 针对双折射晶体引入的高阶色散量对脉冲信噪比影响的情况, 后续将开展实验进行研究.
相关话题/光谱 激光 系统 实验 测量
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 强度调制532 nm激光水下测距
    摘要:激光水下探测在水下目标搜寻、资源勘探等领域具有重要的应用,而散射是激光水下探测面临的主要挑战.载波调制激光雷达具有抗散射、抗干扰的优点,本文利用自行研制的532nm强度调制激光源,在3m长的水箱中搭建激光水下探测系统.532nm激光源最大输出功率为2.56W,强度调制范围为10.0MHz—2. ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 频域反射法光纤延时精密测量
    摘要:本文提出了一种应用于光纤延时系统中实现光纤延时精密测量的新方法,用以提高光纤延时测量的精度和准确性.该方法以1064nm激光调制信号作为光源,通过测量回波信号的幅值和相位信息得到被测通道的频率响应,采用快速傅里叶逆变换得到被测目标的延时信息,实现光纤延时测量.本文通过理论分析和延时测量实验对频 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 超弹性球体入水过程空泡演化及球体变形实验
    摘要:超弹性材料是工程实际中常用的材料,具有很强的非线性力学性能.将超弹性材料应用于入水问题是一个新的跨学科研究方向.与传统的刚性球体入水现象不同,超弹性球体入水后极易发生变形.为了探究该大变形的入水流固耦合问题,本文采用高速摄像方法,对超弹性球体垂直入水问题开展实验研究.基于实验结果,对比分析了球 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 自旋轨道耦合Su-Schrieffer-Heeger原子链系统的电子输运特性
    摘要:在Su-Schrieffer-Heeger(SSH)原子链中,电子在胞内和胞间的跳跃依赖于其自旋时,即SSH原子链存在自旋轨道耦合作用时,存在不同缠绕数的非平庸拓扑边缘态.如何探测自旋轨道耦合SSH原子链不同缠绕数的边缘态是一个重要问题.本文在紧束缚近似下研究了自旋轨道耦合SSH原子链的非平庸 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 原子系综中光学腔增强的Duan-Lukin-Cirac-Zoller写过程激发实验
    摘要:原子系综中的Duan-Lukin-Cirac-Zoller(DLCZ)过程是产生光与原子(量子界面)量子关联和纠缠的重要手段.当一束写光与原子发生作用时,将会产生斯托克斯(Stokes)光子的自发拉曼散射,并同时产生一个自旋波(spin-wave)存储在原子系综中,上述过程即为DLCZ量子记忆 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于径向剪切干涉仪的三维位移测量技术
    摘要:本文提出一种基于双圆光栅径向剪切干涉仪的三维位移测量方法,其测量原理是径向剪切干涉仪所形成的莫尔条纹不仅由二维平面内位移决定,轴向位移会在+1和–1级莫尔条纹之间产生一个特定的相移.首先,基于标量衍射理论对双圆光栅径向剪切干涉仪的+1和–1级莫尔条纹强度分布进行推导,建立了三维位移量与莫尔条纹 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 80.5 MeV/u碳离子诱发铜靶的放射性剩余产物测量
    摘要:高能重带电粒子能直接穿透靶原子核外电子层,与原子核发生直接碰撞,发生散裂反应,产生一系列具有放射性的剩余产物核.重带电粒子诱发靶材放射性剩余核与辐射防护和人员安全有着密切联系,当前,大部分剩余核产额主要依靠蒙特卡罗粒子输运程序进行模拟计算,其准确程度亟需通过实验测量进行准确评估.本文利用能量为 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 温稠密物质中不同价态离子分布对X-射线弹性散射光谱计算的影响
    摘要:在天体物理和惯性约束聚变研究中涉及到的温稠密物质通常包含多种元素的混合,并且每种元素还被电离成多种离子价态,不同价态离子结构及其丰度将直接影响温稠密物质的诊断及其物理性质.同时,从电子结构计算出发来研究宏观物理性质时,还需要考虑温度、密度效应对离子结构的影响.本文从不同价态离子的电子结构计算出 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 利用钟跃迁谱线测量超稳光学参考腔的零温漂点
    摘要:在87Sr光晶格钟实验系统中,通过将自由运转的698nm激光频率锁定在由超低膨胀系数的玻璃材料构成的超稳光学参考腔上,从而获得短期频率稳定性较好的超稳窄线宽激光.超稳光学参考腔的腔长稳定性决定了最终激光频率的稳定度.为了降低腔长对温度的敏感性,使激光频率具有更好的稳定度和更小的频率漂移,利用锶 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 门控下InGaAs/InP单光子探测器用于符合测量的时域滤波特性研究
    摘要:基于砷化镓/磷化铟雪崩光电二极管(InGaAs/InPAPD)的半导体单光子探测器因工作在通信波段,且具有体积小、成本低、操作方便等优势,在实用化量子通信技术中发挥了重要作用.为尽可能避免暗计数和后脉冲对单光子探测的影响,InGaAs/InP单光子探测器广泛采用门控技术来快速触发和淬灭雪崩效应 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.