摘要:激光水下探测在水下目标搜寻、资源勘探等领域具有重要的应用, 而散射是激光水下探测面临的主要挑战. 载波调制激光雷达具有抗散射、抗干扰的优点, 本文利用自行研制的532 nm强度调制激光源, 在3 m长的水箱中搭建激光水下探测系统. 532 nm激光源最大输出功率为2.56 W, 强度调制范围为10.0 MHz—2.1 GHz, 光束发散角约0.5 mrad. 通过在水箱中添加氢氧化镁(Mg(OH)₂)粉末, 测量了不同浑浊度下水的衰减系数. 采用相位测距的方法, 目标反射光的调制信号为探测信号, 对激光源进行调制的电信号作为参考信号, 利用相关运算获得激光的延时时间, 进而可以获得水下目标的距离. 最大调制频率为500 MHz时, 实现了距离为4.3个衰减长度目标的探测, 测距误差约12 cm. 探测距离越远, 测距误差越大, 调制频率越高, 测距精度越高.
关键词: 激光/
强度调制/
水下测距/
相关计算

English Abstract

全文HTML

--> --> -->

水下激光雷达具有空间分辨率高、速度快、效率高和体积小等优点, 可以应用于舰载、机载, 在海洋资源勘探、近海地形测绘、水下目标搜寻等领域具有突出的优势^[1-4]. 水对激光的吸收和散射是水下激光雷达面临的重要挑战^[5]. 吸收会引起探测信号的衰减, 限制探测距离; 散射除了引起信号衰减外, 还会导致强烈的噪声, 甚至淹没目标信号. 蓝绿光波段是水体的透光窗口^[6], 选择蓝绿光作为工作波长可以有效地减少水对探测光的吸收. 载波调制技术是抑制水体后向散射的一种重要方法^[7-9]. 载波调制激光雷达是将激光雷达和微波雷达相结合, 以射频强度调制激光为探测波, 具有较高的空间分辨率和抗湍流干扰能力. 载波调制激光雷达适用于近距离高精度的探测, 采用调制信号作为探测波, 通过提高调制信号的带宽可以获得更高的距离分辨率. 将发射波光强进行高频调制, 目标反射的光子可以保持其强度调制信息, 而在发射源与目标之间由不同距离处水体散射的光子之间会产生干涉相消, 导致高频调制信号消失^[10].
2011年, 电子科技大学张洪敏等^[11]对载波调制激光雷达水下目标探测系统进行了仿真, 仿真表明载波调制激光雷达技术对深海目标探测结果有明显改善, 海水参数和调制参数对探测性能有较大影响. 2014年, Illig等^[12]采用直接调制的方式, 获得了50 mW的442 nm调制激光, 调制频率50—550 MHz. 采用该激光源搭建水下目标探测系统, 采用光电倍增管作为探测器, 利用频域反射法获得了10.2个衰减长度的精确测量, 然后利用盲信号分离技术, 将探测距离提高到了14.7个衰减长度. 2016年, 太原理工大学张明涛等^[13]采用混沌调制激光雷达进行水下测距, 在1.5 m长的水箱中实现了最大1.36 m的探测距离, 平均测距误差为2.3 cm. 2020年, 北京空间机电研究所的沈振民等对混沌脉冲激光雷达和相干双频脉冲激光雷达进行了理论分析, 分别在清水和浊水中测量了水箱中51 cm位置处的反射镜距离, 测距结果分别为54.5和59.0 cm^[14]. 强度调制绿光激光是水下载波调制激光雷达的光源, 目前用于激光水下探测的啁啾强度调制光源多为几十毫瓦量级, 功率较低. 由于水对激光的衰减, 激光水下探测回波信号十分微弱, 给信号的采集和处理带来了难度.
本文采用马赫曾德尔电光调制器对单频1064 nm激光进行强度调制, 经过光纤功率放大器后倍频, 获得了2.56 W的强度调制绿光, 调制范围10 MHz—2.1 GHz. 调制频率为100 MHz时, 调制深度为0.91, 调制频率为300 MHz时频率误差约为1.2 Hz@5 min. 利用设计的激光器作为探测源, 高速硅探测器作为接收器, 搭建水下目标探测系统. 通过在3 m长的水箱中添加氢氧化镁(Mg(OH)₂)粉末来改变水体的衰减系数, 采用PIN探测器实现了距离为4.3个衰减长度目标的探测, 测距误差约12 cm. 由激光雷达方程知, 传输距离的平方与回波信号的功率成反比, PIN探测器和光电倍增管的噪声等效功率分别约为20 pW/Hz^1/2和0.01 pW/Hz^1/2, 原则上采用光电倍增管作为探测器探测距离可以提高45倍.

2

-->

2.1.相位测距原理

相位法测距是将调制信号加载到激光上, 通过测量发射激光的调制信号和回波激光的调制信号之间的相位差来获得测量目标的距离信息^[15].
发射激光的调制信号为

${I_1} = {A_1}\cos ({\rm{2\pi }}f{t_1} + {\varphi _1}), $

式中, ${I_1}$表示发射激光的调制信号强度; ${A_1}$表示发射激光的调制信号幅值; f为调制信号频率; ${t_1}$, ${\varphi _1}$分别表示发射激光调制信号的初始时间和相位.
接收到的回波激光的调制信号为

${I_2} = {A_2}\cos ({\rm{2\pi }}f{t_2} + {\varphi _2}), $

式中, ${I_2}$表示回波激光的调制信号强度; ${A_2}$表示回波激光的调制信号幅值; ${t_2}$, ${\varphi _2}$分别表示回波激光调制信号的时间和相位.
接收端和发射端之间的相位偏移为

$\Delta \varphi = {\rm{2\pi }}f({t_2} - {t_1}) + {\varphi _2} - {\varphi _1}.$

激光接收端和发射端之间的时间差为

$\Delta t = {t_2} - {t_1} + \frac{{{\varphi _2} - {\varphi _1}}}{{{\rm{2\pi }}f}}.$

目标的距离为

$D \!=\! \frac{1}{2}v\Delta t \!=\! \frac{v}{{2f}}\Big(N + \frac{{{\varphi _2} - {\varphi _1}}}{{{\rm{2\pi }}}}\Big) = \frac{\lambda }{{{\rm{2}}n}}\Big(N + \frac{{{\varphi _2} - {\varphi _1}}}{{{\rm{2\pi }}}}\Big), $

式中, v为发射激光在水中的传播速度; N表示回波信号和发射信号之间相差的完整的波长数. 回波信号和发射信号之间的相位差只能计算出来单个周期的相位差. $ \lambda /(2 n)$为相位测距法的测尺长度; $\lambda $为调制信号波长; n为发射激光在水中的折射率. 当测量距离大于测尺长度的时候, 测距结果需要加上完整的波长个数N.
对于相位法测距, 最大测量距离即为测尺长度, 因此采用单一测尺测距, 测量长度会有很大的局限性. 如果需要增大测量距离, 只能降低调制频率, 为了提高测量精度, 需要增大调制频率. 单个调制频率相位测距, 测量长度和测量精度无法同时满足, 因此通常采用多测尺法进行测量^[16-18]. 分散的多测尺法是根据测量距离选择一个较低的调制频率, 保证测尺的长度, 然后采用较高的调制频率提高测量精度. 根据低频调制可以确定高频调制的相位延时的完整波长数N. 随着测量频率的提高, 测尺长度减小, 测量精度提高, 因此可以采用一组低频到高频的调制频率作为探测信号, 既可以测量较远的距离, 也可以保证测量精度. 集中的测尺法是采用两个集中的高频调制进行探测, 频率之间的差值作为测尺, 较高的调制频率保证测量精度, 也可以被称为双频测距^[19].
2 -->

2.2.相关运算原理

载波调制激光雷达技术是利用目标及水体散射对调制信号不同的响应将信号与散射噪声分离, 提高信噪比. 强度调制激光在水中传输时, 由目标直接反射的光子可以保持其强度调制信息, 而散射光子由于传输路径复杂, 不同距离的散射光相互叠加导致高频调制信号的消失. 通过测量回波信号的相位延时可以得到目标的距离, 而相位测量的精度直接决定测距精度. 相关运算法是利用相关函数进行数据分析的方法. 发射激光和接收激光的调制频率相同而具有相关性, 从而可以利用相关运算实现相位差的测量. 由于噪声信号与接收信号频率不同不具有相关性, 相关运算可以消除系统的随机噪声而提高信噪比^[20].
发射信号和接收信号的相关函数可以定义为^[21]

${R_{xy}}(\tau ) = \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int_{ - T/2}^{T/2} {x(t)y(t - \tau )} {\rm{d}}t, $

式中, $x(t)$表示发射信号; $y(t - \tau )$表示回波信号; ${R_{xy}}(\tau )$为互相关函数. 由于发射信号和回波信号的频率相同, 只有一个固定的相位差, 则${R_{xy}}(\tau )$函数会有一个峰值出现. 利用互相关函数检测信号通常在信号已知的条件下进行, 将已知的波形和采集的波形在固定长度内进行相关运算, 当$\tau = {\tau _0}$时, $x(t)$和$y(t)$中的信号部分重合, ${R_{xy}}(\tau )$有最大值, 此时${\tau _0}$即为两个信号之间的时间差, 进而可以得到探测距离:

$D = \frac{\lambda }{{{ {2n}}}}N + \frac{{v{\tau _0}}}{2}.$

实验系统如图1所示, 532 nm强度调制激光经过准直后入射到3 m长的水箱中, 准直光束直径约1 mm, 发散角约0.5 mrad. 水中目标为反射率约0.8的玻璃板, 反射信号被直径1 in (1 in=2.54 cm)、焦距50 mm的透镜接收后聚焦到高速PIN探测器上. 探测器接收的回波信号和射频源发射的参考信号输入到示波器中.
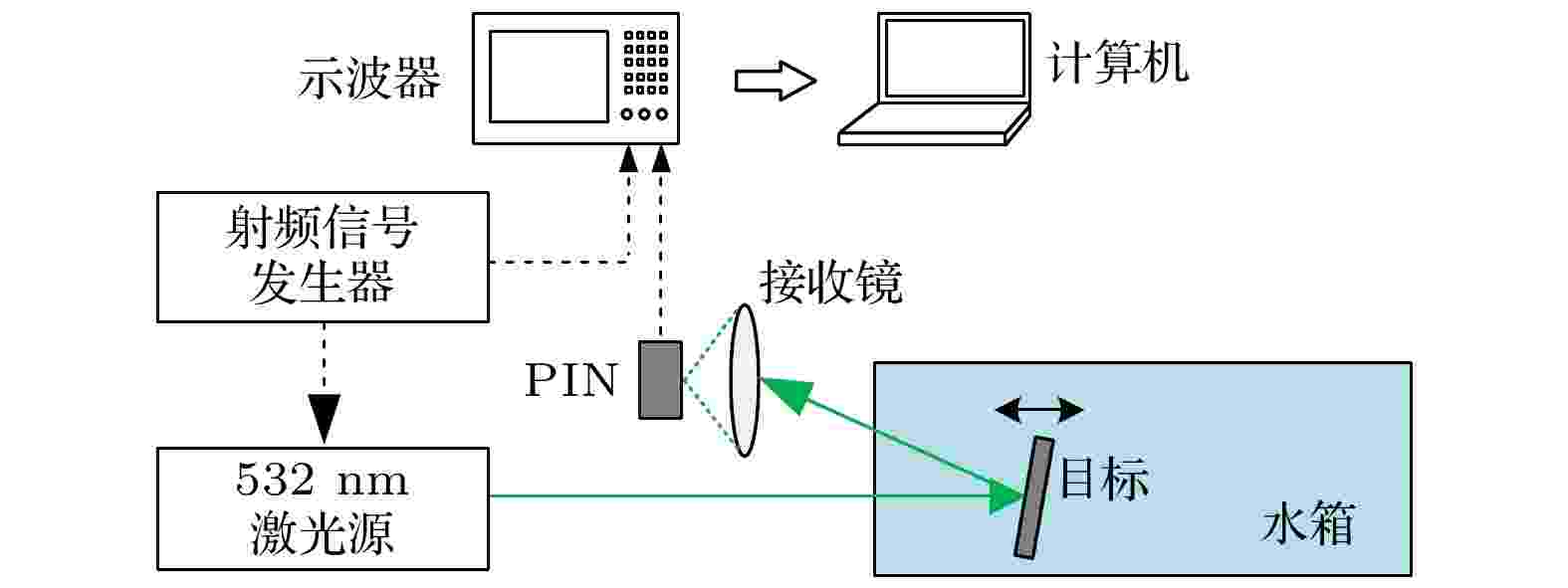图 1 激光水下探测系统
Figure1. Experimental setup of underwater ranging.

将回波信号和参考信号做相关运算, 可以得到回波信号的延时时间, 进而得到目标的距离. 发射系统和接收系统是分离的, 间距约为6 cm, 而且视场重叠较小, 因此接收系统接收到的回波信号中后向散射信号较少, 目标信号的信噪比较高, 容易实现浑浊水体中目标的探测.

2

-->

4.1.水的衰减系数测量

光在水中的衰减遵循比尔-朗伯定律, 将水箱中的目标放置在x₁和x₂处, 则回波的强度分别为

${I_1} = {I_0}{\alpha ^2}\beta \exp ( - c \cdot 2{x_1}), $

${I_2} = {I_0}{\alpha ^2}\beta \exp ( - c \cdot 2{x_2}), $

式中, ${I_0}$为入射光的光强; $\alpha $为水箱入射窗口的透过率; $\beta $为目标的反射率; 则水的衰减系数c为

$c = \frac{{\ln ({{{I_1}} / {{I_2})}}}}{{2({x_2} - {x_1})}}.$

因此, 确定x₁和x₂之间的距离和两个位置处的回波信号功率即可得到水的衰减系数.
Mg(OH)₂粉末难溶于水, 通过在水中添加Mg(OH)₂粉末可以改变水的衰减系数, 从而可以在不同的水体中测量目标的距离. 把水箱入射窗口的内表面作为距离零点, 不同水的衰减系数测量结果如表1所示. 由于实验室的自来水使用频率不高, 在水箱中呈黄绿色, 样本1为实验室的自来水静置24 h以上的水体. 采用源恒通(WGZ-400AS)浊度计, 量程0—400 NTU, 精度0.1 NTU, 静置前测量三次的平均浊度为11.3 NTU, 静置后测量三次的平均浊度为11.2 NTU, 水体比较稳定. 在样本1水体中分别测量0, 0.5, 1.0和1.5 m处回波激光的功率, 以0 m处为基准计算不同距离水的衰减系数分别为0.98, 0.99和1.00 m^–1, 平均衰减系数为0.99 m^–1.

样本	目标距 离/m	回波信号 强度/mW	衰减系 数/m–1	平均衰减 系数/m–1
1	0	160	—	0.99
	0.50	60	0.98
	1.00	22	0.99
	1.50	8	1.00
2	0	261	—	1.72
	0.50	47	1.71
	0.80	17	1.71
	1.00	8	1.74
3	0	216	—	2.97
	0.20	68	2.89
	0.30	35	3.03
	0.50	11	2.98
4	0	230	—	4.03
	0.20	47	3.97
	0.25	30	4.07
	0.40	9	4.05

表1不同水体的衰减系数
Table1.Attenuation coefficient of different water.

在样本1中添加Mg(OH)₂粉末, 打开水箱中的循环泵, 使Mg(OH)₂粉末在水中充分扩散, 再次测量不同距离处水的衰减系数. 当添加Mg(OH)₂颗粒较多, 水的衰减系数较大时, 目标距离较远的回波信号功率较低, 测量误差较大, 因此在较近的距离内测量回波激光的功率. 由于水箱中循环水泵的作用, 水中悬浮的Mg(OH)₂颗粒充分均匀, 认为水箱中各处的衰减系数一致. 4个水体样本的平均衰减系数分别为0.99, 1.72, 2.97和4.03 m^–1, 单位衰减长度对应的距离分别为1.01, 0.58, 0.34和0.25 m.
2 -->

4.2.相位法水下目标距离测量

采用示波器采集调制信号和回波信号的波形, 同时对两个通道进行数据采集. 把水箱入射窗口的内表面作为距离零点, 水的衰减系数为0.99 m^–1, 激光的调制频率为50 MHz时, 回波信号和参考信号的波形如图2(a)所示, 将回波信号和参考信号做相关运算, 结果如图2(b)所示, 峰值对应时间为–0.48 ns. 把目标移动到水中0.5 m的位置, 回波信号和参考信号的波形如图2(c)所示, 将回波信号和参考信号做相关运算, 结果如图2(d)所示, 峰值对应时间为4.158 ns. 水的折射率为1.333@532 nm, 调制频率为50 MHz, 在水中的测尺长度为2.251 m. 0.5 m的距离在一个测尺之内, 则两个位置之间的延时时间为4.638 ns, 距离为0.522 m, 测距误差为2.2 cm. 目标距离的标定为固定在水箱上精度为1 mm卷尺的测量结果, 因此测量误差为激光测距和卷尺测距之间的差值.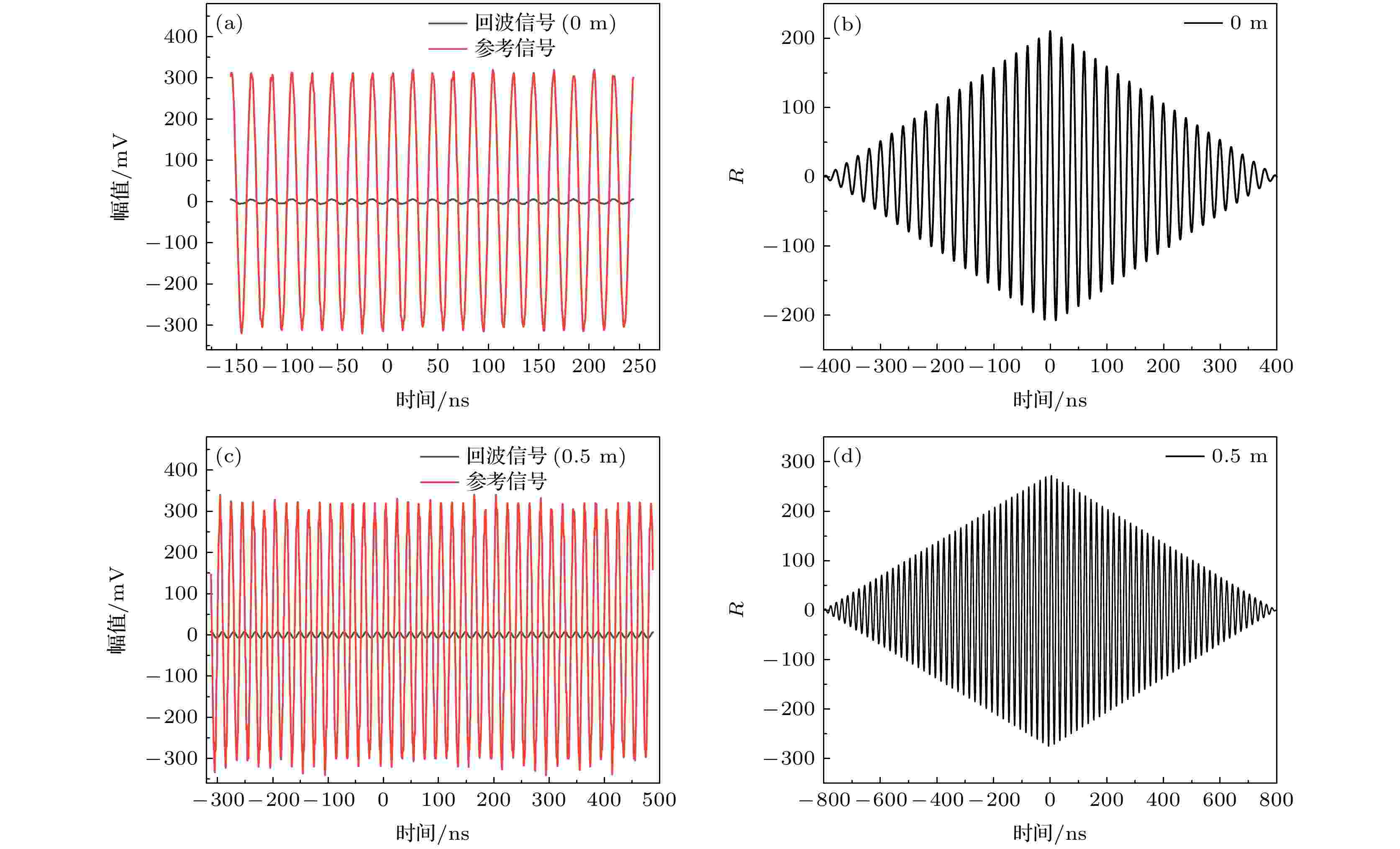
图 2 回波信号和参考信号的波形及相关运算结果　(a), (c) 0和0.5 m处的波形; (b), (d) 0和0.5 m处的相关结果
Figure2. Waveform of echo signal and reference signal, results of correlation calculation: (a), (c) Waveform at 0 and 0.5 m; (b), (d) results of correlation calculation at 0 and 0.5 m.

水的衰减系数为0.99 m^–1, 分别把目标放置在0.5, 1.0, 1.5, 2.0和2.5 m的位置, 采用相位法测距, 每个位置采集五组数据, 不同调制频率下的测距结果如图3所示. 调制频率分别为50, 100, 200, 300, 400和500 MHz, 在水中对应的测尺长度约为2.251, 1.125, 0.563, 0.375, 0.281和0.225 m. 调制频率为50 MHz的测尺基本可以覆盖水箱中的测量距离, 2.5 m位置处的测量结果需要补全一个测尺长度. 调制频率增大, 测尺减小, 测尺长度小于测量长度时可以根据调制频率为50 MHz的测距结果补全相应倍数的测尺长度. 图3(f)为不同距离不同调制频率的测距误差, 随着测量距离的增大, 测量误差增大, 最高达到了7.45 cm. 同一距离, 调制频率越高, 测距误差越小.
图 3 不同距离的测距结果及误差(c = 0.99 m^–1)　(a) 0.5 m; (b) 1.0 m; (c) 1.5 m; (d) 2.0 m; (e) 2.5 m; (f) 测距误差
Figure3. Ranging results and errors at different distances (c = 0.99 m^–1): (a) 0.5 m; (b) 1.0 m; (c) 1.5 m; (d) 2.0 m; (e) 2.5 m; (f) ranging error.

水的衰减系数为1.72 m^–1, 调制频率分别为50, 100, 200, 300, 400和500 MHz, 采用相位法测量不同位置的距离, 测距结果如图4(a)—(e)所示. 当测量距离较近时同一调制频率同一目标的多次测量结果一致性较好. 如图4(e)所示, 多次测量结果比较分散, 与图3(e)相比, 水的浑浊度提高, 测距结果波动增大; 与图4(a)—(d)相比, 测量距离增大, 测距结果波动增大. 图4(f)表明了不同距离不同调制频率的测距结果, 随着测量距离的增大, 测量误差也增大, 最高达到了约12 cm. 由于水的浑浊度增加, 测距误差整体增大. 目标距离为2.5 m时, 调制频率为500 MHz的测距误差明显小于低频调制时的测距误差, 调制频率越高, 测距精度越高.
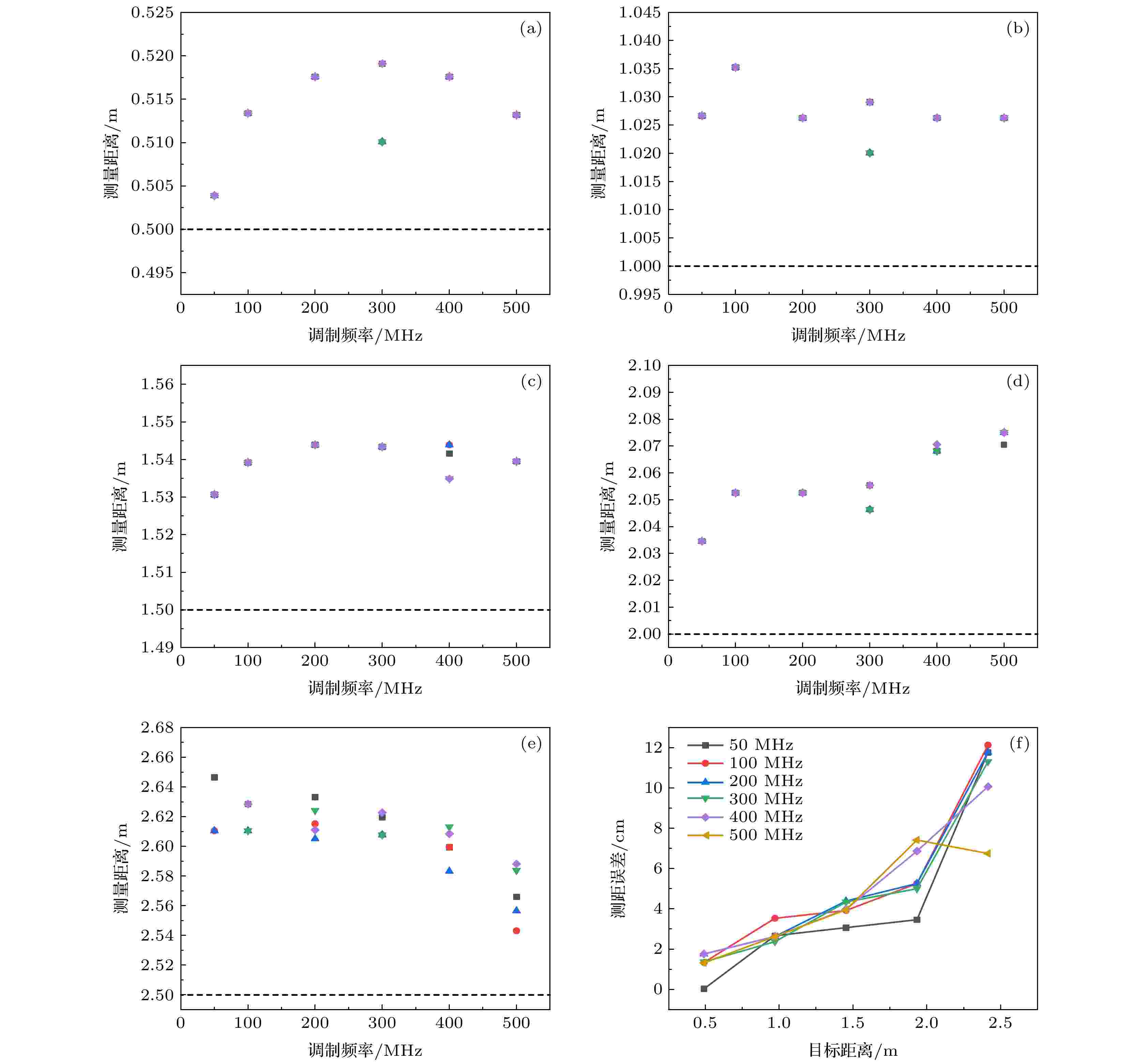图 4 不同距离的测距结果及误差 (c = 1.72 m^–1)　(a) 0.5 m; (b) 1.0 m; (c) 1.5 m; (d) 2.0 m; (e) 2.5 m; (f) 测距误差
Figure4. Ranging results and errors at different distances (c = 1.72 m^–1): (a) 0.5 m; (b) 1.0 m; (c) 1.5 m; (d) 2.0 m; (e) 2.5 m; (f) ranging error.

相位测距的整体测量结果如图5所示, 目标最大距离为4.3个衰减长度 (a.l.)时, 测距结果约为4.5个衰减长度. 随着测量距离的增加, 测距误差增大, 测量结果向远处偏移. 水的浑浊度增加, 探测距离增大, 探测系统接收到的噪声信号越多, 信噪比降低, 从而导致了测距误差增大. 通过在接收端加一个以调制频率为中心的窄带滤波器可以进一步分离散射信号, 提高信噪比. 探测源的调制频率为10.0 MHz—2.1 GHz, 因此通过继续提高探测激光的调制频率可以进一步提高测量精度, 实现近距离内高精度的测量.
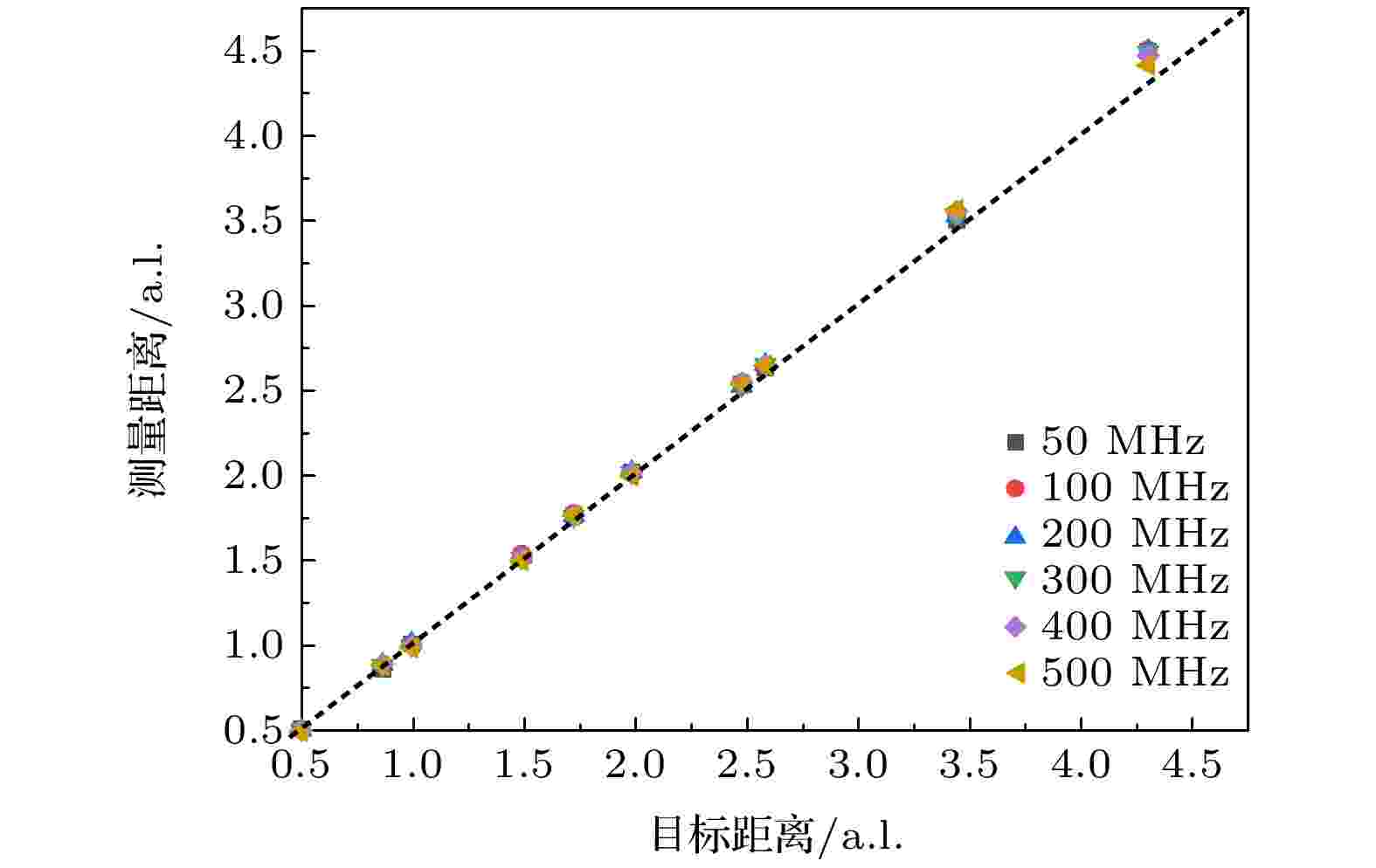图 5 相位法测距结果
Figure5. Ranging results based on phase.

载波调制激光雷达可以有效抑制散射和湍流的影响, 本文采用自行研制的532 nm强度调制激光源在3 m长的水箱中搭建激光水下探测系统, 测量了添加不同Mg(OH)₂水体的衰减系数. 采用相位测距的方法, 分别在50, 100, 200, 300, 400和500 MHz的调制频率对不同距离的目标测距. 利用相关运算获得相位延时时间, 实现了4.3个衰减长度目标的测量, 测距误差约12 cm. 探测距离越远, 误差越大, 调制频率越高, 测距精度越高. 水的衰减系数大, 目标的探测距离较远时, 回波信号的功率微弱, 会被淹没在噪声中. 采用PMT作为接收器, 可以实现微弱信号的探测, 提高测量距离. 采用高频的数据采集卡采集数据, 提高探测信号的调制频率, 可以进一步提高测量精度.