摘要: 针对现有的基于欠采样的频率和二维到达角的联合估计存在结构复杂问题, 本文提出了一种基于调制宽带转换器技术的L型延迟阵列接收结构. 利用延迟通道与未延迟通道采样值之间的相位差可直接估计载频, 进而计算二维到达角, 无需额外的参数配对操作, 避免了配对步骤引入的误差和复杂度的提升. 并结合所提L型延迟阵列结构的特点构造相关矩阵和三线性模型, 提出了两种参数估计算法, 一种基于旋转不变子空间算法, 计算量小, 适用于需要实时处理的场景; 另一种基于正则分解技术, 鲁棒性较好, 适用于信噪比较低的应用场景. 仿真实验表明该方法能较好地从欠奈奎斯特样本中估计目标的载频和二维到达角参数.
关键词: 压缩感知 /
阵列参数联合估计 /
二维到达角 /
阵列式调制宽带转换器 English Abstract Joint estimation of carrier frequency and two-dimensional arrival angle based on L-shaped delay array modulation wideband converter Jiang Si-Yi Fu Ning Qiao Li-Yan Peng Xi-Yuan School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin 150001, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 62071149, 61671177)Received Date: 11 August 2020Accepted Date: 30 December 2020Available Online: 13 April 2021Published Online: 20 April 2021Abstract: As the signal spectrum in modern information technology becomes wider and wider, multi-band signals are distributed in a frequency range of tens of GHz. It covers a very wide spectrum but each RF signal has a very narrow band, and the distribution location of the band (or carrier frequency) is completely unknown. For the receiver, the single-band signals transmitted together constitute a multi-band signal. The sampling rate required to jointly estimate the space domain and frequency domain parameters of these signals is getting higher and higher. Modulated wideband converter system is an analog information conversion system for multiband analog signals, which is based on compressed sensing theory and greatly reduces the sampling rate. First, we propose an L-shaped delay array structure based on modulated wideband converter, which can estimate carrier frequency and two-dimensional arrival angles with a small number of samples. Secondly, two parameter-estimating algorithms are proposed based on the proposed structure. One is based on the estimating of signal parameter via rotational invariance technique (ESPRIT), which requires a small number of computations and is suitable for real-time processing application scenarios; the other algorithm is based on CANDECOMP/PARAFAC (CP) technique, which has better robustness and is suitable for applications with low signal-to-noise ratio. The samples of the delay channels can be directly used to estimate the carrier frequencies, and then the two-dimensional arrival angles are calculated. No additional pairing issue is required between the parameters. Then we give the time complexity analysis and space complexity analysis of the two methods. It can be found that the computational complexity and space storage occupation of the method based on ESPRIT are lower than those of the CP decomposition method. Then the conditions for unique parameter estimation are given. Finally, simulation experiments show that the proposed methods can estimate the carrier frequencies and two-dimensional arrival angles from sub-Nyquist samples. It can be found that the estimation method based on CP decomposition is more robust than the method based on ESPRIT, but at the cost of increased complexity of the algorithm.Keywords: compressed sensing /joint estimation of array parameters /two-dimensional direction of arrival /array modulated wideband converter structure 全文HTML --> --> --> 1.引 言 阵列信号处理已被广泛应用于雷达[1 ] 、声纳[2 ,3 ] 和无线通信[4 ,5 ] 等领域, 通过按一定样式在空间中分布的传感器阵列接收空间电磁信号, 并进行一系列处理得到空时频各域的参数. 在实际应用中, 频率和二维到达角(two-dimensional direction of arrival, 2D-DOA)是对电磁波进行识别的重要特征, 对载频和2D-DOA的联合估计在阵列信号处理领域备受关注.[6 -9 ] 能够在少量样本的情况下准确地恢复稀疏信号, 该理论大大降低了采样率, 具有很高的应用价值. 目前已有不少****将CS理论应用到模拟信号的采样中[10 -15 ] . 其中, 由Mishali和Eldar[14 ,15 ] 提出的MWC系统是一种专门针对多频带模拟信号采样的模拟信息转换系统.[16 ] 利用互素稀疏阵列, 结合闭式中国余数定理实现了欠采样下频率和DOA的联合估计. 沈志博等[17 ] 提出一种CS奇异值分解算法, 但配对步骤较为繁琐. Liu等[18 ,19 ] 提出了一种基于多陪集结构的联合估计方法, 分别基于子空间分解和正则分解/平行因子分析(CANDECOMP/PARAFAC, CP)[20 ] 方法, 但接收阵列结构较为复杂. 接着, 他们又进行了扩展[21 ,22 ] , 利用稀疏阵列减少了所需的阵元个数, 但这种结构对ADC仍有比较高的要求. Stein等[23 ,24 ] 将MWC技术与阵列信号处理相结合, 提出了L型阵列MWC结构来接收信号, 并提出了一种基于旋转不变子空间(estimating signal parameter via rotational invariance techniques, ESPRIT)方法的联合载波DOA恢复算法. Cui等[25 ] 提出了一种基于均匀线性MWC阵列由两阶段估计和参数配对构成的估计方法, 算法复杂且精度有限. Chen等[26 ] 提出了一种基于多个MWC结构的DOA和载频联合估计方法, 鲁棒性较好, 但该结构所需的通道数较多, 硬件成本高. 然而在实际中电磁波存在于三维空间中, 使用2D-DOA来描述目标的方向更为准确, 但目前对基于欠采样的载频和2D-DOA联合估计研究较少. 陈玉龙等[27 ] 提出了一种基于L型阵列的2D-DOA估计的欠采样算法, 但所需的天线阵元个数较多. Esmaeil等[28 ] 提出了一种基于双L型阵列结构的网格CS估计方法, 但是参数估计精度受网格的大小限制. 他们还提出了一种贝叶斯压缩感知算法[28 ] , 方法不依赖网格但步骤复杂且计算量较大.2 节介绍了信号模型; 第3 节首先介绍了L型延迟阵列接收结构, 接着给出了接收信号模型; 第4 节首先对所提的两种方法的原理和步骤进行了详细的阐述. 接着给出了参数估计条件, 最后对复杂度进行了详细的分析. 第5 节给出了本文所提算法的验证结果以验证该算法的正确性和有效性.2.问题描述 考虑M 个远场目标发出的窄带信号${s_i}(t){{\rm{e}}^{{\rm{j}}2{\text{π}}{f_i}}}$ , 其中$i=1, 2, \cdots, M$ . 信号的频率范围为${\cal F}= $ $ [-{{{f_{{\rm{Nyq}}}}} / 2}, {{{f_{{\rm{Nyq}}}}} / 2}{\rm{]}}$ , 其中${f_{{\rm{Nyq}}}}$ 为奈奎斯特频率. ${s_i}(t)$ 为互不相关的基带信号, 带宽不超过B 且远小于调制载频${f_i}$ . 假设信源发出的信号以方位角${\theta _i} \in $ $ ( - {90^ \circ }, {90^ \circ })$ 和俯仰角${\varphi _i} \in ({0^ \circ }, {90^ \circ })$ 的入射方向被天线阵列接收, 为了避免空间模糊, 假设载频、方位角与俯仰角满足[24 ] :$\left\{ {{f_i}} \right\}_{i = 1}^M$ , 俯仰角$\left\{ {{\theta _i}} \right\}_{i = 1}^M$ 和方位角$\left\{ {{\varphi _i}} \right\}_{i = 1}^M$ 参数.3.L型延迟阵列与接收信号模型 23.1.L型延迟阵列结构 3.1.L型延迟阵列结构 提出图1 所示的L型延迟天线阵列结构, 利用延迟通道的采样值可以先估计载频, 进而计算2D-DOA参数, 避免了额外的参数配对操作. 该结构由两个分别沿x 轴和y 轴正方向均匀分布的N 个线性天线阵列$\left\{ {{x_1}, {x_2}, \cdots, {x_N}} \right\}$ 和$\{ {y_1}, {y_2}, \cdots, $ $ {y_N} \}$ 组成, 两个轴在原点共用同一个天线阵元. 相邻阵元之间的间距d 满足$d \leqslant {c / {{f_{{\rm{Nyq}}}}}}$ , 其中c 为光速.图 1 L型阵列MWC结构图Figure1. L shaped array MWC.x 轴的每个阵元后增加一个延迟通道, 在混频之前对接收信号进行固定延时$\tau $ , 如图2 所示.图 2 x 轴延迟通道结构图Figure2. x -axis delay channel.3.2.接收信号模型 -->3.2.接收信号模型 定义${x_n}(t)$ 和${y_n}(t)$ 分别为x 轴和y 轴的第n 个天线阵元接收的信号, ${x'_n}(t)$ 为${x_n}(t)$ 经过延迟$\tau $ 后的信号, 由于目标信号为窄带信号, 有${s_i}(t + \tau ) \approx $ $ {s_i}(t)$ [24 ] , 则接收信号可以表示为$ \tau _i^x = ({d / c})\cos {\theta _i}\cos {\varphi _i} $ , $ \tau _i^y = ({d / c})\sin {\theta _i}\cos {\varphi _i} $ , $\tau $ 为设置的已知延迟时间, 满足$\tau \leqslant {1 / {{f_{{\rm{Nyq}}}}}}$ . 从(2 )式可见各阵元接收的信号类似多频带信号模型, 其频谱示意图如图3 所示.图 3 接收信号频谱示意图Figure3. Spectrum of received signal.${T_p} = 1/{f_p}$ 的 ± 1伪随机序列$p(t)$ 相乘后, 再经过截止频率为${f_p}/2$ 的低通滤波器, 只留下${{\cal{F}}_p} = \left[ { - {f_p}/2, {f_p}/2} \right]$ 内的频谱. 滤波后的信号经过傅里叶变换可得:${\tilde S_i}(f) = \displaystyle\sum\limits_{l = - {L_0}}^{{L_0}} {{c_l}} {S_i}(f - {f_i} - l{f_p})$ , ${S_i}(f)$ 是${s_i}(t)$ 的傅里叶变换形式, ${c_l} = \dfrac{1}{{{T_p}}}\displaystyle\int\nolimits_0^{{T_p}} {p(t)} {{\rm{e}}^{{\rm{j}}2{\text{π}}l{f_p}t}}{\rm{d}}t$ 为伪随机序列$p(t)$ 的傅里叶级数系数, ${L_0} \!=\! \left\lceil {{{{f_{{\rm{Nyq}}}}} / ({2{f_p}}}}) \right\rceil$ 是可以保证${\cal{F}}$ 范围内的所有非零项被搬移到${{\cal{F}}_p}$ 内的最小正整数.${f_s} = {f_p}$ 的速率进行低速采样得到观测值, 将其傅里叶变换后写为矩阵形式可得:${{X}}(f)$ 为$N \times 1$ 的矩阵, 第n 个元素为${X_n}({{\rm{e}}^{{\rm{j}}2{\text{π}}f{T_s}}})$ . ${{W}}(f)$ 是$M \times 1$ 的矩阵, 第i 个元素为${W_i}({{\rm{e}}^{{\rm{j}}2{\text{π}}f{T_s}}}){\rm{ = DTFT\{ }}{{\rm{w}}_i}{\rm{[}}k{\rm{]\} }}$ , 其中${w_i}[k] = {\tilde s_i}(k{T_s})$ . 矩阵$ {A}_{x}=\left[{a}_{1}^{x} {a}_{2}^{x}\cdots {a}_{M}^{x}\right]$ 为阵列流型矩阵, 其中${{a}}_i^x = {[1, {{\rm{e}}^{ - {\rm{j}}2{\text{π}}{f_i}\tau _i^x}}, \cdots, {{\rm{e}}^{ - {\rm{j}}2{\text{π}}{f_i}(n - 1)\tau _i^x}}]^{\rm{T}}}$ .x 轴通道的观测值为${{x}}[k] = [{x_1}[k], \cdots, $ $ {x_N}[k]]^{\rm{T}}$ , 对(4 )式取离散时间傅里叶逆变换, 在时域有:y 轴和x 轴延迟通道的采样 值${{y}}[k] = {[{y_1}[k],\; {y_{2}}[k] \cdots, \;{y_N}[k]]^{\rm{T}}}$ 和${{x'}}[k] \;=\; [{x'_1}[k], $ $ {x'_{2}}[k], \cdots, {x'_N}[k]]^{\rm{T}}$ 有:$ {{{A}}}_{y}=\left[{{{a}}}_{1}^{y}\;\;\;{{{a}}}_{2}^{y}\cdots {{{a}}}_{M}^{y}\right]$ , ${{a}}_i^y = [1,\; {{\rm{e}}^{ - {\rm{j}}2{\text{π}}{f_i}\tau _i^y}},\; \cdots, $ $ {{\rm{e}}^{ - {\rm{j}}2{\text{π}}{f_i}(n - 1)\tau _i^y}}]^{\rm{T}}$ , ${{\varPsi }} \;= \;{\rm{diag}}\;\{ {{\rm{e}}^{ - {\rm{j}}2{\text{π}}{f_1}\tau }},\; {{\rm{e}}^{ - {\rm{j}}2{\text{π}}{f_{2}}\tau }},\; \cdots, $ $ {{\rm{e}}^{ - {\rm{j}}2{\text{π}}{f_M}\tau }}\}$ .${{x}}[k]$ , ${{y}}[k]$ 和${{x'}}[k]$ 中估计信号的载频$\left\{ {{f_i}} \right\}_{i = 1}^M$ , 俯仰角$\left\{ {{\theta _i}} \right\}_{i = 1}^M$ 和方位角$\left\{ {{\varphi _i}} \right\}_{i = 1}^M$ 参数.4.载频与二维DOA联合估计方法 本节给出了基于图1 接收结构所提的两种载频与二维DOA联合估计方法, 一种方法基于ESPRIT技术, 另一种方法基于CP分解. 对两种方法的原理和步骤进行了详细的阐述. 接着给出了参数估计条件, 最后对复杂度进行了详细的分析.4.1.基于ESPRIT的估计方法 4.1.基于ESPRIT的估计方法 首先给出基于ESPRIT的参数联合估计方法, 将采样值分为前N –1项和后N –1项组成的两个子矩阵, 并构造如下的相关矩阵:${{{A}}_{{x_{\rm{1}}}}}$ 和${{A}}_{{y_1}}^{}$ 分别为${{{A}}_x}$ 和${{{A}}_y}$ 的前N –1行,${{{\varPhi }}_x} = {\rm{diag}}\{ {{\rm{e}}^{ - {\rm{j}}2{\text{π}}{f_1}\tau _1^x}}, {{\rm{e}}^{ - {\rm{j}}2{\text{π}}{f_{2}}\tau _1^x}}, \cdots, {{\rm{e}}^{ - {\rm{j}}2{\text{π}}{f_M}\tau _M^x}}\}$ ,${{{\varPhi }}_y} = {\rm{diag}}\{ {{\rm{e}}^{ - {\rm{j}}2{\text{π}}{f_1}\tau _1^y}}, {{\rm{e}}^{ - {\rm{j}}2{\text{π}}{f_{2}}\tau _1^y}}, \cdots, {{\rm{e}}^{ - {\rm{j}}2{\text{π}}{f_M}\tau _M^y}}\}$ .9 )式的矩阵${{R}}$ ,${{R}}$ 进行奇异值分解, 得到前$M$ 个非零奇异值对应的左奇异向量${{U}} = \left[ {{{{U}}_1};{{{U}}_2};{{{U}}_3};{{{U}}_4};{{{U}}_5};{{{U}}_6}} \right]$ . ${{U}}$ 是一个$6(N - 1) \times M$ 的矩阵, ${{{U}}_i}$ 为$(N - 1) \times M$ 的矩阵, $i=1, 2, \cdots, 6$ . 通过推导可得矩阵${{{U}}_i}$ 和对角阵${{{\varPhi }}_x}$ , ${{{\varPhi }}_y}$ 和${{\varPsi }}$ 之间的关系, 定义矩阵${{{V}}_1}$ , ${{{V}}_2}$ 和${{{V}}_3}$ ,$({{{V}}_1} + {{{V}}_2} + {{{V}}_3})$ 进行特征值分解, 这样可以保证矩阵${{{\varPhi }}_x}$ , ${{{\varPhi }}_y}$ 和${{\varPsi }}$ 中元素顺序对应, 可得到特征向量矩阵${\hat{ T}}$ , 进而通过(13 )式—(15 )式计算可以得到${{\hat{ \varPhi }}_x}$ , ${{\hat{ \varPhi }}_y}$ 和${\hat{ \varPsi }}$ ,${f_i}$ , 方位角${\theta _i}$ 和俯仰角${\varphi _i}$ 就可以计算,$\angle ( \cdot )$ 为求复数的相位角, 综上所述, 现将基于ESPRIT的估计方法的步骤总结为如下.输入 各通道Q 快拍采样值${{x}}[k]$ , ${{y}}[k]$ 和${{x'}}[k]$ , 其中$k = 1, \cdots, Q$ ;输出 载频$\left\{ {{f_i}} \right\}_{i = 1}^M$ 、俯仰角$\left\{ {{\theta _i}} \right\}_{i = 1}^M$ 和方位角$\left\{ {{\varphi _i}} \right\}_{i = 1}^M$ ;步骤1 根据(8 )式和(9 )式计算协方差矩阵R 步骤2 对${{R}}$ 进行奇异值分解, 得到左奇异向量${{U}}$ , 根据(10 )式—(12 )式计算矩阵${{{V}}_1}$ , ${{{V}}_2}$ 和${{{V}}_3}$ ;步骤3 对矩阵$({{{V}}_1} + {{{V}}_2} + {{{V}}_3})$ 进行特征值分解, 根据(13 )式—(15 )式计算得到${{\hat{ \varPhi }}_x}$ , ${{\hat{ \varPhi }}_y}$ 和${\hat{ \varPsi }}$ ;步骤4 根据(16 )式—(18 )式计算载频$\left\{ {{f_i}} \right\}_{i = 1}^M$ 、俯仰角$\left\{ {{\theta _i}} \right\}_{i = 1}^M$ 和方位角$\left\{ {{\varphi _i}} \right\}_{i = 1}^M$ .4.2.基于CP分解的估计方法 -->4.2.基于CP分解的估计方法 CP分解[17 ] 可以将一个高维的张量分解成多个秩为1的张量的和, 从而降低待处理参数的维度. 为了使(9 )式中的矩阵${{R}}$ 满足CP分解的模型, 定义一个大小为$6 \times M$ 的矩阵${\cal R} = [{{\cal R}{_1}}\;\;{{\cal R}{_2}}\;\; \cdots $ $ \;\;{{\cal R}{_M}}]$ , 其第i 列向量${{\cal{R}}_i}$ 为${{{R}}_w}$ 中除对角线元素外均为0. 定义一个三阶张量${{{\chi }}_{(N - 1) \times (N - 1) \times 6}}$ , 其正向切片${X}_{k}={R}_{k},\; k=1, 2, \dots, $ $ 6$ , ${{{R}}_k}$ 可以表示为20 )式符合典型的CP分解模型, 阵列流型矩阵${{{A}}_{{x_1}}}$ 和${{{A}}_{{y_1}}}$ 均为范德蒙德矩阵, 当$N \geqslant M + 1$ 时, ${{{A}}_{{x_1}}}$ 和${{{A}}_{{y_1}}}$ 均为满k -秩等于M . 由于信源满足(1 )式, 由(19 )式的定义可以看出, 矩阵${\cal{R}}$ 一定有任意两列独立, 即${k_{\cal{R}}} \geqslant 2$ . 因此有[17 ] , 在不考虑列置换模糊和尺度模糊的条件下, 因子矩阵${{{A}}_{{x_1}}}$ , ${{{A}}_{{y_1}}}$ 和${\cal{R}}$ 可以从张量${{\chi }}$ 中唯一恢复. 通过固定除一个因子矩阵外的所有矩阵的方式, 将CP转化为以下的线性最小二乘的问题:${{{X}}_{(n)}}$ 为张量${{X}}$ 的n -模式矩阵化, 因子矩阵${{\hat{ A}}_{{x_1}}}$ , ${{\hat{ A}}_{{y_1}}}$ 和$\hat {\cal{R}}$ 分别为${{{A}}_{{x_1}}}$ , ${{{A}}_{{y_1}}}$ 和${\cal{R}}$ 的估计值. 利用交替最小二乘法进行循环求解, 可解得三个因子矩阵. 对$\hat {\cal{R}}$ 中的元素计算可得(23 )式—(25 )式, 为了方便将其记为${\hat u_i}$ , ${\hat v_i}$ 和${\hat w_i}$ :${f_i}$ , 方位角${\theta _i}$ 和俯仰角${\varphi _i}$ 参数就可以计算:输入 各通道Q 快拍采样值${{x}}[k]$ , ${{y}}[k]$ 和${{x'}}[k]$ , 其中$k = 1, \cdots, Q$ ;输出 载频$\left\{ {{f_i}} \right\}_{i = 1}^M$ 、俯仰角$\left\{ {{\theta _i}} \right\}_{i = 1}^M$ 和方位角$\left\{ {{\varphi _i}} \right\}_{i = 1}^M$ ;步骤1 根据(8 )式和(20 )式计算三线性模型${{\chi }}$ ;步骤2 利用交替最小二乘法对三线性模型${{\chi }}$ 进行求解, 可求得因子矩阵$\hat {\cal{R}}$ ;步骤3 利用$\hat {\cal{R}}$ 中元素根据(23 )式—(25 )式计算得${\hat u_i}$ , ${\hat v_i}$ 和${\hat w_i}$ ;步骤4 根据(26 )式—(28 )式计算载频$\left\{ {{f_i}} \right\}_{i = 1}^M$ 、俯仰角$\left\{ {{\theta _i}} \right\}_{i = 1}^M$ 和方位角$\left\{ {{\varphi _i}} \right\}_{i = 1}^M$ .4.3.参数估计条件 -->4.3.参数估计条件 由于L型延迟阵列MWC结构是基于MWC理论[14 ,15 ] 展开的, 因此估计条件有一定的一致性, 结合文献[14 ]中MWC理论的重构条件给出如下的参数成功估计的条件.1 )式的M 个互不相关的窄带远场信号$\left\{ {{s_i}(t){{\rm{e}}^{{\rm{j}}2{\text{π}}{f_i}}}} \right\}_{i = 1}^M$ , 使用图1 所示的共有2N –1个阵元的L型延迟阵列MWC结构接收, 当满足以下条件:$d \leqslant {c / {{f_{{\rm{Nyq}}}}}}$ , 阵元个数$N \geqslant M + 1$ , 通道延迟$\tau \leqslant {1 / {{f_{{\rm{Nyq}}}}}}$ ;${f_s} \geqslant {f_p} \geqslant B$ ;$l \in \left[ { - {L_0}, \cdots, {L_0}} \right]$ , ${c_l} \ne 0$ ;$\left\{ {{f_i}} \right\}_{i = 1}^M$ 、俯仰角$\left\{ {{\theta _i}} \right\}_{i = 1}^M$ 和方位角$\left\{ {{\varphi _i}} \right\}_{i = 1}^M$ 参数可成功估计.4.4.复杂度分析 -->4.4.复杂度分析 接下来分析基于ESPRIT的参数估计算法的复杂度. 计算矩阵${{R}}$ 大约需要${N^2} \times Q$ 次复乘, 其中Q 为每通道快拍数, N 为一个轴上的阵元个数. 对${{R}}$ 进行奇异值分解大约需要$6{(N - 1)^3}$ 次复乘, 对矩阵$({{{V}}_1} + {{{V}}_2} + {{{V}}_3})$ 进行特征值分解, 需要${M^3}$ 次复乘, M 为信源个数. 因此, 该算法的时间复杂度大约为$O({N^3} + {N^2}Q + {M^3})$ , 所需的空间复杂度约$O({N^2} + {M^2})$ .${\cal{R}} \odot {{{A}}_{{y_1}}}$ 大约需要${(N - 1)^2} \times M$ 次复乘, 计算${\cal{R}} \odot {{{A}}_{{y_1}}}$ 的伪逆则需要$2(N - 1) \times {M^2} + {M^3}$ 次复乘, 计算${{{X}}_{(1)}}$ 与${\left[ {{{({\cal{R}} \odot {{{A}}_{{y_1}}})}^{\rm{T}}}} \right]^\dagger }$ 的乘积则需要${(N - 1)^3} \times M$ 次复乘. 假设交替最小二乘算法循环I 次, 则CP分解的时间复杂度大约为$O(IM \cdot {N^3} + IN{M^2} + {N^2}Q)$ , 其大小和迭代循环次数有直接关系, 迭代的次数由设定的阈值和最大循环次数有关. 在计算过程中需要存储矩阵${{{X}}_{(k)}}$ 和因子矩阵等, 所需的空间复杂度约为$O({N^3})$ . 可以看出, CP分解方法的单次循环的计算复杂度与ESPRIT方法相当, 但由于CP分解方法是求解优化问题, 需要通过不断重复迭代直到达到收敛条件, 而ESPRIT方法通过一次特征值分解即可求得解析解. 因此无论是计算的时间复杂度还是空间复杂度, 基于ESPRIT的方法均小于CP分解方法.28 ]中的基于CS-OMP的2D-DOA与载频联合估计方法, 利用双L型阵列MWC阵列结构进行信号接收, 用OMP算法进行参数估计, 其所需的时间复杂度大约为$O(N{M^2}{P^2} + {N^3} + $ $ {N^2}(M + Q))$ , 其中P 为分割的网格个数. 空间复杂度大约为$O(N{P^2} + {N^2} + NM)$ , 可见CS-OMP算法复杂度很大程度上由网格的大小决定, 网格越小, 参数估计精度虽然会变高, 但时间复杂度和空间复杂度会急速增长. 将3种方法的复杂度总结如表1 所示. 图4 为M = 3, Q = 160, 迭代次数I = 50时3种算法的时间复杂度, 结果表明ESPRIT方法的复杂度最小, 但是从第5 节仿真实验可以看出CP分解方法在鲁棒性方面有更好的表现.基于ESPRIT的方法 基于CP分解的方法 CS-OMP方法[28 ] 时间复杂度 $O({N^3} + {N^2}Q + {M^2})$ $O(IM \cdot {N^3} + IN{M^2} + {N^2}Q)$ $O(N{M^2}{P^2} + {N^3} + {N^2}(M + Q))$ 空间复杂度 $O({N^2} + {M^2})$ $O({N^3})$ $O(N{P^2} + {N^2} + NM)$
表1 不同方法的复杂度对比Table1. Complexity comparison of different methods.图 4 不同方法在M = 3, Q = 160, 迭代次数I = 50时的复杂度对比图Figure4. Multiplications comparison vs . N with M = 3, Q = 160, and I = 50.5.仿真实验 在本节中, 对本文提出的基于L型延迟阵列MWC结构的ESPRIT算法、CP分解算法以及CS-OMP方法[28 ] 进行对比分析, 探究3种估计方法在不同阵元数、快拍数以及不同信噪比情况下的参数估计表现. 实验中使用的信号均根据2 节中定义的窄带信号模型由仿真生成. 定义[24 ] , 其中${\hat f_i}$ , ${\hat \theta _i}$ 和${\hat \varphi _i}$ 分别为载频、方位角和俯仰角的估计值.$M = 3$ , 奈奎斯特频率f Nyq = 10 GHz, 带宽B = 150 MHz. 伪随机序列$p(t)$ 每周期65个点, 周期频率fp = 1.1B = 154 MHz. 调制载频${f_i}$ 、方位角${\theta _i}$ 和俯仰角${\varphi _i}$ 均在定义范围内随机选取. 设置每个轴的阵元数$N = 6$ , 间距d = 0.03 m. 低通滤波器的截止频率为fp /2=77 MHz, 每通道采样率为${f_s} = {f_p}$ .Q = 100, 每个轴的天线个数从临界最小个数$N = M + 1 = 4$ 到$N = 10$ 递增, 步进值为1. 仿真结果如图5 所示, 可以看出3种方法随着天线个数的增加, 参数估计效果逐渐变好, 这主要因为传感器数量的增加提高了系统对噪声的鲁棒性, 并使其能够处理更多的源信号. 同时可以发现在信噪比为10 dB的情况下, CP分解方法的估计效果要比ESPRIT算法好, 因为CP分解方法可以充分利用多维信息, 直接处理接收数据形成的张量模型, 具有更好的性能. 结合复杂度分析的结论可知, 相比另外两种方法, ESPRIT方法的计算复杂度更低, 运算量较小. 而基于双L型阵列的CS-OMP方法估计精度受网格大小限制, 因此效果不如提出的两种方法.图 5 不同阵元个数下参数估计效果 (a) 载频估计效果; (b) 方位角估计效果; (c) 俯仰角估计效果Figure5. Performance of estimated parameters under different N : (a) Performance of carrier frequency; (b) performance of azimuth angle; (c) performance of elevation angle.Q 的大小对参数估计精确度的影响. 设置信噪比为10 dB, 阵元个数N = 10, Q 的值从40到110, 步进值为10. 参数估计结果如图6 所示, 可以看出随着快拍数Q 的增大, 各方法的信号参数估计效果变好. 所提的阵列结构的总阵元个数为2N – 28 ]中的双L型阵列的总阵元个数为3N – 1=29个. 由于所提方法使用阵元个数较少, 因此在快拍数较少的时候参数估计的表现不如CS-OMP方法, 但是在快拍数大于80时, 所提的两种方法的载频和方位角参数估计效果均比CS-OMP方法好, 这是由于CS-OMP方法的参数估计精度受网格大小的限制.图 6 不同快拍数Q 下参数估计效果 (a) 载频估计效果; (b) 方位角估计效果; (c) 俯仰角估计效果Figure6. Performance of estimated parameters under different$Q$ : (a) Performance of carrier frequency; (b) performance of azimuth angle; (c) performance of elevation angle.Q = 100, 阵元数N = 10. 实验结果如图7 所示, 随着信噪比的增大, 3个方法的参数估计效果均越来越好. 通过对比可以发现, 基于ESPRIT的参数估计方法在信噪比小于20 dB时, 鲁棒性不如CP分解方法, 这是因为ESPRIT方法需要先计算通道采样值间的协方差函数, 而CP分解方法可以直接处理多维的信息, 具有更好的性能. 由于CS-OMP方法阵元个数比所提的阵列结构多, 因此在信噪比较低时效果较好. 但在信噪大于5 dB时, CS-OMP方法的精度受网格限制, 参数估计的误差较大. 同时CS-OMP算法只能重构${\theta _i} \in ({0^ \circ }, {90^ \circ })$ 内的角度, 提出的两种方法均可以恢复在$( - {90^ \circ }, {90^ \circ })$ 之内的角度, 范围较大, 更加适合于实际应用.图 7 不同信噪比下参数估计效果 (a) 载频估计效果; (b) 方位角估计效果; (c) 俯仰角估计效果Figure7. Performance of estimated parameters under different SNR: (a) Performance of carrier frequency; (b) performance of azimuth angle; (c) performance of elevation angle.IM 倍. CS-OMP算法在信噪比较低时对2 D-DOA的估计效果较好, 但信噪比较高时精度受限于网格大小, 计算复杂度随网格的增加会呈指数增长. 同时提出的方法可以估计的方位角范围为$( - {90^ \circ }, {90^ \circ })$ , 而CS-OMP算法可估计范围仅为$({0^ \circ }, {90^ \circ })$ , 因此提出的算法更加具有实用性.6.结 论 本文提出了一种L型延迟阵列MWC的接收结构, 通过增加延迟结构直接估计信号载频, 进而估计2D-DOA参数, 无需额外的参数配对, 避免了配对引入的误差和复杂度的提升. 接着在该阵列结构特点的基础上分别提出了两种参数估计方法, 一种基于ESPRIT方法, 另一种基于CP分解技术, 针对两种方法进行了复杂度分析和仿真, 探究了阵元间距、快拍数以及信噪比对方法估计精度的影响, 并对提出的两种方法以及文献[28 ]中的基于网格的CS-OMP方法进行对比分析, 从实验结果中可以总结出所提方法均可从欠奈奎斯特样本中估计信号的载频和二维DOA参数. 基于ESPRIT方法的计算量较小, 但不足之处是低信噪比条件下表现欠佳, 适用于主动雷达等要求实时性的场合; 而基于CP分解技术的方法鲁棒性更好, 适用于低信噪比的场合, 例如被动雷达、遥感等被动感知的目标探测领域, 但所需计算量较大, 实时处理困难. 本文研究了空间电磁波信号在欠采样条件下的载频和二维到达角估计, 如果在已知信号的某些特征的情况下, 还可以进一步改进来减小算法复杂度或提升抗噪性等. 未来在减小算法复杂度方面可以结合信号已知信息来合理的选取初始值, 或者利用梯度下降等方法加快收敛速度, 减少循环次数; 在增强参数估计精度方面可以利用先验信息设计合理的去噪算法; 也可以利用互质阵列、嵌套阵列等稀疏阵列来减少接收阵列的阵元个数, 降低硬件复杂度和成本. 
















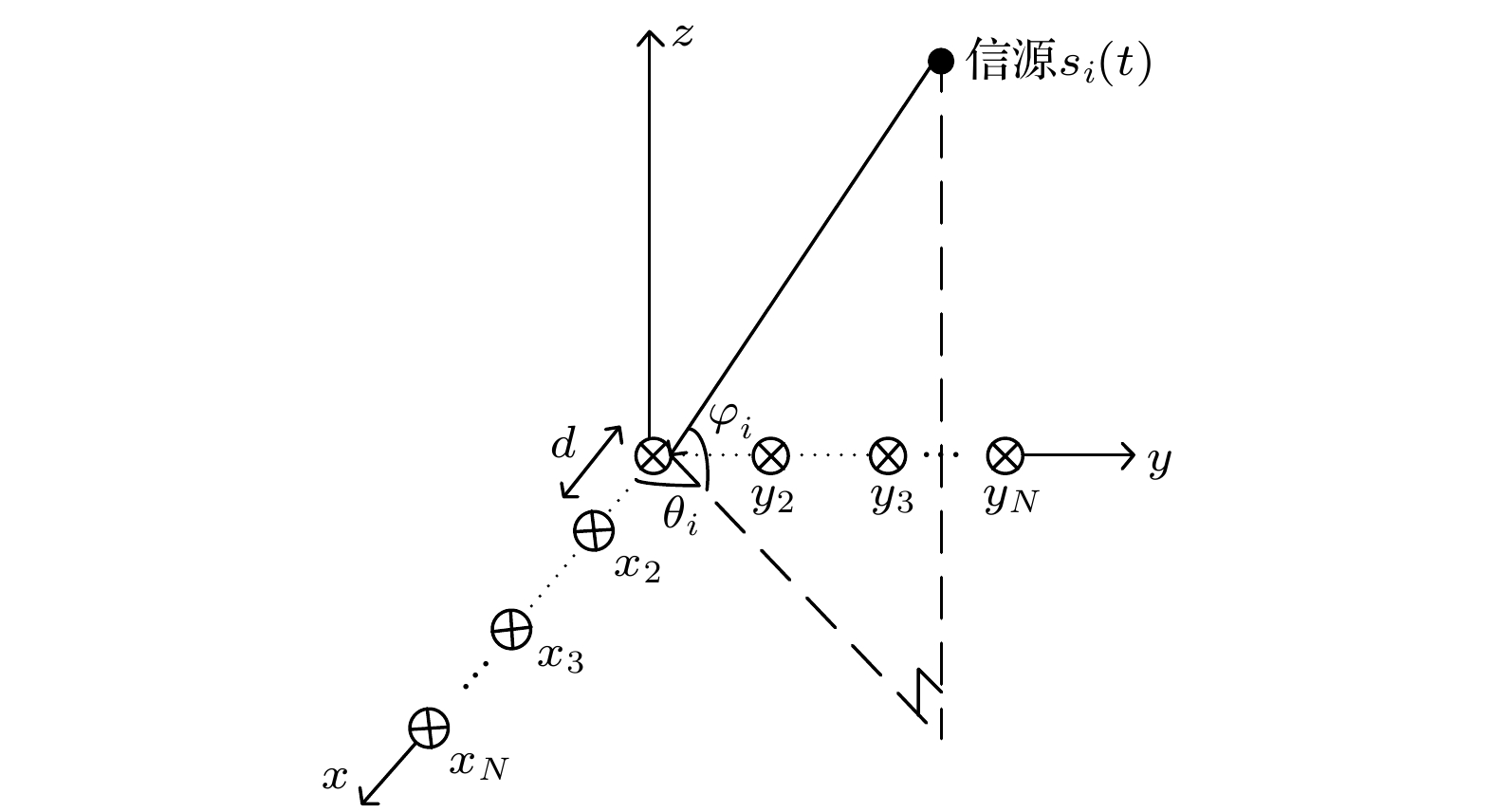 图 1 L型阵列MWC结构图
图 1 L型阵列MWC结构图
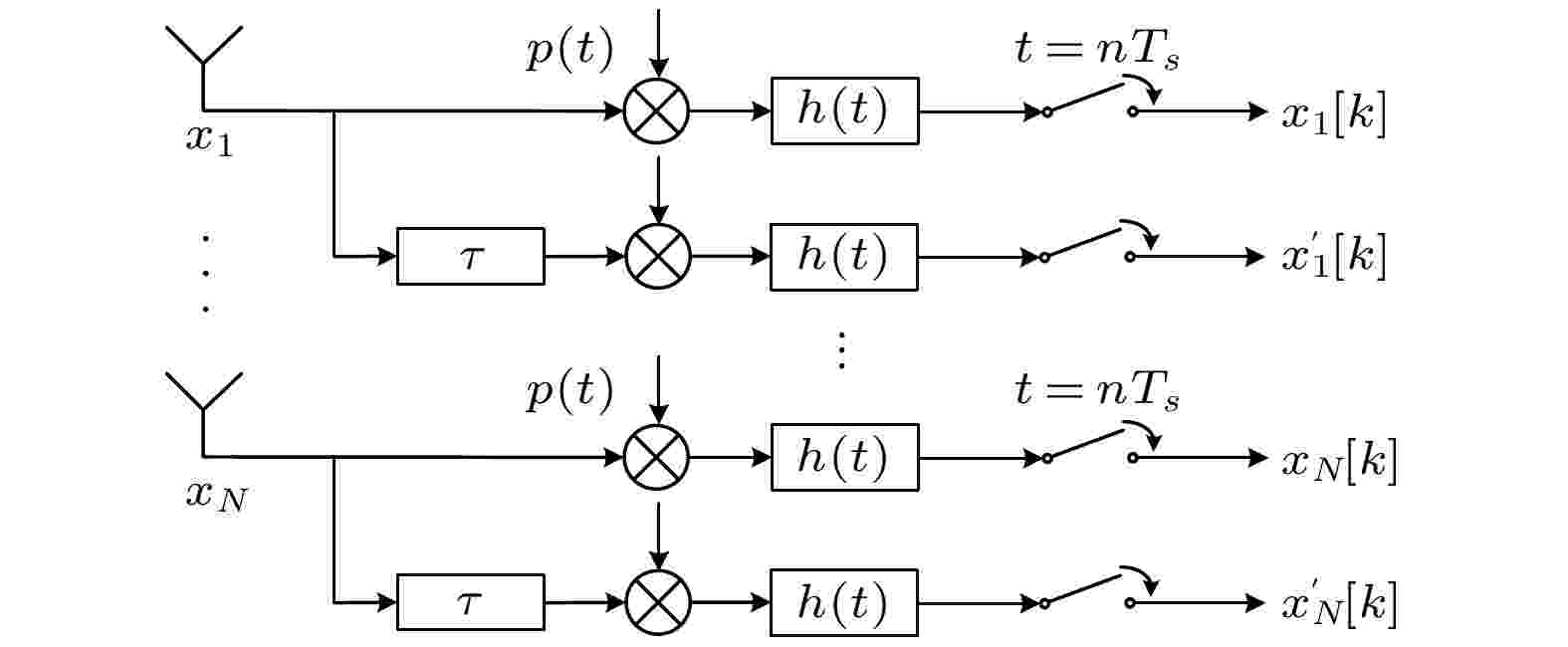 图 2 x轴延迟通道结构图
图 2 x轴延迟通道结构图












 图 3 接收信号频谱示意图
图 3 接收信号频谱示意图


























































































































































































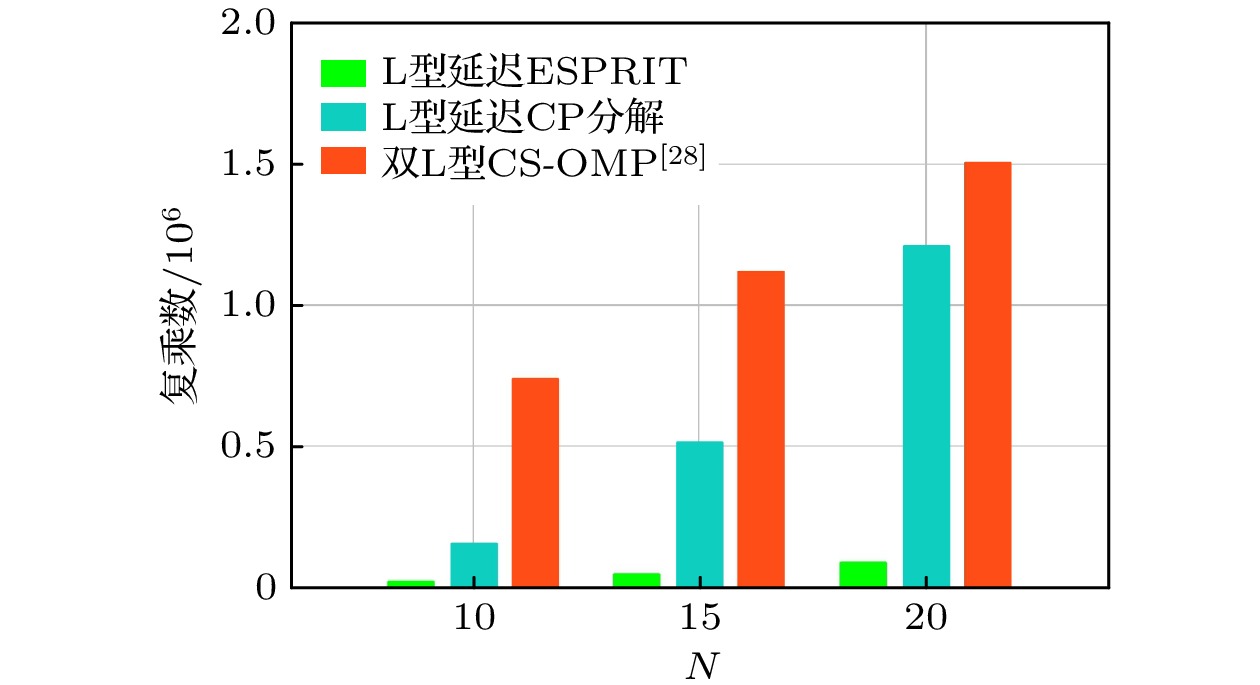 图 4 不同方法在M = 3, Q = 160, 迭代次数I = 50时的复杂度对比图
图 4 不同方法在M = 3, Q = 160, 迭代次数I = 50时的复杂度对比图











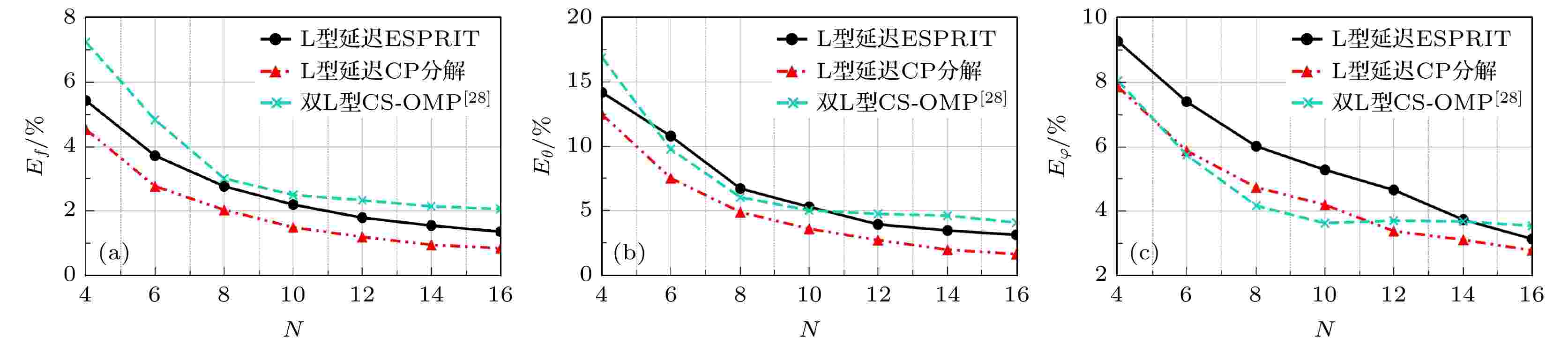 图 5 不同阵元个数下参数估计效果 (a) 载频估计效果; (b) 方位角估计效果; (c) 俯仰角估计效果
图 5 不同阵元个数下参数估计效果 (a) 载频估计效果; (b) 方位角估计效果; (c) 俯仰角估计效果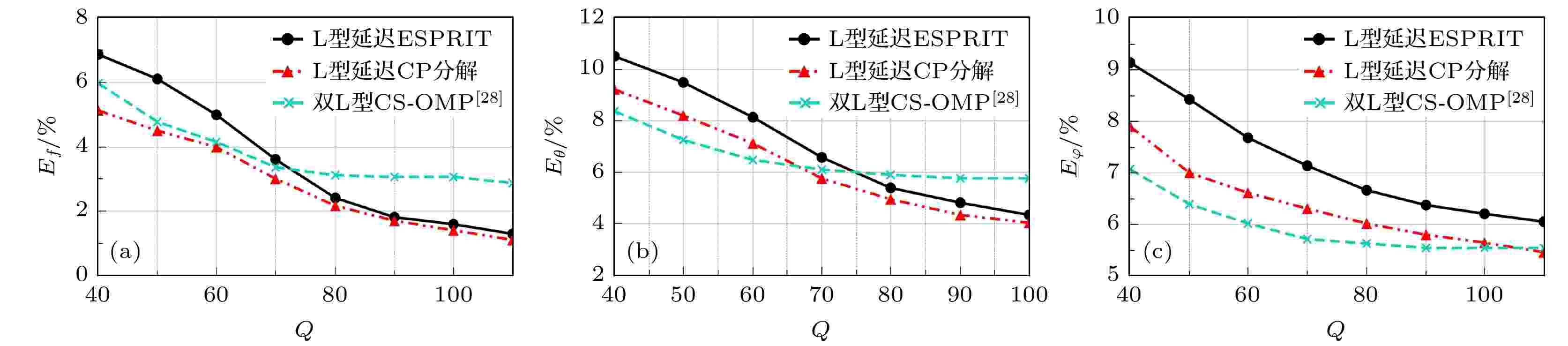 图 6 不同快拍数Q下参数估计效果 (a) 载频估计效果; (b) 方位角估计效果; (c) 俯仰角估计效果
图 6 不同快拍数Q下参数估计效果 (a) 载频估计效果; (b) 方位角估计效果; (c) 俯仰角估计效果


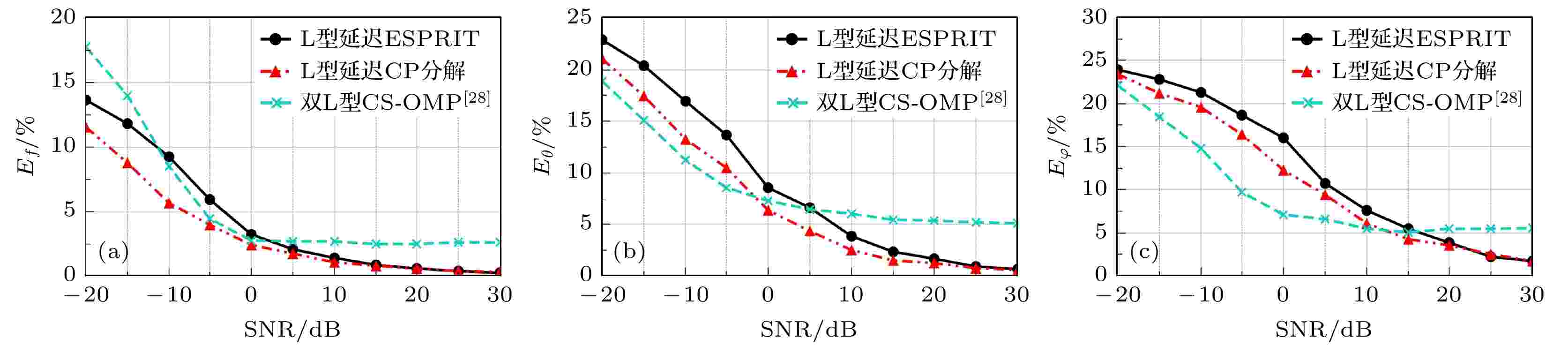 图 7 不同信噪比下参数估计效果 (a) 载频估计效果; (b) 方位角估计效果; (c) 俯仰角估计效果
图 7 不同信噪比下参数估计效果 (a) 载频估计效果; (b) 方位角估计效果; (c) 俯仰角估计效果

