摘要: 系统地研究了最基本的单/双金纳米球系统的共振峰移动、局域场增强和消光谱等光学响应行为. 发现在双金纳米球系统中, 入射光除了能激发每个金纳米球的局域表面等离激元共振模式外, 调整金纳米球间隙可使共振模式间产生强烈耦合, 使系统局域场增强因子进一步提升, 并增强光学传感能力和消光系数. 有趣的是, 受限于有限的局域场增强体积, 具有高局域场增强因子的间隙为2 nm的双金纳米球系统的消光系数大幅降低, 其消光系数和光学传感能力均低于5 nm间隙的系统. 研究表明, 双金纳米球系统的光学传感灵敏度不是由局域场增强幅度直接决定的, 而与系统消光系数有相似的变化行为. 这些结果可指导金纳米双颗粒和多颗粒系统的设计, 为表面拉曼散射增强和光学传感等方面的应用提供创新性思路和方案.
关键词: 金纳米球 /
局域表面等离激元共振 /
光学传感 /
物理机理 English Abstract Correlation of optical sensing with extinction coefficient and local field enhancement in gold nanosphere dimer Xia Wen-Fei Chen Jian-Feng Long Li Li Zhi-Yuan School of Physics and Optoelectronics, South China University of Technology, Guangzhou 510641, China Fund Project: Project supported by the National Key R&D Program of China (Grant No. 2018YFA0306200), the National Natural Science Foundation of China (Grant No. 11974119), the Fundamental Research Fund for the Central Universities, China (Grant No. 2019ZD50), the Innovative and Entrepreneurial Research Team Program of Guangdong Province, China (Grant No. 2016ZT06C594), the Research and Development Projects in Key Areas of Guangdong Province, China (Grant No. 2020B010190001), and the Dongguan Introduction Program of Leading Innovative and Entrepreneurial Talents, China.Received Date: 30 January 2021Accepted Date: 04 March 2021Available Online: 26 April 2021Published Online: 05 May 2021Abstract: In this paper we systematically study the optical extinction, local field enhancement, and resonance peak shift of basic single/double gold nanosphere system. We find that in the double gold nanosphere system, the incident light can excite the coupled resonance modes when the two gold nanospheres are approaching to each other, leading the local field to be enhanced greatly. Interestingly, limited by the scant volume of local field, the extinction coefficient of the double gold nanosphere system of 2 nm gap with a high local field enhancement factor is greatly reduced, so that its optical sensing sensitivity and extinction coefficient are smaller than the 5 nm gap system’s. Studies show that the optical sensing sensitivity of the double gold nanosphere system is not directly determined by the local field enhancement amplitude, but has a similar change behavior to the extinction coefficient of the system. These results can offer us a useful route and hint for designing the gold nanoparticle systems used in the surface Raman scattering enhancement and high performance optical sensing.Keywords: gold nanospheres /localized surface plasmon resonance /optical sensing /physical mechanism 全文HTML --> --> --> 1.引 言 当入射光与金属纳米颗粒相互作用时, 由于金属内部自由电子的集体振荡, 局域表面等离激元共振(localized surface plasmon resonance, LSPR)模式将被激发[1 -4 ] . 金属纳米颗粒的LSPR模式对电磁场有强烈的约束和增强作用, 使其成为纳米科学研究领域的热点, 已在许多场景中得到了应用. 例如在光学领域, 它们被用来实现荧光增强[5 ] 和拉曼增强[6 -14 ] , 使新的非线性光学过程成为可能[15 ,16 ] , 还可以用来制造新型亚波长光学设备, 如纳米激光器[17 -19 ] . 在生物医学领域, 可利用表面等离子体共振峰的移动和表面增强拉曼散射效应来开发新的诊断方法[20 -23 ] . 另外, 在传感研究领域, 也可利用表面等离子体共振峰对介电环境和金属纳米颗粒的几何参数的高敏感性来制造具有超快响应和超高灵敏度的光学传感器件[24 -30 ] .[31 -33 ] , 而其光学响应依赖于金属纳米颗粒的形状、大小、成分和结构[34 ] . 利用偏振共振同步光谱技术, 可对不同尺寸和形状的金纳米颗粒的消光、吸收、散射光谱和散射退极化光谱进行定量研究. 偏振共振同步光谱技术是利用常规荧光分光计获取对应光谱, 该分光计配有一个激发线偏振器和一个检测线偏振器, 由于共振激发和探测是在光谱采集过程中保持激发与探测波长相同的情况下进行测量, 因此也叫同步光谱技术[35 ] . 为了适应不同研究领域与应用场景的需求, 人们利用化学方法生成了不同形状的金属纳米颗粒(包括纳米球、纳米棒和纳米立方体等[36 -40 ] )来改变金属纳米颗粒LSPR模式以调控其光学响应. 例如, 有****研究了单金纳米立方体与单金纳米球的LSPR谱, 发现金纳米立方体比相同大小的金纳米球表现出更高的折射率敏感性[41 ] . 最近, 研究者们还发现将两个或多个金纳米颗粒紧密放置时, 金纳米颗粒间的局部表面等离子体在互相靠近时会强烈耦合, 产生巨大的电磁场增强, 为单分子拉曼检测提供有效的途径[6 -14 ] . 同时, 等离激元耦合可以产生一系列特殊的等离激元模式, 例如高场增强低消光共振模[42 ] 、异常SPR共振模式[43 ] 和Fano共振等[44 -47 ] . 可见, 单/双金纳米颗粒系统可谓金属纳米颗粒表面等离激元研究领域中最为基本的结构, 蕴含着丰富的物理并可能产生更加广泛的应用, 因此, 系统地研究单/双金纳米颗粒系统可为研究复杂金纳米颗粒系统中光与物质相互作用新物理和新应用提供有益指导.2.单金纳米球系统 首先采用FDTD法计算消光谱、共振波谱及近场分布来研究不同折射率背景下单金纳米球系统的光学响应, 模型如图1(a) 所示. 消光系数${Q_{{\rm{ext}}}}$ 表示为${Q_{{\rm{ext}}}} = {C_{{\rm{ext}}}}/({\text{π}}a_{{\rm{eff}}}^{\rm{2}})$ , 其中${a_{{\rm{eff}}}}$ 是有效半径(这里即金纳米球的半径), ${C_{{\rm{ext}}}}$ 是金纳米球消光截面. 归一化场分布为$\left| {{E}} \right|/\left| {{{{E}}_0}} \right|$ , 其中$\left| {{{{E}}_0}} \right|$ 是入射光振幅, $\left| {{E}} \right|$ 是金纳米球结构周围的局域电场振幅. 值得指出的是, 本文所有近场分布图像, 均为归一化场$\left| {{E}} \right|/\left| {{{{E}}_0}} \right|$ 的分布图像. 金纳米球半径r = 50 nm, 本文所用金纳米颗粒的介电常数均取自实验结果[48 ] . 设定入射光沿水平(y 轴)方向入射, 偏振方向沿垂直(z 轴)方向. 为保证计算结果收敛且精确, 仿真过程中网格精度被设置为1 nm × 1 nm × 1 nm, 该网格单元尺寸远小于金纳米球半径以及共振波长.图 1 单/双金纳米球系统结构示意图和入射光波矢及其偏振方向 (a)单金纳米球; (b)双金纳米球Figure1. Schematic diagram of the structure of the single/ double metal nanosphere system and the incident light wave vector and its polarization direction: (a) Single gold nanosphere; (b) double gold nanosphere.$n = 1.0$ 时, 其消光谱中在波长$\lambda = {\rm{ 521\; nm}}$ 处存在一个局域表面等离激元共振峰(用${\lambda _{\rm{p}}}$ 表示共振峰处的波长), 其消光系数为${Q_{{\rm{ext}}}}= $ $ 4.9$ , 如图2(a) 所示, 这与米氏解析理论得到的结果是相符合的[49 ] . 接着将背景折射率从$n = 1.0$ 逐渐增大到$n = 1.3$ , 变化幅度为$\Delta n = 0.3$ , 可以看到共振峰逐渐向右红移, 波长从${\lambda _{\rm{p}}}={\rm{ 521\; nm}}$ 移到${\lambda _{\rm{p}}}={\rm{ 564\; nm}}$ , 红移宽度为$\Delta {\lambda _{\rm{p}}}={\rm{ 43\; nm}}$ . 另外, 在共振峰红移过程中其消光系数也逐渐从${Q_{{\rm{ext}}}}=4.9$ 增强到${Q_{{\rm{ext}}}}=7.4$ . 为了研究共振峰波长与背景折射率之间的关系, 提取了图2(a) 中不同背景折射率下的共振峰波长, 如图2(b) 所示. 通过拟合曲线可以看到, 共振峰波长随背景折射率的增大呈近线性红移.图 2 单金纳米球系统的消光谱、共振波长和电场分布 (a)不同背景折射率下的消光谱; (b)共振波长与背景折射率的关系; (c) n = 1.0时电场分布; (d) n = 1.3时电场分布Figure2. Extinction spectrum, resonance wavelength and electric field distribution of the single metal nanosphere system: (a) Extinction spectrum for different n ; (b) relation between resonance wavelength and n ; (c) electric field for n = 1.0; (d) electric field for n = 1.3.[50 ] 来解释. 根据Drude模型, 材料介电常数实部和虚部分别为${\varepsilon _{\rm{r}}} \!=\! 1 \!-\! \omega _{\rm{p}}^2{\tau ^2}/\left( {1 \!+\! {\omega ^2}{\tau ^2}} \right)$ , ${\varepsilon _{\rm{i}}} = \omega _{\rm{p}}^{\rm{2}}{\tau ^2}/\left[ {\omega \left( {1 + {\omega ^2}{\tau ^2}} \right)} \right]$ , 其中${\omega _{\rm{p}}}$ 为等离子体频率, τ 为弛豫时间. 根据Fr?hlich共振条件$\operatorname{Re} \left( \varepsilon \right) + 2{\varepsilon _{\rm{m}}} = 0$ (其中背景介质的介电常数${\varepsilon _{\rm{m}}} = {n^2}$ ), 得到${\rm{1 - }}\omega _{\rm{p}}^{\rm{2}}{\tau ^2}/\left( {1 + {\omega ^2}{\tau ^2}} \right) = $ $ - 2{\varepsilon _{\rm{m}}}$ , 进一步化简为$1 + 2{n^2} = \omega _{\rm{p}}^{\rm{2}}{\tau ^2}/\left( {1 + {\omega ^2}{\tau ^2}} \right)$ , 背景折射率n 与共振频率ω 呈反比关系, 当背景折射率n 增大时, 共振频率ω 则减小, 即共振峰红移. 另外, 当$n = 1.0$ , $1.1$ , $1.2$ , $1.3$ 时, 平均局域场增强因子分别为1.35, 1.47, 1.59, 1.84. 图2(c) 和图2(d) 分别给出了背景折射率$n = 1.0$ 和$n = 1.3$ 时金纳米球的近场分布. 可以看到, $n = 1.3$ 时的表面场局域效应远好于$n = 1.0$ 时的表面场局域效应. 因此背景折射率的增大导致了金纳米球表面局域场的增强, 进而使得金纳米球的消光系数增大.3.双金纳米球系统 接着研究半径均为r = 50 nm的双金纳米球系统, 结构如图1(b) 所示. 入射平面波传播方向垂直于双球中心连线方向, 而偏振方向则与之平行. 需要强调的是, 本文关注的是光学传感问题, 实际实验中一般采用扩展光束进行照明, 近似于平面光照明, 这不同于常规显微拉曼光谱实验中需要采用高数值孔径物镜进行聚焦激发. 纳米球的体积为V , 把双球系统等效为球体可得到有效半径${a_{{\rm{eff}}}} = $ $ {\left( {\dfrac{3}{{4{\text{π}}}}2 V} \right)^{1/3}} = \sqrt[3]{2}r$ , 这样消光系数可表示为${Q_{{\rm{ext}}}} = $ $ {C_{{\rm{ext}}}}/({\text{π}}a_{{\rm{eff}}}^{\rm{2}})$ , 其中${C_{{\rm{ext}}}}$ 是金纳米球消光截面. 我们知道这样的电磁场配置可有效地激发双金球的纳米间隙等离激元共振模式, 从而产生巨大的局域场增强效应[6 -14 ] . 在计算双金纳米球系统光学响应的过程中, 采用的网格精度为0.1 nm × 0.1 nm × 0.1 nm, 该网格尺寸远小于金纳米球半径、双金纳米球最小间隙以及共振波长, 这保证了计算结果的收敛性及准确性. 另外, 由于等离激元杂化解析理论适用于定性地描述双金纳米球耦合系统中的共振峰劈裂等行为[51 ] , 而对于更为精细的电磁场增强因子及局域场分布通常无法给出精确结果, 因此本文仍采用严格电磁场数值计算方法来求解双金纳米球系统的光学响应.w = 2 nm时, 不同折射率背景下的消光谱如图3(a) 所示, 可看到当背景折射率由n = 1.0增大到n = 1.3时, 共振波长从${\lambda _{\rm{p}}}= $ $ 617\; {\rm{nm}}$ 红移至${\lambda _{\rm{p}}}={\rm{ 733 \;nm}}$ , 红移量$\Delta {\lambda _{\rm{p}}}={\rm{ 116\; nm}}$ . 而消光系数随背景折射率增大则是先增大后减小, 当背景折射率由n = 1.0增大到n = 1.15时, 消光系数从${Q_{{\rm{ext}}}}={\rm{ 11}}{\rm{.2}}$ 逐渐增大至${Q_{{\rm{ext}}}}={\rm{ 11}}{\rm{.7}}$ ; 当背景折射率继续增大至n = 1.3时, 消光系数减小至${Q_{{\rm{ext}}}}={\rm{ 11}}{\rm{.5}}$ . 与单金纳米球系统不同的是, 双金纳米球系统可以通过改变双球间隙来调控光学响应. 图3(b) 给出了双球间隙为5 nm的双金纳米球系统在不同背景折射率下的消光谱. 可以看到, 当背景折射率由1.0增大至1.3时, 共振波长从634 nm红移至763 nm, 红移量大于间隙为2 nm的双金纳米球系统, 达到129 nm. 而消光系数虽也是先增后减, 从12.8 ($n = 1.0$ )增加至13.0 ($n = 1.1$ )后减小到12.7 ($n = 1.3$ ), 但整体消光系数仍要高于间隙为2 nm的双金纳米球系统. 继续增大双金纳米球的间隙至10 nm, 结果如图3(c) 所示, 共振波长从593 nm移动到701 nm, 红移量为$\Delta {\lambda _{\rm{p}}}= $ $ {\rm{ 108\; nm}}$ , 消光系数则是先从10.5 ($n = 1.0$ )增加到10.9 ($n = 1.1$ ), 而后减小至10.8 ($n = 1.3$ ); 相较于w = 5 nm的双金纳米球系统, 其共振峰红移量与消光系数均明显地减小. 进一步调节间隙至20 nm, 共振波长从571 nm移至663 nm, 红移量$\Delta {\lambda _{\rm{p}}}={\rm{ 92\; nm}}$ , 消光效率也从8.5一直增加到9.5, 如图3(d) 所示, 此时共振峰红移量与消光效率均低于间隙为10 nm的情况.图 3 不同间距双金纳米球系统在不同背景折射率下的消光谱 (a) w = 2 nm; (b) w = 5 nm; (c) w = 10 nm; (d) w = 20 nmFigure3. Extinction spectrum of the bimetallic nanosphere system with different spacing under different n : (a) w = 2 nm; (b) w = 5 nm; (c) w = 10 nm; (d) w = 20 nm.$\Delta {\lambda _{\rm{p}}}\!={\rm{ 116\; nm}}$ (w = 2 nm), $\Delta {\lambda _{\rm{p}}}\!={\rm{ 129 \;nm}}$ (w = 5 nm), $\Delta {\lambda _{\rm{p}}}={\rm{ 108\; nm}}$ (w = 10 nm), $\Delta {\lambda _{\rm{p}}}={\rm{ 92\; nm}}$ (w = 20 nm). 在同一折射率背景下, 增大间隙会使得共振峰波长先红移再蓝移, 例如, 背景折射率为1.0时, ${\lambda _{\rm{p}}}={\rm{ 617\; nm}}$ (w = 2 nm), ${\lambda _{\rm{p}}}={\rm{ 634\; nm}}$ (w = 5 nm), ${\lambda _{\rm{p}}}={\rm{ 593\; nm}}$ (w = 10 nm), ${\lambda _{\rm{p}}}= {\rm{ 571\; nm}}$ (w = 20 nm). 另外可以看到, w = 5 nm时不同折射率情况下的消光系数明显高于其他三种情况, 这意味着入射光与双金纳米球系统产生了强烈的相互作用, 使得双金纳米球间发生强烈能量局域, 导致消光系数显著增大.图4 中给出了背景折射率为1.0时不同间隙的双金纳米球系统在共振频率处的近场分布. 可以看到, 当w = 2 nm时, 双金纳米球间隙中心区域存在一个“强热点”, 局域场增强因子为216, 远远大于图1(c) 中的单金纳米球系统的局域场增强因子(约为6.5). 因此, 入射光除了可以在单金纳米球中激发LSPR模式以产生局域场增强外, 金纳米球与球之间的局域场在相互靠近的过程中也会产生强烈耦合, 使得局域场被进一步剧烈增强. 因此, 当间隙增大至5 nm时, 由于双金纳米球间表面局域场的耦合作用减弱, 使其局域场增强因子迅速减小至80.图 4 空气中双金纳米球系统在共振频率处的近场分布 (a) w = 2 nm (λ p = 616 nm); (b) w = 5 nm (λ p = 634 nm); (c) w =10 nm (λ p = 594 nm); (d) w = 20 nm (λ p = 571 nm)Figure4. Near-field distribution of the bimetallic nanosphere system in the air at the resonance frequency: (a) w = 2 nm (λ p = 616 nm); (b) w = 5 nm (λ p = 634 nm); (c) w = 10 nm (λ p = 594 nm); (d) w = 20 nm (λ p = 571 nm).图3 可以看到其消光系数(${Q_{{\rm{ext}}}} = 11.2$ )却小于间隙为5 nm的双金纳米球系统的消光系数(${Q_{{\rm{ext}}}} = 12.8$ ). 这一结果表明, 不同于单金纳米球系统, 在双金纳米球系统中消光系数与局域场增强因子并不是呈正相关关系. 间隙为2 nm的双金球系统中的近场模式展现出高局域场增强系数、低消光系数的特性, 这种特殊的近场模式是由于该近场模式的电场在双金纳米球间隙中有限的区域内高度局域化, 导致了非常强的局域场增强, 但受限于局域场增强的体积, 其消光系数没有想象中的那么大, 而是受到了一定程度的抑制, 以至于小于间隙为5 nm的双金纳米球系统. 继续增大双金纳米球系统的间隙至10 nm, 局域场增强因子减小至39.3, 随着间隙进一步增大至20 nm, 局域场增强因子降至20.7. 这意味着此时继续增大双金纳米球间隙会导致双金纳米球间局域场的耦合作用减弱, 使得系统的场增强作用迅速降低.λ p 与背景折射率n 、共振峰波长λ p 与消光系数${Q_{{\rm{ext}}}}$ 之间的关系, 提取了图3 中不同间隙下的共振峰波长与其消光谱, 如图5(a) 和5(b) 所示. 可以看到, 在同一背景折射率下, 增大双金纳米球间隙, 其共振峰均呈现先红移再蓝移现象; 而在同一间隙宽度下, 共振峰波长随折射率变化均呈近线性关系. 接着, 定义背景折射率灵敏度$\varPhi = \Delta \lambda /\Delta n$ , 以更直接地展现不同间隙的双金纳米球系统中共振峰的移动对不同背景折射率的敏感程度. 通过计算可以得到间隙为1, 2, 5, 10, 20 nm时对应的灵敏度分别为298, 388, 432, 361, 308 nm/RIU. 可以看到, 间隙为5 nm的双金纳米球系统对背景折射率的变化最为敏感, 此时共振峰波长红移量最大. 另外, 在共振峰波长λ p 与消光系数的关系图5(d) 可以看出, 随着间隙的增大, 消光系数呈现出先增大后减小的变化趋势, 间隙为1, 2, 5, 10, 20 nm的双金纳米球系统的消光系数分别为7.3, 11.2, 12.8, 10.5, 8.6. 可以看到, 随着间隙的增大, 消光系数的变化趋势与共振峰红移量的变化趋势是完全一致的, 在间隙为5 nm时消光系数最大, 共振峰红移量最宽, 对背景折射率的变化最为敏感; 而在间隙20 nm时消光系数最小, 共振峰红移宽度最窄, 这也意味着该系统对背景折射率变化的反应最为迟钝. 因此, 双金纳米球系统的光学传感灵敏度并不由局域场增强幅度直接决定, 而与系统消光系数有相似的变化行为.图 5 不同间隙的双金纳米球系统 (a) LSPR共振波长λ p 与背景折射率n 的关系; (b)消光谱; (c)共振峰处的最大场增强因子γ ; (d)共振峰处的消光系数Figure5. Bimetallic gold nanosphere system with different w : (a) Relationship between λ p and background index n ; (b) extinction spectrum; (c) maximum field enhancement for resonance peak; (d) extinction for resonance peak.图5(c) 中给出了不同间隙的双金纳米球系统中的最大局域场增强因子γ 与背景折射率的关系. 可以看到, 在同一背景折射率情况下, 随着间隙逐渐减小, 系统的最大局域场增强因子均是逐渐增大. 接着, 在图5(d) 中给出了不同间隙双金纳米球系统中的消光系数与背景折射率的关系. 可以看到, 在同一背景折射率情况下, 系统的消光系数均是先增大后减小, 变化趋势与光学传感灵敏度的变化趋势有相似的行为. 最后需要说明的是, 当双金纳米球间隙约为1 nm时, 本文使用的FDTD计算方法仍然适用; 但当其间隙远小于1 nm时, 金属中电子-电子之间的库仑作用和泡利不相容原理使得纳米结构中的量子力学效应显现出来, 导致双金纳米球结构的宏观光学响应显著偏离经典电磁理论预测[52 ] , FDTD计算方法便不再适用.4.结 论 本文使用FDTD法系统地研究了金纳米单球和双球系统在不同背景折射率下的消光谱、共振谱及近场分布. 结果表明, 随着背景折射率增大, 单球系统的局域表面LSPR峰随背景折射率的增大呈近线性红移, 变化规律遵循Drude模型. 还研究了不同背景折射率下具有不同间隙的双金纳米球系统的光学响应. 结果表明, 在同一间隙下, 随着背景折射率增大, 共振峰依然呈近线性红移; 而在同一背景折射率下, 在双金纳米球相互靠近过程中其LSPR模式间会发生强烈耦合效应, 使得间隙中的局域场剧烈增强. 但受限于有限的局域场增强体积, 窄间隙(例如2 nm)的双金纳米球系统中会产生特殊的高局域场增强、低消光的共振模式, 从而在逐渐增大间隙的过程中, 可以观察到共振峰先红移再蓝移的现象. 另外, 2 nm 间隙的双球系统其光学传感能力和消光系数低于5 nm间隙的双球系统. 进一步研究表明, 双金纳米球系统的光学传感灵敏度并不由局域场增强幅度直接决定, 而与系统消光系数有相似的变化行为. 以上研究结果提供了一个有效和灵活的优化金纳米球系统设计的新方案, 以满足光学传感和表面增强拉曼散射等方面的应用. 









 图 1 单/双金纳米球系统结构示意图和入射光波矢及其偏振方向 (a)单金纳米球; (b)双金纳米球
图 1 单/双金纳米球系统结构示意图和入射光波矢及其偏振方向 (a)单金纳米球; (b)双金纳米球














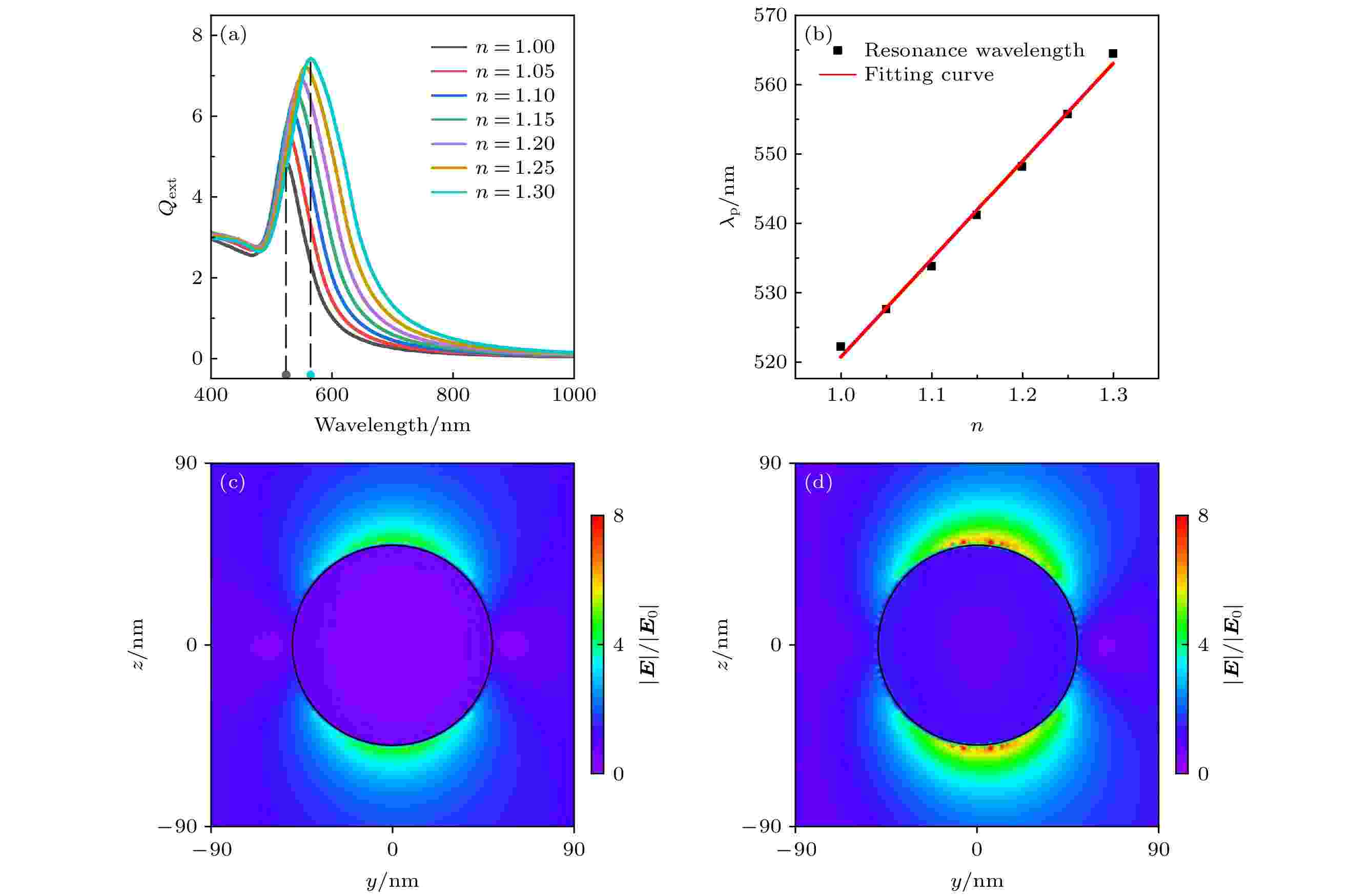 图 2 单金纳米球系统的消光谱、共振波长和电场分布 (a)不同背景折射率下的消光谱; (b)共振波长与背景折射率的关系; (c) n = 1.0时电场分布; (d) n = 1.3时电场分布
图 2 单金纳米球系统的消光谱、共振波长和电场分布 (a)不同背景折射率下的消光谱; (b)共振波长与背景折射率的关系; (c) n = 1.0时电场分布; (d) n = 1.3时电场分布
















































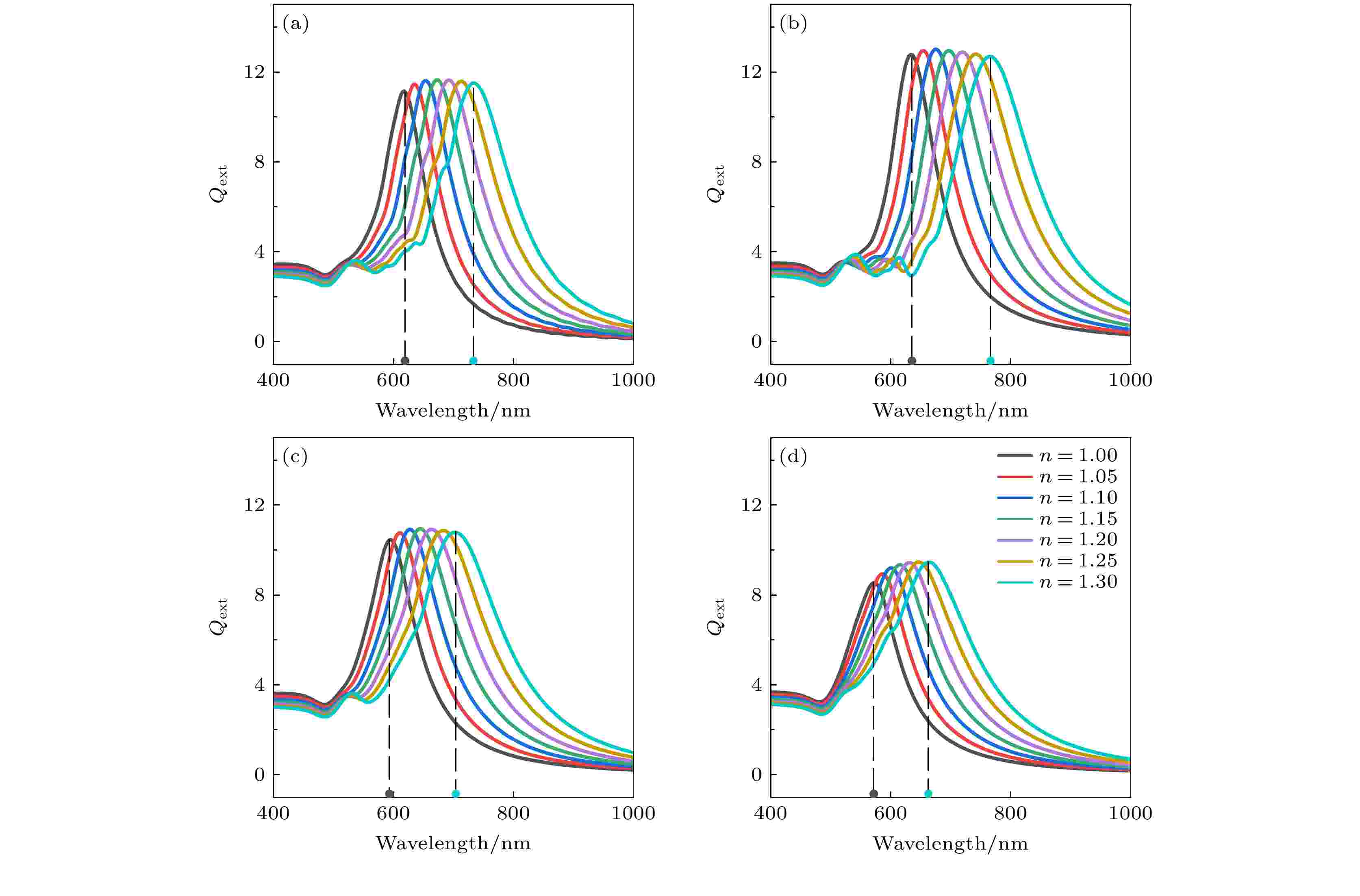 图 3 不同间距双金纳米球系统在不同背景折射率下的消光谱 (a) w = 2 nm; (b) w = 5 nm; (c) w = 10 nm; (d) w = 20 nm
图 3 不同间距双金纳米球系统在不同背景折射率下的消光谱 (a) w = 2 nm; (b) w = 5 nm; (c) w = 10 nm; (d) w = 20 nm







 图 4 空气中双金纳米球系统在共振频率处的近场分布 (a) w = 2 nm (λp = 616 nm); (b) w = 5 nm (λp = 634 nm); (c) w =10 nm (λp = 594 nm); (d) w = 20 nm (λp = 571 nm)
图 4 空气中双金纳米球系统在共振频率处的近场分布 (a) w = 2 nm (λp = 616 nm); (b) w = 5 nm (λp = 634 nm); (c) w =10 nm (λp = 594 nm); (d) w = 20 nm (λp = 571 nm)



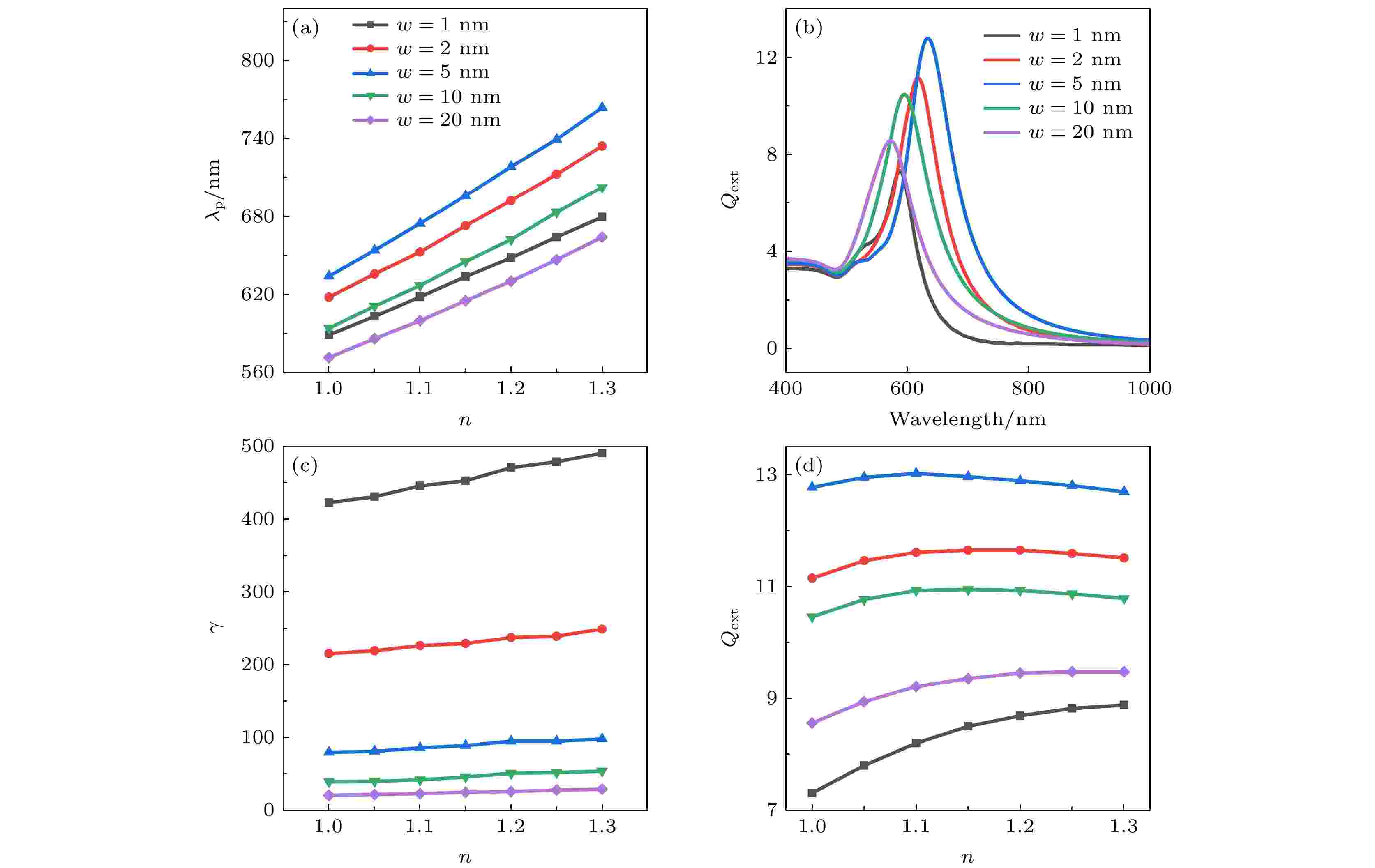 图 5 不同间隙的双金纳米球系统 (a) LSPR共振波长λp与背景折射率n的关系; (b)消光谱; (c)共振峰处的最大场增强因子γ; (d)共振峰处的消光系数
图 5 不同间隙的双金纳米球系统 (a) LSPR共振波长λp与背景折射率n的关系; (b)消光谱; (c)共振峰处的最大场增强因子γ; (d)共振峰处的消光系数