摘要:基于绝缘体上硅的微环谐振器由于成本低、结构紧凑和集成度高等优点, 是构成波分复用器、调制器以及光开关等的核心器件. 然而, 该类器件由于芯层与覆盖层间的高折射率差, 具有较大的偏振相关性, 在诸多使用偏振无关器件的应用中受到限制. 本文基于亚波长光栅和三明治结构设计了一种偏振无关微环谐振器, 通过改变三明治结构中低折射率层SiN_x的折射率, 同时结合耦合区亚波长光栅的结构参数优化, 最终消除微环谐振器的偏振相关性. 运用三维有限时域差分法进行建模仿真, 对器件的结构参数进行了优化. 结果表明, 器件在TE和TM偏振模时的3-dB带宽均小于0.8 nm, 插入损耗均小于0.8 dB, 微环半径仅为10 μm, 并且在谐振波长1552.26 nm附近的两个自由频谱区内实现了偏振无关. 与常见的微环谐振器相比, 本文所提出的器件尺寸小、损耗低, 可用于构成偏振无关的密集波分复用器, 在未来的集成光路中具有较高的应用价值.
关键词: 微环谐振器/
偏振无关/
亚波长光栅/
三明治结构

English Abstract

全文HTML

--> --> -->

在大数据时代, 现代网络通信和人工智能等热点技术兴起, 对信道容量的需求日益突出, 密集波分复用技术应运而生. 密集波分复用器作为其核心器件, 常用的实现方法有: 微环谐振器^[1-3]、阵列波导光栅^[4]、级联马赫-曾德尔干涉仪^[5]和光子晶体^[6]. 其中, 由于微环谐振器拓扑多样, 滤波性能好且与绝缘体上硅(silicon-on-insulator, SOI)技术兼容而备受关注.
SOI是指在绝缘体衬底(SiO₂等)上形成Si波导或Si薄膜, 是一种新型的光电子集成材料. 由于Si与SiO₂材料间折射率差较大, 对光的限制能力强, 弯曲损耗低^[7,8], 因此基于SOI的微环谐振器的弯曲半径较小, 具有更高的集成度^[9]. 但是由于SOI固有的双折射效应, 导致基于SOI的微环谐振器往往有着很强的偏振相关性, 使其在诸多使用偏振无关器件的应用中受到限制. 目前有两种解决方案: 一种方案是使用偏振分集系统^[10]; 另一方案是使所设计的器件本身具有偏振无关性. 本文拟采用后者, 设计偏振无关的微环谐振器.
目前, 已报道的实现SOI型微环谐振器偏振无关的方法有: 1) 采用脊型多模干涉波导, 但存在自由频谱区(free spectral range, FSR)较小以及器件尺寸较大等问题^[11]; 2) 采用十字缝隙波导, 器件尺寸较小, 但插入损耗较大^[12]; 3) 采用亚波长光栅(subwavelength grating, SWG)与梯形波导, 器件Q值较高且插入损耗小于2 dB, 但尺寸较大不利于集成^[13]. 综上, 现有的偏振无关微环谐振器在插入损耗与器件尺寸两者兼顾中存在不足.
针对上述问题, 本文提出一种基于SWG和三明治结构的偏振无关微环谐振器. 通过改变三明治结构中低折射率层SiN_x的折射率, 优化耦合区SWG的结构参数, 可以实现偏振无关. 运用三维有限时域差分法进行建模和分析, 结果表明: 器件尺寸较小且插入损耗较低, 同时在谐振波长1552.26 nm附近的两个FSR内实现了偏振无关, 3-dB带宽小于0.8 nm, 可用于信道间隔为0.8 nm的密集波分复用器.

2

-->

2.1.微环谐振器原理

根据耦合模理论^[14], 当上传/下载型微环谐振器^[15]的微环波导与输入、输出波导之间的距离足够近时, 输入光将通过输入波导芯层外的消逝场不断地耦合进入微环波导, 其中满足谐振条件的光将发生相干干涉, 并很快地达到稳定状态, 从输出端输出. 微环谐振器的谐振条件为

$2{\rm{\pi}} R{n_{{\rm{eff}}}} = m\lambda, $

其中m为微环谐振器的谐振级数, 取正整数; R为微环半径; λ为谐振波长; n_eff为微环波导的模式有效折射率.
反之, 不满足谐振条件的光则不发生干涉, 其大部分从直通端输出, 余下的一小部分则由输出端以背景光的形式输出.
根据耦合模理论, 可以推导出输出端的光强度为^[16]

${\left| D \right|^2} = {\left| {\frac{{{k_1}{k_2}\exp \left[ { - {\rm{j}}\left( {\phi + 2\varphi } \right)} \right]}}{{1 - {t_1}{t_2}\exp \left( { - 2{\rm{j}}\varphi } \right)}}} \right|^2}, $

其中$\phi $为光在微环中传输半圈时产生的相移; $\varphi $为光从输入端开始直到耦合进入微环中时产生的相移; k₁, k₂为微环与输入、输出波导的振幅耦合系数, 相应的振幅透射系数为t₁, t₂. 振幅耦合系数与振幅透射系数满足:

$k_n^2 + t_n^2 = 1,n = (1,2).$

2 -->

2.2.器件结构的设计

所设计的基于SWG和三明治结构的微环谐振器结构如图1(a)所示, 该器件由输入、输出波导与微环波导组成. 器件中除SWG外的波导宽度均为W₁ = 0.5 μm, 满足单模条件; 微环波导中弯曲波导半径为R = 10 μm (R过小, 弯曲损耗过大; R过大, 则FSR过小, 影响波分复用的性能, 故R的取值兼顾了两者); 输入、输出波导与微环波导间的间隔均为g. 此外, 器件中的波导均采用如图1(b)所示的Si/SiN_x/Si三明治结构, Si层厚度H_Si = 0.25 μm, SiN_x层厚度${H_{{\rm{Si}}{{\rm{N}}_x}}}$ = 0.1 μm, 覆盖层为SiO₂. 离子辅助沉积法^[17,18]可调节SiN_x的折射率n(SiN_x)在1.72—3.43范围内变化. 器件中弯曲波导处的SiN_x的折射率为n₂(SiN_x), 其余波导处SiN_x的折射率为n₁(SiN_x). 耦合区的三维结构如图1(c)所示, 该结构在图1(b)所示的三明治结构的基础上, 在Si层引入SWG结构, 如图1(d)所示, 它由两根宽度为W₁, 波导间隔为g的水平直波导和占空比为W₃/Λ、周期Λ = 0.2 μm、宽度为W₃的SWG组成. 其中W₃ = g + 2W₁ + 2L, L = 0.2 μm. SiN_x层采用普通的定向耦合结构, 如图1(e)所示, 波导宽度为W₁, 波导间隔为g.
图 1 基于SWG和三明治结构的偏振无关微环谐振器结构示意图　(a) 俯视图; (b) 波导横截面示意图; (c) 基于SWG和三明治结构的耦合区三维结构示意图; (d) 耦合区Si层俯视图; (e) 耦合区SiN_x层俯视图
Figure1. Schematic configuration of the polarization insensitive ring resonator based on SWG and sandwiched structure: (a) Top view; (b) cross section of the waveguide; (c) three-dimensional schematic configuration of the polarization insensitive coupling region based on subwavelength grating slot waveguides and sandwiched structure; (d) top view of Si layer in coupling region; (e) top view of SiN_x layer in coupling region.

2

-->

3.1.微环谐振器偏振无关的实现

微环谐振器的偏振相关性主要由两个因素造成: 第一, 同一波长时微环耦合区的横电(transverse electric, TE)和横磁(transverse magnetic, TM)偏振模振幅耦合系数不同; 第二, 微环波导的双折射效应导致TE与TM偏振模对应的谐振波长不同. 因此, 需要同时满足耦合区偏振无关和谐振波长的偏振无关, 才能实现微环谐振器的偏振无关.
3 -->

3.1.1.耦合区偏振无关的实现

由(2)式可知微环谐振器输出端的光强度与振幅耦合系数k₁, k₂有关. 因为上、下两个耦合区的结构完全相同, 所以有k₁ = k₂ = k, 此时(2)式变为

${\left| D \right|^2} = {\left| {\frac{{{k^2}\exp \left[ { - {\rm{j}}\left( {\phi + 2\varphi } \right)} \right]}}{{1 - (1 - {k^2})\exp \left( { - 2{\rm{j}}\varphi } \right)}}} \right|^2}.$

由(4)式可知, 当微环波导的半径及器件其他波导长度、宽度不变(即$\phi $和$\varphi $不变)的情况下, 输出端光强度仅与k ²有关. 因此要实现耦合区偏振无关需要满足下面公式:

${k^2}(\lambda,{\rm{TE}}) = {k^2}(\lambda,{\rm{TM}}), $

式中, k ²(λ, TE)和k ²(λ, TM)是波长为λ, TE和TM偏振模时耦合区的k ².
然而, 事实上普通耦合区结构内k ²(λ, TE)远小于k ²(λ, TM). 因此考虑采用三明治结构, 利用Si层和SiN_x层间的电场不连续性, 使得TE和TM偏振模分别在Si层和SiN_x层传播^[19], 如图2所示. 此外, 在三明治结构的Si层中引入了SWG结构. SWG结构如图1(d)所示: 当其周期小于布拉格周期时, 整个结构可当作均匀介质材料, 其等效折射率n_B为
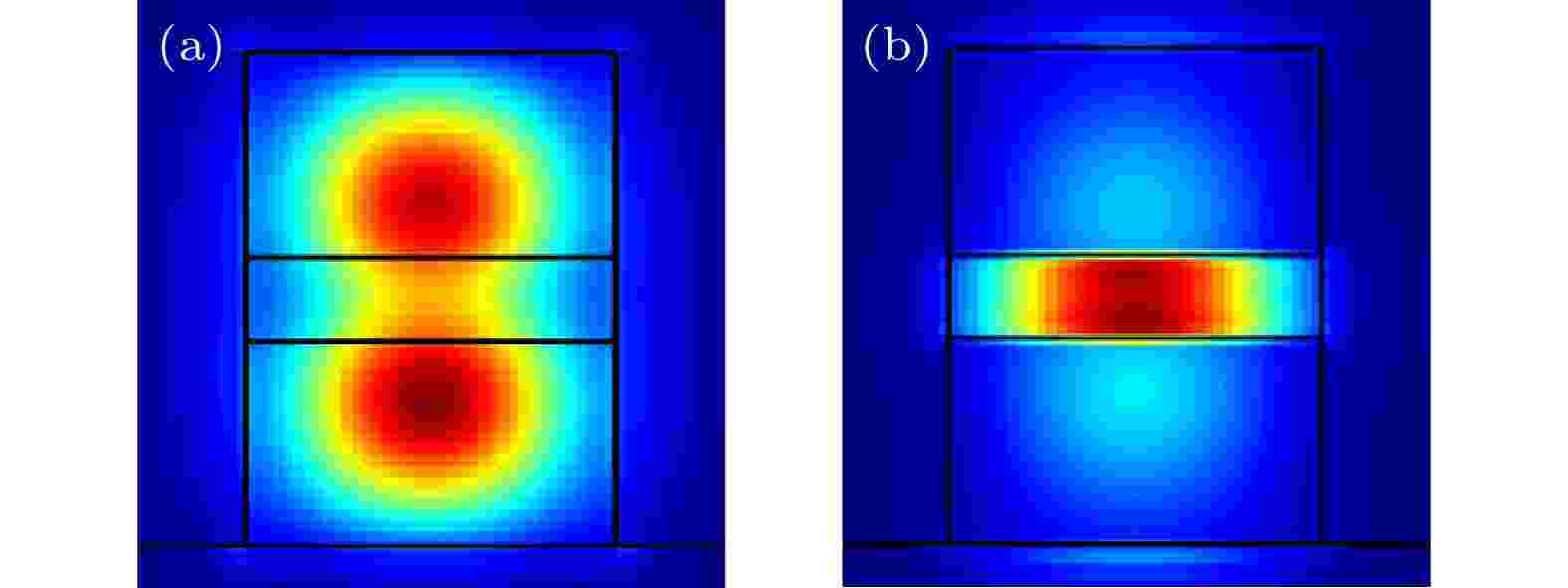图 2 耦合区中的光场分布图　(a) TE偏振模; (b) TM偏振模
Figure2. Field distributions in the coupling region: (a) TE polarization mode; (b) TM polarization mode.

$n_{\rm{B}}^2 \approx \frac{{{W_2}}}{\varLambda }n_{{\rm{GH}}}^2 + \frac{{\varLambda - {W_2}}}{\varLambda }n_{{\rm{GL}}}^2, $

式中, n_GH和n_GL分别为SWG中高和低折射率材料的折射率. 由(6)式可知: 通过改变W₂的值, 可提高SWG的等效折射率. 根据模式耦合原理可以推导出两根相邻直波导间的耦合系数:

$ K=\frac{\omega {\varepsilon }_{{}_{0}}}{4}{ \int _{S}({n}_{3}^{2}-{n}_{1}^{2})}{{{E}}}_{\rm{1t}}\cdot {{{E}}}_{\rm{2t}}{\rm{d}}S.$

式中, ε₀为真空介电常数; ${{{E}}_{{\rm{1 t}}}}$, ${{{E}}_{{\rm{2 t}}}}$分别为两根波导中电场的切向分量; n₁, n₃分别为波导材料的折射率与两根波导间材料的折射率. 由于TE偏振模被局域在Si层中传播, 因此对于k ²(λ, TE)而言n₁, n₃分别为Si的折射率与n_B. 由(7)式知: 通过提高n_B, k ²(λ, TE)的值也会随之增加, 最终实现k ²(λ, TE) = k ²(λ, TM).
下面以g = 0.323 μm, n₁ (SiN_x) = 1.9为例, 讨论W₂对k ²(λ, TE)和k ²(λ, TM)的影响. 由图3可看出, 随着W₂的增加, k ²(λ, TE)和k ²(λ, TM)均单调增加. 其中, 由于TM偏振模主要被限制在SiN_x层传播, 受到W₂变化的影响较小, 因此, k ²(λ, TM)随着W₂的增加其增长幅度缓慢. 而TE偏振模主要被限制Si层的SWG结构中传输, 受到W₂变化的影响大, 因此k ²(λ, TE)随着W₂的增加而快速增加, 所以两者在图中存在交点(图中虚线圈出位置). 在交叉点(W₂ = 0.06 μm)处k ²(λ, TE) = k ²(λ, TM), 此时微环谐振器的耦合区实现偏振无关.
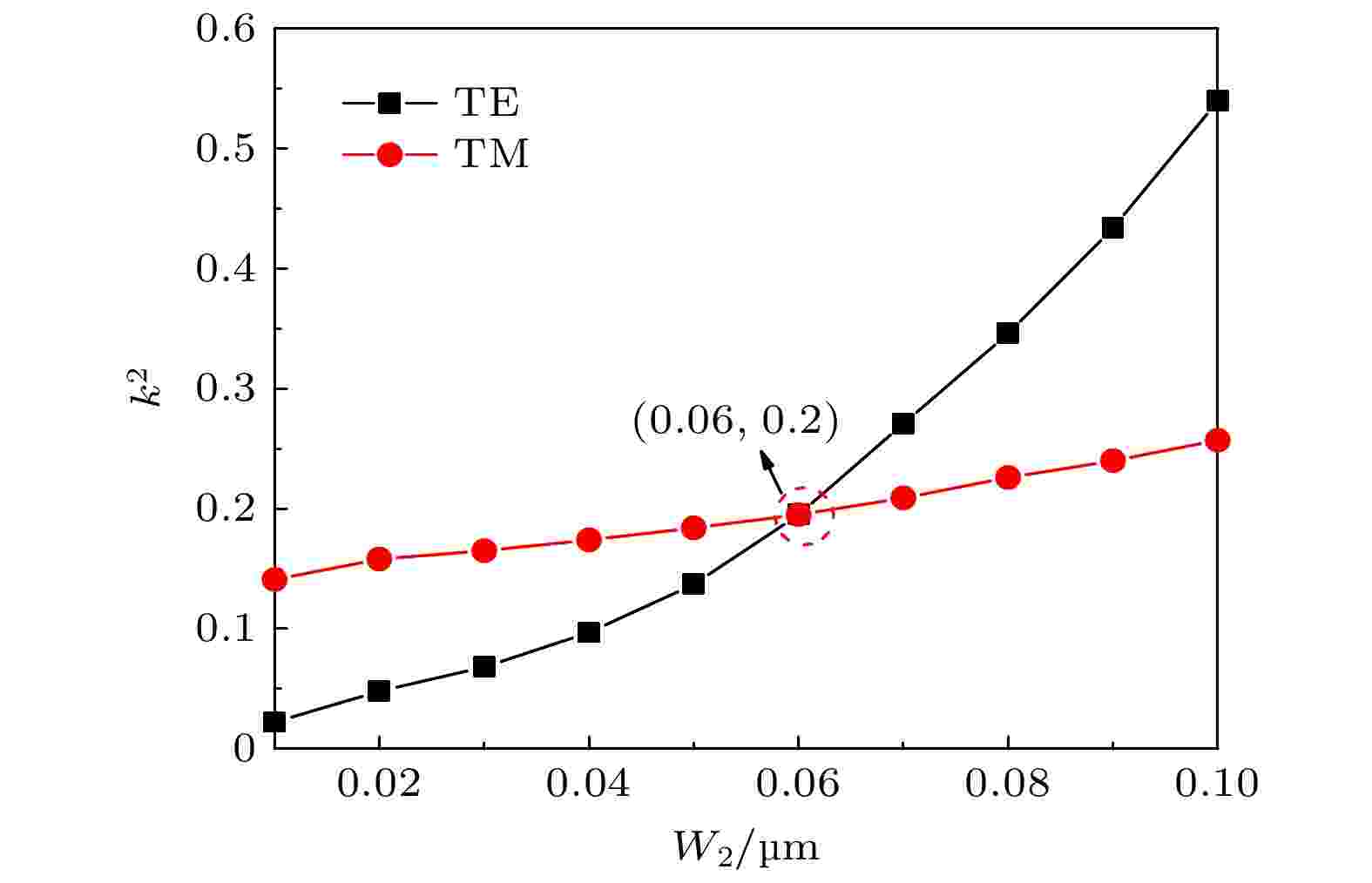图 3 k ²随W₂的变化
Figure3. k ² as a function of W₂.

如上文所述, 当g和n₁(SiN_x)确定时, 可以通过调节W₂得到k ²(λ, TE) = k ²(λ, TM) = k ², 使得耦合区偏振无关. 为了便于后续器件性能优化时提供参数需要, 进一步探讨耦合区满足偏振无关时, k ²受g和n₁(SiN_x)的影响. 如图4(a)所示. k ²随n₁(SiN_x)的减小而增大, 当n₁(SiN_x)固定时, k ²随g的增大而减小. 图4(b)给出了图4(a)中每一组g和n₁(SiN_x)实现耦合区偏振无关时所对应的W₂.
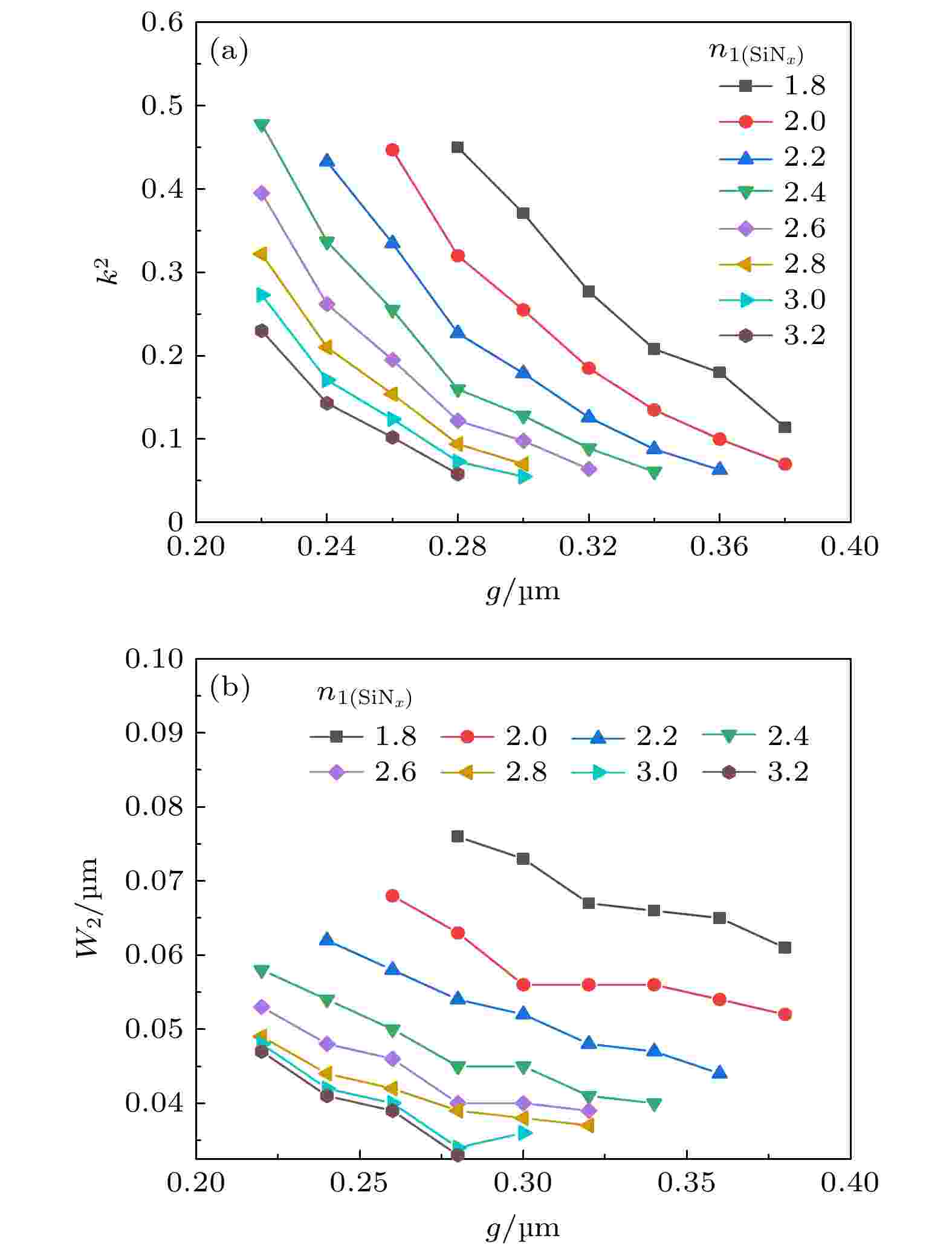图 4 (a) 耦合区满足偏振无关时, 不同n₁(SiN_x)情况下k ²随g的变化; (b) 每一组g和n₁(SiN_x)实现耦合区偏振无关时其对应的W₂
Figure4. (a) k ² as a function of g under different n₁(SiN_x) when the light intensity is polarization-insensitive; (b) W₂ as a function of g under different n₁(SiN_x) when the light intensity is polarization-insensitive

3 -->

3.1.2.谐振波长偏振无关的实现

从(1)式可见: 微环谐振器的谐振波长和微环波导的模式有效折射率有关. 要实现谐振波长偏振无关, 就要求TE和TM偏振模的模式有效折射率相同, 从而使不同偏振模对应的谐振波长相等, 即满足下面公式: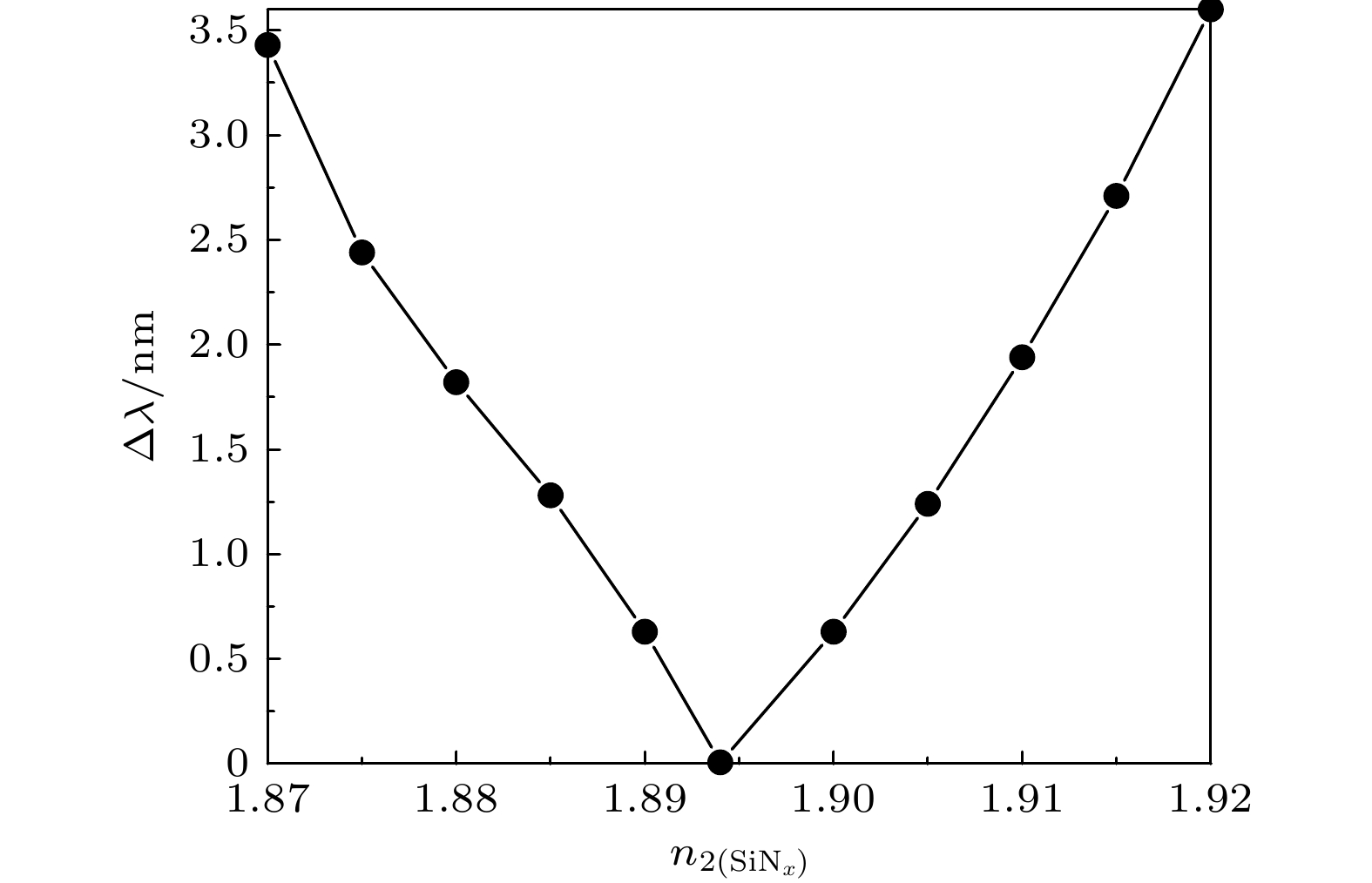

$\Delta \lambda = \left| {\lambda \left( {{\rm{TE}}} \right) - \lambda \left( {{\rm{TM}}} \right)} \right| = 0.$

事实上, 因为SOI波导本身具有双折射效应, TE和TM偏振模的模式有效折射率并不相同. 并且有文献报道: 弯曲波导的引入会加剧器件的偏振相关性^[20]. 为了消除后者造成的影响, 目前主要采用增加弯曲波导半径的方式, 其缺点就是尺寸大, 不利于集成. 为了解决上述问题, 本文拟独立调整弯曲波导中三明治结构内n ₂(SiN_x)的大小, 使得Δλ = 0. 如图2所示, 在三明治结构中TE偏振模与TM偏振模分别在Si层与SiN_x层传播, 因此当n ₂(SiN_x)变化时, λ(TM)的改变量会明显大于λ(TE)的改变量, 从而有效地降低Δλ. 图5为R = 10 μm, g = 0.323 μm, Λ = 0.2 μm, W₂ = 0.06 μm, n₁(SiN_x) = 1.9时, n ₂(SiN_x)变化对Δλ的影响. 从图5可以看出, 随着n ₂(SiN_x)的增加, Δλ先单调减小再单调增加, 且在n ₂(SiN_x) = 1.894时Δλ = 0. 此时TE和TM偏振模的谐振波长完全重合, 实现了谐振波长的偏振无关.
图 5 Δλ随n ₂ (SiN_x)的变化
Figure5. Δλ as a function of n ₂ (SiN_x) in ring.

综上, 当微环谐振器参数取R = 10 μm, g = 0.323 μm, Λ = 0.2 μm, W₂ = 0.06 μm, n₁(SiN_x) = 1.9, n₂(SiN_x) = 1.894时, 可以实现偏振无关的微环谐振器.
2 -->

3.2.微环谐振器性能的优化

对于应用于密集波分复用器的微环谐振器而言, 最重要的性能指标是插入损耗(insertion loss, IL)和3-dB带宽. IL定义公式为

${\rm{IL}}\left( {{\rm{dB}}} \right) = - 10\log \left( {\frac{{{P_{\rm{d}}}}}{{{P_{{\rm{in}}}}}}} \right), $

其中P_d为输出端的输出光功率峰值, P_in为输入端的输入光功率.
3-dB带宽指的是当输出功率下降到峰值的一半时的带宽, 在信道间隔为0.8 nm的密集波分复用器中一般要求3-dB带宽小于0.8 nm^[11].
由(4)式可知, 在弯曲波导半径和器件其他波导长度、宽度不变的情况下, 输出端光强度仅与k ²有关. 而由定义可知: IL和3-dB带宽均与输出端光强度有关, 因此k ²的变化会对IL与3-dB带宽产生直接的影响.
保持结构参数R = 10 μm, Λ = 0.2 μm, W₂ = 0.06 μm, n₁(SiN_x) = 1.9, n ₂(SiN_x) = 1.894不变, 仅通过改变g调整k ²的大小. 图6给出了k ²与g的变化关系, 由图可见, 随着g的增加, k ²从0.35单调递减至0.05.
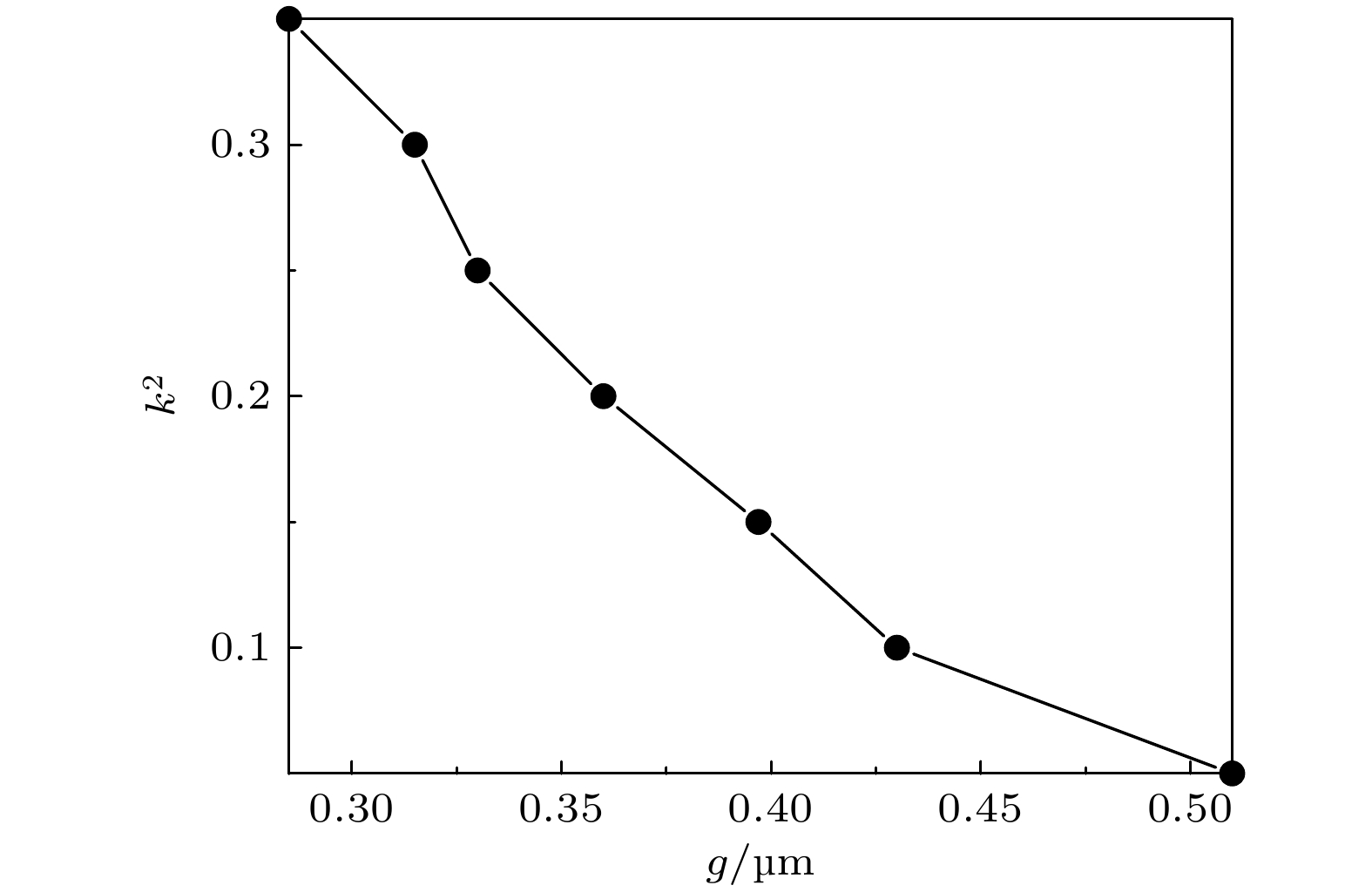图 6 k ²随g的变化
Figure6. k ² of download port as a function of g.

图7(a)展示了k ²对IL的影响, 结果表明: IL随着k ²的增加而减小, 并且在k ² > 0.3时, IL接近0. 为了得到较小的IL, 希望k²的取值尽量偏大. 图7(b)展示了k ²对3-dB带宽的影响. 结果表明: 在k ²从0.05增加至0.35的过程中, 3-dB带宽也从0.3单调递增至1.7. 考虑到3-dB带宽小于等于0.8 nm时, 可应用于信道间隔为0.8 nm的密集波分复用器. 因此, 此处可以选择k ² ≤ 0.2, 结合图7(a)所示, 为了得到较小的IL, 希望k ²的取值尽量偏大, 最终确定k ² = 0.2.
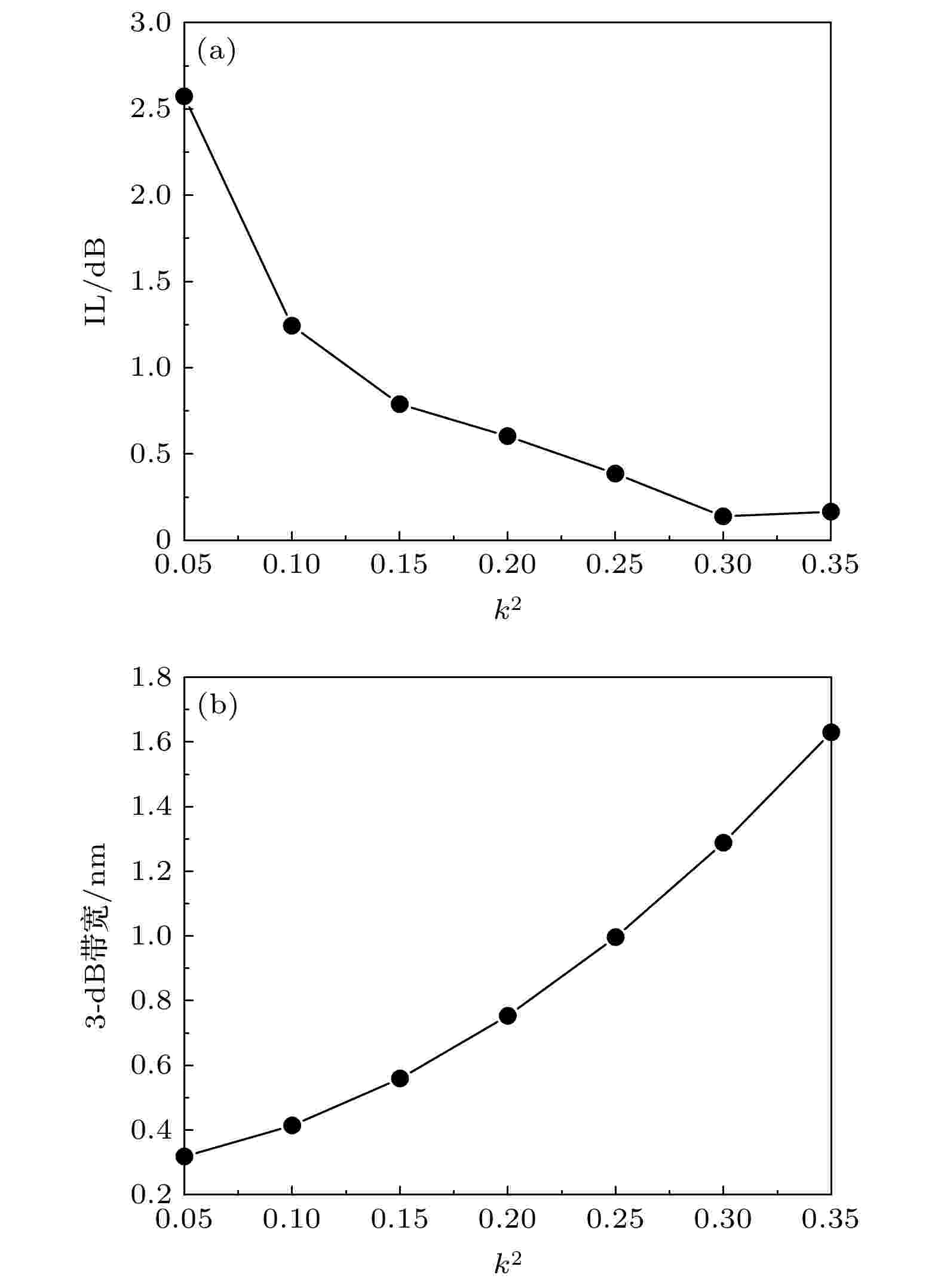图 7 (a) k ²变化对IL的影响; (b) k ²变化对3-dB带宽的影响
Figure7. (a) IL of download port as a function of k ²; (b) 3-dB bandwidth as a function of k ².

k ² = 0.2时, 由前文涉及的图4可知: 存在多种n₁(SiN_x), g与W₂的组合, 能够令器件的耦合区满足偏振无关. 而不同的n₁(SiN_x), g与W₂的组合, 会令器件IL发生改变. 为此, 进一步作参数优化. 图8展示了IL与n₁(SiN_x)的关系: 随着n₁(SiN_x)的增加IL先减小后增加, 在n₁(SiN_x) = 2.8时IL达到最小值, 此时微环耦合区各参数分别为g = 0.24 μm, Λ = 0.2 μm, n₁(SiN_x) = 2.8, W₂ = 0.044 μm. 因为耦合区参数发生变化, 所以需要重新调整n ₂(SiN_x)以实现谐振波长的偏振无关. 采用上文的方法进行调整, 当n ₂(SiN_x) = 2.853时有Δλ = 0.
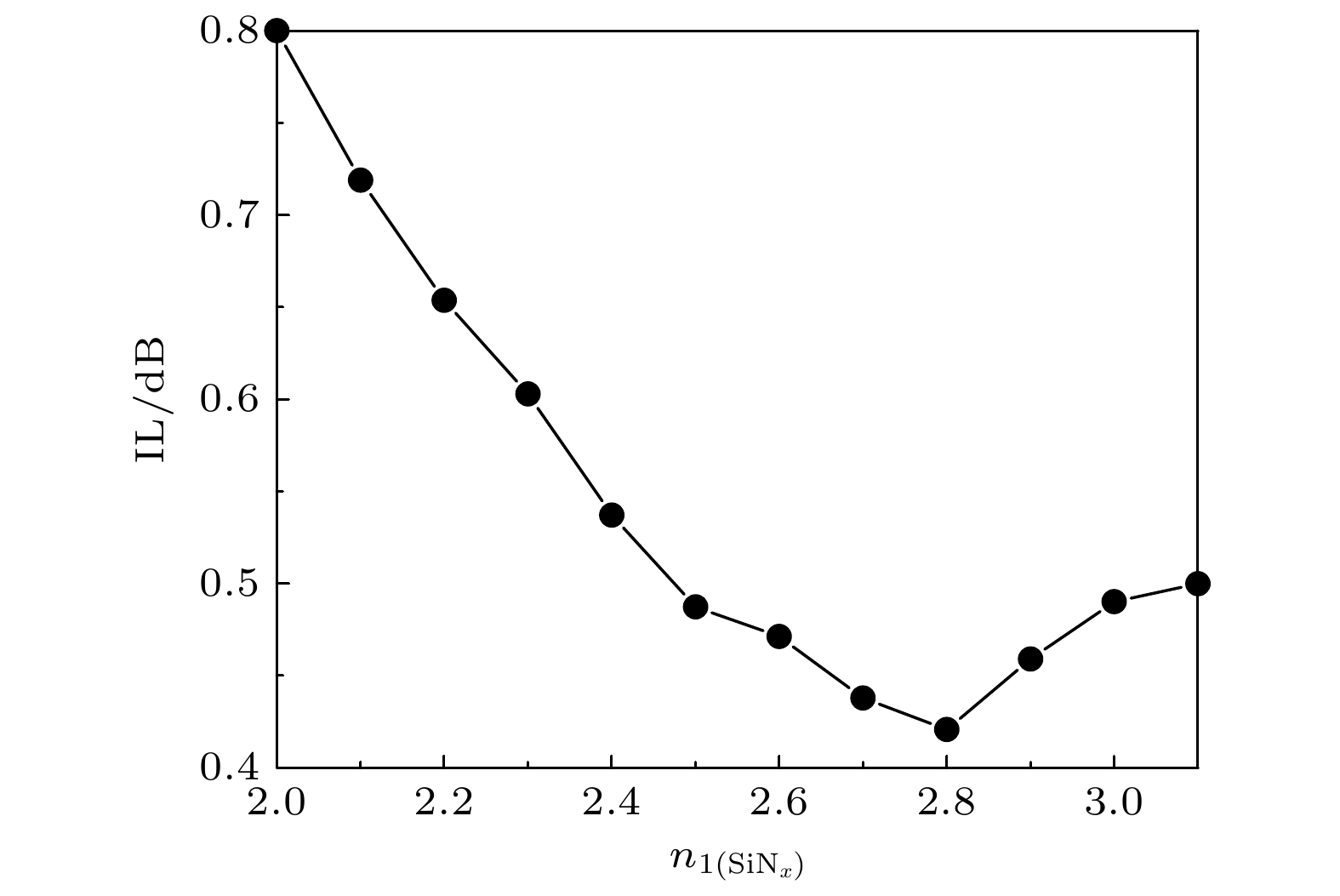图 8 微环谐振器偏振无关且k ² = 0.2时n₁ (SiN_x)变化对IL的影响
Figure8. IL as a function of n₁(SiN_x) when the ring resonator is polarization-insensitive and k ² = 0.2.

此时, TE和TM偏振模时的输出端透过率谱线如图9所示: 在谐振波长1552.26 nm附近, 两者完全重合, 实现了偏振无关.
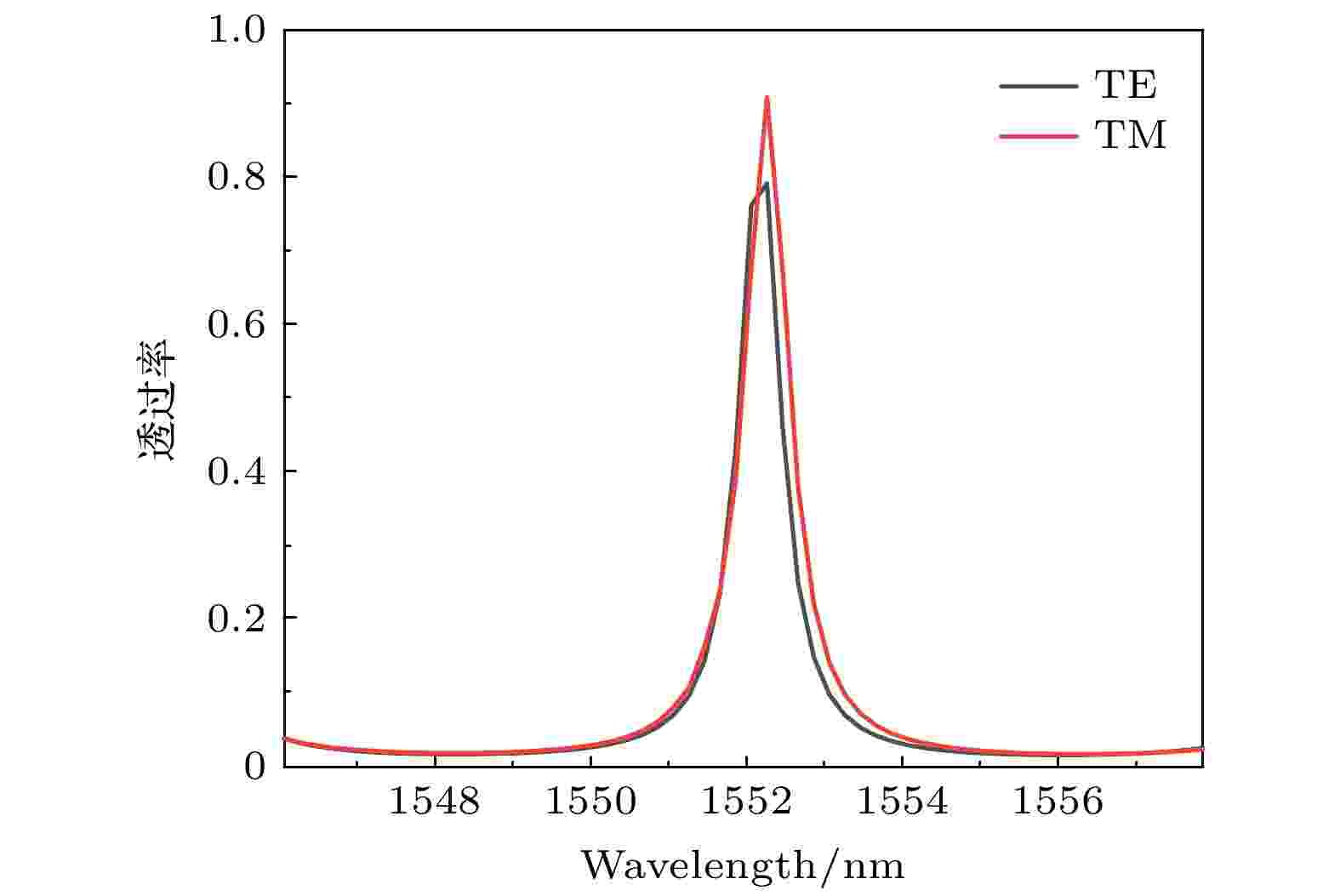图 9 TE和TM偏振模时的输出端透过率谱线
Figure9. Measured transmission spectra with TE- and TM-polarized light inputs for the out port.

综上所述, 所设计的微环谐振器结构参数为R = 10 μm, g = 0.24 μm, Λ = 0.2 μm, n₁(SiN_x) = 2.8, n ₂(SiN_x) = 2.853, W₂ = 0.044 μm, 器件在TE和TM偏振模时的IL分别为0.77与0.42 dB; 3-dB带宽分别为0.68与0.7 nm, 符合通道间隔为0.8 nm的密集波分复用器的性能要求. 表1列出了已报道的偏振无关微环谐振器与所提出器件的性能的比较: 本文中器件的损耗远小于文献[11-13]中提及的, 并且尺寸仅为文献[11,13]中涉及的器件的1/20. 综合考虑器件的损耗与尺寸, 本文设计的器件有着较大的优势.

性能参数	IL/dB	微环半径/μm
文献[11]	< 3	200
文献[12]	< 3	3.7
文献[13]	< 2	200
本文	< 0.8	10

表1偏振无关微环谐振器的性能参数
Table1.Performances of the polarization-insensitive ring resonator.

此外, 需要考虑工艺制作偏差对器件光学性能的影响. 图10(a)—(d)讨论了器件参数W₁, W₂的变化ΔW₁, ΔW₂分别对器件IL和3-dB带宽的影响. 由图10(a)和图10(b)可看出, 器件对W₁的容差性较好, 当ΔW₁在–8—8 nm间变化时, IL < 1 dB, 3-dB带宽小于0.8 nm. W₂主要影响微环谐振器的偏振相关性, 如图10(c)和图10(d)所示, 当ΔW₂在–5—5 nm间变化时, IL < 2 dB, 3-dB带宽小于0.8 nm, 此时器件性能仍然较为良好.
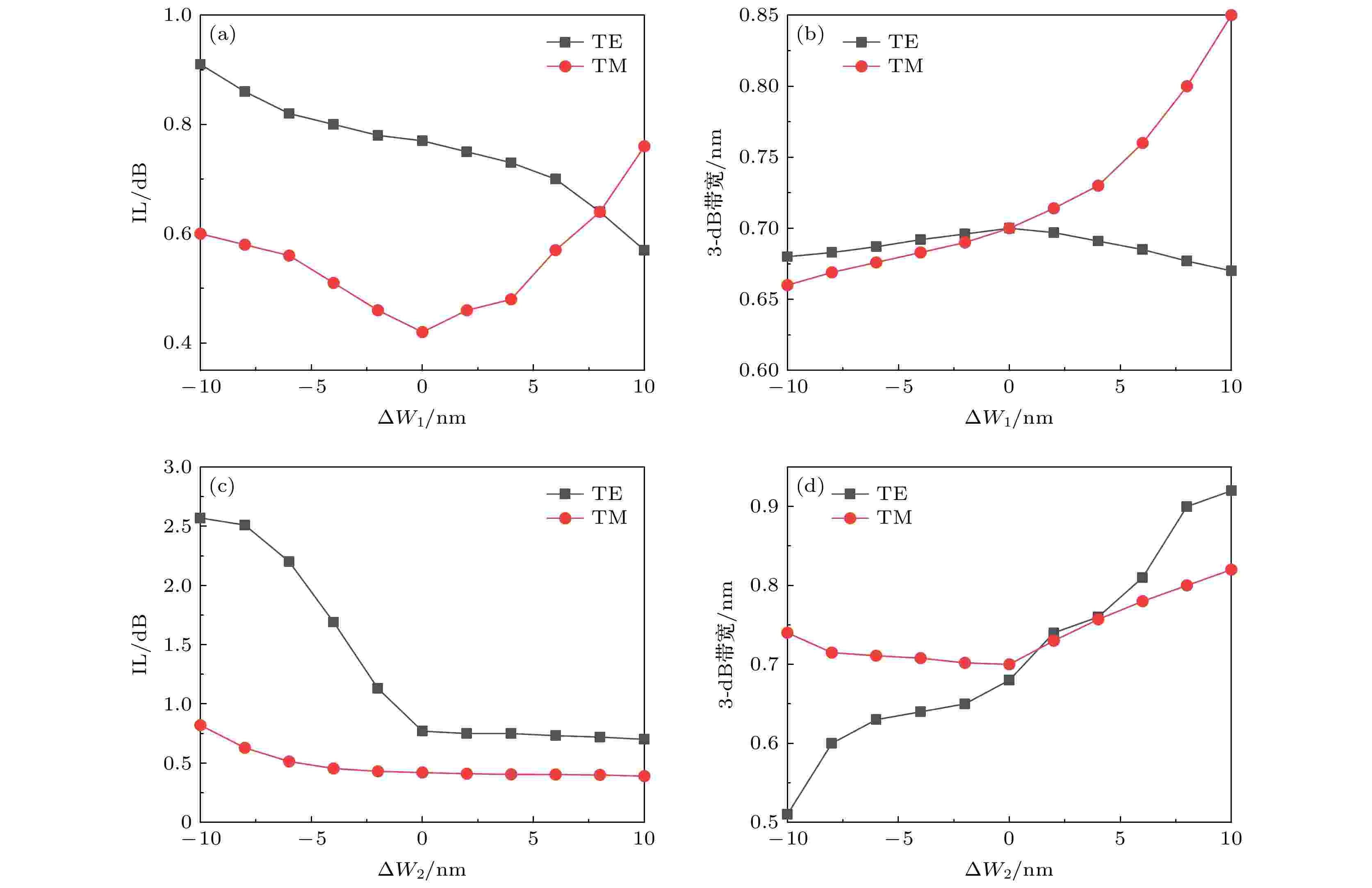图 10 器件性能随结构参数的变化　(a) IL随ΔW₁的变化; (b) 3-dB带宽随ΔW₁的变化; (c) IL随ΔW₂的变化; (d) 3-dB带宽随ΔW₂的变化
Figure10. Performances as functions of structural parameters: (a) IL as a function of ΔW₁; (b) 3-dB bandwidth as a function of ΔW₁; (c) IL as a function of ΔW₂; (d) 3-dB bandwidth as a function of ΔW₂.

本文设计了一种基于SWG和三明治结构的偏振无关微环谐振器. 首先, 讨论如何利用组合结构实现微环谐振器耦合区的偏振无关, 分析了耦合区的结构参数对k ²(λ, TE)和k ²(λ, TM)的影响, 结果表明: 对于不同的g和n₁(SiN_x)组合, 均可通过合理选择W₂使得k ²(λ, TE) = k ²(λ, TM), 从而实现耦合区的偏振无关. 其次, 通过调整弯曲波导处SiN_x层的折射率n ₂(SiN_x)消除了微环谐振器谐振波长的偏振相关性. 最后, 经过参数优化, 使得所设计的微环谐振器在TE和TM偏振模时的3-dB带宽均小于0.8 dB, 插入损耗均小于0.8 dB. 并且, 所设计的微环半径仅为10 μm集成度更高, 插入损耗更低, 可用于信道间隔为0.8 nm的密集波分复用器. 最后对器件的制作容差进行了分析, 仿真结果表明在–8 nm < ΔW₁ < 8 nm, –5 nm < ΔW₂ < 5 nm范围内, 器件性能较好(IL < 2 dB, 3-dB带宽小于0.8 nm). 此外, 本文所设计的微环谐振器可采用感应耦合技术、反应离子刻蚀结合等离子体离子辅助沉积法等实现^[21,22].