摘要: 碳纤维增强复合材料在制造和使用过程中会产生褶皱, 褶皱缺陷的存在使得纤维层起伏不平, 超声波传播至纤维界面时不同声束方向的声能量存在差异. 针对此问题, 提出一种基于声束指向性函数校正的全聚焦阵列成像方法: 制备了含褶皱缺陷的碳纤维增强复合材料试样, 建立超声阵列数据采集实验系统, 捕获全矩阵数据; 考虑超声发射/接收阵元不同声束方向的声能量差异, 提出全聚焦成像方法的校正模型; 将校正前后的全聚焦成像结果与试样的实物图和光学显微镜图像进行对比分析. 实验结果表明: 基于指向性函数校正的全聚焦成像方法能够有效降低背景噪声, 恢复出被检试样的褶皱缺陷和铺层结构等细节信息, 为碳纤维增强复合材料褶皱缺陷的精确表征提供了理论指导.
关键词: 超声相控阵 /
褶皱缺陷 /
全聚焦成像 /
指向性校正 English Abstract Ultrasonic imaging of wrinkles in carbon-fiber-reinforce-polymer composites Zhang Hai-Yan 1 ,Song Jia-Xin 1 ,Ren Yan 1 ,Zhu Qi 2 ,Ma Xue-Fen 3 1.School Institute for Advanced Communication and Data Science, School of Communication and Information Engineering, Shanghai University, Shanghai 200444, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11874255, 11904223)Received Date: 07 January 2021Accepted Date: 08 February 2021Available Online: 09 June 2021Published Online: 05 June 2021Abstract: Carbon-fiber-reinforced-polymer (CFRP) composites are widely used in aerospace, automobile and other industries because of their excellent performances. However, wrinkles will be formed during the manufacturing and service life process of composites, which is detrimental to the fatigue limit and tensile strength. Due to the fiber waviness, the presence of such defects leads to the acoustic energy difference in different beam directions during ultrasonic nondestructive testing. The directly obtained imaging amplitude cannot characterize the wrinkle properly. In order to solve this problem, the total focusing method (TFM) imaging combing the acoustic beam directivity function correction is presented. Firstly, the longitudinal wave signal is excited by an ultrasonic phased array, from which the echo data is collected by full matrix capture (FMC) in both the healthy and defected samples prepared. Then, considering the difference in acoustic energy from different beam directions of each ultrasonic transmitting/receiving array element, a correction TFM is proposed. Finally, the echo signals are post processed while the results are compared with the optical images. No wrinkle information can be indicated from the direct TFM imaging. In contrast, the wrinkles and layer-up information can be recovered from the corrected TFM imaging with an improved signal-to-noise ratio and resolution. Furthermore, owing to the directivity function, the near-surface noise can be effectively reduced and the near-surface fibrous layer information is restored. This method paves the way for the accurate, quantitative and rapid characterizing of wrinkles in real CFRP structures. Keywords: ultrasonic phased array /wrinkle defects /total focus method imaging /directional correction 全文HTML --> --> --> 1.引 言 相比于铝合金等轻质金属材料, 以碳纤维为增强材料, 树脂为基体构成的碳纤维增强复合材料[1 ,2 ] (carbon fiber reinforced polymer, CFRP)具有质量轻、强度高、韧性好和耐腐蚀等优点, 被广泛应用于航空航天、汽车、海洋工程等领域[3 ] , 如: 民用飞机的飞机舱门、机翼、卫星天线、主体骨架结构, 汽车车身和底盘等[4 ,5 ] . 由于CFRP是由两种材料复合而成, 并且制造工艺复杂独特, 加工过程中存在很多不稳定因素, 导致在生产过程中出现富脂、贫脂、褶皱、夹杂和孔隙等缺陷[6 ] . 在服役过程中也会因外部因素诱发分层、断裂、脱粘等不同程度的损伤[7 ,8 ] . 研究表明缺陷的扩展严重降低复合材料的疲劳极限、拉伸强度和寿命[9 ,10 ] , 其中富脂和纤维褶皱等微缺陷很难检测识别, 如果不能及时发现和修复细微缺陷最终将造成重大经济损失和安全事故. 因此对CFRP进行缺陷检测具有重要的研究价值和意义.[11 ] 采用不同频率的探头对CFRP中的分层和富树脂进行检测和表征, 使用时间校正增益抑制系统噪声提高信噪比, 证实了树脂层和分层的反射强度与探头频率相关. Wang等[12 ] 采用超声相控阵对CFRP进行三维损伤量化, 利用重建体积的回波幅度特征, 根据–6 dB下降准则可直接进行损伤识别、定位和量化. Nelson等[13 ] 提出了基于超声回波无损技术的方法, 使用Radon变换方法处理脉冲回波的瞬时幅度数据, 以获得局部区域的纤维分布方向, 叠加瞬时相位数据可定位层界面.[14 ] 提出全聚焦算法(total focus method, TFM), 在API(array performance indicator)的评价系数标准下, TFM的成像效果远高于其他常规相控阵成像方法, 是目前最热门的后处理方法之一. Pain等[15 ] 对不同纤维波纹度的CFRP进行研究, 实验证明回波信号的幅度信息受噪声影响很大, 而相位对信号的衰减相对不敏感, 采用全聚焦瞬时相位成像方法进行表征效果更好. Beatriz等[16 ] 使用三种不同的方法检测和表征CFRP褶皱缺陷, 得出全矩阵捕获和全聚焦成像方法最佳的结论, 采用角度-速度校正方法可实现成像进一步增强. Wilcox等[17 ] 使用与超声波幅度衰减和声束偏转相关的向量函数对全聚焦成像方法进行修正, 可以分辨出缺陷的方向性, 提高了对小缺陷的检测率. 周正干等[18 ] 通过楔块耦合建立双层介质能量衰减模型, 利用衰减校准系数修正全聚焦算法, 扩大了检测角度范围, 降低了漏检率.2.指向性函数校正模型 22.1.全聚焦成像原理 2.1.全聚焦成像原理 全聚焦成像算法是基于全矩阵采集的后处理算法, 图1 是其原理图. 利用超声相控阵捕获全矩阵信号, 由N 个阵元组成的超声探头依次单独激励阵元发射超声信号, N 个阵元同时接收信号, 得到一个N × N 的全矩阵信号.图 1 全聚焦成像算法原理图Figure1. The schematic diagram of TFM imaging.x 方向是探头在表面移动的方向, z 方向是被检测物体的深度方向. 假设在$ (x, z) $ 处为目标聚焦点, 则从第i 个阵元发射超声波到达缺陷, 由第j 个阵元接收到缺陷的散射信号, 超声波的旅行时间为c 为超声波在被检测材料中传播速度, $ {x}_{i} $ 为发射传感器的位置, $ {x}_{j} $ 为接收传感器的位置.N 个传感器所组成的传感器阵列内所有收发组旅行时间所对应的信号幅值进行叠加, 可得到空间内任意网格点$ \left(x, z\right) $ 处的像素值[19 ] , 从而实现缺陷的表征:$ {h}_{ij}\left(t\right) $ 表示第i 个阵元发射超声波第j 个阵元接收得到的回波数据.2.2.全聚焦成像校正算法 -->2.2.全聚焦成像校正算法 图1 中聚焦点A 和B 位于以发射传感器和接收传感器为焦点的椭圆上, 根据椭圆定律可知, 超声波从发射传感器经过A 点和B 点到达接收传感器的距离是相等的, 代入(1 )式两者的旅行时间相等. (2 )式表明全聚焦成像算法中每一点的像素值仅依赖于时间变量, 则在聚焦点A 和B 处的像素值是相同的. 而实际上, 相较于B 点, 声束传播到A 点方向与超声阵列法线方向的夹角更小(图1 中$ {\theta }_{A} < {\theta }_{B} $ ), A 点的超声振幅更大[20 ] . 对于CFRP这种结构复杂的待检测试样, 褶皱的存在使得纤维层起伏不平, 超声波入射到纤维层界面时不同声束方向的声能量存在差异, 常规全聚焦成像方法很难呈现出CFRP的铺层结构和纹理结构, 从而无法实现褶皱缺陷的精确表征, 因此十分必要考虑不同声程的能量影响.[21 ] :d 为阵元宽度, $ \lambda $ 为超声波波长, $ \theta $ 为界面法线方向与声束传播方向的夹角.$ {\theta }_{i} $ , $ {\theta }_{j} $ 分别为聚焦点与发射阵元和接收阵元的夹角.4 )式体现了不同声束方向的声场能量, 综合(2 )式和(4 )式, 校正后的全聚焦成像公式为[22 ] $ H\left({\theta }_{i}, {\theta }_{j}\right) $ 为阵元指向性函数权重因子.3.实 验 搭建实验装置如图2 所示, 实验仪器与材料包括: 计算机、M2M (Multi2000, M2M Inc, Les Ulis, France)相控阵超声波探伤仪、相控阵探头、3块CFRP试样. 相控阵超声探头共有32个发射/接收阵元, 实验时设置激励信号为5个周期的高斯正弦波.图 2 实验装置图Figure2. Experimental device.$ \times $ 80 mm$ \times $ 18 mm, 试样的纤维铺层结构如图6(a) 、图7(a) 、图8(a) 所示, 其中试样A无褶皱, 试样B和试样C褶皱缺陷样式不同. 每块试样可细分为5大层. 第1大层厚6 mm, 其中含有1层玻璃纤维, 40层碳纤维预浸料. 其他4大层的厚度分别为3.0, 2.5, 3.0, 3.5 mm, 其中含有1层玻璃纤维, 20层碳纤维预浸料. 0°和90°碳纤维预浸料交替铺层, 且预浸料中含有树脂纤维, 树脂纤维厚度约为0.003—0.010 mm. 试样上下表面为玻璃纤维. 玻璃纤维和0°/90°碳纤维预浸料平均厚度约为0.15 mm. 图3 给出了试样中有、无褶皱的光学显微镜图像, 其中图3(a) 显示的是试样A的第3大层结构, 图3(b) 是试样B中含有褶皱缺陷的部分显微镜图像, 从中可以清晰地观察到纤维的铺层信息及是否存在褶皱.图 3 CFRP显微镜图 (a)无褶皱; (b)有褶皱Figure3. Microscopic image of CFRP: (a) No wrinkles; (b) wrinkles.图 6 试样A及其成像结果 (a)实物图; (b)图6(a) 的局部放大图; (c)全聚焦成像结果; (d)图6(c) 的灰度图; (e)用指向性函数校正的全聚焦成像结果; (f)图6(e) 的灰度图Figure6. Sample A and imaging results: (a) Sample A; (b) partial enlarged view of Fig.6 (a) ; (c) total focus method; (d) gray scale of Fig.6 (c) ; (e) total focus method corrected by directivity function; (f) gray scale of Fig.6 (e) .图 7 试样B及其成像结果 (a)实物图; (b)图7(a) 的局部放大图; (c)全聚焦成像结果; (d)图7(c) 的灰度图; (e)用指向性函数校正的全聚焦成像结果; (f)图7(e) 的灰度图Figure7. Sample B and its imaging results: (a) Sample B; (b) partial enlarged view of Fig.7(a) ; (c) total focus method; (d) gray scale of Fig.7 (c) ; (e) total focus method corrected by directivity function; (f) gray scale of Fig.7 (e) .图 8 试样C及其成像结果 (a)实物图; (b)图8(a) 的局部放大图; (c)全聚焦成像结果; (d)图8(c) 的灰度图; (e)用指向性函数校正的全聚焦成像结果; (f)图8(e) 的灰度图Figure8. Sample C and its imaging results: (a) Sample C; (b) partial enlarged view of Fig. 8 (a) ; (c) total focus method; (d) gray scale of Fig. 8 (c) ; (e) total focus method corrected by directivity function; (f) gray scale of Fig. 8 (e) .x 轴, 垂直方向为z 轴. 将超声相控阵探头放置于复合材料表面, 32个阵元的排列方向为x 轴方向. 采用纵波激励方式, 纵波在该复合材料板中的传播波速约为$ v=2900\;\mathrm{m}/\mathrm{s} $ , 则波长为$ \lambda $ = $ v/f $ = 0.58 mm. 为了增强复合材料单层的反射, 由该材料单层的共振频率决定超声检测探头的中心频率. 第一阶的共振频率公式满足下式[23 ] :$ {d}_{1} $ 为碳纤维层厚度, $ {d}_{2} $ 为树脂纤维厚度. 如图3(a) 所示, 碳纤维预浸料厚度为0.15 mm (包含树脂纤维, 即$ {d}_{1}+{d}_{2}=0.15 $ ), 代入上式可以计算出样品的共振频率约为$ {f}_{1}=9.67 $ MHz. 当中心频率$ {f}_{\mathrm{c}} $ 满足$0.4 \leqslant {f}_{\mathrm{c}}/{f}_{1}\leqslant1.3$ 时, 单层的反射系数较大[24 ] , 所以选取$ {f}_{\mathrm{c}}= 5$ MHz的探头是可行的, 超声相控阵具体参数配置如表1 所示.参数 值 参数 值 阵元个数 32 阵元宽度/mm 0.9 阵元中心距/mm 1.0 采样频率/MHz 50 中心频率/MHz 5 激励方式 纵波
表1 超声相控阵参数配置Table1. Parameters configuration of ultrasonic phased array.$ \times $ 32个回波信号, 时间窗口长度均为100 μs. 图4 为16号传感器自发自收的前15 μs时域信号. 从中可以观察到幅值很大的表面直达波、幅值较小的损伤散射波及底面反射波.图 4 i = j = 16时域信号Figure4. For i = j =16 time domain signal.图5 为1号传感器发射超声波, 编号为4n (n 为整数)的传感器接收到的前15 μs回波信号. 从图4 可看出: 当接收阵元距离发射阵元较近时, 由于阵元间的电子和机械串扰, 回波信号持续时间较长且混叠了噪声信号, 这种现象在4号和8号阵元的回波信号中较明显. 此外, 由于系统产生的非线性效应, 各阵元接收到的始波信号还延伸至约4 μs处, 如图中的虚线方框位置. 若将这些信号用于全聚焦成像, 将会在材料表面产生盲区, 从而掩盖近表面层的纤维信息.图 5 典型阵列回波信号Figure5. Typical echo signal captured by full matrix.4.结果与讨论 采用图2 中的相控阵实验装置, 选取1个阵元发射纵波, 32个阵元同时接收, 依次激发各个阵元, 最终捕获到32$ \times $ 32的全矩阵数据. 图6 是试样A即无褶皱CFRP的实物图和成像结果, 成像区域为30 mm$ \times $ 20 mm. 其中, 图6(a) 是实物图, 图6(b) 是图6(a) 中方框标记区域的局部放大图, 图6(c) 是直接全聚焦成像结果, 图6(d) 是图6(c) 的灰度图, 图6(e) 是经指向性函数校正后的成像结果, 图6(f) 是图6(e) 的灰度图. 由成像结果可知, 直接全聚焦成像方法(图6(c) 和图6(d) )十分模糊, 基本看不出CFRP的铺层结构, 而指向性函数校正后的全聚焦成像方法可以恢复出纹理信息. 从图6(e) 和图6(f) 可观察出: 试样A含有5大层结构. 由于玻璃纤维相对于碳纤维具有高反射性, 所以较粗明亮纹路为玻璃纤维, 90°碳纤维预浸料中含有更多的树脂纤维, 反射系数随着树脂厚度增加而增大, 所以较细明亮纹路为90°碳纤维, 深色纹路为0°碳纤维. 因加工过程中存在许多不稳定因素, 无法使0°碳纤维和90°碳纤维厚度绝对均匀, 或者因纤维之间存在多次回波, 对成像结果的分辨率产生了影响, 导致层间较粗明亮纹路是由多层方向各异碳纤维组成. 除了第一大层部分纤维纹路被噪声完全覆盖, 其他4大层中可见1层玻璃纤维, 20层碳纤维, 符合图3 中无褶皱试样光学显微镜图像呈现的制造工艺, 且玻璃纤维的成像位置和实际位置基本一致, 具体数值见表2 . 由于声波在传播过程中能量逐渐降低, 反射回波信号较弱, 使得z = 15 mm以下的成像图相对模糊. 研究中还发现, 由于系统产生的非线性效应, 各阵元接收到的始波信号延伸至约4 μs处(图4 ), 将在材料表面产生噪声区域, 如图6(d) 中z 方向0—6 mm区域. 经指向性函数校正后的全聚焦成像可以分辨出4—6 mm的纤维纹路, 如图6(f) 所示. 可见, 基于指向性函数校正的全聚焦成像可以降低近表面噪声, 提高图像的信噪比和分辨率, 恢复出更多细节信息.玻璃纤维 实际位置/mm 成像位置/mm 误差/% 第一层底部 6.0 5.95 0.83 第二层底部 9.0 8.85 1.60 第三层底部 11.5 11.45 0.04 第四层底部 14.5 14.15 2.40 第五层底部 18.0 17.55 2.50
表2 图6(f) 中玻璃纤维的成像位置和实际位置对比Table2. Comparison of imaging position in Fig. 6(f) and actual position of glass fiber.图7 和图8 . 可以观察到, 未校正的图像基本观察不到纤维铺层结构及是否含有褶皱缺陷, 而校正后的图像可以恢复出褶皱信息, 且图7(f) 和图8(f) 中褶皱与实物试样高度一致, 如圆圈标记区域的细节信息与图7(b) 和图8(b) 局部放大图一致, 且缺陷深度与实际深度误差不超过6%. 可见, 经指向性函数校正之后, 全聚焦成像的质量大大提高, 从而可实现褶皱缺陷的精确表征.5.结 论 针对CFRP在制造和使用过程中产生的亚宏观褶皱缺陷, 提出一种全聚焦成像的校正方法, 使用相控阵对3块复杂纤维铺层的CFRP试样进行超声检测, 得到了高质量的重建图像, 能够再现纤维层的细节信息. 主要研究结果包括: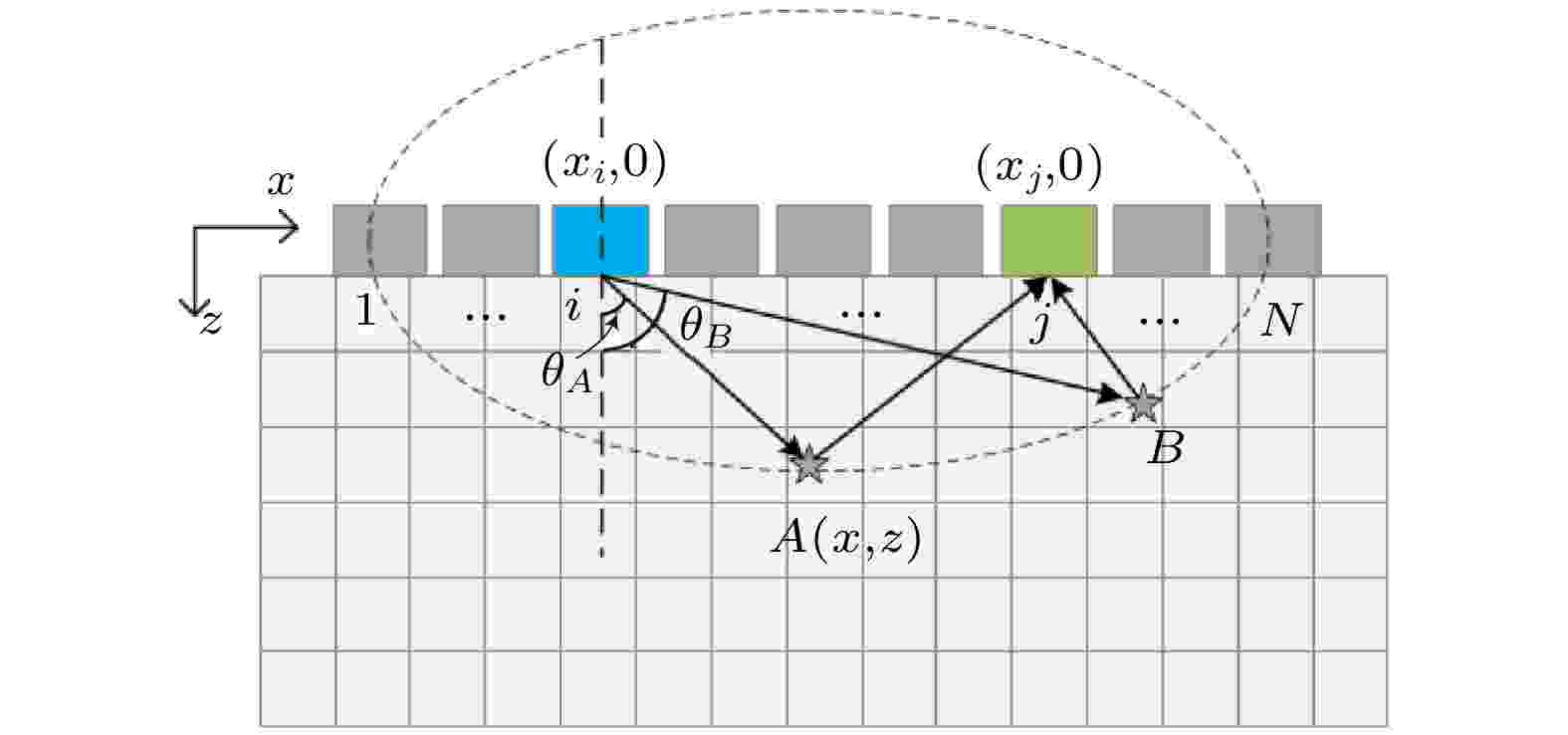 
图 1 全聚焦成像算法原理图
图 2 实验装置图
图 3 CFRP显微镜图 (a)无褶皱; (b)有褶皱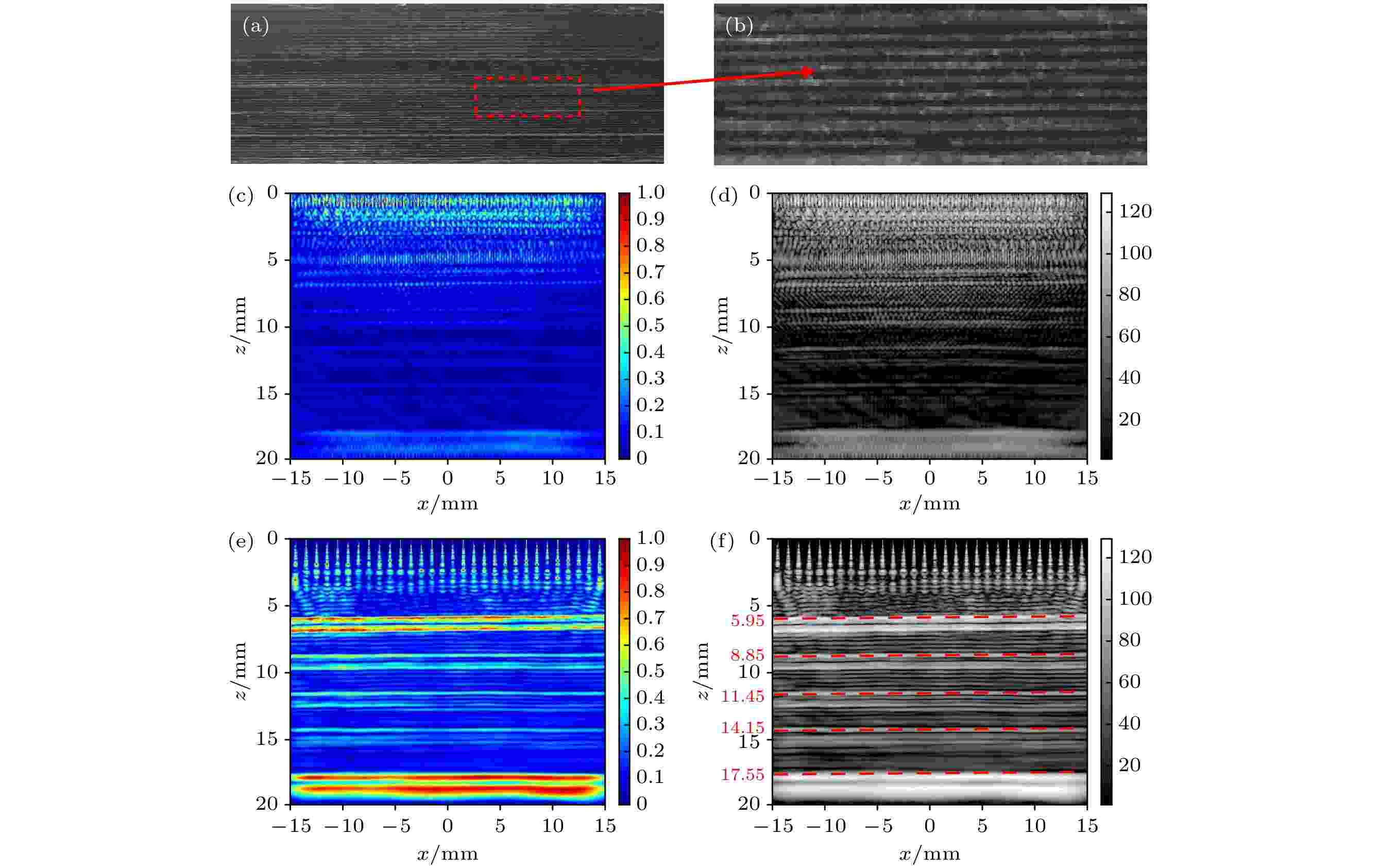
图 6 试样A及其成像结果 (a)实物图; (b)图6(a)的局部放大图; (c)全聚焦成像结果; (d)图6(c)的灰度图; (e)用指向性函数校正的全聚焦成像结果; (f)图6(e)的灰度图
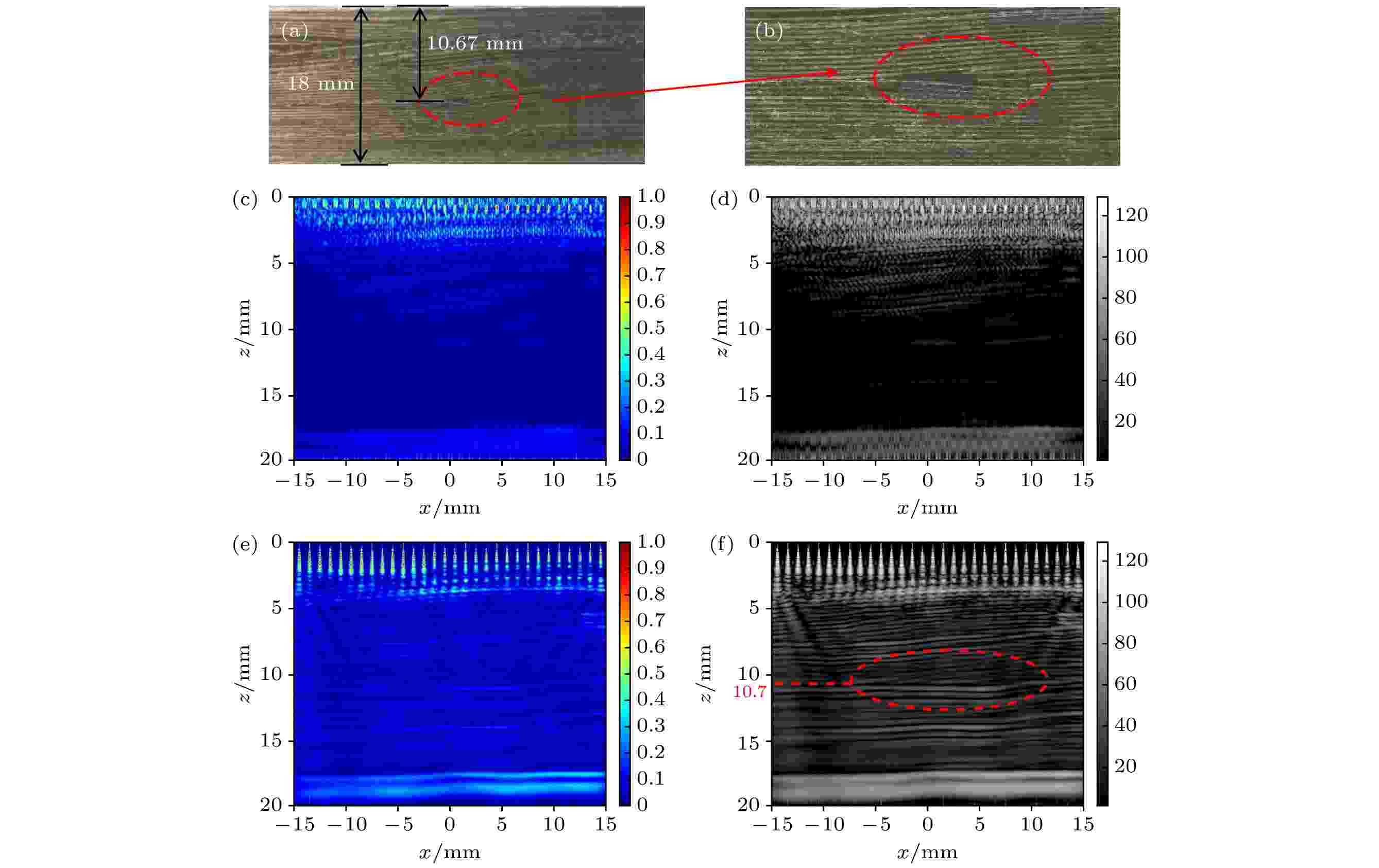图 7 试样B及其成像结果 (a)实物图; (b)图7(a)的局部放大图; (c)全聚焦成像结果; (d)图7(c)的灰度图; (e)用指向性函数校正的全聚焦成像结果; (f)图7(e)的灰度图
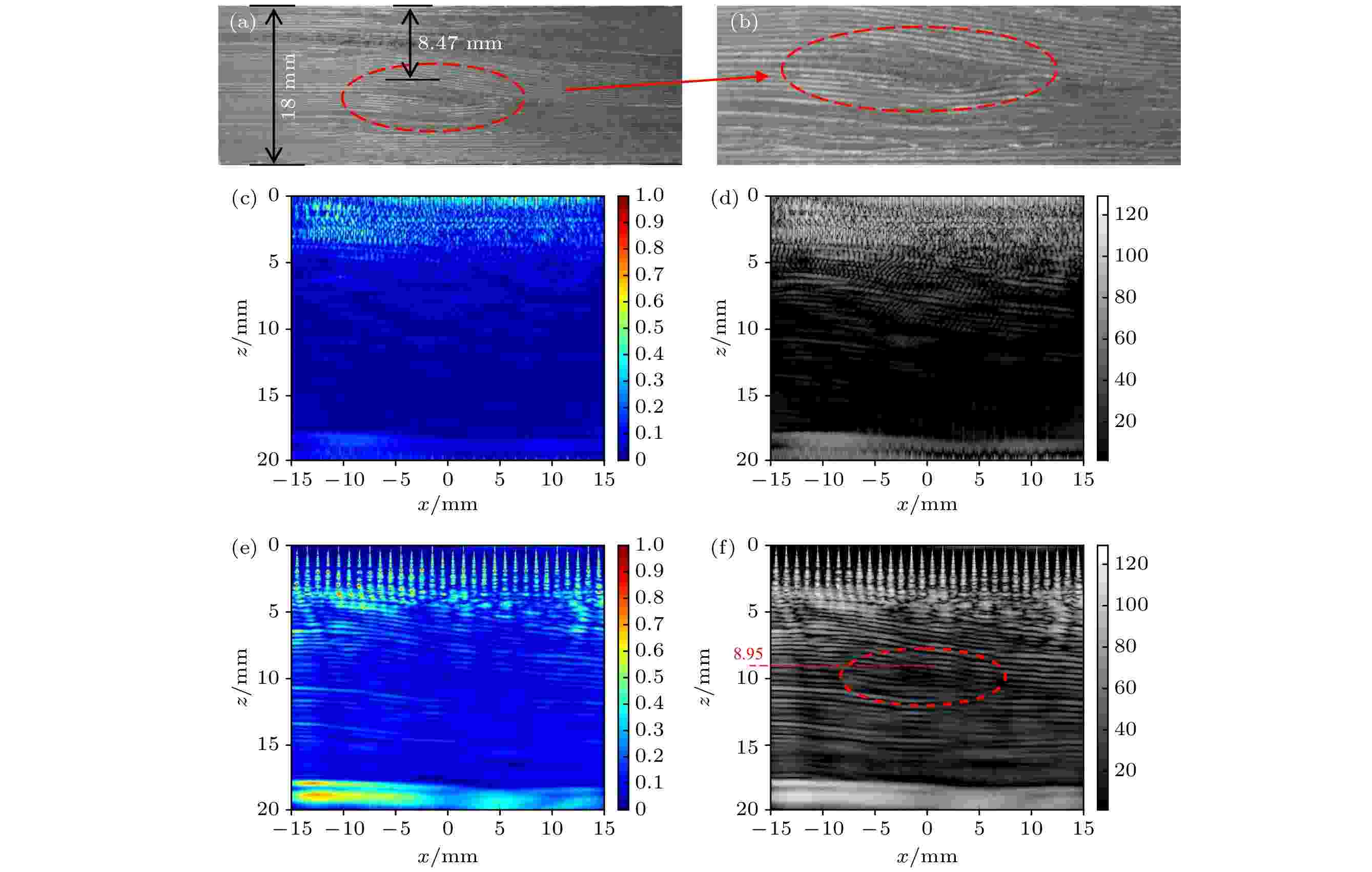图 8 试样C及其成像结果 (a)实物图; (b)图8(a)的局部放大图; (c)全聚焦成像结果; (d)图8(c)的灰度图; (e)用指向性函数校正的全聚焦成像结果; (f)图8(e)的灰度图
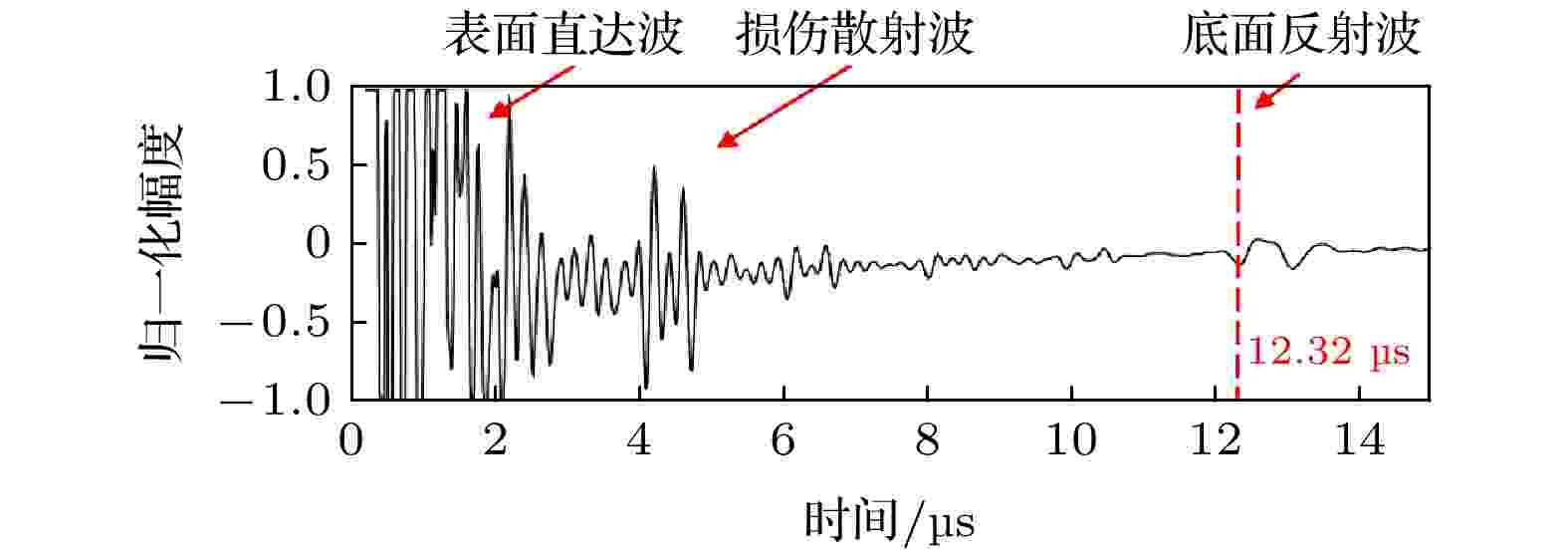图 4 i = j = 16时域信号
图 5 典型阵列回波信号
