全文HTML
--> --> -->Sb2(S,Se)3与铜铟镓硒(Cu(In,Ga)Se2)、非晶硅锗和钙钛矿等多元合金或化合物材料类似, 都可以通过改变元素配比调节材料的禁带宽度. 如果在制备的过程中或者通过后处理的方式, 使化合物中的元素比例随着厚度的变化而变化, 就能够制备出具有渐变能隙结构的吸光层[13-15]. 这种能隙工程的概念已经成功应用在了多种太阳电池的器件结构的设计中, 并使电池性能得到了显著的优化. 在Cu(In,Ga)Se2太阳电池中, Mattheis等[16]制备出了具有Ga梯度的吸光层, 通过导带能级梯度的优化提高了自由电子收集作用, 而改善了后接触界面的复合, 使得电池的短路电流密度(Jsc)得到了有效的提升. 在非晶硅锗太阳电池中, Fan等[17]采用射频等离子体增强化学气相沉积技术, 通过调节锗烷流量制备出具有渐变能隙结构的非晶硅锗吸光层, 使得电池中载流子迁移能力以及被传输层收集的概率得到提升, 使电池的Jsc和稳定性均高于恒定能隙非晶硅锗太阳电池. 在钙钛矿太阳电池仿真研究中, Liu等[18]在器件背接触面一侧引入了渐变能隙结构, 所形成的电子势垒抑制了载流子在界面处的复合, 从而改善了电池性能.
渐变能隙结构也是提高Sb2(S,Se)3太阳电池性能的一项关键技术. Choi等[19]通过有序沉积Sb2S3和Sb2Se3来调整吸光层组分制备了渐变能隙的Sb2(S,Se)3太阳电池, 其PCE高于恒定能隙的Sb2S3和Sb2Se3太阳电池. 而后, Zhang等[20]使用化学浴沉积法, 通过控制Se与Sb2S3薄膜固相反应速率制备了具有渐变能隙的Sb2(S,Se)3薄膜, 发现渐变能隙不仅能够扩宽电池的光谱响应, 还能够促进空穴的输运, 使得电池的Jsc得到了优化, 并制备出了PCE为5.71%的Sb2(S,Se)3太阳电池.
通过以上研究结果可以发现, 渐变能隙结构在多元合金或者化合物电池中都具有很大的研究价值, 对于其内在机理的研究也是十分必要的. 基于此, 我们采用wx-AMPS仿真软件, 对具有递减能隙结构的Sb2(S,Se)3太阳电池进行了建模仿真. 首先通过载流子迁移率的调节探明渐变能隙结构与载流子输运特性的内在关系. 然后在不同厚度和缺陷态的条件下, 将递减能隙与恒定能隙结构的Sb2(S,Se)3太阳电池进行了对比分析. 最后明确了递减能隙结构Sb2(S,Se)3太阳电池的应用条件和优势. 我们的研究结果对具有渐变能隙结构的高性能Sb2(S,Se)3太阳电池的研发提供了理论指导.
Sb2(S,Se)3太阳电池的器件结构为FTO/CdS/Sb2(S,Se)3/Spiro-OMeTAD/Au, 如图1所示. 我们设计了递减能隙的Sb2(S,Se)3太阳电池, 即将Se含量为0%的Sb2S3层设置为起始层, 随着吸光层深度的加深线性增加Se含量, 到吸光层末端对应Se含量为100%的Sb2Se3层. 其中Sb2(S,Se)3的禁带宽度、电子亲和势和介电常数均随着Se含量呈线性变化, 相邻渐变层之间Se含量的差值为1%[23]. 也引入了50% Se含量的恒定能隙Sb2(S,Se)3太阳电池进行比较研究. 通过调节载流子传输层的电子亲和势消除界面势垒对载流子输运的影响. 各层模型的具体参数如表1所列[24-29], 其中将Sb2(S,Se)3吸光层电子的迁移率(μe)由0.1 cm2·V–1·s–1变化至10 cm2·V–1·s–1, 同时固定空穴迁移率(μh)为0.1 cm2·V–1·s–1; Sb2(S,Se)3吸光层的厚度由0.25 μm变化至2 μm; Sb2(S,Se)3吸光层的缺陷态密度由1014 cm–3变化至1017 cm–3. 仿真温度设定在300 K, 太阳光谱选用的是AM 1.5G, 入射光强度为100 mW/cm2.
图 1 Sb2(S,Se)3太阳电池的结构示意图Figure1. Schematic diagram of the Sb2(S,Se)3 solar cell structure.
| 参数 | CdS | Sb2(S,Se)3 | Spiro-OMeTAD |
| 介电常数 | 10 | 10—19 | 3 |
| 电子亲和 势/eV | 3.7—3.87 | 3.7—4.04 | 1.99—2.41 |
| 电子迁移率 (cm2·V–1·s–1) | 100 | 4 | 0.0001 |
| 空穴迁移率/ (cm2·V–1·s–1) | 25 | 0.1 | 0.0001 |
| 施主掺杂 浓度/cm–3 | 1 × 1019 | 0 | 0 |
| 受主掺杂 浓度/cm–3 | 0 | 1 × 1013 | 3 × 1018 |
| 禁带宽度/eV | 2.4 | 1.2—1.7 | 2.91 |
| 导带有效 态密/cm–3 | 2.2 × 1018 | 2.2 × 1018 | 2.2 × 1018 |
| 价带有效 态密/cm–3 | 1.8 × 1019 | 1.8 × 1019 | 1.8 × 1019 |
| 缺陷态密 度/cm–3 | 1 × 1017 | 3 × 1016 | 1 × 1016 |
表1Sb2(S,Se)3 太阳电池材料参数
Table1.Material parameters of the Sb2(S,Se)3 solar cells.
图 2 递减能隙与恒定能隙的Sb2(S,Se)3太阳电池 (a) J-V曲线 ; (b) 能带图; (c) 恒定能隙Sb2(S,Se)3太阳电池能带结构示意图; (d)递减能隙Sb2(S,Se)3太阳电池能带结构示意图Figure2. Sb2(S,Se)3 solar cells with narrowing and constant band gap structure: (a) J-V curves; (b) energy band diagram; (c) energy band scheme of constant band gap Sb2(S,Se)3 solar cell; (d) energy band scheme of narrowing band gap Sb2(S,Se)3 solar cell.
| μe/(cm2·V–1·s–1) | Voc/V | Jsc/(mA·cm–2) | FF/% | PCE/% |
| 0.1 | 0.93 | 20.00 | 52.50 | 9.74 |
| 0.25 | 0.87 | 21.77 | 63.39 | 12.05 |
| 1 | 0.83 | 22.77 | 73.44 | 13.89 |
| 5 | 0.82 | 22.95 | 77.18 | 14.46 |
| 10 | 0.81 | 22.95 | 77.72 | 14.51 |
表2不同μe的Sb2(S,Se)3递减能隙结构太阳电池的性能参数
Table2.Photovoltaic performance of the narrowing band gap structure Sb2(S,Se)3 solar cell with different μe.
Sb2(S,Se)3太阳电池中存在一定强度的内建电场. 在吸光层中产生的光生电子-空穴对会在内建电场的作用下分离, 被两个电极收集并形成电流. 其中电子与空穴的输运性能可以通过漂移速度ν来衡量[30]:
图3给出了改变μe由0.1 cm2·V–1·s–1 提高至10 cm2·V–1·s–1的递减能隙Sb2(S,Se)3太阳电池特性图, 具体性能参数如表2所列. 在递减能隙结构中, 当μe与μh相等时, 附加电场的存在使得自由电子所受电场强度要低于空穴所受电场强度, 导致自由电子的传输受到了抑制. 通过图3(a)不同μe下Sb2(S,Se)3的自由电子浓度可以看到, 此时自由电子在吸光层0.2至0.5 μm处具有最高的浓度, 说明自由电子在电池尾部产生堆积, 不能有效地被电子传输层收集, 导致此处具有最高的载流子复合率, 如图3(b)所示. 此时电池的Jsc和FF最低, 仅有9.74%的PCE. 该电池效率小于50%恒定能隙的Sb2(S,Se)3太阳电池, 这是因为当吸光层中μe与μh相近时, 递减能隙反而会使自由电子传输特性劣化, 使载流子输运变得不平衡, 也说明渐变能隙结构并不适用于所有的电池特性情况.
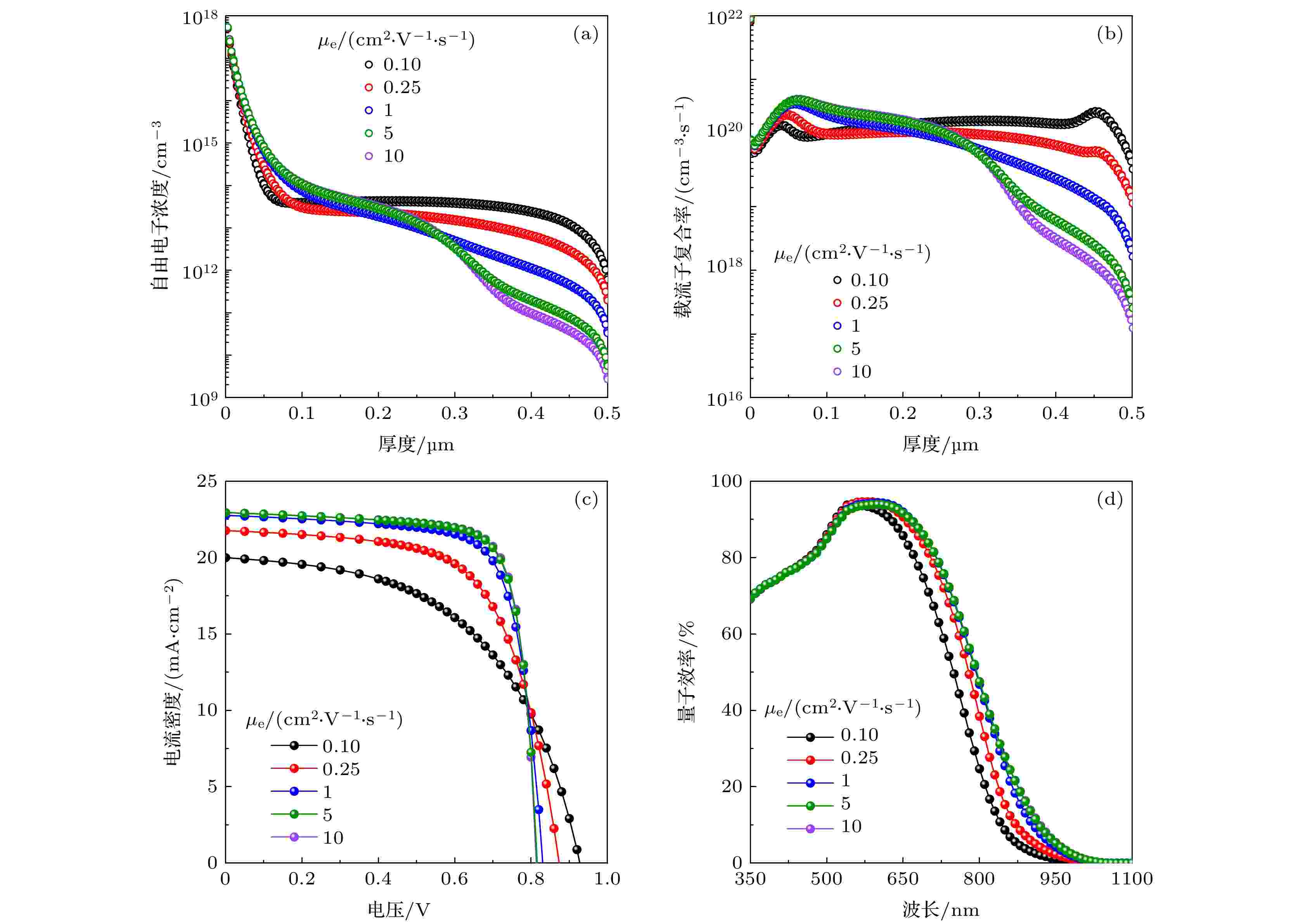图 3 不同μe的递减能隙结构Sb2(S,Se)3太阳电池 (a) 自由电子浓度分布; (b) 载流子复合率分布; (c) J-V曲线; (d) 量子效率曲线Figure3. Narrowing band gap structure Sb2(S,Se)3 solar cells with different μe: (a) Free electron concentration distribution; (b) recombination rate distribution; (c) J-V curves; (d) quantum efficiency curves.
随着μe的提升, 自由电子的输运逐渐克服了渐变能隙所产生的附加电场对电子输运的不利影响, 使更多电池尾端产生的光生自由电子可以输运到电子传输层. 因此, 如图3(a)所示, 递减能隙Sb2(S,Se)3吸光层后半部分的自由电子浓度会随着μe的提高而降低, 也使得这部分的载流子复合率逐渐降低(图3(b)). 图3(d)为不同μe递减能隙Sb2(S,Se)3太阳电池的量子效率曲线. 由于电池后半部分的光生载流子主要源于吸收的长波光子, 因此复合的降低使得电池在600—1100 nm的长波响应得到增强[20,31]. 这也使得Jsc由20.00 mA·cm–2逐渐提高至22.95 mA·cm–2. 载流子复合率的降低也使得电池FF由52.5%提高至了77.72%. 通过上述分析可知, 渐变能隙的设置与载流子的迁移率关系密切, 当吸光层的μe与μh相近时, 是无需引入渐变能隙结构的. 在实验中, 在固定μh为0.1 cm2·V–1·s–1, μe为0.25 cm2·V–1·s–1的情况下就可以得到与恒定能隙Sb2(S,Se)3太阳电池相似的器件性能. 而当μe高于0.25 cm2·V–1·s–1之后, 就能够逐渐体现出递减能隙结构的优势. 当μe为5 cm2·V–1·s–1时, 器件获得了14.46%的PCE, 而在此基础上继续增加μe至10 cm2·V–1·s–1, 电池性能仅有微弱的增长. 这说明递减能隙所产生附加电场的作用在μe为5 cm2·V–1·s–1时就能够发挥的较为充分. 在无机吸光层材料中, 一般情况下μh都是器件性能的限制因素, 因此, 引入递减能隙以平衡调节载流子输运是优化器件性能的有效手段.
目前在实验研究中, 对于不同Se含量的Sb2(S,Se)3的能带位置还没有确定结论[19,20], 因此能带位置的不同是否会对渐变能隙的作用产生影响是一个需要探明的问题. 为此建立了两种模型: 一种为Sb2(S,Se)3的导带随Se含量变化在3.7和4.04 eV之间线性变化; 另一种为Sb2(S,Se)3的导带随Se含量的变化一直固定在3.7 eV. 两种能带位置Sb2(S,Se)3太阳电池的仿真结果如图4所示. 导带位置固定与不固定Sb2(S,Se)3太阳电池的PCE分别为14.56%和14.42%. 两者PCE基本相同, 表明Sb2(S,Se)3导带位置并不会对附加电场产生影响. 当Sb2(S,Se)3太阳电池形成pn结时, 费米能级需要对齐, 虽然在两种模型下Sb2(S,Se)3的导带位置不相同, 但是导带与费米能级之间的距离确是相同的, 如图4(c)所示. 因此在费米能级对齐后, 两种模型所形成的导带和价带形状是基本相同的, 因此能够表现出相同强度的附加电场.
图 4 不同导带位置递减能隙的Sb2(S,Se)3太阳电池 (a) J-V曲线 ; (b) 能带图; (c) 费米能级对齐示意图Figure4. Narrowing band gap Sb2(S,Se)3 solar cells with different conduction band positions: (a) J-V curves; (b) energy band diagram; (c) energy band scheme of Fermi level alignment.
在制备Sb2(S,Se)3薄膜的实验中, 缺陷态密度对应着薄膜质量, 是决定器件性能的重要参数之一. 缺陷态密度也有可能随Se含量的改变而变化[32]. 我们构造了缺陷态密度随Se含量增加由1017 cm–3线性减少到1015 cm–3的递减能隙模型, 发现不同μe的Sb2(S,Se)3递减能隙结构太阳电池性能的变化趋势与缺陷态恒定所展现出的变化规律相同, 如图5所示. 此外, 硅锗薄膜具有与Sb2(S,Se)3相似的能隙可调特性, 在对硅锗薄膜太阳电池渐变能隙结构的理论和实验研究中也得到了与本文相似的结论[33,34]. 基于此, 我们认为在实际的Sb2(S,Se)3太阳电池中, 递减能隙结构能够发挥出平衡载流子输运的作用.
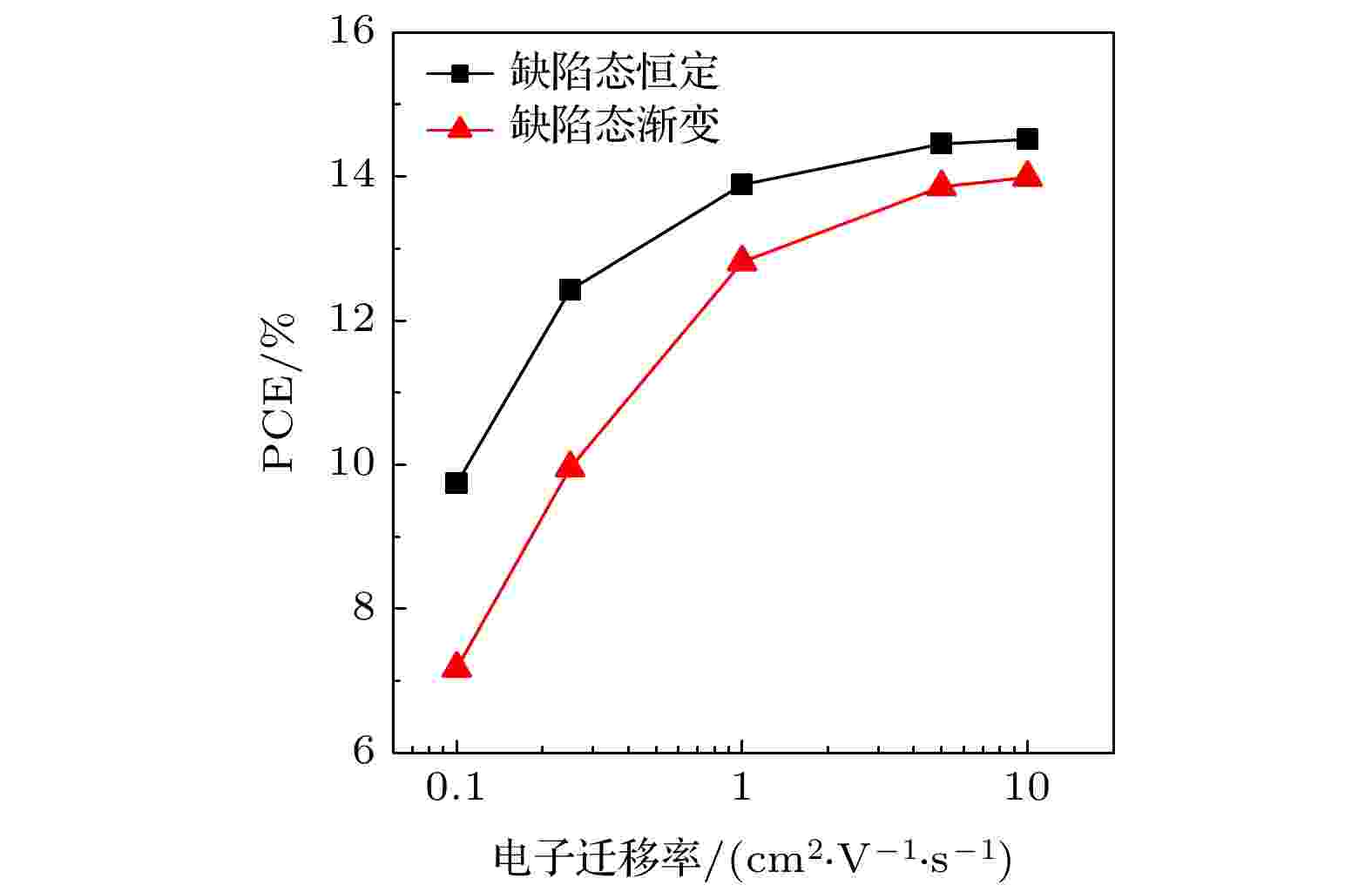图 5 不同缺陷态分布递减能隙的Sb2(S,Se)3太阳电池的PCE随μe的变化Figure5. Narrowing band gap Sb2(S,Se)3 solar cells with different defect state distributions as a function of μe.
鉴于渐变能隙能够优化太阳电池的载流子输运特性, 将不同厚度的缺陷态递减能隙Sb2(S,Se)3太阳电池和恒定能隙Sb2(S,Se)3太阳电池性能进行了对比分析. 图6(a)为不同厚度递减能隙与恒定能隙Sb2(S,Se)3太阳电池的相对效率. 如图6(a)所示, 恒定能隙Sb2(S,Se)3太阳电池在厚度为0.25 μm时取得了最大值, 并且效率会随着厚度的增加而下降. 这是由于当厚度增加时, 不仅内建电场的场强会变弱, 光生载流子输运到传输层的距离也会变长, 这都使得载流子被复合的概率大大增加. 通过图6(b)所示的不同厚度恒定能隙Sb2(S,Se)3太阳电池的载流子复合率分布, 可以看到随着吸光层厚度的增加, 不仅使得吸光层前端的复合率不断提高, 同时也使得高复合的区域被延伸. 当厚度为1.5 μm时, 电池在整个吸光层中会保持高的复合率, 使得电池的性能劣化至厚度为0.25 μm时的 14.12%. 而当采用递减能隙时, 随着厚度的增加, Sb2(S,Se)3太阳电池性能的衰退被大大地缓解了, 电池的各项参数的下降幅度均小于恒定能隙, 其中递减能隙Sb2(S,Se)3太阳电池在吸光层厚度为0.5 μm时获得了最高的效率. 当吸收层厚度为1.5 μm时, 递减能隙太阳电池还能保持厚度为0.25 μm时的40.71%. 从图6(b)所示的递减能隙与恒定能隙Sb2(S,Se)3太阳电池复合率分布的比较可以看出, 递减能隙的Sb2(S,Se)3太阳电池的复合率在吸光层前端有显著降低, 说明此时渐变能隙所产生的附加电场有效地提升了空穴的迁移能力遏制了Sb2(S,Se)3器件性能的劣化. 值得注意的是, 随着锑基太阳电池的发展, 将不同能隙锑基太阳电池结合起来形成多结叠层太阳电池结构将是进一步提高电池性能的有效途径[35]. 此时, Sb2(S,Se)3一般需要作为叠层电池中间电池或者底电池的吸收层. 要想达到各结子电池的电流匹配, 中间电池或者底电池的厚度一般高于1 μm以尽可能吸收长波光子[36]. 递减能隙结构Sb2(S,Se)3太阳电池在厚度较厚的情况下仍可以保持较高的器件性能, 体现了其在叠层太阳电池中的应用潜力.
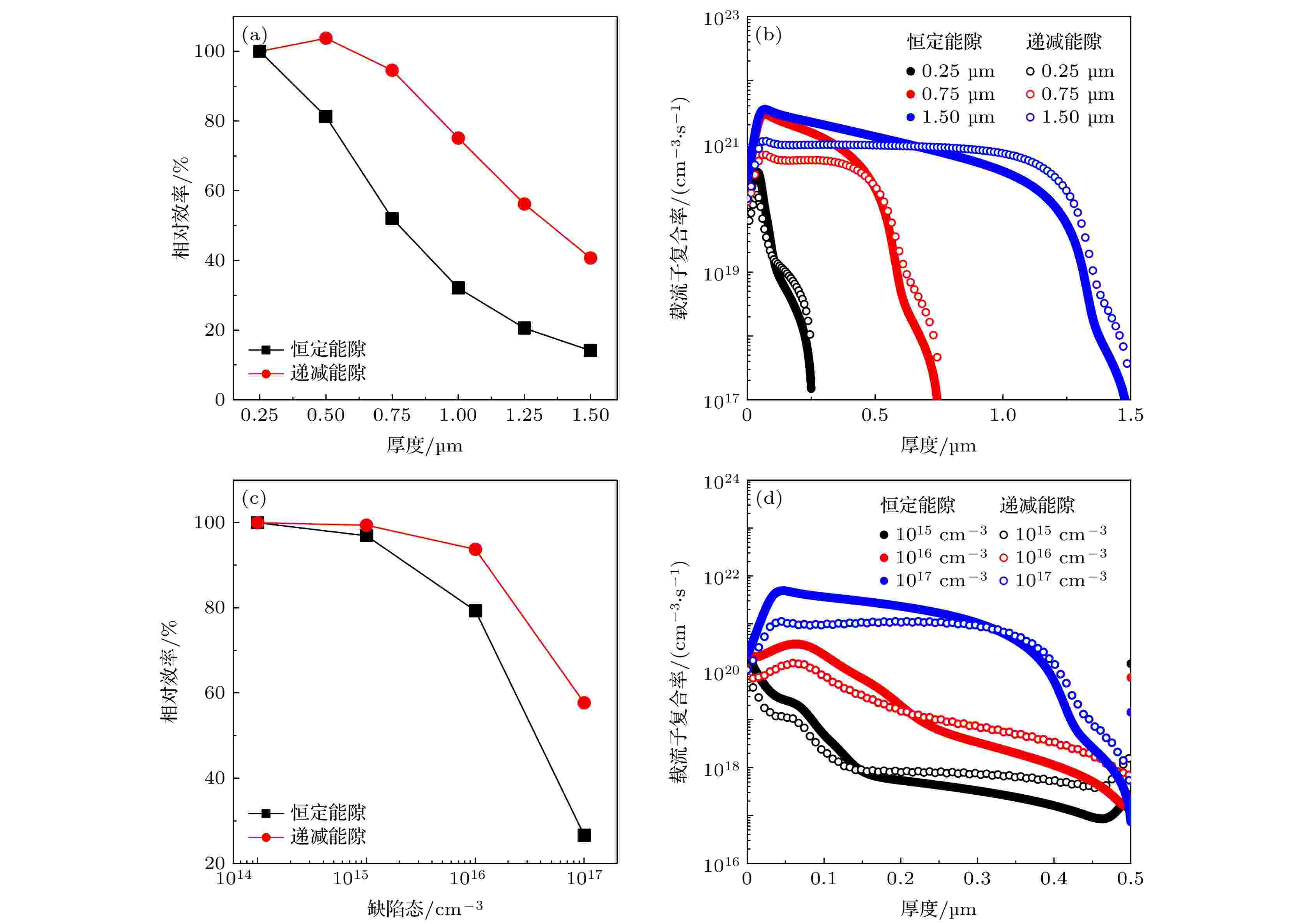图 6 (a) 恒定能隙与递减能隙Sb2(S,Se)3太阳电池的相对效率随厚度的变化, 此处相对效率指的是以厚度为0.25 μm Sb2(S,Se)3太阳电池效率为基准计算出的效率比值; (b) 恒定能隙与递减能隙Sb2(S,Se)3太阳电池的载流子复合率分布随厚度的变化; (c) 恒定能隙与递减能隙Sb2(S,Se)3太阳电池的相对效率随缺陷态密度的变化, 此处相对效率指的是以缺陷态密度为1014 cm–3 Sb2(S,Se)3太阳电池效率为基准计算出的效率比值; (d) 恒定能隙与递减能隙Sb2(S,Se)3太阳电池的载流子复合率分布随缺陷态密度的变化Figure6. (a) Relative PCE of constant band gap and narrowing band gap Sb2(S,Se)3 solar cells with different thicknesses. Here, the relative PCE refers to the PCE ratio calculated by applying the PCE of Sb2(S,Se)3 solar cell with 0.25 μm thick as the denominator; (b) the carrier recombination rate distribution of constant band gap and narrowing band gap Sb2(S,Se)3 solar cells with different thicknesses; (c) the relative PCE of constant band gap and narrowing band gap Sb2(S,Se)3 solar cells with different defect densities. Here, the relative PCE refers to the PCE ratio calculated by applying the PCE of Sb2(S,Se)3 solar cell with the defect density of 1014 cm–3 as the denominator; (d) the carrier recombination rate distribution of constant band gap and narrowing band gap Sb2(S,Se)3 solar cells with different defect densities.
图6(c)给出了不同缺陷态递减能隙与恒定能隙Sb2(S,Se)3太阳电池的相对效率. 在缺陷态小于1015 cm–3时, Sb2(S,Se)3太阳电池性能随着缺陷态的变化基本保持不变, 而当缺陷态密度高于1015 cm–3以后, 两种能隙结构Sb2(S,Se)3太阳电池的性能都会随着缺陷态密度的提高而降低. 我们发现递减能隙Sb2(S,Se)3太阳电池的性能下降速度要低于恒定能隙Sb2(S,Se)3太阳电池, 在缺陷态密度为1017 cm–3时, 递减能隙Sb2(S,Se)3太阳电池仍能保持57.70%的相对效率, 明显高于恒定能隙的26.57%. 通过对比不同缺陷态密度的恒定能隙和递减能隙Sb2(S,Se)3的复合率分布可以发现(图6(d)), 递减能隙结构的优势在于, 可以有效地抑制吸光层前端的载流子复合, 使器件在高缺陷态下仍可以保持较高的器件性能.
总结以上结果发现, 递减能隙在吸光层较厚或缺陷态密度较高的情况下均保持了较高的器件性能, 为进一步探究递减能隙在Sb2(S,Se)3太阳电池中的适用条件. 绘制了递减能隙Sb2(S,Se)3太阳电池与恒定能隙Sb2(S,Se)3太阳电池效率差值的等高线图, 结果如图7所示. 在Sb2(S,Se)3太阳电池厚度很薄, 或者缺陷态很低的情况下, 尽管恒定能隙Sb2(S,Se)3吸光层的μh较低, 但由于此时光生载流子被复合的概率也很低, 使得绝大多数空穴都能够成功被空穴传输层所收集, 因此不会对器件性能造成不利影响. 这导致递减能隙附加电场的作用不能得到体现, 其器件性能要小于恒定能隙Sb2(S,Se)3太阳电池. 而随着吸光层厚度和缺陷态密度的增加, 递减能隙结构的优势能够逐渐显现. 在吸光层缺陷态密度为1015 cm–3时, 递减能隙Sb2(S,Se)3太阳电池在厚度高于1 μm之后具有更高的器件性能. 而当吸光层缺陷态密度为1016 cm–3时, 递减能隙Sb2(S,Se)3太阳电池在厚度高于0.5 μm之后就具有更高的器件性能了. 当Sb2(S,Se)3太阳电池厚度和缺陷态密度分别为1.5 μm和1016 cm–3时, 两种结构太阳电池的PCE具有最大的6.34%的差值, 显示出了递减能隙结构的优势. 而当吸光层厚度和缺陷态密度继续增加, Sb2(S,Se)3太阳电池效率的差值又有所降低, 这是由于此时吸光层的载流子复合率都过高, 这两种结构Sb2(S,Se)3太阳电池的PCE都很低所导致的. 虽然Sb2(S,Se)3太阳电池在近些年得到了快速发展, 但其PCE距离类似结构的碲化镉太阳电池和钙钛矿太阳电池还有较大的优化空间. 其中吸光层材料中较高的缺陷态密度(锑基材料的缺陷态密度比碲化镉材料要高一到两个数量级[37])导致的高复合率是锑基太阳电池效率较低的主要原因之一[38,39]. 因此, 在Sb2(S,Se)3太阳电池中应用渐变能隙是提高电池效率的有效手段. 基于太阳电池吸光层材料中, Cu(In,Ga)Se2材料、非/微晶硅锗材料和钙钛矿材料都具有能隙可调的性质. 本文所总结出的渐变能隙结构的研究成果也可以为以上多元合金或化合物太阳电池的器件结构设计提供理论指导.
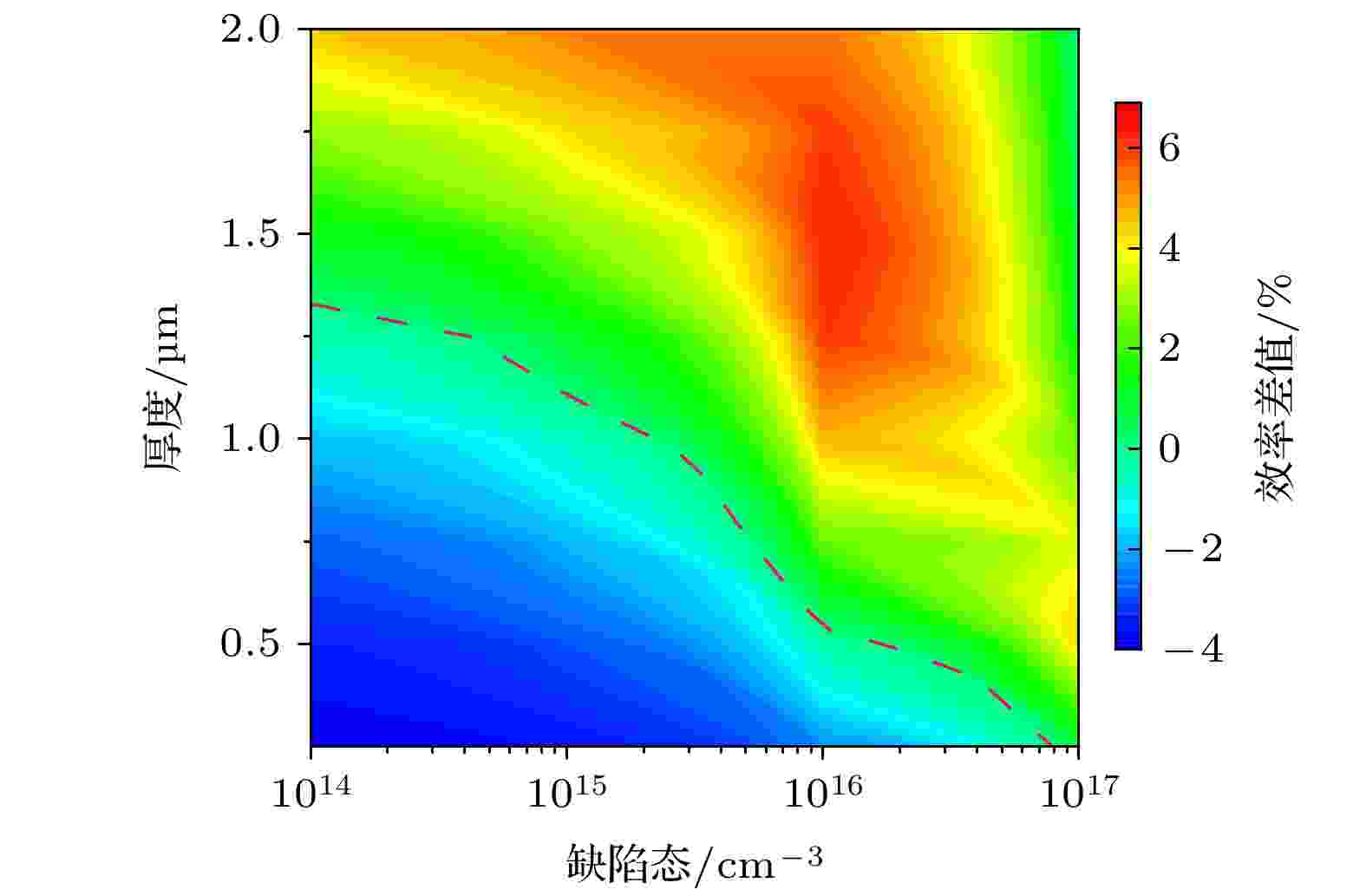图 7 不同厚度与缺陷态下恒定能隙与递减能隙Sb2(S,Se)3太阳电池效率之差的等高线图Figure7. Contour map of the PCE difference between the constant band gap and narrowing band gap structure Sb2(S,Se)3 solar cells with different thicknesses and defect densities.
感谢伊利诺伊大学Rockett教授和刘一鸣博士对wx-AMPS模拟软件的开发.
