摘要:液滴在纳米结构表面的润湿模式研究(Dewetting, Cassie, Partial Wenzel及Wenzel)对强化冷凝、表面自清洁、油水分离等具有重要意义, 现有文献主要研究了液滴在微柱阵列纳米结构表面的润湿行为. 本文采用分子动力学模拟, 研究了纳米结构倾角及表面浸润性对氩液滴在铂固体壁面上润湿模式及其相互转换的影响, 采用了三种纳米结构, 其倾角分别为60° (倒梯形)、90° (长方形)及120° (正梯形); 以本征接触角θ_e表征表面浸润性. 研究表明, 当θ_e < 118°时, 液滴在纳米结构表面均呈Wenzel状态, 即液体向纳米结构缝隙完全渗透; 当118° < θ_e < 145°时, 倒梯形纳米结构有助于液滴保持Cassie状态, 即液体不向纳米结构缝隙渗透, 正梯形纳米结构容易使液滴形成Partial Wenzel状态, 即液体向纳米结构缝隙部分渗透. 分析表明, 三种纳米结构倾角对液滴润湿模式的影响及转换满足自由能最小原理. 本文工作揭示出采用倒置纳米结构, 可使液滴更好维持Cassie模式.
关键词: 液滴/
纳米结构/
润湿模式/
分子动力学

English Abstract

全文HTML

--> --> -->

液滴在固体表面的润湿行为是自然界中普遍存在的物理现象, 广泛应用于印刷工艺、涂料技术、交通运输、航空航天和能源系统等领域^[1]. 众所周知, 润湿状态(Cassie, Partial Wenzel和Wenzel)是影响冷凝液滴生长和脱离的关键因素^[2,3]. 受自然界中“荷叶效应”^[4-6]的启发, 越来越多的****关注超疏水表面的滴状凝结换热及强化机理. 受液滴润湿模式的影响, 超疏水纳米结构表面冷凝存在弹跳、滚动和滑动三种液滴脱落模式^[7], 研究液滴在纳米结构表面的润湿行为对减小液滴脱离尺寸, 促进冷凝液滴脱落, 进而强化滴状冷凝传热有着重要意义.
目前研究的粗糙表面上的润湿状态主要分为Wenzel模型^[8]和Cassie模型^[9]两种理论. Wenzel^[8]认为粗糙表面的存在使得实际固-液接触面积大于所观察到的表面面积, 并假设液滴完全充满纳米结构并润湿壁面. 润湿表面的表观接触角(θ_w)和本征接触角(θ_e)之间满足关系:

$ \cos {\theta _{\rm{w}}} = r\cos {\theta _{\rm{e}}}, $

其中r为粗糙度因子, 表示液滴与固体表面接触的实际面积与投影面积的比值. Cassie和Baxter^[9]进一步拓展了Wenzel方程, 认为液滴在粗糙表面上的接触是一种复合接触, 当表面较疏水时, 液滴不能完全润湿凹槽, 液滴与表面之间有空气存在, 所以表观上的固-液接触面实际上由固-液接触面和气-液接触面共同组成. 复合表面的表观接触角θ_c可以表示为

$ \cos {\theta _{\rm{c}}} = - 1 + f\left( {\cos {\theta _{\rm{e}}} + 1} \right), $

其中f表示与液体接触的实际固体表面占比, 称为相面积分数.
液滴在固体表面的润湿性主要取决于表面的化学组成^[10-15]、微结构形貌^[16-18]和几何结构尺寸^[15,19-21]. He等^[22]采用实验方法研究了水滴在不同浸润性和几何参数的表面上的润湿行为, 研究表明, 当水滴直接在固体基板沉积时形成接触角较大的Cassie润湿状态, 当水滴以一定高度降落到表面时形成接触角较小的Wenzel润湿状态. Bico等^[23]讨论了液滴在纳米结构表面的润湿行为及不同润湿状态转换的可能性. 结果发现增大柱高和柱宽、减小柱间距均有利于Cassie液滴的形成. Marmur^[21]通过计算润湿面积定量评价液滴在粗糙表面的润湿行为. 研究结果补充了Wenzel^[8]和Cassie^[9]理论. 由于实验技术条件和理论模型的限制, 当液滴的特征尺度为微纳米级别时, 表面积与体积的比值明显增大, 宏观尺度下能够忽略的某些影响因素(分子间的范德瓦耳斯力、液体流动出现的壁面滑移效应、传热过程出现的温度阶跃等)变得不容忽视. 因此, 在微纳尺度下, 物理现象所具有的尺度效应和界面效应逐渐成为探究润湿和传热等宏观尺度现象影响机理的重要因素. 近年来, 分子动力学(molecular dynamics, MD)模拟技术快速发展, 并被广泛应用于探究纳米尺度下分子间相互作用及机理. Shi和Dhir^[24]讨论了采用MD模拟得到的水滴在铂表面润湿的接触角和氩液滴在铂表面润湿的接触角, 与实验中水滴在铝表面润湿的接触角的关系, 发现上述三种接触角随体系温度的变化规律一致, 均随温度的增加而降低. Li等^[19]研究了氩液滴在固体铂表面上的润湿行为, 结果表明, 液滴的接触角及总蒸发量随表面浸润性的增加而减小. Yong和Zhang^[25]研究了改变柱高和相面积分数, 汞液滴在固体铜沟槽上的润湿特性, 并将模拟结果与Wenzel^[8]和Cassie^[9]理论预测结果对比, 发现液滴在疏水表面润湿的接触角模拟值与理论计算值符合较好, 然而液滴在亲水表面润湿的接触角模拟值较理论计算值偏大, 造成该现象的原因是纳米尺度下亲水表面高的边缘密度使得钉扎效应明显. Saha等^[18]研究了水滴在不同几何参数(柱高、柱宽、柱间距)的石墨表面上的润湿特性, 发现在最佳柱间距下, 相较水滴在方柱阵列表面上的润湿, 水滴在圆柱阵列表面的润湿具有更高的流动性. Chen等^[15]研究了不同参数(柱高、柱间距和水滴尺寸)对Wenzel状态向Cassie状态自发转换的影响. 结果表明, 水滴在硅表面上润湿状态的转换分为固-液接触面积减小和水滴上升两个阶段. 当柱高位于21.72—48.87 ?时, 上述润湿转换过程发生的概率随液滴尺寸的减小和柱间距的增大而减小.
目前文献对液滴润湿行为的研究主要集中于栏栅形、方柱阵列等规则形状的纳米结构^[15,20], 而低表面张力的流体容易渗入凹槽形成黏滞力较强的润湿接触, 导致液滴不易从表面脱离, 给超疏水表面的制备带来困难, 因此增强能量势垒实现复合接触成为一个重大的挑战. 可重入结构(如“T”或蘑菇形状及悬垂形结构等)逐渐成为研究者关注的焦点. Savoy和Escobedo^[26]采用MD方法模拟了不同尺寸的液滴在“T”形结构上的润湿行为, 发现润湿与方柱相同高度的该结构表面需要克服更高的能量势垒, 一定程度上增强了表面疏水性. Wang等^[27]通过实验方法研究了不同表面边缘角和工质对液滴润湿特性的影响, 结果表明, 尖锐的表面边缘带来的强钉扎作用, 可以显著改变液滴在表面的接触角和润湿状态. Zhu等^[28]采用MD方法研究了不同参数(固体底角、表面浸润性)对水滴润湿状态转换的影响, 研究表明, Cassie态向Wenzel态转换的临界本征接触角对固体底角有很强的依赖性, 而Wenzel态向Cassie态转换的临界本征接触角与固体底角呈相反的规律, 并通过模拟宏观降雨计算了润湿转换的自由能垒, 定量评估Cassie状态的稳定性. 本文提出了三种不同形貌(纵截面分别为倒梯形、长方形和正梯形)的纳米结构表面, 采用MD方法研究纳米结构倾角(60°, 90°和120°)及表面浸润性对液滴润湿行为的影响, 为提高Cassie状态的稳定性、制备亲水材料的超疏水表面和强化滴状凝结换热提供一定指导意义. 本模拟采用开源MD模拟软件LAMMPS实现, 原子位型可视化采用OVTTO软件.

2

-->

2.1.模型构建

本文采用MD方法研究了纳米液滴在不同粗糙表面的润湿行为. 图1(a)为初始状态的MD模型. 模拟体系的大小为L_x × L_y × L_z = 19.58 nm × 19.58 nm × 17.62 nm, x和y方向采用周期性边界条件, z方向采用固定边界条件. 整个体系温度恒定为100 K (本文计算侧重于亚临界压力下的气-液相平衡, 该温度低于氩的临界温度150.7 K, 100 K对应的饱和压力为0.32377 MPa, 同样低于氩的临界压力4.863 MPa). 图1(b)为物理模型的俯视图, 其中红、黄色原子代表固体壁面的Pt原子, 固体基板厚度δ为3σ, 共6层原子. 按照面心立方晶格结构排布, 密度为21.45 × 10³ kg/m³, 晶格常数为1.15σ, 其(111)晶面与液体原子接触. 纳米结构形状如图1(c)所示, 对应三种倾角φ(60°, 90°和120°), 固体原子数为28806—43958个. 蓝色原子代表液滴原子Ar, 因为Ar属于单原子分子, 氩原子间的Lennard-Jones (LG) 势函数具有广泛的理论和实验研究基础, 可定性地表征水滴在固体表面的润湿模拟^[22,29]. 液滴的初始结构为类固体原子排布的面心立方晶格晶格结构, 在体系温度下的饱和密度为1.31 × 10³ kg/m³, 晶格常数为1.72σ. 初始状态, 氩原子全部设置为液体原子, 相空间中气相氩原子数目为零. 根据纳米尺度与原子尺度量级的比较(D ≥ 10σ), 本模拟中液滴直径选取D = 26σ (8.86 nm)^[25,27], 原子数量为7131个, 对应的液滴体积为364.2 nm³.
图 1 (a)初始状态下的模拟系统图; (b)系统俯视图; (c) 纳米结构示意图
Figure1. (a) Diagram of a simulated system in initial state; (b) top view of system; (c) schematic diagram of nanostructure.

前文依据Wenzel^[8]及Cassie和Baxter^[9]的理论分别给出了粗糙度因子r及相面积分数f的定义, 并在图2(a)—(c)中利用不同颜色的线段显示, 其中A_sl代表固-液实际接触面积, A_lv代表气-液接触面积, A_pr代表投影面积. 下面结合图2(d)对相关参数作如下设定, 黑色虚线包围区域作为一个单元, 单个纳米结构顶部宽度设为w, 即上表面圆直径, 高度设为h, 相邻柱间顶部宽度为s, 纳米结构倾角为φ, 粗糙因子r及相面积分数f计算如下:
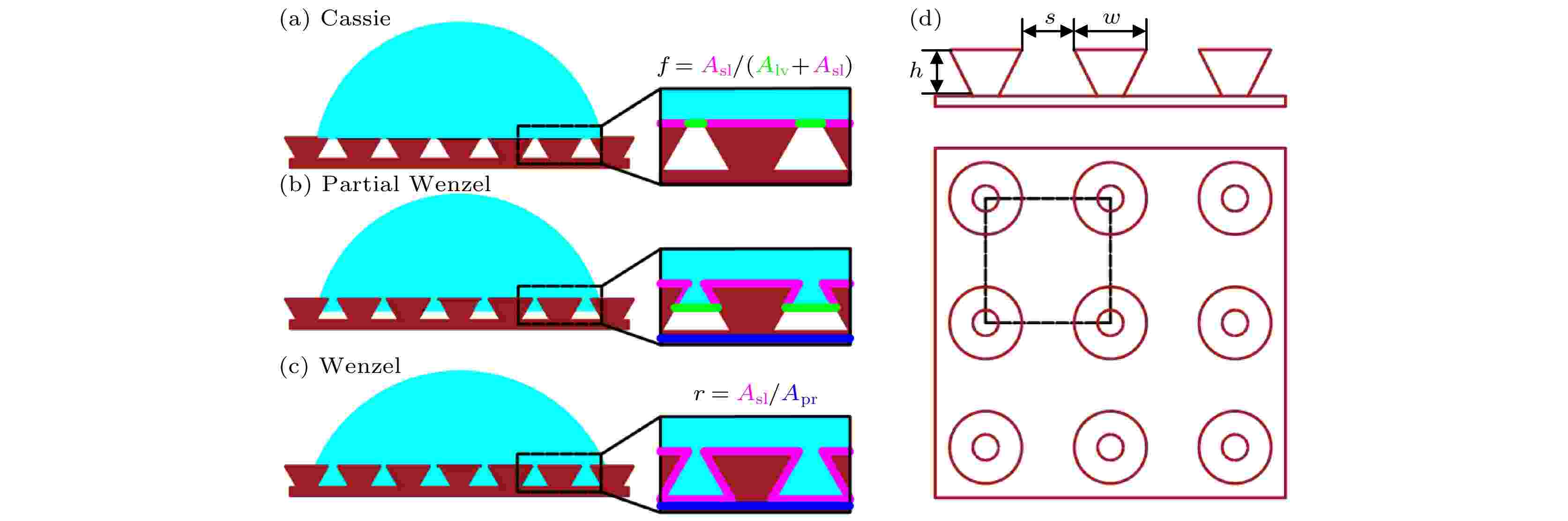图 2 (a) Cassie, (b) Partial Wenzel, (c) Wenzel润湿状态的示意图; (d)粗糙度因子r及相面积分数f确定的示意图
Figure2. Sketches for (a) Cassie, (b) Partial Wenzel and (c) Wenzel wetting states; (d) schematic diagram for determining roughness factor r and phase area fraction f.

$ r = 1 + \frac{{{\rm{\pi }}h\left( {\dfrac{1}{{\sin \varphi }} + \dfrac{1}{{\tan \varphi }}} \right)\left( {w - \dfrac{h}{{\tan \varphi }}} \right)}}{{{{\left( {w + s} \right)}^2}}}, $

$ f = \frac{{{\rm{\pi }}{w^2}}}{{4{{\left( {w + s} \right)}^2}}}. $

将各结构的几何参数代入(3)式和(4)式, 可得不同φ的粗糙因子r和相面积分数f, 具体见表1.

φ/(°)	w /σ	s /σ	h /σ	r	f
60	6.9	4.6	4.025	1.758	0.283
90	6.9	4.6	4.025	1.660	0.283
120	6.9	4.6	4.025	1.509	0.283

表1三种粗糙表面对应的结构参数
Table1.Structural parameters corresponding to three rough surfaces.

2 -->

2.2.模拟体系控制方程

不同种原子间的相互作用采用修正后的LJ势能模型, 表达式为^[30]

$ \phi (r) = 4\alpha {\varepsilon _{{\rm{sl}}}}\left[ {{{\left( {\frac{{{\sigma _{{\rm{sl}}}}}}{r}} \right)}^{12}} - \beta {{\left( {\frac{{{\sigma _{{\rm{sl}}}}}}{r}} \right)}^6}} \right], $

式中r为原子间距, 由Lorentz-Berthelot守则^[31]可得能量参数${\varepsilon _{{\rm{sl}}}} = \sqrt {{\varepsilon _{\rm{l}}} \cdot {\varepsilon _{\rm{s}}}} $, 特征尺寸${\sigma _{{\rm{sl}}}} = ( \sigma _{\rm{s}} + $$ {\sigma _{\rm{l}}} ) / 2$. 调节能量系数α和尺度系数β可以改变固-液间的相互作用力, 得到不同的浸润性. 其中不同类型的原子对应的特征尺寸分别为σ_s = 0.2475 nm, σ_l = 0.3405 nm; 能量参数分别为ε_s = 8.35 × 10^–20 J, ε_l = 1.67 × 10^–21 J. 模拟过程中的截断半径设为3.0σ. 对于距离大于3.0σ的原子, 原子间相互作用可忽略不计.
采用Velocity-Verlet算法求解运动方程, 时间步长取Δt = 0.002346τ, 其中$\tau = \sqrt {m{\sigma ^2}/\varepsilon } $为LJ约化时间常数. 模拟过程对系统采用正则系综(NVT), 维持体系温度为定值T = 0.827ε/k_B, k_B为玻尔兹曼常数, 采取Langevin方法控温. 体系运行100万步(对应时间5 ns)后达到平衡. 为保证数据的有效性, 平衡后再继续运行100万步对相关结果进行统计平均.
通过调节固-液势能参数(α和β)可以改变表面浸润性, 图3(a)为体系内无量纲势能随粒子间距的变化曲线. 势能?随原子间距r的增大先减小后增大, 最后趋于稳定. 势阱深度代表固体原子对液体原子的束缚程度, 随固-液势能参数的增大而增大. 当吸收的能量不足以克服势能壁垒的限制时, 液体原子在平衡位置附近振动, 呈类固体排列. 图3(b)为本征接触角θ_e(液滴站立在光滑表面上时, 在气-液-固三相交点处作气-液界面切线, 此切线与固-液界线间的夹角)随固-液作用参数β的变化曲线. 结果显示, θ_e与β呈线性关系. 本文选取了七种不同的浸润性, α = 0.14, β分别为0.3, 0.35, 0.4, 0.45, 0.5, 0.55和0.6, 对应的θ_e分别为157.6°, 143.5°, 129.4°, 114.5°, 101.3°, 84.6°和68.9°.
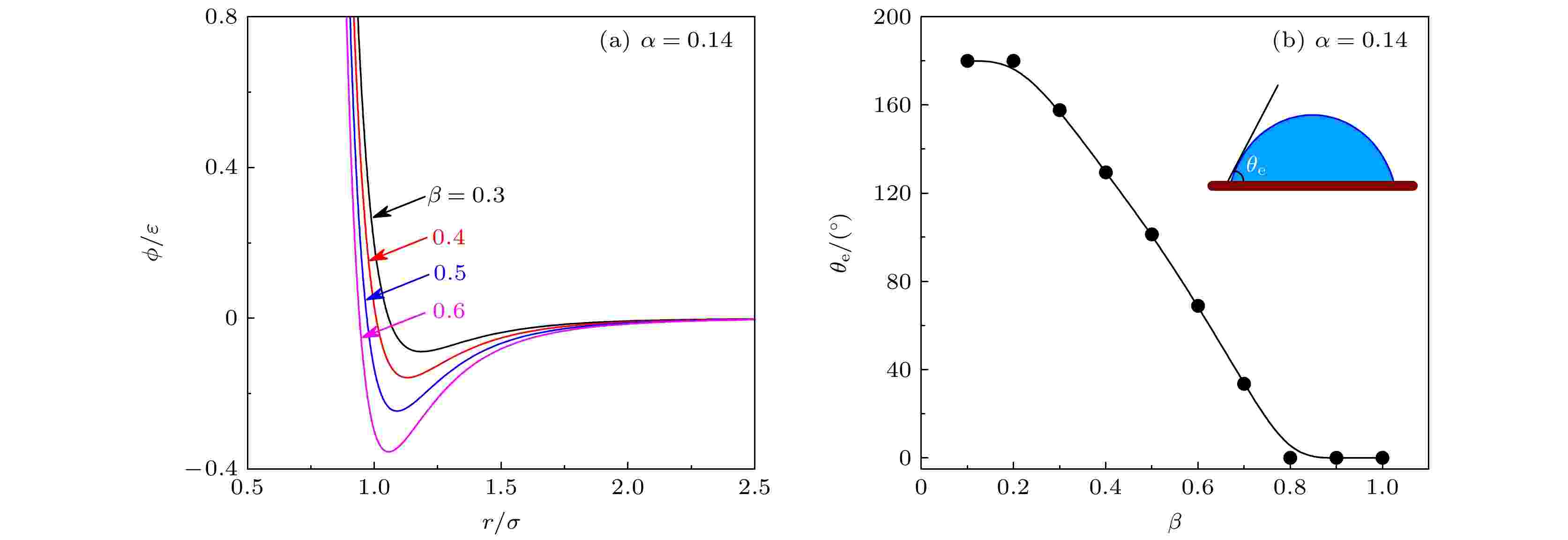图 3 (a)无量纲势能随粒子间距的变化曲线; (b)本征接触角随表面浸润性的变化曲线
Figure3. (a) Variation curves of dimensionless potential energy with particle spacing; (b) change curves of intrinsic contact angle with surface wettability.

2 -->

2.3.接触角的标定

图4给出了三种润湿模式下液滴的密度云图及接触角测量方法. 不同颜色表示不同的数密度范围, 通过拟合连接气-液界面的等密度点, 得到等密度曲线, 图中蓝色实线代表液体主体密度与气体主体密度的平均值, 即ρ* = (ρ_l + ρ_v)/2. 红色区域代表固体基板与纳米结构, 蓝色虚线代表对气-液界面进行圆形拟合得到的液滴外形轮廓线. 不同润湿模式均选取纳米结构顶部与液滴接触部分作为测量基准(图4(d)—(f)中黑色实线所示), 与液滴外部轮廓线做切线, 与水平面夹角即为液滴在粗糙表面的表观接触角θ, 简化表达统一写成接触角. 图4(e)中标示的D代表液滴在粗糙表面的渗透深度, 渗透深度与纳米结构高度之比为渗透率P, 表示液滴的润湿程度. 采用文献[32]中液滴润湿状态的划分方法, 以润湿程度P区分液滴润湿状态, 其中Cassie模式, P ≤ 20%; Wenzel模式, P = 100%; Partial Wenzel模式, 20% < P < 100%.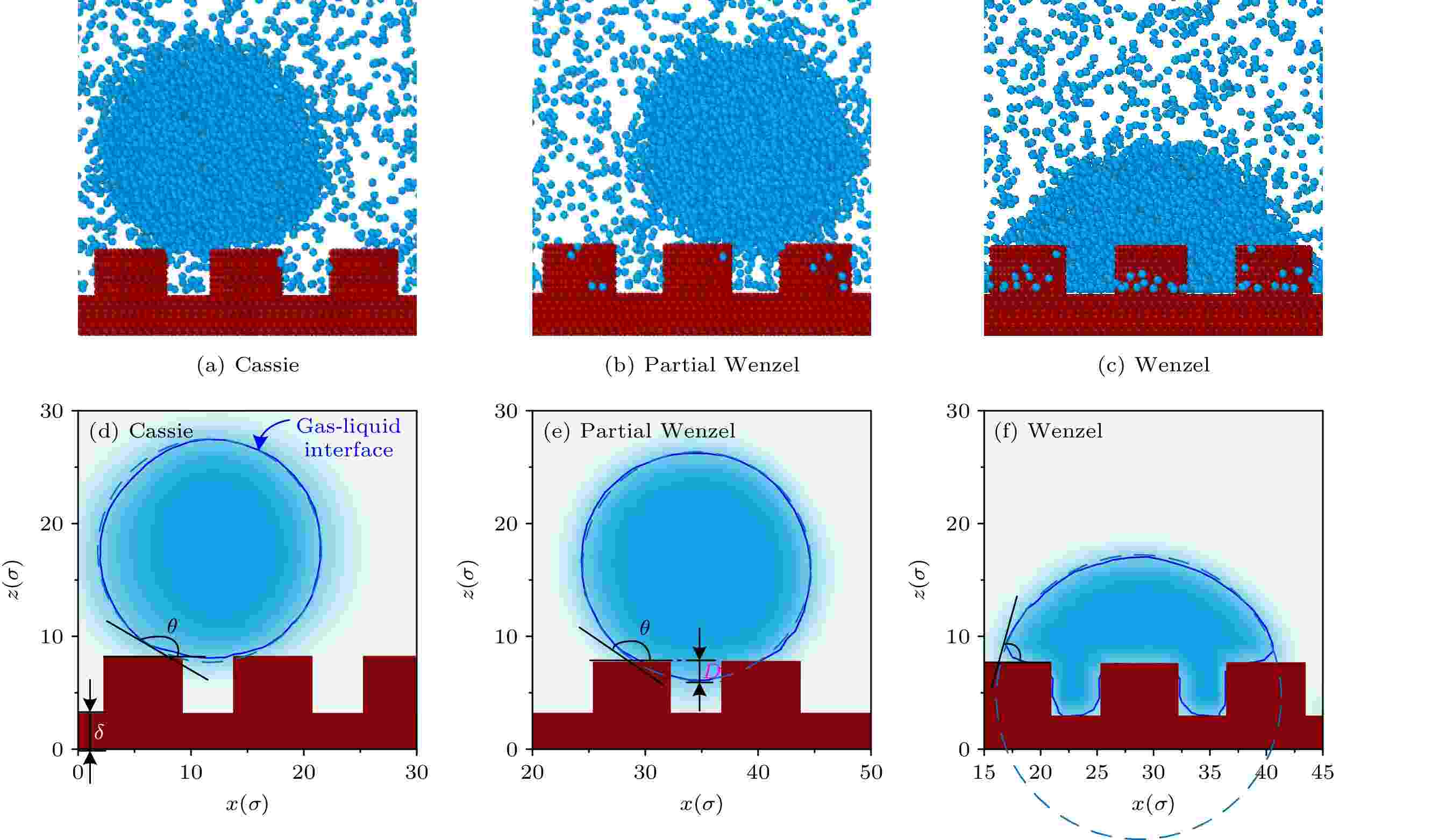
图 4 液滴在粗糙表面上三种润湿模式下的(a)—(c)密度云图及(d)—(f)接触角
Figure4. (a)–(c) Density nephograms and (d)–(f) contact angles of droplets in three wetting modes on rough surfaces.

2

-->

3.1.表面浸润性及纳米结构倾角对接触角的影响

纳米液滴在润湿过程中, 表面张力和分子间作用力是液滴变形与移动的驱动力, 控制液滴在垂直及水平方向的移动. 初始模拟环境为真空状态, 由于空间内压差及分子间力的作用, 在液滴演化过程中, 氩原子逐渐离开液滴进入气相区域发生扩散, 随着气相原子数目不断增多, 气相空间压力趋于饱和, 液滴处于稳定状态. 图5(a)—(c)代表不同θ_e和φ对应的液滴润湿平衡位型图. 当θ_e = 157.6°时, 液滴润湿过程中固-液接触面积较小, 导致表面张力在垂直方向的分量远大于固-液相互作用力, 使得液滴无法稳定在固体表面而发生脱离(Dewetting状态). 王文辉^[33]研究结果中也提到了类似的现象.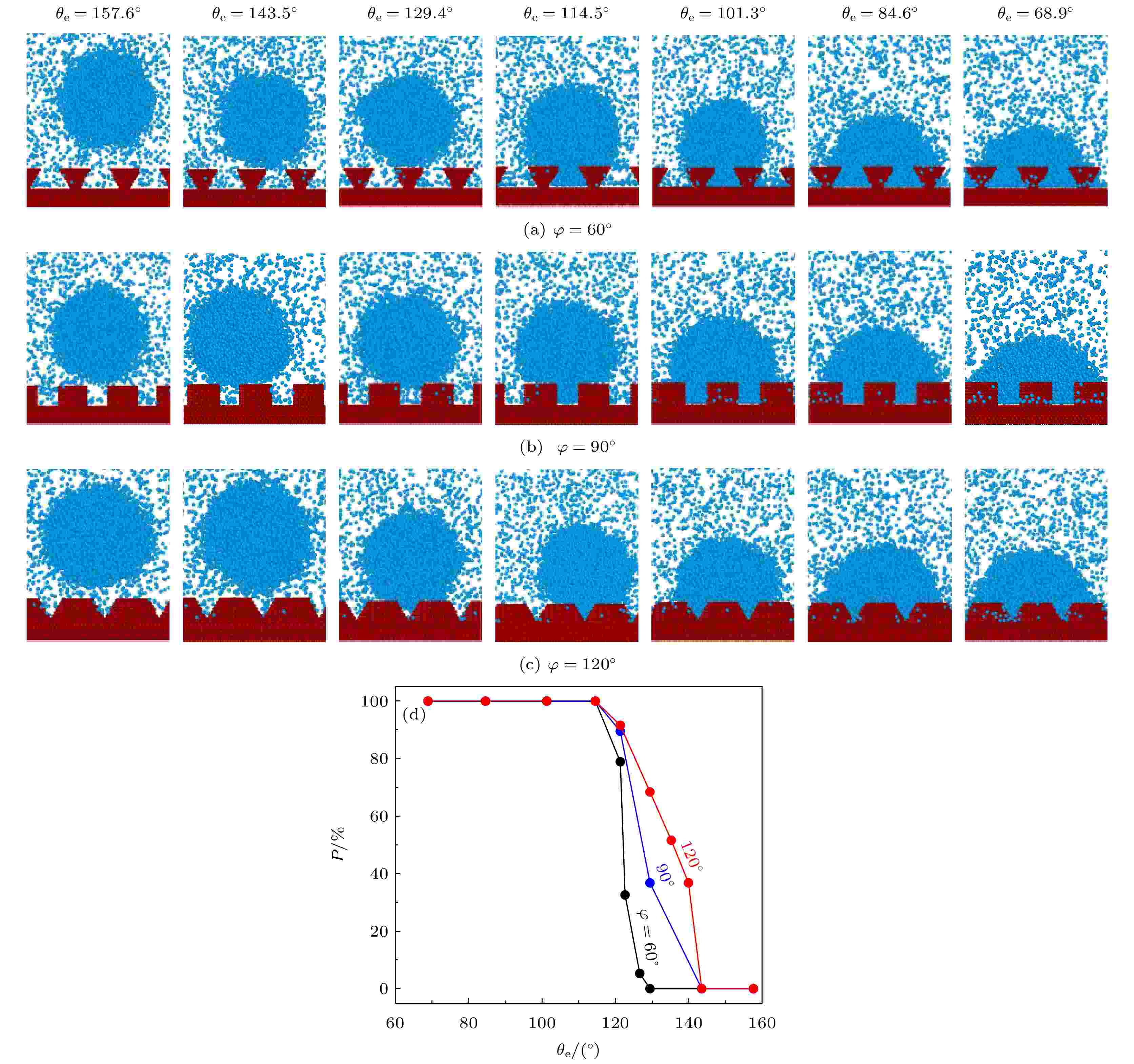
图 5 (a)—(c)当φ = 60°, 90°, 120°时, 不同θ_e的平衡状态位型图; (d) 当φ = 60°, 90°, 120°时, 渗透率随表面浸润性的变化曲线
Figure5. (a)–(c) Bitmaps of equilibrium states for different θ_e with φ = 60°, 90°, 120°; (d) permeability curves with surface wettability with φ = 60°, 90°, 120°.

为表示不同φ和θ_e下液滴在固体表面的润湿程度, 图5(d)给出了渗透率(P)随浸润性(θ_e)的变化曲线. 随着θ_e的减小, 分子间作用力逐渐占主导地位, P由0增至100%, 液滴逐渐向Wenzel模式过渡. 随着φ的减小, P不断减小, 一定程度上降低了液体原子向纳米结构凹槽渗透的能力.
在宏观实际中, 固体表面的各种微小结构对润湿性能都会产生一定影响, 液滴在固体表面的润湿状态和接触角会随着表面浸润性、几何尺寸和纳米结构倾角的改变而发生变化. 如图6(a)所示, 在相同纳米结构倾角(φ)下, 固体表面上的θ随着θ_e的增加而增加. 而在相同浸润性(θ_e)下, 按照润湿模式和液体进入凹槽的数目N_p (N_p的统计方法为: 截取沿z方向7σ的位型图对应的俯视图), 可将θ随着φ的变化划分为I和II两类.
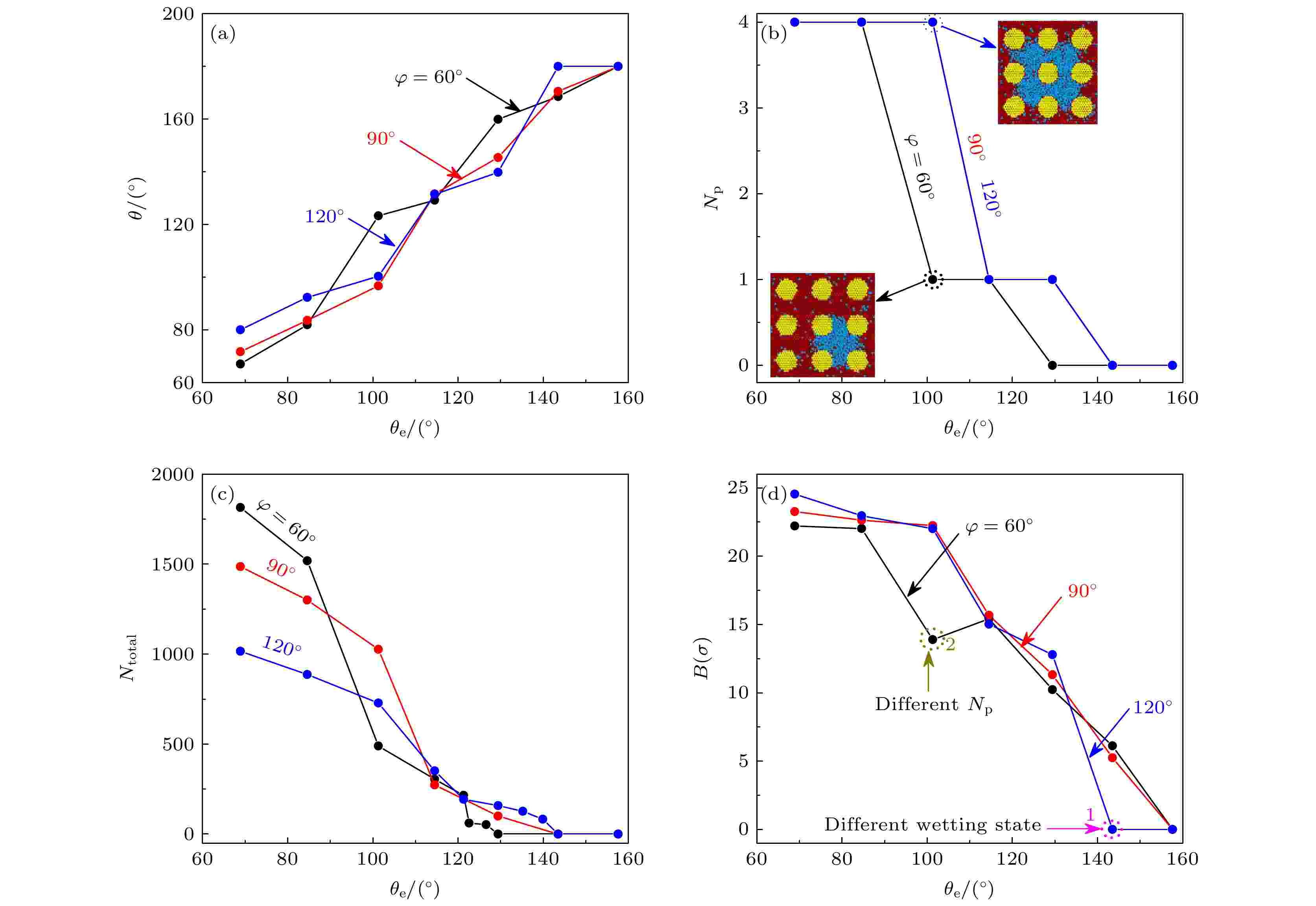图 6 (a)当φ = 60°, 90°, 120°时, 表观接触角随θ_e的变化曲线; (b)液体润湿凹槽数目随θ_e的变化曲线, 其中, φ = 90°和120°时的曲线完全重合; (c)液体原子渗入到凹槽的数量随θ_e的变化曲线; (d)液滴基底圆半径随θ_e的变化曲线
Figure6. (a) Curves of apparent contact angle with θ_e when φ = 60°, 90°, 120°; (b) change curves of the number of liquid wetting grooves with θ_e, where the curves at φ = 90° and 120° are completely coincident; (c) amount of liquid atoms entering the groove varies with θ_e; (d) change curves of the droplet base circle radius with θ_e.

在I类情况下, θ随着φ的增加而增加. 当θ_e = 84.6° (润湿模式与N_p相同)时, 液滴在固体表面呈Wenzel状态(图5(a)—(c)所示), 对应的N_p = 4 (图6(b)所示), 此时θ_60° < θ_90° < θ_120°. 造成上述现象的原因是, 单个凹槽的体积随着φ的增加而减小, 导致纳米结构内部可容纳的总原子数(N_total)随φ的增加而减小(图6(c)所示).
在II类情况下, θ随着φ的增加而减小. 当θ_e = 129.4°(润湿模式不同、N_p相同)时, 随着φ的增加, 润湿模式依次为Cassie, Partial Wenzel和Partial Wenzel, 对应的N_p = 1 (图6(b)), 此时, θ_60° > θ_90° > θ_120°. 主要原因为: φ对液体原子向凹槽内部的渗透能力有一定影响, 且N_total随着φ的增加逐渐增加(图6(c)); 当θ_e = 101.3° (润湿模式相同、N_p不同)时, 液滴在固体表面呈Wenzel状态(图5(a)—(c)), 对应的N_{p, 90°} = N_{p, 120°} = 4和N_{p, 60°} = 1 (图6(c)), 此时, θ_60° > θ_90° > θ_120°. 造成上述现象的原因是: 当液滴外缘位于纳米结构边缘时, 高的表面边缘密度导致近壁面处接触线固定, 限制了液体原子的水平移动.
此外由图6(d)可知, 对于相同纳米结构倾角(φ)的固体表面, 基底圆半径B (指纳米结构顶部固-液接触面积对应的半径)随θ_e的减小而增大, 表明浸润性越强, 液滴在粗糙表面的铺展程度越大. 对于相同浸润性的固体表面, B随φ的增大而增大. 但φ = 120°与60°时, B存在突降, 如图6(d)中1和2标识所示, 其中标识2对应的表面浸润性下, 呈现相反的变化规律. 出现该现象的原因是不同φ对应的润湿状态或N_p不同. 当θ_e = 143.5°时(图6(d)中的标识1), φ = 60°与90°对应的为Cassie状态, 而φ = 120°对应的为Dewetting状态; 当θ_e = 101.3°时(图6(d)中的标识2), φ = 90°与120°对应的N_p = 4, 而φ = 60°对应的N_p = 1.
2 -->

3.2.理论计算与MD模拟比较

3 -->

3.2.1.理论自由能的计算

本节中建立三维空间内液滴在粗糙表面的润湿模型, 假设液滴分布为球型, 每种状态的总能量为液滴和其接触表面之间所产生的所有能量之和. 系统的自由能差可表示为

$\begin{split}\Delta E ={}& \Delta {E_{\rm{int} }} + {E_{\rm{g}}} \\=\;& {A_{{\rm{lv}}}}{\sigma _{{\rm{lv}}}} + {A_{{\rm{sl}}}}({\sigma _{{\rm{sl}}}} - {\sigma _{{\rm{sv}}}}) + {F_{\rm{g}}},\end{split}$

固体表面上的Young方程为

${\sigma _{{\rm{sv}}}} = {\sigma _{{\rm{sl}}}} + {\sigma _{{\rm{lv}}}}\cos {\theta _{\rm{e}}},$

结合(6)式和(7)式得到:

$\Delta E = {\sigma _{{\rm{lv}}}}\left( {{A_{{\rm{lv}}}} - {A_{{\rm{sl}}}}\cos {\theta _{\rm{e}}}} \right) + {F_{\rm{g}}}.$

(6)式对于微观系统的能量计算同样适用^[34,35]. 值得指出的是, 纳米尺度下重力对液滴动力学行为的影响很小, 所以本文忽略了纳米液滴的重力. 即公式中的重力项F_g = 0. 其中, $\Delta {E_{\rm{int} }}$为固体表面上有无液滴时的固-液-气界面能差值; E_g为重力势能; σ_lv为气-液表面张力, A_lv为气-液接触面积, A_sl为固-液接触面积.
对于Cassie模型:

$A_{{\rm{lv}}}^{\rm{C}} = 2{\rm{\pi }}{R^2}\left( {1 - \cos {\theta _{\rm{C}}}} \right) + {\rm{\pi }}{B^2}(1 - f),$

$A_{{\rm{ls}}}^{\rm{C}} = {\rm{\pi }}{B^2}f,$

$\begin{split}\Delta {E_{\rm{C}}} =\;& {\sigma _{{\rm{lv}}}}\{ 2{\rm{\pi }}{R^2}(1 - \cos {\theta _{\rm{C}}}) \\&+ {\rm{\pi }}{B^2}\left[ {1 - f\left( {1 + \cos {\theta _{\rm{e}}}} \right)} \right] \};\end{split}$

对于Wenzel模型:

$A_{{\rm{lv}}}^{\rm{W}} = 2{\rm{\pi }}{R^2}\left( {1 - \cos {\theta _{\rm{W}}}} \right),$

$A_{{\rm{ls}}}^{\rm{W}} = {\rm{\pi }}{B^2}r,$

$\Delta {E_{\rm{W}}} = {\sigma _{{\rm{lv}}}}\left[ {2{\rm{\pi }}{R^2}(1 - \cos {\theta _{\rm{W}}}) - {\rm{\pi }}{B^2}r\cos {\theta _{\rm{e}}}} \right].$

这里R为液滴半径, B为基底圆半径, 表达式为

$B = R\sin \theta.$

3 -->

3.2.2.理论预测与模拟结果的比较

图7(a)—(c)为理论自由能的计算结果, 且对比MD模拟结果(图5), 发现二者符合较好. 当θ_e = 129.4°, φ = 90°时, 理论预测结果显示ΔE_W > ΔE_C, 基于自由能最低原理判断液滴呈Cassie润湿模式, MD模拟结果同样得出该表面浸润性下液滴呈Cassie润湿模式.
图 7 (a)—(c)不同φ和θ_e下的理论自由能值; (d)—(f)不同φ和θ_e下接触角的变化
Figure7. (a)–(c) Theoretical free energy values under different φ and θ_e; (d)–(f) change of contact angle under different φ and θ_e.

由图7(d)—(f)发现, θ随θ_e增加而增加, 变化趋势与φ无关, 但数值上存在略微差别. 通过对处于C (Cassie)和W (Wenzel)两种区域内的模拟值(θ_SIM)与对应润湿模式的预测值(θ_C, θ_w)进行比较, 发现在不同φ值下, θ_C都近似等于θ_SIM; 在大多数情况下θ_w与θ_SIM符合良好. 但θ_e = 68.9°时θ_SIM > θ_w, 此时液滴外缘位于纳米结构边缘(图5), 高表面边缘密度使得接触线固定, 钉扎作用显著, 但Wenzel与Cassie理论模型未考虑上述钉扎效应的影响, 所以理论预测值偏小. 而处于PW (Partial Wenzel)区域的θ_SIM与θ_C, θ_w的大小关系为θ_w < θ_SIM < θ_C, 且渗透程度越高, θ_SIM越接近θ_w. 通过理论公式($\cos {\theta _{{\rm{CW}}}} = \dfrac{f - 1} { r - f }$)计算的C与W润湿模式的转换接触角θ_CW近乎相等 (θ_{CW, 60°} = 123.6°, θ_{CW, 90°} = 121.4°, θ_{CW, 120°} = 125.8°), 均位于PW区域.
3 -->

3.2.3.不同浸润性及纳米结构倾角下的润湿模式分区

为了讨论不同θ_e和φ对润湿模式的影响, 对润湿模式进行统计(如图8所示). 研究发现, 可将φ-θ_e相图划分为4个区域: C, W, PW和DW (Dewetting), 随着θ_e的增加, 液滴逐渐实现W→PW→C→DW的润湿转换.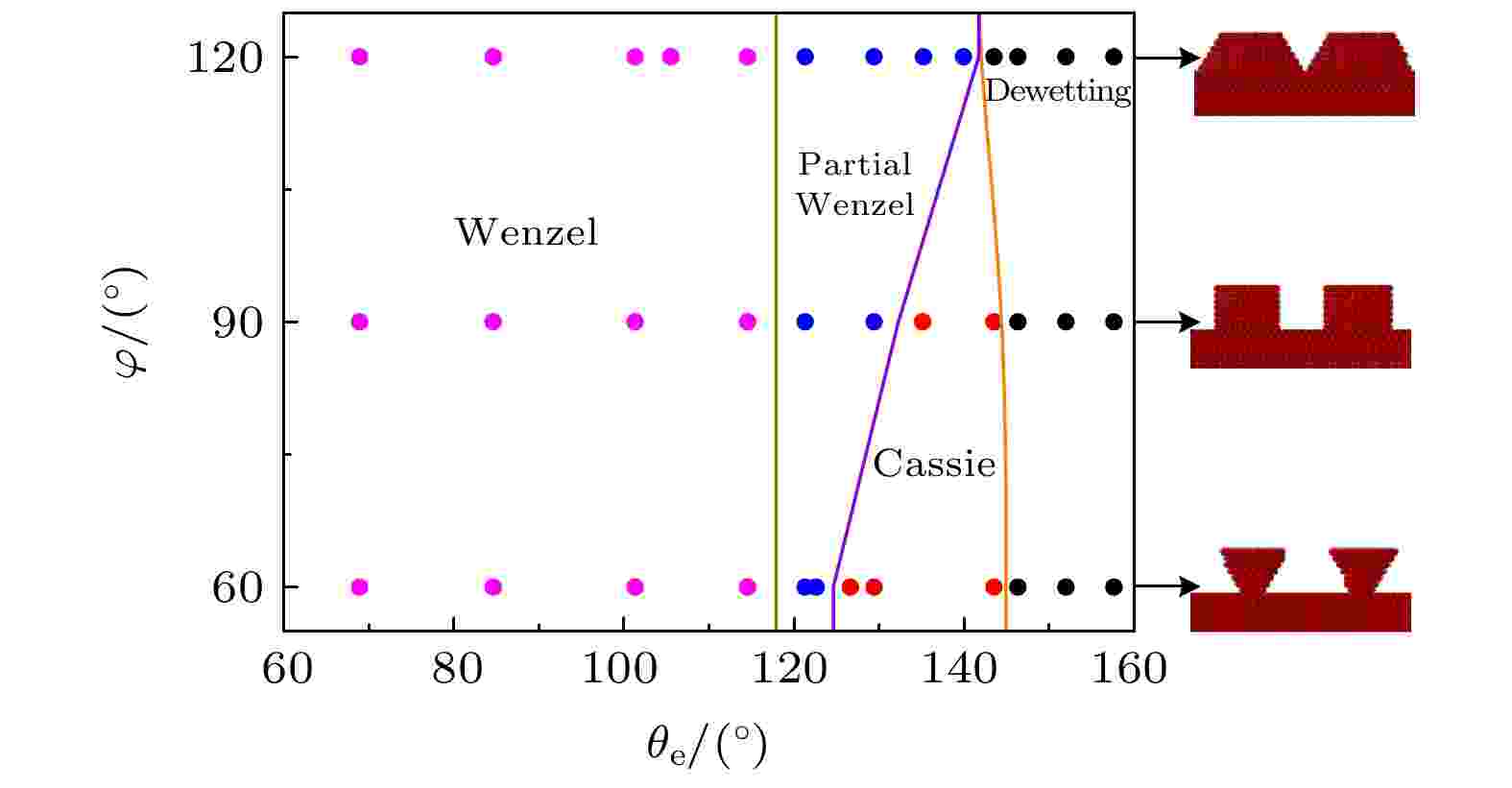
图 8 不同φ和θ_e下的润湿模式分区图
Figure8. Wetting mode partition diagram under different φ and θ_e.

在60° < θ_e < 118°时, 液滴在纳米结构表面呈现W状态, 该润湿状态在相图中占比最高, 约为总区域面积的1/2, 在该区域内表面浸润性占主导作用(即固-液间作用力较强). 随着θ_e的增加(125° < θ_e < 145°), 液滴在纳米结构表面呈现C与PW状态, 且C与PW区域分别呈三角形和反梯形分布, 两种润湿区域所占面积近乎相等. 其中C区域面积随φ的减小而增大, 表明φ减小增强了由锐边效应引起的钉扎作用, 使得壁面外缘可以容纳更多的流体原子; 但当φ较大时(φ ≥ 120°)不存在C状态, 微柱阵列表面的液体原子在毛细力和固-液相互作用力^[27]的共同作用下, 更容易渗透至纳米结构内部, 不利于形成超疏水表面. 在θ_e > 145°时, 液滴在纳米结构表面呈现DW状态, 表面张力占主导作用(即固-液间作用力较弱), 且发现在该区域内固体原子数目随φ的增加而增加.

采用MD方法研究不同纳米结构倾角(φ)及表面浸润性(θ_e)下, 结构尺寸与液滴大小相当时, 纳米氩液滴在粗糙铂表面的润湿行为. 讨论表观接触角的影响因素及检验是否符合Wenzel及Cassie理论预测模型^[8,9], 根据不同结构及浸润性进行润湿模式分区. 具体结论如下:
1)液滴在不同纳米结构倾角(60°, 90°和120°)及浸润性的表面达到润湿平衡后存在四种润湿状态, 分别为Dewetting, Cassie, Partial Wenzel和Wenzel, 随着表面浸润性的减弱, 润湿状态逐渐由Wenzel向Dewetting过渡;
2)通过比较表观接触角模拟值(θ_SIM)与理论预测值(θ_w, θ_C)的大小关系, 发现不同纳米结构倾角在Cassie与Wenzel润湿状态的表观模拟值与预测值基本符合, 而Partial Wenzel润湿状态由于部分液体原子渗入凹槽内, 模拟值较预测值偏小(θ_SIM < θ_C), 且渗透程度越高θ_SIM越接近θ_w;
3)不同润湿模式基本满足自由能最小原理, 根据φ和θ_e对润湿模式进行分区: 随着浸润性θ_e的减小, φ对最终润湿状态的影响减弱, 尤其当θ_e < 118°时, 液滴在纳米结构表面均呈Wenzel状态; 对于超疏水表面(118° < θ_e < 145°), 倒梯形(φ = 60°)纳米结构有利于保持Cassie状态, 而正梯形(φ = 120°)纳米结构容易形成Partial Wenzel液滴, 其一由于φ减小增强了锐边效应引起的钉扎作用, 相同浸润性下降低了液体原子向凹槽内渗透的能力, 其二是当液滴扩散至纳米结构外缘时, 可以容纳更多的流体原子.