全文HTML
--> --> -->在离子径迹特征与器件SEE的关联性研究中, 晶体管SEE收集电荷和存储器SEU的相关研究占绝大多数[2-15], 组合逻辑电路单粒子瞬态(single event transients, SET)的相关研究未见报道. 随着器件特征尺寸的减小和时钟频率的增加, 组合逻辑电路SET造成的软错误急剧增加并逐渐成为SEE软错误的主体[16-21], 开展离子径迹特征与纳米组合逻辑电路SET的关联性研究对准确预估纳米微电子器件在轨SEE软错误率具有重要意义.
本文以纳米CMOS工艺的体硅反相器链为研究载体, 结合TCAD (technology computer aided design)和Geant4耦合仿真, 研究了相同LET值的高低能离子的每核子能量比率、离子LET值、离子入射角度和反相器链偏置电压等参数对相同LET值的高低能离子所导致的纳米反相器链SET脉宽差异的影响, 从离子径迹特征与SET的内在关联角度对影响机制进行了分析.
2
2.1.TCAD模型的建立和校准
针对65 nm体硅CMOS反相器链建立TCAD模型, 考虑到电荷共享的存在, 反相器链选取为四级, 相应的电路原理图和TCAD模型如图1(a)和图1(b)所示. p型金属氧化物半导体(PMOS)晶体管和n型金属氧化物半导体(NMOS)晶体管的栅宽分别为0.32和0.24 μm, 栅长均为60 nm. 晶体管的TCAD模型均通过电学特性校准, 即晶体管TCAD模型的I-V特性曲线与该晶体管HSPICE宏模型的I-V 特性曲线一致, 如图2和图3所示. 当反相器链的输入为逻辑低电平时, NMOS晶体管对SET敏感; 反相器链的输入为逻辑高电平时, PMOS晶体管对SET敏感. 效应仿真中, 离子入射第一级反相器的敏感NMOS或者敏感PMOS, 在第一级反相器的输出端产生瞬态脉冲, 该瞬态脉冲沿反相器链传播至输出端. 仿真考虑的物理模型主要包括: 费米-狄拉克统计模型, 禁带变窄模型, Shockley-Read-Hall (SRH)复合和俄歇复合模型, 考虑掺杂、电场和载流子浓度对迁移率影响的模型, 漂移扩散模型等.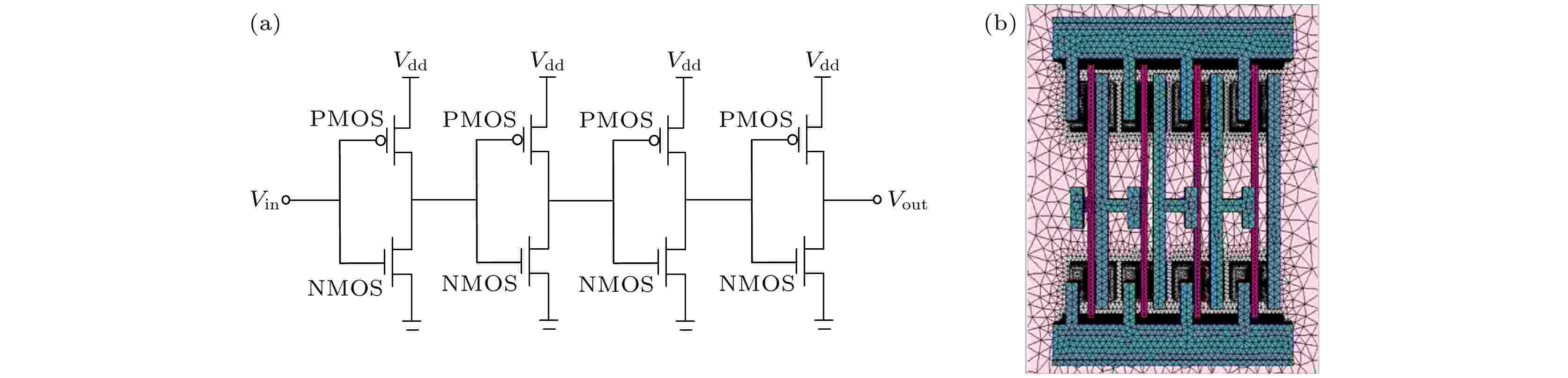
图 1 四级反相器链的(a)电路原理图和(b)三维TCAD模型Figure1. (a) Schematic and (b) three-dimensional TCAD model of the 4-stage inverter chain.
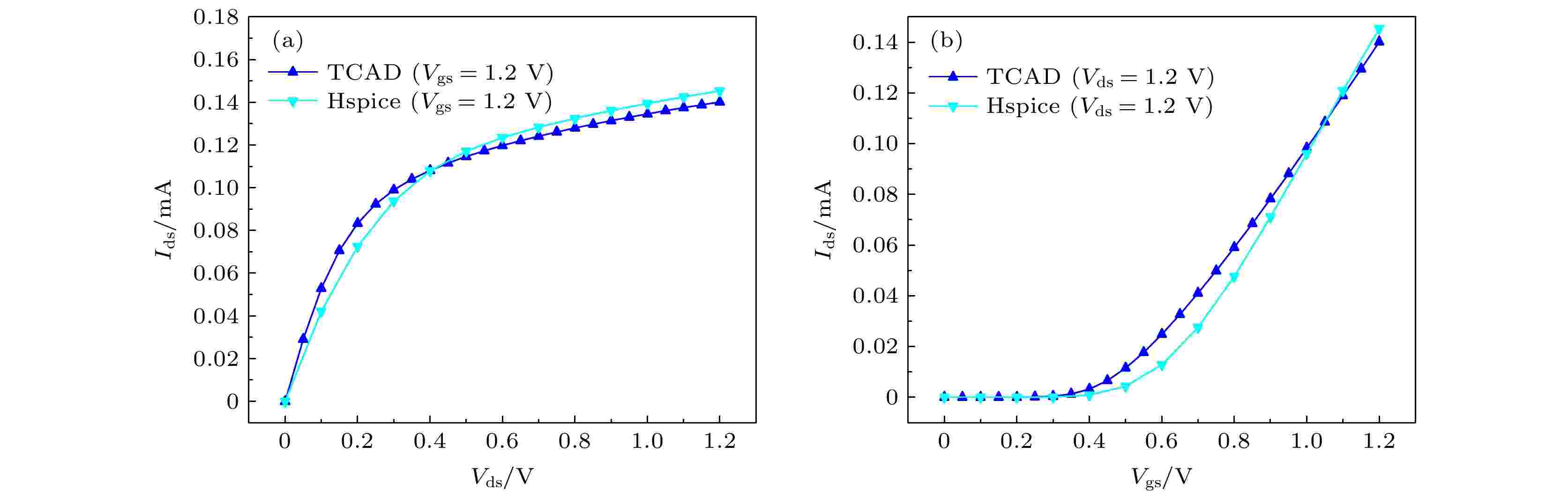图 2 NMOS晶体管的I-V特性校准 (a) Ids-Vds曲线; (b) Ids-Vgs曲线Figure2. Calibration of I-V characteristics of the NMOS transistor: (a) Ids-Vds curves; (b) Ids-Vgs curves.
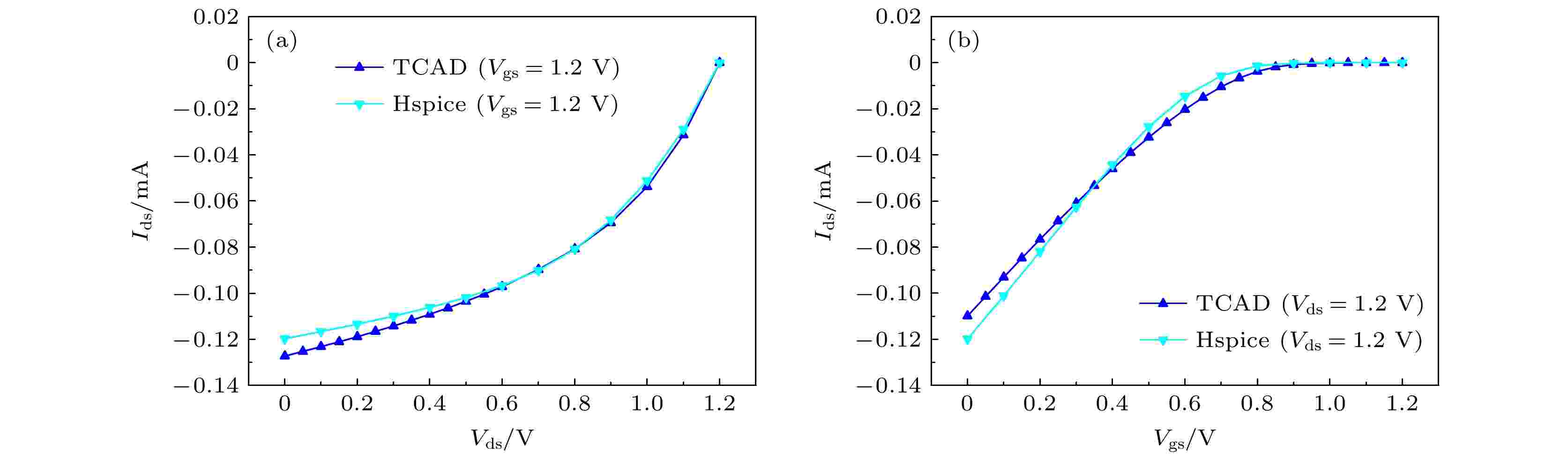图 3 PMOS晶体管的I-V特性校准 (a) Ids-Vds曲线; (b) Ids-Vgs曲线Figure3. Calibration of I-V characteristics of the PMOS transistor: (a) Ids-Vds curves; (b) Ids-Vgs curves.
2
2.2.离子径迹计算程序的开发和结果验证
基于Geant4开发了离子径迹计算程序. Geant4的G4hIonisation类可以用来计算由于带电粒子本身电离损失的能量和次级粒子电离产生的离散式能量损失, 在仅考虑直接电离的情况下, 次级粒子主要是电子, 对于电子与材料相互作用过程的描述选用G4EmLivermorePhysics模型, 在该模型中包括光子、电子和正电子的一系列物理过程, 如康普顿散射、光电效应、韧致辐射和正电子湮灭等. 离子径迹计算程序旨在获取离子径迹的径向能量沉积分布. 考虑到能量沉积围绕径迹中轴线(中轴线由离子入射位置和入射方向共同决定)呈径向对称, 在计算能量沉积分布时, 以径迹中轴线为中心设置一系列同轴圆柱壳, 圆柱壳的半径从内向外依次增大[29], 相邻圆柱壳围成具有一定径向厚度的圆筒状敏感探测器, 敏感探测器相对于径迹中轴线的径向距离为内圆柱壳和外圆柱壳半径的平均值. 为减小各敏感探测器内能量沉积的统计误差, 令1000个离子沿相同方向从同一位置入射硅材料, 统计每一个敏感探测器内的能量沉积, 然后除以相应敏感探测器的体积得到能量沉积密度, 再除以1000归一化到单个离子的能量沉积密度, 该能量沉积密度所对应的沉积位置由敏感探测器相对于径迹中轴线的径向距离来表征, 如此就可以得到单个离子的能量沉积密度随离子径迹径向尺度的变化. 有时在离子径迹计算时, 会将能量沉积密度转化为电子-空穴对密度(离子在硅材料中每沉积3.6 eV的能量可产生一个电子-空穴对).将本文中用Geant4计算的23 MeV·n–1 Kr 离子的径迹数据与文献[30]用Geant4计算的离子径迹数据进行了比较, 这里的径迹数据是指离子入射硅材料生成的电子-空穴对密度随离子径迹径向尺度的变化. 本文和文献[30]均采用G4EmLivermorePhysics模型处理次级电子的输运过程, 对比结果如图4所示. 可以看出, 两者计算的离子径迹数据符合较好, 证明了离子径迹计算程序的可靠性. 值得一提的是, 文献[30]未提供敏感探测器的设置、粒子射程截断值等物理模型参数的选取信息, 本文在进行对比计算时无从参照, 这可能是造成两径迹数据略微存在差异的原因.
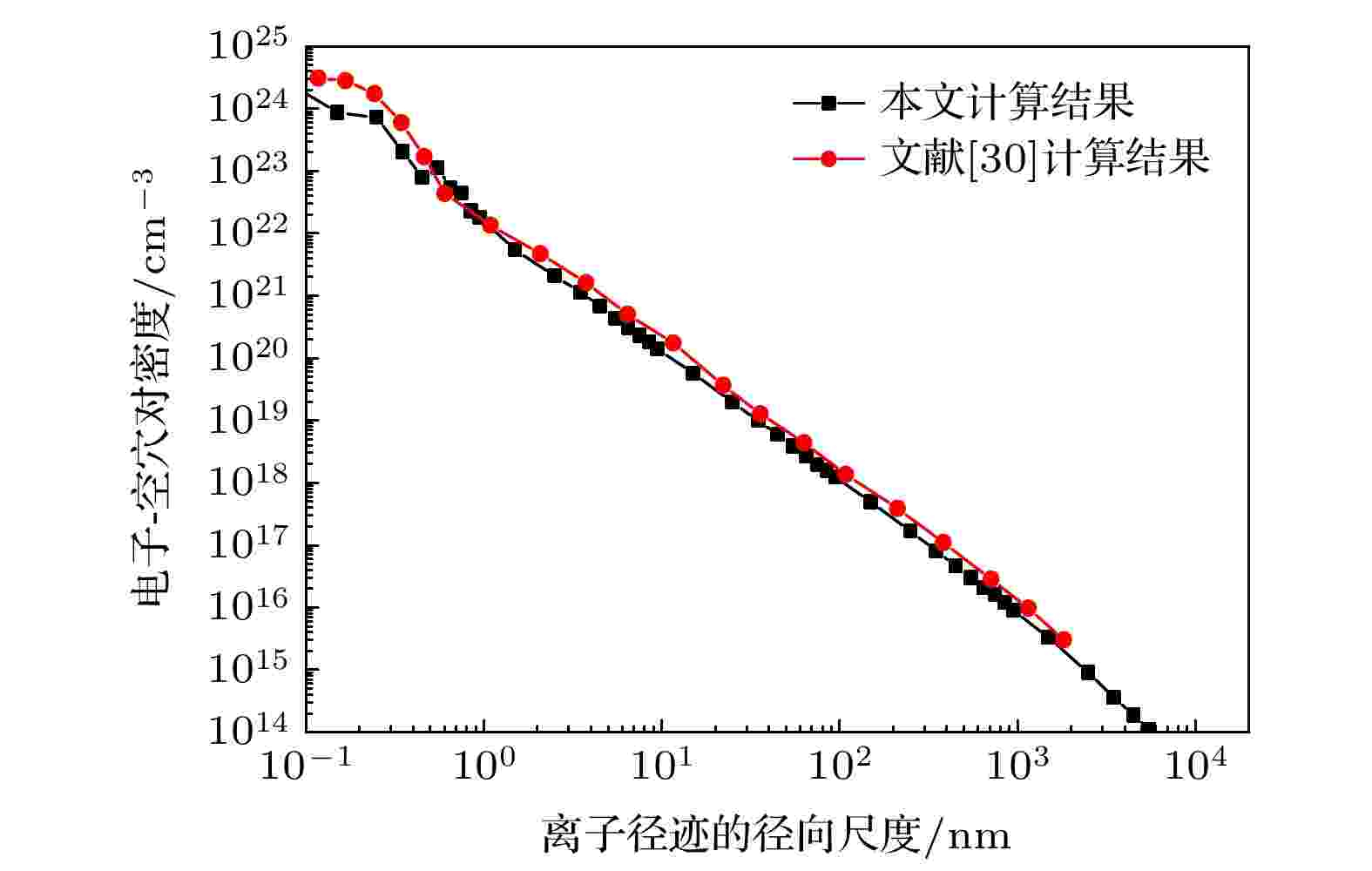图 4 本文和文献[30]通过Geant4计算得到的23 MeV·n–1 Kr离子入射硅材料生成的电子-空穴对密度随离子径迹径向尺度的变化Figure4. Density of electron-hole pairs generated by 23 MeV·n–1 Kr ion incidence into silicon vs. the radial scale of ion track, which are calculated by Geant4. The calculated data of our work and Ref. [30] are compared.
| 离子 分组 | 离子 种类 | 每核子能量 /(MeV·n–1) | 硅表面的LET值/(MeV·cm2·mg–1) | 射程/μm |
| 第一组 | Si | 5.3 | 8.8 | 58 |
| Kr | 83.3 | 8.8 | 1940 | |
| 第二组 | Ti | 3.8 | 21.3 | 38 |
| Xe | 66.7 | 21.3 | 1150 | |
| Ta | 150.3 | 21.3 | 3520 | |
| 第三组 | Br | 3.4 | 41.4 | 36 |
| Ta | 50.3 | 41.4 | 684 |
表1重离子的详细信息
Table1.Detail information of the heavy ions.
图5所示为Geant4计算得到的三组离子入射硅材料生成的电子-空穴对密度随离子径迹径向尺度的变化. 可以看出, 同一组离子中的高能离子的径迹半径为低能离子径迹半径的数倍; 在1—10 nm的径向尺度内, 低能离子产生的电子-空穴对密度明显大于高能离子, 最大差异超过1个数量级; 而在小于零点几纳米的径向尺度内, 高能离子产生的电子-空穴对密度高于低能离子. 上述规律与文献[5]通过Geant4计算得到的高低能离子径迹数据的对比结果在趋势上是一致的.
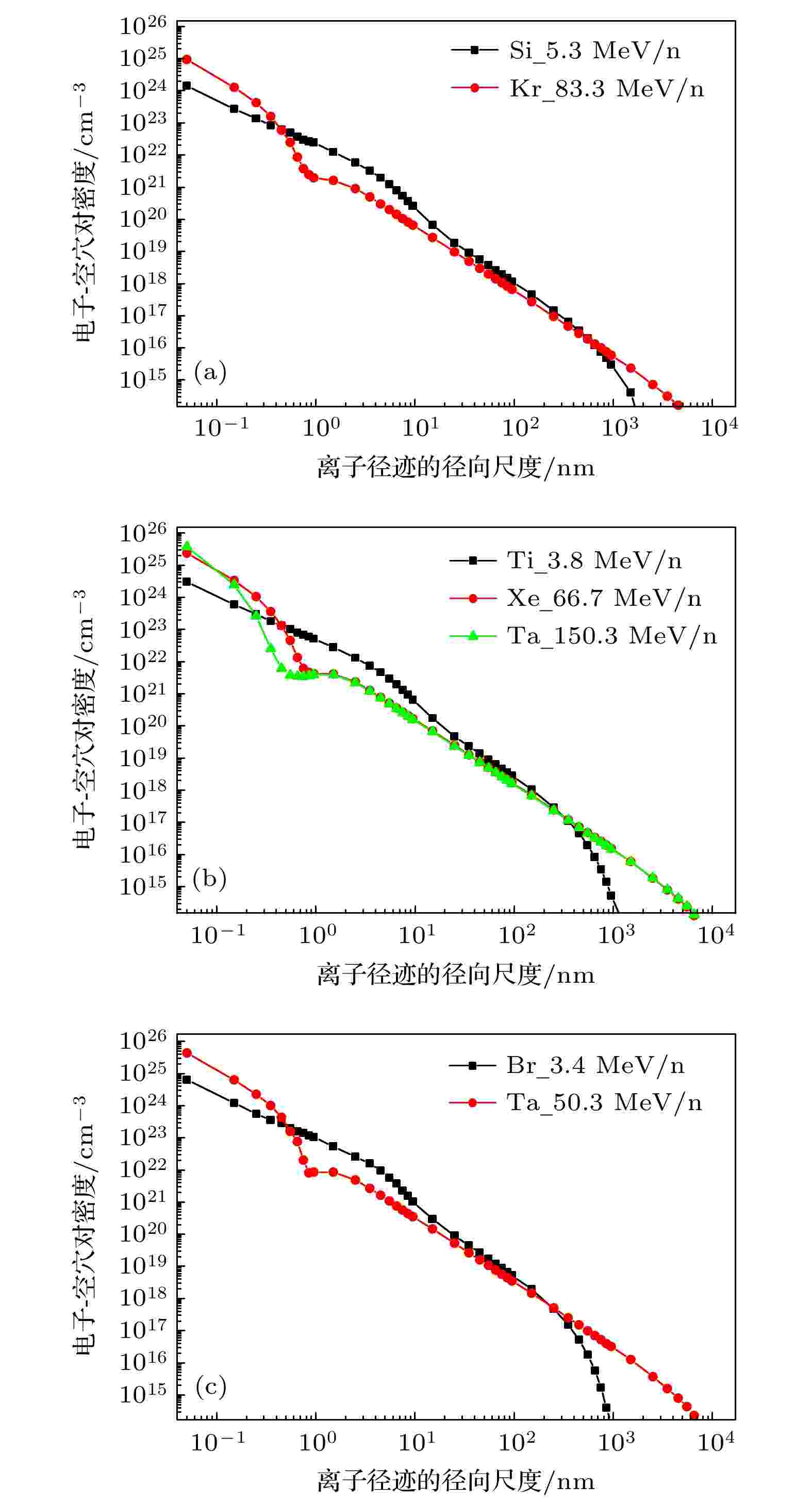图 5 Geant4计算得到的三组离子入射硅材料生成的电子-空穴对密度随离子径迹径向尺度的变化 (a) 第一组高低能离子; (b)第二组高低能离子; (c)第三组高低能离子Figure5. Density of electron-hole pairs generated by ion incidence into silicon vs. the radial scale of ion track: (a) The first group of ions; (b) the second group of ions; (c) the third group of ions.
仿真中, 离子入射位置分布在第一级反相器的有源区(图6), 让离子依次入射图6所示的位置, 记录每一个入射位置所对应的反相器链输出端的SET脉宽(半高宽)Wout, 然后比较高低能离子在每一个入射位置上的Wout差异δ (δ等于低能离子的Wout减去高能离子的Wout), 最后将δ在不同入射位置上的数值通过统计图显示出来.
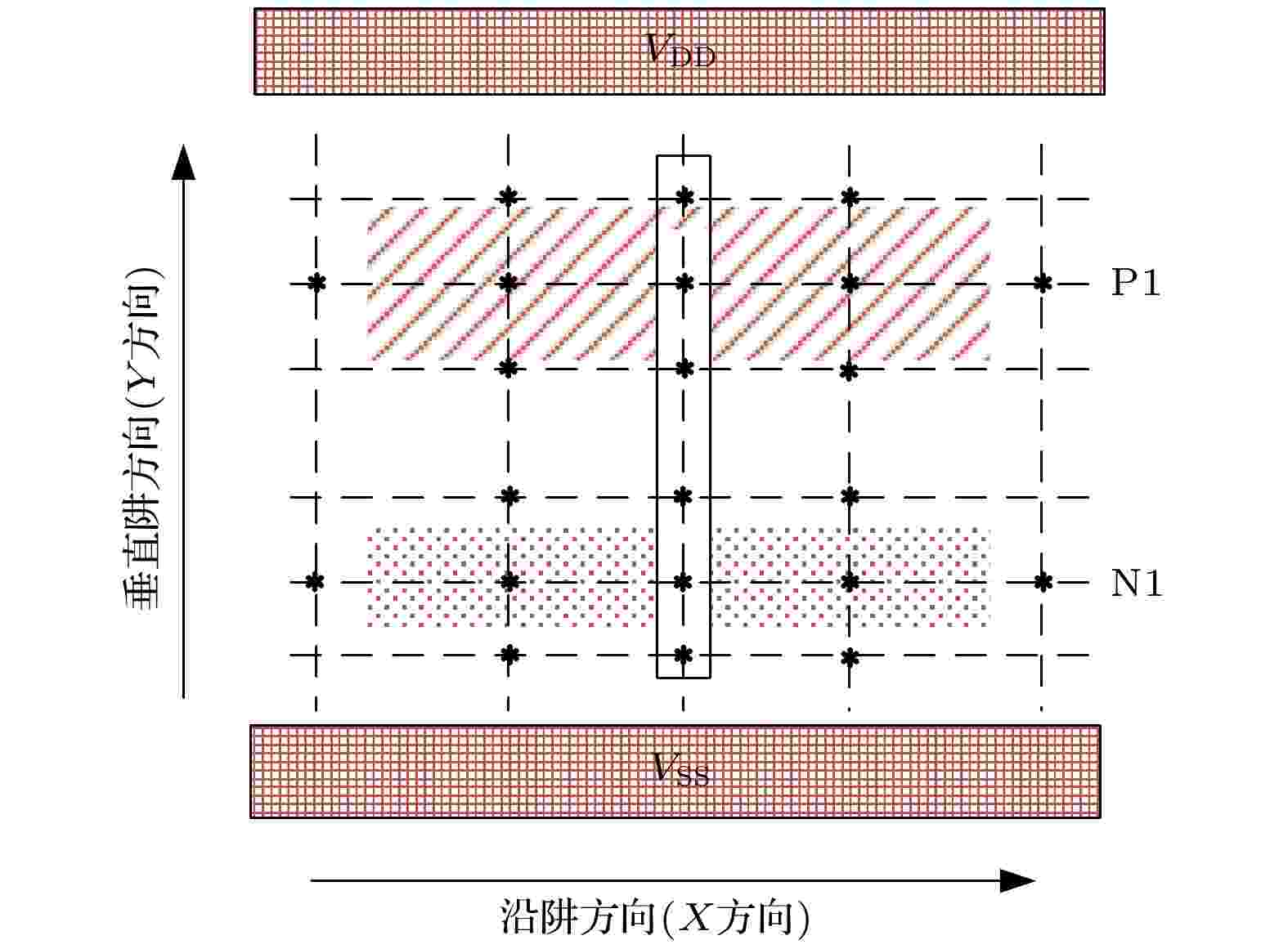图 6 离子入射位置示意图(*表示入射位置)Figure6. Schematic diagram of ion strike locations, where * indicates the ion strike locations.
2
3.1.高低能离子每核子能量比率的影响
第二组的Ti离子为低能离子, Xe和Ta均为高能离子, Xe离子与Ti离子的每核子能量比率约为17.5, 而Ta离子与Ti离子的每核子能量比率更高, 约为39.5. 图7(a)为Ti离子与Xe离子的脉宽差异δ随入射位置的分布, 图7(b)为Ti离子与Ta离子的脉宽差异δ随入射位置的分布. 离子垂直入射, 反相器链偏置电压为1.2 V. 图中X坐标为离子入射位置在沿阱方向的坐标, Y坐标为离子入射位置在垂直阱方向的坐标, Z轴物理量为脉宽差异δ, 图中红色柱代表δ等于0, 黑色柱代表δ小于0, 灰色柱代表δ大于0, 柱的高低代表δ的数值大小. 通过对比发现, 不同入射位置上Ti离子与Xe离子的脉宽差异绝对值均小于50 ps, 但Ti离子与Ta离子的脉宽差异的绝对值最大可达到157 ps. 此外, 计算了各入射位置脉宽差异δ的平方和Σ, 发现图7(a)脉宽差异δ和图7(b)脉宽差异δ的平方和分别为14796和47079. 综上, 高低能离子的每核子能量比率越大, 脉宽差异越明显. 通过图5(b)可以看出, 150.3 MeV·n–1的 Ta离子与3.8 MeV·n–1 的Ti离子的电子-空穴对密度在径迹中心轴附近区域的差异比66.7 MeV·n–1 的Xe离子与3.8 MeV·n–1 的Ti离子的电子-空穴对密度在径迹中心轴附近区域的差异更加明显. 径迹中心轴附近区域的电子-空穴对密度的差异越明显, 电子-空穴对的复合差异就越大, 从而使后续的电荷收集量存在较大差别, 这应该是导致高低能离子的每核子能量比率越大脉宽差异越明显的原因.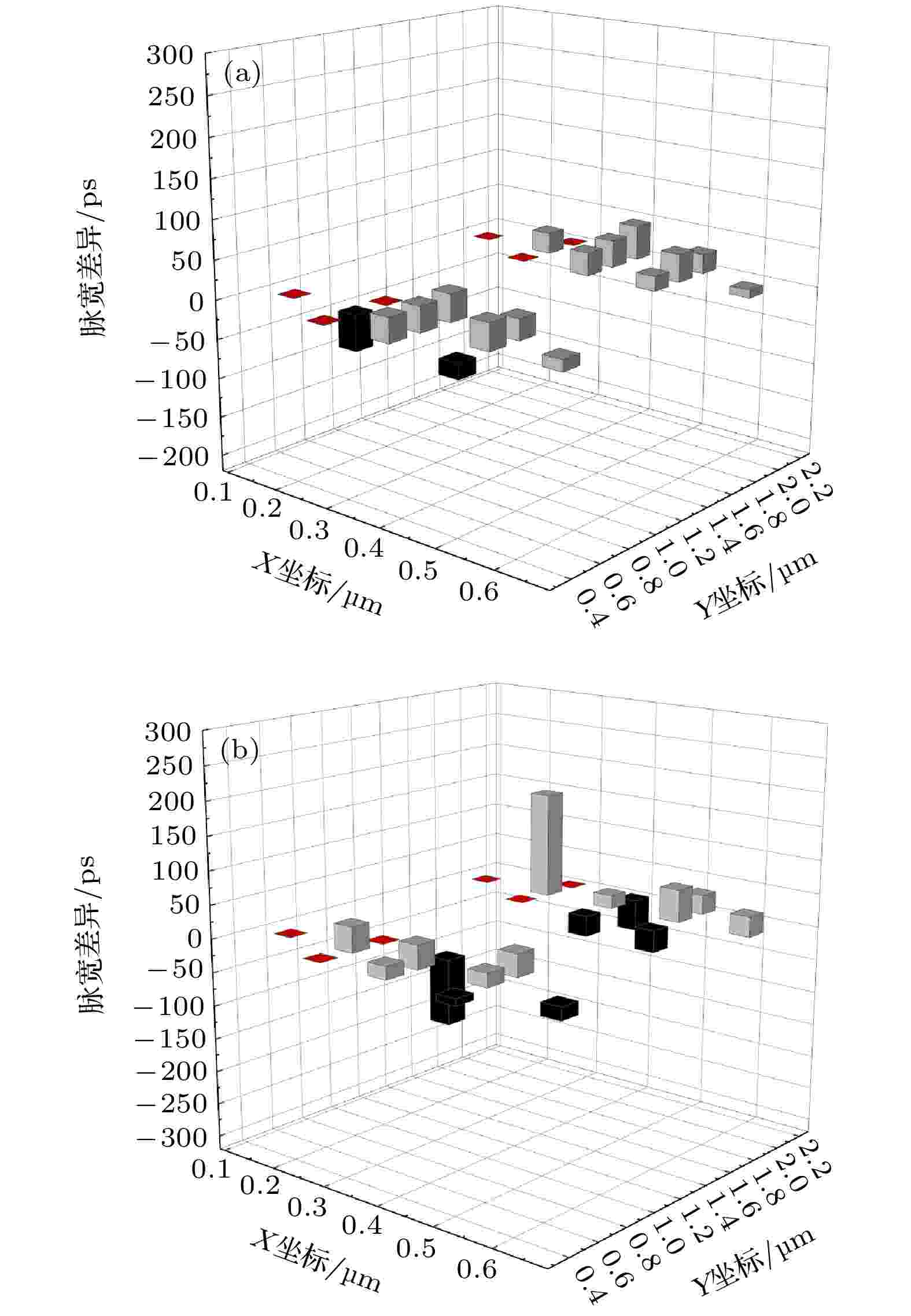
图 7 第二组高低能离子导致的瞬态脉宽差异在不同入射位置上的分布 (a)第二组离子Ti和Xe的比较; (b)第二组离子Ti和Ta的比较Figure7. Distribution of the transient pulse width differences at various strike locations for the second group of ions: (a) Low- and high-energy ions are Ti and Xe respectively; (b) low- and high-energy ions are Ti and Ta respectively.
2
3.2.离子LET值的影响
接下来比较三组离子的脉宽差异分布, 结果如图8所示. 其中第二组离子选取Ti和Xe离子, 以保证高低能离子每核子能量比率尽量与其他两组接近. 对于第一组离子(LET = 8.8 MeV·cm2·mg–1), 多数入射位置下的脉宽差异为0 ps; 对于第二组离子(LET = 21.3 MeV·cm2·mg–1), 多数入射位置下都存在脉宽差异, 但脉宽差异的绝对值均小于50 ps; 而对于第三组离子(LET = 41.4 MeV·cm2·mg–1), 基本所有入射位置下都存在脉宽差异, 且脉宽差异的绝对值最大可达到262 ps. 此外, 三组高低能离子的脉宽差异的平方和Σ分别为6832, 14796和153339. 因此, 随着LET值的增大, 相同LET、不同能量和种类的离子所导致的脉宽差异逐渐明显. 将高低能离子每核子能量比率基本一致的三组离子入射硅材料生成的电子-空穴对密度随离子径迹径向尺度的变化统一示于图9, 可以看出, 在相同径向尺度上, 随着LET值的增大, 高低能离子所产生的电子-空穴对密度的差异逐渐增大(纵坐标为对数坐标), 这将导致高低能离子在电路敏感区及周围的电荷沉积差异更大, 进而使得脉宽差异更明显.
图 8 三组高低能离子导致的瞬态脉宽差异在不同入射位置上的分布 (a)第一组离子Si和Kr的比较; (b)第二组离子Ti和Xe的比较; (c)第三组离子Br和Ta的比较Figure8. Distribution of the transient pulse width differences at various strike locations: (a) Comparison of Si and Kr ions in the first group; (b) comparison of Ti and Xe ions in the second group; (c) comparison of Br and Ta ions in the third group.
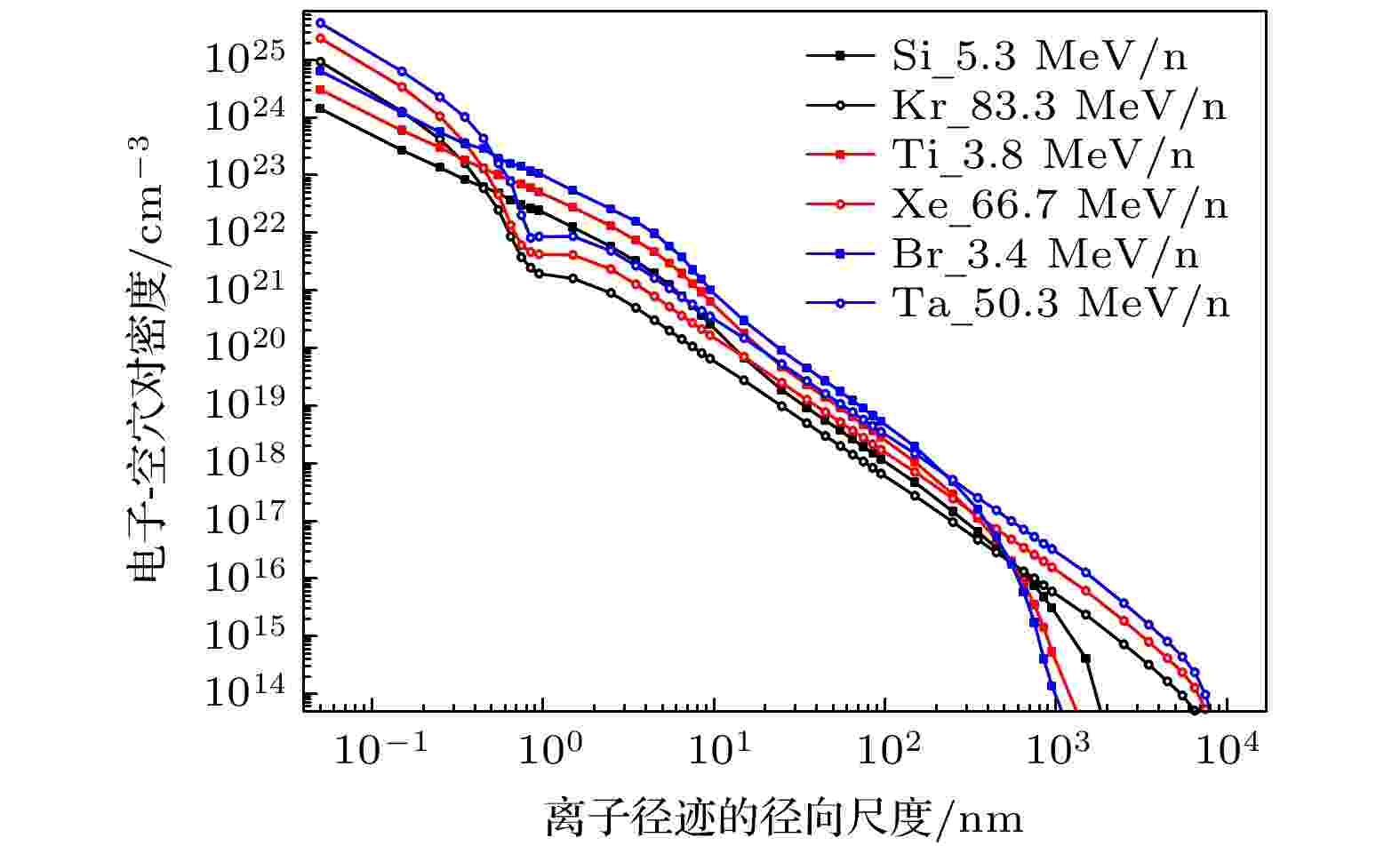图 9 每核子能量比率接近的三组高低能离子入射硅材料生成的电子-空穴对密度随离子径迹径向尺度的变化Figure9. Density of electron-hole pairs generated by ion incidence into silicon vs. the radial scale of ion track. The energy per nucleon ratios of high-energy ion to low-energy ion are similar for the three groups.
2
3.3.离子入射角度的影响
图10所示为第三组的Br和Ta离子在不同入射角度下(沿阱方向30o入射、沿阱方向60o入射、垂直阱方向30o入射、垂直阱方向60o入射)的脉宽差异分布, 表2统计了两种离子在不同入射角度下的脉宽差异的平方和. 通过对比发现, 沿阱方向斜入射的脉宽差异比垂直阱方向斜入射的脉宽差异更加明显. 垂直阱斜入射时, 随着入射角度从30o增加到60o, Σ值从13765变为14131, 两者差别不大. 然而, 沿阱方向斜入射时, 随着入射角度从30o增加到60o, Σ值从93602增加到161159, 两者差别明显, 且沿阱方向60o斜入射与沿阱方向30o斜入射相比, 在更多的入射位置上出现了高能离子脉宽较大的现象(δ小于0). 下面将通过TCAD仿真来研究沿阱方向30o和60o斜入射的差异.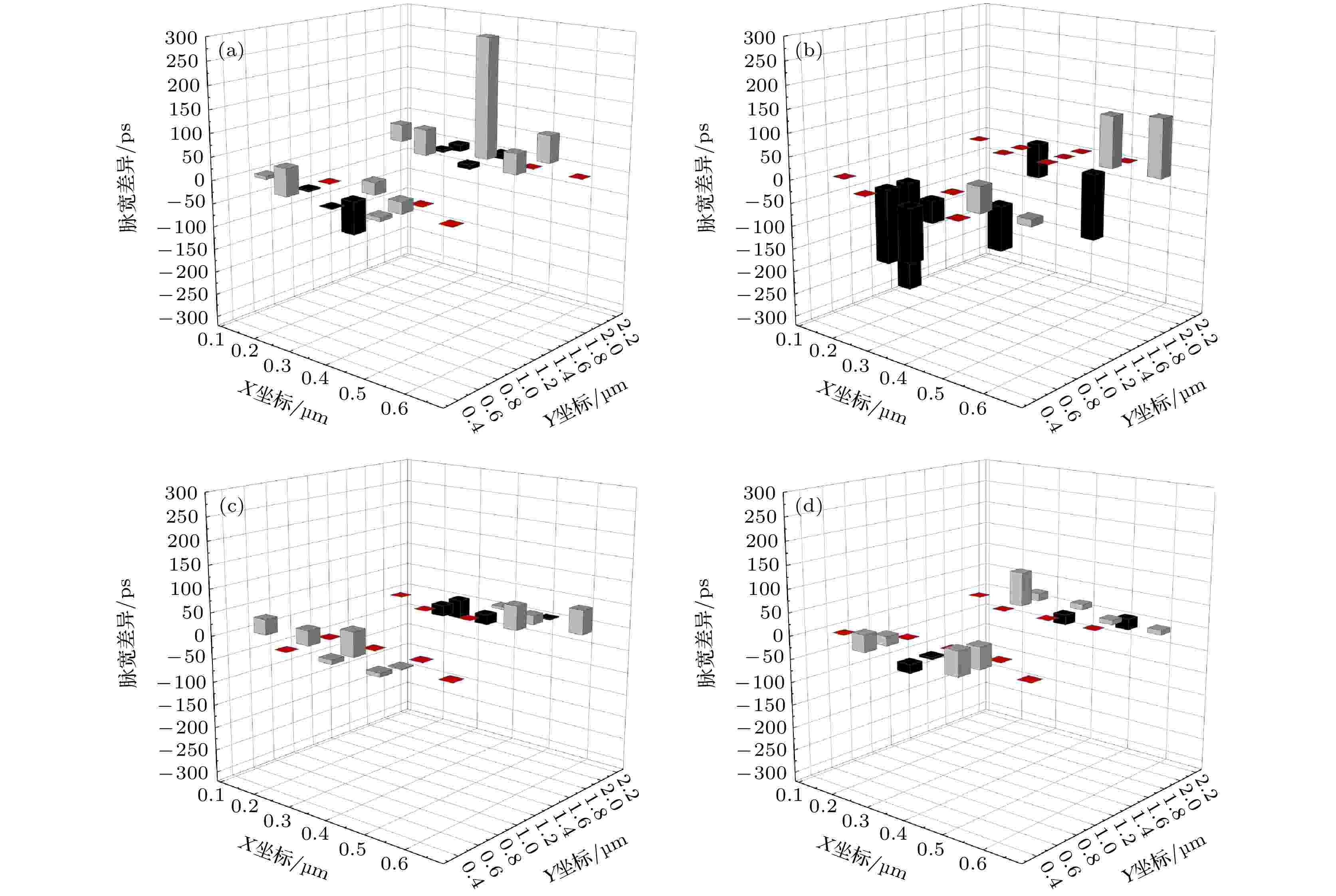
图 10 第三组的 Br和Ta离子在不同入射角度下导致的瞬态脉宽差异随入射位置的变化 (a)沿阱方向30o入射; (b)沿阱方向60o入射; (c)垂直阱方向30o入射; (d)垂直阱方向60o入射Figure10. Distribution of the transient pulse width differences at various strike locations for the Br and Ta ions in the third group at different ion incidence angles: (a) 30o along the well; (b) 60o along the well; (c) 30o across the well; (d) 60o across the well.
| 入射角度 | Σ 值 |
| 沿阱方向30o | 93602 |
| 沿阱方向60o | 161159 |
| 垂直阱方向30o | 13765 |
| 垂直阱方向60o | 14131 |
表2第三组的Br和Ta离子在不同入射角度下导致的瞬态脉宽差异平方和
Table2.Square sum of the transient pulse width differences at various strike locations for the Br and Ta ions in the third group at different ion incidence angles.
图11所示为Br和Ta离子沿阱方向30o入射第一级反相器NMOS漏极附近位置(0.51 μm, 0.77 μm)时, 反相器链各级输出端的SET波形; 图12所示为Br和Ta离子沿阱方向60o入射第一级反相器NMOS漏极附近位置(0.51 μm, 0.77 μm)时, 反相器链各级输出端的SET波形. 可以看出, 离子沿阱方向30o入射时, 随着入射深度的增加, 径迹开始远离反相器的有源区, 后三级反相器收集电荷很少, SET波形受电学屏蔽的影响从第一级反相器输出端开始逐级消减, 到第四级时SET几乎消失. 两离子的效应规律类似, 最终的SET脉宽基本没有差异. 离子沿阱方向60o入射时, 两离子在第一级反相器输出端的SET脉宽略有差异, Br离子导致的SET脉宽稍小, 这可能与Br离子径迹中心轴附近区域的电子-空穴复合率较高有关; 第二级反相器由于脉冲淬熄效应导致输出端SET脉冲基本消失; 第三级反相器通过收集斜入射径迹的扩散电荷而产生SET脉冲, 两离子诱发的SET脉宽相近; 在第四级反相器, Br离子斜入射产生的脉冲淬熄比Ta离子更严重, 最终导致Br离子的SET脉宽较小. 之所以Br离子在第四级反相器的脉冲淬熄更严重, 是因为随着离子径迹向远端反相器下方延伸, 径向电荷分布紧凑的低能Br离子比径向电荷分布较松散的高能Ta离子的电荷收集效率更高, 导致低能Br离子在第四级反相器处的电荷共享更明显. 通过沿阱方向30o和沿阱方向60o的仿真对比发现, 离子入射角度的变化导致电荷收集过程存在差异.
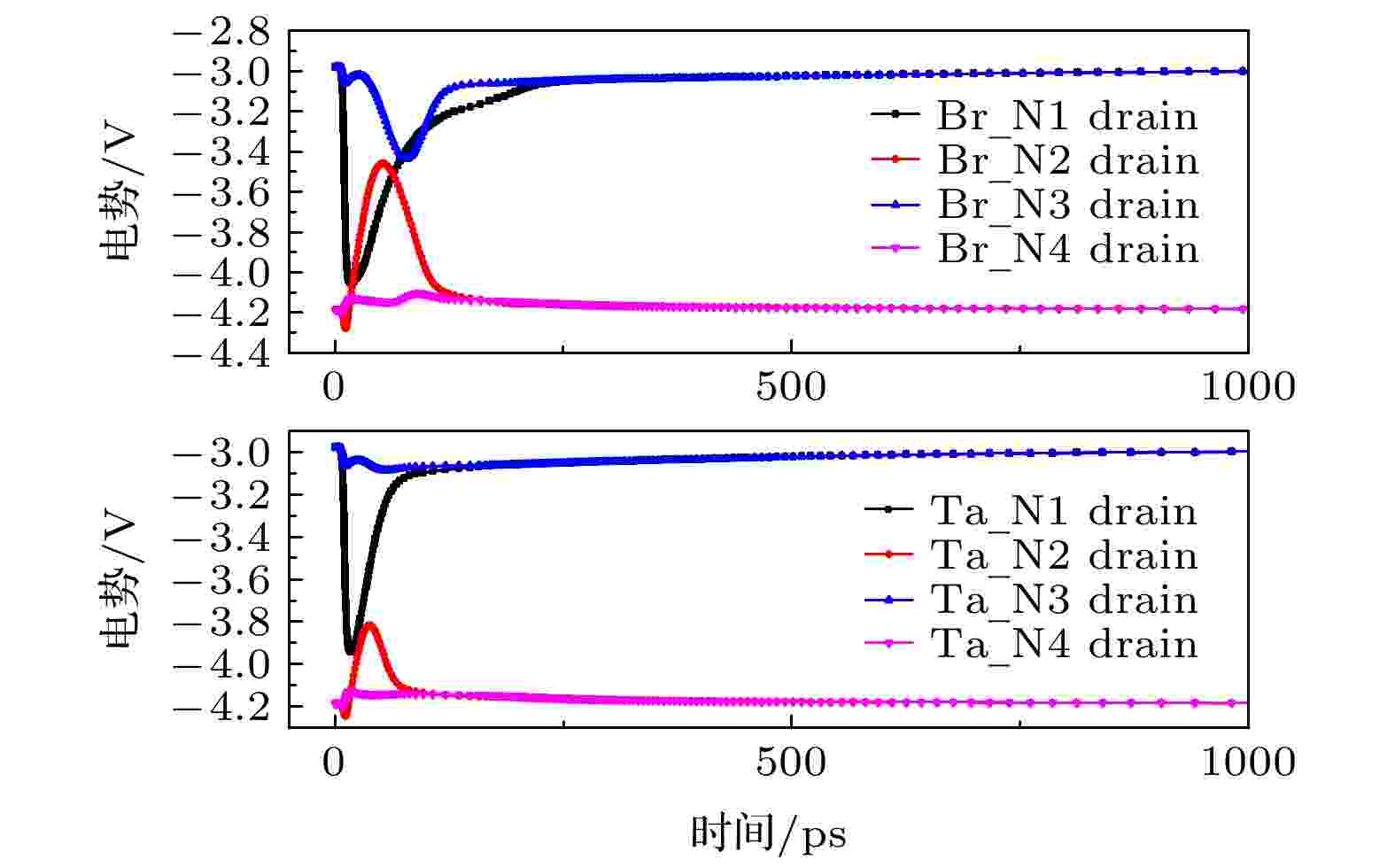图 11 第三组的Br和Ta离子沿阱方向30o入射(0.51 μm, 0.77 μm)时, 反相器链各级输出端的SET波形Figure11. Transient waveforms for N+-drains of the inverter chain, which are induced by Br and Ta ions in the third group. The ion incidence angle is 30o along the well. The strike location is with the coordinate of (0.51 μm, 0.77 μm).
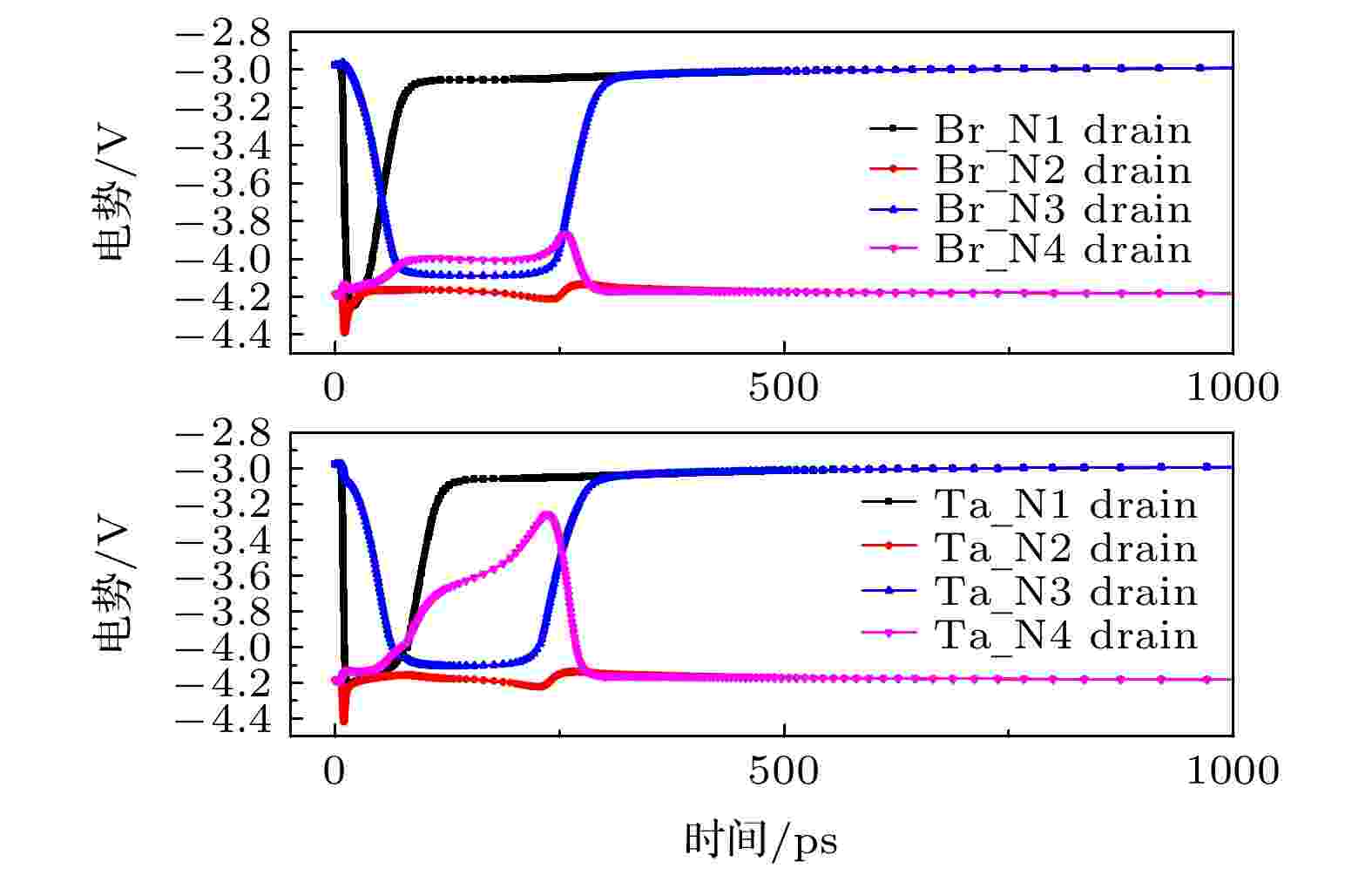图 12 第三组的Br和Ta离子沿阱方向60o入射(0.51 μm, 0.77 μm)时, 反相器链各级输出端的SET波形Figure12. Transient waveforms for N+-drains of the inverter chain, which are induced by Br and Ta ions in the third group. The ion incidence angle is 60o along the well. The strike location is with the coordinate of (0.51 μm, 0.77 μm).
相同LET值的高低能离子入射纳米反相器链后在电荷产生方面存在差异, 离子入射角度的变化导致电荷收集过程存在差异, 两种差异的相互耦合决定了相同LET值的高低能离子的脉宽差异存在一定的离子入射角度依赖性.
2
3.4.反相器链偏置电压的影响
选取第二组的Ti和Xe离子, 为反相器链设置1.0, 1.2和1.4 V的偏置电压, 比较不同偏置电压下高低能离子的脉宽差异, 结果如图13所示. 可以看出, 相同LET值的高低能离子导致的脉宽差异没有表现出明显的偏置电压依赖性, 且通过计算发现, 1.0, 1.2和1.4 V偏置电压下, 高低能离子的脉宽差异的平方和分别为17322, 14796和15583, 也未呈现出明显的偏置电压相关性.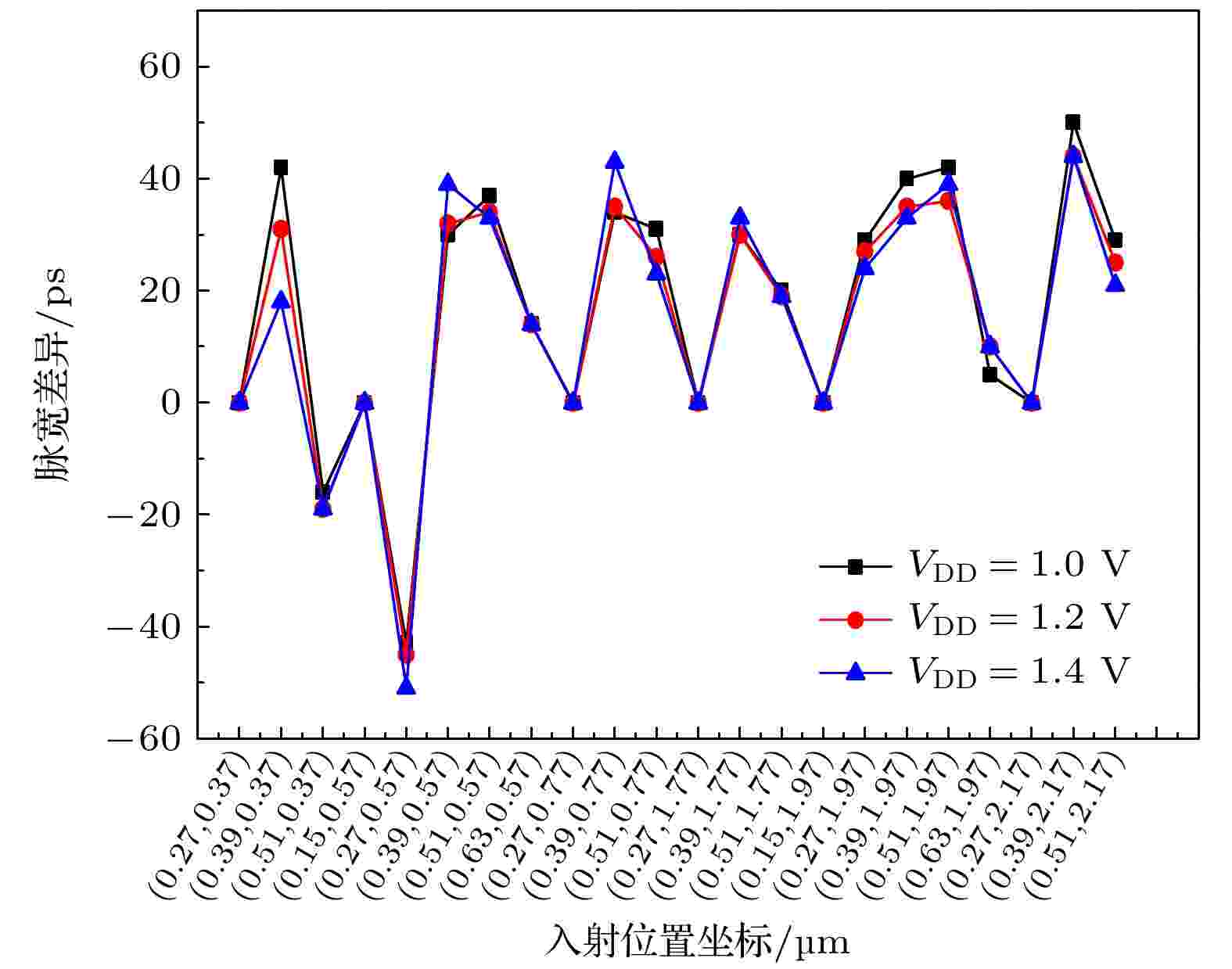
图 13 不同偏置电压下, 第二组的Ti和Xe离子导致的瞬态脉宽差异随入射位置的变化Figure13. Transient pulse width differences under different supply voltages vs. the strike location for the Ti and Xe ions in the second group.
从宏观角度来看, 偏置电压的改变会影响被入射反相器的开态晶体管的驱动电流, 随着偏置电压的升高, 开态晶体管的驱动电流增大, SET脉宽减小, 但这一影响机制与离子径迹无直接关联. 从微观角度来看, 偏置电压会影响反相器有源区的电场分布, 由于高低能离子入射反相器所产生的电子-空穴对分布存在差异, 该差异导致电子、空穴后续的输运和收集过程受电场分布变化的影响会有所不同, 这种影响机制与离子径迹存在关联, 但从图13的仿真结果来看, 在绝大多数离子入射位置上, 这种关联性并不明显, 考虑是偏置电压变化量太小(纳米反相器链在实际工作中, 其偏置电压的可调节范围十分有限), 不足以将电场分布变化所带来的影响呈现出来.
在LET值相同的情况下, 高能离子的径迹半径是低能离子径迹半径的数倍, 若纳米组合逻辑电路对SET非常敏感且相邻敏感单元之间的间距很小, 高能离子更大的径迹覆盖范围将可能导致电路多个敏感单元收集电荷, 产生单粒子多瞬态, 而低能离子可能由于径迹半径较小只产生单个瞬态脉冲; 若纳米组合逻辑电路对SET不太敏感或者相邻敏感单元之间的间距不够小, 高低能离子径迹覆盖范围的差异不会对纳米组合逻辑电路SET产生明显影响.
