全文HTML
--> --> -->值得一提的是, 具有kagome层状晶格结构的材料虽然并非传统意义的二维材料(即由范德瓦耳斯力堆垛的层状材料), 由于其六角网络结构的几何特殊性, 自旋结构主要来源于形成kagome晶格的过渡金属原子电子, 往往伴随有许多新奇的物理、拓扑性质. 具体而言, kagome晶格是具有共角三角形的、以六边形为基本单元的独特二维网格, 类似于石墨烯. 在晶格内, 分子间交换相互作用能形成局部自旋矩的磁耦合, 但同时晶格内存在强烈的几何阻挫效应, 可能也会导致自旋在零温下不呈现长程磁有序. 所以, kagome晶格中的几何阻挫效应的强弱能影响长程磁有序对自旋涨落的竞争, 对材料的基态起重要作用. 另外, 除了磁阻挫, kagome晶格还能容纳不同类型的量子态, 例如狄拉克电子态, 在倒空间中, 两个狄拉克能带的交汇点在布里渊区边界的K和K' 点, 此点可以等价于石墨烯的晶格, 因此会类似地受到晶格对称性的保护[9]. 但与石墨烯晶格不同的是, kagome晶格中垂直于基平面的晶面内并不包含最近邻键合, 因此能在垂直于最近邻键合方向上产生一个电场[10], 使自旋轨道耦合能在kagome晶格的电子结构上扮演重要的角色, 并能进一步产生拓扑非平庸的电子能带[11,12]. 另外, 在电子跳跃模型中, 电子布洛赫波函数的相消干涉能够有效地将电子束缚在kagome晶格的六角形中, 从而导致近无色散的平带电子结构[13], 还有可能在材料中形成长程磁有序. 拓扑kagome磁体在实验上实现了众多以往理论预测的拓扑物理, 是一类新兴的拓扑自旋层状材料. 基于层状磁性材料这一家族出发, 层状磁性拓扑材料不仅同样能将材料的自发磁化维持至极端的二维极限, 具有简单的磁基本单元, 同时, 某些材料在这种极端的二维极限下往往还保留拓扑特性[14]; 还有材料能根据堆垛这些二维极限层来调控其磁性和拓扑特性, 呈现具有层数依赖关系的拓扑特性[15]. 最后需要说明的是, 本综述仅包括层状磁性拓扑材料和具有准二维结构(如kagome层状晶格)的磁性拓扑材料, 其他材料不在本综述的讨论范围内.
上述介绍的层状磁性拓扑材料的构建、制备方式多样, 大多材料都能使用传统的合成方法制备, 例如: 合成本征反铁磁拓扑绝缘体MnBi2Te4系列可以用分子束外延法[16]、真空熔炼法[17,18]、(自助)熔剂法[19,20]、垂直布里奇曼法[21]等; 合成磁性外尔半金属Co3Sn2S2可利用自助熔剂法[22-24]、布里奇曼法[25]、分子束外延法[26]等; 而拓扑kagome磁体中, Mn3Sn则有报道是采用直拉单晶制造法和电弧熔炼法结合的方法[27]或布里奇曼法[28]合成, Mn3Ge可以利用布里奇曼-斯托克巴杰法[29]合成, Fe3Sn2也能通过自助熔剂法[30]合成, 还能通过碘催化的方法熔炼[31], FeSn能通过化学气相传输法合成[14]等. 除了上述合成的体材料, 还可以利用晶体的(准)二维结构特性对块材进行机械剥离或减薄, 得到更小的磁单元结构. 可见, 高质量的层状磁性拓扑材料基本上可以利用传统的方法合成, 因此相对容易开展不同类型的实验研究, 受到更为广泛的关注, 具有一定的潜在应用前景.
2
2.1.磁掺杂拓扑绝缘体
目前领域内研究得最多、历史最悠久的本征拓扑绝缘体是V-VI族多元化合物(Bi,Sb)2(Se,Te)3, 其晶体结构属于
2
2.2.本征磁性拓扑绝缘体
近年发现的具有本征磁序的拓扑绝缘体MnBi2Te4及其系列材料, 兼备非平庸的拓扑性、二维的层状材料结构、磁序来源非掺杂等优点, 克服了磁掺杂导致的磁带隙不均匀性. 同时, 尽管其磁有序温度和磁掺杂拓扑绝缘体接近, 均约为20—30 K, 但由于其磁序主要来自于化学配比组分的过渡金属元素(Mn), 它不仅能实现磁掺杂体系中大多数的物理效应, 而且其实现温度普遍比掺杂体系高至少一个数量级, 因此吸引了非常广泛的关注.3
2.2.1.晶格结构
本征磁性拓扑绝缘体MnBi2Te4是一种A-B-C型密堆垛层状材料, 与本征/磁掺杂拓扑绝缘体不同的是, 它的结构基本单元是由V, VI族元素Bi和Te、过渡金属元素Mn组成七原子层(septuple layer, SL)结构, 形成-VI-V-VI-TM-VI-V-VI-的截面堆垛, 其中过渡金属元素位于SL的中心, 如图1(a)所示[44]. SL层内原子间形成较强的共价键, 而层间VI-VI元素的结合方式则是范德瓦耳斯力相互作用主导. 有趣的是, 通过对MnBi2Te4这类拓扑绝缘体进行晶格结构上的改造, 能形成新的磁序乃至拓扑序, 例如对Mn元素进行过渡金属元素替换[45]或对Bi元素进行Sb替换/掺杂, 可衍生成一大类具有不同磁序的材料[44]. 另外, 如图1(b)所示, 在SL之间插入若干层本征拓扑绝缘体Bi2Te3[46], 即从本征磁性拓扑绝缘体MnBi2Te4出发衍生出MnBi2nTe3n+1系列化合物或超晶格, 同时还取决于材料的厚度、插层结构、表面原子种类等, 也能对材料的磁有序、磁特性进行调控, 甚至形成新的拓扑相[19,46-49].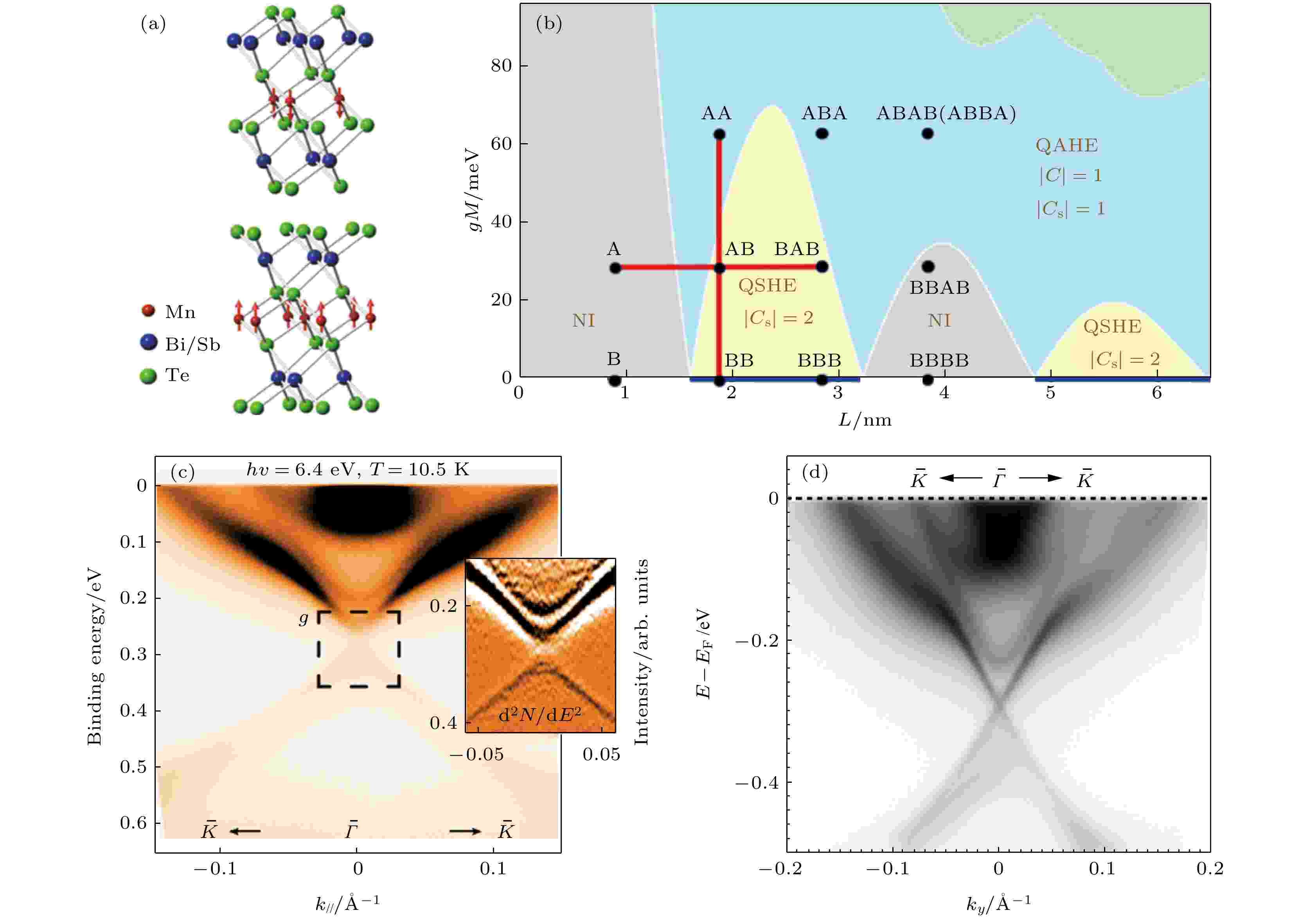
图 1 本征反铁磁拓扑绝缘体MnBi2Te4的晶格结构、磁结构和电子结构 (a)晶格结构示意图, 其中Mn原子的自旋如红色箭头所示, 材料呈A型反铁磁序; (b)理论上不同厚度、磁化强度的MnBi2Te4 能实现的拓扑相; (c), (d)利用角分辨光电子能谱测量的表面能带结构. 图(a)来自文献[44], 图(b)来自文献[46], 图(c)来自文献[21], 图(d)来自文献[57]Figure1. Crystalline, magnetic, and electronic structures of intrinsic antiferromagnetic topological insulator MnBi2Te4: (a) Schematic crystalline structure, the spins of Mn atoms are shown as red arrows, showing a type-A antiferromagnetic order; (b) topological phase diagram of MnBi2Te4 with different thicknesses and magnetizations; (c), (d) angle resolved photoemission spectroscopies of surface electronic structures. (a) is adopted from Ref. [44], (b) from Ref. [46], (c) from Ref. [21], and (d) from Ref. [57].
3
2.2.2.磁结构
根据理论计算和实验研究表明[19,46-49], MnBi2Te4及其大多数的衍生化合物MnBi2nTe3n+1的磁结构均为A型反铁磁序, 即在SL层内Mn是铁磁性耦合, 而层间则是反铁磁性耦合. 通过调节插入本征拓扑绝缘体Bi2Te3的厚度, 能调节反铁磁序的磁特性, 如磁翻转磁场大小和反铁磁层间的交换作用强度等[45], 从而改变实现反常霍尔效应、自旋翻转等效应所需的磁场强度. 近期的理论研究表明, 通过将Bi替换成Sb所形成的MnSb2Te4也具有反铁磁序[50], 但实验结果却表明MnSb2Te4在25 K以下具有自发净磁矩, 结合第一性原理计算证明它可能是亚铁磁性的外尔半金属[51,52], 但这与实验结果有较大差异, 不同的样品合成方法得到的磁有序不一致, 有报道称是具有本征磁性的拓扑绝缘体, 是居里温度为45—50 K的铁磁性[53], 也可能是奈尔温度约为19 K的反铁磁性[54,55]等. 近期X射线衍射和中子衍射的实验揭示[51], 出现这种磁有序差异的可能原因是在所合成的MnSb2Te4中出现Mn和Sb原子的相互替代, 即形成反位无序(antisite disorder), 造成反铁磁序和亚铁磁序的共存, 相对于Mn原来所在的3a位置, Mn原子会在6c位置沿着c轴方向形成反平行的自旋结构, 最终使Mn原子在一个晶胞中贡献约2.1
根据理论计算, 由于MnBi2Te4的A型反铁磁序对拓扑性质可能存在一定的影响, 其拓扑性质会随层数的奇偶性有一定的依赖关系[15]. 近期的反射磁圆二向色性谱研究了从单层到少层的MnBi2Te4在改变层数、温度、外磁场等实验条件的磁行为, 发现MnBi2Te4中自旋翻转所需要的外磁场随其SL层数变化存在一种有趣的奇偶效应[15], 进一步的理论计算表明其中主导的因素可能是材料表面自旋翻转和体自旋翻转的演化. 随着温度升高, MnBi2Te4从反铁磁序演变成顺磁行为. 可见, MnBi2Te4属于一种弱反铁磁体, 能通过一定大小的外磁场作用和特定温度控制, 使不同层数的样品具有不同的磁结构, 进而操纵该材料相关的量子效应.
3
2.2.3.电子结构
在低于奈尔温度时, 虽然MnBi2Te4的反铁磁序破坏了时间反演对称性, 但由于Mn原子层在层内显示出铁磁耦合, 材料总体满足时间反演T和空间平移
然而, 近期不同课题组使用不同的MnBi2Te4样品进行角分辨光电子能谱研究, 各自得到的拓扑表面态结果存在较大分歧. 如图1(c)和图1(d)所示, 近期的几个实验结果[57-59]表明, 在MnBi2Te4面上的拓扑表面态并没有出现本该因反铁磁序而打开的能隙, 反而观察到无能隙狄拉克锥能带; 相反, 在Bi2Te3表面上则出现了能隙, 这与早期的理论、实验结果不一致[21]. 理论上, 一个可能的解释是[57], 由于MnBi2Te4表面磁序与体磁序的不同, MnBi2Te4表面受到时间反演对称性保护而显示出无能隙; 而在Bi2Te3表面, 层间原子轨道的耦合作用导致磁性和杂化共同作用, 最后打开了能隙. 另外, 准粒子干涉实验发现, MnBi2Te4中电子的散射方向、色散关系与理论计算结果不一致[60], 同时实验还发现能带的自旋结构分布也受到层间能带杂化的影响. 当然, 可能的解释也包括不同实验组合成的样品的质量有所不同, 因为MnBi2Te4材料自身的稳定性欠缺, 实验结果更加值得深究. 关于反铁磁拓扑绝缘体MnBi2Te4的拓扑表面态电子结构的研究还需要进一步的实验探索, 不过无论如何, MnBi2Te4表现出不同于传统的本征、磁掺杂拓扑绝缘体中的体表对应关系, MnBi2Te4的表面态似乎不完全由其体态拓扑性质决定.
2
2.3.磁性外尔半金属
除了拓扑绝缘体这一里程碑式的发现, 近年来领域还发现了以外尔半金属(如TaAs[61])、狄拉克半金属(如Na3Bi[62])等为代表的拓扑半金属. 在非磁性的外尔半金属中, 时间反演对称性的存在使得反常霍尔效应为零, 然而, 在磁性外尔半金属中, 非零的贝里曲率的存在, 会产生巨大的反常霍尔效应, 同时进一步的实验表明磁性外尔半金属的反常霍尔角也非常大, 因此磁性外尔半金属能在自旋电子器件中有重要的潜在应用. 然而, 理论上预测的几种磁性外尔半金属, 例如Re2Ir2O7 (Re为稀土元素)[63-68], HgCr2Se4等在实验上尚未观察到理想的反常霍尔效应. 对于Re2Ir2O7, 领域内目前认为在零磁场下仍不能确认这种磁性外尔半金属的主要原因是, 外尔点能随磁序参量而迅速演变, 配对最终会在布里渊区边界湮灭, 造成电荷带隙很容易被打开, 只在磁畴处剩下表面态的金属部分[66]. 另外, 即使在部分Re2Ir2O7 (如Re = Nd, Pr)[66]中发现了非线性的霍尔效应, 且似乎与材料的外尔半金属态[65]、能带接触点的半金属态相关, 但非线性的霍尔效应同时也在具有all-in-all-out (AIAO)的自旋态和电荷带隙[69]的材料(如Re = Eu, Y)[66,70-72]中发现, 因此其微观的物理起源是由于内禀还是外禀因素(例如残余应力[63]、Ir偏离了非磁性的离子态Ir3+而产生铁磁性[72]等)仍然不清晰. 对于HgCr2Se4, 有实验观察到了其半金属特性, 且具有105 K的居里温度, 成为支撑磁性外尔半金属的重要实验证据[73]. 然而, 输运实验上所得到的反常霍尔电阻率不仅较小[73,74], 大约在0.1 mΩ·cm量级, 还需要和普通霍尔效应进行分离和修正; 另外, 实验还发现反常霍尔电阻和电导都与温度T的1/2次方
另外, 近年引起广泛关注的非共线反铁磁材料Mn3Sn和Mn3Ge也被发现具有新颖的拓扑特性, 理论预测和现阶段的实验结果均表明它们也是磁性外尔半金属. 类似于Co3Sn2S2, 在Mn3Sn和Mn3Ge中, 过渡金属Mn也形成了kagome晶格, 具有非共线反铁磁结构, 其磁矩方向可以用大约几百奥斯特的外磁场控制. 另外, 理论计算和近期的实验表明, 在Mn3Sn和Mn3Ge中存在与拓扑特性相关的巨反常霍尔效应、反常能斯特效应、自旋霍尔效应和自旋能斯特效应等丰富的物理效应.
3
2.3.1.晶格结构
如上文所述, Co3Sn2S2是Shandite化合物家族里一类具有kagome晶格的磁性外尔半金属. Shandite 化合物具有M3
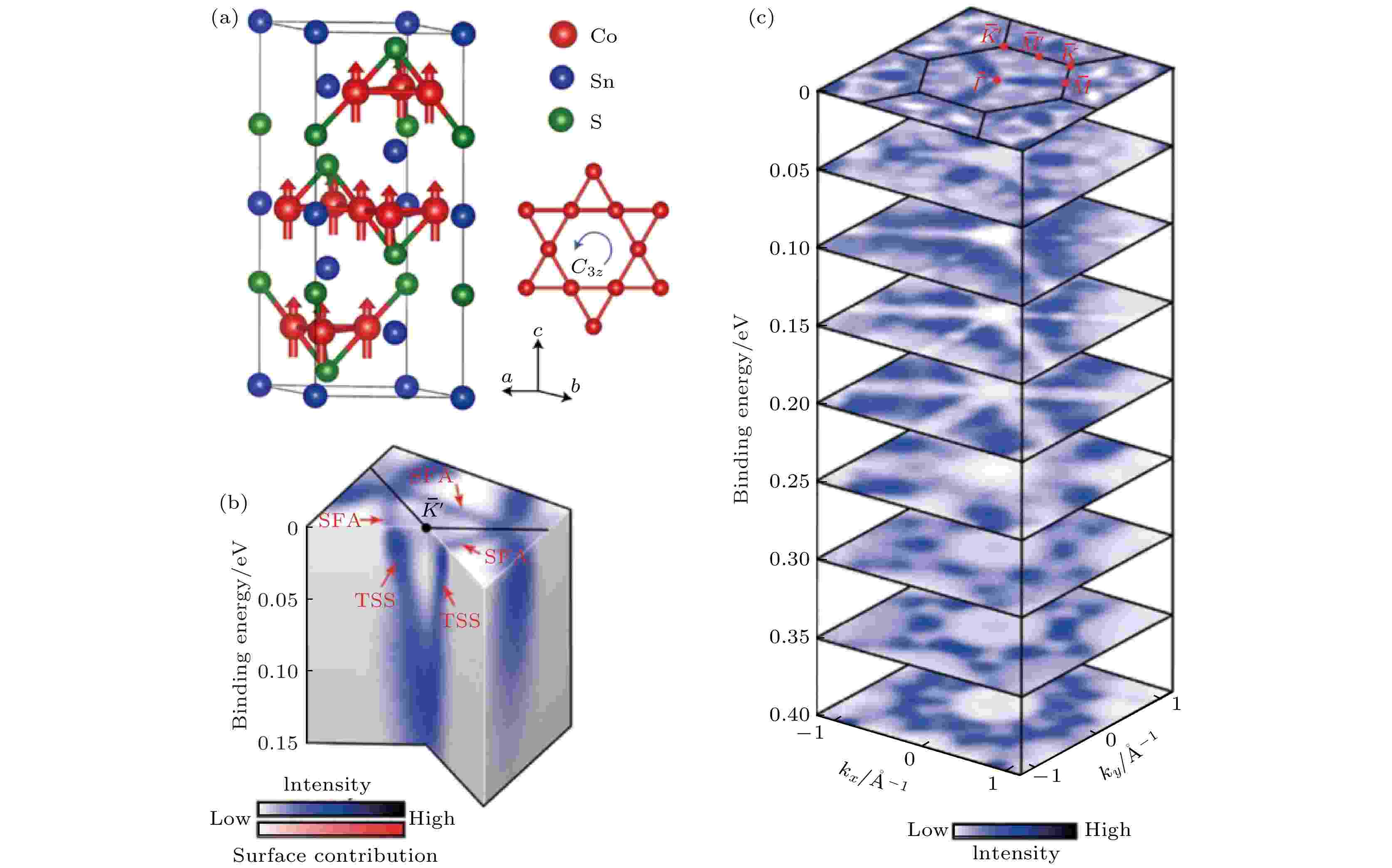图 2 磁性外尔半金属Co3Sn2S2的晶格结构、磁结构和电子结构 (a)晶格结构示意图, 其中Co原子的自旋如红色箭头所示, 材料呈铁磁序; (b), (c)利用角分辨光电子能谱测量的能带结构. 图(a)来自文献[22], 图(b)和图(c)来自文献[82]Figure2. Crystalline, magnetic, and electronic structures of magnetic Weyl semimetal Co3Sn2S2: (a) Schematic crystalline structure, the spins of Co atoms are shown as red arrows, showing a ferromagnetic order; (b), (c) angle resolved photoemission spectroscopies of the electronic structures. (a) is adopted from Ref. [22], (b) and (c) from Ref. [82].
本综述涉及的另一类具有kagome层状晶格的磁性外尔半金属Mn3X (X = Ge, Sn)二元合金, 如图3(a)所示[27], 这系列材料具有Ni3Sn型晶格结构, 属于P63/mmc空间群, 其六边形单元由两层Mn沿着[0001]方向堆叠, 每一层中的Mn原子形成kagome晶格, 而X原子则在一个六边形的中心, 形成如图3(b)的六方准二维结构[27], 可以看作一个扭曲的、由正八面体组成的三角管结构. 这个晶格结构只有在Mn过量的时候才能稳定, 一般情况下Mn会随机占据Sn原子位置.
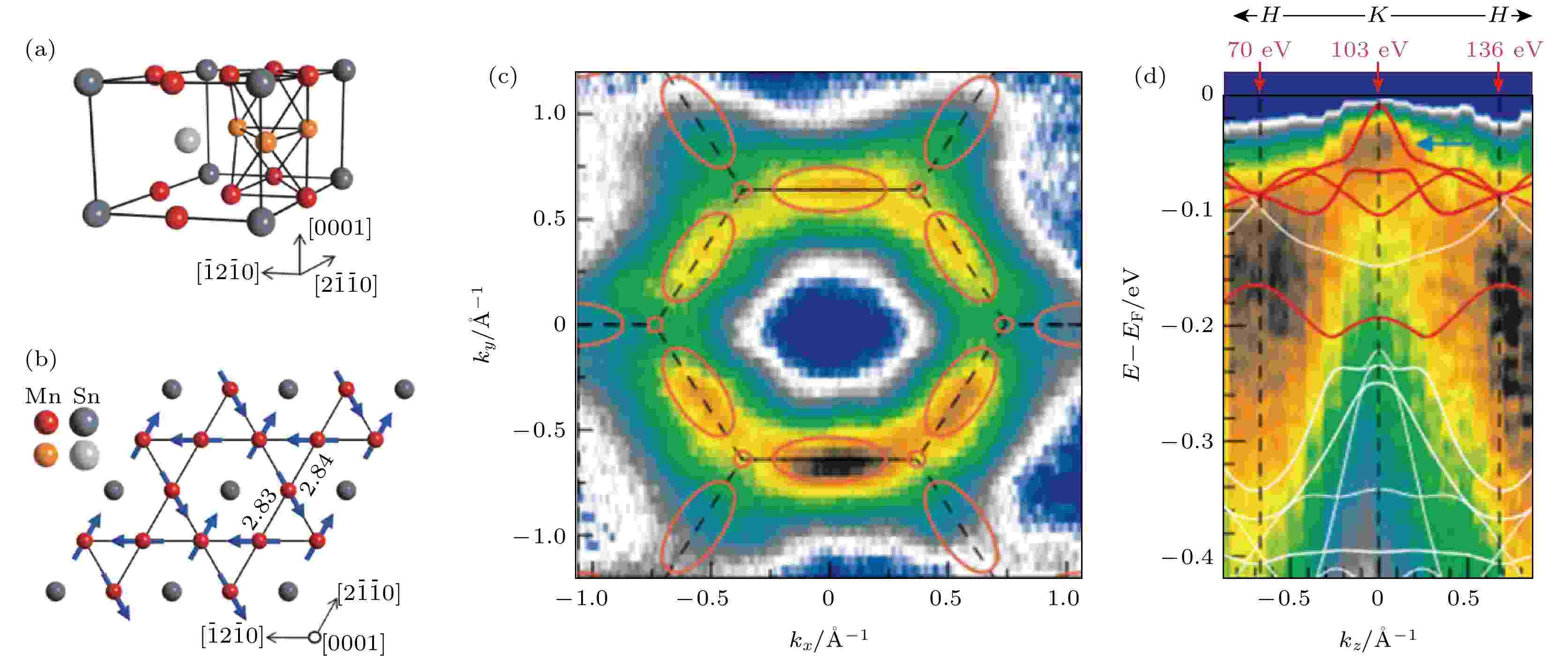图 3 磁性外尔半金属Mn3Sn的晶格结构、磁结构和电子结构 (a), (b)晶格结构示意图, 其中Mn原子的自旋如蓝色箭头所示, 材料呈反铁磁序; (c), (d)利用角分辨光电子能谱测量的能带结构. 图(a)和图(b)来自文献[27], 图(c)和图(d)来自文献[84]Figure3. Crystalline, magnetic, and electronic structures of magnetic Weyl semimetal Mn3Sn: (a), (b) Schematic crystalline structure, the spins of Co atoms are shown as blue arrows, showing an antiferromagnetic order; (c), (d) angle resolved photoemission spectroscopies of the electronic structures. (a) and (b) are adopted from Ref. [27], (c) and (d) from Ref. [84].
3
2.3.2.磁结构
Co3Sn2S2具有本征的垂直铁磁序, 其磁性来自于Co原子所构成的kagome 晶格, 每个Co原子的磁矩强度为
3
2.3.3.电子结构
在能带结构中, 外尔半金属具有优异的拓扑特性, 主要来源是电子体能带结构中的外尔节点, 而这种节点一般由于破缺空间翻转对称性或时间反演对称性所形成, 具有明确的手性, 并且与费米弧表面能带有关. 费米弧从一个外尔节点出发, 在表面二维动量空间内以相反的手性终止于另一个外尔节点, 即一种不连续的费米面结构[81]. 因此, 体态上外尔节点的存在保证了费米弧的形成. 如图2(b)和图2(c)所示, Co3Sn2S2在费米能级附近有三条因能带交叉而产生的节线环, 以及由于强自旋轨道耦合打开而产生的三对外尔节点, 这一预测的能带结构在近期实验上成功被观察到[82]. 同期的实验[24]观察到了由Co原子构成的kagome晶格, 并通过分析电子在不同原子终端面发生弹性散射时的准粒子干涉花样, 获得了不同的表面态费米弧的色散关系. 研究发现[24]在Sn, Co, S三个不同的终端面上施加不同表面电位, 可以修改费米弧的轮廓和外尔点的连通性. 在Sn终端面上能观察到布里渊区内外尔点的费米弧连通性, 而在Co面上, 这种连通性会跨越相邻的布里渊区域, 在S面上, 费米弧会与拓扑平庸的体态和表面状态发生交叠. 此实验结果同时验证了外尔半金属Co3Sn2S2中的拓扑保护和非拓扑保护的电子特性, 确立了其体态-表面态之间的关联.外尔半金属既可以是非磁性的、铁磁性的, 也可以是反铁磁性的, 只要其空间翻转称性(P)和时间反演对称性(T )组成的PT对称性被破缺. 在磁性外尔半金属Mn3X中存在非共线反铁磁自旋结构, 其中的反铁磁交换耦合和Dzyaloshinskii-Moriya 相互作用, 由于破缺了时间反演对称性T, 因此也破缺了PT对称性, 从而允许能带中出现外尔点[83]. 当不考虑材料中的自旋轨道耦合时, Mn3X的能带结构中低能量附近会形成围绕K点的节点环; 当考虑自旋轨道耦合后, 该节点环会演化成K点附近的多对外尔点, 因此一般情况下强自旋轨道耦合是形成外尔半金属的必要条件. 另外, 磁性外尔半金属的一个典型能带特点是某个自旋方向通道在费米能级附近是具有带隙的, 但在另一个自旋通道中则为有强的能带翻转和线性交叉. 近期利用角分辨光电子能谱[84]观察了Mn3Sn的电子结构, 如图3(c)和图3(d)所示, 与上述理论预测基本相符.
2
2.4.磁性狄拉克半金属
3d过渡金属的kagome层状晶格是研究在关联拓扑相中具有对称性保护的电子态的理想平台, 能容纳不同类型的量子磁态. 如上文所述, 在近期发现的磁性外尔半金属中, kagome晶格对拓扑相的形成起了非常重要的作用. 除了磁性外尔半金属, kagome晶格也能成为磁性狄拉克半金属的材料母体, 近期理论和实验都研究表明, 有一系列具有kagome晶格的层状磁性材料具有狄拉克电子的能带结构或电子特性, 是狄拉克半金属的重要候选材料. 尽管磁性外尔半金属、磁性狄拉克半金属的形成并非一定需要kagome晶格, 但具有kagome晶格的磁体与拓扑材料确实具有相当大的重叠部分, 研究具有kagome晶格的磁性材料对寻找新型拓扑材料具有重要的探索意义. 这一节将主要讨论两种具有kagome层状晶格的磁性狄拉克半金属—Fe3Sn2, FeSn.3
2.4.1.晶格结构
在部分具有kagome晶格的二元金属间化合物TmXn (T = Mn, Fe, Co等过渡金属; X = Sn, Ge; m∶n = 3∶1, 3∶2, 1∶1)中, 不同的kagome层、间隔层的堆垛方式能导致不同的准二维电子结构和磁结构, 往往会因此而导致不同的拓扑特性, 此类磁体也称为kagome磁体. 除了上文所述的磁性外尔半金属Mn3X (X = Ge, Sn)以外, 近期发现此类化合物的代表—Fe3Sn2, FeSn, CoSn, 同样具有kagome层状晶格[14,31,85-87], 在存在铁磁序的条件下能承载有质量的狄拉克费米子态, 是磁性狄拉克半金属的重要候选材料. 对于TmXn系列材料, 其kagome晶格由3d过渡金属(T = Mn, Fe, Co)组成, kagome晶格中心则由IV族原子X (X = Sn, Ge)填充, 间隔层由X原子组成, 形成六方晶格. 这些kagome晶格在面内都有不同的平移, 并且由不同的kagome层 (记为A/B)与间隔层(记为S)进行堆垛[14], 如AB, ABSBCSCAS, ASA, 随着X∶T比例的增加, 材料会更显二维性. 对于本节介绍的Fe3Sn2, 如图4(a)所示[85], 它具有双层kagome结构, 空间点群属R
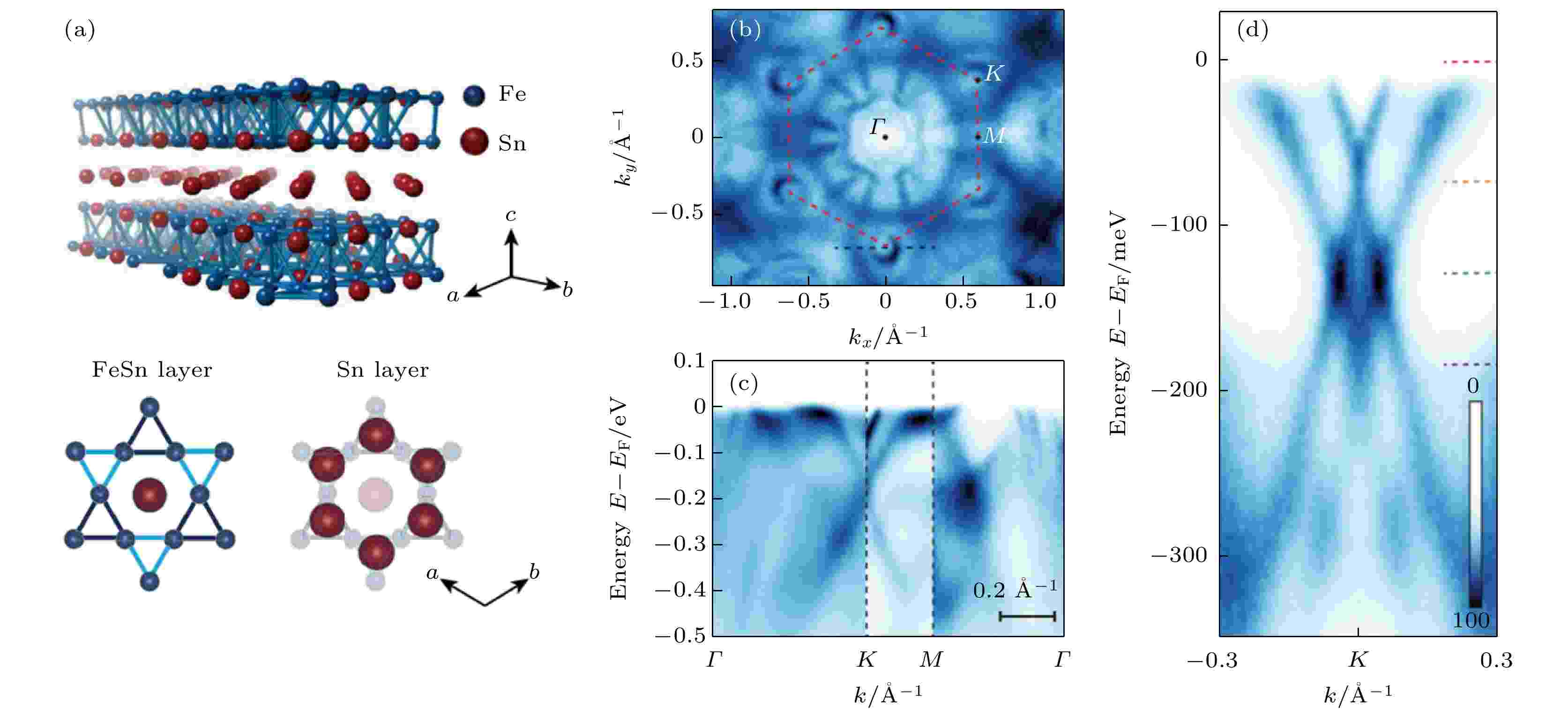图 4 磁性外尔半金属Fe3Sn的晶格结构和电子结构 (a)晶格结构示意图; (b)—(d)利用角分辨光电子能谱测量的能带结构. 图(a)来自文献[85], 图(b)—(d)来自文献[31]Figure4. Crystalline and electronic structures of magnetic Weyl semimetal Fe3Sn: (a) Schematic crystalline structure; (b)–(d) angle resolved photoemission spectroscopies of the electronic structures. (a) is adopted from Ref. [85], (b)–(d) from Ref. [31].
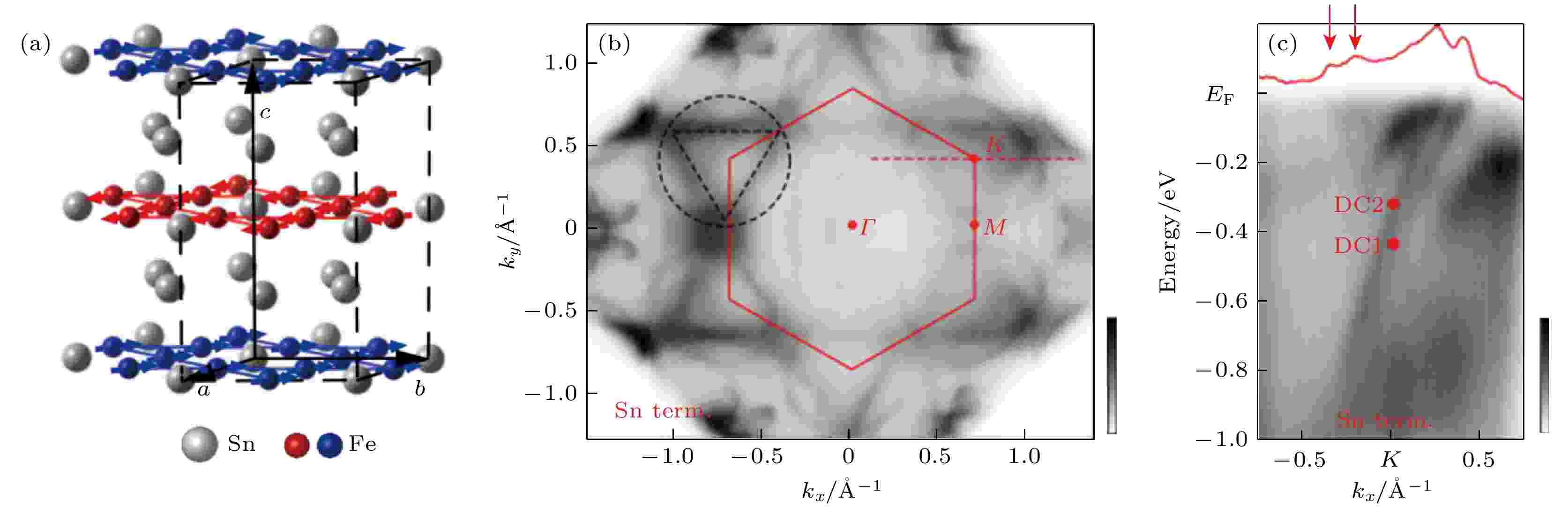图 5 磁性外尔半金属FeSn的晶格结构、磁结构和电子结构 (a)晶格结构示意图, 其中Fe原子的自旋如红、蓝色箭头所示, 材料呈反铁磁序; (b), (c)利用角分辨光电子能谱测量的能带结构. 图(a)来自文献[88], 图(b)和图(c)来自文献[14]Figure5. Crystalline, magnetic, and electronic structures of magnetic Weyl semimetal FeSn: (a) Schematic crystalline structure, the spins of Fe atoms are shown as red and blue arrows, showing an antiferromagnetic order; (b), (c) angle resolved photoemission spectroscopies of the electronic structures. (a) is adopted from Ref. [88], (b) and (c) from Ref. [14].
3
2.4.2.磁结构
早期的实验研究[89]表明Fe3Sn2是一种不寻常的磁性导体, 居里温度高达670 K, 其饱和磁场和饱和磁化强度与温度依赖关系不明显, 在低温下的饱和磁化强度约为每个Fe原子1.9
3
2.4.3.电子结构
如图4(b)—(d)所示, 利用角分辨光电子能谱对Fe3Sn2进行观察, 可以看到, 在布里渊区的K和K′附近存在一对准二维狄拉克锥[31]. 这一对狄拉克锥的中心在K点, 并且有能量上的区分, 如图4(d)所示. 另外, 结合扫描隧道显微术、角分辨光电子能谱、第一性原理计算等手段发现, Fe3Sn2还存在平带电子结构[13]. 这与狄拉克锥型的能带形成鲜明对比, 由于狄拉克锥能带中电子的等效质量为零, 而平带中的电子具有很大的质量, 这两种极端的能带结构同时存在于Fe3Sn2中. 经研究, 影响能带平坦程度的主要因素是kagome晶格内布洛赫波函数的局部破坏程度, 在Fe原子所形成的kagome晶格中, 电子布洛赫波函数的相消干涉能够有效地将电子束缚在kagome晶格的六角形单元中, 从而导致几近无色散的平带. 在结构相对简单的FeSn中, 由于反铁磁kagome结构破缺了每层的空间翻转对称性P和时间反演对称性T, 但服从PT联合对称性, 是实现无质量狄拉克费米子的理想平台. 近期在FeSn的角分辨光电子能谱实验和输运实验中同时观察到狄拉克电子结构(图5(b)和图5(c))、平带以及de Haas-van Alphen量子振荡, 表明FeSn中共存表面态和体态的狄拉克电子[14,88]. 通过理论计算发现, 体狄拉克能带主要来源于局域化的Fe-3d轨道, 而狄拉克表面态表现出完全的二维自旋极化和自旋轨道锁定特性.3.1.本征磁性拓扑绝缘体
如上文所述, MnBi2Te4具有层间反铁磁排布, 其宏观磁性乃至拓扑性质会随着层数的奇偶性发生变化. 理论上, 当MnBi2Te4具有偶数层时, 层间磁矩正好互相抵消, 宏观磁矩为零. 虽然该体系从能带拓扑不变量而言应属于弱拓扑分类, 但是从拓扑场角度而言则能满足静态轴子绝缘体的实现条件, 即轴子场等于π, 本征反铁磁性能使拓扑表面态打开能隙, 是一种天然的轴子绝缘体, 并能产生奇特的拓扑磁电响应. 当MnBi2Te4的层数为奇数时, 体系存在未被抵消的净磁矩, 当材料厚度大于一定值时, 材料的上下表面之间的耦合可以忽略, 原则上能实现量子反常霍尔效应, 即形成陈绝缘体. 然而, 现实材料远不如理论中的模型简单, 下面将从近期针对MnBi2Te4的实验结果, 总结理论、实验发现的重要物理现象.3
3.1.1.量子反常霍尔效应
量子反常霍尔效应自从在磁掺杂拓扑绝缘体中发现后一直是凝聚态物理领域的前沿热点之一. 然而, 掺杂原子的随机性、不均匀性不仅使得所产生的铁磁序欠缺稳定性和均匀性, 还会引入一定的带隙内杂质态、缺陷态, 这使得费米能级的展宽收窄需要极低温条件, 并且不与带隙内的杂质态、缺陷态接触, 才能实现霍尔电导的完全量子化、相应磁阻的极小化. 目前, 在磁掺杂体系中, 这一极低温普遍需要500 mK或更低, 尽管能通过材料结构的优化[91]使磁掺杂拓扑绝缘体实现霍尔电阻量子化的温度提高到1 K左右, 但其磁阻仍需要更低的温度才能进一步降低, 实现无耗散输运. 为了解决极低温这一问题, 近年来领域一直寻找一种非磁掺杂、具有本征磁序的拓扑绝缘体, 期望能从根本上解决磁掺杂的不均匀问题, 将量子反常霍尔效应的实现温度大幅度提高.直至近年, 一个相对比较理想的磁性拓扑绝缘体被理论预测、实验证实, 即上文提到的具有本征反铁磁序的拓扑绝缘体MnBi2Te4, 材料中的磁性主要来源于Mn, 而Mn具有确定化学计量比和确定的原子晶格位置并且有序排列, 材料的奈尔温度在24 K左右. 通过角分辨光电子能谱测量发现[16], 当MnBi2Te4的厚度不小于两个SLs时, 就能观察到具有狄拉克锥型的表面态, 证明它是一个三维拓扑绝缘体. 根据理论计算, 当MnBi2Te4的层厚为奇数且上下表面杂化可忽略时, 材料呈现量子反常霍尔效应, 层厚为偶数时则处于轴子绝缘体相, 并呈现拓扑磁电效应. 有待实验证明的是, 这种具有拓扑轴子表面态的反铁磁拓扑绝缘体的三维体相在外加磁场下能否转变为磁性外尔半金属. 这种外尔半金属的电子结构非常简单, 只有一对外尔点, 是拓扑物理平台理想的研究对象. MnBi2Te4的磁交换带隙约有50 meV, 而磁掺杂拓扑绝缘体的交换带隙宽度从几个meV到几十个meV起伏(取决于其均匀性), 相对而言MnBi2Te4的带隙更稳定、均匀, 有望在更高温度下实现量子反常霍尔效应[45]. 直到2020年, 实验上在1.4 K的温度下, 在5SLs厚的MnBi2Te4样品中观察到零磁场量子反常霍尔效应[20](图6(a)和图6(b)). 有趣的是, 在实现量子反常霍尔效应的样品中调节适当的载流子浓度后, 在高磁场下还能进一步观测到常规的量子霍尔效应. 假如把实现量子反常霍尔效应的零磁场条件放宽, 对样品施加一个强磁场使得样品的反铁磁结构转变成铁磁结构, 能进一步将量子反常霍尔效应的实现温度提高到6.5 K. 这一工作成功地证明了MnBi2Te4是一个能实现量子反常霍尔效应的本征反铁磁拓扑绝缘体. 最近的实验表明[92], 高温量子反常霍尔效应不仅能在MnBi2Te4中实现, 还能在MnBi2Te4系列材料中形成, 如1SL-MnBi2Te4/4QL-Bi2Te3超晶格, 当把费米能级调控到表面带隙内时, 霍尔电导也量子化到
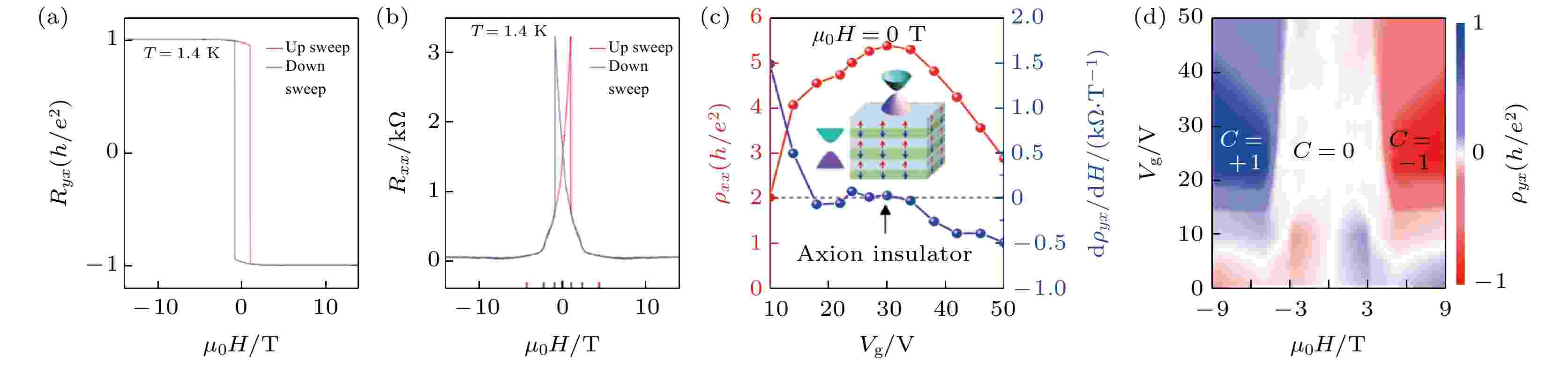图 6 本征磁性拓扑绝缘体的量子反常霍尔效应、轴子绝缘体态 (a)霍尔电阻; (b)磁阻; (c)零磁场下纵向电阻率的栅极电压调制; (d)磁场和栅极电压调制下的相图. 图(a)和图(b)来自文献[20], 图(c)和图(d)来自文献[18]Figure6. Quantum anomalous Hall effect and axion insulating state in the intrinsic antiferromagnetic topological insulator: (a) Hall resistance; (b) magneto-resistance; (c) gate-bias modulated longitudinal resistivity under zero magnetic field; (d) a phase diagram of magnetic field and gate bias. (a) and (b) are adopted from Ref. [20], (c) and (d) from Ref. [18].
3
3.1.2.轴子绝缘体态
理论上在磁性拓扑绝缘体薄膜中, 当两个表面的磁化方向相同时, 两个表面分别贡献的霍尔电导为
3
3.1.3.其他拓扑相和拓扑相变
虽然理论上已经预测在MnBi2Te4中能实现量子反常霍尔效应、轴子绝缘体态, 而目前要制备能实现这两个效应的MnBi2Te4材料仍颇具挑战, 很多实验结果都未能达到量子化的结果[17,19,47], 或需要不同的超晶格结构, 或很高的磁场来使材料变成铁磁态等, 这使对MnBi2Te4的实验研究、物理图像的理解受阻, 因此, 从理论上理解这些实验结果非常具有指导意义. 对于Mn-Bi-Te系列材料(如MnBi2Te4, MnBi4Te7)[19], 2019年, Sun等[46]通过利用有效模型和第一性原理计算发现, 二维多层的Mn-Bi-Te材料能实现多种拓扑相, 不仅仅是量子反常霍尔绝缘体、轴子绝缘体, 实际的实验结果可能还会包括一些其他的量子态或拓扑相, 如时间反演对称的量子自旋霍尔效应、时间反演破缺的量子自旋霍尔效应等. 图1(b)总结了本征拓扑绝缘体Bi2Te3以及磁性拓扑绝缘体Mn-Bi-Te系列的二维结构在磁交换场下的相图, 其中可调参量是层厚和磁交换场强度[46].尽管理论计算表明, 当MnBi2Te4的层数为奇数时, 材料处于量子反常霍尔绝缘相, 偶数层时处于轴子绝缘体相, 但近期的实验[94]发现, 在测量厚度为9SLs和10SLs的器件中, 在外加约5 T的垂直磁场下, 样品的霍尔电阻量子化到半个量子电阻(
另外, 通过Bi2Te3插层所形成的MnBi2nTe3n+1(这里取n = 2, 3为例)系列材料, 即MnBi4Te7, MnBi6Te10, 近期的理论计算和实验结果发现这类材料在低温下与MnBi2Te4类似, 均显示A型反铁磁, 只是随着n的增大(Bi2Te3插层的增加), 层间反铁磁耦合强度会变弱, 使得铁磁序的饱和磁场降低[19], 约1.6 kOe (
2
3.2.磁性外尔半金属
与狄拉克费米子类似, 外尔费米子可以看作动量空间的贝里曲率通量的磁单极子, 自然会对空间中电子的运动造成影响, 一个直接的结果就是导致内禀反常霍尔效应, 以及非零贝里曲率导致的其他物理效应等, 如手性异常、反常能斯特效应. 通常情况下, 当在磁性外尔半金属中实现内禀反常霍尔效应时, 其反常霍尔电导会正比于一对手性相反的外尔费米子在动量空间的间距, 并受到外尔费米子离费米能级的距离的影响. 下面将介绍在磁性外尔半金属中发现的重要物理效应, 典型的包括巨反常霍尔效应、手性异常、拓扑增强反常能斯特效应这三种与外尔点的存在有关的量子效应, 展现出磁与拓扑相互作用下丰富的物理现象.3
3.2.1.巨反常霍尔效应
在磁性外尔半金属中, 外尔节点和节线环都可能产生拓扑增强的贝里曲率, 从而在实验上观察到内禀反常霍尔效应的增强. 这一效应的大小往往取决于费米能级位置的电子占据态以及附近的能带结构. 尽管这一预测在已提出的几种磁性外尔半金属(如Re2Ir2O7, HgCr2Se4, Co基Heusler 化合物等)[98-100]中均未能观察到, 近期实验上首先在磁性外尔半金属Co3Sn2S2观察到了巨大的内禀反常霍尔电导和巨反常霍尔角, 以及关于外尔费米子导致的奇异输运行为[22,23]. 由于Co3Sn2S2的居里温度约为175 K, 在低于这一温度的范围, 如150 K, 实验上观察到了约1130 Ω–1·cm–1的大反常霍尔电导, 并且这一反常霍尔电导对温度的依赖关系并不明显, 如图7(a)所示. 这一结果显示Co3Sn2S2的反常霍尔电导可能主要由非零贝里曲率贡献, 这一曲率对温度不敏感导致所测量的反常霍尔电导在宽温度区间内保持相对较大且稳定的值[22]. Co3Sn2S2样品的载流子浓度低, 这使得Co3Sn2S2具有一个约20%的巨反常霍尔角. 此反常霍尔电导和反常霍尔角比常规磁性材料至少高出一个数量级. 同时, Co3Sn2S2的正磁阻似乎随着磁场增加没有呈现饱和的趋势, 具有补偿型半金属的特征. 进一步的实验表明[101], 通过在Co3Sn2S2中掺杂Ni, 即Co3–xNixSn2S2, 观察到异常增强的反常霍尔电导, 观测值约为1380 S/cm. 通过分离反常霍尔效应的内外禀贡献发现, 内禀反常霍尔电导为1340 S/cm, 因此这种异常增强的反常霍尔电导几乎完全来自于内禀贡献. 另外, 反常霍尔角和反常霍尔因子同时获得增强, 最大值分别达到22%和2.3 V–1. 在Co3Sn2S2中掺杂Ni主要表现为多电子掺杂, 这样的增强现象无法基于刚带模型理解, 目前将这一增强效应归咎于无序的掺杂对贝里曲率产生的影响.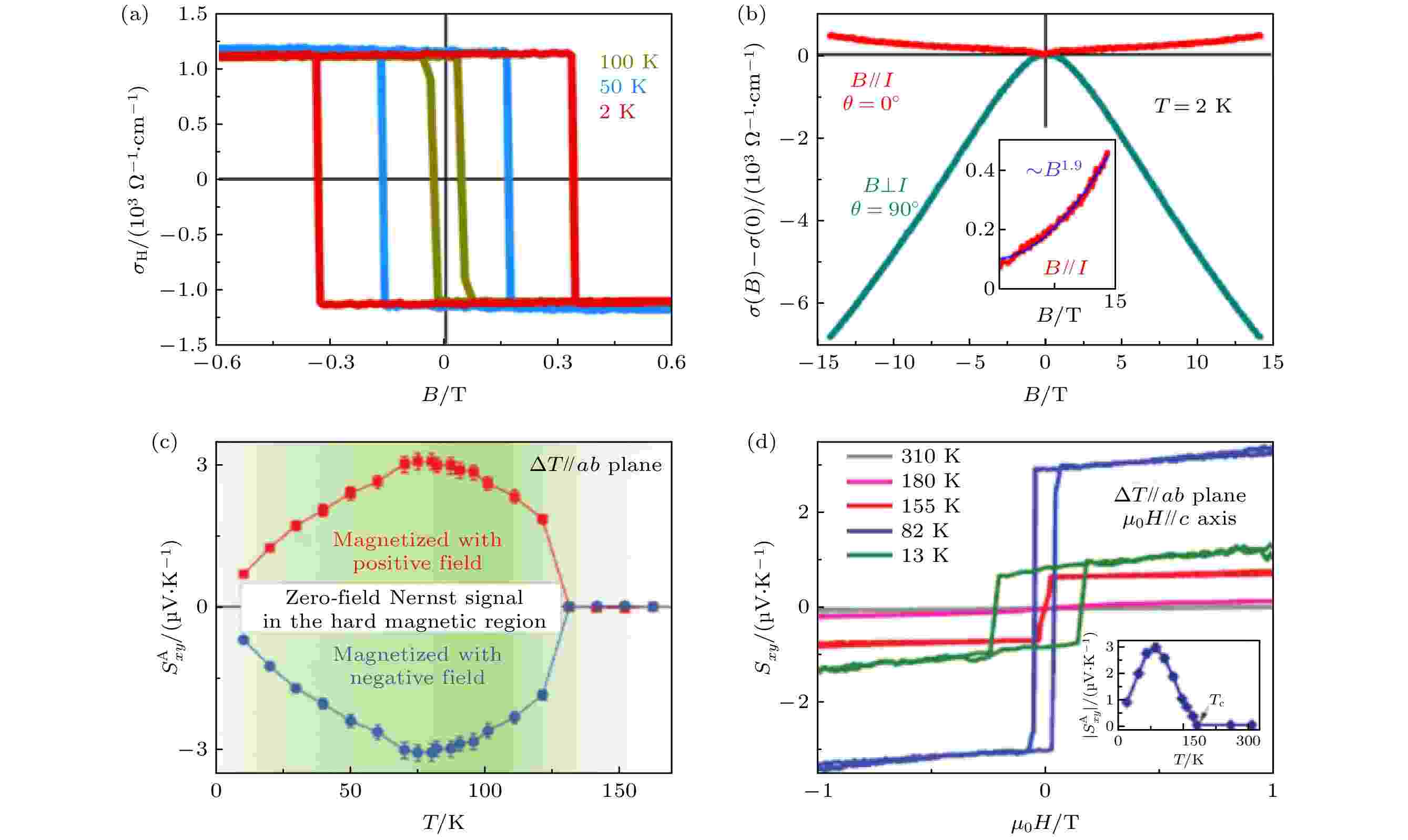
图 7 磁性外尔半金属Co3Sn2S2的反常霍尔效应、手性异常和反常能斯特效应 (a)霍尔电导; (b)磁电导; (c), (d)反常能斯特热功率. 图(a)和图(b)来自文献[22], 图(c)和图(d)来自文献[109]Figure7. Giant anomalous Hall effect, chiral anomaly, and anomalous Nernst effect in magnetic Weyl semimetal Co3Sn2S2: (a) Hall conductance; (b) magneto-electric conductance; (c), (d) anomalous Nernst thermal power. (a) and (b) are adopted from Ref. [22], (c) and (d) from Ref. [109].
对于另一类磁性外尔半金属Mn3X (X = Ge, Sn), 其磁序为反铁磁, 几乎没有净磁矩. 对比于铁磁性材料的反常霍尔效应而言, 理论上Mn3X应该不会表现出反常霍尔效应. 而实验上, Mn3X这种非线性三角反铁磁性却也观察到很大的反常霍尔效应[27-29,102]. 如上文所述, 这源于材料中的手性自旋结构所产生的非零贝里曲率, 且这一反常霍尔效应的主要贡献来源于内禀电子结构, 同时这一来源导致的反常霍尔电导比外禀(净磁矩)因素导致的反常霍尔效应更大. 以Mn3Ge为例[29], 图8(a)显示了Mn3Ge在第一布里渊区的反常霍尔电导分布, 其中在
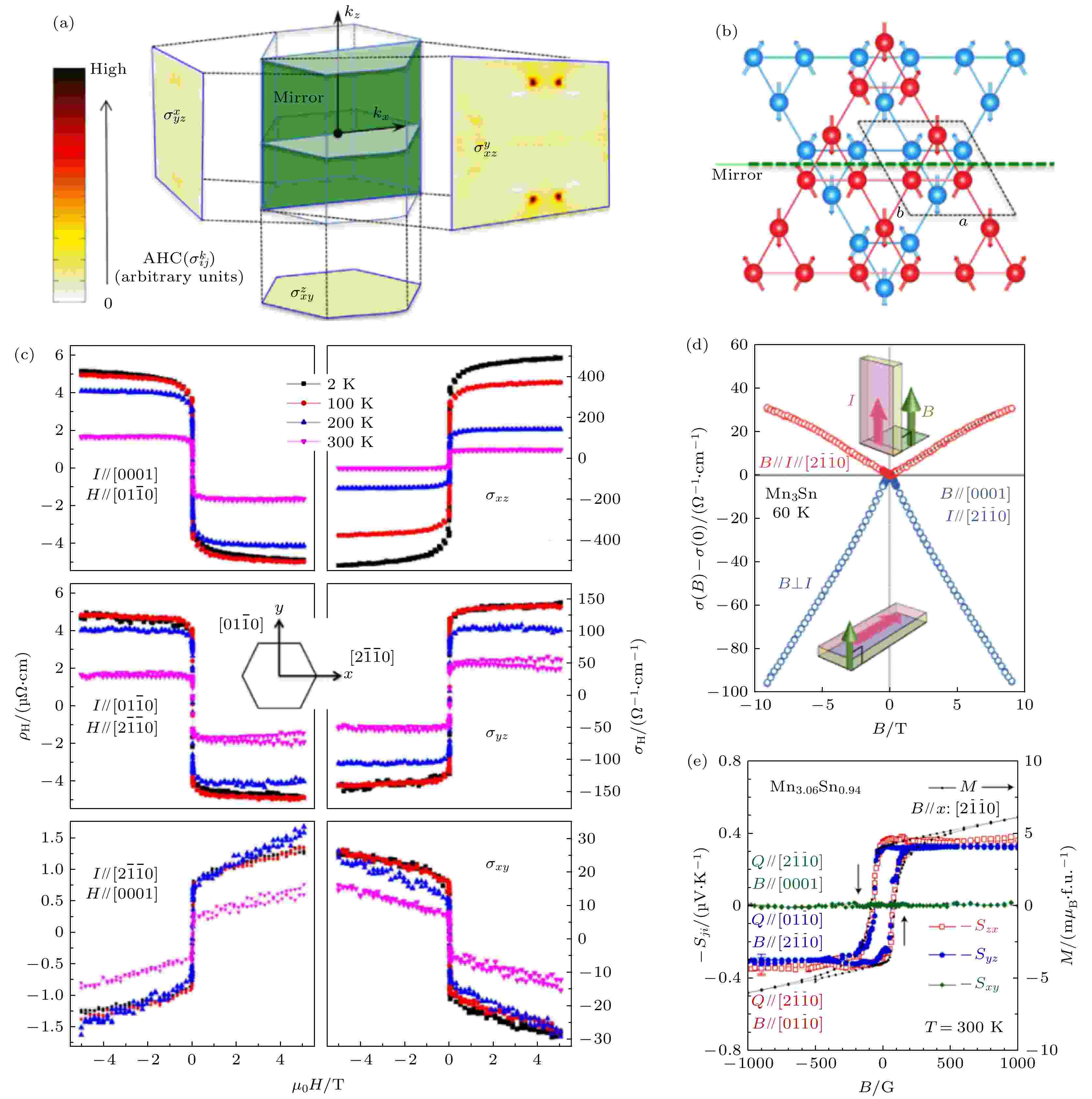图 8 磁性外尔半金属Mn3Ge的反常霍尔效应、Mn3Sn的手性异常和反常能斯特效应 (a)动量空间中Mn3Ge的反常霍尔电导分布; (b)在Mn3Ge中自旋结构的镜面对称性; (c) Mn3Ge的霍尔电阻率; (d) Mn3Sn的面内外的纵向电导; (e) Mn3.06Sn0.94的反常能斯特热功率. 图(a)—(c)来自文献[29], 图(d)来自文献[84], 图(e)来自文献[111]Figure8. Anomalous Hall effect in magnetic Weyl semimetal Mn3Ge, chiral anomalyand anomalous Nernst effect in magnetic Weyl semimetal Mn3Sn: (a) Distribution of anomalous Hall conductance of Mn3Ge in momentum space: (b) spin texture with mirror symmetry in Mn3Ge; (c) Hall resistivity of Mn3Ge; (d) longitudinal conductance of both in- and out-plane for Mn3Sn; (e) anomalous Nernst power of Mn3.06Sn0.94. (a)–(c) are adopted from Ref. [29], (d) from Ref. [84], (e) from Ref. [111].
3
3.2.2.手性异常
在外尔半金属中, 当所加的电流与外加磁场方向平行时, 外尔费米子所在的能带会被朗道能级化, 这一量子化现象会导致手性电荷不守恒, 电荷因此在两个手性相反的外尔节点之间流动, 在宏观实验上表现为负的磁电阻行为. 在对Co3Sn2S2的转角输运测量中发现[22], 当所加的电场与外磁场垂直时, 纵向电阻为正值, 而外加磁场在面内方向时, 纵向电阻则转变为负值, 如图7(b)所示. 这一输运现象被初步认定为外尔费米子导致的手性异常.除了在Co3Sn2S2中观察到上述手性异常的实验现象, Kuroda等[84]也在另一种磁性外尔半金属Mn3Sn中观察到类似的现象. 为了让手性异常在磁电输运中占主导贡献, 实验上合成了一个Mn含量稍高的样品Mn3.06Sn0.94, 这使得费米能级与外尔点之间的距离进一步缩小至约5 meV. 研究发现, 当电流方向沿着
目前为止, 当外加磁场、电场同时在面内方向时出现的负的纵向磁阻效应被视为手性异常存在的重要证据, 但是最近的理论和实验均指出[103-106], 其他机制也可以诱导出负的纵向磁阻, 例如中性/离子杂质导致的轴异常、电流分布的不均匀性、电导涨落等. 另外, 对于没有手性异常的拓扑绝缘体, 在实验上也能够观测到负的纵向磁阻[107,108]. 因此, 负的纵向磁阻不能简单地视为手性异常存在的确切证据. 手性异常的物理特征还待进一步的理论、实验研究.
3
3.2.3.拓扑增强的反常能斯特横向热电效应
与内禀反常霍尔效应类似, 内禀反常能斯特效应也主要受到费米能级附近的电子填充态及贝里曲率分布的影响. 近期对磁性外尔半金属Co3Sn2S2的热输运研究中发现存在拓扑增强的反常能斯特效应[109]. 实验上, Co3Sn2S2在薄膜形式下由于与衬底之间的作用、应力等因素, 其矫顽力显著增强, 高达5 T, 可以使体系保持硬磁单畴状态, 无需施加外磁场即可持续产生能斯特效应. 如图7(c)和图7(d)所示, 在80 K、零外加磁场的实验环境下测得的Co3Sn2S2的横向塞贝克系数约为3 μV/K, 但这一值远高于由于其饱和磁矩(仅为0.9
理论上, 反常能斯特效应能提供一种在费米能级附近对贝里曲率的有效探测方案[75,110], 尤其是对于零磁矩的磁性材料(如反铁磁体). 在近期的实验中, 类似的巨反常能斯特效应也在反铁磁性外尔半金属Mn3X (X = Ge, Sn)中发现[111-113]. 如在Mn含量略高的Mn3.06Sn0.94中, 尽管每个Mn原子磁化强度大约只有0.002
2
3.3.磁性狄拉克半金属
本征的狄拉克半金属中的狄拉克点同时兼具晶体空间翻转对称性与时间反演对称性, 被称为“三维石墨烯”. 但是, 如果晶体空间翻转对称性或时间反演对称性之一被破缺, 例如分别在非中心对称的材料和磁性材料中, 此时的狄拉克点可能会演变为一对外尔节点, 狄拉克半金属也因此会演变成外尔半金属. 晶体空间翻转对称性破缺的外尔半金属已经在TaAs, WTe2等体系中发现, 而时间反演对称性破缺的外尔半金属直至近期才在磁性材料Fe3Sn2, FeSn等中发现. 下面介绍在这些材料中的一些重要实验进展, 主要包括巨反常霍尔效应、巨拓扑霍尔效应以及产生后者的可能的磁斯格明子等拓扑自旋结构, 这些效应在自旋电子、拓扑磁电等研究领域具有重要的价值. 需要说明的是, 在磁性外尔半金属中出现的巨反常霍尔效应、手性异常、拓扑增强的反常能斯特横向热电效应等均可能在磁性狄拉克半金属中出现, 因此这些效应只能说明存在这类拓扑非平庸的电子结构可能会导致的量子效应, 这些效应并不是拓扑非平庸电子结构存在的直接证据.3
3.3.1.巨反常霍尔效应
与磁性外尔半金属类似, 在磁性狄拉克半金属中由于在费米能级附近存在非零贝里曲率的狄拉克费米子能带结构, 能诱导出巨大的反常霍尔电导. 在意识到Fe3Sn2中存在狄拉克费米子的拓扑贡献之前, 实际上已有实验观察到这一巨大的反常霍尔效应[114]. 在室温下, 实验测得Fe3Sn2的饱和霍尔电阻率为3.2 μΩ·cm, 几乎比巡游铁磁体Fe, Ni等高20倍; 反常霍尔系数为6.7 × 10–9 cm/G, 比Fe高3个数量级, 并且正比于纵向电阻率的3.15次方(即
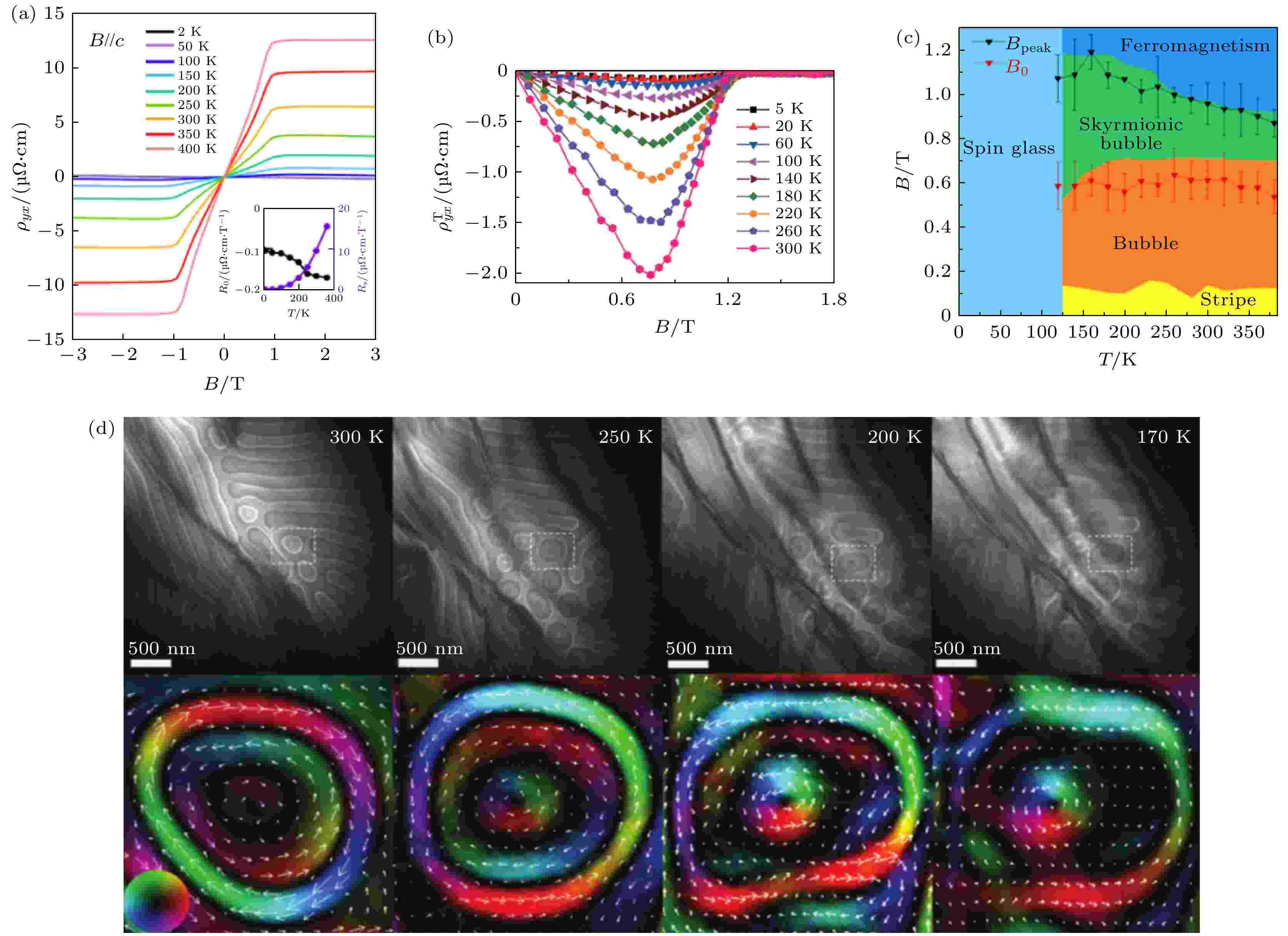图 9 磁性狄拉克半金属Fe3Sn2的反常霍尔效应、拓扑霍尔效应、磁斯格明子磁泡 (a)霍尔电阻率; (b)拓扑霍尔电阻率; (c)温度-磁场下的相图; (d)观察到的斯格明子磁泡. 图(a)来自文献[31], 图(b)来自文献[117], 图(c)来自文献[115], 图(d)来自文献[118]Figure9. Anomalous Hall effect, topological Hall effect, and skyrmion bubble in magnetic Dirac semimetal Fe3Sn2: (a) Hall resistivity; (b) topological Hall resistivity; (c) a phase diagram of temperature and magnetic field; (d) the observed skyrmion bubble. (a) is adopted from Ref. [31], (b) from Ref. [117], (c) from Ref. [115], (d) from Ref. [118].
3
3.3.2.巨拓扑霍尔效应
在Fe3Sn2中, 由于缺陷、杂质、应力或化学配比起伏等原因, 可能形成非共面自旋构型, 使材料同时具有铁磁性和阻挫自旋结构. 磁性材料中的非共面自旋结构与材料的拓扑效应可能存在一定的联系, 近年来引起了广泛的关注. 它主要来源于实空间晶格中标量自旋手性的贝里相位, 从而在实空间中产生一个等效磁场, 当载流子经过这一等效磁场时能感受到等效磁场对它运动时产生的作用力, 这种作用力能对载流子输运产生额外的偏离, 并能在霍尔效应的测量中体现出来, 即拓扑霍尔效应, 亦称为几何霍尔效应. 拓扑霍尔效应通常可在具有拓扑自旋结构(如磁性斯格明子、手性自旋结构等)的材料中观察到, 尤其是在阻挫磁体中经常会观察到此效应. 近日对Fe3Sn2的研究中也观察到了巨大的拓扑霍尔效应[115-117]. 如图9(b)所示, Fe3Sn2在低场时呈现出巨大的拓扑霍尔效应, 在300 K和0.76 T环境下, 测量得的最大拓扑霍尔电阻率约为2.01 μΩ·cm; 当磁场大于1.3 T时, Fe原子的磁矩被完全磁化, Fe3Sn2的阻挫磁结构转变成铁磁性, 此时拓扑霍尔效应因此也消失[117]. 这种实空间的拓扑自旋结构一般只存在于特定的温度、磁场范围, 通过对温度、磁场的调控能把材料体系的磁结构相图刻画出来, 如图9(c)所示[115]. 与破缺材料对称性的拓扑自旋结构不一样, 这种拓扑自旋结构可以在一个中心对称晶格中通过磁阻挫而稳定存在, 而这一效应可能是由于外磁场诱导的拓扑自旋结构和非线性自旋结构共同导致的.3
3.3.3.磁斯格明子和磁泡
近年发现的以磁斯格明子为代表的实空间拓扑磁自旋结构的研究, 不仅为拓扑霍尔效应的来源提供实验依据, 还有望为下一代自旋电子学器件的构建提供新方案. 值得注意的是, 这里的物理载体不限于磁斯格明子, 还包括磁泡这一类研究多年的柱状磁畴结构, 其关键点与磁斯格明子一样, 具有实空间非平庸拓扑性, 即能使这些自旋结构具有高稳定性和抗干扰性. 近期利用洛伦兹透射电子显微镜对Fe3Sn2进行研究[118,119], 观察到了在特定温度区间范围内存在类斯格明子的复杂磁泡、磁涡旋结构, 如图9(d)所示. 但这些复杂磁结构不能用传统磁泡理论来解释, 通过模拟这些磁泡的三维磁结构及其厚度方向积分的面内磁化分布可知, 洛伦兹透射电镜观测的磁结构并非简单的二维磁畴, 而是具有三维厚度调制的三维磁畴. 这一结果为进一步研究磁性狄拉克半金属中拓扑霍尔效应、磁斯格明子等自旋结构提供了直接的实验支撑.作为层状磁性材料和拓扑材料的交叉领域, 层状磁性拓扑材料的家族成员至今仍比较少, 亟待进一步的开发和探索. 一个很重要的例子是, 当前实现量子反常霍尔效应一般是在磁掺杂拓扑绝缘体或者MnBi2Te4家族材料中, 但是实现效应的最高温度仍远低于液氮温度, 这是由此类材料仍存在样品质量等各种相关的问题共同导致的, 因此探索更理想的体系材料是一个极为重要的科学问题. 另外, 在寻找新材料的同时, 还需要专注于其中的一或两种性能优越、有潜在提升价值的层状磁性拓扑材料, 进行更为深入的研究, 并在这些材料基础上进一步探究其中的物理, 对材料进行量子调控等深入研究, 也能对新材料的探索作支撑和辅助作用.
