全文HTML
--> --> -->为什么轨道磁性的研究会与二维材料的发展有着密切的联系呢? 从量子力学角度, 轨道磁性源于非零的贝里曲率[11,12], 而非零的贝里曲率在对称性上要求材料不能同时具有时间反演和空间中心对称性[13]. 最近涌现的二维材料如单层过渡金属硫化物和放在硼氮衬底上的石墨烯都具有诸如有质量型狄拉克的谷能带结构, 在这些谷能带结构中常含有非零的贝里曲率和谷轨道磁矩[14], 因此运动的载流子可产生非零磁矩[6,15]. 以单层过渡金属硫化物为例, 其二维布里渊区为六边形. 在六个转角即狄拉克点附近的电子的低能有效性质可用有质量的狄拉克费米子来描述, 而有质量的狄拉克费米子具有非零的贝里曲率. 即使有非零的贝里曲率, 高晶体对称性如C3等会保证总的可观测效应为零. 所以要观测轨道贝里曲率诱导的磁性响应需要低对称性材料.
二维材料的晶体结构对称性点群种类丰富, 而且具有很好的可调控性. 二维材料的晶体结构可选择性十分广泛. 磁电效应或者谷霍尔效应要求材料不具备对称中心, 并且打破一些镜面对称性, 使得材料的晶体结构选择限定于21个非中心对称点群中的某些低对称性点群. 从低对称性的单斜晶系, 比如1T' 相的过渡金属硫族化合物、三卤化锆或钛等[16]; 到高对称性的四方晶系, 比如硒化铊和砷化镉[17]; 以及六方晶系, 比如石墨烯和2H相的过渡金属硫族化合物[16]. 并且, 二维材料的对称性依赖于层厚和堆叠方式. 比如多层硫化钼点群为具备对称中心的D6h, 而单层硫化钼的点群则降为不具备对称中心的D3h. 二维材料的晶体结构的对称性还可以被外界条件调控, 如衬底、门电压、应力等. 比如, 硼氮衬底上的石墨烯破坏了C3和空间反演对称性, 双层石墨烯加垂直电场破坏了空间反演对称性[6], 加面内应力破坏了镜面对称性[18].
研究二维材料贝利曲率诱导的磁性响应的重要意义在于其易与二维材料本身晶体对称性和量子效应耦合, 产生有趣的物理现象. 许多二维材料具有高电子迁移率和低载流子浓度的特性, 对磁场的效应比较大, 很容易显现量子霍尔效应, 比如石墨烯[19,20]和黑磷[21]. 二维材料的电子结构奇异, 可以实现量子自旋霍尔效应和量子反常霍尔效应, 比如二碲化钨[18,22]和过渡金属五碲化物[23]中存在量子自旋霍尔效应. 另外, 二维过渡金属硫化物材料具有自旋谷锁定效应, 使得谷间的电子散射被抑制, 导致很长的自旋能谷弛豫时间[24]. 轨道磁性与晶体低对称性和强自旋轨道耦合结合, 产生了谷磁电效应[25]和量子非线性霍尔效应[26,27]. 同样, 宏观的轨道磁矩和量子效应的内在物理耦合使我们能够在二维材料中观测到反常霍尔效应和量子反常霍尔效应[1–3].
二维材料及异质结的磁性响应同时与自旋电子学紧密联系. 自旋霍尔效应可将普通电流转换为自旋电流. 它是许多自旋电子器件的应用基础[28], 如自旋轨道力矩磁性随机存储器. 自旋霍尔效应与轨道磁性具有共同的微观机制—贝里相效应[13,28]. 这种紧密联系进一步说明了轨道磁性在电子与信息器件领域的应用前景.
二维材料及异质结的磁性响应是近几年兴起的研究课题, 本文将探讨一系列与电子轨道磁矩或电流引起的磁学响应相关的物理现象. 包括: 1)谷霍尔和磁电效应; 2)量子非线性霍尔效应; 3)转角双层石墨烯中的反常霍尔效应和量子反常霍尔效应. 这三种霍尔效应的物理本质均与贝里曲率诱导的磁响应息息相关. 而为了获得这些磁响应, 材料必须具有降低的晶体维度或对称性. 本文将介绍这些新奇现象现有的物理解释、回顾相关研究的最新发展、讨论其中尚未理解的现象, 并作出展望.
谷霍尔效应首先在石墨烯中被提出[6,30]. 单层石墨烯本身的晶体结构为高对称性的蜂窝结构, 具有反演对称中心, 不存在能谷磁矩, 以致于无法使用光学或电学激发的方法直接在单层石墨烯中观察到谷霍尔效应. 相较于单层本征石墨烯, 在衬底上的单层石墨烯往往和单层二硫化钼一样不具有反演对称中心, 电子在其K和K' 的能带谷中, 具有大小相等和方向相反的能谷磁矩[6,15]. 如果加面内电场, 由于谷霍尔效应的存在, 样品边缘可以积累谷极化载流子(能谷磁矩). 这种边缘能谷磁矩可被光学克尔效应探测到, 如图1(a)所示[22]. 如果用极化光只激发其中一类谷中的载流子, 也可以观测到谷霍尔效应. Mak等[31]在单层二硫化钼中观察到了谷霍尔效应. 他们通过照射不同手性的偏振光, 可以选择性地激发单层二硫化钼K或K' 能带谷中的载流子. 他们的实验印证了观察到谷霍尔效应的关键在于打破材料的中心反演对称性. Gorbachev等[32]在石墨烯超晶格中通过非局域电学测量, 观察到了谷霍尔效应. 在石墨烯超晶格中, 单层石墨烯与氮化硼以A/B方式层叠时打破了晶体反演对称性. 在双层石墨烯或者过渡金属硫族化合物中, 晶体的中心反演对称性可以被施加垂直电场打破. Sui等[33]和Shimazaki等[34]通过施加电场在双层石墨烯中观察到了谷霍尔效应. Lee等[35]通过施加垂直电场打破了双层硫化钼的中心反演对称性, 同样观察到了谷霍尔效应. 通过二维材料的复合, 同样可以打破中心反演对称性. 常温下, Huang等[36]在二硫化钼/二硒化钨异质结中观察到了谷霍尔效应. 此外, 谷霍尔及其相关效应还在单层二硒化钨、二硒化钼和硫化钨等材料中被观察到[37–40]. 磁场与谷效应相互作用的研究同样引起了广泛的兴趣[39–42].
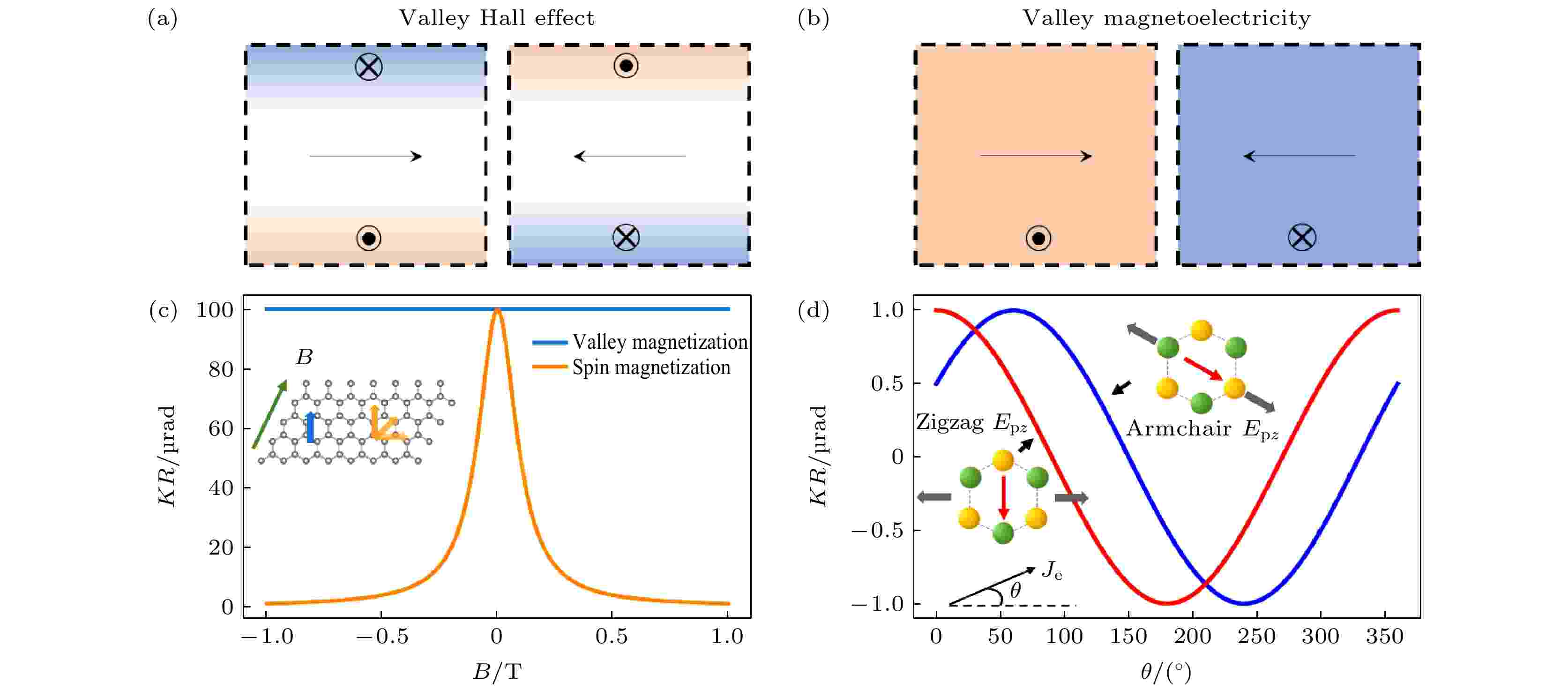图 1 受应力的单层硫化钼谷磁电效应示意图 (a)谷霍尔效应[22]; (b)谷磁电效应[25]; (c)自旋极化引起的磁矩和谷磁电性引起的磁矩在外磁场下的磁光克尔响应; (d)磁光克尔响应与施加电流方向和应力方向的关系Figure1. Sketch of the magnetoelectric effect in monolayer MoS2: (a) Valley Hall effect[22]; (b) valley magnetoelectricity[25]; (c) comparison of magneto-optical Kerr response between spin polarizations induced magnetism and valley magnetization under external magnetic fields; (d) valley magnetization-induced Kerr rotation as a function of the azimuthal angle of current for zigzag and armchair monolayer MoS2.
谷霍尔效应可用于在边缘处产生谷磁矩和探测谷极化电流的谷磁矩, 然而观测到谷霍尔效应往往需要施加圆偏光或者垂直方向的磁场[37–45], 不利于其实际应用[25]. 谷磁电效应(即直接利用电场或者电流控制谷材料的谷磁矩)的发现为谷电子材料的应用提供了便利. 理论上, 产生磁电效应需要打破晶体的中心对称及时间反演对称性[29,46], 但是大多数谷电子材料因为C3对称性的存在而不存在整体的非零谷磁矩(两个边缘存在大小相同方向相反的谷磁矩). 如何通过电学方法产生并控制非零宏观谷磁性成了将谷效应应用于现代电子学的一个关键. 沿着材料特定方向施加应力, 可以打破材料的晶体对称性. 正是基于此方法, Lee等[25]对单层硫化钼施加应力以改变材料晶体结构(如图1(b)所示), 实现了谷磁电效应. 单层硫化钼不具有对称中心, 但具有C3旋转对称性. 施加应力后, 材料的C3对称性降为C1. 时间反演对称性由材料中通过的电流打破[29,47]. 为什么说单层硫化钼中的磁电性是轨道磁性而非自旋磁性引起的呢? 轨道磁矩与自旋磁矩的一个明显差异在于轨道磁矩不显示汉勒效应[48]. 如图1(c)所示, 当面外的自旋磁矩与面内方向的磁场作用, 电子自旋会围绕外磁场方向进动. 在进动过程中, 由于自旋的移相与弛豫, 自旋磁矩在垂直方向的时间平均值会小于零场情况下. 因此, 对于自旋磁矩, 施加面内磁场会导致克尔角度发生偏转. 而对于轨道磁矩, 面内磁场与电子运动轨道平行, 不会引起轨道磁矩的变化. 在单层硫化钼中, 外磁场无法引起克尔角度偏转. 因此, 单层硫化钼的磁电性并非自旋磁矩, 而是轨道磁矩. 单层硫化钼中的磁电性是由轨道磁性引起的另一个证据是其与电流施加方向的关系. 如图1(d)中插图所示, 当应力施加于单层二硫化钼时, 材料内可产生平行(armchair Epz)或者垂直于应力的压电电场(zigzag Epz). 当只向单层二硫化钼施加电流、不施加应力时, K和K' 谷分别产生数量相同但运动方向相反的横向载流子, 以及大小相等方向相反的等效磁场[31]. 因此, 当只施加电流时, 使用磁光克尔显微镜只能观测到材料边缘分别存在的大小相等方向相反的磁矩. 当向样品同时施加电流和应力时, 垂直于电流方向的压电电场分量使得K和K' 谷的费米面沿同一压电电场分量方向倾斜. 受到压电电场的作用, 一个谷中产生的横向载流子数量增加, 另一个谷中数量减少. 由于谷间横向载流子数量不再均衡, 谷中产生的等效磁场虽然方向相反, 但是大小不同. 材料于是表现出谷磁电效应, 并且磁矩均匀存在于材料中, 从而可以被克尔显微镜直接观察到[25]. 轨道磁矩的大小与
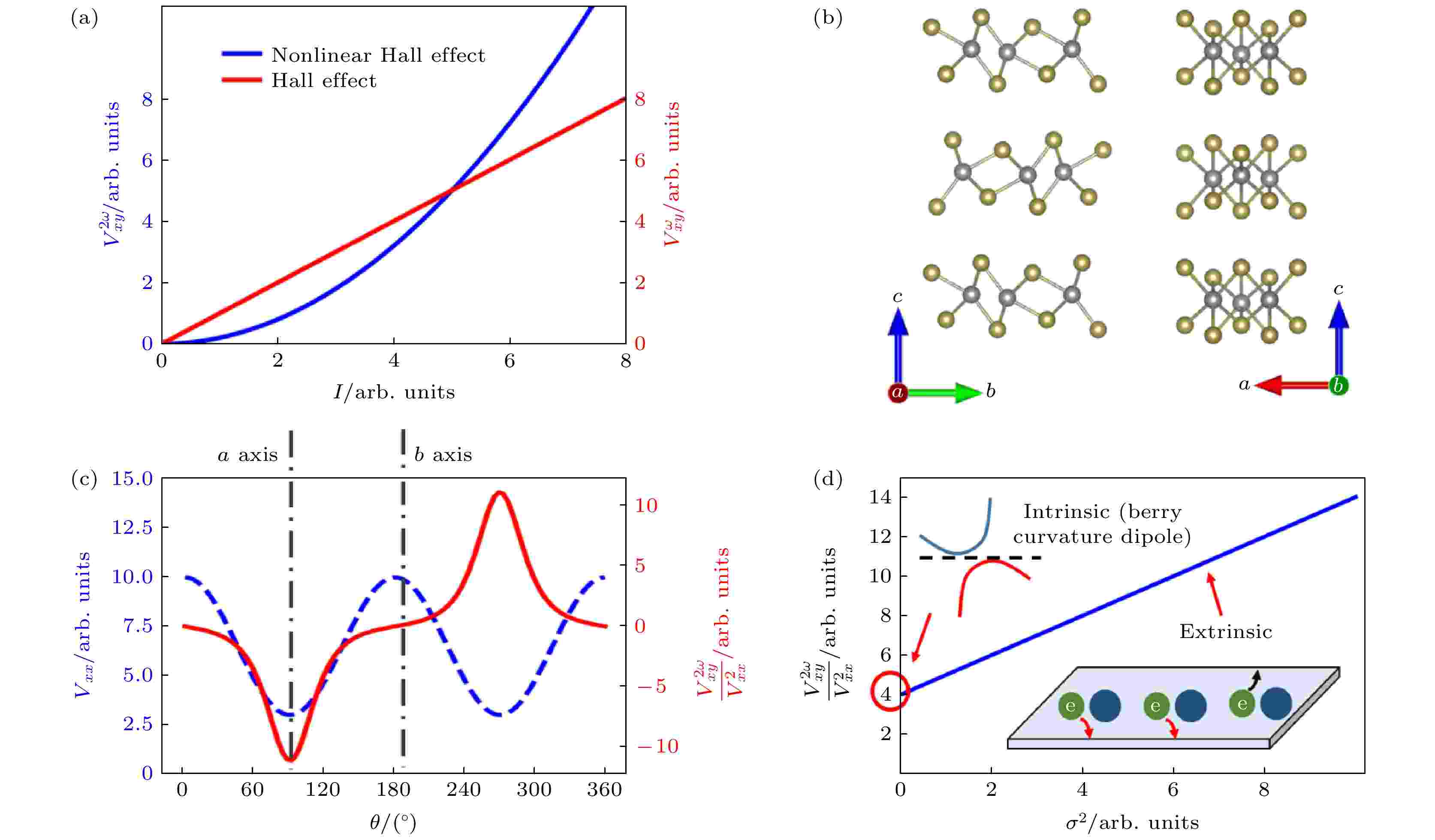图 2 碲化钨中量子非线性霍尔效应示意图 (a)线性和非线性霍尔电压随电流的变化[47]; (b)碲化钨在不同方向上的晶体结构示意图; (c)纵向电压和非线性霍尔电压与电流施加方向的关系[27]; (d)非线性霍尔电压与材料电导率的关系. 插图表示了非线性霍尔效应的两种来源: 贝里曲率和电子偏散射输运[27]Figure2. Illustration of the quantum nonlinear Hall effect: (a) Dependence of linear and non-linear Hall voltage on applied currents[47]; (b) crystal structure of WTe2; (c) angular dependence of longitudinal voltage and non-linear Hall voltage[27]; (d) relationship between nonlinear Hall voltage and conductance. The inset shows two origins of nonlinear Hall voltage: Intrinsic Berry curvature and skew scattering[27].
事实上, 量子非线性霍尔效应确实首先在Td相的二碲化钨中被观察到. 二碲化钨的空间群结构为Pmn21. 如图2(b)所示, 二碲化钨晶体不具备对称中心, 并且平面方向只沿a轴存在对称面, 晶体结构完全满足理论预测的要求. Ma等[26]于2019年首次报道了双层二碲化钨中观察到的量子非线性霍尔效应. 几乎是在同时, Kang等[27]报道了多层二碲化钨中观察到的量子非线性霍尔效应. Ma等[26]在双层二碲化钨中的实验结果与量子非线性霍尔效应是由贝里曲率引起的理论预测十分匹配, 他们认为量子非线性霍尔效应可以作为一种计算贝里曲率的方法. Kang等[27]研究了电流施加方向对横向非线性霍尔电压和纵向电压的影响, 如图2(c)所示, 发现非线性霍尔电压在电流与二碲化钨晶体a轴平行时达到最大值; 当电流与b轴平行时, 非线性霍尔电压消失. 他们认为这一现象与晶体对称性相匹配. 并且, 他们认为施加的面内电流产生了面外轨道磁矩, 从而引起量子非线性霍尔效应. Kang等[27]还研究了不同温度下的量子非线性霍尔效应. 如图2(d)所示, 非线性霍尔电压与电导率的关系可以用以下公式表达:
虽然量子非线性霍尔效应提供了一种测量贝里曲率的电学方法, 许多关于量子非线性霍尔效应的问题仍有待解答. 首先, 目前的理论工作从贝里曲率的角度预测并验证了量子霍尔效应, 然而电子偏散射对量子非线性霍尔效应的影响还需要进一步研究. 其次, 目前只在两种晶体中发现了量子非线性霍尔效应. 量子非线性霍尔效应是否存在于其他同样满足对称性要求并且具有优异量子特性的拓扑绝缘体和过渡金属硫族化合物中? 这仍然是个疑问. 另外, 砷化镉是三维块状材料, 属于C4v点群. Shvetsov 等[56]首次在三维晶体中发现的量子非线性霍尔效应. 因此, 晶体结构对量子非线性霍尔效应影响的研究还需要进一步深入.
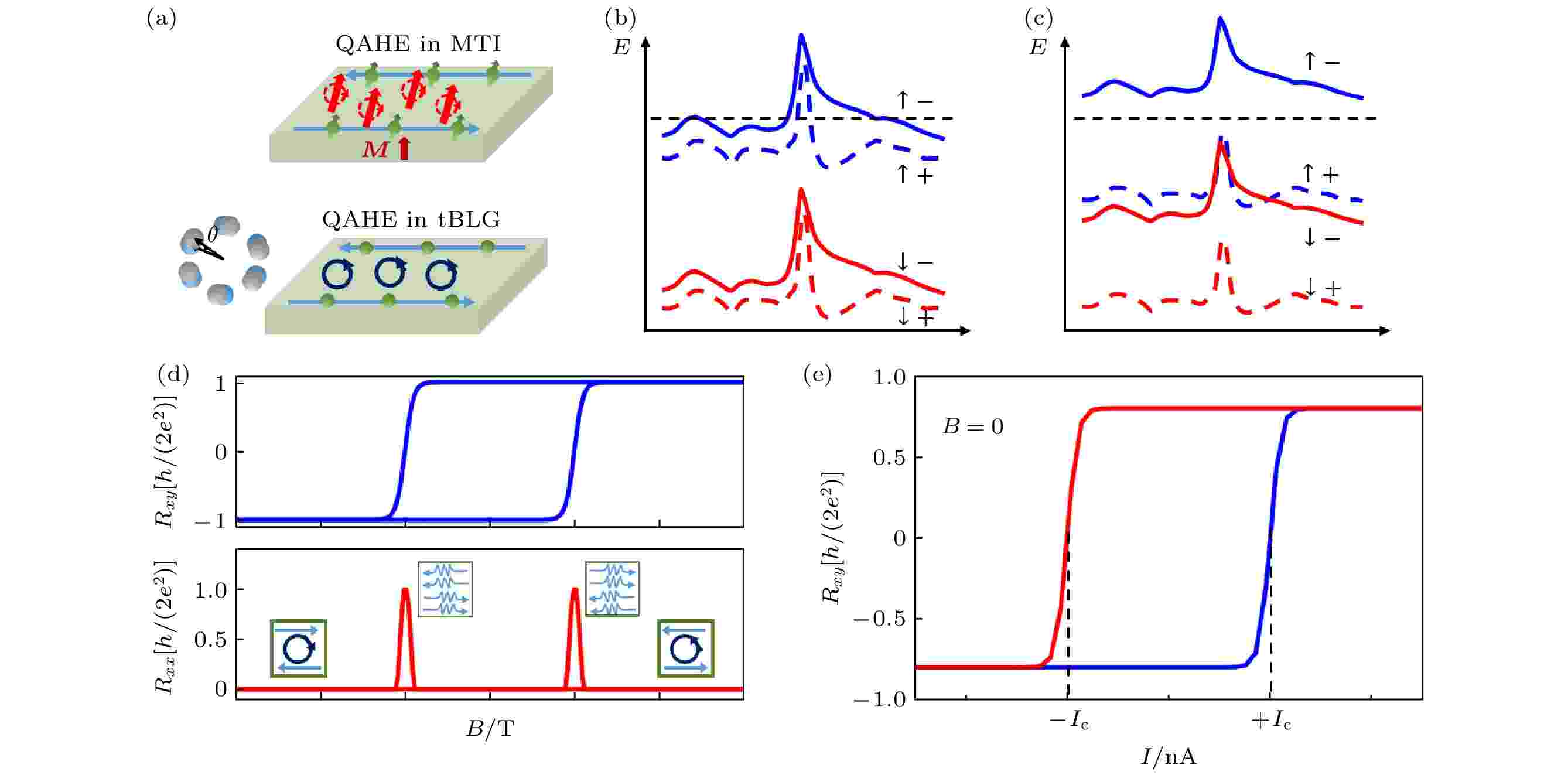图 3 转角双层石墨烯中量子反常霍尔效应示意图 (a)自旋磁化和轨道磁化中量子反常霍尔效应对比示意图; (b)转角双层石墨烯中自旋极化和能谷非极化的导带示意图; (c)转角双层石墨烯中自旋和能谷完全极化的导带示意图; (d)量子反常霍尔态下, 霍尔电阻和纵向电阻随磁场的变化关系, 插图表示材料的导电状态—边缘导电和体导电; (e)电流控制反常霍尔态下磁性翻转示意图Figure3. Illustration of quantum anomalous Hall effect in twisted bilayer graphene (tBLG): (a) Sketch of quantum anomalous Hall effect in spin magnetization and orbital magnetization systems; (b) schematic of fully spin-polarized and but valley-unpolarized conduction bands in a moiré unit cell of tBLG; (c) schematic of fully spin-polarized and valley-polarized conduction bands in a moiré unit cell of tBLG; (d) longitudinal resistance and Hall resistance as a function of magnetic field in the quantum anomalous Hall state, and the insets show the bulk and edge conduction states of material; (e) current control of magnetization switching in the anomalous Hall state.
反常霍尔效应和量子反常霍尔效应在转角双层石墨烯结构中的发现引起了学界对其理论机制的热烈探索. 为了更好地理解魔转角石墨烯中的量子反常霍尔效应, 下面首先简要介绍转角石墨烯中的量子霍尔效应. 当两层石墨烯间的转角小于3°时, 转角石墨烯迷你能带电荷中性点附近的能带是八重简并的, 而远离电荷中性点的能带则是四重简并[61,66–70]. 电荷中性点附近的能带具有拓扑保护的线性色散关系, 而远离的能带则具有拓扑平带结构. 通过电场调节填充系数, 拓扑平带在磁场的作用下可产生量子化的朗道能级, 表现出量子霍尔效应[71–73].
相比于量子霍尔效应, 实现量子反常霍尔效应还需要打破时间反演对称性[50,58]. 魔转角石墨烯并非铁磁体, 也没有掺杂磁性元素, 然而其能带谷中存在轨道磁矩. 因此, 魔转角石墨烯的时间反演对称性很可能是由轨道磁矩打破. 如第2节所述, 石墨烯中相邻能带谷中轨道磁性相反, 并且导带与价带谷中的轨道磁性也相反. 由轨道磁矩引起的宏观磁性只能存在于某些对称性被打破的材料中, 如应力作用下的单层硫化钼[25]. 魔转角石墨烯的对称性结构成为了理解量子反常霍尔效应可能的突破口. 首先, Zhang等[3]认为不能在模型中只考虑转角双层石墨烯结构, 还需要考虑作为保护层的氮化硼与石墨烯的相互作用. 石墨烯与氮化硼的作用打破了转角双层石墨烯在狄拉克点存在的C2T对称性. C2代表2次旋转对称性, T代表时间反演对称性. 打破C2T对称性后, 狄拉克点处的导带和价带的能级被打开. 另外, 在K和K' 的能带谷产生符号相反的磁矩. 他们进一步认为, 观察到的反常霍尔效应可能是由于3/4能带填充的转角双层石墨烯是一个自旋-谷极化的铁磁绝缘体或者是谷极化自旋非极化的费米液体金属. He等[74]计算了氮化硼与转角双层石墨烯异质结的轨道磁电性和电流引起的磁性翻转, 他们同样认为氮化硼与石墨烯间的相互作用打开了狄拉克点处的能带带隙. 然而, 石墨烯与氮化硼的相互作用只是将材料的对称性降低到D6, 此对称性无法允许由面内电流产生面外的磁矩[75,76]. 他们认为除了与石墨烯的相互作用, 氮化硼还引入了应变, 应变将材料对称性进一步降低到C1. 通过引入0.1%的应变, 计算发现狄拉克点附近存在不会被晶体对称性抵消的贝里曲率, 可以成功地解释转角双层石墨烯中产生的面外磁矩. 此外, He等[74]还发现转角双层石墨烯异质结的磁矩与电流引入的电场直接耦合, 可以解释非量子反常霍尔态下弱电流引起的磁性翻转. 然而, 仍然有一些谜题等待解答. 比如Xie和MacDonald[77]以及Bultinck等[78]用平均场的方法计算发现电子库仑相互作用可以导致时间反演对称性的自发破缺, 从而使转角双层石墨烯同时具有自旋和轨道磁性, 但电子库仑相互作用如何导致轨道磁性的微观机理还需要进一步研究. 还比如He等[74]理论分析得出转角双层石墨烯体态存在与电流正比的磁矩, 而Serlin等[2]的分析是说边缘态存在与电流成三次方的磁矩. 总之, 关于转角双层石墨烯中的反常霍尔效应和量子反常霍尔效应的研究还处于最初阶段, 具有极大的研究空间与价值.
1)电流控制量子反常霍尔态轨道磁矩翻转.
目前, 并没有实验表明电流可以翻转量子反常霍尔态下的轨道磁矩, 以实现整量子数的霍尔电阻变化, 可能的原因在于量子霍尔态下只有边缘电导. 不管最后能否实现量子反常霍尔态的磁矩翻转, 目前实验上证实了在接近量子反常霍尔态下, 轨道磁矩可以被非常小的电流翻转. 研究电流控制轨道磁矩的翻转具有深刻的物理与应用价值.
2)从材料的能带及晶体结构考虑, 挖掘更多具有磁性响应的二维材料.
二维材料的磁学响应与其能带和晶体结构有着密切的联系. 从能带的角度来看, 由于轨道磁矩和材料的贝里曲率密切相关. 而贝里曲率往往富集在具有狄拉克点或拓扑结构的材料中, 因此狄拉克、外尔材料和拓扑绝缘体应该是研究的重点. 从晶体结构的角度来看, 二维材料晶体结构的多样性为发现更多具有磁学响应的材料提供了便利. 因此, 可以从具有低对称性同时具有拓扑或狄拉克结构的二维材料中寻找新材料[79–81]. 值得一提的是, 三维拓扑绝缘体的拓扑表面态同样存在非零的贝里曲率[82–84], 然而对其轨道磁矩研究仍然属于空白. 其次, 目前关于晶体结构对轨道磁矩的研究停留在点群层面. 掌握晶体空间群对轨道磁矩的影响, 有利于更准确地发现具有磁性响应的二维材料. 另外, 通过材料间的耦合作用可以打破晶体的对称性以发现具有轨道磁矩的二维材料.
3)二维材料及异质结中的多重物理耦合效应.
二维材料本身可以具有多重吸引人的量子、电子以及自旋特性. 以转角双层石墨烯为例, 在低温下其具有超导、量子反常霍尔效应以及谷霍尔效应[1,2,60,77]. 这些效应间的耦合极具吸引力. 其次, 谷附近富集贝里曲率和轨道磁矩. 贝里曲率可引起自旋霍尔效应产生自旋电流, 其和谷轨道磁矩间的耦合将十分有趣. 最近实现表面、转角石墨烯体系中存在铁电特性[85]. 具有不同特性的二维材料异质结可以引起各种多重物理效应的相互作用, 有望发现新的物理现象.
4)基于含轨道磁性的二维材料的电子、自旋电子、磁光器件的设计及应用.
翻转转角双层石墨烯的磁矩所需要的电流密度远小于目前常用的自旋电子学方法[74]. 这一现象开始显示出轨道磁矩在信息技术中的巨大前景. 在二维材料中发现更多的新型功能, 并将这些功能应用于电子、自旋电子和磁光器件或许能够大幅度提高这些器件的性能.
感谢香港科技大学的罗锦团博士和波士顿学院的马琼博士的讨论.
