摘要: 量子卫星通信是通信领域的研究热点和前沿, 具有理想的信息安全性和覆盖面广的优势, 对于构建全球范围的量子卫星广域网具有重要意义, 而远距离传输信息时网络的可靠性、安全性和路由中继等问题仍需改进. 为了构建性能良好的量子卫星广域网, 本文提出利用蜘蛛网作为一种独特的自然通信拓扑结构, 将自然界蛛网演进为人工蛛网拓扑, 量子信息的传输采用
N 阶量子隐形传态路由方案, 其传输时延基本不变, 在此基础上构建蛛网网络拓扑量子广域网传输模型, 并对构建的网络模型的误码率、吞吐率、安全密钥生成率进行仿真分析. 用抗毁度作为衡量网络拓扑结构可靠性的指标, 以9节点环型网和9节点蛛网为例进行定量和定性分析, 得出蛛网拓扑具有更高的可靠性. 当噪声的平均功率谱密度给定且不存在中继时, 量子态的传输距离越大误码率越大, 这时要考虑引入中继; 当传输距离和噪声功率谱密度一定的情况下, 误码率随着中继节点个数的增多而减小, 因此在蛛网拓扑下要选择合适的路由过程. 随着量子卫星分发纠缠光子对成功概率的增大, 吞吐率逐渐增加; 随着网络中传输时延的增大, 吞吐率逐渐减小, 但在该路由方案下传输时延基本不变, 且蛛网结构的传输时延很小, 因此本文中提出的基于
N 阶量子隐形传态的蛛网网络拓扑量子广域网的吞吐率不会有明显的降低. 当量子信息的传输距离不断增大时, 网络密钥生成率逐渐减小; 随着网络中继节点个数的增多, 密钥生成率逐渐增加. 由此可见, 利用蛛网拓扑以及
N 阶量子隐形传态路由方案构建量子卫星广域网具有很好的优势.
关键词: 蜘蛛网拓扑 /
N 阶量子隐形传态路由方案/
量子卫星广域网 English Abstract Construction strategy and performance simulation of quantum satellite wide area network based on cobweb structure Nie Min 1 ,Han Kai-Jie 1 ,Yang Guang 1,2 ,Zhang Mei-Ling 1 ,Sun Ai-Jing 1 ,Pei Chang-Xing 3 1.School of Communication and Information Engineering, Xi’an University of Posts and Telecommunication, Xi’an 710121, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 61971348, 61201194), the International Scientific and Technological Cooperation and Exchange Program in Shaanxi Province, China (Grant No. 2015KW-013), and Natural Science Basic Research Program of Shaanxi, China (Grant No. 2021JM-464)Received Date: 24 March 2021Accepted Date: 26 April 2021Available Online: 07 June 2021Published Online: 20 July 2021Abstract: Quantum satellite communication is a research hotspot and frontier in the field of communication. It has the advantages of ideal information security and wide coverage, which is of great significance in constructing a global quantum satellite wide area network. However, problems such as network reliability, security and routing relay still need to be improved when transmitting information over long distances. In this paper, the spider web is used as a unique natural communication topology to transform the natural spider web into an artificial spider web topology. The quantum information transmission adopts N-order quantum teleportation routing scheme, and the transmission delay is basically unchanged. On this basis, the spider web topology quantum wide area network transmission model is constructed. The bit error rate, throughput rate and security key generation rate of the network model are simulated and analyzed. Taking 9-node ring network and 9-node cobweb for example, the quantitative analysis and qualitative analysis are both conducted in this paper. The results show that the cobweb topology has higher reliability. When the average power spectral density of the noise is given and there is no relay, the bit error rate increases with the transmission distance increasing, so the introduction of relay should be considered. When the transmission distance and noise power spectral density are constant, the bit error rate decreases with the number of relay nodes increasing, so the appropriate routing process should be selected in the spider web topology. With the increase of the probability of transmitting entangled photon pairs, the throughput rate gradually increases. With the increase of transmission delay in the network, the throughput rate Q gradually decreases. However, the transmission delay is basically unchanged in this routing scheme, and the transmission delay of cobweb structure is very small. Therefore, the throughput rate of the topology quantum WAN of cobweb network based on N-order quantum teleportation proposed in this paper will not significantly decrease. When the transmission distance of quantum information increases, the network key generation rate decreases gradually. With the increase of the number of network relay nodes, the key generation rate increases gradually. Thus, it can be seen that using cobweb topology and N-order quantum teleportation routing scheme to construct a quantum satellite WAN has good advantages.Keywords: spider web topology /N -order quantum teleportation routing schemequantum satellite wide area network 全文HTML --> --> --> 1.引 言 发展量子卫星通信是我国重点战略发展计划, 其发展的最终目标是构建全球广域量子通信网络体系[1 ] . 量子密钥分发(quantum key distribution, QKD)以其无条件安全性引起了****的广泛关注[2 ] , 1984年Bennett和Brassard提出了第一个无条件安全传输的BB84协议, 1992年Bennett在此前研究的基础上又提出了B92协议. 但在实际QKD实现过程中会存在很多安全漏洞, 2012年Lo等[3 ] 首次提出测量设备无关量子密钥分配(measurement-device-independent quantum key distribution, MDI-QKD)协议, MDI-QKD的提出不仅保证QKD协议理论上的安全性, 也消除了窃听者的攻击, 且使通信距离扩大. 随着该协议理论基础的不断完善, 近几年该领域的实验得到了快速的发展, 2020年潘建伟等[4 ] 提出了远距离自由空间MDI-QKD方案, 实现了在19.2 km的城市大气通道上的第一个自由空间MDI-QKD, 这项实验标志着我国向着基于卫星的MDI-QKD迈出了第一步. 同年Yin等[5 ] 实现了基于纠缠的无中继千公里量子保密通信, 这些研究进一步表明通过量子卫星构建全球量子通信网络的方案是可行的.[6 ] ; 2017年9月, 总长2000多公里的“京沪干线”量子保密通信网络正式开通, 同时“京沪干线”与“墨子号”成功对接, 首次实现了洲际量子保密通信[7 ] ; 2011年, 周小清等[8 ] 研究了量子隐形传态网络的互联与路由策略. 2012年, 连涛和聂敏[9 ] 通过分析环境噪声对量子信令远距离传输的影响, 提出了基于纠缠交换的量子信令中继策略. 2013年, 刘晓慧等[10 ] 提出了传输时延小的多阶量子隐形传态量子路由方案, 并分析了其路由策略. 2021年聂敏等[11 ] 根据球形蒲公英量子卫星网络的结构特性, 提出了一种两端纠缠交换的量子路由方案. 2021年1月陈宇翱等[12 ] 提出了约4600 km的天地一体化量子通信网络.N 阶量子隐形传态的量子卫星广域网的误码率、吞吐率以及安全性问题, 通过仿真研究, 为构建性能良好的量子卫星广域网奠定基础.2.蜘蛛网网络拓扑 22.1.蛛网结构及其捕食策略 2.1.蛛网结构及其捕食策略 蛛网结构中圆网是最具代表性的, 且在圆网结构的基础上可以继续进化为别的类型的网[13 ] . 自然界中的圆形蜘蛛网如图1 所示, 结构图如图2 , 其呈现椭圆形并具有一定的对称性, 由捕丝、拖丝、旋转螺旋丝组成, 拖丝按功能又可以划分为框架丝、锚定丝、径向丝. 捕丝具有一定的黏性, 可将猎物粘住; 径向丝支撑整个网结构的稳定[14 ] , 且具有很强的延展性, 可以通过径向丝的振动为蜘蛛提示猎物的位置.图 1 自然界圆形蜘蛛网Figure1. Round spider web in nature.图 2 蛛网结构图Figure2. Cobweb structure diagram.[15 ] , 因此传递蛛网内的振动信息主要是沿着径向丝快速传递到中心区域, 蜘蛛沿着径向丝抵达猎物身边.2.2.人工蛛网演进过程 -->2.2.人工蛛网演进过程 人工蛛网演进过程如图3 所示. 蛛网是由星型、环型拓扑演进而来, 其中星型结构简单且容易管理; 环型拓扑的信息传输误码率很低, 但可靠性差. 蛛网网络拓扑(spider network topology, SNT)除结合这两种拓扑结构的优点之外, 还有很强的抗毁能力, 当通信链路发生故障断开或者出现拥塞时, 由于网络中任意一个节点到另外一个节点的路径不止一条, 可以选择其他路径实现链路之间的连接, 使得信息有效传输.图 3 人工蛛网演进过程 (a) 星型; (b) 环型; (c) 蛛网Figure3. Evolution of artificial cobweb: (a) Star; (b) ring; (c) spiderweb.2.3.SNT与环型拓扑的性能分析 -->2.3.SNT与环型拓扑的性能分析 1)可靠性定量分析H 有g 个节点, 删除其中的c 个节点后, 网络拓扑可以表示为$H\left( c \right)$ , 最终删除m 个节点可以使得网络中的所有节点均为孤立节点, 根据参考文献[16 ,17 ]可知, 网络抗毁度定义为$E\left( c \right)$ 表示删掉c 个节点之后网络的连通度, 表达式为:${e_c}\left( {a, b} \right)$ 表示删掉c 个节点之后节点a 和节点b 之间的连通度, 可表示为:p 为节点a 到达节点b 之间的路径条数, 且均为互不相交的路径; $J\left( d \right)$ 为节点a 到节点b 之间的第d 条路径所需要经过的链路个数.18 ], 假设链路失效的概率为r , 链路有效的概率为s , 网络的全端可靠性为$K\left( {H, S} \right)$ , H 代表网络的拓扑结构, $ H-q$ 是网络H 中除去q 后获得的网络, $ H/q$ 是网络中将q 所连接的两个节点进行合并后得到的网络. 只分析因链路失效而导致的不可靠性, 因子定理为图4 所示, 横轴为链路有效率s , 纵轴为可靠性K . 当链路有效率为0.7时, 环型拓扑的可靠性为0.42, 蛛网拓扑的可靠性为0.81. 因此蛛网结构在可靠性方面更具优势, 随着节点个数的增多, 网络中任意两个节点之间的通信路径不止一条, 网络全端可靠性增加.图 4 环型与蛛网拓扑的网络可靠性分析Figure4. Network reliability analysis of ring and cobweb topologies.3.基于N 阶量子隐形传态路由方案 实现量子通信的关键是量子态远程传送和量子路由, 不同用户之间需要共享量子纠缠[19 ,20 ] . 在进行远距离节点的量子态传输时, 主要存在以下两个问题: 一是量子终端的存储容量有限, 当网络中有很多中继节点时, 其中一个量子设备不可能存储所有可能与之通信的量子设备的纠缠光子对; 二是自由空间中充满了各种环境噪声, 进行远距离的EPR光子对的分发是不可能的. 而N 阶量子隐形传态路由方案是不受这两个问题的限制, 可将量子信息从源节点Alice传输到另外一个远距离且不与之共享EPR纠缠光子对的目的节点Bob处, 需在各个中间节点处进行量子测量和量子门操作, 通过中间节点完成量子态的传输[10 ] . 该路由方案原理如图5 所示图 5 基于N 阶量子隐形传态的量子路由方案Figure5. Quantum routing scheme based on N -order quantum teleportation.3.1.二阶量子隐形传态 3.1.二阶量子隐形传态 以二阶量子隐形传态过程为例进行分析, 假设Alice为源节点, Bob为目的节点, David为中间交换节点, 逻辑线路图如图6 所示.图 6 二阶量子隐形传态逻辑线路图Figure6. Second-order quantum teleportation logic circuit diagram.${\left| 0 \right\rangle _{{A_1}}}{\left| 0 \right\rangle _{{A_2}}}$ , David的两个量子比特分别为${\left| 0 \right\rangle _{{D_1}}}{\left| 1 \right\rangle _{{D_2}}}$ , 那么Bob的量子比特一定是$\alpha \left| 1 \right\rangle + \beta \left| 0 \right\rangle $ . Bob得知自己的状态信息后, 就可以对其进行相应的量子门操作恢复出Alice传输给它的信息$\left| I \right\rangle = \alpha \left| 0 \right\rangle + \beta \left| 1 \right\rangle $ . Bob需要进行的量子门操作如表1 所列.$ {A}_{1} $异或$ {D}_{1} $ $ {A}_{2} $异或$ {D}_{2} $ 量子门操作 0 0 无 0 1 X 门1 0 Z 门1 1 X 门和Z 门
表1 已知测量结果后的量子门操作Table1. Quantum gate operation after known measurement results.3.2.三阶量子隐形传态 -->3.2.三阶量子隐形传态 在分析二阶量子隐形传态的基础上, 讨论三阶量子隐形传态的具体过程, 其需要借助两个中间节点完成量子态传送. 源节点为Alice, 目的节点为Bob, 中间节点分别为David和Gina, 逻辑线路图如图7 所示.图 7 三阶量子隐形传态逻辑线路图Figure7. Third-order quantum teleportation logic circuit diagram.表2 所列.$ {A}_{1} $异或$ {D}_{1} $异或$ {G}_{1} $ $ {A}_{2} $异或$ {D}_{2} $异或$ {G}_{2} $ 量子门操作 0 0 无 0 1 X 门1 0 Z 门1 1 X 门和Z 门
表2 已知测量结果后的量子门操作Table2. Quantum gate operation after known measurement results.N 阶量子隐形传态过程. 由二阶以及三阶量子隐形传态逻辑线路图可知, 各个节点的量子门操作和量子测量是同步完成的, 完成多个节点路由时间与量子隐形传态时间相同.3.3.量子路由方案仿真分析 -->3.3.量子路由方案仿真分析 已有的路由方案很多, 常用的包括量子中继路由方案、量子纠缠交换路由方案等. 参考文献[10 ], 设采用量子中继路由方案时, 传输时间T 为${T_1}$ 表示在量子信息的传输过程中完成量子隐形传态的时间, n 是路由过程使用的中继节点数目.${T'}$ 为${T_2}$ 表示量子纠缠交换时间.N 阶量子隐形传态路由方案时, 传输一个量子态所需要的时间${T''}$ 为w 为在广域网的位置数据库中查找用户具体位置所需的时间, h 为量子卫星分发纠缠光子对的时间. 假设T 1 = 0.8 μs, T 2 = 0.7 μs, $w = 0.01{T_1}$ , $h = 0.01{T_1}$ .图8 所示, 当$n = 4$ 时, T = 4 μs, T' = 3.6 μs, T'' = 0.82 μs; 当$n = 10$ 时, T = 8.8 μs, T' = 7.8 μs, T'' = 0.82 μs. 由此可见, 随着中继节点个数的增多, 前两种路由方案传输时延有明显的增大, 而N 阶量子隐形传态路由方案传输一个量子态的时间基本保持不变, 传输时延小.图 8 三种路由方案量子态传输时间与中继节点个数的关系Figure8. Relationship between the quantum state transfer time and the number of relay nodes.4.基于SNT的量子卫星广域网网络模型 自然界中的蛛网结构与量子卫星通信网络有很多的相似性.图9 所示.图 9 六边形逻辑蛛网拓扑模型Figure9. Hexagonal logic spider web topology model.图10 是SNT量子卫星广域网模型, 量子卫星广域网由量子卫星(quantum satellite)、量子无线基站(router)、量子全局位置数据库(QGPW)、量子局部位置数据库(QLPW)以及地面通信用户组成. 蛛网的中间节点作为quantum satellite, 其余蛛网节点为各个不同的基站, 作为中继转发, 每个基站都配有一个QLPW, 用来查找各个用户的具体位置. 量子卫星的主要任务是生成纠缠光子对, 并将其发送给各个基站, 建立卫星与各个基站之间的量子信道, 实现量子信息的传输.图 10 基于蛛网拓扑的量子卫星广域网Figure10. Quantum satellite wide area network based on cobweb topology.图10 可知网络中只有一个量子卫星, 通过QGPW可以查询到Alice和Bob在同一颗卫星下, 此时QGPW会通知Router1的目的用户Bob的具体位置, 同时在通信的过程中, Router1请求quantum satellite发送纠缠光子对给相应的基站, 建立起卫星与基站之间的量子信道, 利用N 阶量子隐形传态路由方案有效传送Alice所要传送给Bob的信息.5.基于N 阶量子隐形传态的量子卫星广域网性能仿真 25.1.量子信息传输误码率分析 5.1.量子信息传输误码率分析 由于存在环境噪声、人为干扰等因素会导致通信链路失效, 使纠缠粒子的状态发生变化, 从而产生错误的传输. 设量子信息传输误码率为${P_{\rm{r}}}$ [9 ] , 公式为${\sigma ^2}$ 是噪声平均功率谱密度, 其余各参量的含义如表3 所列.L n λ $ {f}_{\rm{T}} $ $ {f}_{\rm{R}} $ $ {F}_{\rm{T}} $ $ {F}_{\rm{R}} $ $ {L}_{\rm{P}} $ 星地间传输距离 中继节点个数 光子波长 发送端望远镜孔径 接收端望远镜孔径 发端望远镜传输因子 收端望远镜传输因子 链路损耗
表3 量子信息传输误码率各参量含义Table3. Meaning of parameters of bit error rate in quantum information transmission.21 ], 应选择透射率较高的大气窗口, 因此本文取$ \lambda = 1550\;{\rm{nm}}$ 进行分析. 其余参数设置为$ n=0$ , ${f_{\rm{T}}} = {f_{\rm{R}}} = 32\;{\rm{mm}}$ , ${F_{\rm{T}}} = {F_{\rm{R}}} = 1$ , ${L_{\rm{p}}} = 5{\text{%}}$ , 噪声的平均功率谱密度分别为1, 2和3 dB/km.${P_{\rm{r}}}$ 与传输距离L 之间的关系. 仿真结果如图11 所示.图 11 误码率与传输距离的关系Figure11. Relationship between BER and transmission distance.${\sigma ^2}$ 一定时, 星地之间传输距离越大, 误码率越大. 在${\sigma ^2} = 1\;{{{\rm{dB}}} / {{\rm{km}}}}$ 条件下, 当传输距离为2000 km时, 误码率为0.049; 当传输距离为4000 km时, 误码率达到0.197. 在量子信息在星地之间的传输距离一定的条件下, ${\sigma ^2}$ 越大, 误码率也越大, 当传输距离为3000 km, ${\sigma ^2} = 1\;{{{\rm{dB}}} / {{\rm{km}}}}$ 时误码率为0.111; ${\sigma ^2} = 3\;{{{\rm{dB}}} / {{\rm{km}}}}$ 时误码率达到0.332. 因此在没有中继的情况下, 传输更远距离时误码率增大, 就需要考虑引入中继.L 为4000 km时, 分析功率谱密度${\sigma ^2}$ 、中继节点个数n 与误码率${P_{\rm{r}}}$ 的关系, 仿真结果如图12 所示, 误码率的其余参量取值同图11 .图 12 误码率与中继节点个数的关系Figure12. Relationship between bit error rate and the number of relay nodes.${\sigma ^2}$ 一定时, 误码率随着n 的增大而减小, 当中继节点数取为6或者更大时, 误码率几乎保持不变, 因此在量子卫星广域网中进行信息传输时要选择合适的路由过程, 使得信息有效传输.5.2.量子广域网吞吐率分析 -->5.2.量子广域网吞吐率分析 基于N 阶量子隐形传态的量子卫星广域网中, 设成功分发纠缠光子对的概率为${P_1}$ 、在QGPW中成功查找位置信息的概率为${P_2}$ 、成功进行量子门操作的概率为${P_3}$ 、接收端成功接收量子信息的概率为${P_4}$ . 那么成功将一个量子态信息传输至目的节点的概率为N 阶量子隐形传态的过程中, 生成纠缠粒子对的时间为h 、在位置数据库中查找信息的时间为w 、进行量子门操作的时间为j 、在中继节点处的传输时延为${T''}$ . 而在N 阶量子隐形传态的过程中, 传输一个量子态的时间不会随着中继节点个数的增多而增大, ${T_1}$ 是量子隐形传态的平均时间, 所以w , h , j 的大小相比于${T{''}}$ 很小, 可以忽略不计, 所以${T_1} = 0.8\;\text{μ}{\rm{s}}$ , 分析吞吐率Q 与${P_1}$ , n 的关系. 根据文献[22 ]可知, 在理想条件下概率均设为0.8, 所以令${P_2}$ , ${P_3}$ , ${P_4}$ 均为0.8, 仿真结果如图13 所示.图 13 吞吐率Q 与${P_1}$ 以及中继节点个数n 的关系Figure13. Relationship between throughput rate Q and P 1 and the number of relay nodes n .${P_1}$ 的增大, 吞吐率Q 也在逐渐增加, 最大可以达到640 kb/s; 随着中继节点个数n 的增大, 吞吐率逐渐降低. 因此在蛛网拓扑结构下, 要选择合适的路由过程使得量子信息的吞吐率尽可能大.${P_1} = {P_2} = {P_3} = {P_4} = 0.8$ 时, 分析吞吐率Q 与传输时延T t 的关系, 其中中继节点个数分别取2, 4, 6, 仿真结果如图14 所示.图 14 吞吐率与传输时延的关系Figure14. Relationship between throughput Q and transmission delay.Q 逐渐减小. 但在N 阶量子隐形传态路由方案下, 传输时延基本不变, 且在蛛网网络拓扑下可选路径多, 传输时延小, 因此本文提出的基于N 阶量子隐形传态的蛛网网络拓扑量子广域网的吞吐率不会随着传输时延的增大有明显的降低.5.3.安全密钥生成率分析 -->5.3.安全密钥生成率分析 网络的安全性主要是指在一定链路条件下所能获得的最高安全密钥生成率. 在量子卫星广域网通信过程中, 进行量子信息传输时仅考虑理想的单光子源, 在单个脉冲中含u 个光子的概率为[23 ] $\varphi $ 为平均光子数, 在一般的量子通信实验中, $\varphi $ 取值为0.1[23 ] , 来获取准单光子源. 根据诱骗态方案, 可知单光子的计数率为$\gamma $ 为量子信道衰减系数, 通常取值为0.2 dB/km, L 为量子信息的传输距离. 考虑单光子计数率后, 可以得到安全密钥生成率为18 )式、(27 )式和(28 )式可知, 影响密钥生成率的参数主要为量子信息的传输距离L , 中继节点个数n , 噪声平均功率谱密度${\sigma ^2}$ .图15 所示. 当$ {\sigma ^2}$ 取3 dB/km, 传输距离L = 2500 km时, 密钥生成率为0.023 bit/s; 传输距离为L = 4000 km, 密钥生成率减小至0.008 bit/s, 因此当量子信息的传输距离增大时, 网络误码率增大, 从而导致安全密钥生成率逐渐减小.图 15 密钥生成率与传输距离的关系Figure15. Relationship between key generation rate and transmission distance.n 的关系如图16 所示, 随着n 的不断增大, 密钥生成率增加, 在蛛网网络拓扑结构中, 任意两个节点之间的通信路径不止一条, 迂回路由多, 可以在网络中选择合适的中继节点个数, 找到最优路径, 使得网络的密钥生成率达到最大, 网络安全性更高.图 16 密钥生成率与中继节点个数的关系Figure16. Relationship between key generation rate and number of relay nodes.6.结 论 本文利用蛛网网络拓扑构建量子卫星广域网, SNT具有高可靠性, 且N 阶量子隐形传态路由方案的传输时延小. 增加中继节点数可以有效降低网络的误码率, 增大量子卫星成功分发纠缠光子对的概率可以提升网络吞吐率, 虽然吞吐率会随着传输时延的增大而减小, 但在该路由方案下传输时延基本不变, 且SNT的传输时延小, 所以量子卫星广域网的吞吐率不会有明显的降低, 且其在一定程度上改进了信息传输的安全性. 因此采用该路由方案以及蛛网网络拓扑构建量子卫星广域网可靠性高、误码率低、吞吐率大, 这为建立全球范围的量子卫星广域网奠定了理论基础. 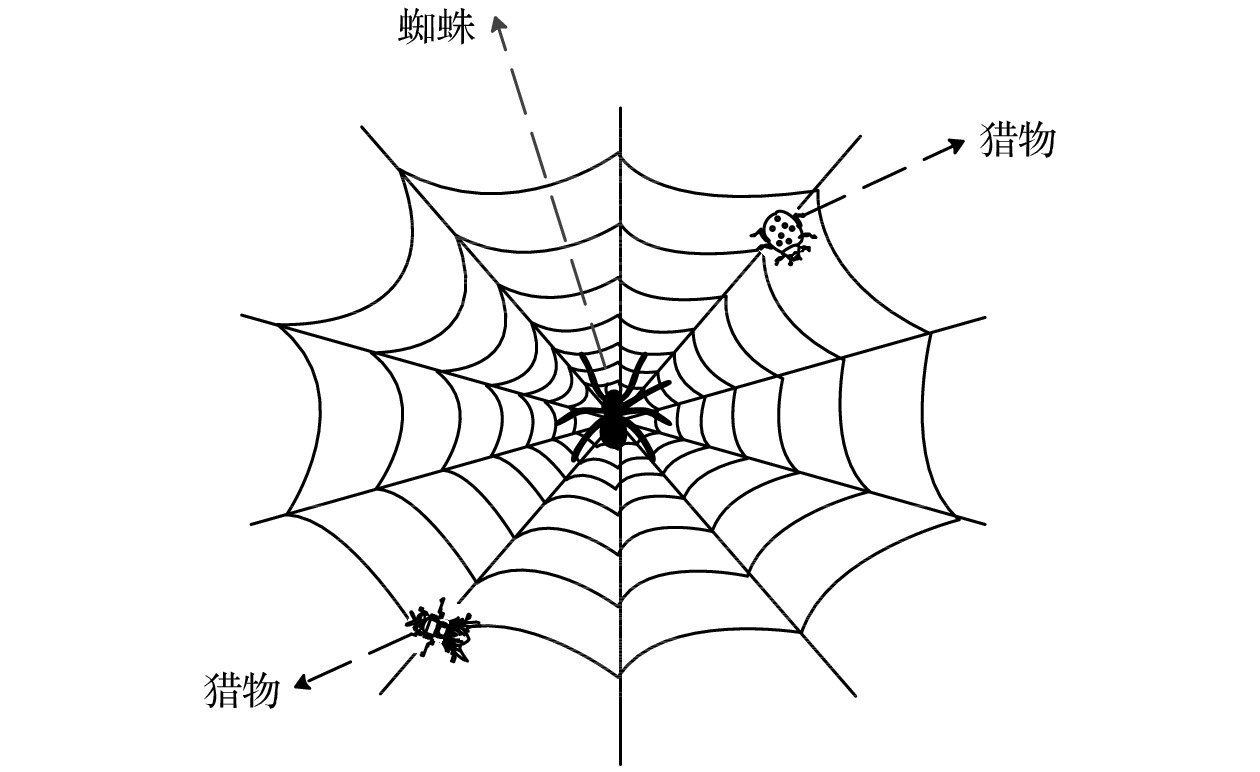 图 1 自然界圆形蜘蛛网
图 1 自然界圆形蜘蛛网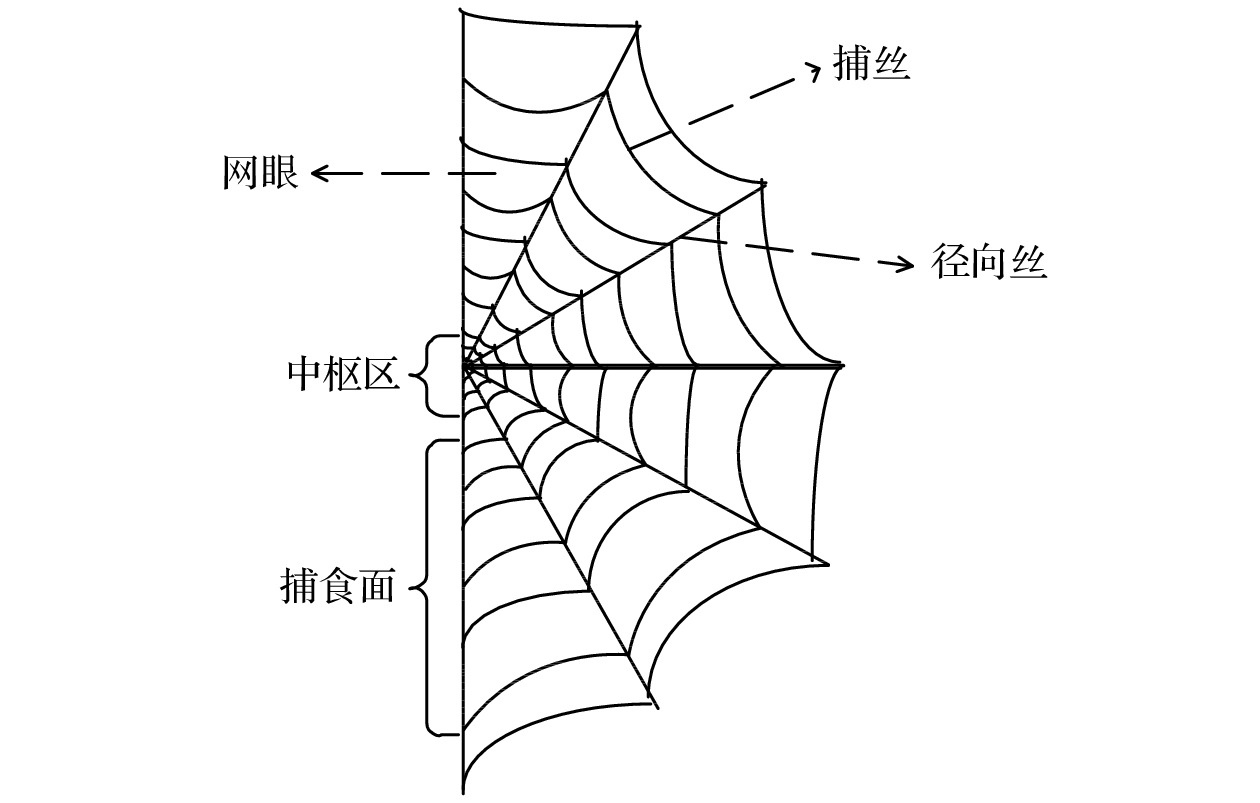 图 2 蛛网结构图
图 2 蛛网结构图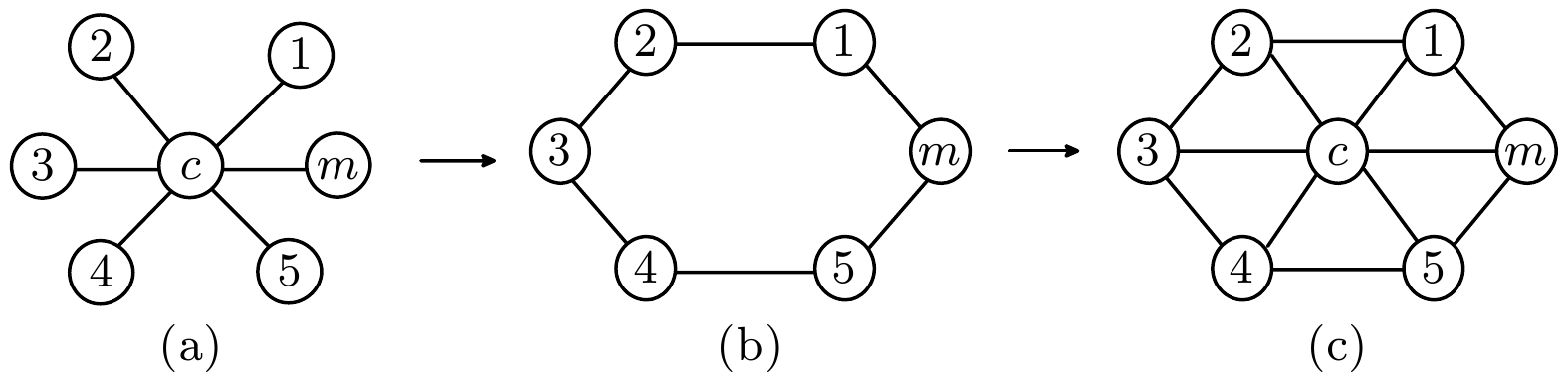 图 3 人工蛛网演进过程 (a) 星型; (b) 环型; (c) 蛛网
图 3 人工蛛网演进过程 (a) 星型; (b) 环型; (c) 蛛网






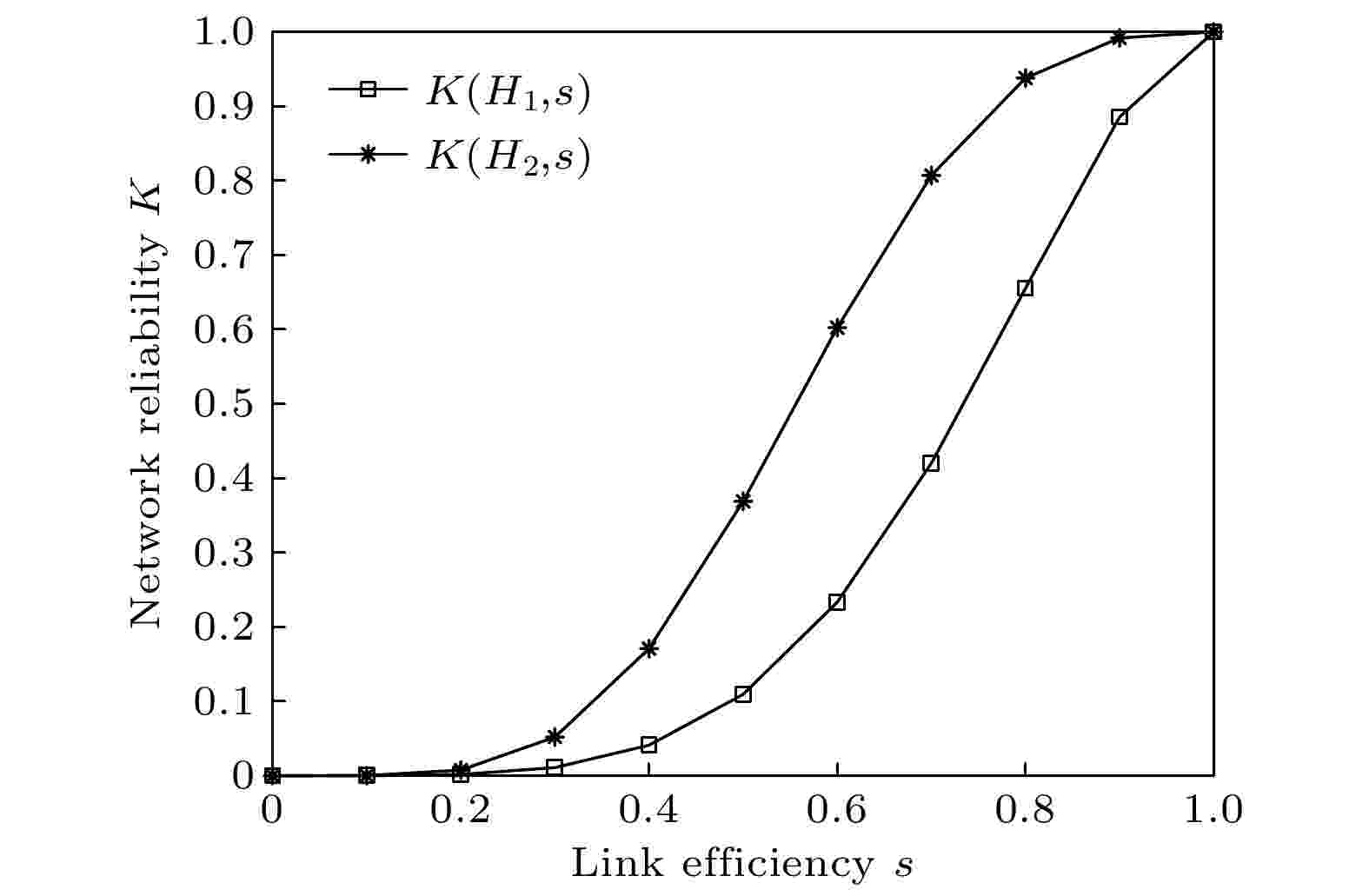 图 4 环型与蛛网拓扑的网络可靠性分析
图 4 环型与蛛网拓扑的网络可靠性分析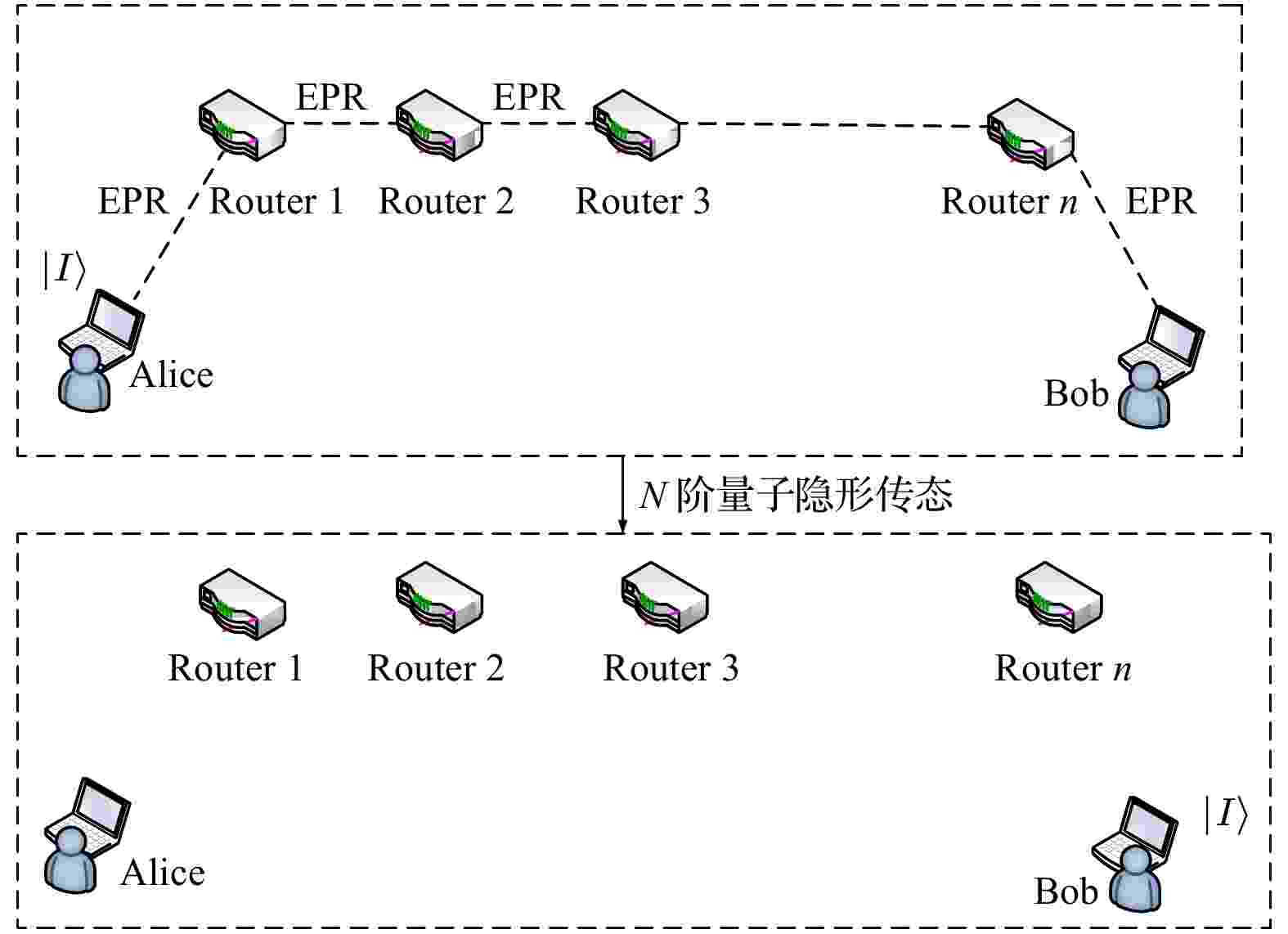 图 5 基于N阶量子隐形传态的量子路由方案
图 5 基于N阶量子隐形传态的量子路由方案 图 6 二阶量子隐形传态逻辑线路图
图 6 二阶量子隐形传态逻辑线路图



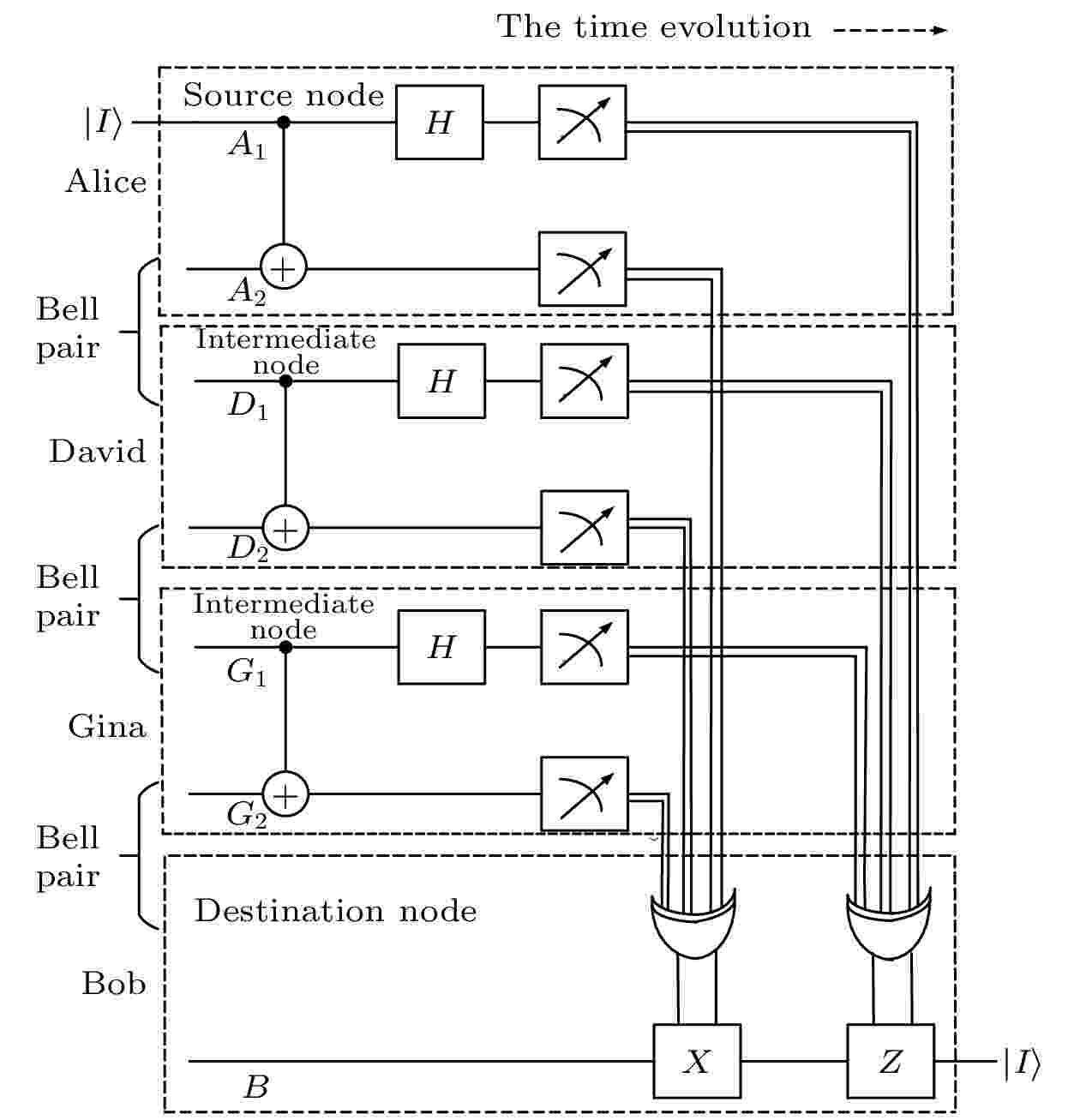 图 7 三阶量子隐形传态逻辑线路图
图 7 三阶量子隐形传态逻辑线路图







 图 8 三种路由方案量子态传输时间与中继节点个数的关系
图 8 三种路由方案量子态传输时间与中继节点个数的关系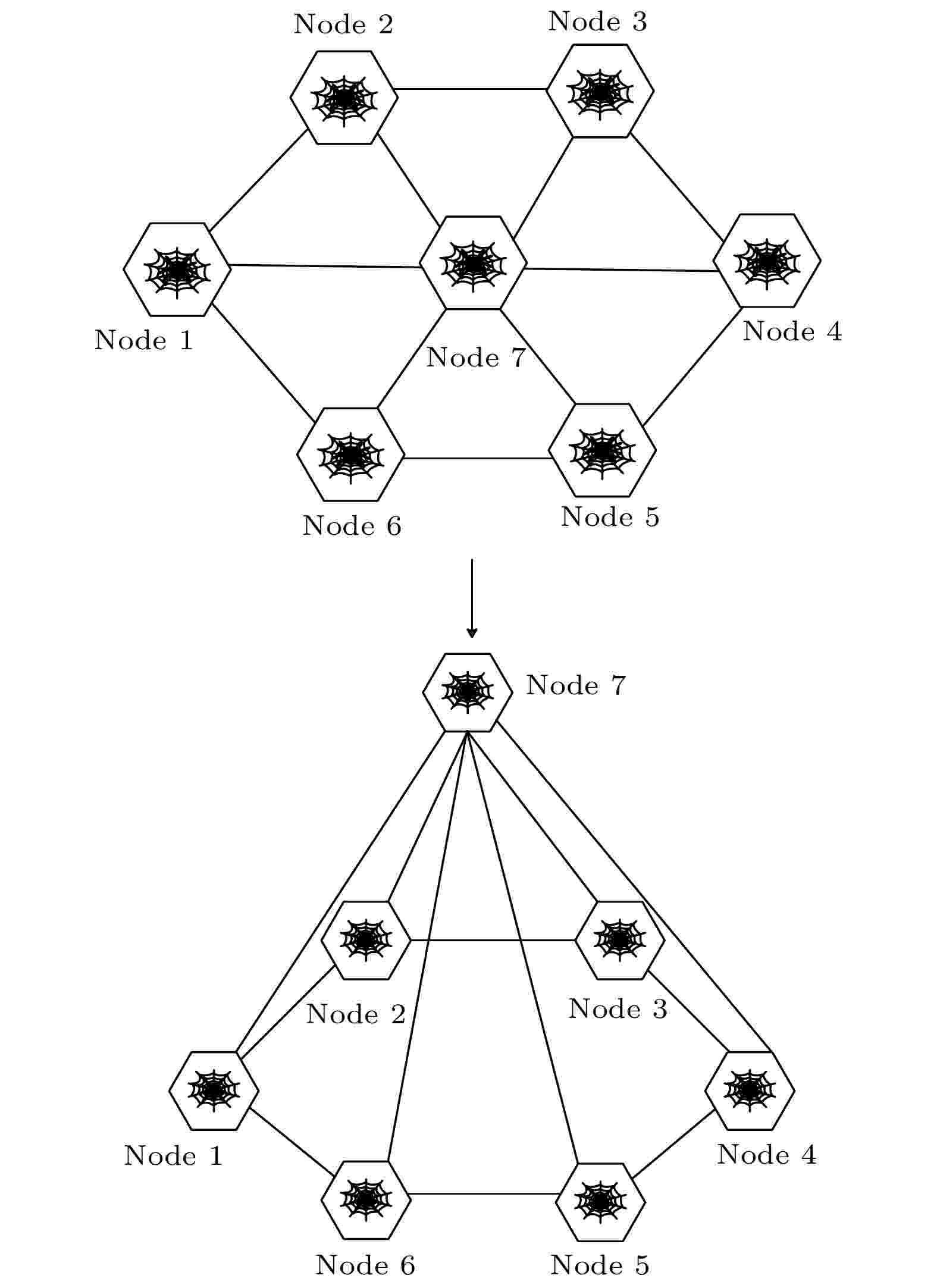 图 9 六边形逻辑蛛网拓扑模型
图 9 六边形逻辑蛛网拓扑模型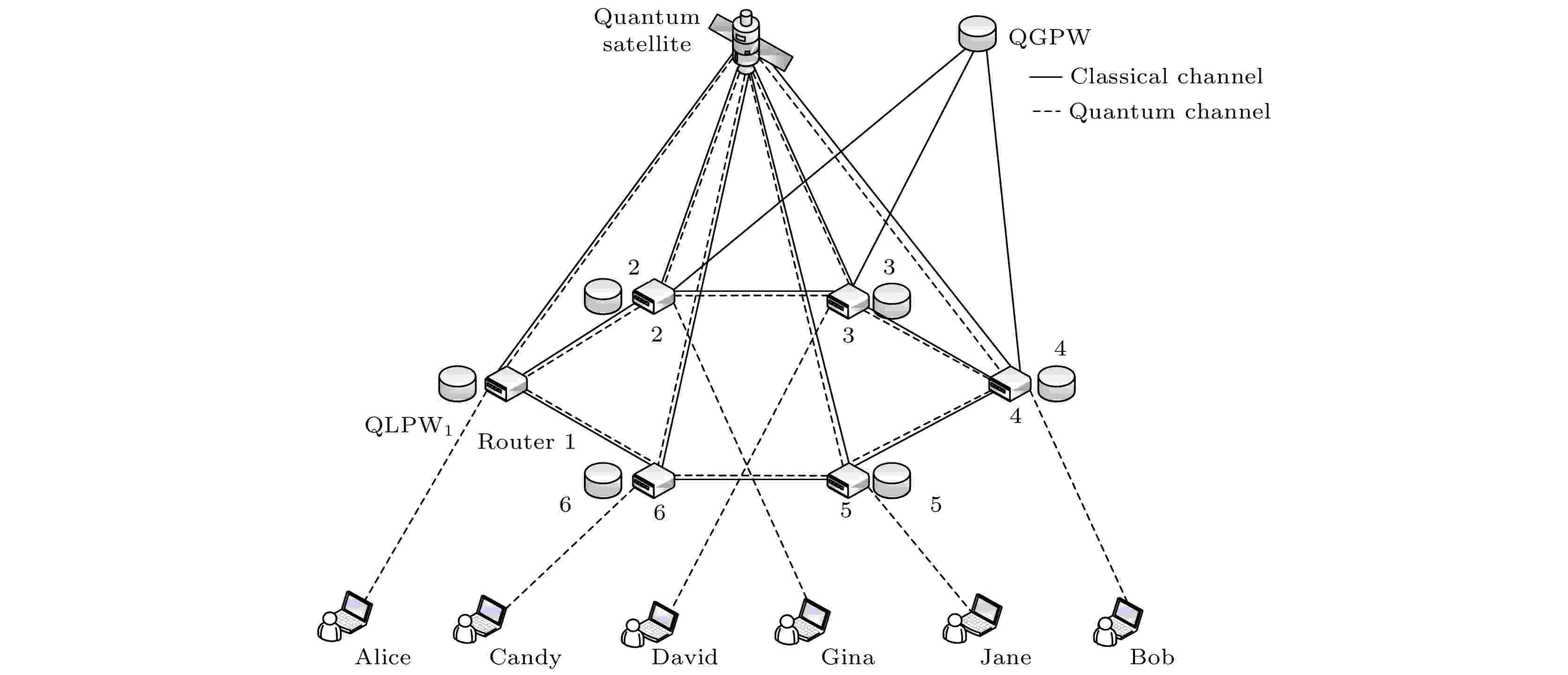 图 10 基于蛛网拓扑的量子卫星广域网
图 10 基于蛛网拓扑的量子卫星广域网







 图 11 误码率与传输距离的关系
图 11 误码率与传输距离的关系










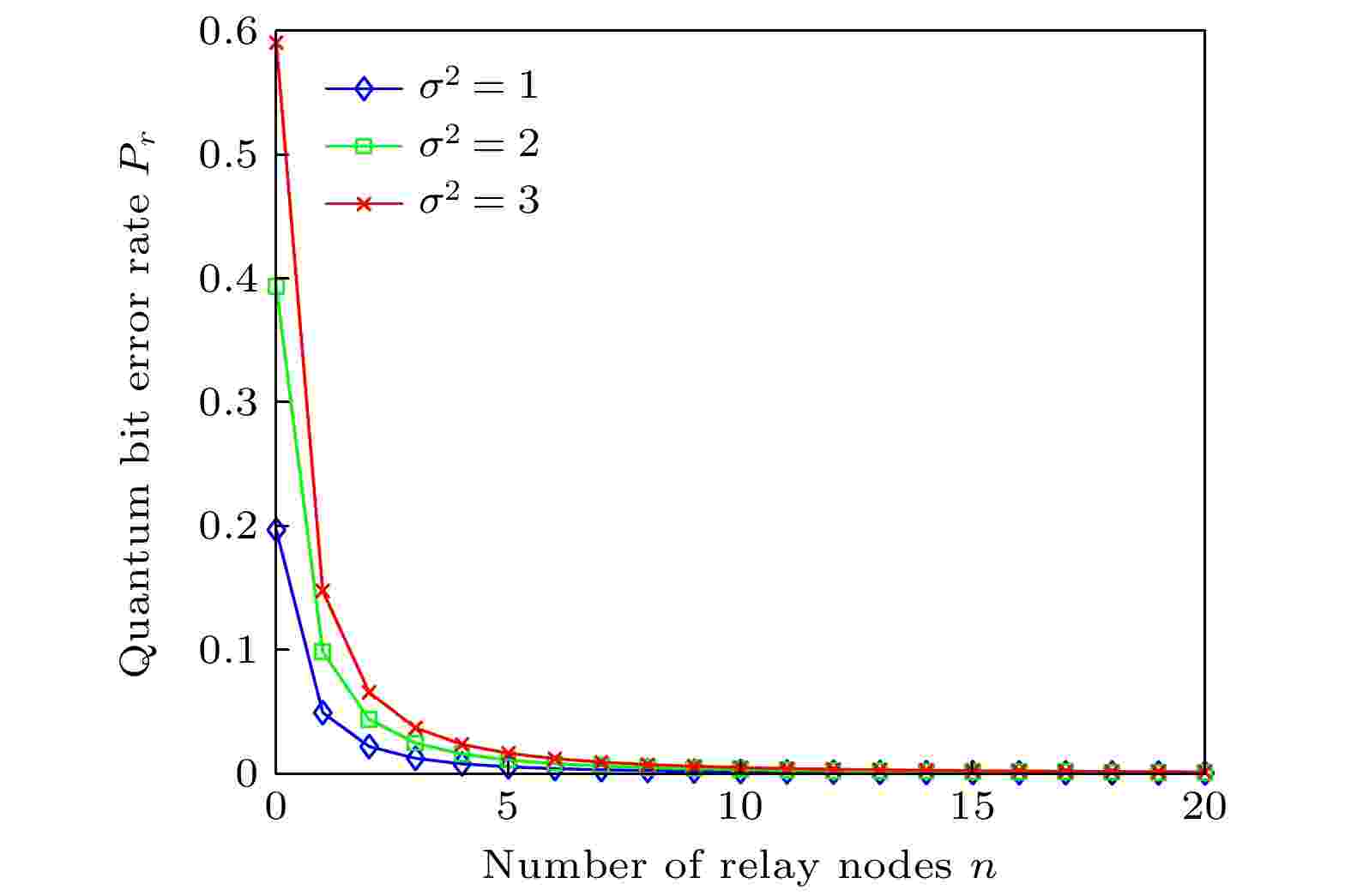 图 12 误码率与中继节点个数的关系
图 12 误码率与中继节点个数的关系












 图 13 吞吐率Q与
图 13 吞吐率Q与


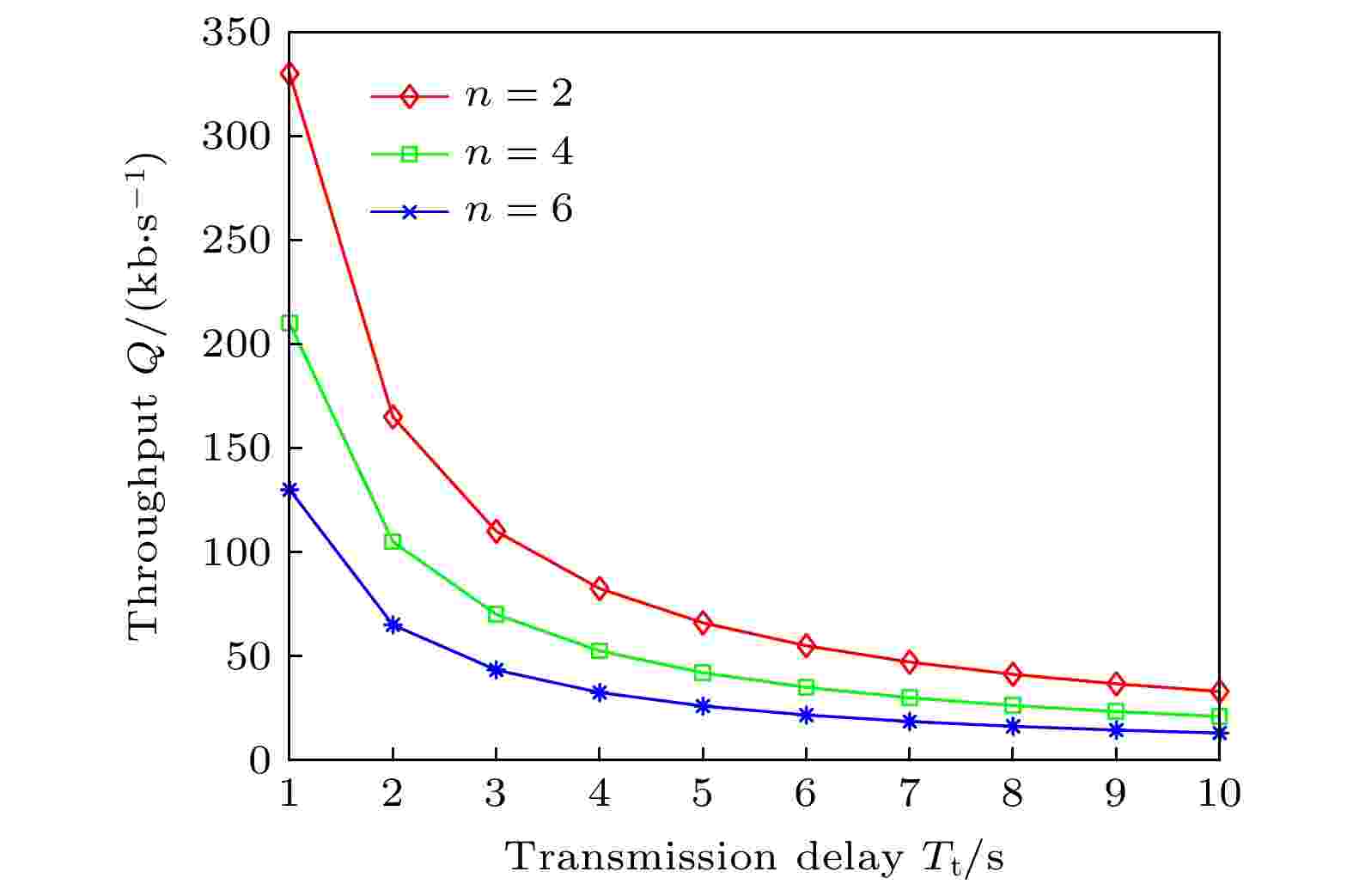 图 14 吞吐率与传输时延的关系
图 14 吞吐率与传输时延的关系






 图 15 密钥生成率与传输距离的关系
图 15 密钥生成率与传输距离的关系 图 16 密钥生成率与中继节点个数的关系
图 16 密钥生成率与中继节点个数的关系