摘要:为了研究疏水表面垂直振动液滴的运动规律, 本文建立了振动液滴的三维模型, 考虑了振动液滴的动态接触角变化过程, 通过流体体积函数和连续表面张力(volume of fluid-continue surface force, VOF-CSF)方法实现了液滴受迫振动的数值模拟, 得到了液滴的四种模态(2, 4, 6和8)动态演化过程、内部流场结构以及动态接触角的变化规律. 随着振动加速度的改变, 液滴可表现出丰富的模态, 而具体模态依赖于振动加速度的频率变化. 以此为基础, 本文对液滴的内部流场结构做了进一步的分析. 在模态2和模态4时, 液滴内部流动从底部向上产生“Y”型流动, 而在模态6和模态8时呈现对称的涡流动. 且共振模态阶数越高, 液滴内部速度平均值越大. 液滴振动时的动态接触角明显偏离静态接触角, 表明液滴振动模型有必要考虑动态接触角. 模拟结果与文献中的实验结果做了对比, 结果符合良好.
关键词: 振动液滴/
模态/
微流动/
数值模拟

English Abstract

全文HTML

--> --> -->

固着表面振动液滴在强化传热、调控蒸发自组装过程以及微流控芯片等领域中有着重要的应用^[1-7]. 早在19世纪就有****开始研究液滴的振动, Kelvin^[8]和Rayleigh^[9]对共振频率下引起无黏自由液滴的动态行为进行了研究. 1932年Lamb^[10]提出了自由液滴在不同的共振模态下的振动频率计算公式, 称为Rayleigh共振频率公式. Strani和Sabetta^[11]在不计重力的情况下, 对附着于固体表面上的非黏性液滴的轴对称振动进行了研究, 与Lamb的研究不同在于, Strani和Sabetta从理论上分析了钉扎在固体表面上的液滴振动, 发现钉扎在固体表面上的液滴的第一模态形状类似于自由液滴的第二模态形状; 研究还发现第n振动模态中的无量纲固有频率可以表示为接触半径与液滴半径之比的函数. 之后, 大量论文讨论自由液滴振动的性质, 主要探讨液滴的振动方向、共振频率、运动方向等方面的特征^[12-17].
为深入研究液滴的振动特性, 大多数文章通过实验研究液滴的振动特性. Brunet等^[14], Noblin等^[15]及Dong等^[16]对在倾斜表面、垂直及水平方向上振动的液滴运动特征进行了研究. 周建臣等^[17]实验研究了液滴在不同频率下的垂直振动特性, 研究发现液滴对外界驱动的不同响应与接触线的振荡行为、变形程度密切相关. 近些年诸多****通过实验研究自由液滴表面出现重力波的振动频率范围^[18-21]. Noblin等^[18]研究了接触角和滞后作用对液滴振动模态的影响, 实验通过改变垂直振动的频率和振幅观察到接触线固着-移动两种类型的振动模态. Shin和Lim^[19], Kim和Lim^[20]以及Park等^[21]针对疏水玻璃片上垂直振动液滴内部的流动规律进行了研究, 实验研究得到液滴垂直振动的2, 4, 6, 8四种振动模态, 在模态2和模态4下液滴内部呈现“Y”型流动, 而在模态6和模态8频率下呈现对称的涡流动, 此外通过粒子图像测速法测量(particle image velocimetry, PIV)发现模态4的流速大于模态2, 模态6和8的流速几乎相同. Ramos^[22]针对超疏水表面微液滴在不同振幅下的振动特性, 得出超疏水表面微液滴可看作自由液滴的结论. 只有少数文章通过数值模拟研究固体表面上液滴的振动问题^[23-25]. James等^[25]实现了固体表面上单个液滴在低频和小振幅垂直振动下的数值模拟, 研究发现振动导致自由液滴表面形成重力波, 当振幅高于临界值时会引发液滴破裂.
基于以上实验研究发现, 液滴内部流动具有清晰的三维特征, 并且接触角变化是关键参数之一. 目前关于液滴振动的研究主要是通过实验测定振动频率、振幅和周期等因素对液滴内部流动产生的影响^[19-21]. 而在实验研究中, 由于透镜效应, 导致无法准确测量到液滴自由界面附近边缘层的流动特征. 因此, 本文在考虑动态接触角的情况下, 建立了三维液滴振动模型, 实现了液滴在疏水表面上垂直振动的三维数值模拟, 获得了液滴在不同频率下垂直振动的四种模态, 预测了不同共振模态下液滴的内部流场结构, 有助于弥补实验测量时由于存在透镜效应而导致液滴自由界面附近边缘层流场不准确的局限性.

2

-->

2.1.物理问题及假定

当基底受到强迫振动时, 液滴随基底垂直上下振动, 当驱动加速度超过某一临界值时, 液滴的内表面和外表面由于振动的影响产生压力差, 在压力差的作用下形成表面波. 随着振动的进行, 表面波叠加形成叶瓣, 导致液滴发生形变. 液滴在上下振动时, 其内部的流动受到几何形状的限制, 在重力和黏性力的共同作用下, 形成涡流动或回流. 故在不同频率下的垂直振动, 液滴内部形成不同的流场结构.
根据已有的实验研究^[19-21]可知液滴在特定的频率下会呈现共振模态. 当液滴处于共振模态时, 表面波叠加形成叶瓣, 叶瓣与叶瓣之间会出现节点, 液滴的振动模态阶数等于节点数. 在共振模态时液滴表面形成的叶瓣是以中心线为轴对称分布, 叶瓣大小和数量相同, 所以液滴内部的微流动是轴对称的. 本文主要研究液滴在垂直振动下的2, 4, 6和8四种共振模态及其内部微流动, 故对三维液滴的振动过程做出如下假设:
1)液滴内部的流动是不可压缩的, 并且在垂直振动下是轴对称的;
2)由于液滴的振动周期远远小于同质量同体积的液滴蒸发的时间, 所以液滴振动过程不考虑自然蒸发;
3)由于本次模拟的液滴半径约为1.14 mm, 小于毛细长度${l_{\rm{c}}}$(${l_{\rm{c}}} = \sqrt {{\sigma /{({\rho _{\rm{l}}}g)}}} $, 约为2.73 mm, 其中$g$是重力加速度, ${\rho _{\rm{l}}}$是液滴密度, $\sigma $是表面张力), 相较于表面张力, 重力对液滴形状的影响可忽略不计, 因此将疏水表面上的微液滴视为球冠形.
基于以上假设, 本文采用VOF-CSF模型^[26,27]对三维液滴的振动过程进行模拟.
2 -->

2.2.VOF模型

本文模拟的液滴振动涉及气液两相和相界面的形变, 需要得到气液两相的交界面, 因此可以采用VOF模型^[26]. 设定空气为主相, 液态水为次相. 气液两相共用一套动量方程, 通过引进相体积分数这一变量, 实现对每一个计算单元相界面的追踪, 气液界面采用几何重建法处理. 模型控制方程如下.
连续性方程:

$\frac{\partial }{{\partial t}}\left( {{\alpha _{\rm{s}}}} \right) + \nabla \cdot \left( {{\alpha _{\rm{s}}}{{{v}}_{\rm{s}}}} \right) = 0, $

其中${\alpha _{\rm{s}}}$为次相体积分数; ${{{v}}_s}$为次相速度. 主相体积分数不能通过该方程求解, 主相与次相体积分数之和为1,

${\alpha _{\rm{p}}} + {\alpha _{\rm{s}}} = 1.$

动量方程:

$\begin{split}&\frac{{\partial \left( {\rho {{v}}} \right)}}{{\partial t}} + \nabla \cdot \left( {\rho {{vv}}} \right) \\=\;& - \nabla p + \nabla \left[ {\mu \left( {\nabla {{v}} + \nabla {{{v}}^{\rm{T}}}} \right)} \right]+ \rho g + F,\end{split}$

式中, $p$为静态压力; ${{v}}$是流体速度, $F$是表面张力所导致的源项; $\rho $和$\mu $分别代表平均密度和动力黏度:

$\rho = {\alpha _{\rm{s}}}{\rho _{\rm{s}}} + \left( {1 - {\alpha _{\rm{s}}}} \right){\rho _{\rm{p}}}, $

$\mu = {\alpha _{\rm{s}}}{\mu _{\rm{s}}} + \left( {1 - {\alpha _{\rm{s}}}} \right){\mu _{\rm{p}}},$

(4)式和(5)式中下标${\rm{p}}$和${\rm{s}}$分别表示主相和次相.
2 -->

2.3.连续表面张力(CSF)模型

动量方程(3)式中的表面张力$F$采用Brackbill等^[27]提出的CSF模型进行处理. CSF模型主要是将VOF计算中附加的表面张力处理为一体积力, 把该体积力作为源项加入到动量方程中. 本文模拟中只涉及水和空气相, 所以(3)式中的体积力$F$在CSF中的表达方程式如下:

$F = \sigma \dfrac{{\rho {\kappa _{\rm{s}}}\nabla {\alpha _{\rm{s}}}}}{{\dfrac{1}{2}\left( {{\rho _{\rm{p}}} + {\rho _{\rm{s}}}} \right)}},$

式中, $\sigma $为气液两相表面张力; ${\kappa _{\rm{s}}}$为次相与主相之间的界面曲率, 通过垂直于相界面的表面局部梯度计算得到:

${\kappa _{\rm{s}}} = - \left( {\nabla \cdot {{n}}} \right),$

式中, ${{n}}$为相界面单位向量, ${{n}}$通过次相体积分数梯度计算得到, 如下式所示:

${{n}} = \frac{{\nabla {\alpha _{\rm{s}}}}}{{\left|\nabla {{\alpha _{\rm{s}}}} \right|}}.$

在VOF模型中采用连续表面张力模型时需要给定壁面接触角, 用于调整壁面附近单元表面的法向, 壁面附近的实际单元的表面法向量表示为:

${{n}} = {{{n}}_w}\cos \left( \theta \right) + {{{t}}_{\rm{w}}}\sin \left( \theta \right), $

式中, ${{{n}}_w}$和${{{t}}_{\rm{w}}}$分别是壁面的单位法向量和切向量; $\theta $为接触角.
2 -->

2.4.接触角模型

(9)式取决于接触角$\theta $, Chernova等^[28]指出, 有必要考虑接触角的动态变化, 才能对液滴的内部流动进行正确的数值模拟. 根据已有的实验研究表明, 动态接触角与接触线移动速度、液体物性、静接触角等因素相关. 本文液滴在疏水表面上振动, 其接触角迟滞现象相对较小, 因此本文忽略接触角迟滞现象, 为了能够同时处理前进接触角和后退接触角, 采用Kistler经验公式^[29]来计算动态接触角:

${\theta _{\rm{D}}} = {f_{{\rm{Hoff}}}}\left[ {Ca + f_{{\rm{Hoff}}}^{ - 1}\left( {{\theta _0}} \right)} \right], $

$\begin{split}&f_{{\rm{Hoff}}}\left( x \right) =\\& \arccos \bigg\{ 1- 2\tanh \bigg[ {5.16{{\Big( {\frac{x}{{1 \!+\! 1.31{x^{0.99}}}}} \Big)}^{0.706}}} \bigg] \bigg\}, \end{split}$

$Ca = \frac{{\mu u}}{\sigma }.$

式中, ${\theta _0}$为初始接触角; ${\theta _{\rm{D}}}$为运动过程中随速度变化的接触角, $Ca$为毛细数; $u$为接触线变化速度.
2 -->

2.5.网格划分与边界条件

如图1所示, 计算区域为正方体空间, 尺寸为 3 mm × 3 mm × 3 mm, 整个计算空间可满足液滴在振动条件下的振动幅度范围和计算要求. 体积为5 $ {\text{μ}}\mathrm{L} $的液滴被布置在XY平面的中心位置上, XY平面是接触角为$115^\circ $的疏水表面, 周围是空气, 其他边界均设置为壁面边界. 网格划分采用非结构化六面体网格, 为了选取合适的最小的计算单元, 尝试不同大小的网格尺寸, 分别用0.02, 0.03, 0.04和0.05 mm的网格尺寸对液滴进行了模拟, 模拟得到的液滴形态和内部流动情况偏差较小, 因此选用网格尺寸为0.04 mm, 既能达到模拟精度, 又可节约计算时间.
图 1 三维模拟计算区域(3 mm × 3 mm × 3 mm)
Figure1. 3D computational domain (3 mm × 3 mm × 3 mm).

底面采用无滑移边界条件, 即液滴和底面接触处的流体速度等于底面的速度. 计算工质为空气和水, 空气为主相, 液态水为次相, 通过改变振动加速度函数的共振频率, 研究不同共振频率对液滴形态变化和内部流动规律的影响. 在基板上施加一个振动加速度, 使液滴做垂直振动:

$a = - {\left( {2{\rm{\pi }}f} \right)^2}A\cos \left( {2{\rm{\pi }}ft} \right), $

其中$a$为振动加速度; f表示液滴的共振频率; $A$为振幅, 模态2, 4, 6和8的振幅$A$分别为0.022, 0.046, 0.013和0.0035 mm.
Lamb^[10]总结出自由微液滴共振模态下的不同共振频率计算公式, 称为Rayleigh共振频率, 表示为

$f = \sqrt {\frac{{n(n - 1)(n + 2)\sigma }}{{3{\rm{\pi }}\rho V}}}, $

其中f表示液滴的共振频率; V, $\rho $和$\sigma $分别指液滴的体积、密度和表面张力; n是不小于2的整数, 表示模态数. 将液滴参数($\rho $= 998 kg/m³, V = 5 $\mathrm{μ}\mathrm{L}$, $\sigma $= 0.0728 N/m)代入(14)式, 计算得到模态2, 4, 6和8的共振频率. 见表1可知, 由Rayleigh方程计算所得的共振频率与实验所得的共振频率较为接近.

Mode n	Rayleigh方程 计算值 f/Hz	共振频率 实验值 f/Hz
2	96	85
4	288	226
6	526	469
8	804	635

表1共振频率的理论值和实验值对比
Table1.Comparisons of theoretical and experimental results for resonance frequency of a 5 ${\text{μ}}\mathrm{L}$ droplet.

2

-->

3.1.振动模态

图2是体积为5${\text{μ}}\mathrm{L}$的液滴放置在水平的115°疏水表面上, 模拟的垂直振动下液滴的四种模态形貌与实验结果^[20]的对比图. 图2(a)是液滴在疏水表面上的共振模态实验结果, 图2(b)是液滴共振模态的模拟结果, 模拟所用共振频率为表1中Rayleigh方程计算值. 由图可知, 模拟所得的液滴模态与实验结果符合较好, 这验证了数学模型的可靠性. 根据前文所提, 因振动形成的波会在液滴表面叠加形成叶瓣, 且共振模态阶数即为节点数. 图2中为了正确识别叶瓣, 叶瓣节点处以箭头突出显示. 如图2所示液滴在四种共振模态中呈现出丰富的形态变化, 表面形成的叶瓣数目和节点数也有所不同. 图2中表明叶瓣数目随着共振模态阶数的增加而增加, 叶瓣尺寸却随之减小. 因此, 当液滴处于模态8时, 由于叶瓣数目较多而叶瓣又较小导致识别困难. 结果表明, 模拟得到的液滴模态与实验中的液滴模态吻合良好.
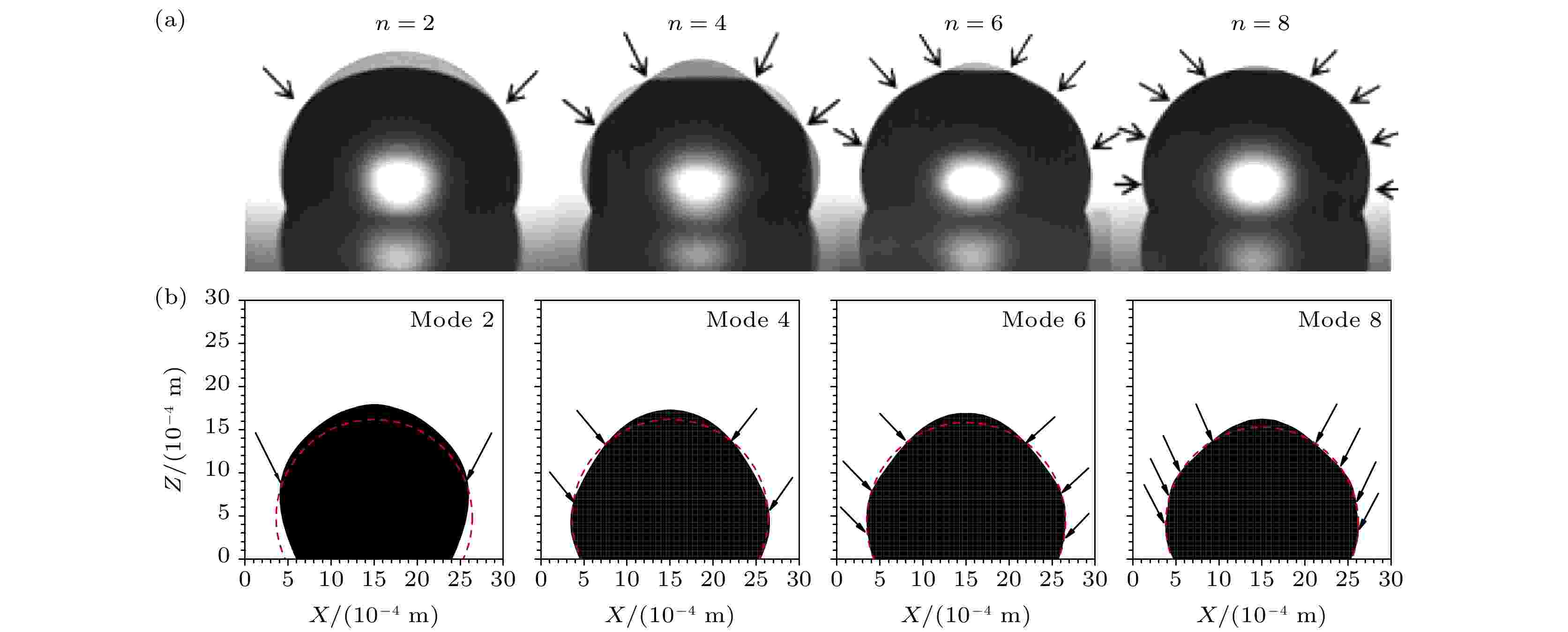图 2 疏水表面上液滴共振模态(2, 4, 6和8)的模拟结果与实验结果对比　(a)实验结果^[20]; (b) 模拟结果
Figure2. Comparisons of the resonance modes (2, 4, 6, and 8) of a vibrating water drop on a hydrophobic surface: (a) Experimental results^[20]; (b) simulation results.

2 -->

3.2.液滴振动模态的动态演化过程

图3是模拟的液滴分别在2, 4, 6和8模态一个周期内的形状变化与实验结果^[21]的对比图. 由图3可知, 模拟所得到的液滴形态的变化与实验结果符合较好. 随着共振模态阶数的增加, 液滴的振动周期越来越短, 约为12.4, 4.0, 2.0和1.2 ms. 这一现象与共振频率以及振动幅度大小有关, 模态阶数越高, 共振频率越大, 振动周期越短. 前一个周期的最后相位与后一周期的第一相位重合. 如图3所示, 液滴在模态6和8中形貌变化更丰富, 在模态2和4中则变化的相对简单. 因为在高阶模态中, 共振频率较大, 液滴表面形成的波不断叠加形成的叶瓣数更多, 导致模态6和8中的液滴呈现更丰富的形貌变化.


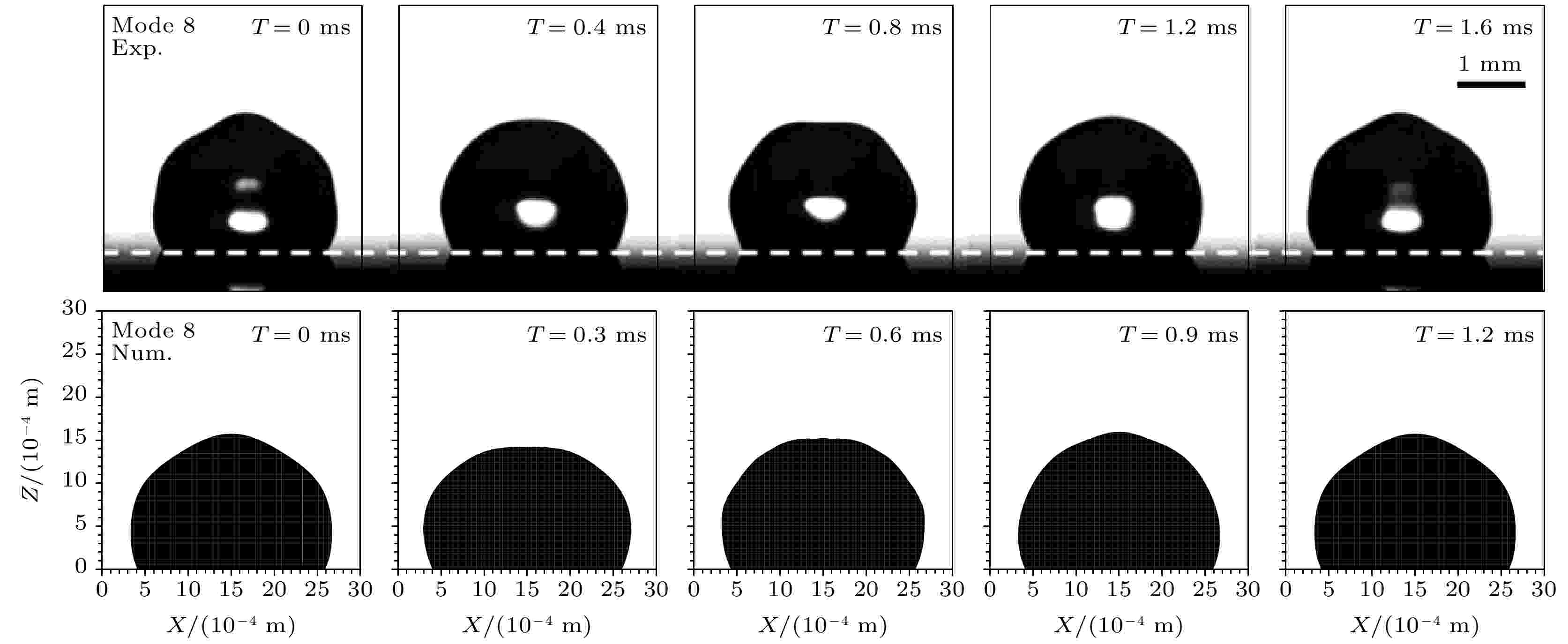图 3 液滴在2, 4, 6和8共振模态下一个振动周期内形貌变化的实验^[21]与模拟结果对比
Figure3. Comparisons between the experimental^[21] and simulation results of the droplet shape evolution during one cycle of the vibration at resonance modes 2, 4, 6 and 8.

2 -->

3.3.液滴振动过程的内部流场结构

目前关于液滴垂直振动的研究主要是通过实验测定液滴振动周期、形状、内部流动方式, 由于实验测量时存在透镜效应, 导致无法准确测量液滴自由界面附近边缘层的流动特征. 为了进一步了解液滴垂直振动时的运动规律, 模拟三维液滴在共振模态2, 4, 6和8下的运动情况, 获得液滴内部的流场结构.
图4是液滴在模态2, 4, 6和8下内部流场的三维视图, 可以看出在每种模态下, 液滴内部的微流动都呈现轴对称的涡流动. 液滴在模态2和4下, 液滴中心流动向上呈现“Y”型, 周围伴随着涡流动; 而在模态6和8时, 液滴中心流动向上到达液滴顶部, 周围同样伴随着涡流动. 为了进一步了解液滴内部的流场结构, 在图5中对液滴内部的二维剖面进行分析并与实验结果对比. 图5是2, 4, 6和8模态下液滴内部的速度场模拟结果与实验结果^[20]对比, 左侧是液滴内部流动的可视化实验结果, 右侧是模拟的液滴内部速度流线图. 随着模态阶数的增加, 多样化的流动模式得到了体现.
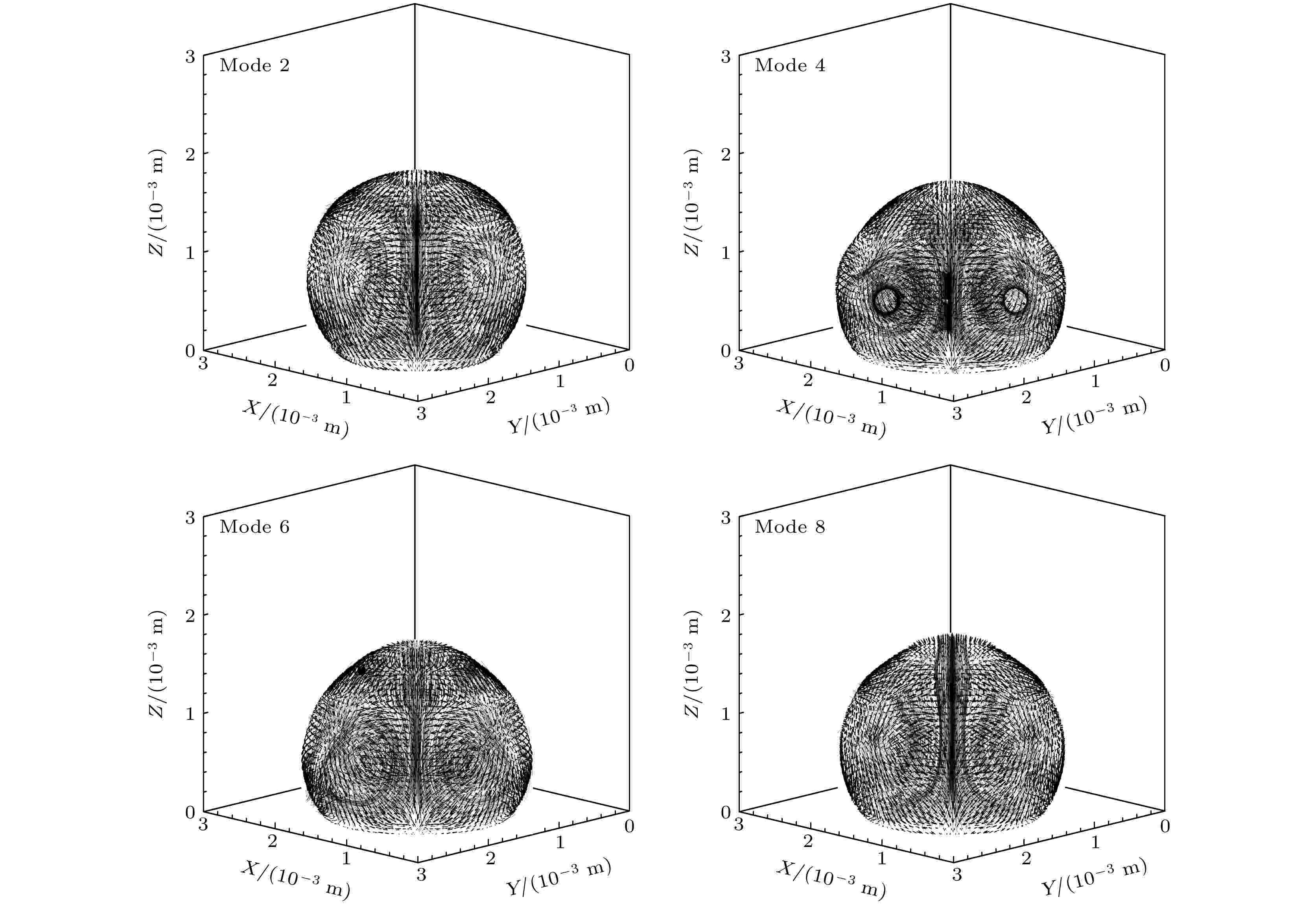图 4 在2, 4, 6和8模态下液滴内部的三维流场图
Figure4. The three-dimensional flow field inside the droplet at modes 2, 4, 6, and 8.

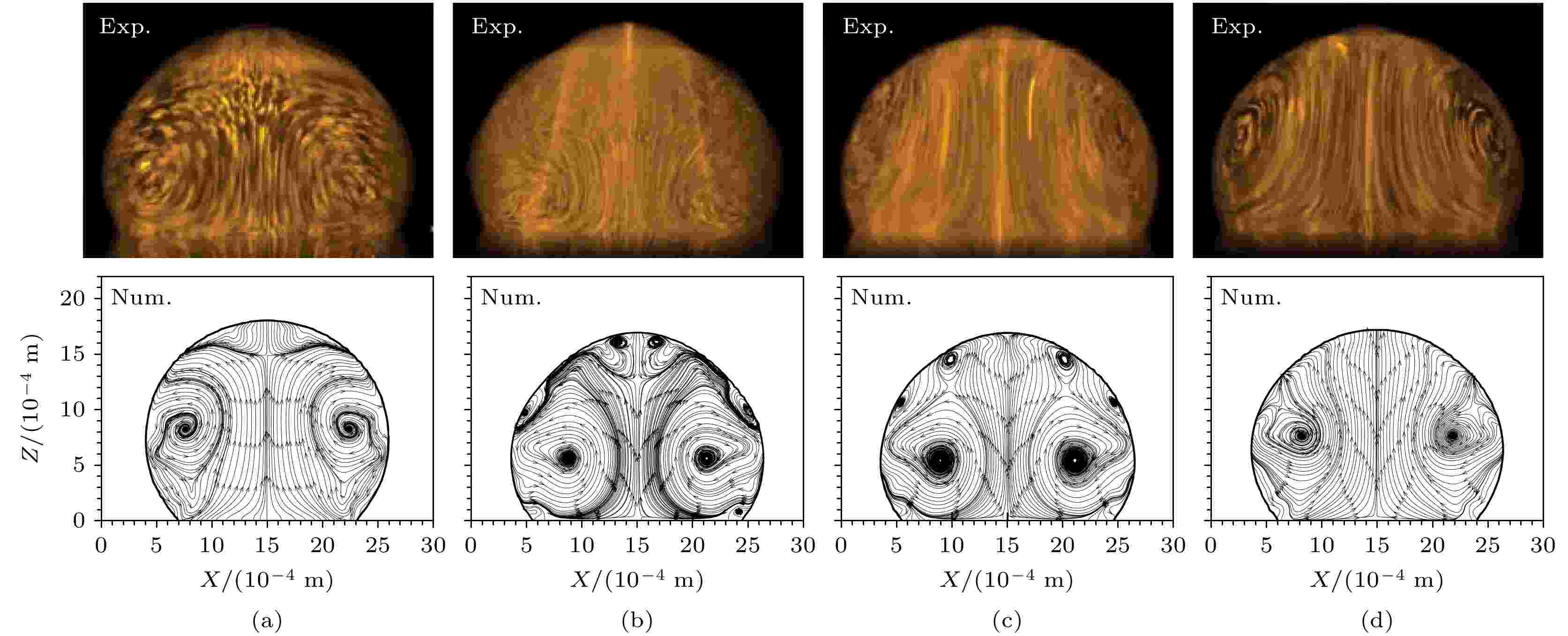图 5 液滴在2, 4, 6和8共振模态下内部流动结构的实验^[20]与模拟结果对比　(a) 模态2; (b) 模态4; (c) 模态6; (d) 模态8
Figure5. Comparisons between the experimental^[20]and simulation results of the internal flow structure of the droplet during the vibration at modes 2, 4, 6 and 8: (a) Mode 2; (b) mode 4; (c) mode 6; (d) mode 2.

图5(a)是液滴在模态2振动时内部的速度场模拟结果. 液滴在振动开始时, 底端的流体受力向上流动, 顶端流体则因为重力影响向下流动, 并在液滴上部形成对称的回流. 随着振动时间的增加, 液滴的主体流动由中间向上, 经过液滴上侧叶瓣叠加的节点处, 再沿着液滴表面回到三相接触线上, 同时在重力和黏性力的共同作用下, 在液滴中心轴两侧形成对称的涡流动. 图5(b)显示了模态4的内部流场, 与模态2流动方式类似, 内部流动皆是自底部中心向上的循环流动, 最后返回液滴的中心. 模态4中的流型更长, 且产生的循环流动位置和大小与模态2不一样, 在液滴上部会形成一个涡环. 故液滴在模态2和模态4中内部流动都呈现“Y”型流动.
图5(c),(d)分别是模态6和模态8的内部流动情况. 如图所示, 与模态2和模态4的流型不同, 以液滴中心线为轴形成两个大尺寸的涡流动, 并且在模态6时, 液滴边缘处出现涡流动, 而在模态8时, 液滴边缘处则没有出现涡流动. 出现这种情况的原因是液滴在模态8时表面形成的叶瓣较多且较小, 几何空间不足以诱导形成回流. 因此, 在模态6和模态8中液滴的内部流动循环变大形成对称的涡流动而不是“Y”型流动.
为了进一步探究液滴的内部流动规律, 对液滴中心底部的垂直速度进行了计算. 在实验测量时, 由于存在透镜效应, 通常是选取某一特定区域测量速度值, 无法准确测量液滴内部完整区域的速度值^[20,21]. 为了与实验测量速度值对比, 选取了同样区域计算了液滴的平均垂直速度, 表2为液滴在四种共振模态下周期内的垂直速度平均值的实验值^[20]与模拟计算值. 从表2中可以看出, 模拟值与实验值呈现同样的趋势, 在模态4时液滴速度平均值约为模态2速度值的两倍; 而模态6和模态8的速度差值不大. 模拟结果与实验结果数值上存在一定的差距. 从速度大小和量级上来看, 模拟的液滴速度应该小于或接近基板速度. 通过估算基板速度发现模拟得到的液滴局部区域平均速度值和基板速度值接近, 因此理论上模拟结果是准确的. 实验和模拟数据之间的差异可能主要是实验条件和测量误差导致.

模态	模拟速度值/(mm·s–1)	实验速度值/(mm·s–1)
2	1.76	0.36
4	3.37	0.79
6	10.43	3.87
8	11.05	3.61

表2液滴在模态2, 4, 6和8下中心底部的平均垂直速度的实验^[20]与模拟对比
Table2.Comparisons between the experimental^[20] and simulation results of averaged vertical velocity at the central bottom region of the droplet in modes 2, 4, 6, and 8.

图6为液滴完整区域在2, 4, 6和8模态下的平均速度随时间的变化曲线图. 从图6中可以看出, 四种模态下的液滴平均速度皆呈现正弦波动变化趋势, 且平均速度的峰值按模态阶数的高低排序, 在模态8时的液滴平均速度峰值达到最大. 在模态2时由于振动频率较低, 液滴内部速度变化趋于平缓, 而其他高频模态下液滴速度波动较大.
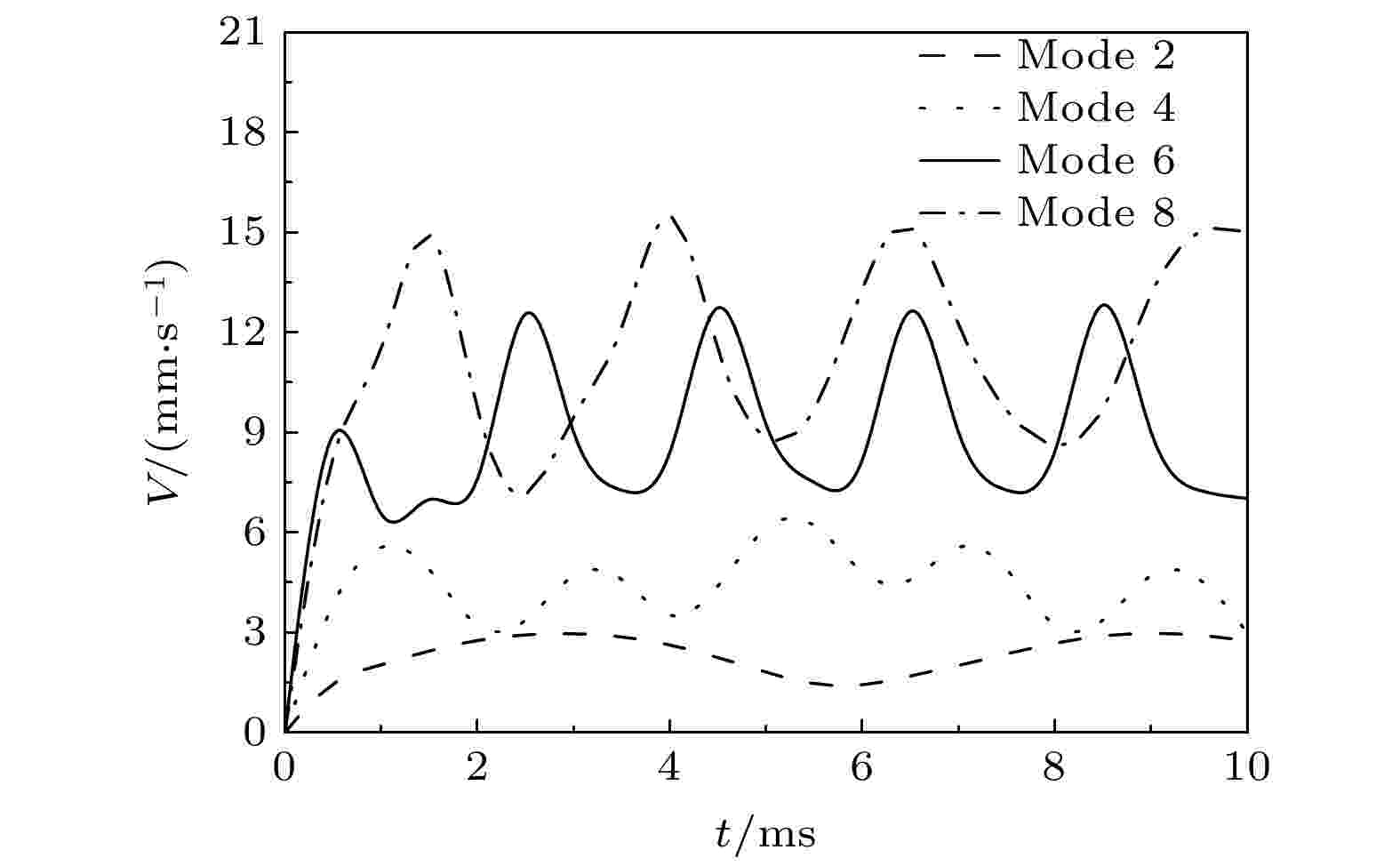图 6 在2, 4, 6和8共振模态下液滴内部平均速度随时间的变化
Figure6. The variations of the velocity with time at modes 2, 4, 6, and 8.

2 -->

3.4.液滴振动过程中动态接触角的变化

液滴在随基板垂直振动过程中, 由于接触角的变化量不为零, 因此有必要考虑接触角变化对液滴振动形态演变的影响. 如图7所示, 考虑动态接触角模拟得到的模态2液滴振动幅值随时间变化曲线(Num.1)和考虑静态接触角模拟得到的模态2液滴振动幅值曲线(Num.2)具有相似的趋势, 但在峰值上有一定的差异, 曲线(Num.1)和实验测得的幅值变化曲线(Exp.)更为接近. 不考虑动态接触角就会导致模拟的液滴高度偏低, 从而影响准确模拟液滴形态演化. 所以, 模拟中考虑了动态接触角的影响.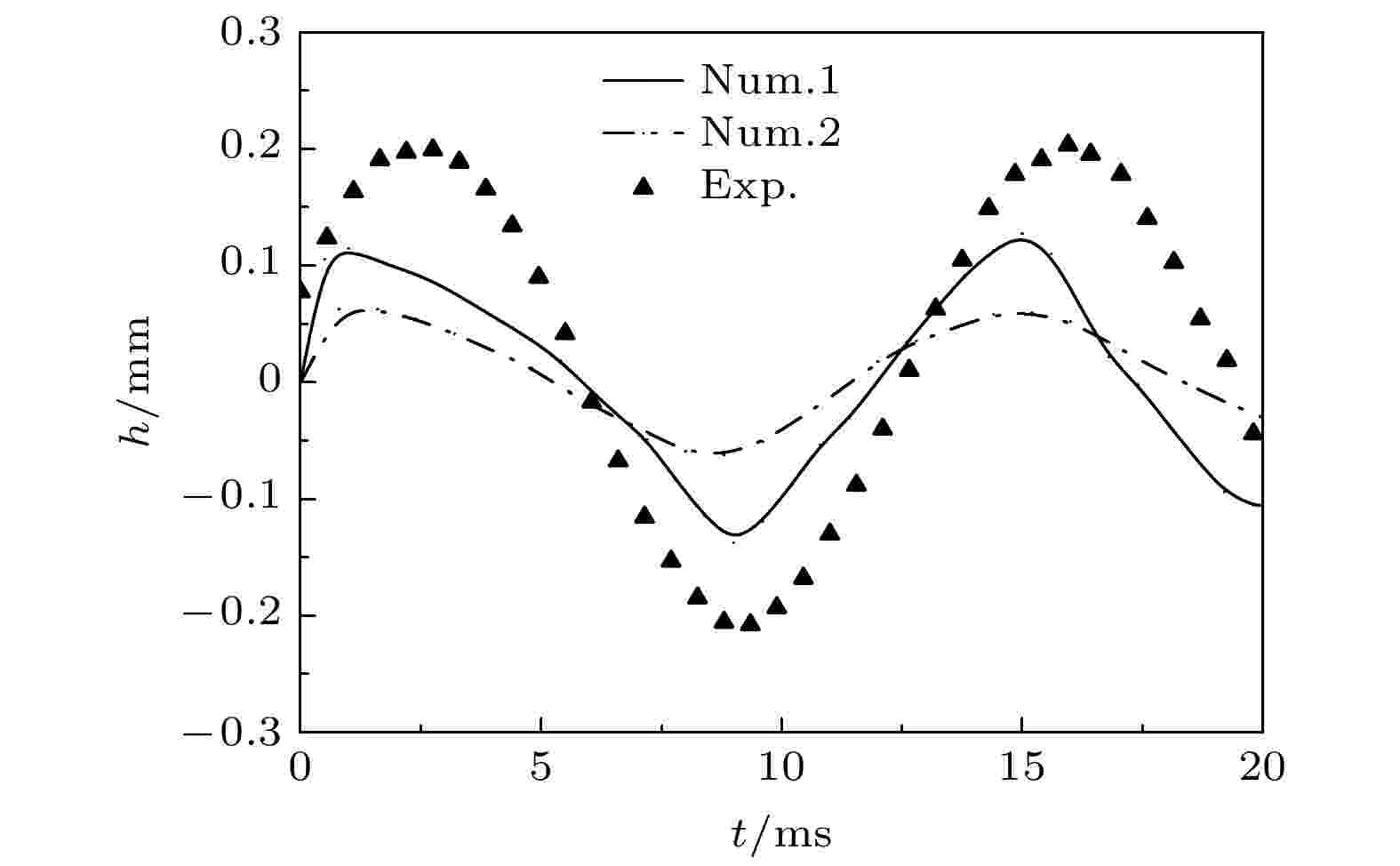
图 7 在模态2时液滴振动幅值随时间的变化. Num.1: 动态接触角; Num.2: 静态接触角; Exp.: 实验^[20]
Figure7. The variations of droplet vibration amplitude with time at mode 2. Num.1: dynamic wetting angle; Num.2: static contact angle; Exp.: experiment^[20].

图8给出了在4种模态下液滴的动态接触角随时间的变化规律. 从图8中可以看到, 在四种不同模态下, 液滴的动态接触角都是以先增大到波峰再减小到波谷这样的趋势变化. 当施加振动加速度后, 液滴的接触线受振动作用, 液滴从接触线附近开始加速运动, 动态接触角开始增大, 此时动态接触角大于静态接触角为前进接触角. 随着振动持续液滴表面形成波瓣导致液滴变形, 液滴边缘的压力逐渐增大, 并且受到黏性阻力和毛细力的阻碍作用, 液滴的运动开始减速, 前进接触角开始减小, 造成接触线停止前进运动, 此时动态接触角接近于静态接触角115°. 由于液滴边缘积累了一定的压力, 在这个压力的作用下, 液滴开始做回复运动, 并造成接触线的加速后退, 动态接触角变小, 此时动态接触角小于静态接触角115°为后退接触角; 随着回复运动的进行, 液滴边缘压力变小, 接触线的后退开始减速, 后退接触角增大直至接近静态接触角. 随着液滴振动的进行, 接触线的前进与后退运动重复之前的变化规律, 动态接触角也随之变化.
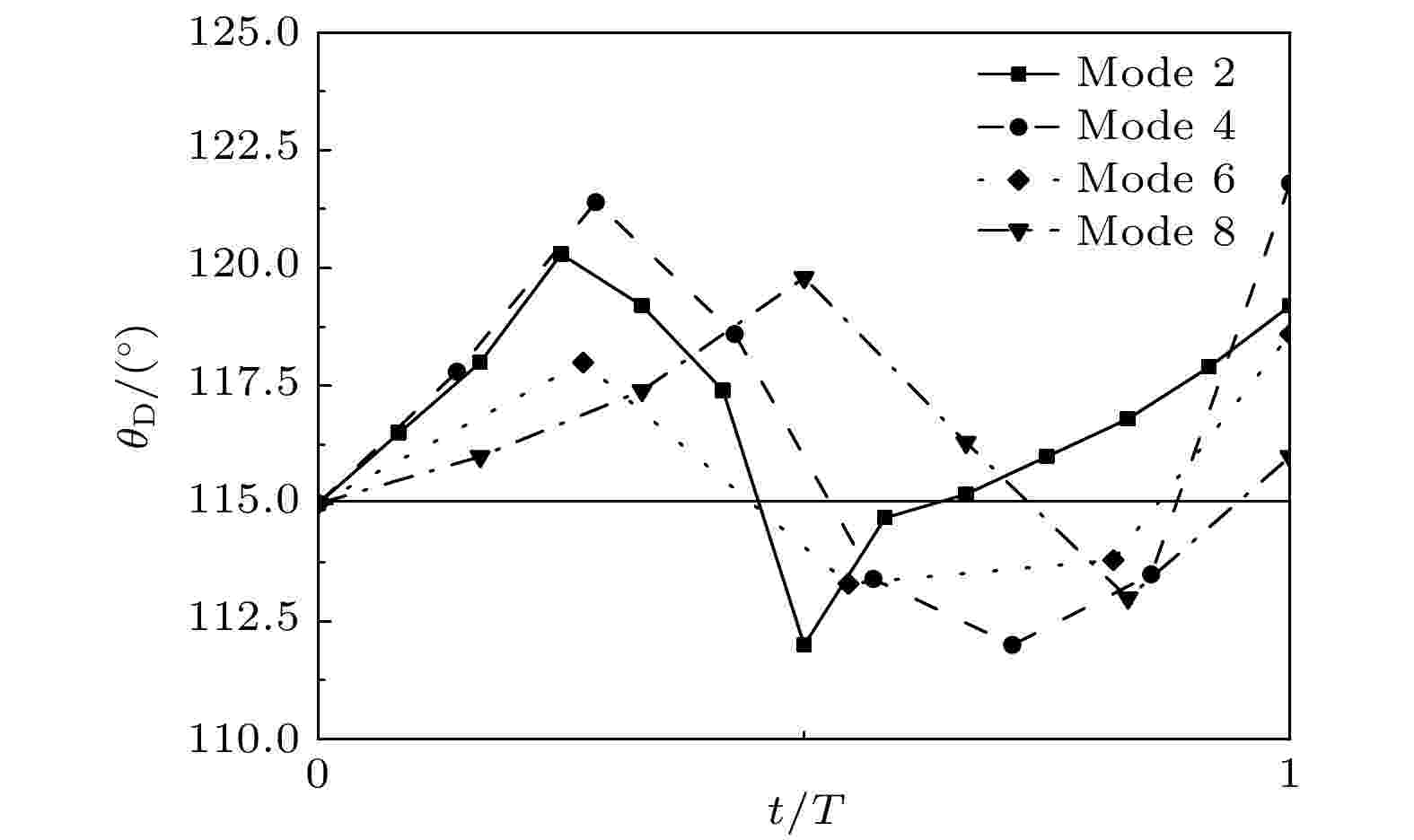图 8 在2, 4, 6和8共振模态下液滴动态接触角随时间的变化
Figure8. The variations of the dynamic contact angle with time at modes 2, 4, 6, and 8.

从图8中还可以看到, 在前进接触角阶段, 接触线的运动速度比较大, 因此动态接触角偏离静态接触角比较多. 在本文的计算条件下, 最大接触角偏离静态接触角接近6°. 综合图7和图8结果, 考虑动态接触角对于准确模拟液滴形态演化尤为重要.
2 -->

3.5.液滴振动过程中润湿面积的变化

液滴在振动过程中会经历铺展和收缩两个过程, 图9为振动周期内液滴润湿面积在2, 4, 6和8共振模态下的变化曲线, 润湿面积皆呈现正弦波动变化趋势, 液滴初始润湿面积约为3.4 mm². 从图9中可以看出, 振动开始时, 液滴的润湿面积逐渐增大, 在大约$\dfrac{1}{4}$T时液滴的润湿面积达到最大值(波峰), 但是接触线并没有停止运动, 而是开始收缩, 润湿面积开始缩小; 在大约$\dfrac{3}{4}$T时, 液滴的润湿面积达到最小值(波谷), 此时接触线速度接近于零, 再之后润湿面积又开始增大重复之前的铺展和收缩运动.
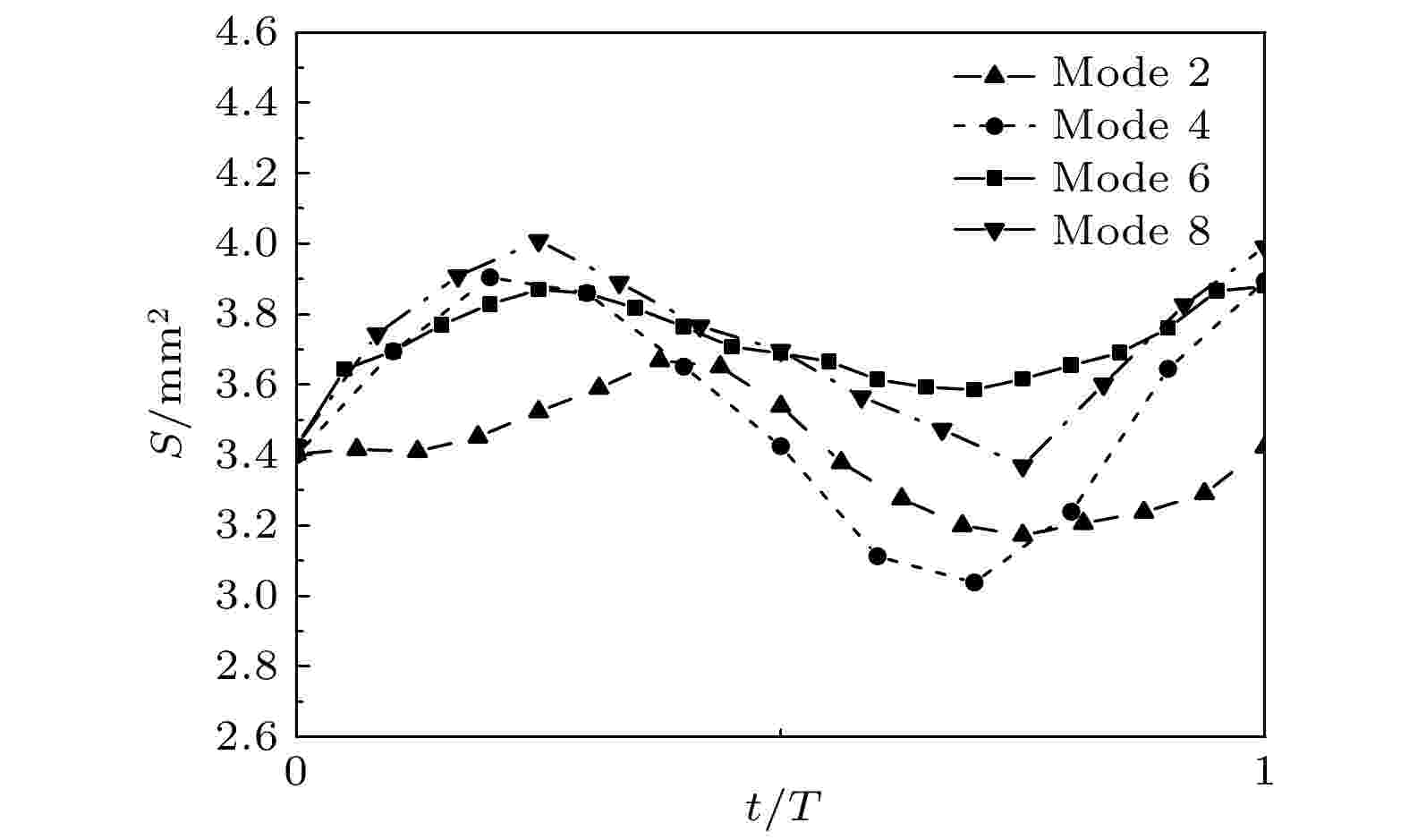图 9 在2, 4, 6和8共振模态下液滴润湿面积随时间的变化
Figure9. The variations of the wetting area with time at modes 2, 4, 6, and 8.

本文依据液滴共振频率与模态的关系以及运动液滴的动态接触角模型, 实现了在115°疏水表面上施加强制性振动时, 放置在疏水性表面上的液滴的不同共振模态(2, 4, 6和8)形状和液滴内部的流动方式的模拟. 结果表明, 模拟所得115°疏水表面上液滴振动的模态与实验结果符合良好. 主要得出以下结论.
1) 液滴在特定的频率下发生共振并且呈现特殊的模态形状, 较高的共振模态阶数有更多的节点叶瓣. 随着模态数的增加, 液滴表面形成的叶瓣数目增加, 尺寸逐渐减小. 在四种共振模态下, 模态阶数越高, 共振频率越大, 周期越短.
2) 在所有模态中, 液滴的内部流动方式呈现轴对称的. 在模态2和模态4时, 内部流动从液滴底部中心开始, 经过液滴上侧叶瓣叠加的节点处, 呈现“Y”型流动方式; 在模态6和模态8中, 液滴内部流动呈现对称的涡流动方式. 且共振模态阶数越高, 液滴内部速度平均值越大.
3) 动态接触角对液滴振动幅值变化有一定的影响, 且动态接触角明显偏离静态接触角, 表明考虑动态接触角对取得正确数值模拟结果的必要性.