摘要:离子引出是激光法分离同位素技术中的关键环节之一, 对产品丰度和产率有重要的影响, 而离子引出中离子和原子间的共振电荷转移过程则会对产品丰度造成污染, 因此在研究离子引出过程时应考虑共振电荷转移的影响. 本文利用粒子模拟(PIC)法以及基于PIC法和杂化PIC法的混合算法研究了考虑共振电荷转移的电场法离子引出过程, 通过对一维平行板法的引出方式进行数值计算, 获得了离子引出过程中共振电荷转移的基本性质和关键影响因素—共振电荷转移截面、引出时间、背景原子密度和蒸气宽度, 并据此得到了离子发生共振电荷转移比例的经验公式; 二维工况下的平行板法、交替偏压法、Π型电场法和M型电场法四种引出方式的计算结果则表明, 在其他条件相同的情况下, M型电场法具有最小的离子引出时间和共振电荷转移损失比例. 本文的研究结论对于指导激光法分离同位素技术中离子引出装置设计和实验工艺设计具有比较重要的参考意义.
关键词: 共振电荷转移/
particle-in-cell法/
鞘层/
屏蔽层

English Abstract

全文HTML

--> --> -->

离子引出过程是激光法分离同位素技术(laser isotope separation, LIS)的核心环节之一, 由光电离产生的离子的引出率直接关系到最终产品的产率, 同时离子引出过程中的各种碰撞过程则会对产品的产率和丰度组成造成影响^[1]. 其中, 关于离子引出率的研究结论已经比较明确, 之前的****通过理论和实验的手段获得了诸多影响离子引出率的关键因素^[2-9]: 引出电压、等离子体密度、等离子体尺寸、电子温度、磁场^[10-14]等等. 但是关于其中碰撞过程的研究则相对较少, 研究结论也有较大的差异^[15,16], 因此考虑碰撞的离子引出过程还有待进一步的研究.
离子引出过程中主要存在以下碰撞过程: 光电离生成的离子和未电离原子间的碰撞(共振电荷转移过程)、电子与未电离原子间的碰撞(二次电离过程)、光电离生成的电子与离子的碰撞(复合过程). 其中复合过程会使精料量下降, 共振电荷转移过程和二次电离过程则会影响产品的同位素丰度组成, 从而影响分离效果. 由于二次电离过程和复合过程对离子总量的影响远小于共振电荷转移过程的影响^[15], 因此在本文的研究中仅考虑共振电荷转移过程对离子引出的影响.
本文采用PIC (particle in cell)法、以及基于PIC法和杂化PIC法的混合算法研究了一维和二维情况下考虑共振电荷转移的离子引出过程. 在一维模拟中重点关注了共振电荷转移过程的特征和主要影响因素, 并根据模拟结果和理论分析给出了离子发生共振电荷转移比例的经验公式; 在二维模拟中分析了平行板电场法、交替偏压法、Π型电场法和M型电场法等四种常见构型下的离子引出过程, 获得了各构型下离子发生共振电荷转移的比例, 并基于离子引出效率和共振电荷转移比例对上述构型进行了对比评价.

PIC方法是一种直接从第一性原理出发的等离子体粒子模拟方法^[17,18], 其模拟的流程图如图1所示. 在完成模拟空间的参数设置、网格划分和粒子信息初始化之后, 计算基本流程如下:
1) 将网格内宏粒子的电荷分配到网格点上获取网格点的电荷和电流;
2) 根据网格点上的电荷和电流以及边界条件求解电磁场方程获取网格点上的电磁场;
3) 根据网格点上的电磁场插值得到宏粒子的受力;
4) 根据经典运动方程或相对论计算得到宏粒子在下一时刻的速度和位置;
5) 处理共振电荷转移.
图 1 PIC法计算流程图
Figure1. Schematic diagram of PIC method.

杂化PIC方法则是在PIC方法的基础上假设电子处于平衡态, 仅计算离子的运动过程. 由于不需要跟踪电子的运动, 因此杂化PIC法的计算量远小于PIC法. 混合算法是作者在处理电场法离子引出问题时提出的一种综合PIC法和杂化PIC法的方法, 相较于PIC法, 混合算法的计算效率更高, 同时比杂化PIC法的适用范围更大, 该算法的详细介绍可参见文献[19].
离子引出过程中, 在一个模拟时间步长Δt内, 离子与背景原子的共振电荷转移几率P_ia为:

${P_{{\rm{ia}}}} = 1 - \exp \left[ { - {\sigma _{{\rm{T,ia}}}}\left( {{v_{{\rm{ia}}}}} \right){n_{\rm{a}}}\left( {{r}} \right){v_{{\rm{ia}}}}\Delta t} \right], $

其中, σ_{T, ia}(v_ia)为相对速度为v_ia的离子和原子的共振电荷转移截面, n_a(r)为位置r处原子的数密度. 为了提高数值计算效率, 带电粒子和中性粒子的共振电荷转移采用零碰撞(null collision)技术以避免遍历每个宏粒子.

2

-->

3.1.一维离子引出过程

本节以一维平行板电场法离子引出为例, 其示意图如图2所示. 在未做额外说明的情况下, 均采用如下的计算条件: 极板间距L = 5 cm; 在未电离前, 金属蒸气在极板间均匀分布, 其原子数密度为4.0 × 10¹¹ cm^–3; 金属蒸气中同时存在A, B两种同位素(其中同位素A为目标同位素), 其丰度均为50%, 两种同位素的相对原子质量均取为200(这种取法不会影响最后的结论). 等离子体宽度为L_p = 3 cm, 位置位于极板中心, 其初始密度分布为均匀分布. 电子温度为0.5 eV, 背景气体中的原子和电离产生的离子温度均为0.1 eV. 本节共计算5个典型算例, 其中同位素B的电离率均为0, 同位素A的电离率、初始离子密度和相应的引出电压等参数详见表1. 共振电荷转移截面取2.0 × 10^–14 cm², 虽然实际的共振电荷转移截面与离子和原子相对速度有关^[20], 但是这种取法不影响本文的结论. 计算时考虑了光电离导致的光作用区内同位素A原子数密度的降低.
图 2 一维平行板电场法离子引出示意图
Figure2. Schematic diagram of one dimensional electric ion extraction of parallel type.

算 例	计算参数
	同位素A 电离率/%	初始离子密 度/(109 cm–3)	引出电 压/kV	背景原子密 度/(1011 cm–3)
1	2.5	5.0	2.0	4.0
2	2.5	5.0	1.0	4.0
3	5.0	5.0	2.0	2.0
4	1.25	5.0	2.0	8.0
5	50	100.0	10.0	4.0

表1一维算例的计算条件
Table1.Simulation parameters in onedimensional cases.

计算时采用的网格数为1000, 网格宽度为5 × 10^–5 m, PIC法和杂化PIC法的时间步长分别为100 ps和1 ns; 该算法已在作者之前工作中通过检验空间步长、时间步长和粒子数的方式完成收敛性检验, 详见文献[19].
图3所示为考虑共振电荷转移条件下, 算例1计算区域内的剩余离子/电子比例随引出时间的变化曲线, 为了方便比较, 图3中同位素B显示的结果为实际结果的100倍(下同). 图4为离子沉积至两侧收集板时的能量分布, 其中图4(a)的显示范围为0—2.5 keV, 图4(b)为0—20.0 eV. 作为对比, 图4中也给出了未考虑共振电荷转移时的计算结果. 图4(a)中的计算结果表明, 当考虑共振电荷转移时, 同位素A, B的离子沉积能量分布可分为三部分: 第一部分离子的沉积能量集中在2.0 keV附近; 第二部分在0—2.0 keV之间近似均匀分布; 第三部分集中在0 keV附近. 当不考虑共振电荷转移时, 同位素A离子的沉积能量只有集中在0和2.0 keV附近的两部分. 这种现象解释如下.
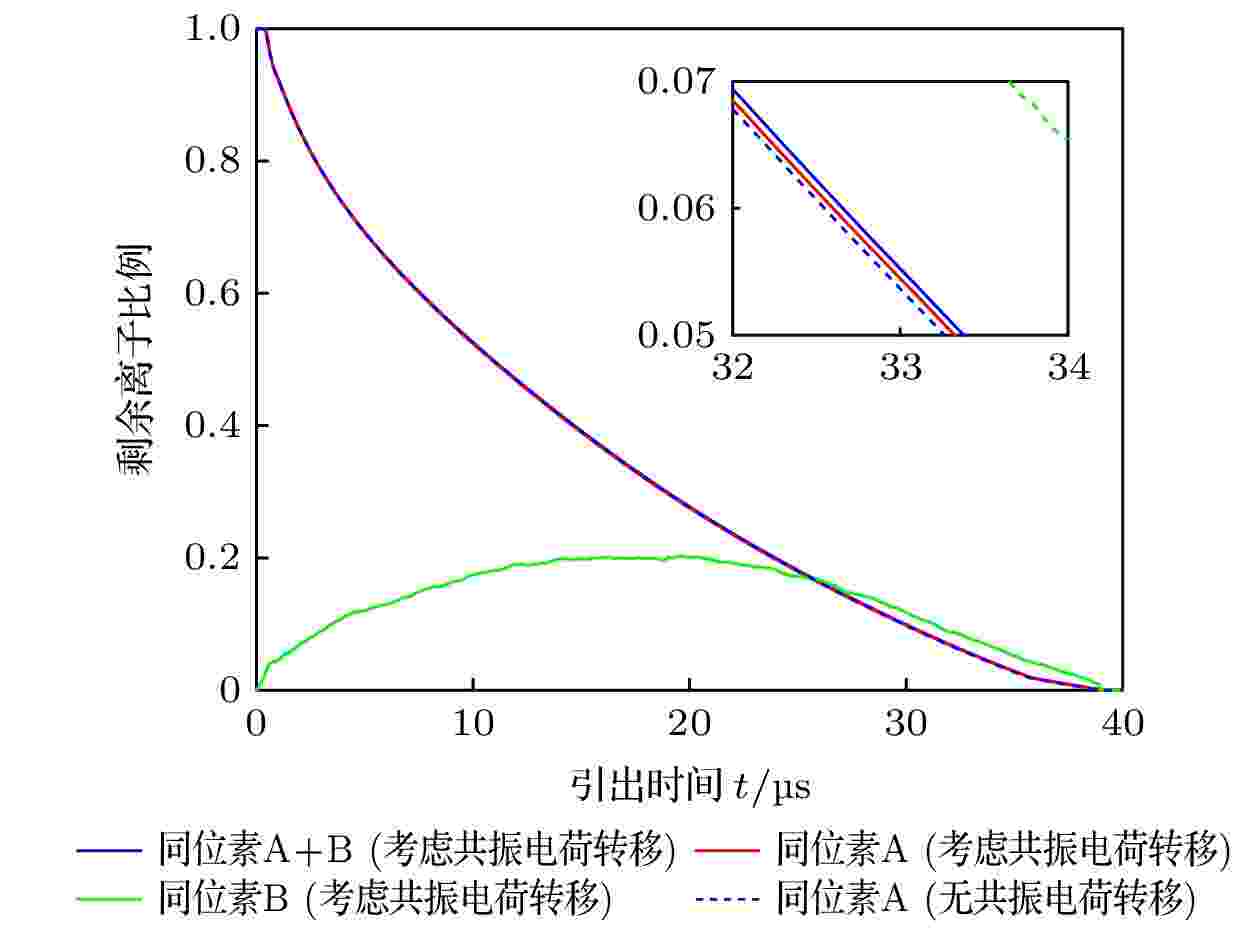图 3 剩余离子比例随引出时间的变化曲线 (算例1)
Figure3. Plots of remaining ion ratio versus extraction time (Case 1).

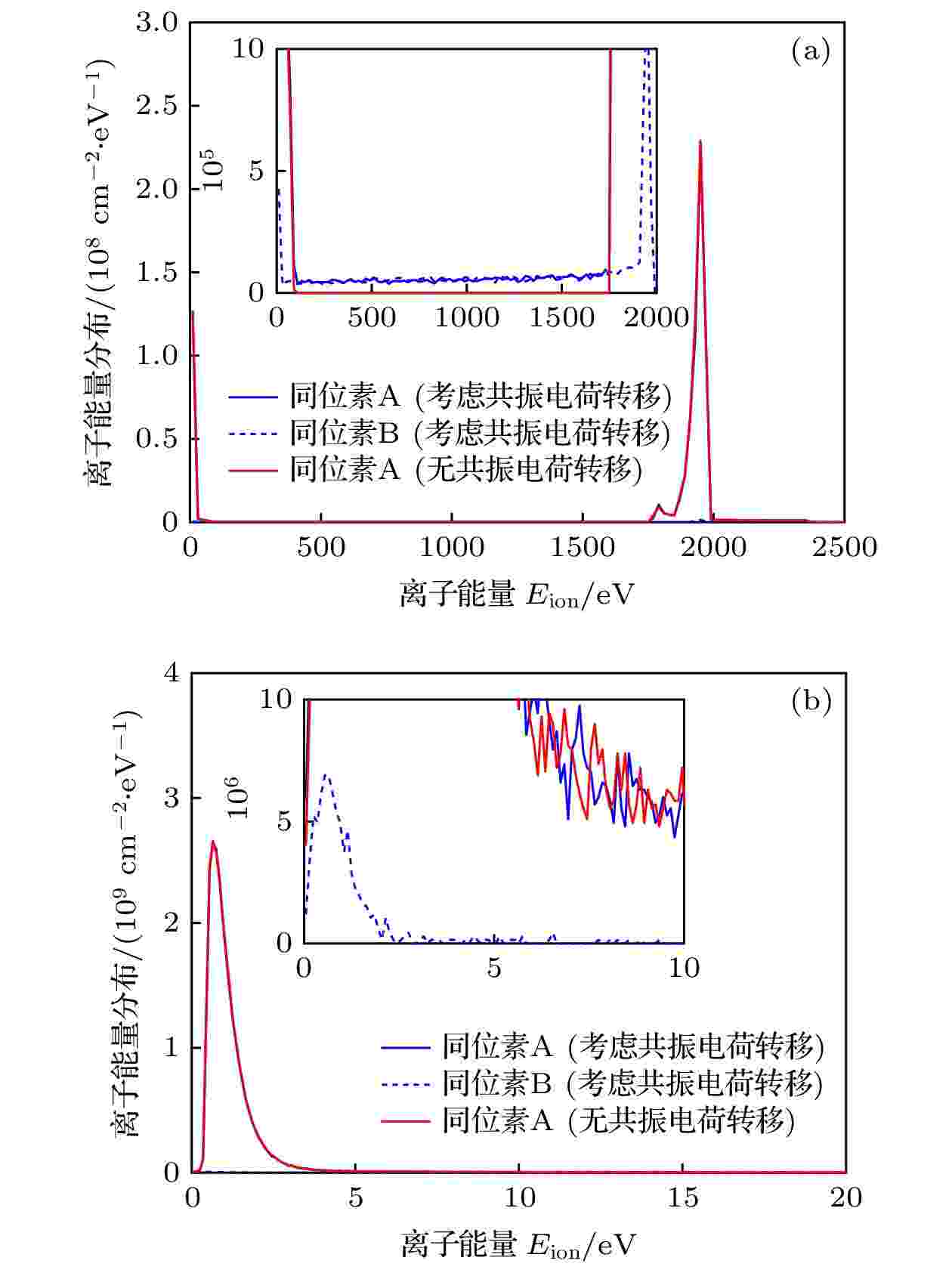图 4 两侧收集板上的离子沉积能量分布 (算例1)　(a) 整体图; (b) 局部放大图
Figure4. Energy distribution of ions deposit on the collection plates (Case 1): (a) General distribution; (b) local distribution.

不考虑共振电荷转移时, 同位素A离子在向负极板运动时被电场加速, 由于鞘层两侧的电势差约为2.0 kV, 因此从负极板引出的离子能量集中在2.0 keV附近. 同时, 正极板附近也会形成微小的鞘层, 小部分被正极板引出的离子的能量为数电子伏, 在图4(b)中则表现为沉积能量集中在0 keV附近. 当考虑共振电荷转移时, 由于引出开始时等离子体中没有同位素B离子, 因此引出过程中的同位素B离子均由共振电荷转移产生. 由同位素B离子的沉积能量分布可以看出, 一部分共振电荷转移发生在屏蔽层中, 因此被引出至收集板时离子的沉积能量集中在2.0和0 keV附近(原理同上); 另一部分共振电荷转移发生在鞘层中, 因此被引出至收集板时同位素B离子能量在0—2.0 keV之间. 同位素A离子的能量分布与同位素B类似, 与不考虑共振电荷转移时的计算结果相比, 一部分同位素A离子的沉积能量分布在0—2.0 keV之间, 这是由同位素A离子在鞘层中与同位素A原子发生共振电荷转移作用所致.
由于发生共振电荷转移的离子和原子只交换电荷, 不交换速度, 因此发生在鞘层中的共振电荷转移相当于使鞘层中离子的平均速度减小了, 从而使离子引出速率略微变慢. 只是由于在鞘层中发生共振电荷转移的离子比例较低, 因此引出速度的下降幅度十分微弱, 如图3所示. 屏蔽层中的共振电荷转移则无此影响. 同位素B剩余离子比例则受到其产生速率和引出速率的共同影响, 因此呈现先增加后减少的趋势.
图4中还有两个现象需要解释: 一是同位素A离子的沉积能量分布曲线中2.0 keV位置处的能量峰左侧均有一个小峰, 这是由于离子引出过程中鞘层形成阶段鞘层内电势波动造成的^[19], 同位素B离子的沉积能量曲线对应能量处未出现明显峰型, 其原因是同位素B离子是由共振电荷转移过程产生, 鞘层形成阶段产生的同位素B离子量少, 因此其沉积能量曲线在2.0 keV附近无其他明显的能量峰; 二是两种同位素2.0 keV位置处的能量峰不是左右对称的, 左侧偏大, 且2.0 keV能量峰峰值处的离子能量小于2.0 keV, 这是由于鞘层剥离和离子在其中的加速运动同时进行, 离子在加速运动中感受到的电场会逐渐减小, 因此电场传递给离子的能量小于2.0 keV. 图5所示为算例1改变不同初始等离子体密度时, 离子运动至两侧收集板时的能量分布. 可以看出, 随着初始等离子体密度的增加, 鞘层剥离速度变慢, 因此能量峰的位置逐渐接近2.0 keV.
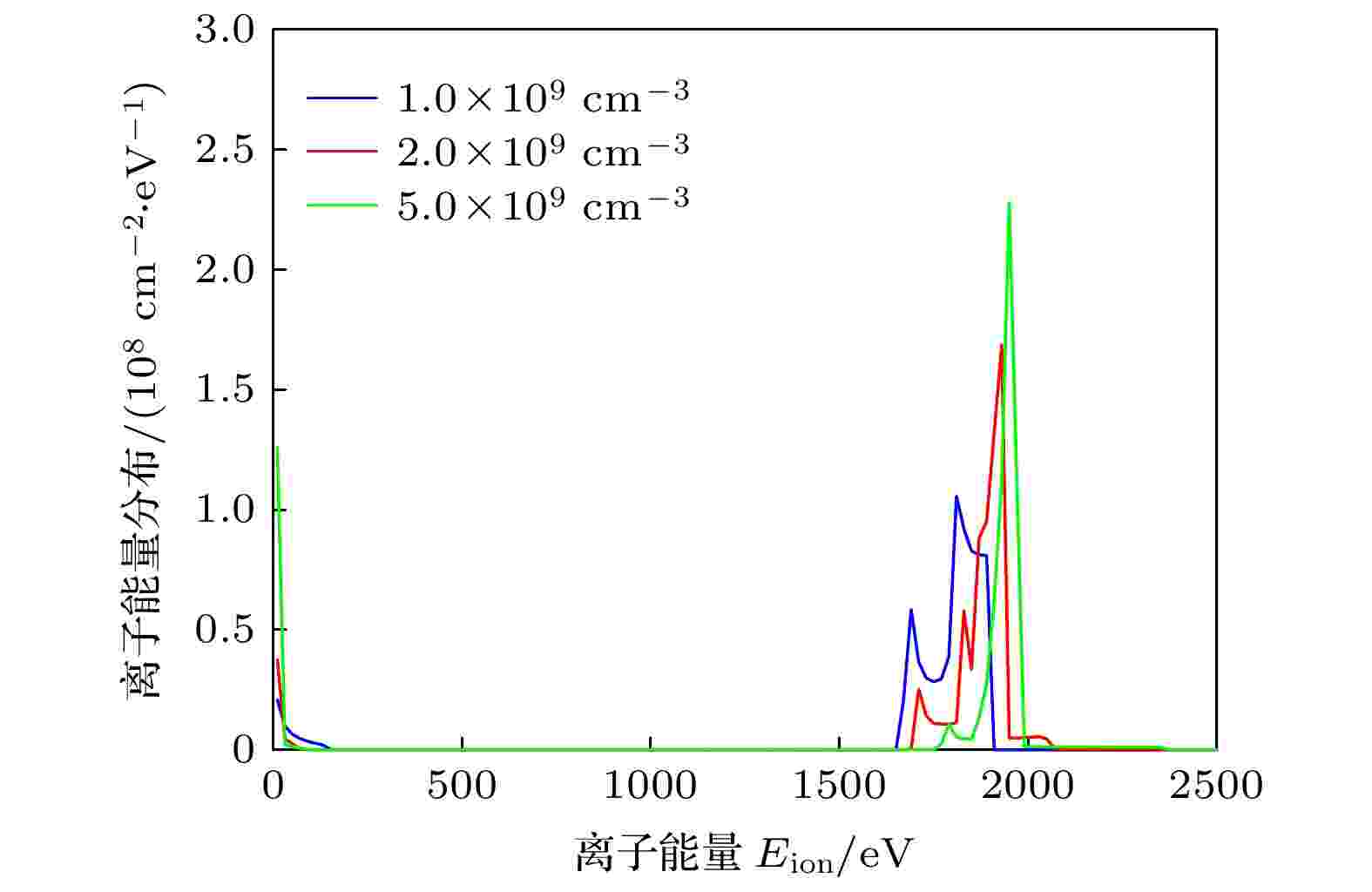图 5 不同初始等离子体密度条件下, 两侧收集板上的离子沉积能量分布(算例1)
Figure5. Energy distribution of ions deposit on the collection plates with several initial plasma densities (Case 1).

由于同位素A离子与A原子之间的共振电荷转移不会影响最终产品的丰度, 因此以下部分只研究同位素A离子与B原子之间的共振电荷转移过程. 图6所示为引出电压分别取1.0和2.0 kV(分别对应算例1和算例2)时, 剩余离子比例随引出时间的变化曲线, 图7给出了相应条件下极板上离子沉积能量分布曲线. 当引出电压分别为1.0和2.0 kV时, 同位素A离子中发生共振电荷转移的比例分别为1.278%和1.151%, 其中, 在屏蔽层中和鞘层中发生的比例分别为0.663%和0.615% (1.0 kV), 0.371%和0.780% (2.0 kV), 计算结果如表2所列. 结合图6中的剩余离子比例随引出时间的变化曲线和(1)式, 可以得到如下结论: 在其他条件不变的情况下, 随着引出电压的升高, 引出时间减小, 离子在屏蔽层中运动的路程减小, 从而使离子屏蔽层中发生共振电荷转移的几率下降(0.663% → 0.371%). 当引出电压分别为1.0和2.0 kV时, 从负极板引出的离子的比例分别为70.24%和84.62%, 由此可得由负极板引出的离子在通过鞘层时发生共振电荷转移的几率从0.876%升至0.921%, 这是因为引出电压的升高使更多的离子由负极板引出, 导致从负极板引出的离子在鞘层中的平均运动路程增长, 发生共振电荷转移的几率升高. 因此随着引出电压的增加, 通过鞘层的离子比例增加, 且离子在鞘层中的平均运动路程略有增长, 这两个原因导致离子在鞘层中发生共振电荷转移的几率增大.
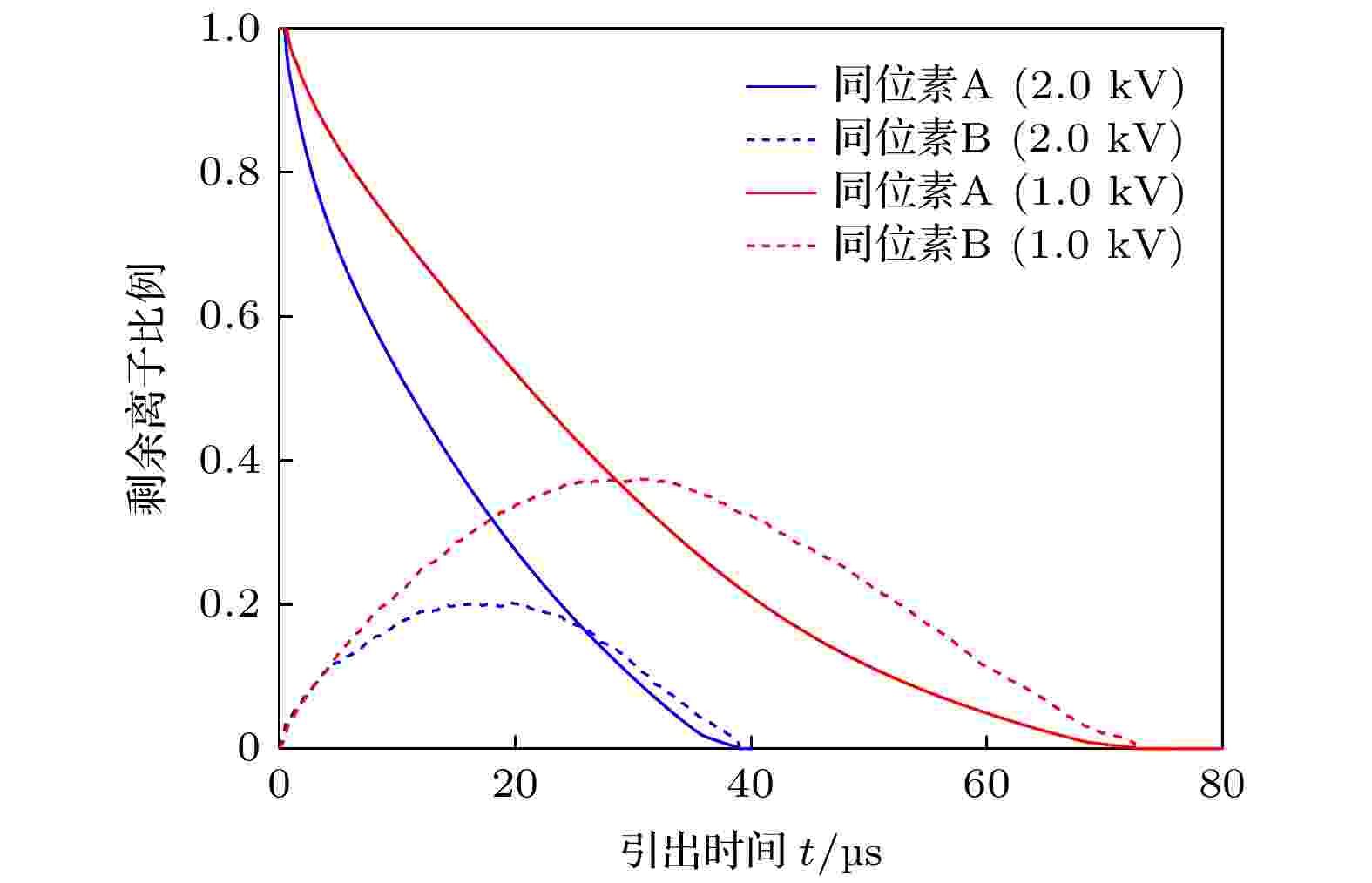图 6 不同引出电压条件下, 剩余离子比例随引出时间的变化曲线(算例1和算例2)
Figure6. Plots of remaining ion ratio versus extraction time with several applied voltages (Case 1 and Case 2).

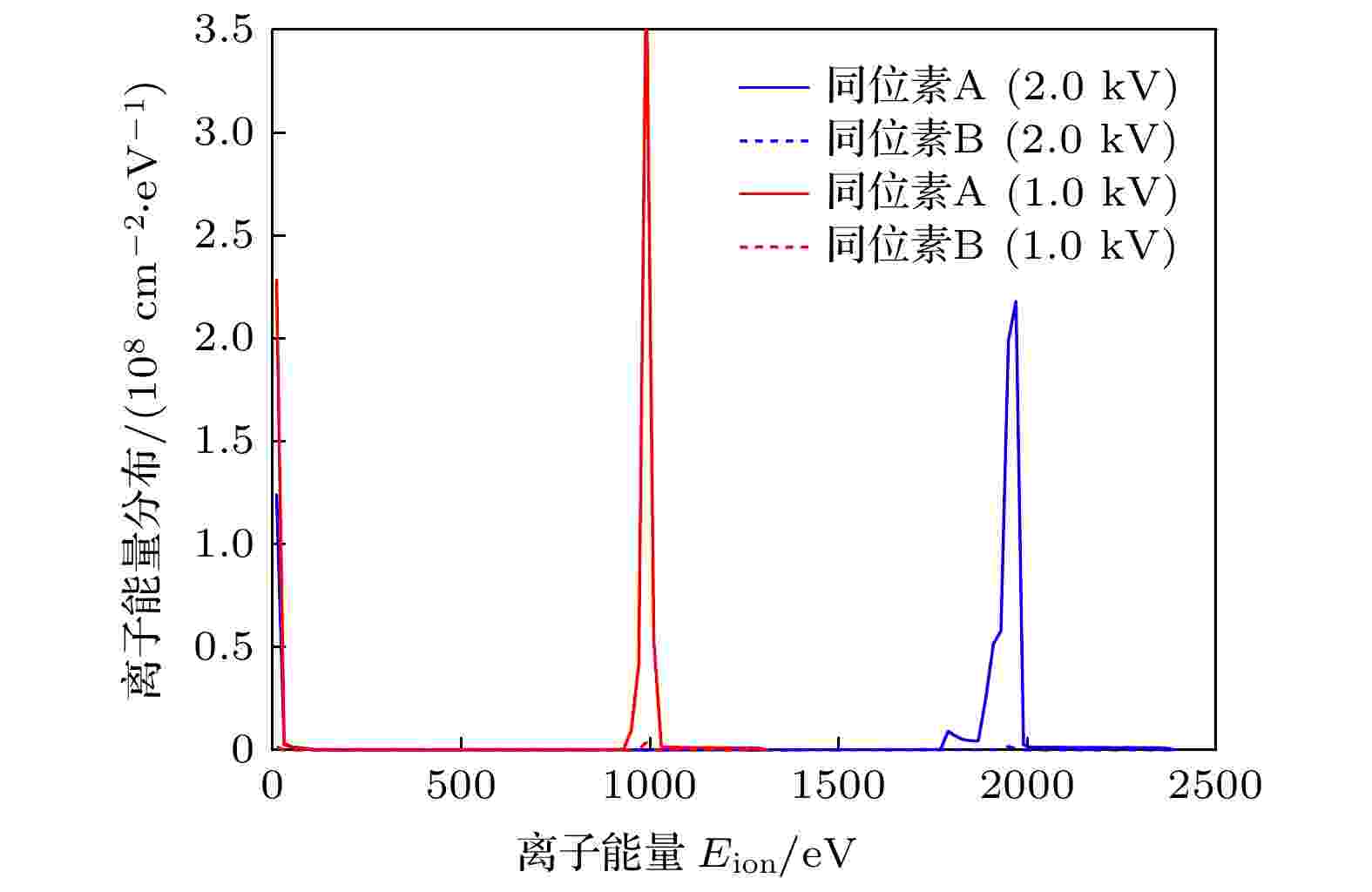图 7 不同引出电压条件下, 两侧收集板上的离子沉积能量分布(算例1和算例2)
Figure7. Energy distribution of ions deposit on the collection plates with several applied voltages (Case 1 and Case 2).

算例	引出时间/μs	负极板引出离子比例/%	共振电荷转移的比例
			鞘层/%	通过鞘层发生共振电荷转移的比例/%	屏蔽层/%	总比例/%
1	37.23	84.62	0.780 (0.846)	0.921 (1.000)	0.371 (0.395)	1.151 (1.241)
2	66.78	70.24	0.615 (0.702)	0.876 (1.000)	0.663 (0.691)	1.278 (1.393)
3	37.20	84.61	0.384 (0.423)	0.454 (0.500)	0.192 (0.200)	0.576 (0.623)
4	37.36	84.65	1.151 (1.693)	1.784 (2.000)	0.740 (0.785)	2.250 (2.478)
5	51.62	75.78	0.654 (0.758)	0.864 (1.000)	0.549 (0.533)	1.203 (1.291)

表2各算例的数值计算结果和公式评估结果
Table2.Simulation and empirical formula results of several simulation cases.

图8所示为背景金属蒸气原子数密度分别取2.0 × 10¹¹, 4.0 × 10¹¹和8.0 × 10¹¹ cm^–3(分别对应算例1、算例3、算例4)时, 剩余离子比例随引出时间的变化曲线. 图9给出了相应条件下极板上离子沉积能量分布曲线. 在背景金属蒸气原子数密度改变时, 同位素丰度和初始离子密度均不变. 在上述三种背景原子蒸气密度下, 同位素A离子中与B原子发生共振电荷转移的比例分别为0.576%, 1.151%和2.250%, 与背景原子蒸气密度基本上成正比, 且背景原子蒸气密度的变化不影响共振电荷转移发生在鞘层中和屏蔽层中的比例.
图 8 不同背景原子蒸气密度条件下, 剩余离子比例随引出时间的变化曲线(算例1、算例3、算例4)
Figure8. Plots of remaining ion ratio versus extraction time with several background atomic densities (Case 1, Case 3, Case 4).

图 9 不同背景原子蒸气密度条件下, 两侧收集板上的离子沉积能量分布(算例1、算例3、算例4)　(a) 整体图; (b) 局部放大图
Figure9. Energy distribution of ions deposit on the collection plates with several background atomic densities (Case 1, Case 3, Case 4): (a) General distribution; (b) local distribution.

图10所示为算例5中剩余离子比例随引出时间的变化曲线, 图11给出了相应条件下极板上离子沉积能量分布曲线. 同位素A离子中与B原子发生共振电荷转移的比例为1.203%, 其中发生在屏蔽层中和鞘层中的比例分别为0.549%和0.654%. 考虑到离子从负极板引出的比例为75.78%, 即可得到由负极板引出的离子在通过鞘层时发生共振电荷转移的几率为0.864%. 另外, 由图11中局部放大部分可以看出, 在5.0—8.0 keV之间, 同位素B的沉积速率略大于同位素A, 这是因为同位素A的电离率较大导致背景原子中同位素A的原子数密度低于同位素B, 在算例1—算例4中此种现象则不明显.
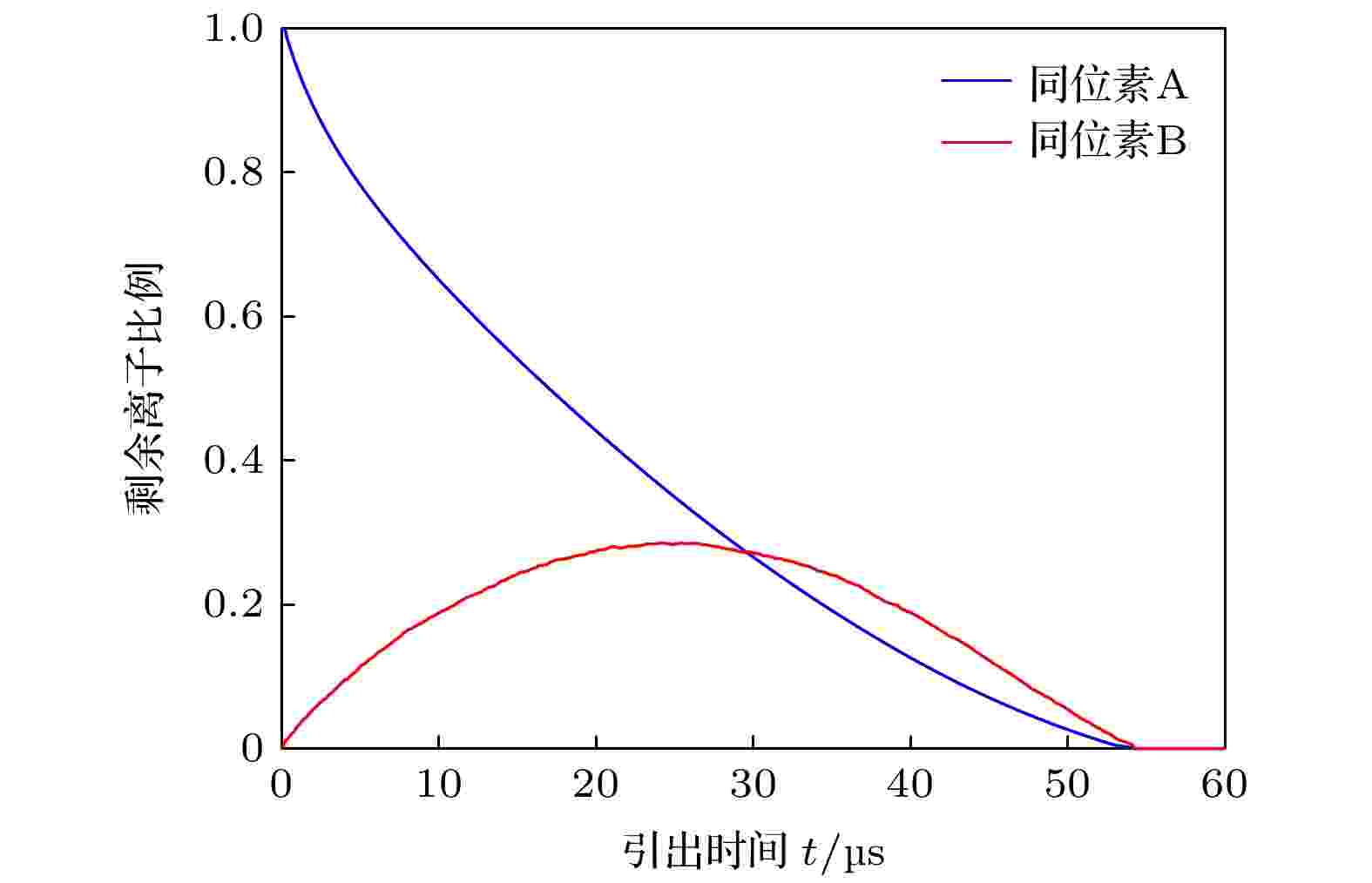图 10 两侧收集板上的离子沉积能量分布(算例5)
Figure10. Plots of remaining ion ratio versus extraction time (Case 5).

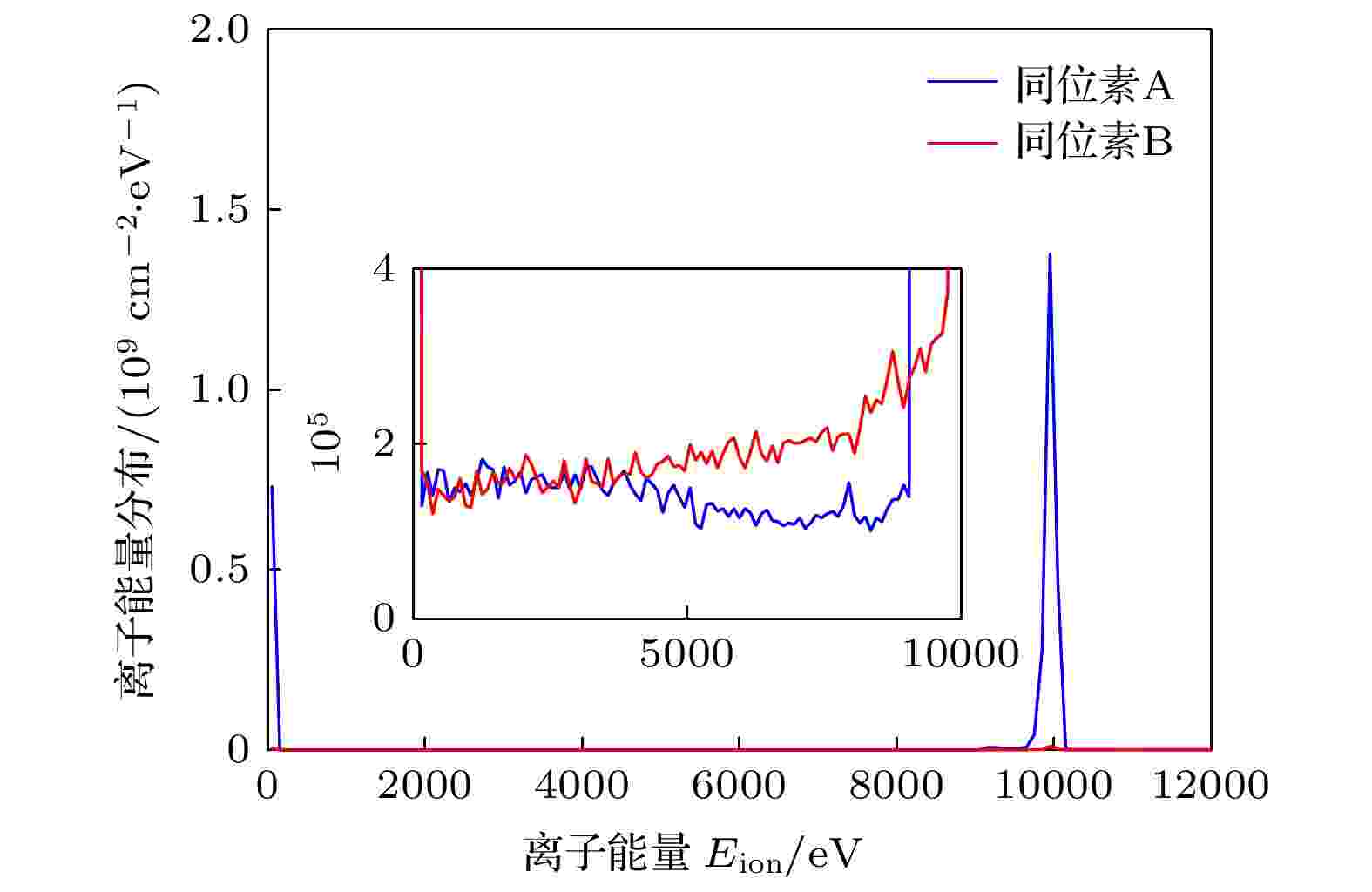图 11 两侧收集板上的离子沉积能量分布(算例5)
Figure11. Energy distribution of ions deposit on the collection plates (Case 5).

通过以上计算结果可以发现: 在电场法离子引出过程中, 屏蔽层和鞘层均会发生共振电荷转移, 根据(1)式, 除了共振电荷转移截面, 离子发生共振电荷转移的几率只受到背景原子密度和离子相对原子运动路程的影响. 屏蔽层中离子和原子均以热速度运动, 因此此区域内的离子发生共振电荷转移的几率主要取决于引出时间, 即可近似为离子停留在屏蔽层中的时间. 因此离子在屏蔽层中发生共振电荷转移的比例P_shield可采用下式估算:

${P_{{\rm{shield}}}} = \frac{1}{2}{n_{\rm{a}}}{\sigma _{{\rm{T,ia}}}} \cdot {v_{{\rm{T,ia}}}} \cdot \tau , $

其中v_T,ia为原子和离子间的平均相对热运动速度, τ为离子引出时间. 另外, 由负极板引出的离子在通过鞘层时发生共振电荷转移的几率P_sheath可采用下式估算:

${P_{{\rm{sheath}}}} = \frac{1}{2}{n_{\rm{a}}}{\sigma _{{\rm{T,ia}}}} \cdot {L_{\rm{a}}}, $

其中L_a为被负极板收集的离子在背景气体中平均运动路程长度的2倍, 在估算时采用背景气体宽度代替. 综上, 离子引出过程中离子发生共振电荷转移的比例P_total可用下式估算:

${P_{{\rm{total}}}} = {P_{{\rm{shield}}}} + {\alpha _{{\rm{cathode}}}} \cdot {P_{{\rm{sheath}}}}, $

其中α_cathode为离子从负极板引出的比例. 由(2)式—(4)式计算得到的共振电荷转移的几率列在表2的括号内, 其中通过鞘层的离子发生共振电荷转移的几率的计算结果均大于模拟结果, 这是因为靠近正极板的离子从正极板引出, 由负极板引出的离子在背景气体中的平均路程长度小于背景气体宽度的一半.
2 -->

3.2.二维离子引出过程

本节计算平行板法、交替偏压法、Π型电场法和M型电场法四种引出构型下的二维离子引出过程, 四种引出构型的示意图如图12所示. 计算参数如下: 左右收集板间距L = 5 cm, 高度H = 6 cm; 尾料板距离左右收集板上沿为2 cm, 其长度为5 cm; 等离子体尺寸为L_p × H_p = 3 cm × 3 cm, 位于左右收集板中心, 其初始密度分布为均匀分布; M型电场法中M极板的长度为5.0 cm, 即M极板下端恰好位于等离子体中心, 上端位于尾料板中心, M极板垂直于尾料板; 金属蒸气在极板间均匀分布, 其原子数密度为4.0 × 10¹¹ cm^–3; 金属蒸气中A, B两种同位素的丰度均为50%, 同位素A的电离率为2.5%, 同位素B的电离率为0, 即等离子体的初始离子密度为5.0 × 10⁹ cm^–3. 其余计算参数同3.1节. 平行板法、Π型法和M型法的引出电压为2.0 kV, 交替偏压法采用频率为1.0 MHz、峰值为2.0 kV的正弦交流电压. 计算时采用的网格数为250 × 400, 网格宽度为2 × 10^–4 m, PIC法和杂化PIC法的时间步长分别为100 ps和1 ns.
图 12 二维电场法离子引出示意图　(a) 平行板电场法; (b) 交替偏压法; (c) Π型电场法; (d) M型电场法
Figure12. Schematic diagram of two dimensional electric ion extraction: (a) Parallel type; (b) alternately biased parallel type; (c) Π-type; (d) M-type.

图13—图16分别为四种引出构型下极板上同位素A和B离子沉积能量分布曲线. 由于共振电荷转移对离子引出时间的影响比较微弱, 本节计算得到的剩余离子/电子比例随引出时间的变化曲线与图3中基本相同, 因此不再赘述. 如图13所示, 平行板电场法中左右极板上同位素A和B离子沉积能量分布与一维工况的模拟结果类似; 在交替偏压法的模拟结果中, 由于极板上的电压是周期性的交变电压, 交变电压的幅值是2.0 kV, 因此沉积能量的最大值明显小于2.0 keV. 且有相当一部分离子从尾料板引出, 这是因为加交变电压的极板有一半的时间是处于正电位, 此时离子从另外一侧的极板和尾料板引出. Π型电场法和M型电场法中左右极板上的离子沉积能量分布与平行板电场法中负极板上的结果类似, 不同点在于Π型电场法中离子沉积能量的峰值在1.2 keV左右, M型电场法则为1.9 keV, 这是因为Π型电场法中等离子体电位小于正极板电位^[19], M型电场法则拥有较快的离子引出速率. M型电场法中沉积在左右极板上的离子能量的最大值接近2.5 keV, 这是由于M型电场法中电子振荡阶段造成等离子体电位高于零电位, 因此在电势回落阶段引出离子的能量大于2.0 keV. 另外, M型电场法中有一部分离子沉积在M极板上, 其沉积能量的分布类似于平行板电场法中正极板上的离子能量分布.
图 13 平行板电场法中, 收集板上的离子沉积能量分布　(a) 同位素A; (b) 同位素B
Figure13. Energy distribution of ions deposit on the collection plates in parallel type: (a) Isotope A; (b) isotope B.

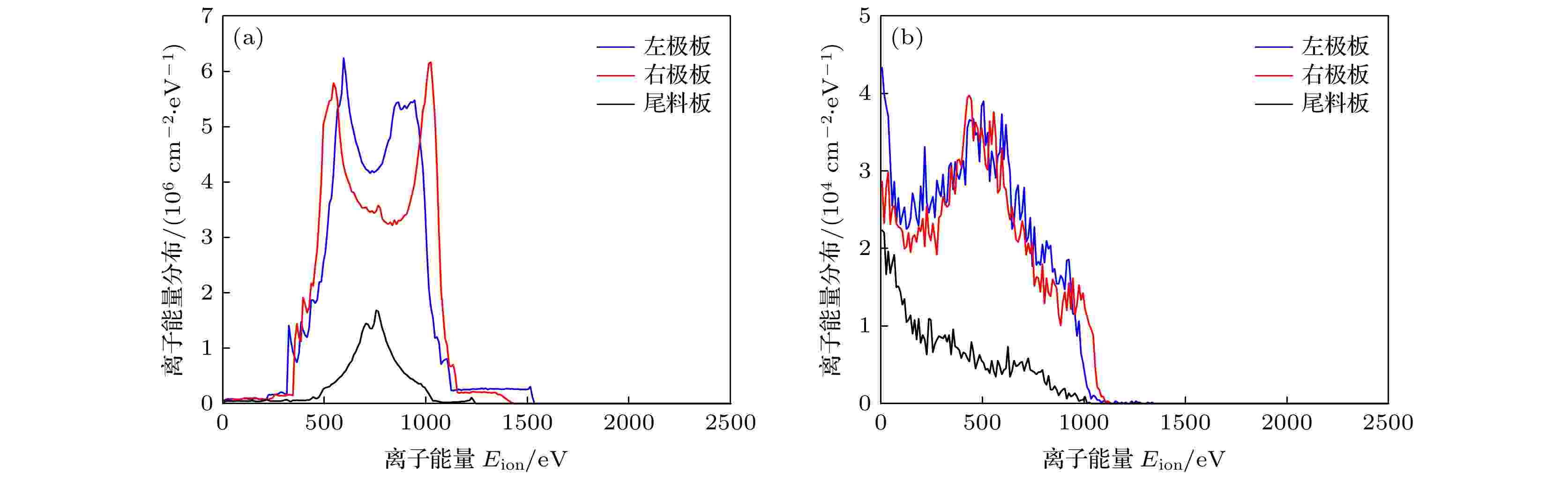图 14 交替偏压电场法中, 收集板上的离子沉积能量分布　(a) 同位素A; (b) 同位素B
Figure14. Energy distribution of ions deposit on the collection plates in alternately biased parallel type: (a) Isotope A; (b) isotope B.

图 15 Π型电场法中, 收集板上的离子沉积能量分布　(a) 同位素A; (b) 同位素B
Figure15. Energy distribution of ions deposit on the collection plates in Π-type: (a) Isotope A; (b) isotope B.

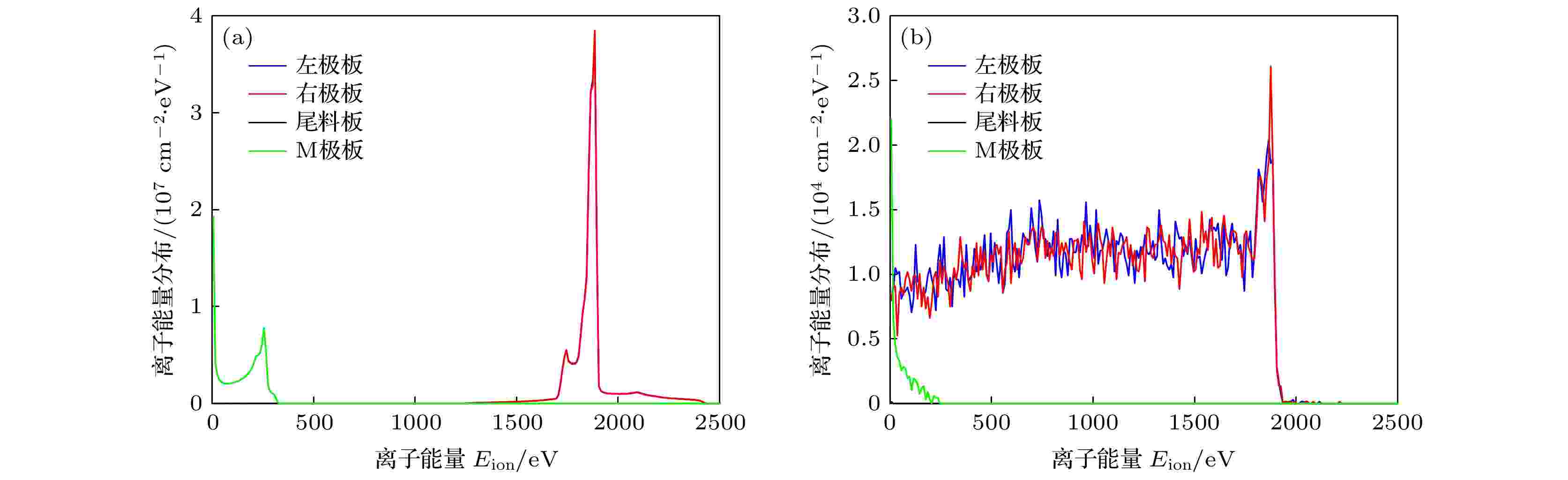图 16 M型电场法中, 收集板上的离子沉积能量分布　(a) 同位素A; (b) 同位素B
Figure16. Energy distribution of ions deposit on the collection plates in M-type: (a) Isotope A; (b) isotope B.

表3给出了四种电场法离子引出构型下同位素A离子中与同位素B原子发生共振电荷转移的比例. 可以看出, 在其他条件相同的情况下, M型电场法离子引出过程中离子发生共振电荷转移的比例最小.

离子引出构型	共振电荷转移比例/%
平行板电场法	1.097
交替偏压电场法	0.911
Π型电场法	0.859
M型电场法	0.640

表3四种引出构型中同位素A离子与同位素B原子发生共振电荷转移的比例
Table3.Resonant charge exchange ratio between A-ion and B-atom in four electrode configurations above.

本文利用混合算法和PIC法计算了考虑共振电荷转移的电场法离子引出过程, 结果表明: 离子在屏蔽层和鞘层中都会发生共振电荷转移, 共振电荷转移过程会略微延长离子引出时间, 发生共振电荷转移的几率主要取决于共振电荷转移截面、引出时间、背景原子密度和蒸气宽度. 在其他条件相同的情况下, M型电场法中离子发生共振电荷转移的比例最小. 结合之前论文中的研究结果, 从缩短引出时间和降低离子发生共振电荷转移比例的角度, M型电场法在本文介绍的四种离子引出构型中表现最优.