摘要: 应用包含链内无序和电子关联的Su-Schriffer-Heeger模型, 研究了共轭聚合物链中无序效应在光激发演化过程中的作用, 尤其是对激子产率的影响. 采用multi-configurational time-dependent Hartree–Fock方法处理电子部分的含时Schr?dinger方程, 而晶格部分的运动则由经典的牛顿方程决定. 研究发现, 加入无序后, 光激发弛豫后的产物与纯净聚合物链中有着定性的不同. 相比于纯净聚合物中光激发下会有一定的概率直接生成极化子对, 考虑无序效应后则更趋向于生成激子, 并且激子的产率很大程度上依赖于无序的类型和强度. 另外还研究了电子-电子相互作用和共轭链长度对激子产率的影响.
关键词: 共轭聚合物 /
激子 /
极化子 /
无序 English Abstract Effects of intrachain disorder on photoexcitation in conjugated polymer chains Fu Cong 1 ,Ye Meng-Hao 1 ,Zhao Hui 1 ,Chen Yu-Guang 1 ,Yan Yong-Hong 2 1.Key Laboratory for Advanced Microstructure Materials of the Ministry of Education, School of Physics Science and Engineering, Tongji University, Shanghai 200092, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11474218, 11575116)Received Date: 30 October 2020Accepted Date: 15 January 2021Available Online: 20 May 2021Published Online: 05 June 2021Abstract: The luminescence efficiency of conjugated polymers has been a central topic in the study of light emitting. The effect of disorder plays an important role in generating excitons after the conjugated polymers have been excited by photons. In this paper, by using the Su-Schriffer-Heeger model, which has been modified to include intrachain disorder and electron correlation, we investigate the effects of disorder on the photoexcitation, especially on the yield of excitons in a conjugated polymer chain. We adopt the multi-configurational time-dependent Hartree–Fock method to solve the multi-electron time-dependent Schr?dinger equation and the Newtonian equation of motion for the lattice vibration. The results show that after the photoexcitation relaxation process, the products of the disordered polymer chain are qualitatively distinct from those of the pure polymer chain. While the pairs of polarons can be generated directly after the photoexcitation in a pure polymer chain, the disorder favors excitons as the products of the photoexcitation, and the yield of excitons depends crucially on the kind and strength of the disorder. Furthermore, the influences of the electron correlation and the conjugation length on the yield of excitons are also discussed. Specifically, we find that in the case of diagonal disorder, when the conjugation length is short and the diagonal disorder is weak, the excitons are mainly generated by the recombination of two lattice defects with a high yield of excitons which will be reduced as the conjugation length increases. The excitons tend to be generated directly with a low yield of excitons which is enlarged as the disorder gets stronger when the conjugation length is long or the diagonal disorder is strong. The on-site Coulomb repulsion favors the generation of excitons as well. The case of off-diagonal disorder is similar to that of diagonal disorder except that the on-site Coulomb potential favors the generation of excitons in the weak disorder regime but depresses the generation of excitons in the strong disorder regime. When both diagonal and off-diagonal disorders are considered, the yield of excitons is dominated by the off-diagonal disorder. We hope that our investigations can provide useful guidance and help for designing organic photoelectric materials and devices.Keywords: conjugated polymer /exciton /polaron /disorder 全文HTML --> --> --> 1.引 言 自从1977年Shirakawa等[1 ] 发现通过掺杂可以将聚乙炔从绝缘体转变成导体后, 共轭聚合物领域得到了迅速的发展. 近年来, 共轭聚合物由于具有良好的导电性能和发光效率[2 ] , 已经成为一类新型电子器件的基础, 被广泛运用到光电(电光)器件中, 例如有机发光二极管[3 ] 、有机场效应管[4 ] 以及聚合物太阳能电池[5 ] 等. 由于有机聚合物材料中普遍存在着较强的电子-声子相互作用, 电荷的注入或光激发会诱导生成孤子、极化子、激子等非线性元激发. 这些元激发在很大程度上决定了材料的光、电、磁等物理性质, 是理解有机材料性质和改善器件性能的重要依据.[6 -12 ] . 根据Onsager理论[6 ,7 ] , 当价带中的电子吸收光子能量跃迁到导带后, 由于共轭聚合物的载流子迁移率比较低并且电荷屏蔽不明显, 导带中的电子和价带中留下的空穴通过库仑相互作用束缚在一起形成激子. 这种库仑束缚能比较小, 大约在$ 0.1—1.0 $ eV (视材料和激子的自旋态而定)[13 ] , 容易被电子的热运动破坏, 从而产生极化子对. 在强外场下, 激子也会因为正负电荷极化而发生解离. 此外还发现, 在有机半导体的施主-受主边界附近激子更容易发生解离[12 ] . 另一种观点认为, 荷电极化子对是共轭聚合物光激发的直接产物[14 -18 ] . Mose等[14 ] 通过测量对苯乙烯瞬时光电导率和光致发光强度随电场的变化发现, 瞬时光电流在低电场下与电场强度成比例, 但在高电场下则随电场强度指数增加; 非线性光电导率的起始场不同于发光猝灭的起始场, 光电流的增加和对应的发光强度的减弱不成比例, 这表明激子作为基本激发, 场诱导的载流子产生不显著. 由于在光激发中激发态的寿命非常短(单态激子的寿命一般在$ 100\; {\rm{ps}}—{\rm{ns}} $ 量级, 而三态激子的寿命可以达到约$ 100\; {\rm{ns}} $ 量级), 因此超快谱学成为了研究光激发的重要实验方法. De Sio等[19 ] 利用超快二维电子谱研究rr-P3HT薄膜中的极化子对产生的动力学过程; Wang等[20 ] 利用瞬态吸收光谱研究了有机光伏异质结J51/N2200中的超快空穴转移过程; 最近, 利用瞬态吸收光谱, Dong等[21 ] 报道了α-6T单质结太阳能电池实现44%的外量子效率以及1.61 V的开路电压. Kersting等[9 ] 利用飞秒发光光谱研究强外电场下聚对苯乙烯中致发光猝灭的时间分辨问题, 实验结果揭示了共轭聚合物的基本激发是有库仑束缚的电子-空穴对, 即激子; 激子的产生和它分裂成电子空穴对之间的延迟, 表明共轭聚合物中的光生载流子不是直接形成的, 而是激子解离的产物. Graupner等[11 ] 利用飞秒分辨光谱直接观察到了聚对苯中的场诱导超快激子解离现象. 而一些聚苯乙烯衍生物MEH-PPV的超快红外活性振动模式的吸收光谱的实验研究[15 -18 ] 发现, 在光吸收后$ 100 $ fs内即探测到了极化子对产生, 远小于激子的寿命, 表明荷电极化子是共轭聚合物光激发直接产生的.[22 ] 采用非绝热动力学方法模拟了聚合物中电子和晶格在光激发后的弛豫过程, 结果表明, 不同能量的激发态最终会弛豫成稳定的晶格结构中的一种, 即中性激子和荷电极化子是可以同时产生的. An等[22 ] 的理论研究基于纯净聚合物链, 只考虑了电子-声子相互作用, 然而在实际的材料中, 多种内部和外部因素都会对共轭聚合物的输运及发光性质产生重要的影响, 例如载流子密度、聚合物结构、无序、杂质、外加电场、压力等[23 -27 ] . 在实际的共轭聚合物材料中, 无序是不可避免的, 大量理论和实验研究已经报道过聚合物中无序和结构的作用[23 -26 ] , 结果表明它们对于有机器件的性能有着非常重要的影响. Monen等[28 ] 研究了共轭聚合物LED中的多分散性效应, 发现能量无序不利于激子的生成; 然而, Konezny等[29 ] 通过实验和数值计算发现, 通过在活动层增加能量无序强度和聚合物的链长, 能够使得器件的效率有所提高. Yuan等[30 ] 模拟了耦合共轭聚合物链中的极化子运动, 发现链间的耦合无序有利于极化子的输运. 此外, 他们还发现对角无序通常对极化子的输运起到抑制作用, 而非对角无序则有利于极化子的输运[31 ] . 可见, 在以聚合物为基础的有机发光二极管中, 无序是一个不可忽略的因素, 人们对于共轭聚合物中的无序效应, 尤其是无序在各种元激发相互作用中所起的作用还缺乏统一的认识. 另一方面, 电子和空穴带相反的电荷, 电子-电子相互作用在正负极化子对的复合和激子的生成中也有着非常重要的作用[32 -34 ] , 理论研究中还需要在一定程度上考虑电子关联效应.[35 ,36 ] 方法处理电子部分的含时Schr?dinger方程, 以同时考虑电子-声子相互作用和电子-电子相互作用, 并通过波函数的投影定量给出各种因素影响下激子态的产率. 第2 节将描述理论模拟中用的模型和计算方法, 第3 节讨论计算结果, 第4 节总结.2.模型和方法 用扩展的Su-Schriffer-Heeger (SSH)模型[37 ,38 ] 来描述一条带有结构无序的聚乙炔链, 体系的哈密顿量为1 )式中第一项表示晶格的弹性势能和动能:K 是σ 键的弹性系数, M 是一个CH单体的质量, $ u_i $ 是格点i 偏离二聚化平衡位置的位移. (1 )式中的第二项则用来描述系统中电子部分的Hamiltonian, 包括π电子的在位势能、相邻格点间的跃迁以及电子-电子关联:$ \varepsilon_{i} $ 是格点i 上π电子的在位势能, $ t_0 $ 是晶格均匀排布时相邻格点间的跃迁积分; $ t_{i} $ 是格点i 和格点$ i+1 $ 间由于引入无序引起的跃迁能改变; $ t_{\rm e} $ 是非简并聚合物中引入的Brazovskii-Kirova对称破缺项[39 ] ; $ \alpha $ 是电子-晶格耦合系数; $ u_i $ 是第i 个格点偏离其平衡位置的距离; $ c_{i, s}^{\dagger}(c_{i, s}) $ 是格点i 上自旋为s 电子的产生(湮灭)算符; $ n_{i, s} = c_{i, s}^{\dagger}c_{i, s} $ 是粒子数算符; U 是同一格点上的库仑相互作用. 在本文的模拟中, $ \varepsilon_{i} $ 和$ t_{i} $ 是满足高斯分布的随机变量(平均值为0, 对应于纯净聚合物链), 分别用来描述体系的对角无序和非对角无序:$ \sigma_\varepsilon $ 和$ \sigma_t $ 分别描述了两种无序的强度. 这样, 结构无序以一种简单且可控制的方式引入到模拟中来. 需要注意的是, 这里的无序是静态的且非关联的. 在后面的数值模拟中, 参数取值采用在聚乙炔中广泛使用的数值[40 ] : $ t_0 = 2.5 $ eV, $ t_{\rm e} = 0.05 $ eV, $ K = 21.0 $ eV/?2 , $ \alpha = 4.1 $ eV/?, $ M = 1349.14 $ eV·fs2 /?2 .6 )式的多体系统的含时Schr?dinger方程一般是不可能的, 需要做适当的近似处理. 本文采用最近发展的MCTDHF方法, 用原子轨道的线性组合系数$ C_{jk_{\mu}} $ 来重写(6 )式中的电子波函数[35 ,36 ] :$\{ C_{jk_\mu} \}$ 是展开系数, $ \{ R_{ij}\} $ 即为有效的瞬时Hamiltonian矩阵, 其表示如下:μ 的Fock矩阵表示为$P_{ij}^{\mu} = \displaystyle\sum\nolimits_{k_{\mu}}C_{ik_{\mu}}C_{jk_{\mu}}^{*}$ 是壳层μ 的投影矩阵, $n^{\mu} = 0, 1, 2$ 是壳层μ 的电子占据数, 在演化过程中保持不变. $ a^{\mu\upsilon},\; b^{\mu\upsilon} $ 是取决于电子波函数组态形式的系数, $ v_{ij} $ 是格点i 和格点j 之间的电子相互作用. 同时电子部分的能量$ V_ {\rm{elec}} $ 可以表示为η 是为了能使得晶格弛豫更快地达到稳定而引入的耗散(阻尼)项, 在这里取室温下的典型值$ \eta = 0.04\omega_Q = 0.04\sqrt{4 K/M} $ . 而密度矩阵$ \rho_{ij} $ 定义为7 )式和(12 )式进行求解, 从而得到电子的演化波函数以及晶格的运动.$ |\psi(t)\rangle $ 投影到$ H_ {\rm{elec}}\{u_i(t)\} $ 的瞬时本征态空间 上 [41 -43 ] . 对于一个给定的瞬时本征态$ |\phi_k\rangle $ , 其对应的产率$ I_k(t) $ 可以写成$ |\phi_k\rangle $ 可以通过自洽迭代求解有效的瞬时Hamiltonian矩阵$ \{ R_{ij}\} $ 得到. 在数值模拟中用两次迭代得到的电子部分能量$ V_ {\rm{elec}} $ (由(10 )式得到)之差$ |\Delta V_ {\rm{elec}}| < 1.0\times 10^{-6} \;{\rm{eV}} $ 作为收敛条件以保证波函数的准确性. 最后, 态$ |\phi_k\rangle $ 可以是任意想要关注的态. 这里主要关注的是激子态, 即最低激发态.3.结果和讨论 在无掺杂(半满)的共轭聚合物中, 系统处在二聚化基态时, 所有的价带能级(用$ \varepsilon_m^{\rm v} $ 表示)是双占据的, 而导带(用$ \varepsilon_n^{\rm c} $ 表示)则是全空的. 在此基础上, 通过改变电子占据状态, 如从能级$ \varepsilon_m^{\rm v} $ 激发一个电子到能级$ \varepsilon_n^{\rm c} $ , 以模拟光激发后晶格以及电子的弛豫过程, 并研究无序等效应对生成物的影响. An等[22 ] 的研究表明, 在纯净聚合物中对于不同能量的光激发, 最终会演化成两种稳定晶格结构中的一种: 奇数能级间的跃迁(如$ \varepsilon_1^{\rm v}\rightarrow\varepsilon_1^{\rm c} $ , $ \varepsilon_3^{\rm v}\rightarrow\varepsilon_3^{\rm c} $ )将演化成单局域自陷态, 这时导带中的电子和价带中的空穴束缚在这一晶格缺陷中, 即自陷激子; 而偶数能级间跃迁(如$ \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c} $ , $ \varepsilon_4^{\rm v}\rightarrow\varepsilon_4^{\rm c} $ )最终将生成两个稳定的局域缺陷结构, 其产物是中性激子和正负荷电极化子对的混合态. 我们首先模拟了纯净聚合物链中光激发后的演化过程, 得到了与上述相同的结果. 而考虑了无序效应后, 我们发现对于奇数能级间的跃迁(如$ \varepsilon_1^{\rm v}\rightarrow\varepsilon_1^{\rm c} $ ), 系统演化的产物没有定性的变化(文章中没有显示); 而偶数能级间跃迁(如$ \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c} $ )后的演化则有定性的不同, 最终的产物更趋向于生成自陷激子态. 因此, 本文对奇数能级间跃迁的演化将不再做更多的讨论, 而着重于研究偶数能级间跃迁后晶格的演化和生成物产率等信息.$ \varepsilon_i $ 的高低来描述对角无序, 并通过高斯分布的标准差$ \sigma_\varepsilon $ 调控其无序强度. 当确定$ \sigma_\varepsilon $ 后, 通过随机数生成器生成一系列决定格点势能的随机数序列$ \varepsilon_i $ . 对于每一组随机参数, 模拟了1000 fs的演化过程, 并在激子的产率达到稳定后做时间上的平均, 得到该组参数下激子的产率. 由于随机数生成的特点, 即使在相同标准差的情况下, 每组随机数序列仍然是不同的. 理论上, 随机样本越多, 随机误差越小. 因此为了确保结果的收敛性, 在每个标准差下模拟了64组样本, 重复上面的过程得到每组样本下激子的产率并对这64组数据做数值平均, 最终得到这一标准差$ \sigma_\varepsilon $ 下激子的产率. 图1 所示为加入无序效应后, 光激发将价带$ \varepsilon_2^{\rm v} $ 上一个电子激发到导带$ \varepsilon_2^{\rm c} $ (电子的初始占据如图1(b) 中的插图所示), 晶格位形的演化过程. 需要注意的是, 由于每次模拟生成的随机数序列不尽相同, 演化的过程和最终位形也有所区别. 结果发现考虑了无序效应后, 对于不同长度的聚合物链, 激子的生成主要有两种机制, 如图1(a) 和图1(b) 所示. 图1(a) 给出了一种典型的演化过程, 这种情况主要出现在短链和较弱的无序强度中. 电子吸收光子能量从价带激发到导带后, 初始的演化与纯净聚合物链中类似, 首先在链上形成两个较浅的晶格缺陷. 在大约200 fs后, 这两个晶格缺陷逐渐靠近并合并为一个较深的缺陷. 随着时间的演化, 这个晶格缺陷缓慢地向着系统能量更低的区域弛豫和移动. 伴随着晶格能量的逐渐耗散, 晶格位形逐渐趋于稳定并形成最终的产物—激子. 在足够长的纯净聚合物链中(可以忽略边界效应), 两个晶格缺陷可以独立分布在链上的不同位置并且相互之间没有影响. 而引入无序后, 遵循向着能量更低方向演化的原则, 初始的两个晶格缺陷则有概率靠得比较近, 从而增加了两者之间的相互作用和波函数的交叠, 并最终合并形成一个晶格缺陷. 考虑到激子本身具有一定的宽度, 因此, 上述情况在短链中尤为明显和重要, 更有利于激子的生成. 另一种典型的演化过程更多地出现在长链和无序强度比较大的情况, 如图1(b) 所示. 这时光激发后晶格直接生成一个缺陷, 并逐渐弛豫达到稳定的激子态. 由于无序的引入破坏了系统的空间反演对称性和平移对称性, 导带的波函数不再是具有对称性的延展态, 取而代之的是在不同的区域有着不同的分布. 光激发后, 同样遵循能量最低的原则, 电子趋向于局域在能量更低的区域, 并进一步直接演化成为激子. 需要注意的是, 比较图1(a) 和图1(b) 可以发现, 后一种机制生成的晶格缺陷要浅于前一种机制生成的晶格缺陷, 相对应的激子产率也要小一些.图 1 加入对角无序后, 电子$ \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c} $ 激发后晶格交错序参量$ \delta_i = (-1)^i(u_{i+1}-u_i)/2 $ 随时间的演化 (a) $ L = 64, \; \sigma_\varepsilon = 0.01 $ eV; (b) $ L = 128, \; \sigma_\varepsilon = 0.10 $ eV, 插图显示了$ \varepsilon_2^{\rm v} $ 上一个电子激发到导带$ \varepsilon_2^{\rm c} $ 后, 电子初始占据状态的示意图Figure1. Dynamical evolution of the staggered bond order parameter $ \delta_{i} = (-1)^{i}(u_{i+1}-u_{i})/2 $ with time for photoexcitation $ \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c} $ : (a) $ L = 64, \; \sigma_\varepsilon = 0.01 $ eV; (b) $ L = 128, \; \sigma_\varepsilon = 0.10 $ eV. The inset shows the initial electronic levels for a photoexcitation process of $ \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c} $ .$ L = 64, \; L = 96, \; L = 128 $ 三种长度的聚合物链. 同时, 由于电子和空穴分别带相反电荷, 电子关联在激子的生成中也有着重要作用, 在数值计算中也加入了电子-电子相互作用, 具体分别是$ U = 0 $ , $ U = 1.0 $ eV, $ U = 2.0 $ eV和$ U = 3.0 $ eV四种强度的库仑势. 图2 给出了不同链长、无序强度和电子关联下激子的产率. 首先可以明显地发现, 由于电子关联提供了一个电子和空穴间有效的吸引机制, 几乎所有情况下, 同一格点上的库仑相互作用都有利于激子的生成, 即激子的产率随着U 的增加而增大. 另外, 由于无序的引入破坏了系统的空间反演对称性和电子-空穴对称性, 即使非常小的无序强度也会对系统的演化产生决定性的影响, 尤其对于比较短的链, 无序的作用尤为重要. 从图2(a) 可以发现, 即使在很小的无序强度下, 如$ \sigma_\varepsilon = 0.01 $ eV, 最终演化的产物主要为激子, 其产率接近70%. 对于较长的聚合物链, 如$ L = 128 $ 时, 在较小的无序强度下则更趋向于生成极化子对, 激子的产率很小, 与纯净的聚合物链类似; 同时在这种情况下电子关联则起着主导作用, 并非常明显地提高激子的产率, 如图2(c) 所示. 对于$\varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c}$ 的光激发, 可以发现在短链(如$ L = 64, $ $ L = 96 $ )和无序度较弱时激子的生成主要来自于两个晶格缺陷之间的复合, 并且激子的产率随着链长的增加有所减小(链变长不利于复合). 这种机制下生成的激子有较大产率, 在短链中接近70%. 而当无序度增大时, 电子波函数则倾向于在部分区域有较大分布, 从而在局部直接生成激子. 这种机制下生成的激子产率较小, 并且随着无序度的增加其产率有所增加. 因此, 结合这两种机制的共同作用, 激子的产率随着无序度的增加有一个先变小再变大的过程, 对应的激子产生机制也由复合为主转变成直接生成为主. 而长链中(如$ L = 128 $ )则由于激发后电荷分布的不同倾向于生成深浅不同的两个缺陷, 同时随着无序强度的增加电荷的分布呈更为不平衡的趋势, 这时系统的演化主要为上面提到的第二种机制, 激子的产率也随着$ \sigma_\varepsilon $ 的变大明显地增加.图 2 激子的产率在不同链长和电子关联下随着对角无序强度的变化 (a) $ L = 64, \; \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c} $ ; (b) $ L = 96, \; \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c} $ ; (c) $L = $ $ 128, \; \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c}$ ; (d) $ L = 64, \; \varepsilon_4^{\rm v}\rightarrow\varepsilon_4^{\rm c} $ ; (e) $ L = 96, \; \varepsilon_4^{\rm v}\rightarrow\varepsilon_4^{\rm c} $ ; (f) $ L = 128, \; \varepsilon_4^{\rm v}\rightarrow\varepsilon_4^{\rm c} $ Figure2. Dependence of the yield of the exciton on the strength of diagonal disorder: (a) $ L = 64, \; \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c} $ ; (b) $ L = 96, \; \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c} $ ; (c) $ L = 128, \; \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c} $ ; (d) $ L = 64, \; \varepsilon_4^{\rm v}\rightarrow\varepsilon_4^{\rm c} $ ; (e) $ L = 96, \; \varepsilon_4^{\rm v}\rightarrow\varepsilon_4^{\rm c} $ ; (f) $ L = 128, \; \varepsilon_4^{\rm v}\rightarrow\varepsilon_4^{\rm c} $ .图2(d) —图2(f) 给出了$ \varepsilon_4^{\rm v}\rightarrow\varepsilon_4^{\rm c} $ 的光激发后激子的产率. 相较于$ \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c} $ 时生成两个晶格缺陷, 这时光激发后首先生成四个晶格缺陷, 它们彼此之间靠得更近, 即使在较长链中(比较图2(c) 和图2(f) )也有较多的交叠和耦合, 这更有利于直接复合成激子. 所以这时不同链长和无序强度下的演化主要遵循多个晶格缺陷间的复合, 只有在长链和强无序时有较小的概率生成一深一浅两个晶格缺陷(文章中没有显示). 因此如图2(d) —图2(f) 所示, 激子的产率在三种链长下随着无序的变化曲线基本相似, 只是随着链长的增加略有减小.$ t_i $ 来描述系统中的对角无序. 结果发现, 在非对角无序强度比较小时, 光激发后晶格的演化与对角无序时类似, 主要通过晶格缺陷间的复合生成激子. 而在大无序强度时虽然主要机制也是直接生成激子, 但和图1(b) 中不同的是除了生成主要产物激子外, 还会在链上的其他区域生成一些局域和稳定的小晶格缺陷(文章中没有显示). 这是由于非对角无序影响最近邻格点间的交叠积分, 其直接决定了电子在链上的跃迁. 系统无序度增大时, 跃迁能的大范围变化使得激发电子的波函数趋向于局域在更多的区域, 从而进一步演化成局域晶格缺陷. 图3 给出了加入非对角无序时激子的产率在不同链长L 和在位库仑势U 下随着无序强度$ \sigma_{t} $ 的变化. 首先对于$ \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c} $ , 不同于只考虑对角无序时电子关联基本有利于激子的生成, 可以发现电子关联在无序度较小时有利于激子的生成而无序度较大的时候则不利于激子的生成. 在无序度比较小时, 两种无序在激子生成的机制上类似, 电子关联引起电子-空穴间的有效吸引有利于激子的生成. 另外, 相比于只考虑对角无序时的情况(图2 ), 可以发现这时电子关联对激子产率的影响变小. 而当无序变强时, 在电子-电子相互作用的影响下, 聚合物链上会生成更多且比没有电子关联时更深一些的局域晶格缺陷, 从而束缚一定的电荷, 同时这也导致激子的产率相应减小, 这在强电子关联时尤为明显, 如图3(a) —图3(c) 所示. 类似于对角无序中的机理, 在电子关联较弱时, 短链中激子的产率随着无序的增加先减小再增大, 在长链中则随着无序度的增加同时增加. 最后, 对于$ \varepsilon_4^{\rm v}\rightarrow\varepsilon_4^{\rm c} $ 的光激发, 由于晶格首先生成四个缺陷, 在短链中随着非对角无序的增加会有更高的概率相互复合成一些较浅的晶格缺陷, 也使得激子的产率减小; 而在长链中, 这种复合的概率相对较小, 激子的产率在强无序时有所增加, 正如图3(d) —图3(f) 所示.图 3 激子的产率在不同链长和电子关联下随着非对角无序强度的变化 (a) $ L = 64, \; \varepsilon_2^{\upsilon}\rightarrow\varepsilon_2^c $ ; (b) $ L = 96, \; \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c} $ ; (c) $L = 128, $ $ \; \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c}$ ; (d) $ L = 64, \; \varepsilon_4^{\rm v}\rightarrow\varepsilon_4^{\rm c} $ ; (e) $ L = 96, \; \varepsilon_4^{\rm v}\rightarrow\varepsilon_4^{\rm c} $ ; (f) $ L = 128, \; \varepsilon_4^{\rm v}\rightarrow\varepsilon_4^{\rm c} $ Figure3. Dependence of the yield of the exciton on the strength of off-diagonal disorder: (a) $ L = 64, \; \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c} $ ; (b) $L = $ $ 96, \; \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c}$ ; (c) $ L = 128, \; \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c} $ ; (d) $ L = 64, \; \varepsilon_4^{\rm v}\rightarrow\varepsilon_4^{\rm c} $ ; (e) $ L = 96, \; \varepsilon_4^{\rm v}\rightarrow\varepsilon_4^{\rm c} $ ; (f) $ L = 128, \; \varepsilon_4^{\rm v}\rightarrow\varepsilon_4^{\rm c} $ .$ \sigma_{t} $ 和$ \sigma_{\varepsilon} $ ($ \sigma_{t} = \sigma_{\varepsilon} $ )来描述两种无序强度. 图4 给出了同时考虑两种无序时激子产率随无序强度和链长以及激发能量的变化. 对比图2 和图3 中激子产率曲线变化的整体趋势, 可以明显地发现, 在同时考虑两种无序的情况下, 无论是$ \varepsilon_{2}^{\rm v}\rightarrow\varepsilon_{2}^{\rm c} $ 还是$ \varepsilon_{4}^{\rm v}\rightarrow\varepsilon_{4}^{\rm c} $ 的光激发, 激子产率的变化曲线与只考虑非对角无序情况时非常相似. 正如前文所述, 由于非对角无序影响最近邻格点间的交叠积分, 直接决定了电子在链上的跃迁, 从而进一步影响多个晶格缺陷能否复合以及最终演化的产物和产率的大小. 因此, 与对角无序相比, 非对角无序在光激发后的演化过程中起主要作用, 非对角无序对光生激子的影响会更大.图 4 两种无序同时存在时, 激子的产率在不同链长和电子关联下随着无序强度的变化 (a) $ L = 64, \; \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c} $ ; (b) $L = 96, $ $ \; \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c}$ ; (c) $ L = 128, \; \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c} $ ; (d) $ L = 64, \; \varepsilon_4^{\rm v}\rightarrow\varepsilon_4^{\rm c} $ ; (e) $ L = 96, \; \varepsilon_4^{\rm v}\rightarrow\varepsilon_4^{\rm c} $ ; (f) $ L = 128, \; \varepsilon_4^{\rm v}\rightarrow\varepsilon_4^{\rm c} $ Figure4. Dependence of the yield of the exciton on the strength of both diagonal and off-diagonal disorder: (a) $ L = 64, \; \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c} $ ; (b) $ L = 96, \; \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c} $ ; (c) $ L = 128, \; \varepsilon_2^{\rm v}\rightarrow\varepsilon_2^{\rm c} $ ; (d) $ L = 64, \; \varepsilon_4^{\rm v}\rightarrow\varepsilon_4^{\rm c} $ ; (e) $ L = 96, \; \varepsilon_4^{\rm v}\rightarrow\varepsilon_4^{\rm c} $ ; (f) $L = 128, \; \varepsilon_4^{\rm v}\rightarrow\varepsilon_4^{\rm c}$ .4.总 结 应用包含了链内无序和电子-电子相互作用的扩展SSH模型, 通过非绝热近似方法求解电子和晶格的耦合方程, 研究了共轭聚合物链中无序效应在光激发演化过程中的作用. 发现偶数能级间跃迁后的晶格演化与纯净聚合链中有着定性的不同: 相比于纯净聚合物中光激发下可以有一定的概率直接生成极化子对, 考虑了无序效应后则更趋向于生成激子. 系统地研究了无序类型、无序强度、光激发能量、电子关联以及共轭链长度对光激发的演化过程和生成产物的影响, 并且通过波函数投影定量给出了激子态的产率. 希望这些理论结果能够给有机光电材料和器件的设计提供有益的指导和帮助. 
















































































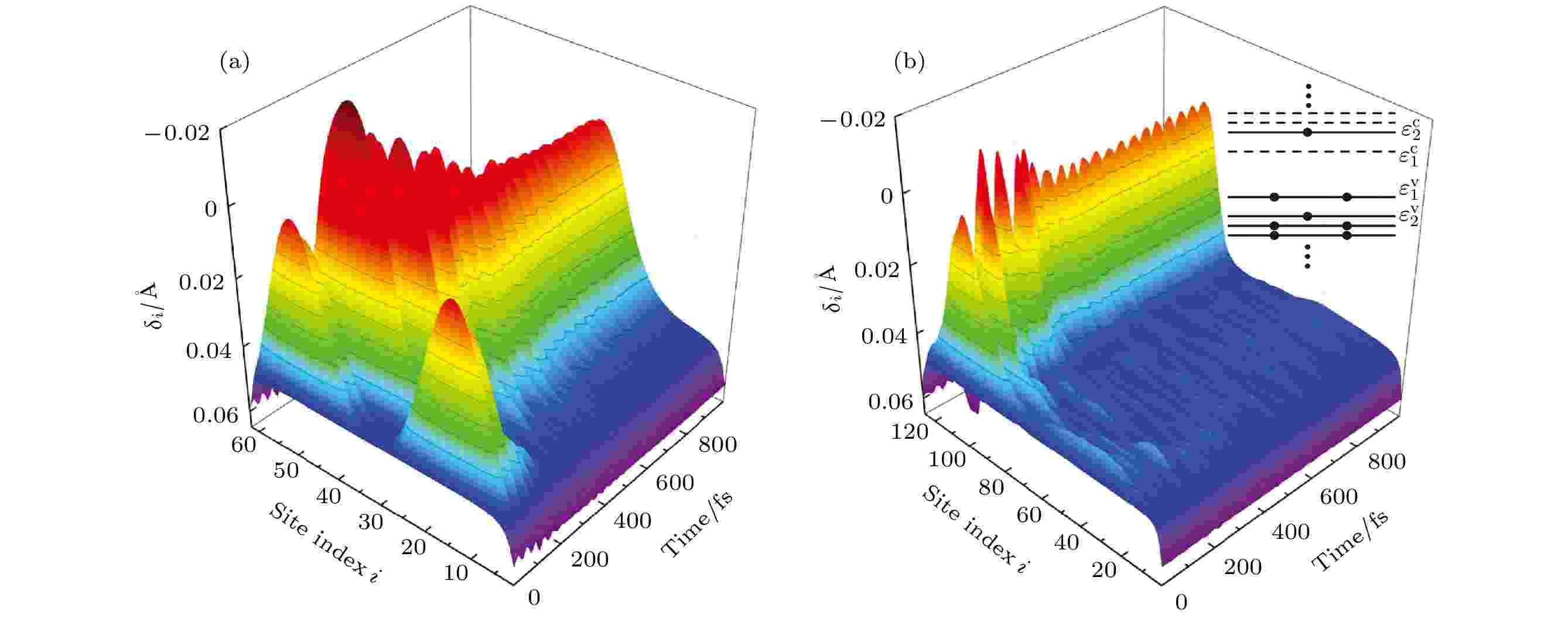 图 1 加入对角无序后, 电子
图 1 加入对角无序后, 电子


























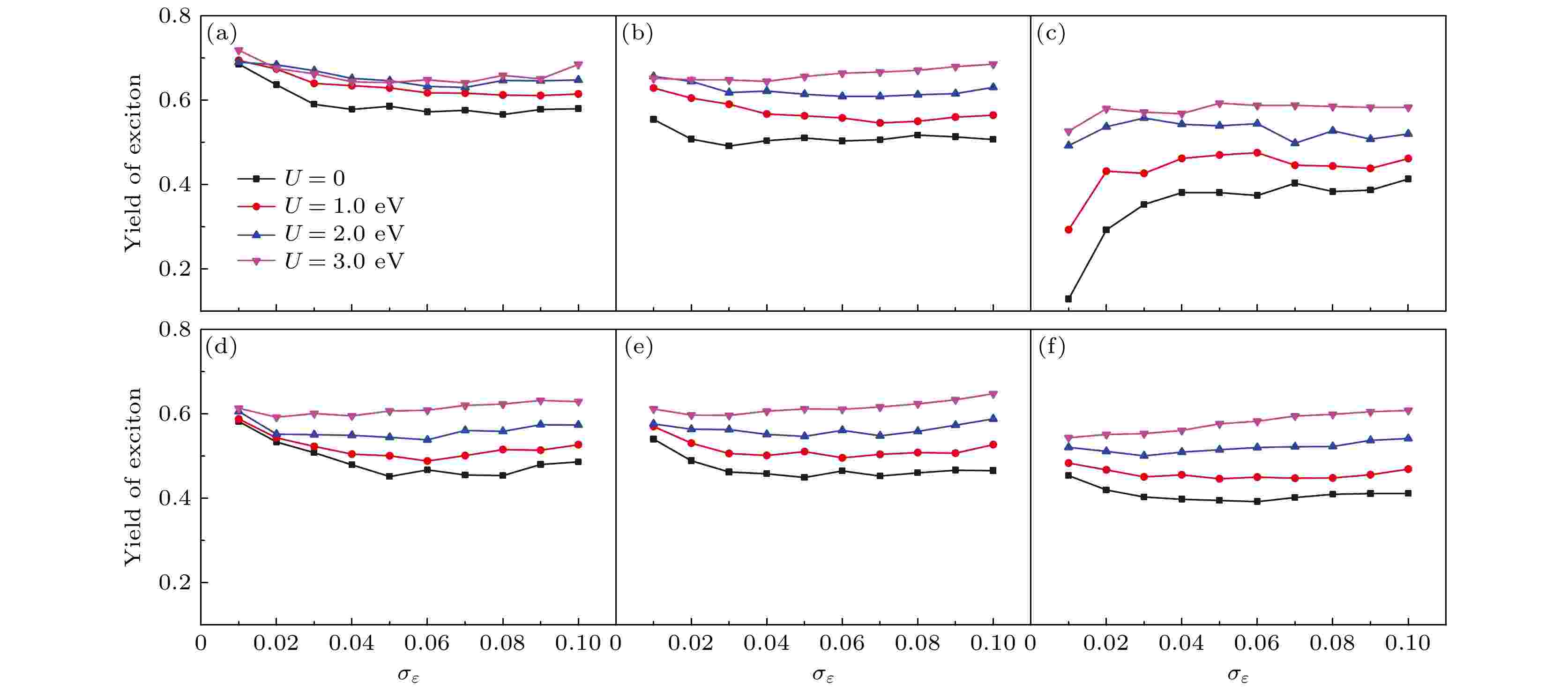 图 2 激子的产率在不同链长和电子关联下随着对角无序强度的变化 (a)
图 2 激子的产率在不同链长和电子关联下随着对角无序强度的变化 (a) 


















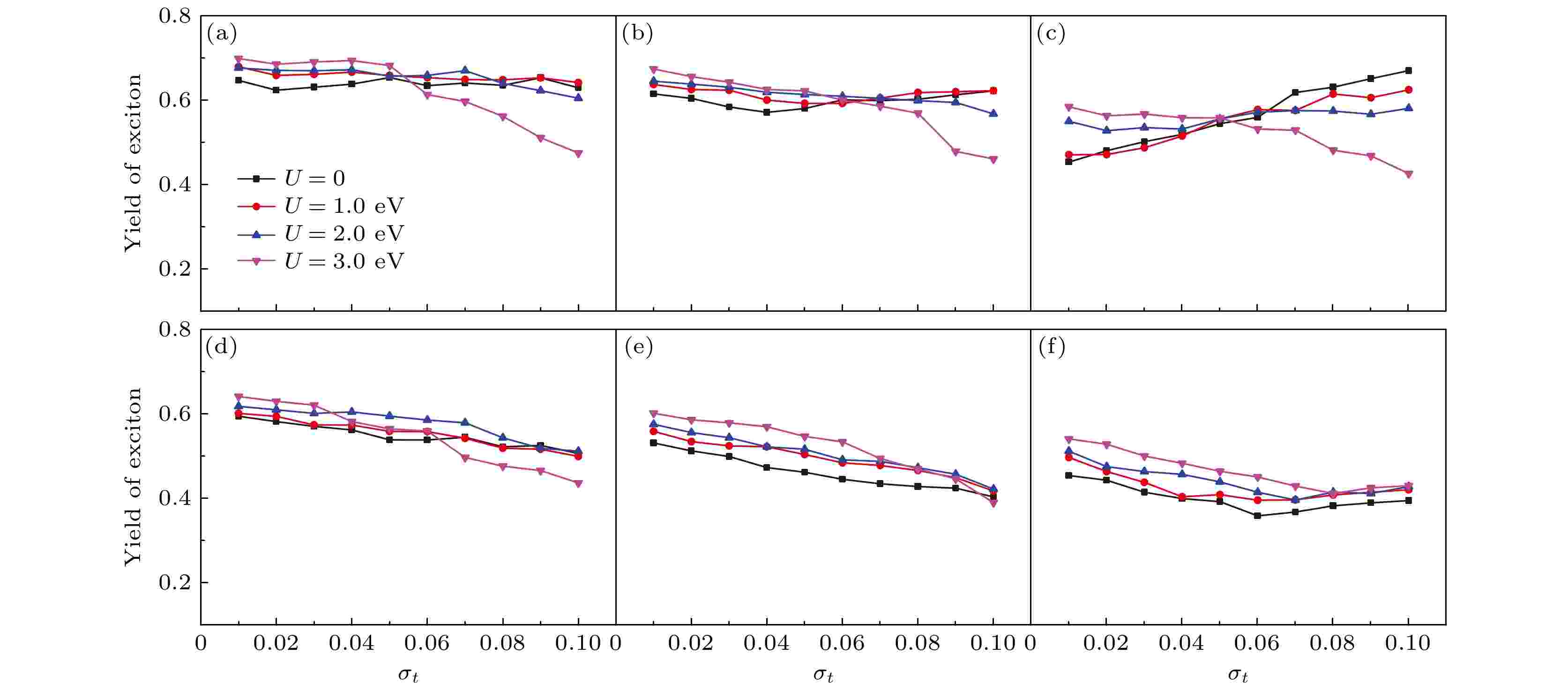 图 3 激子的产率在不同链长和电子关联下随着非对角无序强度的变化 (a)
图 3 激子的产率在不同链长和电子关联下随着非对角无序强度的变化 (a) 


















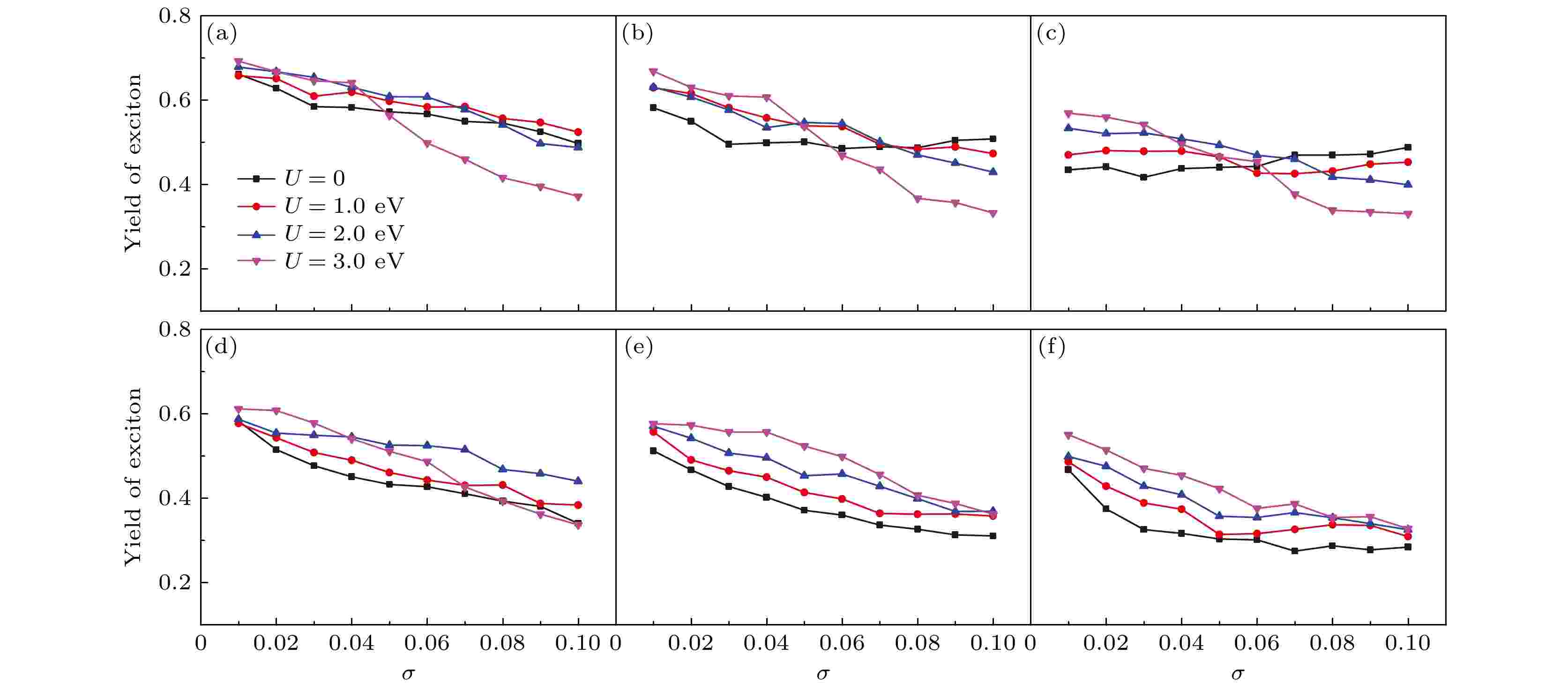 图 4 两种无序同时存在时, 激子的产率在不同链长和电子关联下随着无序强度的变化 (a)
图 4 两种无序同时存在时, 激子的产率在不同链长和电子关联下随着无序强度的变化 (a) 












