摘要:本文建立了高气压下的氦气放电模型, 通过与试验对比, 验证了模型的有效性, 并利用该模型对高气压下“场致发射”的影响进行了探讨. 通过Fowler-Nordheim方程将电流密度转化为电子通量, 并将电子通量添加到COMSOL相应的壁边界条件中进行仿真, 在宏观层面(击穿电压)以及微观层面(空间电子密度)进行分析. 研究发现, 场致发射电流密度J由电场强度E、场增强因子$\beta $以及金属逸出功W共同决定; $\beta = 300$时场致发射的影响可以忽略, 而对于$\beta = 400$、电场强度10 MV/m以上的工况, 场致发射对击穿的影响较大; 对于以铜为平行平板电极的氦气击穿来说, 电场强度E小于8 MV/m 时可以忽视场致发射的作用; 在微观层面上, 场致发射能够给放电空间提供新的“种子电子”, 进而提升整个空间的电子密度, 使得粒子碰撞反应加剧, 最终导致击穿.
关键词: 场致发射/
氦气/
高气压/
击穿电压

English Abstract

全文HTML

--> --> -->

高温气冷堆(high-temperature gas-cooled reactor, HTGR)作为第四代反应堆堆型之一, 由于其具有较高的固有安全性和热电转化效率等优势, 近年来得到了广泛关注^[1]. 氦气具有中子吸收截面小、化学性质稳定、高比热、高导热系数等特点, 故被选用为HTGR的一回路冷却剂. HTGR在运行工况下的氦气压力高达7 MPa, 这就给工作在氦气环境下的主氦风机及其电磁轴承、电气贯穿件等电气设备的绝缘设计带来了挑战, 故研究高气压下的氦气击穿特性具有十分重要的工程意义^[2]. 在7 MPa下, 平行极板间的电场强度最高时可达10 MV/m, 在此高场强下, 场致发射将是一个不可忽视的放电机制. 因此, 探究场致发射对高气压氦气平行极板击穿电压的影响就非常重要.
早在1928年Fowler和Nordheim就提出了金属场致发射理论. 在金属中, 若存在外电场, 金属表面势垒将变形, 这时将有部分导带的电子“透过”势垒而脱离金属表面, 该现象称为“场致发射”. 场致发射在真空放电中起着重要作用, 它常常是高真空中气体击穿的原因^[3]. 迄今为止, 不少研究者探究了场致发射现象. Little等^[4]利用电子显微镜发现, 多种金属表面上都存在微凸, 达微米量级, 这会使得尖端处电场放大倍数达100以上, 达到场致发射条件. 张喜波等^[5]分析认为, 场致发射电流会持续加热电流通道内的气体, 导致气体温度上升和通道内气体分子数密度降低, 由于电子平均自由程与气体分子数密度成反比, 因此随着平均自由程的增大, 电子更容易获得足以导致“雪崩”的能量, 进而降低了对间隙电场强度的要求, 即场致发射电流的加热效应在某种程度上抵消了增大气压对击穿场强的提升效果. 徐翱等^[6]建立了微间隙气体放电形成过程的仿真模型, 并分析了考虑和不考虑场致电子发射对这种微间隙气体放电形成过程的影响, 讨论得到了间隙间距在2—5 μm范围时, 形成微间隙气体放电过程的主要因素是阴极场致电子发射和随后的离子增强场致电子发射; 而当间隙间距小于1 μm 时, 场致电子发射将会在微间隙气体放电过程中起主要作用. 气体放电的主要机制是电子碰撞电离(electron impact ionization, EII), 二次电子发射(secondary electron emission, SEE)和场致电子发射(field emission, FE)^[7]. Wallash等^[8]分析认为, 当电极间隙d > 5 μm时, EII 和SEE 占主导地位; 当电极间隙 d < 5 μm时, FE 占主导地位. 潜力等 ^[9]研究了碳纳米管在大气压环境中的场致发射特性, 实验结果表明碳纳米管场致发射阴极与阳极间距在100—200 nm时, 可以在1 atm(1 atm=101325 Pa)的空气以及惰性气体环境中发射电子, 电子与气体分子碰撞的几率很低, 气体原子被电子碰撞后电离几率也很低. 孙强等^[10]在研究氮气火花开关击穿机制时发现, 如果需要阴极-触发极、阳极-触发极同时击穿的话, 其阴极-触发极之间的外加电压需要大于1.18 kV、阳极-触发极之间的外加电压需要大于3 kV, 而考虑触发极的场致发射后, 该击穿阈值可以显著降低. 当钨暴露于氦等离子体流时, 表面将会有纳米结构的钨束. Sinelnikov等^[11]研究发现若钨表面有纳米级的束状钨时, 场致发射的场增强因子能达数千, 其能在1—5 MV/m 的电场强度下得到单位为μA/cm²的场致发射电流密度. 而Shin等^[12]也发现若钨表面有纳米级的束状钨时, 由于场致发射的增强, 触发电弧放电的几率将会增大.
当前关于场致发射的研究主要集中在微米间隙下场致发射的影响以及场致发射的应用, 而关于毫米间隙下的场致发射对击穿影响的研究较少. 因此, 有必要探究毫米间隙下场致发射对击穿的影响. 本文通过对比1 MPa下不同温度以及不同间隙时氦气击穿电压的仿真值和实验值, 验证了高气压氦气仿真模型的有效性, 并利用该模型从宏观和微观两个角度探究了7 MPa下场致发射的影响.

2

-->

2.1.控制方程

在放电过程中, 氦气原子(He)的数密度可近似认为无变化, 且取决于气体的温度和压强. 计算中涉及的其他粒子主要有5种, 即电子(e)、氦原子离子(He⁺)、氦分子离子(${\rm{He}}_2^+ $)、氦激发态原子(He^*)以及氦激发态分子(${\rm{He}}_2^* $). 本文采用流体模型进行数值仿真, 等离子体控制方程主要有泊松方程、重粒子连续性方程、电子连续性方程.
泊松方程用于求解等离子体区域的电场E和电势$\varphi $:

$E = - \nabla \varphi , $

${\varepsilon _{\rm{r}}}{\nabla ^2}\varphi = - \frac{\rho }{{{\varepsilon _0}}}, $

其中, $\rho $为空间电荷密度; ${n_i}$是正离子数密度; ${\varepsilon _0}$是真空介电常数, 即8.85 × 10¹² F/m; ${\varepsilon _{\rm{r}}}$是氦气的相对介电常数, 值为1.000074, 可近似取1.
重粒子(氦原子除外)的连续性方程如下:

$\rho \frac{{\partial {w_k}}}{{\partial t}} = \nabla \cdot {{{\varGamma }}_k} + {S_k},~~ k = 1,2,3,4, $

其中$\rho $是气体密度; 对于第k种重粒子, ${{{\varGamma }} _{{k}}}$是迁移扩散通量, ${S_k}$是源项, ${w_k}$是质量分数.
电子的连续性方程如下:

$\frac{{\partial {n_{\rm{e}}}}}{{\partial t}} + \nabla \cdot {{{\varGamma }} _{\rm{e}}} = {S_{\rm{e}}}$

$\frac{{\partial {n_{\rm{\varepsilon }}}}}{{\partial t}} + \nabla \cdot {{{\varGamma }} _{\rm{\varepsilon }}} = {S_{\rm{\varepsilon }}} - {\rm{e}}{{{\varGamma }} _{\rm{\varepsilon }}} \cdot {{E}}$

其中, n_e和n_ε分别为电子数密度和电子能量密度; ${{{\varGamma }} _{\rm{e}}}$和${{{\varGamma }} _{\rm{\varepsilon }}}$分别是电子数密度通量和电子能量通量; E是空间的局部电场强度; ${S_{\rm{e}}}$是电子密度净增加量的源项, 其数值通过反应列表电子参与的碰撞综合计算得到; ${S_{\rm{\varepsilon }}}$是电子能量的源项, 表示碰撞过程中交换的能量的总和.
2 -->

2.2.等离子体化学反应

本文在仿真中考虑了21个碰撞反应, 碰撞过程相应的反应式、速率常数和反应能见表1. 模型中的$\alpha $系数及输运参数见表2.

反应式	速率常数	反应能/eV	参考文献
${\rm{e}} + {\rm{He}} \to {\rm{2 e}} + {\rm{H}}{{\rm{e}}^ + }$	$\alpha {V_{\rm{e}}}/{N_{{\rm{He}}}}$	24.6	[13]
${\rm{e }}+ {\rm{H}}{{\rm{e}}^{\rm{*}}} \to {\rm{2 e}} + {\rm{H}}{{\rm{e}}^ + }$	$1.5 \times {10^{ - 13} }\sqrt { {T_{\rm{e} } } } \exp \left( { - \dfrac{ {4.77} }{ { {T_{\rm{e} } } } } } \right)$	4.78	[13]
${\rm{e}} + {\rm{He}}_{\rm{2}}^{\rm{*}} \to {\rm{2 e}} + {\rm{He}}_{\rm{2}}^ + $	$9.75 \times {10^{ - 16} }T_{\rm{e} }^{0.71}\exp \left( { - \dfrac{ {3.4} }{ { {T_{\rm{e} } } } } } \right)$	3.4	[13]
${\rm{H}}{{\rm{e}}^{\rm{*}}} + {\rm{H}}{{\rm{e}}^{\rm{*}}} \to {\rm{e}} +{\rm{ He }}+{\rm{ H}}{{\rm{e}}^ + }$	$8.7 \times {10^{ - 16} }\sqrt {\dfrac{ { {T_{\rm{g} } } }}{ {0.025} } }$	0	[13]
${\rm{He}}_{\rm{2}}^{\rm{*}} + {\rm{He}}_{\rm{2}}^{\rm{*}} \to {\rm{e}} + {\rm{3 He }}+{\rm{ H}}{{\rm{e}}^ + }$	$8.7 \times {10^{ - 16} }\sqrt {\dfrac{ { {T_{\rm{g} } } }}{ {0.025} } }$	0	[13]
${\rm{He}}_{\rm{2}}^{\rm{*}} + {\rm{He}}_{\rm{2}}^{\rm{*}} \to {\rm{e}} +{\rm{ 2 He}} +{\rm{ He}}_{\rm{2}}^ + $	$2.03 \times {10^{ - 15} }\sqrt {\dfrac{ { {T_{\rm{g} } } }}{ {0.025} } }$	0	[13]
${\rm{e}} + {\rm{He}} \to {\rm{e }}+ {\rm{H}}{{\rm{e}}^{\rm{*}}}$	$\dfrac{ {1.6 \times { {10}^{ - 15} }\exp \left( { - 350/{x^2} } \right)} }{ { {x^{0.3} }\left( {1 + 0.43{x^{1.2} } } \right)} }$	19.8	[13]
${\rm{e }}+ {\rm{H}}{{\rm{e}}^{\rm{*}}} \to {\rm{e}} + {\rm{He}}$	$3 \times {10^{ - 15} } + \dfrac{ {5 \times { {10}^{ - 13} }\exp \left( { - 1.398/{T_{\rm{e} } } } \right)} }{ {1 + 5\exp \left( { - 0.602/{T_{\rm{e} } } } \right)} }$	–19.8	[13]
${\rm{e}} + {\rm{He}} \to {\rm{e}} + {\rm{He}}$	横截面数据	0
${\rm{2 He }}+{\rm{ H}}{{\rm{e}}^ + } \to {\rm{He}} +{\rm{ He}}_{\rm{2}}^ + $	$1 \times {10^{ - 43}}$	0	[13]
${\rm{2 He }}+{\rm{ H}}{{\rm{e}}^{\rm{*}}} \to {\rm{He}} +{\rm{ He}}_{\rm{2}}^{\rm{*}}$	$8.1 \times {10^{ - 48}}T\exp \left( { - 650/T} \right)$	0	[13]
${\rm{e }}+ {\rm{H}}{{\rm{e}}^ + } \to {\rm{H}}{{\rm{e}}^{\rm{*}}}$	$6.76 \times {10^{ - 19}}{T_{\rm{e}}}^{ - 0.5}$	–4.78	[14]
${\rm{e }}+ {\rm{H}}{{\rm{e}}^ + } \to {\rm{He}}$	$1.327 \times {10^{ - 27}}{n_{\rm{e}}}T_{\rm{e}}^{ - 4.4}$	–24.6	[14]
${\rm{e}} + {\rm{He}}_{\rm{2}}^ + \to {\rm{He}} +{\rm{ H}}{{\rm{e}}^{\rm{*}}}$	$5 \times {10^{ - 15}}$	0	[13]
${\rm{e}} + {\rm{He}}_{\rm{2}}^ + \to {\rm{He}}_{\rm{2}}^{\rm{*}}$	$5 \times {10^{ - 15} }({ { {T_{\rm{g} } } } }/{ { {T_{\rm{e} } } } })$	–3.4	[13]
${\rm{e}} +{\rm{ He }}+{\rm{ H}}{{\rm{e}}^ + } \to {\rm{He}} +{\rm{ H}}{{\rm{e}}^{\rm{*}}}$	$1 \times {10^{ - 38}}{\left( {{T_{\rm{e}}}/{T_{\rm{g}}}} \right)^{ - 2}}$	0	[13]
${\rm{2 e}} + {\rm{He}}_{\rm{2}}^ + \to {\rm{e + 2 H}}{{\rm{e}}^{\rm{*}}}$	$6.186 \times {10^{ - 39}}{T_{\rm{e}}}^{ - 4.4}$	0	[15]
${\rm{2 e}} + {\rm{He}}_{\rm{2}}^ + \to {\rm{e}} + {\rm{He}}_{\rm{2}}^{\rm{*}}$	$7.1 \times {10^{ - 32}}$	0	[15]
${\rm{e }}+ {\rm{He }}+ {\rm{He}}_{\rm{2}}^ + \to {\rm{He}} +{\rm{ He}}_{\rm{2}}^{\rm{*}}$	$5 \times {10^{ - 39} }({ { {T_{\rm{g} } } } }/{ { {T_{\rm{e} } } } })$	0	[13]
${\rm{e }}+ {\rm{He }}+ {\rm{He}}_{\rm{2}}^ + \to {\rm{2 He }}+{\rm{ H}}{{\rm{e}}^{\rm{*}}}$	$5 \times {10^{ - 39}}$	0	[15]
${\rm{2 e}} + {\rm{He}}_{\rm{2}}^ + \to {\rm{e}} +{\rm{ He }}+{\rm{ H}}{{\rm{e}}^{\rm{*}}}$	$2.8 \times {10^{ - 32}}$	0	[15]
注: ${V_{\rm{e}}}$表示电子迁移速度(迁移率与场强的乘积), ${N_{{\rm{He}}}}$是氦原子数密度, 由理想气体状态方程求得; ${T_{\rm{e}}}$和${T_{\rm{g}}}$分别是以eV表示的电子温度和气体温度, T 表示以K为单位的气体温度; x 表示以${\rm{Td}}$ ($1~{\rm{ Td} } = {10^{ - 17} }\;{\rm{ V} } \cdot {\rm{c} }{ {\rm{m} }^{\rm{2} } }$)为单位的约化场强; 横截面数据来源于https://fr.lxcat.net/home/中的 Phelps 数据库; 表中二体反应(两种反应物)的速率常数单位是m3/s, 三体反应(三种反应物)的速率常数单位是m6/s.

表1模型考虑的粒子碰撞过程
Table1.Collision processes considered in the model.

参数	计算式	参考文献		参数	计算式	参考文献
α/m–1	$0.41 p{ {\rm{e} }^{ - 18.116 p/E} }$	[16]		De/(m2·s–1)	$2.3 \times {10^{24}}{T_{\rm{e}}}/{N_{{\rm{He}}}}$	[17]
	$ + 1.93 p{ {\rm{e} }^{ - 84.541 p/E} } $			Dp/(m2·s–1)	$3.25 \times {10^{22}}{T_{\rm{e}}}/{N_{{\rm{He}}}}$	[17]
μe/(m2·s–1·V–1)	$2.83 \times {10^{24}}/{N_{{\rm{He}}}}$	[17]		Di/(m2·s–1)	$4.88 \times {10^{22}}{T_{\rm{e}}}/{N_{{\rm{He}}}}$	[17]
μp/(m2·s–1·V–1)	$3.25 \times {10^{22}}/{N_{{\rm{He}}}}$	[17]		Dm/(m2·s–1)	$\dfrac{ {5.6} }{ {133.3 p} }{\left( {\dfrac{ { {T_{\rm{g} } } }}{ {0.025} } } \right)^{1.5} }$	[17]
μi/(m2·s–1·V–1)	$4.88 \times {10^{22}}/{N_{{\rm{He}}}}$	[17]		Dj/(m2·s–1)	$\dfrac{ {4.1} }{ {133.3 p} }{\left( {\dfrac{ { {T_{\rm{g} } } }}{ {0.025} } } \right)^{1.5} }$	[17]
注: 电子(e)、氦原子离子(He+)、氦分子离子(${\rm{He}}_2^+ $)、氦激发态原子(He*)以及氦激发态分子(${\rm{He}}_2^* $), 分别对应下标e, p, i, m和j.

表2模型中的$\alpha $系数及输运参数
Table2.$\alpha $ coefficient and transport parameters in the model.

2 -->

2.3.几何模型与初边值条件

在COMSOL中选择二维轴对称模型, 其中r = 0处为对称轴, 铜电极半径为3 cm, 上边界AD为阳极, 下边界BC为阴极(如图1所示).
图 1 模型几何结构
Figure1. Geometry of the model.

本文设定初始电子密度为10¹⁰ m^–3, 电子温度根据其与局部电场的关系得到, 数值^[18]为$1.5 \times $$ \left( {1.987 \times {{10}^{ - 6}}\left| E \right| + 3.822} \right){\rm{ eV}}$; 根据电中性原则, ${\rm{H}}{{\rm{e}}^ + }$和${\rm{He}}_{\rm{2}}^ + $的数密度之和也为10¹⁰ m^–3, 不妨假设初始时${\rm{H}}{{\rm{e}}^ + }$和${\rm{He}}_{\rm{2}}^ + $分别占$30\% $和$70\% $; ${\rm{H}}{{\rm{e}}^{\rm{*}}}$和${\rm{He}}_{\rm{2}}^{\rm{*}}$的初始摩尔分数设为${10^{ - 20}}$(表示粒子与氦原子数密度之比).
电子通量和电子能量通量的边界条件如下^[19,20]:

${{n}} \cdot {{{\varGamma }} _{\rm{e}}} = \frac{1}{2}\sqrt {\frac{{8{k_{\rm{B}}}{T_{\rm{e}}}}}{{{\rm{\pi }}{m_{\rm{e}}}}}} {n_{\rm{e}}} - \sum {{\gamma _{\rm{i}}}} ({{n}} \cdot {{{\varGamma }} _{\rm{i}}}), $

${{n}} \cdot {{{\varGamma }} _{\rm{\varepsilon }}} = \frac{5}{6}\sqrt {\frac{{8{k_{\rm{B}}}{T_{\rm{e}}}}}{{{\rm{\pi }}{m_{\rm{e}}}}}} {n_{\rm{\varepsilon }}} - \sum {{\gamma _{\rm{i}}}\mathop {{\varepsilon _{\rm{i}}}}\limits^ - } ({{n}} \cdot {{{\varGamma }} _{\rm{i}}}).$

对于铜电极, 二次电子发射系数${\gamma _{\rm{i}}}$在阴极BC处取$0.19$^[21], 阳极AD处取0, 二次电子平均能$\mathop {{\varepsilon _{\rm{i}}}}\limits^ -$取15.3 eV. ${m_{\rm{e}}}$是电子质量. n是指向边界的单位法向量, ${{{\varGamma }} _{\rm{i}}}$是边界的离子通量.
重粒子的边界条件如下^[19,20]:

${{n}} \cdot {{{\varGamma }} _k} = {M_k}{R_{s,k}} + {\alpha _s}{M_k}{c_k}{\mu _{k,m}}{z_k}\left( {{{E}} \cdot {{n}}} \right), $

${R_{s,k}} = {c_k}\sum\limits_{i = 1}^N {{v_{i,k}}} \frac{1}{4}\sqrt {\frac{{8R{T_{\rm{g}}}}}{{\pi {M_{\rm{m}}}}}} , $

其中${{{\varGamma }} _k}$代表物质k的通量向量, ${M_k}$, ${c_k}$分别代表重物质k的摩尔质量和摩尔浓度, ${R_{s, k}}$指物质k的表面反应速率, ${{{\mu}} _{{k} {, }{\rm{m}}}}$指迁移率. ${{{z}}_{{k}}}$指电荷数. 若${{E}} \cdot {{n}} \geqslant {\bf{0}}$, ${\alpha _{\rm{s}}}$取1, 否则, 取0. $ {v}_{i, k}$表示第i表面反应中第k物质的化学计量系数, ${{M} _{\rm{m}}}$是平均摩尔质量. 模型的边界条件如表3所示.

边界	$ \varphi $	$ {n}_{\rm{e}} $	$ {n}_{\rm{\varepsilon }} $	ni	$ {n}_{\rm{n}} $
AD	$ {V}_{a} $	(6)	(7)	(8)	(8)
BC	$ 0 $	(6)	(7)	(8)	(8)
AB, CD	$\dfrac{\partial \varphi }{\partial r}=0$	$ -{{n}}\cdot {{\varGamma }}_{\bf{e}}=0 $	$ -{{n}}\cdot {{\varGamma }}_{\bf{\varepsilon }}=0 $	$ -{{n}}\cdot {{\varGamma }}_{{k}}=0 $	$ -{{n}}\cdot {{\varGamma }}_{{k}}=0 $

表3模型边界条件
Table3.Boundary conditions in the model.

试验^[13]采用一组平行平板电极来研究毫米级间隙高压氦气击穿特性, 电极与陶瓷绝缘板通过螺栓紧固件连接(如图2所示). 板电极直径为100 mm(后改用60 mm, 对击穿电压无明显影响), 厚度为10 mm, 边缘处留有半径为3 mm的圆倒角, 用以减小电场的边缘效应.
图 2 平行平板
Figure2. Parallel plate.

本文的仿真参数与的实验参数保持一致, 如表4所示.

参数	值
温度/℃	25, 105, 155, 180
压强/ MPa	1, 7
间距/ mm	0.25, 031, 0.53, 3.02
半径/ cm	3
外加电压	直流

表4实验与仿真参数
Table4.Parameters of experimentand simulation.

本文将模型计算的仿真电压值与试验测量电压值进行了对比, 结果见图3. 实验采用1 mA作为击穿判据, 仿真也采用1 mA作为击穿判据, 超过1 mA视为击穿, 反之, 视为未击穿.
图 3 1 MPa下实验值与仿真值　(a) 25 ℃; (b) 105 ℃; (c) 155 ℃ (d) 180 ℃
Figure3. Experimental value and simulation value at 1 MPa: (a) 25 ℃; (b) 105 ℃; (c) 155 ℃; (d) 180 ℃.

从图3 中可以看出1 MPa下仿真数据与实验数据较为符合, 仅仅在3.02 mm时误差达到$10{\text{%}} $左右, 1 mm以内基本相符. 通过与实验数据的对比, 本文所采用的高气压氦气放电模型得到了验证, 该模型可以定性用于研究高气压下的场致发射及相关的氦气放电机理.

相比于1 MPa, 7 MPa在相同间隙下的击穿电压更大(如图4所示), 故电场强度也更大(如图5所示). 7 MPa下的部分试验工况电场强度达到10 MV/m, 在如此高场强下, 场致发射是否会对击穿产生较大影响值得深入研究.
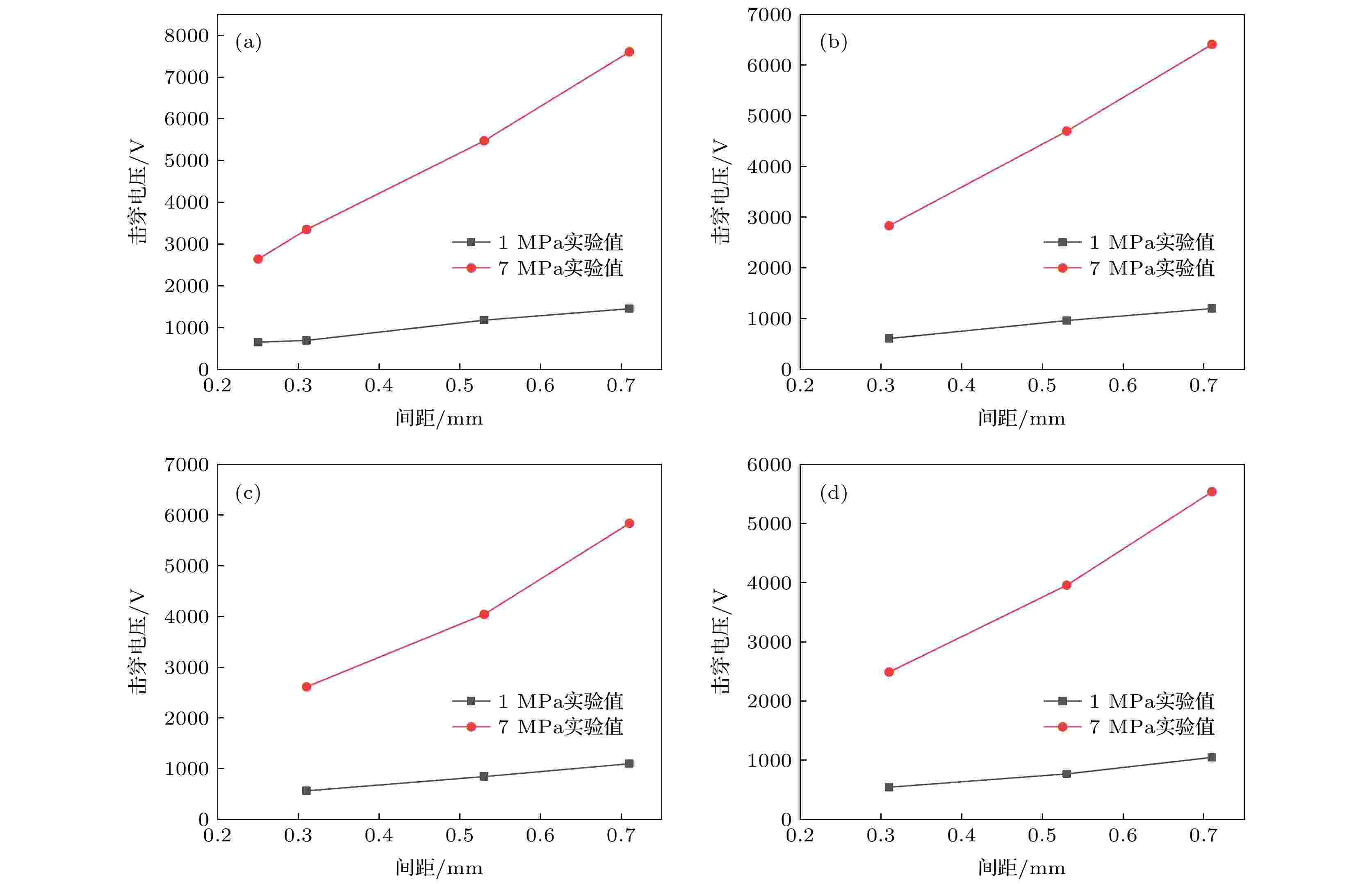图 4 1 MPa和7 MPa下的实验值　(a) 25 ℃; (b) 105 ℃; (c) 155 ℃; (d) 180 ℃
Figure4. Experimental value at 1 MPaand7 MPa: (a) 25 ℃; (b) 105 ℃; (c) 155 ℃; (d) 180 ℃.

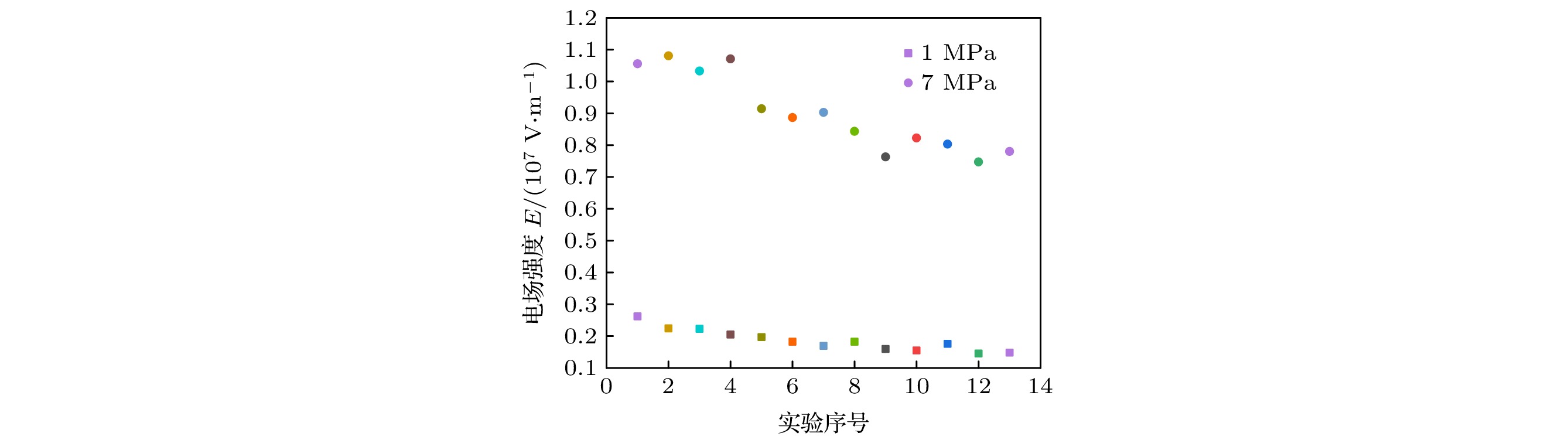图 5 1 MPa和7 MPa下的实验击穿场强
Figure5. Experimental breakdown field strength at 1 MPa and 7 MPa.

2

-->

4.1.场致发射理论

场致发射电流密度的 Fowler-Nordheim 公式^[5]可以简化为

$ \begin{split} J =\;& {{1.4 \times {{10}^{ - 14}}{{{\beta}} ^2}{E^2}}}/{W}\\ &\times\exp \bigg( {9.25{W^{ - \tfrac{1}{2}}} - 6.51 \times {{10}^9} \times \frac{{{W^{\tfrac{3}{2}}}}}{{{{\beta}} E}}} \bigg), \end{split}$

其中, J是电流密度大小, 单位为${\rm{A}}/{{\rm{m}}^2}$; 电场强度E单位为${\rm{V}}/{\rm{m}}$; 金属逸出功W单位是${\rm{eV}}$, 铜的逸出功为${\rm{4}}.65\;{\rm{ eV}}$; $\beta $是金属表面微凸的场增强因子, 对于平行铜板电极可取300—400^[5].
从图6中可以看出场致发射电流密度J随$\beta $的增大近似呈指数增大, 随电场强度E的增大也近似呈指数增大, 随金属逸出功W的增大近似呈指数减小.
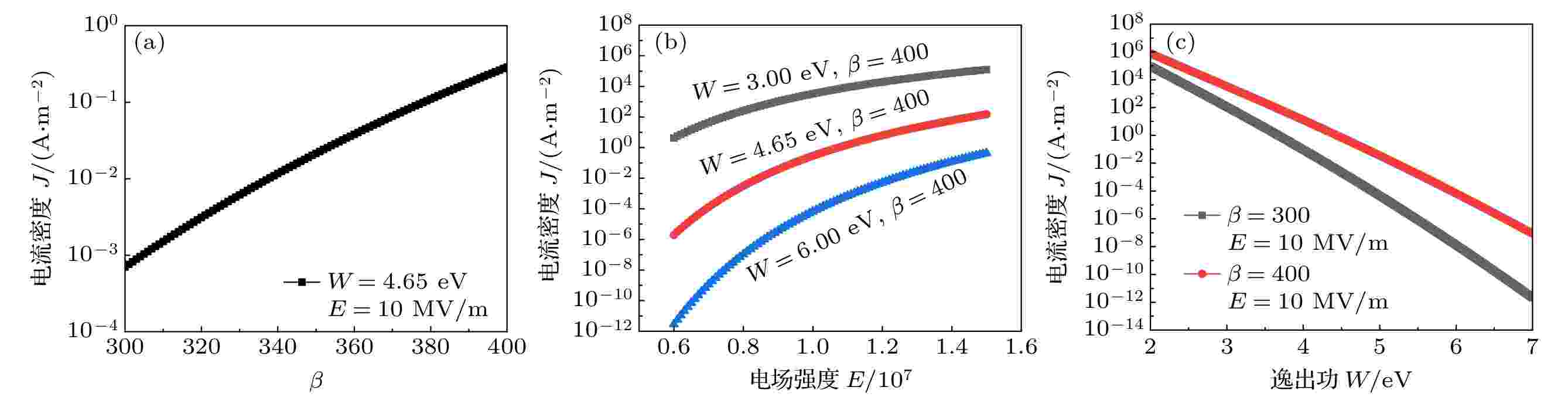图 6 电流密度的影响因素　(a) $\beta $; (b) E; (c)W
Figure6. Influencing factors of current density: (a) $\beta $; (b) E; (c)W.

2 -->

4.2.COMSOL仿真

本文在COMSOL模型的阴极处添加一个电子通量来代替场致发射效应. 此时电子通量和电子能量通量在阴极BC处的边界条件为

$ {{n}} \cdot {{{\varGamma }} _{\rm{e}}} = \frac{1}{2}\sqrt {\frac{{8{k_{\rm{B}}}{T_{\rm{e}}}}}{{{\rm{\pi }}{m_{\rm{e}}}}}} {n_{\rm{e}}} - \left[ {\sum {{\gamma _{\rm{i}}}} ({{n}} \cdot {{{\varGamma }} _{\rm{i}}}) + {{n}} \cdot {{{\varGamma }} _{\rm{t}}}} \right], $

${{n}} \cdot {{{\varGamma }} _{\rm{\varepsilon }}} = \frac{5}{6}\sqrt {\frac{{8{k_{\rm{B}}}{T_{\rm{e}}}}}{{{\rm{\pi }}{m_{\rm{e}}}}}} {n_{\rm{\varepsilon }}} - \left[ {\sum {{\gamma _{\rm{i}}}\mathop {{\varepsilon _{\rm{i}}}}\limits^ - } ({{n}} \cdot {{{\varGamma }} _{\rm{i}}}) + {\varepsilon _{\rm{t}}}\left( {{{n}} \cdot {{{\varGamma }} _{\rm{t}}}} \right)} \right], $

其中${\varepsilon _{t}}$是电子能量, 数值^[15]为$1.5 \times ( 1.987 \times {{10}^{ - 6}} $$ \left| E \right| + 3.822 ){\rm{ eV}}$. 通过阴极附近的电荷量来建立等式, 将场致发射电流密度转化为电子通量${{{\varGamma }} _{\rm{t}}}$, 具体流程如图7. $\Delta t$表示时间微元, $\Delta S$表示面积微元:
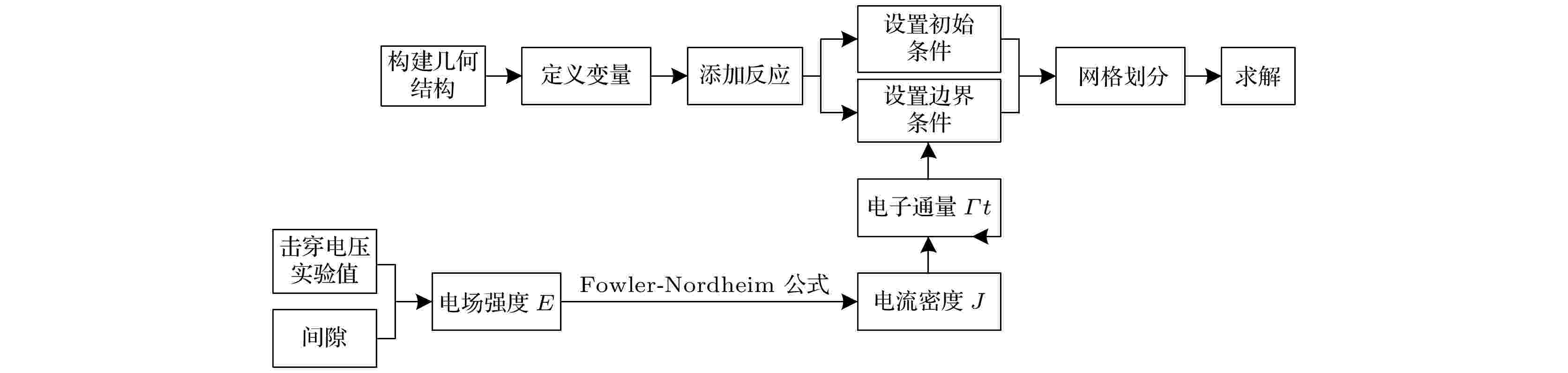图 7 流程图
Figure7. Flow chart.

${{{\varGamma }} _{\rm{t}}} \times \Delta t \times \Delta S \times {q_e} = J \times \Delta t \times \Delta S, $

${{{\varGamma }} _{\rm{t}}} = {J}/{{{q_{\rm{e}}}}}.$

2 -->

4.3.微观层面场致发射影响

本文从微观角度初步探讨了场致发射的影响. 对于氦气放电来说, 击穿的本质可以认为是带电粒子密度的急剧增大. 当电压达到临界击穿电压时, 带电粒子的消耗率小于带电粒子的生成率, 带电粒子骤增引发电流突变, 从而导致击穿.
本文研究了场致发射电子通量对初始时刻以及后期击穿时刻电子密度的影响. 以气压为7 MPa、温度为25 ℃、间距为0.25 mm的工况为例. 未考虑场致发射电子通量时电压为3365 V未击穿, 3375 V时击穿; 考虑场致发射电子通量时, 3365 V也能够击穿($\beta = 400$).
本文模型采用二维轴对称, 放电空间是一个圆柱空间, 电子密度在径向可以近似同步变化, 故研究将焦点集中于如图8所示电子密度在轴向的变化. 图8(a)未考虑场致发射, 电压为3365 V; 图8(b)考虑了场致发射, 电压为3365 V. 从图8(a)可以看出, 未考虑场致发射时, 阴极附近的电子密度率先降低, 21 ns时整个空间的电子密度保持相对的稳定, 约在10⁸ m^–3量级. 从图8(b)可以看出, 若考虑场致发射电子通量, 由于阴极相当于一个“电子源”, 源源不断提供电子, 故阴极附近出现高电子密度区域, 该区域不断向阳极扩散, 21 ns时整个空间的电子密度保持相对稳定, 接近10¹³ m^–3量级. 对比可以看出, 场致发射的存在会使初始阶段的空间电子密度大大提升, 提高接近5个数量级. 电子密度的提升会加剧电离, 当电离程度急剧加大时, 全部带电粒子的密度将会剧增, 就可以导致击穿.
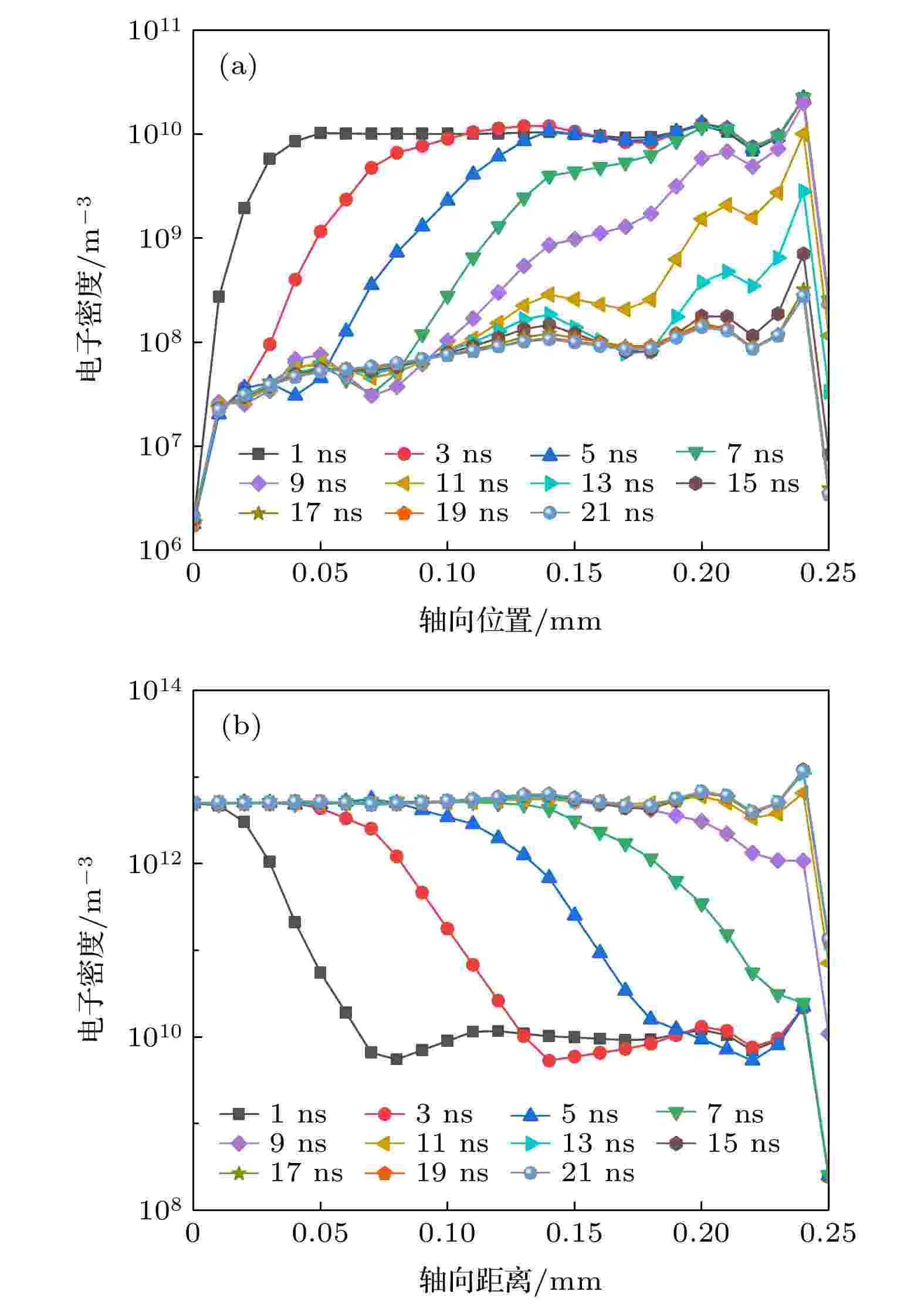图 8 轴向位置的电子密度
Figure8. Electron density in Z axis.

图9描述了3365 V和3375 V(临界击穿电压)时空间平均电子密度的变化, 可以看出, 场致发射的存在会使初期空间电子密度长时间保持在高水平, 使得放电后期反应的激烈程度增加, 最后导致击穿.
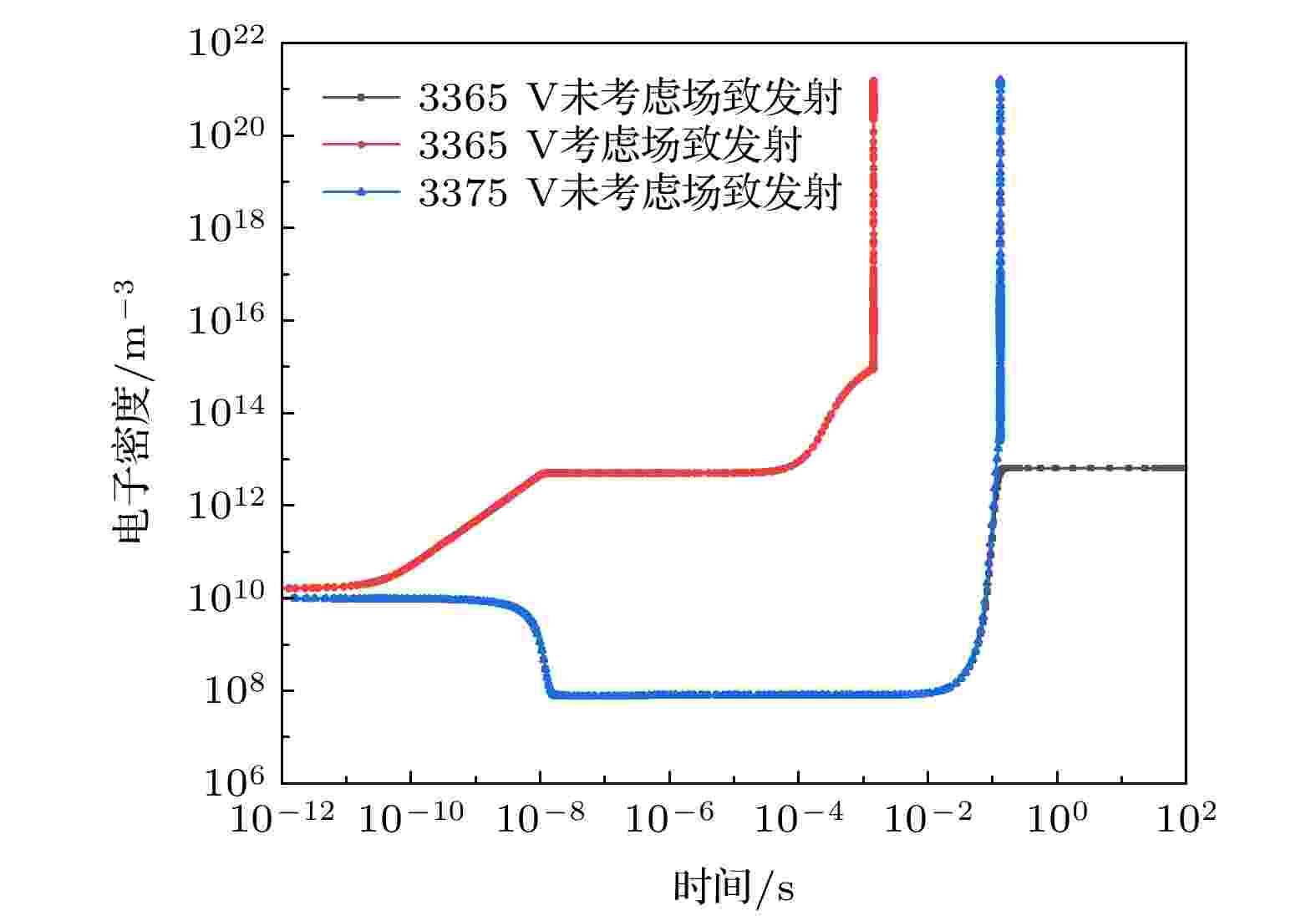图 9 电子密度演化图
Figure9. Evolutiondiagramofelectron density.

2 -->

4.4.宏观层面场致发射的影响

3 -->

4.4.1.理论分析

本文探究了场致发射对击穿电压的影响, 实验过程以1 mA为判据, 电流超过1 mA为击穿, 故在仿真中也以1 mA为判据. 电场强度E由实验值的击穿电压求得, 铜的逸出功$W = 4.65\;{\rm{ eV}}$, 电流密度J随$\beta $的增大 近似呈指数增大($\beta $的取值为300—400), 故只需要讨论$\beta = 300$和$\beta = 400$就可以将电流密度J的范围确定, 这样就能全面考虑场致发射的影响.
本文中试验和仿真对于击穿的判据均为1 mA, 可以根据(6) 式计算$\beta = 300$和$\beta = 400$时25 ℃和180 ℃下的场致发射电流.
从表5可以看出$\beta = 300$时, 场致发射电流(最大为$1.17 \times {10^{ - 5}}\;{\rm{ A}}$)相比击穿判据(${10^{ - 3}}\;{\rm{ A}}$)太小, 基本不到$1\% $, 故$\beta = 300$时对击穿几乎没有影响. $\beta = 400$时, 温度25 ℃, 场致发射电流都大于击穿判据$\left( {{{10}^{ - 3}}\;{\rm{ A}}} \right)$, 故25 ℃时, 场致发射对击穿影响较大; 180 ℃时, 场致发射电流在10^–6—10^–5 A量级, 故该条件下场致发射对击穿几乎没有影响.

温度/℃	间距/mm	实验值/V	场强/(MV·m–1)	I/A
				$\beta = 300$	$\beta = 400$
25	0.25	2640	10.56	$7.01 \times {10^{ - 6}}$	$2.2 \times {10^{ - 3}}$
	0.31	3350	10.81	$1.17 \times {10^{ - 5}}$	$4.2 \times {10^{ - 3}}$
	0.53	5475	10.33	$4.24 \times {10^{ - 6}}$	$1.5 \times {10^{ - 3}}$
	0.71	7605	10.71	$9.65 \times {10^{ - 6}}$	$2.8 \times {10^{ - 3}}$
180	0.31	2490	8.03	$6.20 \times {10^{ - 9}}$	$9.62 \times {10^{ - 6}}$
	0.53	3960	7.47	$7.02 \times {10^{ - 10}}$	$1.81 \times {10^{ - 6}}$
	0.71	5540	7.80	$2.64 \times {10^{ - 9}}$	$5.00 \times {10^{ - 6}}$

表5场致电流
Table5.Current of field emission.

此外, 从表5可以得出: $\beta \in \left[ {300, 400} \right]$, 电场强度在8 MV/m以下时, 场致发射电流不到${10^{ - 5}}\;{\rm{ A}}$(占击穿判据的1%), 故可以认为电场强度在8 MV/m以下时, 场致发射对击穿没有影响.
3 -->

4.4.2.仿真论证

仿真结果表明$\beta = 300$时, 考虑场致发射电子通量几乎对击穿结果没有影响(如图10所示). $\beta = 400$时, 温度为25 ℃时, 考虑场致发射电子通量对击穿结果影响较大; 温度为180 ℃时, 考虑场致发射电子通量几乎对击穿结果没有影响(如图10所示). COMSOL仿真结果十分符合理论分析结果
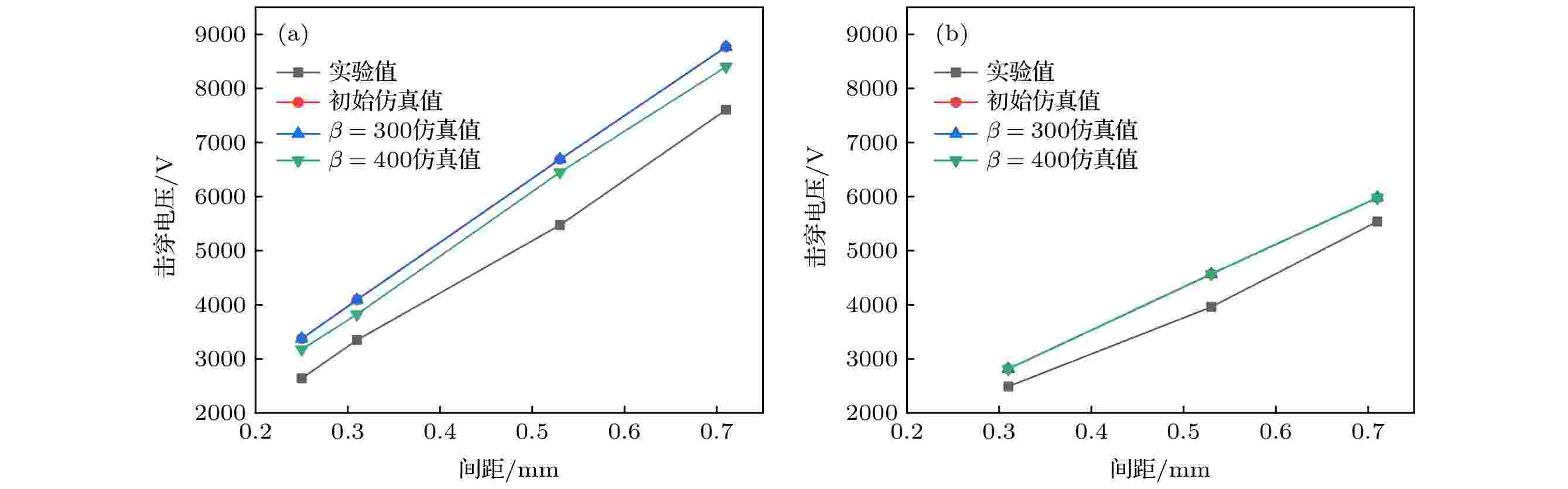图 10 7 MPa下实验值与仿真值　(a) 25 ℃; (b) 180 ℃
Figure10. Experimental value and simulation value at 7 MPa: (a) 25 ℃; (b) 180 ℃.

本文针对场致发射对高气压下氦气平行极板的击穿电压影响进行了理论与数值仿真研究, 通过理论和仿真研究, 可以发现:
(1) 7 MPa下电场强度E达到10 MV/m左右, $\beta = 300$时场致发射的影响可以忽略, 而对于$\beta = 400$, 电场强度10 MV/m以上的工况, 场致发射对击穿的影响较大;
(2)对于以铜$\left( {W = 4.65\;{\rm{ eV}}} \right)$为平行平板$( \beta \in $$ \left[ {300, 400} \right] )$电极的氦气击穿来说, 电场强度E小于8 MV/m时, 场致发射电流不到击穿判据$\left( {{{10}^{ - 3}}\;{\rm{ A}}} \right)$的$1{\text{%}} $, 故本文认为电场强度E小于8 MV/m时可以忽视场致发射的作用.
(3)本文认为场致发射能够给放电空间提供新的“种子电子”, 进而提升整个空间的电子密度, 使得粒子碰撞反应加剧, 最终导致击穿.
可以看出, 即使考虑场致发射, 7 MPa下的仿真数据和实验仍有较大差距. 分析认为差距主要来自两个方面: 第一, 由于材料加工工艺的原因, 平板电极材料表面会存在许多凸起, 而本文的场增强因子$\beta \in \left[ {300, 400} \right]$, 该经验取值可能偏低; 第二, 氦气的激发态粒子和氮气、氧气之间存在彭宁电离, 实验过程中可能混入微量的空气杂质, 空气杂质对击穿电压造成了一定影响. 在后续的工作中, 后续将深入探究空气杂质对高气压氦气放电特性的影响.