摘要:ZrO₂陶瓷耐高温、耐腐蚀、抗辐照性能强, 是极具前景的反应堆惰性基质燃料和锕系元素固化材料. 本文联合使用热峰模型和分子动力学方法, 模拟了核辐射环境下ZrO₂的相变过程: 基于热峰模型, 从快速重离子注入后能量沉积和传导的多物理过程出发, 建立热扩散方程, 求得ZrO₂晶格温度时空演变特性; 然后运用分子动力学方法模拟了该热峰作用下, 单斜ZrO₂相变的微观物理过程. 研究发现, 电子能损为30 keV·nm^–1的单一快速重离子注入后, ZrO₂中心产生一个半径为7 nm的柱形径迹, 径迹中心晶格迅速熔融, Zr原子配位数由7降至4—6, 2 ps时开始结晶并形成空洞, 空洞周围为非晶区, 非晶区外Zr原子配位数变为8, 同时X射线衍射(X-ray diffraction, XRD)计算和分析结果确认发生了单斜相向四方相的转变. 随着热峰能量向周围传递, 相变区逐渐扩大. 经热峰计算和分子动力学模拟, 辐照诱导ZrO₂由单斜相转为四方相的快速重离子的电子能损阈值为21 keV·nm^–1.
关键词: ZrO₂/
相变/
热峰/
分子动力学

English Abstract

全文HTML

--> --> -->

随着核能的不断开发利用, 高放射性核废料持续增多, 如何有效地提高核燃料利用率并减少放射性核废料, 已成为核能可持续发展所必须解决的关键问题. 近年来研究发现, 在反应堆以及加速器驱动的次临界系统中, 采用惰性基质燃料能够有效地促进钚的回收利用和次锕系元素的嬗变, 从源头上降低核废物中长寿命放射性元素的含量^[1,2]. 氧化锆(ZrO₂)陶瓷耐高温、耐腐蚀、抗辐照性能强, 是惰性基质燃料的候选材料之一^[3,4]. 然而, ZrO₂在不同温度下呈现三种不同的晶相, 1170 ℃以下为单斜相, 1170—2370 ℃之间为四方相, 2370—2715 ℃之间为立方相. ZrO₂在加热冷却过程中, 可发生单斜至四方相变(1100—1250 ℃), 以及四方至单斜相变(1050—700 ℃), 后者的剪切应变为16%—18%, 导致体积增加约5%^[5]. 核反应堆的强辐射环境可诱导ZrO₂发生相变, 这将对ZrO₂在核工业方面的应用产生极大影响, 例如惰性基质燃料相变引起的体积和应力变化将可能损坏燃料棒结构, 损伤核反应装置, 带来核泄漏风险^[1,2,6]. 因此, 研究ZrO₂在高能粒子辐照下的相变行为具有重要工程意义.
近20年来, 利用加速器技术对ZrO₂在不同种类和能量的快速重离子作用下的抗辐照性能进行了广泛研究^[7-12]. 研究发现, 单斜ZrO₂晶体在快速重离子辐照下可以转化为四方相, 并且能够在室温下稳定存在. 当前主要采用热峰模型对快速重离子诱导材料相变现象进行机理解释^[13-15], 即快速重离子辐照促进材料局部温度升高, 超过材料的相变温度, 从而诱导相变. 但热峰模型只能定量计算辐照后材料内部的温度分布, 不能直观地反映材料微观结构变化^[16]. 分子动力学能够模拟几百皮秒和几十纳米时空范围内材料微观结构演化, 已广泛应用于材料的低能辐照损伤研究中^[17,18]. 然而快速重离子辐照材料时, 能量损失过程由电子非弹性碰撞主导. 分子动力学无法描述电子与电子以及电子与声子之间的相互作用, 因此不能模拟高能粒子对材料的辐照损伤作用.
本文结合热峰模型和分子动力学两种方法的优势, 对快速重离子辐照下, ZrO₂由单斜相转化为四方相的微观过程进行模拟, 并计算诱导ZrO₂相变的快速重离子的电子能损阈值. 首先, 利用热峰模型描述快速重离子入射后, ZrO₂内部电子激发、电子-声子能量耦合、电子-电子以及声子-声子能量传递过程, 计算得出晶格温度; 然后, 根据晶格温度标定体系原子动能, 将其作为分子动力学模拟初始条件, 研究ZrO₂微观结构演化, 并通过X射线衍射(X-ray diffraction, XRD)计算确定ZrO₂相变类型; 随后, 根据Zr原子配位数变化具体分析ZrO₂相变过程; 最后, 改变入射离子的电子能损, 进行多次热峰计算和分子动力学模拟, 确定诱导ZrO₂发生相变的快速重离子的电子能损阈值.

2

-->

2.1.热峰模型

热峰模型认为快速重离子穿过靶材料时, 首先以离子运动路径为轴线形成圆柱形的电离核心区域, 称为径迹. 在大约10^–16至10^–15 s时间内将能量传递给靶材电子系统; 随后, 径迹中心电子通过热传导将部分能量传递给径迹周围电子; 同时, 通过电子-声子耦合作用将部分能量传递给原子; 径迹中心原子获得能量后, 通过晶格振动将能量传递给径迹周围原子. 热峰模型的热过程可以通过以下两个耦合微分方程描述^[19-21], 分别对应电子和原子系统.

${C_{\rm{e}}}({T_{\rm{e}}})\frac{{\partial {T_{\rm{e}}}}}{{\partial t}} \!=\! \frac{1}{r}\frac{{\partial \left[ {r{K_{\rm{e}}}\left( {{T_{\rm{e}}}} \right)\dfrac{{\partial {T_{\rm{e}}}}}{{\partial r}}} \right]}}{{\partial r}} - g\left( {{T_{\rm{e}}} \!-\! {T_{\rm{a}}}} \right) + A\left( {r,t} \right),$

${C_{\rm{a}}}({T_{\rm{a}}})\rho \frac{{\partial {T_{\rm{a}}}}}{{\partial t}} \!=\! \frac{1}{r}\frac{{\partial \left[ {r{K_{\rm{a}}}\left( {{T_{\rm{a}}}} \right)\dfrac{{\partial {T_{\rm{a}}}}}{{\partial r}}} \right]}}{{\partial r}} \!+\! g\left( {{T_{\rm{e}}} - {T_{\rm{a}}}} \right).$

式中, T_e和T_a, C_e和C_a, K_e和K_a分别为电子和原子的温度、比热容和热导率, C_e取1 J·cm^–3·K^–1, K_e取2 J·cm^–1·s^–1·K^–1[22], C_a^[23,24]和K_a^[24-26]为随温度变化的量, 其表达式分别为

${C_{\rm{a}}} \!=\! \left\{ {\begin{aligned}& {\rm{565}}.{{4272 + 61}}.{\rm{164}} \times {\rm{1}}{{\rm{0}}^{ - 3}}{T_{\rm{a}}} \\& - 114.1728 \times {{10}^5}{T_{\rm{a}}}^{ - 2},&{{T_{\rm{a}}} < 2715{{,}}} \\ &{800}, &{{T_{\rm{a}}} \geqslant 2715{{,}}} \end{aligned}} \right.$

${K_{\rm{a}}} = \frac{{2400}}{{{T_{\rm{a}}}}}\left( {\frac{2}{3}\sqrt {\frac{{420}}{{{T_{\rm{a}}}}}} + \frac{{{T_{\rm{a}}}}}{{3 \times 420}}} \right).$

ρ为晶体质量密度, 取5.68 g·cm^–3; g为电子-声子耦合系数, 由电子平均自由程λ决定, g = K_e/λ, 对于ZrO₂, λ = 4.5 nm^[14]; A(r, t)为入射离子在半径r, 时间t时沉积在电子系统的能量密度, 其表达式为

$A\left( {r,t} \right) = AD\left( r \right)\alpha {{\rm{e}}^{ - \alpha t}}.$

式中, D(r)为初始沉积能量空间分布, 指数因子α = 1/τ, τ为电子能量沉积时间, 取10^–15 s, 可调参数A表达式为

$\int_{t = 0}^\infty {\int_{r = 0}^{r = {r_{\rm{m}}}} {A\left( {r,t} \right)2{\rm{\pi}} r{\rm{d}}r{\rm{d}}t = {S_{\rm{e}}}} } .$

式中, r_m为电离径迹半径, S_e为入射离子的电子能损值, 对于给定能量和种类的入射离子, 其电子能损值可由SRIM软件包^[27]求得.
数值求解热峰方程, 获取ZrO₂原子温度的时空分布.
2 -->

2.2.分子动力学模拟

建立如图1所示的单斜ZrO₂原胞模型, 将其扩展为40a₀ × 10b₀ × 40c₀的超晶胞模型, 模型尺寸为20.5816 nm × 5.2075 nm × 21.2428 nm, 共包含1.92 × 10⁶个原子. 其中a₀ = 5.1454 ?, b₀ = 5.2075 ?, c₀ = 5.3107 ?, 为单斜ZrO₂的晶格常数.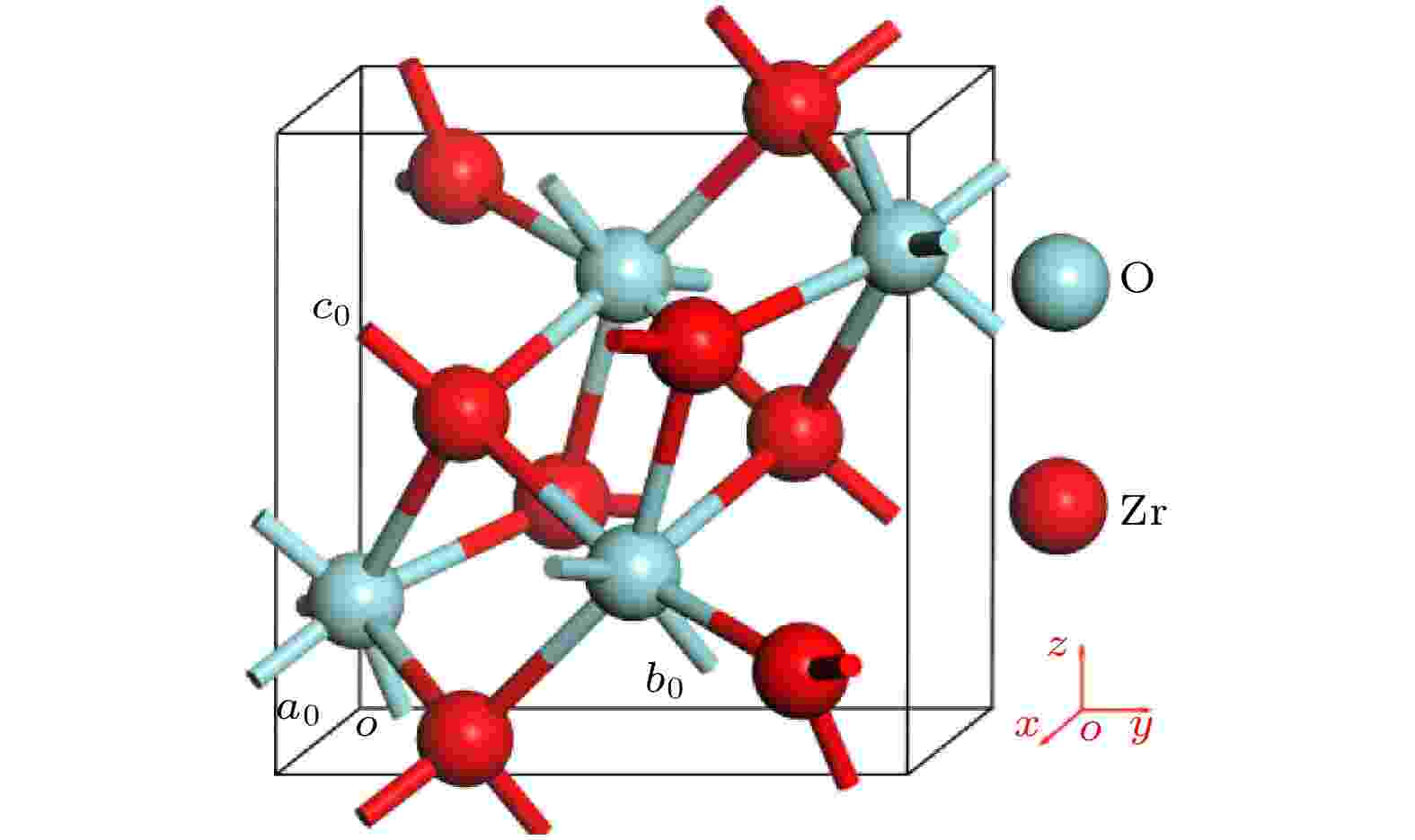
图 1 单斜ZrO₂原胞结构模型
Figure1. The crystal structure of monoclinic ZrO₂.

计算采用LAMMPS软件^[28], ZrO₂原子间相互作用力采用Buckingham势函数^[29,30]描述, 势能表达式为

${U_{ij}} = \frac{{{q_i}{q_j}}}{{{r_{ij}}}} + A\exp \left( {\frac{{ - {r_{ij}}}}{\rho }} \right) - \frac{C}{{r_{ij}^6}}.$

式中, 第一项为长程库伦势, 后两项为短程Buckingham势; q_i和q_j分别为原子i和j的电荷, r_ij为原子间距, A, ρ, C为可调参数. 在快速重离子辐照下, 热峰中心区域原子处于非平衡态, 原子间距小于平衡距离, 相互作用力为较强的斥力. Buckingham势能够准确模拟平衡态下ZrO₂原子间相互作用, 然而, 由其描述的原子间近核作用力为相互吸引力, 与实际不符. 因此, 采用普适的Ziegler-Biersack-Littmark (ZBL)库伦屏蔽势^[27]对Buckingham势的近核力进行修正, 并用Fermi函数将两种势函数平滑连接^[31]:

${U_{ij}} = {f_{\rm{F}}}\left( {{r_{ij}}} \right) \cdot {U_{{\rm{Buckingham}}}} + \left( {1 - {f_{\rm{F}}}\left( {{r_{ij}}} \right)} \right) \cdot {U_{{\rm{ZBL}}}},$

${f_{\rm{F}}}\left( {{r_{ij}}} \right){{ = }}{1}/ [{{1{{ + }}{{\rm{e}}^{ - {A_{\rm{F}}}\left( {{r_{ij}} - {r_{\rm{c}}}} \right)}}}}].$

式中, r_ij为原子间距; r_c, A_F为可调参数, r_c决定两种势函数间连接点的选取, A_F控制连接处的平滑程度.
模拟过程中采用三维周期性边界条件, 截断半径取1.6 nm. 采用自适应时间步长^[32], 即根据原子速度和受力情况, 实时更新积分步长, 限制每个原子在单个步长内最大移动距离为0.5 ?, 最大动能变化为100 eV, 并设置最大允许步长为1 fs.
热峰注入前, 采用NVT系综进行10 ps弛豫, 使用Nose-Hoover恒温器进行300 K热浴. 随后, 如图2所示, 将热峰沿[010]方向注入, 根据热峰模型计算得出的晶格温度标定原子动能. 采用NVE系综对弛豫阶段进行模拟, 并将X和Z方向3 ?厚边界层与300 K Berendsen恒温器连接, 模拟能量通过热传导耗散到环境的过程.
图 2 热峰注入靶材料示意图(S_e = 30 keV·nm^–1)
Figure2. Diagram of thermal spike injection into target material (S_e = 30 keV·nm^–1).

2

-->

3.1.热峰作用下的晶格温度时空演化

图3展示了不同位置和不同时刻的晶格温度变化趋势, 入射离子的电子能损为30 keV·nm^–1, 为实验值(10—50 keV·nm^–1)的中位数.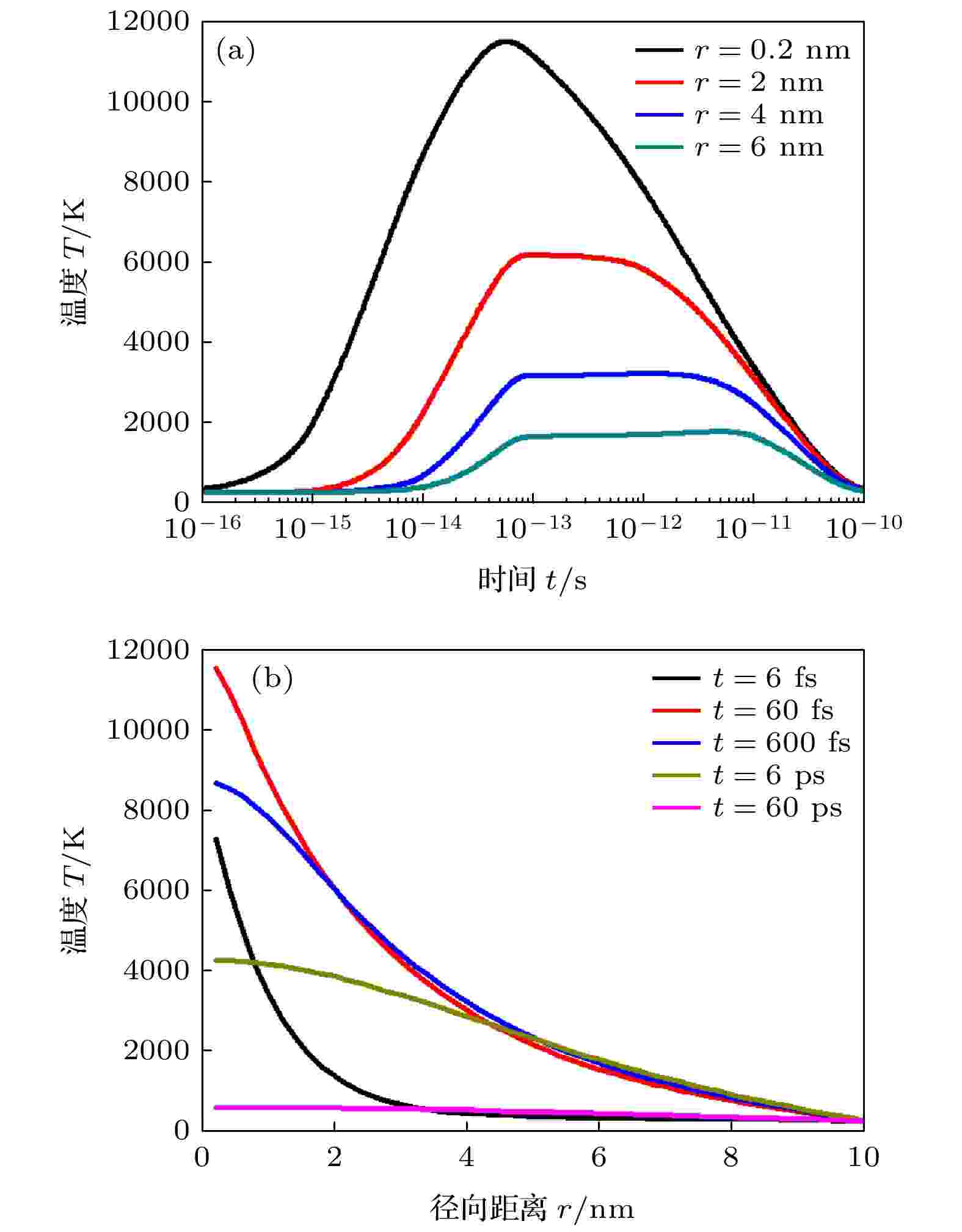
图 3 晶格温度分布曲线　(a) 不同位置晶格温度随时间演化; (b) 不同时刻晶格温度的径向分布
Figure3. Distributions of lattice temperature: (a) Evolution of lattice temperature at different radial distances; (b) radial distribution of lattice temperature at different times.

由图3可知, 在电子能损为30 keV·nm^–1的快速重离子辐照下, ZrO₂径迹周围晶格温度迅速升高, 60 fs时各处温度基本已达最大值, 径迹中心温度最高接近12000 K, 远超ZrO₂熔点(2715 ℃). 径迹中心温度达到峰值后迅速降低, 距径迹中心较远的晶格温度达到峰值后, 先维持一段时间再缓慢下降, 径迹内各处温差随时间减小, 60 ps时各处温度已接近环境温度300 K. 热峰作用下, 距径迹中心4 nm内晶格温度会超过熔点(2715 ℃), 6 nm内晶格温度会超过单斜相至四方相的相变温度(1170 ℃).
2 -->

3.2.热峰作用下的晶格温度时空演化

由热峰模型得出的晶格温度径向分布, 反映了快速重离子辐照后, 沉积在不同位置处的原子动能. 根据计算结果, 60 fs时径迹内各处温度基本已达最大值, 故取此时刻晶格温度, 标定不同位置处原子动能. 经分子动力学模拟, 得出不同时刻ZrO₂微观结构变化如图4所示.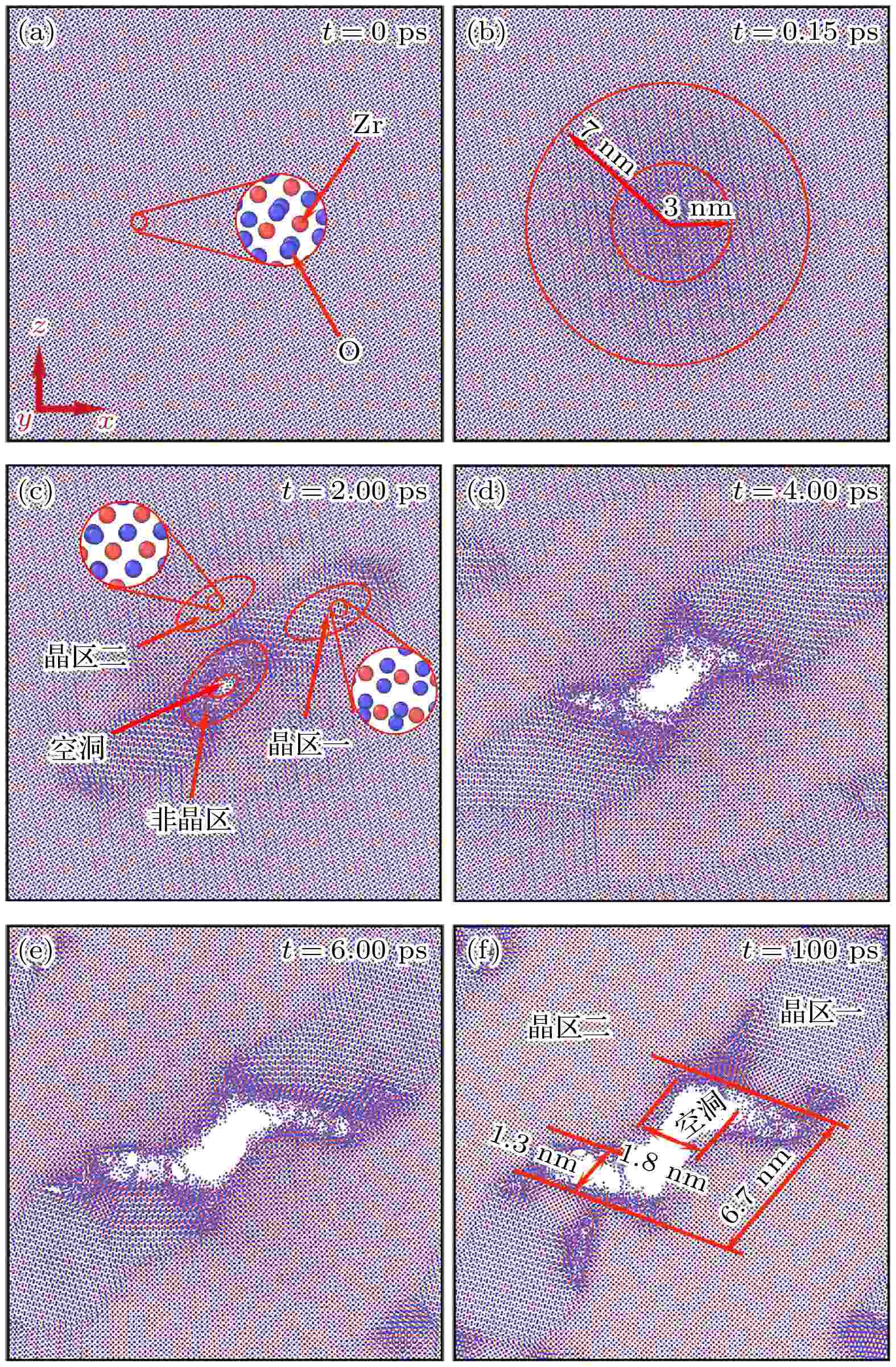
图 4 不同时刻ZrO₂原子结构变化. 所有原子沿热峰注入方向投影在(010)平面上
Figure4. Atomic structure of ZrO₂ at different times. All the atoms are projected on (010) plane along the injection direction of thermal spike.

由图4可知, 0 ps时体系原子处于热平衡态. 热峰注入后, 中心区域原子能量较高, 受热激发离开初始晶格位置, 并与周围原子发生剧烈碰撞. 0.15 ps时, 产生一个熔融的柱形径迹, 距离热峰中心3 nm内原子无序程度较高, 3至7 nm内原子无序程度较低. 2 ps时径迹中心开始形成空洞, 空洞外围为高度无序的非晶区, 非晶区周边原子熔融重排, 形成了两种不同的晶区(晶区一和晶区二). 在(010)投影平面上, 晶区二内Zr, O原子空间分布均匀, 且Zr原子位于临近4个O原子的对称中心, O原子位于临近4个Zr原子的对称中心; 晶区一内Zr与Zr原子间距较远, O与O原子间距较近, 且O原子不处于临近Zr原子的对称中心位置. 由4, 6和100 ps的微观结构可知, 随着能量由径迹中心向四周传递, 重结晶过程逐渐发展至整个体系, 空洞、晶区一和晶区二的尺寸逐渐增大, 100 ps时体系已达平衡态.
XRD图谱能够反映材料成分、形态以及内部原子排列结构等信息, 广泛应用于物质的晶体结构表征. 取100 ps时晶区二内部分原子坐标, 进行分子动力学计算, 获得辐照后ZrO₂晶体XRD图谱^[33], 并与辐照前XRD图谱以及单斜(m-ZrO₂)、四方(t-ZrO₂)标准谱进行对比, 结果如图5所示.
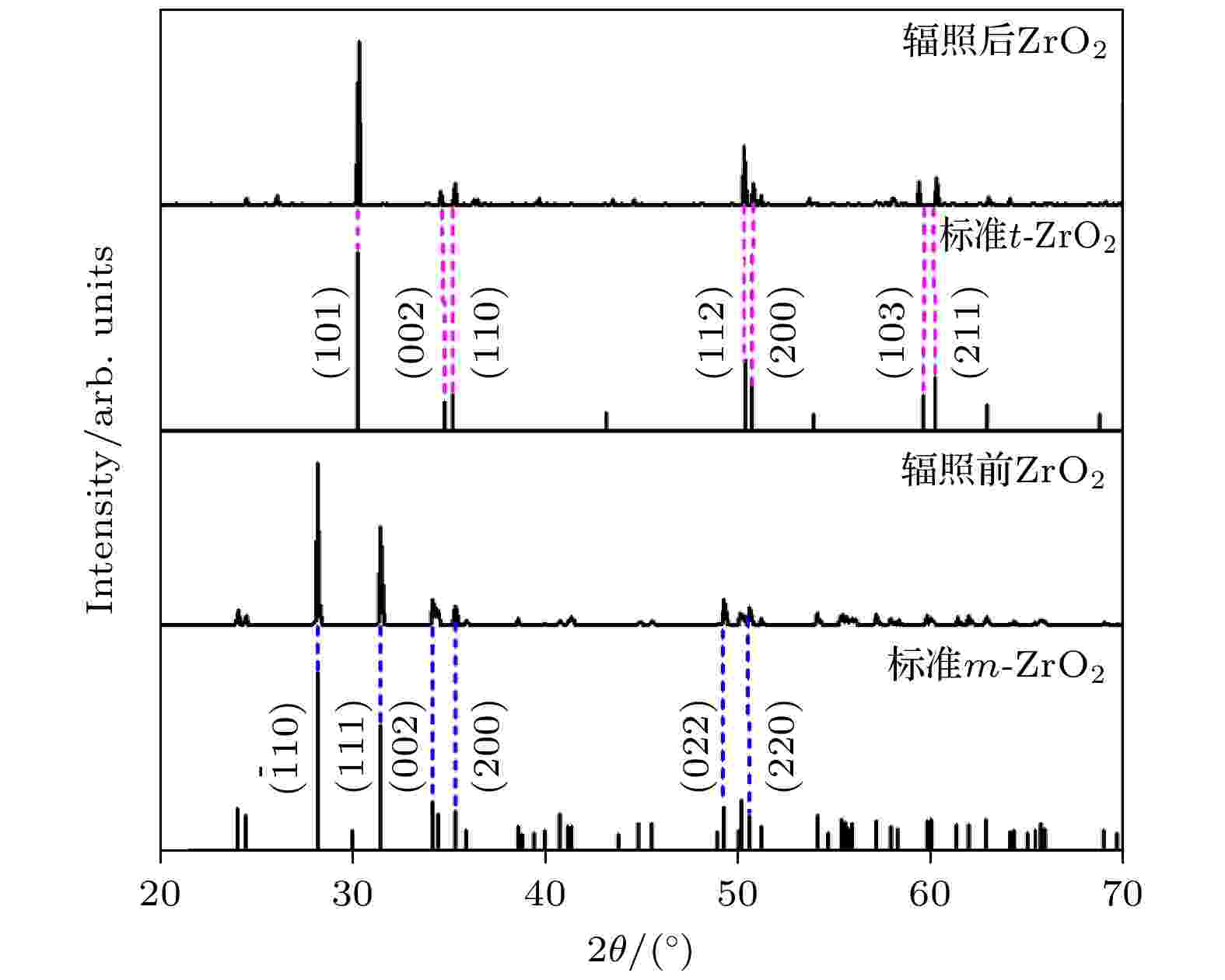图 5 辐照前后以及标准ZrO₂ XRD图谱
Figure5. XRD patterns of pristine, ion-irradiated and standard ZrO₂.

由图5可知, 辐照前XRD图谱在28.2°, 31.5°, 34.2°, 35.3°, 49.3°和50.1°出现衍射峰, 分别对应m-ZrO₂的($ {\overline{1}} 11$), (111), (002), (200), (022), (220)晶面衍射(JCPDS. No 83-0936), 表明辐照前ZrO₂为单斜相. 经快速重离子辐照后, 单斜相特有的特征峰消失, 并且在30.3°, 34.6°, 50.3°, 50.8°, 59.4°, 60.3°出现新的特征峰, 与t-ZrO₂的(101), (002), (112), (200), (103), (211)衍射晶面良好对应(JCPDS. No 88-1007), 证明在快速重离子辐照作用下, ZrO₂由单斜相转为了四方相.
ZrO₂晶体中, 单斜相的Zr原子配位数为7, 四方相的Zr原子配位数为8, 因此可根据Zr原子配位数的变化情况研究辐照条件下ZrO₂相变过程. 图6展示了不同配位数的Zr原子空间分布随时间演化过程.
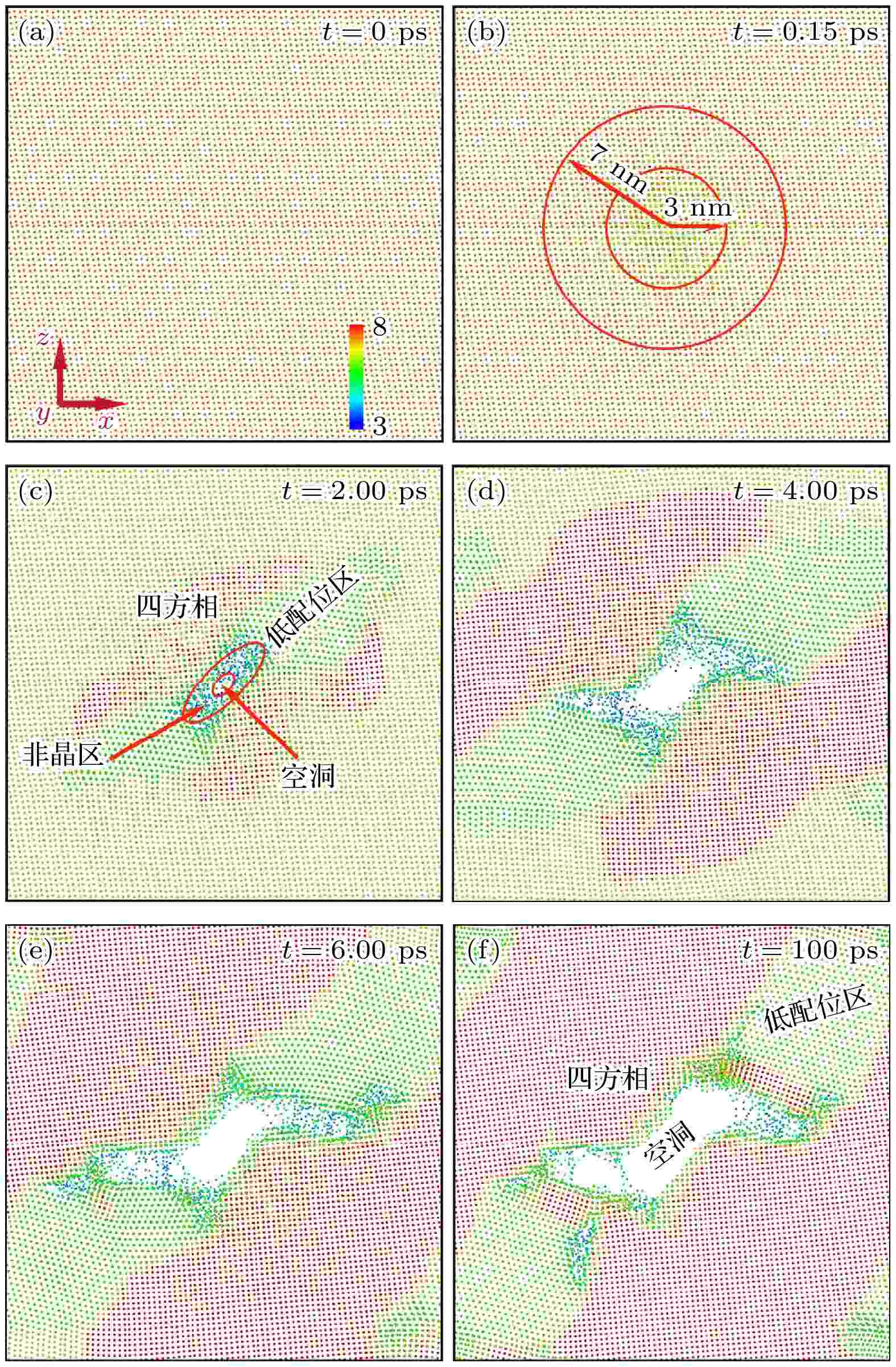图 6 不同时刻不同配位数Zr原子空间分布. 所有原子沿离子入射方向投影在(010)平面上, 颜色不同代表配位数不同
Figure6. Spatial distribution of Zr atoms with different coordination number at various times. All the atoms are projected on (010) plane along the injection direction of thermal spike. Different coordination numbers are distinguished by the atomic color.

如图6所示, 初始时刻所有Zr原子配位数均为7, 表明ZrO₂为单斜相. 0.15 ps时, 距热峰中心7 nm范围内形成一个熔融的柱形径迹, 其中28%的Zr原子配位数降为6, 4.4%的Zr原子配位数降为5, 距径迹中心3 nm范围内, 47.8%的Zr原子配位数降为6, 14.8%的Zr原子配位数降为5, 0.7%的Zr原子配位数降为4, 表明越靠近径迹中心, 原子无序程度越高. 随着能量向四周传递, 径迹中心温度逐渐降低, 原子发生结晶重排, 2 ps时, 径迹中心出现空洞, 其周边由配位数为3或4的Zr原子组成非晶区, 非晶区两侧生长出两种不同的晶相, 分别为配位数为8的四方相以及配位数为6的低配位相. 由4, 6和100 ps微观结构可知, 随着能量继续由中心向四周传递, 四方相以及低配位相逐渐发展至整个体系, 同时空洞范围不断扩大. 4和6 ps时, 四方相区域内仍有部分Zr原子配位数为7, 100 ps时, 四方相区域内所有Zr原子配位数均为8, 表明随着时间推移, 相变区域变得更加致密有序. 100 ps时, 空洞周边部分低配位相逐渐转变为四方相, 将两侧相变区连接起来. 本文模拟所得到的空洞, 在实验中尚未得到验证. 然而, 单斜ZrO₂密度为5.65 g/cm³, 四方ZrO₂密度为6.10 g/cm³, 一定质量的ZrO₂由单斜相转为四方相后, 体积减小约7.4%. 本文分子动力学模拟中采用的系综为NVE系综, 模拟过程中体系体积固定, 因此, 在NVE系综下进行ZrO₂由单斜相至四方相的相变模拟, 必然导致空洞的产生. 此外, 在其他材料(如Ge^[31], Fe-Cr^[34]合金等)的辐照损伤研究中, 曾观察到空洞的产生.
2 -->

3.3.辐照诱导单斜ZrO₂相变的电子能损阈值

为获得辐照诱导ZrO₂由单斜相转为四方相的快速重离子的电子能损阈值, 在电子能损为15—30 keV·nm^–1范围内进行了多次热峰计算和分子动力学模拟. 图7展示了Zr原子配位数随电子能损值变化趋势.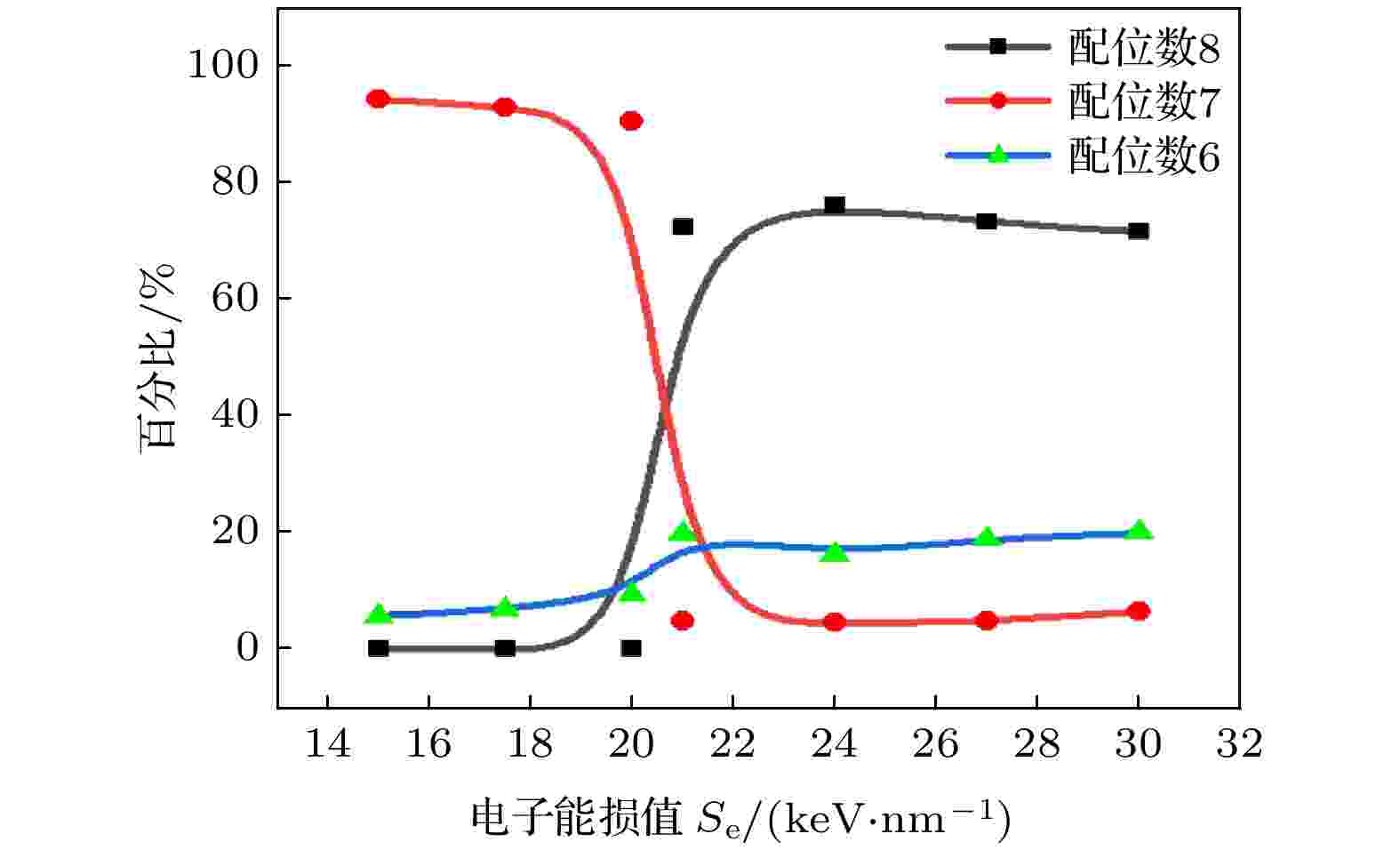
图 7 配位数随电子能损值变化
Figure7. The change of coordination number with electronic energy loss.

如图7所示, 电子能损值为15—20 keV·nm^–1时, 配位数为7的Zr原子个数随电子能损值增加而减少, 未出现配位数为8的Zr原子, 表明ZrO₂仍保持单斜相. 当电子能损值为21 keV·nm^–1时, 72.4% Zr原子配位数由7变为8, 表明ZrO₂已经由单斜相转为四方相. 由此得出辐照诱导单斜ZrO₂相变的快速重离子的电子能损阈值为21 keV·nm^–1. 电子能损值为21—30 keV·nm^-1时, 随着电子能损值增加, 配位数为8的Zr原子个数先增加后减小, 占Zr原子总数比例在71.5%—76%之间.
当入射离子电子能损分别为20和21 keV·nm^–1时, 辐照后不同配位数的Zr原子空间分布如图8所示.
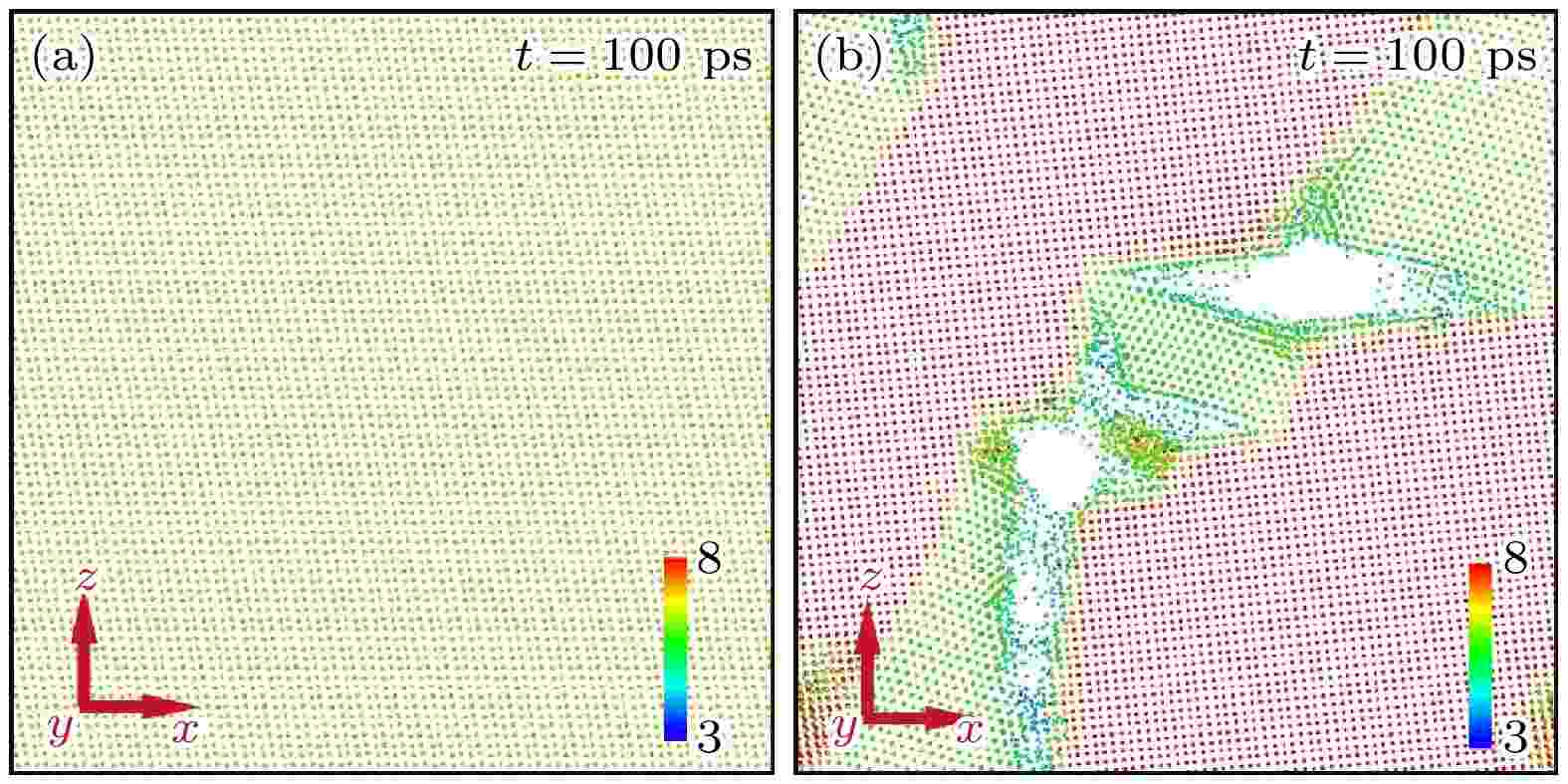图 8 不同配位数Zr原子空间分布　(a) 电子能损值为20 keV·nm^–1; (b)电子能损值为21 keV·nm^–1. 所有原子沿离子入射方向投影在(010)平面上, 颜色不同代表配位数不同
Figure8. Spatial distribution of Zr atoms with different coordination number: (a) S_e = 20 keV nm^–1; (b) S_e = 21 keV nm^–1. All the atoms are projected on (010) plane along the injection direction of thermal spike. Different coordination numbers are distinguished by the atomic color.

如图8所示, 电子能损值为20 keV·nm^–1时, 辐照未能造成ZrO₂由单斜相至四方相的转变. 在热峰作用下, 部分原子离开其正常晶格位置, 成为点缺陷, 点缺陷的引入使得部分Zr原子配位数降为6或5, 点缺陷在空间上均匀分布. 电子能损值低于20 keV·nm^–1时, 不同配位数Zr原子的空间分布图与图8(a)相似. 当快速重离子电子能损值为21 keV·nm^–1时, 72.4% Zr原子配位数由7变为8, 并且在空间上形成连续致密的排列结构, 表明ZrO₂已经由单斜相转为四方相. 当电子能损值低于27 keV·nm^–1时, 低配位相和四方相中心未形成连续空洞, 与图8(b)相似, 这是由于热峰温度较低, 中心原子动能较小, 不足以引起足够剧烈的碰撞使得热峰中心所有原子运动到足够远的区域, 随着系统快速淬火, 原子迅速冷却, 形成非连续的空洞. 当电子能损值高于27 keV·nm^–1时, 低配位相和四方相中心形成连续空洞, 不同配位数Zr原子空间分布与图6(f)相似.
根据热峰模型^[13,35], 快速重离子辐照后, 材料相变区域面积σ与入射离子的电子能损S_e存在如下关系:

$ {\sigma \left( {{S_{\rm{e}}}} \right) = {\rm{\pi }}a_0^2\ln \left( {{S_{\rm{e}}}/{S_{{\rm{et}}}}} \right)},\;\;\;{{S_{{\rm{et}}}} \leqslant {S_{\rm{e}}} \leqslant 2.7{S_{{\rm{et}}}}} ,$

$ {\sigma \left( {{S_{\rm{e}}}} \right) = {\rm{\pi }}a_0^2{S_{\rm{e}}}/2.7{S_{{\rm{et}}}}},\;\;\;{{S_{\rm{e}}} > 2.7{S_{{\rm{et}}}}} .$

式中, a₀为热峰温度的初始分布半径; S_et为入射离子的电子能损阈值.
经热峰模型计算和分子动力学模拟得出, 辐照致单斜ZrO₂相变的快速重离子的电子能损阈值为21 keV·nm^–1, 与实验值12 keV·nm^–1存在一定误差^[7-10], 这主要与辐照剂量以及势函数的准确性有关. 模拟条件为单离子入射, 对应的辐照剂量为2.37 × 10¹¹ ions·cm^–2, 而实验中通常辐照剂量较大, 为10¹²—10¹⁵ ions·cm^–2, 可能存在同一区域被多个离子辐照的情况. 此外, 分子动力学模拟中采用普适的Ziegler-Biersack-Littmark (ZBL)库伦屏蔽势修正的Buckingham势描述ZrO₂原子间相互作用力, 其与真实的原子间作用力相比存在一定差异, 这将导致模拟结果与实验结果存在一定偏差. 未来可开发更为准确的势函数, 开展多个离子同时入射以及多个离子先后入射的研究, 模拟高剂量快速重离子辐照对材料的损伤作用.

本文结合了热峰模型和分子动力学的优势, 模拟了快速重离子辐照下, ZrO₂由单斜相转为四方相的微观物理过程, 并计算了辐照诱导ZrO₂相变的快速重离子的电子能损阈值. 首先, 基于热峰模型, 考虑快速重离子辐照单斜ZrO₂时, 电子激发、电子-声子能量耦合以及电子-电子、声子-声子能量传导多物理过程, 建立热扩散方程, 求得ZrO₂晶格温度时空演变特性. 然后, 运用分子动力学方法模拟了热峰作用下ZrO₂相变的微观物理过程. 热峰注入后, ZrO₂中心形成一个半径为7 nm的径迹, 径迹中心晶格迅速熔融; 2 ps时熔融区逐渐冷却重结晶, 其中心开始形成空洞, 空洞外围为高度无序的非晶区, 非晶区外围生成四方相和低配位相; 随着能量由径迹中心向四周传递, 四方相和低配位相逐渐发展至整个体系, 同时空洞尺寸随之增大. 经热峰计算和分子动力学模拟, 辐照诱导单斜ZrO₂相变的快速重离子的电子能损阈值为21 keV·nm^–1, 高于实验值12 keV·nm^-1, 主要原因为: 1) 入射离子剂量的模拟值小于实验值; 2) 分子动力学中采用势函数描述的原子间相互作用力与真实情况存在一定误差, 未来可开发更精确的势函数描述ZrO₂原子间相互作用力, 开展高剂量快速重离子辐照下, 材料辐照损伤的模拟研究. 本文建立的研究方法可有效地模拟高能离子对材料辐照损伤的微观物理过程, 将来可用于其他惰性基质燃料(如YSZ/ZrO₂-PuO₂等)的高能辐照损伤研究.