摘要:当前, 尽管集成电路制造工艺水平不断提高, 但受到量子效应的限制, 器件尺寸的缩小使业界遇到了可靠性低、功耗大等瓶颈, 微电子行业延续了近50年的“摩尔定律”将难以持续. 2004年二维材料—石墨烯的问世, 为突破集成电路的功耗瓶颈带来了新的机遇. 由于低维特性, 二维材料在一层或者几层原子厚度中表现出丰富多样的电学、磁学、力学和光学等物理特性. 其中, 铁磁性在信息处理、存储等技术上有着广泛的应用价值. 然而, 目前在实验上合成的具有铁磁性的二维材料屈指可数. 同时, 在二维系统中长程有序磁态会因为热涨落的因素在有限温度内受到强烈的抑制, 无法在室温下保持铁磁性, 这为后续工作带来了不可忽视的限制与挑战. 因此实现二维磁性材料室温下的铁磁有序及其调控是现阶段需要解决的重大问题. 本综述详细地介绍了二维磁性材料的发展过程、制备方法及其优越性能, 并着重阐述了调控二维磁性材料居里温度的方法. 最后, 扼要地分析并展望了二维磁性材料在未来的应用前景.
关键词: 二维磁性材料/
居里温度/
新型二维自旋电子器件

English Abstract

全文HTML

--> --> -->

基于半导体器件的超大规模集成电路是整个信息产业的基础, 它直接推动消费类电子、计算机、航空航天及国防信息化等相关产业的发展. 然而, 随着传统半导体的发展, 其特性和工艺都遇到了瓶颈, 更先进的制程工艺使其逐渐逼近出现量子限制效应的临界点, 集成电路的发展之路变得不再明朗. 因此, 许多研究机构都在致力于从材料、器件到系统的各个层面探究突破集成电路性能瓶颈的方案, 其中自旋电子学有望超越当前硅基集成电路技术, 实现低功耗、智能化、高速度、高集成度和非易失性的新型电子器件, 成为国际上的研究热点. 其中, 与CMOS工艺兼容的非易失自旋电子器件—磁隧道结(magnetic tunnel junction, MTJ)具有降低芯片的静态功耗、实现存算一体、抗高能离子辐照以及提高系统的可靠性等诸多优势^[1–5], 被认为是取代传统存储器的关键技术之一, 获得了学术界及产业界的广泛关注^[6–10]. 因此, 加速推进MTJ在数据存储及计算方面的应用, 对超大规模集成电路在“后摩尔时代”克服性能瓶颈具有重大意义. 然而, 随着基于MTJ的新型存储器的发展, 很多新技术诸如自旋转移矩和自旋轨道矩在读写速度、功耗和耐久性等方面仍存在着亟待解决的问题. 因此, 在赶超现有的集成电路技术的基础上, 发展新材料、新器件和新技术是一种有效的途径.
2004年, 英国曼彻斯特大学Andre Geim和Kostya Novoselov成功从石墨材料剥离出石墨烯, 首次实现了单原子层二维材料的制备^[11–15]. 二维材料是指电子仅在两个维度上自由运动而另一维度限制在纳米尺度的材料, 原子以层状的形式存在, 通过范德瓦耳斯力即分子间作用力堆叠在一起, 层内原子以化学键进行连接^[16–20]. 石墨烯近似于蜂巢结构, 由碳原子构成六角型, 是通过强共价键结合的二维材料, 其单层可稳定存在; 石墨烯具有良好的热导率、极高的透明度以及高载流子迁移率等优越特性, 有望在诸多领域中实现跨越式的突破. 因此, 以石墨烯为代表的二维材料将会为未来科技的发展提供更多的机遇, 书写半导体领域的新格局. 2018年, 瑞士洛桑联邦理工大学研究人员^[21]开发出一种新算法, 对超过10 万种已知的化合物进行搜索与结构分析. 结果显示, 其中1036 种材料更适合剥离, 可提供新颖的结构原型以及大量的材料组合来实现丰富多样的物理、化学特性, 带来科学上的重大发现和技术方面的大幅提高. 随着研究人员对二维材料的基础研究愈发深入, 推广其应用变得尤为重要. 开发基于二维材料的新器件具有重要意义, 特别是近几年来新兴的二维磁性材料更是备受瞩目. 相比于传统的三维空间结构, 二维磁性材料通过较弱的范德瓦耳斯相互作用与相邻层结合, 使得匹配度不同的原子层结合成为可能, 进而创建广泛的范德瓦耳斯异质结构, 摆脱晶格匹配和兼容性的限制. 从而有望实现具有电路微型化、力学柔韧性、三维堆叠高密度、响应速率快和高开关比性能的磁传感器和非易失随机存储器等新型自旋电子学器件. 因此, 探索新型二维磁性材料, 将为未来信息科技的发展注入更大的潜能, 并在多个领域表现出广泛的应用前景, 带动真正的科技革命^[22–24].
2017年, 来自美国加州大学伯克利分校的张翔课题组^[25]和华盛顿大学许晓栋课题组^[26]分别基于单层CrI₃ 和双层Cr₂Ge₂Te₆两种材料进行研究, 相关工作发表在《Nature》杂志上, 两种材料的厚度在少层或者单层时依靠磁各向异性来抑制二维晶体中存在的热涨落, 实现长程有序磁态. 该工作依托于实验现象首次发现了二维材料中本征磁性的存在, 为探索合适的二维磁性材料提供了有效的解决办法. 这些材料由于解理能很低, 很容易通过类似最早制备单层石墨烯的机械剥离手段得到任意厚度的薄层. 但该技术对原材料的质量具有较高的要求, 且由于胶带解理的方法会使二维材料随机分布在衬底上, 因此很难大量制备, 无法投入实际应用以实现产业化. 同时, CrI₃和Cr₂Ge₂Te₆的居里温度(Curie temperature, T_c)均远低于室温. 因此, 寻找在室温下维持铁磁有序且可以进行大面积制备的新型二维磁性材料成为目前关键性的科学问题.
到目前为止, 人们一直在理论和实验上致力于室温居里温度的突破. 此前的理论计算表明一些具有本征铁磁性的二维材料可以维持至室温^[27–30]. 但是, 实验进展并不顺利, 要么材料难以实现, 要么真实居里温度远低于室温. 目前, 仅少数二维磁性材料被报道具有室温的居里温度, 其调控主要基于电场、应变及界面工程效应等方法^[31–33]. 2018年, 复旦大学张远波课题组^[33]利用固态电解质作为栅极制备了基于Fe₃GeTe₂薄层的离子场效应晶体管器件, 通过电压调控将居里温度提高至室温. 2020年, 武汉大学的何军课题组^[34]报道了二维磁性材料Cr₂Te₃重构后居里温度从160 K提高到280 K. 此外, 本课题组利用拓扑绝缘体(Bi₂Te₃)与Fe₃GeTe₂之间的界面工程效应将Fe₃GeTe₂的铁磁性维持至远超室温以上^[31]. 为尽早实现室温二维自旋电子器件, 本综述重点围绕如何提高二维磁性材料的居里温度展开探讨: 从二维材料的制备方法与磁性起源入手, 探索二维材料的磁特性与调控; 随后深入讨论调控居里温度的方法背后所蕴含的物理机理; 最后展望二维磁性材料的未来发展前景, 其诸多优势有望代替MTJ中的传统磁性薄膜, 实现与集成电路技术高度契合且融功能器件于一体的新型室温二维自旋电子器件, 实现里程碑式的突破.

2

-->

2.1.二维磁性材料的制备方法

二维材料涵盖了石墨烯、黑磷、拓扑绝缘体、二维磁性材料和过渡金属硫族化合物等不同类型的层状范德瓦耳斯(van der Waals, vdW)材料. 目前, 制备二维材料的方法多种多样, 包括机械剥离法^[35,36]、化学气相沉积法^[37–41]、液相剥离法^[42–46]和物相沉积法^[47]等多种方法, 其中机械剥离法和分子束外延技术是主流的制备二维磁性材料的手段.
3 -->

2.1.1.机械剥离法

机械剥离法是通过克服相邻薄膜之间的范德瓦耳斯力从而将薄膜从块状样品中剥离出来的一种机械手段. 该方法剥离的方向包括沿着法向力和侧向力两个方向, 在理想情况下可以将薄膜一层一层地从块状样品中剥离出来. 该方法最早应用在石墨烯的获取中, 通过此方法可以控制石墨的剥落以获得高质量薄膜. 图1给出了在高定向热解石墨(highly oriented pyrolytic graphite, HOPG)表面上解理单层石墨烯的方法, 将透明胶带作用于材料表面, 通过施加法向力进行剥离^[36]. 在多次重复该法向力后, 石墨层会变得越来越薄, 最终得到单层石墨烯. 该方法一经发现, 立即引起了二维材料研究的热潮, 研究人员使用该方法制备了除石墨烯以外的其他多种二维材料. 目前, 通过机械剥离法已成功制备出包括CrI₃, CrGeTe₃, Fe₃GeTe₂ (FGT), Fe₅GeTe₂等的多种二维磁性薄膜. 特别是, 二维磁性材料CrI₃的层状结构的磁性依赖实验结果为研究磁性与层数的关系提供了重要的实验依据. 研究发现了CrI₃的层间磁性耦合作用, 该材料在单层时具有铁磁性, 双层时具有反铁磁性. 由于退磁效应使双层CrI₃的磁矩衰减, 在三层及块状样品中层间铁磁耦合得以保留, 表现为铁磁性^[26]. 另外, 二维磁性材料Fe₅GeTe₂在少层厚度的情况下, 其居里温度可维持至接近室温, 表现出巨大的潜力^[48]. 虽然机械剥离方法制备的二维材料具有缺陷少、表面平整等诸多优势, 但该方法存在着生产效率低、可控性较差等缺点, 从而难以实现大规模合成, 无法进行工业化量产.
图 1 单层石墨烯机械剥离流程^[36]
Figure1. Mechanical peeling process of single-layer graphene^[36].

3 -->

2.1.2.分子束外延法

分子束外延(molecular-beam epitaxy, MBE)是一种在超真空环境下(< 10^–11 Torr (1 Torr $ \approx $133.322 Pa))的物相沉积技术. 如图2(a)所示, 具有一定热运动的原子或分子以束流的形式喷射到衬底表面, 以外延生长的方式沉积在衬底表面并形成单晶, 同时配合反射高能电子衍射(reflection high-energy electron diffraction, RHEED)可实时监控外延生长变化过程^[47]. 薄膜的具体生长过程如图2(b)所示, 具有一定动能的分子束喷射到一定温度的衬底上, 其中部分原子会在接触表面后直接反射脱离衬底, 或附着于衬底后脱附蒸发到腔体中. 另一部分原子在附着于衬底后聚集成晶核, 之后原子在表面不断扩散迁移, 沿衬底晶格生长为晶体薄膜. 该技术具有明显的优势, 包括可精准控制生长的厚度、组分、掺杂浓度等.
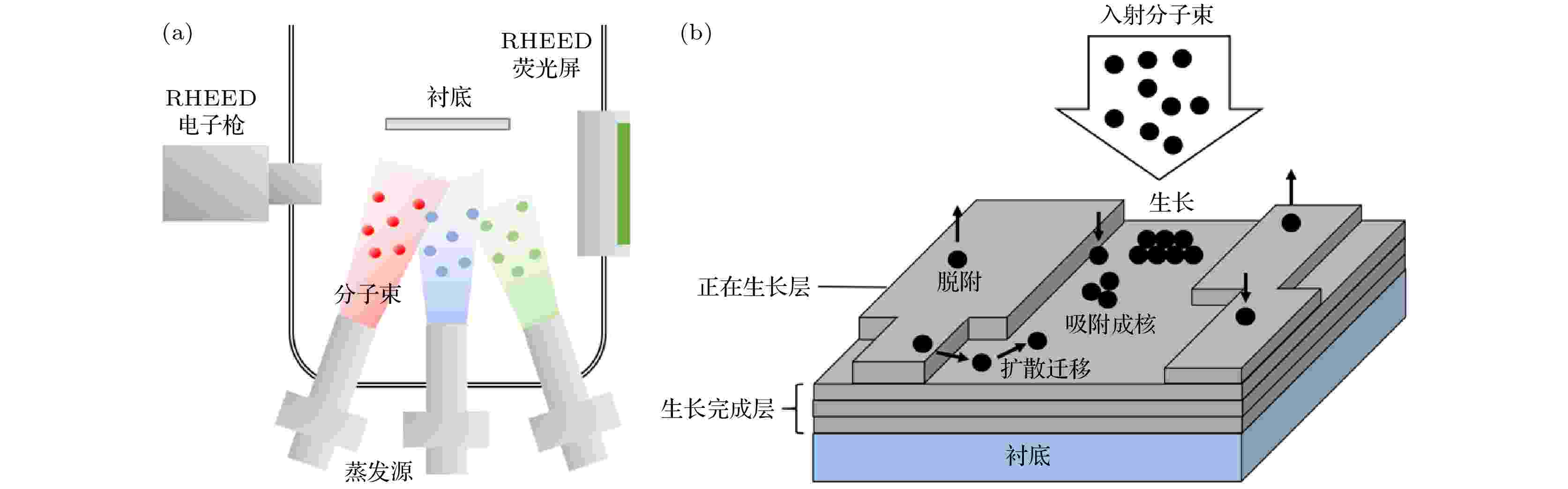图 2 (a) 分子束外延生长腔示意图; (b) 薄膜生长过程示意图
Figure2. (a) Schematic diagram of molecular beam epitaxial growth cavity; (b) schematic diagram of film growth process.

目前, 已报道的可通过分子束外延技术生长的二维磁性材料包括VSe₂, MnSe₂以及FGT. 特别是本课题组已实现在蓝宝石衬底上对二维磁性材料FGT的可控制备, 通过RHEED衍射观察到的尖锐条纹可推断出薄膜的高质量特征, 并可以通过调节Fe的浓度精准调控居里温度, 为后续的工作奠定了坚实的基础^[31].
2 -->

2.2.二维磁性材料的磁性起源

2.1节主要整理了二维磁性材料的制备方法. 接下来围绕二维磁性材料的磁性起源及新特性进行阐述. 在宏观角度上, 铁磁性的产生是由于存在长程有序排列的磁矩^[17]. 由于具有时间反演对称性的自发打破, 相邻自旋之间的相互作用(交换耦合), 使其倾向于特定的方向有序排布; 当外加磁场强度增大时, 这些区域的合磁矩定向排列程度会随之增加并最终达到某一极限值. 然而, 长期以来研究人员认为在二维系统中材料的长程有序磁态会因为热涨落的存在而受到强烈抑制^[49–51]. 因此, 一个系统能否在有限居里温度下经历相变, 取决于热波动的有效性. 在一个三维系统中, 磁性相变总是会在某一特定温度下发生. 然而一维情况下, 只有在温度T = 0 K时, 系统才可能实现长程磁有序. 因此, 对于处在这两种极端情况间的二维系统来说, 情况更加复杂. 在这种情况下, 任何温度下长程磁矩的存在都取决于相关的自旋分量n, 称为自旋维数, 通常由系统的物理参数决定. 根据Mermin-Wagner-Hohenberg定理, 在任何温度下, 热扰动都会破坏自旋维数为3 (各向同性Heisenberg模型)的二维系统的长程磁序^[52]. 也就是说, 由于热扰动的存在, 各向同性Heisenberg模型中的二维自发磁化行为是不存在的. 这在很长一段时间内都困扰着科学家, 阻碍了二维系统中磁性的研究和发展. 直到2017年, 科学家在二维材料中发现了本征磁性, 从而打破了僵局. 研究表明, 材料的磁各向异性会抑制热扰动对长程磁序的影响, 从而使得二维Ising铁磁体中存在本征磁性成为可能^[26]. 该Ising模型表明, 当n = 1, 居里温度$ {T}_{\rm{c}} $大于0 K时, 材料会发生磁有序相的相变^[53,54]. 在这种情况下, 系统的各向异性在自旋波谱中打开了一个缺口, 从而抑制了热波动的影响. 同时, 向二维磁性材料施加非常小的磁场将产生更强的有效磁各向异性, 打开更大的自旋波激发间隙.
2017年, 美国加州大学伯克利分校的张翔课题组^[25]通过磁光克尔技术揭示了Cr₂Ge₂Te₆ (CGT)薄层样品的铁磁性, 图3(a)所示为CGT的原子结构图, 清晰地展现了原子的分布, 测量结果表明CGT的居里温度会随着厚度的减薄而降低. 研究发现块材的居里温度(T_c)约为68 K, 而双层薄膜的T_c仅约为30 K. CGT作为一种近于理想的二维Heisenberg铁磁体, 为研究自旋行为提供了新的方向, 具有重大意义. 华盛顿大学许晓栋课题组^[26]通过机械剥离法制备了单层CrI₃晶体, 用磁光克尔技术证明了单层CrI₃是伊辛(Ising)铁磁体(图3(b)), 其居里温度为45 K, 且自旋朝面外方向排列. CrI₃材料由于解理能很低, 面内材质较坚硬, 很容易通过剥离来得到独立存在的薄层. 因此, CrI₃也成为了二维铁磁材料的一个重要突破口. 2017年, 复旦大学修发贤课题组^[55]报道了利用分子束外延技术制备的晶圆级FGT二维磁性薄膜(图3(c)), 通过原位反射高能电子衍射振荡证实了其二维逐层生长模式. 同时, 霍尔电阻测量结果表明, 块状FGT的居里温度为216.4 K, 且易磁化轴沿面外取向. 与面内磁各向异性相比, 垂直磁各向异性(perpendicular magnetic anisotropy, PMA)可以提供更低的开关电流. 这对于MTJ以及磁性随机存储设备具有重要意义.
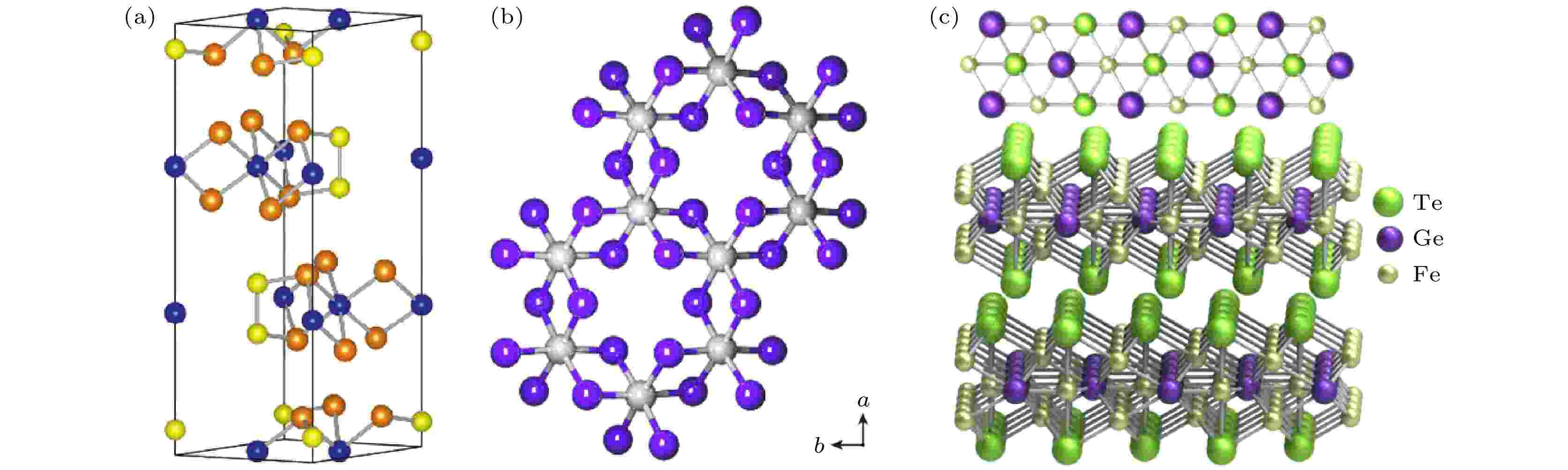图 3 (a) Cr₂Ge₂Te₆的原子结构视图^[25], 其中蓝色、黄色和橘色的球分别代表Cr, Ge和 Te原子. (b) 单层CrI₃的平面内原子结构视图, 其中灰色和紫色的球分别代表Cr和I原子^[26]. (c) Fe₃GeTe₂的面内和面外原子结构视图, 其中黄色、紫色和绿色的球分别代表Fe, Ge和 Te原子^[55]
Figure3. (a) Atomic structure view of Cr₂Ge₂Te₆. The blue, yellow, and orange balls represent Cr, Ge, and Te atoms, respectively^[25]. (b) In-plane atomic structure view of a single layer of CrI₃. The gray and purple balls represent Cr and I atoms, respectively^[26]. (c) In-plane and out-of-plane atomic structure views of Fe₃GeTe₂. The yellow, purple and green balls represent Fe, Ge and Te atoms, respectively^[55].

2

-->

3.1.二维磁性材料的新特性

第2节主要介绍了目前主流的新型二维磁性材料, 其新奇的物理现象蕴含着更多的机遇和挑战. 以FGT材料为例, 2018年, 澳大利亚皇家墨尔本理工大学Wang课题组^[56]报道了具有不同厚度的单晶金属FGT纳米薄片相关磁学输运的测量结果. 该研究表明FGT具有单一的硬磁相, 方形的磁滞回线以及较大的矫顽力(在2 K时高达550 mT). 同时, 研究结果证明了FGT的居里温度对薄膜厚度的依赖性, 如图4(a)所示, 当FGT薄膜的厚度大于25 nm时, 厚度对T_c并未产生较大的影响. 然而, 当厚度从25 nm减小到8 nm时, T_c急剧下降. 既然FGT具有巡游金属特性, 其自旋与自旋之间的耦合甚至沿着面外的方向也可扩展到多原子层, 这种沿着面外的耦合范围可表达为^[56]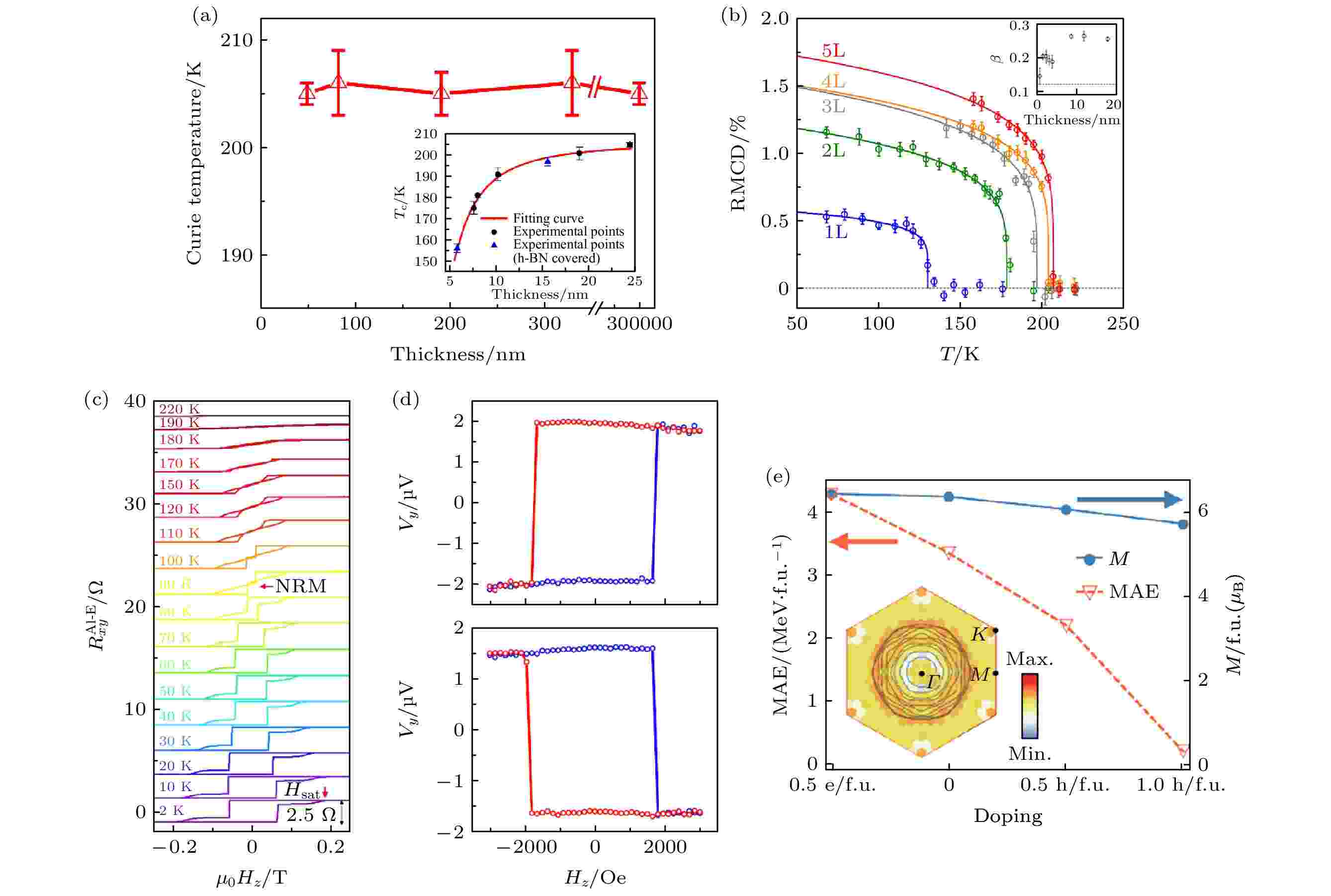
图 4 (a), (b) FGT薄膜的居里温度随厚度的依赖关系^[56,57]; (c)不同温度下30 nm FGT/O-FGT薄膜器件的反常霍尔电阻与垂直磁场的关系, 其中在90 K温度下出现负的剩磁^[58]; (d) FGT薄膜的能斯特信号横向电压与垂直磁场的关系, 温度梯度分别为$\nabla {T_x} = 1.3\;{\rm{K}} \cdot {{\text{μ} }}{{\rm{m}}^{ - 1}}$和$\nabla {T_x} = - 1.1\;{\rm{K}} \cdot {\text{μ} }{{\rm{m}}^{ - 1}}$^[59]; (e) Fe_3–xGeTe₂薄膜的磁晶各向异性能与磁化强度随掺杂浓度变化的关系^[60]
Figure4. (a), (b) Thickness-dependent Curie temperature of FGT films for critical analysis^[56,57]; (c) relationship between the anomalous Hall resistance of 30 nm thick FGT/O-FGT device and the perpendicular magnetic field under different temperatures, where the negative remanence magnetization appears at 90 K^[58]; (d) relationship between the transverse voltage of the Nernst signal of FGT film and the perpendicular magnetic field with temperature gradient of $\nabla {T_x} = 1.3\;{\rm{K}} \cdot {\text{μ} }{{\rm{m}}^{ - 1}}$ and $\nabla {T_x} = - 1.1\;{\rm{K}} \cdot {\text{μ} }{{\rm{m}}^{ - 1}}$, respectively^[59]; (e) change of the magnetocrystalline anisotropy of Fe_3–xGeTe₂ film and the magnetization with doping concentration^[60]

$1 - {T_{\rm{c}}}\left( n \right)/{T_{\rm{c}}}\left( \infty \right) = {\left[ {\left( {{N_0} + 1} \right)/2n} \right]^\lambda }{\rm{,}}$

其中$ n $为原子层数, $ {N}_{0} $为自旋-自旋耦合范围, $ \lambda $为临界指数. 对居里温度-厚度的拟合临界分析结果表明, 当FGT的厚度低于5.8 nm时, 该材料的铁磁性由三维状态变为二维状态, 揭示了其在未来自旋电子应用中的普适性. 同年, 许晓栋课题组^[57]再次通过光学测量手段进一步证明了原子层厚度的FGT薄膜的二维巡游铁磁性(图4(b)). 该工作同样证明了可剥落的范德瓦耳斯磁体FGT在减薄至单层时表现出强大的二维铁磁性, 并具有很强的垂直各向异性. 依赖于层数的研究表明, 厚度小于4 nm (5层)的三维Ising铁磁性发生了从三维到二维的转变行为, 同时居里温度(T_c)从207 K迅速降至单层中的130 K, 并突出了巡游铁磁性的物理特性. 韩国标准科学研究所Hwang课题组^[58]发现在脱落的二维磁性材料FGT上会自然形成氧化层(O-FGT), 并且在FGT和O-FGT层之间存在反铁磁耦合(antiferromagnetic coupling, AFC). 基于第一性原理计算得出, 在每层的界面处形成的氧化物会在各层之间引发反铁磁耦合. 如图4(c)所示, AFC会引起异常的磁滞回线, 其中包括双磁化反转曲线, 在特定温度范围内会产生负的剩磁. 2019年, 约翰霍普金斯大学Xu课题组^[59]观察到FGT中大的反常能斯特效应, 反常霍尔角和能斯特角约为0.07和0.09, 远大于普通铁磁体的霍尔角(图4(d)). 根据莫特关系可知, 这些大角度表示在费米能级附近的大贝里曲率, 这与最近提出的将FGT用作拓扑节线半金属候选物的提议是一致的, 提供了FGT作为拓扑铁磁体的证据, 并证明了在自旋卡诺电子应用中使用二维磁性材料及其能带拓扑的可行性. 磁各向异性在范德瓦耳斯磁体中具有特殊的重要性, 因为它不仅影响磁性和自旋输运性质, 同时对稳定二维极限下的磁序也是至关重要的. 韩国科学技术学院自旋电子学中心Jang课题组^[60]报道了空穴掺杂有效地调制了范德瓦耳斯铁磁体的磁各向异性, 并探讨了这种效应的物理成因. Fe_3–xGeTe₂纳米薄片对空穴掺杂的磁各向异性有着显著的抑制作用, 该工作对二维磁体中电子结构和磁性之间的复杂联系进行了充分的研究, 并提出了一种通过掺杂来调控磁性的方法(图4(e)).
2 -->

3.2.二维磁性材料的界面磁调控

2018年, 麻省理工学院Jarillo-Herrero课题组^[61]通过旋转双层石墨烯之间的角度实现了最高温度为1.7 K的超导特性. 这一重大发现突显了界面的重要性, 为二维材料的发展提供了新机遇, 再一次掀起了二维材料在当今凝聚态物理领域的研究新热潮. 一般来说, 广义Heisenberg哈密顿量源于电子的性质, 是通过除自旋以外的所有自由度积分得到的. 因此, 电子结构的改变会修正系统的有效自旋哈密顿量, 这体现了二维材料对外部操作的敏感性^[62].
2018年, 为了探索二维磁性材料的界面调控作用, 华盛顿大学许晓栋课题组^[63]和康奈尔大学Shan课题组^[64]分别利用电压调控了CrI₃的磁性(图5). 双层CrI₃表现为具有磁场驱动磁性相变的层状反铁磁体. 许晓栋课题组^[63]通过磁光克尔效应(magneto-optic Kerr effect, MOKE)显微镜在双层CrI₃中观察到静电门控制的磁性相变. 在临界磁性相变的磁场附近, 通过电压调控可实现铁磁态与反铁磁态间的转变. 其次, 在零磁场下, 净磁化强度可以通过栅极电压连续调控. 两种磁矩方向相反的反铁磁态均显示出了MOKE信号对栅极电压的线性依赖, 但符号相反. 而Shan课题组^[64]利用CrI₃-石墨烯垂直异质结构并通过电子掺杂, 来控制单层及双层CrI₃的磁性能. 在单层CrI₃中, 掺杂可以显著地改变饱和磁化强度、矫顽力以及居里温度. 更进一步地, 在双层CrI₃中, 高于2.5 × 10¹³ cm^–2的电子掺杂能诱发实现零磁场下的反铁磁态到铁磁态的转变. 利用电压进行磁调控这一方法再次证实了二维材料的外场敏感性.
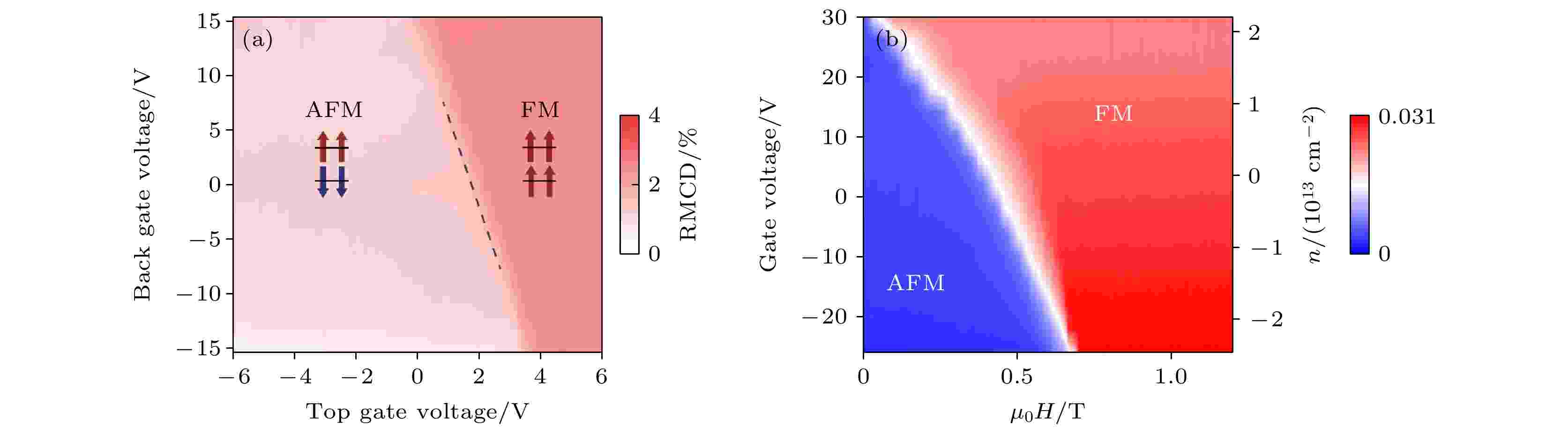图 5 (a) 在μ₀H = 0.78 T时, RMCD强度与顶栅电压和背栅电压的关系, 可以看出在双层CrI₃中利用静电门控制的磁性转变^[63]; (b) 4 K时双层CrI₃中栅极电压-掺杂密度-磁场相位图, 可以看出双层CrI₃中利用电子掺杂控制的磁性转变^[64]
Figure5. (a) RMCD signals under the top gate and back gate voltage at μ₀H = 0.78 T. Magnetic transition can be controlled by electrostatic gate in double-layer CrI₃^[63]. (b) Gate voltage-electron doping density-magnetic field phase diagram in double layer CrI₃ at 4 K. Magnetic transition can be controlled by electron doping in double-layer CrI₃^[64].

作为目前热门的研究方向, 迄今为止, 人们一直致力于在理论与实验上寻找居里温度较高的二维磁性材料^[65]. 在之前的研究中, 通过密度泛函理论(density functional theory, DFT)计算预测了几种居里温度在室温及以上的磁性二维材料, 包括VS₂/WS₂范德瓦耳斯异质结(487 K)^[29], VS₂/MoS₂范德瓦耳斯异质结(485 K)^[29], NiCI₃ (400 K)^[30], CrGeTe₃ (314 K)^[28]及Cr₂C (300 K)^[27]等, 如表1所列. 然而, 寻找室温二维磁性材料的实验研究并不容易, 要么难以合成, 要么居里温度远低于理论值. 到目前为止, 在二维磁性块体中, 实验已经证明FGT存在接近室温的居里温度(约220 K)以及强的垂直磁各向异性, 然而这仍无法应用在室温自旋电子器件中. 因此, 在针对二维磁性材料展开的众多研究中, 将居里温度提高至室温甚至以上一直是这个领域中的研究热点.

2D材料/异质结构	$ {T_{\rm{c}}}/K $	计算/制造方法
VSe2/MoS2和VSe2/HOPE vdW heterostructure	> 300	MBE
VS2/WS2 vdW heterostructure	487	DFT
VS2/MoS2 vdW heterostructure	485	DFT
VTe2	128	DFT
MnSe2/GaSe和MnSe2/SnSe2 vdW heterostructure	> 300	MBE
MnSe2	286	DFT
MnS2	253	DFT
MnI2	15	DFT
NiI2	63	DFT
CrSCI	150	DFT
CrSBr	160	DFT
CrSI	170	DFT
CrI3	45	机械剥离法
CrI3	161	DFT
CrI3	95	DFT
CrCl3	49	DFT
CrBr3	73	DFT
CrF3	41	DFT
CrTe3	71	DFT
NiCl3	400	DFT
CrGeTe3	30	机械剥离法
CrGeTe3	314	DFT
CrGeTe3	130	DFT
CrSiTe3	214	DFT
CrSiTe3	90	DFT
CrSiTe3	170	DFT
Cr3Te4	2057	DFT
Fe3GeTe2	20—300	机械剥离法
Fe3GeTe2	270—300	机械剥离法
Cr3C	> 300	DFT

表1部分二维磁性材料的汇总^[65]
Table1.Summary of some two-dimensional (2D) magnetic materials^[65].

2018年, 南佛罗里达大学的Batzill课题组^[66]利用MBE技术, 在MoS₂和HOPG衬底上生长VSe₂, 其铁磁性可以维持至室温(图6(a)), 并利用Se作为覆盖层对薄膜进行保护, 以达到防氧化的目的. 相较于多层厚度的薄膜, 单层薄膜的磁矩显著增强. 进一步地, 这种铁磁排列非常牢固, 在单层中观察到了电荷密度波的跃迁, 这可能是导致磁性增强的原因. 同年, 加州大学河滨分校Kawakami课题组^[67]同样利用MBE技术生长硒化锰(MnSe_x)薄膜, 该材料也存在室温铁磁性(图6(b)), 磁性及结构表征进一步证明该铁磁性源自单层MnSe₂晶相. 然而, 随着MnSe_x薄膜生长厚度的增加, 薄膜内会产生非磁性共价化合物α-MnSe, 此时薄膜室温铁磁性可能源于MnSe₂单层或者其与α-MnSe层的界面耦合磁性. 该工作也通过DFT计算预测了MnSe₂单层薄膜具有稳定的铁磁性, 与实验结果一致. 这些鼓舞人心的结果为实现室温二维自旋电子器件应用提供了重要的探索方向. 然而, 其不足之处在于VSe₂或MnSe₂块状形式不具有铁磁性, 且MnSe₂在多层结构时易相变成共价α-MnSe相, 这些不易控制性将增加器件制备的难度. 此外, VSe₂具有面内磁各向异性, 相比于PMA自旋电子器件, 已被证明具有较差的可扩展性. 尽管上述材料在实际器件应用中有较大的难度, 但这仍然为寻找高居里温度材料提供了一种途径. 因此, 为实现可在室温下工作的二维自旋电子器件, 需要探索更优、更稳定且具有更强的PMA特性的二维铁磁材料或异质结构.
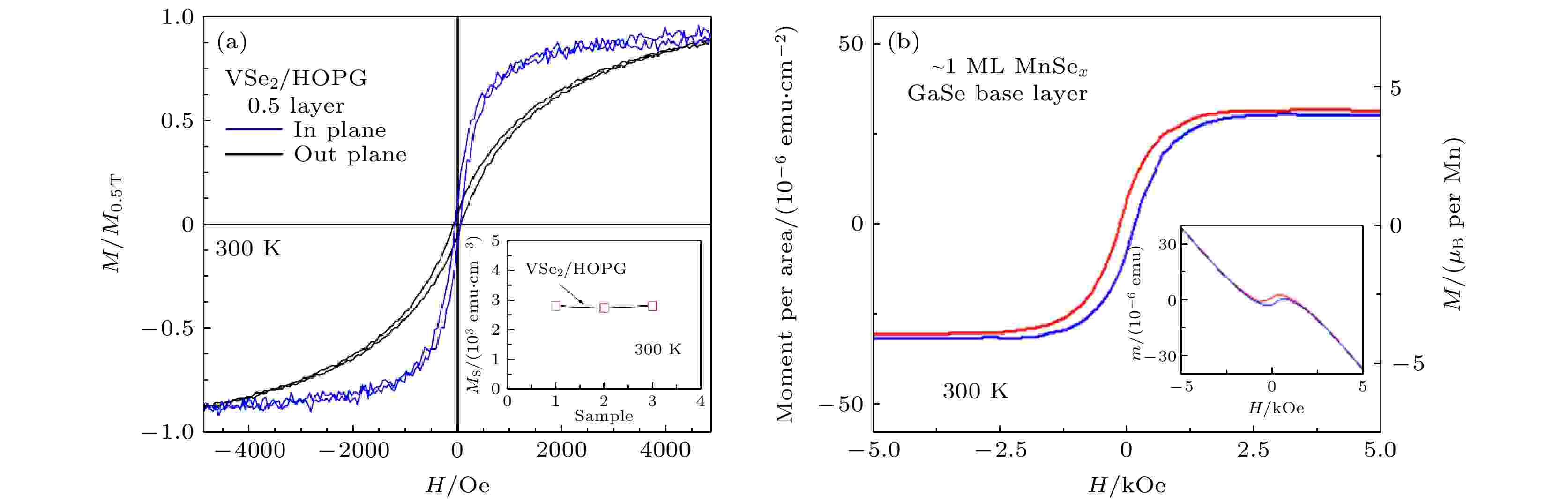图 6 (a) HOPG上单层VSe₂在300 K处的面内和面外磁滞回线^[66]; (b) MnSe_x在300 K处的面外磁滞回线^[67]
Figure6. (a) In-plane and out-of-plane hysteresis loops of a single layer of VSe₂ on HOPG at 300 K^[66]; (b) out-of-plane hysteresis loops of MnSe_x at 300 K^[67].

由图7(a)可知, 中国科学院金属研究所张志东课题组^[68]通过静电门控, 证明少层二维磁性半导体CGT器件可以实现源漏电阻的栅极可调. 而且, 克尔测量结果表明当样品在居里温度以下时, 可通过双极调控磁化强度, 其起源可能来自于费米能级调控时自旋极化能带结构中的再平衡. 而Verzhbitskiy等^[69]通过在CGT薄膜制成的晶体管器件中进行静电掺杂, 如图7(b)所示, 显著提高了居里温度(高于140 K). 实验表明, 载流子掺杂可以调控CGT的居里温度, 并改变其磁各向异性能的符号, 从而导致磁易轴由面外变为面内. 2018年, 复旦大学张远波课题组^[33]制备了基于FGT薄层的离子场效应晶体管器件, 将固态电解质覆盖于FGT和旁侧栅极上, 施加正向的栅极电压可以将锂离子插入进FGT的层间间隙中, 引起大约每层10¹⁴ cm^–2的电子浓度增加, 改变费米面上的态密度, 从而将居里温度提高至室温(图7(c)).
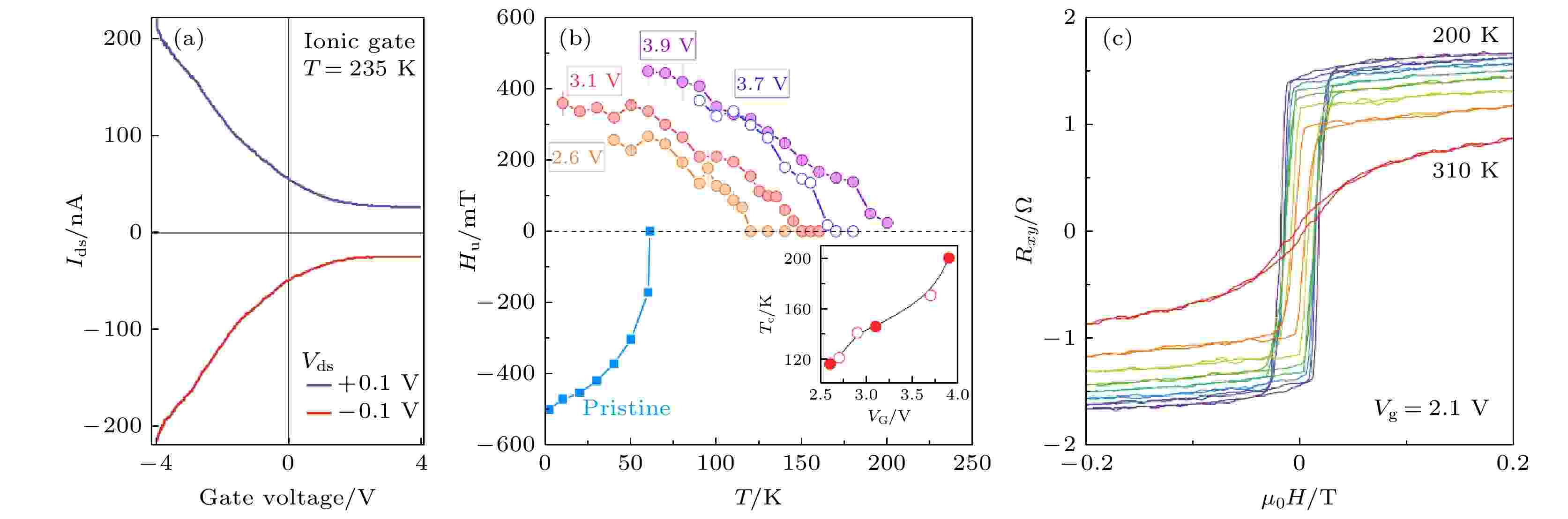图 7 (a) CGT薄膜在不同栅电压下的场效应曲线^[68]; (b)静电掺杂的CGT薄膜器件在不同栅电压下居里温度的变化^[69]; (c)栅电压调控的四层FGT薄膜的霍尔曲线^[33]
Figure7. (a) Field-effect I_ds curves of CGT film^[68]; (b) variation of Curie temperature of CGT device with electron doping under different voltages^[69]; (c) gate-voltage controlled Hall curves of four-layer FGT flake^[33].

此外, 化学掺杂也是一种有效提高二维磁性材料居里温度的方法. 复旦大学修发贤课题组^[55]利用分子束外延技术在蓝宝石及砷化镓衬底上生长FGT薄膜, 并测量其居里温度为216.4 K. 进一步发现, 通过增加Fe的组分, FGT的居里温度不断增加(图8(a)). 2019年, 美国田纳西州橡树岭国家实验室May课题组^[48]合成了Fe_5–xGeTe₂的新型范德瓦耳斯化合物, 通过提高Fe的浓度, 使块状材料的居里温度维持在室温(T_c = 310 K), 少层薄膜的居里温度接近室温(T_c = 280 K), 如图8(b)所示. 2020年, 浦项科技大学Kim课题组^[70]通过改变Fe的浓度制备了Fe₄GeTe₂材料, 该材料同样显示出接近室温的铁磁有序(图8(c)), 以及大的磁化强度和高电导率, 即使在低至7层的薄膜中也具备这些特征, 同时垂直磁各向异性得到了显著改善. 加州大学伯克利分校邱子强课题组^[71]通过使用Ga注入来提高FGT材料的居里温度, 他们的研究证明以10^–3 Ga ?^–3的浓度注入FGT铁磁体时, 可以实现超出室温居里温度. 此外, 其磁各向异性也从低温下的平面外转变为高于本征居里温度以上时的平面内(图8(d)). 上述结果证明了Fe_3+xGeTe₂ (x ≤ 2)具有多种物理特性以及对外部操作具有高敏感性等优势, 在半导体器件领域将表现出巨大的潜在应用价值, 以及广阔的前景.
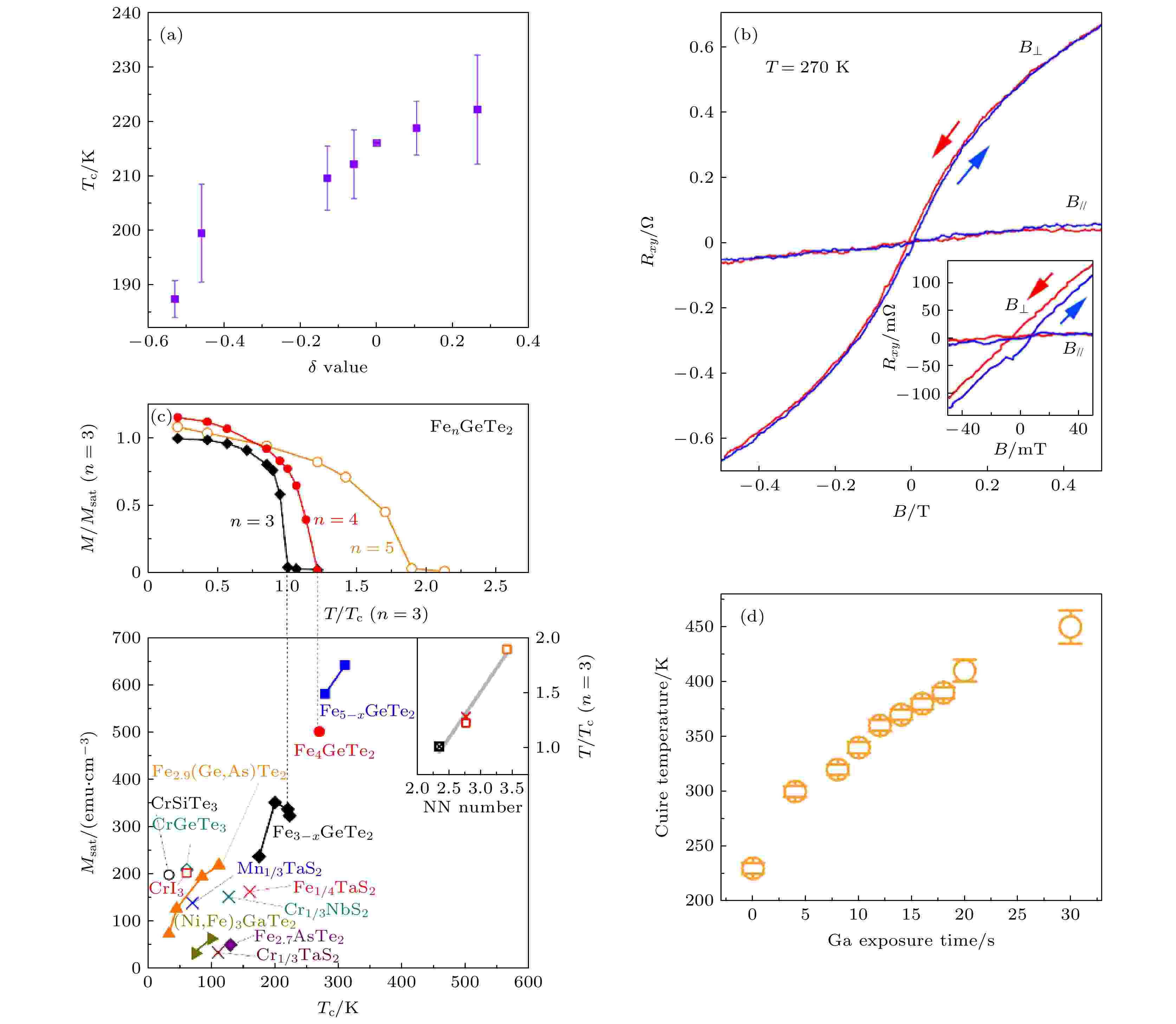图 8 (a), (b), (c) 改变Fe的浓度调控FGT薄膜居里温度的变化^[55,48,70]; (d) 改变Ga的曝光时间调控FGT薄膜居里温度的变化^[71]
Figure8. (a), (b), (c) Changing the concentration of Fe to regulate Curie temperature of FGT films^[55,48,70]; (d) exposure time of Ga-controlled Curie temperature of FGT film^[71].

此外, 其他一些方法也成功地提高了二维磁性材料的居里温度至室温以上. 由图9(a)可知, 加州大学伯克利分校邱子强和北京大学李佳课题组^[72]通过使用聚焦离子束将FGT图案化为微米级菱形结构, 使得FGT薄膜的磁畴相从230 K以下的平面外条纹磁畴转变为高于230 K直至370 K的平面内涡旋磁畴相. 中国科学院大学顾波课题组^[32]通过DFT理论预测了居里温度为144 K的二维磁性半导体—Cr₂Ge₂Se₆的存在. 进一步指出通过施加3%的应变可以将其居里温度增加至326 K, 施加5%的应变可增加至421 K, 远高于室温, 如图9(b)所示.
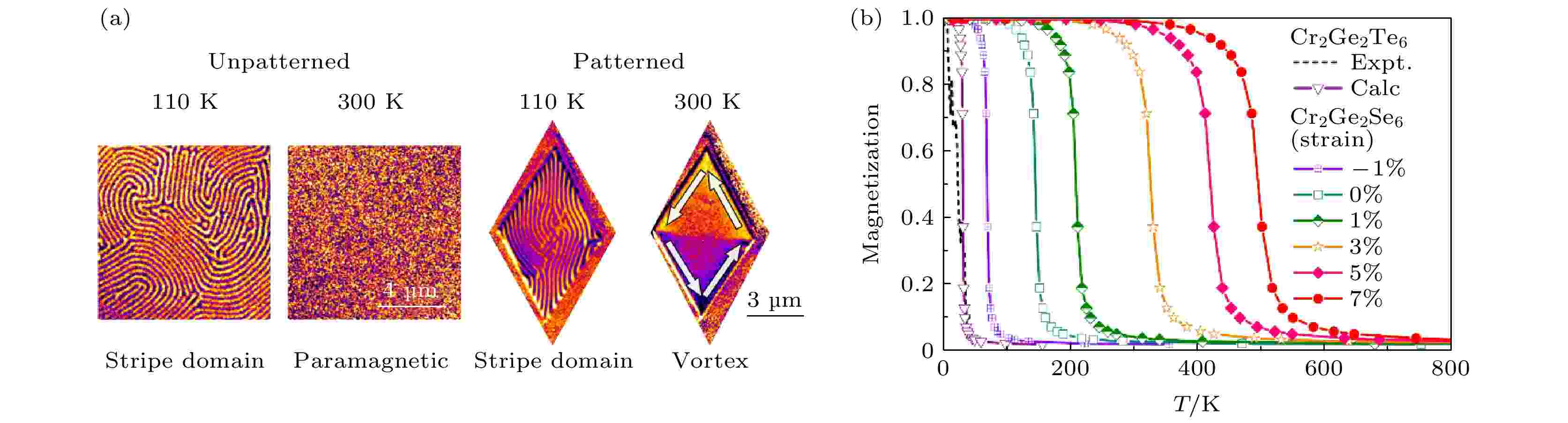图 9 (a) 图形诱导FGT薄膜铁磁性的变化^[72]; (b) 应变诱导CGT薄膜居里温度的变化^[32]
Figure9. (a) Pattern induces the variation of ferromagnetism of FGT film^[72]; (b) strain induces the variation of Curie temperature of CGT film^[32].

最近有研究表明, 利用两种材料间的界面耦合会诱导出稳定的铁磁序, 可以极大地提高二维磁性材料的居里温度. 复旦大学修发贤课题组^[55,73]通过制备FGT/MnTe及FGT/CrSb异质结, 利用铁磁层/反铁磁层界面之间的交换作用来增强磁性. 相较于纯FGT薄膜, FGT/MnTe异质结的矫顽场增加了50%以上(图10(a))^[55]; 而利用层间的近邻效应, FGT/CrSb异质结成功将4层纯FGT的居里温度从140.3 K提高至286.7 K, 接近室温, 如图10(b)所示^[73]. 2020年, 中国科学院大学顾波课题组^[74]基于DFT计算提出了具有强自旋轨道耦合的异质结构, 其中非磁性半导体层(PtSe₂)可使得二维磁性半导体(Cr₂Ge₂Te₆)的磁各向异性能大幅度增强, 并通过哈密顿量模型分析了Dzyaloshinskii-Moriya相互作用以及单离子各向异性有助于居里温度的增强. 该工作进一步验证了界面工程效应的重要性, 尤其是强自旋轨道耦合异质界面效应为二维磁性材料的磁性增强研究拓宽了思路, 具有重要的启发意义.
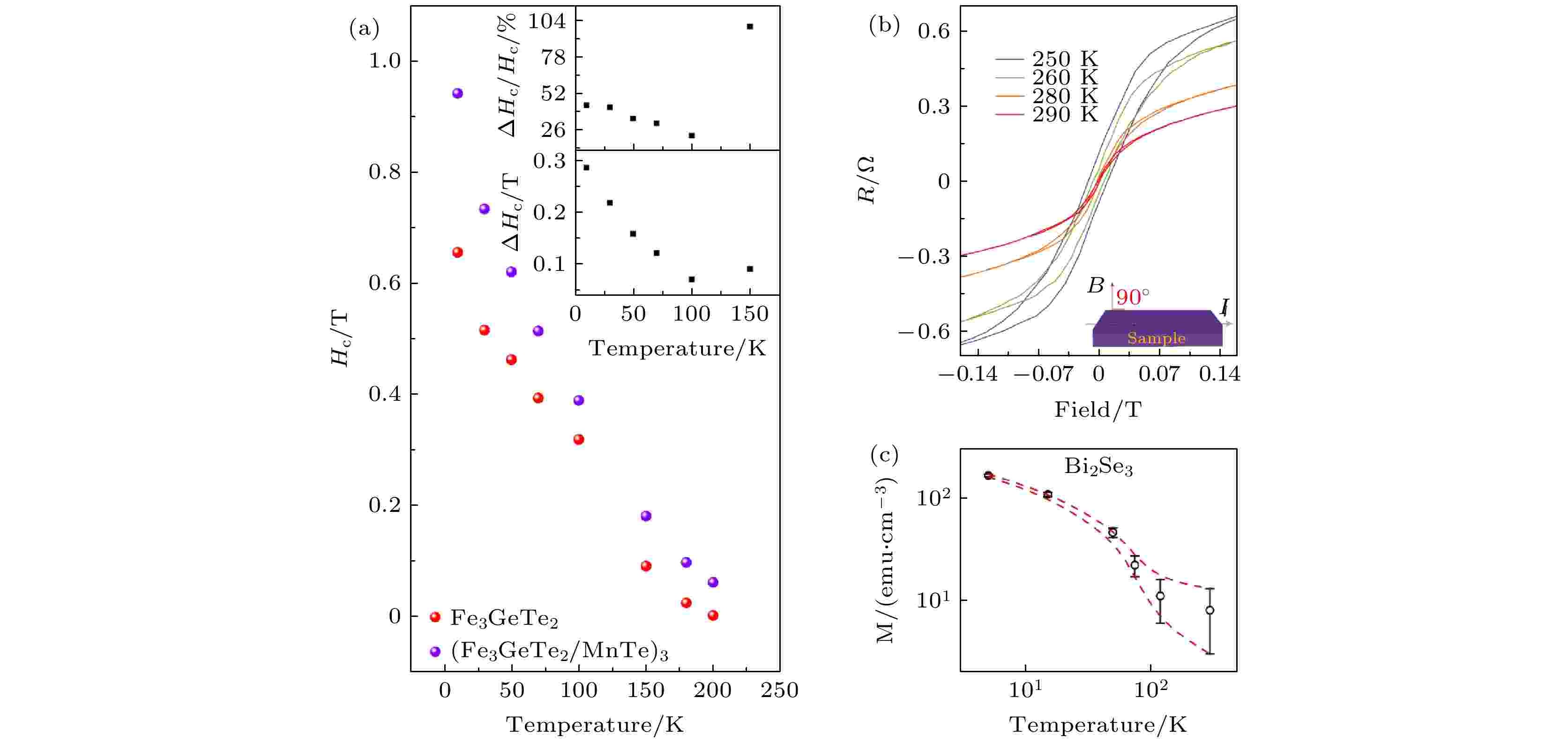图 10 (a) 反铁磁MnTe增强Fe₃GeTe₂铁磁性^[55]; (b) 反铁磁CrSb近邻效应诱导居里温度的变化^[73]; (c) EuS/Bi₂Se₃界面增强居里温度^[77]
Figure10. (a) Antiferromagnetic MnTe induced Fe₃GeTe₂ ferromagnetism enhancement^[55]; (b) antiferromagnetic CrSb proximity-induced Curie temperature increase^[73]; (c) EuS/Bi₂Se₃ interfacial-enhanced Curie temperature^[77].

拓扑绝缘体作为一种二维范德瓦耳斯材料, 近年来继石墨烯之后成为凝聚态物理领域的另一个研究热点. 拓扑绝缘体具有强的自旋轨道耦合引起的非平庸拓扑表面态, 尤其当打破时间反演对称后, 会带来许多新奇的特性, 如量子反常霍尔效应等^[75,76]. 因此, 利用拓扑绝缘体的强自旋轨道特性有望用来调控二维磁性材料的居里温度. 此前, 麻省理工学院Katmis和Moodera课题组^[77]制备了铁磁绝缘体EuS与拓扑绝缘体Bi₂Se₃的异质结构, 其界面铁磁性可持续到室温以上, 如图10(c)所示.
2020年, 本课题组利用MBE技术生长了可控厚度的Bi₂Te₃/FGT异质结, 成功利用界面工程效应提高了FGT的居里温度(230 K)至室温以上(400 K), 通过改变FGT的厚度进一步验证了界面的重要性^[31]. 理论方面, 该工作基于DFT以及基于Ising模型的蒙特卡罗模拟来计算, 哈密顿量为

$\begin{split}H =\;& {H_0} - {J_1}\sum\limits_{\left\langle {ij} \right\rangle } {{S_i}} \cdot {S_j} - {J_2}\sum\limits_{ \langle\langle ij \rangle\rangle } {{S_i}} \cdot {S_j} \\&- {J_3}\sum\limits_{\langle \langle\langle ij \rangle\rangle\rangle } {{S_i}} \cdot {S_j}{\rm{,}}\end{split}$

其中, $ {S}_{i} $, $ {S}_{j} $表示在i和j位置上的自旋; $ {J}_{1} $, $ {J}_{2} $, $ {J}_{3} $分别表示第一、第二及第三近邻交换耦合系数, $ {J}_{1} $与$ {J}_{3} $表征铁磁性, $ {J}_{2} $表征反铁磁性.
值得注意的是, 表2的计算结果表明在单层Bi₂Te₃/FGT异质结中的层内磁性相互交换作用远大于单层纯FGT. 通过数值发现$ {J}_{1} $比$ {J}_{2} $和$ {J}_{3} $大得多, 且基态与居里温度T_c均主要取决于$ {J}_{1} $, 结论证实了界面耦合会引起磁性薄膜获得更高的居里温度T_c. 实验方面, 如图11(a)所示, 电阻随温度变化的曲线图表现出金属的特性, 表明该异质结与FGT薄膜的导电性质相似. 然而, 曲线在100 K以下时剧烈下降, 原因可能是Bi₂Te₃和FGT的协同导电引起的. 随后, 如图11(b)—(d)所示, 通过向器件施加平面外和平面内的磁场, 其反常霍尔曲线证明了异质结超越室温的铁磁性和垂直磁各向异性. 阿罗特图可以进一步精准地确定居里温度, 例如图11(e)确定了Bi₂Te₃(8)/FGT(5)的居里温度约为380 K. 更进一步地, 图11(f)通过磁光克尔技术再次验证了室温铁磁性. 通过系统研究具有不同厚度的FGT异质结构的铁磁性, 验证了拓扑绝缘体界面增强FGT居里温度(图11(g)—(i)). 此工作提出了一种利用拓扑异质结来提高二维磁性材料居里温度的方法, 证明了界面效应的重要性, 对研究调控居里温度具有一定的启发意义.

	E0	EFM /eV	EAFM-In /eV	EAFM-L /eV	J1 /meV	J2 /meV	J3 /meV
Pure FGT	0	–11.441	–10.703	–11.272	3.675	–1.817	0.663
Bi2Te3/FGT	0	–16.400	–15.196	–15.742	5.906	–2.923	1.064

表2FGT和Bi₂Te₃/FGT磁性相互交换作用
Table2.Magnetic interaction of FGT and Bi₂Te₃/FGT.

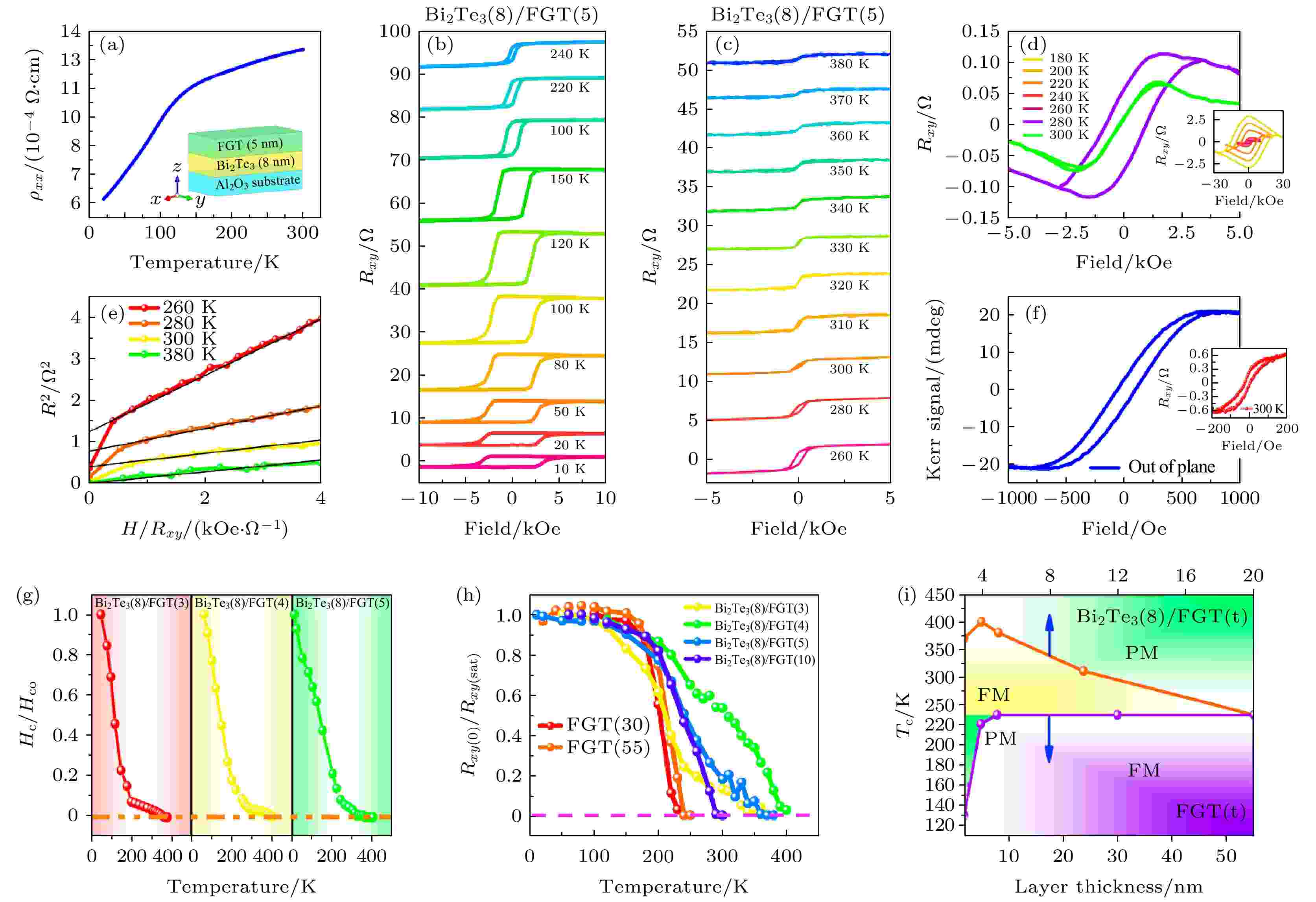图 11 (a) Bi₂Te₃(8)/FGT(5)异质结构随温度变化的电阻率; (b), (c) 不同温度下的面外反常霍尔曲线; (d) 不同温度下的面内反常霍尔曲线; (e) 阿罗特图来精准表征居里温度; (f) 300 K下异质结构的磁光克尔信号; (g), (h), (i) 不同厚度下异质结构的居里温度表征^[31]
Figure11. (a) Resistivity of Bi₂Te₃(8)/FGT(5) heterostructure with the variation of temperature; (b), (c) out-of-plane anomalous Hall curves under different temperatures; (d) in-plane anomalous Hall curves under different temperatures; (e) Arrott plot for characterizing the Curie temperature; (f) magneto-optical Kerr signal of the heterostructure at 300 K; (g), (h), (i) thickness-dependent Curie temperature^[31].

在进行二维磁性材料磁特性以及居里温度调控研究的同时, 研发新型二维自旋电子器件有望解决现有硅基电子器件尺度缩小引起的功耗瓶颈. 2018年, 日内瓦大学Morpurgo课题组^[78]设计了基于FGT/h-BN/FGT的隧穿自旋阀器件, 其中FGT由剥离法制备, 厚度分别为7和20 nm, 两层FGT皆可由磁场进行翻转. 绝缘体h-BN用作隧穿层, 厚度为1—2个原子层, 该器件呈现了隧道磁电阻(TMR)效应, 即两层FGT处于平行状态时, 器件呈现低阻态; 两层FGT处于反平行状态时, 器件呈现高阻态. 最终该器件在低温(4.2 K)下实现了160%的隧穿磁阻率. 2019年, 皇家墨尔本理工大学Wang课题组^[79]设计了FGT/graphite/FGT范德瓦耳斯异质结构并进行了磁阻研究. 在常规巨磁阻(giant magnetoresistance, GMR)中, 三层结构显示出对称的磁阻效应: 当两个铁磁层中的磁矩指向相反方向时, 三层结构呈现高阻态; 当磁矩指向相同方向时, 三层GMR器件将处于低阻态. 然而该范德瓦耳斯异质结中的磁阻具有明显的高、中和低阻态. 这种独特的特征揭示了与之前截然不同的物理机理. 经过理论计算, 三种电阻行为归因于自旋动量锁定在graphite/FGT界面处感应的自旋极化电流. 由此可知, 不同材料耦合形成的范德瓦耳斯异质结体现出来截然迥异的特性, 在自旋电子学应用中将具有巨大的潜力. 同时, 加州大学河滨分校Shi 课题组^[22]针对FGT/Pt异质结构中的自旋轨道矩翻转进行了探索, 通入Pt层的电荷流可以产生自旋轨道矩, 进而实现FGT磁化方向的翻转. 该工作为实现基于二维磁性材料的自旋轨道矩器件指明了方向.
综上所述, 探索高居里温度的二维磁性材料并进一步制备在室温下工作的新型二维自旋电子器件, 将是二维磁性材料迈向实际应用的重要一步, 有望加速自旋芯片的应用, 从而推动集成电路产业的发展. 因此, 如何构建低功耗、高集成度、非易失性和智能化的新型低维自旋电子器件, 亟需研究人员进一步探索和研究.

目前, 二维磁性材料的制备大多依赖于机械剥离技术, 且其新颖的自旋特性以及原型器件也仅在低温下工作, 这大大限制了未来的实际应用, 因此, 实现高居里温度将是推动其进一步发展的先决条件. 本篇综述着重聚焦于探讨二维磁性材料居里温度的调控方法, 从二维磁性材料的制备方法着手, 以CrI₃, Cr₂Ge₂Te₆, Fe₃GeTe₂为范例, 分析了二维磁性材料的长程有序磁态以及优越的物理特性. 在调控居里温度的方法中, 无论是理论分析还是实验现象, 均揭示了电子能带结构的改变会导致系统中有效自旋哈密顿量的修正, 证明了二维磁性材料的多功能性及其对外部操作的敏感性, 诸如门控、应变以及界面工程效应等. 进一步地, 可扩展到由二维磁性材料组成的磁性异质结以及开发新的概念器件, 有望在能源环境、电子信息、航空航天、生物医药等领域引起革命性的突破.