摘要: 获得粒子能级布居是研究非平衡等离子体辐射性质的一个重要方面. 对于复杂三维等离子体, 采用细致碰撞辐射模型虽然精确, 但计算耗费大. 本文提出了一种束缚态特征温度法, 能够快速计算得到非平衡等离子体中的粒子能级布居. 对非平衡氖等离子体算例的研究表明, 本文方法是有效的, 在等离子体非平衡程度不太高时与碰撞辐射模型符合较好. 在计算效率上, 本文方法比碰撞辐射模型至少提高了3000倍, 可极大节约计算资源和成本, 在工程计算中有重要实际意义.
关键词: 非平衡 /
等离子体 /
能级布居 English Abstract A simplified method of calculating electronic energy level populations in nonequilibrium plasmas He Xin 1 ,Jiang Tao 2 ,Gao Cheng 1 ,Zhang Zhen-Fu 1 ,Yang Jun-Bo 1 1.College of Liberal Arts and Sciences, National University of Defense Technology, Changsha 410073, China Fund Project: Project supported by the National Numerical Windtunnel of China (Grant No. NNW2019ZT3-B07) and the National Natural Science Foundation of China (Grant No. 12074430)Received Date: 14 December 2020Accepted Date: 07 February 2021Available Online: 12 July 2021Published Online: 20 July 2021Abstract: In order to investigate the radiative properties of plasma in non local thermodynamic equilibrium (NLTE), it is of great importance to determine energy level populations, which are often obtained by the so-called collisional-radiative (CR) model. As is well known, the CR model is accurate but computationally costly, and thus it is difficult to be applied to engineering calculations for such as complex three-dimensional plasmas. In this work, a bound-state characteristic temperature (BCT) method is proposed, which can be used to calculate quickly the energy level populations in non-equilibrium plasmas. In this method, we assume that for each kind of ionization stage, the bound-state population is Boltzmannian at a certain characteristic temperature. The assumed characteristic temperature is related to the degree of none-equilibrium and may be different from the electronic temperature of the plasma. Based on a modified Saha equation, the assumed characteristic temperature can be calculated easily, and then the energy level populations are obtained conveniently. Five cases of non-equilibrium neon plasma at variable electronic temperatures and densities are investigated and compared with the results from a CR model. Good agreement is found between them if the degree of non-equilibrium is not very large. It shows that the present method is effective and at least 3000 times faster in computation time than the CR model. The method is very useful in engineering applications. Keywords: nonequilibrium /plasmas /energy level populations 全文HTML --> --> --> 1.引 言 在天体物理、X射线激光物理和约束聚变等领域中[1 ] , 常常需要掌握等离子体的辐射特性, 进而研究其中辐射的输运与分配[2 ] . 为了获得辐射参数, 必须知道等离子体中粒子的能级布居.[3 ] . 然而, 很多情况下的等离子体处在非局域热动平衡状态(non-LTE, NLTE)[4 ] . 计算NLTE等离子体中的粒子能级布居是辐射特性研究必须面对的问题.[5 ] . 根据原子参数的精密程度, 研究者发展了基于不同层次的CR模型, 如平均原子模型[6 -9 ] 、超组态模型[10 -14 ] 、细致组态模型[15 -21 ] 和细致能级模型[22 ,23 ] 等. 一般说来, 细致能级模型因为考虑了不同电荷态离子的能级结构, 计算精度最高, 但是计算耗费大; 而超组态模型把大量能量相近的精细能级近似处理成一个“能级”, 虽节省了计算时间, 但降低了计算精度[24 -26 ] . 因此研究者们提出了一些兼顾计算精度和计算时间的CR模型和方法[27 -29 ] . 例如Hansen等[27 ] 使用混合了细致能级模型和超组态模型的方法获得原子参数和能级布居; Bauche等[29 ] 在超组态模型中引入“有效温度”的概念, 能够方便获得相应能级上的粒子占据数. 虽然CR模型的种类很多[26 ] , 但很多时候为了准确模拟NLTE等离子体辐射性质, 需要选取足够多数量的量子态, 使得速率方程组规模很大. 大规模的速率方程组求解复杂, 计算量大, 通常要借助高性能计算平台. 在三维尺度、参数梯度大的等离子体工程计算中, CR模型虽然精度高, 但难于实际应用. 因此, 研究能够保证一定精度同时低成本、高效率的计算方法, 一直是研究者不断追求的目标, 也具有重要且实际的意义.2.束缚态特征温度法 本文不考虑处于完全热非平衡态的等离子体. 在一般情况下的NLTE等离子体中, 可认为自由电子服从某一自由电子温度${T_{\rm{e}}}$ 的麦克斯韦速度分布[2 ] . 考察NLTE等离子体中原子序号为$A$ 的$z$ 价粒子${A^{z + }}$ ($0 \leqslant z \leqslant A$ , $z = 0$ 表示原子), 设其电离能为${I^z}$ , 如图1 所示.图 1 ${A^{z + }}$ 的束缚态及连续态Figure1. Bound and continuum states of ${A^{z + }}$ .${I^z}$ 能级可看作${A^{z + }}$ 的束缚态. 引入${A^{z + }}$ 的束缚态特征温度$T_{\rm{b}}^z$ , 即假设${A^{z + }}$ 各束缚态上的占据数服从温度为$T_{\rm{b}}^z$ 的Boltzmann分布, 则${I^z}$ 能级上的“粒子数”$N_I^z$ 满足:${N^z}$ 为${A^{z + }}$ 粒子数, $g_I^z$ 为${I^z}$ 能级的简并度, $k$ 为Boltzmann常数, ${Q^z}(T_{\rm{b}}^z) = \displaystyle\sum\nolimits_j g_j^z \exp \left[ {\frac{ - E_j^z} {kT_{\rm{b}}^z}} \right]$ 为${A^{z + }}$ 在特征温度$T_{\rm{b}}^z$ 下的配分函数($E_j^z$ 和$g_j^z$ 分别为${A^{z + }}$ 第$j$ 束缚态的能量和简并度).${I^z}$ 能级上的粒子可看作由处于基态的${A^{(z + 1) + }}$ 与速度为零的自由电子构成. 由于自由电子服从${T_{\rm{e}}}$ 下的麦克斯韦速度分布, 则$N_I^z$ 还满足[30 ] :$N_0^{z + 1}$ 和$g_0^{z + 1}$ 分别为${A^{(z + 1) + }}$ 基态的占据数和简并度, ${N_{\rm{e}}}$ 为自由电子数, ${m_{\rm{e}}}$ 为自由电子质量, $h$ 为Planck常数. 类似地, 引入${A^{(z + 1) + }}$ 的束缚态特征温度$T_{\rm{b}}^{z + 1}$ , (2 )式可转化为${N^{z + 1}}$ 为${A^{(z + 1) + }}$ 粒子数, ${Q^{z + 1}}(T_{\rm{b}}^{z + 1})$ 为${A^{(z + 1) + }}$ 在特征温度$T_{\rm{b}}^{z + 1}$ 下的配分函数.1 )式和(3 )式, 有$T_{\rm{b}}^z$ . 进而, 根据Boltzmann公式$N_j^z = $ $ {{{N^z}g_j^z\exp \left[ {{{ - E_j^z} / {(kT_{\rm{b}}^z)}}} \right]} / {{Q^z}(T_{\rm{b}}^z)}}$ , 可得到${A^{z + }}$ 粒子的各能级占据数.$T_{\rm{b}}^A = {T_{\rm{e}}}$ (因为$z = A$ 对应于粒子完全电离), 然后按照“倒序”依次求解出$T_{\rm{b}}^{A - 1}$ , $T_{\rm{b}}^{A - 2} ,\cdots,$ $T_{\rm{b}}^0$ , 详细计算流程如图2 所示. 实际上, 总存在某个电离度范围$p \leqslant z \leqslant q$ , 不在该电离度范围的粒子丰度相对很小. 此时, 可近似认为$T_{\rm{b}}^{q + 1} = {T_{\rm{e}}}$ ($q + 1 \leqslant A$ ), 然后依次求解出$T_{\rm{b}}^q$ , $T_{\rm{b}}^{q - 1},\cdots,$ $T_{\rm{b}}^p$ , 进而计算主要粒子的能级布居.图 2 计算流程图Figure2. Calculation flowchart.$T_{\rm{b}}^z = {T_{\rm{e}}}$ ($0 \leqslant z \leqslant A$ ), 那么(4 )式自然过渡为LTE条件下的Saha方程[30 ] .3.算例与讨论 表1 列出了5种条件的NLTE氖(Ne)等离子体, 其中e– 代表自由电子. 为了便于将本文计算的能级布居与CR模型结果进行直接对比, 表中Ne粒子百分数、自由电子(e– )数密度均采用了与CR模型相同的数据[22 ] . 另外, 表中未列出丰度小于10–6 的粒子. 算例1—算例3主要研究Ne核总数密度相同、${T_{\rm{e}}}$ 不同的情况; 算例4和算例5分别与算例2和算例3对应, 主要研究${T_{\rm{e}}}$ 相同、Ne核总数密度不同的情况.算例1 算例2 算例3 算例4 算例5 $k{T_{\rm{e}}}$/eV 5 15 40 15 40 Ne核总数密度/${\rm{c}}{{\rm{m}}^{ - 3}}$ 1018 1018 1018 1020 1020 ${\rm{Ne}}$粒子数含量/% 0.0258 ${\rm{N}}{{\rm{e}}^ + }$粒子数含量/% 5.2017 ${\rm{N}}{{\rm{e}}^{2 + }}$粒子数含量/% 88.6853 0.0015 5.0406 ${\rm{N}}{{\rm{e}}^{3 + }}$粒子数含量/% 6.0863 0.4202 38.9713 0.0002 ${\rm{N}}{{\rm{e}}^{4 + }}$粒子数含量/% 0.0008 19.4618 48.9205 0.0299 ${\rm{N}}{{\rm{e}}^{5 + }}$粒子数含量/% 67.8883 0.0037 6.9899 1.0996 ${\rm{N}}{{\rm{e}}^{6 + }}$粒子数含量/% 12.1407 0.6767 0.0777 15.7779 ${\rm{N}}{{\rm{e}}^{7 + }}$粒子数含量/% 0.0874 20.1261 48.7610 ${\rm{N}}{{\rm{e}}^{8 + }}$粒子数含量/% 79.1935 34.3313 ${\rm{N}}{{\rm{e}}^{9 + }}$粒子数含量/% ${\rm{N}}{{\rm{e}}^{10 + }}$粒子数含量/% e– 数含量/(1018 cm–3 ) 2.01 4.92 7.79 351.00 712.00
表1 算例参数Table1. Cell parameters.4 )式, 计算能级布居还用到各价Ne粒子的电离能(见表2 ). 等离子体环境中, 由于屏蔽效应, 原子(或离子)的电离能相比于孤立原子会下降. 表2 中的数据由计算而得(等离子体条件: $k{T_{\rm{e}}}$ 为40 eV, Ne核数密度为1020 cm–63 ). 在本文所研究的等离子体条件下, 电离能下降值变化不大, 因此忽略不同条件(自由电子温度、核总数密度)对Ne粒子电离能的影响.原子(离子) 电离能/eV ${\rm{Ne}}$ 19.441 ${\rm{N}}{{\rm{e}}^ + }$ 40.565 ${\rm{N}}{{\rm{e}}^{2 + }}$ 63.007 ${\rm{N}}{{\rm{e}}^{3 + }}$ 93.588 ${\rm{N} }{ {\rm{e} }^{4 + } }$ 123.924 ${\rm{N}}{{\rm{e}}^{5 + }}$ 157.561 ${\rm{N}}{{\rm{e}}^{6 + }}$ 201.788 ${\rm{N}}{{\rm{e}}^{7 + }}$ 230.156 ${\rm{N}}{{\rm{e}}^{8 + }}$ 1183.642 ${\rm{N}}{{\rm{e}}^{9 + }}$ 1345.217
表2 Ne原子及离子电离能Table2. Ionization energy of neon atom and ions.${T_{\rm{e}}}$ 下的Boltzmann公式和Saha方程计算而得:5 )式和(6 )式的比值$\alpha $ (对同种粒子的任意能级均相等). 显然, 对平衡等离子体, $\alpha = 1$ ; 反之, $\alpha $ 偏离1. 为评估本文计算结果与CR模型的符合程度, 对各能级计算出二者的比值$\delta $ ($\delta = 1$ 表示完全符合).图3 为算例1条件下本文计算的能级布居与CR模型结果的对比. 图中, $1.00 < \alpha \leqslant 2.13$ , 可知等离子体是弱非平衡的. 如图3(a) , (b) , (d) , (e) , 对于Ne, Ne+ , Ne3+ 和Ne4+ , $\delta $ 与1的平均偏差不大于10%, 说明本文计算的能级布居与CR模型符合很好. 如图3(c) 所示, 对于Ne2+ , $\delta $ 与1的平均偏差稍大(–31%), 这可能主要是由于Ne2+ 的电离能数据存在误差.图 3 算例1的非简并能级布居Figure3. Non-degenerate electronic level populations for Case 1.图4 为算例2条件下能级布居结果对比. 图中, $1.71 \leqslant \alpha \leqslant 30.08$ , 较算例1有所增大, 可知此条件下等离子体的非平衡程度提高. 对于各价Ne离子(除图4(d) 中的Ne5+ ), $\delta $ 与1的平均偏差都在17%以内, 说明此条件下计算出的能级布居与CR模型符合较好.图 4 算例2的非简并能级布居Figure4. Non-degenerate electronic level populations for Case 2.图5 为算例3条件下能级布居结果对比. 此条件下, $7.63 \!\leqslant\! \alpha \!\leqslant\! 40484$ , 说明非平衡程度进一步增大. 如图5(a) 所示, 对于Ne5+ , $\delta $ 与1的平均偏差为38%. 如图5(b) —图5(d) , 对于Ne6+ , Ne7+ 和Ne8+ , $\delta $ 与1的平均偏差不大于20%. 结果表明, 此条件下本文计算得到的能级布居与CR模型偏离不大.图 5 算例3的非简并能级布居Figure5. Non-degenerate electronic level populations for Case 3.图3 —图5 可知, 在Ne核总数密度为1018 cm–3 条件下, 对于弱非平衡态, 本文计算的能级布居与CR模型符合很好; 随着非平衡程度增大, 本文计算结果与CR模型之间逐渐产生偏离.图6 为算例4条件下能级布居计算结果. 对于各价Ne离子, $\alpha $ 均接近1, 说明等离子体处于近平衡态. 此条件较算例2的非平衡程度降低, 主要归因于Ne核总数密度增大. 图6 中, $\delta $ 与1的平均偏差不超过10%, 说明计算结果与CR模型符合很好. 对比图6 与图4 可知, 在$k{T_{\rm{e}}}$ = 15 eV条件下, 若非平衡程度提高, 则本文得到的能级布居与CR模型的偏离增大, 这与图3 —图5 反映的现象类似.图 6 算例4的非简并能级布居Figure6. Non-degenerate electronic level populations for Case 4.图7 为算例5条件下能级布居计算结果. 相比于算例3, 由于Ne核总数密度增加, 等离子体非平衡程度降低($1.03 \leqslant \alpha \leqslant 218$ ). 对于图7(e) 中的Ne7+ , $\delta $ 与1的平均偏差稍大(–13.5%); 对于图7 中其他各价Ne离子, $\delta $ 与1的平均偏差都不大于7.8%. 因此, 此条件下得到的能级布居与CR模型符合较好. 对比图7 与图5 发现, 现象与$k{T_{\rm{e}}}$ = 15 eV时类似.图 7 算例5的非简并能级布居Figure7. Non-degenerate electronic level populations for Case 5.$1.00 < $ $ \alpha \leqslant 2.13$ )时, 本文方法与CR模型非常符合(平均偏差基本在10%以内); 随着非平衡程度的增大($2.13 < \alpha \leqslant 218$ ), 与CR模型逐渐产生偏差(平均偏差基本在30%以内); 若非平衡程度不太高($\alpha \leqslant $ $ 40484$ ), 与CR模型符合较好(平均偏差不超过38%).表3 给出了5个算例总耗时对比, 忽略程序语言效率及计算平台性能的差别, 本文方法比CR模型至少提高了3000倍. 在误差允许范围内, 这将在参数梯度大、复杂三维非平衡等离子体的工程计算中产生巨大效益.程序语言 计算平台 CPU 总耗时 CR模型 Fortran IBM服务器 Intel Xeon E5649: 6核2.53 GHz 约24 h 本文方法 Matlab Thinkpad笔记本电脑 Intel Core i5-3320 M: 2核2.60 GHz 约28 s
表3 计算耗费对比Table3. A comparison of calculation cost.4.结 论 提出了一种用于计算非平衡等离子体中原子及离子能级布居的简化方法. 以几种条件(5 eV $\leqslant $ $ k{T_{\rm{e}}} \leqslant$ 40 eV, 1018 cm–3 $ \leqslant $ 核数密度 $ \leqslant $ 1020 cm–3 )的非平衡Ne等离子体为例, 计算研究了粒子的能级布居, 并与CR模型进行了对比. 结果表明: 1)该方法是有效的, 当等离子体非平衡程度不太高时与CR模型符合较好; 2)计算速度比CR模型至少提高了3000倍, 可大大节约计算成本, 对于复杂三维等离子体计算非常有用. 
图 1 
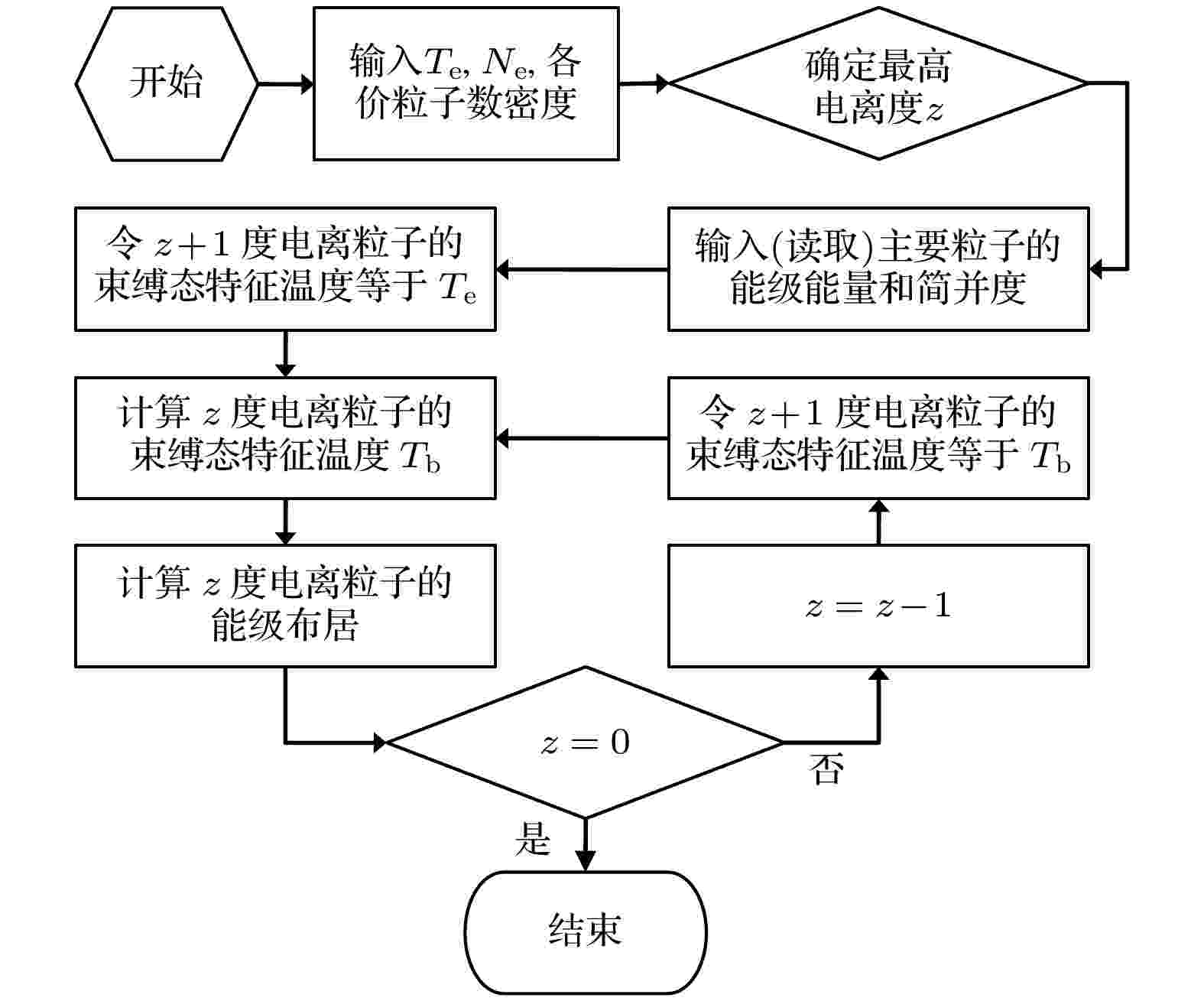图 2 计算流程图
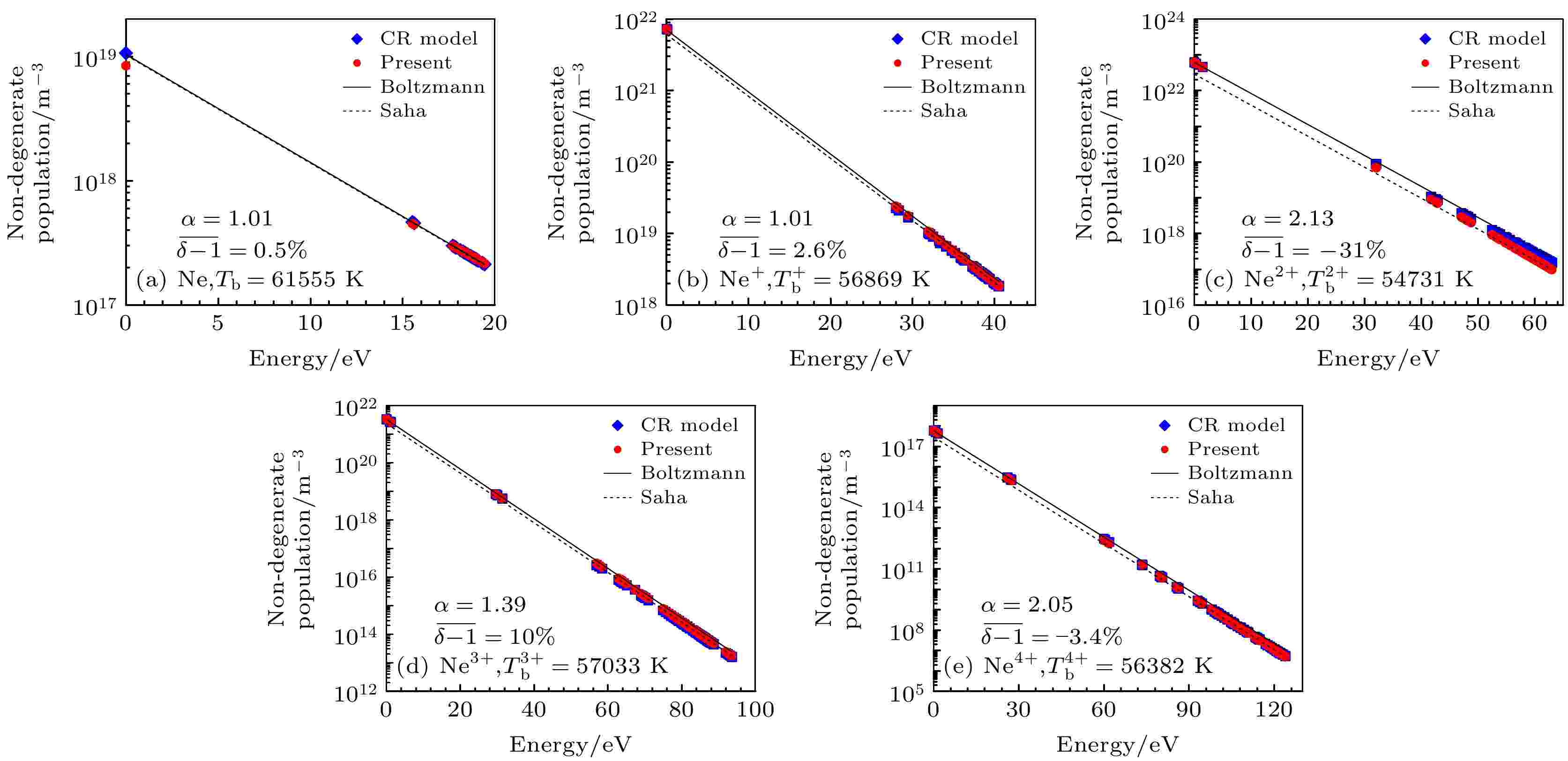图 3 算例1的非简并能级布居
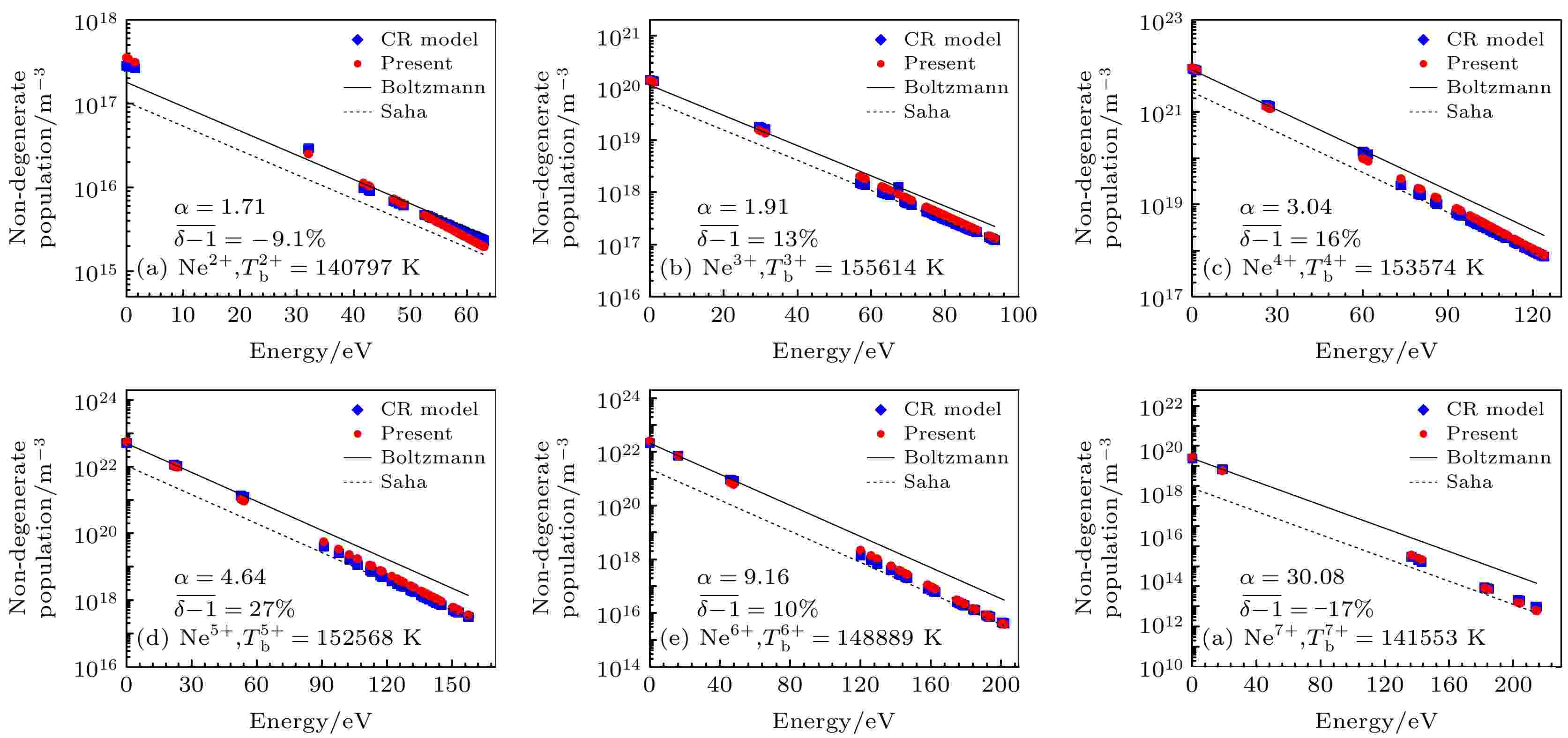图 4 算例2的非简并能级布居
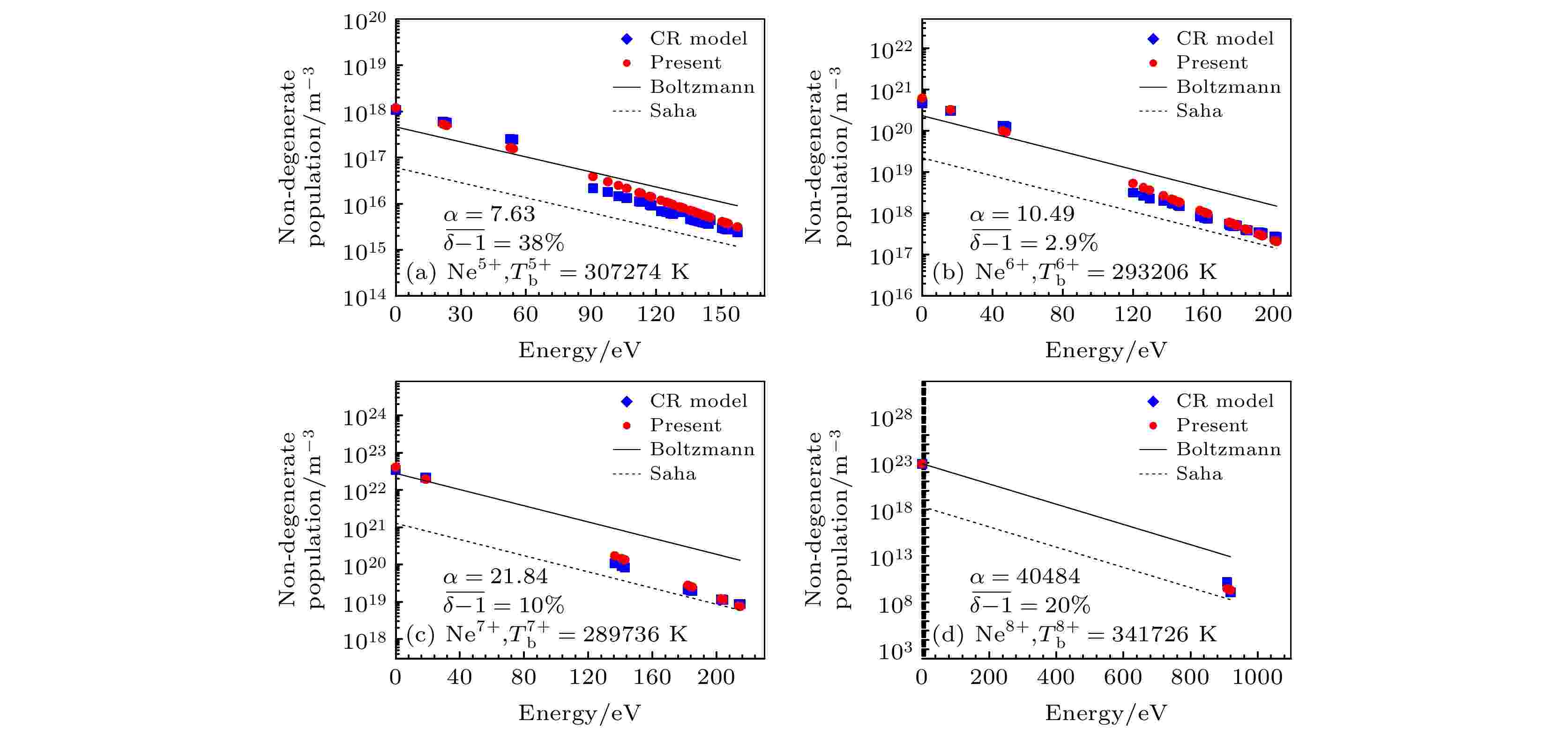图 5 算例3的非简并能级布居
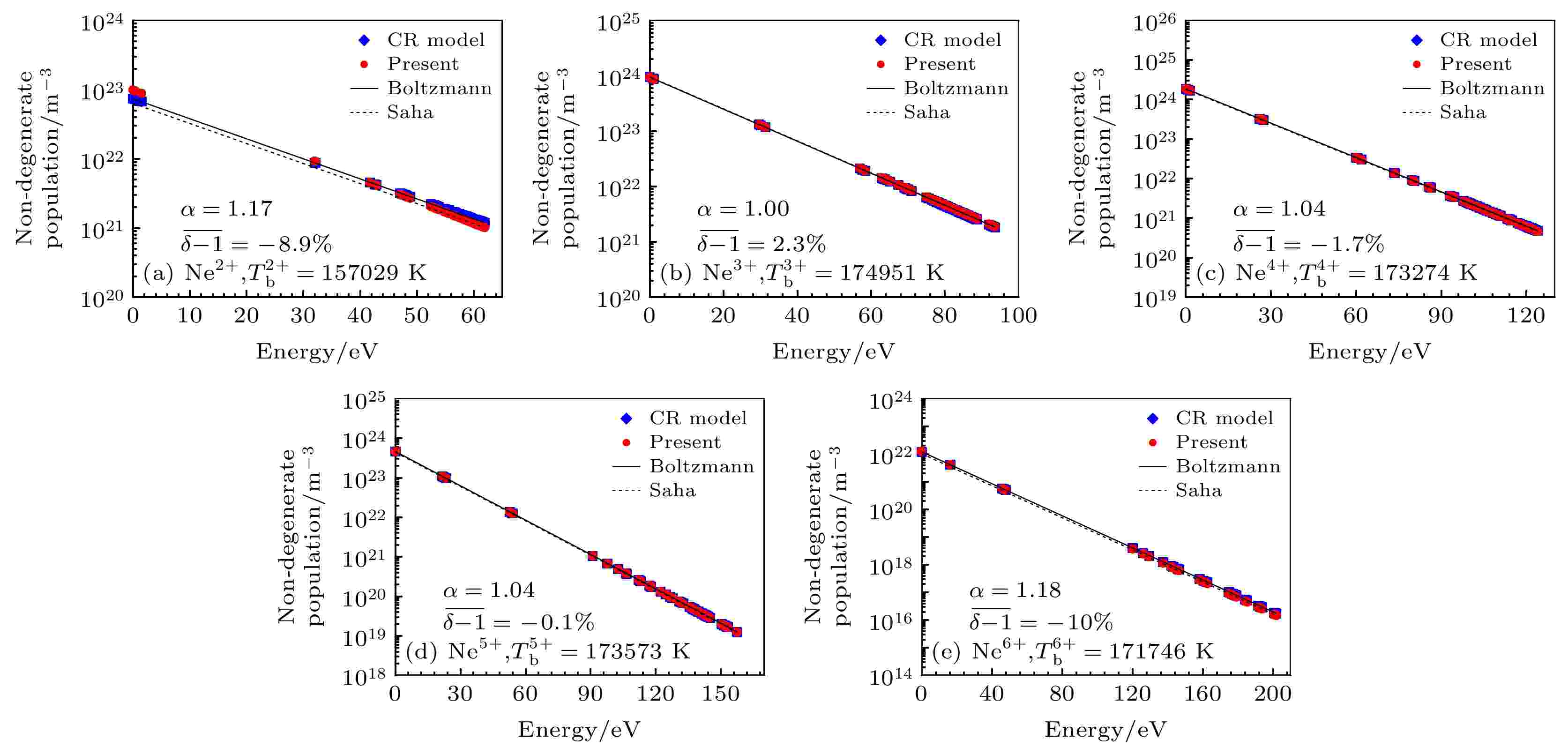图 6 算例4的非简并能级布居
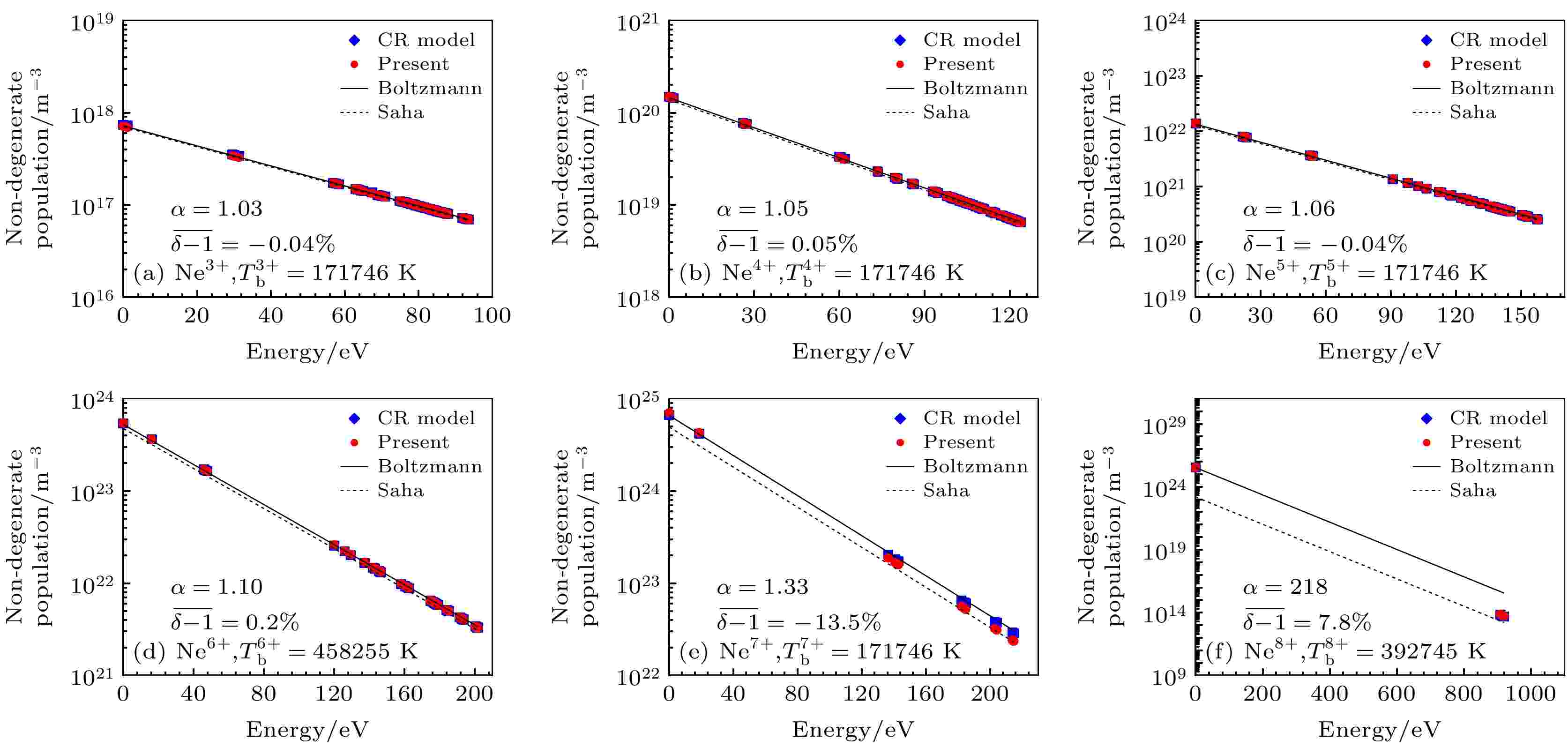图 7 算例5的非简并能级布居
