摘要: 非晶合金具有独特物理和力学性能, 如何建立非晶合金微观结构非均匀性与物理/力学性能之间的关联是非晶固体的重要研究课题之一. 微合金化是调控非晶合金微观结构有效手段之一. 本研究以玻璃形成能力优异的Zr
50– x Cu
34 Ag
8 Al
8 Pd
x (
x = 0, 2)非晶合金为模型合金, 借助差示扫描量热仪和电磁声转换设备, 研究非晶合金铸态、弛豫态和结晶态热流和剪切模量随温度的演化规律, 以及物理时效(低于玻璃转变温度)过程剪切模量的变化随时间演化规律. 基于自间隙原子理论, 利用热流曲线表征非晶合金在相同热历史剪切模量热效应. 通过分析铸态和弛豫态自间隙缺陷浓度和激活能谱, 发现结构弛豫导致自间隙缺陷浓度减小, 诱导剪切模量随温度演化偏离软化过程, 并伴随体系放热. 与此同时, 研究发现添加微量Pd元素可抑制模型合金体系原子迁移, 增加特征弛豫时间. 本研究从非晶合金模量热效应角度进一步理解非晶合金微观结构非均匀性.
关键词: 非晶合金 /
缺陷浓度 /
剪切模量 /
微观结构非均匀 English Abstract Evolution of defect concentration in Zr50– x 34 Ag8 Al8 Pdx x = 0, 2) amorphous alloys derived using shear modulus and calorimetric data Cheng Yi-Ting 1 ,Andrey S. Makarov 2 ,Gennadii V. Afonin 2 ,Vitaly A. Khonik 2 ,Qiao Ji-Chao 1 1.School of Mechanics, Civil Engineering and Architecture, Northwestern Polytechnical University, Xi’an 710072, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 51971178), the Natural Science Foundation of Shaanxi Province, China (Grant No. 2019JM-344), and the Russian Science Foundation (Grant No. 20-62-46003)Received Date: 03 February 2021Accepted Date: 26 February 2021Available Online: 15 July 2021Published Online: 20 July 2021Abstract: Amorphous alloys exhibit unique physical and mechanical properties, which are closely connected with their microstructural heterogeneity. The correlation between structural heterogeneity and mechanical properties is one of the important issues of amorphous alloys. Micro-alloying is an effective way to tune the mechanical and physical properties of amorphous alloys. In the present study, Zr50– x 34 Ag8 Al8 Pdx x = 0 and 2) amorphous alloys with ability to form excellent glass are chosen as model alloys. The evolutions of heat flow and shear modulus in different states (as-cast, relaxed and crystalline) with temperature of Zr50– x 34 Ag8 Al8 Pdx x = 0 and 2) glass system are studied by differential scanning calorimetry (DSC) and electromagnetic-acoustic transformation (EMAT) technique, respectively. The experiment demonstrates that a decrease of the shear modulus is accompanied by the endothermic heat flow and vice versa. The correlation between the heat flow and shear modulus is investigated according to the interstitialcy theory. The calculations of the interstitialcy defect concentration and activation energy spectra suggest that the microstructure remains stable at relatively low temperatures. When temperature increases, the interstitialcy defect structure is activated. Compared with that in the as-cast state, the interstitialcy defect concentration in the relaxed state is reduced by structural relaxation, indicating that temperature-dependent shear modulus softening is inhibited. At temperatures above glass transition temperature, a rapid growth of interstitialcy defect concentration results in the accelerated shear softening, which is accompanied by significant endothermic heat flow. It is noted that the minor addition of palladium reduces the interstitialcy defect concentration in the Zr50– x 34 Ag8 Al8 Pdx x = 0 and 2) metallic glass systems. It is suggested that the introduction of Pd reduces the atomic mobility and increases the characteristic relaxation time. In parallel, the change of shear modulus as a function of the aging time (below the glass transition temperature) is studied by using EMAT equipment. The results indicate that the interstitialcy defect concentration decreases in the physical aging process, which is accompanied by an increase of shear modulus. The interstitialcy defect concentration and shear modulus change towards the quasi-equilibrium state with aging time increasing. A reduction of the interstitialcy defect concentration leads to a decrease of the shear modulus change upon microalloying by Pd into Zr50– x 34 Ag8 Al8 Pdx x = 0 and 2) metallic glass system.Keywords: amorphous alloy /defect concentration /shear modulus /microstructural heterogeneity 全文HTML --> --> --> 1.引 言 非晶态物质在自然界中广泛存在, 其组成单元具有长程无序特征. 非晶合金又称金属玻璃, 由单个原子通过各向同性的金属键组成, 是一种兼具金属和玻璃特性的简单“原子玻璃”[1 ] . 非晶合金的简单结构使其成为研究非晶态材料物理和力学行为的优异模型体系, 不仅可以洞悉非晶态材料结构弛豫、结晶和玻璃化转变等物理现象, 而且可以深入探讨如屈服强度、塑性流变和韧脆性转变等独特力学行为的物理机制[1 ] . 非晶合金物理和力学性能与其微观结构信息密切相关, 当金属熔体随温度降低冷却至熔化温度以下, 熔液黏度迅速增加, 若冷却速率足够快导致形核结晶过程被抑制, 致使液体原子结构在狭窄温度区间内偏离平衡态进而被“冻结”形成玻璃, 这一狭窄温度区间内的现象被称为玻璃转变[2 ,3 ] . 玻璃转变过程没有相变发生, 通常被认为是一个动力学过程[4 ] . 基于非晶合金形成机理, 其微观结构“缺陷”形式与传统晶态材料点缺陷、线缺陷等缺陷形式不同. 在极速快冷过程中, 熔体不同区域原子排布或相对疏松或相对密集, 因此非晶合金存在物理/力学行为非均匀性, 如密度、能量、模量和弛豫行为等, 大量研究中将非晶合金的微观结构非均匀性定义为“缺陷”[5 ,6 ] . 许多基于“缺陷”定义的理论模型为构建非晶固体物理和力学行为的微观结构起源被提出. Wang等[7 ] 提出流变单元模型可以描述非晶合金的物理和力学参数随物理时效时间的演化过程. Perez等[8 ,9 ] 提出准点缺陷理论通过量化“缺陷”浓度联系非晶合金微观结构与其宏观动力学行为. Spaepen将针对液体提出的自由体积模型应用到玻璃结构, 阐明了其弛豫与流变行为[10 ] .[11 ] . 与此同时, 晶态材料作为非晶态固体的基态, 相应晶体状态与非晶合金物理/力学性能存在内禀性关联[12 ] . 非晶合金的弛豫和晶化过程伴随体系放热和吸热, 剪切模量随之发生改变[13 ,14 ] . 一般, 不可逆结构弛豫过程导致剪切模量增大, 同时玻璃体系放热, 而可逆结构弛豫表现为冷却过程中体系放热和升温过程中体系吸热现象, 剪切模量软化总是在吸热过程中发生[6 ] . 与对应晶态合金相比, 非晶合金具有较小的剪切模量, 晶化过程中剪切模量突变增大同时体系剧烈放热[6 ] . 非晶合金微观结构在弛豫和晶化过程中改变, 即“缺陷”改变诱导模量在此过程中软化和增强, 非晶合金“缺陷”与弛豫、晶化现象及剪切模量间的联系对于深入探究其物理/力学性能的微观结构起源具有十分重要的研究意义[15 ] . Khonik等[12 ] 在自间隙原子理论基础上建立了非晶合金剪切模量与热流的联系, 通过自间隙原子理论量化体系“缺陷”, 解释了非晶合金弛豫和晶化过程微观结构演变, 以及剪切模量与“缺陷”的关联.[5 ] . 同时, 微合晶化是调控非晶合金物理/力学性能的有效手段之一, 已有研究表明在Zr50 Cu34 Ag8 Al8 非晶合金中引入2%(文中的元素百分比指原子百分比) Pd元素, 得到的Zr48 Cu34 Ag8 Al8 Pd2 非晶合金展现出更优异的玻璃形成能力和压缩塑形[16 ] . 然而关于其性能提升的微观机制仍不明确, 微量添加Pd元素对玻璃体系微观结构作用仍待研究. 本研究选取玻璃形成能力良好的Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金作为模型体系, 以差式扫描量热分析(differential scanning calorimetry, DSC)和电磁声转换(electromagnetic acoustic transformation, EMAT), 基于自间隙原子理论框架, 研究微合金化对非晶合金热流和剪切模量的影响, 探究微合金化前后非晶合金微观结构的改变, 进而深入了解非晶合金物理和力学性能的微观结构起源.2.自间隙原子理论 22.1.理论模型 2.1.理论模型 自间隙原子理论由Granato提出, 并成功揭示了金属熔化现象与自间隙型缺陷的关联[17 ,18 ] . 自间隙原子理论认为哑铃型间隙存在于各类晶体结构中, 而熔化现象与自间隙型缺陷的增殖相关[17 ] . 熔融状态下自间隙缺陷仍为可识别结构单元, 在快速冷却过程中熔融体缺陷形式被冻结, 进而被非晶合金所“继承”[12 ] . 非晶合金的结构弛豫和晶化现象与自间隙缺陷浓度的变化密切相关[19 ] . 在结构弛豫和晶化过程中伴随玻璃体系放热和吸热效应, 导致体系“缺陷”浓度和剪切模量变化[13 ,14 ] . 自间隙原子理论可建立相互表征的热流与模量关系, 热流W 和瞬时剪切模量G 的关系可表示为[20 ] $\dot T$ 表示升温速率; ${G_{{\rm{rT}}}}$ 是非晶合金室温剪切模量; ${\mu _{{\rm{rT}}}}$ 是相应晶体合金室温剪切模量; $\mu $ 是相应晶体合金的瞬时剪切模量; $\beta $ 为剪切敏感系数, 对于非晶合金, 一般$\beta $ 取值范围为15—25, 可建立较好的热流与模量关系[21 ,22 ] ; ρ 为合金密度, 在实验过程中认为是常量[23 ] .[2 ] . 自间隙原子理论认为, 自间隙缺陷弹性能导致非晶合金相对于晶体结构内能过剩[20 ,24 ] . 考虑热流W 与焓H 的关系[20 ] :U 是体系内能; P 是环境压力; V 为样品体积, 在结构弛豫和晶化过程中可认为是常量[14 ] . 因此可得内能与剪切模量具有以下关系[25 ] :[20 ] 5 )式可知晶态材料$\Delta U = 0$ . 在结构弛豫和晶化过程中. 非晶合金自间隙缺陷弹性能以热量形式耗散, 溢出内能$\Delta U$ 在此过程中减小[20 ,24 ] .2.2.实 验 -->2.2.实 验 本文将Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金所需元素(纯度均为99.9%以上)按照原子百分比配备, 借助水冷铜模吸铸法制备板状样品. 熔炼全程处于氩气保护, 并在熔炼前利用钛锭清除残余氧气, 所有母合金锭均反复熔炼5次以上确保其化学成分均匀. 模型体系的玻璃特性由Philips PW3830型X射线衍射(X-ray diffraction, XRD)设备测定. Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金XRD衍射图显示宽泛的“馒头峰”, 表明体系微观结构不存在晶化相, 具有非晶态特征[26 ] . 利用低速水冷切割机将确认为非晶态的板状材料切割为5 mm × 5 mm × 2 mm大小的样品, 将样品表面打磨光滑并置于无水乙醇溶液中采用超声振荡清洗干燥后进行EMAT实验.50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金热性能分析采用Hitachi DSC 7020型差示扫描量热仪器测定. 非晶合金原位剪切模量通过电磁超声变换测定, 样品尺寸为5 mm × 5 mm × 2 mm. EMAT利用非接触式电磁声变换方式, 在测试过程中样品不直接接触激磁和接收线圈, 最大程度减小对样品的扰动[27 ] . 通过接收线圈记录震动频率f , 样品剪切模量G (T )表示为[25 ] $g(T)$ 为剪切模量变化; ${f_{{\rm{rT}}}}$ 是室温震动频率.50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金在升温过程中铸态、弛豫态和完全晶化态的热流和剪切模量随温度演化规律, 升温速率均为3 K/min. 将铸态试样由室温升温至715 K得到弛豫态试样, 降温后由室温再次升温至823 K得到完全晶化态样品, 再次降温后第三次升温获得晶化态试样的热流和剪切模量随温度演化规律. 借助EMAT原位测定Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金在18 h物理时效过程中剪切模量随时间的演化过程, 物理时效温度分别为615 K和625 K.3.实验结果 Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金铸态、弛豫态和晶态热流分别利用DSC测定, 切线法得到Zr50 Cu34 Ag8 Al8 和Zr48 Cu34 Ag8 Al8 Pd2 非晶合金玻璃转变温度T g 分别为680 K和689 K. 图1(a) 和图1(b) 插图分别显示Zr50 Cu34 Ag8 Al8 和Zr48 Cu34 Ag8 Al8 Pd2 非晶合金以室温为初始温度, 进行3次升温实验测定热流曲线, 升温过程如图1(d) 所示. Run1: 铸态样品升温至715 K得到弛豫后样品. Run1过程显示玻璃体系在500 K < T < T g 范围中放热, T g < T (过冷液相区)时体系吸热. Run2: 弛豫态样品升温至823 K得到完全晶化样品. Run2过程在500 K < T < T g 范围内体系放热反应消失而过冷液相区吸热热流基本保持不变, 随着温度继续升高, 玻璃体系在晶化过程伴随剧烈放热反应. Run3: 晶态样品再次升温至823 K. Run3过程中晶体持续吸热软化, 热流曲线不再波动表明弛豫和晶化反应已充分完成. 本文热流曲线规律与其他典型非晶合金具有一致特征[20 ] . 图1(a) 和图1(b) 为Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金铸态和弛豫态热流曲线, 为消除晶态影响, 铸态和弛豫态热流分别为${W_{{\rm{ini}}}} = {W_{{\rm{Run1}}}} - {W_{{\rm{Run3}}}}$ 和${W_{{\rm{rel}}}} = {W_{{\rm{Run2}}}} - $ $ {W_{{\rm{Run3}}}}$ . 图1(c) 为Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金的铸态热流曲线. 可以看到Zr48 Cu34 Ag8 Al8 Pd2 非晶合金放热峰绝对值更小, 表明在Zr50 Cu34 Ag8 Al8 非晶合金中引入Pd元素可抑制玻璃体系弛豫过程.图 1 (a) Zr50 Cu34 Ag8 Al8 和(b)Zr48 Cu34 Ag8 Al8 Pd2 非晶合金DSC曲线. Run1为由室温升温至715 K的过程, Run2为室温升温至823 K的过程, Run3为室温升温至823 K的过程. 升温速率为3 K/min; (c) Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金铸态DSC曲线; (d)升温过程示意图Figure1. (a) DSC curves of Zr50 Cu34 Ag8 Al8 and (b) Zr48 Cu34 Ag8 Al8 Pd2 metallic glasses. Run1, Run2 and Run3 correspond to heating from room temperature up to 715 K, 823 K and 823 K, respectively; (c) DSC curves of Zr50– x 34 Ag8 Al8 Pdx x = 0, 2) metallic glasses (as-cast state) on an enlarged scale; (d) schematic diagram of heating process.g (T )可借助EMAT技术进行无损测定[20 ] . 由(6 )式可知, 根据材料室温剪切模量G rT 可获得升温过程中非晶合金剪切模量值. 材料剪切模量G 可通过弹性模量E 和泊松比ν 得到. 已有文献报道Zr50 Cu34 Ag8 Al8 和Zr48 Cu34 Ag8 Al8 Pd2 非晶合金的室温铸态弹性模量E 分别为102 GPa和96 GPa[28 ] , 同时Zr基非晶合金ν 为0.4[6 ] . 由此可得Zr50 Cu34 Ag8 Al8 和Zr48 Cu34 Ag8 Al8 Pd2 非晶合金室温铸态剪切模量G rT 分别为36.43 GPa和34.29 GPa. EMAT测试结果显示Zr50 Cu34 Ag8 Al8 非晶合金铸态、弛豫态和结晶态的室温剪切模量分别为36.43, 38.59和51.57 GPa. Zr48 Cu34 Ag8 Al8 Pd2 非晶合金铸态、弛豫态和晶化态室温剪切模量分别为34.29, 36.24和46.86 GPa. 需要注意的是弛豫和晶化导致模型合金剪切模量升高, 同时微合金化后模型合金剪切模量略微降低.图2 为Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金3次升温过程中剪切模量随温度的演化过程, EMAT实验条件设置与热流测定实验一致. Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金剪切模量G 随温度演化具有以下4个典型特征[19 ] : 1)升温过程中剪切模量持续软化, 500 K < T < T g 时, 铸态(Run1)非晶合金剪切模量在结构弛豫作用下软化受抑制. Zr基非晶合金中可普遍观察到这一现象, 而Pd基非晶合金中无明显减缓剪切模量软化现象[29 ] . 2)弛豫态(Run2)非晶合金室温剪切模量变大, 升温过程中没有发生结构弛豫, 剪切模量持续软化. 3) T g < T 时, 非晶合金铸态和弛豫态剪切模量演化曲线重合, 并随温度升高加速软化. 4)晶态(Run3)非晶合金室温剪切模量明显增大, 随温度升高剪切模量呈现线性下降. 剪切模量软化过程与热流曲线存在明显关联, 结构弛豫抑制剪切模量软化并伴随体系放热, T g < T 时体系吸热同时剪切模量软化过程加速. 根据自间隙原子理论, 可量化热流与剪切模量的关系. 据(1 )式可得到热流W (T )对剪切模量随温度演化的描述[20 ] :图 2 (a) Zr50 Cu34 Ag8 Al8 和(b) Zr48 Cu34 Ag8 Al8 Pd2 非晶合金剪切模量在3次升温过程中随温度演化过程Figure2. Evolution of the shear modulus with temperature during three subsequent heating runs of (a) Zr50 Cu34 Ag8 Al8 and (b) Zr48 Cu34 Ag8 Al8 Pd2 metallic glasses.$W(T)$ 分别为${W_{{\rm{ini}}}}$ 和${W_{{\rm{rel}}}}$ , 密度取7.1 g/cm3 [23 ] . 图2 实线部分由(8 )式所得, 取参数$\beta $ 为12可较好地利用热流数据构建Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金剪切模量随温度演化过程.4.非晶合金缺陷浓度热效应 非晶合金热流和剪切模量热效应必然与其微观结构相关, 前已述及自间隙原子理论认为非晶合金中存在哑铃型“缺陷”, 探索非晶合金“缺陷”演化历程对于理解其物理和力学性能十分重要[12 ] . 铸态和弛豫态非晶合金升温过程中剪切模量G 与自间隙缺陷浓度c 具有以下关系[12 ] :c 可表示为[12 ] $\alpha $ 为常量1. 图3(a) 为Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金铸态和弛豫态自间隙缺陷浓度随温度演化过程. 当T < 500 K时, 玻璃体系自间隙缺陷浓度保持不变, 随温度继续升高, 铸态非晶合金自间隙缺陷浓度呈现下降趋势, 此时体系发生结构弛豫. 当T g < T , 铸态和弛豫态非晶合金自间隙缺陷浓度随温度演化曲线重合(图3(a) ), 这与图2 中铸态和弛豫态剪切模量软化过程一致. 需要注意的是Zr48 Cu34 Ag8 Al8 Pd2 非晶合金需要更高的温度完成结构弛豫, 与此同时相同状态下其自间隙缺陷浓度更低, 表明微合晶化降低“缺陷浓度”、抑制体系原子移动性、延长弛豫时间. Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金弛豫态自间隙缺陷浓度在升温过程中不再降低, 表明结构弛豫过程在第一次升温过程中完成. Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金弛豫后自间隙缺陷浓度均减小约0.5%, 玻璃体系自间隙缺陷的弹性能随之释放, 导致内能降低.图 3 Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金的(a)铸态和弛豫态自间隙缺陷浓度以及(b)自间隙缺陷浓度随温度的变化率(${{{\rm{d}}c(T)} / {{\rm{d}}T}}$ )随温度的演化Figure3. (a) Evolution of the defect concentration in the as-cast and relaxed samples and (b) the rate of defect concentration change (${{{\rm{d}}c(T)} / {{\rm{d}}T}}$ ) as a function of temperature for Zr50– x 34 Ag8 Al8 Pdx x = 0, 2) metallic glasses.${{{\rm{d}}c(T)} / {{\rm{d}}T}}$ )随温度演化过程可直观对比升温过程中玻璃体系“缺陷”浓度变化. 图3(b) 为Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金${{{\rm{d}}c(T)} / {{\rm{d}}T}}$ 与温度的关系. 可以看到微合晶化前后${{{\rm{d}}c(T)} / {{\rm{d}}T}}$ 与温度关系曲线几乎重合. T < 500 K时${{{\rm{d}}c(T)} / {{\rm{d}}T}}$ 为0表明体系微观结构没有明显改变, 图1 和图2 中热流和剪切模量均保持常数. 温度继续升高, 铸态非晶合金${{{\rm{d}}c(T)} / {{\rm{d}}T}}$ 为负值, 表明“缺陷”浓度减小, 而弛豫态非晶合金“缺陷”浓度随温度升高逐渐增大, 其${{{\rm{d}}c(T)} / {{\rm{d}}T}}$ 为正. 结构弛豫过程完成, 铸态和弛豫态非晶合金${{{\rm{d}}c(T)} / {{\rm{d}}T}}$ 演化曲线重合, 此时${{{\rm{d}}c(T)} / {{\rm{d}}T}}$ 为正值, 系统吸热致使“缺陷”浓度迅速增大, 体系内能升高, 剪切模量加速软化. 注意到微合金化前后结构弛豫开始温度相同, 而微量Pd元素引入导致弛豫结束所需温度更高, 再次证明微合金化降低原子移动性及增加弛豫时间.[26 ] . 晶化过程伴随大规模原子重排, 非晶合金中“缺陷”浓度急剧下降, 这导致晶化后剪切模量显著升高. 玻璃转变温度以下至晶化温度以上的循环升温实验表明, 结构弛豫造成“缺陷”浓度大幅降低,宏观表现为非晶合金内耗降低[30 ] .[31 ] . 升温速率固定时特征激活能E 0 近似于潜在激活能, 其中${E_0} = AT$ , 升温速率为3 K/min时, $A \approx 3.17 \times {10^{ - 3}}\;{\rm{eV/K}}$ [12 ] . 激活能谱${n_0}({E_0})$ 表示单位激活能可激发的自间隙缺陷浓度, 激活能谱${n_0}({E_0})$ 可由铸态和弛豫态剪切模量表示[12 ] :50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金激活能谱图如图4 所示. 激活能谱图可大致分为3个区域: 1)低能量区域(1 eV < E 0 < 1.4 eV), ${n_0}$ =0表明较低的能量无法改变玻璃体系自间隙缺陷浓度; 2)${n_0}$ 随特征激活能增大而迅速升高, “缺陷”随能量增大被激活, 此时发生结构弛豫, 原子重排导致自间隙缺陷浓度发生改变; 3)${n_0}$ 达到峰值后迅速衰减为0, 结构弛豫完成致使可激活“缺陷”浓度迅速减小. Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金激活能谱图表明在“缺陷”激活能量区间, 结构弛豫速率随能量增大而加快, 因此图3(b) 中${{{\rm{d}}c(T)} / {{\rm{d}}T}}$ 为负且随温度升高绝对值变大. 注意到1 eV < E 0 < 2 eV区域, Pd元素添加前后单位激活能可激活“缺陷”浓度一致. 对于Zr48 Cu34 Ag8 Al8 Pd2 非晶合金在2 eV < E 0 < 2.06 eV区域, 单位激活能可激活“缺陷”浓度略微减小, 在2.06 eV < E 0 < 2.2 eV区域, 单位激活能可激活“缺陷”浓度略微增大. 这说明合金体系微观结构非均匀性变化. 同时2% Pd元素引入导致激活能谱略微变宽, 合金完成结构弛豫需要更大能量激励, 表明Pd元素添加抑制原子移动性, 增加微观结构非均匀性.图 4 Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金的激活能谱Figure4. Activation energy spectra for Zr50– x 34 Ag8 Al8 Pdx x = 0, 2) metallic glasses.48 Cu34 Ag8 Al8 Pd2 非晶合金玻璃转变温度T g 更高. 本文T g 为玻璃态向过冷液体转变过程中, 结构演化开始的温度. 结构演化与原子重排相关, 然而Pd元素添加导致激活原子运动所需能量更多, 同时“缺陷”浓度减小抑制原子迁移, 因此Pd元素添加致使玻璃转变温度T g 升高.5.物理时效对缺陷浓度的影响 前文讨论了“缺陷”浓度在玻璃升温过程中的演化, 同时物理时效过程通常伴随“缺陷”持续减少[5 ] , 本节将讨论物理时效过程Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金剪切模量和自间隙缺陷浓度随物理时效时间的演化规律. 根据自间隙原子理论, 剪切模量的变化$g(T)$ 与物理时效时间t 的关系可表示为[31 ] k 为玻尔兹曼常数, 取值$1.3806 \times {10^{ - 23}}\;{{\rm{J}} / {\rm{K}}}$ ; ${N_0}$ 为激活能谱, 近似为常量; τ 为拟合参数. 图5 为Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金物理时效过程中$g(T)$ 和自间隙缺陷浓度c 随物理时效时间的演化过程, 考虑到Zr50 Cu34 Ag8 Al8 和Zr48 Cu34 Ag8 Al8 Pd2 非晶合金玻璃转变温度不同, 选择物理时效温度分别为615 K和625 K. 如图5 所示, 剪切模量的变化$g(T)$ 随物理时效时间的延长先快速增长后趋于平缓, 注意到微合金化后剪切模量的变化$g(T)$ 减小. 图中实线为(12 )式拟合曲线, 表明自间隙原子理论能够很好地描述非晶合金物理时效过程. Zr50 Cu34 Ag8 Al8 和Zr48 Cu34 Ag8 Al8 Pd2 非晶合金拟合结果${N_0}$ 分别为$5.67 \times {10^{ - 3}}\;{\rm{ e}}{{\rm{V}}^{{\rm{ - 1}}}}$ 和$5.50 \times $ $ {10^{ - 3}}\;{\rm{ e}}{{\rm{V}}^{ - {\rm{1}}}}$ , ${N_0}$ 与“缺陷”浓度激活难易程度相关, ${N_0}$ 越小表明激活“缺陷”所需能量越少[12 ] . 综上所述, 添加微量Pd元素导致模型合金原子移动性降低, 结构弛豫过程受抑制, 致使剪切模量的变化$g(T)$ 减小.图 5 物理时效过程中Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金剪切模量的变化$g(T)$ 和自间隙缺陷浓度随物理时效时间的演化过程.Figure5. Сhange of the shear modulus $g(T)$ and defect concentration with the aging time for Zr50– x 34 Ag8 Al8 Pdx x = 0, 2) metallic glasses10 )式可得到物理时效过程中自间隙缺陷浓度随物理时效时间演化过程, Zr50 Cu34 Ag8 Al8 和Zr48 Cu34 Ag8 Al8 Pd2 非晶合金的$\mu (T)$ 分别选用615和625 K时相应晶态剪切模量. 结果表明Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)非晶合金自间隙缺陷浓度随物理时效时间的增长逐渐降低并趋于稳态. 在实验时间窗口范围, Zr50 Cu34 Ag8 Al8 和Zr48 Cu34 Ag8 Al8 Pd2 非晶合金自间隙缺陷浓度最终达到2.43%和2.17%, 与图2(a) 中弛豫态室温自间隙缺陷浓度接近.50– x 34 Ag8 Al8 Pdx x = 0, 2)玻璃体系对比分析表明, 非晶合金塑性提高的微观结构起源并非“缺陷”增加. 非晶合金不存在晶体材料中位错、孪晶等变形机制, 然而非晶合金存在相对于基体结构和动力学异质性的区域, 这些区域具有较低的黏度、模量和强度, 以及具有较高能量和原子移动性, 类似于晶体中“缺陷”[7 ] . 在热/力激励下这些区域首先发生局部原子迁移, 引发宏观塑性变形, 因此调控“缺陷”浓度是改善非晶合金塑性的重要手段[32 ] . 非晶合金的“缺陷”即为原子排布疏松区域, 一般认为, 提高非晶合金“缺陷”浓度可提高其塑性变形能力. Yu等[33 ] 在La基非晶合金薄带拉伸实验中实现了室温附近的拉伸塑性, 并发现该材料具有明显的结构非均匀性. Shen等[34 ] 对比不同冷却速率下“缺陷”含量不同的Ti基非晶合金, 发现非晶合金“缺陷”含量越高塑性变形能力越强. Ketov等[35 ] 将非晶合金在液氮中浸泡几分钟后迅速升温至室温并保持几分钟, 循环数十次后非晶合金压缩塑性显著增加, 通过热/动力学测试, 结果均表明合金“缺陷”含量增加. 另外, 应力松弛[36 ] 、高温蠕变[37 ] 和室温缠绕[38 ] 等方法也能通过改变“缺陷”浓度增强合金室温塑性. Qiao等[39 ] 通过0.5% Dy元素添加致使CuZrAl合金体系塑性明显提高, 准点缺陷理论分析表明微合金化导致合金“缺陷”浓度升高. 文献报道微量Pd元素添加导致压缩断裂后断面剪切带丰富[28 ] , 这可能与微合金化导致微观结构非均匀性增加, 进而促进变形过程剪切带的形成和增殖相关, 致使其压缩塑性提高.6.结 论 自间隙原子理论可有效建立非晶合金弛豫过程中热流和剪切模量关系, 并且可描述物理时效过程剪切模量的变化$g(T)$ 随物理时效时间的演化.50– x 34 Ag8 Al8 Pdx x = 0, 2)玻璃体系自间隙缺陷浓度, 抑制其原子移动性和结构弛豫过程, 导致玻璃体系特征弛豫时间延长. 激活能谱反应了模型合金微观结构非均匀性改变, Pd元素引入导致结构非均匀性增大, 这可能与Zr50– x 34 Ag8 Al8 Pdx x = 0, 2)玻璃体系室温塑性增强相关.$g(T)$ 减小. 














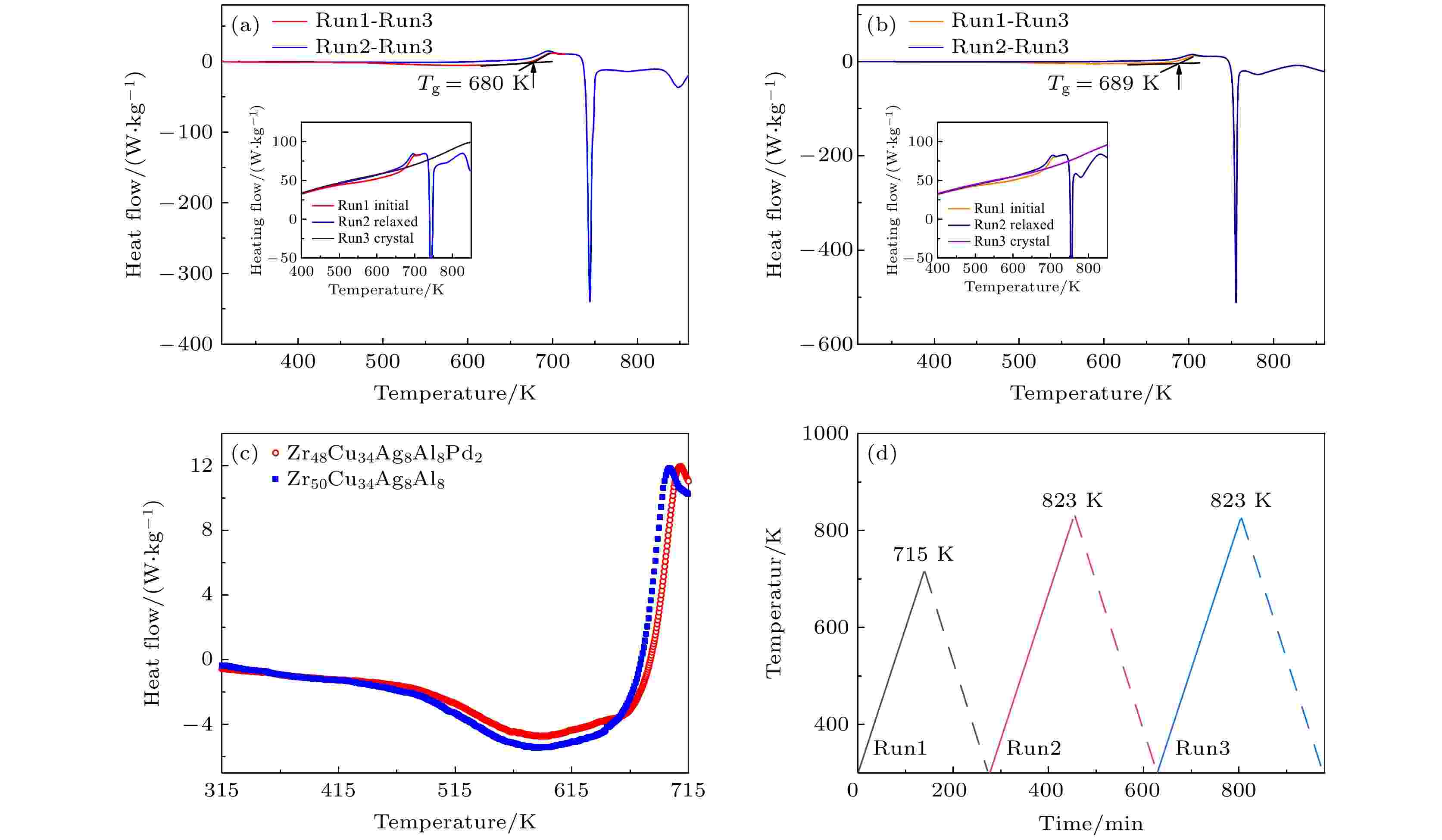 图 1 (a) Zr50Cu34Ag8Al8和(b)Zr48Cu34Ag8Al8Pd2非晶合金DSC曲线. Run1为由室温升温至715 K的过程, Run2为室温升温至823 K的过程, Run3为室温升温至823 K的过程. 升温速率为3 K/min; (c) Zr50–xCu34Ag8Al8Pdx(x = 0, 2)非晶合金铸态DSC曲线; (d)升温过程示意图
图 1 (a) Zr50Cu34Ag8Al8和(b)Zr48Cu34Ag8Al8Pd2非晶合金DSC曲线. Run1为由室温升温至715 K的过程, Run2为室温升温至823 K的过程, Run3为室温升温至823 K的过程. 升温速率为3 K/min; (c) Zr50–xCu34Ag8Al8Pdx(x = 0, 2)非晶合金铸态DSC曲线; (d)升温过程示意图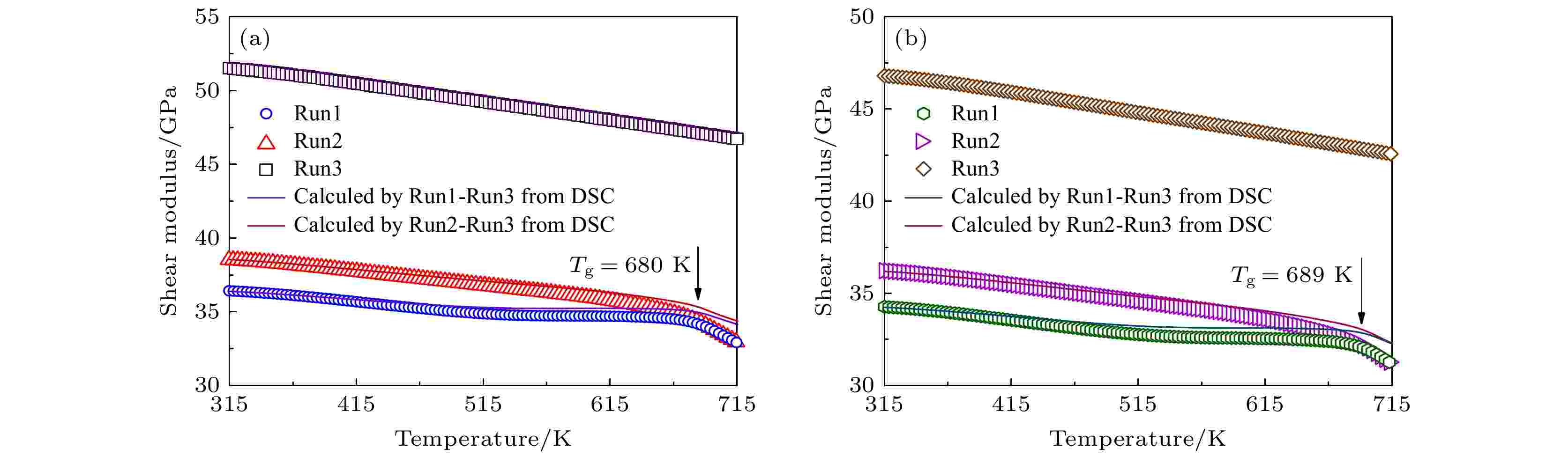 图 2 (a) Zr50Cu34Ag8Al8和(b) Zr48Cu34Ag8Al8Pd2非晶合金剪切模量在3次升温过程中随温度演化过程
图 2 (a) Zr50Cu34Ag8Al8和(b) Zr48Cu34Ag8Al8Pd2非晶合金剪切模量在3次升温过程中随温度演化过程




 图 3 Zr50–xCu34Ag8Al8Pdx (x = 0, 2)非晶合金的(a)铸态和弛豫态自间隙缺陷浓度以及(b)自间隙缺陷浓度随温度的变化率(
图 3 Zr50–xCu34Ag8Al8Pdx (x = 0, 2)非晶合金的(a)铸态和弛豫态自间隙缺陷浓度以及(b)自间隙缺陷浓度随温度的变化率(

















































































 图 4 Zr50–xCu34Ag8Al8Pdx (x = 0, 2)非晶合金的激活能谱
图 4 Zr50–xCu34Ag8Al8Pdx (x = 0, 2)非晶合金的激活能谱




































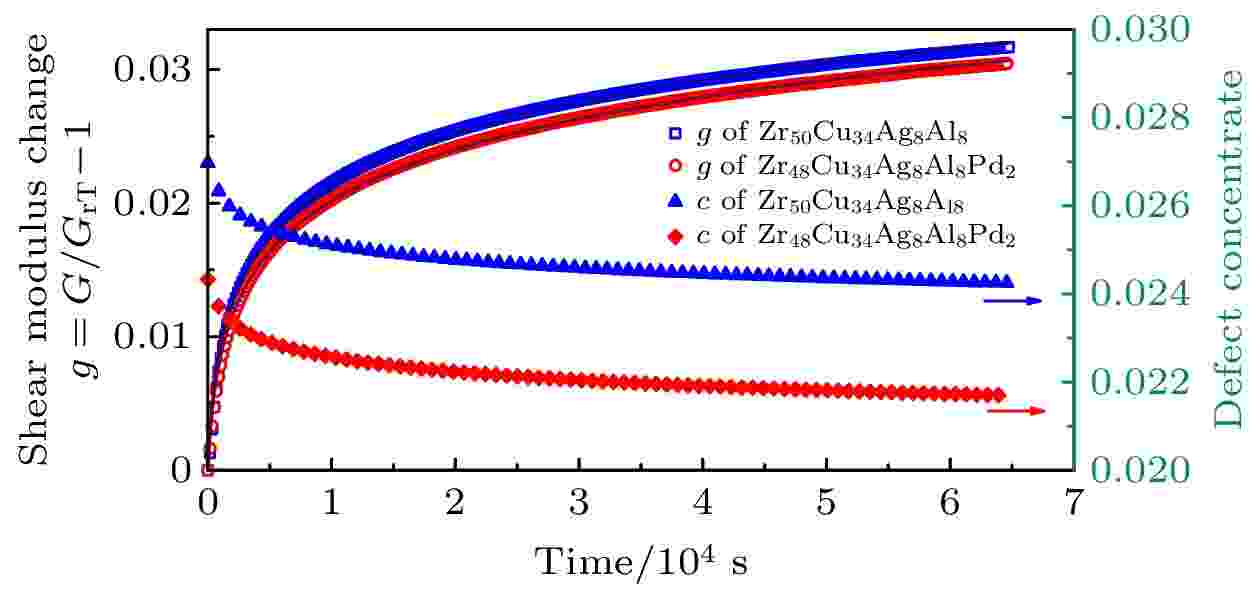 图 5 物理时效过程中Zr50–xCu34Ag8Al8Pdx(x = 0, 2)非晶合金剪切模量的变化
图 5 物理时效过程中Zr50–xCu34Ag8Al8Pdx(x = 0, 2)非晶合金剪切模量的变化




