摘要:以L型步行通道内的单向行人流为研究对象, 基于可控实验与微观仿真研究行人转弯行为. 首先, 构建转弯区无障碍物、障碍物沿转弯区对角线布局、以及障碍物垂直转弯区对角线布局三种实验场景, 通过行人可控实验分析行人移动轨迹、速度分布等行为特征; 然后, 基于L型通道内的行人微观行为, 改进基于Voronoi图的速度修正仿真模型, 制定并嵌入行人通过L型通道的转弯规则; 最后, 分别对有/无障碍物以及非对称L型通道场景进行仿真研究, 模拟再现行人的转弯行为, 分析研究不同阶段行人速度与个体密度的分布情况. 研究发现: 基于行人的移动行为, L型通道可分为垂直直行区域、过渡区域、转弯区域和水平直行区域; 行人在通过转弯区域时会形成“隐形瓶颈”和“弯道三角形闲置区域”, 产生一定的流线压缩; 改进的仿真模型, 可以模拟再现行人通过弯道区域时呈现光滑弧线的移动轨迹, 并能观察到“隐形瓶颈”和“弯道三角形闲置区域”现象; 同时, 行人流依次通过L型通道的四个区域时, 其速度分布情况与行人实验数据相吻合, 呈现先增后减再增“波浪式”变化的特点. 该仿真模型也模拟再现了由于转弯行为导致行人局部密度变化的情况, 彼此印证了行人速度与局部密度变化的统一性. 对“隐形瓶颈”的认知, 有助于合理利用和设计L型通道转弯区域.
关键词: 行人动力学/
L型通道/
速度修正模型/
Voronoi图/
隐形瓶颈

English Abstract

全文HTML

--> --> -->

在大型行人步行设施内, 通常存在90o L型步行通道. 由于行人的转弯行为特征与通道转弯处的空间特点, 会对转弯区行人流移动产生特殊影响. 对L型通道转弯处的行人流特征研究, 可以揭示行人转弯的移动规律, 有助于合理设计行人聚集场所和步行设施^[1-3], 科学地制定行人组织方案和疏散策略^[4], 提高步行设施内行人流移动效率, 避免和缓解行人拥堵等. 目前, 行人动力学特征研究主要包括基于微观行为仿真与实证实验分析研究两种方式^[5]. 基于微观行为的仿真模型主要包括离散仿真模型与连续仿真模型. 离散仿真包括: 元胞自动机模型^[6,7], 领域模型^[8]等; 连续仿真模型包括: 社会力模型^[9], 离心力模型^[10]以及基于启发式方法的模型等^[5,11-13]. 研究对象主要包括步行通道或疏散空间等不同设施、有无障碍物等不同空间布局的移动或疏散行人流等. 步行通道主要包括不同角度及尺寸的L型、T型、U型和Y型等不同场景. 基于实证实验分析研究主要包括实景行人实验, 可控行人实验, 虚拟现实行人实验等^[14].
在基于微观行为的仿真模型中, 社会力模型作为基于力的连续模型, 以假想社会力描述行人之间的相互作用; 行人运动受自驱动力、排斥力和接触摩擦力等合力的影响^[9]. 传统社会力模型可以克服元胞自动机模型中行人移动方向和速度固化等问题, 模拟再现平滑的行人移动轨迹, 定量描述行人之间的动态特性和相互作用; 尽管在模拟行人微观行为与再现宏观现象方面有较强优势, 但仍有参数复杂难以准确合理校准^[15]、会出现行人抖动和重叠现象^[16]、仿真少量行人会出现行人死锁现象^[13]、无法有效仿真有拐角的复杂场景^[17]等不足. 为克服传统社会力模型的缺点, 从多种角度对其进行了修改完善, 包括自驱动力改进^[18], 排斥力改进^[19], 引入引力^[20], 引入离心力^[17], 引入其他参数^[19], 引入行人停止机制^[16]等. 在基于启发式方法的模型中^[11-13], 将启发式方法整合到行人建模中处理复杂情景并模拟更平滑的行人移动轨迹. Moussaid等^[11]认为行人行为模式是通过改变速度大小和方向来实现, 并引入行人视觉信息, 提出一种简单的行为启发式模型来捕捉行人行为中的潜在规律. 基于Voronoi图特有的几何特性, 将Voronoi图引入行人动力学领域, 建立基于Voronoi图的启发式模型, 用于确定行人的个人空间、领域、安全距离、邻居、局部密度、速度以及移动规则等^[5,12,13]. Wu等^[21]基于Voronoi图, 考虑目标行人周围不同距离和方向行人对其移动速度的影响, 构建速度修正模型, 简化模型参数标定, 克服社会力模型中行人抖动和重叠问题, 在通道场景取得很好的仿真效果.
仿真模型也被广泛应用于存在行人转弯的L型通道场景的研究中, 如果没有额外规则, 行人选择基本的最短路径策略移动, 会忽略局部不规则空间对行人动力学的影响, 从而导致仿真结果出现不合逻辑的现象, 如行人分布不合理, 行人在最近弯道转角处排队拥挤, 外部转角区域利用率不足, 增加行人通过时间等^[22]. 因为行人在弯道转角处的移动行为明显不同于直通道中的行为, Ma等^[20]调查了北京西直门地铁站出入口转弯区域行人的移动行为, 研究发现行人在移动过程中倾向于向弯道转角内侧靠近, 转弯过程中速度先减小后增大, 于是通过引入引力和分段函数对社会力仿真模型进行了改进. Dias等^[17]将行人步行过程分为直行、转弯、再直行三个阶段, 在行人转弯过程中引入阻力和离心力, 改进传统社会力模型. Li等^[23]将具有转角的复杂场景划分为多个区域, 分别计算每个区域的静态领域场, 并引入边界规则来处理相邻区域. Dias和Lovreglio^[24]通过受控实验收集轨迹数据校准“离散表示”和“连续表示”两种静态领域模型, 通过似然函数优化方法发现“连续表示”更符合实际数据. Yanagisawa等^[25]提出一种线性递减的转弯函数, 根据行人在转向时的偏离角度修改转移概率. Dias等^[26]将最小加速度和三分之一幂定律引入行人动力学仿真中, 用于模拟弯道区域的行人运动. Zeng等^[27]通过考虑弯道中一个或多个中间目的地, 并改变所需方向, 引导行人移动到所需路径. Guo和Tang^[28]基于启发式方法, 将弯道转弯行为规则和传统微观仿真方法结合模拟行人转弯.
在行人动力学实证实验分析研究中, 可控行人实验一般以行人作为研究主体, 对行人或实验场景进行一定设计或限制; 因其可以对人群属性及环境参数进行灵活设置, 可以提前准备和重复实验, 所以能较为真实地反映行人行为并被广泛采用. 现有的可控实验主要包括: 有无障碍物及其不同布局的通道、房间、瓶颈等场景. 在疏散场景中, 在出口前合理放置障碍物可以在某些条件下提高疏散效率^[25,29]. 行人移动轨迹是行人动力学研究中最为基础和有效的数据和研究内容, 主要包含身体摇摆和主要行进方向^[30]. 随着技术不断进步, 行人自动识别和轨迹提取技术取得显著发展, Boltes等^[31,32]开发了基于视频的Petrack软件用于自动或半自动识别并确定行人移动位置和轨迹. 基于行人微观移动的轨迹, 研究人员发现行人在移动过程中有侧向行走倾向^[10,33,34].
行人动力学实证实验分析方法, 已被应用于存在行人转弯的L型通道场景研究中. Dias等^[17]通过行人实验提取轨迹, 观察到行人在弯道转弯区域有固定转弯起始点和完成点, 存在减速和加速现象, 并且以恒定角速度逐渐改变行走方向. Courtine和Schieppati^[35]发现行人在弯道转弯区域的行走速度低于直线路段. Hicheur等^[36]和Imai等^[37]发现降低行人在弯道转弯区域的速度可以降低行人躯干、四肢和头部之间的不对称、不平衡, 使行人平稳高效通过弯道. Illera等^[38]发现当行人在高转弯角(例如90o)通道跑步时, 行人潜意识可能认为会撞到墙, 导致犹豫情绪, 从而降低移动速度. Guo和Tang^[28]发现行人对弯道转弯内侧路线的偏好会对行人排队产生影响, 增加转弯角会对行人排队产生负面影响. Shiwakoti等^[39]认为弯道转弯角越大, 行人在步行汇合区域速度下降越明显. Kirik等^[40]在行人实验中发现在弯道转弯后行人流量和密度会减小, 但速度会提高, 行人移动轨迹倾向于向弯道内侧靠近, 行人转弯行为可能会造成行人流紊乱.
在现有的微观行人仿真与实证实验研究中, 发现连续仿真模型相比离散仿真模型可更精细地再现行人微观行为, 但传统的连续仿真模型仍然存在各种问题. 基于Voronoi图的速度修正模型结合了Voronoi图特征以及连续和离散仿真模型的优点, 简化了模型参数标定, 提高了准确性, 克服了行人仿真过程中的重叠性和抖动性, 而且具有良好拓展性; 目前主要用于直通道等简单行人场景仿真, 对于复杂场景, 如L型通道的研究较少.
本文通过可控行人实验, 分析行人在转弯区无障碍物、障碍物沿转弯区对角线布局、障碍物垂直转弯区对角线布局三种实验场景的行人移动轨迹和速度, 以及行人在90o L型通道垂直直行区域、过渡区域、转弯区域和水平直行区域的移动特征, 研究不同场景布局下的流线压缩现象, 以及行人在转弯区域的“隐形瓶颈”和“弯道三角形闲置区域”; 然后, 基于行人在不同区域的移动特征制定行人通过L型弯道的转弯规则, 改进基于Voronoi图的速度修正模型, 对有无障碍物及非对称L型通道场景进行仿真研究, 模拟再现行人通过弯道区域时呈现光滑弧线移动轨迹的行为过程, 并对行人移动过程的速度和个体密度进行分析, 以验证仿真模型的有效性.

2

-->

2.1.实验设置

2020年10月11日下午, 在北京交通大学主校区机械工程楼南侧广场, 通过将10个带伸缩带的隔离栏布置成90o L型通道. 在有无障碍物及其不同布局的L型通道内, 以正常非恐慌状态行走的方式进行单向行人流转弯行为控制实验. 同时, 在广场附近高层建筑10层楼道窗户处, 架设一台25帧/秒的高清摄像机, 以鸟瞰状对实验进行全程拍摄, 如图1所示. 本次实验共招募志愿者60名参与实验, 其中, 男22名, 平均身高176 cm; 女38名, 平均身高164 cm. 本次实验视频用Petrack行人识别软件处理^[3,31,32], 通过标定多个地面坐标, 对摄像机及软件参数进行修正标定, 消除拍摄偏角影响. 同时, 为了在后期视频处理中, 配合及验证Petrack软件的颜色识别模式对不同颜色的敏感程度, 并追踪行人头部(帽子); 选取红色/黄色帽子作为实验道具, 要求志愿者不得身穿红色/黄色衣服及鞋子, 需听从工作人员指挥佩戴红色/黄色帽子在指定区域内以正常速度行走.
图 1 实验场景拍摄设置
Figure1. Experimental scene shooting settings.

根据生活常识及相关的行人实验研究, 设置常见的L型通道出入口尺寸, 以满足多名行人(如5人)可并排通过的尺寸需求. 入口处通道宽度${W_1}$为2.6 m, 长度${L_1}$为11.5 m, 长度${L_3}$为8.6 m, 出口处通道宽度${W_2}$为2.9 m, 长度${L_2}$为6.6 m, 如图2所示. 在实验中, 戴红色或黄色帽子的行人数量相同, 各为30名, 所有志愿者均从通道底端A口进入, 以正常速度单向移动, 形成稳定行人流, 经过弯道转弯, 从通道右端B口出去. 在实验过程中, 随着L型通道中人数的变化, 通道中行人整体密度变化为0—1.45 P/m². 实验根据有无障碍物及障碍物连线与转弯区域对角线的关系分为3个场景, 分别为: 转弯区无障碍物场景1、障碍物沿转弯区对角线布局场景2、障碍物垂直转弯区对角线布局场景3, 分别如图2、图3和图4所示. 志愿者听从工作人员指挥, 在每个场景均行走3次.
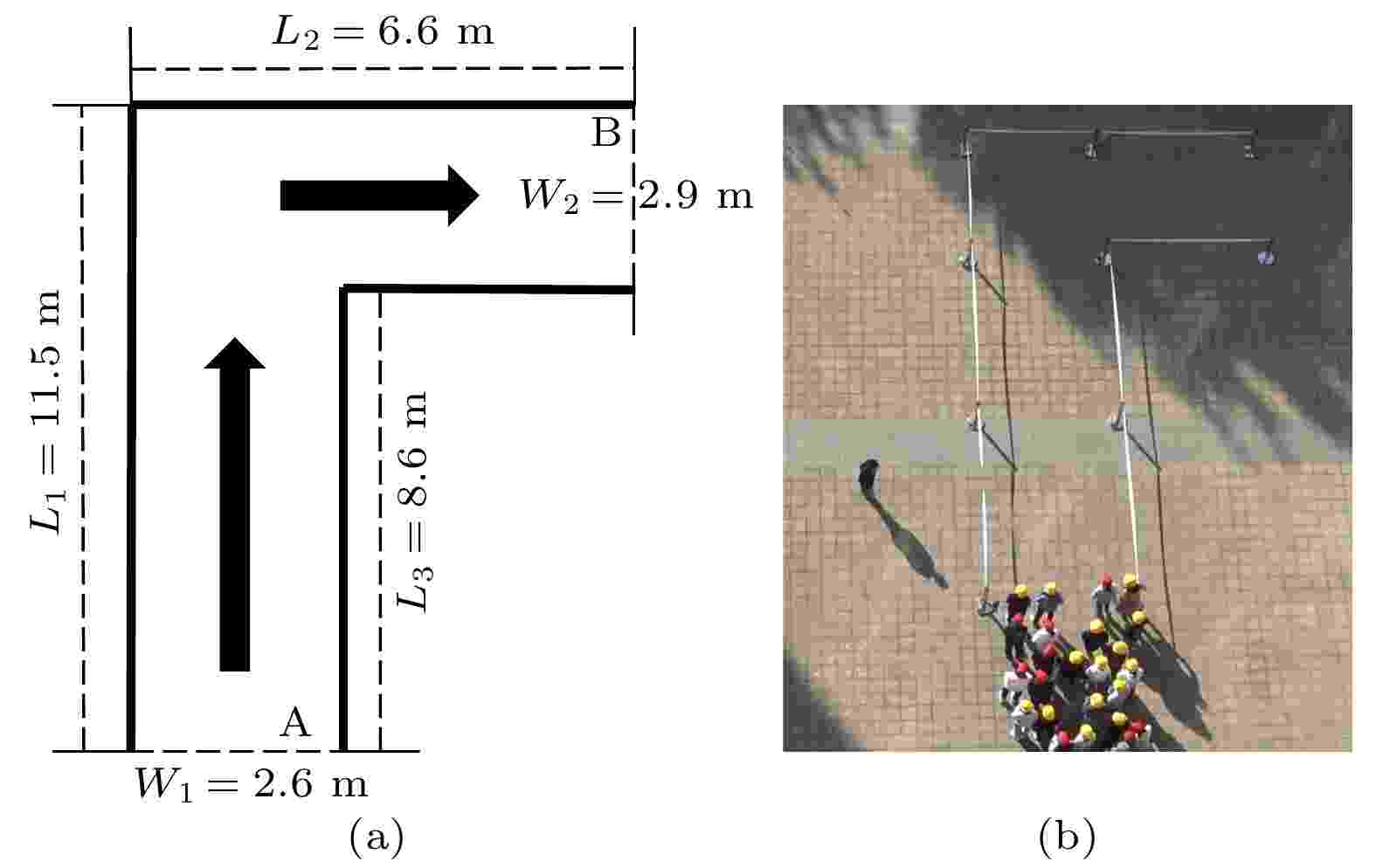图 2 行人在L型通道移动的实验场景1　(a) L型通道设置; (b) 行人实验截图
Figure2. Experimental Scenario 1 of pedestrian movement in an L-shaped corridor: (a) The L-shaped corridor setting; (b) pedestrian experiment screenshot.

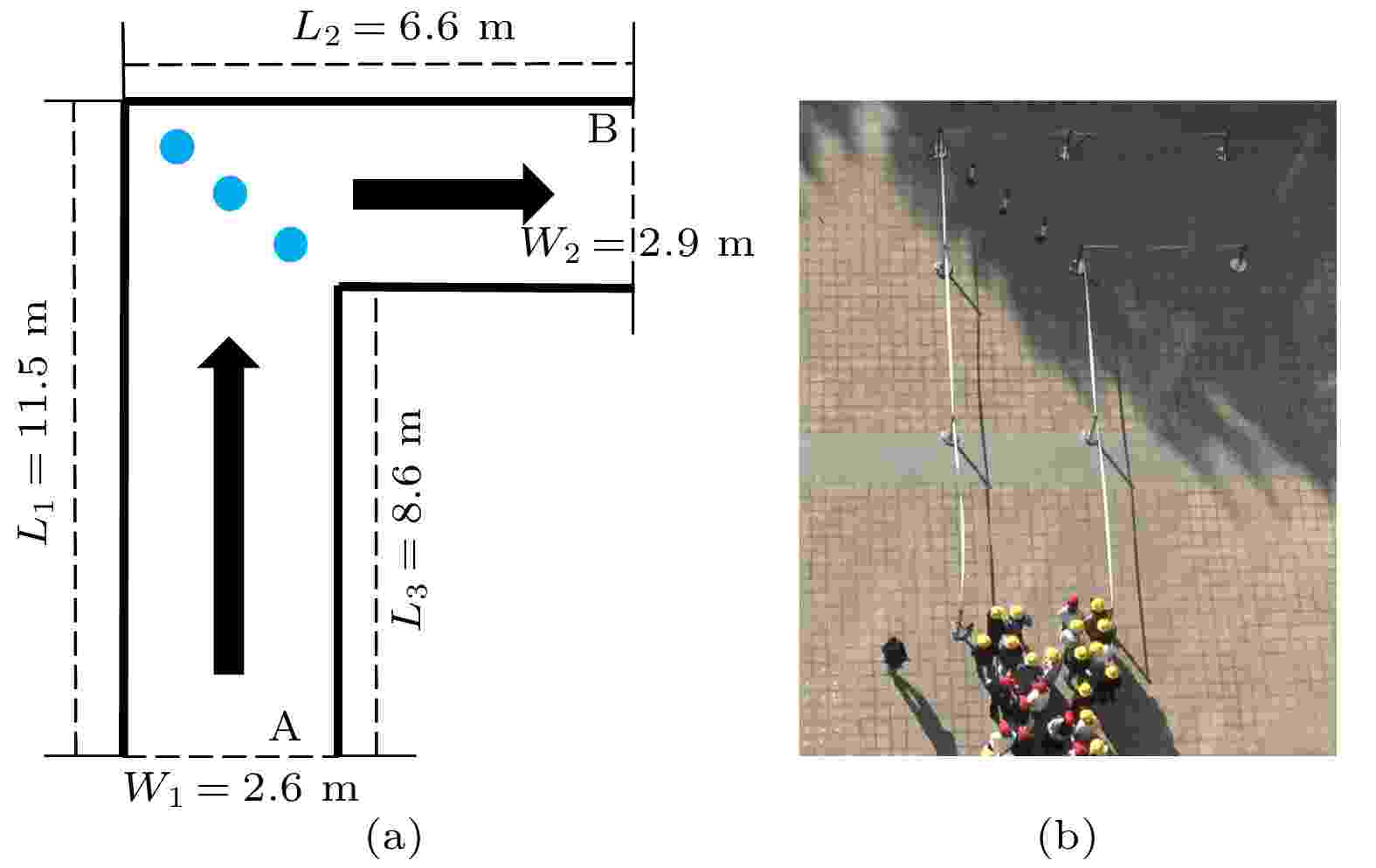图 3 行人在带有障碍物的L型通道移动的实验场景2 　(a) L型通道设置; (b)行人实验截图
Figure3. Experimental Scenario 2 of pedestrian movement in an L-shaped corridor with obstacles: (a) The L-shaped corridor setting; (b) pedestrian experiment screenshot.

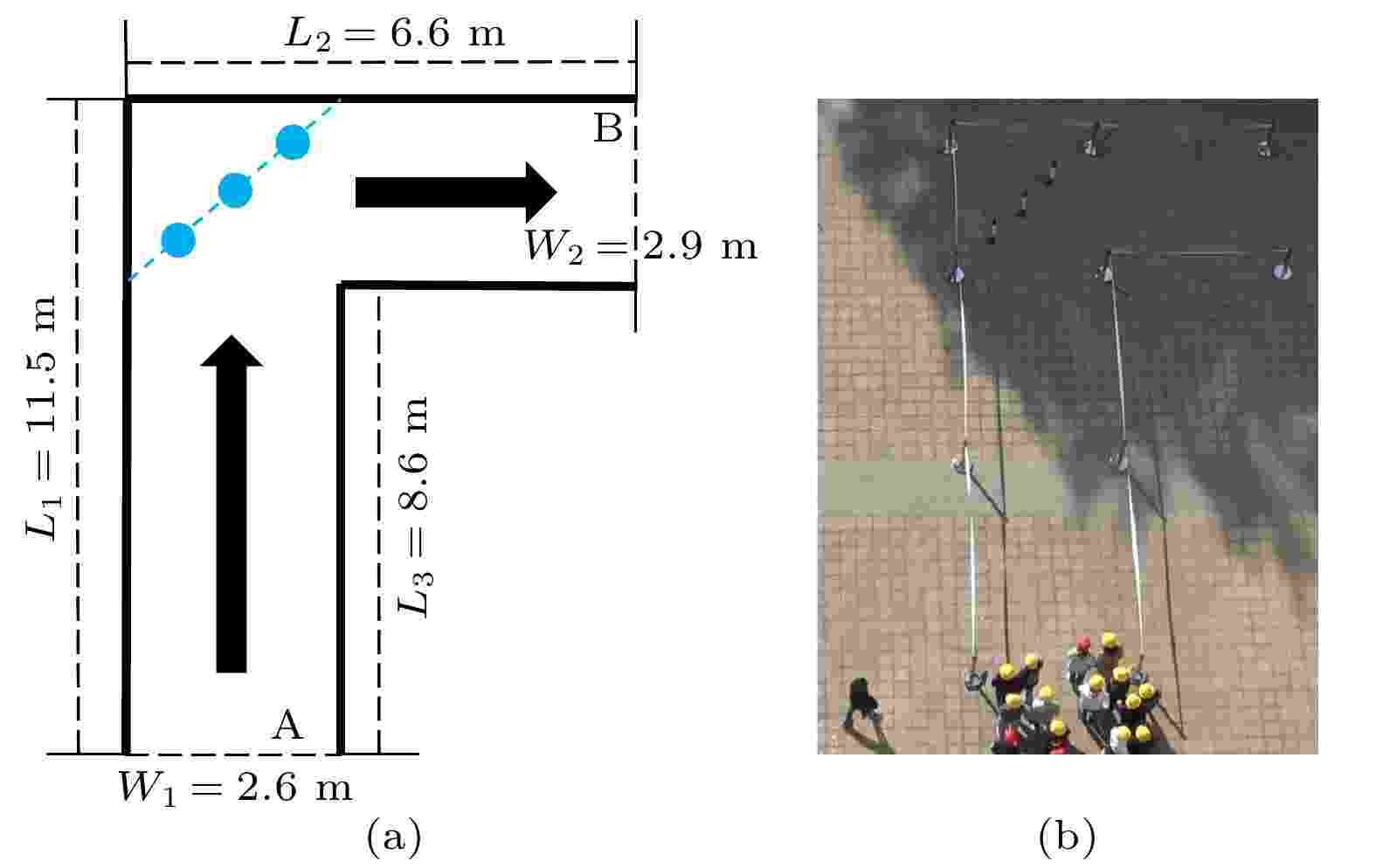图 4 行人在带有障碍物的L型通道移动的实验场景3 　(a) L型通道设置; (b) 行人实验截图
Figure4. Experimental Scenario 3 of pedestrian movement in an L-shaped corridor with obstacles: (a) The L-shaped corridor setting; (b) pedestrian experiment screenshot.

在实验场景2中, 为了研究障碍物对L型通道转弯区域的行人分流作用, 在转弯区域对角线处, 均匀布置了3个障碍物分流, 如图3所示. 根据实验观察, 行人在通过L型通道转弯区域会出现一定的“流线压缩”现象. 为了与行人通过L型无障碍物通道转弯区域的轨迹进行对比, 在场景3中, 在转弯区域与通道壁组成三角形区域处设置了3个障碍物, 以观察行人通过L型有障碍物通道转弯区域的流线压缩现象, 如图4所示.
2 -->

2.2.实验分析

实验结束后, 通过Petrack软件对实验视频划定观察区域, 使用颜色识别模式追踪行人头部, 识别行人佩戴的红色/黄色帽子, 并克服阴影区域对追踪的影响. 设定视频的起始坐标, 从行人进入L型通道开始, 每隔25帧(0.04 s)根据行人的高度和视角计算获取行人相应的地面位置, 如图5所示.
图 5 通过Petrack软件对行人进行识别追踪
Figure5. The pedestrians are identified and tracked by Petrack software.

1) 实验场景1
在实验场景1中, 选取一组代表性行人移动轨迹进行分析, 如图6所示. 可以观察到, 行人移动过程中会形成4—5列轨迹簇, 行人以近似平滑的弧线轨迹通过L型通道转弯区域.
图 6 行人在场景1无障碍物的L型通道行走的视频截图
Figure6. The video screenshots of pedestrians walking in the L-shaped passage without obstacles in Scene 1.

基于观察区域内所有行人在观察时间内连续移动的地面坐标, 绘制连续的行人移动轨迹线, 可以观察到行人整体通过L型通道时形成了稳定的弧形曲线, 如图7(a)所示. 选取行人在通道入口水平面A不同出发位置有代表性的几条连续行人轨迹线, 可以发现行人在正常非恐慌移动过程中, 很少会出现乱串行为, 基本按照自身的移动轨迹以稳定弧线通过转弯处, 且行人在移动过程中不是以直线移动, 而是不停来回抖动存在拉链效应的侧向位移, 如图7(b)所示.
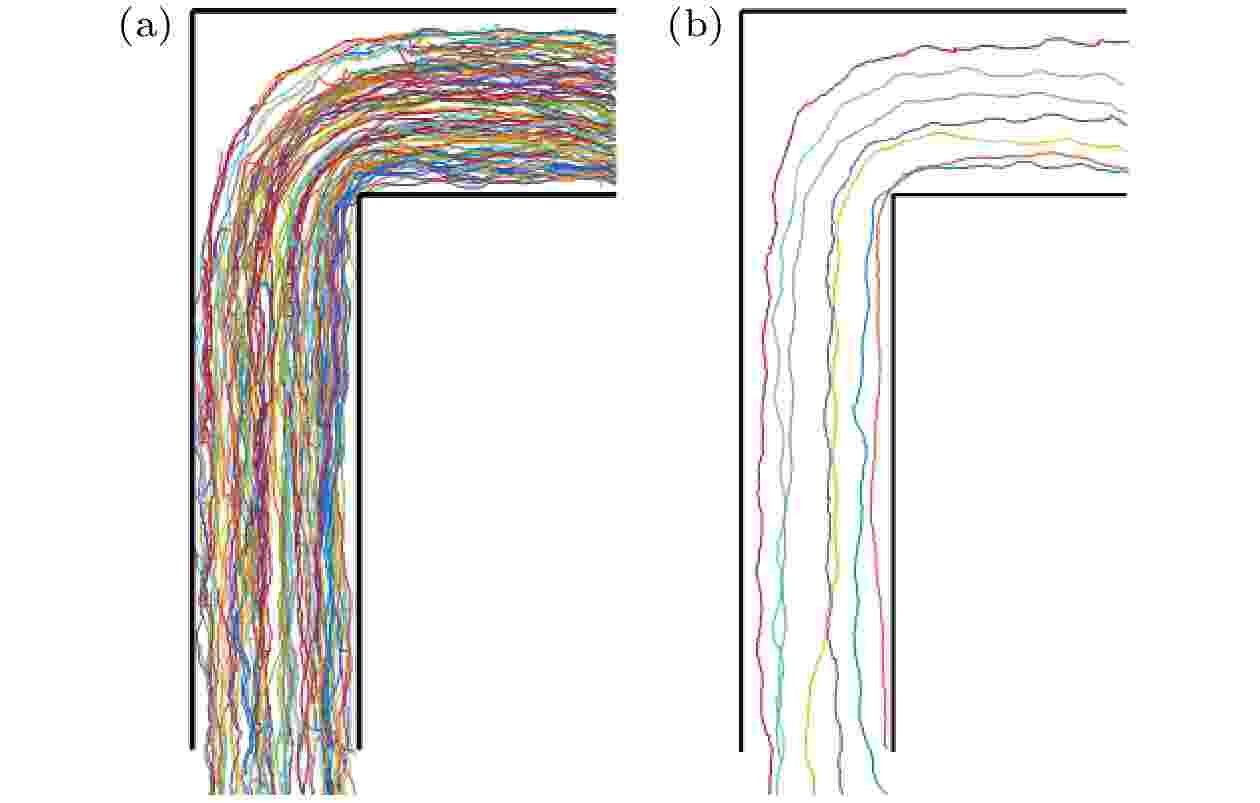图 7 行人在场景1无障碍物L型通道的移动轨迹　(a) 原始移动轨迹; (b)简化移动轨迹
Figure7. The paths of pedestrians in the L-shaped corridor without obstacles in Scene 1: (a) The original moving track of the pedestrians in the L-shaped corridor; (b) the simplifying moving track of the pedestrians in the L-shaped corridor.

以图7(b)简化的行人移动轨迹为例进行分析, 可以发现行人在通过L型通道时, L型通道分为直行区域、过渡区域、拐弯区域和直行区域. 其中, ${Z_1}$和${Z_4}$分别为垂直和水平直行区域, 行人基本以既定速度方向直行通过; ${Z_2}$为过渡区域, 行人向弯道内侧靠拢, 且${Z_2}$左侧区域的速度方向调整较大, ${Z_2}$右侧区域的速度方向调整较小; ${Z_3}$为弯道转弯区域, 行人实现转弯, 且行人均不会进入弯道三角形闲置区域${Z_0}$中进行绕远, 如图8(a)所示. 在行人通过转弯区域时, 可以发现, 行人移动轨迹线基本是以弯道处顶点O为圆心的圆弧, 具有相同的圆心角θ. 越外围的行人, 其绕行弧长λ越大; 越内侧的行人, 其绕行弧长λ距离越小, 如图8(b)所示. 同时, 转弯区域的对角线${d_0}$可以看作传统的有形瓶颈, 由有效瓶颈${d_1}$和无效瓶颈${d_2}$两部分组成, 即${d_0} = {d_1} + {d_2}$, 行人在直通道的通行瓶颈宽度为${d_3}$, 且${d_1} < {d_3}$, 有效瓶颈${d_1}$可以看作是转弯区的“隐形瓶颈”, 行人在转弯区域的移动轨迹集中在隐形瓶颈内, 且发生流线压缩现象, 如图8(c)所示.
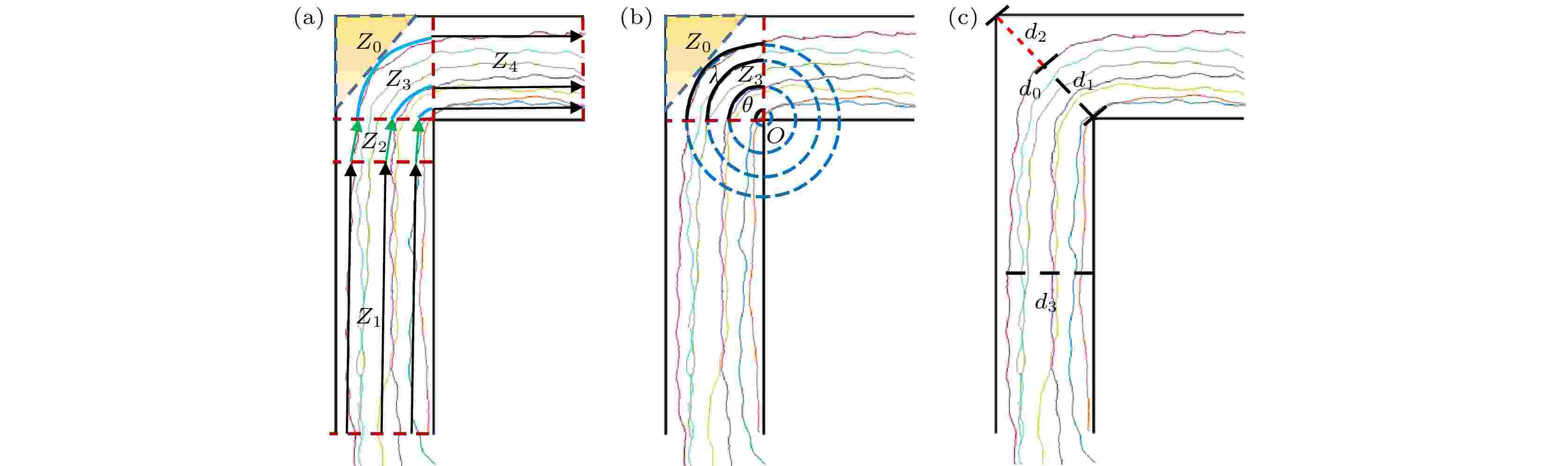图 8 行人在场景1无障碍物的L型通道移动的特征分析　(a) 行人在通道移动的四区域; (b) 行人在转弯区域的转弯特征; (c) 行人在通道移动的隐形瓶颈
Figure8. Analysis on the characteristics of pedestrian movement in an L-shaped corridor without obstacles in Scene 1: (a) Four types of areas where pedestrians move in the corridor; (b) the turning characteristics of pedestrians in the turning area; (c) the invisible bottleneck of pedestrian movement in the corridor.

2) 实验场景2
在实验场景2中, 在L型通道转弯对角线处均匀放置了3个防撞柱, 将转弯处的瓶颈均匀分成了4个小型瓶颈${P_1}-{P_4}$供行人通过, 每个瓶颈宽度${W_3}$约为1.1 m, 如图9所示.
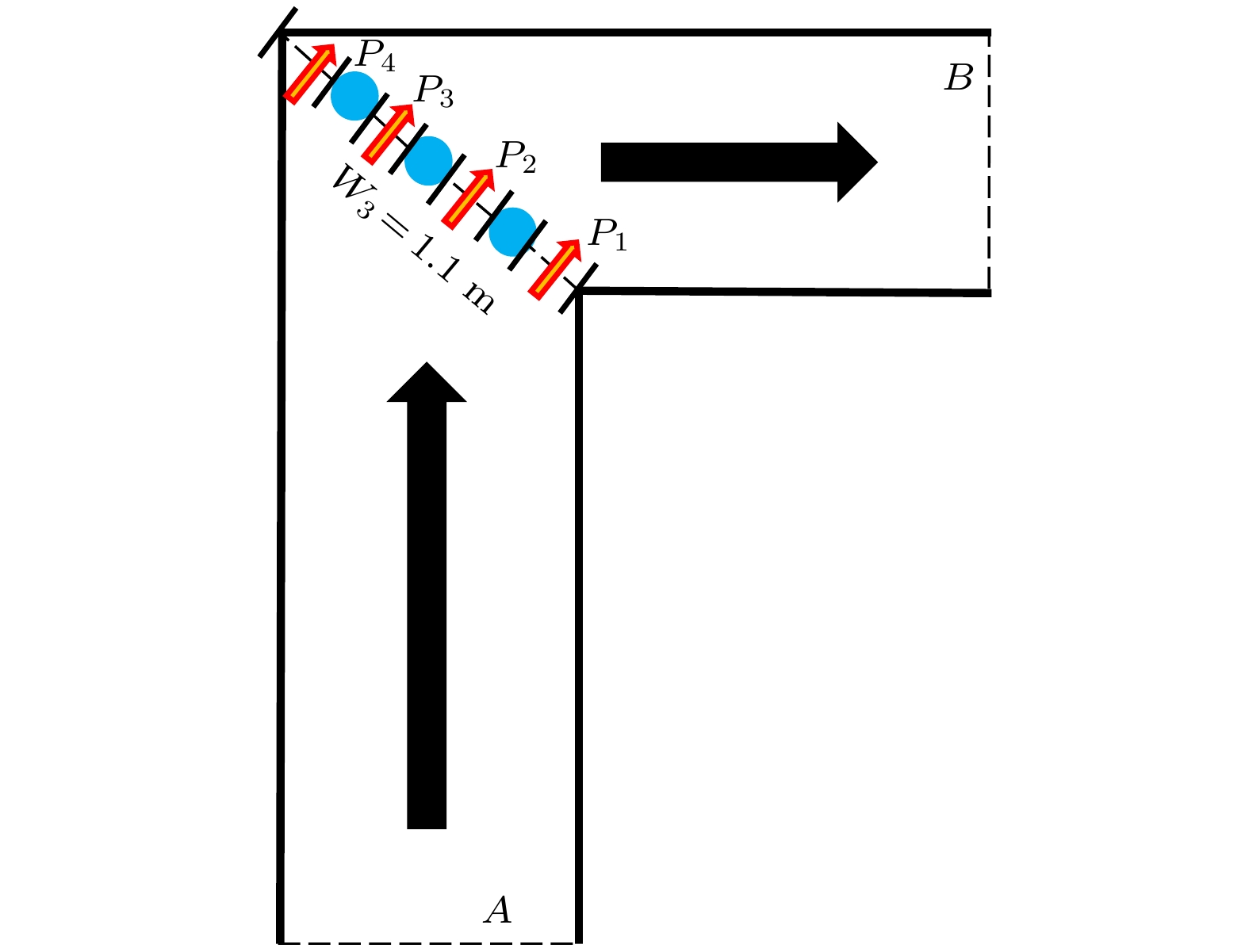图 9 场景2中L型通道转弯处的小型瓶颈设置
Figure9. A small bottleneck setting at an L-shaped corridor bend in Scene 2.

在实验场景2中, 选取一组代表性的行人移动轨迹, 可以发现行人在移动过程中, 主要从靠近弯道内侧的3个小型瓶颈${P_1}-{P_3}$通过, 通行人数比例为11∶12∶7, 没有行人从外围的小型瓶颈${P_4}$通过, 如图10所示.
图 10 行人在场景2有障碍物的L型通道行走的视频截图
Figure10. The video screenshots of pedestrians walking in the L-shaped corridor with obstacles in Scene 2.

基于观察区域内所有行人在观察时间内连续移动的地面坐标, 绘制连续的行人移动轨迹线, 可以明显观察到行人在通过弯道区域时, 会从两侧绕过障碍物, 降低行人聚集通过的程度, 在障碍物前的避免碰撞区域和障碍物后的未占据区域形成菱形空白区域${Z_5}$和${Z_6}$, 且行人均不会进入弯道三角形闲置区域${Z_0}$中进行绕远, 如图11所示.
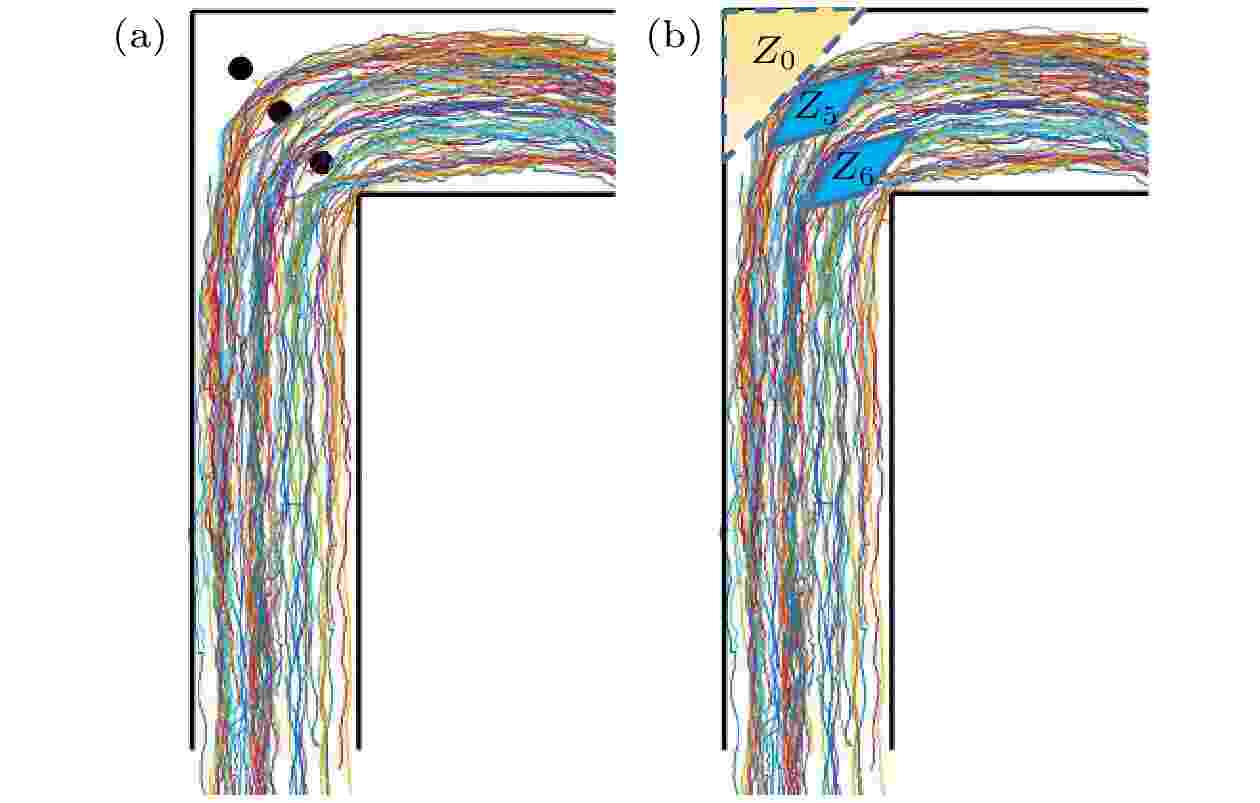图 11 行人在场景2有障碍物的L型通道移动的特征分析
Figure11. Analysis on the characteristics of pedestrian movement in an L-shaped corridor with obstacles in Scene 2.

3) 实验场景3
在实验场景3中, 将3个障碍物放置在弯道三角形闲置区域${Z_0}$的斜边处, 行人在移动过程中不会与障碍物碰撞, 依序通过弯道, 如图12所示.
图 12 行人在场景3有障碍物的L型通道行走的视频截图
Figure12. The video screenshots of pedestrians walking in the L-shaped corridor with obstacles in Scene 3.

基于观察区域内所有行人在观察时间内连续移动的地面坐标, 绘制连续的行人移动轨迹线. 相较场景1和场景2, 场景3因放置障碍物压迫减小了行人转弯移动空间, 但行人在通过弯道过程中, 仍会与障碍物组成的边缘相隔一定距离, 留下间隙空间${Z_{{\rm{gap}}}}$, 如图13所示.
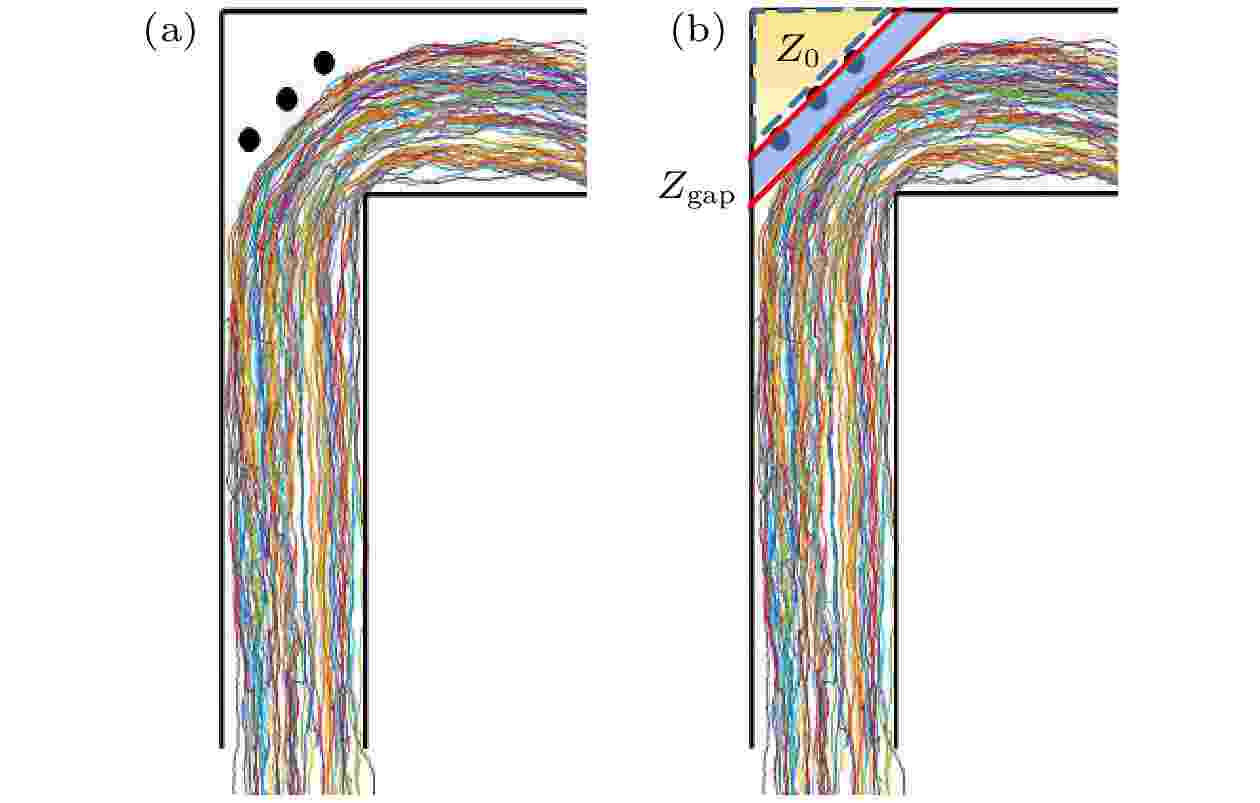图 13 行人在场景3有障碍物的L型通道移动的特征分析
Figure13. Analysis on the characteristics of pedestrian movement in an L-shaped corridor with obstacles in Scene 3.

4) 对比分析
通过对比分析, 3个场景的弯道三角形闲置区域${Z_{01}}-{Z_{03}}$的面积大小关系, 为${Z_{03}} > {Z_{01}} > {Z_{02}}$. 可以明显看到, 由于障碍物压缩区域面积、行人远离障碍物的心理及行为需求, 相较场景1和场景2, 场景3的闲置区域${Z_{03}}$的面积最大, 即行人的弯道可行区域的面积最小; 而且三个场景的隐形瓶颈宽度${d_{02}} > {d_{01}} > {d_{03}}$, 场景3的流线压缩现象最明显, 如图14所示.
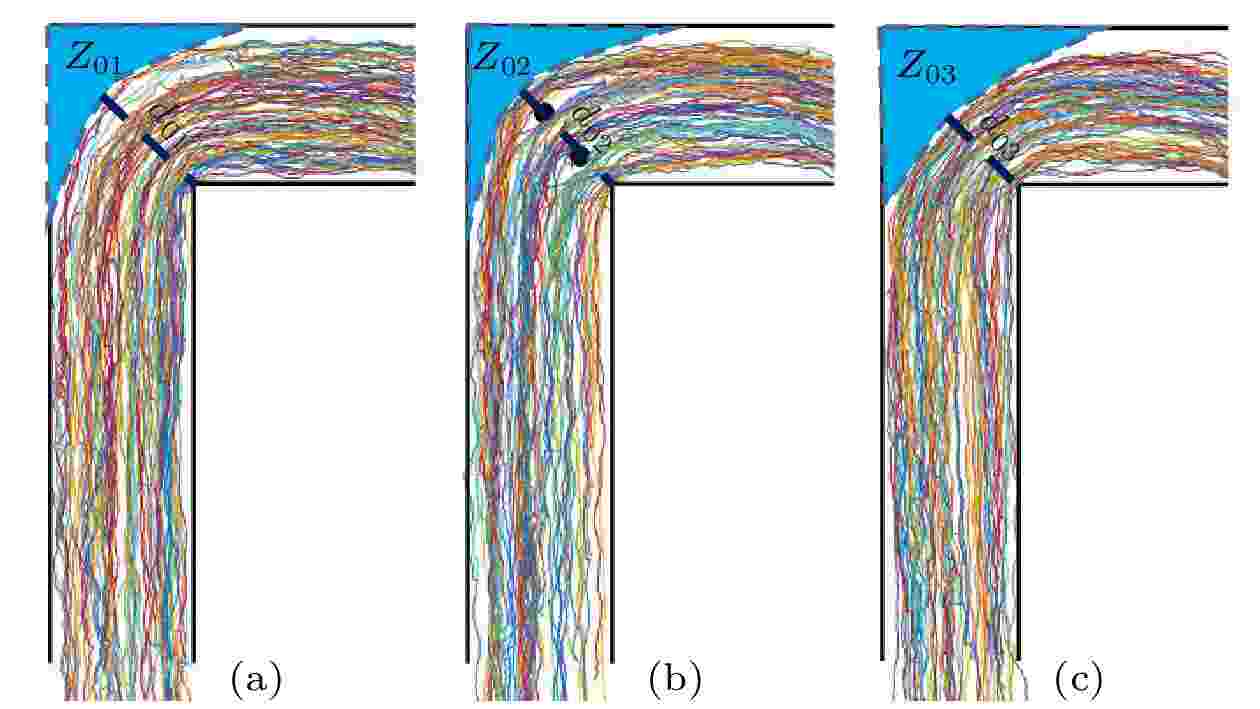图 14 不同场景的弯道三角形闲置区域面积大小对比　(a) 场景1的弯道三角形闲置区域面积; (b) 场景2的弯道三角形闲置区域面积; (c) 场景3的弯道三角形闲置区域面积
Figure14. Comparisons of the area size of the curve triangle idle area in different scenes: (a) The area size of the curve triangle idle area in Scene 1; (b) the area size of the curve triangle idle area in Scene 2; (c) the area size of the curve triangle idle area in Scene 3

因为行人速度分布的离散和随机性, 选取典型的行人速度变化过程, 统计分析3个场景行人通过L型通道速度随时间的变化过程, 如图15所示. 行人通过通道共需要约16 s, 速度变化过程呈波浪变化曲线. 在垂直直行区域, 行人速度逐渐提高到稳定状态1.1 m/s左右; 在过渡和转弯区域, 通过隐形瓶颈时, 速度逐渐降低, 在转弯区域中间速度降到最低0.8 m/s左右; 离开转弯区域后, 在水平直行区域速度又逐渐提高到稳定状态1.1 m/s左右.
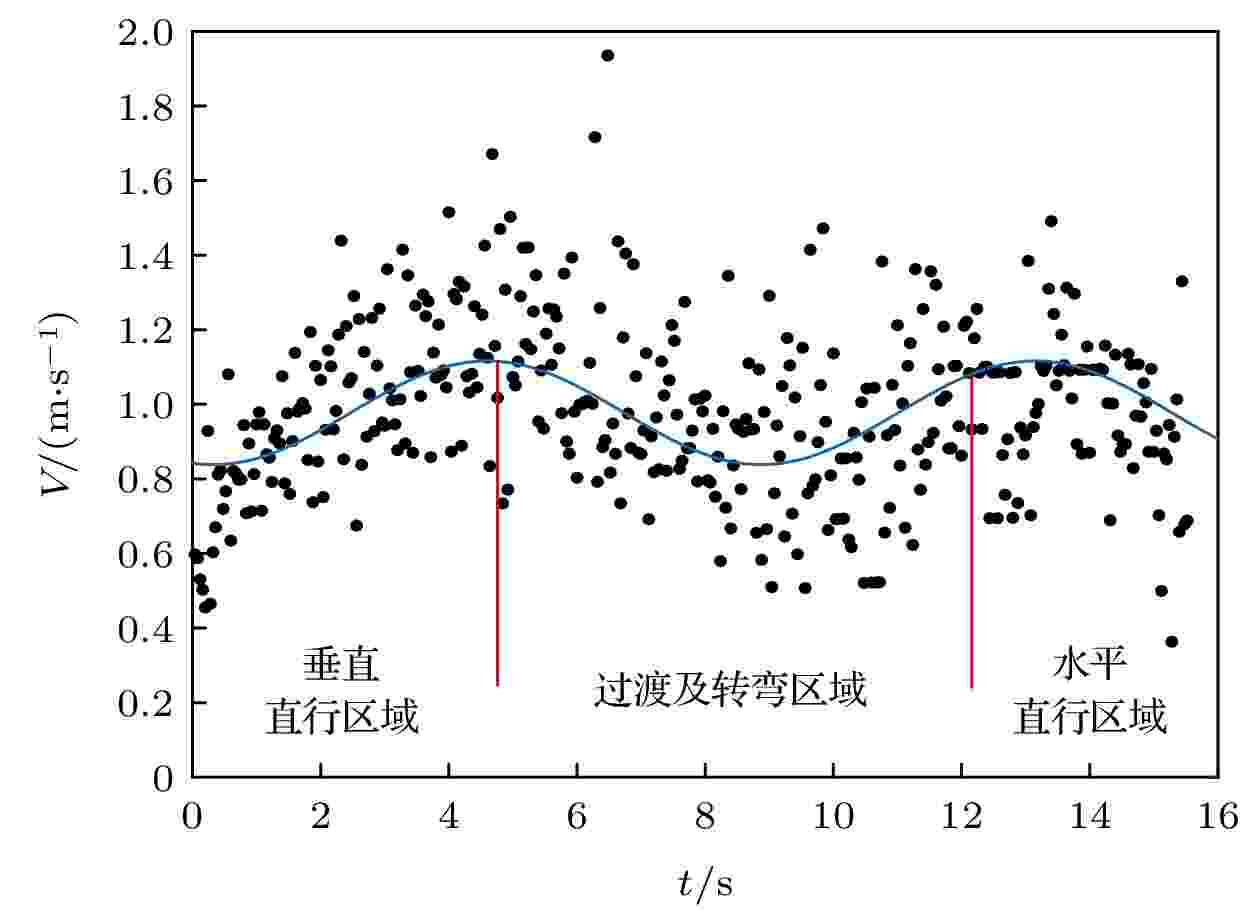图 15 行人在L型通道的速度变化过程
Figure15. The velocity change process of pedestrians in L-shaped corridor.

通过拉伸L型直通道, 形成类似房间行人疏散的场景, 可以更明显地看到在传统认知中由两侧物理边界形成的有形瓶颈${d_{\rm{t}}}$处, 行人流易形成轨迹紊乱和速度降低现象, 如图16(a)所示. 在常见的L型直通道中, 行人在通过有形瓶颈${d_{\rm{t}}}$之前, 虽然没有两侧的物理边界, 但实际上自发形成并经过了隐形瓶颈${d_{\rm{b}}}$, 同时会生成弯道三角形闲置区域${Z_0}$和一定程度的流线压缩, 如图16(b)所示.
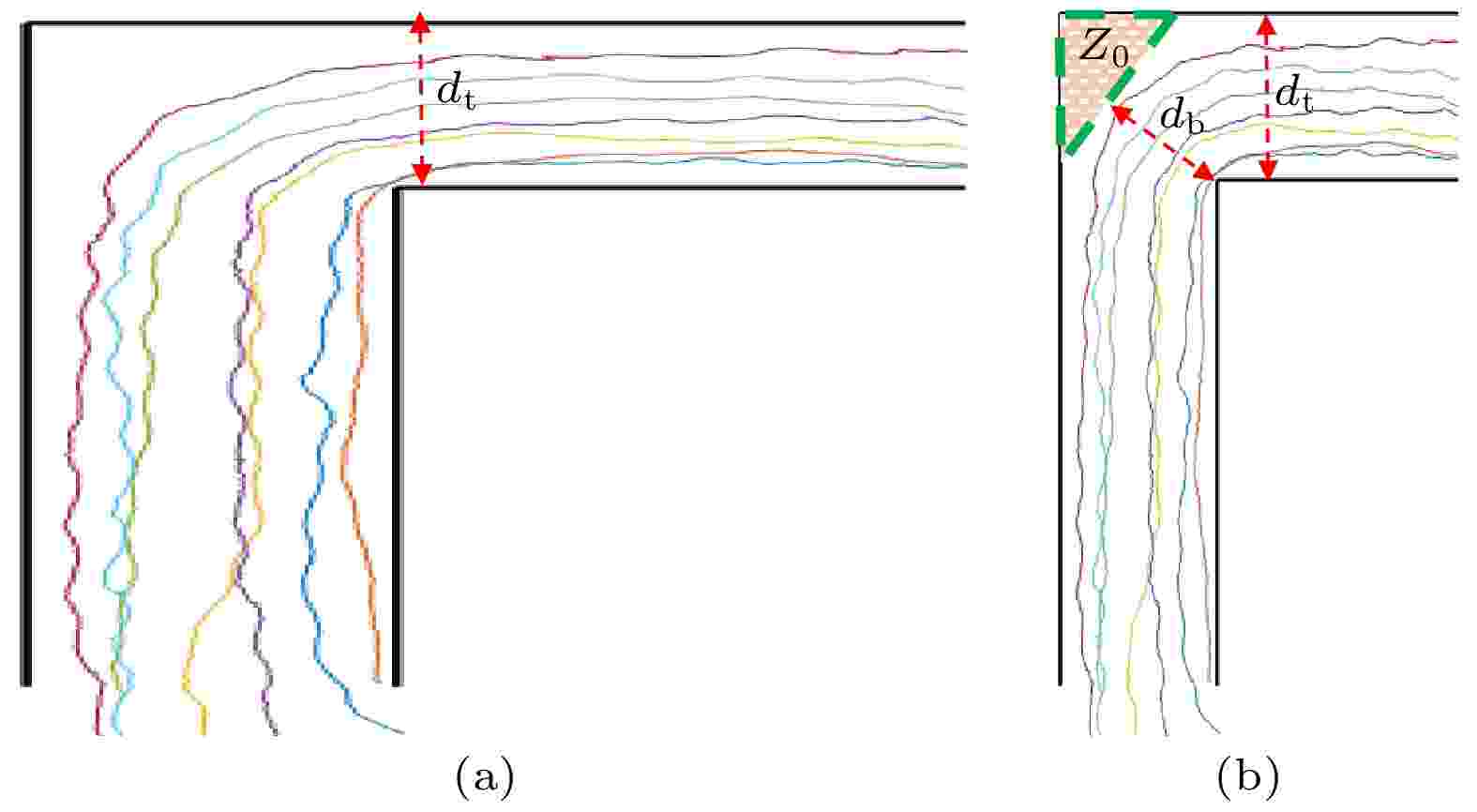图 16 通道中的瓶颈　(a) 传统认知的有形瓶颈; (b) 通道中的隐形瓶颈和有形瓶颈
Figure16. Bottlenecks in the corridor: (a) The physical bottleneck of traditional cognition; (b) invisible and visible bottlenecks in the corridor.

2

-->

3.1.行人速度修正模型

基于Voronoi图的速度修正模型具有良好的仿真效果, 仿真的基本图与实证数据良好吻合, 且具有良好的拓展性^[19]. 模型认为在目标行人视野前方一定范围内的周围行人, 会对目标行人的移动决策产生影响; 但目标行人视野后方的周围行人, 对目标行人的影响较小; 而且视野前方不同方向和距离的周围行人, 对目标行人移动速度的影响各不相同, 如图17所示.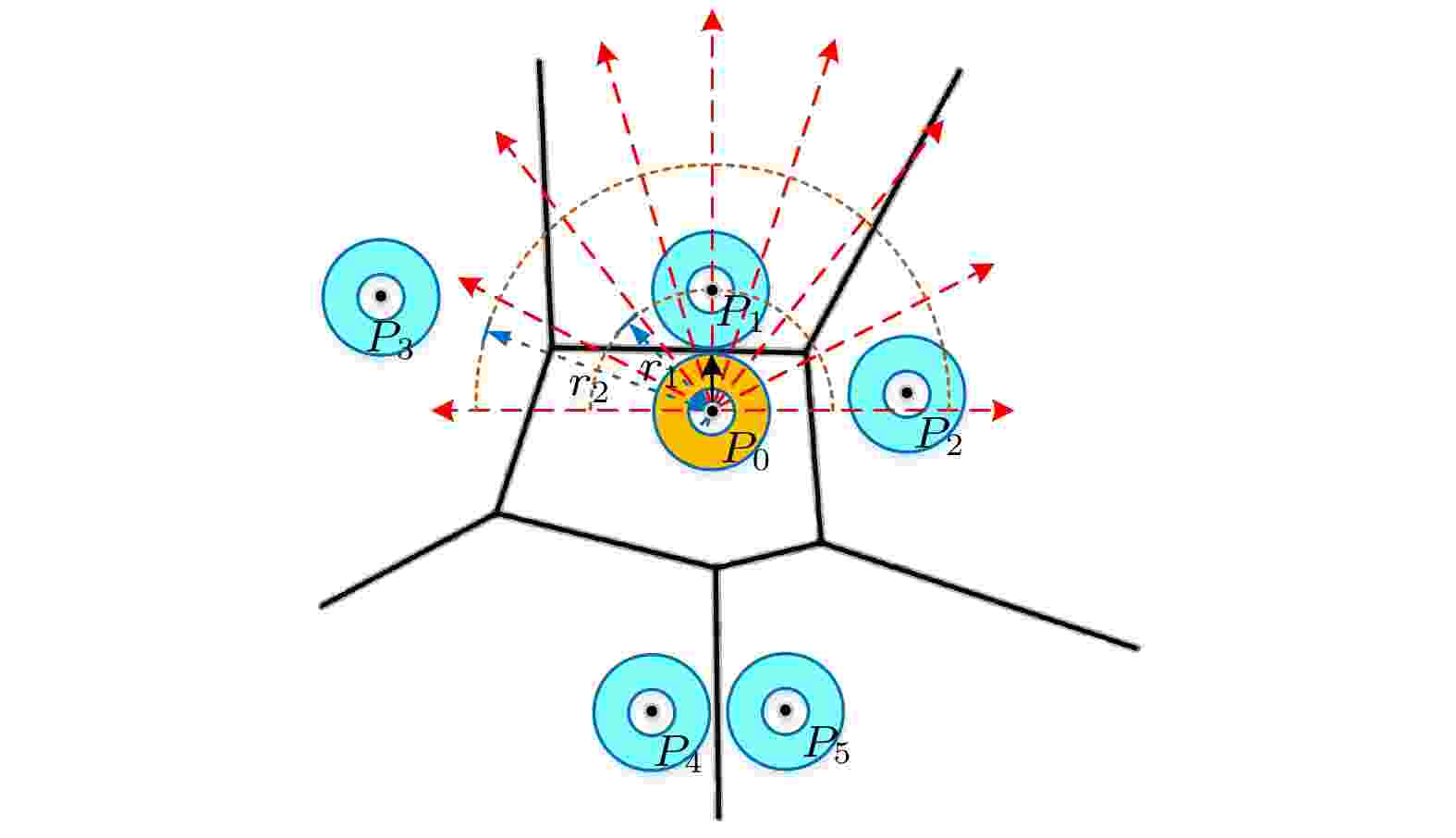
图 17 周围行人对目标行人的速度影响^[19]
Figure17. Velocity effects of surrounding pedestrians to the target pedestrian^[19].

模型设定行人在正常移动时主要受自驱动速度, 周围行人和障碍物排斥速度的影响. 行人在不同速度影响下的位置更新过程, 如(1)式—(4)式所示:

${v_i}(t) = {v_0} + \sum\limits_{j( \ne i)} {{v_{ij}}} + \sum\limits_W {{v_{i{\rm{w}}}}} ,$

${v_{ij}} = {v_0} \times g(({d_{ij}} - {r_{ij}}) \times {\theta _{ij}}) \times {{{n}}_{ij}},$

${v_{i{\rm{w}}}} = {v_0} \times g({d_{iw}} - {r_i}) \times {{{n}}_{i{\rm{w}}}},$

${s_i}(t + \Delta t) = {s_i}(t) + {v_i}(t) \times \Delta t,$

其中${v_i}(t)$为目标行人${P_i}$在时刻t的合速度, 目标行人在移动过程中, 会受来自周围行人的速度${v_{ij}}$和来自墙壁W的速度${v_{i{\rm{w}}}}$的影响, ${v_{\rm{0}}}$为目标行人的初始移动速度.
${v_0} \times g[({d_{ij}} - {r_{ij}}) \times {\theta _{ij}}] \times {{{n}}_{ij}}$表示目标行人受周围行人的排斥心理. 在目标行人视野范围内, 若${d_{ij}} - {r_{ij}} \leqslant {d_{{\rm{m}}1}}$, 当${\theta _{ij}} = 0$时, $g(x)$函数取值为${k_1}$; 当${\theta _{ij}} \ne 0$时, $g(x)$函数取值为${k_2}$. 若${d_{{\rm{m}}1}} < {d_{ij}} - $$ {r_{ij}} \leqslant {d_{{\rm{m2}}}}$, $g(x)$函数取值为${k_3}$; 若${d_{ij}} - {r_{ij}} > {d_{{\rm{m2}}}}$, $g(x)$函数取值为${k_4}$. 其中, ${d_{ij}}$表示两行人质心间的距离, ${r_{ij}}$表示两行人半径之和, ${\theta _{ij}}$表示两行人位置与目标行人速度方向的夹角, ${{{n}}_{ij}}$为周围行人质心指向目标行人质心的单位向量.
${v_0} \times g({d_{i{\rm{w}}}} - {r_i}) \times {{{n}}_{i{\rm{w}}}}$表示目标行人受来自墙壁W的速度影响, 与来自周围行人的速度影响类似, 在目标行人视野范围(180o)内, 若${d_{i{\rm{w}}}} - {r_i} \leqslant $$ {d_{{\rm{m}}3}}$, $g(x)$函数取值为${k_5}$; 若${d_{i{\rm{w}}}} - {r_i} > {d_{{\rm{m}}3}}$, $g(x)$函数取值为${k_6}$. 其中, ${d_{i{\rm{w}}}}$为目标行人与墙壁W的垂直距离, ${r_i}$为目标行人的半径, ${{{n}}_{i{\rm{w}}}}$为与墙壁垂直且指向目标行人的单位向量. 通过仿真实验测定, 速度修正模型中各参数的取值如表1所列^[19].

参数	取值	单位	参数	取值
${v_0}$	1	${\rm{m}}/{\rm{s}}$	${k_1}$	1.0
${r_i}$	0.3	m	${k_2}$	0.6
${d_{{\rm{m}}1}}$	0	m	${k_3}$	0.2
${d_{{\rm{m}}2}}$	0.5	m	${k_4}$	0
${d_{{\rm{m}}3}}$	0.25	m	${k_5}$	0.8
$\Delta t$	0.5	s	${k_6}$	0

表1速度修正模型参数取值^[19]
Table1.Parameter values of velocity correction model^[19].

2 -->

3.2.L型通道转弯规则

根据行人实验, 行人${P_{\rm{i}}}$通过典型的直角L型通道(图18)时, 通过区域由直行区域(${Z_1}$)、过渡区域(${Z_2}$)、转弯区域(${Z_3}$)和直行区域(${Z_4}$)组成. 行人通过直行区域时, 行人以原本的自驱动速度前进, 速度方向为${{{n}}_{i1}}$, 如(5)式所示; 行人通过过渡区域时, 设行人在与转弯区域${Z_2}$的垂直距离为${L_0}$时, 行人${P_{\rm{i}}}$的坐标为(${x_i}, {y_i}$), 直通道左侧${Z_{21}}$的行人倾向于向弯道内侧$\delta \cdot W$处靠近, 右侧${Z_{22}}$的行人依旧向前行进, 速度方向为${{{n}}_{i2}}$, 如(6)式所示; 行人通过弯道转弯区域时, 行人以近90o圆弧轨迹通过弯道, 行人不断调整自驱动速度方向, 其时变速度方向设定为${{{n}}_{i\theta }}$.
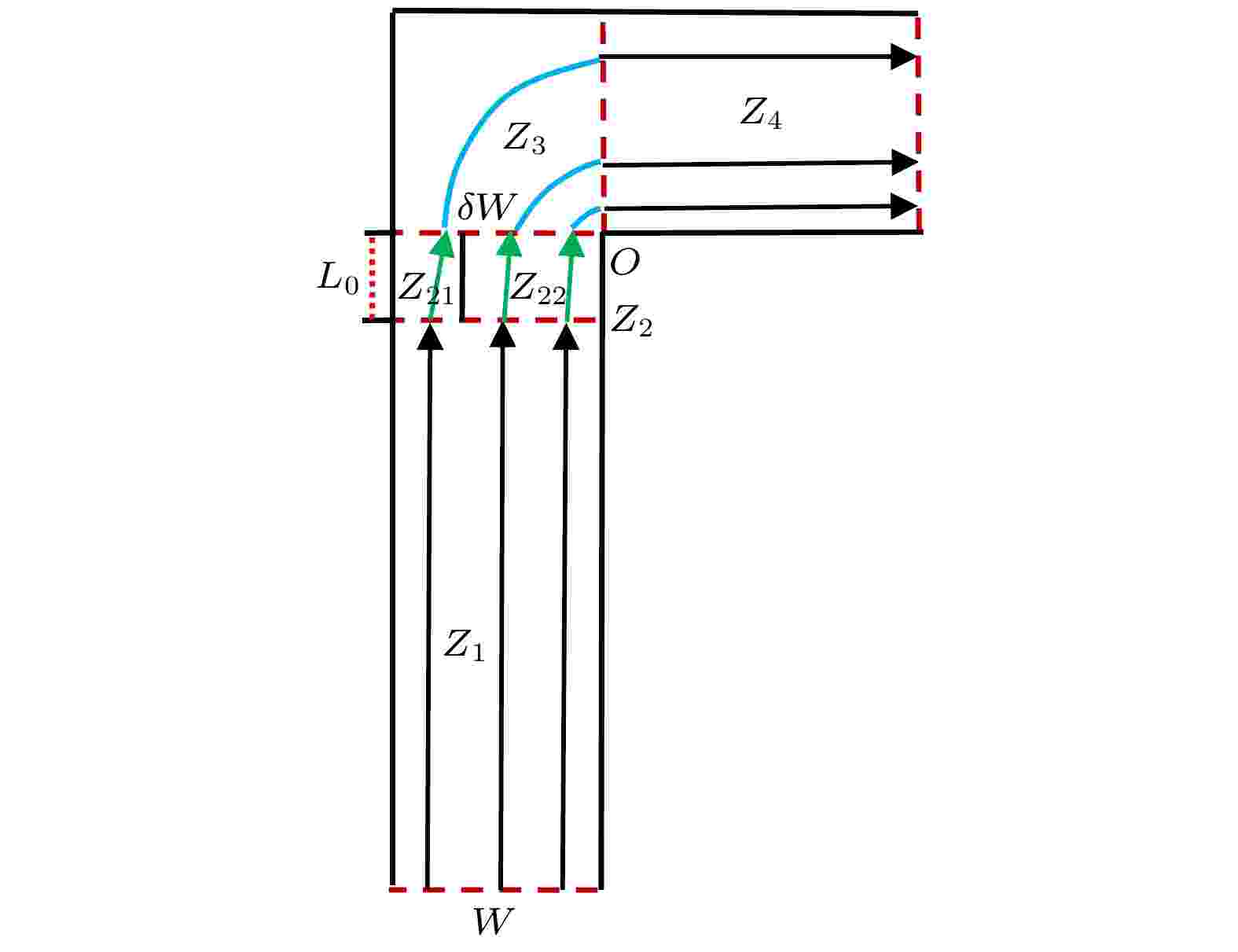图 18 行人通过90o L型通道的过程分析
Figure18. Process analysis of pedestrians passing through the 90o L-shaped corridor.

${{{n}}_{i1}} = \left\{ {\begin{aligned} &{[0,1],}&{P_i} \in {Z_1}, \\ &{[1,0],}& {P_i} \in {Z_4},\end{aligned}}\right.$

${{{n}}_{i2}} = \left\{ {\begin{aligned} &\frac{{(\delta \cdot W,L) - ({x_i},{y_i})}}{{{\rm{norm}}((\delta \cdot W,L) - ({x_i},{y_i}))}},&{P_i} \in {Z_{21}}{{ , }} \\ & [0,1]{{ }},&{P_i} \in {Z_{22}}{{ }}{{.}} \end{aligned}} \right.$

在每仿真时间步长内, 行人走过的类弧长路段对应的圆心角$w'$可由(7)式—(9)式联合计算得到, 如(10)式所示. 设定行人到达转弯区域起始点的坐标为(${x_{il}}, {y_{il}}$), 转弯区域内侧圆心O点的坐标为(${x_0}, {y_0}$), 行人通过转弯区域的自驱动速度方向${{{n}}_{i\theta }}$可由(10)式—(11)式联合计算得到. 行人在转弯区域${Z_3}$的自驱动速度变化过程, 如图19所示. 行人在转弯区域内速度转向到正对水平直行区域时, 完成速度转向过程.
图 19 行人通过转弯区域的自驱动速度时变过程(箭头方向为行人的自驱动速度方向)
Figure19. The time-varying process of pedestrians' self-driven velocity through the turning area. (The arrow direction is the direction of pedestrians' self-driven velocity).

$\lambda = \frac{{\theta \cdot {\rm{\pi }} \cdot R}}{{180}} = v \cdot t,$

$\frac{t}{{\Delta t}} = \frac{\theta }{\omega },$

$w' = w \cdot \alpha ,$

$w' = \frac{{180 \cdot v \cdot \Delta t \cdot \alpha }}{{{\rm{\pi }} \cdot R}},$

${{{n}}_{i\theta }} = \frac{{({x_o} - R \cdot \cos (q \cdot w'),{y_0} + R \cdot \sin (q \cdot w')) - ({x_{il}},{y_{il}})}}{{{\rm{norm}}(({x_o} - R \cdot \cos (q \cdot w'),{y_0} + R \cdot \sin (q \cdot w')) - ({x_{il}},{y_{il}}))}},$

其中R为行人在转弯区域距离圆心O点的半径; θ为圆心角; λ为弧长; v为行人通过转弯区域的速度大小; t为行人通过转弯区域的时间; $\Delta t$为仿真时间步长, ω为每仿真时间步长内行人走过的弧长对应的圆心角; α为修正系数; $\omega '$为修正后每仿真时间步长内行人走过的弧长对应的圆心角; q为行人进入转弯区域后的仿真时间步数.
行人自驱动速度${v_0}$的方向为${{{n}}_0}$, 如(12)式所示; 对(1)式进行修正后, 如(13)式所示, 可得行人在90o L型通道的速度:

${{{n}}_0} = \left\{ \begin{aligned}&{{{n}}_{i1}},\;\;\;{P_i} \in {Z_1}{{ , }}{P_i} \in {Z_4}{{ ,}}\\ &{{{n}}_{i2}},\;\;\;{P_i} \in {Z_2}{{ ,}}\\ &{{{n}}_{i\theta }},\;\;\;{P_i} \in {Z_3}{{ ,}}\end{aligned} \right.$

${{{v}}_{{i}}}(t) = {v_0} \cdot {{{n}}_0} + \sum\limits_{j( \ne i)} {{{{v}}_{ij}}} + \sum\limits_W {{{{v}}_{i{\rm{w}}}}} .$

行人通过转弯区域时, 步行轨迹是模型转弯区域规则与行人速度修正规则双重作用的结果. 转弯规则描述了行人移动的趋势, 而行人速度修正规则描述了实际移动过程中行人之间的相互关系.
2 -->

3.3.L型通道仿真验证

由于行人整体密度受场地面积和空间分布的影响较大, 而基于Voronoi元胞的形状随行人位置变化而变化的特征, 可以计算得到个体行人的局部密度, 可以较好地反映每个行人实时的个体密度变化情况^[13,21]. 因此, 在行人流仿真过程中, 设定绿色、黄色、橙色和红色四种颜色, 分别描述低密度、中密度、中高密度和高密度的四种局部密度状态. 根据实验和仿真经验, 设定δ为0.25, ${L_0}$为1.5 m, $\Delta t$为0.1, α为1.8.
在90o L型无障碍通道的仿真场景中, 设定竖向通道为3 m × 13 m, 横向通道为3 m × 10 m; 在竖向通道底端3 m × 2 m的范围内生成初始位置固定的20个行人, 如图20所示.
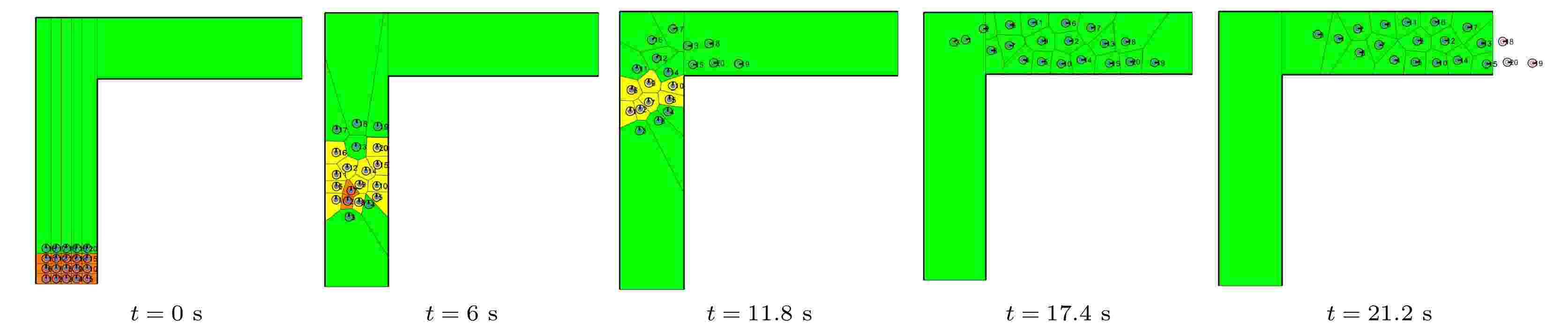图 20 行人通过L型无障碍物通道的仿真过程($ {W_1} = 3\;{\rm{m}}$, $ {L_1} = 13\;{\rm{m}}$, $ {W_2} = 3\;{\rm{m}}$, $ {L_2} = 10\;{\rm{m}}$) (a) t = 0 s; (b) t = 6.0 s; (c) t = 11.8 s; (d) t = 17.4 s; (e) t = 21.2 s
Figure20. The screenshots of the simulation process of pedestrians passing through the L-shaped corridor without obstacles (${W_1} = 3\;{\rm{m}}$, ${L_1} = 13\;{\rm{m}}$, ${W_2} = 3\;{\rm{m}}$, ${L_2} = 10\;{\rm{m}}$).: (a) t = 0 s; (b) t = 6.0 s; (c) t = 11.8 s; (d) t = 17.4 s; (e) t = 21.2 s.

通过仿真观察, 行人在开始阶段在垂直通道内向上方移动, 接近转弯区时向弯道内侧靠近, 通过转弯区后向右方移动, 最后通过水平通道离开系统, 仿真时长为28.3 s, 仿真过程如图20所示.
通过仿真也可以发现, 行人通过90o L型无障碍通道的仿真轨迹线与行人实验的移动轨迹线吻合, 行人以较光滑的圆弧轨迹通过弯道区域, 如图21(a)所示. 通过行人仿真移动轨迹线, 可明显地观察到转弯区域的隐形瓶颈${d_{\rm{b}}}$和弯道三角形闲置区域${Z_{\rm{0}}}$, 以及多列行人簇. 仿真结果与行人实验观察结果相吻合, 如图21(b)所示.
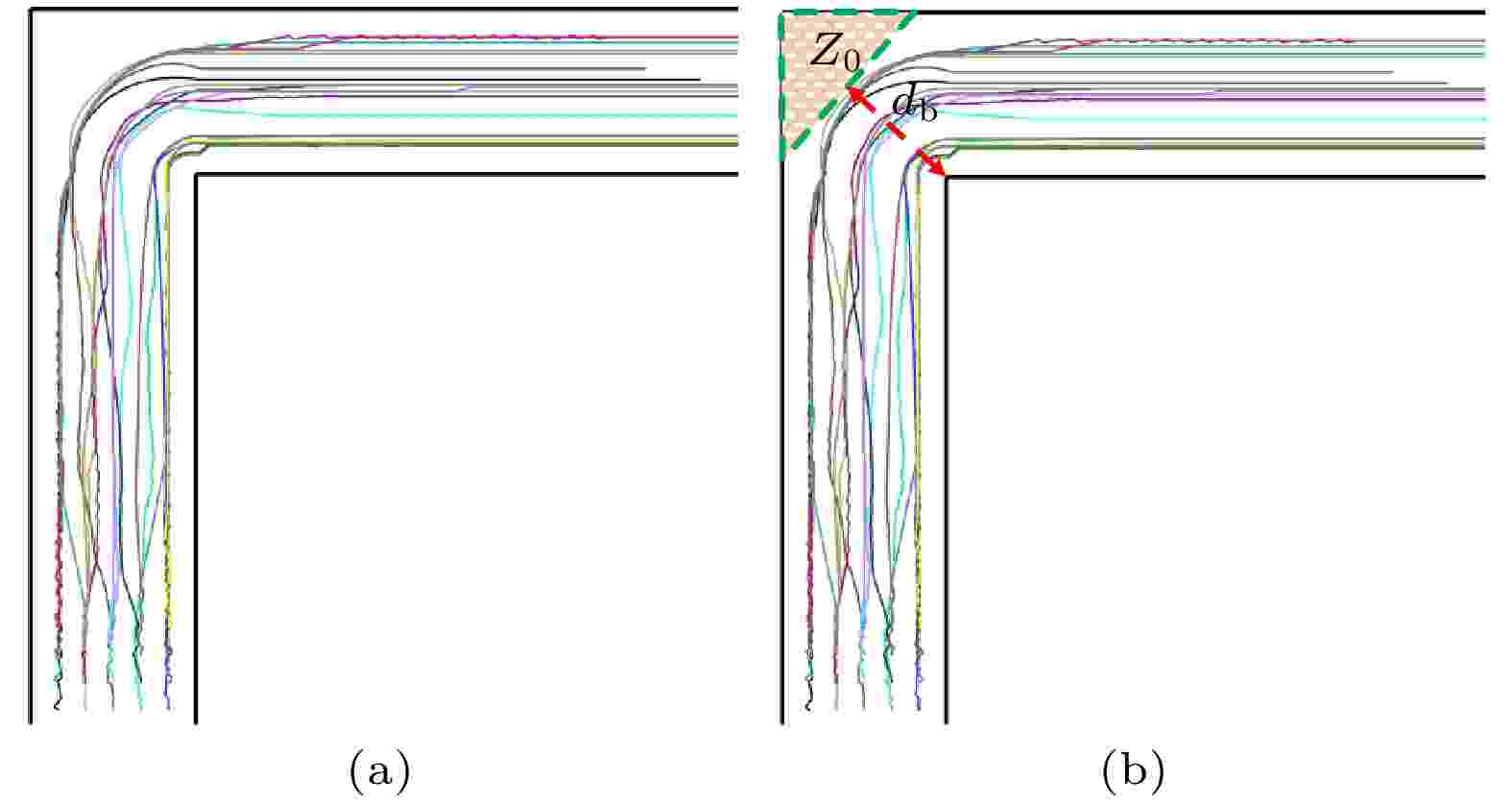图 21 行人仿真通过L型无障碍通道的轨迹线　(a) 行人移动轨迹线; (b) 在转弯区域形成的弯道三角形闲置区域和隐形瓶颈
Figure21. Pedestrian simulation of the path lines through the L-shaped corridor without obstacles: (a) The pedestrian movement trajectory; (b) the triangular idle area of the curve and the invisible bottleneck formed in the turning area.

由图20可知, 在$ t = 6\;{\rm{s}}$, $ t = 11.8\;{\rm{s}}$和$ t = 17.4\;{\rm{s}}$时, 行人分别分布在L型无障碍通道的垂直直行区域、过渡及转弯区域和水平直行区域; 分别统计各阶段行人速度、个体局部密度情况如图22和图23所示. L型无障碍通道位置与直角坐标系的对应关系如图22(a)所示. 行人在垂直直行区域的速度大都保持在较高的稳定状态(约1 m/s), 但由于前方行人的阻挡, 后方行人速度相对较低, 如图22(b)所示; 行人在过渡及转弯区域的速度变化较大, 出现了不同程度的降低; 但当行人离开转弯区域时, 速度又恢复到了较高的稳定状态, 如图22(c)所示; 行人在水平直行区域的速度均保持在较高的稳定状态(约1 m/s), 但由于后方的行人仍处于转弯区域内, 其速度仍相对较低, 如图22(d)所示.
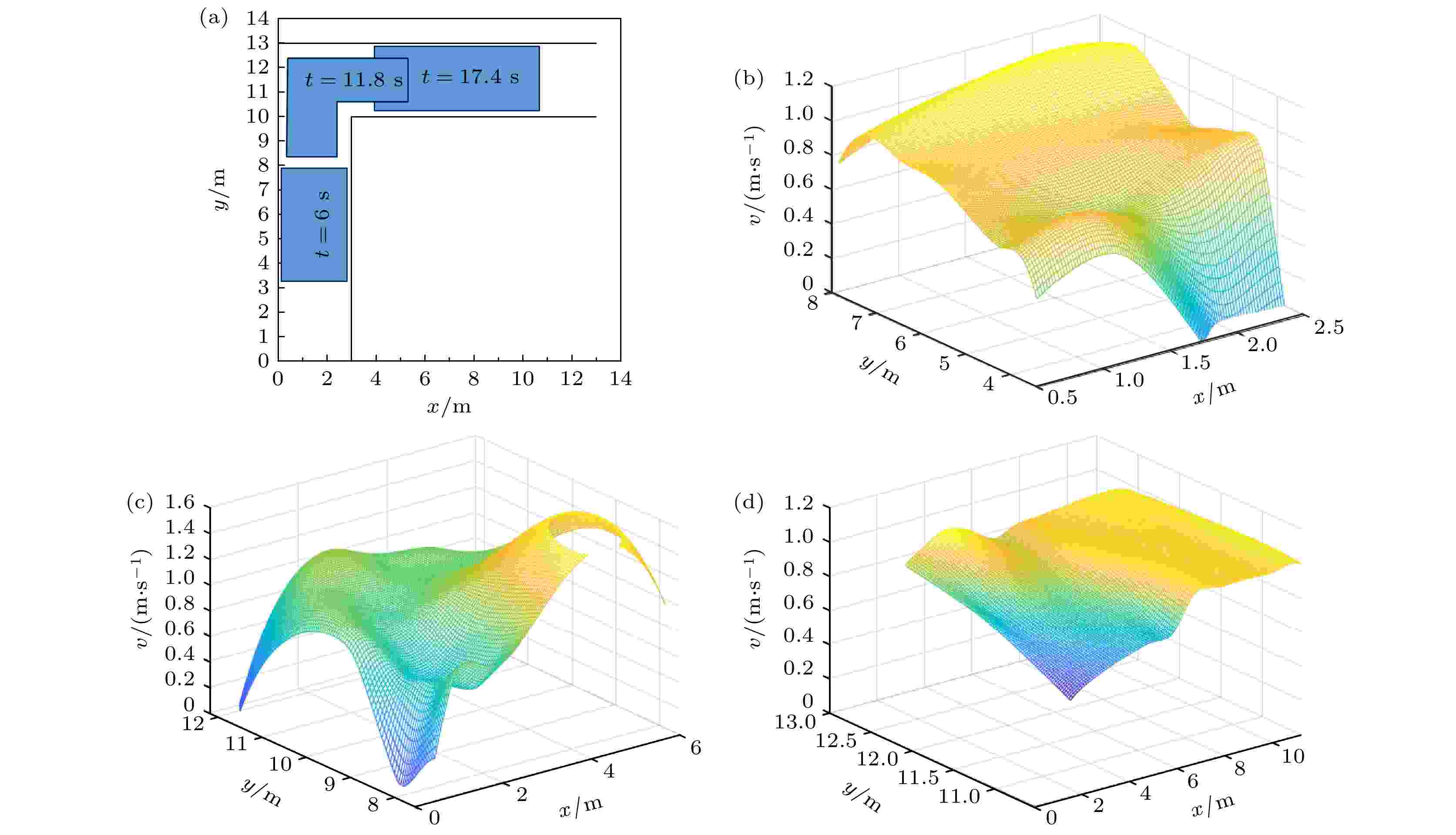图 22 L型无障碍通道内不同时刻行人速度分布情况　(a) L型无障碍物通道位置与直角坐标系的对应关系; (b) 行人在垂直直行区域的速度, t = 6.0 s; (c) 行人在过渡及转弯区域的速度, t = 11.8 s; (d) 行人在水平直行区域的速度, t = 17.4 s
Figure22. The velocity distribution of pedestrians at different times in L-shaped corridor without obstacles: (a) Corresponding relation between the position of L-shaped straight corridor without obstacles and Cartesian coordinate system; (b) the velocity of pedestrians in vertical straight-ahead areas, t = 6.0 s; (c) the velocity of pedestrians in transition and turning areas, t = 11.8 s; (d) the velocity of pedestrians in horizontal straight-ahead areas, t = 17.4 s.

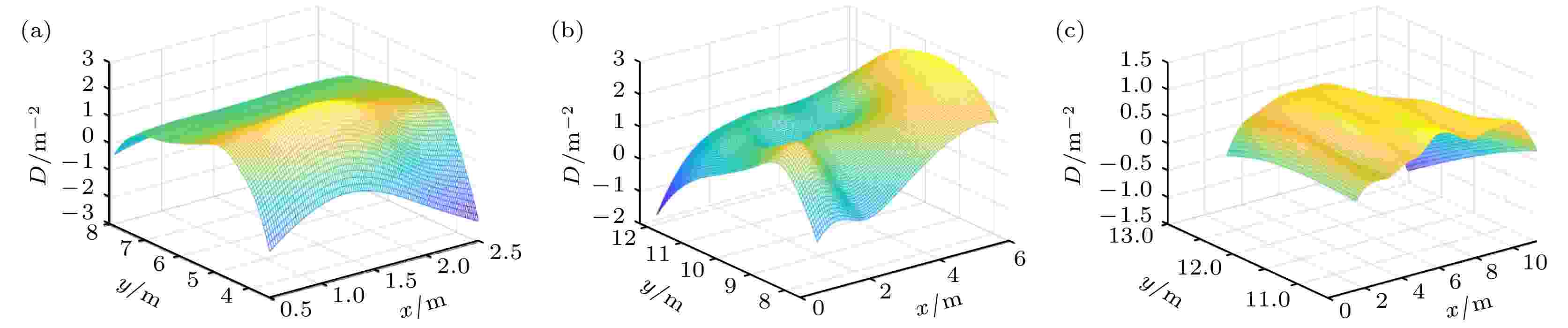图 23 L型无障碍通道行人个体局部密度的变化情况　(a) 行人在垂直直行区域的个体局部密度, t = 6.0 s; (b) 行人在过渡及转弯区域的个体局部密度, t = 11.8 s; (c) 行人在水平直行区域的个体局部密度, t = 17.4 s
Figure23. The variation trend of the individual local density of pedestrians in L-shaped straight corridor without obstacles: (a) The individual local density of pedestrians in vertical straight-ahead areas, t = 6.0 s; (b) the individual local density of pedestrians in transition and turning areas, t = 11.8 s; (c) the individual local density of pedestrians in horizontal straight-ahead areas, t = 17.4 s.

同时, 行人在垂直直行区域的个体局部密度大都保持在较低的稳定状态, 接近于1 P/m²; 但在中后方区域, 由于前方行人的阻挡, 后方行人的低速度导致了个体局部密度相对较高, 在2 P/m²左右, 如图23(a)所示. 行人在过渡及转弯区域的个体局部密度变化较大, 在过渡区域及刚到水平直行区域的行人较拥挤, 个体局部密度相对较高, 而在转弯区域的行人速度及个体密度均较低, 如图23(b)所示; 行人在水平直行区域的个体局部密度均较低, 低于1 P/m², 如图23(c)所示.
在L型通道转弯区域对角线处分别设置3个半径为0.25 m的圆形障碍物, 障碍物坐标分别为(0.75, 12.25), (1.5, 11.5), (2.25, 10.75), 其他设置与L型无障碍通道相同. 行人通过转弯区域的仿真过程如图24所示. 由图24可见, 行人在转弯区域有效地避开了障碍物.
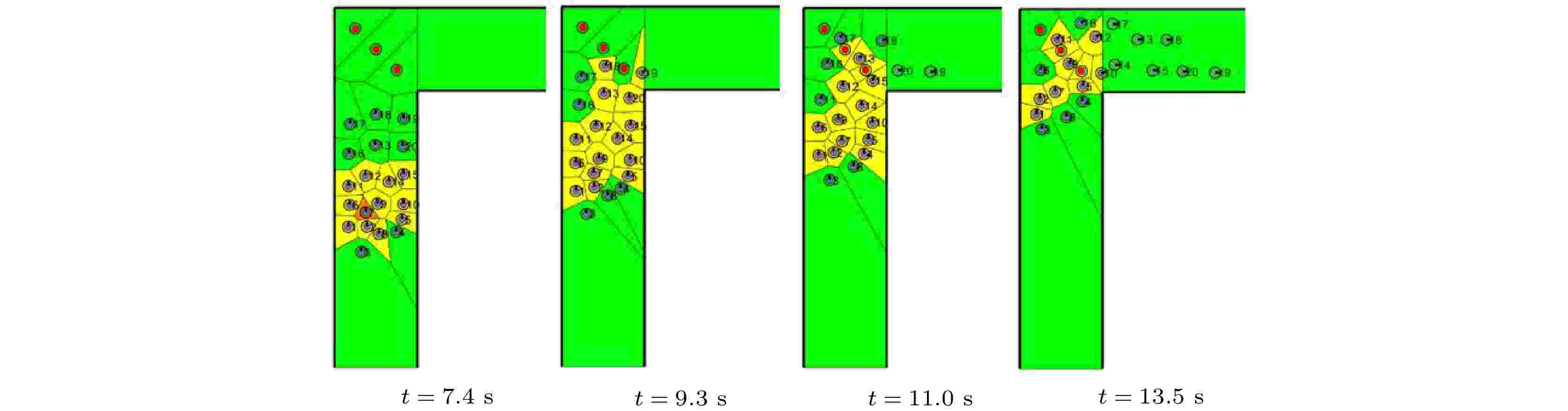图 24 行人通过L型有障碍通道的仿真过程($ {W_1} = 3\;{\rm{m}}$, $ {L_1} = 13\;{\rm{m}}$, $ {W_2} = 3\;{\rm{m}}$, $ {L_2} = 10\;{\rm{m}}$)　(a) t = 7.4 s; (b) t = 9.3 s; (c) t = 11.0 s; (d) t = 13.5 s
Figure24. The screenshots of the simulation process of pedestrians passing through the L-shaped corridor with obstacles ($ {W_1} = 3\;{\rm{m}}$, ${L_1} = 13\;{\rm{m}}$, $ {W_2} = 3\;{\rm{m}}$, $ {L_2} = 10\;{\rm{m}}$): (a) t = 7.4 s; (b) t = 9.3 s; (c) t = 11.0 s; (d) t = 13.5 s

由图24可知, 在$ t = 7.4\;{\rm{s}}$, $ t = 9.3\;{\rm{s}}$, $ t = 11\;{\rm{s}}$和$ t = 13.5\;{\rm{s}}$时, 行人分别分布在L型有障碍通道的直行、过渡及转弯区域的各个阶段, 现分别统计各阶段的行人速度与个体局部密度情况, 如图25和图26所示. L型有障碍通道位置与直角坐标系的对应关系如图25(a)所示. 行人在垂直直行及过渡区域的速度大都保持在较高的稳定状态(约1 m/s), 但后方行人由于前方行人的阻挡, 其速度相对较低, 如图25(b)所示. 行人在部分过渡及有障碍物转弯区域的速度变化较大, 出现了不同程度的降低; 但当行人离开转弯区域后, 速度又恢复到了较高的稳定状态, 如图25(c)所示. 行人在部分过渡、转弯及水平直行区域的速度出现了分化, 过渡及水平直行区域的行人速度保持在较高的稳定状态约1 m/s, 而在转弯区域的速度相对较低, 如图25(d)所示. 当行人大部分处于转弯及水平直行区域时, 转弯区域的行人速度较低, 而处于水平直行区域的行人速度恢复到较高的稳定状态约1 m/s, 如图25(e)所示.
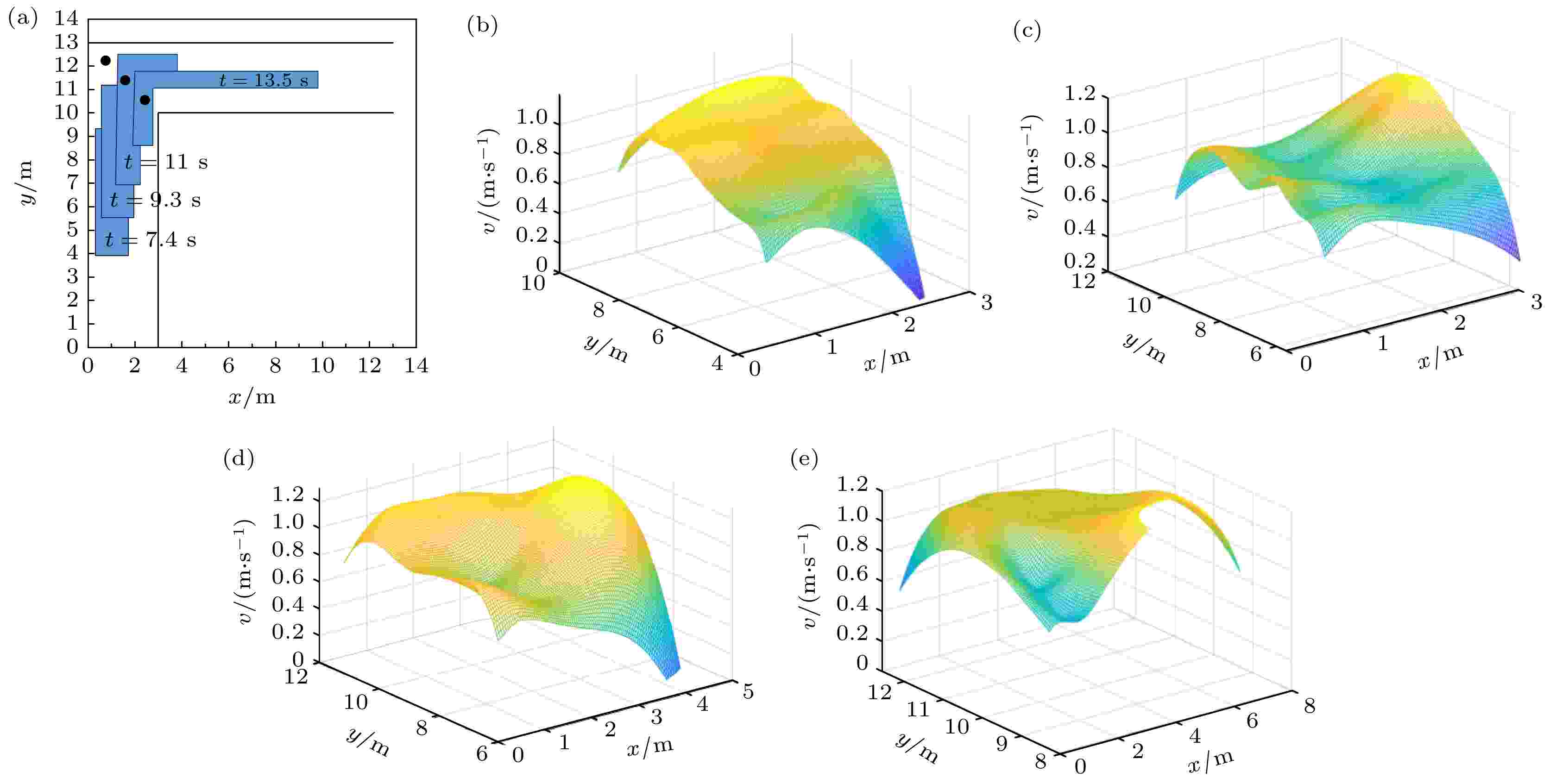图 25 L型有障碍通道行人速度的变化趋势　(a) L型有障碍通道位置与直角坐标系的对应关系; (b) 行人接近转弯区域的速度, t = 7.4 s; (c) 行人刚进入转弯区域的速度, t = 9.3 s; (d)行人部分处于转弯区域的速度, t = 11.0 s; (e) 行人大部分通过转弯区域的速度, t = 13.5 s
Figure25. The variation trend of pedestrian velocity in L-shaped corridor with obstacles: (a) Corresponding relation between the position of L-shaped corridor with obstacles and Cartesian coordinate system; (b) the velocity at which pedestrians approach the turning area, t = 7.4 s; (c) the velocity at which the pedestrians first enter the turning area, t = 9.3 s; (d) the velocity at which the pedestrians part are in the turning area, t = 11.0 s; (e) the velocity at which the pedestrians pass through the turning area for the most part, t = 13.5 s.

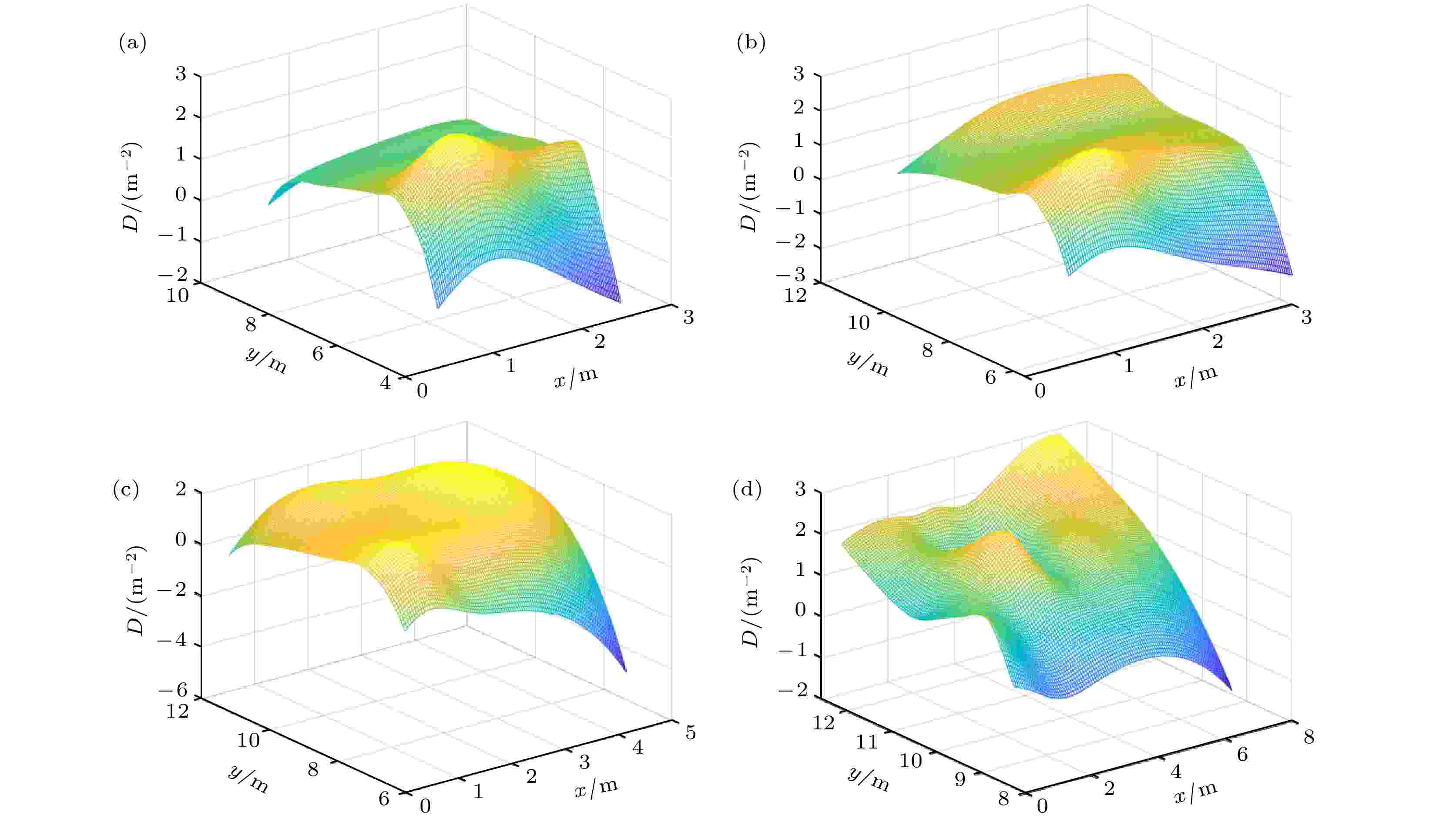图 26 L型有障碍通道行人个体局部密度的分布情况　(a) 行人接近转弯区域的个体局部密度, t = 7.4 s; (b) 行人刚进入转弯区域的个体局部密度, t = 9.3 s; (c) 行人部分处于转弯区域的个体局部密度, t = 11.0 s; (d) 行人大部分通过转弯区域的个体局部密度, t = 13.5 s
Figure26. The individual local density distribution of pedestrians in L-shaped corridor with obstacles: (a) The individual local density at which pedestrians approach the turning area, t = 7.4 s; (b) the individual local density at which the pedestrians first enter the turning area, t = 9.3 s; (c) the individual local density at which the pedestrians part are in the turning area, t = 11.0 s; (d) the individual local density at which the pedestrians pass through the turning area for the most part, t = 13.5 s.

同时, 在刚接近转弯区域时的行人个体局部密度, 大都保持在较低的稳定状态, 接近于1 P/m², 但由于中后方区域行人的低速度导致其较高的个体局部密度, 约2 P/m², 如图26(a)所示. 刚进入转弯区域时行人个体局部密度变化较大, 在转弯区域和垂直直行区域中部的行人个体局部密度较高, 如图26(b)所示. 行人部分处于转弯区域时的个体局部密度较高, 约2 P/m², 如图26(c)所示. 行人在大部分通过转弯区域时其个体局部密度变化较大, 在转弯区域即将到达水平直行区域的个体局部密度较高, 但仍处于末尾过渡区域和到达水平直行区域的个体局部密度较低, 如图26(d)所示.
通过对比分析, 行人通过L型有障碍通道转弯区域的速度, 略低于无障碍物转弯区域的速度, 且有较好的行人分流秩序; 但通过有障碍转弯区域的个体局部密度要大于无障碍物转弯区域的密度.
为了进一步证明该仿真模型对不同尺寸L型通道的适用性, 在图20仿真场景的基础上, 通过扩大垂直直通道的宽度, 同时缩减水平直通道的宽度, 设置非对称的L型通道进行仿真研究. 设定δ为0.7, α为2.5, 其他参数保持不变. 仿真初始时刻, 在垂直直通道底部随机生成20个行人. 行人通过L型通道的仿真过程, 如图27所示.
图 27 行人通过非对称L型通道的仿真过程(${W_1} = 6\;{\rm{m}}$, ${L_1} = 12\;{\rm{m}}$, ${W_2} = 2\;{\rm{m}}$, ${L_2} = 10\;{\rm{m}}$)　(a) t = 0.2 s; (b) t = 4.5 s; (c) t = 12.5 s; (d) t = 204 s
Figure27. The screenshots of the simulation process of pedestrians passing through an asymmetric L-shaped corridor (${W_1} = 6\;{\rm{m}}$, ${L_1} = 12\;{\rm{m}}$, ${W_2} = 2\;{\rm{m}}$, ${L_2} = 10\;{\rm{m}}$): (a) t = 0.2 s; (b) t = 4.5 s; (c) t = 12.5 s; (d) t = 204 s.

以90o L型步行通道内的单向行人流为研究对象, 基于可控实验与微观仿真研究行人的转弯行为. 构建通道转弯区无障碍物、障碍物沿转弯区对角线布局、障碍物垂直转弯区对角线布局三种实验场景, 通过行人实验获取不同实验场景下的行人移动轨迹. 分析发现行人在正常非恐慌情况下, 在移动过程很少出现乱串行为, 且存在轻微抖动的拉链效应侧向位移; 基于行人的移动行为, L型通道可分为垂直直行区域、过渡区域、转弯区域和水平直行区域. 在过渡区域行人会向弯道内侧靠拢, 基本按照稳定弧线通过转弯区域. 在转弯过程中, 距转弯中心越外围行人, 绕行弧长距离越大; 越内侧行人, 绕行弧长距离越小. 行人移动会形成多列轨迹簇, 在转弯区域会形成不被行人使用的“弯道三角形闲置区域”; 且在瓶颈处会观察到物理瓶颈的有效部分与无效部分, 以及“隐形瓶颈”现象. 当在转弯区域对角线处设置障碍物时, 可以明显地观察到行人在通过弯道时, 在障碍物前的避免碰撞区域和障碍物后的未占据区域形类菱形空白区域. 当在转弯区域垂直对角线处设置障碍物时, 虽然障碍物压缩了行人的可行转弯移动空间, 但行人在移动过程中不会与障碍物接触, 且会与障碍物组成的边缘相隔一定距离, 留下间隙空间. 不同实验场景均会出现不同程度的流线压缩现象, 且不同场景的“弯道三角形闲置区域”面积大小不同. 同时, 通过对行人通过L型通道不同区域的速度分布情况分析, 发现行人在通过弯道转弯区域时会降低速度.
基于L型通道的行人微观行为, 改进基于Voronoi图的速度修正仿真模型, 制定并嵌入行人通过L型通道的转弯规则, 分别对有/无障碍物以及非对称L型通道场景进行仿真研究. 改进的仿真模型, 能有效地模拟再现行人通过弯道区域时呈现光滑弧线的移动轨迹, 并能观察到“隐形瓶颈”和“弯道三角形闲置区域”现象; 同时, 行人流依次通过L型通道的四个区域时, 其速度分布情况与行人实验数据相吻合, 呈现先增后减再增“波浪式”变化的特点. 该仿真模型也模拟再现了由于行人转弯行为所导致局部密度变化的情况, 彼此印证了行人速度与局部密度变化的统一性.
根据行人实验和仿真结论, 对行人通过L型通道微观与宏观行为的认知有利于合理利用和设计L型通道转弯处区域, 如减小弯道区域面积大小, 修改转弯处通道线型节省空间、在弯道三角形闲置区域设置垃圾桶、广告牌, 在隐形瓶颈处设置隔离柱合理引导分离人群以提高秩序等.