摘要:量子计算在近十年取得了长足的进展. 随着量子调控技术达到前所未有的高度, 包括超导量子比特、光量子器件、原子系综等在内的量子实验平台都进入到了崭新的时代. 目前在特定计算任务上超越经典的量子计算优势也已经被报道. 其中一种可以有效运用可控量子器件的计算方案是采用绝热量子计算. 绝热量子计算中算法的选择与研究至关重要, 其将直接决定量子计算优势是否能够最大限度地被挖掘. 本综述主要介绍近期机器学习在绝热量子算法设计方面的应用, 并讲述该计算架构在3-SAT和Grover搜索等问题上的应用. 通过与未经机器学习优化设计的绝热量子算法对比, 研究表明机器学习方法的应用可以极大提高绝热量子算法的计算效率.
关键词: 绝热量子计算/
量子算法/
量子模拟/
机器学习

English Abstract

全文HTML

--> --> -->

量子计算概念最早可以追溯到20世纪80年代, 当时Benioff^[1]提出了量子图灵机概念, Feynman^[2]有了量子模拟的想法. 而后Deutsch^[3]提出量子线路模型来实现普适量子计算, Yao^[4]证明了量子线路模型与量子图灵机的等价性—两者可以在多项式时间内互相模拟. 在量子算法方面, 1994年Shor^[5]基于量子线路模型提出了可在多项式时间内求解质因数分解问题的量子算法. 由于质因数分解问题的困难性是Rivest-Shamir-Adleman (RSA) 公钥加密体系安全性的保障, 这一由Shor提出的多项式量子算法引起了密码学和相关实验领域的高度关注^[6–12]. 量子计算有了从理论研究走向实际应用的趋势, 量子计算机的研发开始引起多方投入^[13]. 同时, 人们也从量子信息理论和量子计算复杂度的角度展开研究, 期待设计出更多具有显著量子计算优势的量子算法^[14–17].
目前已知的具有超越经典计算优势的量子算法主要可以归为三大类^[16]. 第一类是利用量子傅里叶变换寻找周期的量子算法, 包括Shor算法^[5]、Simon算法^[18]、以及Hallgren算法^[19]等. 第二类是以有量子加速的Grover搜索算法^[20]为基础的搜索及优化算法—可以在$ O(\sqrt{N}) $时间内完成对N个项目的搜索. 第三类是在量子计算机上对复杂的量子多体体系进行高效模拟. 这是基于Feynman“利用量子计算机来进行量子模拟”的想法^[2]. 量子系统的希尔伯特空间会随量子自由度(比如原子数等)的数目指数增长, 所以如果用经典计算机来模拟量子多体系统需要大量的内存资源和计算资源. 而量子计算机可以直接用量子比特进行计算, 具有对复杂量子多体系统模拟的天然优势. 这一方面对量子化学计算、材料科学的复杂微观物理机制(如高温超导)的揭示等具有重要科学价值.
量子算法与经典算法的很大一点不同是量子力学允许的量子操作、量子叠加和量子纠缠很难直接与直观经验建立联系, 甚至是反直觉的. 这极大地增加了量子算法设计的难度, 同时使得人们在经典计算算法设计上积累的经验很难被直接借用^[16].
在开发设计量子算法时, 我们期待设计出能够相比于经典计算更高效的量子算法. 对于可以在量子计算机上以多项式时间解决的问题, 人们把它们归为BQP (bounded-error quantum polynomial time)复杂类. 目前人们还没有一个普适的理论来确定这类问题的边界, 在后文中我们将对此做更具体的介绍. 虽然通常人们不认为量子计算能够指数加速NP-complete问题, 但在具体算法设计中, 任何能够提升量子计算能力的设计方法和技巧都值得尝试^[21]. 在量子计算的发展进程中, 我们也可以适当借鉴经典计算领域的发展. 设计出具有量子优势的量子算法还有待于量子研究领域与经典计算研究领域的深度交融.
Farhi等^[22,23]在2001年提出了与量子线路模型相应的绝热量子计算模型—AQC (adiabatic quantum computation). 在绝热量子计算中, 我们首先会构造一个非平庸的问题哈密顿量, 其基态编码了我们关心问题的答案. 然后我们让系统从一个与问题哈密顿量非对易的平庸哈密顿量基态开始做演化, 一直演化到这个编码的问题哈密顿量. 如果整个演化过程是完全绝热的并且基态与激发态之间始终存在能级差^[24], 我们最后也就能获得问题哈密顿量的基态, 即这个计算问题的正确解. 这也就将一个计算问题变成了一个哈密顿量求基态的问题. 绝热量子计算模型可以看作连续时间的量子计算, 其与离散时间的量子线路模型的等价性也在理论上得到了证明^[25,26]. “演化体系哈密顿量”这一想法与量子模拟非常接近. 而人们在量子模拟及量子控制方面也具备了很多理论知识和实验经验^[27–30]. 所以绝热量子计算概念的提出不但给我们提供了一种全新的普适量子计算框架, 而且有利于将我们对量子模拟的物理直觉与量子算法设计结合起来以打开新思路. 后文将详细介绍绝热量子计算的算法设计.
经典计算领域的算法设计复杂程度也在愈趋加大, 如何实现经典算法的自动化设计也变得越来越重要. 对于一个问题, 如果存在多种可以解决的算法, 那么如何高效地挑选一个最优的算法就非常关键. 这就涉及算法选择问题(algorithm selection)^[31]; 而对于一个算法, 在不同的问题例子中如何去优化算法构型(algorithm configuration)^[32]也相当重要. 我们将在后文中详细介绍机器学习在经典算法设计领域的应用. 另一方面, 近些年机器学习也在处理量子多体问题上, 特别是在物态的相分类^[33–37]、多体波函数的表示及基态制备^[38–41]、优化量子操控^[42–45]等方向上有了一系列的应用.
虽然经典与量子算法的设计领域差别很大, 但两者的复杂性使得它们都面临着巨大挑战. 通过借鉴机器学习在经典算法设计与量子多体物理中的成功应用, 我们也希望机器学习方法能辅助量子算法设计. 这不仅会帮助我们设计出具有量子优越性的算法, 同时设计获得的量子算法也有望实现机器学习的量子加速^[46]. 我们期待这两个领域的交融会碰撞出灵感的火花.

本节将对绝热量子计算的概念以及绝热量子计算中问题哈密顿量的编码方案与自旋玻璃物理的联系进行介绍. 而后, 给出三个具体计算问题的哈密顿量构造方案. 最后讨论运用绝热量子计算模型探索BQP复杂类的研究途径.
2

-->

2.1.绝热量子计算

绝热量子计算作为一种普适的量子计算框架^{[22,23,25,26,47]}, 其原理是将一个计算问题变成量子体系求基态的问题. 设想有两个非对易的哈密顿量$H_{\rm{b}}$和$H_{\rm{p}}$, 其中初始哈密顿量$H_{\rm{b }}$的基态非常容易制备, 而问题哈密顿量$H_{\rm{p}}$的基态则编码了我们所关心问题的解. 让量子系统从初始哈密顿量$H_{\rm{b }}$的基态开始演化, 直到系统到达问题哈密顿量$H_{\rm{p}}$. 一般可以用以下含时哈密顿量来刻画该过程:

$ H(s(t/T)) = [1-s(t/T)]H_{\rm{b}}+s(t/T)H_{\rm{p}}, $

其中$ s(t/T) $为哈密顿量的演化路径(从$ 0 $变化到$ 1 $), T为总的演化时间. 如果演化时间T足够长并且系统的基态与激发态之间始终存在能级差^[24], 那么由绝热定理可以保证, 这个量子系统将时刻处于瞬时哈密顿量的基态. 量化绝热条件是绝热定理成立的必要条件^[48]. 由此, 可以估计出绝热演化时间$T\gg O(\varDelta_{\min}^{-2})$^[22,49,47], 其中$\varDelta_{\min}$为基态与第一激发态之间的最小能隙. 通过测量演化T时间后的系统状态, 将得到问题哈密顿量的基态, 即问题的解.
绝热量子计算在被提出之时就将目标指向解决NP-complete和NP-hard问题^[22,23]. 而后, 对其是否能够超越经典计算的质疑也接踵而来—因为对于这类NP-complete和NP-hard问题, 其最小能隙呈指数减小, 所以绝热量子计算需要的时间是指数增长的. 其并不能做到相比于经典算法的指数加速, 但可能在系数因子上会比经典的算法更优^[50–55].
2 -->

2.2.哈密顿量编码

本节将介绍绝热量子计算哈密顿量编码与自旋玻璃问题的关联. 也将介绍三个典型计算问题的哈密顿量构造方法.
3 -->

2.2.1.哈密顿量编码与自旋玻璃问题

在理论和实验中, 总可以将绝热量子计算的哈密顿量编码为伊辛自旋模型的量子形式^[56,57]. 一个经典的伊辛自旋模型可以写作:

$ H(s_1,s_2,\cdots,s_n) = \sum\limits_{i < j}J_{ij}s_is_j+\sum\limits_{i = 1}^nh_is_i. $

在绝热量子计算中, 通过将自旋$ s_i $写成泡利算符形式来得到问题哈密顿量$H_{\rm{p}}$:

$ H_{\rm{p}} = H(\sigma_1^z,\cdots,\sigma_n^z), $

其中$ \sigma_i^z $为作用在第i个自旋上的泡利Z算符, $ J_{ij} $和$ h_i $为实数. 可以将初始哈密顿量$H_{\rm{b}}$设置为:

$ H_{\rm{b}} = \frac{1}{2}\sum\limits_i[{\mathbb{1}}-\sigma_i^x], $

其中$ \sigma_i^x $为作用在第i个自旋上的泡利X算符.
这样的问题哈密顿量构造与物理中的自旋玻璃模型可以一一对应. 自旋玻璃问题是一个在凝聚态物理和统计及计算物理领域中悠久且丰富的物理问题^[58–60]. 自旋玻璃问题和NP(nondeterministic polynomial) 问题的联系也备受关注. 这种关联给了我们从物理角度来理解计算中的困难的机会^[61–63]. Karp^[64]在1972年研究发现21个组合及图论计算问题都可以在多项式时间归约到一个NP-complete问题上, 也就证明了它们都是NP-complete问题. Lucas^[65]研究了这些典型NP-complete问题如何编码为自旋玻璃形式的问题哈密顿量. 一般人们也会把这类编码后的问题叫作QUBO (quadratic unconstrained binary optimization) 问题.
3 -->

2.2.2.基于绝热量子计算的Grover搜索算法

基于线路模型的Grover搜索算法被证明具有超越经典搜索算法的平方加速^[20]. 这个搜索问题是指在$ N = 2^n $个项目中寻找到标记的项. 对于一个函数$ f:\{0, 1\}^n\mapsto\{0, 1\} $, 只有被标记的项$ f(m) = $$ 1 $, 对于任意的$ x \neq m, \ f(x) = 0 $. 我们的目标是用最少的询问神谕(oracle)次数来找到这个标记的项目m. 对应到绝热量子计算, 可以将初始哈密顿量写成$H_{\rm{b}} = \mathbb{1}-|\psi_0\rangle \langle \psi_0 |$, 以及问题哈密顿量$H_{\rm{p}} = \mathbb{1}-|m\rangle\langle m|$, 其中$|\psi_0\rangle = 1/\sqrt{2^n}\displaystyle\sum\nolimits_{i = 0}^{2^n-1}|i\rangle$, $ |m\rangle $为某一个被标记的态. 在这样的哈密顿量构造下, 如果将演化路径简单地选择为$ s = t/T $, 其中的最小能隙出现在$ s = 1/2 $:

$ \varDelta_{\min} = \varDelta(s = 1/2) = \frac{1}{\sqrt{N}} = \frac{1}{\sqrt{2^n}}. $

由绝热定理条件可知, $T\gg1/\varDelta_{\min}^2\sim O(2^n))$^[47], 这与经典搜索算法的复杂度一致. 所以在绝热量子计算中简单地选择线性哈密顿量演化路径不会使得Grover搜索问题具有量子加速. 而在如此编码下, 研究表明: 可以解析地优化哈密顿量演化路径以使得上述Grover搜索问题在绝热量子计算中依旧具有平方的量子加速^[66].
3 -->

2.2.3.基于绝热量子计算的3-SAT算法

布尔可满足性问题(Boolean satisfiability problem)中含有n个布尔变量$ z_i $, 由其组成了一系列子句 (clause) $ C_\alpha $, 其中每一个子句$ C_\alpha $内都含有k个变量并以“或”($ \vee $)连接, 如: $C_\alpha = $$ ( b_1\vee b_2\vee\dots\vee b_k)$, 其中$b_i\in\{z_1, z_2, \cdots, z_n, \neg z_1, $$ \neg z_2, \cdots \neg z_n\}$. 最终我们希望找到一串布尔变量$ z_i $, 使得所有用“与”($ \land $)连接的子句都得到满足, 即:

$ \varPhi \equiv C_1 \land C_2 \land\dots\land C_r = 1. $

如果每个子句中有相同变量个数$ k = 2 $, 这类问题称作2-SAT. 这类问题可以在经典计算中有效地被解决, 归属于复杂类P. 而对于$k\geqslant3$的情况, 这类问题都是NP-complete问题, 它们可以在多项式时间内互相转化. Farhi等^[22]提出绝热量子计算时就尝试对3-SAT问题进行测试. 为了构造3-SAT问题哈密顿量, 我们举例一个涉及三个布尔变量$ z_{i_C}, z_{j_C}, z_{k_C} $的子句C, 并且对此定义一个经典的能量函数:

$ \begin{split}&h_C(z_{i_C},z_{j_C},z_{k_C}) \\=\;& \left\{ \begin{aligned} &0, \quad{\text{如果}} z_{i_C},z_{j_C},z_{k_C} {\text{使得子句}}C{\text{满足}} ; \\ &1, \quad{\text{如果}} z_{i_C},z_{j_C},z_{k_C} {\text{使得子句}}C{\text{不满足}}.\end{aligned} \right. \end{split}$

定义$h(z_1, z_2, \cdots, z_n) = \sum_C h_C$并且将其在以泡利Z算符本征矢为计算基下对角化成量子算符形式的问题哈密顿量$H_{\rm{p}}$, 也就是对应于:

$ H_{\rm{p}} |z_1\rangle|z_2\rangle\dots |z_n\rangle = h(z_1,z_2,\cdots,z_n)|z_1\rangle|z_2\rangle\cdots |z_n\rangle. $

于是, 这就将3-SAT问题的解编码到了$H_{\rm{p}}$的基态上.
3 -->

2.2.4.基于绝热量子计算的质因数分解算法

质因数分解问题是希望将一个大数N分解为两个质因数p和q, 也就是实现$ N \rightarrow p \times q $的分解. RSA公钥加密体系的安全性正是基于当前经典算法无法在多项式时间内求解质因数分解问题. 在经典计算领域, 大家尝试了求解该问题的不同方法, 如基于启发式算法的设计^[67], 机器学习方法^[68,69], 以及仿生算法^[70,71]和随机架构算法^[72]等. 而在量子计算领域, Shor算法可在多项式时间内解决质因数分解问题^[5]. 但Shor算法对量子比特数量和门的保真度要求很高, 在目前的实验条件下^[73], 还只能在比较小的数字上做分解^[9,74]. 另一方面, 近些年大家对在绝热量子计算中实现质因数分解也做了大量工作^{[75,76,47,77,78,55]}. 在绝热量子计算质因数分解问题中, 构造问题哈密顿量一般有两种主要方式. 一种是直接将问题写成损失函数$f_{\rm{cost}} = $$ (N-p \times q)^2$^[79], 为了避免其中耦合强度出现指数增长, 人们提出了另一种基于乘法表的损失函数构造方法^[77]. 其中, 通过将二进制数映射为泡利算符, 继而引入额外的量子比特将高阶耦合项降到二阶, 人们可以将这一问题约化到前文提到的QUBO问题, 并得到相应的问题哈密顿量.
2 -->

2.3.绝热量子计算与BQP复杂类

自从Shor^[5]提出质因数分解的多项式算法以来, 量子计算领域获得了更广泛的关注, 也涌现出许多不同新的研究方向. 然而不同于量子计算复杂度理论、量子密码学以及量子纠错等领域的快速发展, 量子算法设计作为量子计算研究的核心问题之一, 特别是设计出相比经典算法具有指数加速的量子算法, 并没有如人们想象中那样顺利推进. 对于这一现象, Shor^[16]指出, 一个可能的原因, 是由于人们没有像设计经典算法一样好的直觉设计量子算法. 而找到能充分展现量子计算机超越经典计算机能力的BQP问题具有十分重要的现实意义.
在计算复杂度理论中, BQP问题是指在量子计算机上存在多项式规模的量子线路并且出错概率小于1/2求解的一类判定问题(decision problem)^[80], 简言之, 就是能在量子计算机上在多项式时间内求解的问题. 与其类似的经典计算问题是BPP(bounded-error probabilistic polynomial time)问题, 它被定义为能在多项式时间内被概率图灵机以有界的错误率求解的判定问题. 虽然在具体问题中, 如质因数分解^[5]、二次符号权重计数问题(quadratically signed weight enumerator problem)^[81]、琼斯多项式估计(approximation of Jones polynomials)^[82,83], local Hamiltonian本征值采样问题(LHES)、相位估计采样问题(PES)、酉矩阵平均本征值估计(LUAE)^[84]等问题上量子计算可以做到指数加速, 但BQP计算复杂类的边界仍然是未解决的理论问题. 在量子计算机上可以高效解决的问题仍有待进一步探索.
前文提到, 由于人们缺少量子世界观以及量子线路模型难以提供好的算法设计直觉, 那么绝热量子算法会是寻找BQP问题的一条途径. 量子线路模型被证明能以多项式量级的步骤转换为一个绝热量子算法^[25]. 因此利用量子线路模型定义的BQP问题, 也可以等价地在绝热计算机上定义. 若对于要求解的问题有已知的量子线路算法, 那么可以根据已知的线路模型中的一系列门操作构造出初始哈密顿量和问题哈密顿量, 使得问题哈密顿量的基态为历史态$\dfrac{1}{\sqrt{L+1}}\displaystyle\sum\nolimits_{l = 0}^{L} |\alpha(l)\rangle\otimes|1^{l}0^{L-l}\rangle$, 其中$ |\alpha(l)\rangle $表示原来的线路模型中每个时刻对应的逻辑态, $ |1^{l}0^{L-l}\rangle $是标记演化时刻的时间态. 于是原本线路模型中的求解过程转换成为寻找问题哈密顿量的基态. 这个转换过程花费的步骤呈多项式增长. 在线路模型中, 质因数分解问题^[5]就是一个典型的BQP问题. 通过绝热量子算法判定的BQP问题也有典型的例子, 如胶合树问题^[85]. 如果机器学习方法可以辅助设计绝热算法, 就有望通过这种方式找到更多的BQP问题, 进而探索BQP复杂类的边界.

本节将首先对机器学习的几个方向及其在经典算法设计中的应用做简要介绍. 而后介绍量子与经典组合算法以及机器学习在量子控制中的应用.
2

-->

3.1.机器学习分类

1956年的达特茅斯会议中, “用机器来模仿人类学习以及其他方面的智能”的观点被首次提出^[86]. 机器学习往往面对的是大量的数据, 通过学习来拟合出其中的复杂关系. 我们期待机器能自行学会数据中的关联, 并能给出符合人类逻辑认知甚至超越人类能力的预判. 近些年来, 机器学习在图像识别^[87]、自然语言处理^[88]以及策略游戏^[89]等方面表现出令人称叹的能力, 其中非常值得一提的就是误差逆传播算法(error back propagation)^[90]在多层神经网络中的应用. 一个多层神经网络可被分为输入层、隐藏层和输出层, 其中每一个隐藏层和输出层的神经元中都含有激活函数(可被激活或抑制来模仿生物的神经元机能). 在训练时我们将信号逐层向前传递直到输出层, 而后将误差逆传递来更新权重. 我们期待训练好的网络会有很强的表示能力与泛化能力. 也即是, 对于一个完全陌生的输入数据, 网络也能给出符合预期甚至超越人类认知的判断. 机器学习的方法主要有三大类^[91]: 监督学习、无监督学习和强化学习. 监督学习中具有代表性的是处理“分类”和“回归”问题. 需要给机器大量的带标签数据. 机器通过学习数据特征和标签的关联, 获得对新数据进行预测的能力. 如果预测的结果是离散的, 就属于“分类”; 如果预测的结果是连续的, 就属于“回归”. 对于无监督学习, 给机器的是不带标签的数据, 也就是希望机器能够自己发现数据之间的共同特征, 将相关的部分归为一类进行“聚类”. 强化学习^[89]则是让智能体与环境进行有探索地交互来训练获得最大奖励. 智能体在某一个状态$ s_t $下根据策略做出动作a, 并且获得环境的奖励r, 到达下一个状态$ s_{t+1} $. 其中的会用到Q值来表示在某个状态下做不同动作的未来奖励的估计. 对于像围棋这样的游戏, 状态空间会随着格点个数指数增长. 考虑到要存下这么多状态空间需要大量内存, 在近期的强化学习中都采用了神经网络的强大表示能力来表示Q值. 在人类专家知识输入不断减少的情况下, 强化学习智能体在策略游戏中依旧表现得非常出色^[92–95].
2 -->

3.2.机器学习在经典算法设计中的应用

随着经典算法设计变得越来越复杂, 机器学习也被用在设计经典算法上. 1976年Rice^[31]就提出了“算法选择问题”, 他将“算法选择问题”与“没有免费午餐定理”^[96]相提并论—对于任何算法, 想要其表现好于其他算法就必须付出代价. 换句话说, 即没有一个普适的最好算法来解决一大类问题. 在面对拥有多种求解算法的一类问题(特别是NP-hard问题)中, 不同问题实例的求解效果不尽相同. 如何挑选出其中最好的算法就显得非常关键^[97]. 下面通过回顾在经典领域的自动化算法设计, 期待能对量子算法的设计有一些启发.
在早期工作中, 人们通过将算法选择问题映射为马尔科夫决策过程, 利用强化学习选择算法来使得算法运行时间最短^[98]以及并行不同算法加速求解组合搜索问题^[99]. 为了预测不同算法在具体问题求解中的所需时间, 需要根据人类专家知识预先选择出可能影响问题计算时间的特征, 将一系列问题的特征和和真实算法所需运行时间作为数据集, 通过学习利用回归方式预测每个算法在具有某些特征的问题上求解所需时间^[100,101]. 值得一提的是, 连续多年蝉联SAT比赛冠军的SATzilla^[102]在处理3-SAT问题时会利用预设的求解算法在短时间内求解那些简单的问题实例. 而对于那些没有在短时间内被求解的问题实例, 其将根据问题特征来挑选出预测的最好算法进行求解. 曾经用于分类的元学习(meta-learning)也被运用到算法选择中^[103], 不同的机器学习方法在算法选择问题上的表现也得到了评估和对比^[104]. 机器学习在推荐系统(特别是在购物网站)中的成功应用也推动了自动化算法推荐系统的出现^[105].
与算法选择问题相应的, 算法本身就具有许多可被调整的参数. 手动对大量的参数进行“调参”不仅费时也非常依赖于专业知识. 算法构型的设计^[32]就是在高维参数空间中选择出最佳的算法构型参数. 目前已开发的一系列算法构型设计工具包^[106–109]都可以给出优化的固定参数算法构型. 但人工智能算法在计算过程中需要不断迭代, 最佳的算法参数一般会随着整个程序运行的时间而发生变化. 为此, 利用强化学习^[110]以及基于启发式算法^[111]的动态算法构型设计框架也被提出.
算法选择问题是希望获得一个选择机制以在面对新的问题实例时挑选出最佳的算法, 而算法构型设计是对算法本身的参数做优化. 在经典计算算法设计上人们也有将两者进行融合^[112]以获得对困难问题的高效计算.
2 -->

3.3.量子与经典组合算法

量子算法的设计与研究并不是一蹴而就的. 在研究与设计量子算法的过程中, 人们也会将经典算法中的一些思想与手段加以利用, 进而设计出量子与经典的组合算法. 一般地, 这些组合算法按照形式可以分为以下两类.
其一是利用量子系统具有的优越性来实现一些经典算法, 其中具有代表性的是量子机器学习(quantum machine learning, QML). 量子机器学习领域主要研究如何借助量子系统中的叠加与纠缠等性质来实现经典机器学习算法的加速^[113]. 在机器学习算法中, 有很多算法本质上都可以分解为基于矩阵的一些线性代数运算. 在这些线性代数运算中, 对于傅里叶变换^[5]、寻找矩阵特征值与特征向量^[15]以及求解线性方程组^[114,115]等运算, 都有着相比经典算法有指数或者多项式级别加速的量子算法. 这一系列具有量子加速的线性代数运算(quantum basic linear algebra subroutines, qBLAS)^[113]可以加速许多机器学习领域中的算法, 例如最小二乘法^[116]、梯度下降法与牛顿法^[117]、半正定规划^[118]、主成分分析^[119]、拓扑分析^[120]、支持向量机^[121]等. 在这些机器学习算法的实现中, 为了避免经典数据的输入与读取成为限制算法效率的瓶颈, 量子随机读取内存(quantum random access memory, qRAM)^[122]技术被提出, 并旨在极大地提升数据读取的效率. 量子机器学习的另一大研究领域是利用量子模拟器或可编程量子线路以建立量子深度学习网络(deep quantum learning network)^[123,124]. 基于玻尔兹曼分布的量子玻尔兹曼机(quantum Boltzmann machine)将神经网络表示成为伊辛模型下量子自旋及其间的相互作用, 通过训练和优化过程使得量子系统可以学习到数据的概率分布^[125]. 相较于经典版本, 量子玻尔兹曼机可以更有效地加速训练过程^[126], 同时在自旋相互作用模型的选取上也更具灵活性^[125]. 除此之外, 量子机器学习不仅可以和经典机器学习一样接收经典信息并进行处理, 还可以直接处理量子系统与量子过程产生的量子信息^[113].
其二则是将量子态的制备、演化与测量过程与经典的优化算法相结合, 利用经典计算机调节并优化量子计算过程中的相应参数. 其中具有代表性的算法有量子近似优化算法(quantum approximate optimization algorithm, QAOA)与变分量子本征求解(variational quantum eigensolver, VQE)算法. 量子近似优化算法, 最初由Farhi与Goldstone^[127]在2014年提出, 主要被用于解决一些NP-hard的组合优化问题. 一般地, 量子计算机的演化过程可以用$ 2 p $个幺正算符来描述, 其中p为预先设定的正整数决定量子线路的深度^[127]. 量子近似优化算法利用经典的优化算法调节这些算符, 进而影响对应的量子计算过程, 并通过迭代最终使演化结果能够很好地近似对应组合优化问题的最优解. 量子近似优化算法不仅被证明具有通用计算的能力^[128], 同时还在例如连续优化^[129]、线性代数^[130]等领域中的一些问题中有着良好的表现. 除此之外, 它也被认为具有实现量子优越性的潜力^[131], 并且在谷歌“悬铃木”^[132]、D-Wave 2000 Q^[133]等量子计算硬件上表现出了良好的适配性, 但是该算法的量子计算优势还需要更准确地刻画^[134].
Peruzzo等^[135]在2014年提出的变分量子本征求解算法, 则是为了解决量子化学领域的相关问题. 变分量子本征求解算法借助变分原理, 通过预先拟设(ansatz)来选择量子初态与量子线路, 并在量子演化后利用哈密顿量平均(Hamiltonian averaging)的手段估计能量期望值, 最终利用经典的非线性优化过程优化参数直至寻找到符合要求的近似解^[136]. 尽管理论上传统求解特征值的量子相位估计算法有着很好的性能, 但它对于量子系统的相干性有着很高的要求. 相对地, 变分量子本征求解算法对于相干性的要求大大降低^[135]. 目前, 在不同的量子计算硬件上, 变分量子本征求解算法可以很好地求解$ {\rm{H}}_2 $^[137]、$ {\rm{HeH}}^+ $^[135,138]、$ {\rm{LiH}} $^[139,140]、$ {\rm{BeH}}_2 $^[139] 等分子系统的基态能量问题以及$ {\rm{H}}_2 $^[141] 等分子系统的激发态能量问题.
2 -->

3.4.机器学习在量子控制中的应用

经典最优控制理论通常需要对物理系统建立一个数学模型, 其基本目的是控制系统来根据参考轨迹运动或者根据目标函数优化系统的动力学^[142]. 但如果这个数学模型过于复杂以至于无法解析得到参考路径之时, 那么机器学习就是一个可供选择的方式^[143,144]. 与经典控制类似的量子控制在量子计算与量子信息的应用中起到至关重要的作用, 其核心是控制量子动力学过程向既定的方向(比如特殊的量子态)去演化, 简单来说就是对量子系统的控制^[27].
对于传统的贝叶斯优化, 需要知道系统动力学的知识^[145]. 而在机器学习方法下, 可以将量子系统视为一个黑箱—此时量子控制的策略会根据系统结果的输出, 来近似知道对应的动力学过程^[146,147]. 人们可以利用机器学习在量子计算及量子测量中进行量子调控^[148–153], 实现在高维量子多体系统中的非凸优化^[154,42], 以及利用神经网络对控制脉冲进行设计^[155]等.
近些年, 强化学习在量子系统优化控制中的应用也备受关注. 如在量子线路模型中, 通过在强化学习的环境中加入不同的控制误差来训练优化智能体以实现普适的量子控制^[43]. 另外, 强化学习在实现高保真度目标态的快速制备^[45,156,157]、量子线路优化^[158]、控制非平衡量子热力学过程^[159]以及在量子开放系统中进行最优化控制并与传统优化方法进行对比^[160–162], 结合强化学习与量子绝热捷径技术实现对单个量子比特进行更快更鲁棒地控制^[163,164]等领域得到广泛应用.
机器学习(特别是强化学习)在有噪声的中等规模量子(NISQ)^[73]控制中与传统量子优化方法, 如GRAPE^[165]、CRAB^[166]一并成为了新的一种量子最优化控制方法, 并且能够帮助人们对自旋玻璃物理以及对量子相变物理进行控制, 辅助建立更直观的物理图像^[42,45,167].

本文第2节谈到绝热量子计算的定义, 了解到为了避免出现从基态向激发态的跃迁 (Landau–Zener transition)^[168,169], 原则上需要给系统很长的演化时间. 在绝热量子计算中, 人们通过解析局部优化哈密顿量演化路径, 使系统在最小能隙处降低演化速率来保证不发生跃迁, 并实现了Grover搜索问题的平方加速^[66].
必须要指出的是, 想要在复杂的量子多体系统中做到对整个能谱的全局认知本身就非常困难. 所以对于复杂量子多体体系, 很难解析地知道这些最小能隙的位置来局域地优化哈密顿量演化路径^[170–172]. 而在经典及量子最优化控制部分的介绍中, 我们已经谈到可以尝试将复杂的物理系统看作黑箱, 利用机器学习来获取最优化的控制.
本节将具体介绍我们利用强化学习辅助设计绝热量子算法的一个工作^[173]. 从前文的介绍中了解到绝热量子计算的表现与演化路径密切相关. 在接下来的内容中, 所说的绝热量子算法的设计就对应于绝热演化的路径设计. 我们在第2节中介绍了几个计算问题的哈密顿量编码方式. 而对于给定一个计算问题, 总有不同的问题实例. 如在Grover搜索问题中对不同的目标态的搜索以及在3-SAT问题中不同子句的选择, 这都会使不同问题实例具有不同的答案. 绝热算法设计或者说哈密顿量演化路径设计不能依赖于具体的某一个问题实例. 这也就有别于对具体目标量子态制备^[45]以及实现快速的量子门操作^[174,155,43], 如何学习并自动化设计绝热量子计算中哈密顿量演化路径以使得计算过程体现出量子优势就是一个量子算法设计问题^{[173,175,176]}. 对此, 我们构造了自动化绝热量子算法设计框架, 如图1. 这一框架特别适合对那些很难被求解但容易被验证的问题进行绝热算法设计, 如Grover搜索问题、质因数分解问题、3-SAT问题等等. 在该框架中, 我们参数化哈密顿量演化路径为:
图 1 强化学习辅助绝热量子算法设计的示意图^[173]. 其中强化学习中的智能体(agent)根据绝热量子计算(AQC)输出的结果来获取奖励, 并根据深度神经网络近似表示的Q值表格来选择动作更新绝热量子算法
Figure1. Schematic diagram of the reinforcement learning approach for quantum adiabatic algorithm design^[173]. The learning agent collects the reward according to the result obtained from adiabatic quantum computing (AQC) and produces an action to update the quantum adiabatic algorithm based on its Q table represented by a deep neural network.

$ s\left(\frac{t}{T}\right) = \frac{t}{T}+\sum\limits_{m = 1}^{C} b_m\sin\left(\frac{m\pi t}{T}\right), $

其中C为截断阶数. 当C趋于无穷时, 这样的参数化形式就是完备的. 强化学习中智能体(agent)的状态s为需要设计的哈密顿量演化路径中的全部参数$ b_m $, 称作“路径态”(path state). 智能体的动作a是对路径态中参数$ b_m $的操作, 其根据绝热量子计算机的输出结果对错来获得不同奖励r, 即答案正确奖励为1, 答案错误奖励为0. 强化学习的目标是最大化奖励, 所以通过让智能体从线性路径开始对路径参数进行调整, 也就能优化设计出好的绝热量子算法. 这样的框架就非常适合在D-wave机器^[177]中应用. 值得一提的是, 在训练智能体的时候, 将同一系统规模的大量问题实例一起输入并对最后的表现进行平均, 这样的处理能够让算法设计更为鲁棒.
智能体中深度神经网络近似地表示Q值表格, 并用其来估计当前状态下选择不同动作的未来累积奖励. 在例如围棋游戏中, 智能体的动作是离散的. 而这里通过类似模拟退火的方式连续化了强化学习智能体的动作, 实现了自动化设计具有量子加速的绝热量子Grover搜索算法. 其中固定系统总的演化时间T与系统规模n的关系为$ T = \sqrt{2^n} $. 人们解析地得到了基于第2节中介绍的Grover搜索算法哈密顿量编码方式下的具有量子加速的绝热算法^[66]. 在这一演化时间内, 线性的演化路径会大概率以失败告终. 而利用强化学习自动化绝热量子算法设计框架获得的算法, 其可以在这一演化时间内到达与解析获得的算法^[66]相当的结果(成功概率99.9% 以上), 在过程中甚至有超越解析算法^[66]的表现, 如图2. 通过对系统的能谱以及强化学习得到的路径进行观察, 发现演化路径在能隙最小处变化得最缓慢, 出现了平台^[173]. 这个重要特征与解析结果^[66]是一致的.
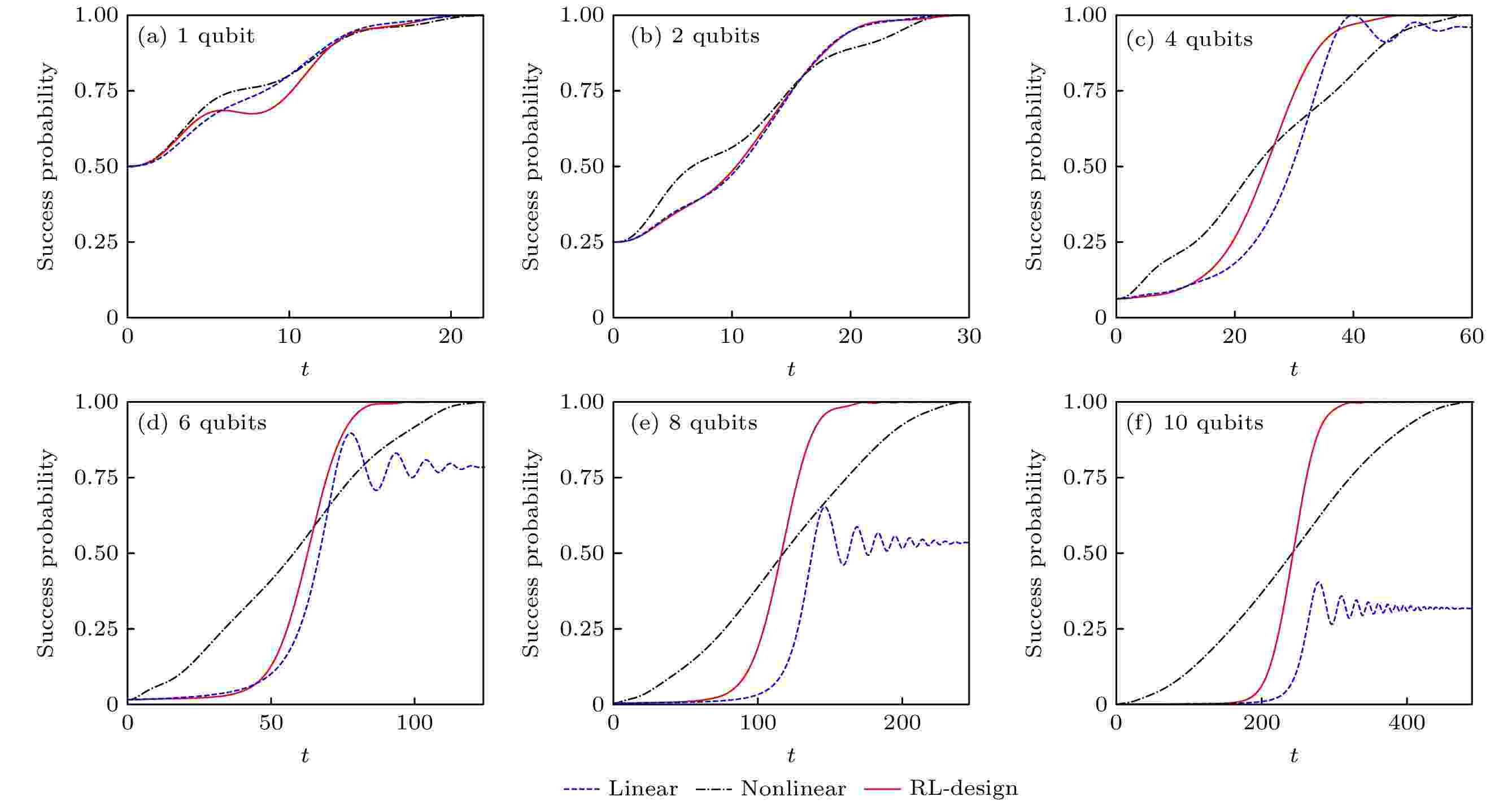图 2 强化学习辅助设计的绝热量子算法在Grover搜索问题上的表现^[173]. 其中成功概率(success probability)是演化终态与目标态交叠的平方, 总的演化时间T与系统规模n的关系为$ T = \sqrt{2^n}$. 图中蓝色虚线表示的线性演化路径成功概率会随着系统尺寸增大不断降低. 红色实线和黑色虚线分别表示强化学习设计得到的演化路径和解析获得的非线性路径^[66]的表现. 在选择的演化时间下, 两者的成功概率都能接近于1, 说明两者都具有平方的量子加速
Figure2. Performance of reinforcement learning designed quantum adiabatic algorithm in success probability for Grover search problem^[173]. The success probability is obtained by taking the square of wave-function overlap of the final evolved quantum state with the target state. The total adiabatic evolution time is chosen as $ T = \sqrt{2^n}$ where n is the system size. The blue dashed line denotes the success probability of linear path which decreases as increasing the system size. The red solid line and black dashed line denote the performance of the reinforcement learning designed path and the nonlinear path^[66], respectively. Given the choice of total evolution time, the success probability close to 1 by both implies that they both exhibit quadratic quantum speed up.

我们测试了强化学习在量子比特数量拓展过程中的表现, 如图3. 其中线性演化路径的结果非保真度(infidelity)增长得很快, 说明其计算表现能力不佳(前文中提到其被证明没有量子加速). 我们测试了将在10 qubits系统强化学习得到的路径直接用到11—16 qubits上, 发现虽然保真度会有下降但这也会比直接用线性路径更好. 而如果将在i qubits系统中强化学习得到的路径用到$ i+1 $ qubits系统并计算其非保真度. 这样拓展具有远超线性路径的表现能力, 其结果的非保真度都接近于1%. 对于另一种实验友好的编码方式, 即如果将初始哈密顿量写成$H_{\rm{b}} = \dfrac12 \displaystyle\sum\nolimits_i[\mathbb{1}-\sigma_i^x]$, 解析的方法^[66]无法得到最优的演化路径, 而基于强化学习的方式依旧可以获得这一具有平方加速的量子算法^[173].
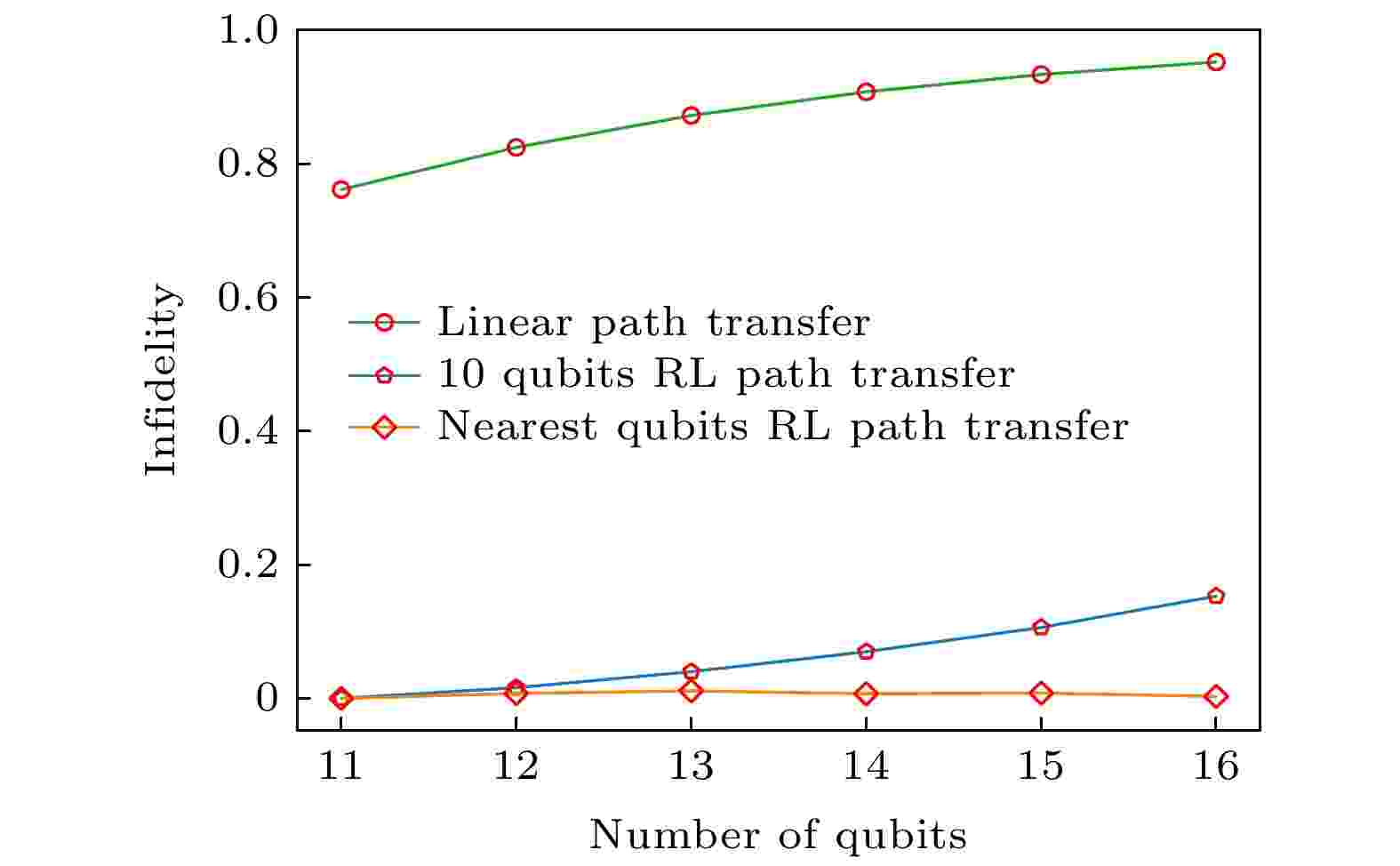图 3 强化学习在Grover搜索问题的绝热量子算法设计中的拓展性^[173]. 其中绿线是线性路径的表现, 蓝线是将10 qubits系统中强化学习学到的路径推广到更大系统, 橘线是将在n qubits系统强化学习获得的路径推广到$ n+1$qubits系统
Figure3. Transferability of reinforcement learning based quantum adiabatic algorithm design for Grover search problem^[173]. The green line denotes the infidelity of linear path. The blue line denotes the infidelity of the path obtained by training the 10 qubits system. The orange line denotes the performance of applying the path learned from the n qubits system to the $ n+1$ qubits system.

在对3-SAT这个NP-complete问题研究中, 我们对10 qubits系统且仅对包含3个子句的问题进行强化学习来获得绝热量子算法. 将这样设计得到的算法直接推广到其他不同子句数量的问题上, 其表现能力与一般的线性演化路径相比具有明显的提升. 这样获得的绝热算法具备一定的可迁移性^[173].
在这个工作中^[173], 我们利用强化学习优化设计了参数$ s(t) $. 也可以将其推广, 将初始哈密顿量和问题哈密顿量前的参数在保证边界条件下分别优化. 有研究表明, 这样的分别优化会有更好的表现^[178,179]. 人们也考虑在演化过程中设计加入额外的哈密顿量, 并且让这些额外的哈密顿量在初始和结束演化时关闭来提升绝热量子计算的能力^[180,172,47]. 此外, 强化学习在自动化设计优化量子线路^[181–183]、完成在量子模拟中的哈密顿量构造^[184]、优化量子纠错码^[185]、优化数字量子模拟^[186]以及容错量子计算^[187]等量子计算方面也有广泛应用.

量子计算因其具有超越经典计算的优势而受到高度关注. 其中量子计算算法的设计开发与量子计算的硬件实现都至关重要. 本文对绝热量子计算、机器学习及其在经典算法设计中的应用做了回顾, 介绍了机器学习, 特别是强化学习在量子最优化控制中以及绝热量子计算算法设计中的具体应用. 我们看到了机器学习在设计经典算法和求解量子多体物理上的成功应用, 也期待机器学习能够对复杂且违反经典直觉的量子算法设计提供更多帮助. 这不仅能够更好地将量子计算优势挖掘出来, 量子计算的计算优势也能更有力地加速机器学习对大量数据的处理. 我们预期量子计算与机器学习的交融会给这两个领域带来新的契机和突破.