摘要:超表面可以对入射光场的相位、偏振、幅度等自由度进行精确调控, 为发展下一代基于量子态片上实验平台提供了一种新途径, 具有重要的应用前景. 本文提出了一种新型的超表面结构, 即具有不同占空比的硅结构光栅单元构成的超透镜, 在焦平面上可形成聚焦光环. 研究了在焦平面上环形光场的强度分布和不同数值孔径超透镜的聚焦特性. 采用这种超透镜聚焦光环来构建一个氟化镁(MgF)分子的光学存储环, 计算了MgF分子在聚焦光场中所受的光学势和偶极力, 对MgF分子束在存储环运动过程进行了Monte-Carlo模拟. 研究结果表明, 设计的超表面结构具有很好的聚焦特性, 聚焦光环的光场强度比入射光增强了55.1倍; 同时可以实现对MgF分子的装载并囚禁在表面存储环内.
关键词: 超表面/
超构透镜/
光学囚禁/
光栅

English Abstract

全文HTML

--> --> -->

超表面是由亚波长厚度的阵列单元构成的二维平面材料. 通过调整每个单元结构的几何参数, 如形状、大小和旋转角度, 能够独立地与电场和磁场分量相互作用, 进而实现对入射光的相位、振幅、偏振、角动量等特性的有效操控^[1-3]. 目前采用超表面结构相继成功研制了各种新颖的类似于普通光子学中的透镜、反射镜、波导、光栅和偏振调控等光学元器件. 其中超透镜的设计和应用吸引了极大的关注^[4-12]. 超表面单元在亚波长尺度上对光的相位、偏振态、色散等属性有着独特响应, 而且可以抑制高阶衍射光, 2016年哈佛大学Capasso教授小组^[5]首先报道了可见光波段的超透镜, 这种透镜具有亚波长分辨成像功能和高效聚焦的特性, 可以与当时最好的商用物镜相媲美. 2017年南京大学祝世宁和台湾蔡定平联合研究小组^[6]将聚焦效应和色差效应的相位组合在一起, 实现了在近红外波段的宽带消色差反射型超透镜. 2018年, 在可见光波段的, 透射型的连续宽带消色差超构透镜也被Wang等^[7]和Chen等^[8]实现了. 随后多功能的超透镜及应用被相继报道.
超冷原子实验装置的微型化一直受到传统光学元件(如反射镜、透镜、分束器等)的尺寸所约束. 超表面可以对入射光场进行多自由度精确调控, 相比较于由微结构金属线和磁性薄膜构成的原子芯片来说, 超表面光学原子芯片可以为发展下一代基于超冷原子及其量子态片上实验平台提供新方法和新思路, 具有重要的应用前景^[13-16]. 为了达到光学系统体积小和功耗降低的目的, 几种基于超表面的微型原子磁光阱(magneto-optical trap, MOT)方案被报道^[17-22]. 英国Arnold小组最早采用超表面光栅结构来研究反射式原子MOT, 2013年他们报道了超表面光栅原子MOT实验, 对于圆形光栅结构, 可以囚禁6 × 10⁷个铷原子^[17]. 2020年, 南方科技大学李贵新小组^[20]也报道了超表面透射式原子MOT的方案, 一束左旋圆偏振激光透过原子光学芯片被分为五束右旋圆偏振态可控的光束, 将所有反射光束在四极磁场的中心相交, 形成了一单束原子MOT, 捕获的铷原子数为10⁷个, 原子温度约35 μK. 超表面原子MOT可以应用于便携式的冷原子钟^[22]. 最近, 笔者课题组^[23,24]也提出了利用超透镜的会聚光场来实现MgF分子的光学囚禁的方案. 综上所述, 目前的超透镜都是将反射光束或者透射光束会聚到一个焦点上, 对于在其焦平面上形成一个聚焦光环的方案还没有报道. 聚焦光环可以构建适用于冷分子囚禁的光学储存环, 囚禁在储存环内的分子可以与激光场或者分子之间不断地相互作用, 因此分子储存环给冷碰撞提供了很好的实验平台. 与电场或磁场的储存环(原子芯片)相比, 纯光学储存环不需要考虑分子的极性(电偶极矩)和顺磁性(磁偶极矩)等特性, 任何分子都可以进行光学囚禁^[25,26].
本文提出了一种超透镜结构, 在焦平面上可形成聚焦光环. 首先, 介绍了这种超透镜的设计原理, 研究了在焦平面上环形光场的强度分布和有不同数值孔径的超透镜的聚焦特性. 其次, 采用超透镜聚焦光环来构建一个MgF分子的光学存储环, 计算了MgF分子在聚焦光场中所受的光学势和偶极力, 采用Monte-Carlo模拟方法对存储环中MgF分子的运动动力学过程进行了研究.

2

-->

2.1.周期性单元结构的设计

超表面对电磁波的相位调控分为以下几种方式: 传输型相位、几何型相位、电路型相位等. 本文主要应用传输型相位来设计超表面存储环, 电磁波通过在传输过程中产生的光程差来实现相位调控, 用公式可以表示为

$ \phi =\frac{2{\rm{\pi }}{n}_{\rm{eff}}d}{\lambda }, $

其中, λ, d, n_eff分别表示入射光波长、光学器件不同位置的厚度及该位置的有效折射率, ?即为该位置对应相位调控大小. 传统的光学器件主要通过改变器件的厚度d来实现对于光程的调控, 传输相位型超构表面近乎二维平面, 为了工艺制造上可行, 一般使器件保持厚度d不变, 通过改变不同位置的有效折射率n_eff来实现对相位的累积. 而有效折射率n_eff的改变一般是通过在折射率较低材料的衬底上构建折射率较高材料的微结构, 通过改变不同位置微结构的形状和结构参数来影响共振进行调控的.
图1(a)展示了本文设计的超构表面所应用的周期性结构单元, 其衬底采用SiO₂材料, 上面生长Si材料微结构. SiO₂衬底的晶格周期宽度设为P, 上面的Si柱宽度设为W, 高度设为H. 改变晶格单元上的Si柱的结构即可调控超表面该位置的有效折射率n_eff, 进而实现对入射光波前相位的调控. 要实现波导效应, Si柱高度需要满足一定的条件使其对相位的调控覆盖2π的相位范围. 入射光波长为1064 nm, 硅柱高度需要半个波长左右, 经过仿真扫描不同范围的结构参数, 把高度H设置为480 nm. 图1(b)和1(c)给出了晶格宽度P和硅柱宽度W分别与透射率之间的变化规律. 纵坐标为占空比, 定义为硅柱宽度W与晶格宽度P的比值, 即占空比(duty cycle) = W/P. 仿真模拟采用时域有限差分法(finite difference time domain, FDTD)进行扫描.
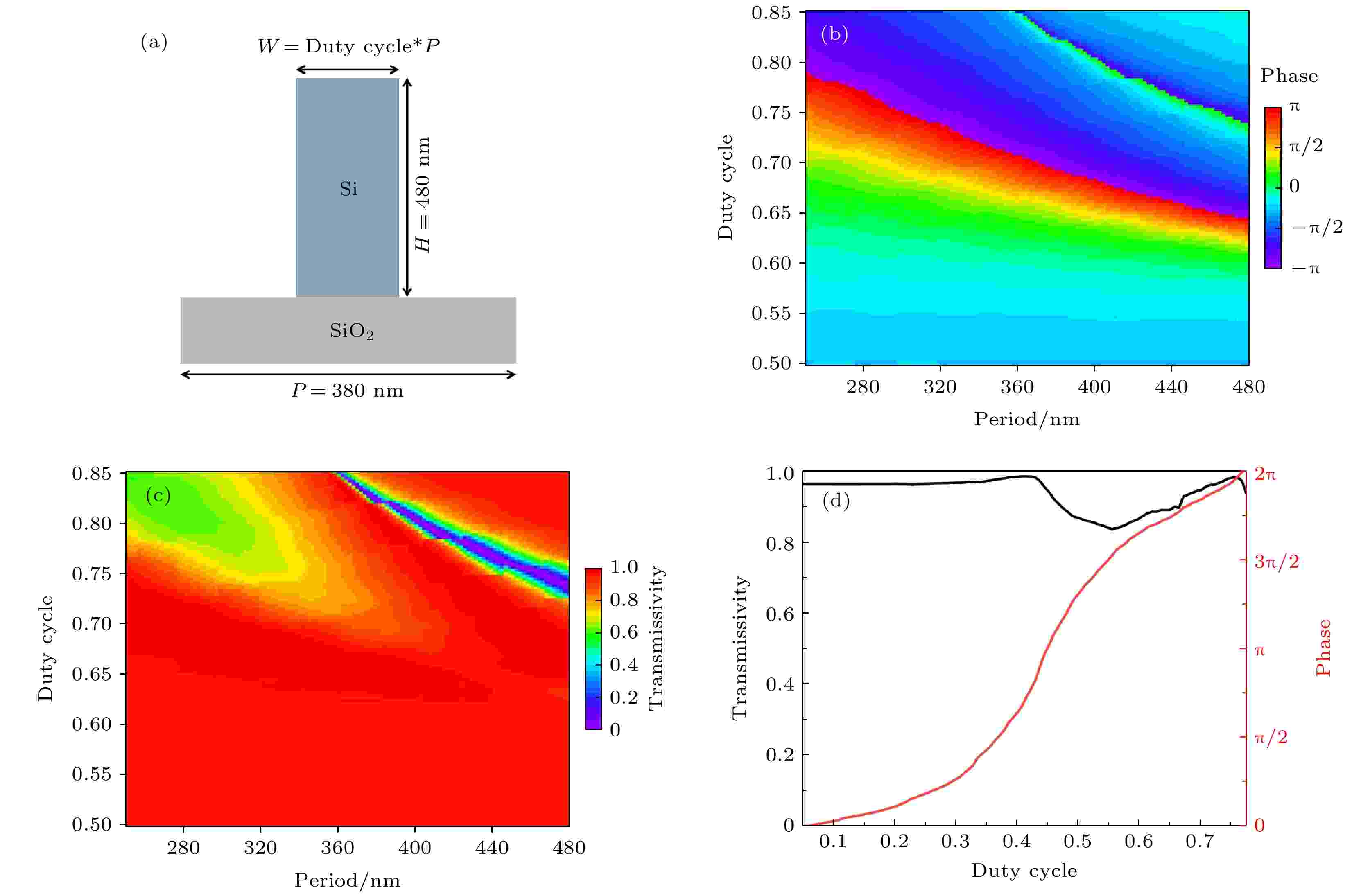图 1 (a)单元结构的示意图, Si柱宽度为W, 高度为H, SiO₂基底的在周期为P; (b)和(c)分别表示扫描单元衬底周期和占空比得到的相位、透射率二维图; (d)当P = 380 nm时, 相位和透射率分别与占空比之间的关系, 黑色实线为透射率曲线, 红色实线为相位变化曲线
Figure1. (a) Schematic diagram of the unit structure, the width of the Si column is W, the height is H, and the period of the SiO₂ substrate is P; (b) and (c) represent the two-dimensional diagram of the phase and transmittance obtained by scanning the period and duty cycle of the unit structure, respectively; (d) when P = 380 nm, the dependence of the phase and transmittance on the duty cycle, respectively, the black solid line is the transmittance curve, and the red solid line is the phase change curve.

为了设计超平面环形透镜, 单元结构对于相位的调控不仅要覆盖2π相位范围, 而且还要具有高透射率. 从图1(b)中可以看出, 当占空比从0.05变化到0.8, 图中周期P大于340 nm区域的颜色变化范围覆盖了全色域, 即选择这个区域的结构参数可实现对于相位调控0—2π范围的全覆盖, 同时满足图1(c)中接近红色的高透射率区域即可完成对于周期P的筛选. 最后把周期P = 380 nm作为一个优化的选择, 改变硅柱宽度W的仿真结果如图1(d)所示, 红线表示当光栅的占空比从0.05变化到0.75, 相位覆盖了2π的范围, 黑线表示占空比变化的时单元结构保持着大于80%的透射率. 这样确定了周期性单元晶格的结构参数: P = 380 nm, H = 480 nm, 占空比范围在0.05—0.76, 用于调控传输相位.
2 -->

2.2.超表面储存环的设计

超表面光学储存环设计本质上就是在芯片表面形成环形光场, 也就是设计超表面环形透镜, 如图2(a)所示. 光束入射到平面环形透镜, 在其焦平面上形成聚焦的光环. 设计原理是在一条半径方向上的光栅阵列的相位排布能将入射光会聚到焦平面, 这样的一维光栅阵列结构旋转一圈扩展成二维光栅圆环阵列就能将径向入射光在每个半径方向上汇聚至焦平面, 最终形成聚焦光环.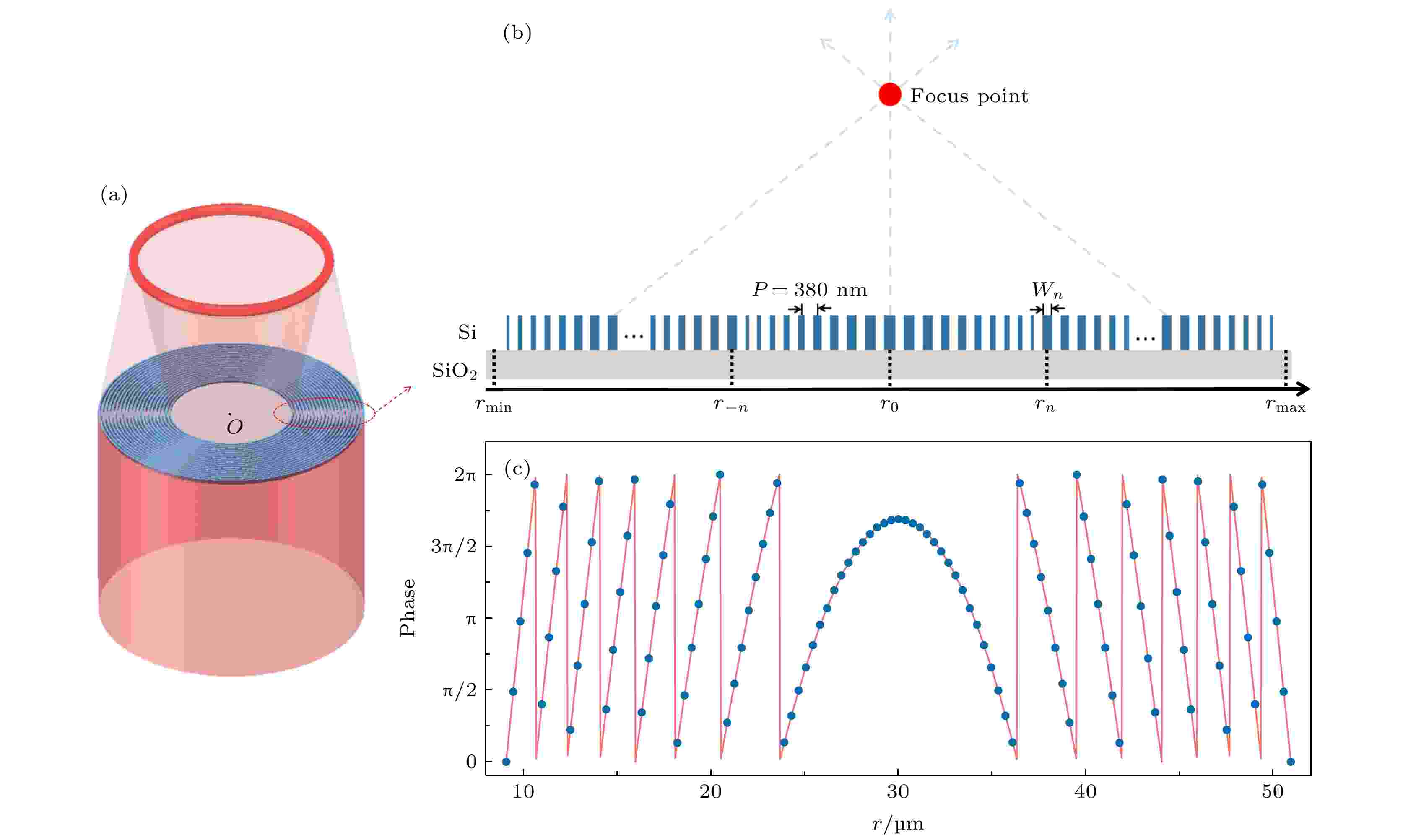
图 2 超表面环形透镜设计原理图　(a)超表面环形光场形成的原理图; (b)半径方向截面光栅排布结构示意图; (c)当焦距f = 22 μm时, 对应的相位分布图, 红色实线为所需相位曲线, 蓝色原点为单元结构实际所需的分立相位值
Figure2. Design principle diagram of the metasurface ring lens: (a) Principle diagram of the formation of the ring light field; (b) layout structure diagram of the cross section of the half grating; (c) corresponding phase distribution for f = 22 μm, the red solid line is the required phase curve, and the blue dot is the discrete phase value required by the unit structure.

图2(b)是半径方向的光栅截面示意图, 为了会聚这个方向上的入射光, 通过光栅阵列表面的透射光相移需要满足凸透镜相位分布方程. 设计的光栅阵列由111个单元构成, 除中心单元外左右各55个单元对称分布, 单元结构中心位置坐标和对应每个单元结构需要对应的相位大小需要满足的公式如下:

${r_{n + 1}} = {r_n} + P,$

${\phi _n} = - \frac{{2{\rm{\pi }}}}{\lambda }\left[ {\sqrt {{{({r_n} - {r_0})}^2} + {f^2}} - f} \right],$

式中, r₀为最中间位置的单元结构中心对应位置, r_n为从中间开始右数第n个单元结构中心位置对应坐标, f为设定的焦距, λ为设置的入射光波长, ${\phi _n}$即为求得的中心位置在r_n坐标上的单元结构所需要的相位值. 由于对称性要求, r_-n位置上的单元结构所需相位值和r_n相同. 以焦距为f = 22 μm为例, 按照(2)式和(3)式算出了每个光栅单元所需的相位分布, 把中心位置坐标r₀设置为30 μm, 如图2(c)所示, 红色实线为所需的连续相位曲线, 表示形成透镜所需的相位在0—2π之间往复. 当相位大于2π时, 可以将其映射为0到2π之间的等价值, 因此图2(c)中红色曲线呈锯齿状, 每个锯齿对应一个不同的2π周期. 蓝色圆点表示111个单元结构实际对应的分立的相位值, 这样根据图1(d)的相位、占空比对应曲线, 就能获得每个位置上的单元结构对应的占空比, 进而得出每个单元结构对应的Si结构宽度W_n, 从而获得设计整个光栅阵列所需的结构参数. 这样设计好的一维结构光栅阵列在二维上扩展成圆环阵列, 能够改变入射光波前相位, 使其在超透镜表面形成环形焦线. 最终设计的超透镜内径r_内 = 9 μm, 外径r_外 = 51 μm, 宽度R_w = r_外 – r_内 = 42 μm, 把超透镜的数值孔径定义为NA = sin(tan^–1(R_w/2f), 预期的焦点在f₀ = 22 μm, r₀ = 30 μm位置, NA = 0.69.

使用全场有限元模拟(COMSOL multiphysics)对设计好的超表面光栅阵列进行仿真模拟. 入射光为1064 nm径向偏振光. 最后对网格进行划分, Si柱排布区域网格划分最密集, 最小单元长度为λ/22, 约为48 nm, 其他部分最大单元长度为λ/10, 约为106 nm. 图3(a)为仿真得到的焦平面的二维光强分布图, 光环半径定义为环形光强最大位置距原点的距离, 即光学储存环的中心半径, 中心半径的设计值r₀ = 30 μm, 模拟光场获得的中心半径${r'}$ = 29.3 μm, 误差率约为2%. 图3(b)为焦平面上对应的一维光强度分布图, 可以看出相对与入射光强度, 聚焦光环的光强度最大值为55.1, 也就是说可以焦平面上的光强度比入射光强度增强了55.1倍. 焦点处光强度分布的半高全宽FWHM = 0.8 μm. 图3(b)中的2张插图为焦平面上的二维光强度分布图. 焦距的设计值f₀ = 22 μm, 实际值${f'}$ = 22.4 μm, 误差率为1.8%. 实际的${r'}$和${f'}$与实际值都稍有差别的原因分析主要有两点: (1)超透镜相位改变是分立的单元阵列, 相位改变不连续, 造成了一定的误差; (2)当超透镜由一维旋转扩展成二维时, r₀内外的超表面面积不同.
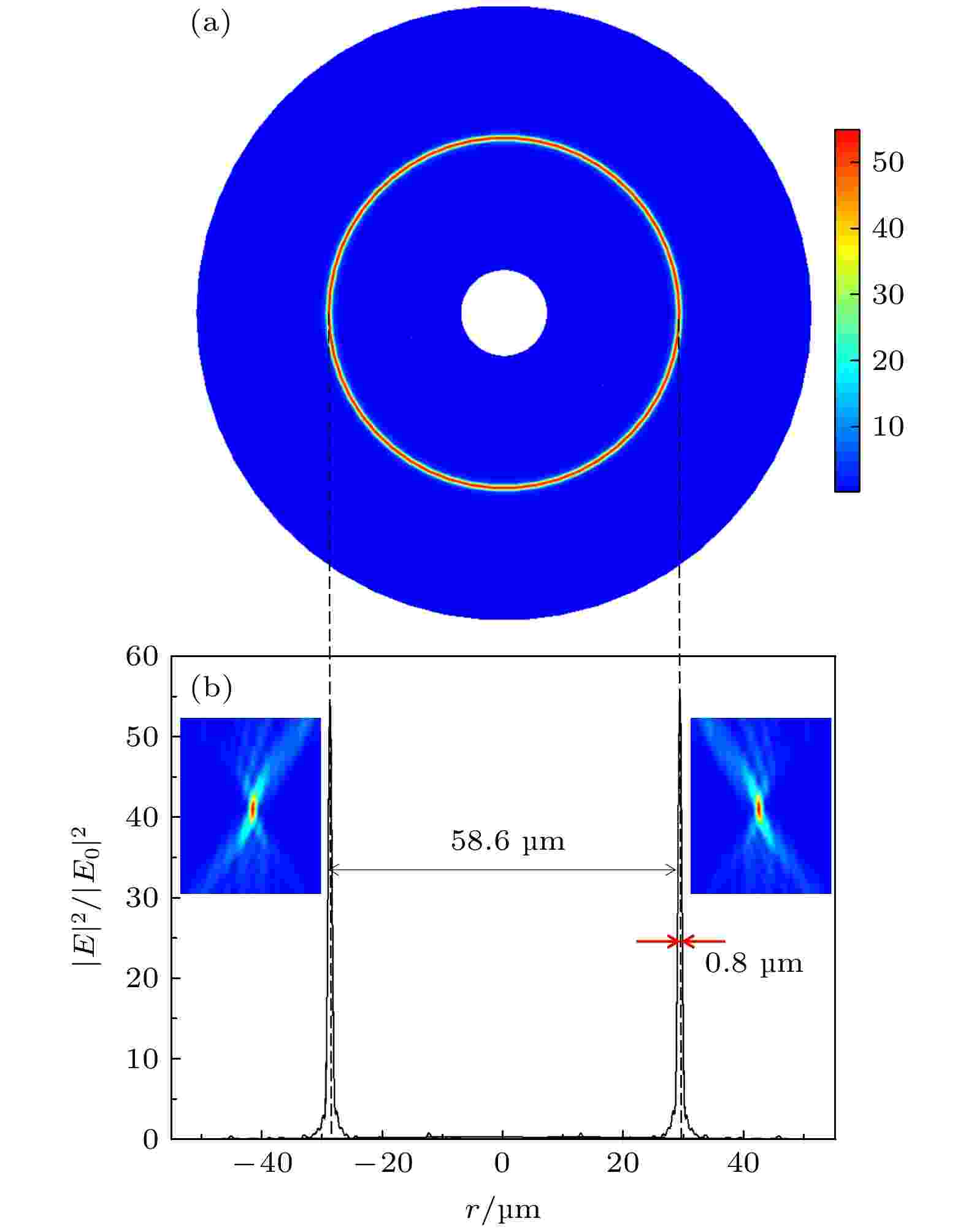图 3 超表面环形光场的光强分布　(a)焦平面上二维光强度分布; (b)焦平面上一维光强度分布
Figure3. Intensity distribution of ring light field on the metasurface: (a) Two-dimensional intensity distribution on focal plane; (b) one-dimensional intensity distribution on focal plane.

接下来讨论具有不同数值孔径(NA)的超表面环形透镜的聚焦特性. 根据2.2节的方法设计了多种数值孔径的超表面环形透镜的结构. 当芯片宽度R_w = 42 μm, 把焦距设计半径f由34 μm变化到6 μm, 对应的数值孔径NA由0.52变化到0.96. 不同数值孔径时焦平面上相对光强最大值如图4所示. 图4中的插图为对应点的二维光强分布图. 当f = 34 μm, 即NA = 0.52时, 焦点位置最大相对光强|E|²/|E₀|² = 46.8, 二维光强分布图最长和最短半高全宽大小为(6.2 μm, 0.8 μm). 当f = 13 μm, 即NA = 0.85时, 相对光强|E|²/|E₀|² = 56.2, 对应的光强度图最长和最短半高全宽为 (2.0 μm, 0.8 μm). 当NA增大逐渐要突破衍射极限, 光强也开始慢慢减弱, 当f = 6 μm, 即NA = 0.96时, 相对光强|E|²/|E₀|² = 33.4, 对应的光强度图最长和最短半高全宽为1.37 μm和0.8 μm. 可以看出, 焦平面聚焦光环的最大光强度的大小随着超透镜焦距的减小出现先增大然后再变小的趋势; 而且焦平面上光斑的水平方向的尺寸不随数值孔径的改变而发生变化, 竖直方向的尺寸随着数值空间的增大而减小.
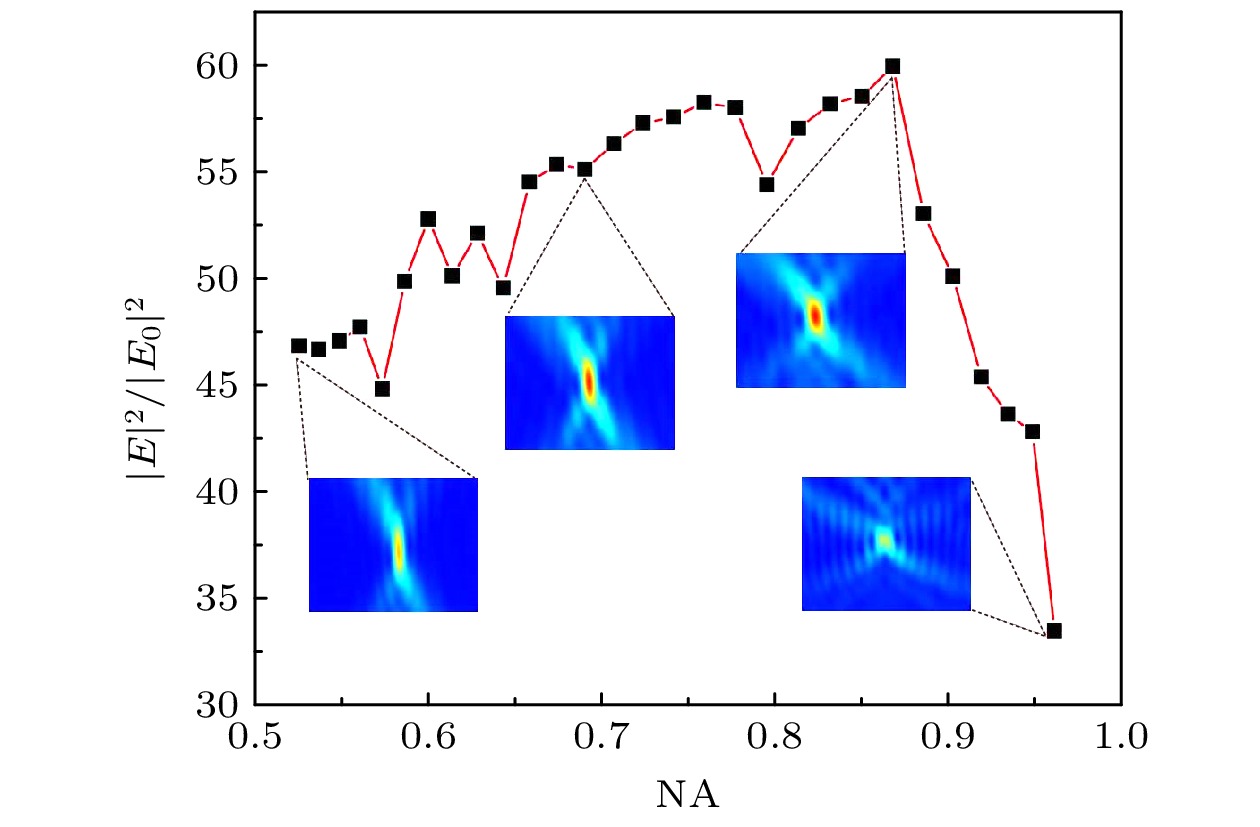图 4 数值孔径NA对焦平面上聚焦光环的最大光强的影响
Figure4. Effect of numerical aperture NA on the maximum intensity of the ring light field on the focal plane.

当中性分子在非均匀激光场中运动时, 分子将被感应出一个电偶极矩, 从而因受到激光场的偶极相互作用而改变分子的运动状态. 当光场为蓝失谐时, 相互作用势为排斥势, 分子被推向光强最弱处; 当光场为红失谐时, 相互作用势为吸引势, 分子被吸引到光强最强处. 本文设计的这种具有强聚焦能力的超表面环形透镜可以为囚禁冷分子提供足够大的光学囚禁势. 超表面透镜在焦平面形成一个聚焦的点时, 可以形成一个冷分子红失谐光阱. 如果在焦平面形成聚焦光环, 就可以形成一个冷分子红失谐的环形光阱, 也就是冷分子储存环.
当中性分子在激光场中受到交流Stark效应时, 受到交流电磁场和光学偶极力的相互作用, 其相互作用势为^[23]

$I(r) = \frac{1}{2}\sqrt {\frac{{{\varepsilon _0}}}{{{\mu _0}}}} \left| {E \cdot E} \right| = \frac{1}{2}c{\varepsilon _0}{\left| E \right|^2}, $

$\begin{split}\;& {U_{{\rm{dip}}}} =- \frac{1}{{2{\varepsilon _0}c}}{\rm{Re}} (\alpha ) \cdot I(r) \\=\,& - \frac{1}{{2{\varepsilon _0}c}}{\rm{Re}} (\alpha ) \cdot \frac{1}{2}c{\varepsilon _0}{\left| E \right|^2} = - \frac{1}{4}\alpha \cdot {\left| E \right|^2}, \end{split}$

$ {U}_{\rm{dip}}=kT, $

其中, α表示分子极化率, ${\varepsilon _0}$为真空介电常数, c为真空中的光速, k为玻尔兹曼常数, ${U_{{\rm{dip}}}}$即为分子在光场中的偶极势, 通常用温度T来表示分子阱深度. 如果研究对象是氟化镁分子, 将超透镜聚焦光环光场处的横截面的光场强度代入, 就可以得到氟化镁分子在光场中的偶极势, 并对偶极势求导就可得到分子在光场中所受的偶极力. MgF分子的平均极化率α = 4.56 × 10^–40 Cm²/V, 入射光功率为1 W. MgF分子在聚焦光环光场中所受光学势和偶极力带入电场强度, 如图5所示. 从图5可以看出, MgF分子在光场中的偶极势分布曲线对称, 且最大偶极势约为32 μK, 这足以捕获来自传统多普勒冷却后装载到MOT之后分子温度最低达到几个微开的超冷MgF分子. 相应的偶极力大小和方向随着r变化, 且偶极力最大为8.2 × 10^–22 N, 这比MgF分子所受的重力大1.1 × 10⁴倍. 这表明MgF分子所受到的偶极力足够大以平衡分子所受的重力.
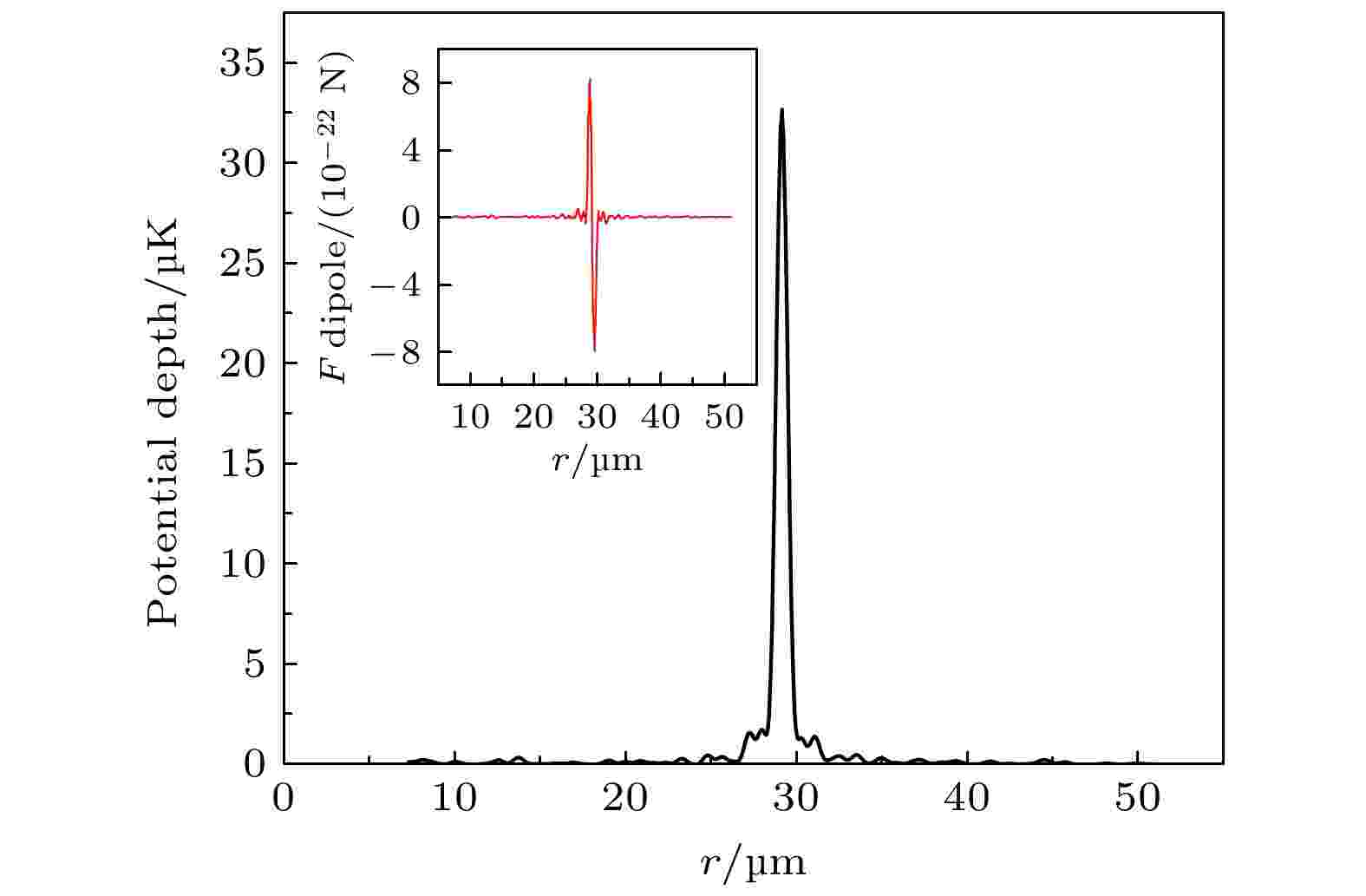图 5 MgF分子在环形聚焦光场中所受光学势和偶极力(见插图)
Figure5. Optical potential and dipole force(inset firure) of MgF molecule in ring focused light field.

储存环也是一种环形光学势阱, 然而, 它并不是在空间上一点有最大囚禁势能, 而是在一个圆环上势能都一样大. 分子可以装在这种环形的光学势阱中, 也就是分子的存储环. 为了验证设计的光学储存环的囚禁效果, 我们进行了MgF分子三维Monte-Carlo动力学过程的模拟. 模拟的条件如下: MgF分子束切向呈高斯速度分布, 中心速度为0.2 m/s, 在10 μK玻尔兹曼速度分布之内, 沿储存环切向入射^[27,28]. 观测区域为光环上MgF分子束入射点相对180°的小区域. 在储存环上一个很小的区域内考察分子数目随时间演化的关系, 也就是探测区域内分子数目随时间演化的关系, 结果如图6所示. 从图6可以看到, 分子波包在开始时纵坐标峰值为4.3 × 10⁴个, 波包大约1 ms经过一次观测区域, 波包高度逐渐变矮, 在做圆周运动过程中分子波包不断拉长, 大约在5 ms后, 探测区域分子数目趋于稳定, 约为4 × 10³, 表明了分子已经扩散到了整个光学储存环空间中. 探测区域内分子数随时间越来越少, 这是因为分子波包具有一定的速度展宽, 在做圆周运动过程中分子波包不断拉长, 最终稀释到整个储存环区域. 图7为单个氟化镁分子在储存环中运动轨迹的三维立体图, 分子在z方向的运动在焦平面附近0.25 μm的范围内; 红色虚线为在xoy平面的运动轨迹投影, 分子在r方向上运动在光束半径附近0.37 μm的范围内.
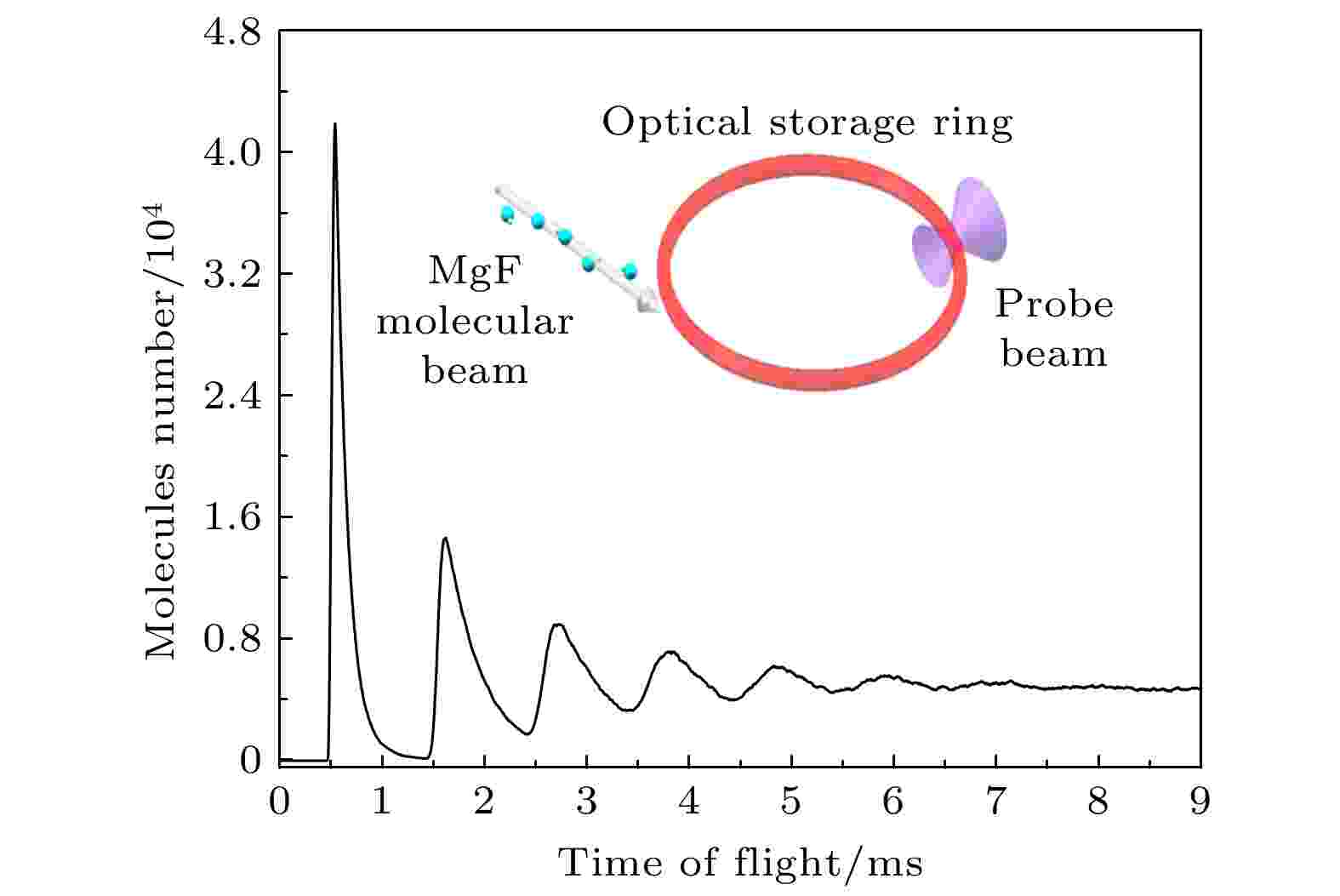图 6 MgF分子束在存储环运动若干圈的飞行时间谱. 插图是探测原理示意图
Figure6. Time-of-flight spectrum of MgF molecular beam moving in the storage ring for several cycles. The illustration is the schematic diagram of molecule detection.

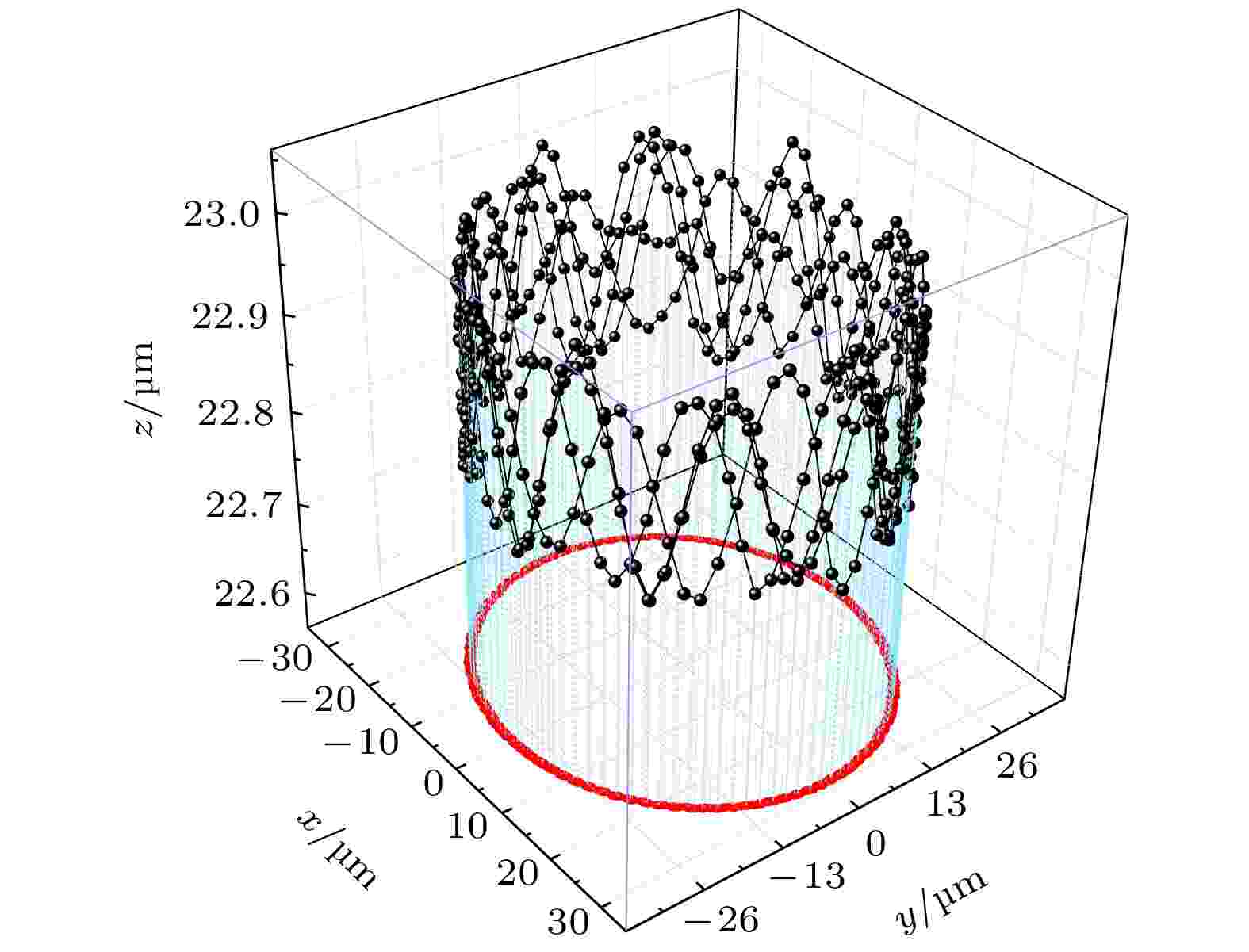图 7 单个MgF分子在表面储存环中运动运动轨迹图, 其中红色虚线为分子在储存环中运动的俯视图, 也就是运动轨迹在xoy平面的投影
Figure7. Motion trajectory of a single MgF molecule in the surface storage ring, in which the red dotted line is the top view of the motion of the molecule in the storage ring, that is, the projection of the motion trajectory on the xoy plane.

本文利用传输型相位超表面结构单元设计了光学存储环的方案. 这种结构由不同占空比的硅结构光栅单元构成, 在焦平面上可形成聚焦光环. 设计的焦距为22 μm的超表面环形透镜, 聚焦光环的光场强度比入射光增强了55.1倍, 焦点处光强度分布的半高全宽为0.8 μm. 随着数值孔径的增大, 焦平面上最大光强度先增大后减小; 同时焦平面上光斑的水平方向的尺寸不随数值孔径的改变而发生变化, 竖直方向的尺寸随着数值空间的增大而减小. 最大偶极势约为32 μK, 可以将10 μK的冷分子囚禁在光学存储环中. 本文所设计的超表面存储环结构具有易于设计制作, 波前调控灵活的特点, 对于研究储存环内分子的冷碰撞和反应具有潜在的应用前景.