摘要:二维冰是典型的原子制造技术获得的新型原子级材料, 其结构和成核生长在材料科学、摩擦学、生物学、大气科学和行星科学等众多领域具有至关重要的作用. 虽然二维冰的结构性质已被广泛研究, 但对其电学和光学性质知之甚少. 本文通过密度泛函理论和线性响应理论计算了二维冰相I在零温时的主要电学、光学、介电性质和红外光谱. 其次, 利用从头算分子动力学方法模拟得到了二维冰相I在有限温度下的声子振动态密度. 本文的结果揭示了原子级二维冰相I的电子结构, 同时展示了其独特的光吸收机理, 有助于二维冰相I的进一步实验表征和原子级操控. 由于表面上的二维冰可以促进或抑制三维冰的形成, 这对于设计和研发防结冰材料具有潜在的应用价值. 此外, 二维冰本身也可以作为一种特殊的二维材料, 为高温超导电性、深紫外探测、冷冻电镜成像等研究提供全新的标准材料.
关键词: 原子级二维冰相I/
电子结构/
光学性质/
理论模拟

English Abstract

全文HTML

--> --> -->

冰是一种常见的物质, 它的结构和成核生长在材料科学、摩擦学、生物学和大气科学等许多领域都起着至关重要的作用^[1-8]. 早在20世纪20年代, Bragg等^[9]利用X射线表征首次得到了冰的晶体结构, 从此揭开了冰晶体结构研究的序幕. 经过近百年的研究和探索, 迄今为止人们已经发现了18种冰的晶相(三维冰相)^[10-13], 其中自然界中最常见的冰相是六边形冰相^[14-16]. 然而, 冰在二维极限下能稳定存在吗? 这个问题一直以来存在很大争议^[17-19]. 一般认为, 在单分子层极限下, 二维冰具有许多不饱和氢键, 需要依靠与基底的相互作用才能形成稳定结构. 通常情况下二维冰的结构非常依赖于衬底的结构和对称性.
最近有实验发现在双层石墨烯间会形成一种与表面结构无关的四方二维冰相^[20], 这种二维冰起初被质疑是NaCl的晶体结构^[21], 随后Algara-Siller等^[22,23]进行了进一步的验证, 证实了四方二维冰相的存在. 这些讨论激发了人们进一步研究受限二维冰的浓厚兴趣. 界面上的二维水(冰)结构广泛存在^[24-26], 界面上的单层有序水, 也可以认为是一种二维冰. 例如, Chen等^[27]使用量子蒙特卡罗(quantum Monte Carlo, QMC)方法研究了单层方形冰在高压下的稳定性, 结果表明单层方形冰在高压下是稳定存在的, 这支持了Algara-Siller等^[20]的研究结果. 但是这种状态的低维冰往往存在于金属表面^[28-30]和绝缘体表面^[31,32]的水冰层, 或是石墨和石墨烯^[33,34]等强约束的受限空间内^[35,36]. 而关于二维冰是否能独立且稳定存在的问题依然悬而未决. 直至2020年初, Ma等^[37] 首次在金衬底上成功生长了单晶二维冰, 并利用高分辨率原子力显微镜技术展示了其两层六边无旋堆垛结构的亚原子分辨成像, 将其命名为二维冰相I. 他们展示了二维冰内相互饱和且稳定的氢键结构, 并从理论上揭示了原子级二维冰的特殊生长机制. 这一发现不仅从理论上加深了人们对二维冰成核和生长的理解, 同时也证实了二维冰在作为原子制造新型材料方面存在巨大的应用潜力^[38]. 面对实际中的设计制造, 则需要我们对二维冰的结构、电子、介电和光学等特性进行进一步的理论研究, 从而为其在高温超导电性、深紫外探测、冷冻电镜成像等领域应用提供理论基础.
由于物质的光电性质与原子分子的振动特性息息相关, 因此不同冰相的振动光谱, 如拉曼和红外光谱(infrared, IR)^[39,40] 一直都是人们关注的焦点. 通过粒子速度自关联函数的傅里叶变换得到的^[41] 振动态密度(vibrational density of states, VDOS), 直接反映了微观振动特征. 一方面VDOS在不同体系中具有不同的特征振动频率以及频率峰值, 其振动特征谱可以用作分子指纹^[42,43]. 另一方面, 从VDOS中提取本征振动模式^[44]可以体现粒子振动的动力学特征. 基于经典力场和从头算分子动力学, 目前对体相冰的振动谱及其介电性质已有众多理论研究^[45,46]. 2011年Aragones等^[47]研究并总结了冰Ih, III, V, VI和VII不同相的偶极介电常数随温度和压力的变化. 后来也有研究逐步向特定条件下二维冰的可能结构搜索及其相关性质计算等方向展开^[27,48-50]. Ghasemi等^[51]使用密度泛函理论(density functional theory, DFT)和密度泛函微扰理论(density functional perturbation theory, DFPT)开展了二维冰和体相冰的电子和离子介电常数以及相应的频率依赖性等研究. 现有的研究一方面主要集中在体相冰与特定构型二维冰的结构研究与性质计算, 人们对二维冰相I的相关特性还知之甚少; 另一方面由于存在氢键、共价键及范德瓦尔斯(van der Waals, vdW)等复杂的相互作用, 在利用DFT计算二维冰相I的振动特性时还缺乏涵盖不同相互作用的模型描述对其振动特性的影响.
DFT计算中考虑不同交换关联泛函对体相冰及液态水的性质预测具有明显差异. Santra等^[52]对比了半局部、杂化和vdW三种交换关联泛函对冰Ih和六个质子有序冰等相关性质的影响, 结果表明考虑vdW效应后的相变压力更加接近实验所得到的相变压力. 此外, 基于非局域关联性发展的revised Vydrov and Van Voorhis (rVV10)^[53] vdW泛函可以准确地考虑vdW作用和一些非局域效应. 强约束且正则化(strongly constrained and appropriately normed, SCAN)^[54]的泛函和含动能项的广义梯度近似(meta-generalized gradient approximation, meta-GGA)可以同时考虑共价键、氢键和vdW相互作用, 在描述水的结构和动力学方面更加精确^[55]. Peng等^[56]结合rVV10非局域关联泛函与SCAN泛函, 既对水中短程相互作用进行优化, 同时又对长程vdW相互作用进行准确描述, 被称为SCAN + rVV10泛函. 该泛函被广泛地应用到水的结构建模和特性计算中^[57].
本文使用四种不同的交换关联泛函对二维冰相I的结构、电子和光学性质以及振动特性进行了系统研究. 使用DFT和DFPT计算了0 K下的电子能带结构、光学性质和红外光谱. 使用从头算分子动力学(ab initio molecular dynamics, AIMD)模拟了有限温度下的径向分布函数(radial distribution function, RDF)和VDOS. 为原子级二维冰相I的电子、介电和光学性质及振动特性提供了基准理论数据.

二维冰相I的原胞构型由12个原子组成, 分别在x方向和y方向进行3 × 3周期性扩展, 在z方向设置10 ?的真空层, 建立了具有周期性边界条件的108个原子的二维六边形结构. 互锁双层冰结构的顶视图、斜视图和侧视图如图1所示. 在DFT计算中, 使用PBE^[58]和SCAN泛函来处理价电子之间的交换关联相互作用. 用rVV10非局域密度泛函和vdW-DF-ob86^[59,60]泛函计算水分子间的vdW相互作用. 用超软赝势^[61]来处理离子实与价电子之间的相互作用. 用模守恒赝势^[62]来精确描述原子散射特性.
图 1 二维冰相I的结构的顶视图、斜视图和侧视图. 顶部水层的H和O原子分别用白色和红色圆球表示, 底部水层的H和O原子分别用深蓝色和浅蓝色圆球表示
Figure1. Top, oblique and side views of the structure of two-dimensional ice I. H and O atoms in the top water layer are denoted as white and red spheres, respectively. H and O atoms in the bottom water layer are shown by dark blue and light blue spheres, respectively.

基于DFT和DFPT, 使用Quantum-ESPRESSO(QE)^[63]软件计算了0 K的电子能带结构、介电函数和红外光谱. 在DFT的自洽计算中, k点网格设置为12 × 12 × 1, 而在非自洽计算中, 对于局域态密度(partial density of states, PDOS)计算, 将其设置为24 × 24 × 1. PDOS计算使用0.01 Ry的高斯展宽, 总能量收敛阈值设置为10^–9 eV.
二维冰相I的AIMD同样使用QE程序计算. 首先构建14.1 ? × 14.1 ? × 12.5 ?的三斜盒子作为超原胞, 包含36个水分子. 采用正则系综(NVT)进行AIMD模拟, 温度设为120 K, 由速度标定恒温算法控制. 模拟时间为40 ps, 时间步长设为20.67 a.u. (1 fs). 这里, 我们选择120 K的温度对二维冰相I进行模拟, 是由于实验上冰的生长在120 K停止, 样品立即冷却至5 K, 以确保较长时间的成像^[37]. 因此, 我们在考虑不同温度效应对二维冰相I的影响时, 选择从5 K开始. 通过分子动力学模拟得到的VDOS可以包含二维冰相I非简谐振动特性的影响. 首先计算出速度自关联(velocity autocorrelation, VAC)函数, 然后通过VAC函数的傅里叶变换获得VDOS:

$I\left( \omega \right) = 2\int_0^\infty {C(t)\cos \omega t} {\rm{d}}t, $

$\begin{split}C(t)\equiv\;& \frac{{\left\langle {v({t_0} + t) \cdot v({t_0})} \right\rangle }}{{\left\langle {{v^2}({t_0})} \right\rangle }} \\=\;& \frac{{\displaystyle\sum\limits_{j = 1}^{{n_{\rm{t}}}} {\displaystyle\sum\limits_{i = 1}^N {{v_i}({t_{0j}} + t) \cdot {v_i}({t_{0j}})} } }}{{\displaystyle\sum\limits_{j = 1}^{{n_{\rm{t}}}} {\displaystyle\sum\limits_{i = 1}^N {v_i^2({t_{0j}})} } }}, \end{split}$

其中, $\left\langle {\;} \right\rangle$ 表示系综平均, N是二维冰相I中的原子数, n_t是不同轨迹时间起点的数目. 本文中, 以20个时间步长的间隔将n_t设为100.

2

-->

3.1.二维冰相I的结构

二维冰相I是一个互锁的双层冰结构, 由两个平坦的六边形水层组成, 如图1所示. 平面中水分子之间的夹角为108.9°. 在每个水层中, 一半的水分子平行于基底, 另一半垂直于基底, 一个OH向上或向下. 一层中的垂直水与另一层中的平行水形成氢键, 从而导致完全饱和的氢键结构. 图2给出了120 K时不同泛函的二维冰相I的RDF.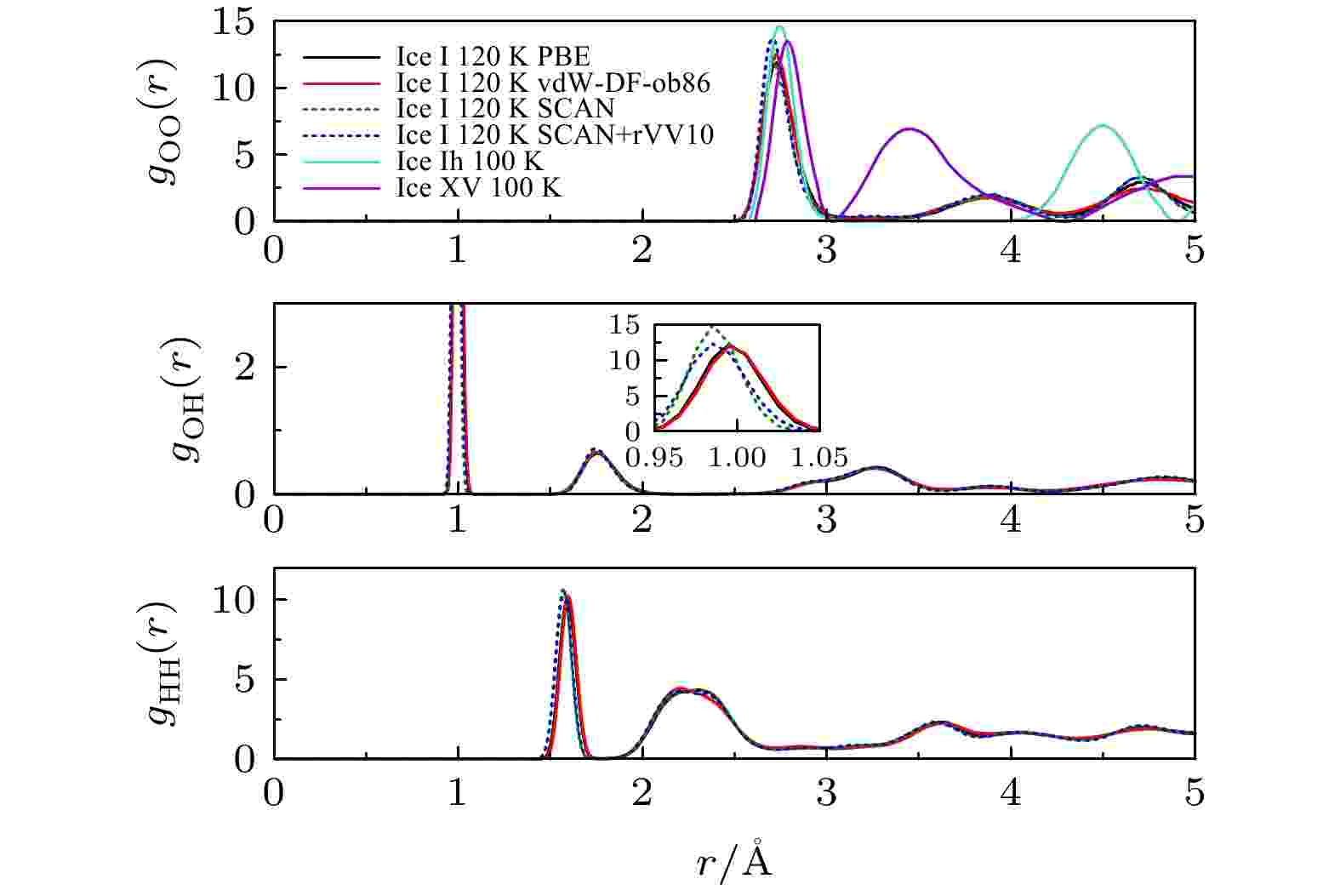
图 2 在120 K温度下, 二维冰相I在不同泛函的径向分布函数(g_OO, g_OH和g_HH)及与冰Ih, XV相在100 K的g_OO的对比. 插图显示了在0.95—1.05 ?距离范围内的g_OH的曲线图
Figure2. Radial distribution functions (g_OO, g_OH and g_HH) of two-dimensional ice I in different functionals at 120 K and the comparison with the g_OO of the ice Ih and XV phase at 100 K. The insets show elaborations of the g_OH plots within the 0.95–1.05 ? distance range.

对于PBE/vdW-DF-ob86、SCAN和SCAN + rVV10泛函的g_OO(r)的第一个峰的位置分别在2.725 ?、2.695 ?和2.705 ?, 这与单层六边冰相^[50]及冰相I^[64]的g_OO(r)值近似. 此外, 我们还比较了100 K时, 冰相Ih和XV的g_OO(r)^[65]. 无论是液态水还是冰, 水分子中氧原子之间的最近邻距离几乎相同, 约为2.8 ?左右. 也就是说, 在非常高的压力下形成的所有冰相都满足Bernal-Fowler规则的质子无序性^[66], 其中每个水分子与周围分子形成四个氢键, 其四面体构型具有两个短的O—H间距(给体质子)和两个长的O—H间距(受体质子). 从体相冰过渡到二维冰相, 可以形成密度更大的晶体结构, 其中最近邻氧氧距离基本相同, 但四面体键合方式却不同. 从图2中可以看出, 三种冰相结构的g_OO(r)的第一个峰几近相同, 但第二个峰不同. 冰相Ih具有典型的六边形结构, 其中水分子氢键结合成六元环, 而冰XV是高压冰相, 与其他冰相相比具有更高的密度, 其原因是内部互锁但不相互连接的特殊晶格结构所致. 特别地, 与二维冰相I和冰相Ih相比, 高压冰XV具有较大的g_OO(r)第一近邻半径和较小的第二近邻氧距离, 从而导致总体上更致密的结构. 尽管冰Ih也具有部分六边形氧构型, 但是与二维冰相I的堆积几何结构不同, 因此g_OO(r)第二近邻氧距离也不同.
图2中g_OO(r)值可以看出, SCAN泛函考虑vdW作用时, 氧氧的距离略有增加, 而PBE和vdW-DF-ob86泛函的氧氧的间隔明显大于SCAN和SCAN + rVV10. 通过g_OH(r)的第一个峰表征的OH共价键分别为0.985 ? (SCAN/SCAN + rVV10)、0.995 ? (PBE/vdW-DF-ob86); 第二个峰是在氧与氢之间沿着氢键的距离, 约为1.745 ?. 而g_HH(r)中具有明显的三个峰, 第一个峰位于1.565 ? (SCAN)、1.575 ? (SCAN + rVV10)、1.595 ? (PBE/vdW-DF-ob86)对应分子内H-H距离; 2.25 ?处为水二聚体的相邻氢原子之间的距离; 水二聚体中相对氢原子之间的距离为3.6 ?. 在SCAN泛函考虑vdW作用后, g_HH(r), g_OH(r)和g_OO(r)的结果一致, 即氢氢、氧氢和氧氧距离略有增加. 而PBE和vdW-DF-ob86泛函的g_HH(r), g_OH(r)和g_OO(r)间距明显大于SCAN和SCAN + rVV10. 这可能是由于交换关联泛函SCAN的强约束效应减小了原子间的距离.
此外, 我们使用vdW-DF-ob86泛函研究了不同温度(从5 K到150 K)对二维冰相I的结构的影响. 如图3所示, 随着温度升高, g_OO(r)的第一个峰变宽, 但其位置基本保持不变. 在30 K时, 第二个峰几乎消失, 表明这个配位壳层随着温度的升高而坍塌. 而且第一个峰的高度与5 K时相比显著降低. 虽然第一个峰的强度逐渐减小, 但当温度高于60 K以上, 氧氧RDF的特征变得非常相似, 在3.85 ?和4.70 ?附近有较大的展宽特征峰. 其原因在于, 随着温度升高, 更容易克服氢键的束缚而激发水分子, 从而使四面体氢键网格急剧坍塌, 在高温下趋于均匀. 随着温度升高, 与g_OO(r)的第一个峰的变化相似, g_OH(r)和g_HH(r)的第一个峰变宽, 但位置保持不变.
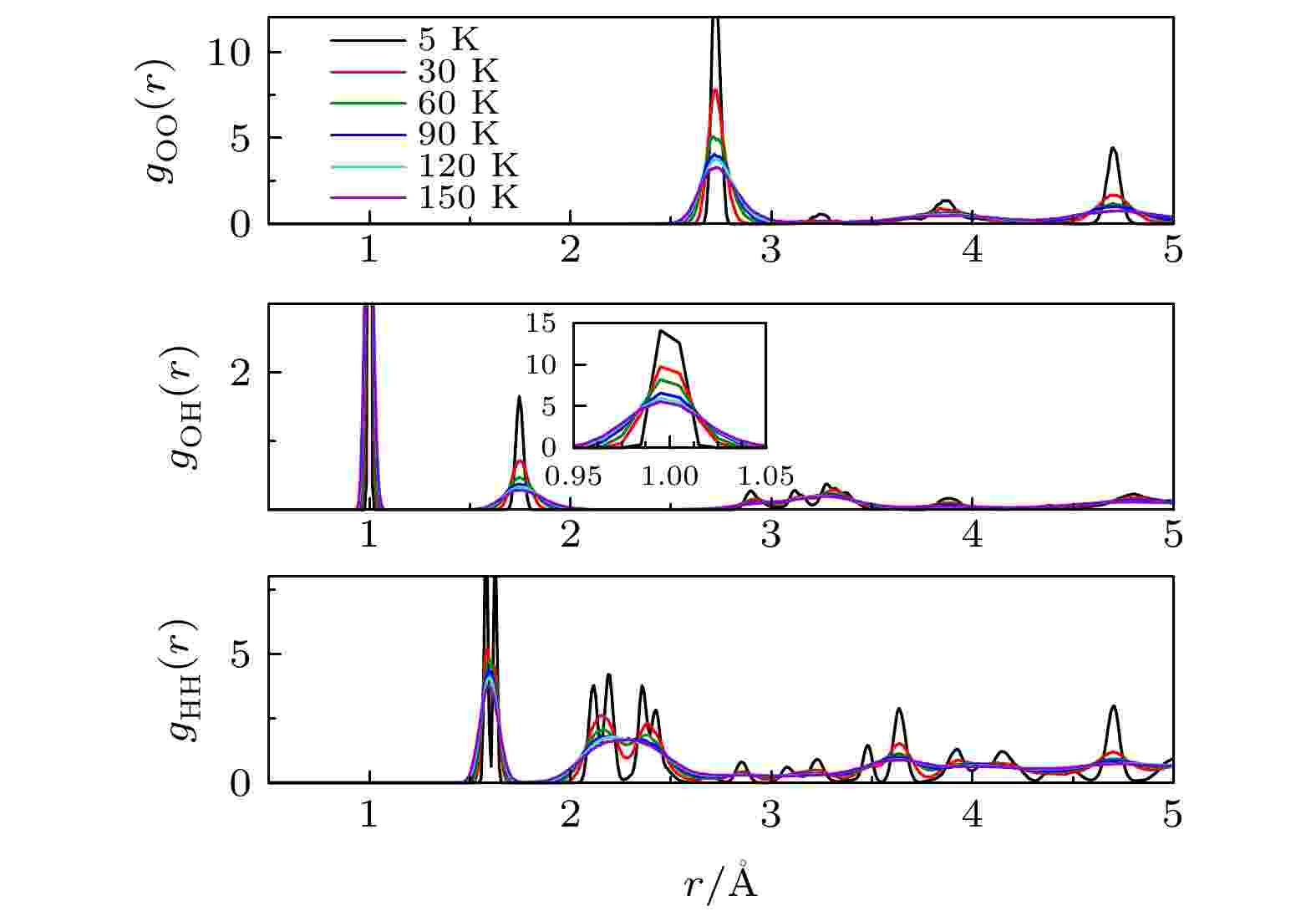图 3 从头算分子动力学模拟的二维冰相I在不同温度的径向分布函数. 插图显示了在0.95—1.05 ?距离范围内的g_OH的曲线图
Figure3. Radial distribution functions of two-dimensional ice I at different temperatures from ab initio simulations. The insets show elaborations of the g_OH plots within the 0.95–1.05 ? distance range.

2 -->

3.2.电子能带结构

二维冰相I的不同泛函的电子能带结构和对应的PDOS如图4所示. 我们发现对于PBE, vdW-DF-ob86, SCAN和SCAN + rVV10泛函, 能量的间接带隙分别为5.730, 5.582, 6.325, 6.266 eV. 其中, PBE和vdW-DF-ob86之间的能量带隙相差很小, 同样SCAN和SCAN + rVV10的能量带隙相差也很小. 但是, 可以看出在考虑了vdW作用后, 能量带隙减小了. 此外, 我们发现SCAN和SCAN + rVV10泛函的能量带隙大于PBE和vdW-DF-ob86泛函的能隙. 这可能也是由于SCAN泛函本身的强约束效应导致. 这里, 我们得到的二维冰相I的能隙、电子能带结构和PDOS与其他二维冰相^[51,67] 的结果略有不同, 这主要归因于二维冰相I的双层互锁结构, 导致带隙比其他冰相略大0.2 eV左右.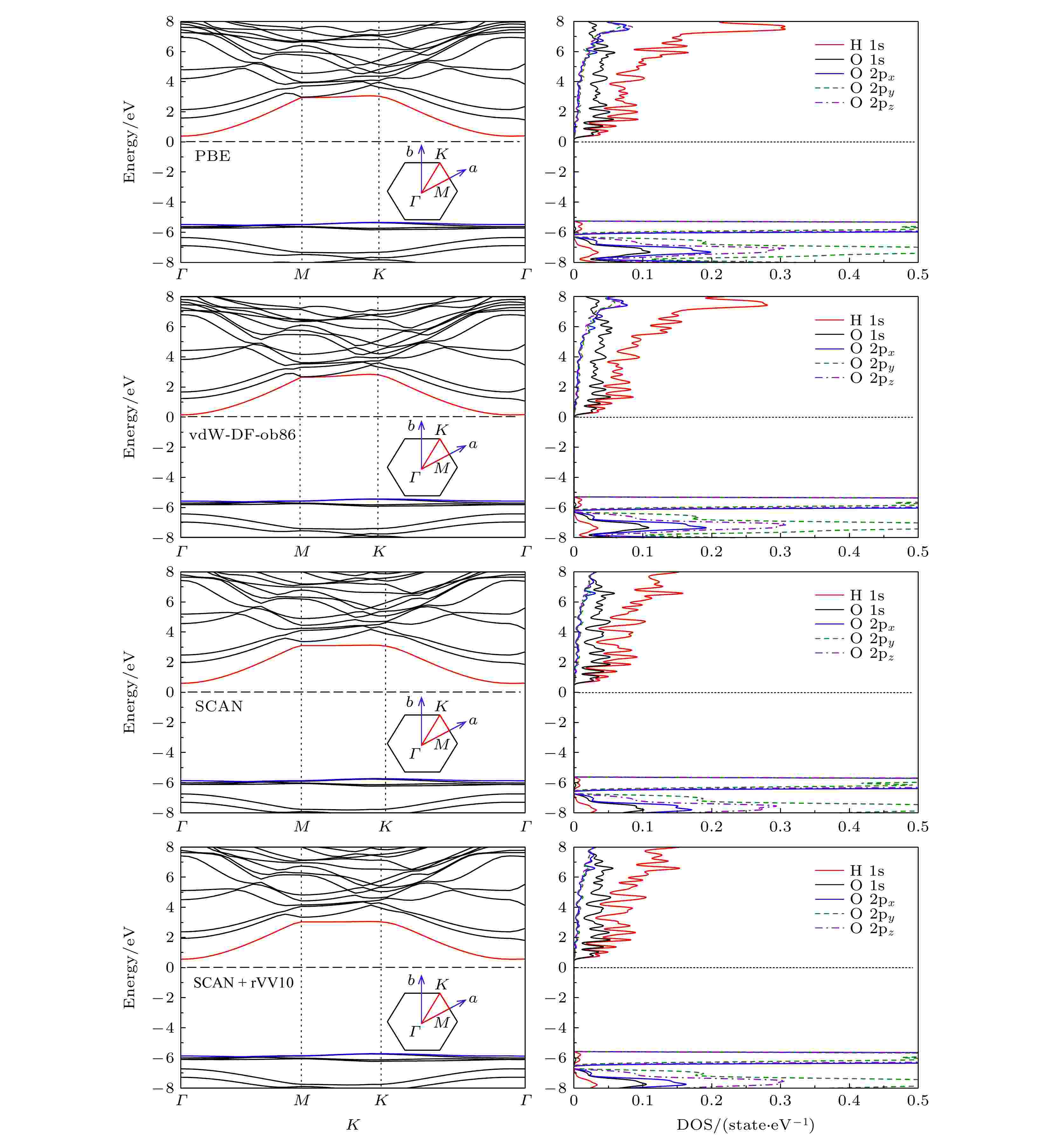
图 4 二维冰相I在不同泛函的电子能带结构. 插图显示了相应的布里渊区
Figure4. The electronic band structure of the two-dimensional ice I in different functionals. The insets show the corresponding Brillouin zones.

此外, 在二维冰相I中, O原子和H原子在中间层sp²杂化, 形成蜂窝结构, 如电子能带图中的导带部分. 在双层二维冰中, 每层二维冰相I之间的相互作用都很弱, 例如氢键和vdW相互作用, 这会减小二维冰相I的带隙. 从图4可以看出, 导带起伏很大. 实际上, 能带越宽, 该能带中电子的有效质量越小, 非局域性越强, 组成该能带的原子轨道的可扩展性越强, 这可以通过PDOS结果证明.
2 -->

3.3.光学性质

使用模守恒赝势在0—30 eV的能量范围内计算了二维冰相I的介电函数${\varepsilon _{{\rm{el}}}}(\omega )$. 为了提高介电函数计算的准确性, 我们将二维冰相I的k点网格设为12 × 12 × 1. 通过计算能级之间的偶极跃迁来获得介电函数. 介电函数由与频率相关的实部${\varepsilon ^{\rm{r}}}(\omega )$和虚部${\varepsilon ^{\rm{i}}}(\omega )$组成:

${\varepsilon _{{\rm{el}}}}(\omega ) = {\varepsilon ^{\rm{r}}}(\omega ) + {\rm{i}}\left[ {{\varepsilon ^{\rm{i}}}(\omega )} \right], $

介电函数的虚部^[68]根据(4)式得到

$\begin{split}{\varepsilon ^{\rm{i}}}\left( \omega \right) =\;& \frac{{4{{\rm{\pi }}^2}}}{{{m^2}{\omega ^2}}}\sum _{V,C}\int _{BZ}{{\rm{d}}^3}k\frac{2}{{{{\left( {2{\rm{\pi }}} \right)}^3}}} {\left| {e{M_{CV}}\left( K \right)} \right|^2} \\&\times\delta \left[ {{E_C}\left( k \right) - {E_V}\left( k \right) - h\omega } \right]. \end{split}$

而介电函数实部可以由虚部通过Kramers-Kronig关系^[69]变换得到. 通过能带结构, 可以计算得到全部的光学常数. 本文给出了二维冰相I在不同泛函的光学性质, 如图5所示给出了二维冰相I的介电函数的实部和虚部$\left( {{\varepsilon ^{xx}}, {\varepsilon ^{yy}}, {\varepsilon ^{zz}}} \right)$. 此处, x和y表示平面内分量, 而z分量垂直于x-y平面. PBE和vdW-DF-ob86泛函的介电常数几乎相同, 约为1.431, 且SCAN和SCAN + rVV10泛函的介电常数也基本相同, 约为1.393, 但值小于PBE和vdW-DF-ob86泛函的介电常数. 这表明采用SCAN和SCAN + rVV10泛函, 二维冰相I具有更好的绝缘性, 这与能带图中SCAN和SCAN + rVV10具有较大的带隙一致. PBE泛函的实部约等于vdW-DF-ob86的实部, 同样SCAN泛函的实部也约等于SCAN + rVV10的实部. 与低能区域(0—10 eV)中的SCAN和SCAN + rVV10相比, 介电函数的实部在PBE和vdW-DF-ob86中具有更大的值, 这可能是由于SCAN泛函的强约束性. 对于二维冰相I, 实部和虚部中${\varepsilon ^{xx}} \ne {\varepsilon ^{yy}}$, 这是由于实部和虚部都具有二维六边形冰的各向异性晶格.
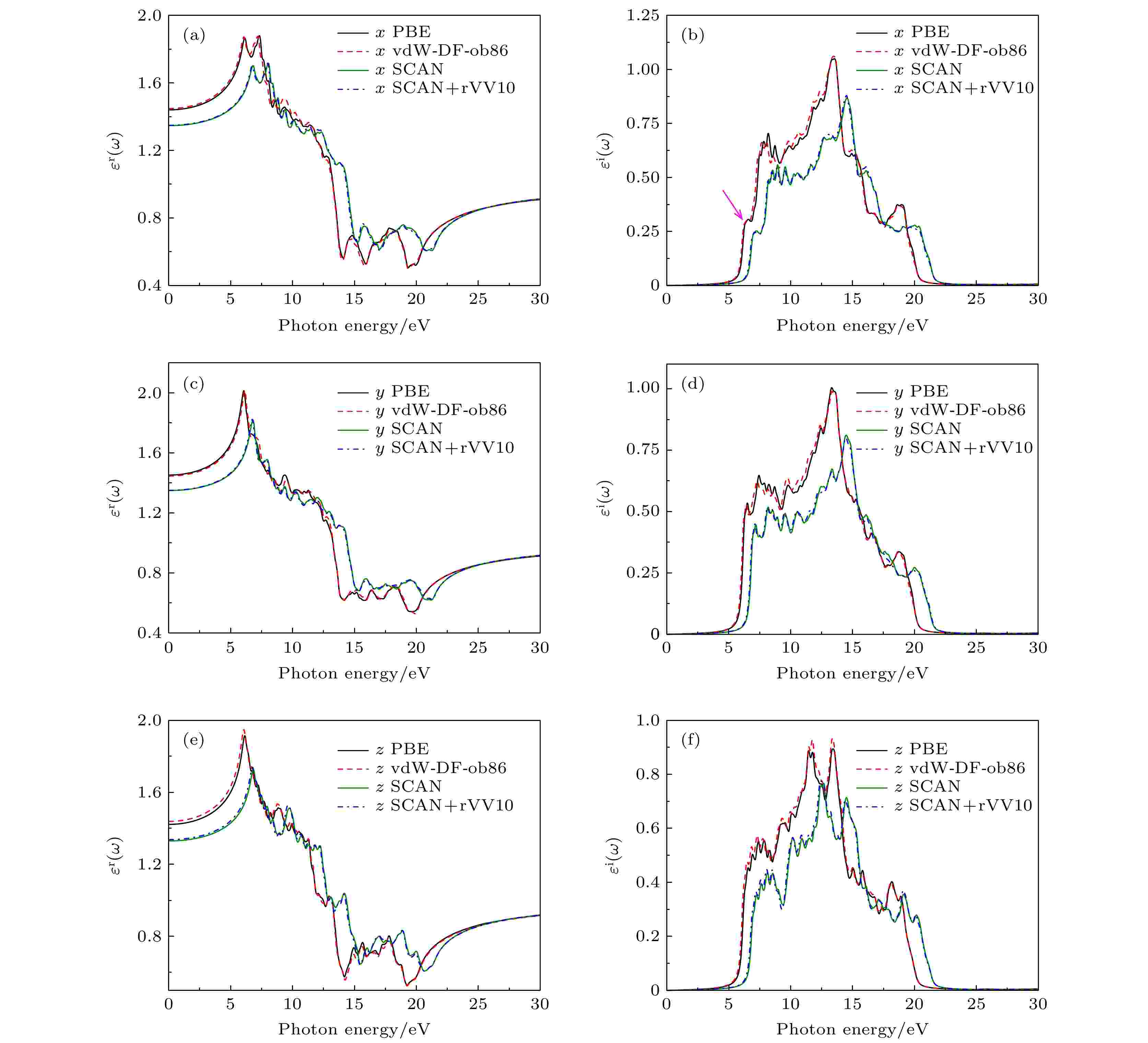图 5 二维冰相I在不同泛函的介电函数的实部　(a), (c), (e)和虚部(b), (d), (f). 其中, x和y表示平面内分量, 而z分量垂直于x-y平面. 粉色虚线箭头表示能隙
Figure5. The real (a), (c), (e) and imaginary (b), (d), (f) part of dielectric function of the two-dimensional ice I in different functionals. Here, x and y denote the in-plane components, while z component is perpendicular to x-y plane. The pink-dashed arrows refer to the energy gap.

通过分析介电函数的虚部可以了解二维冰相I的吸收行为. ${\varepsilon ^{\rm{i}}}(\omega )$函数中的特征峰对应于光传输, 这主要归因于从p价带到s导带的带间跃迁, 这从图4的PDOS可看出. 例如, 第一个吸收峰对应于能隙(图5(b)粉色虚线箭头). 与PBE和vdW-DF-ob86泛函相比, SCAN和SCAN + rVV10泛函的${\varepsilon ^{\rm{i}}}(\omega )$的主峰发生了蓝移, 这与图4的带隙相对应(SCAN和SCAN + rVV10泛函的带隙明显大于PBE和vdW-DF-ob86泛函的带隙). 这说明较大的带隙会导致吸收光谱向较大的能量移动. 实际上, ${\varepsilon ^{\rm{i}}}(\omega )$中计算出的第一个临界点与从价带最大值到导带最小值(带隙)的跃迁有关. 且二维冰相I的吸收能量范围分别在紫外光谱(> 3.2 eV)和可见光谱(介于2和3.2 eV之间)中. 在低能区, 二维冰相I的介电函数实部比其他二维冰^[51,70,71]略大0.1—0.2左右, 这可能是由于二维冰相I双层互锁的几何堆积结构导致. 与其他二维冰相比, 二维冰相I的峰值略高0.2左右. 但从峰的位置来看, 二维冰相I与其他二维冰的结果是一致的.
2 -->

3.4.振动特性

分别使用DFPT和AIMD模拟对二维冰相I的IR和VDOS进行了理论研究. 基于准谐波近似得到0 K时的IR光谱. 这里给出了PBE、vdW-DF-ob86和SCAN + rVV10泛函的IR光谱如图6(a)所示. 可以看出, IR光谱具有四个主要特征峰, 在低频区和高频区PBE和vdW-DF-ob86泛函的IR光谱基本一致: 在约259 cm^–1处有一个明显的峰, 以839 cm^–1为中心出现宽频带, 在1638 cm^–1处有一个窄峰(分子内弯曲), 分子内伸缩带的中心在3186 cm^–1处. 相比之下, SCAN + rVV10泛函的IR光谱的峰的位置略有不同, 前两个峰出现蓝移, 高频区的两个峰出现红移. 这主要是因为低频峰是由分子间摆动引起, 分子间摆动模式增强, 而分子内H—O—H弯曲振动和O—H键伸缩振动减弱.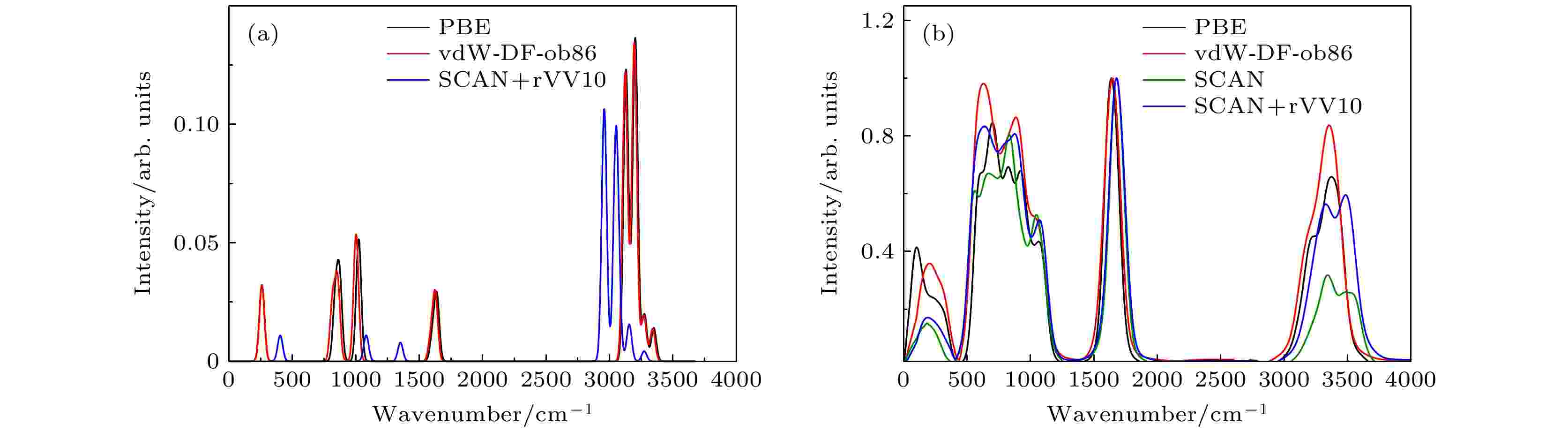
图 6 (a)谐波近似下, 不同泛函PBE, vdW-DF-ob86和SCAN + rVV10的二维冰相I的IR; (b) 二维冰相I在不同泛函的振动态密度
Figure6. (a) IR of the two-dimensional ice I with different functionals PBE, vdW-DF-ob86 and SCAN+rVV10 under harmonic approximation; (b) the vibrational density of states of the two-dimensional ice I in different functionals.

图6(b)为二维冰相I的不同泛函的的VDOS. 其振动峰可以表征为分子间摆动, 转动, 分子内(H—O—H)弯曲和(O—H)伸缩. 分子间摆动峰出现在约203 cm^–1处, 此峰处于太赫兹(THz)频率范围, 与氢键振动相关. 转动峰出现在629 cm^–1处, 它是由相邻分子之间的静电库仑相互作用引起的. O-H键与相邻分子的氧的排列即O—H···O氢键配置进一步软化了O—H键的动力学. 如图2所示, g_OH(r)除了1 ?处之外还有一个峰在1.745 ?处, 而这个峰正好介于g_OH(r)与g_OO(r)(2.7 ?)之间, 这反映的是水分子之间通过氢键相互作用连接在一起. 氢键振动引发的分子间相对运动可以在振动谱中反映出来. 图2显示g_HH(r)在2.25 ?处存在一个峰. 然而, 分子内O—H伸缩振动在某种程度上向更高的频率移动. 由于H—O—H弯曲而产生的峰值在1645 cm^–1处, 伸缩的O—H键在3325 cm^–1处断裂. 此外, 我们发现二维冰相I的分子内弯曲振动和O—H伸缩振动区域与实验和理论上得到的冰Ih相^[72-74]以及其他冰相^[75]的结果非常相似, 分别在1500—1800 cm^–1和3000—3600 cm^–1处, 如图7所示. 图7(a)中, 与冰Ih相的实验和理论值相比, 二维冰相I的O—H伸缩振动峰发生了蓝移, O—H伸缩振动更剧烈. 虽然冰Ih相和二维冰相I都存在氢键网格结构, 但由于二维冰相I的特殊双层互锁结构导致分子间氢键相互作用减弱, 分子内O—H共价键增强. 图7(b)中, 二维冰相I的H—O—H弯曲振动峰和实验中的结晶冰及理论中的六方冰相比, 出现了较大的展宽. 这是由于与三维冰相比, 双层的二维冰相I中存在两种弯曲振动模式, 分别为平行水分子和垂直水分子的贡献, 导致其比三维冰的分子内弯曲振动峰变宽.
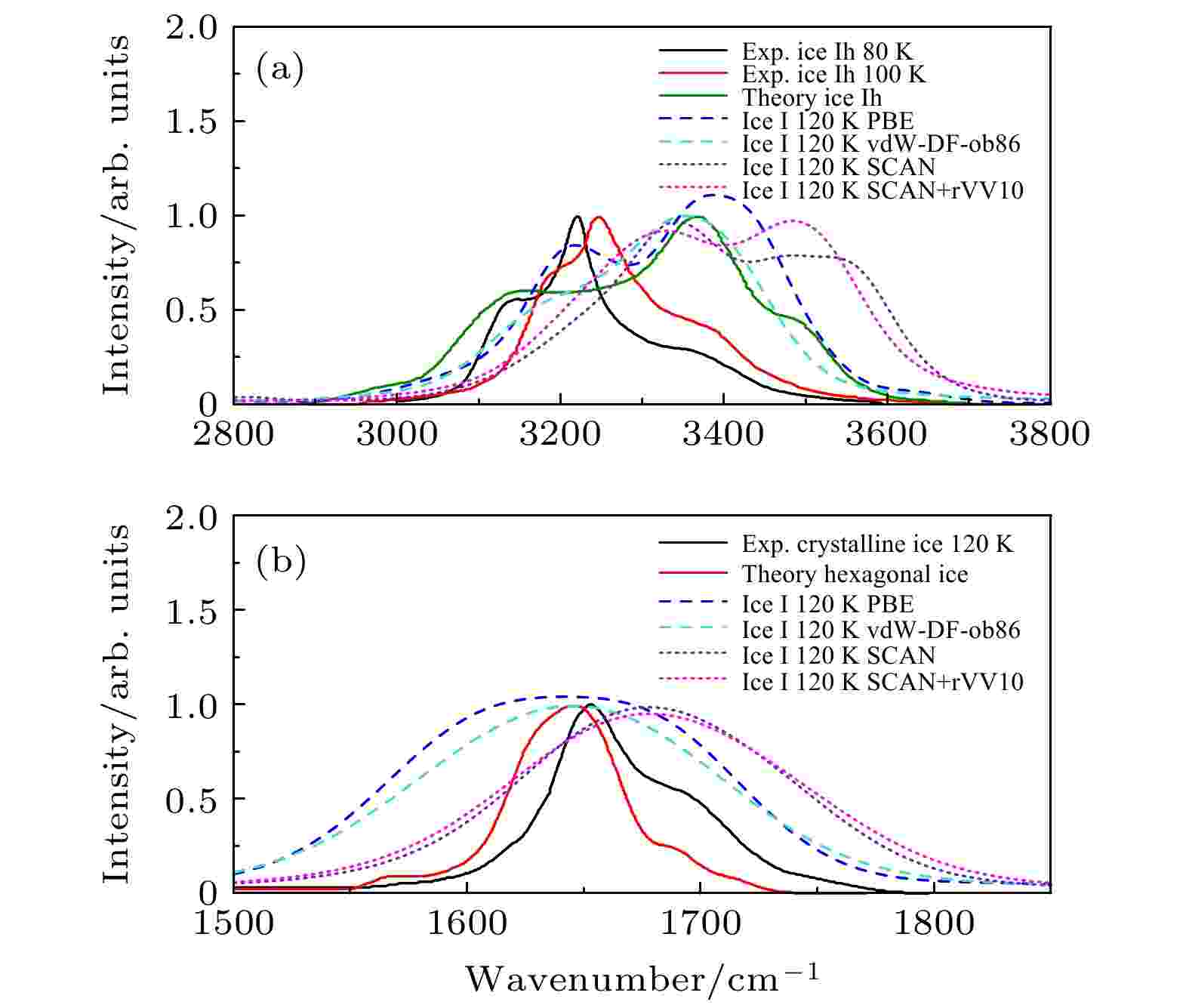图 7 (a)二维冰相I和实验^[72,76]及理论的冰Ih相^[75]的分子内伸缩振动谱; (b) 二维冰相I和实验^[77]及理论的其他冰相^[75]的分子内弯曲振动谱
Figure7. (a) Intramolecular stretching vibration spectra of two-dimensional ice I and experimental^[72,76] and theoretical ice Ih^[75]; (b) intramolecular bending vibration spectra of two-dimensional ice I and experimental^[77] crystalline ice and theoretical hexagonal ice^[75].

二维冰相I在不同温度下的VDOS如图8所示. 可以看出, 随着温度的升高, 1500—1750 cm^–1的分子内弯曲振动峰逐渐变宽, 弯曲峰的位置出现了少许红移, 表明温度越高, 弯曲振动越弱. 而氢键束缚的O—H伸缩振动峰和自由氢原子的O—H伸缩振动峰随着温度升高不仅变宽, 而且彼此之间略有移动. 在90 K时, 3325 cm^–1附近自由氢原子的O—H伸缩振动峰明显增长, 然后随着温度升高回落到氢键束缚的O—H伸缩振动峰的相同高度. 这是由于自由氢原子的O—H伸缩模式比氢键束缚的O—H伸缩模式热激发更快, 导致在90 K出现明显增长的峰. 高温下, 氢键对氢原子的束缚减弱, 两类O—H伸缩振动峰几乎趋于一致, 振动谱上两个频带由于展宽而合并成一个带. 随温度升高, O—H伸缩振动峰发生蓝移, O—H伸缩振动更剧烈, 这与实验中受限超冷水在不同温度效应的O—H伸缩振动特性一致^[40]. 分子间振动峰在低温下具有明显的特征, 低频段(小于1000 cm^–1)的分子间振动峰随着温度的升高向更低频方向移动. 由于温度升高, 氢键被破坏, 分子间摆动模式逐渐减弱.
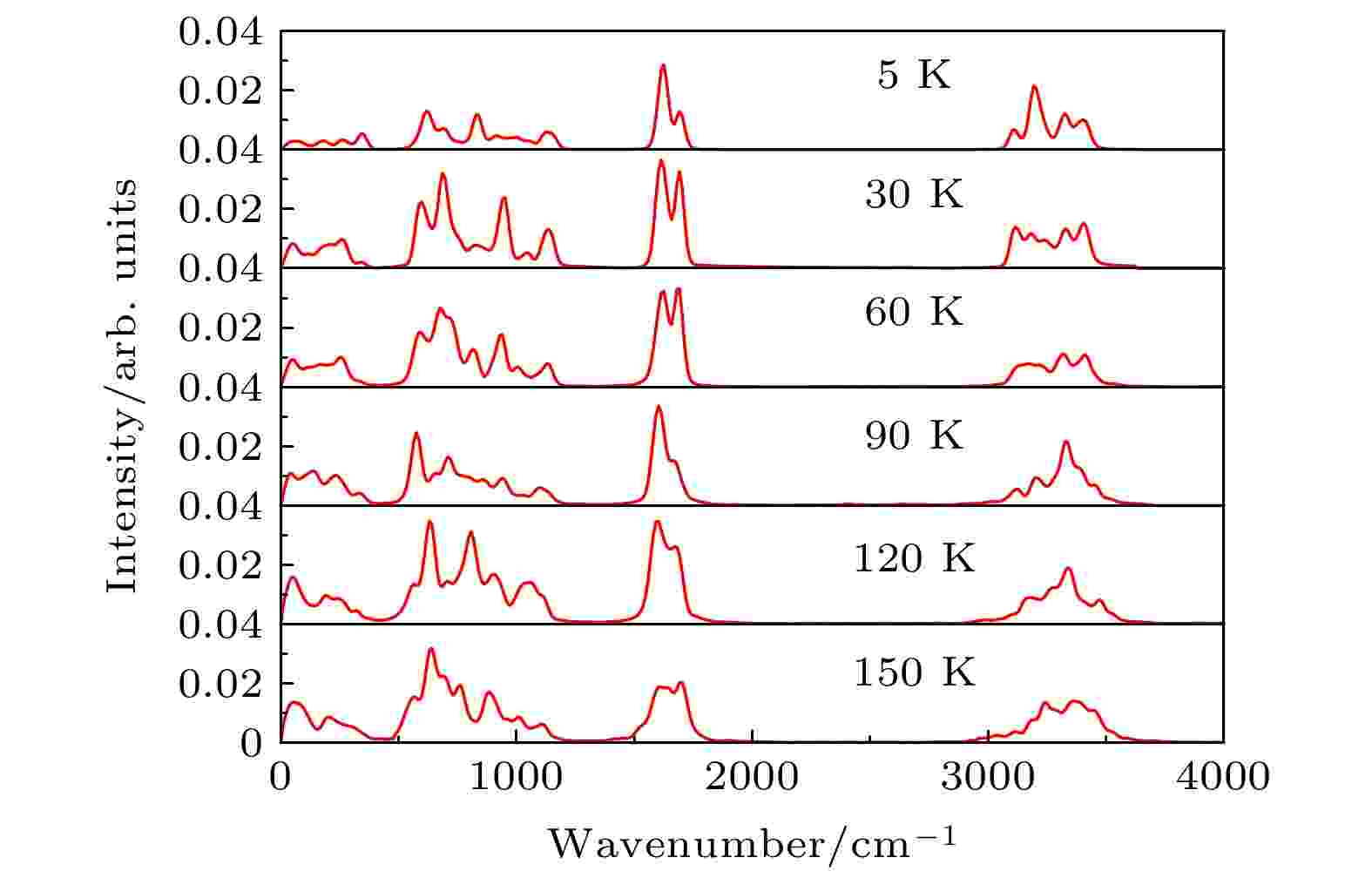图 8 二维冰相I在不同温度下的振动态密度
Figure8. The vibrational density of states of the two-dimensional ice I at different temperatures.

利用DFT和DFPT方法使用四种不同泛函系统研究了二维冰相I在0 K时的电子能带结构、光学性质和IR光谱. 通过AIMD模拟研究了二维冰相I在有限温度下的结构性质和振动特性, 并系统研究了不同交换关联泛函和不同温度效应对二维冰相I的结构性质、振动特性的影响. 首先, 对于二维冰相I的结构, 无论是SCAN还是PBE泛函在考虑vdW作用后, 对原子间距几乎没有影响, 而SCAN和PBE泛函对比则相差较多. 由此可见影响结构原子间距离的主要原因是SCAN泛函的强约束效应, 且SCAN泛函更好地体现了中程的范德瓦尔斯相互作用, 在描述晶格常数和长程相互作用方面, 比GGA具有更高的精度. 当温度高于60 K以上, 由于热涨落效应, 二维冰相I的水分子之间的四面体氢键网络结构会坍塌, 然后随着温度升高向各向同性均匀结构转变. 其次, 二维冰相I是间接带隙, 其光学性质表现出了各向异性晶格. 且二维冰相I的吸收能量范围分别在紫外光谱(> 3.2 eV)和可见光谱(介于2和3.2 eV之间)中. 不同泛函的计算结果表明, SCAN和SCAN + rVV10泛函计算出的带隙大于PBE和vdW-DF-ob86, 且主峰发生了蓝移, 说明较大的带隙会导致吸收光谱向较大的能量移动, 而vdW作用对光学性质影响很小. 最后, 从二维冰相I的振动特性方面看, SCAN + rVV10泛函与PBE和vdW-DF-ob86相比, 其IR光谱的前两个峰出现蓝移, 高频区的两个峰出现红移. 因而考虑SCAN的强约束效应会导致二维冰相I的分子间摆动模式增强, 而分子内H—O—H弯曲振动和O—H键伸缩振动减弱. vdW作用对振动性质的影响仍然不明显. 从温度效应考虑二维冰相I的振动谱, 发现随着温度升高, 低频段的分子间摆动模式减弱, 分子内弯曲和伸缩振动峰变宽, 随温度升高, O—H伸缩振动峰发生蓝移. 本文的结果揭示了原子级二维冰相I的电子结构, 同时展示了其独特的光吸收机理, 有助于二维冰相I的进一步实验表征和原子级操控. 由于二维冰是典型的原子制造技术获得的新型原子级材料, 对于设计和研发防结冰材料具有潜在的应用价值, 可以为高温超导电性、深紫外探测、冷冻电镜成像等研究提供全新的平台.