全文HTML
--> --> -->二维原子晶体作为个体, 其本身具有的优异特性已备受关注. 在一种可以将二维原子晶体“拾取”并精确地在预定位置“释放”的“pick-up”转移技术被发明后[36], 该领域涌现的一个新的研究方向是以单个二维原子晶体为基本单元, 通过垂直方向上的堆叠构建多层结构[37]. 这种叠层结构的层间仍以范德瓦耳斯力结合, 因此被称为“范德瓦耳斯异质结”或“二维垂直异质结”[38,39]. 与外延生长的层状半导体异质结不同, 二维异质结的界面不存在共价键, 因此制备过程不受界面晶格匹配条件的限制; 异质结界面可以达到近乎原子级的平坦, 不受界面原子相互扩散和偏析的影响; 二维原子晶体的选择范围广泛, 可制备多种物理性质不同的叠层结构[40-43].
关于二维原子晶体的结构、特性、制备及应用等已有较多论述[9-13,44-47], 本文主要聚焦二维原子晶体转移堆叠、高质量电子器件制备及其电学输运研究方面的进展. 究其历史, 转移堆叠技术起源于该领域研究初期中面临的一个重要问题: 二维原子晶体的表面完全暴露, 因此很容易受到衬底的影响, 致使其电学输运测量结果严重偏离本征态[48]. 通过第一代(聚合物基)转移技术将石墨烯转移到h-BN上可以有效提高其载流子迁移率, 就此拉开了转移技术发展的序幕[49]; pick-up转移技术的发明淘汰了第一代转移技术[36,37], 实现了无污染的洁净界面、多层结构的任意堆叠及层间转角的控制, 使得叠层异质结的研究得以迅速发展. 随着转移工艺和器件结构的不断优化, 器件质量不断提高, 包括分数量子霍尔效应、霍夫施塔特蝴蝶能谱在内的多种电子关联态陆续被报道[50,51]. 尤其近两年来, 在石墨烯莫尔超晶格中发现了平带结构以及超导、莫特绝缘体及轨道磁性等奇特电子关联态, 掀起了二维异质结研究的又一股热潮[52,53].
转移堆叠技术是目前二维原子晶体电学输运特性研究的实验基础, 作为转移堆叠之前的必要的准备步骤, 本文首先介绍二维原子晶体的机械剥离及快速表征的主要手段; 在此基础上, 介绍几代主要的转移堆叠方法的发展和进步, 及其对二维电子器件质量的影响. 针对电学输运研究中利用高质量电子器件, 本文将介绍无序性、电学接触以及几种重要器件结构的最新进展, 特别是适合于二维原子晶体叠层异质结的器件结构及电学调控手段.
2.1.机械剥离和快速识别
制备叠层结构的第一步是获得单层或少层的二维原子晶体. 整体而言, 晶圆级二维原子晶体生长仍面临较大的挑战[12,44]. 目前高质量器件仍主要采用机械剥离的单层或少层晶体, 因此本文简要介绍机械剥离方面的进展. 机械剥离技术本质上是一个晶体解理过程[54]. 相较于层内的强共价键, 层状晶体的层间范德瓦耳斯力较弱. 如果施加一个垂直于层基面的拉伸应力, 则可以使晶体从层间解理. 机械剥离的操作过程并不复杂, 以石墨烯为例, 如图1(a)所示[55]: (1)首先将片状石墨放置在透明胶带上; (2), (3)然后将胶带反复对折数次以减薄石墨晶体; (4)再将粘有薄层石墨的胶带覆盖在目标衬底上并撕下胶带; (5)利用光学显微镜在衬底上寻找单层及少层石墨烯. 需要特别指出, 所谓的单层及少层石墨烯是通过衬底与石墨烯之间的结合力, 从胶带上的薄石墨中解理出来的, 并不是把胶带上通过反复折叠产生的石墨烯直接粘贴到衬底上. 机械剥离自首次报道以来就被普遍采用, 对于几乎所有二维原子晶体都适用; 剥离过程不需要复杂精密的设备, 非常易于实施. 除机械剥离外, 还可以利用超声辅助液相剥离以及电化学插层等方式获得单层及少层的二维原子晶体[56]. 相比而言, 机械剥离是一个物理过程, 不会引入多余杂质, 可以获得表面极为清洁的样品[1,54]. 因此, 机械剥离法非常适合于研究二维原子晶体的本征物理特性.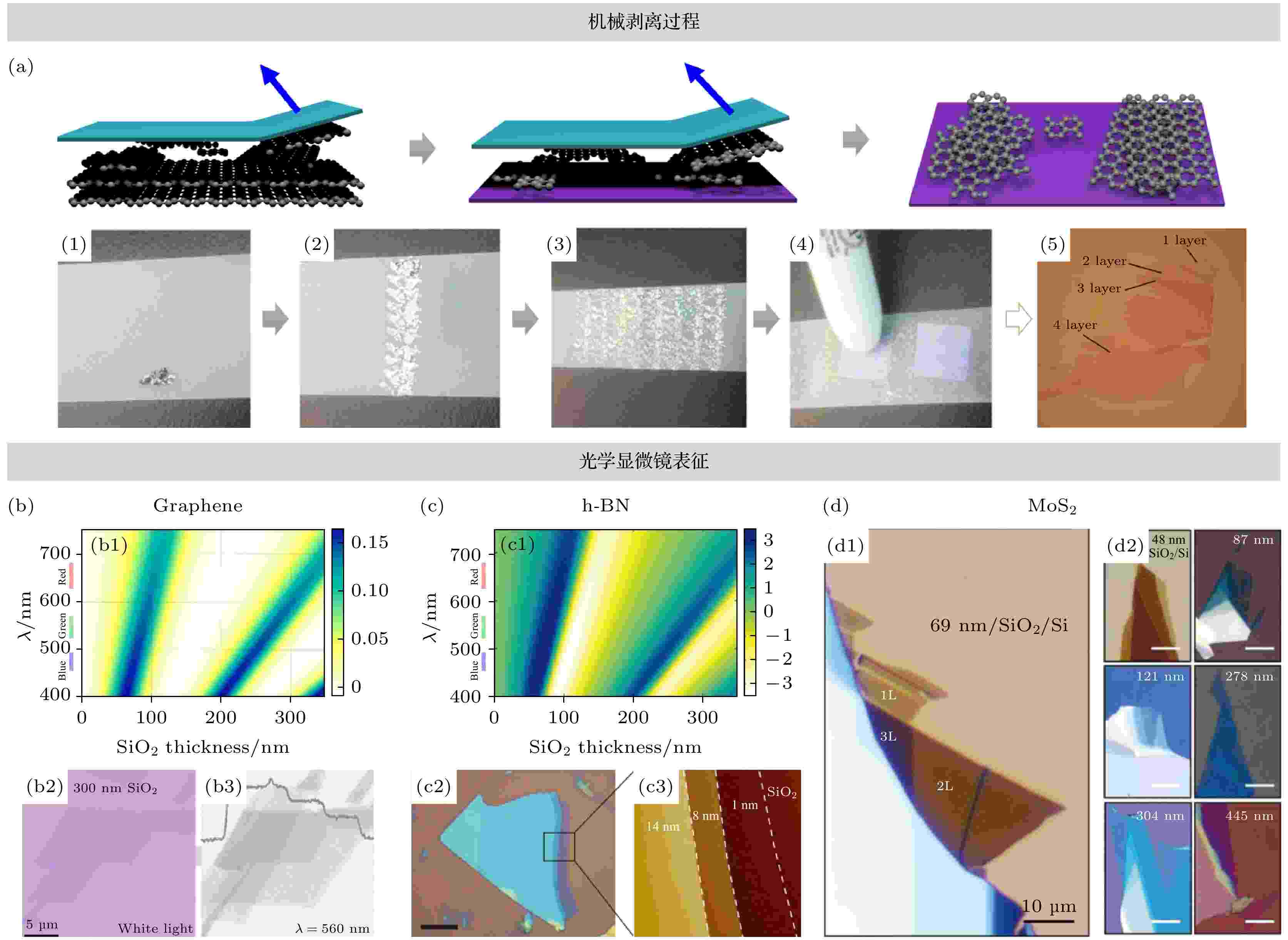
图 1 二维原子晶体的机械剥离及层数的快速识别 (a)石墨烯的机械剥离过程示意图, 以及具体步骤的照片((1)—(4))和样品的光学照片((5)), 其中可以看到不同层数的样品[55]; (b)石墨烯[57]和(c)h-BN[49,58]在不同厚度SiO2上(即Si/SiO2衬底), 不同波长的入射光下的光学对比度变化规律, 以及相应光学照片和原子力显微镜图片; (d) SiO2上MoS2的光学照片, 也可以看出对比度随着SiO2的厚度变化显著[59]Figure1. Mechanical exfoliation and rapid identification of layer number for two-dimensional atomic crystal (2DACs): (a) Schematic diagram of the mechanical exfoliation process of graphene, photos of the individual exfoliation steps ((1)–(4)) and optical images of the sample ((5)), in which flakes with different layers can be observed[55]. Optical contrast of graphene[57] (b) and h-BN[49,58] (c) on Si/SiO2 substrate with different thickness of SiO2 for the incident light with different wavelengths, and corresponding optical images and atomic force microscope (AFM) images. (d) Optical images of MoS2 on SiO2, exhibiting that optical contrast varies notably with the thickness of SiO2[59].
机械剥离的二维原子晶体如果长时间在空气中暴露, 表面会吸附尘埃颗粒、水蒸汽以及气体分子等, 导致微观结构和物理性质显著变化[48,57]. 因此, 转移堆叠的第二步是快速识别样品的层数及形貌, 然后根据器件制备的需求选择合适的晶体, 进一步更精确地表征. 层数是二维原子晶体的最关键参数之一, 其测量方法有多种, 但实际叠层转移过程要求能够快速地初步判断层数. 由于光的吸收以及界面干涉和衍射过程, 衬底上的二维原子晶体由于厚度不同会产生显著的光学对比度差异, 所以光学显微镜是最简单和常用的手段. 除了二维原子晶体本身的层数, 衬底厚度对光学对比度也有很大影响. 如单层石墨烯在不同厚度SiO2上的光学对比度会也明显不同(图1(b))[58], h-BN和MoS2也存在类似规律(图1(c)和图1(d))[49,59,60]. 这一点在使用聚合物对二维原子晶体进行转移堆叠时需加以考虑, 通常需要调整聚合物的厚度以获得最佳的光学对比度. 但利用光学显微镜识别二维原子晶体的层数不可避免会产生偏差, 精确测量层数和形貌还需要借助光谱表征[61,62]或者原子力显微镜等手段[1,19].
机械剥离法制备的二维原子晶体一般仅有几微米到几百微米, 因此增大样品的尺寸(或面积)是机械剥离法的主要研究内容之一[54]. 剥离过程涉及三部分: 块材(各种层状晶体)、粘接材料(如胶带)和衬底(SiO2/Si, 蓝宝石等). 研究表明, 增强块材/衬底之间的结合力有助于剥离大尺寸二维原子晶体. 例如, Huang等[63]对SiO2/Si衬底的表面进行等离子体处理, 增强了块材和衬底之间的结合力, 显著提高了石墨烯等二维原子晶体的剥离尺寸. 增强块材/粘接材料之间的粘接力也有利于剥离较大尺寸的二维原子晶体. 这里所说的粘接材料通常是胶带, 也可以是其他与层状晶体表面存在较强结合力的材料(如金属薄膜或氧化物薄膜). 如Desai等[64]基于金对硫族元素的强亲和势, 报道了一种金辅助剥离法. 将沉积在过渡金属二硫族化合物(TMDCs)晶体表面的一层金薄膜作为粘接材料(即“金胶带”), 实现了大尺寸单层TMDCs的剥离. 最近, Huang等[65]基于对金属/层状晶体界面吸附能和层间键能的理论计算对该法进行了系统优化, 开发出一种普适性的超大面积金辅助剥离法. 该方法具有很好的普适性, 能够剥离毫米级二维半导体、铁磁体和超导体等, 如图2(a)所示. 然而, 金辅助剥离法尚有不足, 特别是金薄膜需要腐蚀液才能去除, 所以极易引入杂质(图2(b))[66]. Deng等[67]报道了一种Al2O3辅助剥离法, 即利用沉积的Al2O3薄膜与层状晶体的新鲜解理面之间的较强结合力, 解理出单层铁磁体Fe3GeTe2[34]和拓扑绝缘体MnBi2Te4. 如图2(c)所示, Al2O3薄膜在后续工艺中可直接用作衬底, 从而避免液相腐蚀过程.
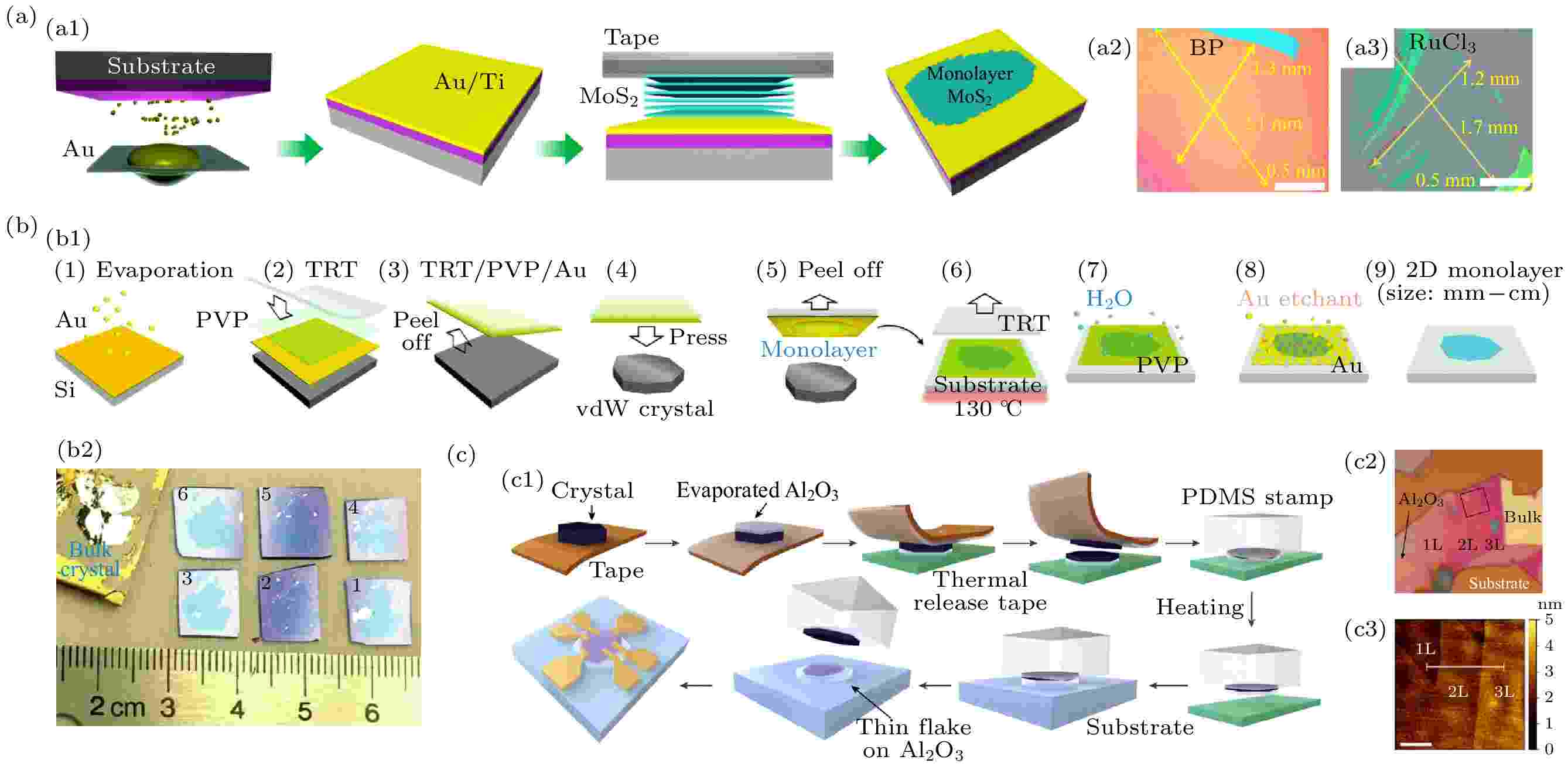图 2 大尺寸二维原子晶体的剥离技术 (a)金辅助的超大面积剥离法的示意图以及利用该法制备的毫米级黑磷和三氯化钌(RuCl3)的光学照片[63]; (b)金辅助剥离后的湿法去除金薄膜的过程和大面积样品的照片[64]; (c) Al2O3辅助剥离法及器件制备过程示意图, 以及制备的Fe3GeTe2样品的光学照片和原子显微镜图片[65]Figure2. Exfoliation technique of large-sized 2DACs: (a) Schematic illustration of the ultra-large area Au-assisted exfoliation and optical images of millimeter-sized black phosphorus and ruthenium trichloride (RuCl3) obtained by this method[63]; (b) wet chemical removal of gold films after Au-assisted exfoliation and optical images of large-area flakes[64]; (c) schematic of Al2O3-assisted exfoliation and device fabrication process, optical images and AFM images of Fe3GeTe2 flakes[65].
机械剥离法虽然取得了较大进展, 但也面临诸多问题. 转移过程中需要的胶带或者其他粘接材料不可避免地会引入污染, 因此大尺寸二维原子晶体的超洁净剥离技术仍需进一步研究. 又如, h-BN是目前该领域最为常用的绝缘电介质, 但相较于石墨烯和TMDCs, 大尺寸二维h-BN的剥离很困难, 因此亟需探索大尺寸h-BN的剥离技术. 整体而言, 由于层状材料的元素组成、晶体结构及层间结合力不同, 增大某种二维原子晶体的剥离尺寸需要针对性的系统研究.
2
2.2.二维原子晶体的转移堆叠技术
32.2.1.转移堆叠技术概述
如上文所述, 机械剥离是将二维原子晶体从块材解理到衬底上的过程. 与之相比, 转移堆叠则是将二维原子晶体从某一衬底移动到另一种衬底或另一种二维原子晶体(下文统称为目标衬底)表面的过程, 转移介质一般不再是常用的胶带, 而是具备一定粘性的透明聚合物薄膜, 如图3所示[55]. 转移堆叠技术有多种, 但基本过程和设备大致相似. 制备叠层结构的转移台一般包括三部分: 配备长焦镜头的光学显微镜、透明载玻片和精密微定位器. 长焦镜头可以提供大的工作距离, 保证转移过程中能够大幅度升降载玻片, 已实现在不同平面上的聚焦. 微定位器主要用于承载二维原子晶体, 通常配备两个: 一个微定位器固定在可旋转基座上, 装配有真空吸盘和温控系统, 用于固定目标衬底和控制转移过程的温度; 另一个微定位器则用于移动载玻片(承载了另一种二维原子晶体). 微定位器不仅可以在x, y和z方向相对调整, 还可以倾斜和旋转.
图 3 转移堆叠过程示意图和常用转移台的照片[55]Figure3. Schematic of the transfer and stacking process and photos of commonly used probe station[55].
以典型的石墨烯/h-BN叠层结构为例, 尽管这两种材料在空气中都比较稳定, 但晶体尺寸一般小于100 μm, 且二维结构异常脆弱, 因此将石墨烯转移到h-BN表面需要克服一系列技术难题, 本文以此为例介绍转移堆叠方法的发展过程. 转移堆叠方法可以从不同角度进行分类[68-70], 由于本文主要聚焦高质量器件, 因此重点关注不同转移方法获得的界面(或表面)质量.
3
2.2.2.聚合物基转移法
2010年, 美国哥伦比亚大学的Dean等[49]首次采用聚合物(聚甲基丙烯酸甲酯, PMMA)作为转移介质制备了石墨烯/h-BN叠层结构(也称为PMMA转移法), 如图4(a)和图4(b)所示. 首先将石墨烯剥离到PMMA薄膜/水溶性聚合物薄膜/SiO2/Si衬底上. 通过改变旋涂条件可以调整PMMA薄膜的厚度, 达到与石墨烯之间的理想光学对比度. 然后将整个衬底浸入去离子水中, 待水溶聚合物溶解后PMMA薄膜漂浮在水面上, 石墨烯则附着于薄膜表面. 使用载玻片捞起漂浮的PMMA薄膜, 加热干燥后将载玻片翻转(承载石墨烯的一面朝下), 用微定位器固定. 同时, 将h-BN剥离到另一SiO2/Si衬底上, 并在基座上固定. 然后使用显微镜和微定位器, 将载玻片上的石墨烯与基座上的h-BN对准. 令二者接触后升高基座的温度, 保温一段时间可使PMMA薄膜与载玻片分离, 从而将石墨烯转移到h-BN上. 最后, 将制作好的叠层浸入丙酮或在H2/Ar中退火, 去除表面残留物.
图 4 (a)PMMA转移过程的具体步骤示意图以及(b)对应的光学照片[49]; (c)石墨烯在SiO2和h-BN衬底表面的形貌图和电荷密度图[71]; (d)石墨烯分别在SiO2和h-BN衬底上的转移特性曲线[49]Figure4. (a) Schematic of individual steps of the PMMA transfer process and (b) the corresponding optical images of the flakes taken for each step[49]; (c) topography and charge density maps of graphene on SiO2 and h-BN[71]; (d) transfer curves of graphene on SiO2 and h-BN substrates[49].
PMMA转移法在转移堆叠及高质量器件的发展过程中具有重要意义. 扫描隧道显微镜(STM)的早期研究表明, 石墨烯在SiO2/Si衬底上通常是高度无序的[71], 实际的电学特性相对于其本征态也会发生显著变化[48,51]. h-BN是一种与石墨烯结构类似的宽带隙绝缘体(约6 eV), 能够为石墨烯提供原子级平坦的衬底. 在h-BN衬底上, 石墨烯的表面粗糙度和电荷密度不均匀性都显著降低(图4(c)). 基于PMMA转移法制备的石墨烯/h-BN叠层结构, 石墨烯载流子迁移率可以到60000 cm2/(V·s), 比以SiO2为衬底的器件提高了一个数量级(图4(d))[49], 但远未达到石墨烯迁移率的理论预测值.
3
2.2.3.叠层结构的界面污染
聚合物基转移法虽然实现了转移堆叠过程, 但仍存在诸多严重的问题. 漂浮在液体中的二维原子晶体/PMMA薄膜需要用载玻片捞起, 该操作极易引起二维原子晶体产生皱纹或吸附液体分子. 类似的水基转移法都存在类似的问题[72]. 针对该问题, Taychatanapat等[73]利用聚乙烯醇(PVA)代替了水溶性聚合物, 即利用胶带将PMMA/PVA复合薄膜从SiO2/Si衬底上机械剥离下来, 然后制备叠层结构, 避免了从溶液中捞起的过程. 此外, 利用聚二甲基硅氧烷(PDMS)或聚丙烯酸酯碳酸酯(PPC)取代PVA也有助于提高叠层转移的效率[74,75]. Zomer等[76]则利用Elvacite(丙烯酸树脂)取代PMMA, 即将Elvacite作为“牺牲层”, 一旦其接触加热的衬底就会熔化, 从而将二维原子晶体从胶带释放到目标衬底.然而, 无论采用任何聚合物, 二维原子晶体都不可避免地要与之直接接触, 最终在接触处产生残留聚合物. 特别是在制备多叠层结构时, 连续接触聚合物导致聚合物残留会更为严重, 如图5(a)所示[37]. 由于转移堆叠通常在大气中进行, 堆叠过程中界面处通常会形成气泡和褶皱. 这些杂质、气泡和褶皱都会导致额外的无序, 减小叠层的可用面积. 器件加工的过程中需要人为地避开杂质和气泡(如图5(b)所示)[77], 从而增加了器件工艺和结构的复杂程度. 高质量电子器件要求叠层结构的所有界面必须洁净[48,51], 因此以PMMA转移法为代表的聚合物基转移方法目前已经较少应用于高质量电学器件的制备, 只在局域电学测量如STM研究中偶有采用[78].
图 5 (a)聚合物基转移法导致的界面杂质及气泡的AFM图[37]; (b)利用含有气泡的叠层制备的器件光学照片, 其中将顶栅电极设计为复杂形状是为避开气泡[77]Figure5. (a) AFM images of interfacial impurities and bubbles resulting from polymer-based transfer process[37]; (b) optical images of the devices fabricated with stacks containing bubbles, in which the complex top gate shape was designed to avoid the bubbles[77].
3
2.2.4.pick-up转移法
Wang等[36]基于二维原子晶体之间的范德瓦耳斯力开发了一种pick-up转移法(或称为范德瓦耳斯拾取转移法), 其主要特点是整个转移过程中二维原子晶体不接触任何聚合物, 从而彻底消除了叠层界面的聚合物残留和气泡聚集, 基本过程如图6(a)所示. 以h-BN/石墨烯/h-BN叠层为例, 首先在SiO2/Si衬底上旋涂适当厚度的PPC薄膜, 然后将h-BN剥离到PPC层上(选择较厚的h-BN有利于减少叠层中的褶皱). 使用透明胶带将PPC薄膜从SiO2/Si衬底上剥离下来, 并粘贴到固定于载玻片表面的PDMS上, 然后将载玻片翻转并安装到微定位器上. 载玻片上的h-BN与SiO2/Si衬底上的石墨烯对准, 然后加热到PPC的玻璃化转变温度(约40 ℃)以上使其体积发生膨胀. 由于范德瓦耳斯相互作用较强, 相比于SiO2/Si衬底, 石墨烯更倾向于粘附在h-BN上. 冷却过程中, PPC转变为玻璃态, 体积发生收缩, 从衬底上拾取石墨烯. 重复相同过程, 可以继续拾取底部的h-BN. 根据具体的叠层结构, 可以连续拾取所需的二维原子晶体. 整个叠层完成后, 将其加热到较高温度便可从PDMS中释放PPC膜, 从而将叠层释放到最终衬底上.
图 6 (a) pick-up转移法的过程示意图; 所制备的叠层结构的(b)光学照片、(c) AFM图像和(d)截面TEM图像; (e)器件的转移特性曲线. 插图分别为器件的光学照片和低温电学输运测量结果[36]Figure6. (a) Schematic of the pick-up transfer process; (b) optical images, (c) AFM images and (d) cross-sectional TEM images of the obtained h-BN/graphene/h-BN stacks; (e) transfer curves of the device. The left and right insets are optical images of the device and low-temperature electrical transport measurements, respectively[36].
pick-up转移法最显著的优势在于叠层内部的所有界面都未与任何聚合物接触, 从而可以获得极为洁净的界面[48,51]. 不仅如此, 由此构建的h-BN封装叠层结构可以在器件制备过程避免石墨烯受外界影响, 对于高质量器件而言意义重大. 从图6(b)—图6(d)可以看出, 叠层界面处没有任何污染. 石墨烯的室温载流子迁移率可达105 cm2/(V·s)量级的理论值, 如图6(e)所示. 值得注意的是, 拾取过程中石墨烯会沿着上层h-BN的边缘被撕裂, 因此pick-up转移法制备的叠层结构的最终尺寸严格受限于h-BN的尺寸, 这也为一种独特的叠层转移技术创造了机遇, 即2.3小节中将要讨论的“撕裂+堆叠”法.
2
2.3.莫尔超晶格的制备
基于pick-up转移法带来的巨大进步, 研究者们在叠层结构的界面质量和结构可控性等方面取得了一系列进展, 最为典型的例子是莫尔超晶格的构建. 叠层结构界面处存在一个独特的自由度, 即层间转角θ. 该自由度在传统的二维量子阱中是不存在的, 能够导致出现一系列奇异的物理现象. 在石墨烯/h-BN叠层中, 两者晶格对齐(θ接近0°)时由于晶格间的微小失配(约1.6%)会形成周期性的莫尔超晶格, 如图7(a)所示[79]. 类似地, 两个单层石墨烯之间的旋转也能产生莫尔超晶格. 莫尔超晶格能够引入莫尔周期势, 从而强烈地改变二维原子晶体的本征能带结构[50-53]. 有关莫尔超晶格器件的进展会在3.4小节中详细讨论, 这里主要以石墨烯/h-BN和转角双层石墨烯为例, 介绍莫尔超晶格的制备技术.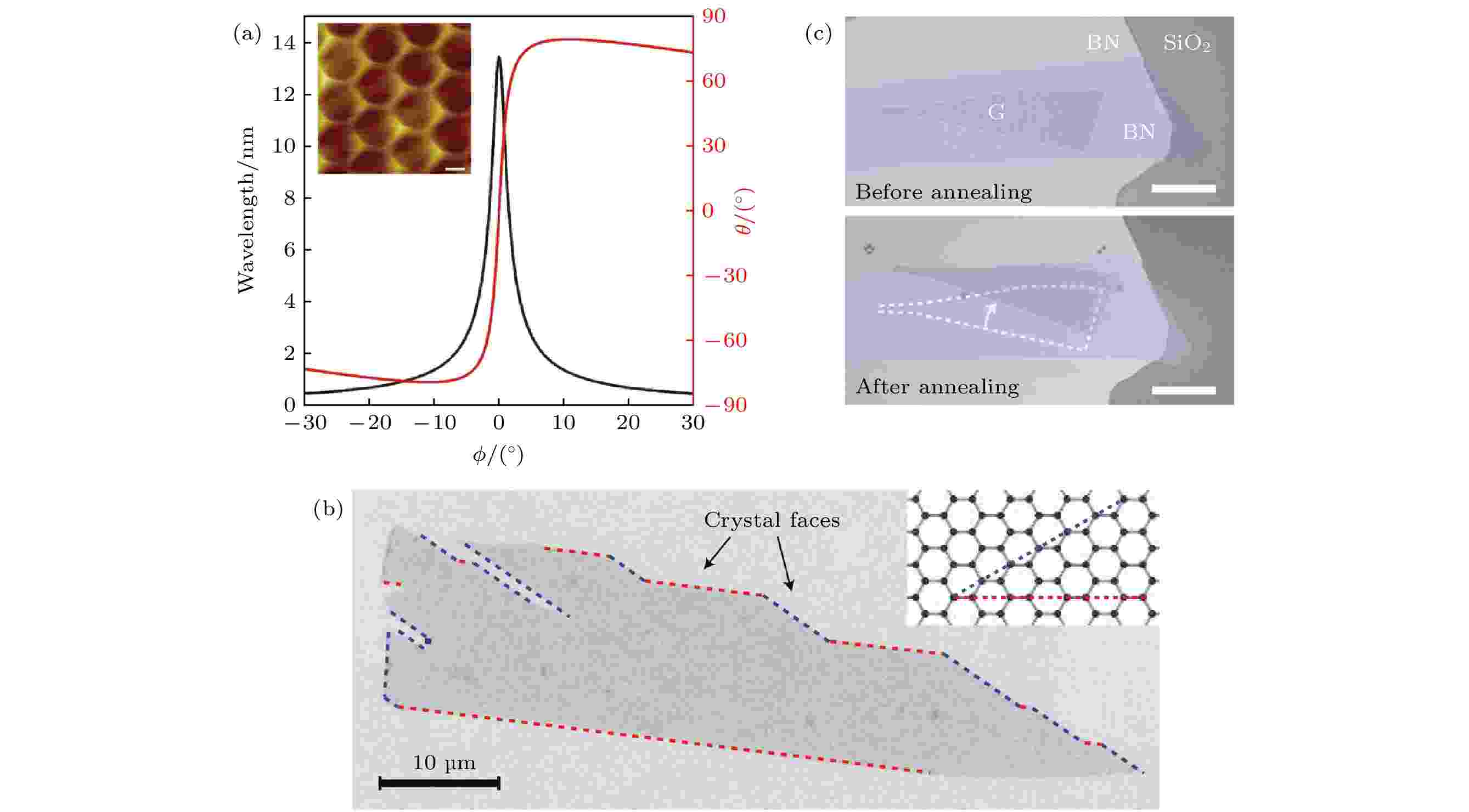
图 7 (a)石墨烯/h-BN莫尔超晶格的波长(黑色)和超晶格旋转角(红色)与层间转角的关系曲线, 插图为波长11.5 nm的莫尔超晶格的STM图像[79]; (b)单层石墨烯晶体边缘对应特定的晶向, 插图为石墨烯晶格模型中标示出的对应晶向[7]; (c)退火前后, h-BN/石墨烯/h-BN叠层的光学照片[81]Figure7. (a) Plot of the wavelength of the graphene/h-BN moiré superlattice (black) and the rotation angle of the superlattice (red) as function of the rotation angle between layers[79]. The inset represents STM image of the moiré superlattice with a wavelength of 11.5 nm. (b) edges of the monolayer graphene crystal correspond to specific crystal orientation[7]. The inset shows the corresponding crystal orientation denoted with dashed line in the lattice model. (c) optical images of h-BN/graphene/h-BN stacks before (upper penal) and after (lower penal) annealing[81].
实现石墨烯/h-BN叠层的晶格对准有几种基本方法. 在机械剥离过程中, 二维原子晶体通常按照特定的晶面解理, 因此晶体的笔直边缘通常指示特定的晶向, 如图7(b)所示[7]. 因此, 实现两种晶格对准的最简单方式是选择石墨烯和h-BN的特定直边, 并在堆叠过程中转动转移台, 控制选定直边之间的夹角大小.
例如, Ponomarenko等[80]通过对准石墨烯和h-BN的直边实现了对叠层转角的控制, 对准精度约为1°. 除了在堆叠转移过程中人为控制转角, Wang等[81]研究发现, h-BN/石墨烯/h-BN叠层在退火过程中, 石墨烯的一个边缘与h-BN的一个边缘会自发地形成大致对齐的结构(图7(c)). 这种晶格相对运动可能是热诱导的体系能量过渡到最低态, 因此可以通过退火使石墨烯自发旋转到与h-BN晶格对准的位置.
石墨烯莫尔超晶格的出现实际早于石墨烯/h-BN莫尔超晶格. 在剥离石墨烯的早期实验中, 利用STM在HOPG表面就曾发现随机形成的莫尔超晶格, 在转角很小时发现了体系中存在范霍夫奇点. 如2.2.4小节所述, 在利用pick-up技术制备石墨烯/h-BN叠层结构的过程中, 石墨烯通常会沿h-BN的边缘被撕裂. Kim等[82]基于这一实验现象, 在拾取过程中选择性地撕裂同一片石墨烯制备了转角双层石墨烯莫尔超晶格, 这种方法也被称为“tear and stack”法(“撕裂+堆叠”法). 如图8(b)所示, 首先利用h-BN拾取石墨烯的一半, 然后将SiO2/Si衬底(即样品台基座)旋转一定角度后, 再拾取剩余的另一半石墨烯, 最后拾取底层h-BN. 由于这两片单层石墨烯来自同一片石墨烯, 二者晶体取向完全相同, 因此样品台的旋转角就是双层石墨烯的层间转角, 如图8(c)所示[83]. 对于TMDCs还可以使用二次谐波等光学手段推测晶向, 以此为参考辅助转角控制. 对于较厚的二维原子晶体, 可利用AFM针尖或等离子蚀刻等方法将其切割(图8(d)). 利用STM证实, “撕裂+堆叠”法制备的叠层中的确形成了莫尔超晶格(图8(e))[82]. 与对准笔直边缘法相比, “撕裂+堆叠”法能够更精确地控制层间转角; 但在撕裂过程中会对二维原子晶体施加剪切应力, 小幅度改变其面内取向, 导致转角稍微偏离预期值. 由于魔角双层石墨烯中的电子关联态对转角极为敏感, 因此亟需开发转角精确可控的转移方法.
图 8 (a)“撕裂+堆叠”法制备石墨烯莫尔超晶格的过程示意图以及相应的光学照片[82]; (b)转移台的旋转过程示意图[83]; (c)“切割+堆叠”法制备石墨烯莫尔超晶格叠层的光学照片; (d)制备的莫尔超晶格的STM图像[82]Figure8. (a) Schematic diagram of the preparation process of graphene moiré superlattice by “tearing + stack” method and the corresponding optical images[82]; (b) schematic of the rotating the stage (supporting the underlying graphene) during “tearing + stack” process[83]; (c) optical images of the graphene moiré superlattice prepared by “tearing + stack” method; (d) STM image of the obtained graphene/h-BN moiré superlattice[82].
2
3.1.器件中的无序
33.1.1.无序对于电学输运的影响
所谓的“无序”主要包括晶体缺陷产生的本征无序和周围环境导致的外部无序[48,57]. 本征无序主要包括原子缺陷, 例如空位、反位、替代、边缘和晶界等, 是在天然形成或人工合成晶体的过程中产生的, 通常需要通过生长工艺的优化才能改善. 外部无序的主要来源包括应变、吸附物、衬底表面粗糙度、衬底中的带电杂质以及环境导致的氧化等. 二维原子晶体按照定义来讲几乎完全是表面, 因此非常容易受到多种外部无序的影响. 最典型的, 衬底诱导的无序性可以导致静电势变化、电荷载流子散射、能带结构局部改变以及激子复合中心等, 显著影响二维原子晶体的电学性质[71,84-86].对于石墨烯而言, 目前通过机械剥离法已经能够获得质量很高的二维单晶, 因此外部无序是影响其输运特性的主要因素. 下面以石墨烯为例, 讨论外部无序对电学输运特性的影响, 以及如何通过转移堆叠和器件工艺降低器件中的无序. 由于量子霍尔效应与样品中的无序密切相关, 本文以可观测到的量子霍尔态为评价无序的标准(图9). 尽管剥离的石墨烯其本征缺陷密度已经很低, 但受限于SiO2衬底的无序, 低温下石墨烯的载流子迁移率仅为103—104 cm2/(V·s). 早期利用直接剥离到SiO2/Si上的石墨烯仅能观察到四重简并的整数量子霍尔效应. 理论和实验研究都证实, 衬底表面电荷的不均匀分布和表面吸附物引起的电势无序是低温下主要的载流子散射机制[87,88]. 通过刻蚀沟道下方的SiO2所构建的悬浮器件可以大幅降低石墨烯中的电荷不均匀性, 液氦温度下载流子迁移率提高至200000 cm2/(V·s)[89-91], 从而可观测到分数量子霍尔效应[92,93]. 但悬浮结构本身要承受栅极的静电力吸引, 结构比较脆弱, 无法大范围调控沟道载流子浓度.
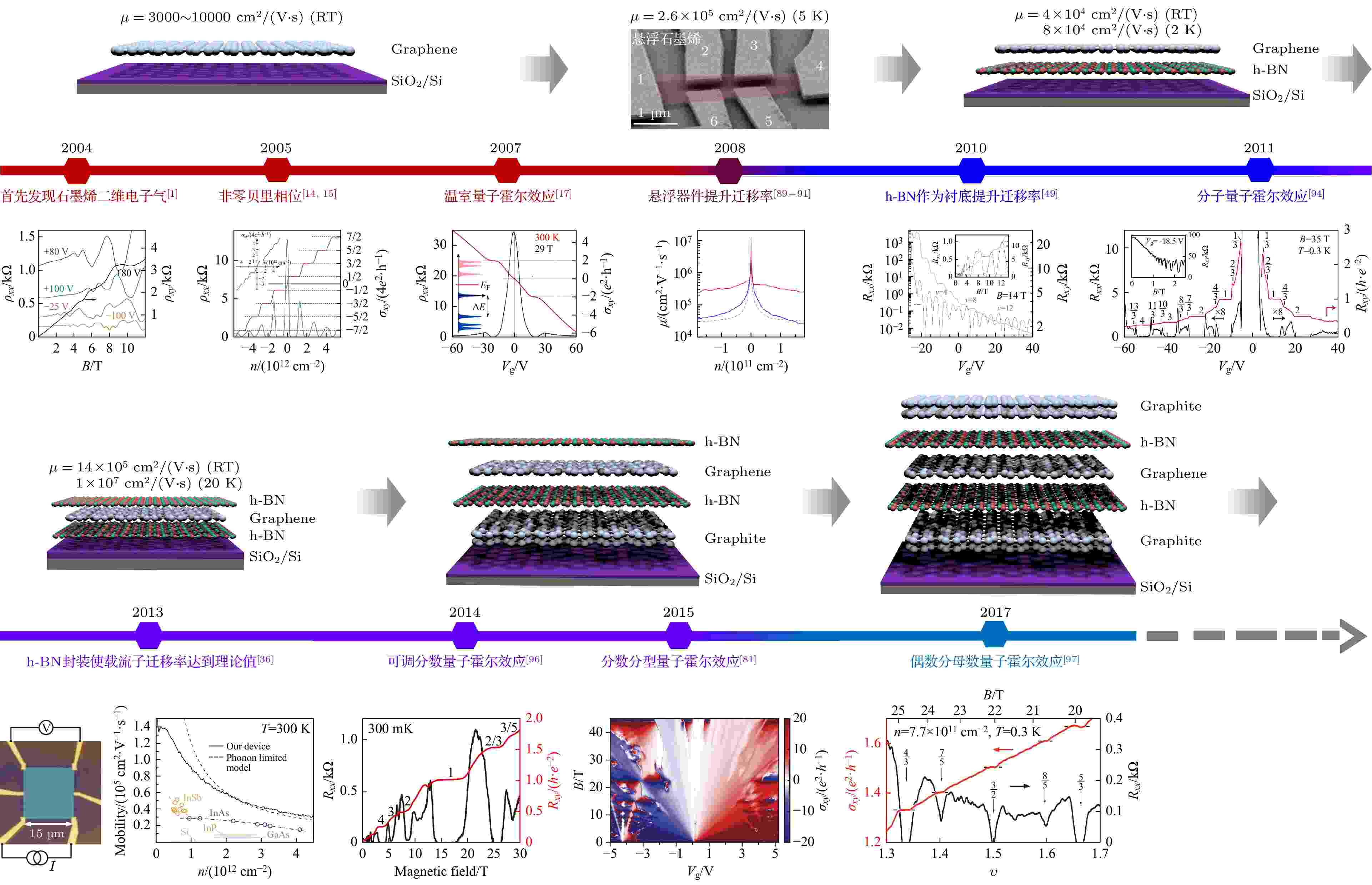图 9 石墨烯器件的无序降低以及由此带来的器件质量提升, 以可观测到的量子霍尔态为评价标准Figure9. Progress of reducing the disorder in graphene-based devices and the resulting improvement of device quality, evaluated by the observable quantum Hall state.
3
3.1.2.h-BN封装叠层结构
与SiO2/Si衬底相比, 利用PMMA转移法将石墨烯转移到h-BN衬底上能够显著提升器件质量, 由此可以观察到四重简并朗道能级的解除[49]以及分数量子霍尔效应和量子霍尔铁磁性等[94,95]. PMMA转移法制备的器件仍然受到转移堆叠和电极图案化过程中残留聚合物的影响, 所以这类器件在液氦温度下载流子迁移率可达到60000—100000 cm2/(V·s), 仍低于悬空的石墨烯器件.Wang等[36]利用pick-up拾取技术制备h-BN“封装”的石墨烯器件, 即构建封装叠层结构, 能够将石墨烯与外界环境有效隔绝. 在半导体产业中, “封装(Packaging)”通常指将测试过的晶圆进行加工得到独立芯片的过程. 而对于二维原子晶体, “封装(Encapsulation)”指的是利用h-BN将二维原子晶体双面“包覆”起来的过程. 封装石墨烯叠层器件显示出弹道输运特性, 其室温电子平均自由路径达到微米量级, 室温迁移率达到理论值100000 cm2/(V·s); 低温电子平均自由程大于20 μm, 迁移率大于1000000 cm2/(V·s), 这为高质量二维电子器件奠定了极其重要的基础[36,37].
封装叠层结构已经在最大程度上消除了器件层中无序的影响. 然而研究发现, 封装叠层的上方或下方的金属栅极会导致静电势波动, 进而影响器件的电学输运性质. 为解决该问题, 使用pick-up转移法引入薄层石墨作为栅极可以使沟道附近的电势波动最小化. 2014年, Maher等[96]首次利用薄层石墨作为底栅极封装的双层石墨烯器件, 观察到双层石墨烯上的分数量子霍尔态. 最近, 利用这种无序极低的器件在实验上已经观察到了偶数分母分数量子霍尔态[97-100], 这类器件中的无序密度已降低到109 cm–2以下.
即便如此, 朗道能级的展宽分析证实, 石墨烯器件的无序性仍比GaAs/AlGaAs量子阱高约两个数量级[48]. 无序的起源尚不明确, 可能是叠层界面存在少量环境中的杂质(例如水或碳氢化合物分子), 也可能是h-BN含有的微量氧或碳杂质所致. 迄今为止, 除了“条纹”相外[101], GaAs异质结器件的几乎所有量子霍尔效应现象都可以在石墨烯叠层器件中观察到. 随着石墨烯器件质量的持续提高, 相信更多量子霍尔效应现象都可以被研究. 以石墨烯为代表的二维单晶具有更强的电子相互作用以及调节载流子浓度的能力, 这使得能够更广泛地调控量子霍尔态.
对于以TMDCs为代表的化合物二维原子晶体而言, 其晶体质量尚不及石墨烯, 缺陷密度在1011—1012 cm–2范围内, 所以本征无序和外部无序在其电学输运研究中都需要考虑. 关于TMDCs中的本征缺陷及如何改善已有较多系统的论述, 这里不再赘述. 本文主要讨论外部无序对其输运特性的影响以及如何通过器件工艺加以改善. TMDCs包含了多种过渡金属与硫族元素形成的二维原子晶体, 除半导体(MoS2, WS2, MoSe2和WSe2)外, 还包含超导体(NbSe2)和拓扑绝缘体(WTe2)等[4,9], 本文主要以二维半导体MoS2为例讨论器件无序问题.
与石墨烯类似, 衬底在单层MoS2中诱导的无序在STM测量中也可以观察到, 如图10(a)所示[102]. 研究表明, 单层MoS2的电子迁移率既受到材料内部声子散射的影响, 又受到衬底中无序性的影响[103,104]. 室温下, 单层MoS2在SiO2/Si衬底上的迁移率通常约为10 cm2/(V·s), 远低于预测的声子散射极限值(约400 cm2/(V·s))(图10(b))[105]. 如图10(c)所示, 通过高κ电介质钝化(如HfO2或Al2O3)或h-BN封装都可以减少这种无序, 显著提高MoS2的室温载流子迁移率[106-108]. 低温下, SiO2/Si衬底上的MoS2器件在低载流子浓度时甚至表现出近绝缘特性, 这表明产生了无序诱导的局域化. HfO2钝化可以消除低载流子浓度下的绝缘行为, 但高载流子浓度下的迁移率依然较低. 相比之下, h-BN封装叠层结构可以将单层MoS2的迁移率提高大约一个数量级(图10(d))[108]. 高κ电介质钝化层通常采用与传统半导体工艺兼容的原子层沉积(ALD)制备, 更适合于研究在室温工作的微电子器件; 电学输运测量通常在低温强磁场下进行, 因此h-BN封装叠层结构更适合于高质量电子器件的输运研究.
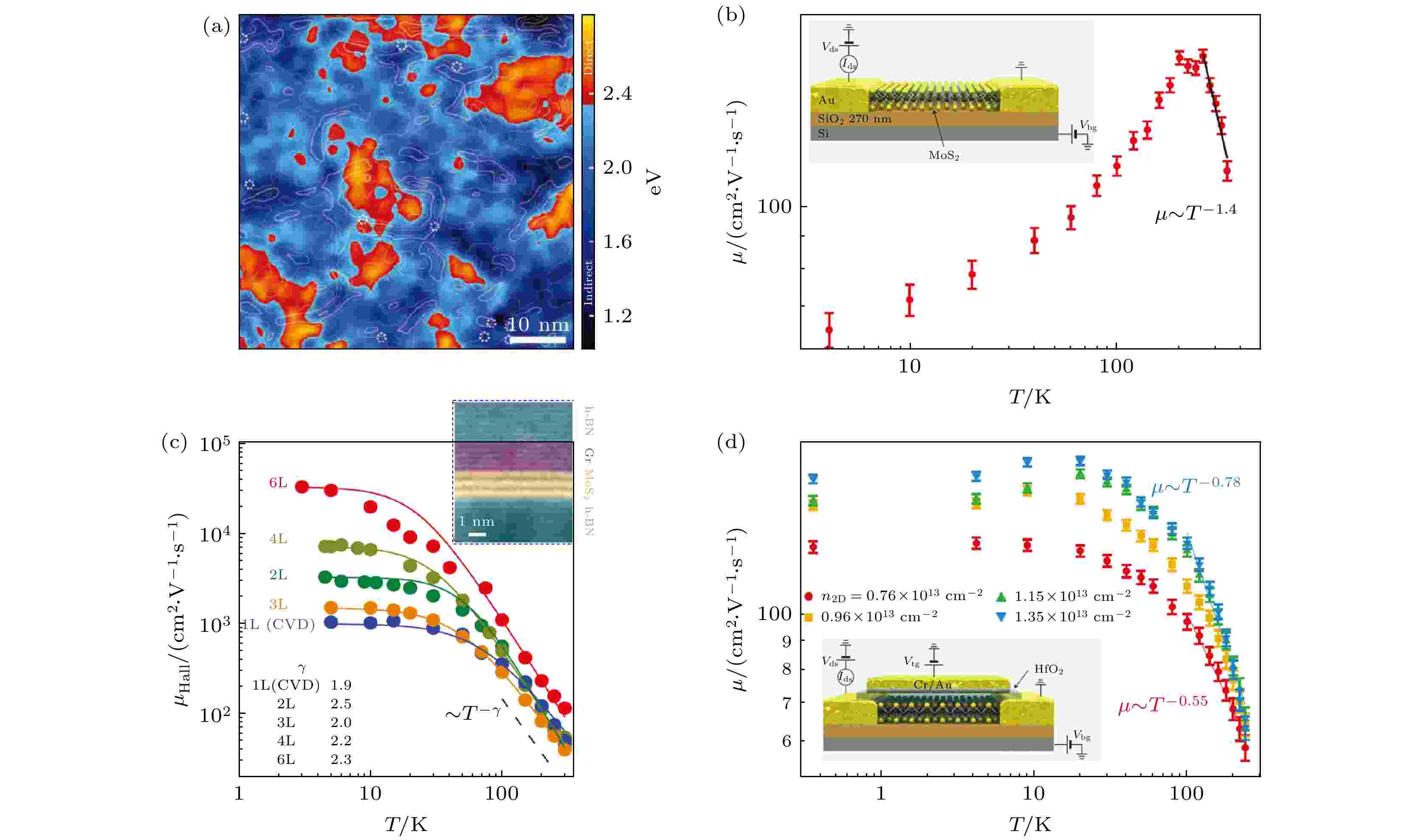图 10 (a)基于STM测量结果推导出的SiO2/Si衬底上MoS2的能带结构变化[102]; (b) SiO2/Si衬底上MoS2的迁移率随温度的变化, 插图为器件结构示意图[104]; 通过(c) h-BN封装技术[109]和(d) HfO2钝化技术[107]屏蔽外部无序后, MoS2的迁移率随温度的变化Figure10. (a) Variation of energy band structure of MoS2 on SiO2/Si substrate, deduced from STM measurements[102]; (b) Plots of MoS2 mobility as function of temperature on SiO2/Si substrates[104]. The inset illustrates the device structure. The mobility of MoS2 vs. temperature after screening the external disorder by (c) encapsulation with h-BN[109] and (d) passivation with HfO2[107].
需要指出的是, 封装叠层结构对TMDCs中无序性的降低程度远小于石墨烯, 这很大程度上是由于TMDCs晶体的质量远未达到结构近乎完美的石墨烯晶体[48,57,110]. 整体而言, 封装叠层器件已经使低温强磁场下TMDCs的电学输运测量可以实施. 对于二维半导体而言, 电学接触问题实际更为严重, 因此关于将在3.3.3小节中详细讨论.
石墨烯、h-BN和MoS2等研究较多的二维原子晶体在空气中比较稳定, 机械剥离和转移堆叠过程都可以在空气中进行, 封装叠层结构也在电极工艺中起到很好的保护作用. 而对于许多敏感型二维原子晶体而言, 环境中的水和氧导致的氧化是首要问题, 例如二维半导体、超导体、拓扑绝缘体及铁磁体等. 空气氧化会严重影响这类二维原子晶体的结构, 甚至使其完全瓦解, 无法进行电学输运特性研究[111,112]. 在手套箱内的惰性气氛中进行机械剥离, 并采用封装叠层结构可以很好地保护敏感型二维原子晶体以研究其物理特性, 例如二维半导体(BP)、超导体(NbSe2)、拓扑绝缘体(WTe2)以及铁磁体(CrI3)等[31,32,113,114], 如图11所示.
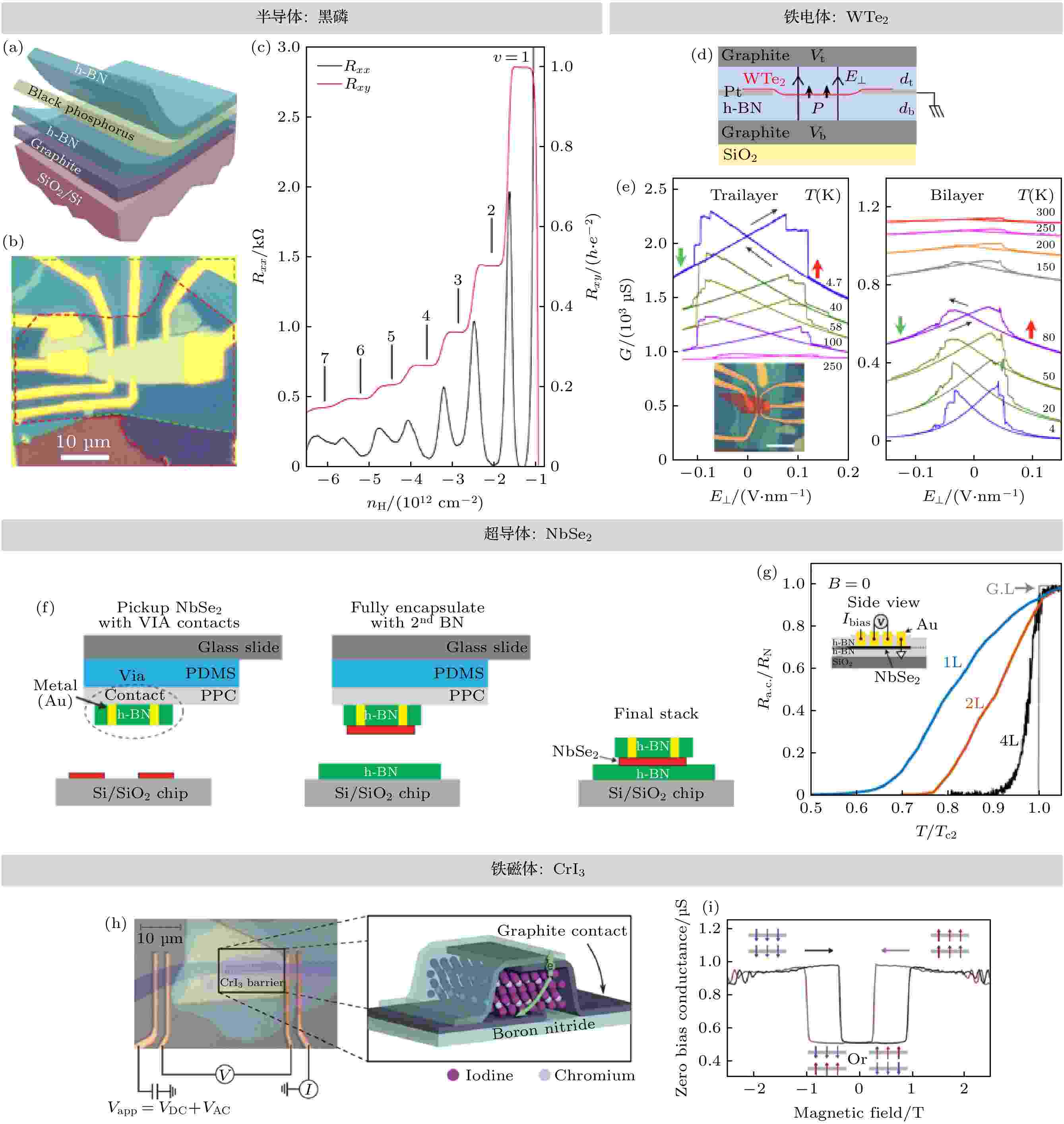图 11 h-BN封装结构用于空气敏感型二维原子晶体的电学输运、磁学及铁电极化特性的研究 (a)—(c)半导体: BP[113]; (d), (e)铁电体: WTe2[31]; (f), (g)超导体: NbSe2[114]; (h), (i)铁磁体: CrI3[32]Figure11. Study on the electrical transport, magnetic and ferroelectric polarization characteristics of unstable 2DACs with h-BN encapsulation: (a)?(c) semiconductor: black phosphorous[113]; (d), (e) ferroelectric: WTe2[31]; (f), (g) superconductor: NbSe2[114]; (h), (i) ferromagnet: CrI3[32].
2
3.2.二维原子晶体的电学接触
电学接触的质量也是影响电子器件质量的关键因素之一. 实验上通常利用接触电阻(Ω·μm)来衡量接触特性, 最理想的是获得低电阻的欧姆接触. 总体上讲, 对于石墨烯而言, 一维边缘接触结构很好地解决了接触电阻的问题, 石墨烯电学输运研究的主要问题在于如何进一步降低无序以及丰富调控手段. 而对于二维半导体而言, 电学接触问题则较为复杂, 实现理想的欧姆接触仍是电学输运测量所面临的主要挑战之一.3
3.2.1.石墨烯的边缘电学接触
h-BN封装叠层结构是目前降低二维原子晶体外部无序的最有效方法, 同时也对电极接触工艺提出额外要求. 采用传统的开槽工艺很难保证刻蚀h-BN的过程不破坏包裹在叠层内部的二维原子晶体. 针对封装叠层结构, Wang等[36]开发了一种独特的边缘电学接触工艺. 如图12(a)所示, 首先将整个叠层结构进行刻蚀, 只暴露石墨烯边缘; 再沉积金属, 自然形成一维边缘接触. 边缘电学接触工艺与封装叠层结构完美匹配, 因此可以最大程度地还原二维原子晶体的本征特性. 原因主要在于一维边缘接触能够实现较好的界面成键和较低的隧穿势垒, 有利于从电极向石墨烯的面内晶格注入载流子(图12(b)和图12(c)). 实验表明, 石墨烯器件的边缘接触电阻值可低至100 Ω·μm (图12(d)), 目前石墨烯的电学输运特性研究普遍采用这种接触结构.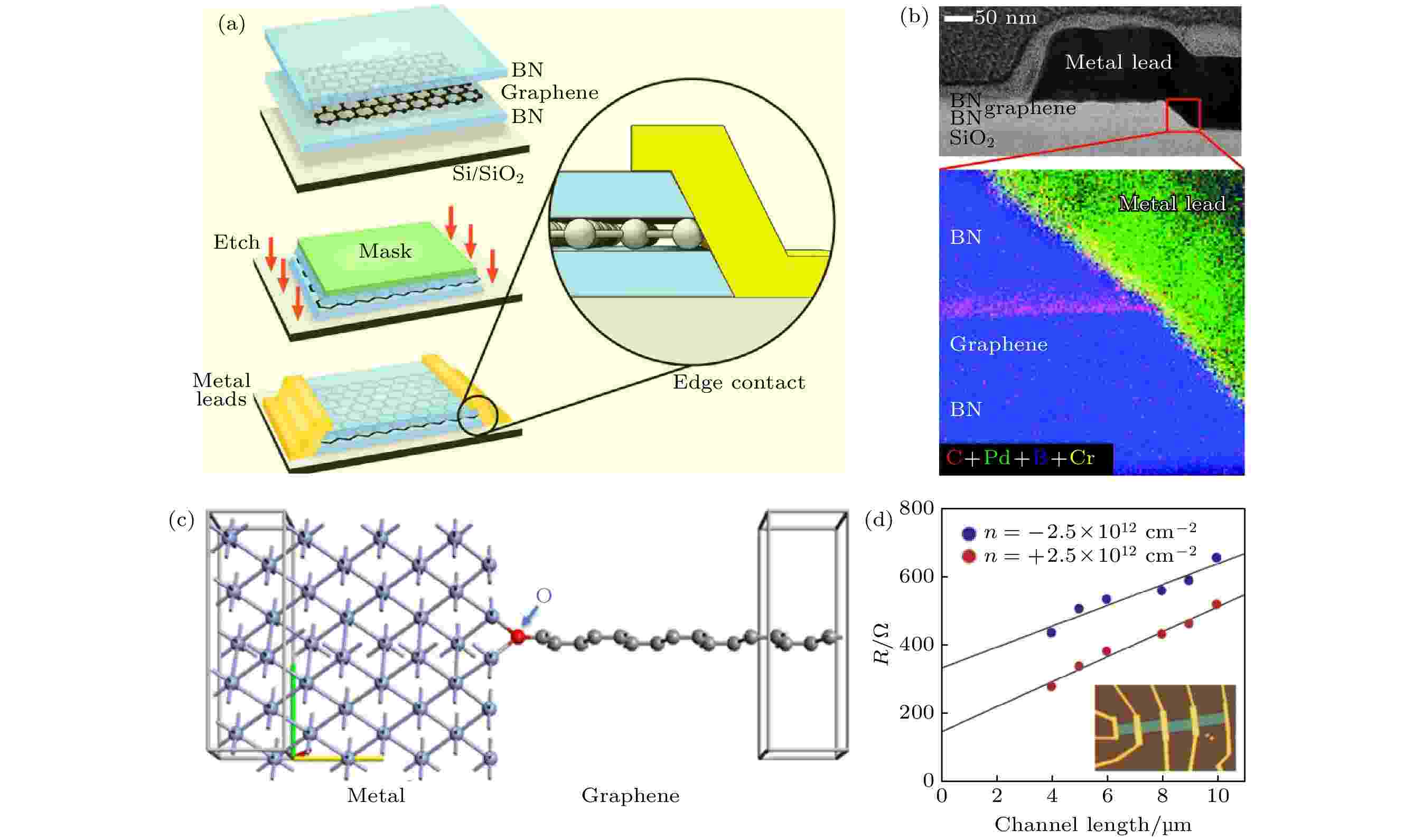
图 12 (a)石墨烯的一维边缘接触结构的工艺示意图; (b)截面TEM图像及相应的EDS图像; (c)接触界面的原子结构示意图; (d)接触电阻与沟道长度的关系曲线[36]Figure12. (a) Schematic of the one-dimensional edge contact process for graphene devices; (b) cross-sectional TEM image and corresponding EDS mapping; (c) atomic structure diagram of contact interface; (d) Plot of the contact resistance as function of the channel length[36].
3
3.2.2.基于石墨烯电极的“混合型”边缘电学接触
一维边缘接触适用于石墨烯, 但不适用于二维半导体. 针对二维半导体, 一种折衷的方法是首先在叠层内部利用石墨烯与二维半导体形成平面范德瓦耳斯接触, 然后再利用石墨烯作为电极制作边缘接触, 即构建以石墨烯为电极的“混合型”边缘电学接触. 如图13(a)和图13(b)所示, Cui等[109]通过将石墨烯电极转移到MoS2上构建了这种“混合型”边缘接触结构, 实现了较好的欧姆接触, 观测到了MoS2的SdH震荡(图13(c)). Bandurin等[116]也采用了相似结构, 将石墨烯电极置于InSe底部, 再制作石墨烯边缘电学接触, 观测到了InSe中的整数量子霍尔效应(图13(d)—图13(f)). 混合型边缘接触也可用于空气敏感型二维原子晶体. 例如Tsen等[117]首先利用h-BN依次拾取定位好的石墨烯电极和NbSe2, 制备了混合型接触结构, 由此研究了NbSe2的超导特性(图13(g)和图13(h)). 混合型边缘接触在二维半导体器件中应用较广[118], 但值得注意的是, 尽管石墨烯电极可以有效地向二维半导体注入载流子, 但是石墨烯的狄拉克点与二维半导体的导带和价带通常存在偏移, 因此需要对石墨烯进行额外的静电掺杂才能降低接触势垒. 此外, 混合型边缘接触也增加了叠层的步骤和复杂性.
图 13 “混合型”边缘接触结构及电学输运测量结果 (a)—(c) MoS2[109]; (d)—(f) InSe[116]; (g), (h) NbSe2[117]Figure13. Mixed edge contact configuration and the corresponding electrical transport measurements: (a)?(c) MoS2[109]; (d)?(f) InSe[116]; (g), (h) NbSe2[117].
3
3.2.3.金属/二维半导体界面的费米能级钉扎效应
低的接触电阻是开展二维半导体电学输运测量研究的前提. 遗憾的是, 二维半导体与金属电极之间通常存在较大的接触电阻. 理论上讲, 任何金半接触肖特基势垒的高度都仅取决于金属功函数和半导体电子亲和势之间的差值. 与传统半导体类似, 金属费米能级常常被钉扎在二维原子晶体/电极的界面态能级处, 导致最终肖特基势垒的高度与金属功函数无关. 关于金属/二维原子晶体界面费米能级钉扎的起源目前尚无定论, 但是无论具体机制如何, 费米钉扎效应都会导致较大的接触电阻[119-122]. 传统半导体工艺中, 对电极区域的材料进行替代掺杂是降低接触电阻的常用策略, 但不适用于二维原子晶体, 这是由于替代掺杂过程极有可能改变甚至破坏原有的二维晶格结构. 尽管二维原子晶体的表面掺杂已经取得了一些进展, 但掺杂效果很有限, 且极易引入额外无序. 利用金属电极使接触区域的二维原子晶体发生局域相变[123,124], 或者通过在金属/二维原子晶体界面插入隧穿绝缘层[125-127]等手段在一定程度上可以降低接触电阻, 但是这些方法大多难以兼容封装叠层结构, 因此就很难应用于电学输运测量. 迄今为止, 较为理想的二维半导体电学接触主要是通过叠层工艺构建范德瓦耳斯型金半接触实现的. 通过避免直接沉积金属的过程, 可以缓解界面缺陷态导致的费米能级钉扎效应.3
3.2.4.顶电极范德瓦耳斯接触工艺
采用传统的金属沉积工艺制备顶电极接触在电学输运研究中也有报道[128-130], 但是很难获得理想的金属/二维半导体界面. 以金属/MoS2接触为例, 常用的沉积(蒸发、溅射等)工艺会在界面处产生大量的缺陷、应变和金属扩散, 如图14(a)和图14(b)所示[131]. 这些无序会在二维半导体表面产生大量能隙态, 形成费米能级钉扎. Liu等[131]将预先图案化的金属电极转移到二维半导体的表面, 形成范德瓦耳斯接触, 避免了金属沉积过程可能引入的无序(图14(d)和图14(e)).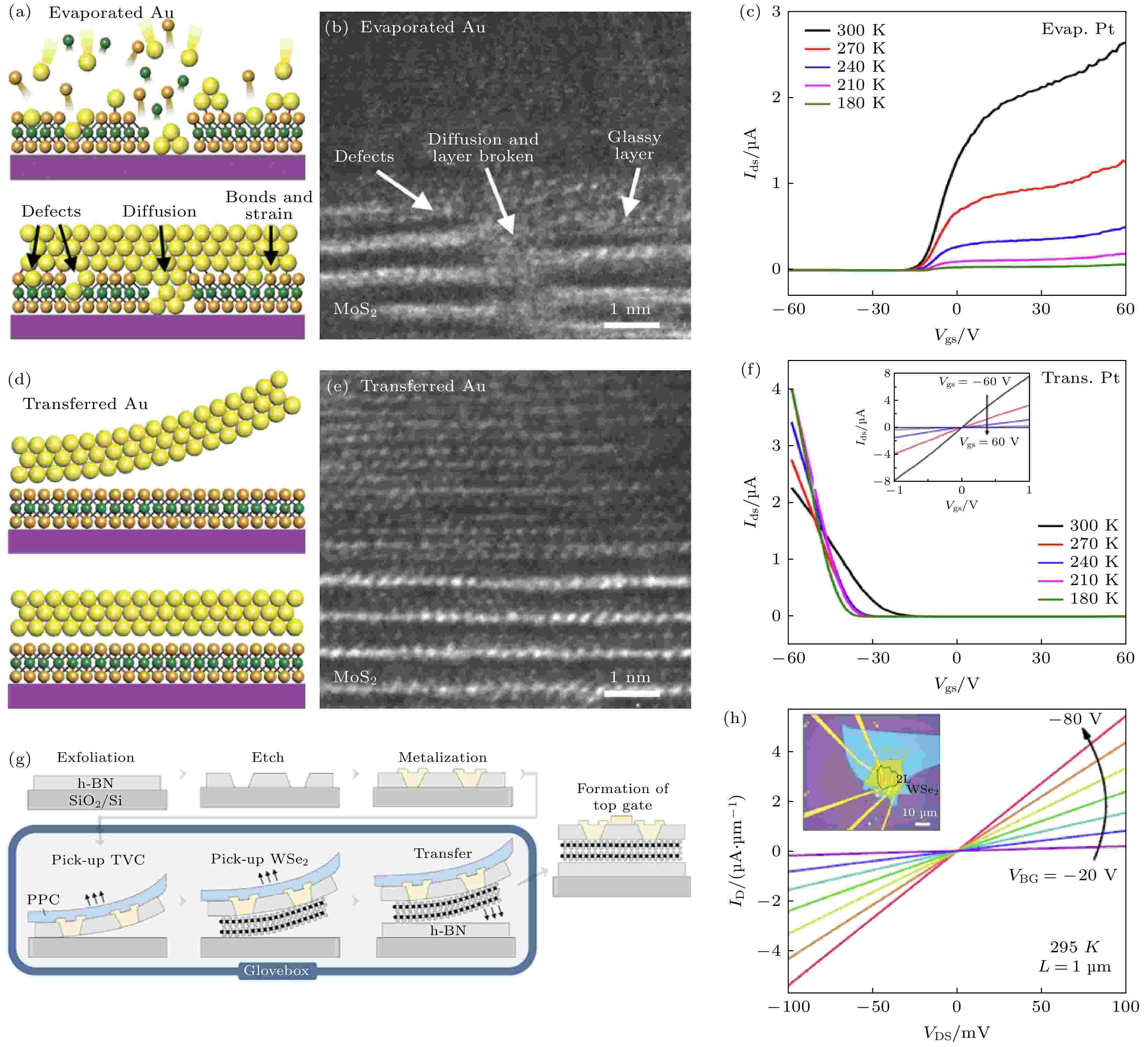
图 14 顶电极范德瓦耳斯接触工艺. 在MoS2表面直接沉积(a)—(c)金属电极和(d)—(f)转移金属电极形成的界面原子结构示意图、相应的界面TEM图像和转移特性曲线, 其中图(f)中的插图为不同栅压下的输出特性曲线[132]; (g)兼容h-BN封装结构的顶电极范德瓦耳斯接触结构的工艺流程示意图; (h)基于顶电极范德瓦耳斯接触的WSe2器件的输出特性曲线[114]Figure14. van der Waals contact between the top electrodes and TDACs. The schematic of atomic structure at the interface, the TEM images of the interface and the corresponding transfer curves of the contacts formed by (a)?(c) the direct deposition of metal electrode and (d)?(f) transferring metal electrode on the MoS2, respectively[132]. The inset in panel (f) is the output curves. (g) Schematic of the fabrication process for top electrode with van der Waals contact structure, compatible with h-BN encapsulation. (h) Output curves of WSe2 device with top electrodes[114].
这种方法制备的金属/MoS2界面几乎无缺陷, 能有效缓解费米能级钉扎效应(图14(c)和图14(f)). Jung等通过图案化的h-BN上沉积金属制备了图案化的电极, 再利用范德瓦耳斯拾取法制备了顶电极接触的WSe2器件, 电学测试显示出很好的欧姆接触特性(图14(g)和图14(h))[132]. 由于封装叠层结构是降低无序的有效手段, 这种与封装结构兼容的顶电极工艺较为适合二维半导体的输运特性研究. 此外, 基于封装叠层的顶电极工艺还适用于空气敏感型二维原子晶体, 例如, Benyamini等[114]利用这种接触结构研究了单层NbSe2的超导特性.
3
3.2.5.底电极范德瓦耳斯接触工艺
目前, 二维半导体电学输运研究利用的主要是底电极范德瓦耳斯接触工艺. 与顶电极工艺相比, 底电极接触与封装叠层结构的兼容性更好. 例如, Movva等[133]在SiO2/Si衬底上预先沉积Pt底电极, 再将WSe2转移到Pt电极上形成范德瓦耳斯接触, 如图15(a)和图15(b)所示. 如图15(c)和图15(d)所示, 器件接触在室温和底线下都显示出优良的欧姆特性. Fallahazad等[134]进一步在h-BN上直接沉积底电极, 从而制备了底电极接触的WSe2封装叠层器件; 采用石墨栅极进一步降低器件的无序, 实验上观察到了WSe2中的SdH振荡(图15(e)和图15(f)). 采用“底电极+双石墨栅极”的器件结构, 研究者们后续报道了MoSe2和MoS2的电学输运测量结果(图15(g)—图15(k))[135-137]. 但迄今为止, 二维半导体的接触电阻问题仍未彻底解决, 尚未在二维半导体中观察到分数量子霍尔效应. 底电极工艺也适用于研究空气敏感型材料, 如Fatemi等[138]制备了底电极接触的单层WTe2器件, 并研究了其超导特性(图15(l)—图15(m)), 在单层NbSe2的超导特性研究中也经常采用底电极接触结构[26,27].
图 15 底电极范德瓦耳斯接触 (a)结构和(b)工艺示意图.(c), (d)表征欧姆接触特性的I-V特性曲线[133]. 基于底电极范德瓦耳斯接触的WSe2 ((e), (f))[134], MoS2 ((g)?(i)), MoSe2 ((j), (k))和WTe2 ((l)?(n))的电学输运测量结果[135-138]Figure15. (a) Schematic and (b) fabrication process of van der Waals contact between bottom electrodes and WSe2[133]. (c), (d) I-V curves indicating ohmic contact. Electrical transport measurements of WSe2 (e), (f)) [134], MoS2 ((g)?(i)), MoSe2 ((j), (k)) and WTe2 ((l)?(n)) using bottom electrode contacts[135-138].
2
3.3.几种新型器件结构
范德瓦耳斯拾取法制备的封装叠层结构能够大幅降低器件的无序, 使得二维原子晶体的电学输运特性研究取得了一系列进展. 虽然Hall bar仍然是最常用的器件结构, 但是其电学测量精细程度需要进一步提升. 此外, 一些常用的电学调控手段, 例如离子液体掺杂[139]等无法直接应用于叠层异质结. 近年来, 几种新颖的器件结构陆续被报道, 在分数量子霍尔效应、玻色-爱因斯坦凝聚以及其他电子基态调控研究方面获得很大突破. 需要指出的是, 这些器件结构之间并非完全独立, 实验上可以相互结合使用.3
3.3.1.可降低边缘无序的器件
即便对于无序最低的封装叠层结构, 器件的边缘仍然是本征无序性的主要来源之一. 体电子态测量不受边缘模式的影响, 诸如量子电容、Corbino圆盘以及局域栅极等器件结构都可以用于研究分数量子霍尔效应的精细结构. 量子电容是研究强磁场下体电子态的有效手段之一, 在III-V族异质结器件输运研究中已有采用[140-142]. 石墨烯研究初期也有研究者尝试构建电容测量装置[143-145], 但是大多受制于叠层中较高的无序, 测量结果并不理想. 从结构上讲, 包含顶栅和底栅的封装叠层结构本身就可以视为一个电容结构, 其极低的无序非常有利于量子电容的研究. 例如, Young等[95]测量了以石墨为底栅的双层石墨烯封装结构的量子电容, 发现在倾斜磁场下出现了量子自旋霍尔态(图16(a)和图16(b)). Zibrov等[98]制备了双石墨电极的石墨烯封装叠层器件, 进一步降低器件无序, 观察到半整数朗道能级填充时的偶数分母分数量子霍尔态, 这些态中可能存在能够容纳非阿贝尔任意子的Pfaffian相. 电容测试法在二维半导体的关联电子态研究方面更具优势, 可以规避接触电阻的问题. 例如, Shi等[146]通过测试双石墨栅极的单层WSe2封装叠层器件的量子电容, 观察到了最低的三个朗道能级中的分数量子霍尔态, 特别是在第二朗道能级中也观察到偶数分母分数量子霍尔态, 如图16(c)—图16(e)所示.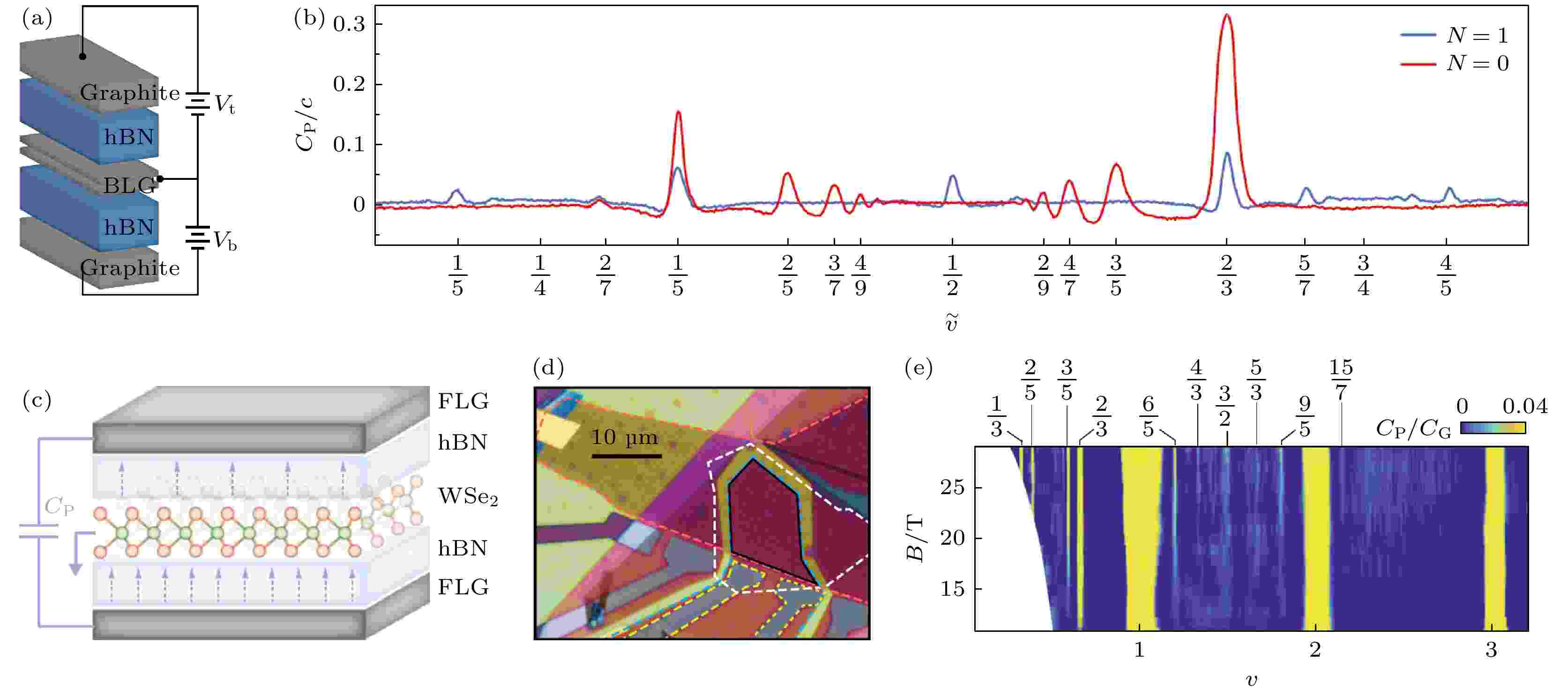
图 16 叠层器件的量子电容测试法 (a)双层石墨烯的量子电容测量示意图; (b) N = 1和N = 0朗道能级的不同填充数对应的量子电容[95]; WSe2的(c)量子电容测量结构示意图, (d)光学照片以及(e)不同填充数对应的量子电容随磁场的变化关系[146]Figure16. Quantum capacitance measurement of devices based on stacks: (a) Schematic of quantum capacitance measurement of bilayer graphene; (b) quantum capacitance of different filling factors of N = 1 and N = 0 Landau levels [95]; (c) schematic of quantum capacitance measurement, (d) optical image and (e) the relationship between quantum capacitance and magnetic field for various filling factors of WSe2 [146].
迄今为止, 利用传统的Hall bar结构难以观测量子电容测量结果中的细节特征, 因此无法对分数量子霍尔态进行深入研究. 在Corbino圆盘结构中, 电流经过器件边缘和中心的圆环路径, 由于内外边缘态产生的边缘电流相互抵消, 因此能够排除电极边缘模式的影响. 早期采用氧化物等电介质构建的Corbino器件由于存在较高的无序, 体输运特征在一定程度上被掩盖[147-149]. Zhu等[150]证实基于封装叠层结构的Corbino器件能够改善电学输运测量结果(图17(a)和图17(b)). 在此基础上通过进一步优化工艺, 利用石墨作为顶电极和底电极, Polshyn等[151]和Zeng等[152]制备成新型的Corbino器件(图17(c)—图17(f)), 探测到了在更高填充数的分数量子霍尔态. Li等[153]在此基础上制备了双电层结构的Corbino器件(图17(g)和图17(h)), 通过引入库仑拖拽效应从本质上改变了输运特征(有关库仑拖拽的内容详见3.3.2小节), 除了观察到原有的分数量子霍尔态之外, 还观察到了更加新颖的电子关联态.
图 17 Corbino结构的石墨烯器件的电学输运特性 (a)金属栅极的Corbino器件的光学照片和结构示意图; (b)器件电阻随位移场的变化曲线[150]; (c)基于石墨栅极的Corbino器件的微加工过程示意图[152]; (d)双电层结构的Corbino器件的测量装置示意图; (e)纵向电导率随填充数的变化, 其中涌现出一系列符合复合费米子模型的新的分数量子霍尔态[153]Figure17. Electrical transport properties of Corbino devices based on graphene: (a) Schematic and optical image of the Corbino device with metal gate; (b) relationship between the resistance and displacement field[150]; (c) schematic of the fabrication process of Corbino device with top and bottom gate[152]; (d) Corbino device with the electric double layer (EDL) structure; (e) variation of the longitudinal conductivity with filling factor, in which a series of emergent fractional quantum hall states corresponding to the composite fermion model appear[153].
传统的半导体异质结输运研究一般是通过图案化栅极来定义局域耗尽区, 单层石墨烯由于缺乏能隙而不能通过耗尽直接使栅极下方的沟道区域绝缘, 且栅极的边缘结构和蚀刻工艺都不可避免地会引入各种无序[154,155]. 叠层结构的优势在于可以将石墨电极图案化, 从而在降低二维电子气无序的同时, 通过施加静电场定义实际Hall bar的几何形状. Ribeiro-Palau等[157]首先将单层石墨烯制作成Hall bar, 然后将石墨顶电极加工成尺寸更小的“Local bar”, 利用在强磁场下石墨烯的v = 0绝缘态进行输运测量, 如图18(a)和图18(b)所示. 其中, 石墨顶电极的低无序起到重要作用, Local bar器件在N = 0和N = 1朗道能级中出现了丰富的分数量子霍尔态. Chen等[158]采用相似的Local bar结构, 观察到了N = 2朗道能级中的可重入整数量子霍尔效应(RIQHE). 这些观察结果与高迁移率GaAs/AlGaAs量子阱中的实验结果相似, 证实了器件具有较高的质量. 最近, Zhou等[159]在Corbino结构中利用“Local bar”结构的石墨顶电极和底电极分别定义两个耗尽区, 在朗道能级的分数填充附近观察到了斯格明子(图18(c)和图18(d)).
图 18 基于局域定义的石墨栅极研究石墨烯器件的电学输运特性 (a)局域定义的石墨顶栅器件结构示意图; (b)器件纵向电导率与局域石墨栅压关系曲线, 在N = 0和N = 1朗道能级中可以观测到大量的分数量子霍尔态[157]; (c)基于局域石墨栅极的Corbino器件的结构示意图; (d)器件的纵向电导率与局域石墨栅压的关系曲线[159]Figure18. Electrical transport properties of graphene devices with locally defined graphite gates[157]: (a) Locally defined graphite top gate structures and optical images; (b) Relationship between the longitudinal conductivity and the local gate voltage, and a large number of fractional quantum Hall states can be observed within the N = 0 and N = 1 Landau levels; (c) schematic of Corbino device with local graphite gates; (d) Relationship between the longitudinal conductivity and the local gate voltage[159].
3
3.3.2.双电层(EDL)器件
激子是一种玻色子, 目前普遍采用光学测量手段研究二维原子晶体叠层异质结中的激子特性. 自首次在GaAs/AlGaAs量子阱中观察到库仑拖拽现象以来, 双电层(EDL)结构引起了广泛的关注, 其中的空间间接激子在高载流子浓度下会产生超流的玻色-爱因斯坦凝聚(BEC), 是利用电输运测量激子特性的一种重要手段[160,161]. 相较于传统的GaAs体系, 石墨烯/h-BN/石墨烯封装叠层是一种层间相互作用更强的EDL结构: h-BN作为隔离介质的层间距最小可达~1 nm, 比GaAs体系小一个数量级[162,163]; 石墨烯的载流子可调谐范围大, 可以达到“零绝缘层”的极限. Gorbachev等[165]采用聚合物基转移法, 首次制备了由两个单层石墨烯和h-BN隔离层组成的EDL结构, 如图19(a)—图19(d)所示. 测量结果虽未观察到清晰的BEC, 但仍可以清楚地看到零磁场下的库仑拖拽现象, 显著优于以氧化物隔离介质的EDL结构[166]. 近年来利用石墨栅极的封装叠层EDL器件, 最终观察到了与GaAs量子阱中类似的驱动层中的可重入整数量子霍尔效应, 这是层间相干性和激子超流性的有力证据(图19(e)—图19(h))[167-169], 目前已经将EDL中层间结合态的研究扩展到分数量子霍尔态[161].
图 19 零磁场下石墨烯双电层(EDL)结构的库仑拖曳效应研究利用聚合物基转移法制备的石墨烯EDL器件的 (a)示意图, (b)光学照片, (c)测量结构示意图, (d)拖拽电阻率的相图[165]; 利用pick-up转移法制备的(e)器件结构示意图以及(f)叠层结构和(g) EDL器件的光学照片; (h)拖拽电阻与两层石墨烯的朗道能级填充数的关系曲线[168]Figure19. Coulomb drag effect of graphene electric double layer (EDL) in zero magnetic field: (a) Schematic, (b) optical image, (c) measurement setup and phase diagram of drag resistivity of graphene EDL device prepared by polymer-based transfer method (d) [165]; (e) structure diagram, (f) optical image of the stack and (g) final EDL device fabricated by the pick-up transfer method; (h) curves of drag resistance as function of total Landau level filling factors of two layers of graphene[168].
3
3.3.3.介电环境及近邻效应
二维原子晶体的电子基态对微观环境极为敏感, 在研究其本征特性时需要排除环境中各种无序, 同时还可以利用衬底有效地调控电子态[170]. 封装叠层结构则既可以合理利用各种外界调控手段, 又能避免各种无序的不利影响.理论预言, 二维电子系统同时受到磁场和周期性势场的作用时会表现出自相似的递归能谱, 即Hofstadter蝴蝶能谱. 而与晶格势能量尺度相匹配的磁场极大, 此前研究者们曾尝试在GaAs量子阱中通过构建介电超晶格引入外部周期势, 然而图形化工艺大幅增加了二维电子气的无序[171-176].
封装叠层结构在这方面具备独特优势, 例如Forsythe等[177]将石墨烯封装转移堆叠到了二维介电超晶格上, 如图20(a)—图20(c)所示. 叠层中底层的h-BN较薄, 当向栅极施加偏压时, 介电超晶格能够调制石墨烯的二维电子气, 观察到了次级狄拉克锥以及Hofstadter蝴蝶能谱. 由于介电超晶格的周期较大, 仅在B = 3.0 T的磁场下可以达到?/?0 = 1 (石墨烯/h-BN天然超晶格需要超过20 T的强磁场). 最近, Li等[178]又将石墨烯封装转移堆叠到一维介电超晶格上, 观察到了主要狄拉克锥和次级狄拉克锥在平行于超晶格基矢的方向上逐渐变平的奇特现象, 如图20(d)—图20(g)所示.
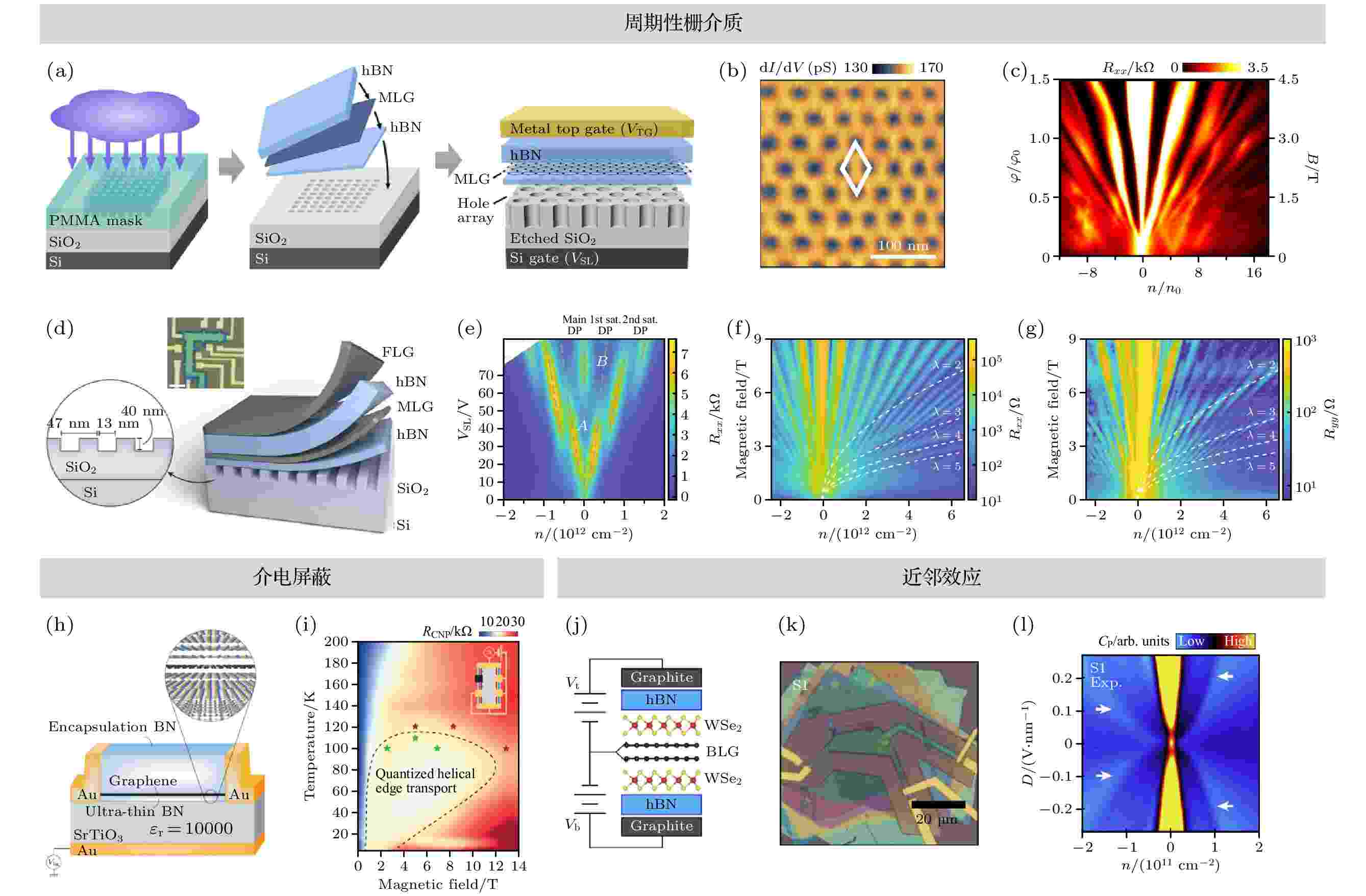图 20 利用介电环境及近邻效应调控石墨烯中电子基态 (a)以二维周期性介质为栅极的石墨烯叠层结构的制备工艺示意图; 周期性外部电场作用下的石墨烯的(b)STM图和(c)朗道能级扇形图[177]; (d)基于一维周期性栅介质的石墨烯叠层结构示意图; (e)石墨烯的纵向电阻率与载流子浓度和底栅电压的关系[178]; Rxx (f)Figure20. Tuning the ground state of electrons in graphene by changing the dielectric environment and proximity effects: (a) Schematic of the fabrication process of graphene stack based on two-dimensional periodic gate dielectric pattern; (b) STM image and (c) Landau fan diagrams of graphene under the applied periodic electric field[177]; (d) schematic of graphene stack with one-dimensional periodic gate dielectric; (e) relationship between longitudinal resistivity and carrier concentration with periodic gate voltage in the graphene device[178]; (f), (g) the Landau fans of Rxx and Ryy, respectively; (h) schematic of the device based on a high-κ gate dielectric; (i) relationship between the resistance of main Dirac point with the temperature and magnetic field[182]; (j) schematic of capacitance measurement for WSe2/h-BN/WSe2 stack and (k) optical images of the device; (l) relationship between the quantum capacitance of the main Dirac point with the displacement field and carrier concentration[194].
二维电子气中, 电子-电子的库仑相互作用是决定电子基态的关键因素, 因此利用衬底介电特性直接调控库仑相互作用是研究强关联体系的手段之一. 对于石墨烯而言, 一方面, 库仑相互作用会导致一系列新物态的产生, 例如悬浮器件由于与衬底空间上完全分离, 可以视为介电常数极低的系统. 因此, 悬浮器件中的库仑相互作用很强, 能够观察到一系列强关联电子态[179]. 另一方面, 强电子关联导致的涨落也能破坏长程序, 理论预测石墨烯基态在垂直磁场下是铁磁有序的拓扑绝缘体[3,180], 而库仑相互作用反而会使量子霍尔铁磁性不稳定[181]. 在3.1.2小节中讨论的利用HfO2栅极提高TMDCs的迁移率, 主要是基于其高介电常数对衬底电荷无序的屏蔽效应. 很容易推断, 如果能继续大幅提高栅介质的介电常数, 则二维原子晶体中电子和电子之间的库仑相互作用也可能被屏蔽. 为观测石墨烯中的本征铁磁有序, Veyrat等[182]将石墨烯封装转移堆叠到高介电常数的SrTiO3(STO)衬底上, 其中底层较薄的h-BN使衬底能够有效屏蔽石墨烯中的库仑相互作用. 如图20(g)和图20(h)所示, 基于低温下STO的高介电屏蔽特性(εr ≈ 10000), 观察到了石墨烯中铁磁相的螺旋边缘输运特性.
除了对叠层结构施加特定的外部影响, 还可以利用叠层内部邻近效应调控电子结构. 例如, 自旋-轨道耦合(SOC)是实现物质的时间反演不变拓扑的关键, 但是单层石墨烯的本征SOC较弱, 仅能打开μeV量级的带隙[183-185], 难以在实验上直接观察, 而通过掺杂等常规手段诱导SOC会给体系带来很大的无序[186-188]. 研究表明, 利用相邻二维原子晶体之间的近邻效应可以显著增强石墨烯中的SOC, 同时避免掺杂引起的诸多不利影响[189-193]. 例如, Island等[194]通过在双层石墨烯封装叠层异质中插入强SOC的WSe2, 并利用体电容测试法(图20(i)—图20(k)), 在石墨烯电荷中性点附近观察到一个由SOC驱动的能带反转产生的不可压缩相, 证实了近邻效应可以增强石墨烯的SOC.
2
3.4.莫尔超晶格器件
33.4.1.莫尔体超晶格概述
当叠层中相邻的两层二维原子晶体具有非常接近的晶格常数[78,195], 或具有相同的晶格常数但相互旋转时[52,53], 会产生周期性调制的莫尔超晶格, 其晶格周期远远大于晶体的原子晶格. 莫尔超晶格是最近几年二维原子晶体研究领域最热门的课题之一, 形成了“转角电子学(twistronics)”这一崭新的领域[196].石墨烯/h-BN对准的叠层结构是第一个莫尔超晶格体系. 由于微小的晶格失配, 石墨烯与h-BN之间的晶格对准能够形成莫尔超晶格, 会诱导产生次级狄拉克锥, 该体系研究的重点是莫尔势场和磁场在相近长度范围内的相互作用[50,51]. 理论预言, 莫尔超晶格体系能够产生的一系列自相似能级被称为Hofstadter蝴蝶的分形能谱[197]. 如3.3小节所述, 在GaAs/AlGaAs量子阱中直接设计能实现分形能谱的介电超晶格极具挑战性. 虽然利用STM能够观测石墨烯/h-BN莫尔超晶格的范霍夫奇点, 但是早期研究石墨烯中较高的无序阻碍了电学输运特性的研究. 到2013年, 基于转移堆叠的技术进步才利用电学输运实验证实了石墨烯/h-BN莫尔超晶格的分形能谱(图21(a)和图21(b))[77,198,199].
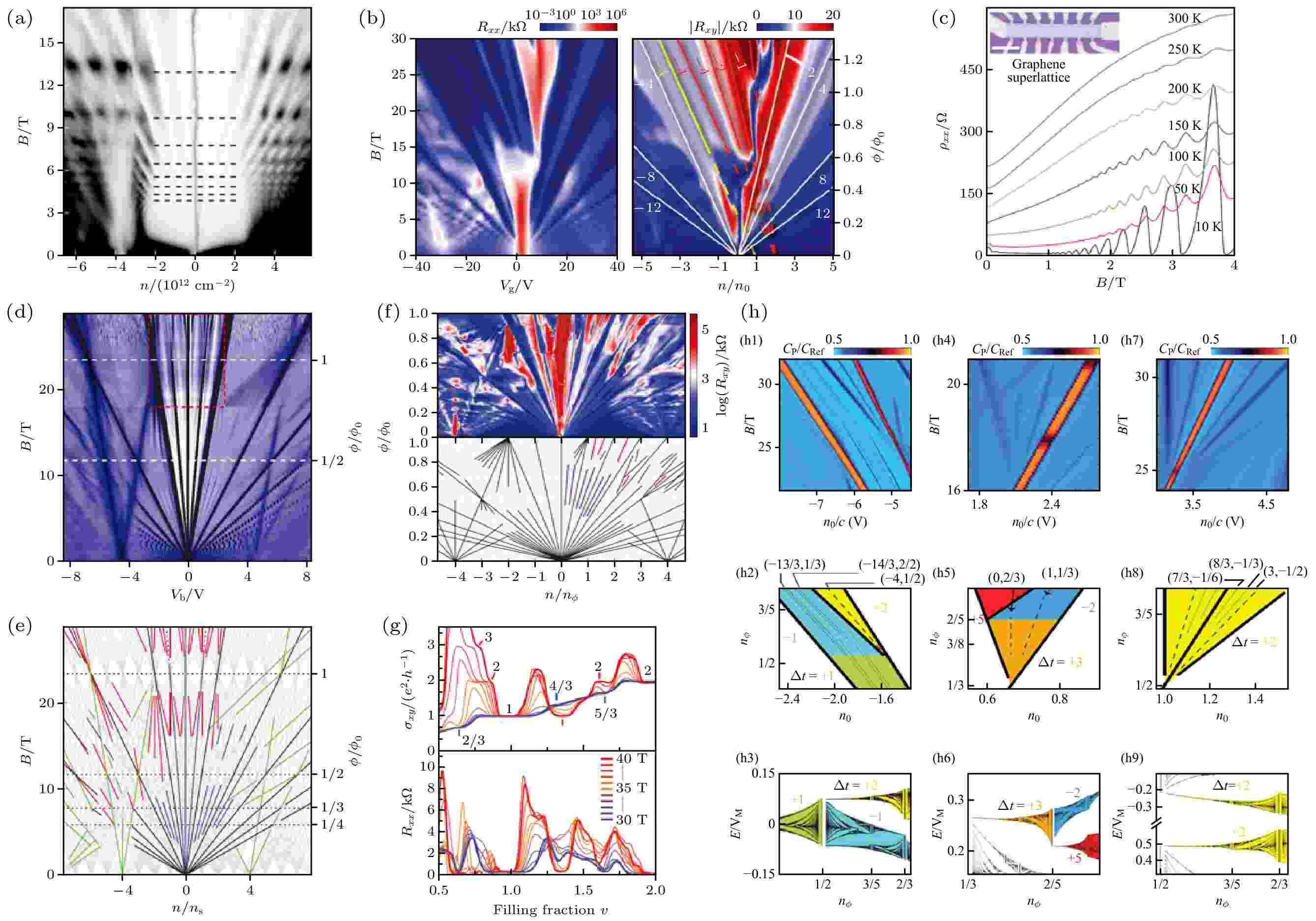图 21 石墨烯/h-BN莫尔超晶格的电学输运特性 (a) Geim课题组[77]和(b)Kim课题组[198]报道的Hofstadter蝴蝶分形能谱; (c)室温附近观测到的SdH振荡[201]; (d)实验观测到的对称破缺整数量子霍尔态(红色虚线框标识)和(e)对应的Wannier图(彩色实线标识了态密度极小值)[200]; (f), (g) t为整数和s非零的量子霍尔态[80]; (h)电容测量中观察到的t为分数和s为零的量子霍尔态[202]Figure21. Electrical transport properties of graphene/h-BN moiré superlattice: (a) Hofstadter butterfly fractal spectrum reported by Geim’s group[77] and (b) Kim’s group[198]; (c) SdH oscillations observed near room temperature[201]; (d) observed quantum Hall ferromagnetic states and (e) theoretically predicted Landau fan diagram[200]; (f), (g) quantum Hall state with integer t and non-zero s[80]; (h) quantum Hall state where t is a fraction and s is zero observed in the capacitance measurement[202].
石墨烯/h-BN莫尔超晶格在强磁场中会产生丰富的量子霍尔态序列, 可以使用以下公式跟踪其轨迹:
魔角石墨烯体系是最近涌现出的另一种莫尔超晶格体系, 二维原子晶体与莫尔超晶格的耦合也会强烈改变电子的能带结构, 研究的重点是魔角诱导出现的平带, 因此魔角体系也可以称为莫尔平带体系(区别于本征的平带系统)[203-206]. 平带内, 电子相互作用占主导地位, 会出现新奇的关联电子态. 近年来, 得益于转移堆叠方法的逐步完善[82,83,207], 魔角石墨烯的研究取得了一系列重要的突破. 如图22所示, 在魔角双层石墨烯中, 由于层间杂化能量和动量空间中转角决定的能带移动之间的相互作用, 首次在转角(1.1 ± 0.1)°的狭窄范围内产生了平带, 观察到了一系列关联电子态[208,209]. 在ABC三层石墨烯/h-BN异质结[210-212]和转角双层-双层石墨烯中[213-216], 通过施加垂直位移场诱导体系出现了半导体能隙, 丰富了平带系统的调控手段; 在转角单层-双层石墨烯[217,218]和转角三层石墨烯[219]中, 也发现了类似的电子关联行为; 将魔角石墨烯进一步与h-BN晶格对准, 由于其能谷简并度的打破而观察到了轨道磁性[220-225]. 有关二维原子晶体莫尔超晶格物理已经有很多专门的综述[52,206], 本文将从电子器件的角度, 概述基于其他二维原子晶体的莫尔超晶格及石墨烯莫尔超晶格的结构及平带调控方面的进展.
图 22 石墨烯莫尔平带系统 单层-单层石墨烯莫尔超晶格(魔角双层石墨烯)器件的 (a)示意图, (b)电子相图和(c)能带结构[209]; (d), (e)魔角双层石墨烯中的轨道铁磁性[222]; 双层-双层石墨烯莫尔超晶格的(f)器件结构和晶格结构示意图以及(g)电阻率随位移场的变化关系图[215]; ABC三层石墨烯/h-BN莫尔超晶格器件的(h)结构示意图和(i)纵向电阻率随位移场的变化关系图, 其中插图为器件的光学照片[212]; 转角三层石墨烯莫尔超晶格的(j)器件结构示意图和(k)纵向电阻率随位移场和莫尔单胞填充数的变化关系图[219]Figure22. Graphene moiré flat band system: (a) Schematic, (b) electronic phase diagram and (c) energy band structure of a monolayer-monolayer graphene moiré superlattice (magic-angle twisted bilayer graphene, MATBG) device[209]; (d), (e) orbital ferromagnetism in MATBG[222]; (f) schematic of device geometry and (g) relationship between the resistivity and the displacement field of the twisted bilayer-bilayer graphene (twisted double bilayer graphene, TDBG) moiré superlattice[215]; (h) schematic and (i) relationship between the longitudinal resistivity and the displacement field of the ABC trilayer graphene/h-BN moiré superlattice device. The inset in panel (i) is the corresponding optical image[212]. (j) Schematic of device structure and (k) relationship of the longitudinal resistivity with the displacement field and the filling factors of the moiré unit cell of the twisted trilayer graphene moiré superlattice[219].
3
3.4.2.转角TMDCs
目前已经在包括双层石墨烯、单层-双层石墨烯、双层-双层石墨烯、ABC三层石墨烯/h-BN及转角三层石墨烯等多个基于石墨烯的莫尔超晶格中实现了孤立平带. 二维原子晶体的材料种类繁多, 物理性质丰富多样, 可以预见莫尔超晶格的广阔研究空间. 但是, 魔角石墨烯系统的可调性仍然受到很大限制, 例如在转角双层-双层石墨烯中, 由于对整个能带结构的附加位移场效应, 狭窄的魔角范围不仅没有拓宽反而得到了有效保持; 而在ABC三层石墨烯/h-BN莫尔超晶格中, 最大莫尔波长由石墨烯和h-BN晶格失配固定. 有关转角2H相TMDCs的理论工作预测, 其莫尔布里渊区中也存在平带和范霍夫奇点, 平带宽度随转角连续变化, 无需施加额外的位移场[226-228]. 与石墨烯相比, TMDCs的能级简并度更低且存在强的SOC, 因此转角TMDCs有望成为研究三角晶格单能带Hubbard模型及各种新奇物态的理想平台[229-231].就器件工艺而言, 基于撕裂-堆叠拾取转移法和一维边缘电学接触, 石墨烯莫尔超晶格体系输运研究的关键技术瓶颈已经得以解决. 迄今为止, 对于大量的二维半导体, 例如转角TMDCs, 关联电子态的研究仍以光学手段为主[232-240], 以及基于扫描探针的局域电学测量研究[241-243]. 但整体而言, 转角TMDCs的电学输运研究严重受制于接触电阻的问题. Wang等[244]在转角TMDCs的电学输运研究方面取得了突破性进展, 利用3.2.5小节中所述的Pt底电极工艺实现了较好的低温欧姆接触, 研究了转角双层WSe2中的关联电子特性. 器件制备方法与“撕裂和堆叠”方法大致相同, 器件结构如图23(a)和图23(b)所示. 研究发现, 在转角4°—5.1°的双层WSe2中, 平带半填充处出现了电阻峰; 在转角为4°和4.2°时, 观测到了对应莫尔微带全填充时的电阻峰, 证实了由转角导致的莫尔超晶格会产生平带(图23(c)). 对于转角5.1°的器件, 通过调控电场可以得到最强的关联态, 温度低于3 K时在半填充两侧观察到了零电阻现象(图23(d)). 转角TMDCs的显著优势在于系统中平台的带宽和掺杂可以独立变化, 且由于体系中材料的种类繁多, 为其他电子关联态, 如激子凝聚、自旋液体、铁磁有序等的研究提供了一个新的平台.
图 23 转角WSe2器件中的电子关联态[241]底电极接触的器件 (a)结构示意图和(b)光学照片; (c)零磁场时, 不同转角的器件的纵向电阻随载流子浓度的变化关系图, 重点标示了其中的半填充电子态的电阻; (d)转角WSe2器件的电子相图Figure23. Correlated electronic states in a twisted WSe2 device[241]: (a) Schematic and (b) optical image of the device with bottom electrode; (c) curves of the longitudinal resistance vs. the carrier concentration for devices with different twisted angles under zero magnetic field. The resistance of the half-filling state is marked. (d) The phase diagram of the twisted WSe2 device.
3
3.4.3.莫尔超晶格器件的原位研究
对于莫尔超晶格系统而言, 层间转角和距离是影响层间耦合的两个关键因素. 采用“撕裂+堆叠”技术制造的器件通常无法原位改变二维原子晶体之间的转角, 因此对器件层间耦合特性的研究带来了不便性. 但实验上研究转角对电学输运特性的影响通常要制备一系列不同转角的器件, 这往往会增加实验的复杂程度. 原子力显微镜除用于常规的形貌和层数表征外, 还可以利用针尖的作用力操纵二维原子晶体面内取向[245]. Ribeiro-Palau等[246]和Finney等[247]通过将二维原子晶体的边缘与原子力显微镜尖端对齐, 在石墨烯/h-BN叠层结构中实现了转角的原位控制, 从而实现了对层间耦合特性的动态控制(图24(a)—图24(e)), 阐明能隙性质与动态转角和莫尔耦合强度之间的关系非常有助于验证相关的理论模型. 此外, 通过施加压力可以直接改变层间距离, 如Yankowitz等研究压力对于石墨烯/h-BN[248]和转角石墨烯莫尔超晶格[249]中的层间耦合强度的影响. 结果表明, 石墨烯/h-BN莫尔超晶格中, 石墨烯的能隙随层间距离的微弱减小而显著增大(图24(f)—图24(h)); 在转角石墨烯中, 通过压力改变层间距可以在转角大于魔角的器件中出现超导态和关联绝缘态, 证实了可以使用压力在非魔角的情况下产生平带的理论预言(图24(i)—图24(k)).
图 24 (a)利用AFM针尖原位调控石墨烯/h-BN莫尔超晶格的装置示意图; (b)—(d)不同转动时, 叠层结构的AFM图像[246]; (e)石墨烯的次级狄拉克点随原位转角的变化关系;石墨烯/h-BN莫尔超晶格的静压力测试(f)装置和原理示意图及(g)装置照片[248]; (h)主要狄拉克点和次级狄拉克点的带隙随压力的变化; (i)魔角石墨烯器件的结构示意图; (j)莫尔原胞半填充处的关联绝缘态随压力的变化; (k)有(蓝色曲线)/无(灰色曲线)静压的情况下, 器件的纵向电导率随载流子浓度及相应莫尔单胞填充数的变化曲线[249]Figure24. (a)Schematic of the graphene/h-BN moiré superlattice in situ controlled by AFM tip; (b)?(d) AFM images of the stack with different twisted angels[246]; (e) relationship between the secondary Dirac point of graphene and the in situ controllable twisted angles[248]; (f) top, cartoon of the piston-cylinder pressure cell. Bottom, schematic of the graphene stack under ambient and high pressure. (g) optical images of the device; (h) bandgaps as a function of pressure; (i) schematic of the magic angle graphene device[249]; (j) plots of the conductance (left penal) and resistance (right penal) of the half-filling states as function the pressure; (k) dependence of longitudinal conductivity on the carrier concentration and the corresponding filling factors of the moiré unit cell with (blue curve) and without (grey curve) high pressure.
3
3.4.4.转角体系的关联电子态调控
除层间转角、层间距和位移场等调控方法之外, 如3.3小节所述, 微观介电环境也会显著影响转角石墨烯的电子基态. 典型例子是魔角石墨烯与封装底层中的h-BN晶格对准能够打破石墨烯的能谷简并度, 使体系出现轨道铁磁性[220-225]. 平带结构中超导态和关联绝缘体态之间的关系是强关联物理研究的重要内容之一, 至今尚无定论. 通过改变叠层的介电环境可以控制体系的库仑能量大小, 从而系统研究超导态和关联绝缘态. 平带中出现关联绝缘体的条件是电子的库仑能远大于动能, 如果魔角石墨烯与石墨电极之间的距离小于摩尔单胞尺寸, 则极化电荷可在该尺度上屏蔽库仑相互作用. 例如Stepanov等[250]通过减小叠层结构中魔角石墨烯和石墨栅极之间的距离(即h-BN的厚度), 有效屏蔽了系统中电子相互作用, 观察到了关联绝缘体的淬灭, 而关联绝缘体消失后空出的相空间由超导圆顶所占据, 如图25(a)和图25(b)所示. Liu等[251]基于类似的叠层结构, 研究了双层石墨烯对魔角石墨烯的库仑屏蔽作用及其对电子关联态的影响. 输运测量结果表明, 随着库仑屏蔽作用的增强, 关联绝缘体相逐渐消失, 而超导相的稳定性则逐渐增强(图25(c)—图25(e)). 此外, 类似于利用WSe2诱导Bernal双层石墨烯SOC的实验, 也可以利用WSe2诱导魔角石墨烯中的SOC, 例如Arora等[252]在魔角石墨烯叠层中插入了单层WSe2(图25(f)), 输运测量结果表明, 在三个非魔角的转角器件中都可以清晰地看到超导转变, 如图25(g)—图25(i)所示. 磁输运测量结果进一步证实了WSe2诱导的SOC能够破坏魔角石墨烯的自旋-能谷对称性, 因此可以在转角远小于魔角的情况下稳定超导态. Lin等[253]研究了WSe2的近邻效应对魔角石墨烯中电子相互作用的影响, 证实WSe2的SOC可以诱导魔角石墨烯出现显著的反常量子霍尔效应, 即产生了轨道铁磁性(图25(j)—图25(k)).
图 25 转角石墨烯器件中关联电子态的外部调控 (a)通过调控叠层结构中魔角石墨烯和石墨栅极之间的h-BN的厚度调控系统中电子相互作用; (b)随着库仑屏蔽作用的增强, 关联绝缘体逐渐淬灭[250]. (c)利用Bernal双层石墨烯调控魔角石墨烯的器件结构示意图; (d)在不同的双层石墨烯载流子浓度下, ν = 2填充对应的电导随温度变化曲线及(e)能隙随双层石墨烯载流子浓度的变化曲线[251]; (f)魔角石墨烯/单层WSe2叠层结构示意图; (g)—(i)三个非魔角的转角石墨烯器件中的超导转变; (j)利用单层WSe2的近邻效应调控魔角石墨烯的器件结构示意图[252]; (k)器件的横向电阻和纵向电阻随载流子浓度及相应朗道能级填充数的变化曲线; (l) ν = 1和(m) ν = 2填充对应的电子态的轨道磁性测量结果[253]Figure25. Tuning of interaction between electrons in twisted graphene devices: (a) Interaction between electrons can be tuned by adjusting the thickness of the h-BN between the MATBG and the graphite gate in the stack; (b) with enhancing the Coulomb screening effect, the correlated insulator phase is quenched[250]. (c) Schematic of the device utilizing Bernal bilayer graphene to tune MATBG; (d) under different carrier concentration in Bernal bilayer graphene, plots of the conductance corresponding to ν = 2 filling vs. temperature and (e) energy gap vs. carrier concentration in bilayer graphene[251]; (f) schematic of MATBG/monolayer WSe2 stack; (g)?(i) superconducting transition observed in the three twisted devices with non-magic angles[252]; (j) schematic of the device to tune the MATBG using the proximity effect of monolayer WSe2; (k) curves of the transverse (upper curve) and longitudinal (lower curve) resistance vs. the carrier concentration (the filling factor of the Landau level). Orbital magnetic measurement of the electron states corresponding to (l) ν = 1 and (m) ν = 2 filling[253].
