摘要: 高效率的网络分析方法对于分析、预测和优化现实群体行为具有重要的作用, 而加权机制作为网络重构化的重要方式, 在生物、工程和社会等各个领域都有极高的应用价值. 虽然已经得到越来越多的关注, 但是现有加权方法数量还很少, 而且在不同拓扑类型和结构特性现实网络中的效果和性能有待继续提高. 本文提出了一种新型的双模式加权机制, 该方法充分利用网络的全局和局部的重要拓扑属性(例如节点度、介数中心性和紧密中心性), 并构建了两种新型的运行模式: 一种是在原始模式中通过增加桥边的权重来提高同步能力; 另一种是在逆模式中通过弱化桥边的权重来提高聚类检测. 此外, 该加权机制仅受单一参数
$ \alpha $ 的影响, 非常便于调控. 在人工基准网络和现实世界网络中的实验结果均验证了该模型的有效性, 可以广泛应用于大规模的现实世界网络中.
关键词: 复杂网络 /
加权策略 /
通信邻域图 /
聚类结构 English Abstract A new tunable weighting strategy for enhancing performance of network computation Li Hui-Jia 1 ,Huang Zhao-Ci 1 ,Wang Wen-Xuan 1 ,Xia Cheng-Yi 2 1.School of Science, Beijing University of Posts and Telecommunications, Beijing 100876, China Fund Project: Project supported by Fundamental Research Funds for the Central Universities of China (Grant No. 2020XD-A01-2) and the National Natural Science Foundation of China (Grant No. 71871233)Received Date: 09 March 2021Accepted Date: 02 April 2021Available Online: 07 June 2021Published Online: 05 September 2021Abstract: For many real world systems ranging from biology to engineering, efficient network computation methods have attracted much attention in many applications. Generally, the performance of a network computation can be improved in two ways, i.e., rewiring and weighting. As a matter of fact, many real-world networks where an interpretation of efficient computation is relevant are weighted and directed. Thus, one can argue that nature might have assigned the optimal structure and weights to adjust the level of functionality. Indeed, in many neural and biochemical networks there is evidence that the synchronized and coordinated behavior may play important roles in the system’s functionality. The importance of the network weighting is not limited to the nature. In computer networks, for example, designing appropriate weights and directions for the connection links may enhance the ability of the network to synchronize the processes, thus leading the performance of computation to improve. In this paper, we propose a new two-mode weighting strategy by employing the network topological centralities including the degree, betweenness, closeness and communication neighbor graph. The weighting strategy consists of two modes, i.e., the original mode, in which the synchronizability is enhanced by increasing the weight of bridge edges, and the inverse version, in which the performance of community detection is improved by reducing the weight of bridge edges. We control the weight strategy by simply tuning a single parameter, which can be easily performed in the real world systems. We test the effectiveness of our model in a number of artificial benchmark networks as well as real-world networks. To the best of our knowledge, the proposed weighting strategy outperforms previously published weighting methods of improving the performance of network computation.Keywords: complex networks /weighting strategy /communication neighbor graph /community structure 全文HTML --> --> --> 1.引 言 复杂网络理论[1 -3 ] 是一种分析大规模复杂系统的有力工具, 在过去十年里已经涌现出一系列相关研究成果, 例如聚类划分技术、疾病传播和免疫策略、交通驱动模型、同步分析、级联失效、异常值搜索算法等等. 在这些成果中, 拓扑计算和结构分析是研究复杂网络内在特性的最有效途径, 并使得理解网络功能特征成为可能. 其中, 最重要的拓扑特征之一是聚类结构[3 -8 ] . 它在探测聚类时将节点分成若干子集, 子集之间应有清晰的边界约束, 同一组成员之间比不同组成员拥有更多的关联. 聚类信息有助于理解和分析网络的结构特征和功能特性.[9 ,10 ] 提出的模块度函数Q 是最为常用的一种探测指标, 用以评价聚类划分[2 ] 的好坏. 给定一个划分${P}_{k}=({G}_{1}, {G}_{2}, \cdots , G_{K})=(\left({V}_{1}, {E}_{1}\right), $ $ \left({V}_{2}, {E}_{2}\right), \cdots, \left({V}_{K}, {E}_{K}\right))$ , K 是聚类的数目, 模块度函数Q [9 ] 定义如下:L 是网络中边的总数目, $ l({V}_{s}, {V}_{s}) $ 和$l\left({V}_{s}, {\overline{V}}_{s}\right)$ 分别代表聚类s 内部以及s 与网络中剩余部分之间的边的数目. 通常来说, Q 值较大意味着该聚类结构较好[11 -16 ] . 此外, Boccaletti等[17 ] 根据网络中的同步局域化理论提出了一种新的动态聚类检测方法(opinion changing rate model, OCR). 他们将改进的Kuramoto同步模型应用到网络的每个节点中, 利用社团内部连接紧密而同步速度快的特征, 利用权重技术使得网络聚类之间的边权逐渐降低, 直到网络聚类划分获得最大的模块度Q 值. 复杂网络中另一个广泛存在的现象是同步[18 -24 ] . 在连通网络中, 每个节点通过网络连接, 在动力系统的演化下, 与网络其他节点进行耦合. 在足够强的耦合作用下, 节点的状态会随着时间的延长达到同步(状态一致). 在许多加权网络中, 可以调整网络的结构和权重, 以提升节点状态获得达到同步的能力. 事实上, 已有研究结果表明, 在许多社会和生物网络研究中, 同步行为会在调节系统和组织功能中发挥重要作用.[21 -30 ] , 但是总体来说数量还很少, 而且对于不同拓扑类型和结构特性的现实网络, 特定加权算法的效果和性能仍不清楚, 还有待继续分析和验证. 而且现有方法(在第2 节详细说明)通常仅利用一种节点中心度来定义网络边权, 对于结构相对均匀的网络, 效果不理想; 而且对于相对稀疏的现实网络, 调控参数的影响不明显. 另外, 目前加权之后的动态网络中的各种隐藏特征, 如聚类结构和同步能力之间的相互关系, 仍未能得到很好的解释和分析.$ \alpha $ 的控制, 可以很方便地进行调控. 对于聚类探测, 通过在人工基准网络(包括GN基准和LFR基准), 以及若干现实网上进行测试, 验证了本文提出的加权机制不仅有助于提高探测精度, 而且还能缓解模块度优化的分辨率限制问题. 关于同步性, 通过在具有不同结构特性的无标度网络和Watts-Strogatz网络上进行测试, 验证了加权机制在提升网络同步性能上的高效表现. 通过比较, 本文提出的加权机制在提高网络计算能力方面要优于其他以往发表的加权方法.1 节和第2 节分别梳理复杂网络的基本理论及国内外相关的工作; 第3 节引入本文使用的加权机制并提出对应的双模式加权算法; 第4 节对加权机制如何增强网络同步性能及其对聚类结构探测的影响进行详细分析; 第5 节对加权机制分别运用于人工网络和大量现实世界网络进行试验; 第6 节对全文进行总结, 并提出一些未来研究中值得深入考虑的问题.2.相关工作 基于现实数据重构复杂网络是了解和控制复杂系统的基本方式, 而作为网络重构的重要组成部分, 网络加权已经开始得到越来越多的关注. Chavez等[21 ] 提出了一种通过拉普拉斯矩阵的非对角线元素$ {l}_{ij} $ 来增强同步能力的加权方案, 其加权后的元素$ {l}_{ij}^{\mathrm{w}} $ 定义如下:$ \alpha $ 为调控参数, $ {B}_{ij} $ 是节点i 和j 之间的边介数中心度, $ \alpha \approx 1 $ 相当于最优的同步能力. 与之相似, Wang等[22 ] 提出网络可以被视为是加权无向网络和加权有向网络的叠加. 基于现实网络的特征, 他们假设了一个合适的梯度场, 并定义权重$ {l}_{ij}^{\mathrm{w}} $ 如下:$ \alpha $ 值的增大, 网络同步化总是会随之提升. 然而, 同时应当注意避免$ \alpha $ 值过高, 否则会导致网络断开和分裂. 为了解决这个问题, Jalili等[23 ] 在节点介数中心度方法的基础上提出了一种新的加权方法, 其中权重$ {l}_{ij}^{\mathrm{w}} $ 定义如下:$ {B}_{j}B $ 和$ {B}_{ij}B $ 分别代表节点j 与边$ {e}_{ij} $ 之间的介数中心度. 该加权机制被用来提高网络的同步性能. 但是上述加权算法仅仅利用一种节点中心度来定义网络边权, 对于结构相对均匀的网络, 效果不理想. 而且对于相对稀疏的现实网络, 调控参数的影响不明显.[31 ] 讨论了一种新型加权机制, 用以缓解网络聚类中的模块度缺陷, 即分辨率极限[32 ] 和极端限制[33 ] 等问题. 该加权机制利用了网络的局部和全局信息, 其中每条边的权重定义如下:$ {c}_{ij} $ 定义为共同邻居比例, $ {B}_{ij} $ 是边介数中心度. 利用Clauset-Newman-Moore方法[10 ] 进行试验, 验证了该加权机制能够显著地优化社团探测的速度与精度. 但是仿真分析也表明, 当网络规模较小时, 其加权效果不明显. 而且虽然该方法可以用来加强社团内部的团内边, 但是却无法明显降低团间边的权重, 从而阻碍了该加权算法的进一步应用. 另外现有的网络加权方法还包括模拟退火算法[25 ] 、文献计量方法[26 ] 、随机游走算法[27 ] 、级联动力学方法[28 ] 、变分贝叶斯方法[29 ] 和概率推断方法[30 ] 等. 但总体来说, 当前加权算法的数量还很少, 而且对于不同拓扑类型和结构特性的现实网络, 特定加权算法的效果和性能仍不清楚, 还有待继续分析和验证.3.复杂网络基本理论 23.1.基本定义 3.1.基本定义 假设$ G(V, E) $ 是一个无向连通图, V 为节点集, E 为边界集. 这里考虑三个最常用的衡量拓扑结构和信息流通的中心度指标.节点度 节点度$ {k}_{i} $ [34 ] 表示节点i 相连的边的数量, 根据邻接矩阵$ {\boldsymbol{A}}=\left({a}_{ij}\right) $ 将其定义为$ {a}_{ij} $ 是节点i 和节点j 之间的邻接矩阵值. 还可以将节点度扩展到加权网络得到节点强度的概念.节点强度 节点强度$ {s}_{i} $ [35 ] 是节点i 相关联的边的权重总和, 定义如下:$ {w}_{ij} $ 为节点i 和节点j 之间的边的权重值.介数中心度 一个节点在信息传播中的重要性可以通过其介数中心度[36 ] 来计算, 定义为$ {\sigma }_{ij}\left(u\right) $ 为节点i 和节点j 之间的通过节点u 的最短路径的数量, $ {\sigma }_{ij} $ 是节点i 和节点j 之间的最短路径的总数量. 介数中心度的概念还可以拓展到边. 边$ {e}_{ij} $ 的介数中心度$ {B}_{ij} $ 表示通过该边的最短路径的数量, 在信息传播研究中常用来表示流通负载.紧密中心度(closeness) 节点i 的紧密中心度[36 ] 定义为一个网络中其他节点到节点i 的平均距离的倒数$ {D}_{ij} $ 是节点i 和节点j 之间最短路径的长度; $ {C}_{i} $ 用来测量一个节点与其他节点的(平均)紧密程度. 为了定义该中心性与最短路径的直接(正比例)关系, 还可以将其定义为$ {C}_{i} $ 的倒数: ${C}_{i}=\dfrac{1}{{C}_{i}}= $ $ \dfrac{1}{n-1}{\displaystyle\sum }_{j\in V}{D}_{ij}$ .k -邻域图 k -邻域图[37 ,38 ] 定义为将节点i 和节点j 连接起来的最短路径上的点的集合, 其中i 和j 之间的最短距离值小于等于k . 由于邻域关系是不对称的($ i\to j $ ), 因此根据k -邻域图的定义得到的可能是一个有向子图. 在特定网络中, 节点i 的k -邻域图被构造为特定的相似性度量(这里指最短路径距离)下显示与i 最相似的子图. 然而在大多数应用中, k 的值难以直接给定, 以致其应用领域受到限制.3.2.双模式加权算法 -->3.2.双模式加权算法 1)通信邻域图k -邻域图定义的启发, 为了增强网络信息流, 本文提出了一个新的拓扑定义——通信邻域图(communication neighbor graph, CNG), 并进一步提出一种新的加权算法. 通信邻域图的具体定义如下.通讯邻域图 假设$ G(V, E) $ 是一个无自循环的无向网络, 其中节点的数量$ \left|\left|V\right|\right|=N $ . 对于G 中的节点来说, $ {\zeta }_{ij} $ 是节点i 与节点j 之间的最短路径(路径为节点序列集合). 节点i 通过节点j 的通信邻域图用$ {\varPi }_{i\to j} $ 表示, 其定义为: 给定节点u , 如果满足通过节点i 与u 之间的最短路径长度大于节点j 与u 之间的最短路径长度, 即$ l\left({\zeta }_{iu}\right) > $ $ l\left({\zeta }_{ju}\right) $ , 那么节点u 属于$ {\varPi }_{i\to j} $ . 如果节点i 和节点u 之间存在一条以上的最短路径, 那么就认为$ {\zeta }_{iu} $ 是其中任意一条. 根据通信邻域图CNG的定义, 对于特定节点u , 假定节点i 与节点u 之间有边相连, 如果$ {\zeta }_{iu} $ 经过节点j , 那么节点u 就属于$ {\varPi }_{i\to j} $ .$ {\varPi }_{i\to j} $ 与$ {\varPi }_{j\to i} $ 是不同的. 对于任意一对相邻的节点i 和j 来说, 节点j 一定属于$ {\varPi }_{i\to j} $ . 另外, 任一节点$ u\ne i $ 属于且仅属于节点i 的一个通讯邻域图. 图1(a) 给出了两个相邻节点的通信邻域图的例子. 当网络是稠密且规模不大时, 该定义是非常直观的.图 1 (a)节点4和节点5之间边对应的通讯邻域图; (b)网络中的桥边Figure1. (a) Communication neighborhood graph corresponding to the edge between node 4 and node 5; (b) bridge side in the network.图1(b) 所示. 如果节点具有大的度、介数中心性和紧密中心性, 那么它更有可能具有高信息吞吐量, 因此这些节点及其所连的边更可能成为瓶颈. 在本文模型中, 这种可能性被假设为与单一实数成正比, 即定义图中每个节点的$ \gamma $ 值.$ \gamma \left(u\right)\in R $ 表示属于$ {\varPi }_{i\to j} $ 中节点u 的一个特定指标, ${\boldsymbol{\varGamma }}\left({\varPi }_{i\to j}\right)=\{\gamma \left({u}_{1}\right), $ $ \gamma \left({u}_{2}\right), \cdots, \gamma \left({u}_{k}\right)\}$ 且是$ {\varPi }_{i\to j} $ 中所有节点的$ \gamma $ 值集合, 其中$ u\in {\varPi }_{i\to j} $ . 那么, 本文的加权机制定义如下:$ \psi $ 为任意实数集中的单一实数相关的函数. 这是一种具有代表性的加权方法, 可以用来加强与网络通信相关的多种计算与应用.$ \psi $ 为一个集合所有元素的加和, 即如果${\boldsymbol{X}}=\{{x}_{1}, {x}_{2}, \cdots, {x}_{N}\}$ , 那么$\psi \left({\boldsymbol{X}}\right)= $ $ {{\displaystyle\sum }_{i=1}^{N}{x}_{i}}$ , 同时$\psi \left({\boldsymbol{X}}\right)={\displaystyle\sum }_{i=1}^{N}{x}_{i}$ . 定义节点u 的加权参数为$ \alpha \in R $ , 且$ {k}_{u} $ , $ {B}_{u} $ 和$ {\widetilde {C}}_{u} $ 分别为网络G 中节点的度、介数中心性和紧密中心度$ {C}_{u} $ 的倒数. $ \varepsilon $ 设定为0.01, 以避免$ \gamma $ 值为0. 设计加权参数$ \gamma $ 是为了反映瓶颈节点u 的各项参数, 包括度$ {k}_{u} $ , 介数中心性$ {B}_{u} $ 和紧密中心度$ {C}_{u} $ , 如果各项参数比较大, 则$ \gamma $ 也比较大, 节点u 成为瓶颈节点的概率也会很大. 那么, 节点j 到节点i 的权重为$ {\varPi }_{i\to j} $ 表示节点i 通过节点j 的通信邻域图. (12 ) 式表示的加权机制的原理为当传输线路 $ i\to j $ 比较重要时, 其通信邻域图$ {\varPi }_{i\to j} $ 的规模也会相应比较大. 则当$ \alpha > 0 $ 时, (12 )式的分子项${\displaystyle\sum }_{u\in {\varPi }_{i\to j}}\gamma \left(u\right)$ 和相应的权重$ {W}_{ij} $ 也会相应比较大, 从而实现了加权机制增强重要通信边的权重的目的. 这里, 分母项的设置是为了实现标准化, 权重矩阵的对角线元素被设置具有零行和属性, 即${W}_{ii}=-{\displaystyle\sum }_{k}{W}_{ij}=1$ .12 )式)中, 分母的标准化项使得入度更加均匀. 另外, $ \gamma $ 函数((11 )式)增强了以高$ \gamma $ 值节点为起点的路径, 并且进一步使得网络流量更加趋向于流向这类节点. 这个过程使节点的负载分配更加倾向于平均. 总而言之, 本文提出的加权策略使负载分布更加均匀化, 同时降低了平均路径长度. 本文加权算法具体流程如算法1所示. 本算法由于需要计算节点的介数、度、紧密度三种中心性度量, 时间复杂度分别为O(n 3 ), O(n 2 )和O(n 3 ), 因此总的时间复杂度为O(n 3 ).算法1 网络加权算法流程G , 其节点数为n , 边数为m ; 加权参数$ \alpha .$ W $ {k}_{u} $ , $ {B}_{u} $ 和$ {\widetilde {C}}_{u} $ , 分别为网络G 中节点的度、介数中心性和紧密中心度$ {C}_{u} $ 的倒数;6 )式和(11 )式计算节点u 的加权值$ \gamma \left(u\right) $ ;12 )式更新网络中边的加权值w ij $ \gamma $ 值是相等的, 加权机制并不能增强网络的传输容量. 因此, 本文的加权机制旨在通过降低瓶颈节点的限制, 使网络层次结构趋于平坦以提高传输容量. 这种加权机制对具有非均匀层次结构和瓶颈节点的网络(如无标度网络)来说很有效率. 反之, 均匀网络或无瓶颈节点的网络则不具备这种加权机制的优势. 此外, 本文的加权策略还有一个重要优点: 只受一个参数调控, 即参数$ \alpha $ , 可以用来控制加权权重的异质程度(即非均匀性). 这里有三种典型的情况:$ \alpha > 0~(\alpha < 0) $ , 在通信邻域图中, 具有高$ \xi $ 值的节点对信息传输会有更多(更少)的贡献. 特别地, 在同质(均匀)网络中, 节点呈现出均匀的负载和度分布, 那么节点的$ \xi $ 值和随之得到的加权值也会变得均匀. 在这种情况下, 改变$ \alpha $ 不会导致权重和网络传输效率发生显著变化. 类似地, 当网络负载分布和度分布是异质(非均匀)时, 不同的$ \alpha $ 会导致权重和网络传输效率发生显著变化. 因此, 在异质(同质)网络中, $ \alpha $ 会有更多(更少)的影响.$ \alpha =0 $ 时, $ \gamma $ 值将退化为对所有节点u 都有$ \gamma \left(u\right)=1 $ . 值得注意的是, 这种情况与无权网络或者标准化仅仅应用于节点度的情况不同. 在这种情况下, 仅考虑每个通信邻域图的节点数量, 它在$ \gamma $ 值分布的方差较小的网络中将会相当有效, 即$ \gamma $ 值的同质性.$ \alpha < 0 $ 并不会产生负值, 但是会使得信息传输能力下降(即具有高$ \xi $ 值的节点对信息传输会有更少的贡献). 根据本文框架, 我们提出了利用转置权重矩阵以降低传输能力的逆加权方案. 为了能够更方便地转换, 权重矩阵被定义为$ 0\leqslant \rho \leqslant 1 $ , 表示传输程度. 例如, 当$ \rho =1 $ 意味着高传输流量, 而$ \rho =0 $ 意味着低传输流量.逆模式加权机制 在(12 )式的加权机制中, 设定参数$ \alpha < 0 $ , 定义为逆模式加权机制. 根据(12 )式, 在逆模式加权机制中, 即具有高$ \xi $ 值的节点对信息传输会有更少的贡献, 从而会使得网络流量更加趋向于避开这类节点, 使得信息传输能力下降. 为了能够更方便地转换, 权重矩阵被定义为(13 )式. 逆模式加权算法如算法2所示.算法2 逆模式加权算法流程G , 其节点数为n , 边数为m ; 加权参数$ \alpha < 0 $ ; 传输程度参数$0\leqslant \rho \leqslant 1.$ W 11 )式计算节点u 的加权值$ \gamma \left(u\right) $ ;12 )式更新网络中边的加权值$ {w}_{ij}^{*} $ ;13 )式更新网络中边的加权值$ {w}_{ij}^{*} $ .$ \alpha $ 的影响, 将其应用到著名的BA网络中, 分别考虑$ \alpha =2 $ 和$ \alpha =6 $ 两种情况, 结果如图2 所示. 可以看出, 受加权机制的影响, 节点强度和节点度会出现明显异化. 此外, 当$ \alpha =6 $ 时, 节点强度和节点度的关系的分布相较于$ \alpha =2 $ 时更加分散. 这是因为$ \alpha $ 的值越大, 更多的边会得到较大的权重值. 该结果与前面加权机制的分析相符合. 因此, 通过本文的加权策略, 权重分布、节点强度以及度的关系均依赖于参数$ \alpha $ 的值, 该加权网络比相应的二进制无权网络提供了更多的信息.图 2 参数α 取不同值时BA模型中节点强度s 和节点度k 之间的关系(N = 5000) (a) $ \alpha =2 $ ; (b) $ \alpha =6 $ Figure2. Relationship between node strength s and node degree k in BA model (N = 5000) with different values of parameter α : (a) $ \alpha =2 $ ; (b) $ \alpha =6 $ .4.复杂网络的属性分析 许多研究[20 ,39 ,40 ] 发现, 网络中信息传输的难易程度可以解释为同步能力, 并且它们都被网络拓扑矩阵的特征值所限制. 由此直接引出本文提出的加权方案, 它可以试图通过改善信息流以增强同步能力. 然而, 并不是所有的应用都需要提高同步能力, 有些反而需要降低, 比如降低网络的同步性有助于辨别网络中的聚类结构[17 ] . 本节将分析加权机制对网络同步能力的作用, 并进一步分析其对聚类探测及其效率的影响, 从而有效验证加权机制的高效性. 除了同步和聚类分析, 本文加权机制还可以有效应用于网络流行病传播关键路径识别、免疫策略分析、演化博弈分析、路由策略设计、交通拥塞预防等多个方面.4.1.同步性分析 4.1.同步性分析 首先说明加权机制增强网络同步性能的原因. 设${\lambda }_{1}\leqslant {\lambda }_{2}\leqslant, \cdots, \leqslant {\lambda }_{N}$ 为加权矩阵W N 个特征值. 根据文献[41 ], 矩阵W $ {\lambda }_{N}/{\lambda }_{2} $ 越小, 则意味着该网络具有更大的同步能力. 如上所述, 网络通信的能力可以被解释为在网络中信息流动的难易程度. 更确切地说, 可以将动态方程写作:W W W 推论1 加权机制((12 )式)得到的权重矩阵的所有特征值是实数, 且值介于0—2之间.证明 权重矩阵W $ {\boldsymbol{L}}^{\mathrm{w}} $ , 写作$ {\boldsymbol{L}}^{\mathrm{w}}={\boldsymbol{M}}{\boldsymbol{Q}} $ , 其中Q $ {Q}_{ij}=-\psi \left({\boldsymbol{\varGamma }}\left({\varPi }_{i\to j}\right)\right) $ . 容易看出, W ${\lambda }_{i}(i=1, \cdots, N)$ 与$ {{\boldsymbol{M}}}^{1/2}{\boldsymbol{Q}}{{\boldsymbol{M}}}^{1/2} $ 的特征值相等, 即是实数且非负的, 且最小特征值$ {\lambda }_{1}=0 $ . 另一方面, Gerschgorin循环定理[42 ] 证明了$ {\boldsymbol{L}}^{\mathrm{w}} $ 的每个特征值都在一个半径为1的圆的内部, 因此$0= $ $ {\lambda }_{1}\leqslant $ $ {\lambda }_{2}\leqslant, \cdots, \leqslant {\lambda }_{N}\leqslant 2$ . 证明完毕.超中心节点 网络中具有最大$ \gamma $ 值的节点被称为网络的超中心节点.定理1 令$ G(V, E) $ 为一个无向网络, 对于每一对节点u 和v , 选择它们之间的最短路径$ S{P}_{uv} $ , 并根据通信邻域图的定义确定通信邻域图运用加权机制((12 )式). 如果该邻域图具有唯一的超中心节点, 那么当$ \alpha \to +\infty $ 时, 通过移除超中心节点的输入边, 剩余网络将会退化到一个以超中心节点为根节点的有向生成树, 因此总有一条有向路径可以从超中心节点通向其他所有节点.证明 根据(12 )式, 当$ \alpha \to +\infty $ 时, 可以得到$ \psi \left({\boldsymbol{\varGamma }}\left({\varPi }_{i\to j}\right)\right)\approx \mathrm{max}\left\{{\boldsymbol{\varGamma }}\left({\varPi }_{i\to j}\right)\right\} $ , 从而有 ${\displaystyle\sum }_{k}\psi\times $ $ \left({\boldsymbol{\varGamma }}\left({\varPi }_{i\to j}\right)\right)\approx \underset{k}{\mathrm{max}}\left\{\mathrm{max}\left\{{\boldsymbol{\varGamma }}\left({G}^{i\to k}\right)\right\}\right\}$ . 现在, 假设节点$ {u}^{*} $ 是唯一的超中心节点, 即网络中具有最大的$ \gamma $ 值的节点. 当$ \alpha \to +\infty $ 时, 如果$ {u}^{*}\in {\varPi }_{i\to j} $ 并收敛于0, 权重$ {W}_{ij} $ 将收敛于1. 换言之, 每个节点$ i\ne {u}^{*} $ 只保持一条边连接网络中具有最大$ \gamma $ 值的那个节点. 由于$ {u}^{*} $ 的输入边被删除了, 也就是所有到$ {u}^{*} $ 的输入边的权重都等于0, 仅保留N – 1条有向边. 因此, 从节点$ {u}^{*} $ 到网络中所有其他节点都有一条有向路径, 且仅保留有N – 1条边, 由此得到的网络结构是一个有向生成树, 其中具有最大$ \gamma $ 值的节点是根节点. 证明完毕.推论2 根据参考文献[41 ], 定理1中得到的有向生成树的特征值比$ {\lambda }_{N}/{\lambda }_{2}=1 $ , 意味着该网络具有最大的同步能力. 简单来说, 由于生成树的根拥有最大的$ \gamma $ 值, 因此在所得的生成树中, 大多数节点都在树的较低层次上, 也就是说大多数节点与根节点的平均距离较短. 值得一提的是, 当$ \alpha \to +\infty $ 时, 如果不移除根节点的输入边, 那么特征值比$ {\lambda }_{N}/{\lambda }_{2}=2 $ , 也就是说, $0={\lambda }_{1} < {\lambda }_{2}= $ $ {\lambda }_{3}, \cdots, ={\lambda }_{N-1} < {\lambda }_{N}=2$ . 如果超中心节点并不唯一, 当$ \alpha \to +\infty $ 时, 网络将退化为有向图, 其中所有超中心节点都属于边权重相等的团. 此外, 该团中的任意节点都能与图中的所有其他节点相连, 即对于网络中的每个节点来说, 都有一条有向路径通向每个超中心节点. 基于上述可以发现, 只有参与这些路径的边被留下来, 而其他的边都将会消失.4.2.聚类结构分析 -->4.2.聚类结构分析 前文已经提到, 在一些应用中, 有时候还需要降低同步能力, 如辨别网络中的聚类结构[17 ] . 本文提出的加权策略对聚类结构探测也有很强的影响, 并且可以进一步发现聚类结构与同步性之间的隐藏关系. 首先给出聚类结构的弱定义:聚类结构的弱定义 Radicchi等[43 ] 分别从弱定义和强定义这两方面给出了衡量聚类结构的量化标准, 其中弱定义被认为是一个子图集合能够成为聚类结构的最弱标准, 即聚类是网络的子图集合, 子图内部的边的密度高于子图之间的边的密度. 给定一个网络$ G=(V, E) $ , 其中V 是节点集, E 是边界集, $ {\boldsymbol{A}}=\left({a}_{ij}\right) $ 为其邻接矩阵, 令$ {V}_{\mathrm{s}}\subset V $ 为一个特定子图, $ {\overline {V}}_{\mathrm{s}}=V\backslash {V}_{\mathrm{s}} $ 为网络其余的节点集, 那么在弱灵敏度条件下$ {\boldsymbol{V}}_{\mathrm{s}} $ 能够成为一个聚类的条件是:$L\left({V}_{\mathrm{s}}, {V}_{\mathrm{s}}\right)={\displaystyle\sum }_{i\in {V}_{\mathrm{s}}}{\displaystyle\sum }_{j\in {V}_{\mathrm{s}}}{a}_{ij}$ , $L\left({V}_{\mathrm{s}}, {\overline {V}}_{\mathrm{s}}\right)= $ $ {\displaystyle\sum }_{i\in {V}_{\mathrm{s}}}{\displaystyle\sum }_{j\notin {V}_{\mathrm{s}}}{a}_{ij}$ . 在弱定义下的网络聚类中, $ {V}_{\mathrm{s}} $ 内部的边的个数至少应该超过其连接网络剩余部分的边个数的一半.推论3 如果$ {e}_{ij} $ 是一个类间边, 那么邻域图$ {\varPi }_{i\to j} $ 和$ {\varPi }_{j\to i} $ 很可能是两个相邻的聚类. 此外, 在极端情况下, 如果网络是二划分且$ {e}_{ij} $ 是唯一的类间边, 根据聚类结构的弱定义, $ {\varPi }_{i\to j} $ 和$ {\varPi }_{j\to i} $ 将是严格的网络聚类.证明: 根据弱定义, 如果一个网络拥有聚类结构, 由于存在高密度的类内边, 一个随机游走者将会在一个聚类中停留很多的时间. 这意味着一个节点到同一聚类内的节点的路径长度通常比到不同聚类的节点的路径长度短. 如图2 中$ \alpha =2 $ 时, $ {\varPi }_{i\to j} $ 中的节点到节点j 的路径长度比到节点i 的路径长度都要长. 相反, $ {\varPi }_{j\to i} $ 中的节点到节点i 的路径长度比到节点j 的路径长度长. 因此可以得出结论: $ {\varPi }_{i\to j} $ 和$ {\varPi }_{j\to i} $ 很可能是两个不同的聚类. 此外, 如果$ {e}_{ij} $ 是唯一的类间界, 根据聚类结构的弱定义, 这个结论是严格的. 证明完毕.$ \alpha $ 的值并在示例网络中删除$ {W}_{ij} < 0.5 $ 的边. 如图3 所示, 当$ \alpha $ 值从2增加到4, 聚类结构会显著增强.图 3 应用加权机制后网络的动态演化示例图Figure3. Example of dynamic evolution of network after applying weighting mechanism.$ R={l}^{\mathrm{o}\mathrm{u}\mathrm{t}}/{l}^{\mathrm{i}\mathrm{n}} $ 在解决模块度优化问题上发挥着十分重要的作用. 为了满足弱定义的标准, 这个比率的区间应该为[0, 2].定理2 令$ {l}^{\mathrm{o}\mathrm{u}\mathrm{t}} $ 为类间边的数量, $ {l}^{\mathrm{i}\mathrm{n}} $ 为类内边的数量, 那么比率$ R={l}^{\mathrm{o}\mathrm{u}\mathrm{t}}/{l}^{\mathrm{i}\mathrm{n}} $ 可以用来有效量化网络中的聚类结构.证明 对于特定的网络G , 其相对的超图$ {G}^{*} $ 定义为一个有向加权的C 团结构, 其中的每个节点对应于G 的一个聚类. 在$ {G}^{*} $ 中, 节点r 和节点s 之间的边用$ {l}_{\mathrm{o}\mathrm{u}\mathrm{t}}^{rs}/{l}_{\mathrm{i}\mathrm{n}}^{r} $ 来加权, 其中$ {l}_{\mathrm{o}\mathrm{u}\mathrm{t}}^{rs} $ 代表G 中聚类r 和聚类s 之间的团间边数量, $ {l}_{\mathrm{i}\mathrm{n}}^{r} $ 代表聚类r 内部边的数量. $ {G}^{*} $ 对应的$ C\times C $ 拉普拉斯矩阵${\boldsymbol{F}}= $ $ \left\{{F}_{rs}\right\}$ 是不对称的, 但是可以变换为$ {\boldsymbol{F}}={\boldsymbol{\varDelta }}\varTheta $ , 其中$ \varDelta =\left\{{\varDelta }_{rs}\right\} $ 是一个对称的零行和矩阵, 其非对角元素为$ {\varDelta }_{rs}=-{l}_{\mathrm{o}\mathrm{u}\mathrm{t}}^{rs} $ , 对角元素为${\varDelta }_{rr}={\displaystyle\sum }_{r\ne s}{l}_{\mathrm{o}\mathrm{u}\mathrm{t}}^{rs}$ , 且$\varTheta =\mathrm{diag}\left\{1/{l}_{\mathrm{i}\mathrm{n}}^{1}, \cdots, 1/{l}_{\mathrm{i}\mathrm{n}}^{c}\right\}$ . 那么可以将F F F F $ {\lambda }_{1}^{*}=0 $ , 次小特征值$ {\lambda }_{2}^{*} > 0 $ .[42 ,44 -46 ] , $ {\lambda }_{2}^{*} $ 能够量化超图的连通性, 从而衡量不同聚类的性质和互相关联的程度. 应该注意到, $ {\lambda }_{2}^{*} $ 已经过标准化, 所以它应该是一维的. 这里, 可以得出$ {\lambda }_{2}^{*}\approx {l}_{\mathrm{o}\mathrm{u}\mathrm{t}}/{l}_{\mathrm{i}\mathrm{n}} $ . 特殊情况下, 如果C 个聚类都具有相等规模$ {N}_{c}=N/C $ , 那么类内边数量$ {l}_{\mathrm{i}\mathrm{n}}^{r} $ 和类间边$ {l}_{\mathrm{o}\mathrm{u}\mathrm{t}}^{r} $ 数量对所有聚类来说都是一样的. 此时, 由$ {l}_{\mathrm{i}\mathrm{n}}^{r}={l}_{\mathrm{i}\mathrm{n}}/C $ 和$ {l}_{\mathrm{o}\mathrm{u}\mathrm{t}}^{r}={l}_{\mathrm{o}\mathrm{u}\mathrm{t}}/C $ , 可以得到$ L=C\left({l}_{\mathrm{i}\mathrm{n}}^{r}+0.5{l}_{\mathrm{o}\mathrm{u}\mathrm{t}}^{r}\right)={l}_{\mathrm{i}\mathrm{n}}+0.5{l}_{\mathrm{o}\mathrm{u}\mathrm{t}} $ : 由$\varDelta = $ $ CI/{l}_{\mathrm{i}\mathrm{n}}$ , 可以得到$ {\lambda }_{2}^{*}={l}_{\mathrm{o}\mathrm{u}\mathrm{t}}/{l}_{\mathrm{i}\mathrm{n}}={l}_{\mathrm{o}\mathrm{u}\mathrm{t}}^{r}/{l}_{\mathrm{i}\mathrm{n}}^{r} $ . 证明完毕.[32 ] 发现了聚类探测的分辨率限制问题, 表明对于优化模块度Q ((1 )式)的算法, 如果$ {l}_{\mathrm{i}\mathrm{n}}^{r} $ 的取值区间不在[0, L ]内, 那么模块度优化算法将无法检测到这些聚类. 直观地看, 如果引入一种加权策略, 能够有效扩大这个限制区间, 那么许多优化算法就能够在一个较大的限制范围内探测到准确聚类. 为了分析简便, 假设权重之和边的个数L 保持相等. 这里, 加权网络中所有的量都以上尖号为区分, 即$ \widehat{R} $ . 首先, 回顾一个关于聚类规模边界的定理[32 ] .定理3 聚类规模对模块度函数Q 的影响有如下限制:$ R={l}^{\mathrm{o}\mathrm{u}\mathrm{t}}/{l}^{\mathrm{i}\mathrm{n}} $ . 如果合并聚类i 和聚类j 不能提高模块度函数Q 的值, 那么对于聚类i 和聚类j 的规模有如下约束条件[31 ] :j , 有i , 有i 和聚类j 之间的团间边权重之和为$ {R}_{ij}{l}_{j}^{\mathrm{i}\mathrm{n}}={R}_{ji}{l}_{i}^{\mathrm{i}\mathrm{n}}={l}_{ij}^{\mathrm{o}\mathrm{u}\mathrm{t}} $ .L . 如果$ {\hat{l}}_{i}^{\mathrm{i}\mathrm{n}} $ 和$ {\hat{l}}_{i}^{\mathrm{o}\mathrm{u}\mathrm{t}} $ 分别表示聚类i 的类内边权重之和以及聚类i 与其他聚类节点的类间边权重之和, 那么有$ {\widehat{R}}_{i}= $ $ {\hat{l}}_{i}^{\mathrm{o}\mathrm{u}\mathrm{t}}/{\hat{l}}_{i}^{\mathrm{i}\mathrm{n}} $ , $ {\widehat{R}}_{ij}={\hat{l}}_{ij}^{\mathrm{o}\mathrm{u}\mathrm{t}}/{\hat{l}}_{i}^{\mathrm{i}\mathrm{n}} $ . 利用加权模块度函数Q , 根据定理3, 可以推导出聚类规模的上下界为$ {\widehat{R}}_{ij} $ 的值, 因此能提高聚类探测规模的上限.$ {\widehat{R}}_{i} $ , $ {\widehat{R}}_{j} $ 和$ {\widehat{R}}_{ij} $ 的值, 聚类探测规模的下限不一定会降低. 然而, 如果假设对所有i 都有${\widehat{R}}_{i}\leqslant 2$ , 将得到下限的区间:$ {\widehat{R}}_{ij} $ 逐渐减少, 可以发现该区间的上下两端都将减少, 表明引入本文加权机制后, 聚类探测规模的下界会减少.5.实 验 本节将上述加权机制运用在人工网络和大量现实世界网络中. 结果表明, 这种加权机制可以分别利用原模式和逆模式来提高网络同步能力以及增强聚类结构检测能力.5.1.同步性 5.1.同步性 在本文提出的加权策略中, 唯一的调整参数是$ \alpha $ . 通过改变$ \alpha $ 参数, 可以控制权重值的异质性和特征值比$ {\lambda }_{N}/{\lambda }_{2} $ .[2 ] 和Watts-Strogatz小世界网络[1 ] 作为基准模型网络, 并将本文加权机制应用其中. 无标度网络的节点度分布服从幂律特性, 即该模型有两个参数, 其中节点初始边数$ {k}_{0} $ 控制平均度, 即$ \left\langle k \right\rangle \approx 2{k}_{0} $ . 另外, 参数$\beta $ 调整控制网络度分布的异质性, 当$ \beta $ 增加时, 网络的异质性会减少到特定程度.图4 给出了在无标度网络上的实验结果, 其中数据点为50次实验结果的平均值. 图4(a) 为特征值比$ {\lambda }_{N}/{\lambda }_{2} $ 和参数($ \alpha $ , $ \left\langle k \right\rangle $ )的对应关系, 这里网络的平均度用$ \left\langle k \right\rangle $ 表示. 设$ \alpha =1 $ , 对于所有的平均度$ \left\langle k \right\rangle $ , 可以得到$ {\lambda }_{N}/{\lambda }_{2} < 2 $ , 这比文献[23 ]的最优情况还要好, 而又优于文献[21 , 22 , 39 ]的研究结果. 对于较大的平均度$ \left\langle k \right\rangle $ , 权重分布和度分布的同质性增加, 这表示$ \gamma $ 值将更加均匀, 而$ \alpha $ 的影响也会较弱. 所以, 无论$ \alpha $ 的大小, 加权过程都将显著提高网络同步能力. 对于平均度$ \left\langle k \right\rangle $ 较低的网络, 由于网络中异质性较高, 因此较大的$ \alpha $ 将会得到更好的结果. 接下来研究网络的异质性(非均匀性), 该性质可以用参数$ \beta $ 来衡量. 已有研究表明, 网络度分布的异质性是影响同步性能最重要的因素之一. 无标度网络中特征值比$ {\lambda }_{N}/{\lambda }_{2} $ 和参数$ \alpha $ , $ \beta $ 的关系如图4(b) 所示. 对于不同的$ \beta $ , 因为无标度特征导致节点度的非均匀性, 参数$ \alpha $ 的影响作用会更加显著. 此外可以看出, 随着$ \beta $ 值增加, 网络非均匀性降低, 得到的加权网络的同步性会逐渐变差.图 4 (a) 无标度网络中$ {\lambda }_{N}/{\lambda }_{2} $ 与($ \alpha $ , $ \left\langle k \right\rangle $ )的对应关系(N = 500, $ \beta =0 $ ); (b)无标度网络中$ {\lambda }_{N}/{\lambda }_{2} $ 与($ \alpha $ , $ \beta $ )的对应关系(N = 500, $ \left\langle k \right\rangle =4 $ )Figure4. (a) Corresponding relationship (N = 500, $ \beta =0 $ ) in scale-free networks between $ {\lambda }_{N}/{\lambda }_{2} $ and ($ \alpha $ , $ \left\langle k \right\rangle $ ); (b) Corresponding relationship (N = 500, $ \left\langle k \right\rangle =4 $ ) in scale-free networks between $ {\lambda }_{N}/{\lambda }_{2} $ and ($ \alpha $ , $ \beta $ ).$ \left\langle k \right\rangle =2{k}_{0} $ , 和重连概率P . 图5 给出了在Watts-Strogatz网络中应用本文加权算法的结果, 图中数据点为50次实验结果的平均值. 其中, 图5(a) 为特征值比$ {\lambda }_{N}/{\lambda }_{2} $ 随参数$ \alpha $ 和网络平均度$ \left\langle k \right\rangle $ 的变化情况. 和无标度网络相似, 当平均度$ \left\langle k \right\rangle $ 增加时, 网络的异构程度随之降低$ \alpha $ , 从而降低$ \alpha $ 的贡献程度. 可以看出, 当平均度$ \left\langle k \right\rangle $ 非常高时, $ \alpha $ 对特征值比$ {\lambda }_{N}/{\lambda }_{2} $ 几乎没有影响. 图5(b) 为特征值比$ {\mathrm{\lambda }}_{{N}}/{{\lambda }}_{2} $ 随参数$ \alpha $ 和重连概率P 的变化情况. 当P 较小时, 网络度分布几乎是均匀的, 但是节点的负载分布却是极度非均匀的. 这是由于极少数的重连边可以被视作捷径, 它们承担着很高的负载, 导致负载的分布具有高度的不均匀性. 随着重连概率P 的增加, 网络重连边的数量会逐渐增加, 负载分布会因此变得越来越均匀. 在这种情况下, 虽然度分布的方差会逐渐增加, 但仍不足以提升$ \gamma $ 值的异质程度. 因此, 增加P 会使$ \gamma $ 值分布更加均匀, 从而降低加权机制的贡献程度. 特别地, 当P = 1时, Watts-Strogatz网络等同于完全随机图.图 5 (a) Watts-Strogatz网络中$ {\lambda }_{N}/{\lambda }_{2} $ 与($ \alpha $ , $ \left\langle k \right\rangle $ )的对应关系(N = 500, P = 0.1); (b) Watts-Strogatz网络中$ {\lambda }_{N}/{\lambda }_{2} $ 与($ \alpha $ , P )的对应关系(N = 500, $ \left\langle k \right\rangle =4 $ )Figure5. (a) Corresponding relationship (N = 500, P = 0.1) in Watts-Strogatz networks between $ {\lambda }_{N}/{\lambda }_{2} $ and ($ \alpha $ , $ \left\langle k \right\rangle $ ); (b) corresponding relationship (N = 500, $ \left\langle k \right\rangle =4 $ ) in Watts-Strogatz networks between $ {\lambda }_{N}/{\lambda }_{2} $ and ($ \alpha $ , P ).[21 ] 、Wang方法[22 ] 、Jalili方法[23 ] 、Khadivi方法[31 ] 、模拟退火(SA)算法[25 ] 、随机游走(RW)算法[27 ] 、变分贝叶斯(VB)算法[29 ] 、概率推断(PL)方法[30 ] 和本文方法, 结果列在表1 中, 其中设定$ \alpha =4 $ . 可以看出, 本文使用的加权机制的性能超过了其他所有的加权方法. 值得一提的是, 对于所有的现实世界网络, 随着$ \alpha $ 的增加, 特征值$ {\lambda }_{N}/{\lambda }_{2} $ 比都将收敛于2. 现实世界网络 N $ \left\langle k \right\rangle $ $ {\lambda }_{N}/{\lambda }_{2} $ Chavez Wang Jalili Khadivi RW SA VB PL This work 蛋白质结构网络2 53 4.64 20.92 20.54 6.06 5.83 5.61 4.87 4.43 4.59 4.27 海豚网络 62 5.12 16.89 43.01 6.83 6.22 6.04 5.33 5.07 5.30 4.95 蛋白质结构网络1 95 4.48 63.1 262.2 23.5 19.82 15.71 13.65 10.59 11.88 8.45 蛋白质结构网络3 99 4.37 43.75 299.85 13.07 10.84 10.27 9.87 9.14 9.00 8.02 中国航空网络 203 18.48 13.25 5.79 3.29 2.88 2.23 2.08 1.83 1.76 1.55 电子邮件通讯 1133 9.62 8.63 5.81 5.40 4.04 3.86 3.91 3.84 3.54 3.77 酵母蛋白质交互作用 1458 2.67 52.44 269.07 25.60 17.63 15.61 13.21 10.76 12.66 9.52 蛋白质交互作用 2840 2.92 34.87 41.60 16.50 13.85 11.48 10.47 8.94 9.87 5.50 中国电力网络 865 5.20 49.77 133.8 25.43 20.90 23.44 15.19 12.04 10.56 5.04 科学家合作网络 4380 3.25 68.31 273.14 38.69 25.87 20.02 17.36 10.42 11.77 7.21 因特网AS2 7690 4.00 12.90 3.26 2.94 2.15 2.04 2.10 1.91 1.59 1.88 因特网AS5 8063 4.10 12.88 3.41 3.37 2.56 2.27 2.09 1.97 2.20 1.83
表1 在现实世界网络中使用8种不同加权策略的实验结果对比, 其中RW代表随机游走方法, SA代表模拟退火方法, VB代表变分贝叶斯方法, PL代表概率推断方法Table1. Comparison of experimental results using eight different weighting strategies in real world networks, in which RW represents random walk method, SA stands for simulated annealing method, VB stands for variational Bayesian method, PL stands for probability inference method.5.2.聚类探测 -->5.2.聚类探测 1)人工基准网络[9 ,11 ] 已经广泛应用于对不同聚类算法的效率评估. GN网络共包括128个节点, 这些节点被分配到4个聚类中, 每个聚类包含32个节点, 每个聚类内部点之间连边和与类外节点连边的概率分别为$ {p}_{\mathrm{i}\mathrm{n}} $ 和$ {p}_{\mathrm{o}\mathrm{u}\mathrm{t}} $ . 因此, 对于每个节点, 它们在聚类内部的边的个数和与其他类节点关联的边的期望分别为$ {z}_{\mathrm{i}\mathrm{n}}=31{p}_{\mathrm{i}\mathrm{n}} $ 和$ {z}_{\text{out}}=96{p}_{\text{out}} $ , 可以看出$ {z}_{\mathrm{i}\mathrm{n}}\text{+}{\text{z}}_{\mathrm{o}\mathrm{u}\mathrm{t}}\text{=16} $ .[47 ] 提出了LFR基准网络, 它可以通过调整相关参数来符合现实网络中的无标度特征. 在该基准网络中, 节点的度分布和聚类规模遵循幂律分布. 此外, 还需要设定一些其他参数, 包括节点最大度、节点平均度、节点总数、聚类最大规模和最小规模以及最重要的混合参数$ \mu $ . 混合参数$ \mu $ 的取值区间为[0, 1], 决定了LFR基准图的聚类模糊性程度: $ \mu $ 越大, 聚类就越难被正确划分. 可以看出, GN基准网络是LFR基准网络的一个特例. 由于GN基准网络和LFR基准网络的社团都是预先给定的, 而不同划分算法得到的结果是不同的, 因此这里利用正确率R (正确划分的节点和全部节点的比值)衡量划分的正确性.图6(a) 的原加权网络中, $ \alpha $ 取2和4, 在逆加权网络中, $ \alpha $ 取–2和–4, 数据点为50次实验结果的平均值. 图6(a) 给出了在GN基准网络上应用加权策略前后的平均正确率R 的对比. 可以看出, 当$ \alpha =4 $ 和$ \alpha =2 $ 时, 加权策略的原模式都提高了平均正确率R , 而相应的两个逆模式 ($ \alpha =-4 $ 和$ \alpha =-2 $ )都会降低平均正确率R . 与$ \alpha =4 $ 的情况相比, 在$ \alpha =2 $ 的情况下, 平均正确率R 会下降约2—3倍. 而且在逆模式中, 当${z}_{\mathrm{o}\mathrm{u}\mathrm{t}}\leqslant 6.5$ 时, $ \alpha =-4 $ 的情况与$ \alpha =-2 $ 相比, 平均正确率R 会降低2倍以上.图 6 (a) GN基准网络中使用加权机制(逆加权机制)前后平均比率R 的对比; (b) LFR基准网络中使用加权机制(逆加权机制)前后平均比率R 的对比Figure6. (a) Comparison of average ratio R before and after using weighting mechanism (inverse weighting mechanism) in GN benchmark network; (b) comparison of average ratio R before and after using weighting mechanism (inverse weighting mechanism) in LFR benchmark network.$ \mu $ 在区间[0, 0.5]内变化. 从图6(b) 可以看出, 加权策略的原模式会显著提高平均正确率R , 而相应的逆模式会降低平均正确率R . 与$ \alpha =4 $ 的情况相比, 在$ \alpha =2 $ 的情况下, 平均正确率R 会下降约4—5倍. 另外, 在逆加权模式也会得到相似的结果. 比较两种基准网络, 对于提高平均正确率R , 加权策略在LFR基准网络中会取得更好的效果.$ \alpha $ 值的加权机制对网络赋权, 然后利用一些著名的聚类算法运行并测试其准确性. 这里使用在信息论中被广泛研究的标准化互信息(normalized mutual information, NMI)来衡量聚类结果的准确性[40 ] . NMI位于区间[0, 1]内, 其值的大小表明真实聚类和模型结果之间重叠的比例. 特别地, 当NMI的值为1时, 算法结果与真实聚类完全相同, 具有最高的划分效率. 真实划分X 和模型结果Y 之间的标准化互信息NMI的数学定义为$ {c}_{X} $ 和$ {c}_{Y} $ 分别表示真实划分X 和模型结果Y 中的聚类数量. 在(21 )式, $ {N}_{ij} $ 代表真实划分中聚类i 和实验结果中聚类j 之间重叠的节点数量, $ {N}_{i} $ 和$ {N}_{j} $ 分别表示矩阵N 中第i 行和第j 列值的总和.图7(a) 和图7(b) 给出了利用两种著名算法, 即模拟退火法(SA)[48 ] 和Duch-Arenas法(DA)[49 ] , 在运用加权机制的网络上的实验结果, 图中数据点为50次实验结果的平均值. 其中, SA算法被证明是效果最好的聚类算法之一, 然而其计算复杂性也较高. 与SA相比, DA不仅在模块化优化方面具备一定可靠性, 而且计算过程也相对简单. 从图7(a) 和图7(b) 可以看到, 当$ \alpha $ 值从–2降低到–4, 逆加权模式对应的NMI值越来越高, 要优于无权网络. 相反, 在原加权模式中, 当$ \alpha $ 值从2增加到4, 加权网络的NMI相对于无权网络的NMI却越来越少. 这些结果均验证了本文的加权策略的有效性. 此外, 通过比较两种方法发现, 图7(a) 中$ \alpha =4 $ ($ \alpha =-4 $ )和$ \alpha =2 $ ($ \alpha =-2 $ )两种情况的NMI差异区间小于图7(b) . 这可能是因为, 即使是在无权网络中, SA都拥有更高的精确度, 难以通过加权策略提高它的表现. 但是对于DA来说, 通过提高$ \alpha $ , 加权机制能够大幅提高它的计算精度.图 7 在LFR网络中运用加权机制(逆加权机制), 当取不同的$ \alpha $ 值时, 利用(a) SA算法和(b) DA算法后NMI的计算值Figure7. Weighted mechanism (inverse weighted mechanism) is used in LFR network. When the $ \alpha $ value is different, the NMI value is calculated by using (a) SA algorithm and (b) DA algorithm.图8 所示, 图中数据点为50次实验结果的平均值. 考虑两种不同聚类规模条件下的LFR基准网络, 其中, 每个聚类的节点数量在10—50之间为小聚类网络, 在20—100之间为大聚类网络. 为了增强这两种LFR基准网络的可比性, 规定它们的区别仅限于聚类的规模大小, 其他方面的性质则完全相同. 图8 验证了在逆加权网络中, SA和DA算法的准确性都得到提升. 此外, 通过比较不同规模LFR网络的聚类结果可以看出, 大聚类网络中两种算法的精确度更低, 这可能是因为小聚类网络中具有更多的类间边, 而类间边更可能是被加权的. 并且通过比较两种方法, 图8(a) 显示的小聚类和大聚类LFR网络(无论是逆加权网络还是加权网络)之间的NMI区间差距小于图8(b) , 原因与图7 相同, 完美证明了本文加权机制的有效性.图 8 在LFR网络中运用加权机制(逆加权机制), 当$ \alpha =4 $ ($ \alpha =-4 $ )并考虑聚类规模时, 利用(a) SA算法和(b) DA算法后NMI的计算值Figure8. The weighted mechanism (inverse weighted mechanism) is used in LFR network. When α = 4 (α = –4) and considering the cluster size, the NMI calculated by (a) SA algorithm and (b) DA algorithm.表2 中列出. 这里使用了7种广泛使用的网络, 并标识了相应的文献出处. 为了便于比较, 提供了关于7种网络已发表方法中的最优模块度Q 值[56 ] . 本文计算了当$ \alpha =4 $ 时三种代表性算法, 即SA[48 ] , DA[49 ] 和CNM[10 ] 的加权前后模块度Q 值, 其中“/”左右表示加权后和加权前的模块度Q 值, 结果如表2 所列. 这三种算法的精确度虽然并不处于最顶级的行列, 然而正如表2 所列, 在应用加权策略后, 结果非常接近已发表的最优值, 并且计算过程更加简便. 网络 文献 最优Q SA[48 ] DA[49 ] CNM[10 ] 中国航空网络 [11 ] — 0.644/0.525 0.589/0.428 0.577/0.483 空手道俱乐部 [50 ] 0.420 0.416/0.342 0.411/0.351 0.413/0.376 《悲惨世界》 [51 ] 0.561 0.554/0.389 0.539/0.406 0.531/0.395 海豚社会网络 [52 ] 0.531 0.527/0.375 0.521/0.362 0.517/0.356 电子邮件 [53 ] 0.579 0.568/0.462 0.543/0.436 0.538/0.444 爵士乐 [54 ] 0.446 0.439/0.333 0.437/0.341 0.431/0.328 PGP密钥签名 [55 ] 0.878 0.883/0.674 0.843/0.705 0.872/0.754
表2 在不同现实网络使用加权策略得到的实验结果, 其中“/”左右表示加权后和加权前的模块度Q 值Table2. Experimental results are obtained by using weighting strategy in different real networks, where /’s left or right represents the modularity Q value after or before weighting.[21 ] 、Wang方法[22 ] 、Jalili方法[23 ] 、Khadivi方法[31 ] 、模拟退火(SA)算法[25 ] 、随机游走(RW)算法[27 ] 、变分贝叶斯(VB)算法[29 ] 、概率推断方法[30 ] 和本文方法, 用以对比不同加权方法的聚类效果. 聚类算法统一使用CNM方法[10 ] , 并计算当$ \alpha =4 $ 时的模块度Q 值. 结果列在表3 中, 可以看出, 本文所使用的加权机制的性能超过了其他所有的加权方法, 从而验证了本文加权算法的高效性. 网络 Chavez Wang Jalili Khadivi RW SA VB PL This work 空手道俱乐部 0.316 0.322 0.351 0.362 0.374 0.381 0.390 0.386 0.413 中国航空网络 0.449 0.478 0.423 0.432 0.506 0.543 0.564 0.578 0.603 《悲惨世界》 0.357 0.369 0.399 0.411 0.439 0.457 0.488 0.433 0.531 爵士乐 0.338 0.347 0.353 0.361 0.383 0.399 0.42 0.387 0.431 PGP密钥签名 0.583 0.678 0.676 0.715 0.744 0.786 0.839 0.820 0.872 海豚社会网络 0.357 0.381 0.371 0.374 0.406 0.444 0.483 0.500 0.517 电子邮件 0.368 0.409 0.431 0.443 0.471 0.499 0.503 0.495 0.538
表3 在现实世界网络中使用不同加权策略的实验结果对比, 这里网络聚类算法利用CNM算法, 其中RW代表随机游走方法, SA代表模拟退火方法, VB代表变分贝叶斯方法, PL代表概率推断方法Table3. Comparison of experimental results using different weighting strategies in the real world network. CNM algorithm is used as the network clustering algorithm, in which RW represents the random walk method, SA represents the simulated annealing method, VB represents the variable dB method, and PL represents the probability inference method.6.结 论 随着“大数据”技术的不断涌现和发展, 如何处理大规模网络已经成为了巨大的现实挑战[57 ,58 ] . 同时, 作为一个开放性问题, 提高网络同步性能或聚类探测的算法效率往往非常困难. 为此, 本文提出一个新型双模式加权机制, 通过加权改变网络拓扑结构来提高同步性能或聚类探测的算法效率. 该加权机制包括两种模式: 一是通过提高桥点的权重以增强同步能力的原始模式: 二是通过减少桥点的权重以提高聚类探测效率的逆模式. 这种加权机制仅受一个参数$ \alpha $ 的影响, 因此非常便于实施. 通过在人工基准网络和现实世界网络上的实验分析, 检验了模型的有效性和高效性. 特别地, 通过比较发现, 本文提出的加权策略在效率上优于以往发表的提升网络计算效率的加权方法. 






























































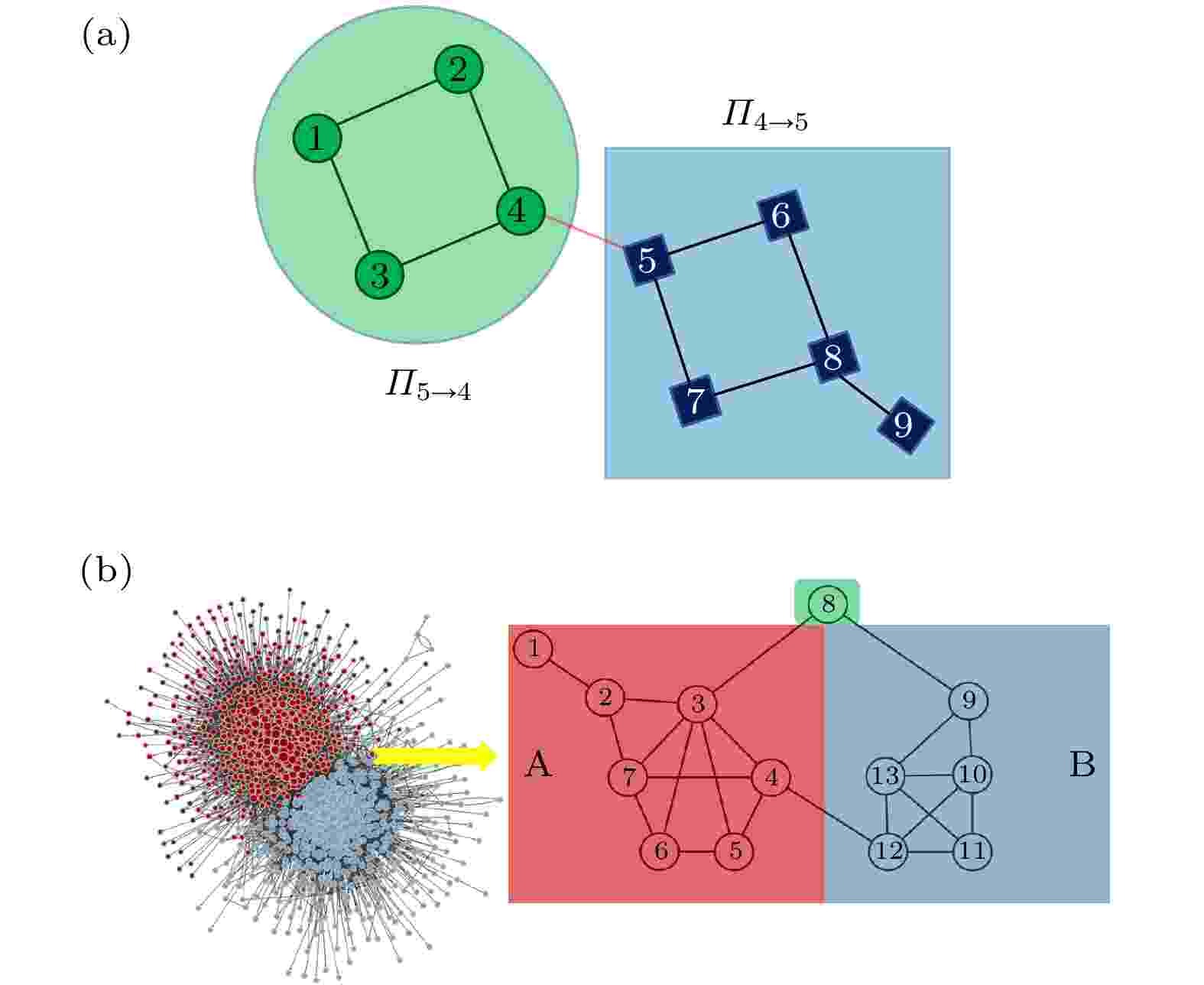 图 1 (a)节点4和节点5之间边对应的通讯邻域图; (b)网络中的桥边
图 1 (a)节点4和节点5之间边对应的通讯邻域图; (b)网络中的桥边


















































































































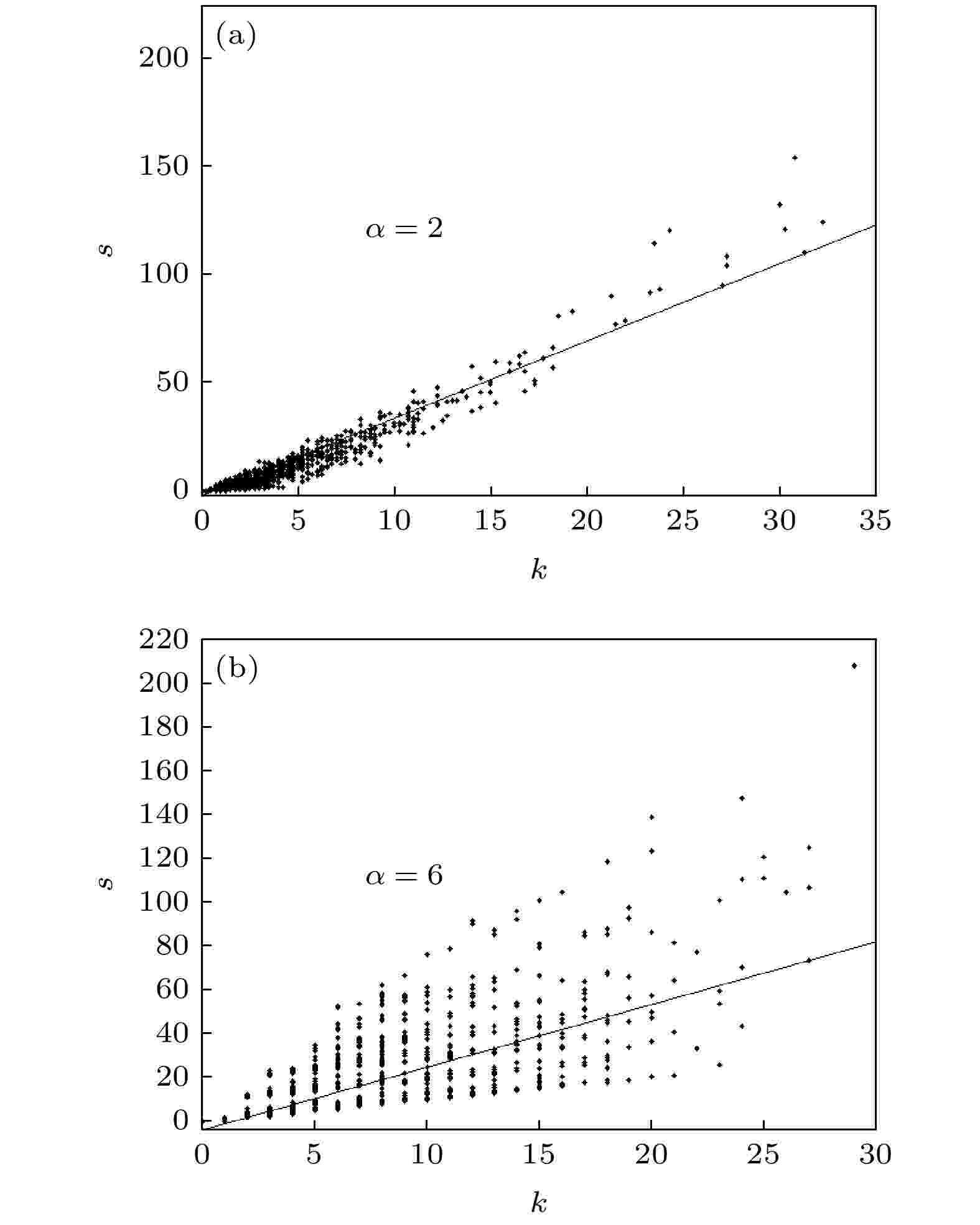 图 2 参数α取不同值时BA模型中节点强度s和节点度k之间的关系(N = 5000) (a)
图 2 参数α取不同值时BA模型中节点强度s和节点度k之间的关系(N = 5000) (a) 



































































































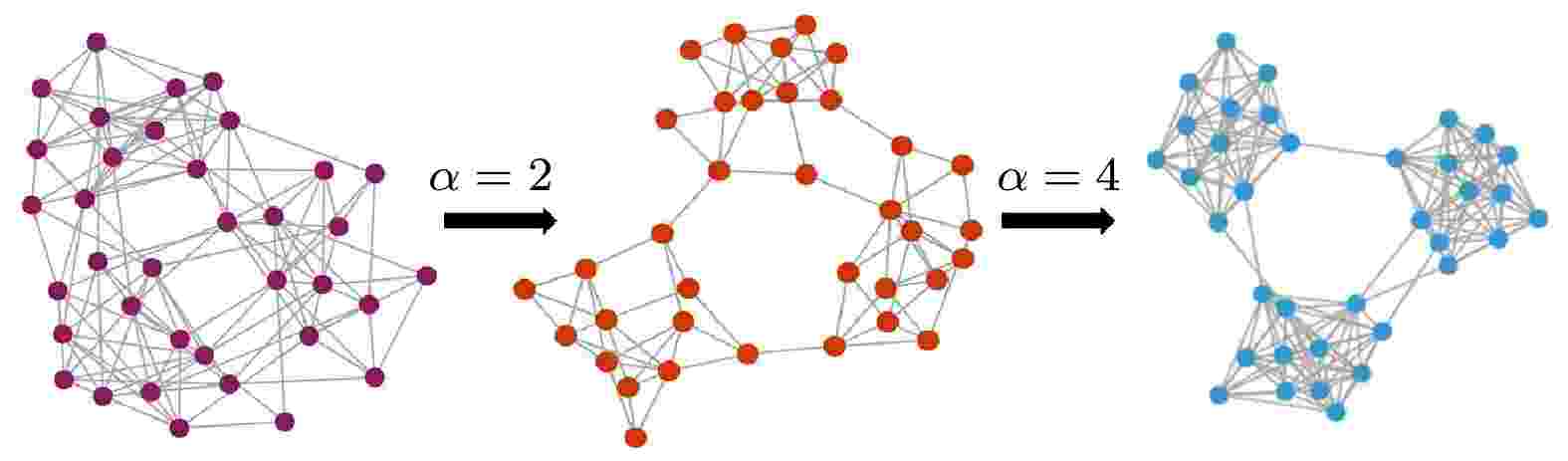 图 3 应用加权机制后网络的动态演化示例图
图 3 应用加权机制后网络的动态演化示例图



















































































































































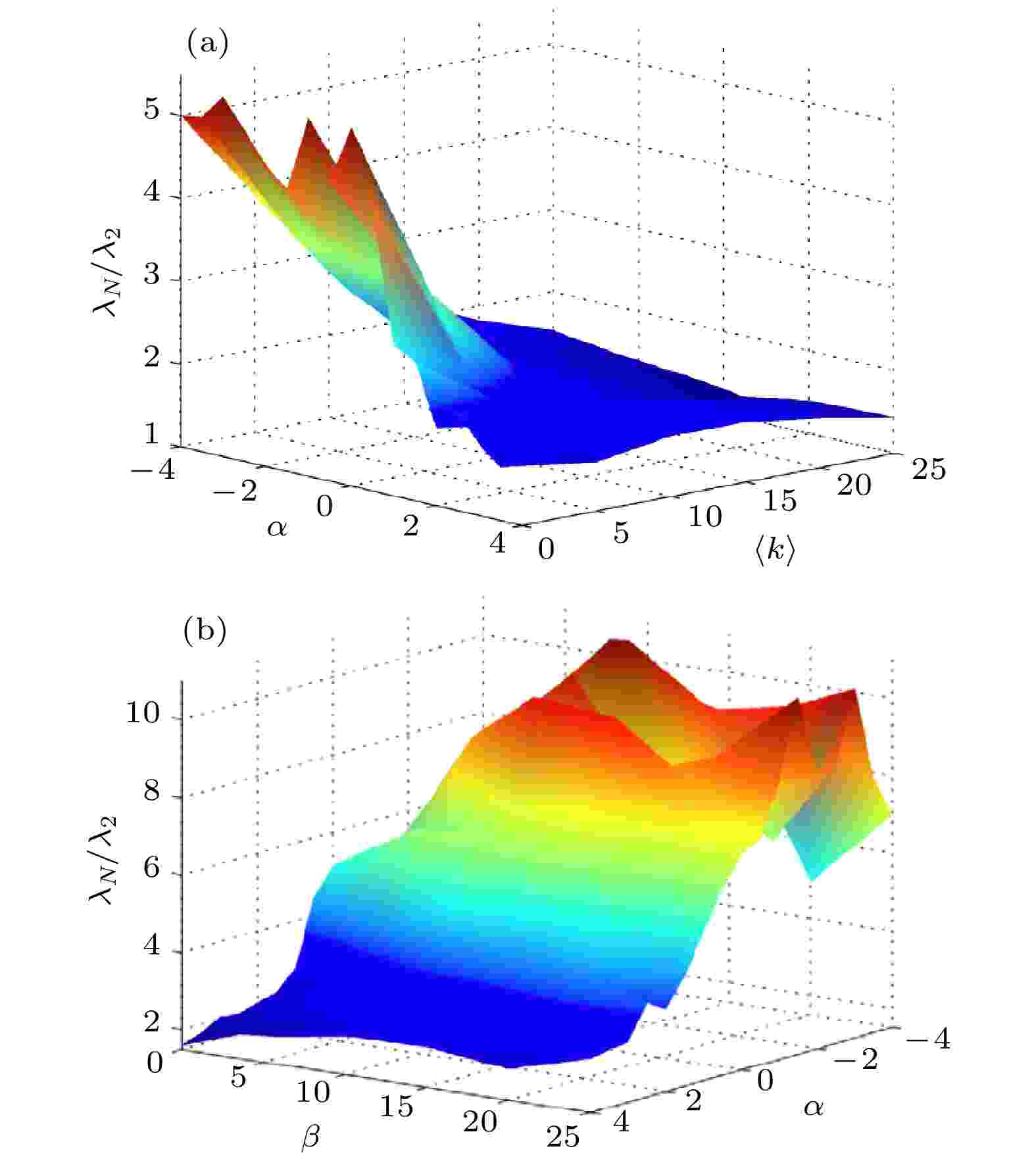 图 4 (a) 无标度网络中
图 4 (a) 无标度网络中



































































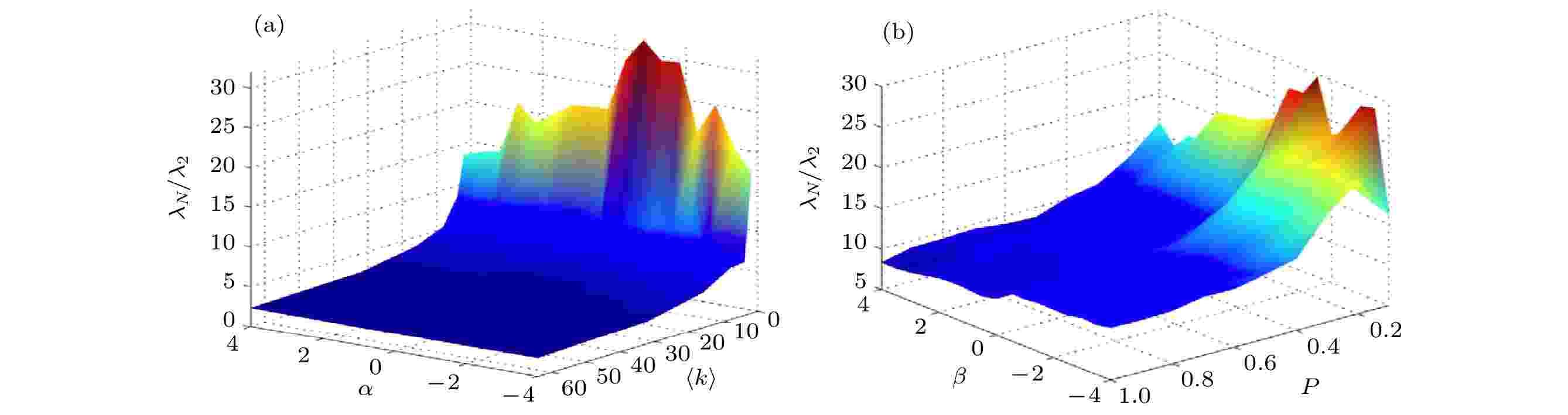 图 5 (a) Watts-Strogatz网络中
图 5 (a) Watts-Strogatz网络中

























































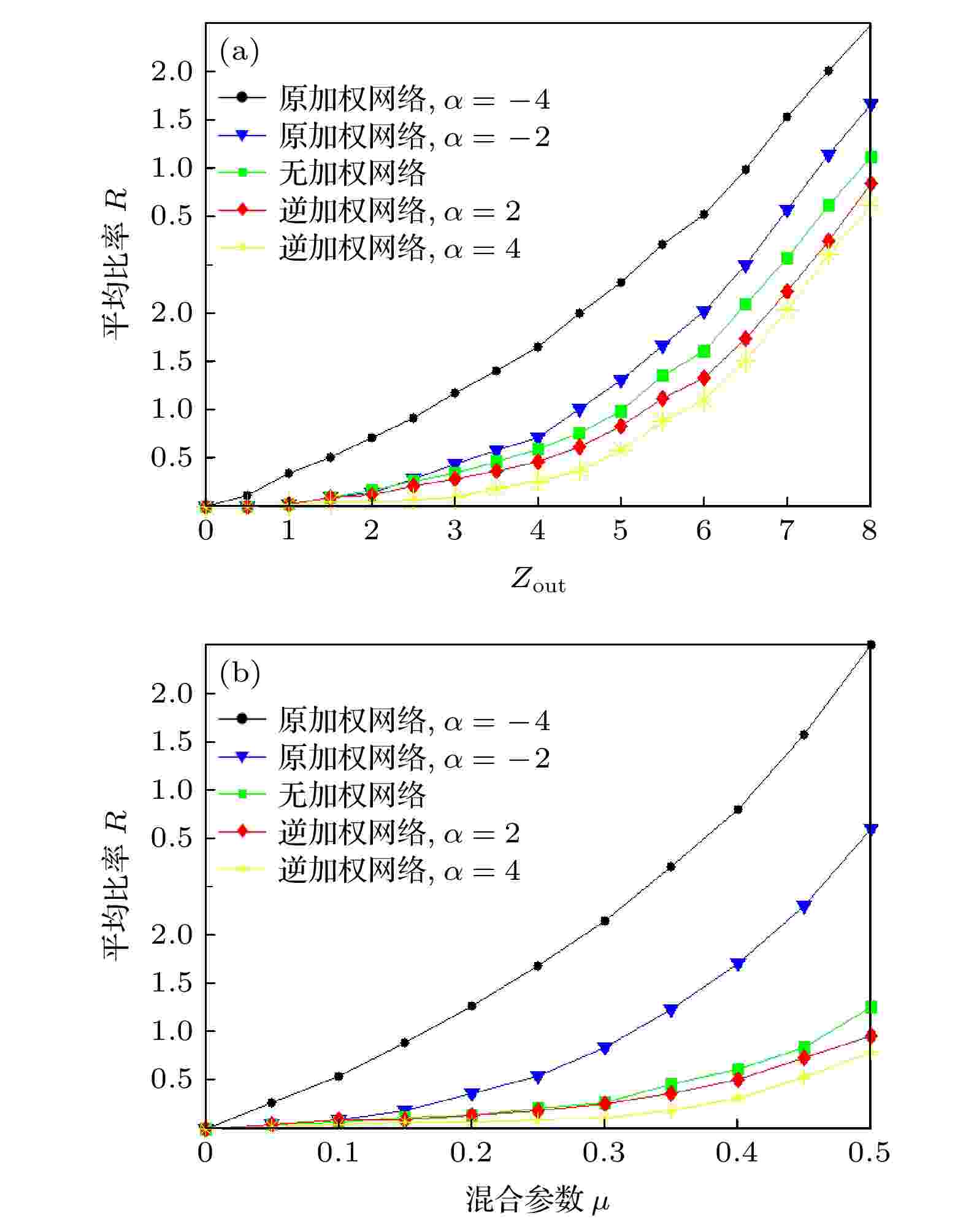 图 6 (a) GN基准网络中使用加权机制(逆加权机制)前后平均比率R的对比; (b) LFR基准网络中使用加权机制(逆加权机制)前后平均比率R的对比
图 6 (a) GN基准网络中使用加权机制(逆加权机制)前后平均比率R的对比; (b) LFR基准网络中使用加权机制(逆加权机制)前后平均比率R的对比





















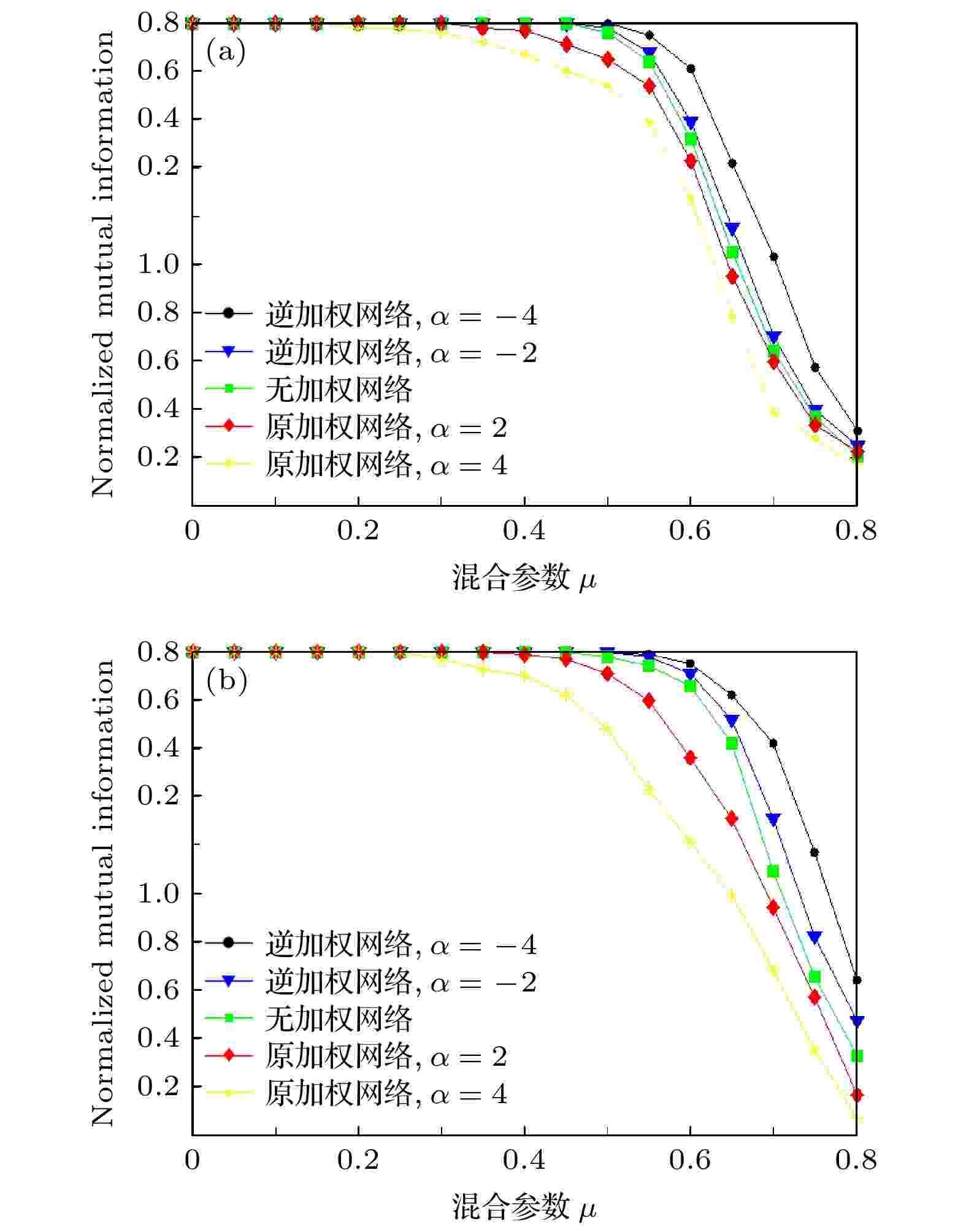 图 7 在LFR网络中运用加权机制(逆加权机制), 当取不同的
图 7 在LFR网络中运用加权机制(逆加权机制), 当取不同的

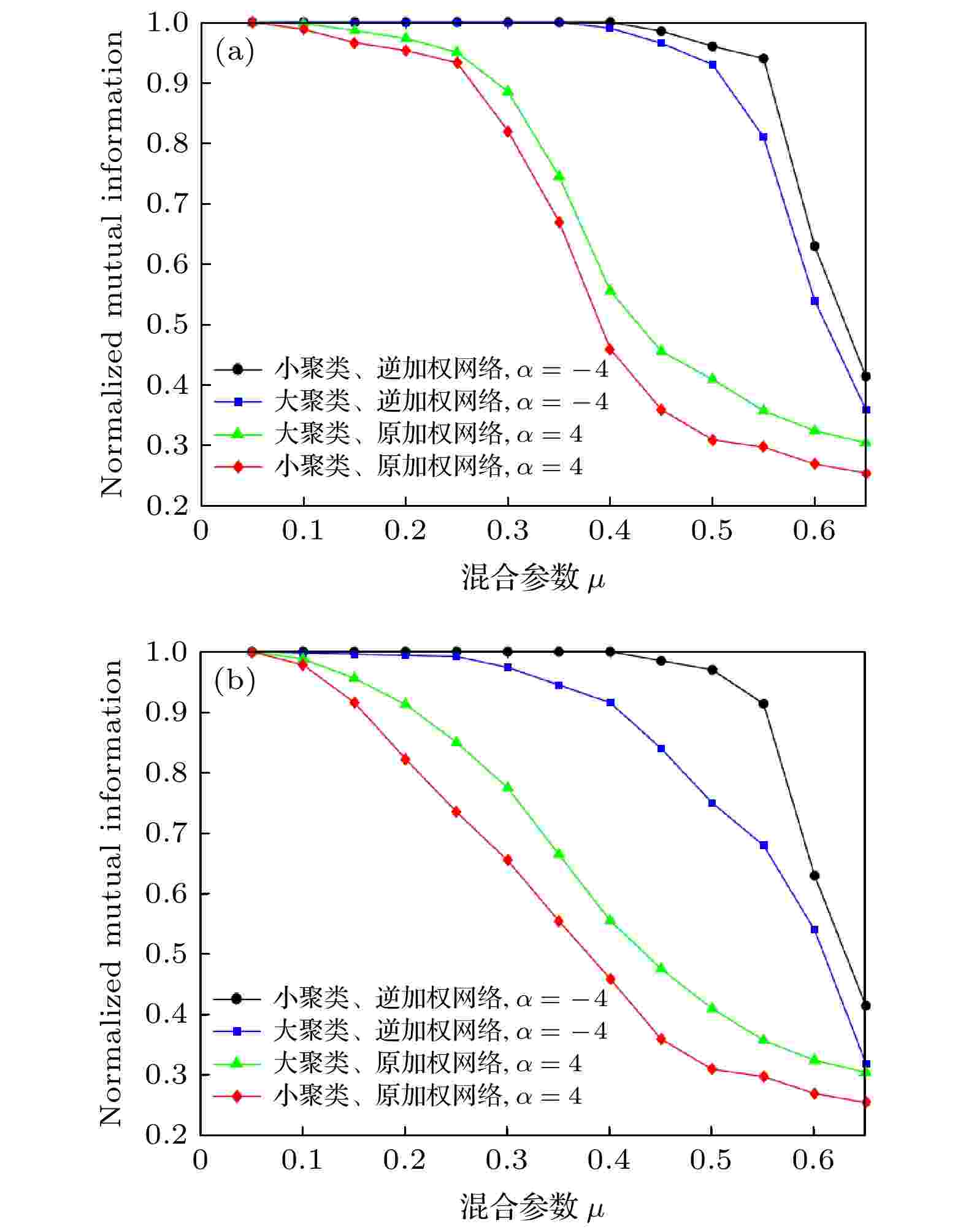 图 8 在LFR网络中运用加权机制(逆加权机制), 当
图 8 在LFR网络中运用加权机制(逆加权机制), 当





