删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

三维数值模拟射频热等离子体的物理场分布

本站小编 Free考研考试/2021-12-29
摘要:射频热等离子体的产生包含了丰富、复杂的物理场分布, 正确认识这些物理场分布对射频热等离子体在工业领域的应用有指导作用. 本文建立了三维射频热等离子体的热-电-磁-流动强耦合数学物理模型, 考虑了感应线圈的真实螺线管结构, 开发了用于计算三维射频热等离子体复杂电磁场的C++程序代码, 计算了射频热等离子体重要物理场, 如温度场、流场和电磁场的分布情况. 结果表明, 射频热等离子体各物理场分布具有三维非对称效应, 感应线圈结构对温度场和流场的空间分布有重要影响. 研究结果对优化、控制射频热等离子体的实际应用过程有重要的指导意义.
关键词: 温度场/
流场/
电磁场/
射频热等离子体/
三维数值模拟

English Abstract


全文HTML

--> --> -->
1.引　言
射频热等离子体因具有高温、高焓、高化学活性特征, 被认为是绝佳的高温热源和化学反应源[1,2], 在诸多高新技术领域有重要应用, 特别是在难熔微米级粉末球形化[3,4]、纳米颗粒合成[5,6]以及等离子体喷涂[7,8]方面展现出独特优势, 是近些年备受人们关注的研究热点.
射频热等离子体通常是在大气压或者近大气压下产生, 其产生原理类似于感应加热, 因而有时也被称为射频感应耦合热等离子体. 一般认为, 射频热等离子体的放电方式有两类, 即感应线圈内的电场激发和磁场激发, 相应地被命名为E放电和H放电. 这种热等离子体的产生过程可以描述为: 首先在感应线圈上施加高电压形成高的电场强度, 强电场击穿工作气体(通常为惰性气体)形成初始电离, 随着高频振荡振幅增大, 气体电离程度急速上升, 电导率增加, 这时E放电占主导地位, 当电导率增加并达到某一临界值时, 感应线圈的磁能开始释放, 等离子体吸收磁场能, 从而形成并维持稳定的等离子体, 此后的过程H放电占主导地位[9]. 日本科学家Razzak等[10]利用CCD相机记录了射频放电热等离子体的产生过程, 发现E放电所用时间约为1 ms, 而且放电主要是在约束管的边缘, 呈环状. 经过模式转换后H放电成为主放电过程, 此时, 放电由边缘向中心扩散, 形成稳定的等离子体, 并在上游气流的作用下向发生器喷口喷射出来, 形成等离子体射流. 此外, 帕邢定律表明, 气体击穿电压是电极距离和气压乘积的函数. 线圈匝间距一定的情况下, 增加气压使得带电粒子平均自由程缩短, 带电粒子在自由程中获得的能量减小, 这不利于放电; 另一方面带电粒子在线圈匝间渡越时发生的碰撞次数增多, 这有利于放电, 因此存在最小击穿电压. 经过大量的实验我们发现, 当等离子体炬内气压为40 kPa, 电源阳极电压升高到6 kV即可点燃等离子体[11]. 这种射频热等离子体的主要特点是高温(约104 K)、高焓(约107 J/kg)、低速(约30 m/s). 这对粉末颗粒球化、纳米颗粒合成极具优势. 高温可使原料颗粒在极短的时间内发生熔融/汽化; 低速可确保颗粒在等离子体中有较大的“滞留时间”, 从而可充分吸收等离子体能量, 进而发生完全的熔融/汽化.
获得射频热等离子体的空间物理场分布有两种手段, 一是实验诊断, 二是数值模拟. 但由于射频热等离子体具有以下特点: 1)等离子体温度极高; 2)稳定性差, 极易受到气流的作用发生淬灭; 3)受到强烈的电磁干扰作用和等离子体发生器空间狭小使得诊断异常困难. 这为实验上获得射频热等离子体物理场分布带来了困难. 为此, 人们建立了各种数学物理模型, 通过数值模拟研究射频热等离子体物理场分布. 数值模拟获得射频热等离子体的物理场分布是经济有效的方法, 同时可有效克服诊断困难的问题. 典型的数值模拟工作是加拿大Sherbrooke大学Xue等[12]建立的二维扩展场磁流体力学模型, 采用麦克斯韦方程组计算感应线圈产生的电磁场, 采用流体力学方程解算等离子体的流动特性, 并将电磁场产生的焦耳热和洛伦兹力项引入到流体力学方程解算等离子体温度场特征. Xue等[12]在感应线圈外建立了一个扩展场区域, 巧妙且有效地解决了电磁场的不自洽问题和磁场边界的问题. Bernardi等[13]在此模型的基础上发展了一种偶极子边界模型(DPBC Model)给出了更精确的电磁场边界条件. Shigeta研究组[14]和Tanaka[15]进一步细化了此方面的工作, 考虑了等离子体的热力学非平衡和化学非平衡效应, 进一步模拟了等离子体真实的物理场特征. 以上二维模型均采用了等离子体发生器的轴对称假定, 将激发线圈视为一个个与等离子体炬同轴的圆环, 忽略了线圈存在的倾角和等离子体三维效应. 通常, 这种三维效应被认为与线圈形状、匝数、倾角有关[16,17], 这些参数会直接影响电磁场的位形, 进而影响等离子体温度场和速度场的分布. 为了更精确地计算射频热等离子体真实的符合实际的物理场分布, 我们建立了三维射频热等离子体数学物理模型, 考虑了感应线圈的实际螺线管结构, 并考虑了等离子体流动过程中存在的湍流效应(在二维模型中大多将等离子体简单地视为层流流动状态), 给出了符合真实的物理场分布. 然而, 由于三维模型中电磁场和流场的强耦合, 以及热力学及输运参数是温度的非线性函数, 使得计算十分复杂, 计算量大, 收敛困难. 为此, 我们利用FLUENT程序包并进行二次开发, 自行编制适用于计算射频热等离子体物理场分布的用户自定义函数(UDF)程序代码, 计算得到了各物理场的三维分布情况. 射频热等离子体物理场分布, 如温度场、速度场、电导及黏性分布研究对于粉末颗粒球化, 纳米颗粒合成是非常重要的. 如等离子温度分布与颗粒在等离子体的熔融过程直接相关; 等离子体速度大小和分布情况会影响颗粒在等离子体中的滞留时间, 从而影响颗粒的熔融和蒸发等热物理过程; 再如, 等离子体电导率与金属颗粒在等离子体的传热过程有关, 等离子体黏性分布对颗粒在等离子体的运动有重要影响. 获得这些物理场分布对研究颗粒在等离子体中的热物理行为有重要的指导意义.
2.数学物理模型
2
2.1.几何模型
-->

2.1.几何模型

本文模拟的实体几何模型源于核工业西南物理研究院自制的用于粉末球化的射频热等离子体炬和反应腔室, 几何结构和网格结构如图1所示, 具体几何尺寸见表1. 如图1(a)所示, 等离子体炬由陶瓷约束管、石英制送气管以及同轴的线圈组成, 线圈圈数是5, 通入电流的频率f 为3 MHz. 等离子体炬内中心轴处置有送料枪, 用于送入原料颗粒到等离子体高温区. 用于产生和约束热等离子体的气体是氩气, 送料载气同为氩气. 此三路气体(放电气、冷却气和送料气)分别由图1(a)中所示的3个入口被送入到等离子体炬内. 放电气由石英制送气管通入, 在线圈上施加的高电压将其击穿形成等离子体, 并沿着等离子体炬出口喷射出来. 冷却气沿着陶瓷约束管的内表面被高速送入到等离子体炬中, 它主要用于冷却陶瓷约束管壁使之免受高温而损坏. 在等离子体炬下方置有反应腔室, 原料通过等离子体处理后会进入反应腔室进行冷却、凝固甚至反应生成目标颗粒. 等离子体炬和反应腔室都进行了水冷处理, 本数值模拟中, 相关壁面的温度被设置为300 K. 图1(b)所示为网格结构图. 将整个计算域分成四部分: I 管区域、II 扩展区域、III 线圈区域以及IV等离子体区域. I管区域采用源于面的Cooper网格, 其他区域采用四面体网格, 总网格数为445904, 节点数为132751. 在处理计算区域的过程中, 人为地将等离子体炬外部空气区域扩展至100 mm处, 视扩展区域边缘处的矢势为零. 此外, 将扩展区设置为固体区域而不是流体, 这样做的好处是可将空气区域的热物理属性设置为固定值, 避免空气区域参与计算质量连续性方程、动量方程和能量方程, 大大减少了计算量的同时, 还可以使迭代计算变得容易收敛.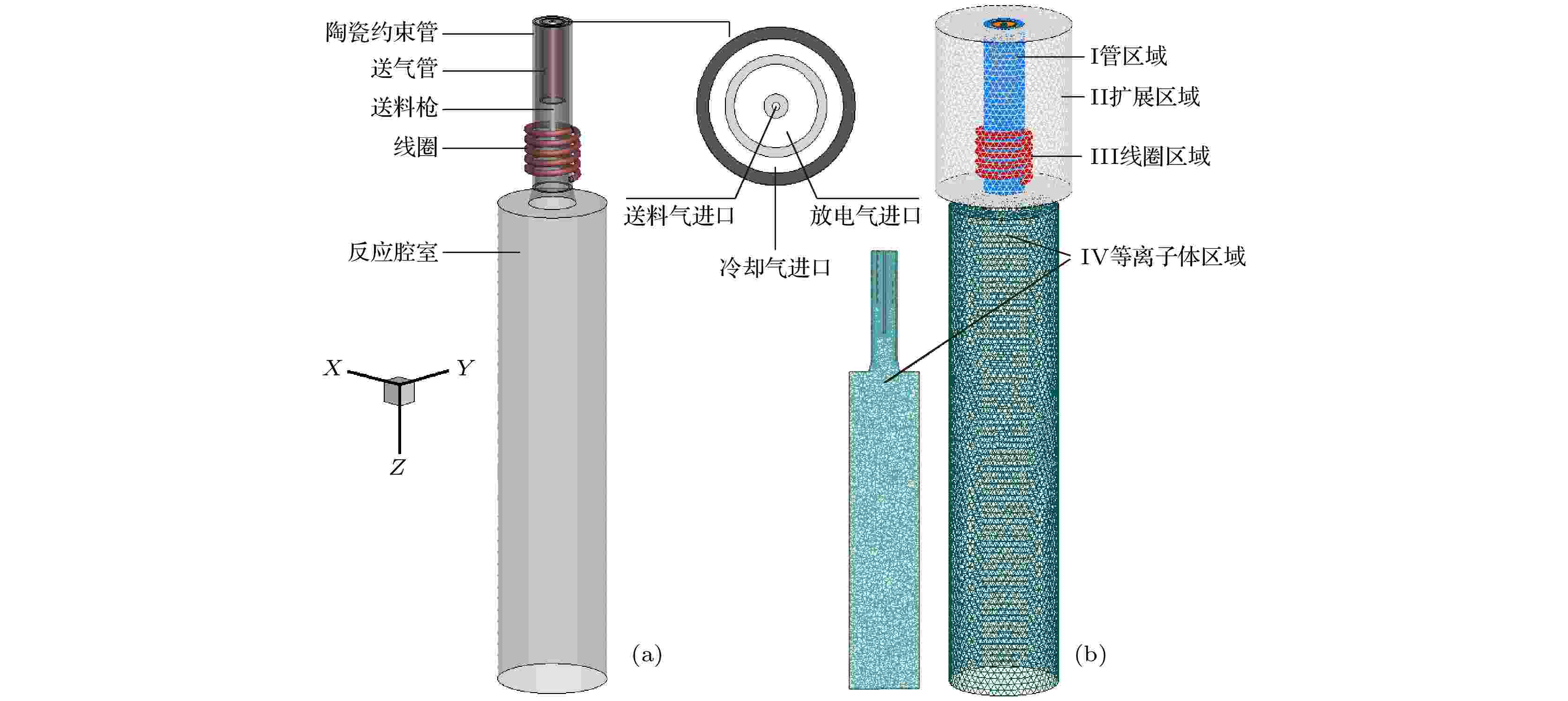
图 1 等离子体炬及腔室　(a)几何结构示意图; (b)计算域和网格结构
Figure1. Plasma torch system: (a) Geometric structure; (b) computational domain and grid.

参数名称数值
陶瓷约束管内半径/外半径/长度/mm25/29.5/252
送气管内半径/外半径/长度/mm15.5/19/120
送料枪内半径/外半径/长度/mm1.5/4.5/186
线圈半径/轴向节距/mm37/15
线圈螺线管半径/mm5
线圈匝数5


表1等离子体炬及腔室几何尺寸表
Table1.Dimensions of the plasma system sketched in Fig. 1

2
2.2.控制方程
-->

2.2.控制方程

在二维射频热等离子体模型中, 为了简化计算, 将几何结构简化为完全轴对称结构, 线圈视为一个个与等离子体炬同轴的圆环, 忽略线圈存在的倾角. 在模拟三维射频热等离子体各物理场分布时, 考虑了线圈的三维结构以及线圈的实际倾角, 使各物理场更接近真实分布. 同时, 为了突出物理问题的重要部分, 省略一些小量, 使问题得到简化, 作如下假定: 假定等离子体处于局域热力学平衡态, 电子温度与重粒子温度相等, 即组分中出现的温度可以用单一的等离子体温度T代替; 等离子体在炬内的流动属于定常流动, 即不考虑等离子体随时间的演化过程, 考虑了等离子体中在低雷诺数下的湍流效应. 忽略能量源项中的压力做功项(小项).
3
2.2.1.电磁场方程
-->
2.2.1.电磁场方程
基于以上假设, 将等离子体看成带电的流体, 或者称为磁流体, 即等离子体既具有流体属性, 又具有电磁属性. 根据麦克斯韦方程组, 线圈中流过的变化的电流驱动产生变化的电磁场, 变化的电磁场将能量耦合到等离子体炬中使得气体放电产生等离子体并得以维持. 因此可以利用麦克斯韦方程组来处理流经线圈的射频电流激发的电磁场分布:
${\boldsymbol{\nabla}} \cdot {\boldsymbol{E}}=\frac{\rho }{{\varepsilon }_{0}},$
${\boldsymbol{\nabla}} \cdot {\boldsymbol{B}}=0,$
${\boldsymbol{\nabla}} \times {\boldsymbol{E}}=-\frac{\partial {\boldsymbol{B}}}{\partial t},$
${\boldsymbol{\nabla}} \times {\boldsymbol{B}}={\mu }_{0}{\varepsilon }_{0}\frac{\partial {\boldsymbol{E}}}{\partial t}+{\mu }_{0}{\boldsymbol{J}},$
其中E和B分别是电场强度和磁感应强度, $ \rho $是电荷密度, $ {\mu }_{0} $是自由空间的磁导率, $ {\varepsilon }_{0} $是自由空间的介电常数, J为电流密度. 利用矢量恒等式${\boldsymbol{\nabla}} \cdot $$ \left({\boldsymbol{\nabla}} \times {\boldsymbol{A}}\right)=0$, 可将B写成
${\boldsymbol{B}}={\boldsymbol{\nabla}} \times {\boldsymbol{A}},$
其中A为磁矢势. 对于电场E, 其源于电荷密度和变化的磁场两部分. 因此, 可以将其写成
${\boldsymbol{E}}={{\boldsymbol{E}}}_{\rho }+{{\boldsymbol{E}}}_{B},$
其中, $ {{\boldsymbol{E}}}_{\rho } $和$ {{\boldsymbol{E}}}_{B} $可表达如下:
${\boldsymbol{{\boldsymbol{\nabla}} }} \cdot {{\boldsymbol{E}}}_{\rho }={\boldsymbol{\nabla}} \cdot \left(-{\boldsymbol{\nabla}} \varphi \right)=\frac{\rho }{{\varepsilon }_{0}},$
${\boldsymbol{\nabla}} \times {{\boldsymbol{E}}}_{B}=-\frac{\partial {\boldsymbol{B}}}{\partial t}=-\frac{\partial }{\partial t}({\boldsymbol{\nabla}} \times {\boldsymbol{A}}),$
${{\boldsymbol{E}}}_{B}=-\frac{\partial {\boldsymbol{A}}}{\partial t},$
方程(7)中的$ \varphi $是电势. 将(7)式和(9)式代入到(6)式, 这样电场强度E可表达如下:
${\boldsymbol{E}}=-{\boldsymbol{\nabla}} \varphi -\frac{\partial {\boldsymbol{A}}}{\partial t}\text{.}$
进一步地, 利用矢量恒等式${\boldsymbol{\nabla}} \times {\boldsymbol{\nabla}} \times {\boldsymbol{A}}= -{{\boldsymbol{\nabla}} }^{2}{\boldsymbol{A}}+ $$ {\boldsymbol{\nabla}} ({\boldsymbol{\nabla}} \cdot {\boldsymbol{A}})$, 可将(4)式表达为
$\begin{split}{\boldsymbol{\nabla}} \times {\boldsymbol{B}}=\;&{\boldsymbol{\nabla}} \times {\boldsymbol{\nabla}} \times {\boldsymbol{A}}=-{{\boldsymbol{\nabla}} }^{2}{\boldsymbol{A}}+{\boldsymbol{\nabla}} ({\boldsymbol{\nabla}} \cdot {\boldsymbol{A}})\\=\;&{\mu }_{0}{\varepsilon }_{0}\frac{\partial {\boldsymbol{E}}}{\partial t}+{\mu }_{0}{\boldsymbol{J}}\text{.}\end{split}$
将(10)式代入(11)式并化简得
${{\boldsymbol{\nabla}} }^{2}{\boldsymbol{A}}=-{\mu }_{0}{\varepsilon }_{0}\frac{\partial }{\partial t}\left(-\nabla \varphi -\frac{\partial {\boldsymbol{A}}}{\partial t}\right)-{\mu }_{0}{\boldsymbol{J}}+{\boldsymbol{\nabla}} ({\boldsymbol{\nabla}} \cdot {\boldsymbol{A}})\text{.}$
现在考虑方程(12)右边的${\boldsymbol{\nabla}} ({\boldsymbol{\nabla}} \cdot {\boldsymbol{A}})$, 磁矢势A的一般形式为
$ A\left(r\right)=\frac{{\mu }_{0}}{4\mathrm{\pi }}\iiint \frac{J\left({r}'\right)}{r-{r}'}{\mathrm{d}}^{3}{r}'\text{,}$
其中, 电流密度可由电荷守恒方程给出,
$\nabla \cdot J=-\frac{\partial \rho }{\partial t}\text{.} $
联立(13)式和(14)式可得到
$\nabla \cdot A\left(r\right)=-\frac{{\mu }_{0}}{4\mathrm{\pi }}\iiint \frac{\rho \left({r}'\right)}{r-{r}'}{\mathrm{d}}^{3}{r}'=-{\mu }_{0}{\varepsilon }_{0}\frac{\partial \varphi }{\partial t}\text{,}$
其中电势$\varphi \left(r\right)=\dfrac{{\mu }_{0}}{4\mathrm{\pi }{\varepsilon }_{0}}\displaystyle\iiint \dfrac{\rho \left({r}'\right)}{r-{r}'}{\mathrm{d}}^{3}{r}'$.
这样, 将(15)式代入(12)式化简后得到
${\boldsymbol \nabla }^{2}{\boldsymbol{A}}={\mu }_{0}{\varepsilon }_{0}\frac{{\partial }^{2}{\boldsymbol{A}}}{\partial {t}^{2}}-{\mu }_{0}J\text{.}$
电流密度J包括线圈电流密度$ {J}_{\mathrm{c}} $和感应等离子体电流密度$ {J}_{\mathrm{i}} $. 因此可写成,
$J={J}_{\mathrm{c}}+{J}_{\mathrm{i}},$
其中, $ {J}_{\mathrm{c}} $可写成 ${J}_{\mathrm{c}}= {I}/{S}$, I为流经感应线圈的电流, S为线圈铜管的横截面积; $ {J}_{\mathrm{i}} $ 可由欧姆定律给出${J}_{\mathrm{i}}=\sigma E=\sigma \Big(-{\boldsymbol{\nabla}} \varphi -\dfrac{\partial {\boldsymbol{A}}}{\partial t}\Big)$, $ \sigma $为等离子体电导率. 这样方程(16)可写成
$ {{\boldsymbol{\nabla}} }^{2}{\boldsymbol{A}}={\mu }_{0}{\varepsilon }_{0}\frac{{\partial }^{2}{\boldsymbol{A}}}{\partial {t}^{2}}-\frac{{\mu }_{0}I}{S}+{\mu }_{0}\sigma \left(\nabla \varphi +\frac{\partial {\boldsymbol{A}}}{\partial t}\right)\text{.}$
假定A 按正弦规律变化, 角频率为$ \omega =2\mathrm{\pi }f $, 其中f为频率, 可以将A 表述如下:
$A\left(r,t\right)=A\left(r\right){\mathrm{e}}^{\mathrm{i}\omega t},$
$\varphi \left(r,t\right)=\varphi \left(r\right){\mathrm{e}}^{\mathrm{i}\omega t}\text{.}$
将(19)式代入(18)式可得
${\boldsymbol \nabla }^{2}{\boldsymbol{A}}=-\frac{{\mu }_{0}I}{S}+{\mu }_{0}\sigma {\boldsymbol \nabla} \varphi +(\mathrm{i}\omega {\mu }_{0}\sigma -{\mu }_{0}{\varepsilon }_{0}{\omega }^{2}){\boldsymbol{A}}\text{.}$
对于等离子体区, $ I=0 $, 对于线圈区域, $ \sigma =0 $, 方程(21)可分别简化为
${\boldsymbol \nabla }^{2}{\boldsymbol{A}}={\mu }_{0}\sigma {\boldsymbol \nabla} \varphi +(\mathrm{i}\omega {\mu }_{0}\sigma -{\mu }_{0}{\varepsilon }_{0}{\omega }^{2}){\boldsymbol{A}},$
$ {\boldsymbol \nabla }^{2}{\boldsymbol{A}}=-\frac{{\mu }_{0}I}{S}{-\mu }_{0}{\varepsilon }_{0}{\omega }^{2}{\boldsymbol{A}}\text{.}$
在方程(22)的右边中含有电势 $ \varphi $, 接下来通过方程(1)和方程(10)推导求解电势 $ \varphi $的方程.
${\boldsymbol \nabla }^{2}\varphi =-\frac{\rho }{{\varepsilon }_{0}}-{\boldsymbol \nabla} \left(\frac{\partial {\boldsymbol{A}}}{\partial t}\right)\text{.}$
将(15)式代入(24)可得到
${\boldsymbol \nabla }^{2}\varphi =-\frac{\rho }{{\varepsilon }_{0}}+{\mu }_{0}{\varepsilon }_{0}\frac{{\partial }^{2}\varphi }{\partial t}=-\frac{\rho }{{\varepsilon }_{0}}-{\mu }_{0}{\varepsilon }_{0}{\omega }^{2}\varphi \text{.} $
为了计算磁矢势方程(22)和方程(23)以及电势方程(25), 获得它们的分布, 进而获得磁感应强度B和电场强度E的分布, 需要在FLUENT中采用用户自定义标量(UDS)方法将磁矢势A和 $ \varphi $看成自定义标量进行计算设置, UDS可解算如下形式的方程:
$\begin{split}& \frac{\partial \rho {\varnothing }_{k}}{\partial t}+\frac{\partial }{\partial x}\left(\rho u{\varnothing }_{k}-{\tau }_{k}\frac{{\partial \varnothing }_{k}}{\partial x}\right)={S}_{{\varnothing }_{k}}, \\ &\qquad\qquad k=\mathrm{1,2},\cdots, {n},\end{split}$
此处 $ {\tau }_{k} $ 和 $ {S}_{{\varnothing }_{k}} $分别是第k个UDS对应的扩散系数和源项; $ \rho, u $是流体的密度和速度. 方程(26)左端的第一项是时间项, 第二项包含对流项和扩散项. 将方程(26)与方程(22)、方程(25)相对照可得, $ {\tau }_{k}=1 $, $ \varnothing ={\boldsymbol{A}} $ 或$ \varphi $. 对应的各个源项使用C++编程通过用户自定义函数(UDF)的方式写入到FLUENT解算器, 从而参与迭代运算.
在进行二维数值计算时, 将磁矢势A写成复数形式, $ {\boldsymbol{A}}={{\boldsymbol{A}}}_{\mathrm{R}}+\mathrm{i}{{\boldsymbol{A}}}_{\mathrm{I}} $, 并将其代入到磁矢势方程(22)分开计算磁矢势A的实部和虚部. 本文三维数值计算射频热等离子体时采用同样的处理方式, 将磁矢势写成同样的复数形式并投影到x, y和z方向上. 电势 $ \varphi $ 也作同样的处理.
${A}_{x}={A}_{\mathrm{R}x}+\mathrm{i}{A}_{\mathrm{I}x},$
${A}_{y}={A}_{\mathrm{R}y}+\mathrm{i}{A}_{\mathrm{I}y},$
${A}_{z}={A}_{\mathrm{R}z}+\mathrm{i}{A}_{\mathrm{I}z},$
$\varphi ={\varphi }_{\mathrm{R}}+\mathrm{i}{\varphi }_{\mathrm{I}}\text{.}$

3
2.2.2.流体力学方程
-->
2.2.2.流体力学方程
如前文所述, 本文将射频热等离子体视为具有电磁属性的流体, 因此需解算流体力学方程, 考虑质量、动量和能量输运方程. 它们在笛卡尔坐标系下的具体形式可表述如下:
${\boldsymbol \nabla} \cdot \left(\rho {\boldsymbol{u}}\right)=0,$
$\begin{split}{\boldsymbol \nabla} \cdot \left(\rho {\boldsymbol{u}}{\boldsymbol{u}}\right)=\;&-{\boldsymbol \nabla} P+{\boldsymbol \nabla} \cdot \bigg[\mu ({\boldsymbol \nabla} {\boldsymbol{u}}+{\boldsymbol \nabla} {{\boldsymbol{u}}}^{\mathrm{T}})\\&-\frac{2}{3}\mu {\boldsymbol \nabla} \cdot \left({\boldsymbol{u}}{\boldsymbol{I}}\right)\bigg]+{\boldsymbol{J}}\times {\boldsymbol{B}},\end{split}$
${\boldsymbol \nabla} \cdot \left(\rho {\boldsymbol{u}}h\right)={\boldsymbol \nabla}\cdot \left(\frac{k}{{C}_{\mathrm{p}}}{\boldsymbol \nabla} h\right)+{\boldsymbol{J}}\times {\boldsymbol{E}}-Q,$
式中$ \rho $, $ k $, $ {C}_{\mathrm{p}} $, $ \mu $, $ T $, $ h $和 $ {\boldsymbol{u}} $ 分别是等离子体密度、热导率、热容、黏性系数、温度、比焓和速度. $ P $是腔室压力, $ {\boldsymbol{E}} $是电场强度, $ {\boldsymbol{B}} $是磁感应强度, $ J $是等离子体内电流密度, $ Q $是体积辐射热, ${\boldsymbol \nabla} {{\boldsymbol{u}}}^{\mathrm{T}}$是矢量梯度张量${\boldsymbol \nabla} {\boldsymbol{u}}$的转置, $ {\boldsymbol{I}} $是单位张量. 其中, 体积辐射热的表达式为$Q=5600\left(T-9500\right) +181(T- $$ 9500)^{2}$[18], 单位为W/m3.
等离子体尾焰处具有一定的湍流效应, 对于射频热等离子体常采用标准$k\text{-}\omega$模型来描述这种湍流效应, 其控制方程表示为
${\boldsymbol \nabla} \cdot \left(\rho {\boldsymbol{u}}k\right)={\boldsymbol \nabla} \cdot {(\varGamma }_{k}{\boldsymbol \nabla} k)+{G}_{k},$
${\boldsymbol \nabla} \cdot \left(\rho {\boldsymbol{u}}\omega \right)={\boldsymbol \nabla} \cdot {(\varGamma }_{\omega }{\boldsymbol \nabla} \omega )+{G}_{\omega }, $
式中$ k $和$ \omega $分别为湍流动能和动能耗散率; $ {G}_{k} $是由平均速度梯度所致湍流能量源项; $ {G}_{\omega } $是的$ \omega $源项; $ {\varGamma }_{k} $和$ {\varGamma }_{\omega } $是有效扩散系数,
${\varGamma }_{k}=\mu +\frac{{\mu }_{t}}{{\sigma }_{k}},$
${\varGamma }_{\omega }=\mu +\frac{{\mu }_{t}}{{\sigma }_{\omega }},$
其中$ {\sigma }_{k} $和$ {\sigma }_{\omega } $分别为$ k $和$ \omega $的湍流Prandtl 数, 湍流黏性系数 $ {\mu }_{t} $ 可由(38)式表示, 相关的参数见文献[19].
${\mu }_{t}={\alpha }^{*}\frac{\rho k}{\omega }.$
方程(31)—(35)分别是连续性方程、动量守恒方程、能量守恒方程和湍流方程, 结合上文推导的电磁场方程(21)和方程(25), 构成了本数学物理模型的控制方程. 给定合适的、符合实验条件的初始值和边界条件, 即可计算出射频热等离子体的各物理场分布.
2
2.3.初始和边界条件
-->

2.3.初始和边界条件

图2为射频电源电路框图. 射频电源电子管阳极电流是$ {I}_{\mathrm{\alpha }} $, $ {I}_{\mathrm{\beta }} $是经放大并去直流后的回路电流, 放电倍数为1.7. $ {I}_{\mathrm{\gamma }} $是放电线圈所在槽路电流, 即流过耦合线圈的电流, $ q $是槽路因子. 本电源的槽路因子$ q $ = 40.
${I}_{\mathrm{\alpha }}\times 1.7={I}_{\mathrm{\beta }},$
${I}_{\mathrm{\gamma }}={I}_{\mathrm{\beta }}\times q\text{.}$
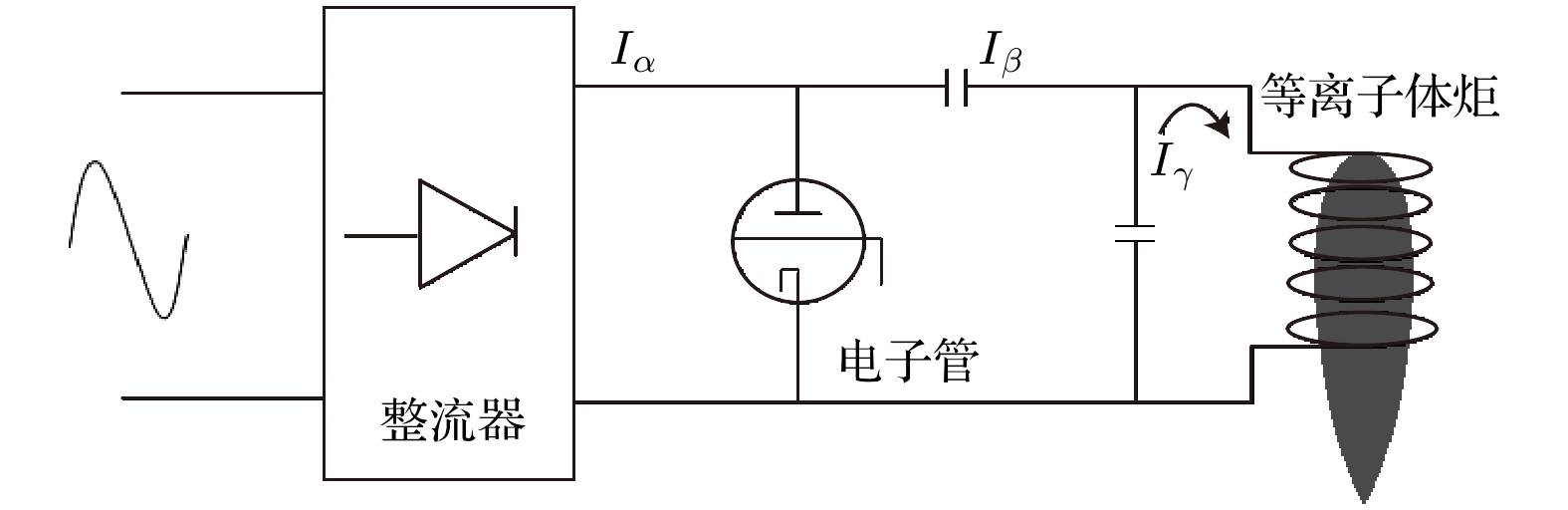图 2 射频电源电路框图
Figure2. Diagram of radio frequency power supply circuit.

实验测量等离子体稳定后, 射频电源阳极电流为$ {I}_{\mathrm{\alpha }}=5 \;{\rm{A}}$, 因此有, $ {I}_{\mathrm{\beta }}=5\times 1.7=8.5 \;{\rm{A}}$. 在数值模拟中, 设置流经线圈的电流为${I}_{\mathrm{\gamma }}=8.5\times 40= $$ 340\;{\rm{A}}$. 等离子体的初始温度设置为6000 K, 其意义相当于物理上的引燃等离子体过程. 速度和磁矢势的初始值为零. 热等离子体热力学及输运参量, 如等离子体电导率、热导率、热容及黏性系数, 是温度的非线性函数等数据引自文献[20]并进行数据拟合后进入到FLUENT中进行迭代计算. 扩展区和约束管热导率分别为0.0242和1.047 W/(m·K).
对于等离子体炬进口, 分别有送料气Q1、放电气Q2和冷却气Q3, 送气量按照实验要求设定, 不考虑送粉的情况下, Q1设置为0, Q2和Q3分别为1.0和6.0 m3/h. 在FLUENT下对应的进气速度分别为0.4和2.009 m/s.
进口处的边界条件为$ T{|}_{\mathrm{i}\mathrm{n}\mathrm{l}\mathrm{e}\mathrm{t}}=0 $, $\dfrac{\partial {\boldsymbol{A}}}{\partial z} \Big|_{\mathrm{i}\mathrm{n}\mathrm{l}\mathrm{e}\mathrm{t}}=0$.
出口处的边界条件为$\dfrac{\partial T}{\partial z}\Big|_{\mathrm{o}\mathrm{u}\mathrm{t}\mathrm{l}\mathrm{e}\mathrm{t}}=0$, $\dfrac{\partial (\rho u)}{\partial z}= $$ \dfrac{\partial v}{\partial z}=\dfrac{\partial w}{\partial z} \Big|_{\mathrm{o}\mathrm{u}\mathrm{t}\mathrm{l}\mathrm{e}\mathrm{t}}=0$, $\dfrac{\partial {\boldsymbol{A}}}{\partial z}\Big|_{\mathrm{o}\mathrm{u}\mathrm{t}\mathrm{l}\mathrm{e}\mathrm{t}}=0$.
壁面边界条件分为管壁、腔室壁面和外部扩展区壁面, 它们对应的边界分别命名为Wall-q, Wall-c和Wall-out. 管壁和腔室壁面都进行了循环水冷却, 扩展区的温度为室温, 在FLUENT 中, 这些温度都设置为300 K. 管壁的速度为无滑移速度边界条件, 扩展区的边界处的磁矢势符合远场边界条件.
$ T{|}_{\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l}\text{-}\mathrm{q}}=T{|}_{\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l}\text{-}\mathrm{c}}=T{|}_{\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l}\text{-}\mathrm{o}\mathrm{u}\mathrm{t}}=0, $
$ u=\mathrm{w}{|}_{\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l}\text{-}\mathrm{q}}=0, $
$ {\boldsymbol{A}}{|}_{\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l}\text{-}\mathrm{o}\mathrm{u}\mathrm{t}}=0\text{.} $
本文借助Gambit 2.2.30软件建立等离子体炬的几何模型, 并进行网格划分, 利用UDF技术将自编的适用于计算电磁场方程的C程序引入到商业软件FLUENT 15.0进行数值计算, 采用二阶迎风格式对控制方程进行离散, 并运用基于压力和速度耦合的SIMPLE 算法进行迭代计算, 利用TECPLOT 360对计算结果进行后处理.
3.计算结果与讨论
2
3.1.磁矢势、电场及磁场分布
-->

3.1.磁矢势、电场及磁场分布

射频热等离子体通常在大气压或者近大气压下产生, 其产生原理类似于感应加热, 因而有时也称射频感应耦合热等离子体. 与感应加热不同的是, 射频热等离子体的加热对象不是金属而是气体, 其基本原理都是基于法拉第电磁感应定律. 因而, 电磁场的分布对于射频热等离子体的产生及维持是极其重要的.
图3—5分别为磁矢势Ax, Ay和Az在YZ, XZ和YZ平面上的剖面图. 从图3可以看到, 磁矢势Ax的实部ARx和虚部AIx的最大值分别为2.53 × 10–4和3.93 × 10–5 T·m. 图4表明磁矢势Ay和Ax的值相当, 云图显示他们的最大值分布在近线圈区域, 并向外递减. 轴向磁矢势Az也具有相同的分布(图5), 但其实部和虚部的最大值为1.94 × 10–5和4.39 × 10–7 T·m, 约低于Ax和Ay一个量级. 这表明磁矢势的方位角强烈影响射频热等离子体的电磁行为.
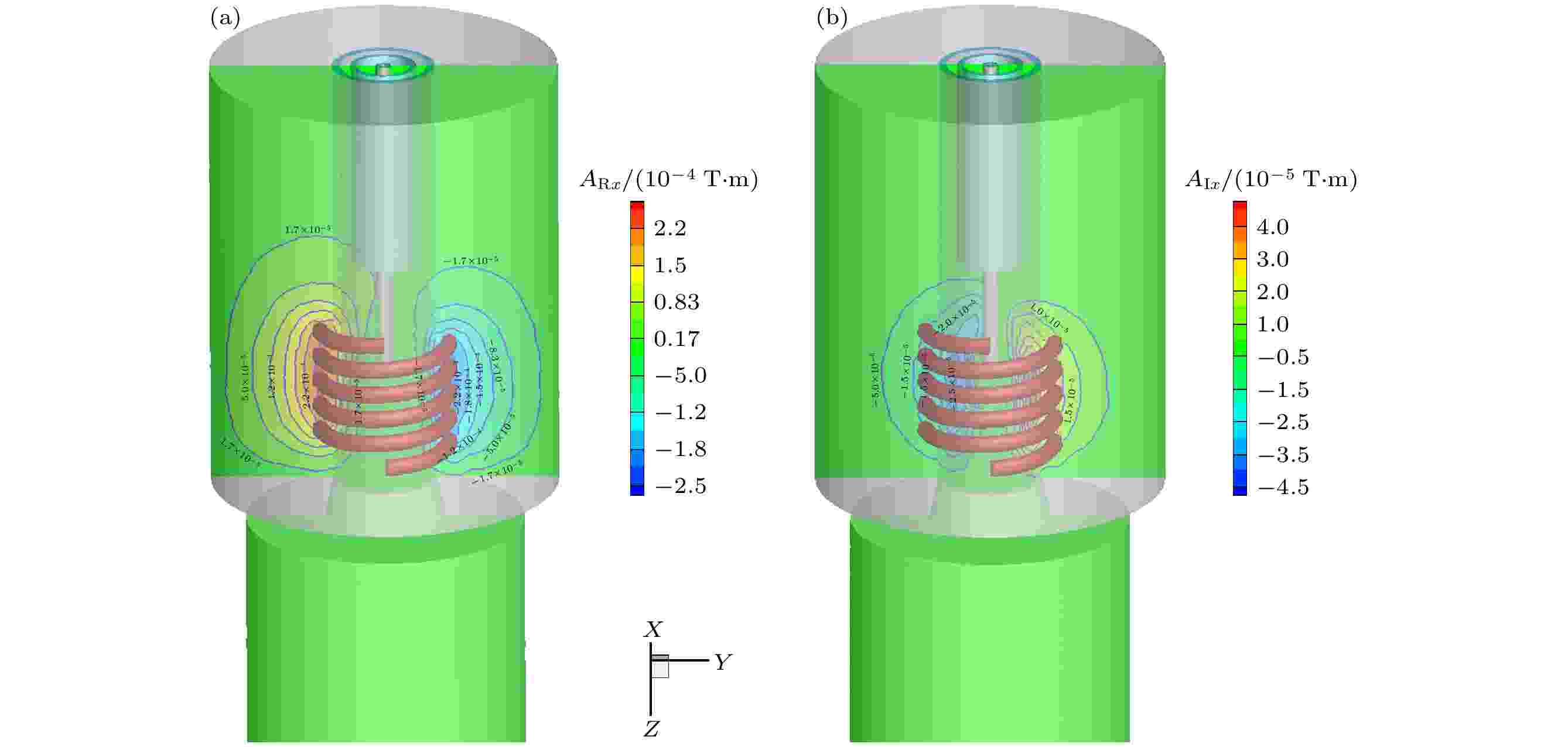图 3 磁矢势Ax分布图　(a)实部; (b)虚部
Figure3. Distribution of magnetic vector potential Ax: (a) Real part; (b) imaginary part.

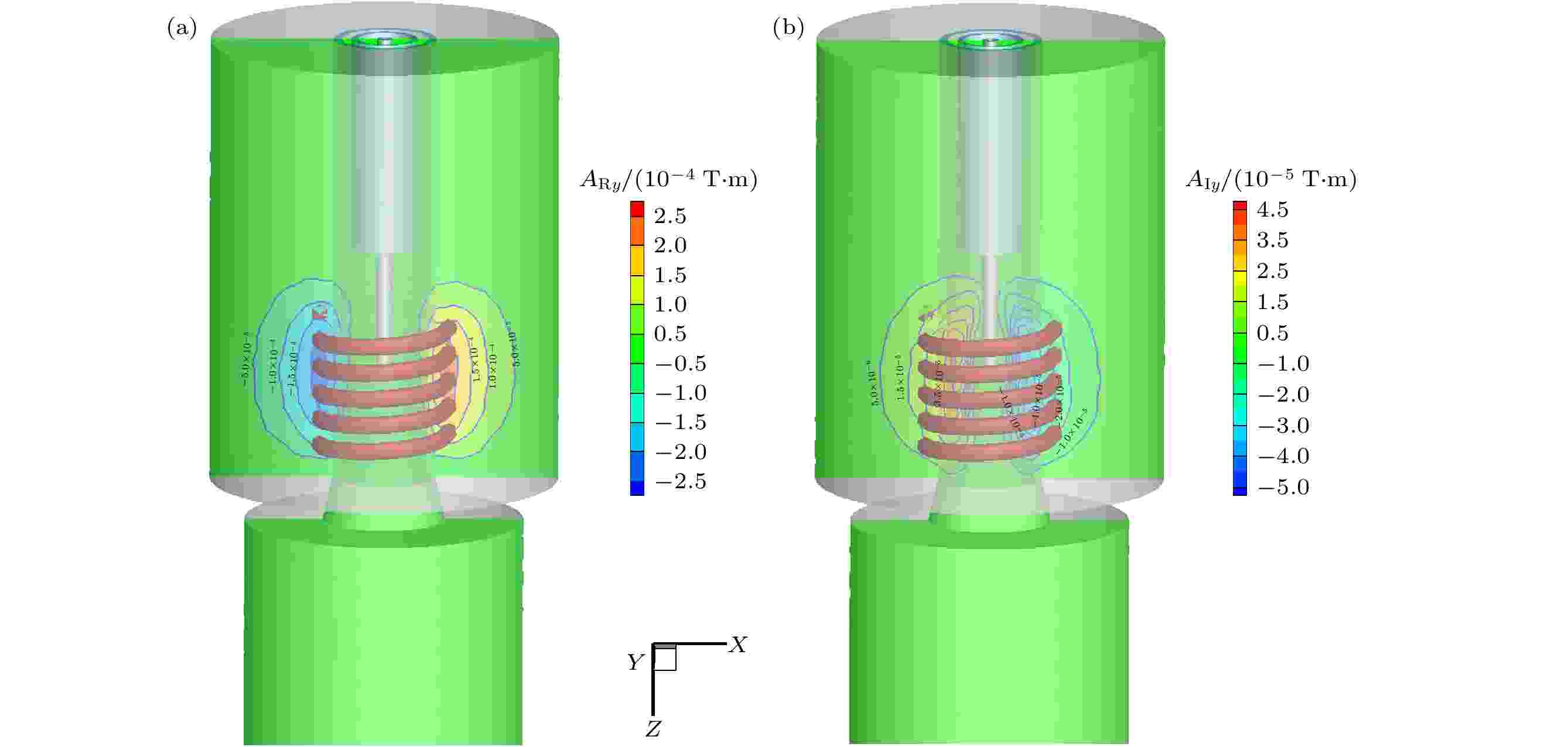图 4 磁矢势Ay分布图　(a)实部; (b)虚部
Figure4. Distribution of magnetic vector potential Ay: (a) Real part; (b) imaginary part.

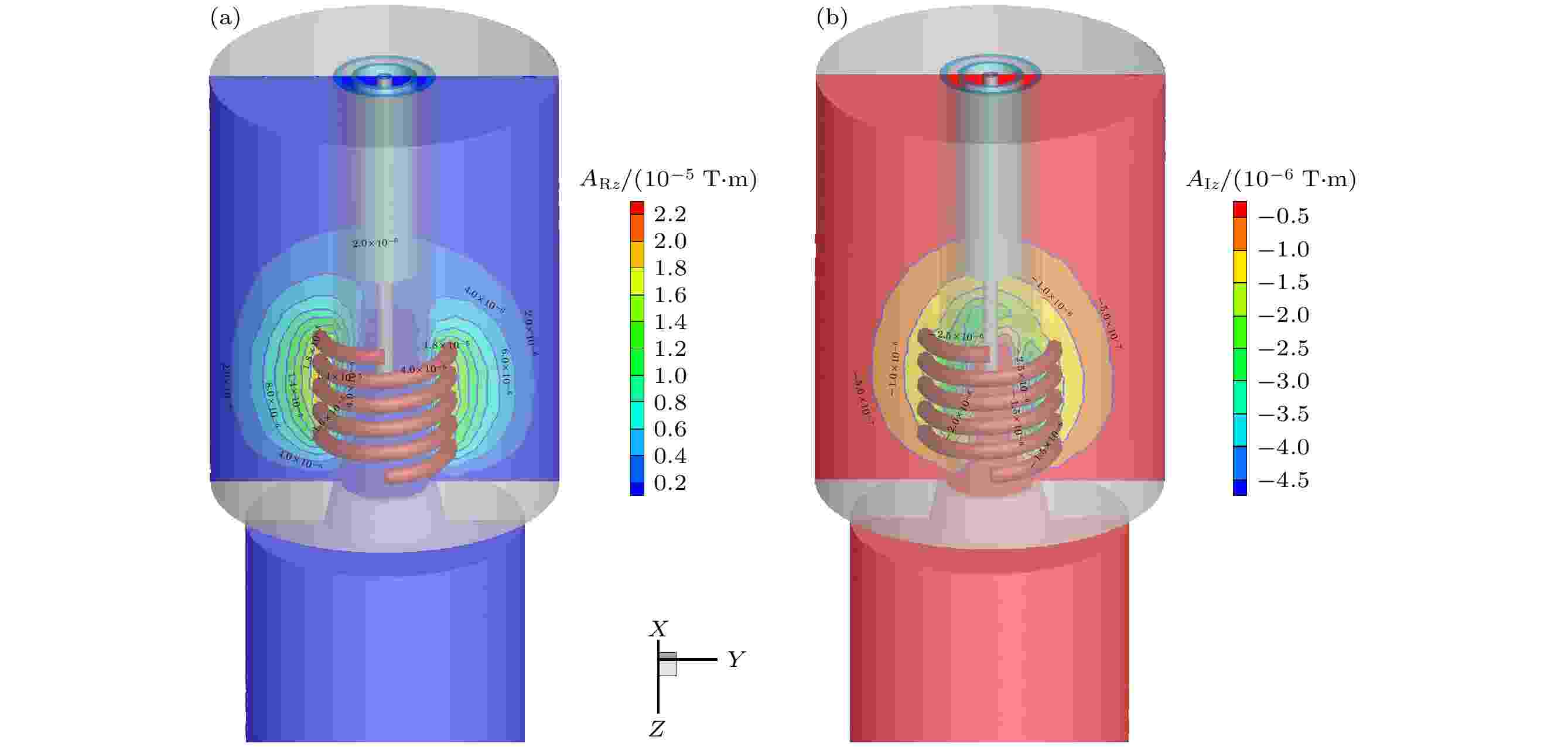图 5 磁矢势Az分布图　(a)实部; (b)虚部
Figure5. Distribution of magnetic vector potential Az: (a) Real part; (b) imaginary part.

由电磁感应定律可知, 感应线圈产生的磁场主要沿轴线方向分布. 如(5)式所示$ {\boldsymbol{B}}={\boldsymbol{\nabla}} \times {\boldsymbol{A}} $, 则有 ${B}_{\mathrm{R}z}=\dfrac{\partial {A}_{\mathrm{R}y}}{\partial x}-\dfrac{\partial {A}_{\mathrm{R}x}}{\partial y}$, ${B}_{\mathrm{I}z}=\dfrac{\partial {A}_{\mathrm{I}y}}{\partial x}-\dfrac{\partial {A}_{\mathrm{I}x}}{\partial y}$, 由这两个公式可计算得到Bz的分布. 图6给出了在YZ平面上, 等离子体炬轴向磁感应强度Bz的分布情况. 图6(a)所示为实部分布, 其中线图显示磁场垂直于线圈, 且主要分布在线圈附近, 形成闭合曲线. 图6中的云图显示靠近线圈处磁感应强度具有最大值. 实部和虚部的最大值分别为3.72 × 10–2 T和5.52 × 10–3 T. 在等离子体区的磁场相对较小, 这是感应线圈产生的磁场与等离子体区感应电流产生的磁场相互作用的结果[21].
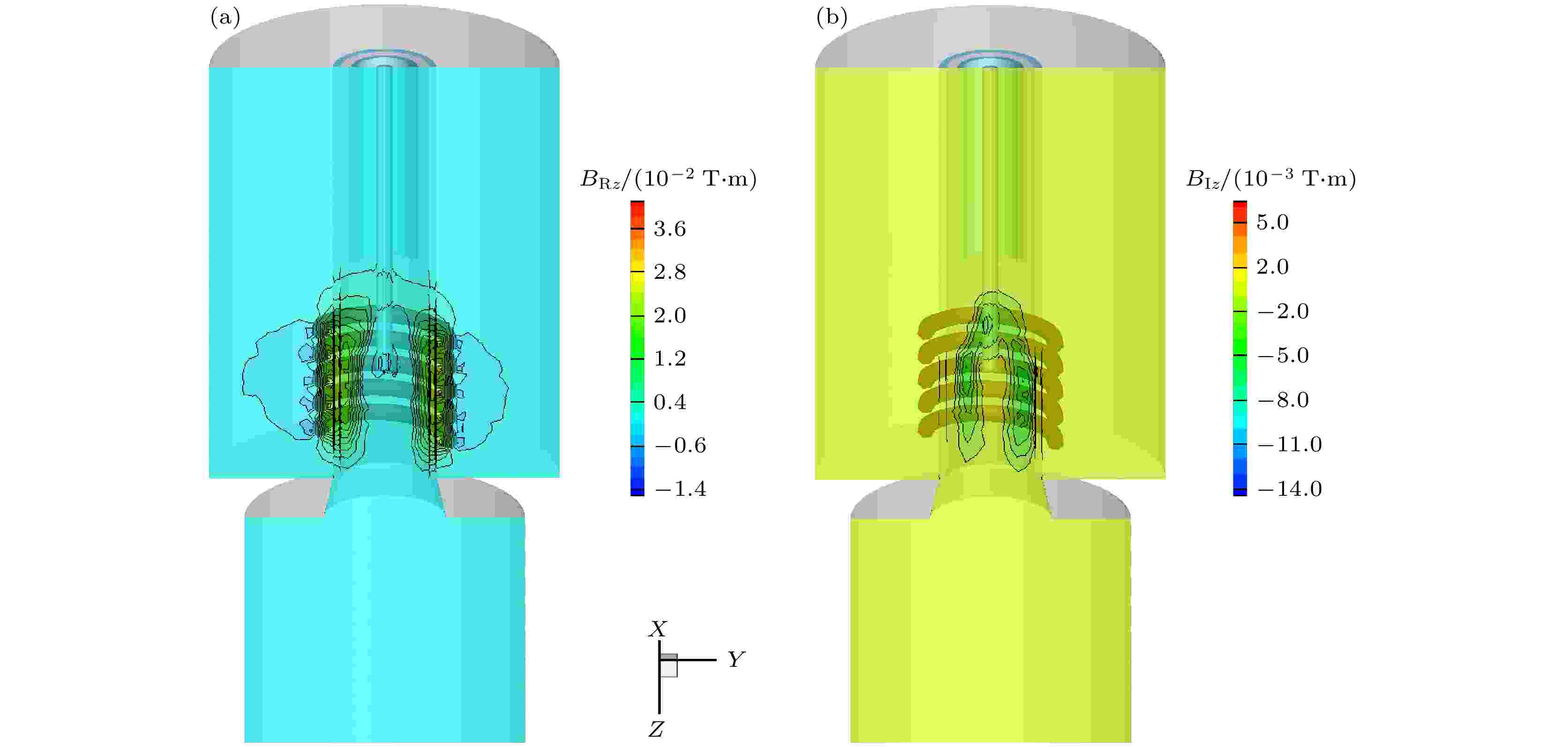图 6 YZ平面上的磁感应强度B分布　(a)实部; (b)虚部
Figure6. Distribution of magnetic flux density on YZ plane: (a) Real part; (b) imaginary part.

仅考虑由变化的磁场产生的电场, 则由(9)式得到 ${\boldsymbol{E}}=-\dfrac{\partial {\boldsymbol{A}}}{\partial t}=-\mathrm{i}\omega {\boldsymbol{A}}$. 从上文得知Ax, Ay的值较Az大一个量级, 因此, Ex和Ey同样比Ez大一个量级. 计算结果表明各电场分量的最大值分别为, ERx = 776 V/m, EIx = 4250 V/m, ERy = 686 V/m, EIy = 4640 V/m, ERz = 66.9 V/m, EIx = 369 V/m. 因此, 电场分布主要集中在XY平面, 呈现与感应线圈同轴的环形分布. 图7给出了XY平面上的合电场分布, 电场的最大值约为800 V/m. 从等离子体炬的侧上方观察, 可以看到电场的分布主要集中在线圈内部的主放电区域. 考虑到线圈的非对称性, 电场的分布并非二维模拟所呈现的闭合圆环, 而是呈现非对称性的环形分布. 此外, 在线圈外部电场呈现急剧下降趋势, 这与预期是一致的.
图 7 XY平面上的电场E分布, z = 180 mm
Figure7. Electric field distribution on the XY plane, z = 180 mm.

2
3.2.温度场、热焓及焦耳热分布
-->

3.2.温度场、热焓及焦耳热分布

如前文所述, 射频热等离子体各物理场分布具有三维效应, 并非二维模型所示的对称性分布[4]. 图8所示为射频热等离子体的三维温度场分布图. 图8(a)—(c)分别为YZ, XZ, XY面上的温度场剖面图, 可以看到, 最高温度约为11000 K, 平均温度约为9000 K, 分布在线圈覆盖区, 这里是主放电区域. 由于强烈的感应放电, 能量耗散主要发生在感应线圈内部. 这种放电呈现环形, 类似变压器的次级线圈, 图8(c)所示的XY平面上的温度分布显示了这种环形放电的基本特征. 线圈覆盖区下端主要通过对流及传热过程进行热量传递, 因此这里的温度相对较低, 约为6000 K左右, 与实验上采用原子发射光谱法获得的等离子体温度较为符合[22]. 此外, 由于线圈的非对称结构, 存在一定的偏转角, 这造成等离子体的温度场分布也呈现非对称结构, 特别是在等离子体尾焰处, 等离子体温度分布向一端偏转(如图8(a)所示), 这与实验观察是一致的. 真实的三维线圈结构对等离子体的温度分布有重要影响, 除此之外, 其他线圈参数(如线圈匝数、匝间距、线圈半径等)皆对等离子体温度分布有一定影响. 增加线圈匝数, 等离子体温度、体积以及总耗散功率会相应地增加. 增加匝间距和半径, 等离子体温度和总耗散功率有相反的变化[23,24]. 需要指出的是, 在管壁附近及等离子体尾焰处, 电子温度和重粒子温度会有一些偏差, 等离子体是偏离局域热力学平衡态. 特别是在管壁附近, 由于水冷及冷却气的作用, 这种差别会更加明显.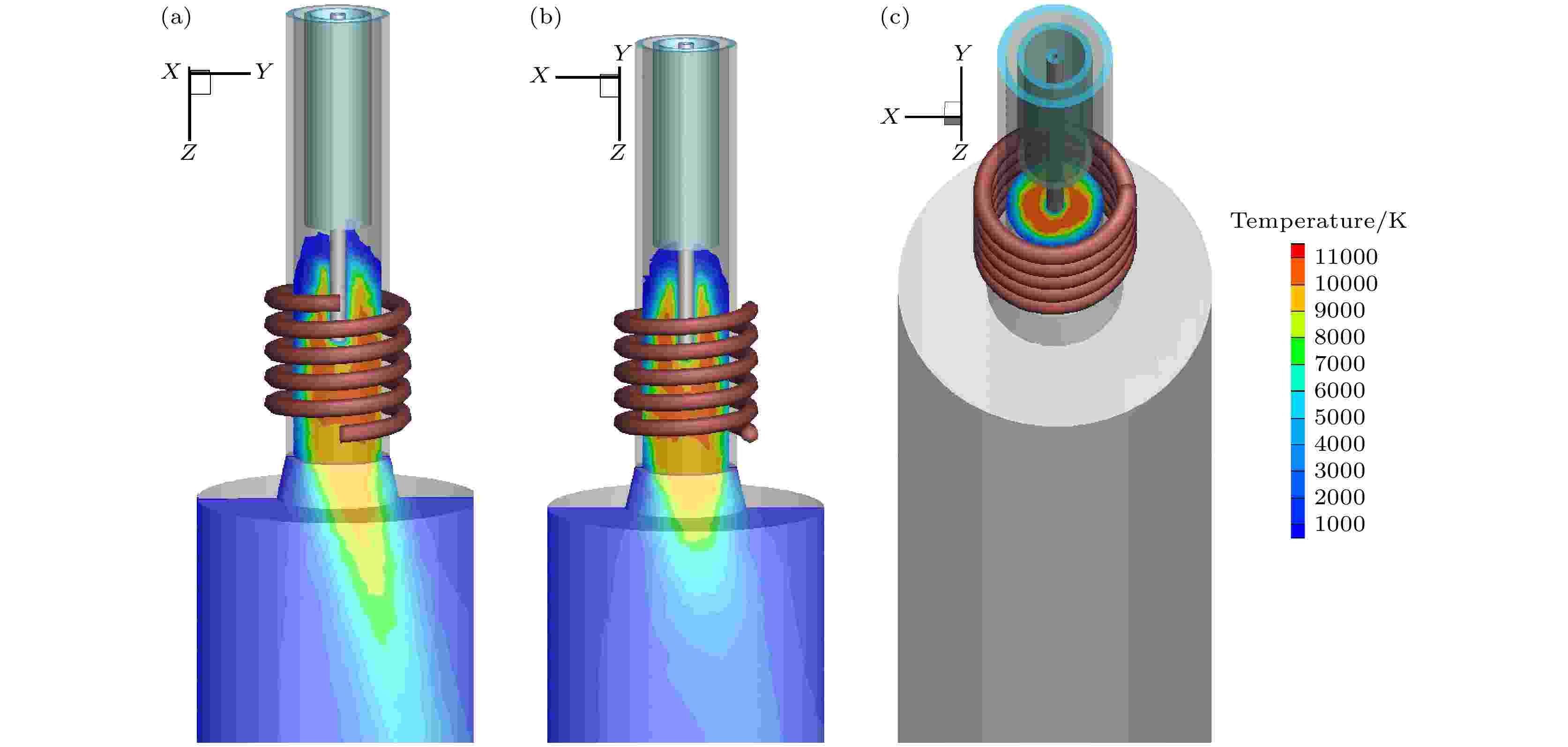
图 8 温度场场分布图　(a) YZ平面; (b) XZ平面; (c) XY平面, z = 180 mm
Figure8. Temperature field distribution: (a) YZ plane; (b) XZ plane; (c) XY plane, z = 180 mm.

感应电流的振荡频率是影响等离子体温度分布的另一个重要因素. 众所周知, 高频率的振荡电流会产生趋肤效应, 趋肤厚度$\delta $可由下式决定:
$\delta =\sqrt{1/\left(\mathrm{\pi }{\mu }_{0}f\sigma \right)},$
其中$ {\mu }_{0} $是自由空间的磁导率, $ f $是振荡频率, $ \sigma $是等离子体电导率. 取等离子体的平均温度为9000 K, 对应的电导率为 $\sigma \!=\! 1935.8\;\Omega \cdot \mathrm{m}$, ${\mu }_{0} \!=\! 4\mathrm{\pi }\!\times\! {10}^{-7}\;\mathrm{H}/\mathrm{m}$, $f \!=\! 3\;\mathrm{M}\mathrm{H}\mathrm{z}$, 则趋肤厚度为6.6 mm. 若振荡频率增加, 则趋肤厚度变小. 这意味着放电区域变薄, 等离子体高温区也向约束管边缘移动, 这会导致等离子体炬壁面的温度增加, 这对等离子体炬的使用寿命是不利的. 此外, 振荡频率的选择对射频热等离子体炬的尺寸优化有指导意义. 由以上分析可知, 趋肤厚度随着振荡频率的升高而减小, 同时, 等离子体中的焦耳热将集中于更窄的区域中, 因此, 减小振荡频率可以有效增加趋肤深度且使等离子体的能量耗散分布更加均匀. 同时, 趋肤厚度会影响射频热等离子体炬效率. 研究表明, 当放电约束管半径约为趋肤深度的1.5倍时, 耦合效率最高[25]. 在实际应用过程中, 为防止约束管过热, 通常以一股大气流作为冷却气用以保护放电约束管内壁.
图9(a)和图9(b)给出了感应线圈覆盖区放电过程中所耗散的焦耳热分布. 焦耳热主要分布在主放电区域, 同样呈环形分布, 其平均值约为3.0 × 108 W/m3. 大部分耗散的焦耳热会直接导致等离子体温度和速度的提高. 由于氩热等离子体具有较高的热容, 且随着温度的升高, 热容呈指数增长(当温度为10000 K, 热容达3000 J/ (kg·K)), 其对应的焓值也较高. 图9(c)给出了焓值分布图, 焓值分布与等离子体温度分布相似, 焓值最高可达1 × 107 J/ kg, 平均值约为5 × 106 J/ kg, 等离子体尾焰处的焓值约为2.0 × 106 J/ kg, 这与实验室测量是相符的[26]. 射频热等离子体的高温、高焓特性, 使其在材料热处理方面极具优势.
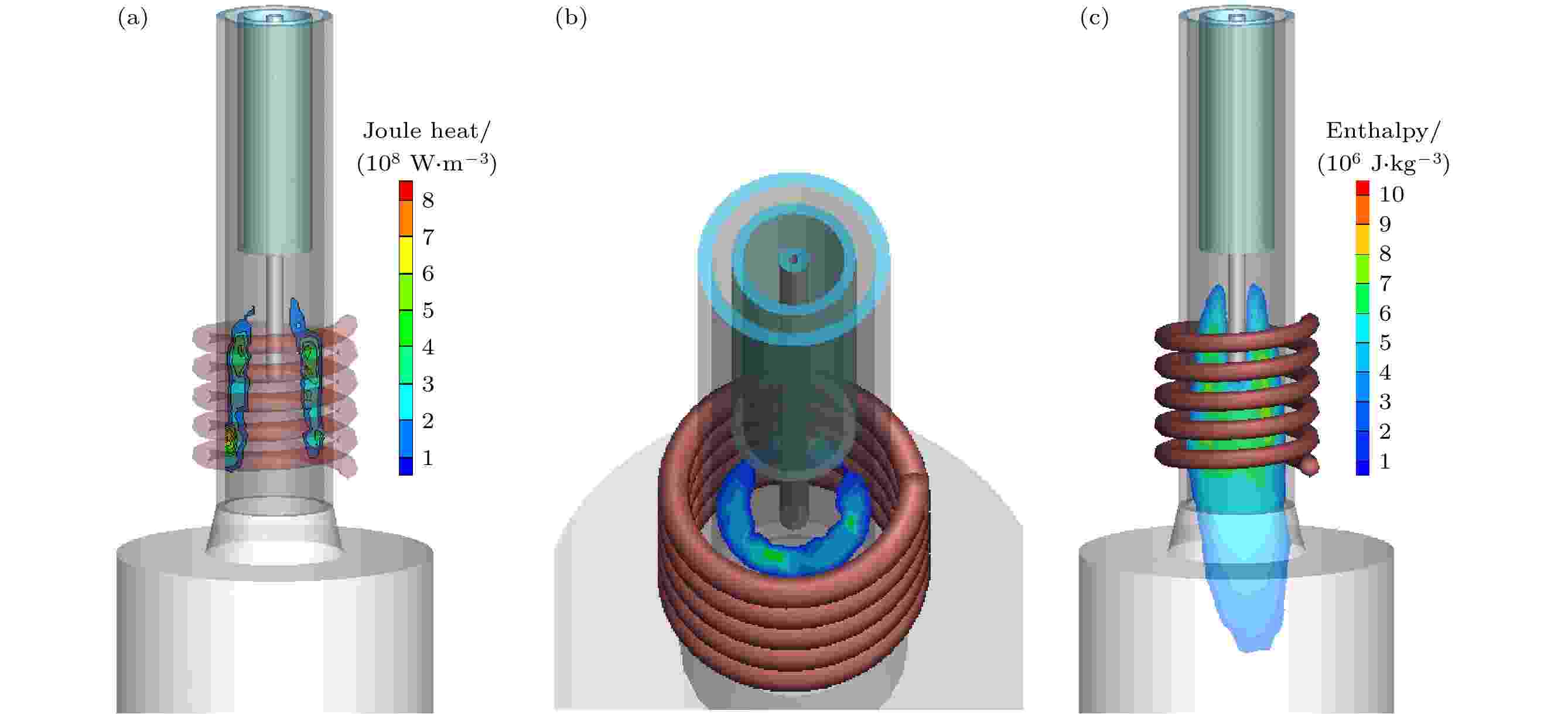图 9 (a)焦耳热分布; (b) XY 平面上的焦耳热, z = 180 mm; (c)焓值分布
Figure9. (a) Joule heat distribution; (b) Joule heat distribution on the XY plane, z = 180 mm; (c) enthalpy distribution.

2
3.3.电导率、热导率及黏性分布
-->

3.3.电导率、热导率及黏性分布

图10给出了射频热等离子体的电导率、热导率和黏性分布情况. 等离子体的电导率具有不均匀性, 最大值主要分布在环形放电区域内, 最大值为4289 A/(V·m), 远小于铜的电导率5.81 × 107 A/(V·m), 这表明尽管射频热等离子体具有极高的温度, 但它的电离率并不高(< 10%)[20]. 射频热等离子体电导率主要贡献源于电子, 离子对它的贡献可忽略. 环形放电区较高的电导率表明本区域具有较高的电子密度, 放电剧烈, 是主放电区域, 这与前文的分析结果是一致的. 此外, 等离子体电导率是温度的非线性函数, Raizer 推导出它们的关系如下[27]: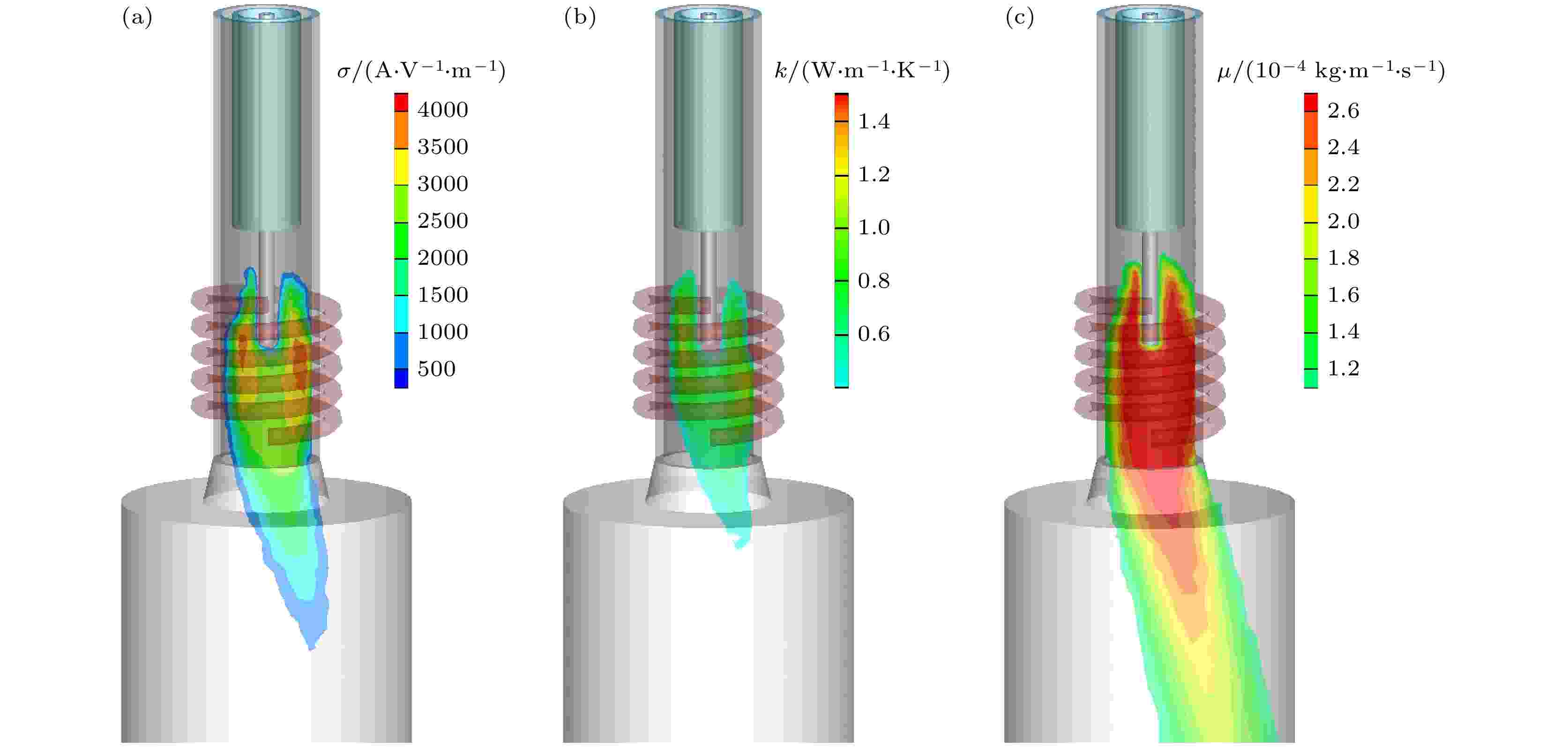
图 10 (a)电导率分布; (b)热导率分布; (c)黏性系数分布
Figure10. (a) Electrical conductivity distribution; (b) thermal conductivity distribution; (c) viscosity distribution.

$\sigma = 1.9 \times {10^2} \times \frac{{{T^{1.5}}}}{{{\rm{ln}}\varLambda }}~{\rm{A}}/({\rm{V}} \cdot {\rm{m}}),$
其中, $ \mathrm{l}\mathrm{n}\varLambda $ 为库仑对数. 等离子体电导率是等离子体温度的指数型函数, 温度升高等离子体电导率急剧增大, 当等离子体温度低于6000 K时, 电导率几乎可以忽略不计, 这与我们的模拟结果是相符的, 如图10(a)所示, 特别是在水冷管壁附近以及等离子体尾焰处, 等离子体电导率的分布趋近于零.
图10(b)所示为氩气射频热等离子体的热导率分布, 与等离子体温度及电导率的分布情况类似, 这是由于等离子体热导率也是温度的函数. 此外, 热导率的平均值约为1.0 W/(m·K), 与石英玻璃的热导率相当, 可见, 氩气射频热等离子体具有较小的热导率. 为此, 通常将部分氢气通入氩气热等离子体提高其导热性能[14,28]. 图10(c)给出了氩气射频热等离子体的黏性分布情况, 可看到黏性较高的区域分布在感应线圈覆盖的等离子体高温区域, 最高值为2.7 × 10–4 kg/(m·s). 在等离子体中, 由于电子的质量较小, 黏性主要的贡献来源于重粒子. 在高温区的黏性高意味着本区域具有较高的黏性阻力, 这对注入到等离子体中的颗粒(固体颗粒或液滴)有重要影响[28-30].
2
3.4.速度场、流场及洛伦兹力分布
-->

3.4.速度场、流场及洛伦兹力分布

图11(a)所示云图为等离子体的速度场分布, 最大流速约为40 m/s, 分布在线圈覆盖区下游(红色区域), 这表明, 冷气流以Q1 = 0.4 m/s, Q2 = 2.009 m/s的初始速度送入到等离子体炬中, 经过线圈区域发生放电形成等离子体后, 其流动过程急剧加速, 在线圈下游段速度达到最大. 如前文所述, 在这一区域放电所耗散的焦耳热能有向动能的转化过程. 尽管如此, 如果与直流电弧热等离子体相比较, 射频热等离子体也是相对低速的, 直流电弧热等离子体的速度可达200—300 m/s, 这也是射频热等离子体的重要特征之一. 射频热等离子体的低速可使原料颗粒在等离子体中有较长的滞留时间, 确保其有效加热熔融, 这对材料处理是有益的. 图11(b)所示矢量图是等离子体流场分布图. 图中显示, 气流沿着管壁向内平缓流动, 在线圈覆盖区及其上端处的流动异常复杂, 存在回流现象, 等离子体流动呈现从内向外的翻滚, 然后沿着中心线方向收缩并喷射出来. Boulos [21]称这种复杂流动是由电磁泵效应所致. 图11(c)二维模拟结果显示, 这种回流现象具有对称性. 事实上, 三维模拟结果显示, 由于线圈的非对称性, 这种回流现象并非二维模拟结果所示的等离子体流动呈对称性, 三维模拟结果更趋于实际的等离子体流动过程. 为了更清晰地观察线圈区域的复杂流动状态, 将图11(b)进行放大, 从图12可以看到, 在线圈上端处出现一个流线密集的回流区域, 另一端存在一个半径较大的回流. 在线圈下端进行密集的束流并沿着出口喷射出来. 这种回流的形成和带电粒子受到径向上的洛伦兹力有关. 图13给出了单位体积的洛伦兹力Fx的分布图, Fx的平均值约为6000 N/m3, 方向指向轴线. 径向上的洛仑兹力使带电粒子向内(中心线)运动, 从而使等离子体在线圈区沿径向流动. 此外, 这种回流现象可能与线圈区域的负气压梯度也有关[31]. 在实际应用过程中, 为了避免这种复杂流动对送料的影响, 通常将送料枪出口位置越过这一复杂流动区, 置于线圈的第二圈平面处. 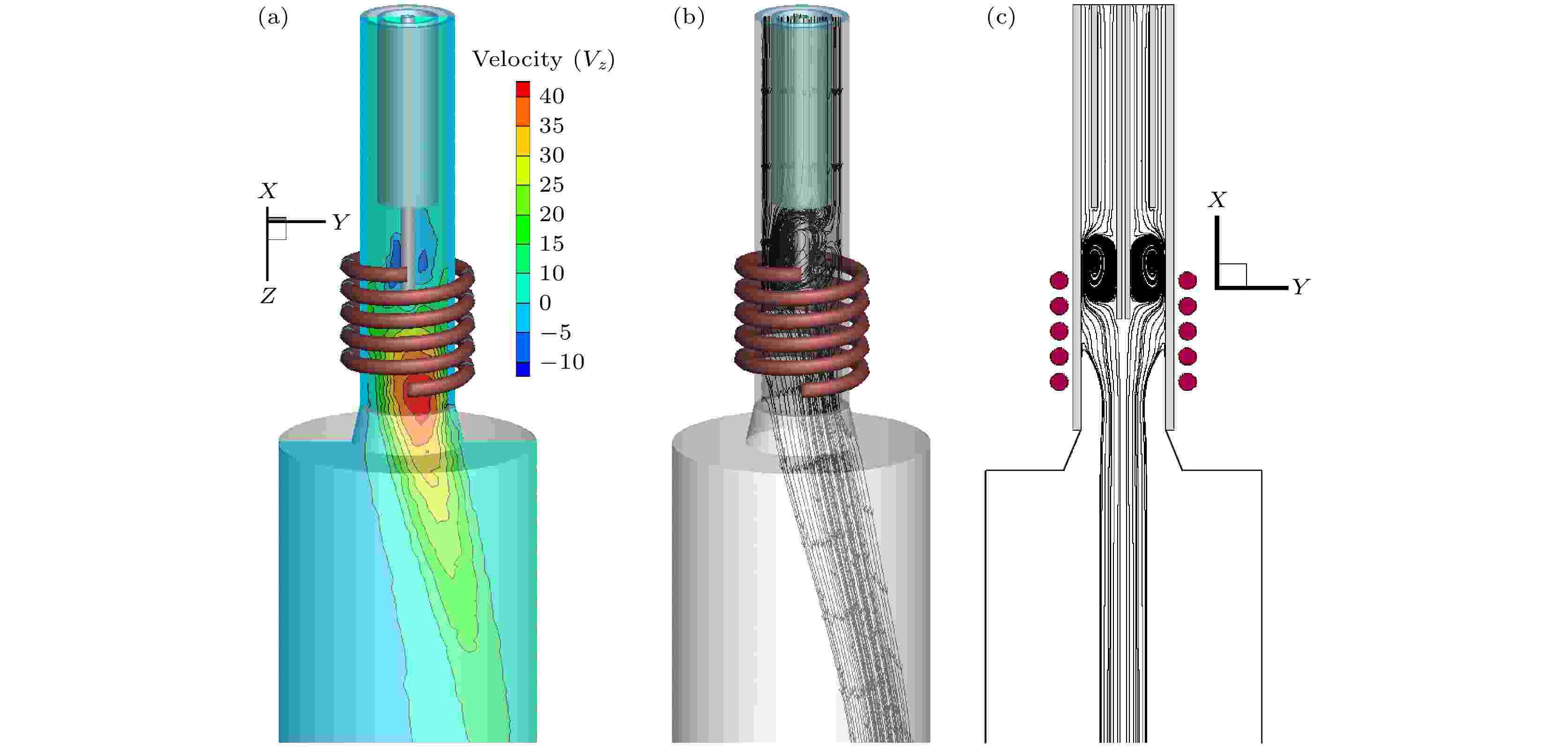此外, 在等离子体尾焰处存在一定的湍流效应, 如前文所述我们采用标准$k\text-\omega$模型来描述这种湍流效应. 从图11(b)所示的流场分布图可以看到, 这种湍流效应并不十分明显, 这与直流电弧热等离子体较强的湍流流动是不同的. 实验表明射频热等离子体尾焰处的湍流流动也是不明显的, 与本文的模拟结果是一致的.
图 11 (a)速度场Vz; (b)流场; (c)二维流场[4]
Figure11. (a) Velocity field Vz; (b) flow field; (c) two dimensional flow field[4].

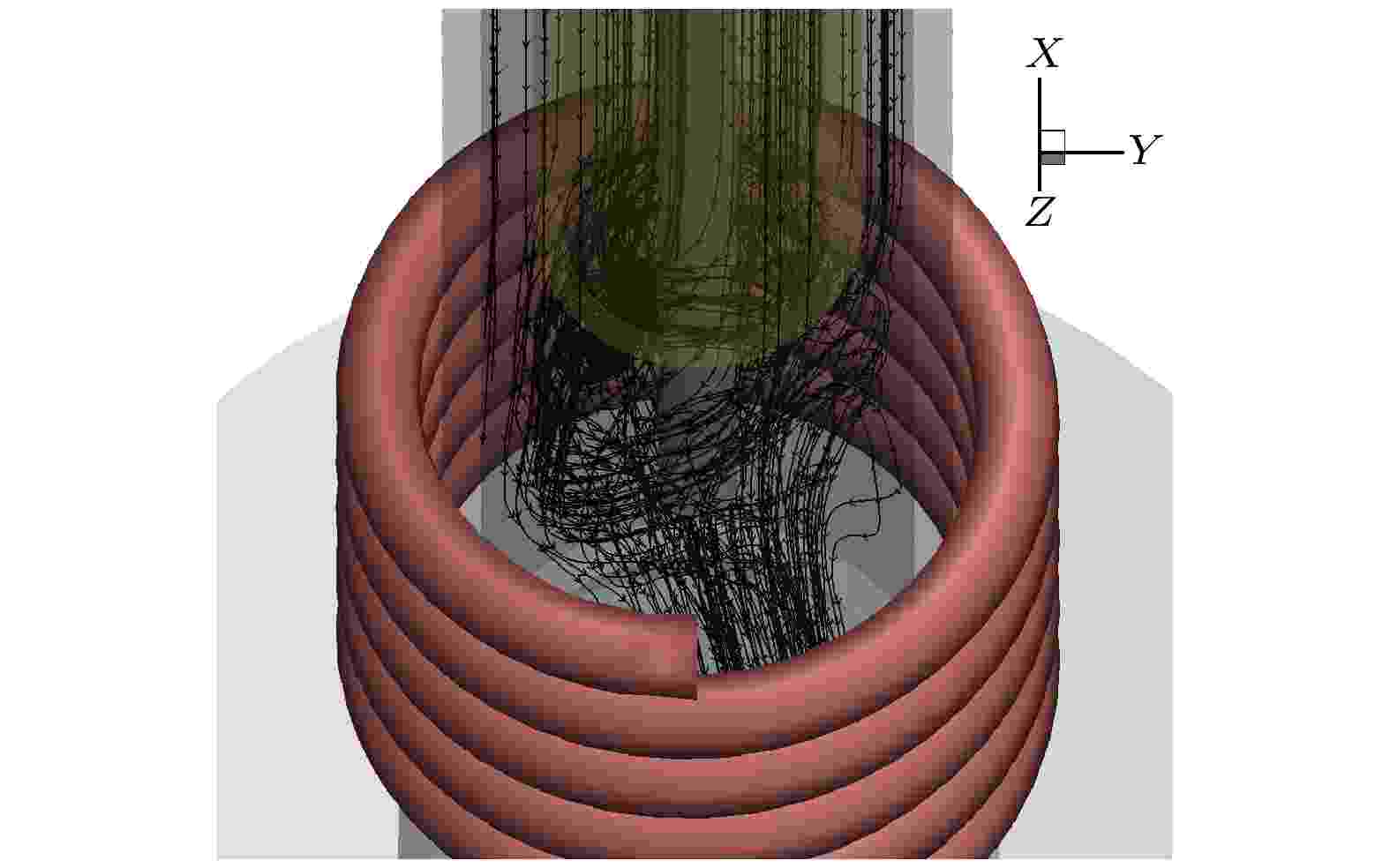图 12 射频热等离子体流场放大图
Figure12. Magnified view of radio frequency thermal plasma flow field.

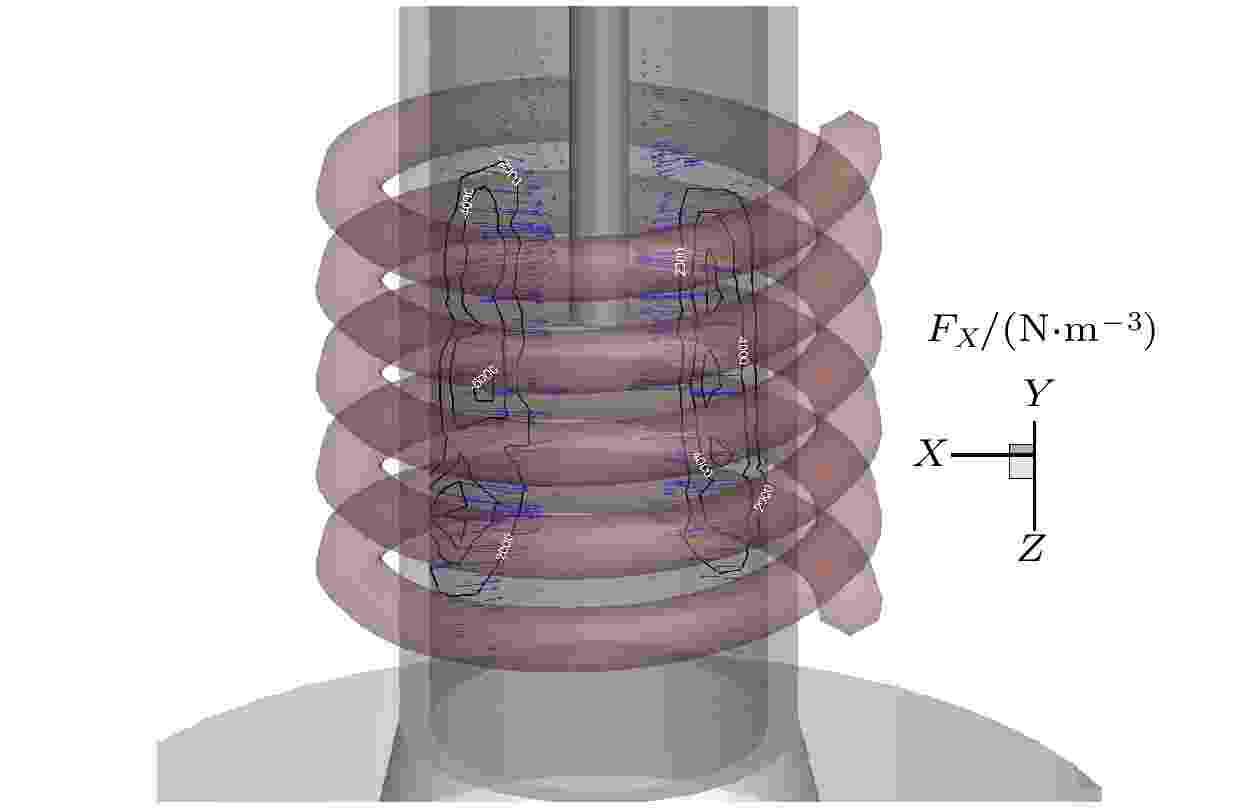图 13 洛伦兹力Fx矢量分布图
Figure13. Lorentz force distribution(Fx).

4.结　论
本文建立了更贴近真实结构、更复杂的三维射频热等离子体的数学物理模型, 将射频热等离子体视为磁流体, 利用FLUENT软件解算流体力学方程, 结合自行开发的C++程序解算电磁场方程, 计算分析了射频热等离子体的物理场分布, 特别是温度场和流场分布, 从物理上揭示了各物理场分布的原因, 为射频热等离子体在粉末球化、纳米颗粒合成及等离子体喷涂等实际应用提供理论指导. 通过分析讨论各物理场分布可以得出如下结论:
1)射频热等离子体的各物理场, 如温度场、流场和电磁场具有三维特征. 在二维轴对称情况下, 感应线圈实际结构对等离子体物理场分布的影响可忽略不计. 然而, 大多数情况下当考虑感应线圈的实际形状时, 它对等离子体的非对称性产生重要影响. 射频热等离子体物理场的三维非对称性特征对实际应用的工艺过程设计具有指导意义.
2)射频热等离子体三维温度场、焦耳热及电导率分布揭示了射频热等离子体放电的环形结构, 温度极值分布在这一环形区域. 受振荡频率影响较大的趋肤效应是放电呈环形分布的主要原因. 这一结论对射频热等离子体炬的设计具有参考意义.
3)与二维数值模拟不同, 三维模拟结果给出了更复杂更贴近实际的等离子体流场分布. 由于感应线圈的非对称性, 线圈覆盖区等离子体回流也具有非对称性. 此外, 等离子体尾焰处的湍流效应并不明显.
相关话题/物理 计算 电磁场 等离子体 结构
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 一个圆柱形双栅场效应晶体管的物理模型
    摘要:圆柱形双栅场效应晶体管(CSDGMOSFET)是在围栅MOSFET器件增加内部控制栅而形成,与双栅、三栅及围栅MOSFET器件相比,圆柱形双栅MOSFET提供了更好的栅控性能和输出特性.本文通过求解圆柱坐标系下的二维泊松方程,得到了圆柱形双栅MOSFET的电势模型;进一步对反型电荷沿沟道积分, ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 神经微管振动产生纳米尺度内电磁场作用
    摘要:生物体经过神经元进行信息处理产生指令,控制各种功能和活动.神经元可通过神经微管维持动态生长,辅助蛋白转运等,微管蛋白可产生电磁信号进行信息交换.微管蛋白具有强极性分布,本文通过研究微管不同振动模式产生的电磁特性,分析微管周围的电磁场分布和相互作用.结果表明,微管蛋白在太赫兹波段有众多振动模式. ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 褶皱状蜂窝结构的单层二维材料研究进展
    摘要:以石墨烯为代表的二维材料具有新颖的物理特性和潜在的应用前景.但石墨烯的零带隙限制了它在半导体器件中的应用,寻找新的半导体型替代材料成为当前的一个研究热点.作为黑磷的单层,磷烯具有褶皱状蜂窝结构.它具有可调直接带隙、高载流子迁移率和面内各向异性等独特的性质,引起了人们的广泛关注.磷烯的发现开辟了 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于波动与扩散物理系统的机器学习
    摘要:物理学在机器学习中的应用以及两者的交叉融合正引起广泛关注,尤其是在波动系统和扩散系统中.本文重点关注波动与扩散物理系统和机器学习之间的内在联系以及对机器学习算法和物理实现的推进作用,综述了波动系统和扩散系统中的机器学习研究,介绍了部分最新研究成果.文中首先讨论了监督学习的波动系统实现,包括神经 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于蛛网结构的量子卫星广域网构建策略及性能仿真
    摘要:量子卫星通信是通信领域的研究热点和前沿,具有理想的信息安全性和覆盖面广的优势,对于构建全球范围的量子卫星广域网具有重要意义,而远距离传输信息时网络的可靠性、安全性和路由中继等问题仍需改进.为了构建性能良好的量子卫星广域网,本文提出利用蜘蛛网作为一种独特的自然通信拓扑结构,将自然界蛛网演进为人工 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 金属-介质-金属多层结构可调谐Fabry-Perot共振及高灵敏折射率传感
    摘要:顶层透光、底层不透光的金属-介质-金属多层结构可以产生窄带完美吸收共振,用于测量介质层待测液体的折射率变化.本文通过构建Fabry-Perot共振解析模型,准确复现了该结构的响应光谱,给出了其共振波长、品质因子、半高全宽和灵敏度的解析表达式,并分析了介质层厚度对光谱的谐振波长和线宽的调谐机制, ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 疏水表面振动液滴模态演化与流场结构的数值模拟
    摘要:为了研究疏水表面垂直振动液滴的运动规律,本文建立了振动液滴的三维模型,考虑了振动液滴的动态接触角变化过程,通过流体体积函数和连续表面张力(volumeoffluid-continuesurfaceforce,VOF-CSF)方法实现了液滴受迫振动的数值模拟,得到了液滴的四种模态(2,4,6和8 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 一种计算非平衡等离子体中粒子能级布居的简化方法
    摘要:获得粒子能级布居是研究非平衡等离子体辐射性质的一个重要方面.对于复杂三维等离子体,采用细致碰撞辐射模型虽然精确,但计算耗费大.本文提出了一种束缚态特征温度法,能够快速计算得到非平衡等离子体中的粒子能级布居.对非平衡氖等离子体算例的研究表明,本文方法是有效的,在等离子体非平衡程度不太高时与碰撞辐 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于单元辐射叠加法的结构声源声场重建方法
    摘要:为了提高分布式结构声源的声场重建精度,本文提出了基于单元辐射叠加法的结构声源声场重建方法.该方法首先利用声场叠加原理和结构振声传递特性,建立了结构声源表面振动与辐射声场之间的振声传递关系解析表达式,得到便于快速计算的振声传递矩阵,能够解决连续分布、相干结构噪声源的声传播模型精细化表征问题.然后 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • In<sub>1+</sub><i><sub>x</sub></i>Te化合物的结构及热电性能研究
    摘要:InTe化合物中In+的孤对电子引发的晶格非谐性振动使得其具有本征极低的热导率,因此被认为是一种具有潜力的中温热电材料.然而,较低的电输运性能使得InTe的热电性能不高.在本工作中,采用熔融、退火结合放电等离子活化烧结工艺制备了一系列In1+xTe(x=0,0.001,0.003,0.005, ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.