摘要: 研究了纳米机械谐振器耦合量子比特系统中的声子阻塞现象. 发现在弱驱动的条件下, 非厄米哈密顿量的所有本征值都等于零时, 出现了强声子反聚束现象. 于是提出了零本征值方法来诱导声子阻塞. 本文详细分析了此方法对声子阻塞的影响, 给出了最佳条件并解释了背后的物理机理. 不同于传统的声子阻塞和非传统的声子阻塞, 不管是强非线性还是弱非线性, 都可以实现声子的反聚束效应.
关键词: 声子阻塞 /
纳米机械谐振器 /
量子比特 English Abstract Phonon blockade induced by a non-Hermitian Hamiltonian in a nanomechanical resonator coupled with a qubit Liao Qing-Hong 1,2 ,Deng Wei-Can 1 ,Wen Jian 1 ,Zhou Nan-Run 1 ,Liu Nian-Hua 3 1.Department of Electronic Information Engineering, Nanchang University, Nanchang 330031, China Received Date: 25 December 2018Accepted Date: 27 February 2019Available Online: 01 June 2019Published Online: 05 June 2019Abstract: Nanomechanical resonator has important applications in the field of high-precision detection because it has a high-Q factor, high vibration frequency, small size, and other excellent characteristics. Superconducting qubit has very large magnetic dipole moments, so it can be easily combined with nanomechanical resonator. Furthermore, the system parameters including frequency and coupling strength can be designed according to requirements beforehand, which makes a superconducting qubit an ideal artificial atom. Compared with natural atom, superconducting qubit has abundant energy levels. For these reasons, nanomechanical system has aroused wide interest in the engineering, electron, physical and other fields of science and technology. According to the recent research, a new approach to the zero eigenvalues of non-Hermitian Hamiltonian is applied to the optomechanical system. It was found that the scheme is superior to conventional photon blockade (CPB) and unconventional photon blockade (UPB) in the cavity quantum electrodynamics (QED) system. So we propose a scheme to induce phonon blockade in order to explore a new avenue to the research about phonon blockades in the quantum open system. We study the phonon blockade in an optomechanical system that a qubit is coupled with nanomechanical resonator (NAMR) driven by two external weakly driving fields respectively in this way. In this paper, the Hamiltonian of such a system can be treated by the non-Hermitian Hamiltonian and it can be described in the form of matrix. Then the phenomenon of phonon blockade occurs when all the eigenvalues in the form of matrix are equal to zero. It is found that strong phonon antibunching can be triggered in both strong and weak nonlinearity when we use the method which has been already used in a gain optical cavity system. The distinct result reflects the advantage of our approach which possesses some outstanding characters between the ordinary methods (conventional phonon blockade and unconventional phonon blockade). In addition, the effect of our avenue on phonon blockade is analyzed and also the distinction between the conventional phonon blockade (CPNB) and unconventional phonon blockade (UPNB) is compared with each other in detail. By analytical calculation, the optimal conditions are given and the underlying physical mechanism is explained. In the comparison between CPNB and UPNB, we show the superiority of our scheme through some graphs. Finally, we describe briefly the measurements of phonon blockade in the NAMR-qubit system via a superconducting cavity. The proposal may provide a theoretical way to guide the manufacture of phonon devices in the future. The results obtained here may have a great significance and application in the field of quantum information processing and precision measurement.Keywords: phonon blockade /nanomechanical resonator /qubit 全文HTML --> --> --> 1.引 言 超导量子电路作为人工设计的量子力学系统, 显示了宏观的量子相干性, 可以用来研究量子光学和原子物理的现象[1 ] . 在超导量子电路中, 超导传输线谐振器代替传统的光学腔, 超导量子比特扮演自然原子的角色. 超导量子比特作为宏观的人工原子, 其他超导量子器件, 例如超导传输线、机械纳米振子等的强耦合, 可以实现一种崭新的全固态的腔量子电动力学(cavity quantum electrodynamics, C-QED)结构, 而且这些人工的原子和光场, 具有以前微腔QED没有的可控性和可集成化的优点. 包含超导量子比特和纳米机械振子的混合量子电路是另一种新兴的混合量子系统[2 ] . 这种混合量子电路的有趣的理论研究和有实质性进展的实验结果, 证明了该系统可以作为未来量子器件, 并拥有广泛的应用[2 -4 ] .[5 ] 发现机械谐振器在超低温(超导)条件下的振动可以激发量子效应, 产生单个量子(声子). 随后, 清华大学Liu等[6 ] 根据这个实验, 研究了纳米机械谐振器(nanomechanical resonator, NAMR)中的声子阻塞效应. 声子阻塞, 顾名思义, 类似于光子阻塞[7 ] , 是一种纯量子现象. 这种现象是在非线性机械振荡器[8 ] 中, 第一个声子被外部驱动场激发, 第二个声子被第一个声子阻挡导致不能传输. 光子阻塞效应的一项重要应用是可以用于实现理想的单光子源[9 ,10 ] , 而声子阻塞效应同样可以作为实现单声子源的机制之一[11 ,12 ] . 类比于产生光子阻塞的两种机制, 声子阻塞同样地对应两种发生机制. 声子阻塞的实现有两种主要的物理机理: 基于失谐机制的声子反聚束需要较大的非线性来改变系统的能级结构, 这被称为传统声子阻塞(conventional phonon blockade, CPNB)[13 -16 ] . 除了第一种物理机理外, 还可以获得强声子反聚束, 即利用双声子激发的不同路径产生的破坏性干涉, 即使在非线性远小于腔模的衰减率(弱非线性)的条件下也能实现, 称为非传统声子阻塞(unconventional phonon blockade, UPNB)[16 -19 ] .[20 ] 、光学模式与机械模式之间产生的二阶非线性相互作用导致的强声子反聚束现象[21 ] 、机械谐振器与两能级系统耦合的光力系统的双色二阶边带的生成[22 ] . 多模光力系统[23 ] 、有限温度下耦合非线性微米/纳米机电系统的谐振器的声子反聚束效应并与热噪声的关系[24 ] 、机械振动位移的平方耦合的声子阻塞现象研究[25 ] 、光声阻塞现象[26 ] 、俘获多个离子的库仑晶体中声子阻塞研究[27 ] 等.[28 -44 ] . 其中包含了量子纠缠[28 ] 、兰姆位移[31 ] 、光子统计特性[44 ] 等. 本文研究NAMR-量子比特系统中的声子统计性质, 其中的系统是由一个纳米机械谐振器耦合一个超导量子比特(以下简称量子比特)组成. 这里利用了非厄米哈密顿量的零本征值方法, 并假设$\kappa < 0$ , 研究了NAMR-量子比特系统中的声子统计特性. 同时给出探测声子阻塞或声子统计特性的方法.2.NAMR-量子比特系统的物理模型 图1 研究的是由一个纳米机械谐振器(右边)耦合一个量子比特(左边)组成的物理系统. 纳米机械谐振器受到一个强度为$\varepsilon $ 的外加场驱动, 量子比特受到一个强度为$\varOmega $ 的外加场驱动. 整个系统的哈密顿量为[16 ] 图 1 NAMR-量子比特系统的物理模型图Figure1. Schematic diagram of the nanomechanical resonator coupled with a qubit.$\hbar = 1$ , ${\sigma _ + }$ 和${\sigma _ - }$ 是量子比特的上升和下降算符, 其跃迁频率是${\omega _0}$ ; a 和${a^ + }$ 表示NAMR中声子的湮灭和产生算符, 其频率是${\omega _{\rm{m}}}$ ; g 是量子比特与NAMR的耦合强度; 量子比特的外加驱动场振幅是$\varOmega $ , 频率是${\omega _{\rm{q}}}$ ; NAMR的外加驱动场振幅是$\varepsilon $ , 频率是${\omega _{\rm{a}}}$ ; $\phi $ 是两个外加驱动场的相位差.${\omega _{\rm{q}}} = {\omega _{\rm{a}}} = {\omega _{\rm{d}}}$ 和${\omega _0} = {\omega _{\rm{m}}}$ , 在以入射光频率旋转的框架中, 得出哈密顿量:$\varDelta \equiv {\omega _0} - {\omega _{\rm d}} = {\omega _{\rm m}} - {\omega _{\rm d}}$ .3.非厄米哈密顿量作用下的声子阻塞效应的零本征值 23.1.声子阻塞的条件分析 3.1.声子阻塞的条件分析 考虑机械模衰减率$\kappa $ 和量子比特自发辐射速率$\gamma $ . 所以, 整个系统可以用非厄米哈密顿量描述为$n + 1$ , 在基矢$\left| {n, e} \right\rangle $ 和$\left| {n + 1, g} \right\rangle $ 下, 可得到非厄米哈密顿量的矩阵形式:$\varOmega , \varepsilon \ll \left| \kappa \right|$ .4 )式中的矩阵, 可得知其两个特征值:$n = 0$ . 而且要使得(5 )式特征值取到实数, 则满足条件$\left| g \right| = \dfrac{\gamma }{2}$ 时, 两个特征值相等, 即${\omega _ \pm } = \varDelta $ . 所有特征值取0时需满足$g \gg \dfrac{\gamma }{2}$ 时, 有$\sqrt {16{g^2} - 4{\gamma ^2}} \simeq 4g$ , 此时特征值$\omega _ \pm \simeq \varDelta \pm g$ .$\varDelta = \mp g$ 时, 这一对特征值相等并且取得最小值0. 此时可以知道特征值为零的条件为:图2 中的系统能级可知, 系统参数条件满足(8 )式或(9 )式时, 可出现声子阻塞现象.图 2 外加驱动场共振的情况下声子阻塞现象的能级图 (a)满足(8 )式时的能级图, 其中$\omega _ \pm ^{\left( 1 \right)} = {\omega _{\rm{m}}}$ 和$\omega _ \pm ^{\left( 2 \right)} = 2{\omega _{\rm{m}}} \pm $ $2g + {\rm{i}}\dfrac{\gamma }{2}$ ; (b)满足(9 )式时的能级图, 其中$\omega _ \pm ^{\left( 1 \right)} = {\omega _{\rm{m}}} \pm g$ 和$\omega _ \pm ^{\left( 2 \right)} = 2{\omega _{\rm{m}}} \pm \sqrt 2 g + {\rm{i}}\dfrac{\gamma }{2}$ Figure2. Schematic energy-level diagram explaining the occurrence of the phonon blockade by the driving field satisfying the resonance condition: (a) Energy-level diagram when Eqs. (8 ) are satisfied, where $\omega _ \pm ^{\left( 1 \right)} = {\omega _{\rm{m}}}$ and $\omega _ \pm ^{\left( 2 \right)} = 2{\omega _{\rm{m}}} \pm$ $ 2g + {\rm{i}}\dfrac{\gamma }{2}$ ; (b) energy-level diagram when Eqs. (9 ) are satisfied, where $\omega _ \pm ^{\left( 1 \right)} = {\omega _{\rm{m}}} \pm g$ and $\omega _ \pm ^{\left( 2 \right)} = 2{\omega _{\rm{m}}} \pm \sqrt 2 g + {\rm{i}}\dfrac{\gamma }{2}$ .$\gamma $ 设为正数, $\kappa $ 设为负数. 事实上, 在光学腔中, 腔模衰减率${\kappa _{\rm{C}}} < 0$ 已被广泛地研究[45 ,46 ] , 而且已经有实验实现了这个参数[47 -51 ] . 本文基于此, 做出了相应的假设, 即声子场衰减系数$\kappa < 0$ . 实际上已有实验通过相干驱动声子技术[5 ,52 -54 ] 、引入声子激光[55 -57 ] 和直接驱动机械振子[58 ,59 ] 等方式来提供机械增益. 这里简要讨论直接驱动纳米机械谐振器来产生力学增益的可能性[60 ] . 外场驱动在可分辨边带条件下, 对应于纳米机械谐振器中声子冷却的斯托克斯散射过程被极大抑制, 给纳米机械谐振器提供能量的反斯托克斯过程得到了增强并占主要优势.3.2.数值模拟方法 -->3.2.数值模拟方法 通过计算系统的主方程来研究二阶关联函数. 系统的密度矩阵为:$\ell \left( {\hat o} \right)\hat \rho = \hat o\hat \rho {\hat o^ + } - \dfrac{1}{2}{\hat o^ + }\hat o\hat \rho - \dfrac{1}{2}\hat \rho {\hat o^ + }\hat o$ .$\partial \rho /\partial t = 0$ . 通过二阶关联函数${g^{\left( 2 \right)}}\left( 0 \right)$ 来研究声子的统计特性.$\left( {\dfrac{{\partial \rho }}{{\partial t}} = 0} \right)$ 得出${g^{\left( 2 \right)}}\left( 0 \right)$ . 二阶关联函数${g^{\left( 2 \right)}}\left( 0 \right) < 1$ 对应于亚泊松分布的统计特性. 通过计算关联函数, 可以知道声子阻塞效应是否会发生.3.3.结果分析 -->3.3.结果分析 下面通过计算机数值模拟分析研究声子阻塞效应, 比较和分析(8 )式和(9 )式. 系统中腔模的希尔伯特空间被截取到5维, 以耗散率$\gamma $ 作为基本单位来设定其他参数. 图3 给出了不同条件下($g/\gamma = 0.5$ , 2.0, 4.0) ${g^{\left( 2 \right)}}\left( 0 \right)$ 与$\varDelta /\gamma $ 的关系图, 可以得出出现声子阻塞的特点.图 3 在不同的$g/\gamma $ 关系下, 二阶关联函数${g^{\left( 2 \right)}}\left( 0 \right)$ 与$\varDelta /\gamma $ 的关系图 (a) $\kappa /\gamma = - 1$ , $\varepsilon /\gamma = 0.1$ , $\varOmega = 0$ , $\varepsilon \ne 0$ ; (b) $\kappa /\gamma = - 1$ , $\varOmega /\gamma = 0.1$ , $\varepsilon = 0$ , $\phi = 0$ Figure3. Logarithmic plot (of base e) of the zero-delay-time second-order correlation functions ${g^{\left( 2 \right)}}\left( 0 \right)$ as a function of $\varDelta /\gamma $ for different $g/\gamma $ with $\kappa /\gamma = - 1$ : (a) $\varepsilon /\gamma = 0.1$ , $\varOmega = 0$ , $\varepsilon \ne 0$ ; (b) $\varOmega /\gamma = 0.1$ , $\varepsilon = 0$ , $\phi = 0$ .$g/\gamma = 0.5$ , 当出现${g^{\left( 2 \right)}}\left( 0 \right)$ 的波谷, 即${g^{\left( 2 \right)}}\left( 0 \right) \ll 1$ 时, 对应于强声子反聚束现象. 此时$\varDelta /\gamma = 0$ , 与(8 )式相对应.$g/\gamma = 2$ , 当出现${g^{\left( 2 \right)}}\left( 0 \right) \ll 1$ 时, 此时$\varDelta /\gamma = $ $\pm 2$ , 对应于(9 )式. 也就是说, 在条件$g/\gamma = 0.5$ 下比在条件$g/\gamma = 2$ 下出现的反聚束现象更强. 这是因为这里只取了$\left| g \right| \gg \dfrac{\gamma }{2}$ 的一个近似值. 只要随着g 的增大, 近似效果越明显, 反聚束效应就会越强, 例如图3 中的$g/\gamma = 4$ .3.4.与CPNB和UPNB比较 -->3.4.与CPNB和UPNB比较 现在讨论在非厄米特哈密顿量作用下产生声子阻塞效应在零本征值下的物理机理.图4 描述了基于不同路径干涉的情况下的声子阻塞现象的能级情况. 绿色箭头描述的是第一条路径$\left| {1g} \right\rangle \to \left| {2g} \right\rangle $ , 振幅为$\sqrt 2 \varepsilon $ ; 蓝色箭头是第二条路径$\left| {1g} \right\rangle \to \left| {0e} \right\rangle \to \left| {1e} \right\rangle \to \left| {2g} \right\rangle $ , 振幅$\dfrac{{g \times \varepsilon \times \sqrt 2 g}}{{\dfrac{\kappa }{2} \times \left( {\dfrac{\kappa }{2} + \dfrac{\gamma }{2}} \right)}}$ , 其中$\dfrac{\kappa }{2}$ 和$\left( {\dfrac{\kappa }{2} + \dfrac{\gamma }{2}} \right)$ 分别是$\left| {0e} \right\rangle $ 衰减到$\left| {0g} \right\rangle $ 和$\left| {1e} \right\rangle $ 衰减到$\left| {1g} \right\rangle $ 的衰减率.图 4 UPNB能级图Figure4. Schematic energy-level diagram of unconventional phonon blockade.8 )式或者(9 )式的情况, 驱动场频率${\omega _{\rm{d}}}$ 如果等于$\omega _ \pm ^{\left( 1 \right)}$ , 那就满足了单激发数共振条件, 同时产生单声子的可能性就大大增加. 在这里, 由于失谐, 产生双声子的可能性并没有像单声子那样大.[16 ] :${g^{\left( 2 \right)}}\left( 0 \right) \approx 2{p_2}/p_1^2$ , 这里${p_2} = {\left| {{C_{2g}}} \right|^2} + {\left| {{C_{2e}}} \right|^2}$ 是产生双声子的几率, ${p_1} = {\left| {{C_{1e}}} \right|^2} + {\left| {{C_{1g}}} \right|^2}$ 是产生单声子的几率. 由于是在弱驱动的条件下, 所以${p_1} \gg {p_2}$ . 在单激发数下的零本征值的条件, ${p_1}$ 可以急剧增大, 导致的结果是${g^{\left( 2 \right)}}\left( 0 \right) \approx 0$ . 这样, 就可以出现声子阻塞现象.图5 比较了CPNB, UPNB和本文方案的区别. 不管是在强非线性还是弱非线性的限制下, 本文方案都可以实现声子的反聚束现象. 实现该方案的物理机理和CPNB相同, 都是由于失谐所造成的声子的反聚束. 实现CPNB的最佳条件如下:图 5 本文方案与CPNB和UPNB的区别Figure5. Different parameter range for the CPNB, the UPNB, and the present scheme.$\kappa $ 与$\gamma $ 之间的定量关系. 这是因为仅仅考虑了(2 )式中的特征频率, 而没有引入$\kappa $ 与$\gamma $ . 这就导致了在$\varDelta = \left| g \right|$ 的条件下, 不能得到$\left| g \right| ={\gamma }/{2}$ 这个条件(见图6 ), 而只能注意到$\varDelta = \left| g \right| = 0$ . 本文方案最显著的特点就是加入了$\kappa /\gamma = - 1$ 这个条件. 事实上, 如果(9 )式中的条件变为$\kappa > 0$ 和$\gamma > 0$ , 那么就变成了(13 )式, 也就是说变为了CPNB.图 6 二阶关联函数${g^{\left( 2 \right)}}\left( 0 \right)$ 和平均声子数$N = \left\langle {{a^ + }a} \right\rangle = \left[ {{\rm{Tr}}\left( {{\rho _s}{a^ + }a} \right)} \right]$ 的对数图像 (a), (b) $\varepsilon /\gamma = 0.1$ , $\varOmega = 0$ ; (c), (d) $\varOmega /\gamma = 0.1$ , $\varepsilon = 0$ , $\phi = 0$ . 其他参数为$\kappa /\gamma = - 1$ .Figure6. The logarithmic plot (of base e) of the zero-delay-time second-order correlation functions ${g^{\left( 2 \right)}}\left( 0 \right)$ and average photon numberN : (a) and (b) $\varepsilon /\gamma = 0.1$ , $\varOmega = 0$ ; (c) and (d) $\varOmega /\gamma = 0.1$ , $\varepsilon = 0$ , $\phi = 0$ . The shared parameters: $\kappa /\gamma = - 1$ .图7 和图8 比较了本文方案和CPNB, UPNB的不同. 结果表明, 在设定相应的参数下, 本文方案得出的声子阻塞效果比其他两种方案要好. 这是因为非厄米哈密顿量的作用方式更贴合主方程. 这就导致了在其他条件相同时, 本文方案会比直接使用(2 )式的更精确. CPNB的触发是由于声子场频率与驱动场频率不同步(失谐)而导致的, 而UPNB的触发是通过两个不同路径的量子干涉产生的. 因此, 当作用方式是量子干涉时, 声子的反聚束会对干涉中的相位差极其敏感, 所以干涉路径的改变会使反聚束的区域发生剧烈变化. 然而, 在本文方案中, 驱动场的改变导致量子干涉路径的改变并不会对反聚束的物理环境产生影响. 所以本方案中的强声子反聚束与UPNB方案的物理机理不同.图 7 二阶关联函数${g^{\left( 2 \right)}}\left( 0 \right)$ (对数)与$\varDelta /\gamma $ 的关系图, 其中$\varepsilon /\gamma = 0.1$ , $\varOmega = 0$ (a) $g/\gamma = 0.5$ , $\kappa /\gamma = - 1$ (本文方案), $\kappa /\gamma = 1$ (UPNB); (b) $g/\gamma = 5$ , $\kappa /\gamma = - 1$ (本文方案), $\kappa /\gamma = 1$ (CPNB)Figure7. The logarithmic plot (of base e) of the zero-delay-time second-order correlation functions ${g^{\left( 2 \right)}}\left( 0 \right)$ as a function of $\varDelta /\gamma $ . The shared parameters: $\varepsilon /\gamma = 0.1$ , $\varOmega = 0$ . Other parameters: (a) $g/\gamma = 0.5$ , $\kappa /\gamma = - 1$ (our scheme), $\kappa /\gamma = 1$ (UPNB); (b) $g/\gamma = 5$ , $\kappa /\gamma = - 1$ (our scheme), $\kappa /\gamma = 1$ (CPNB).图 8 二阶关联函数${g^{\left( 2 \right)}}\left( 0 \right)$ (对数)与$\varDelta /\gamma $ 的关系图, $\varOmega \ne 0$ , $\varepsilon = 0$ , $\phi = 0$ (a) $\varOmega /\gamma = 0.1$ , $g/\gamma = 0.5$ , $\kappa /\gamma = - 1$ (本文方案), $\kappa /\gamma = 1$ (UPNB); (b) $\varOmega /\gamma = 2$ , $g/\gamma = 10$ , $\kappa /\gamma = - 1$ (本文方案), $\kappa /\gamma = 1$ (CPNB)Figure8. The logarithmic plot (of base e) of the zero-delay-time second-order correlation functions ${g^{\left( 2 \right)}}\left( 0 \right)$ as a function of $\varDelta /\gamma $ : $\varOmega \ne 0$ , $\varepsilon = 0$ , $\phi = 0$ . Other parameters: (a) $\varOmega /\gamma = 0.1$ , $g/\gamma = 0.5$ , $\kappa /\gamma = - 1$ (our scheme), $\kappa /\gamma = 1$ (UPNB); (b) $\varOmega /\gamma = 2$ , $g/\gamma = 10$ , $\kappa /\gamma = - 1$ (our scheme), $\kappa /\gamma = 1$ (CPNB).4.声子阻塞效应的探测 通过测量光学腔场的输出光子的相关性, 可以间接观测到NAMR中的声子阻塞现象. 对于NAMR-量子比特系统, 我们参照了文献中的测量方法[16 ] . 在最近的实验中, 一个量子比特耦合一个NAMR以后, NAMR再耦合一个超导腔组成了一个三体系统[61 ] . 假设这个超导光腔通过辐射压相互作用耦合到NAMR, 就可以通过研究超导光腔中的光子统计特性, 来研究NAMR中的声子统计特性, 从而观察NAMR中的声子阻塞现象. 声子统计特性探测模型见图9 .图 9 声子统计特性探测模型Figure9. The detecting model of the statistical properties of the phonons.${\omega _{\rm b}}$ , 在以入射光频率${\omega _{\rm{b}}}$ 旋转的框架中, 整个系统的总哈密顿量为b 和${b^ + }$ 表示超导腔中光子湮灭和产生算符, 超导腔的共振频率为${\omega _{\rm{c}}}$ ; J 是超导腔与NAMR的耦合强度; ${\varOmega _{\rm{c}}}$ (假定为实数)是超导腔的外加驱动场振幅; ${\varDelta _{\rm{b}}}$ 满足共振条件${\varDelta _{\rm{b}}} \equiv {\omega _{\rm{c}}} - {\omega _{\rm{b}}} = {\omega _{\rm{m}}}$ .$b \to b + \alpha $ . 这里$\alpha $ 在频率为${\omega _{\rm{b}}}$ 驱动光场中的稳态平均场. 在强驱动的条件下, $\left| \alpha \right| \gg 1$ . 同样地, 可以将${H_{{\rm{om}}}}$ 再在旋波近似下, 哈密顿量变为$H_{{\rm{om}}}^\prime = {\omega _{\rm{m}}}{b^ + }b + G{a^ + }b + {G^*}a{b^ + }, $ 其中光力系统有效的耦合强度$G = g\alpha $ , 同样假定$\left| G \right| \ll {\omega _{\rm{m}}}$ , 在相互作用哈密顿量的演化下, 声子场和腔场之间形成纠缠态, 探测腔场光子统计特性可以实现对声子阻塞或声子统计特性的探测[61 ] .5.结 论 研究了在非厄米哈密顿量作用下的NAMR-量子比特系统的零本征值条件下的声子统计特性. 充分利用了零本征值方法, 通过分析和计算, 得到了强声子反聚束的最佳条件, 同时引入二阶关联函数讨论了声子阻塞效应. 通过主方程的稳态求解, 分析了各种条件对声子阻塞的影响, 结果发现都能很好地匹配声子阻塞现象. 比较了本方案与CPNB和UPNB的区别, 发现本文方案在强非线性和弱非线性条件下都能实现强声子反聚束现象. 阐明了这种声子阻塞的物理机理是不同于UPNB的失谐原理. 最后, 简要分析了利用外加超导腔去间接地探测NAMR中的声子统计特性的方法. 本文的研究结果将在量子信息处理以及精密测量等研究领域具有重要的意义和应用前景. 


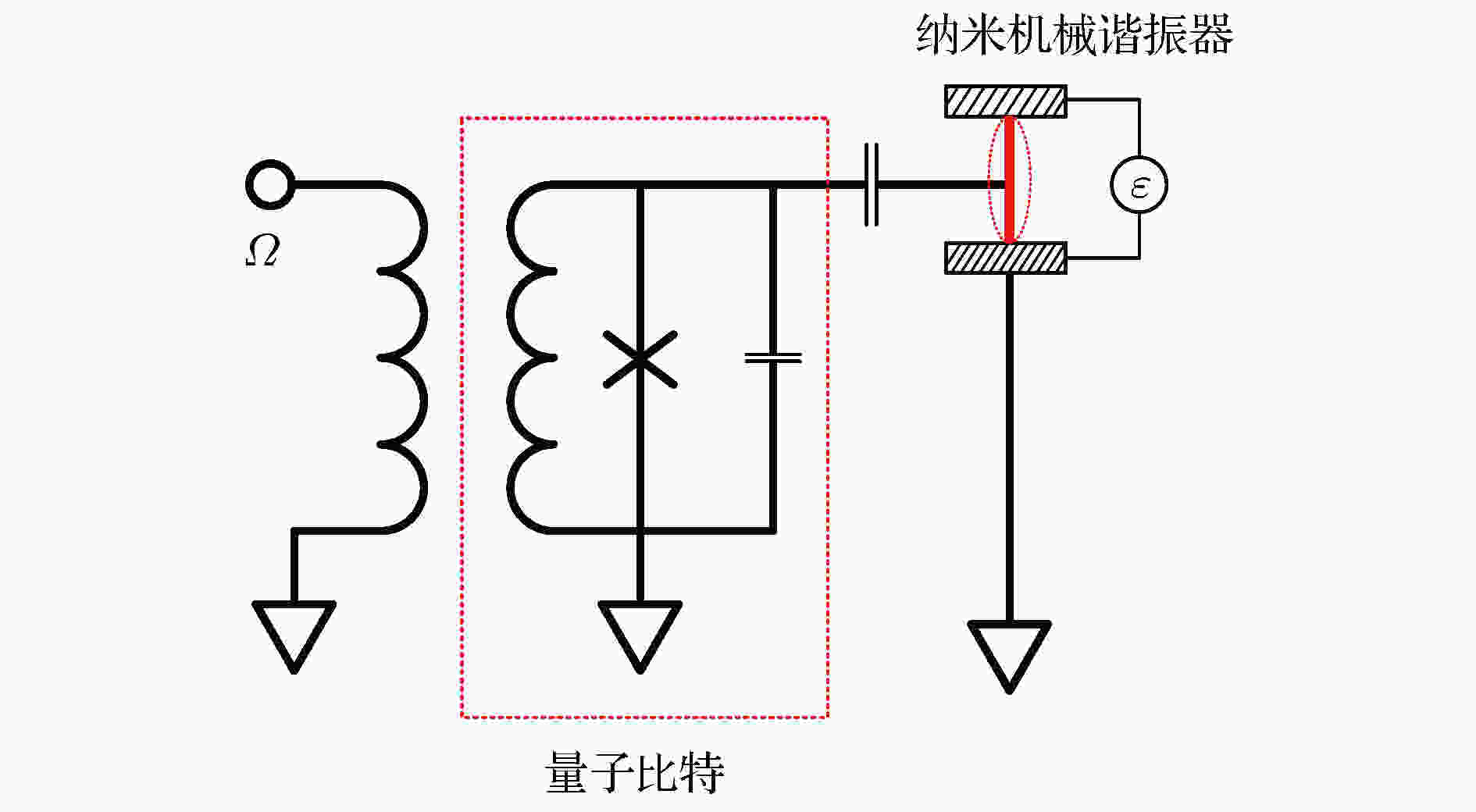 图 1 NAMR-量子比特系统的物理模型图
图 1 NAMR-量子比特系统的物理模型图


























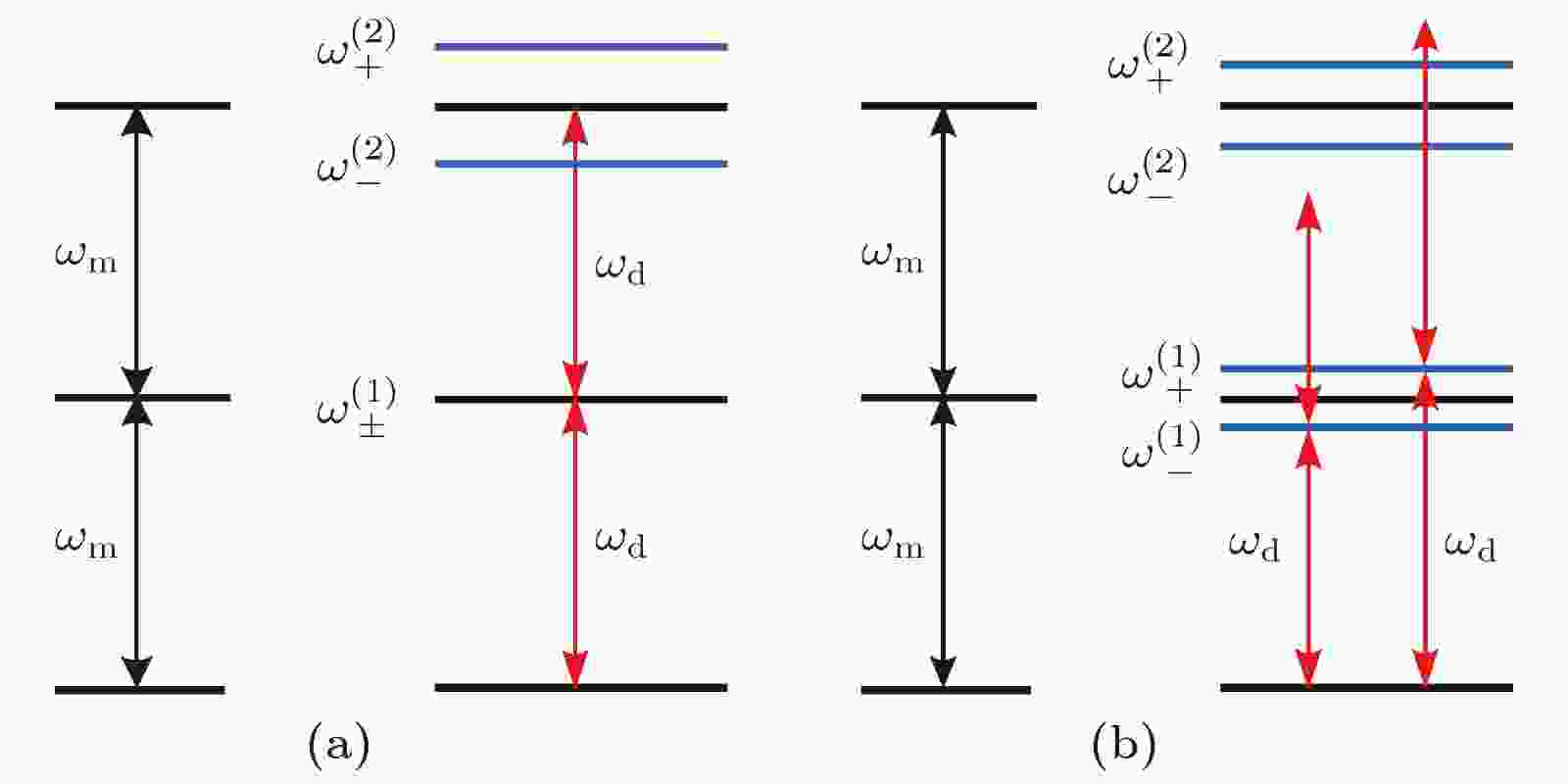 图 2 外加驱动场共振的情况下声子阻塞现象的能级图 (a)满足(8)式时的能级图, 其中
图 2 外加驱动场共振的情况下声子阻塞现象的能级图 (a)满足(8)式时的能级图, 其中























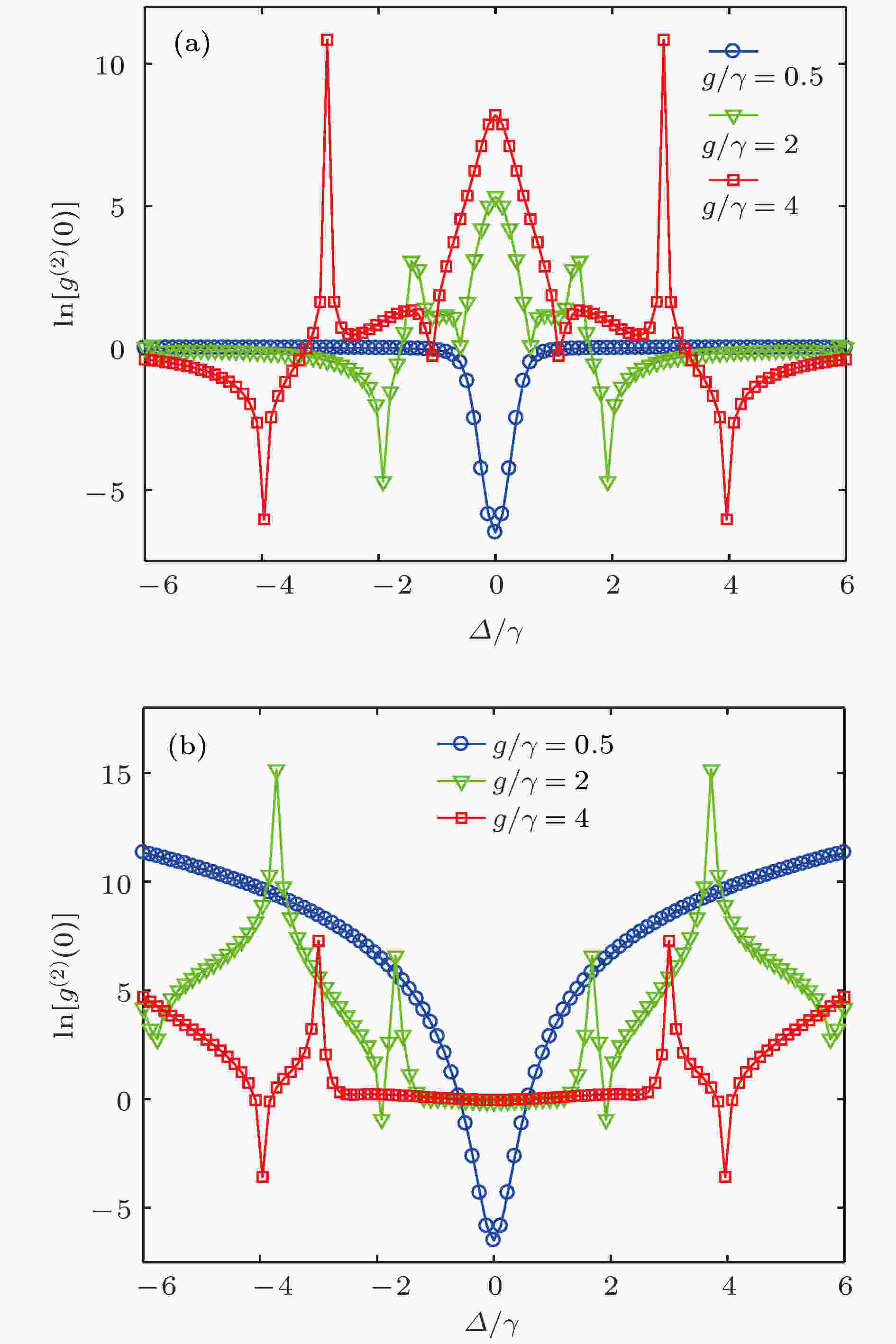 图 3 在不同的
图 3 在不同的














































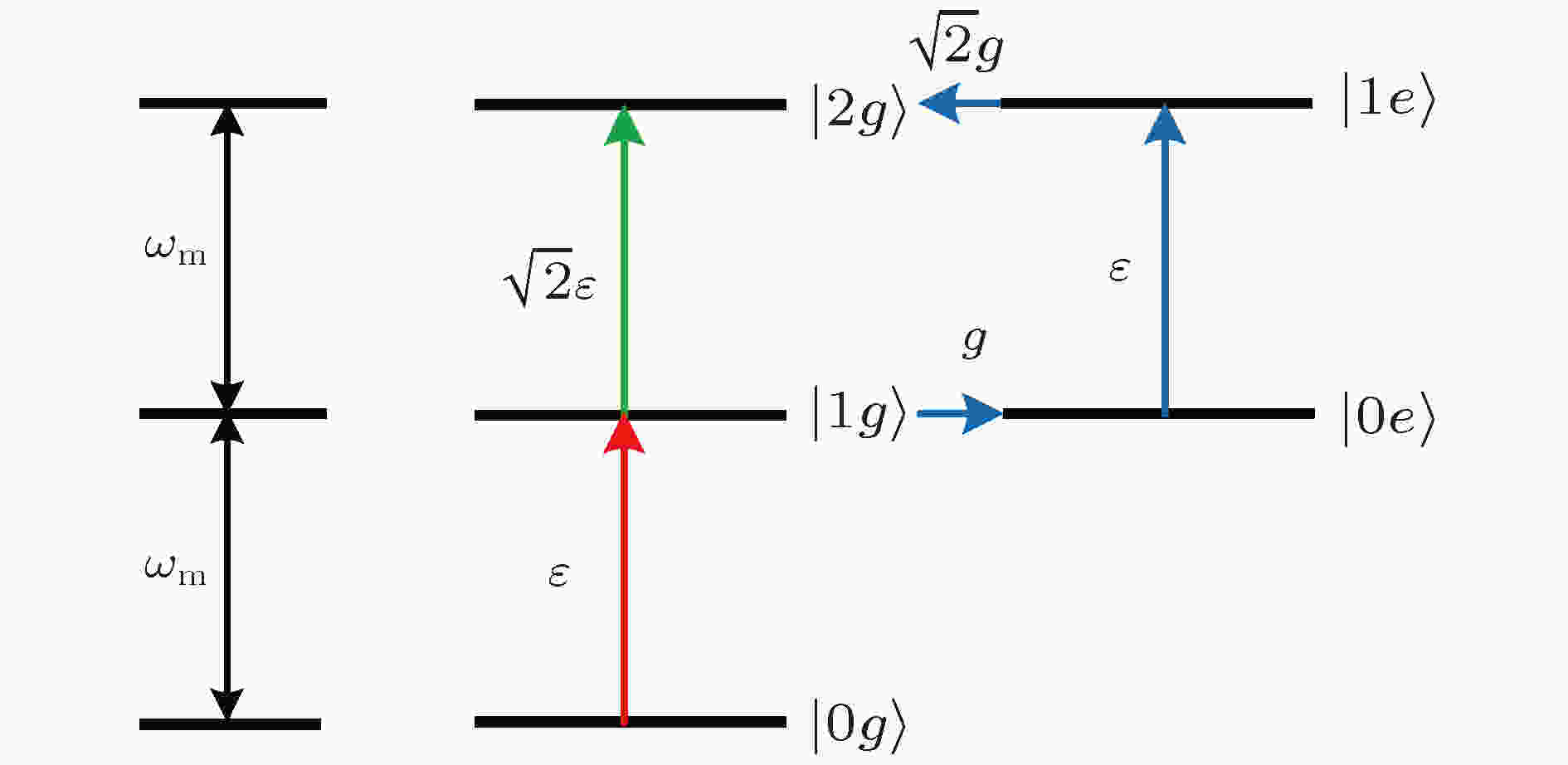 图 4 UPNB能级图
图 4 UPNB能级图







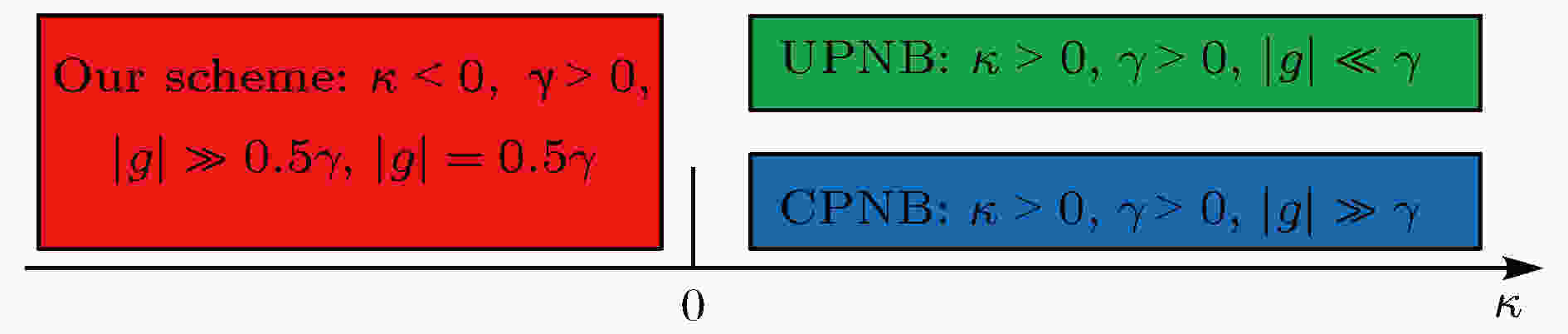 图 5 本文方案与CPNB和UPNB的区别
图 5 本文方案与CPNB和UPNB的区别













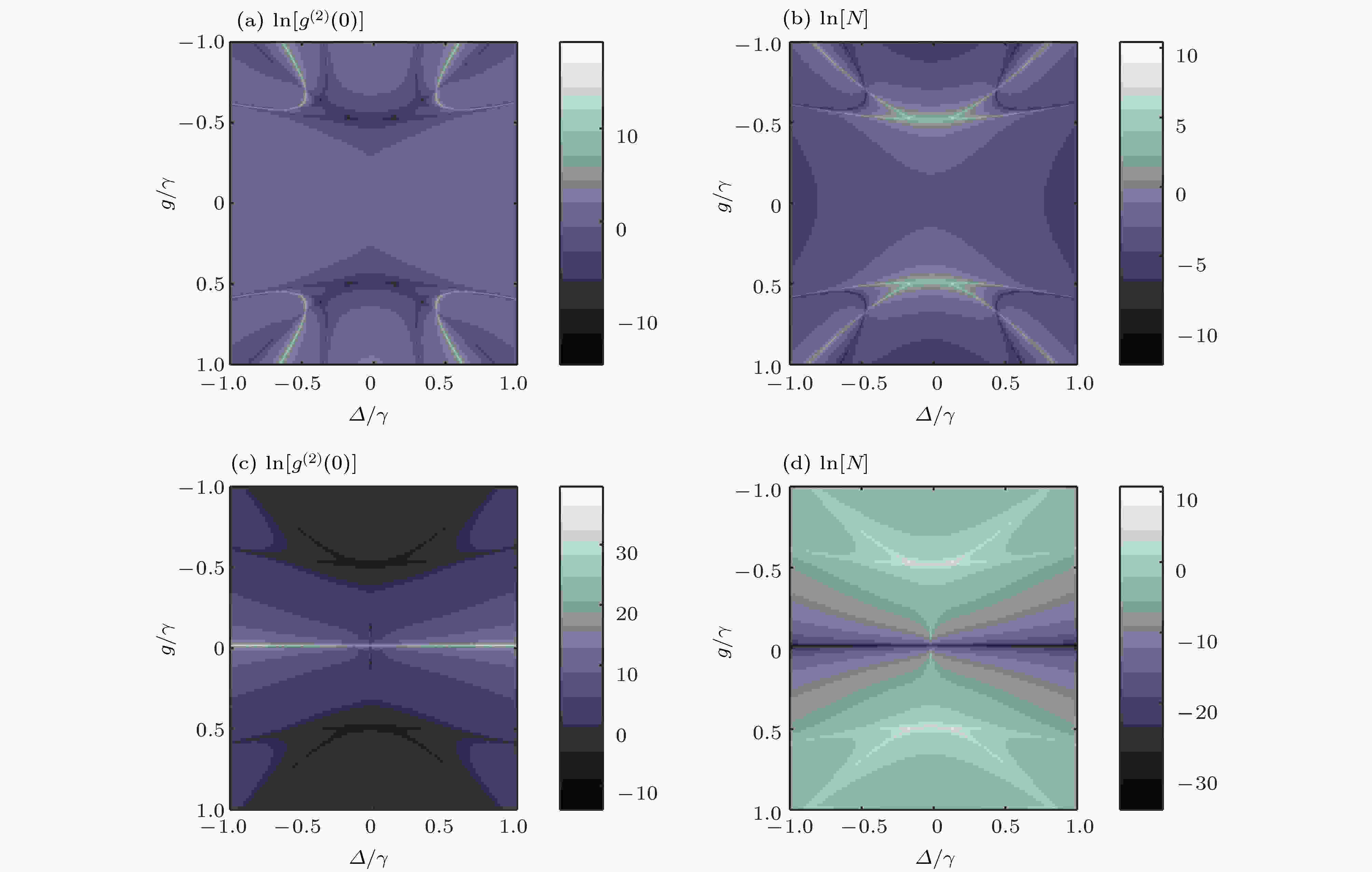 图 6 二阶关联函数
图 6 二阶关联函数














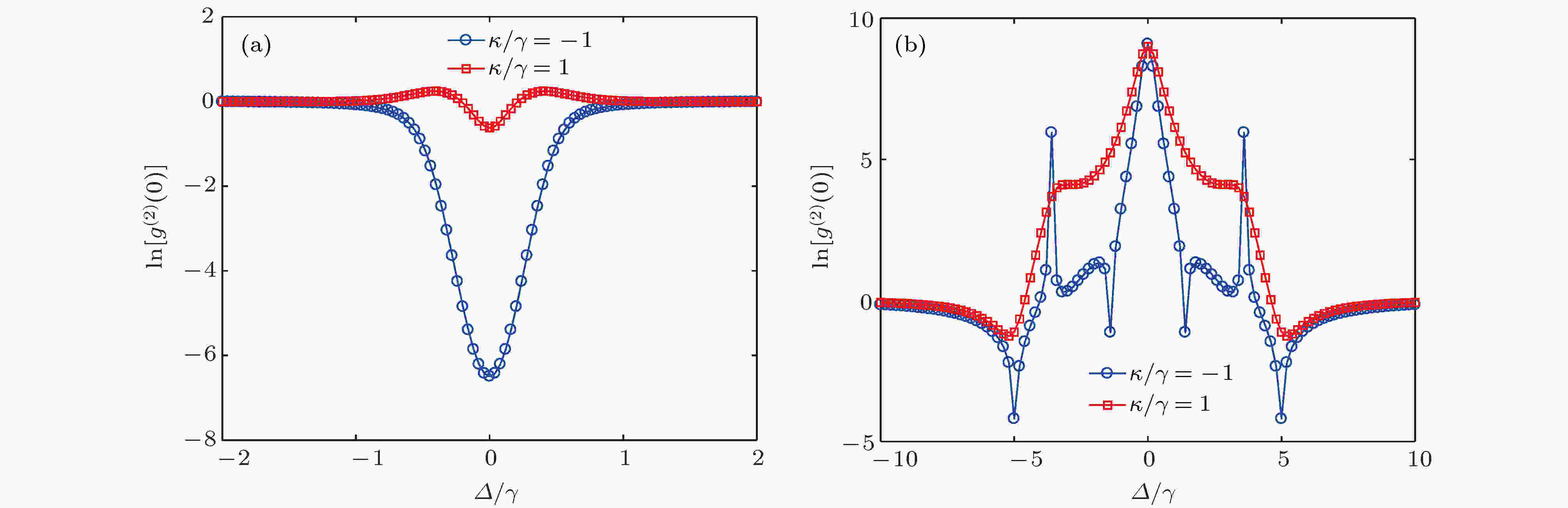 图 7 二阶关联函数
图 7 二阶关联函数



























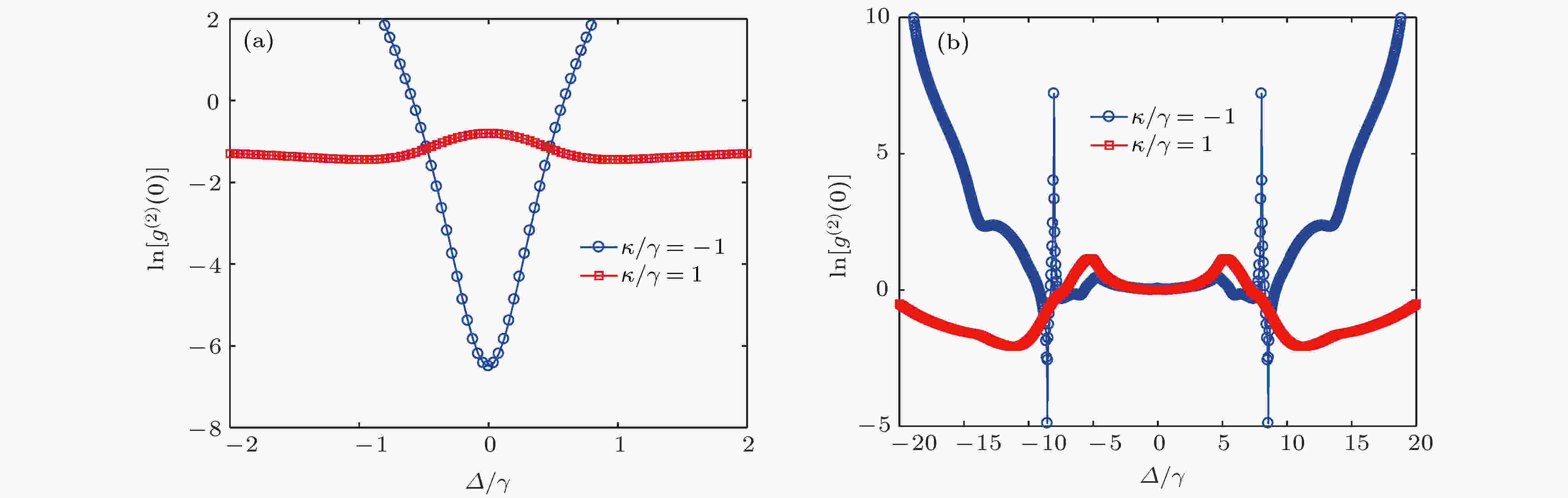 图 8 二阶关联函数
图 8 二阶关联函数

































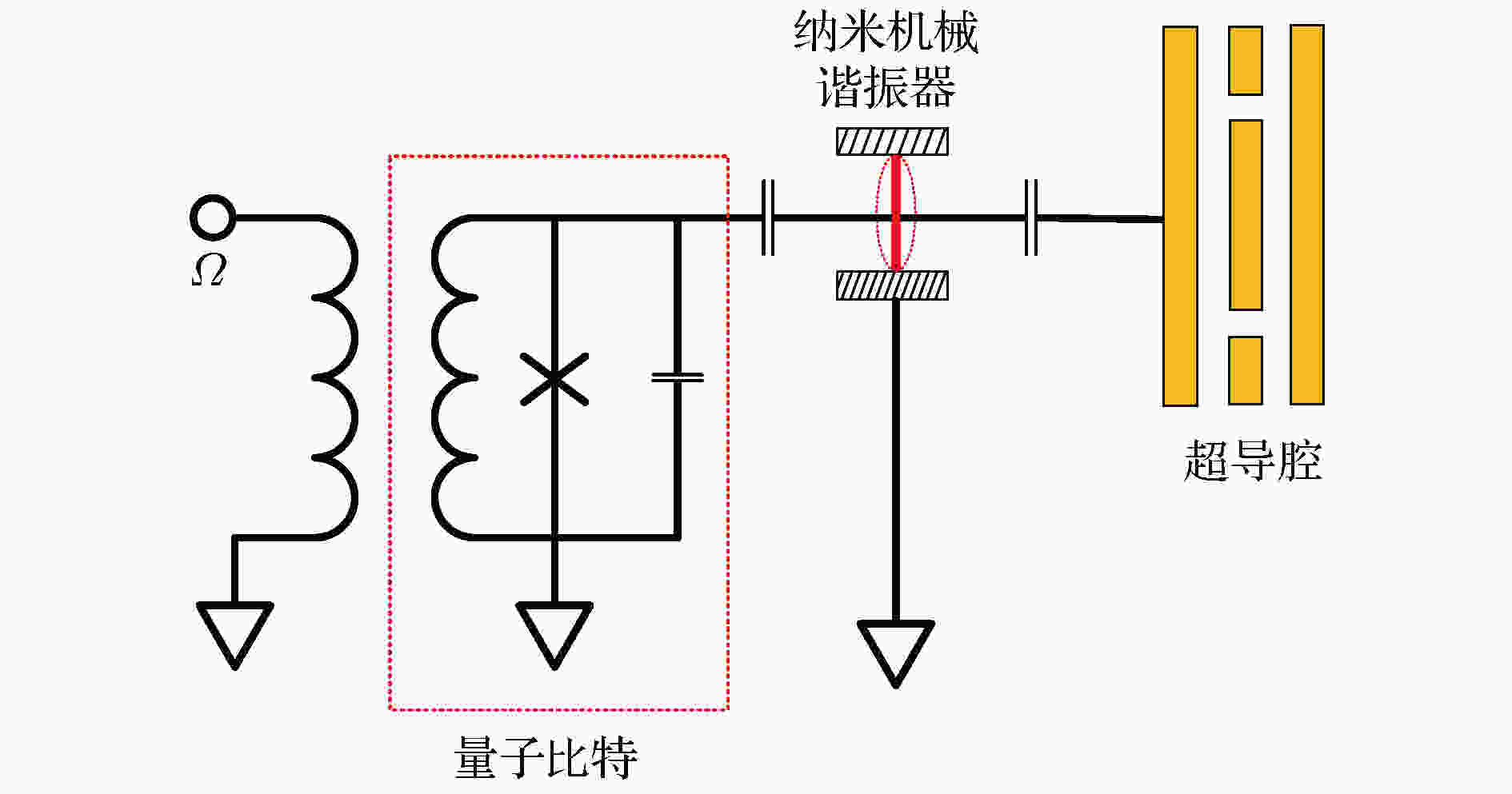 图 9 声子统计特性探测模型
图 9 声子统计特性探测模型














